Abstract
The Yang-Baxter equation first appeared in a paper by the Nobel laureate, C.N. Yang, and in R.J. Baxter’s work. Later, Vladimir Drinfeld, Vaughan F. R. Jones and Edward Witten were awarded Fields Medals for their work related to the Yang-Baxter equation. After a short review on this equation and the Yang-Baxter systems, we consider the problem of constructing algebra factorizations from Yang-Baxter systems. Our sketch of proof uses braided categories. Other problems are also proposed.
1. Introduction
The Yang-Baxter equation first appeared in a paper by the Nobel laureate, C.N. Yang, and in R.J. Baxter’s work. At the 1990 International Mathematics Congress, Vladimir Drinfeld, Vaughan F. R. Jones and Edward Witten were awarded Fields Medals for their work related to the Yang-Baxter equation.
This equation plays a crucial role in many areas of mathematics, physics and computer science. Many scientists have used the axioms of various algebraic structures or computer calculations in order to produce solutions for it, but the full classification of its solutions remains an open problem.
In our previous special issue on Hopf algebras, quantum groups and Yang-Baxter equations, several papers [1,2,3,4,5,6], as well the feature paper [7], covered many topics related to the Yang-Baxter equation.
The interest in the Yang-Baxter equation is also motivated by its many applications and interpretations. As an example of categorical interpretation, let us consider the following extension for the duality between finite dimensional algebras and coalgebras to the category of finite dimensional Yang–Baxter structures (from [8] and, also, [4]). That duality can be illustrated by the following diagram:
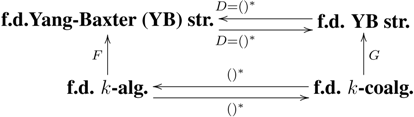 The previous duality extension resembles the duality extension from [9]. Furthermore, the extension of the duality between finite dimensional algebras and coalgebras could lead to further developments of the current paper.
The previous duality extension resembles the duality extension from [9]. Furthermore, the extension of the duality between finite dimensional algebras and coalgebras could lead to further developments of the current paper.

The following list of recent papers could be an introduction and a motivation to study Yang-Baxter systems: [10,11,12,13,14].
The next section provides a mathematical background on Yang-Baxter systems, and Section 3 contains the main problems and results.
2. Preliminaries
We work over the field k, and all the unadorned tensor products are tensor products over k.
The identity map on a k-vector space V is denoted by .
All the algebras considered are k-algebras, and they are associative and with a unity; the product in a k-algebra A is denoted by , while the unit map is denoted by .
For any vector spaces V and W, denotes the natural bijection defined by .
Let be a k-linear map. Define , and . Each of the is thus a linear endomorphism of .
Definition 2.1 An invertible k-linear map, , is called a Yang-Baxter operator (or, simply, a YB operator) if it satisfies the equation:
Equation (1) is usually called the braid equation. It is a well-known fact that the operator R satisfies (1) if and only if satisfies the quantum Yang-Baxter equation:
Example 2.2 ([15]) If A is a k-algebra, then for all non-zero , the linear map:
is a Yang-Baxter operator.
This construction played an important role in the construction of Yang-Baxter systems from algebra factorizations (see [16]).
Yang-Baxter systems were introduced in [17], as a spectral-parameter independent generalization of quantum Yang-Baxter equations related to non-ultralocal integrable systems, previously studied in [18].
Yang-Baxter systems are conveniently defined in terms of Yang-Baxter commutators. Consider three vector spaces, , and three linear maps, , and . Then, a Yang-Baxter commutator is a map defined by:
In terms of a Yang-Baxter commutator, the quantum Yang-Baxter Equation (2) is expressed simply as .
Definition 2.3 Let V and be vector spaces. A system of linear maps,
is called a WXZ-system, or a Yang-Baxter system, provided the following equations are satisfied:
The next remark plays an important role in this paper.
Remark 2.4 Given a WXZ-system as in Definition 2.3, one can construct a Yang-Baxter operator on , provided the maps are invertible. This is a special case of a gluing procedure described in ([19], (Theorem 2.7)) (cf. [19], (Example 2.11)). Let , , . Then, the linear map:
given by: , and for all , ,
is a Yang-Baxter operator.
Definition 2.5 An algebra A is said to be entwined with an algebra B if there exists a linear map satisfying the following four conditions:
- (1)
- ,
- (2)
- ,
- (3)
- ,
- (4)
- ,
The map ϕ is known as an algebra factorization map, and the triple is called an algebra factorization.
3. Algebra Factorizations, Yang-Baxter Systems and Braided Categories
Let be a Yang-Baxter operator on V.
For an integer , let , .
On the tensor algebra, , we consider the following product:
for: , , and , ,
Although the invertibility of R is not essential for the following theorem, we assume that R is invertible in order to give a proof for it using braided categories.
Theorem 3.1 Starting with a WXZ-system as in Definition 2.3 and Remark 2.4, using the above notations and denoting by , , , we have the following properties.
- (i)
- and are k-algebra structures.
- (ii)
- There exists an algebra factorization, , defined by
Proof. A direct proof was presented in [20].
Another approach to this problem could be via braided algebras, and this was done in the revision of [20].
Now, we would like to prove it using the properties of a braided category. We start by proving (ii).
We use Remark 2.4 in order to obtain a new Yang-Baxter operator defined over , which will generate the braiding of a monoidal category.
The objects of this category are: .
The morphisms of this category are endomorphisms of and their tensor products.
Now: can be extended to a braiding.
The restrictions of the braiding generated by to subspaces of the form:
imply that ϕ is an algebra factorization.
The proof of part (ii) includes the proof for part (i). □
Remark 3.2 From the previous theorem, has an algebra structure associated with that algebra factorization. It is an open problem to study the relation between that structure and (see Remark 2.4).
Remark 3.3 In a natural way, gets a bialgebra structure (if R is invertible).
The map, , extends naturally to T(V). This can be done using the fact that any can be thought of as a sum of products of n elements from V and requesting that . The fact that R is invertible is essential here. The associativity of μ implies .
The coassociativity of Δ follows from the fact that . For , follows from the definition of Δ.
We define , and by a similar argument we have (because ε is an algebra morphism).
The compatibility between Δ and ε follows, because and .
Remark 3.4 From the previous theorem, Remarks 3.2 and 3.3 and the assumption that U is invertible, it follows that inherits a bialgebra structure. This can be done in the same spirit as Remark 3.3. (The invertibility of U is a key ingredient.)
This new bialgebra structure is different from any kind of bicrossed product of bialgebras presented in Section IX.2 of [21].
Conflicts of Interest
The author declares no conflicts of interest.
References
- Kanakoglou, K. Gradings, braidings, representations, paraparticles: Some open problems. Axioms 2012, 1, 74–98. [Google Scholar] [CrossRef]
- Underwood, R.G. Quasi-triangular structure of Myhill-Nerode bialgebras. Axioms 2012, 1, 155–172. [Google Scholar] [CrossRef]
- Schmidt, J.R. From coalgebra to bialgebra for the six-vertex model: The star-triangle relation as a necessary condition for commuting transfer matrices. Axioms 2012, 1, 186–200. [Google Scholar] [CrossRef]
- Nichita, F.F.; Zielinski, B. The duality between corings and ring extensions. Axioms 2012, 1, 173–185. [Google Scholar] [CrossRef]
- Links, J. Hopf algebra symmetries of an integrable Hamiltonian for anionic pairing. Axioms 2012, 1, 226–237. [Google Scholar] [CrossRef]
- Hoffnung, A.E. The Hecke bicategory. Axioms 2012, 1, 291–323. [Google Scholar] [CrossRef]
- Nichita, F.F. Introduction to the Yang-Baxter equation with open problems. Axioms 2012, 1, 33–37. [Google Scholar] [CrossRef]
- Nichita, F.F.; Schack, S.D. The duality between algebras and coalgebras. Ann. Univ. Ferrara 2005, 51, 173–181. [Google Scholar]
- Morris, S.A. Pontryagin Duality and the Structure of Locally Compact Abelian Groups; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Kouloukas, T.E.; Papageorgiou, V.G. Entwining Yang-Baxter maps and integrable lattices. Math. Phys. 2011, 93, 163–175. [Google Scholar] [CrossRef]
- Lebed, V. Braided Systems, Multi-Braided Tensor Products and Bialgebra Homologies. 2013. arxiv 1305.0944. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1305.0944 (accessed on 3 September 2013).
- Nichita, F.F. Lie algebras and Yang-Baxter equations. Bull. Transylv. Univ. Brasov, Ser. III: Math. Inf. Phys. 2012, 5, 195–208. [Google Scholar]
- Nichita, F.F.; Parashar, D.; Zielinski, B. Semi-entwining structures and their applications. ISRN Algebra 2013, 817919:1–817919:9. [Google Scholar]
- Nichita, F.F.; Popovici, B.P. Yang-Baxter operators from (G, θ)-lie algebras. Rom. Rep. Phy. 2011, 63, 641–650. [Google Scholar]
- Dăscălescu, S.; Nichita, F. Yang-Baxter operators arising from (co)algebra structures. Commun. Algebra 1999, 27, 5833–5845. [Google Scholar] [CrossRef]
- Brzeziński, T.; Nichita, F.F. Yang-Baxter systems and entwining structures. Comm. Algebra 2005, 33, 1083–1093. [Google Scholar] [CrossRef]
- Hlavaty, L.; Snobl, L. Solution of the Yang-Baxter system for quantum doubles. Int. J. Mod. Phys. 1999, A14, 3029–3058. [Google Scholar] [CrossRef]
- Hlavaty, L.; Kundu, A. Quantum integrability of nonultralocal models through Baxterization of quantized braided algebra. Int. J. Mod. Phys. 1996, A11, 2143–2165. [Google Scholar] [CrossRef]
- Majid, S.; Markl, M. Gluing operations for R-Matrices, quantum groups and link-invariants of Hecke type. Math. Proc. Cambridge Philos. Soc. 1996, 119, 139–166. [Google Scholar] [CrossRef]
- Berceanu, B.; Nichita, F.; Popescu, C. Algebra Structures Arising from Yang-Baxter Systems. 2010. arXiv:1005.0989. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1005.0989 (accessed on 3 September 2013).
- Kassel, C. Quantum Groups; Springer Verlag: New York, NY, USA, 1995. [Google Scholar]
© 2013 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
