The first step in our change point detection approach is to infer the number of change points in a region of data and the approximate time of each change point. The second step is to refine the initial estimates of the time of each change point.
Functions such as the breakpoint function in R [
26] attempt to both infer the number of change points and their approximate times using a piecewise linear change detection technique described in [
21]. Alternatively, wavelet-based change detection and the lag-one differencing option can infer the number of change points and their approximate times.
4.1. Finding the Correct Number of Change Points and the Approximate Times of Each Change Point
Wavelet change detection performance [
23] can be measured on the basis of three criteria: (1) Good detection (low rate of false positives and false negatives in locating change points); (2) Good localization (accurate estimate of the exact change point location); and (3) Low response per change point, which expands on (1) by considering the number of change points inferred to be associated with a single true change point. References [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25] are among the many references that describe wavelet change point detection using some type of synthesis of wavelet coefficients at each of multiple scales. For example, [
23] presented a computational approach to synthesize wavelet coefficients over multiple scales. Reference [
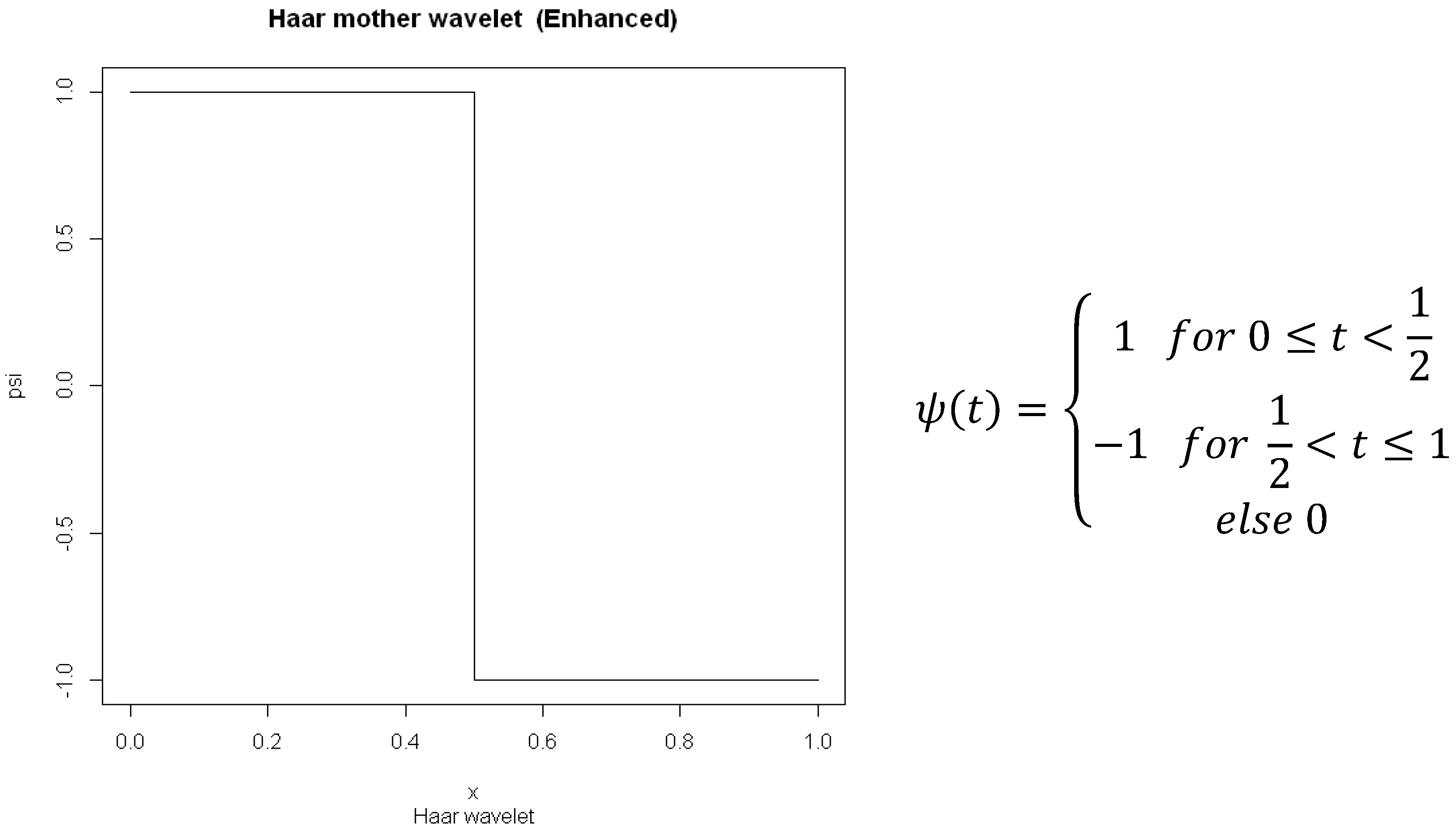
15] presented a different computational approach for signals that are piecewise polynomial (such as our SM signals that are piecewise linear). Because piecewise polynomial signals impact wavelet coefficients at multiple scales (see
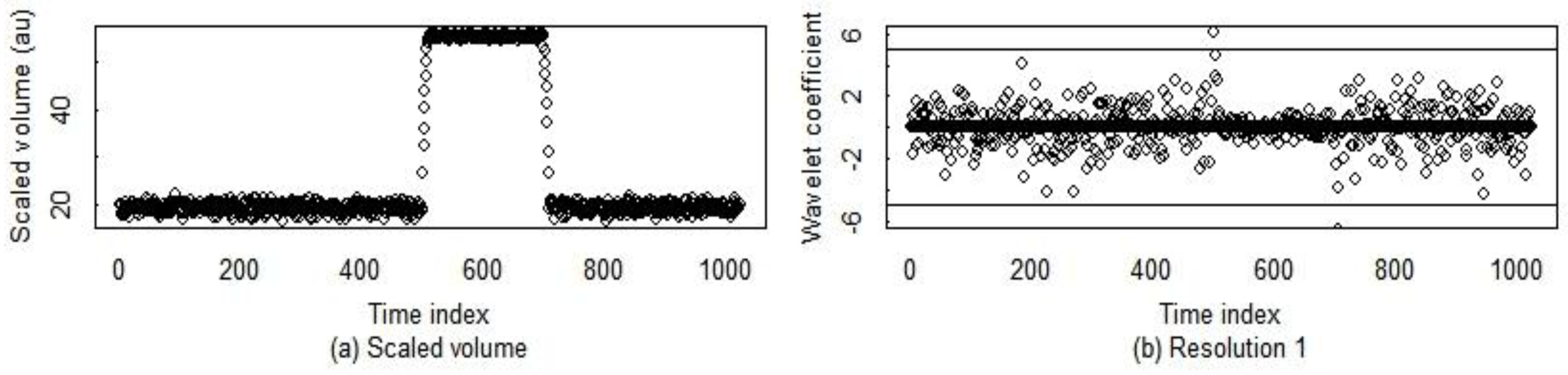
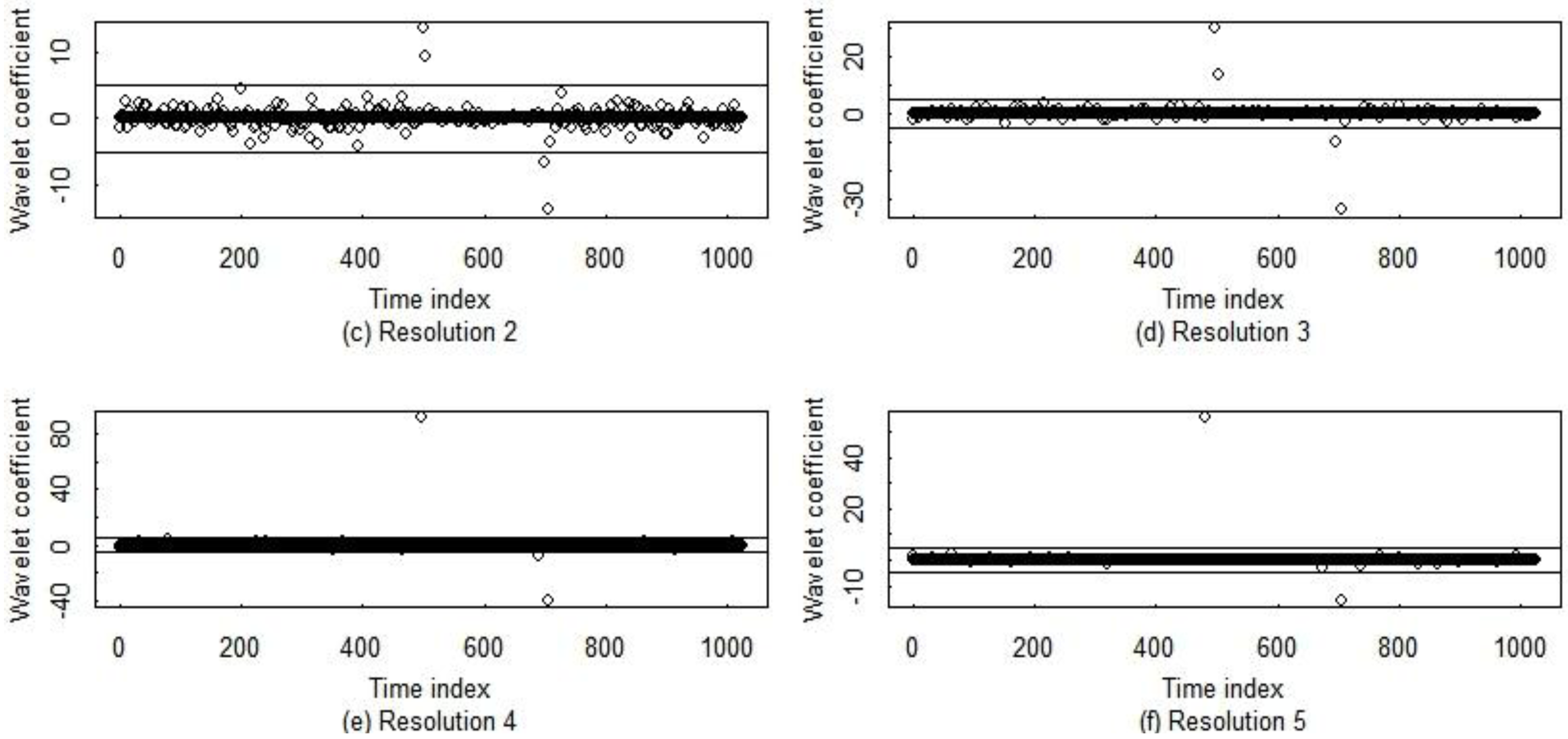
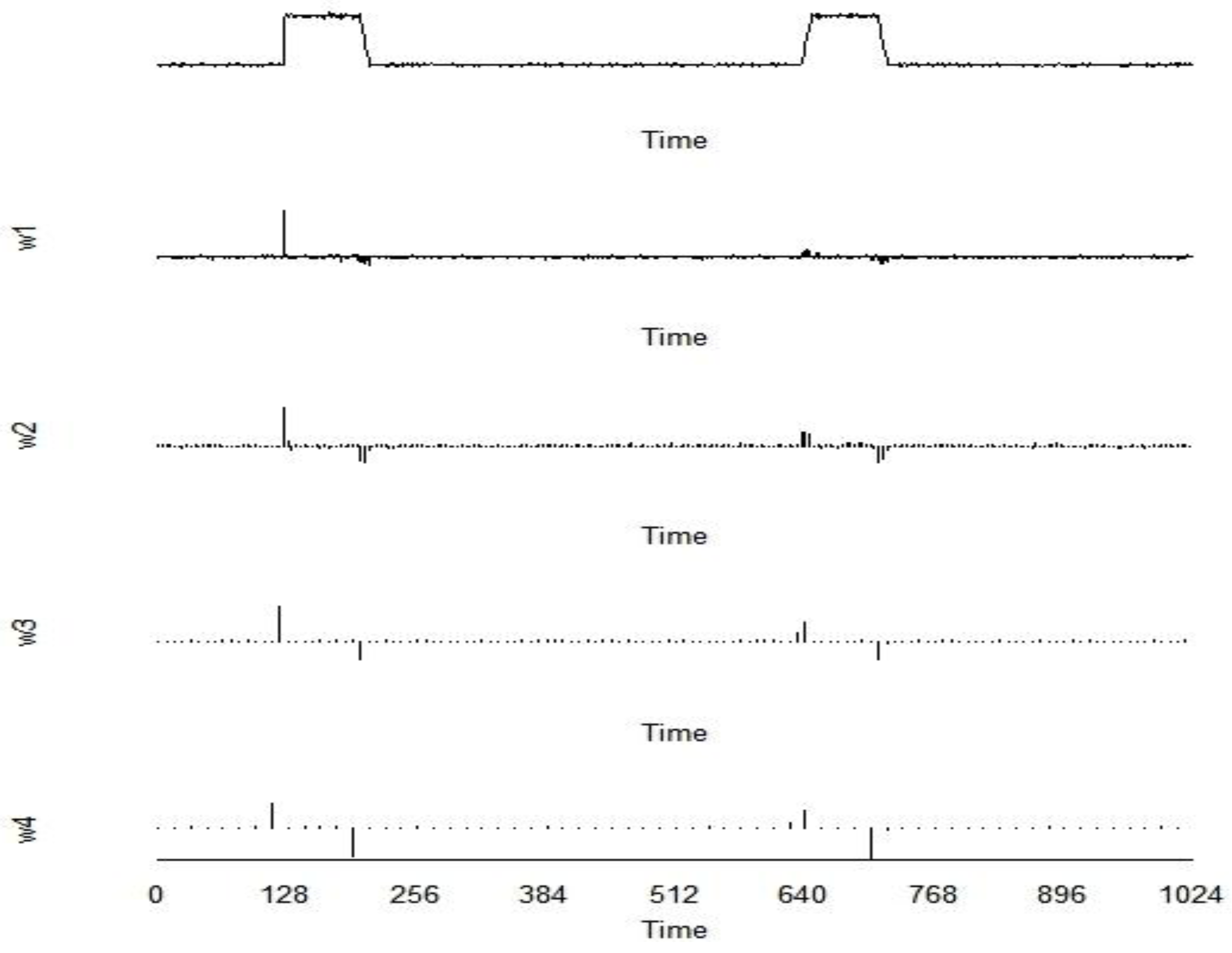
Figure 3 and
Figure 4), [
15] relied on a piecewise polynomial approximation that departed from conventional orthogonal wavelet bases.
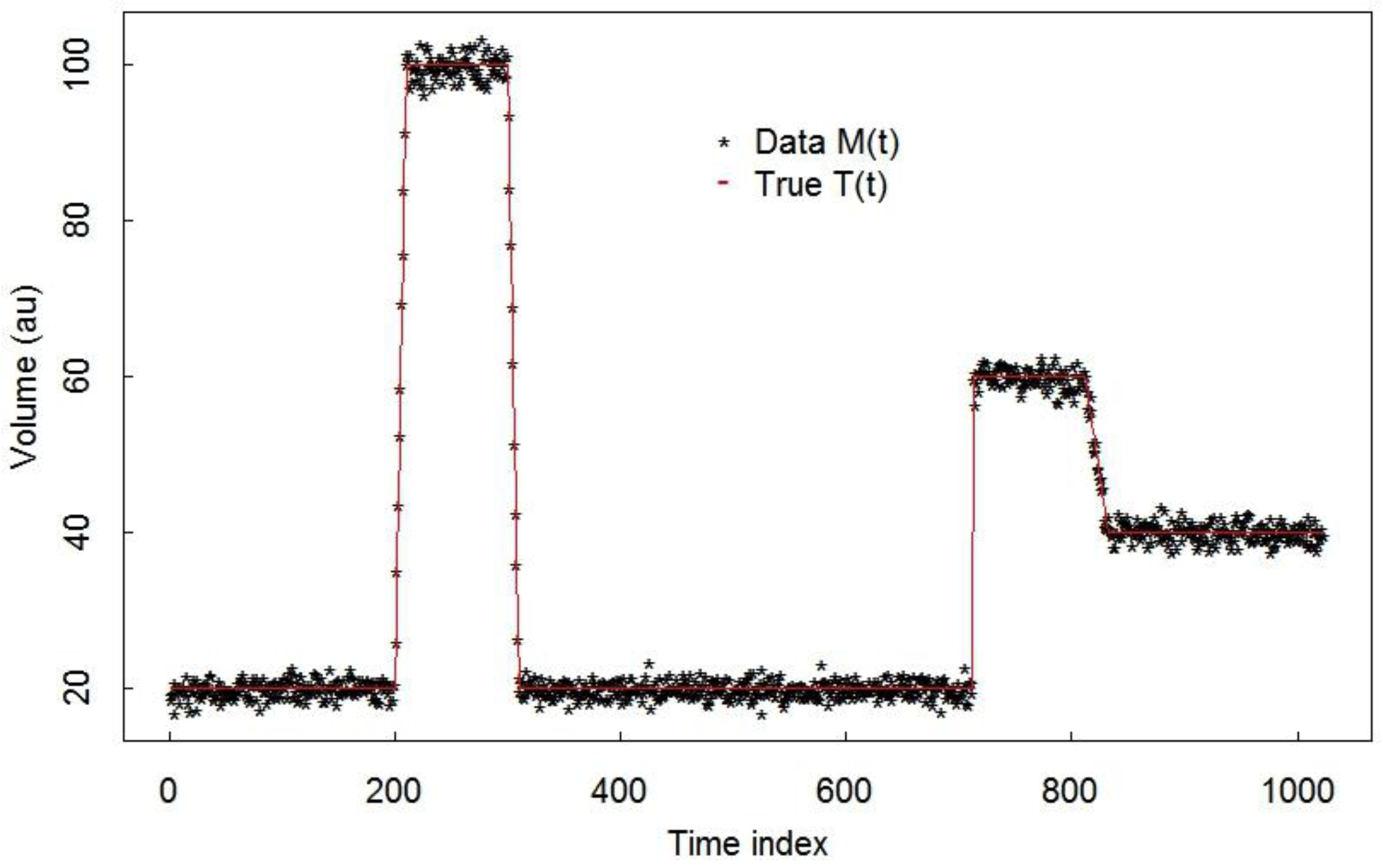
In our SM signals, we know there is a distinct start and stop time index during which a receipt or shipment occurs. Therefore, our approach is to find the change region associated with each event (receipt or shipment) and then find the start and stop indices of that event. Candidate methods are then compared based on their ability to locate each approximate change “region”, without any “breakdown”, which is our informal term for failure to infer the correct number of change regions [
7].
However, in multiple simulations of SM data, we found that no method, not the breakpoints method, not the simple lag-one differencing, and no multi-resolution wavelet-based method, gives adequately reliable change detection for the desired range of
σR and
σA values unless the correct number of change points is known. For example,
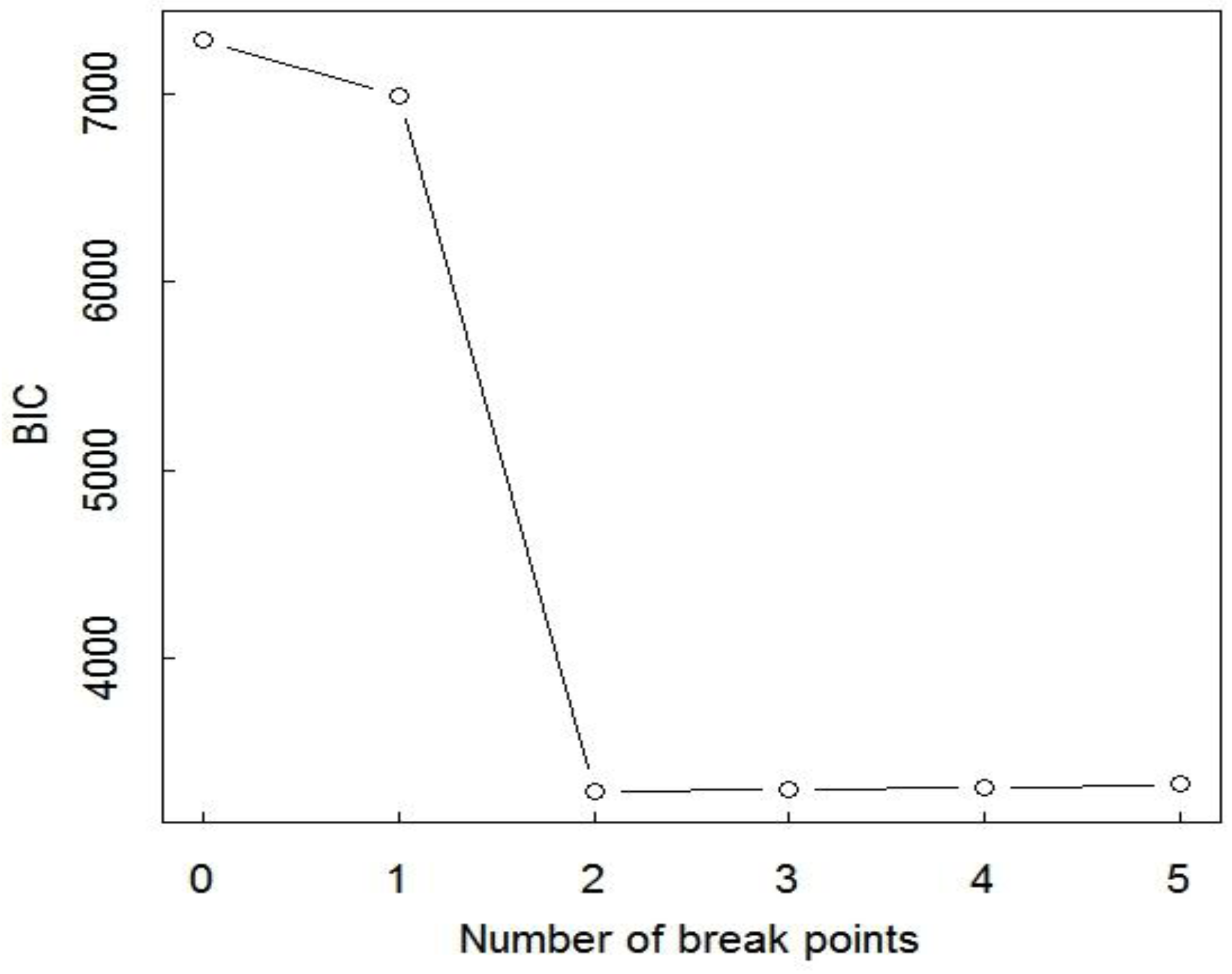
Figure 5 illustrates that breakpoints finds only two of the four change points in the first tank cycle data such as in
Figure 1. The Bayesian information criterion (BIC) is used in breakpoints to infer the number of change points. The BIC is defined as BIC = −2log(maxlikelihood) +
plog(
n), where maxlikelihood is the maximum likelihood (corresponds to the usual least squares regression estimate in the case of Gaussian data) and
p is the number of model parameters to penalize for the number of breakpoints. The model having the smallest BIC is preferred, and changes in BIC of less than approximately 10 are commonly assumed to be noise. Therefore,
Figure 5 shows that breakpoints selected only two of four change points, failing to detect a slope change within each transfer. In addition, breakpoints is slow to run on 1024 data points despite its use of a relatively fast dynamic programming algorithm to try many options for the number of change points and locations.
Figure 5.
An example of the Bayesian information criterion (BIC) for breakpoints applied to data such as the first tank cycle in
Figure 1. The true number of change points is four.
Figure 5.
An example of the Bayesian information criterion (BIC) for breakpoints applied to data such as the first tank cycle in
Figure 1. The true number of change points is four.
Similarly,
Figure 4 illustrates that standard multi-resolution wavelet-based change detection is not tuned to our SM application. For example, the resolution 1 and 2 wavelet coefficient plots show multiple change points occurring during the gradual shipment. Therefore, an approach such as that used in [
15] or in the lag-one-differencing change detection option to concatenate contiguous change points (“sub-events”) into a single shipment event is needed. Fortunately, as we show below, wavelet-based change detection is highly effective for finding change point regions, which we then refine to an estimated start and stop time of, for example, the shipment in
Figure 4.
To the best of our knowledge, wavelet literature assumes purely additive error models [
12,
27,
28] rather than the combination of additive and multiplicative errors in Equation (1) that are more appropriate for SM data [
10]. Therefore, we evaluated whether transforming to approximately unit variance prior to wavelet-based change detection was helpful. If the true value
Tt at each time step
t were known exactly, then rescaling
M(
t) by dividing by
would convert the time series to a unit variance time series with purely additive error. Because
Tt is unknown, it must be estimated using
, which we obtained using an initial Haar-based wavelet transform. Because of estimation error in
the scaled
M(
t) has only approximately unit variance, and departures from unity tend to occur near the change points. All quantitative results are for the option that first scales
M(
t) to approximately unit variance prior to performing change detection; however, whether to transform the simulated SM data to approximately unit variance by first performing an initial smoothing made very little difference in the ability of Haar wavelets to find approximate change point regions.
4.2. Refining the Initial Estimate of the Time of Each Change Point
As discussed above, all methods we consider first locate an approximate change “region”. Then, because we anticipate a slope change in T(t) at the start and stop times of each change region, we apply breakpoints to find the approximate start and stop times of each change region, specifying to breakpoints that there are two change points in a small change region. Next, we refine the initial change point estimate. To do so, a simpler version of breakpoints that estimates only one change point at a time (see the Supplemental Information), suitable for data regions that are known to contain only one change point is applied near the estimated start time and near the estimated stop time. For comparison, a multi-scale wavelet option (see the Supplemental Information) is also applied to data regions that are known to contain only one change point. The multi-scale wavelet option applies wavelets only to the 16 time indices near each change point.
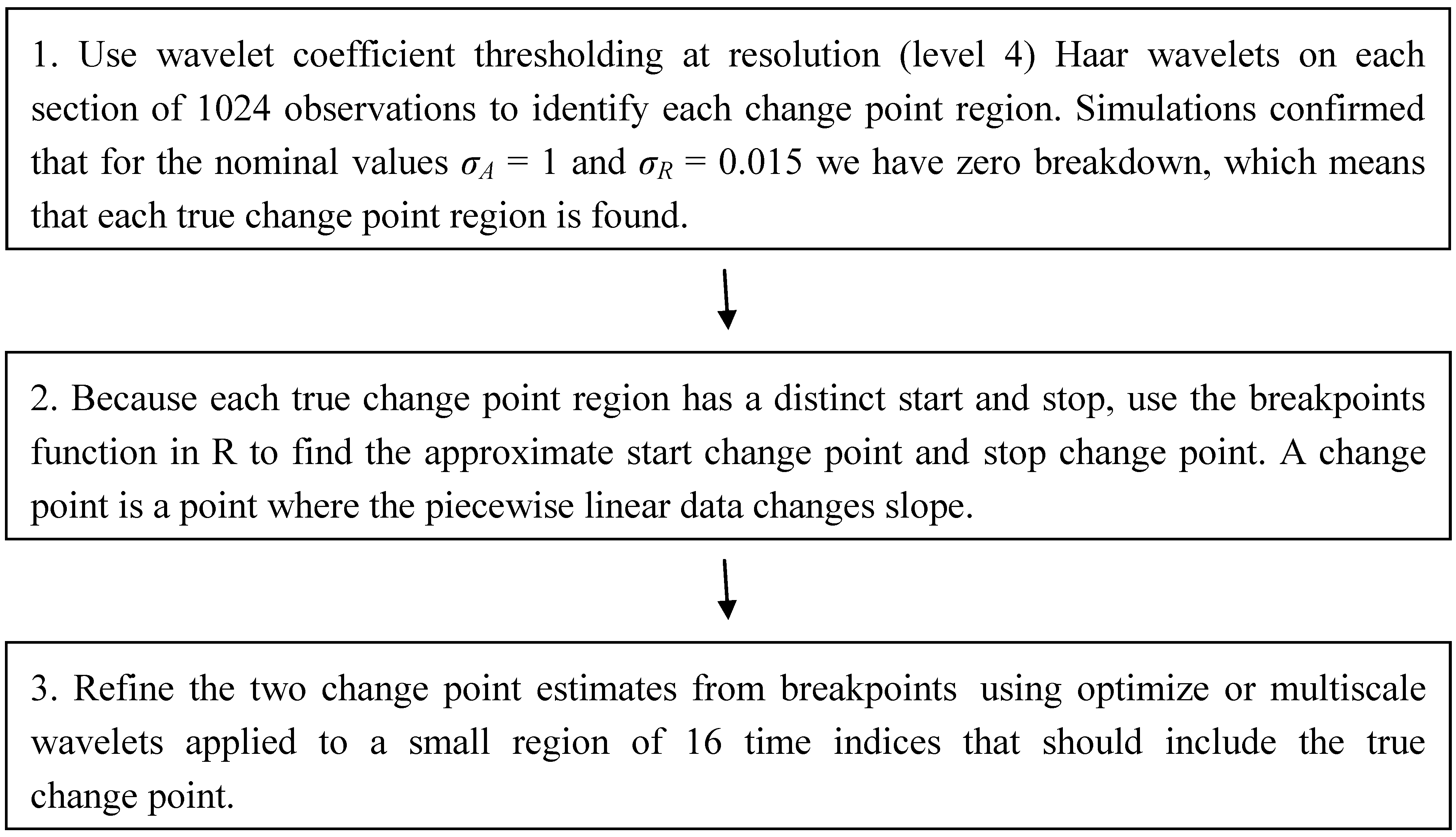
We summarize our change point detection approach in
Section 4.1 and
Section 4.2 with a block 3-step scheme as follows.
4.3. Qualitative and Quantitative Simulation Results
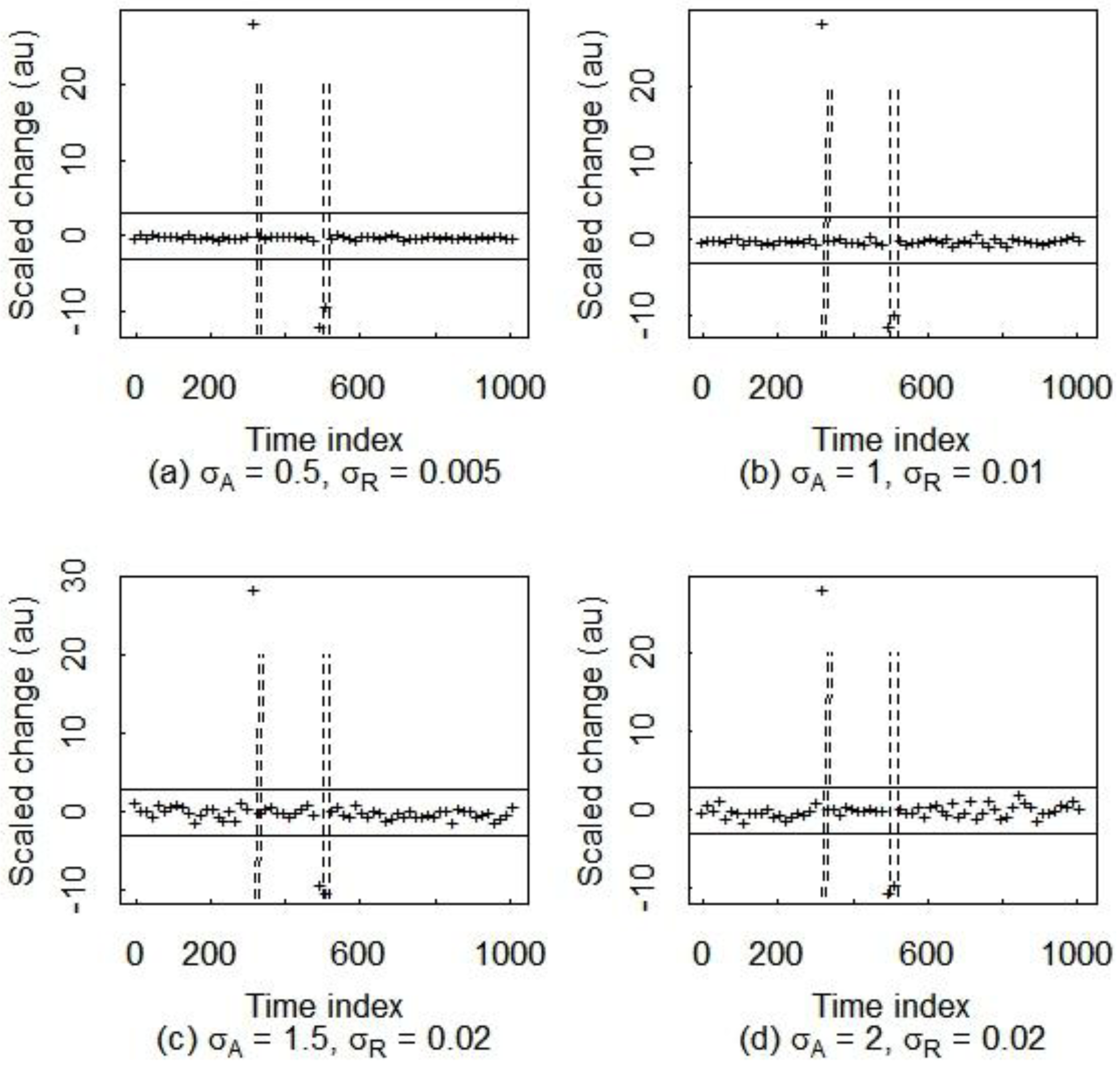
Figure 6 illustrates the lag-one differencing option for approximate change region detection for the gradual receipt and shipment in the first tank cycle in
Figure 1. As
σA and
σR in Equation (1) increase in going from subplots (a) to (d) in
Figure 6, the gradual receipt and shipment regions become very difficult to detect. Recall that
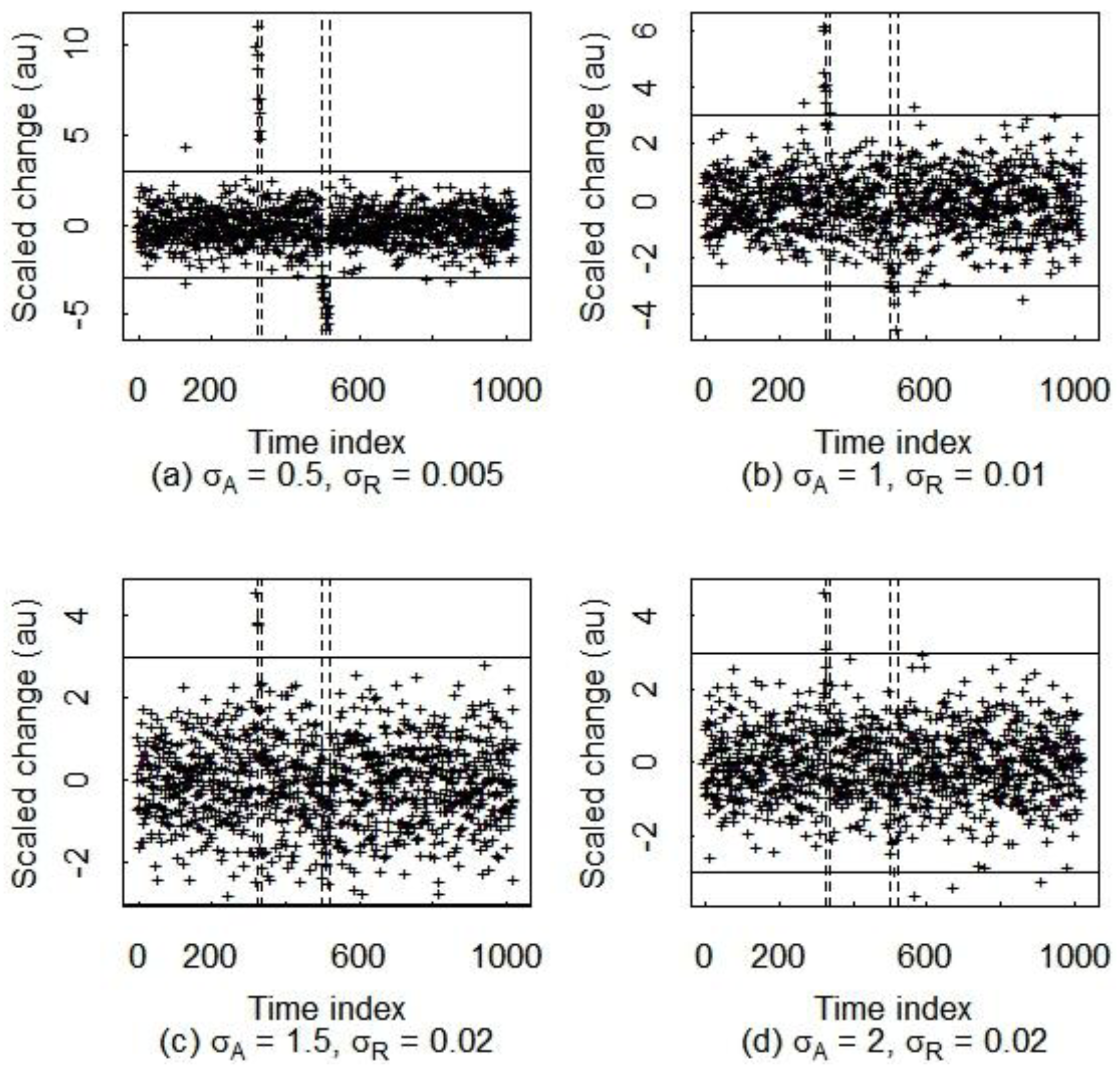
Figure 4 illustrated the potential of Haar-wavelet based change detection for a gradual receipt and gradual shipment. Comparing
Figure 7 to
Figure 6, note that Haar-wavelet based change region detection performs much better than the lag-one differencing. More quantitatively, using repeated sets of 1000 simulations of data as in
Figure 3 with a gradual receipt and gradual shipment, we found that the breakdown
σA and
σR values (the
σA and
σR values at or above which the method to find each change region results in finding the wrong number of change regions) are approximately 1 and 0.03 for lag-one differencing and are approximately 8 and 0.12 for Haar
-wavelet based change detection, which are both well above the values anticipated for our SM application. Of course the breakdown point depends on the rate of change of
T(
t) during each change region. But this example is representative of SM data, demonstrating a large advantage of a wavelet-based method to locate approximate change-point regions. We therefore have implemented Haar wavelet based change detection using high resolution to find approximate change point regions in sections of typically 512 or 1024 observations.
Figure 6.
The scaled lag-one change for increasing values of
σA and
σR in Equation (1). Note that the abrupt shipment is easily detected but that the more gradual receipt is less easily detected. The two true change regions are indicated with vertical dashed lines. The values
σA and
σR in Equation (1) increase in going from subplots (
a) to (
d) in
Figure 6, beginning with
σA = 0.5 and
σR = 0.005 in (
a).
Figure 6.
The scaled lag-one change for increasing values of
σA and
σR in Equation (1). Note that the abrupt shipment is easily detected but that the more gradual receipt is less easily detected. The two true change regions are indicated with vertical dashed lines. The values
σA and
σR in Equation (1) increase in going from subplots (
a) to (
d) in
Figure 6, beginning with
σA = 0.5 and
σR = 0.005 in (
a).
Figure 7.
The scaled change arising from the Haar-wavelet coefficient monitoring for increasing values of σA and σR in Equation (1) in subplots (a–d). Note that both the gradual shipment and the gradual receipts are easily detected for (a–d) as σA and σR increase. The two true change regions are indicated with vertical dashed lines.
Figure 7.
The scaled change arising from the Haar-wavelet coefficient monitoring for increasing values of σA and σR in Equation (1) in subplots (a–d). Note that both the gradual shipment and the gradual receipts are easily detected for (a–d) as σA and σR increase. The two true change regions are indicated with vertical dashed lines.
Table 1 lists the root mean squared errors (RMSEs) for the breakpoints method of the estimated change points (receipt start and stop and shipment start and stop) both without and with refinement by the “one change-point at a time” option using optimize and also for the multi-scale wavelet option mentioned in
Section 4.2 (see the Supplemental Information). Recall that Haar-based wavelet change detection is used in all cases to first find the approximate location of each change point. The
Table 1 entries were calculated using 1000 sets of simulations at nominal values of
σA (1.0) and
σR (0.015) for a tank cycle similar to that in
Figure 1, with a gradual receipt and gradual shipment, both occurring over 10 time steps. We verified by repeating the set of 1000 simulations that the RMSEs are repeatable across sets of 10
4 simulations to within approximately ±0.01 or less.
Table 1.
The root mean squared errors (RMSEs) for change point detection with and without refinement using the optimize function using 104 simulations.
Table 1.
The root mean squared errors (RMSEs) for change point detection with and without refinement using the optimize function using 104 simulations.
| Event | Breakpoints without refinement | Optimize to refine | Multi-Scale wavelets to refine |
|---|
| Receipt Start | 1.0 | 0.14 | 0.83 |
| Receipt Stop | 5.3 | 0.22 | 1.7 |
| Ship Start | 3.9 | 0.23 | 1.0 |
| Ship Stop | 2.0 | 0.15 | 0.81 |
The RMSEs in
Table 1 are a good high level summary of performance in the 10
4 simulations. Notice that the optimize option leads to very good (low) RMSE and the multiscale wavelet option is also quite effective, without having been tuned to this change detection problem (see the Supplemental Information). Using optimize, the start of the receipt was estimated as
t = 499, 500, or 501 (the true was 500 in all 10
4 simulations) with relative frequency 0.003, 0.995, and 0.002, respectively, so the RMSE is very small (0.14). The RMSE value of 1.7 for the receipt using multi-scale wavelets to refine the initial estimate from breakpoints can probably be reduced by more careful tuning of the multiscale wavelet approach (see the Supplemental Information). Estimation behavior without and with refinement was similar for the shipment. Qualitatively, we expect lower RMSE at the start of the receipt and at the end of the shipment because relative errors have smaller impact at the lower volumes.
Because refinement using optimize is simple and has slightly better performance than refinement using our implementation of multi-scale wavelets, we recommend Haar-based wavelets with resolution 4 to find each change point region. Certainly, we might find a multi-scale wavelet option that is more tuned to this type of SM that bundles together steps one and two. However, it is known that the change point location initial estimate will need some type of refinement [
15,
23]. For example, we verified by simulation that varying the location of the change point relative to the data length and/or changing the parity of the change point location [
29] leads to additional variation between the estimated and true change point location. In addition, the Supplemental Information gives a numerical example of noise in the estimated change point location using multi-scale wavelets. Future work will consider in more detail whether there are performance or implementation advantages to using a “purely wavelet” based change detection.
To summarize this section, Haar-based wavelet change detection with resolution level 4 as in
Figure 4 has the best breakdown and so is recommended for finding the approximate location of each change point region. Then, a very simple application of breakpoints to find the start and stop of each change region, or optimize (our preference) to refine the initial estimate of each change point within the change region completes the procedure.
Figure 5 illustrates the excellent performance (high breakdown of Haar-based wavelet change region detection).
Table 1 summarizes the RMSEs with and without either the optimize-based or the multi-scale-wavelet-based refinement step.