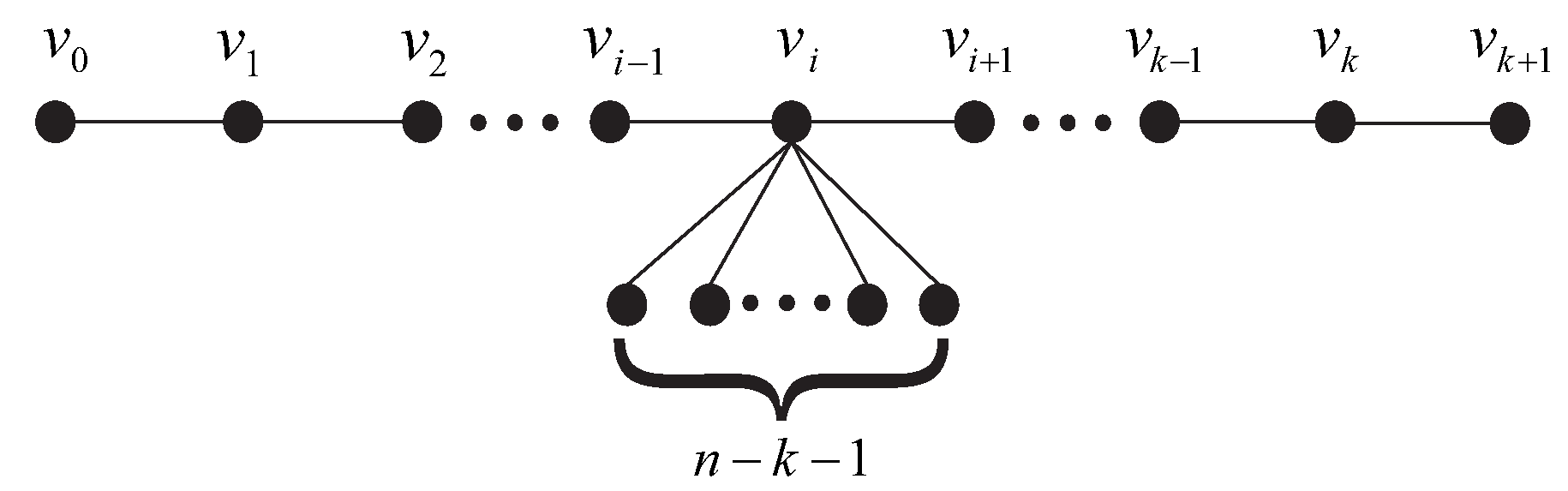The (n-1)-th Laplacian Immanantal Polynomials of Graphs

Abstract

Let ${\chi }_{n-1}\left(\sigma \right)$ denote the irreducible character of the symmetric group $S_n$ corresponding to the partition $(n-1,1)$. For an $n\times n$ matrix $M=\left(m_{i,j}\right)$, we denote its $(n-1)$-th immanant by $d_{n-1}\left(M\right)$. Let G be a simple connected graph and let $L\left(G\right)$ and $Q\left(G\right)$ denote the Laplacian matrix and the signless Laplacian matrix of G, respectively. The $(n-1)$-th Laplacian (respectively, signless Laplacian) immanantal polynomial of G is defined as $d_{n-1}(xI-L\left(G\right))$ (respectively, $d_{n-1}(xI-Q\left(G\right))$). In this paper, we partially resolve Chan’s open problem by establishing that the broom graph minimizes $d_{n-1}\left(L\left(T\right)\right)$ among all trees with given diameter. Furthermore, we give combinatorial expressions for the first five coefficients of the $(n-1)$-th Laplacian immanantal polynomial $d_{n-1}(xI-L\left(G\right))$. We also investigate the characterizing properties of this polynomial and present several graphs that are uniquely determined by it. Additionally, for the $(n-1)$-th signless Laplacian immanantal polynomial $d_{n-1}(xI-Q\left(G\right))$, we show that the multiplicity of root 1 is bounded below by the star degree of G.

1. Introduction

Let $G=\left(V\right(G),E(G\left)\right)$ be a simple connected graph with vertex set $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$ and edge set $E\left(G\right)=\{e_1,e_2,\dots ,e_m\}$. Let $n=\left|V\right(G\left)\right|$ and $m=\left|E\right(G\left)\right|$ denote the number of vertices and edges, respectively. The degree matrix $D\left(G\right)=\mathrm{diag}(d_1,d_2,\dots ,d_n)$ is defined where $d_i=d\left(v_i\right)$ (or $d_i\left(G\right)$) denotes the degree of vertex $v_i$. The adjacency matrix $A\left(G\right)=\left(a_{i,j}\right)$ is defined as

$$a_{i,j}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{v}_i\mathrm{and}{v}_j\mathrm{are}\mathrm{adjacent},\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The Laplacian matrix of G is $L\left(G\right)=D\left(G\right)-A\left(G\right)$ and its signless Laplacian matrix is $Q\left(G\right)=D\left(G\right)+A\left(G\right)$.

Let $S_n$ denote the symmetric group of degree n, let $\lambda$ be a partition of n and let ${\chi }_{\lambda }$ be the irreducible character of $S_n$. The immanant function $d_{\lambda }$ with respect to the character ${\chi }_{\lambda }$, acting on an $n\times n$ matrix $M=\left(m_{i,j}\right)$, is defined as

$$d_{\lambda }\left(M\right)=\sum _{\sigma \in S_n}{\chi }_{\lambda }\left(\sigma \right)\prod _{i=1}^n{m}_{i,\sigma \left(i\right)}.$$

(1)

In particular, when $\lambda =(k,1^{n-k})$, we call $d_{(k,1^{n-k})}\left(M\right)$ the hook immanant of M, abbreviated as $d_k\left(M\right)$. For hook immanants, $d_1\left(M\right)$ corresponds to the determinant of M; $d_2\left(M\right)$ to the second immanant; and $d_n\left(M\right)$ to the permanent of M (i.e., $per\left(M\right)$).

Specific to the focus of this paper, we will pay particular attention to the case $k=n-1$. The $(n-1)$-th immanant is defined as

$$d_{n-1}\left(M\right)=\sum _{\sigma \in S_n}{\chi }_{n-1}\left(\sigma \right)\prod _{i=1}^n{m}_{i,\sigma \left(i\right)},$$

(2)

where the character ${\chi }_{n-1}$ corresponds to the partition $(n-1,1)$ and can be computed as ${\chi }_{n-1}\left(\sigma \right)=F\left(\sigma \right)-1$; Here, $F\left(\sigma \right)$ denotes the number of fixed points of the permutation $\sigma$. A key property derived from this character formula is the following combinatorial expression for $d_{n-1}\left(M\right)$:

$$d_{n-1}\left(M\right)=\sum _{i=1}^n{m}_{i,i}per\left(M\left(i\right)\right)-per\left(M\right),$$

(3)

where $M\left(i\right)$ denotes the submatrix of M obtained by deleting the i-th row and i-th column. The computational complexity of $d_{n-1}\left(M\right)$ can be established via reduction from the permanent. Since computing the permanent of a matrix is #P-complete [1] and since the permanent can be reduced to computing $d_{n-1}\left(M\right)$ for a constructed matrix $M^{\prime }$ (see, e.g., the construction in [2]), it follows that computing $d_{n-1}\left(M\right)$ for a general matrix M is also #P-complete.

Bürgisser [2] showed that computing the hook immanant of M is VNP-complete. These immanants of graph-related matrices have been extensively investigated in the literature (see, e.g., [3,4,5,6,7,8]). In particular, concerning the Laplacian immanant of trees, Chan and Lam [9] established lower bounds for $d_{\lambda }\left(L\left(G\right)\right)$ among trees with given diameter and proposed the following open problem:

Problem 1.

For each partition λ of n, determine which tree(s) with given diameter minimize $d_{\lambda }\left(L\left(G\right)\right)$?

With regard to Problem 1, Brualdi and Goldwasser [10] proved that among all trees with given diameter, the broom graph minimizes $per\left(L\right(T\left)\right)$. Given the computational complexity of immanants, attention naturally shifts to specific cases of immanants. In particular, this intrinsic complexity motivates our study of immanant properties on specific structured matrices, such as the Laplacian matrices of trees. Among hook immanants, the case $k=n-1$ represents one of the more elementary yet non-trivial cases, which leads us to the following problem:

Problem 2.

For the partition $(n-1,1)$ of n, determine which tree(s) with given diameter minimize $d_{n-1}\left(L\left(G\right)\right)$?

Let I be the $n\times n$ identity matrix. For any $n\times n$ matrix $M=\left(m_{i,j}\right)$, its hook immanantal polynomial is defined as

$$d_k(xI-M)=d_{(k,1^{n-k})}(xI-M).$$

Among the family of hook immanantal polynomials, the characteristic polynomial and the permanental polynomial $per(xI-M)$ (i.e., $d_n(xI-M)$) have been the most widely studied [11,12,13]. Yu [14] derived explicit expressions for immanantal polynomials via fundamental subgraphs. Further investigations into the hook immanantal polynomial can be found in [15,16,17,18,19]. In particular, Merris [20] investigated the roots and coefficients of the second Laplacian immanantal polynomial. For hook immanantal polynomials, Merris posed the following problem about the star degree:

Problem 3.

Is the star degree of G always a lower bound for the multiplicity of 1 in $d_k(xI-L\left(G\right))$?

Wu et al. [17] answered this question affirmatively for the case of the second immanantal polynomial. Since Merris’s problem involves $L\left(G\right)$, we are naturally led to consider its analogue for the signless Laplacian matrix $Q\left(G\right)$. For $Q\left(G\right)$, Faria [15] proved that the multiplicity of the root 1 in $per(xI-Q(G\left)\right)$ equals the star degree of G. These results, combined with the fact that evaluating $d_{n-1}(xI-M)$ is #P-complete for general matrices [2], motivate us to study the specific case of the hook immanantal polynomial $d_{n-1}(xI-Q\left(G\right))$ and to propose the following extension of Problem 3:

Problem 4.

Is the multiplicity of the root 1 in $d_{n-1}(xI-Q\left(G\right))$ related to the star degree of G?

This paper focuses on Problems 2 and 4, investigating the fundamental properties of the $(n-1)$-th Laplacian immanantal polynomial and providing solutions to these problems. The paper is structured as follows. In Section 2, we first investigate the fundamental properties of the coefficients of the $(n-1)$-th Laplacian immanantal polynomial. Alongside this, we address Problem 2 by showing that the broom graph minimizes $d_{n-1}\left(L\left(T\right)\right)$. Section 3 investigates the properties of the $(n-1)$-th Laplacian immanantal polynomial. In the final section, we resolve Problem 4 by showing that the multiplicity of the root 1 in $d_{n-1}(xI-Q\left(G\right))$ is bounded below by the star degree of G that has a non-zero star degree.

2. Coefficients of the $(\mathit{n}-\mathbf{1})$-th Laplacian Immanantal Polynomial and the Solution to Problem 2

For an $n\times n$ matrix $M=\left(m_{i,j}\right)$, by Equation (2), the $(n-1)$-th immanantal polynomial is expressed as

$$d_{n-1}(xI-M)=c_0\left(M\right)x^n-c_1\left(M\right)x^{n-1}+\dots +{(-1)}^n{c}_n\left(M\right).$$

(4)

First consider the $(n-1)$-th immanantal polynomial for an $n\times n$ matrix $M=\left(m_{i,j}\right)$. Let ${\mathcal{S}}_{k,n}$ denote the collection of all k-element subsets of $\{1,2,\dots ,n\}$. For $Y\in {\mathcal{S}}_{k,n}$, let $M\left[Y\right]$ denote the principal $k\times k$ submatrix corresponding to Y. Define $M\left\{Y\right\}$ as the $n\times n$ matrix satisfying

$$M{\left\{Y\right\}}_{ij}=\left\{\begin{array}{cc}{m}_{i,j}\hfill & \mathrm{if}i,j\in Y,\hfill \\ {\delta }_{i,j}\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where ${\delta }_{i,j}$ is the Kronecker delta. Then $M\left\{Y\right\}$ is permutationally similar to the direct sum of $M\left[Y\right]$ and the $(n-k)$-order identity matrix. This similarity is realized by applying a permutation that brings all indices in Y to the first k positions. Under this permutation, the matrix transforms into an explicit block diagonal structure: the upper-left $k\times k$ block is precisely $M\left[Y\right]$ and the lower-right $(n-k)\times (n-k)$ block is the identity matrix, as all off-block entries are zero by the definition of $M{\left\{Y\right\}}_{ij}={\delta }_{ij}$ for i or $j\notin Y$.

By Equation (4), the coefficient $c_k\left(M\right)$ of $x^{n-k}$ in the expansion of $d_{n-1}(xI-M)$ arises from selecting a k-subset Y of indices where the term $-m_{i,j}$ is chosen (no x contribution), while the remaining indices contribute $x{\delta }_{i,j}$ (enforcing fixed points). The matrix $M\left\{Y\right\}$, which retains elements of M on Y and is identity elsewhere, encodes this constraint. Unlike the permanent, whose character is multiplicative ($per\left(M\right\{Y\left\}\right)=per\left(M\right[Y\left]\right)$), the character ${\chi }_{n-1}$ for the $(n-1)$-th immanant is not multiplicative [21]. Thus, $d_{n-1}\left(M\left\{Y\right\}\right)$≠$d_{n-1}\left(M\left[Y\right]\right)$ and $d_{n-1}\left(M\left\{Y\right\}\right)$ computes the weighted sum over the subgroup $S_Y$ (permutations that are the identity outside Y). Therefore, from (2) we have

$$c_k\left(M\right)=\sum _{Y\in {\mathcal{S}}_{k,n}}{d}_{n-1}M\left\{Y\right\}.$$

(5)

Let $S_Y$ be the subgroup of $S_n$ consisting of permutations that fix all elements outside Y, which is isomorphic to the symmetric group $S_k$ acting on Y. Since each permutation in $S_Y$ has $n-k$ more fixed points than its corresponding permutation in $S_k$, from (2) and (5) we obtain

$$c_k\left(M\right)=\sum _{Y\in {\mathcal{S}}_{k,n}}\left(d_{n-1}M\left[Y\right]+(n-k)perM\left[Y\right]\right).$$

(6)

It is essential to clarify the precise meaning of the notation $d_{n-1}$ in this context. In Equation (5), $d_{n-1}$ operates on an $n\times n$ matrix, employing the character ${\chi }_{n-1}$ of the symmetric group $S_n$. However, in Equation (6), the same symbol $d_{n-1}$ is applied to the principal submatrix $M\left[Y\right]$, which is a $k\times k$ matrix. Strictly speaking, the corresponding immanant for a matrix of order k should be denoted as $d_{k-1}$, utilizing the character ${\chi }_{k-1}$ of $S_k$. To ensure notational consistency while maintaining readability, we hereby establish the following convention: throughout this work, the symbol $d_{n-1}$ will represent the hook immanant for square matrices of any order. Formally, for any $p\times p$ matrix B, we define:

$$d_{n-1}\left(B\right):=\sum _{\sigma \in S_p}{\chi }_{p-1}\left(\sigma \right)\prod _{i=1}^p{b}_{i,\sigma \left(i\right)},$$

where ${\chi }_{p-1}$ is the character of $S_p$ corresponding to the partition $(p-1,1)$. Under this convention, $d_{n-1}\left(M\left[Y\right]\right)$ in Equation (6) unambiguously denotes the $(k-1)$-th immanant of the $k\times k$ submatrix $M\left[Y\right]$. This complication does not occur for the permanent because the trivial character $\chi \left(\sigma \right)=1$ remains irreducible upon restriction to subgroups. This stability follows from the fact that the trivial representation is one-dimensional [21] and is therefore irreducible and multiplicative under any subgroup restriction. Consequently, for permutations that are identity outside subset Y, the permanent satisfies the multiplicative identity $per\left(M\left\{Y\right\}\right)=per\left(M\left[Y\right]\right)·per\left(I_{n-k}\right)=per\left(M\left[Y\right]\right)$, where $I_{n-k}$ is the identity matrix of order $n-k$. This is unlike the $(n-1)$-th immanant, which corresponds to a higher-dimensional irreducible representation whose character may decompose upon restriction.

Let $B=\left(b_{i,j}\right)$ be a $k\times k$ matrix ($k\ge 2$). By Equation (3), we obtain

$$d_{n-1}\left(B\right)=\sum _{i=1}^k{b}_{i,i}perB\left(i\right)-per\left(B\right),$$

(7)

where $B\left(i\right)$ denotes the submatrix of B obtained by deleting the i-th row and column. Substituting this expression for $d_{n-1}\left(M\left[Y\right]\right)$ from Equation (7) into (6), we obtain for each subset Y:

$$\begin{array}{ccc}& & d_{n-1}\left(M\left[Y\right]\right)+(n-k)perM\left[Y\right]\hfill \\ & =& \left(\sum _{i=1}^k{m}_{Y_i,Y_i}perM\left[Y\right]\left(i\right)-perM\left[Y\right]\right)+(n-k)perM\left[Y\right]\hfill \\ & =& \sum _{i=1}^k{m}_{Y_i,Y_i}perM\left[Y\right]\left(i\right)+(n-k-1)perM\left[Y\right].\hfill \end{array}$$

Therefore, summing this identity over all $Y\in {\mathcal{S}}_{k,n}$ yields the desired expression for the coefficient $c_k\left(M\right)$:

$$\begin{array}{cc}\hfill c_k\left(M\right)& =\sum _{Y\in {\mathcal{S}}_{k,n}}\left(\sum _{i=1}^k{m}_{Y_i,Y_i}perM\left[Y\right]\left(i\right)+(n-k-1)perM\left[Y\right]\right)\hfill \\ \hfill & =\left(\sum _{Y\in {\mathcal{S}}_{k,n}}\sum _{i=1}^k{m}_{Y_i,Y_i}perM\left[Y\right]\left(i\right)\right)+(n-k-1)q_k\left(M\right)\hfill \\ \hfill & =\left(\sum _{Y\in {\mathcal{S}}_{k-1,n}}\left(\sum _{i\notin Y}{m}_{i,i}\right)perM\left[Y\right]\right)+(n-k-1)q_k\left(M\right),\hfill \end{array}$$

(8)

where $M\left[Y\right]\left(i\right)$ denotes the submatrix of $M\left[Y\right]$ obtained by deleting the row and column corresponding to the i-th element of Y (thus directly analogous to the notation $B\left(i\right)$ introduced in Equation (7)) and $q_k\left(M\right)$ denotes the coefficient of ${(-1)}^k{x}^{n-k}$ in the permanental polynomial $per(xI-M)$.

Now consider the special case $M=L\left(G\right)$. Rewriting Equation (8) gives

$$c_k\left(G\right)=(n-k-1)q_k\left(G\right)+\sum _{Y\in {\mathcal{S}}_{k-1,n}}\left(\sum _{i\notin Y}d\left(v_i\right)\right)perL\left(G\right)\left[Y\right],$$

(9)

where $q_k\left(G\right)=q_k\left(L\left(G\right)\right)$. If G is a regular graph with $d\left(v_t\right)=r$ ($1\le t\le n$), then

$$c_k\left(G\right)=(n-k-1)q_k\left(G\right)+(n-k+1)r{q}_{k-1}\left(G\right).$$

(10)

Theorem 1.

Let $G_1$ and $G_2$ be two regular graphs. Then the following statements are equivalent

(i) 

$per(xI-L\left(G_1\right))=per(xI-L\left(G_2\right))$;

(ii) 

$d_{n-1}(xI-L\left(G_1\right))=d_{n-1}(xI-L\left(G_2\right))$;

(iii) 

$per(xI-A\left(G_1\right))=per(xI-A\left(G_2\right))$.

Proof. 

The equivalence of (i) and (ii) follows from (10) since $c_k\left(G\right)$ can be expressed in terms of $q_k\left(G\right)$. If (iii) holds, since the leading coefficients are equal and the coefficients of $x^{n-2}$ are identical, $G_1$ and $G_2$ must have the same number of vertices n, edges m and thus the same regularity r. Substituting $(x-r)$ into $per(xI+A\left(G_1\right))=per(xI+A\left(G_2\right))$ yields (i). Reversing the steps shows that (i) implies (iii). □

We extend some definitions to facilitate subsequent analysis. Let $\mathrm{deg}\left(G\right)=(d_1,d_2,\dots ,d_n)$ denote the degree sequence of a graph G. For any edge $e=\{v_i,v_j\}\in E\left(G\right)$, the edge-deleted degree sequence ${\mathrm{deg}}_e\left(G\right)$ is obtained by removing the entries $d_i$ and $d_j$ from $\mathrm{deg}\left(G\right)$. Let $a_k$ denote the k-th elementary symmetric function. For a graph G, define $a_k\left(G\right)=a_k\left(\mathrm{deg}\left(G\right)\right)$. Then, for $k\ge 3$, let

$$b_k\left(G\right)=\sum _{e\in E\left(G\right)}{a}_{k-2}\left({\mathrm{deg}}_e\left(G\right)\right).$$

Theorem 2.

Let G be a graph with n vertices and m edges and let $L\left(G\right)$ denote its Laplacian matrix. The $(n-1)$-th Laplacian immanantal polynomial admits the expansion

$$d_{n-1}(xI-L\left(G\right))=\sum _{k=0}^n{(-1)}^k{c}_k\left(G\right)x^{n-k},$$

where the coefficients are given by:

$$\begin{array}{ccc}\hfill c_0\left(G\right)& =& n-1,\hfill \\ \hfill c_1\left(G\right)& =& (n-1)a_1\left(G\right)=2m(n-1),\hfill \\ \hfill c_2\left(G\right)& =& (n-1)a_2\left(G\right)+m(n-3),\hfill \\ \hfill c_3\left(G\right)& =& (n-1)a_3\left(G\right)+(n-3)b_3\left(G\right)-2(n-4)T\left(G\right),\hfill \\ \hfill c_4\left(G\right)& =& (n-1)a_4\left(G\right)+(n-3)b_4\left(G\right)+(n-5)[\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)-\sum _{i=1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{d_i}{2}}\right)+2C_4\left(G\right)]\hfill \\ & & -2(n-4)\sum _{i=1}^n{d}_i[T\left(G\right)-T\left(G\left(v_i\right)\right)].\hfill \end{array}$$

Here, $T\left(G\right)$ counts triangles in $G, T\left(G\left(v_i\right)\right)$ counts triangles containing vertex $v_i$ and $C_4\left(G\right)$ counts quadrilaterals.

Proof. 

The coefficient of the highest-degree term $x^n$ in the polynomial, denoted $c_0\left(G\right)$, is given by ${\chi }_{n-1}\left(\mathrm{id}\right)=n-1$. The coefficient $c_1\left(G\right)$ equals the product of ${\chi }_{n-1}\left(\mathrm{id}\right)$ and the trace of the Laplacian matrix, i.e., $c_1\left(G\right)=(n-1)a_1\left(G\right)=2m(n-1)$. For $n\ge 3$, the coefficient of $x^{n-2}$ is determined by two types of permutations: the identity permutation $\sigma =\mathrm{id}$, contributing $(n-1)a_2\left(G\right)$ and the transpositions corresponding to the endpoints of each edge in G (where ${\chi }_{n-1}\left(\sigma \right)=n-3$), leading to $c_2\left(G\right)=(n-1)a_2\left(G\right)+m(n-3)$.

For the coefficient $c_3\left(G\right)$, the analysis of $L\left(G\right)$ involves three parts: the contribution from the identity permutation, $(n-1)a_3\left(G\right)$; the contribution from transpositions of edge endpoints, $(n-3)b_3\left(G\right)$; and the contribution from 3-cycles (and their inverses) corresponding to triangular structures in G, $-2(n-4)T\left(G\right)$. Specifically, for any permutation $\sigma \in S_n$ containing a 3-cycle $(i,j,k)$ where $\{i,j\},\{j,k\},\{i,k\}\in E\left(G\right)$ (forming a triangle in G), the calculation of $F\left(\sigma \right)-1$ shows that the character ${\chi }_{n-1}\left(\sigma \right)=n-4$. Given that the off-diagonal entries of the Laplacian matrix satisfy $l_{ij}=l_{jk}=l_{ik}=-1$, each 3-cycle and its inverse contribute $-2(n-4)$ to $c_3\left(G\right)$. The total contribution from all 3-cycles is $-2(n-4)T\left(G\right)$. Thus, $c_3\left(G\right)=(n-1)a_3\left(G\right)+(n-3)b_3\left(G\right)-2(n-4)T\left(G\right)$.

For the coefficient $c_4\left(G\right)$, we provide a systematic classification of all permutation types in $S_n$ with support on precisely 4 vertices that yield non-zero products in $L\left(G\right)$. The analysis reveals five distinct types of such permutations that contribute to this coefficient:

Type I: 

Identity permutation: This type contributes $(n-1)a_4\left(G\right)$, accounting for all ways of selecting 4 vertices and using their diagonal entries.

Type II: 

Single transposition: These permutations consist of one transposition (an edge) and two fixed points. Each has ${\chi }_{n-1}\left(\sigma \right)=n-3$ and contributes a product equal to $d\left(p\right)d\left(q\right)$ for the fixed points p and q. Summing over all edges and all vertex pairs not incident to the edge results in the term $(n-3)b_4\left(G\right)$, where $b_4\left(G\right)={\sum }_{e\in E\left(G\right)}{a}_2\left({\mathrm{deg}}_e\left(G\right)\right)$.

Type III: 

Two disjoint transpositions: These permutations have ${\chi }_{n-1}\left(\sigma \right)=n-5$ and contribute a product of 1. The number of such permutations is equal to the number of pairs of vertex-disjoint edges, given by $\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)-{\sum }_{i=1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{d_i}{2}}\right)$, leading to the term $(n-5)\left[\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)-{\sum }_{i=1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{d_i}{2}}\right)\right]$.

Type IV: 

4-cycles: A 4-cycle permutation has ${\chi }_{n-1}\left(\sigma \right)=n-5$ and yields a non-zero product if and only if its vertices form a 4-cycle in G, contributing a product of 1. Each undirected 4-cycle corresponds to two cyclic orders, giving the term $2(n-5)C_4\left(G\right)$.

Type V: 

3-cycle with an isolated fixed point: These permutations have ${\chi }_{n-1}\left(\sigma \right)=n-4$. Specifically, consider any permutation $\sigma \in S_n$ containing a 3-cycle $(i,j,k)$ where $\{i,j\},\{j,k\},\{i,k\}\in E\left(G\right)$ (forming a triangle in G) with an arbitrary fixed point $v_p$ ($p\notin \{i,j,k\}$). For each such permutation, the product of the relevant entries from $xI-L\left(G\right)$ is ${(-1)}^3·d_p=-d_p$ and thus its total contribution to the coefficient is ${\chi }_{n-1}\left(\sigma \right)·(-d_p)=-(n-4)d_p$. The off-diagonal entries $l_{ij}=l_{jk}=l_{ik}=-1$ and the diagonal entries (particularly $d_p$ of the fixed point $v_p$) yield the observed character value. The inverse permutation contributes an identical amount, so for each triangle $\Delta$ and each vertex $v_p\notin \Delta$, the combined contribution is $-2(n-4)d_p$. Summing over all triangles $\Delta$ and all vertices $v_p$ not in $\Delta$ gives: $-2(n-4){\displaystyle \sum _{\Delta }}{\displaystyle \sum _{v_p\notin \Delta }}{d}_p.$

This double sum is equivalent to $-2(n-4){\sum }_{i=1}^n{d}_i[T\left(G\right)-T\left(G\left(v_i\right)\right)]$, since for a fixed vertex $v_i$, $T\left(G\right)-T\left(G\left(v_i\right)\right)$ counts exactly the number of triangles that avoid $v_i$.

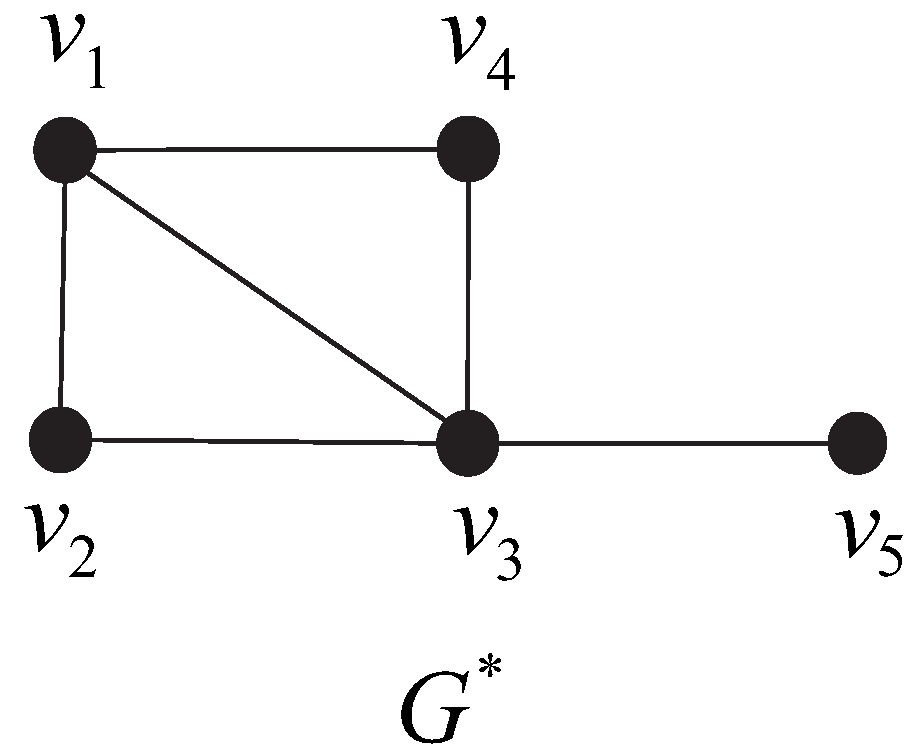
For example, consider the Graph $G^{\ast }$ with 5 vertices illustrated in Figure 1. This graph contains two triangles: ${\Delta }_1=\{v_1,v_2,v_3\}$ and ${\Delta }_2=\{v_1,v_3,v_4\}$. The degrees of the vertices are $d_1=3$, $d_2=2$, $d_3=4$, $d_4=2$ and $d_5=1$. The number of triangles incident to each vertex is given by: $T\left(G\left(v_1\right)\right)=2$ (as $v_1$ belongs to both ${\Delta }_1$ and ${\Delta }_2$), $T\left(G\left(v_2\right)\right)=1$ (only in ${\Delta }_1$), $T\left(G\left(v_3\right)\right)=2$ (both triangles), $T\left(G\left(v_4\right)\right)=1$ (only in ${\Delta }_2$) and $T\left(G\left(v_5\right)\right)=0$ (in no triangle). We now evaluate the expression: ${\displaystyle \sum _{i=1}^5}{d}_i\left[T\left(G\right)-T\left(G\left(v_i\right)\right)\right]=3(2-2)+2(2-1)$

$+4(2-2)+2(2-1)+1(2-0)=0+2+0+2+2=6.$

This result is corroborated by a direct computation: for triangle ${\Delta }_1$, the vertices not belonging to it are $v_4$ and $v_5$, whose degrees sum to $2+1=3$; for triangle ${\Delta }_2$, the external vertices are $v_2$ and $v_5$, with degree sum $2+1=3$. The total is therefore $3+3=6$, which agrees with the previous calculation. Then we obtain: $-2(n-4){\displaystyle \sum _{i=1}^n}{d}_i[T\left(G\right)-T\left(G\left(v_i\right)\right)]=-2\times (5-4)\times 6=-12.$

Figure 1. Graph $G^{\ast }$ with 5 vertices.

Figure 1. Graph $G^{\ast }$ with 5 vertices.

Summing the contributions from all five types yields the final expression:

$$\begin{array}{ccc}\hfill c_4\left(G\right)& =& (n-1)a_4\left(G\right)+(n-3)b_4\left(G\right)+(n-5)[\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)-\sum _{i=1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{d_i}{2}}\right)+2C_4\left(G\right)]\hfill \\ & & -2(n-4)\sum _{i=1}^n{d}_i[T\left(G\right)-T\left(G\left(v_i\right)\right)].\hfill \end{array}$$

□

Lemma 1

(Bapat [22]). Let M be a positive semidefinite matrix. Then

$$perM\ge 0.$$

Note that every principal submatrix of the Laplacian matrix $L\left(G\right)$ of a graph G is positive semidefinite; this follows from the well-known property that the Laplacian matrix $L\left(G\right)$ of G itself is positive semidefinite, and all principal submatrices of any positive semidefinite matrix inherit this positivity. By Lemma 1 and Equation (9), we derive the following inequality for $c_k\left(G\right)$:

Theorem 3.

Let G be a graph with n vertices, and $c_k\left(G\right)$ the coefficient of ${(-1)}^k{x}^{n-k}$ in $d_{n-1}(xI-L\left(G\right))$. Then

$$0\le c_k\left(G\right)\le (n-k-1){(n+k-2)}^k+(n-1)(n-k+1){(n+k-3)}^{k-1}.$$

Proof. 

Since the Laplacian matrix $L\left(G\right)$ is positive semidefinite, every principal submatrix $L\left(G\right)\left[Y\right]$ is also positive semidefinite. By Lemma 1, it follows that $perL\left(G\right)\left[Y\right]\ge 0$ for all $Y\subset V\left(G\right)$. Furthermore, the diagonal entries $d\left(v_i\right)$ and the coefficient $(n-k-1)$ are nonnegative. Therefore, from Equation (9), we conclude that $c_k\left(G\right)\ge 0$. On the other hand, it is not difficult to observe that the upper bound for the permanent of k-th order principal submatrices of the complete graph $K_n$, obtained using the diagonal dominance matrix permanent bound [23], serves as an upper bound for the permanent of k-th order principal submatrices of any graph G. Thus, Equation (9) can be transformed into:

$$\begin{array}{cc}\hfill c_k\left(G\right)& =(n-k-1)q_k\left(G\right)+\sum _{Y\in {\mathcal{S}}_{k-1,n}}\left(\sum _{i\notin Y}d\left(v_i\right)\right)perL\left(G\right)\left[Y\right]\hfill \\ \hfill & \le (n-k-1)\prod _{i=1}^k\left(|l_{i,i}|+\sum _{j\ne i}\left|l_{i,j}\right|\right)\hfill \\ \hfill & +\sum _{Y\in {\mathcal{S}}_{k-1,n}}\left(\sum _{i\notin Y}{d}_i\left(K_n\right)\right)\prod _{i=1}^{k-1}\left(|l_{i,i}|+\sum _{j\ne i}\left|l_{i,j}\right|\right)\hfill \\ \hfill & =(n-k-1){(n+k-2)}^k+(n-1)(n-k+1){(n+k-3)}^{k-1},\hfill \end{array}$$

where ${\mathcal{S}}_{k-1,n}$ denotes the collection of all $(k-1)$-element subsets of $\{1,2,\dots ,n\}$. □

At the end of this section, we characterize the broom graph as the minimizer of $d_{n-1}\left(L\left(G\right)\right)$ among trees with given diameter. First, we introduce necessary notations and lemmas.

Let G be a simple graph and $W\subseteq V\left(G\right)$ be a vertex subset. Denote by $L_W\left(G\right)$ the principal submatrix of the Laplacian matrix $L\left(G\right)$ obtained by deleting rows and columns corresponding to vertices in W. When $W=\left\{v\right\}$, we simply write $L_v\left(G\right)$; when $W=\{u,v\}$ with $uv\in E\left(G\right)$, we write $L_{uv}\left(G\right)$. For any vertex $v\in V\left(G\right)$, let ${\mathcal{C}}_G\left(v\right)$ denote the collection of all cycles in G containing v and $N\left(v\right)$ the set of vertices adjacent to v.

Let $B={\left(b_{s,t}\right)}_{n\times n}$ be a symmetric matrix over the complex field. For any $1\le i,j\le n$, define a symmetric matrix $B_{\left[ij\right]}={\left(b_{s,t}^{i,j}\right)}_{n\times n}$ where

$$b_{s,t}^{i,j}=\left\{\begin{array}{cc}{b}_{s,t},\hfill & \mathrm{if}(s,t)\ne (i,j)\mathrm{and}(s,t)\ne (j,i),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Thus, $B_{\left[ij\right]}=B_{\left[ji\right]}$ is obtained by replacing the $(i,j)$-th and $(j,i)$-th entries of B with zeros. For example, if

$$B=\left(\begin{array}{ccc}{b}_{1,1}& b_{1,2}& b_{1,3}\\ b_{1,2}& b_{2,2}& b_{2,3}\\ b_{1,3}& b_{2,3}& b_{3,3}\end{array}\right),$$

then

$$B_{\left[12\right]}=B_{\left[21\right]}=\left(\begin{array}{ccc}{b}_{1,1}& 0& b_{1,3}\\ 0& b_{2,2}& b_{2,3}\\ b_{1,3}& b_{2,3}& b_{3,3}\end{array}\right),B_{\left[33\right]}=\left(\begin{array}{ccc}{b}_{1,1}& b_{1,2}& b_{1,3}\\ b_{1,2}& b_{2,2}& b_{2,3}\\ b_{1,3}& b_{2,3}& 0\end{array}\right).$$

Clearly, if $b_{i,j}=0$, then $B=B_{\left[ij\right]}=B_{\left[ji\right]}$.

Lemma 2

(Chan and Lam [9]). Let $C[n;k;i]$ denote the caterpillar graph of diameter k$C(k;\underset{i-1}{\underbrace{0,\dots ,0}},n-k-1,\underset{k-1-i}{\underbrace{0,\dots ,0}})$ (see Figure 2), where $n-k-1$ pendant vertices are attached at the i-th position along the diameter. For any tree T with n vertices and diameter k, there exists an index $i\in \{1,2,\dots ,\lfloor {\displaystyle \frac{k}{2}}\rfloor \}$ depending on λ such that

$$d_{\lambda }\left(L\left(T\right)\right)\ge d_{\lambda }\left(L\left(C[n;k;i]\right)\right).$$

Moreover, the inequality is strict unless $T\cong C[n;k;j]$ for some $j\in \{1,\dots ,k-1\}$.

Lemma 3.

Let G be a simple graph and $v\in V\left(G\right)$ a vertex. Then

$$\begin{array}{ccc}\hfill d_{n-1}\left(L\left(G\right)\right)& =& d\left(v\right)\left[per\left(L_v\left(G\right)\right)+d_{n-1}\left(L_v\left(G\right)\right)\right]+\sum _{u\in N\left(v\right)}{d}_{n-1}\left(L_{uv}\left(G\right)\right)\hfill \\ & & +2\sum _{C\in {\mathcal{C}}_G\left(v\right)}{(-1)}^{\left|V\right(C\left)\right|}{d}_{n-1}\left(L_{V\left(C\right)}\left(G\right)\right).\hfill \end{array}$$

Proof. 

Let $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$. By definition of $d_{n-1}\left(L\left(G\right)\right)$, we consider the product terms $l_{1,\sigma \left(1\right)}{l}_{2,\sigma \left(2\right)}\dots l_{n,\sigma \left(n\right)}$ corresponding to permutations $\sigma$ in the expansion of the Laplacian matrix $L\left(G\right)$, where $l_{i,j}$ denotes the $(i,j)$-entry of $L\left(G\right)$. Note that $l_{i,i}=d\left(v_i\right)$ and for $i\ne j$, $l_{i,j}=-1$ if $v_i{v}_j\in E\left(G\right)$, otherwise $l_{i,j}=0$. Thus, if $l_{1,\sigma \left(1\right)}{l}_{2,\sigma \left(2\right)}\dots l_{n,\sigma \left(n\right)}\ne 0$, then for every $j\in \{1,\dots ,n\}$, either $j=\sigma \left(j\right)$ or $v_j{v}_{\sigma \left(j\right)}\in E\left(G\right)$. Without loss of generality, let $v=v_1$, so $l_{1,1}=d\left(v\right)$.

Considering $\sigma$ as a product of disjoint cycles, let ${\gamma }_1$ be a cycle in $\sigma$ and write $\sigma ={\gamma }_1{\sigma }^{\prime }$. Define the set $P=\{\sigma \mid l_{1,\sigma \left(1\right)}{l}_{2,\sigma \left(2\right)}\dots l_{n,\sigma \left(n\right)}\ne 0\}$. Based on the length of ${\gamma }_1$, we partition P into three cases:

• $S_1=\{\sigma \in P\mid {\gamma }_1=\left(1\right)\}$ (fixed point at 1);
• $S_2^j=\{\sigma \in P\mid {\gamma }_1=\left(1j\right)\}$ (transposition corresponding to edge $v{v}_j$);
• $S_C=\{\sigma \in P\mid {\gamma }_1$ is a cycle of length $\ge 3$ containing v}.

Since $S_1$, $S_2^j$ (for any $j\ne 1$), and $S_C$ are pairwise disjoint with $P=S_1\cup \left({\cup }_{v_j\in N\left(v\right)}{S}_2^j\right)\cup \left({\cup }_{C\in {\mathcal{C}}_G\left(v\right)}{S}_C\right)$, we have:

$$\begin{array}{cc}\hfill d_{n-1}\left(L\left(G\right)\right)& =\sum _{\sigma \in S_n}{\chi }_{n-1}\left(\sigma \right)\prod _{i=1}^n{l}_{i,\sigma \left(i\right)}\hfill \\ \hfill & =\sum _{\sigma \in S_1}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}+\sum _{v_j\in N\left(v\right)}\sum _{\sigma \in S_2^j}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}\hfill \\ \hfill & +\sum _{C\in {\mathcal{C}}_G\left(v\right)}\sum _{\sigma \in S_C}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}.\hfill \end{array}$$

□

Remark 1.

For the $(n-1,1)$ Young diagram (a first row of $n-1$ boxes and a second row of 1 box), the Murnaghan-Nakayama rule for ${\chi }_{(n-1,1)}\left(\sigma \right)$ simplifies to:

• For a length-1 cycle (fixed point): Remove one of two possible length-1 rim hooks (last box of the first row or the single box of the second row), giving ${\chi }_{(n-1,1)}\left(\sigma \right)={\chi }_{(n-2,1)}\left({\sigma }_1\right)+{\chi }_{(n-1)}\left({\sigma }_1\right)$ where ${\sigma }_1$ is σ with the fixed point removed.
• For a length-2 cycle (transposition): Remove the unique length-2 rim hook consisting of the last two consecutive boxes of the first row. This leaves the $(n-3,1)$ Young diagram, so ${\chi }_{(n-1,1)}\left(\sigma \right)={\chi }_{(n-3,1)}\left({\sigma }_2\right)$ where ${\sigma }_2$ is σ with the transposition removed.
• For a length-$l\ge 3$ cycle: Remove the unique length-l rim hook consisting of the last l consecutive boxes of the first row. This leaves the $(n-l-1,1)$ Young diagram, so ${\chi }_{(n-1,1)}\left(\sigma \right)=$
  ${\chi }_{(n-l-1,1)}\left({\sigma }_3\right)$ where ${\sigma }_3$ is σ with the l-cycle removed.

Using Remark 1 to compute the character values for each case, we proceed as follows:

1.

For $\sigma \in S_1$ with ${\gamma }_1=\left(1\right)$:

$$\begin{array}{cc}\hfill & \sum _{\sigma \in S_1}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}\hfill \\ \hfill & =d\left(v\right)\sum _{\begin{array}{c}{\sigma }_1\\ {\gamma }_1{\sigma }_1\in S_1\end{array}}[{\chi }_{(n-1)}\left({\sigma }_1\right)+{\chi }_{(n-2,1)}\left({\sigma }_1\right)]l_{2,{\sigma }_1\left(2\right)}\dots l_{n,{\sigma }_1\left(n\right)}\hfill \\ \hfill & =d\left(v\right)\left[per\left(L_v\left(G\right)\right)+d_{n-1}\left(L_v\left(G\right)\right)\right].\hfill \end{array}$$

2.

For $\sigma \in S_2^j$ with ${\gamma }_1=\left(1j\right)$:

$$\begin{array}{cc}\hfill & \sum _{\sigma \in S_2^j}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}\hfill \\ \hfill & =\sum _{\begin{array}{c}{\sigma }_2\\ {\gamma }_1{\sigma }_2\in S_2^j\end{array}}{\chi }_{(n-3,1)}\left({\sigma }_2\right)l_{2,{\sigma }_2\left(2\right)}\dots l_{(j-1),{\sigma }_2(j-1)}{l}_{(j+1),{\sigma }_2(j+1)}\dots l_{n,{\sigma }_2\left(n\right)}\hfill \\ \hfill & =\sum _{u\in N\left(v\right)}{d}_{n-1}\left(L_{uv}\left(G\right)\right).\hfill \end{array}$$

3.

For each permutation $\sigma \in S_C$, the cycle ${\gamma }_1$ corresponds to a cycle C of length $l\ge 3$ in the graph, with sign ${(-1)}^{\left|V\right(C\left)\right|}$ and contributing a factor of 2 (since the cycle is reversible). Therefore,

$$\begin{array}{ccc}& & \sum _{\sigma \in S_C}{\chi }_{(n-1,1)}{l}_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}\hfill \\ & =& 2\sum _{\begin{array}{c}{\sigma }_3\\ {\gamma }_1{\sigma }_3\in S_C\end{array}}{(-1)}^{\left|V\right(C\left)\right|}{\chi }_{(n-l-1,1)}\left({\sigma }_3\right)l_{i_1,{\sigma }_3\left(i_1\right)}\dots l_{i_{n-l},{\sigma }_3\left(i_{n-l}\right)}\hfill \\ & =& 2\sum _{C\in {\mathcal{C}}_G\left(v\right)}{(-1)}^{\left|V\right(C\left)\right|}{d}_{n-1}\left(L_{V\left(C\right)}\left(G\right)\right),\hfill \end{array}$$

where $i_1,\dots ,i_{n-l}$ are the vertices of the graph $G-V\left(C\right)$.

Combining these results yields:

$$\begin{array}{ccc}\hfill d_{n-1}L\left(G\right)& =& d\left(v\right)\left[per\left(L_v\left(G\right)\right)+d_{n-1}\left(L_v\left(G\right)\right)\right]+\sum _{u\in N\left(v\right)}{d}_{n-1}\left(L_{uv}\left(G\right)\right)\hfill \\ & & +2\sum _{C\in {\mathcal{C}}_G\left(v\right)}{(-1)}^{\left|V\right(C\left)\right|}{d}_{n-1}\left(L_{V\left(C\right)}\left(G\right)\right).\hfill \end{array}$$

To facilitate subsequent proofs, for the n-vertex path graph $P_n$, we employ the standard vertex labeling in which vertices are labeled consecutively as $v_1,v_2,\dots ,v_n$ with $v_i=i$ for $1\le i\le n$ and edges are given by $\{v_j,v_{j+1}\}$ for $1\le j\le n-1$.

Lemma 4.

Let $P_n$ be the path graph with n vertices and $L\left(P_n\right)$ its Laplacian matrix. Given $B_{\left[ij\right]}$ as defined earlier, for $n\ge 5$ and any $\left[ij\right]\ne \left[12\right]$,

$$d_{n-1}\left(L{\left(P_n\right)}_{\left[12\right]}\right)<d_{n-1}\left(L{\left(P_n\right)}_{\left[ij\right]}\right).$$

Proof. 

The proof proceeds by induction on n. By path symmetry, we may assume $i,j\le \lceil n/2\rceil$. The base case $n=5$ is verified by computation (see Appendix A): $d_4\left(L\left(P_5\right)\left[12\right]\right)=48<52=d_4\left(L\left(P_5\right)\left[23\right]\right)$. By Lemma 3, when we delete the second vertex $v_2$ from the left in the path graph $P_n$ (under the standard labeling where vertices are labeled $v_1,v_2,\dots ,v_n$ consecutively), which is adjacent to the pendant vertex $v_1$ on one side and vertex $v_3$ on the other side. By applying Lemma 3 to vertex $v_2$ of $P_n$ (adjacent to $v_1$ and $v_3$), we derive:

$$\begin{array}{ccc}\hfill & & d_{n-1}\left(L\left(P_n\right)\right)\hfill \\ & =& 2d_{n-1}\left(L{\left(P_{n-1}\right)}_{\left[12\right]}\right)+2per\left(L{\left(P_{n-1}\right)}_{\left[12\right]}\right)+d_{n-1}\left(L_{v_1{v}_2}\left(P_n\right)\right)+d_{n-1}\left(L_{v_2{v}_3}\left(P_n\right)\right).\hfill \\ & =& 2d_{n-1}\left(L{\left(P_{n-1}\right)}_{\left[12\right]}\right)+2per\left(L{\left(P_{n-1}\right)}_{\left[12\right]}\right)+d_{n-1}\left(L_{v_1{v}_2}\left(P_n\right)\right)+d_{n-1}\left(L{\left(P_{n-2}\right)}_{\left[12\right]}\right).\hfill \end{array}$$

(11)

Based on the proof of Lemma 3, the following recursive relation is obtained: for a cycle of length 2, ${\chi }_{(n-1,1)}\left(\sigma \right)={\chi }_{(n-3,1)}\left({\sigma }_2\right)$, where ${\sigma }_2$ is the permutation after removing the corresponding cycle. From the definition of the $(n-1)$-th immanant $d_{n-1}\left(L\left(P_n\right)\right)$ and the proof of Lemma 3, we have:

$$\begin{array}{ccc}\hfill d_{n-1}\left(L\left(P_n\right)\right)& =& \sum _{\sigma \in S_n}{\chi }_{n-1}\left(\sigma \right)\prod _{i=1}^n{l}_{i,\sigma \left(i\right)}\hfill \\ & =& \sum _{\sigma \in S_1}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}+\sum _{v_j\in N\left(v\right)}\sum _{\sigma \in S_2^j}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\hfill \\ & & \dots l_{n,\sigma \left(n\right)}\hfill \\ & =& \sum _{\sigma \in S_1}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}+\sum _{\begin{array}{c}{v}_j\in N\left(v\right)\\ j\ne 2\end{array}}\sum _{\sigma \in S_2^j}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\hfill \\ & & \dots l_{n,\sigma \left(n\right)}+\sum _{\begin{array}{c}{v}_j\in N\left(v\right)\\ j=2\end{array}}\sum _{\sigma \in S_2^j}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}\hfill \\ & =& \sum _{\sigma \in S_1}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\dots l_{n,\sigma \left(n\right)}+\sum _{\begin{array}{c}{v}_j\in N\left(v\right)\\ j\ne 2\end{array}}\sum _{\sigma \in S_2^j}{\chi }_{(n-1,1)}\left(\sigma \right)l_{1,\sigma \left(1\right)}\hfill \\ & & \dots l_{n,\sigma \left(n\right)}+\sum _{\begin{array}{c}{\sigma }_2\\ {\gamma }_1{\sigma }_2\in S_2^j\\ j=2\end{array}}{\chi }_{(n-3,1)}\left({\sigma }_2\right)l_{3,{\sigma }_2\left(3\right)}\dots l_{\left(j\right),{\sigma }_2\left(j\right)}\dots l_{n,{\sigma }_2\left(n\right)}\hfill \\ & =& d_{n-1}\left(L{\left(P_n\right)}_{\left[12\right]}\right)+d_{n-1}\left(L_{v_1{v}_2}\left(P_n\right)\right).\hfill \end{array}$$

(12)

Then we can combine Equations (11) and (12) to obtain:

$$d_{n-1}\left(L{\left(P_n\right)}_{\left[12\right]}\right)=2d_{n-1}\left(L{\left(P_{n-1}\right)}_{\left[12\right]}\right)+2per\left(L{\left(P_{n-1}\right)}_{\left[12\right]}\right)+d_{n-1}\left(L{\left(P_{n-2}\right)}_{\left[12\right]}\right).$$

The inequality follows because, as established by Corollary 2.13 in Ref. [10], we have $perL{\left(P_{n-1}\right)}_{\left[12\right]}$ ≤$perL{\left(P_{n-1}\right)}_{\left[ij\right]}$ for all $\left[ij\right]\ne \left[12\right]$ and the induction hypothesis applies. □

Theorem 4.

Let T be a tree with n vertices and diameter k. Then

$$d_{n-1}\left(L\left(T\right)\right)\ge d_{n-1}\left(L\left(C[n;k;1]\right)\right),$$

with equality holding if and only if T is the broom graph $C[n;k;1]$.

Proof. 

By Lemma 2, it suffices to prove that $d_{n-1}\left(L\left(C[n;k;j]\right)\right)>d_{n-1}\left(L\left(C[n;k;1]\right)\right)$ for $j\ne 1$. We proceed by induction on n. For the base case $n=k+1$, the broom graph $C[n;k;1]$ reduces to the path graph $P_{k+1}$, which is the unique tree with diameter k and $n=k+1$ vertices. Now consider $n>k+1$. By Lemma 3, removing any $n-k-1$ pendant vertices v with their incident edges $uv$ from $C[n;k;1]$, we obtain $d_{n-1}\left(L\left(C[n;k;1]\right)\right)=per\left(L_v\left(C[n;k;1]\right)\right)+d_{n-1}\left(L_v\left(C[n;k;1]\right)\right)+d_{n-1}\left(L_{uv}\left(C[n;k;1]\right)\right)$. The linearity of the permanent yields $per\left(L_v\left(C[n;k;1]\right)\right)=per\left(L(C[n;k;1]-v)\right)+per\left(L_{uv}\left(C[n;k;1]\right)\right)$, which combined with Equation (7) gives $d_{n-1}\left(L_v\left(C[n;k;1]\right)\right)=d_{n-1}\left(L(C[n;k;1]-v)\right)+d_{n-1}\left(L_{uv}\left(C[n;k;1]\right)\right)$, where $L_{uv}\left(C[n;k;1]\right)$ reduces to the direct sum of an $(n-k-2)$-identity matrix and $L{\left(P_k\right)}_{\left[12\right]}$.

According to Equation (6), we have

$$\begin{array}{ccc}\hfill & & d_{n-1}\left(L\left(C[n;k;1]\right)\right)\hfill \\ & =& per\left(L_v\left(C[n;k;1]\right)\right)+d_{n-1}\left(L_v\left(C[n;k;1]\right)\right)+d_{n-1}\left(L_{uv}\left(C[n;k;1]\right)\right)\hfill \\ & =& \mathrm{per}\left(L(C[n;k;1]-v)\right)+\mathrm{per}(L_{uv}\left(C[n;k;1]\right)+d_{n-1}L(C[n;k;1]-v))\hfill \\ & & +d_{n-1}\left(L_{uv}\left(C[n;k;1]\right)\right)+d_{n-1}\left(L_{uv}\left(C[n;k;1]\right)\right)\hfill \\ & =& \mathrm{per}\left(L\left(C[n-1;k-1;1]\right)\right)+per\left(L{\left(P_k\right)}_{\left[12\right]}\right)+d_{n-1}\left(L\left(C[n-1;k-1;1]\right)\right)\hfill \\ & & +2d_{n-1}\left(L_{uv}\left(C[n;k;1]\right)\right).\hfill \\ & =& \mathrm{per}\left(L\left(C[n-1;k-1;1]\right)\right)+per\left(L{\left(P_k\right)}_{\left[12\right]}\right)+d_{n-1}\left(L\left(C[n-1;k-1;1]\right)\right)\hfill \\ & & +2[d_{n-1}\left(L{\left(P_k\right)}_{\left[12\right]}\right)+(n-k-2)per\left(L{\left(P_k\right)}_{\left[12\right]}\right)].\hfill \end{array}$$

(13)

Similarly, we have

$$\begin{array}{ccc}\hfill & & d_{n-1}\left(L\left(C[n;k;i]\right)\right)\hfill \\ & =& \mathrm{per}\left(L\left(C[n-1;k-1;i]\right)\right)+per\left(L{\left(P_k\right)}_{\left[ij\right]}\right)+d_{n-1}\left(L\left(C[n-1;k-1;i]\right)\right)\hfill \\ & & +2[d_{n-1}\left(L{\left(P_k\right)}_{\left[ij\right]}\right)+(n-k-2)per\left(L{\left(P_k\right)}_{\left[ij\right]}\right)].\hfill \end{array}$$

(14)

Brualdi and Goldwasser [10] proved that among all trees with given diameter, the broom graph minimizes $per\left(L\right(T\left)\right)$. Combining Equations (13) and (14) with Lemma 4 and the induction hypothesis completes the proof of the theorem. □

3. The Properties of the $(\mathit{n}-\mathbf{1})$-th Laplacian Immanantal Polynomials

In this section, we investigate the properties and prove that complete graphs with at most three edges removed are uniquely determined by their $(n-1)$-th Laplacian immanantal polynomials. We begin by establishing several fundamental lemmas that will be crucial for our main results.

Lemma 5

(Merris, Theorem 2 [20]). Let G be a graph with n vertices and m edges and $L\left(G\right)$ its Laplacian matrix. Then

$$\begin{array}{c}\hfill d_2\left(L\left(G\right)\right)=2m\kappa \left(G\right).\end{array}$$

where $\kappa \left(G\right)$ denotes the number of spanning trees in G.

Lemma 6

(Johnson and Peirce [24]). Let A be an $n\times n$ positive semidefinite Hermitian matrix, $n>2$. Then

$$d_2\left(A\right)\le d_{n-1}\left(A\right).$$

If $n\ge 4$, equality holds if and only if A has a zero row, A is diagonal, or A has rank 1. If $n=3$, then $d_2\left(A\right)=d_{n-1}\left(A\right)$ holds as an identity.

Lemma 7

(Liu, Theorem 5 [25]). Let $G=\left(V\right(G),E(G\left)\right)$ be a graph with n vertices and m edges and let $d_1,d_2,\dots ,d_n$ be its degree sequence. For any two vertices i and j ($1\le i<j\le n$), let $G_{i,j}$ denote the subgraph obtained by deleting vertices i and j from G and let $\left|E\right(G_{i,j}\left)\right|$ denote the number of edges in this subgraph. Then the following identities hold:

$$\begin{array}{ccc}\hfill \sum _{\begin{array}{c}{v}_j{v}_k\in E\left(G\right)\\ 1\le j<k\le n\end{array}}\sum _{i\ne j,k}{d}_i& =& 2m^2-\sum _{i=1}^n{d}_i^2.\hfill \\ \hfill \sum _{1\le i<j<k\le n}{d}_i{d}_j{d}_k& =& {\displaystyle \frac{4}{3}}{m}^3-m\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{1}{3}}\sum _{i=1}^n{d}_i^3.\hfill \\ \hfill \sum _{1\le i<j\le n}{d}_i{d}_j\left|E\left(G_{i,j}\right)\right|& =& \sum _{i=1}^n{d}_i^3-{\displaystyle \frac{5}{2}}m\sum _{i=1}^n{d}_i^2+\sum _{v_i{v}_j\in E\left(G\right)}{d}_i{d}_j+2m^3.\hfill \\ \hfill \sum _{1\le i<j<k<l\le n}{d}_i{d}_j{d}_k{d}_l& =& -{\displaystyle \frac{1}{4}}\sum _{i=1}^n{d}_i^4+{\displaystyle \frac{2}{3}}m\sum _{i=1}^n{d}_i^3+{\displaystyle \frac{2}{3}}{m}^4-m^2\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{1}{8}}{\left(\sum _{i=1}^n{d}_i^2\right)}^2.\hfill \end{array}$$

Theorem 5.

Let G be a simple connected graph with at least one edge. Then the polynomial $d_{n-1}(xI-L\left(G\right))$ has no zero roots.

Proof. 

Assume 0 is a root of $d_{n-1}(xI-L\left(G\right))$. By Lemmas 5 and 6, $c_n\left(G\right)=d_{n-1}\left(L\left(G\right)\right)\ge d_2\left(L\left(G\right)\right)=2m\kappa \left(G\right)>0$, which proves the theorem. □

Theorem 6.

Let G be a simple connected graph with at least one edge. Then the polynomial $d_{n-1}(xI-L\left(G\right))$ has no negative real roots.

Proof. 

The $(n-1)$-th Laplacian immanantal polynomial of G is

$$d_{n-1}(xI-L\left(G\right))=\sum _{k=0}^n{(-1)}^k{c}_k\left(G\right)x^{n-k}.$$

By Theorem 2, we have

$$c_0\left(G\right)=n-1>0,c_1\left(G\right)=2m(n-1)>0.$$

and $c_n\left(G\right)>0$. For $2⩽k⩽n-1$, $n-k-1⩾0$. Since $L\left(G\right)$ is positive semidefinite, $q_k\left(G\right)>0$ and ${\displaystyle \sum _{Y\in S_{k-1,n}}}\left({\displaystyle \sum _{t\notin Y}}{d}_t\left(G\right)\right)perL\left(G\right)\left[Y\right]>0$, so by Equation (6) we have $c_k\left(G\right)>0$.

Observe that ${(-1)}^k{c}_k\left(G\right)x^{n-k}=c_k\left(G\right){(-{\displaystyle \frac{1}{x}})}^k{x}^n$. If n is odd, for all real $\lambda <0$, $c_k\left(G\right){(-{\displaystyle \frac{1}{\lambda }})}^k>0$ and ${\lambda }^n<0$. If n is even, for all real $\lambda <0$, $c_k\left(G\right){(-{\displaystyle \frac{1}{\lambda }})}^k>0$ and ${\lambda }^n>0$. Thus for all $\lambda <0$, $d_{n-1}(xI-L\left(G\right))<0$ when n is odd and $d_{n-1}(xI-L\left(G\right))>0$ when n is even. Therefore, any connected graph G with at least one edge has no negative real roots in $d_{n-1}(xI-L\left(G\right))$. □

Substituting the expressions for $a_k\left(G\right)$ and $b_k\left(G\right)$ into Theorem 2, we obtain:

Corollary 1.

Let G be a graph with n vertices and m edges and $L\left(G\right)$ its Laplacian matrix. Then:

$$d_{n-1}(xI-L\left(G\right))=\sum _{k=0}^n{(-1)}^k{c}_k\left(G\right)x^{n-k}$$

where the coefficients satisfy:

$$\begin{array}{ccc}\hfill c_0\left(G\right)& =& n-1;\hfill \\ \hfill c_1\left(G\right)& =& (n-1)a_1\left(G\right)=2m(n-1);\hfill \\ \hfill c_2\left(G\right)& =& -{\displaystyle \frac{1}{2}}(n-1)\sum _{i=1}^n{d}_i^2+2m^{2}n-2m^2+mn-3m;\hfill \\ \hfill c_3\left(G\right)& =& {\displaystyle \frac{1}{3}}(n-1)\sum _{i=1}^n{d}_i^3-(mn-m+n-3)\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{10}{3}}{m}^{2}n-{\displaystyle \frac{22}{3}}{m}^2-2(n-4)T\left(G\right);\hfill \\ \hfill c_4\left(G\right)& =& -{\displaystyle \frac{1}{4}}(n-1)\sum _{i=1}^n{d}_i^4+({\displaystyle \frac{2}{3}}mn-{\displaystyle \frac{2}{3}}m+n-3)\sum _{i=1}^n{d}_i^3-(m^{2}n-m^2+{\displaystyle \frac{5}{2}}mn-{\displaystyle \frac{15}{2}}m\hfill \\ & & +{\displaystyle \frac{1}{2}}n-{\displaystyle \frac{5}{2}})\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{1}{8}}(n-1){(\sum _{i=1}^n{d}_i^2)}^2+(n-3)\sum _{\left(v_i{v}_j\right)\in E\left(G\right)}{d}_i{d}_j\hfill \\ & & +2(n-4)\sum _{i=1}^n{d}_{i}T\left(G_{v_i}\right)+2(n-5)C_4\left(G\right)-4m(n-4)T\left(G\right)\hfill \\ & & +{\displaystyle \frac{2}{3}}{m}^4(n-1)+2m^3(n-3)+{\displaystyle \frac{1}{2}}{m}^2(n-5)+{\displaystyle \frac{1}{2}}m(n-5).\hfill \end{array}$$

Here, $T\left(G\right)$ counts triangles in G, $T\left(G\left(v_i\right)\right)$ counts triangles containing vertex $v_i$ and $C_4\left(G\right)$ counts quadrilaterals.

Proof. 

We derive the expressions for $c_k\left(G\right)$ by substituting the combinatorial definitions of $a_k\left(G\right)$ and $b_k\left(G\right)$ into Theorem 2, using the identities established in Lemma 7 to handle the resulting summations. The calculations proceed as follows:

$$\begin{array}{ccc}\hfill c_2\left(G\right)& =& (n-1)a_2\left(G\right)+m(n-3)=(n-1)(2m^2-{\displaystyle \frac{1}{2}}\sum _{i=1}^n{d}_i^2)+m(n-3)\hfill \\ & =& -{\displaystyle \frac{1}{2}}(n-1)\sum _{i=1}^n{d}_i^2+2m^{2}n-2m^2+mn-3m.\hfill \\ \hfill c_3\left(G\right)& =& (n-1)a_3\left(G\right)+(n-3)b_3\left(G\right)-2(n-4)T\left(G\right)\hfill \\ & =& (n-1)\sum _{1\le i<j<k\le n}{d}_i{d}_j{d}_k+\sum _{\begin{array}{c}{v}_j{v}_k\in E\left(G\right)\\ 1\le j<k\le n\end{array}}\sum _{i\ne j,k}{d}_i-2(n-4)T\left(G\right)\hfill \\ & =& (n-1)[{\displaystyle \frac{4}{3}}{m}^2-m\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{1}{3}}\sum _{i=1}^n{d}_i^3]+(n-3)(2m^2-\sum _{i=1}^n{d}_i^2)-2(n-4)T\left(G\right)\hfill \\ & =& {\displaystyle \frac{1}{3}}(n-1)\sum _{i=1}^n{d}_i^3-(mn-m+n-3)\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{10}{3}}{m}^{2}n-{\displaystyle \frac{22}{3}}{m}^2-2(n-4)T\left(G\right).\hfill \\ \hfill c_4\left(G\right)& =& (n-1)a_4\left(G\right)+(n-3)b_4\left(G\right)+(n-5)[\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)-\sum _{i=1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{d_i}{2}}\right)+2C_4\left(G\right)]\hfill \\ & & -2(n-4)\sum _{i=1}^n{d}_i[T\left(G\right)-T\left(G\left(v_i\right)\right)]\hfill \\ & =& (n-1)\sum _{1\le i<j<k<l\le n}{d}_i{d}_j{d}_k{d}_l+(n-3)\sum _{1\le i<j\le n}{d}_i{d}_j|E\left(G_{i,j}\right)|+(n-5)[\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)\hfill \\ & & -\sum _{i=1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{d_i}{2}}\right)+2C_4\left(G\right)]-2(n-4)\sum _{i=1}^n{d}_i[T\left(G\right)-T\left(G\left(v_i\right)\right)]\hfill \\ & =& (n-1)[-{\displaystyle \frac{1}{4}}\sum _{i=1}^n{d}_i^4+{\displaystyle \frac{2}{3}}m\sum _{i=1}^n{d}_i^3-m^2\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{1}{8}}{(\sum _{i=1}^n{d}_i^2)}^2+{\displaystyle \frac{2}{3}}{m}^4]\hfill \\ & & +(n-3)[\sum _{i=1}^n{d}_i^3-{\displaystyle \frac{5}{2}}m\sum _{i=1}^n{d}_i^2+\sum _{v_i{v}_j\in E\left(G\right)}{d}_i{d}_j+2m^3]+(n-5)[\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)-\sum _{i=1}^n\left({\displaystyle \genfrac{}{}{0pt}{}{d_i}{2}}\right)\hfill \\ & & +2C_4\left(G\right)]-2(n-4)\sum _{i=1}^n{d}_i[T\left(G\right)-T\left(G\left(v_i\right)\right)]\hfill \\ & =& -{\displaystyle \frac{1}{4}}(n-1)\sum _{i=1}^n{d}_i^4+({\displaystyle \frac{2}{3}}mn-{\displaystyle \frac{2}{3}}m+n-3)\sum _{i=1}^n{d}_i^3-(m^{2}n-m^2+{\displaystyle \frac{5}{2}}mn-{\displaystyle \frac{15}{2}}m\hfill \\ & & )\sum _{i=1}^n{d}_i^2+(n-3)\sum _{\left(v_i{v}_j\right)\in E\left(G\right)}{d}_i{d}_j+{\displaystyle \frac{1}{8}}(n-1){(\sum _{i=1}^n{d}_i^2)}^2+{\displaystyle \frac{2}{3}}{m}^4(n-1)+2m^3(n-3)\hfill \\ & & +{\displaystyle \frac{1}{2}}(m^2-m)(n-5)-{\displaystyle \frac{1}{2}}(n-5)\sum _{i=1}^n(d_i^2-d_i)+2(n-5)C_4\left(G\right)\hfill \\ & & +2(n-4)\sum _{i=1}^n{d}_{i}T\left(G_{v_i}\right)-4m(n-4)T\left(G\right).\hfill \\ & =& -{\displaystyle \frac{1}{4}}(n-1)\sum _{i=1}^n{d}_i^4+({\displaystyle \frac{2}{3}}mn-{\displaystyle \frac{2}{3}}m+n-3)\sum _{i=1}^n{d}_i^3-(m^{2}n-m^2+{\displaystyle \frac{5}{2}}mn-{\displaystyle \frac{15}{2}}m\hfill \\ & & +{\displaystyle \frac{1}{2}}n-{\displaystyle \frac{5}{2}})\sum _{i=1}^n{d}_i^2+{\displaystyle \frac{1}{8}}(n-1){(\sum _{i=1}^n{d}_i^2)}^2+(n-3)\sum _{\left(v_i{v}_j\right)\in E\left(G\right)}{d}_i{d}_j\hfill \\ & & +2(n-4)\sum _{i=1}^n{d}_{i}T\left(G_{v_i}\right)+2(n-5)C_4\left(G\right)-4m(n-4)T\left(G\right)\hfill \\ & & +{\displaystyle \frac{2}{3}}{m}^4(n-1)+2m^3(n-3)+{\displaystyle \frac{1}{2}}{m}^2(n-5)+{\displaystyle \frac{1}{2}}m(n-5).\hfill \end{array}$$

□

Theorem 7.

The following can be deduced from the $(n-1)$-th Laplacian immanantal polynomial of a graph G:

(i) 

The number of vertices.

(ii) 

The number of edges.

(iii) 

The sum of squares of vertex degrees.

Proof. 

(i) is obvious. From Corollary 1, we have the number of edges $m={\displaystyle \frac{1}{2(n-1)}}{c}_1\left(G\right)$ and

$$\sum _{i=1}^n{d}_i^2\left(G\right)=-{\displaystyle \frac{2}{n-1}}\left[c_2\left(G\right)-2m^{2}n+2m^2-mn+3m\right].$$

Thus (ii) and (iii) hold. □

From Theorem 1, we know that if regular graph G is determined by its permanental polynomial, then G is also determined by its $(n-1)$-th Laplacian immanantal polynomial. In the subsequent research of this section, we consider the case of non-regular graphs.

Let H be a subgraph of G and denote by $G-E\left(H\right)$ the subgraph obtained by deleting all edges of H from G. Let ${\mathcal{G}}_n$ denote the collection of all graphs obtained by deleting at most 3 edges from the complete graph $K_n$. These graphs are labeled as $G_{ij}$ where $1\le i\le 3$ and $0\le j\le 4$, as illustrated in Figure 3.

Lemma 8

(Zhang et al. [26]). Let $H\subseteq K_n$ be a graph with l edges and $G=K_n-E\left(H\right)$. Then

$$T\left(G\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{3}}\right)-l(n-2)+\sum _{\nu \in V\left(H\right)}\left({\displaystyle \genfrac{}{}{0pt}{}{d\left(\nu \right)}{2}}\right)-T\left(H\right),$$

where $T\left(G\right)$ denotes the number of triangles (3-cycles) in a graph G (or similarly, $T\left(H\right)$ for graph H).

From Theorem 7 and

Table 1. Sum of squared degrees for some graphs in ${\mathcal{G}}_n$.

Graph	${\sum }_{\mathit{i}\in \mathit{V}\left(\mathit{G}\right)}{\mathit{d}}_{\mathit{i}}^2$
$G_{20}$	$n^3-2n^2-7n+14$
$G_{21}$	$n^3-2n^2-7n+12$
$G_{30},G_{32}$	$n^3-2n^2-11n+24$
$G_{31}$	$n^3-2n^2-11n+20$
$G_{33}$	$n^3-2n^2-11n+22$
$G_{34}$	$n^3-2n^2-11n+18$

, we easily obtain the following lemmas:

Lemma 9.

The graphs $K_n$, $G_{10}$, $G_{20}$, $G_{21}$, $G_{31}$, $G_{33}$ and $G_{34}$ are uniquely determined by their $(n-1)$-th Laplacian immanantal polynomials.

Lemma 10.

The graphs $G_{30}$ and $G_{32}$ are uniquely determined by their $(n-1)$-th Laplacian immanantal polynomials.

Proof. 

From Table 1, we have

$$\sum _{i=1}^n{d}_i^2\left(G_{30}\right)=\sum _{i=1}^n{d}_i^2\left(G_{32}\right)=n^3-2n^2-11n+24.$$

Using Corollary 1 and Lemma 8, we calculate

$$\begin{array}{ccc}\hfill c_3\left(G_{30}\right)-c_3\left(G_{32}\right)& =& {\displaystyle \frac{1}{3}}(n-1)\left(\sum _{i=1}^n{d}_i^3\left(G_{30}\right)-\sum _{i=1}^n{d}_i^3\left(G_{32}\right)\right)\hfill \\ & & -2(n-4)(T\left(G_{30}\right)-T\left(G_{32}\right))\hfill \\ & =& {\displaystyle \frac{1}{3}}(n-1)·(-6)-2(n-4)·1\hfill \\ & =& -4n+10.\hfill \end{array}$$

This implies that graphs $G_{30}$ and $G_{32}$ are uniquely determined by their $(n-1)$-th Laplacian immanantal polynomials. □

From Lemmas 9 and 10, we directly obtain the following theorem:

Theorem 8.

All graphs in the collection ${\mathcal{G}}_n$ are uniquely determined by their $(n-1)$-th Laplacian immanantal polynomials.

4. The Solution of Problem 4

We begin with the following definitions: A pendant star of a graph is a maximal subgraph consisting of all pendant edges connected to a common central vertex. By this definition, we define the degree of a pendant star as the number of its pendant vertices (or pendant edges) minus 1. Furthermore, for any graph, we define its star degree as follows: if the graph contains pendant stars, the star degree equals the sum of the degrees of all pendant stars; otherwise, the star degree is zero. In this section, we prove that when a graph G has positive star degree, the multiplicity of 1 as a root of the polynomial $d_{n-1}(x{I}_n-Q\left(G\right))$ is at least the star degree, thereby answering Problem 4. To this end, we first recall the following result on immanants of isomorphic matrices, which will be critical for our proof.

Proposition 1

([8]). Let $M_1$ and $M_2$ be two isomorphic $n\times n$ matrices and let λ be an arbitrary partition of n. Let $d_{\lambda }$ denote the immanant function associated with the irreducible character ${\chi }_{\lambda }$ of the symmetric group $S_n$. Then there exists a permutation matrix P such that

$$\begin{array}{c}\hfill d_{\lambda }\left(M_1\right)=d_{\lambda }\left(P^{-1}{M}_{2}P\right).\end{array}$$

Corollary 2.

Let $M_1$ and $M_2$ be two isomorphic $n\times n$ matrices, $d_{n-1}$ denote the $(n-1)$-th immanant. Then there exists a permutation matrix P such that

$$d_{n-1}\left(M_1\right)=d_{n-1}\left(P^{-1}{M}_{2}P\right).$$

Let C be an $n\times n$ matrix. According to Equation (2) and Corollary 2, we can conclude: If $c_n=c_{n-1}=\dots =c_{n-(p-1)}=0$, then 0 is a root of $d_{n-1}(xI-C)$ with multiplicity at least p.

Let I be the identity matrix of order n, $C=Q\left(G\right)-I$ and suppose 0 is a root of $d_{n-1}(xI-C)$ with multiplicity at least p. Then

$$\begin{array}{cc}\hfill d_{n-1}(xI-Q\left(G\right))& =d_{n-1}(xI-(C+I))\hfill \\ \hfill & =d_{n-1}((x-1)I-C)\hfill \\ \hfill & ={(x-1)}^n-c_1{(x-1)}^{n-1}+c_2{(x-1)}^{n-2}-\dots +{(-1)}^n{c}_n.\hfill \end{array}$$

Therefore, 1 is a root of $d_{n-1}(xI-Q\left(G\right))$ with multiplicity at least p.

If $A{\left(G\right)}_1$ and $A{\left(G\right)}_2$ are adjacency matrices corresponding to two different labelings of the same graph G, then there exists a permutation matrix P such that $A{\left(G\right)}_1=P^{-1}A{\left(G\right)}_{2}P$. This conclusion also applies to $Q{\left(G\right)}_1=D{\left(G\right)}_1+A{\left(G\right)}_1$ and $Q{\left(G\right)}_2=D{\left(G\right)}_2+A{\left(G\right)}_2$, where $A{\left(G\right)}_1=P^{-1}A{\left(G\right)}_{2}P$ and $D{\left(G\right)}_1=P^{-1}D{\left(G\right)}_{2}P$. By Corollary 2, the $(n-1)$-th immanantal polynomial of the matrix $Q\left(G\right)=D\left(G\right)+A\left(G\right)$ is independent of the specific labeling of the graph.

In the proof of Theorem 9, we will use $d_{n-1}(Q\left(G\right)-xI)$ instead of $d_{n-1}(xI-Q\left(G\right))$, as they have the same roots.

Theorem 9.

Let G be a simple connected graph. If the star degree of G is not zero, then the multiplicity of the root 1 in the polynomial $d_{n-1}(xI-Q\left(G\right))$ is greater than or equal to the star degree of G.

Proof. 

We consider only simple connected graphs and further assume that the number of vertices $\left|V\right(G\left)\right|\ge 2$, otherwise Theorem 9 holds trivially.

When the star degree $p>0$, the graph contains r pendant stars ($r\ge 1$), each containing $k_1,\dots ,k_r$ pendant vertices ($k_i\ge 1$), respectively, with ${\displaystyle \sum _{i=1}^r}(k_i-1)=p$. We can label the vertices as follows: label the r central vertices as $v_n,v_{n-1},\dots ,v_{n-r+1}$; label the $k_1$ pendant vertices adjacent to $v_n$ as $v_1,\dots ,v_{k_1}$, the $k_2$ vertices adjacent to $v_{n-1}$ as $v_{k_1+1},\dots ,v_{k_1+k_2}$ and so on; the remaining $n-r-{\displaystyle \sum _{i=1}^r}{k}_i$ non-pendant vertices can be arbitrarily labeled as $v_{k_1+\dots +k_r+1},\dots ,v_{n-r}$.

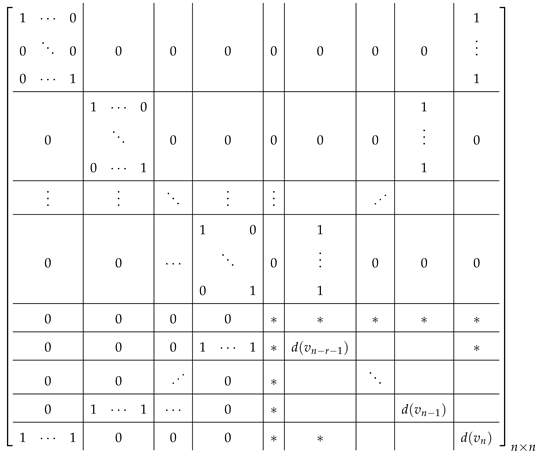
With this labeling Q(G) has the form

Under this notation, the matrix $Q\left(G\right)$ satisfies $d_j\ge 2$ for $j=k_1+k_2+\dots +k_r+1,\dots ,n$. We need to prove that the root 1 of the polynomial $d_{n-1}(Q\left(G\right)-xI)$ has multiplicity at least p, which is equivalent to showing that the root 0 of the polynomial $d_{n-1}(Q\left(G\right)-I-xI)$ has multiplicity at least p.

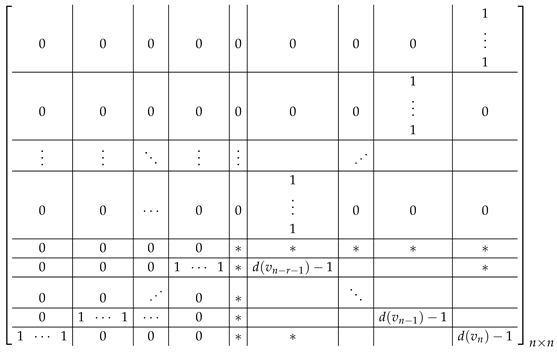
Consider the matrix $Q\left(G\right)-I$, which has the following block structure:

We first prove that 0 is a root of multiplicity at least p for $d_{n-1}(Q\left(G\right)-I-xI)$. Given $k_1+\dots +k_r=h$ with ${\displaystyle \sum _{t=1}^r}(k_t-1)=p$ (implying $h-r=p$), observe that $Q\left(G\right)-I$ and all its submatrices are nonnegative. Every principal submatrix of order $n-(p-1)$ contains a $[h-(p-1\left)\right]\times \left[\right(n-r)-(p-1\left)\right]$ zero submatrix and since $(h-p+1)+(n-r-p+1)=n-p+2=n-(p-1)+1>n-(p-1)$. Therefore, by Frobenius-König theorem, all order $n-(p-1)$ principal minors of $Q\left(G\right)-I$ have $\mathrm{per}=0$. In fact, all submatrices of order $n-(p-1)$ have an $[h-(p-1\left)\right]\times \left[\right(n-r)-(p-1\left)\right]$ zero submatrix which appears in the top left corner and thus the conditions of Frobenius and Konig’s theorem are satisfied for all these submatrices. By the Laplace expansion for permanents, we can conclude that the permanent of all submatrices of order k of $Q\left(G\right)-I$, with $p-1\le k\le n$, is zero; in particular, the permanent of all principal submatrices of order k (that is, the permanental polynomial coefficient $q_k$), $p-1\le k\le n$, is zero. From Equation (9) $(c_k\left(G\right)=(n-k-1)q_k\left(G\right)+{\sum }_{Y\in {\mathcal{S}}_{k-1,n}}\left({\sum }_{i\notin Y}d\left(v_i\right)\right)perL\left(G\right)\left[Y\right])$ and its consequences, we conclude that the $d_{n-1}$ of all principal submatrices of order k, $p-1\le k\le n$, is zero. Furthermore, the same argument shows that the coefficients $c_n,\dots ,c_{n-(p-1)}$ are also zero, establishing that 0 is a root of multiplicity at least p for $d_{n-1}(Q\left(G\right)-I-xI)$. Consequently, 1 is a root of multiplicity at least p for $d_{n-1}(Q\left(G\right)-xI)$. □

Remark 2.

When the star degree of G is zero, there exist graphs G with star degree zero such that either $d_{n-1}(Q\left(G\right)-I)=0$ or $d_{n-1}(Q\left(G\right)-I)\ne 0$. We know that when $d_{n-1}(Q\left(G\right)-I)=0$, then 1 is a root of $d_{n-1}(Q\left(G\right)-xI)$; when $d_{n-1}(Q\left(G\right)-I)\ne 0$, then 1 is not a root of $d_{n-1}(Q\left(G\right)-xI)$.

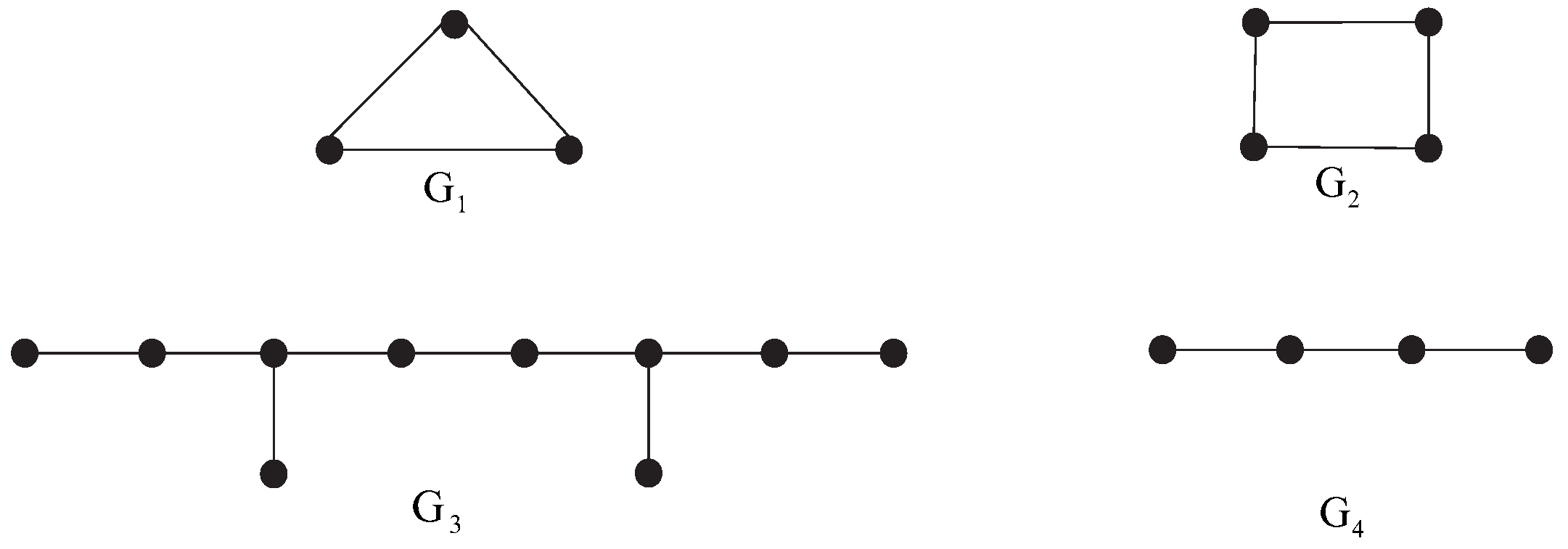
We provide four specific examples (see Figure 4) to illustrate that when the star degree of G is zero, the multiplicity of the root 1 in $d_{n-1}(xI-Q\left(G\right))$ may equal the star degree of G or may be greater than the star degree of G.

(a) There exists a graph G without pendant stars (i.e., G has no pendant vertices) and $d_{n-1}(Q\left(G\right)-I)=0$.

Example: For graph $G_1$ shown, $d_{n-1}(Q\left(G_1\right)-I)=d_2(Q\left(G_1\right)-I)=0$.

(b)   There exists a graph G without pendant stars and $d_{n-1}(Q\left(G\right)-I)\ne 0$.

Example: For graph $G_2$ shown, $d_{n-1}(Q\left(G_2\right)-I)=d_3(Q\left(G_2\right)-I)=3\ne 0$.

(c)   There exists a graph G containing pendant stars of degree zero (i.e., all pendant stars contain exactly one pendant vertex) and $d_{n-1}(Q\left(G\right)-I)=0$.

Example: For graph $G_3$ shown, $d_{n-1}(Q\left(G_3\right)-I)=d_9(Q\left(G_3\right)-I)=0$.

(d)   There exists a graph G containing pendant stars of degree zero and $d_{n-1}(Q\left(G\right)-I)\ne 0$.

Example: For graph $G_4$ shown, $d_{n-1}(Q\left(G_4\right)-I)=d_3(Q\left(G_4\right)-I)=-1\ne 0$.

5. Conclusions

In this paper, we establish fundamental properties of the $(n-1)$-th Laplacian immanantal polynomial and offer solutions to two problems: we prove that the broom graph minimizes $d_{n-1}\left(L\left(T\right)\right)$ over trees with given diameter (addressing Problem 2) and show that the multiplicity of 1 in $d_{n-1}(xI-Q\left(G\right))$ is bounded below by the star degree of G (addressing Problem 4). These results make concrete progress on Chan’s problem (Problem 1) by fully resolving the case of the $(n-1)$-th immanant and broadening the reach of Merris’s problem (Problem 3) on star degree. Furthermore, Merris [8] pointed out that studying the immanantal polynomial for determining a graph is a good question. we prove that a regular graph G is determined by its permanental polynomial if and only if it is determined by its $(n-1)$-th Laplacian immanantal polynomial and provide examples of non-regular graphs characterized by the latter.

While our work resolves the case for the $(n-1)$-th Laplacian immanantal polynomial, several challenging problems remain open. These include Chan’s problem for arbitrary partitions $\lambda$ (Problem 1), the minimization of other hook immanants $d_k$ where $k\ne n-1$, a complete resolution of Merris’s question across all hook immanants (Problem 3) and a full characterization of non-regular graphs determined by their $(n-1)$-th Laplacian immanantal polynomials. The VNP-completeness associated with these problems further underscores the depth and difficulty of this research area.