Analysis of a Retrial Queueing System Suitable for Modeling Operation of Ride-Hailing Platforms with the Dynamic Service Pricing

Abstract

Effective operation of any service system requires optimal organization of the sharing of resources between the users (customers). To this end, it is necessary to elaborate on the mechanisms that allow for the mitigation of congestion, i.e., the accumulation of many users requiring service. Due to the randomness of the user’s arrival process, congestions can occur even when an arrival rate is constant, e.g., the arrivals are described by the stationary Poisson process, which is assumed in the majority of existing papers. However, congestions can be more severe if the possibility of fluctuation of the instantaneous arrival rate exists. Such a possibility is an inherent feature of many systems and can be taken into account via the description of arrivals by the Markov arrival process (MAP). This makes the problem of congestion avoidance drastically more challenging. In many real-world systems, there exists the possibility of customer admission control via dynamic pricing. We propose a novel predictive mechanism of dynamic pricing. Decision moments coincide with the transition moments of the underlying process of the MAP. A customer may join or balk the system or postpone joining the system depending on the current cost. We illustrate the application of this mechanism in a multi-server retrial queueing model with dynamic service pricing. The behavior of the system is described by a multidimensional Markov chain with state-inhomogeneous transitions. Its stationary distribution is computed and may be used for solving the various problems of system revenue maximization via the choice of the proper pricing strategy.

1. Introduction

1.1. Importance of Ride-Hailing Platforms and Their Analysis

With ride-hailing services offering a widely accessible, cost-effective, and on-demand transportation option, people’s daily lives have undergone a significant transformation. These platforms mostly consist of smartphone apps that link passengers with nearby drivers in an easy and convenient way, making the booking and payment procedure fast and simple. Users can call a car to their precise position and arrive at their destination with a few clicks, frequently in a matter of minutes. The majority of drivers are regular people who have consented to use private vehicles for travel, converting their vehicles into makeshift taxis. Peer-to-peer models that offer more flexibility, lower pricing, and a greater variety of cars have completely changed the traditional taxi industry. Additionally, the platforms streamline the entire process by utilizing cutting-edge technologies like digital payments and Global Positioning Systems (GPS) tracking, doing away with the necessity of paying cash and guaranteeing a smooth journey. Several of these platforms have strengthened their position as all-encompassing integrated mobility solutions by adding extra services like food and grocery delivery in addition to the fundamental trip ordering functionalities. Taxi ordering platforms are anticipated to become more and more useful in people’s daily lives as the population of cities continues to increase and the need for relatively cheap and convenient transportation options rises.

Ride-hailing platforms like Uber, Lyft, Bolt, DiDi, Caocao, etc., which use dynamic pricing methods, may represent a significant shift in the transportation sector. These platforms usually raise costs during times of high demand, such as rush hour or significant events, by using real-time supply and demand data to continuously alter their fares. By encouraging more drivers to work when there is a need, this dynamic pricing system strives to guarantee consistent accessibility for clients. Clients, however, may experience a price shock as a result of this, as they can be shocked to discover that, in comparison to the regular rate, fares increase many times during peak hours. According to ride-hailing businesses, this methodology helps them better balance supply with demand fluctuations. However, critics argue that this could make transportation unaffordable for low-income people who rely on these services. The ability to quickly change prices depending on market conditions is a key competitive advantage of the taxi ordering model, but it has also generated significant debate about fairness, transparency, and access. As these platforms continue to grow and evolve, the dynamic nature of their pricing structures is likely to remain a central and controversial aspect of the taxi-ordering experience. The study of various aspects of taxi operation has become very popular in the last few years, for example, see the very extensive list of references in a recent study [1], as well as the paper [2].

Due to the high practical value of ride-hailing platforms and the necessity to properly balance the interests of taxi businesses and clients, it is important to build and analyze the adequate mathematical models of their operation. It is well known that a powerful tools for solving the problems of capacity planning, performance evaluation, optimization, and optimal control entails employing various real-world service systems with randomness of some of their elements, including transportation systems, which is the theory of queues. Due to the random duration of the inter-arrival and service times, situations in ride-hailing platforms are possible when congestion occurs, i.e., the queue length becomes long. To avoid congestion occurrence and long waiting by the users, a certain control by users entering the system (users admission control) should be applied.

1.2. Admission Control with Dynamic Pricing

In general, the users of queueing systems can be heterogeneous with respect to (i) the requirement for the service system resource (e.g., the required throughput of a channel, capacity of a vehicle or an aircraft, etc.), which may determine the distribution of service time of different types of users; (ii) requirements to the quality of service (e.g., delay-sensitive and delay-tolerant, business or economy class, elastic and inelastic, etc. users); and (iii) importance for the system, including the financial value or providing critical missions. Admission control for heterogeneous users can be effectively implemented based on various priority schemes.

Because the users of ride-hailing platforms are more or less homogeneous, in this paper, we restrict ourselves to the case of homogeneous users. In this case, a control by users admission to the system can be implemented by the service provider (server) or the users themselves.

The scenario when the decision is made by the service provider is better described in the existing literature. The server can somehow regulate the rate of the arrival flow and also directly control the admission of arriving users to the system. For example, there are some active management schemes, which suppose dropping some users based on some rule, that can be applied. Information about the history of research and the state of the art in the field of admission control at the beginning of the 21st century can be found, e.g., in surveys [3,4]. The current literature on this topic is huge. Note that the tool of Markov Decision Processes ($MDP$) is very popular in that literature.

The scenario where the decision maker is the user became very popular during the last few years. The corresponding direction in queueing theory is called strategic queues; see, e.g., [5,6,7]. In models considered within that direction, the user defines the utility of joining the system and then makes a decision to balk or join it. Variants of observable, almost unobservable, and fully unobservable queues are usually dealt with. Problems of the individual and social optimization are considered.

In this paper, having in mind applications for optimization of operation of ride-hailing platforms, we consider a mixed scenario when the final decision maker is the user, but the server can imply on the user’s decision, since the decision of the user takes into account the available information about the current price of entering the service. Even if some servers are idle at the moment of a user’s arrival, the user may conclude that the offered price of service is too high and decide not to join the system. The user can permanently leave the system or postpone his/her trial to enter the service. Decisions relating to the online change of the price are made by the server. The difference with the usual admission control, where the fate of the user is decided directly by the server, is that here the server can only push for the user’s solution desired for the server. The server can offer a low price if he is interested in accepting the user or a high price in the contrary case. But the final decision is made by the user.

The reasons for the application of dynamic pricing under a properly chosen policy of control, which is advocated, e.g., in a long-standing paper [8], are clear. The main two of them are as follows: (i) congestion avoidance via making the admitted traffic smoother by means of discouragement of arrivals during periods of congestion when there is a long queue and encouragement during periods when the servers are idle or the queue is short; (ii) receiving more revenue by the server due to the possibility of setting a high tariff during peak times and due to the possible higher throughput of the system. Such revenue is usually defined as the difference between the payment obtained by the server from the users and the charge paid to the users due to the service level agreement violation (user’s loss or waiting longer than the preassigned limit value). A discussion of the advantages of dynamic pricing over static pricing can be found again in [8]. It is worth noting that the appearance of the conditions in [8] for the application of dynamic pricing have drastically enhanced due to the development of telecommunication technologies (including mobile communications and the creation of GPS) and the digitization all spheres of human life, including the automatic account and billing of various services. Therefore, in this paper, we analyze the system with this type of pricing.

1.3. Brief Literature Review

The literature about queueing systems with dynamic pricing is already pretty extensive, and we do not pretend to present its complete survey. We cite here only a few papers. The paper [9] is often cited as the first paper devoted to the problem of finding the optimal dynamic pricing policies. In this paper, the problem of maximizing the expected reward in an $M/M/s$-type queue was considered. In order to encourage or discourage a user’s arrival, the cost of service was decreased or increased. The cost was chosen from the finite set of existing costs at all moments of the jumps in the number of users in the system. All distributions characterizing the behavior of the system were defined as exponential. A survey of the relevant literature was done. Using the theory of semi-Markov Decision Processes (semi-$MDP$), the monotonicity of the strategy of control was shown (optimal price is a non-decreasing function of the number of users in the system), and the computational algorithm for defining the optimal parameters of the strategy (thresholds) was presented.

In [10], a rental firm with two types of users, contract users and walk-in users, was considered. The former contract users were controlled by the admission policy, and the walk-in users were controlled by the pricing policy. It was demonstrated that optimal policies are monotone with respect to the system parameters. In [11], a similar model was analyzed. It was shown that when the revenue brought in by walk-in users is large, the optimal policies are not always monotonous in the number of contract users in the system. In [12], a general framework to investigate how an optimal policy varies with changes in system parameters was proposed in the context of so-called event-based dynamic programming; see, e.g., [13].

The paper [14] is one of the rare papers where the arrival and service rates were not constant. They were assumed to be bounded, periodic functions of time. Applying $MDP,$ the authors showed that, under the infinite horizon discounted and average reward optimality criteria, for each fixed time, optimal pricing and admission control strategies are nondecreasing with respect to the number of users in the system. They proposed a pointwise stationary approximation of the optimal policies and suggested a heuristic to improve the implementation of this approximation, wherein they showed its usefulness via a numerical study. In [15], an inventory model with the Markov Modulated Poisson Process ($MMPP$) flow of demands with three different pricing policies (static, depending on the state of the underlying process of the $MMPP$ and depending also on the stock) was considered. Inventory models are in some sense similar to queueing models, and the hybrid queueing–inventory models became a popular subject of research.

Different aspects of the application of dynamic pricing in the analysis of ride-hailing taxi platforms are discussed, e.g., in papers [16,17,18,19,20,21,22,23,24].

1.4. The Main Contributions of the Paper

1. Practically all previously considered models in the literature of the implementation of the dynamic control by prices assume a reactive-type control. The decision maker reacts to the change in a current queue length. Consideration of only this type of control is explained by the fact that the overwhelming majority of the existing literature suggests that the arrival flow is described by a stationary Poisson process, in which arrival moments are more or less uniformly distributed on the time axis. Queue length fluctuates if the service time variance is not large, though not essentially. The single piece of information used for admission control is the observed queue length. Therefore, to mitigate fluctuation of the queue and maximally avoid congestion, the decision maker should react to the decrease or increase in the queue length by the increase or decrease in the price of customers admission (and service).

The imposition of the assumption that the arrivals are defined by the stationary Poisson process, which is made by the vast majority of authors, is easily understandable. The nice properties of this process (which stem from the properties of the exponential distribution of inter-arrival times) allow researchers to drastically simplify the mathematical study because, during the description of the interesting real-world process by the Markovian random process, it is not necessary to account for the residual time until the arrival of the next user. This reduces the dimension of the considered process (often to one) and drastically simplifies the analysis. However, the results of such an analysis can be negligible if the coefficient of variation of the inter-arrival times is not close to 1 and (or) the coefficient of correlation of sequential inter-arrival times is not close to zero. The value of the actual loss probability or average waiting time can be several orders larger than the one computed under the assumption that the flow is described (or approximated) by the stationary Poisson process with a rate equal to the rate of the real arrival process. The difference between the actual and approximated values of the loss probability or mean waiting time is especially large for the coefficient of variation that is essentially larger than 1 and (or) the positive coefficient of correlation. Our experience dealing with different real-world systems (communication systems, contact centers, and websites) shows that the real arrival flows can have, namely, such values of the coefficients of variation and correlation. Therefore, modeling of these systems with the help of the stationary Poisson process leads to huge errors in their performance evaluation.

In this paper, we suggest a much more general, advanced, and adequate model of arrival process for many real-world systems (see, e.g., [25]). Such a process was offered by M. Neuts as a versatile point arrival process that is currently known in the literature as the Markov Arrival Process ($MAP$), see, e.g., [26,27,28,29,30,31,32,33,34]. One of the simple and tractable versions of the $MAP$ is the $MMPP$. Arrivals of the users in the $MMPP$ are defined as follows. There is a finite set of stationary Poisson processes and a continuous-time Markov chain with the finite state space, which is called the underlying process of arrivals. During the stay of the underlying process in some fixed state, the users arrive in the stationary Poisson processes with the corresponding rate. After the jump of the underlying process to another state occurs, the stationary Poisson process with the changed rate defines the arrivals. The $MMPP$ process is a good model of many real flows because it is known that the rate of generation of users’ demands in the real-world systems during the day and night definitely fluctuates depending on the exact time. For example, it may sharply increase during the morning and evening rush hours, rainy times, and periods before and after some public events like concerts, sporting events, etc. Therefore, the $MMPP$ is definitely much better suited for describing real traffic than the stationary Poisson process. It is worth mentioning here that the problem of constructing the $MAP$ and $MMPP$ based on the time stamps defining the real traffic is already well addressed in the literature; see, e.g., [35].

In this paper, we suppose that the arrivals are defined by the $MAP$ or its particular case as $MMPP$, and decisions about the dynamic change in price are not made as the reaction to the current queue length. Instead, we assume available information about the state of the underlying process of the $MAP$, and the decision moments are the epochs of the jumps of the underlying process. We suppose that the price of service should be higher during the stay of the underlying process in the states with a higher instantaneous arrival rate. Therefore, we suppose that the price of service can, e.g., increase if congestion still does not occur, but the underlying process has made the jump to the state with more intensive arrival of customers. It can be said that we use the predictive type of control. The price can be increased when the growth of the queue has not yet occurred but is anticipated to occur very soon. For example, this could occur if it starts raining or a concert finishing time approaches, but the burst of demand still does not arrive. Correspondingly, the price can be decreased when the decrease in the queue still has not occurred but should happen. The earlier (predictive) increase in the price allows the provider to receive a higher profit due to a slightly earlier start of decreasing the acceptance of users who are ready to pay only a low price and create some reserve of open cars in anticipation of the approaching arrival of users who can pay a higher price. Correspondingly, soon after the end of a concert or football game, the server can reduce the price (reduce surge multiple) even if the high load has not disappeared. This can allow for the avoidance of possible starvation of open cars when the rate of the user’s demands drops to a low level.

Thus, the first important contribution of the paper consists of the more adequate account of the nature of real flows, offering and analyzing another principle of the dynamic price control implementation than the one used in the literature.

2. The second important contribution of this paper consists of the consideration of the possibility to postpone the decision by a user about joining or balking the system via the consideration of a retrial phenomenon. The importance of accounting for the possibility of customer retrials is evident from the point of view of the applications to modeling ride-hailing platforms. For example, if the offered price of the taxi seems too high to the user immediately after the end of a concert or a game, the user can visit a cafe around the concert hall to drink a cup of coffee and then try to call a taxi later on when the demand of users (and the price of the service) drops to the desired level.

The proposed retrial queueing model is amenable to analytical and numerical study. This study has used, as background, the results of analysis of queues with the $MAP$ arrival process; see, e.g., the book [29] and paper [36]. Also, this analysis uses the experience of analyzing retrial queues and queues with impatient users. Well-known surveys of the research in retrial queues are given, e.g., in the books [37,38] and papers [39,40,41]. Results of the analysis of the multi-server retrial queues with the $MAP$ are presented, in particular, in the papers [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62].

1.5. Possible Applications

The analyzed queueing model was mainly oriented to the use for description and optimization of the operation of ride-hailing taxi platforms. Among the other promising applications of the proposed model and dynamic pricing mechanism, part of which is listed in [8], we can mention that the suggested model can also be suitable for the description and optimization of operation and pricing in different transportation networks (aviation, railway, cargo, maritime, bus, car-sharing, etc.), various food and goods delivery systems and hypermarkets, entertainment places, etc., where the cost of purchase may be reduced via the provision of promotions and discounts during low demand time intervals. Another potential application of the proposed model, which is actively discussed in the literature, is control by electric vehicle charging stations; see, e.g., [63,64].

1.6. Justification of the Assumptions About Parameters of the System and Their Availability

It is worth noting the following:

•

Congestions in the stationary operating queueing system with reliable servers mainly occur due to the probability of randomly occurring long durations of service or bursts in arrivals. It is clear that the $MAP$, which is characterized by the jumping instantaneous arrival rate, much better fits to reflect bursts than the stationary Poisson arrival process assumed in the overwhelming majority of the existing papers in the field of dynamic pricing.

•

Describing possible applications of the model, we focused on $MMPP$ as the most easily tractable case of the $MAP.$ However, we present analysis of the model under the general assumptions about the $MAP.$ As another easily tractable case of the $MAP$ beyond the $MMPP$, we explore the cases when the permanent arrival rate takes place during the intervals having phase-type ($PH$) distribution or the inter-arrival times within periods, with the fixed average instantaneous rate having a $PH$ distribution.

•

As already mentioned, the problem of constructing the matrices defining the $MAP$ based on the observation of time stamps of real traffic is already well studied in the literature. Additionally, even without having more exact information, the service provider can suppose the shape of the $MAP$ flow arriving today based on the available information about its shape during the corresponding time intervals yesterday or on the same day, e.g., Monday, of the previous week. Adjusting the model of the flow to special events like concerts, games, rain, heat, etc., as well as weekends or holidays, can also be easily done.

•

Information about the value of the probability that the user will postpone or cancel the journey under different states of the underlying process and values of surge multiples is easily accessible from the database of the service provider as the frequency of occurrence of the corresponding events. Note that these events are continuously monitored and registered by the platform of the service provider. In many ride-hailing applications, for the user’s convenience, the system automatically gives information about the current values of multiple surges. The color in the corresponding window of the screen of the user’s smartphone varies from green in the case of a cheap tariff through yellow to red in the case of an expensive tariff. The final decision of a user to start or postpone a journey is also registered.

•

Although here we successfully get rid of the non-realistic assumption that inter-arrival times have the exponential distribution imposed in the majority of known papers, we assume that service times have an exponential distribution. This assumption seems quite restrictive, although it is quite common in the existing research. It is clear that it would be better to relax this assumption and suppose that service time has a more general $PH$ distribution; see [29,32,65,66,67]. This can be theoretically easily done at the expense of introducing additional components in the construction of the Markov chain describing the dynamics of the system. This generalization does not lead to more mathematical difficulties in analysis. However, this generalization essentially increases the size of the blocks of the generator of the chain.

Let W be the number of possible states of the underlying process of the arrival process and N be the number of servers. Then, the size of blocks of the generator of the chain in the case of the exponential service time distribution is $W(N+1).$ Now, let the service time distribution be of $PH$-type and M be the number of possible states of the underlying process of the $PH$ distribution. The size of blocks of the generator of the chain describing the behavior of the system depends on the selection of the random process that defines simultaneous service of customers in the servers.

If this random process is defined by states of the underlying process of the $PH$ distribution of the service time in each busy server, the size of blocks of the generator of the chain describing behavior of the system increases from $W(N+1),$ which we had in the case of the exponential service time distribution, to $W{\displaystyle \frac{M^{N+1}-1}{M-1}}.$ Even in the case that $M=2,$ this number that becomes equal to $W(2^{N+1}-1)$ can be huge when N is large. Note that consideration of the $PH$ distribution with $M=2$ allows us to fit exactly or approximately the variance in the service time distribution.

If, following [68], this random process is defined as the number of servers currently having the corresponding phases of the underlying process, the size increases from $W(N+1),$ which we had in the case of the exponential service time distribution, to $W\left({\displaystyle \genfrac{}{}{0pt}{}{N+M}{M}}\right).$ If $M=2,$ this number is equal to $W{\displaystyle \frac{(N+2)(N+1)}{2}}.$ For large N, this number is also very large.

Because in numerical examples we intend to use a large number $N,N=200,$ of servers (cars in a potential application for dynamically fixing the offered price by a taxi provider in a small town), we decided to restrict ourselves to the case of exponential distribution of service times.

Note that the assumption about the exponential distribution of service time is not as restrictive here as it may seem at first glance. Experience of the calculation of various performance characteristics of multi-server queues with $BMAP$ or $MAP$ arrival flow and $PH$ distribution of service time, see, e.g., [60,69,70], shows the following. In contrast to single-server queues, where the variance of service time has a significant impact, in multi-server queues, only the mean service rate matters when the number of servers is large. Higher moments of the distribution of service time, including its variance, have quite a small impact. Therefore, the use of exponential distribution of service time is well justified in our model. In constrast, as was already mentioned above, the use of exponential distribution of inter-arrival times may lead to huge errors and is not appropriate.

1.7. Structure of Presentation

The rest of the paper is organized as follows. Application of the idea of linking the predictive dynamic pricing in ride-hailing systems to the state of the underlying process of arrivals is demonstrated via the consideration of the multi-server retrial queueing system with the $MAP$ arrival process. Generally speaking, the price of service is higher when arrivals are more intensive and is lower when arrivals are rare. The mathematical model of this queueing system is described in detail in Section 2. A multidimensional stochastic process describing the behavior of the considered queueing system is introduced in Section 3. Its generator is obtained there. The sufficient conditions for the ergodicity and non-ergodicity of this process are presented, and the computation of its steady-state distribution is discussed briefly in Section 4. Formulas for the calculation of various performance characteristics of the system in terms of the computed vectors of the stationary probabilities are presented and briefly explained in Section 5. Numerical illustrations, including consideration of optimization problems, are given in Section 6. Section 7 concludes the paper.

2. Mathematical Model

We consider a retrial queueing system that models the operation of a fragment of a ride-hailing system. The system has N identical servers and no buffer. Its scheme is depicted in Figure 1. The server corresponds to a vehicle that can provide service to the users (clients, passengers, etc.) residing in the fragment of the system under study.

Users enter the system according to the $MAP$; for more information, see, for example, [26,27,28,29,30,31,32,33,34]. The $MAP$ is an essential generalization of the well-known stationary Poisson process in which inter-arrival times have an exponential distribution with the fixed parameter. Customers’ arrivals in the $MAP$ are possible only at the moments of the jumps of the so-called underlying process of arrivals. This process is an irreducible continuous-time Markov chain ($MC$) ${\nu }_t,t\ge 0,$ with the finite state space $\{1,2,...,W\}.$ The generator, D, of this $MC$ is represented as the sum of two square matrices $D_0$ and $D_1$ of size $W.$ Entries of the non-negative matrix $D_1$ contain the rates of transitions of the $MC$ ${\nu }_t$ within its state space that are accompanied by users’ arrivals. The diagonal entries of the matrix $D_0$ are negative. The modulus of an entry defines the rate of the exit of $MC$ from the corresponding state. The non-diagonal entries of the matrix $D_0$ are non-negative and define the rates of transitions of the $MC$ ${\nu }_t$ within its state space that are not accompanied by users arrival. The stationary Poisson process is the particular case of the $MAP$ when $W=1$, and the matrices $D_0$ and $D_1$ become scalars.

The average intensity $\lambda$ of the arrival of users, who would like to order a taxi, to the fragment of the ride-hailing system under study is determined by the formula $\lambda =\mathit{\theta }{D}_1\mathbf{e},$ where $\mathit{\theta }=({\theta }_1,\dots ,{\theta }_W)$ is the row vector of stationary probabilities of the $MC$ ${\nu }_t.$ This vector is the only solution to the system $\mathit{\theta }D=\mathbf{0},\mathit{\theta }\mathbf{e}=1.$ Here, $\mathbf{e}$ is an appropriately sized column vector consisting of ones, and $\mathbf{0}$ is a row vector consisting of zeros.

We denote by ${\lambda }_{\nu },$ $\nu =\overline{1,W},$ the value ${\lambda }_{\nu }={\left(D_1\right)}_{\nu }\mathbf{e}$ of the average arrival rate in the state $\nu .$ Here, ${\left(D_1\right)}_{\nu }$ is the $\nu$th row of the matrix $D_1.$ Notation like $\nu =\overline{1,W}$ means that the variable $\nu$ admits the values from the set $\{1,2,...,W\}.$

Without loss of generality, we assume that the states of the process ${\nu }_t$ are enumerated in the ascending order of the rates ${\lambda }_{\nu },$ i.e., ${\lambda }_1<{\lambda }_2<\cdots <{\lambda }_W.$

An arriving user, who sees the idle servers (open cars), may decide, independently of each other, whether to start the service, balk the system, or postpone service depending on the current value of the price of the service offered by the system (via the mobile ride-hailing application). This price is defined, besides the length of the suggested journey, by the basic tariff and the multiplying factor (surge multiple). The multiplying factor may dynamically vary: during the time intervals, when the demand for service is higher, the multiplying factor is larger.

It is usually assumed in the literature that the value of the multiplying factor, reflecting the demand for service in the system, is defined by the current value of the queue length. This is absolutely reasonable in the case of the constant user arrival rate. Here, to account for the nature of real flows in real-world systems, we suggest that the arrival process of users is defined by the $MAP$ or its special case, $MMPP,$ in which the matrix $D_1$ is the diagonal matrix with the diagonal entries equal to the users arrival rate during the interval with the fixed state of the underlying process. An instantaneous arrival rate is piecewise-constant and may change at the moments of jumps in the underlying process of the $MMPP.$ Therefore, in contrast to other models considered in the literature, we assume that the offered price of the service depends on the current value of the underlying process, not on the length of the queue. It is obvious that the current length of the queue significantly depends on the current state of the underlying process of the $MAP.$ Generally speaking, the queue has to be longer when users intensively arrive. However, the increase in the queue basically occurs with some delay after the underlying process jumps to the state with a larger instantaneous arrival rate. Correspondingly, the decrease in the queue occurs with a delay after the underlying process jumps to the state with a smaller instantaneous arrival rate. Thus, the transition of the underlying process is the primary factor. The change in queue length is, in general, the consequence of this transition. This explains our choice of the moments when the dynamic price can be changed.

We denote the multiplying factor for a user arriving during the stay of the underlying process ${\nu }_t$ in the state $\nu$ by $c_{\nu },\nu =\overline{1,W}.$ The multiplying factors are ordered as $0\le c_1\le c_2\le \cdots \le c_W.$ Some multiplying factors can be less than 1 to encourage users to receive service when the arrival rate to the system is low. Some others can be quite large to encourage some low budget users to voluntarily balk the system without receiving service.

A user entering the system when all servers are busy (i.e., there are no open cars) with the probability $p_1$ decides to postpone their travel and will make attempts to obtain service later (it is said that he/she goes to the orbit). With the probability $1-p_1,$ he/she leaves the system forever (decides to cancel the trip or use an alternative kind of transport).

A user entering the system when at least one server is idle receives in the application information about the offered price and decides whether the price is suitable for him/her. We denote as $q_{\nu }=q_{\nu }\left(c_{\nu }\right),\nu =\overline{1,W},$ the probability that this price is suitable for the user if the current state of the underlying process ${\nu }_t$ is $\nu$. If the user decides that the offered price is suitable, he/she starts the service. Otherwise, with the probability $1-q_{\nu }$, he/she does not start service. He/she leaves the system permanently with the probability $1-p_1.$ With the probability $p_1,$ the user goes to the orbit and retries for service later.

The mechanism of user retrial is supposed to be as follows. If at an arbitrary moment the number of users that plan to make the retrials (stay in the orbit) is equal to $i,i>0,$ then the total rate of retrials is equal to ${\alpha }_i$ such that $\underset{i\to \infty }{lim}{\alpha }_i=\infty ,{\alpha }_0=0.$ The most popular dependence of ${\alpha }_i$ on i is of the form ${\alpha }_i=i\alpha$, where $\alpha$ is interpreted as an individual retrial rate. An attempt is considered successful if at least one server is idle and the offered service price satisfies the user. The probability of the last event is also given by $q_{\nu },\nu =\overline{1,W}.$ If the attempt is unsuccessful, the user returns to the orbit with the probability $p_2,0\le p_2\le 1,$ and with the probability $1-p_2$ leaves the system permanently.

The service (journey) time of a user has an exponential distribution. We assume that the parameter of the service time distribution ${\mu }_{\nu }$ also depends on the current state $\nu$ of the underlying arrival process. For example, in a possible application for modeling a taxi service, the time of day, weather conditions, and occurrence of traffic jams have an impact not only on the rate of customers arrival but also on the trip duration. The average duration of the journey is equal to ${\mu }_{\nu }^{-1},\nu =\overline{1,W}.$

The final aim of the study is to determine the optimal values of the multiplying factors $c_{\nu },\nu =\overline{1,W},$ that should be chosen by the system manager at which the system’s revenue, defined below, would be at its maximum. To this end, we have to have the possibility to compute the main stationary performance characteristics of the system for any admissible set of parameters of the system and the multiplying factors. To obtain such a possibility, in the next sections, we describe the behavior of the system by a suitably constructed multidimensional $MC$ and analyze this $MC.$

For the reader’s convenience, we present

Table 1. Main notations.

N	the number of servers
${\nu }_t,t\ge 0$	the underlying process of the $MAP$
$D_0$ and $D_1$	the matrices that define the $MAP$
W	the state space dimension of the underlying process of the $MAP$
$\mathit{\theta }$	the row vector of stationary probabilities of the $MC$ ${\nu }_t$
$\lambda$	the average intensity of users arrival
${\lambda }_{\nu },$$\nu =\overline{1,W}$	the average arrival rate in the state $\nu$
$c_{\nu },\nu =\overline{1,W}$	the price multiplying factor for a user arriving during the stay of the underlying process ${\nu }_t$ in the state $\nu$
$p_1$	the probability that a user goes to the orbit when all servers are busy
$q_{\nu },\nu =\overline{1,W}$	the probability that the price is suitable for the user if the current state of the underlying process ${\nu }_t$ is $\nu$
${\alpha }_i,i>0$	the total rate of retrials if at an arbitrary moment the number of users in the orbit is equal to i
$p_2$	the probability that the user returns to the orbit if the attempt is unsuccessful
${\mu }_{\nu },\nu =\overline{1,W}$	the average service rate if the current state of the underlying process ${\nu }_t$ is $\nu$
${\mu }_{\nu }^{-1},\nu =\overline{1,W}$	the average duration of the journey if the current state of the underlying process ${\nu }_t$ is $\nu$

where the denotations used for the parameters of the model are summarized.

3. Process of the System States

Let

$i_t,$ $i_t\ge 0,$ be the number of users in the orbit,

$n_t,$ $n_t=\overline{0,N},$ be the number of busy servers, and

${\nu }_t,{\nu }_t=\overline{1,W},$ be the state of the underlying process of the $MAP$ at time $t,t\ge 0.$

The behavior of the system under study is described by the process ${\xi }_t=\{i_t,n_t,{\nu }_t\},$ $t\ge 0,$ that is a regular, irreducible, continuous-time $MC$.

Let Q be the generator of the $MC$ ${\xi }_t,t\ge 0.$ It is the matrix with the entries $Q_{(i,n,\nu ),(j,n^{\prime },{\nu }^{\prime })},i,j\ge 0,n,n^{\prime }=\overline{0,N},\nu ,{\nu }^{\prime }=\overline{1,W},$ that have the following meaning. The number $Q_{(i,n,\nu ),(i,n,\nu )}$ is negative. Its module is equal to the rate of the exit of the process ${\xi }_t$ from the state $(i,n,\nu ).$ The entry $Q_{(i,n,\nu ),(j,n^{\prime },{\nu }^{\prime })}$, where at least one of the relations $i\ne j,n^{\prime }\ne n,{\nu }^{\prime }\ne \nu$ holds well, defines the transition rate of the $MC$ ${\xi }_t$ from the state $(i,n,\nu )$ to the state $(j,n^{\prime },{\nu }^{\prime }).$

To simplify denotations, along with the standard notion of the state $(i,n,\nu )$ of the $MC$ ${\xi }_t,$ let us introduce the notion of the macro-state $(i,n)$ as the set $(i,n)=\left(\right(i,n,1),(i,n,2),\dots ,(i,n,W)$ and the notion of the level i of the $MC$ ${\xi }_t$ as the set of macro-states $\left(\right(i,0),(i,1),\dots ,(i,N\left)\right),i\ge 0.$

Correspondingly, introduce the matrix $Q_{i,j}^{(n,n^{\prime })}={\left(Q_{(i,n,\nu ),(j,n^{\prime },{\nu }^{\prime })}\right)}_{\nu ,{\nu }^{\prime }=\overline{1,W}}$ of transition rates between the macro-states $(i,n)$ and $(j,n^{\prime })$ and the matrix $Q_{i,j}$ consisting of the blocks $Q_{i,j}^{(n,n^{\prime })},n,n^{\prime }=\overline{0,N}.$ The matrix $Q_{i,j}$ defines transition rates from the states that belong to the level i and the states that belong to the level $j.$ The generator Q is the infinite-size matrix consisting of the blocks $Q_{i,j},i,j\ge 0.$

Theorem 1.

The generator $Q={\left(Q_{i,j}\right)}_{i,j\ge 0}$ has the following block-tridiagonal structure:

$$Q=\left(\begin{array}{cccccc}{Q}_{0,0}& Q_{0,1}& O& O& O& \dots \\ Q_{1,0}& Q_{1,1}& Q_{1,2}& O& O& \dots \\ O& Q_{2,1}& Q_{2,2}& Q_{2,3}& O& \dots \\ O& O& Q_{3,2}& Q_{3,3}& Q_{3,4}& \dots \\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right).$$

The non-zero blocks $Q_{i,j},|i-j|\le 1,$ have the following form.

The matrix $Q_{i,i}$ has the block-tri-diagonal structure

$$Q_{i,i}=\left(\begin{array}{ccccccc}{Q}_{i,i}^{(0,0)}& Q_{i,i}^{(0,1)}& O& O& \dots & O& O\\ Q_{i,i}^{(1,0)}& Q_{i,i}^{(1,1)}& Q_{i,i}^{(1,2)}& O& \dots & O& O\\ O& Q_{i,i}^{(2,1)}& Q_{i,i}^{(2,2)}& Q_{i,i}^{(2,3)}& \dots & O& O\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ O& O& O& O& \dots & Q_{i,i}^{(N-1,N-1)}& Q_{i,i}^{(N-1,N)}\\ O& O& O& O& \dots & Q_{i,i}^{(N,N-1)}& Q_{i,i}^{(N,N)}\end{array}\right),i\ge 0,$$

(1)

where the diagonal blocks $Q_{i,i}^{(n,n)}$ have the form

$$Q_{i,i}^{(n,n)}=D_0+(1-p_1)D_1(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\})-n\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\}-$$

$$-{\alpha }_i{I}_W+p_2{\alpha }_i(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\}),n=\overline{0,N-1},$$

$$Q_{i,i}^{(N,N)}=D_0+(1-p_1)D_1-N\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\}-(1-p_2){\alpha }_i{I}_W,$$

the up-diagonal blocks $Q_{i,i}^{(n,n+1)}$ have the form

$$Q_{i,i}^{(n,n+1)}=\mathrm{diag}\{q_1,q_2,\dots ,q_W\}{D}_1,n=\overline{0,N-1},$$

and the sub-diagonal blocks $Q_{i,i}^{(n,n-1)}$ have the form

$$Q_{i,i}^{(n,n-1)}=n\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\},n=\overline{1,N}.$$

The matrix $Q_{i,i+1}$ is the block-diagonal of the form

$$Q_{i,i+1}=\mathrm{diag}\{Q_{i,i+1}^{(n,n)},n=\overline{0,N}\},i\ge 0,$$

(2)

where the matrices $Q_{i,i+1}^{(n,n)}$ are given by the formula

$$Q_{i,i+1}^{(n,n)}=p_1(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\})D_1,n=\overline{0,N-1},$$

$$Q_{i,i+1}^{(N,N)}=p_1{D}_1,i\ge 0.$$

The matrix $Q_{i,i-1}$ is the block-two-diagonal of the form

$$Q_{i,i-1}=\left(\begin{array}{ccccccc}{Q}_{i,i-1}^{(0,0)}& Q_{i,i-1}^{(0,1)}& O& \dots & O& O& O\\ O& Q_{i,i-1}^{(1,1)}& Q_{i,i-1}^{(1,2)}& \dots & O& O& O\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ O& O& O& \dots & O& Q_{i,i-1}^{(N-1,N-1)}& Q_{i,i-1}^{(N-1,N)}\\ O& O& O& \dots & O& O& Q_{i,i-1}^{(N,N)}\end{array}\right),i\ge 1,$$

(3)

where the diagonal and up-diagonal blocks are given by the formulas

$$Q_{i,i-1}^{(n,n)}=(1-p_2){\alpha }_i(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\}),n=\overline{0,N-1},$$

$$Q_{i,i-1}^{(N,N)}=(1-p_2){\alpha }_i{I}_W,$$

$$Q_{i,i-1}^{(n,n+1)}={\alpha }_i\mathrm{diag}\{q_1,q_2,\dots ,q_W\},n=\overline{1,N-1}.$$

Here,

$I_W$ is the identity matrix of size $W,$

O is the zero matrix of size defined from the context, and

the notation $\mathrm{diag}\{q_1,q_2,\dots ,q_W\}$ means the diagonal matrix with the diagonal entries given in the brackets.

Proof. 

The proof of Theorem 1 is routinely implemented by means of careful analysis of intensities of various transitions of the $MC$ ${\xi }_t$ during the interval of infinitesimal length and rewriting the intensities of these transitions in block matrix form.

Since no more than one user can enter or leave the orbit during an interval of infinitesimal length, the matrices $Q_{i,j},i,j\ge 0$ are zero matrices for all $i,j$ such that $|i-j|>1.$ The blocks $Q_{i,j},|i-j|\le 1,$ consist of the matrices ${\left(Q_{i,j}\right)}_{n,n^{\prime }}$ of the transition rates of the $MC$ ${\xi }_t$ from the macro-state $(i,n)$ to the macro-state $(j,n^{\prime })$, where $n,n^{\prime }=\overline{0,N}$.

The blocks $Q_{i,i},i\ge 0,$ have block-tri-diagonal structure (1). This stems from the fact that the transition from the macro-state $(i,n)$ to the macro-state $(i,n^{\prime })$ for $n,n^{\prime },|n-n^{\prime }|>1$ is not possible because not more than one user can start or finish service during an interval of infinitesimal length.

The diagonal entries of the diagonal blocks $Q_{i,i}^{(n,n)},n=\overline{0,N},$ of the matrices $Q_{i,i}$ are negative. Their moduli define the intensities of leaving the corresponding state of $MC$ ${\xi }_t$. The events that lead to the change of the $MC$ state are the following:

(a) The underlying process of the $MAP$ changes its states except in the cases when the underlying process of the $MAP$ transits from one state to the same state with a user’s arrival, and this user leaves the system permanently (he/she does not move to the orbit). In the latter case, the exit from the state does not occur. Up to the sign, the intensities of these events are defined by the diagonal entries of the matrix $D_0+(1-p_1)D_1(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\})$ if $n=\overline{0,N-1},$ and by the diagonal entries of the matrix $D_0+(1-p_1)D_1$ if $n=N$ (i.e., all servers are busy).

(b) A service completion occurs on one of the busy servers. The intensities of this event are defined by the entries of the matrix $n\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\},n=\overline{1,N}.$

(c) A user leaves the orbit (starts service or leaves the system forever). The intensities of these events are defined, up to the sign, by the entries of the matrix $-{\alpha }_i{I}_W+p_2{\alpha }_i(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\})$ if $n=\overline{0,N-1},$ and by the entries of the matrix $-(1-p_2){\alpha }_i{I}_W$ if $n=N.$

The non-diagonal entries of the diagonal blocks $Q_{i,i}^{(n,n)}$ of the matrices $Q_{i,i}$ are non-negative. They define the $MC$ transition rates that do not lead to the change of the components i and n. These transitions can occur if the $MAP$ underlying process makes a transition without the generation of a user or changes its state with the generation of a user that leaves the system upon arrival. The intensities of such events are given by the corresponding non-diagonal entries of the matrix $D_0+(1-p_1)D_1(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\}).$

The blocks $Q_{i,i}^{(n,n+1)},n=\overline{0,N-1},$ of the matrices $Q_{i,i}$ define the intensities of the event that leads to the increase in the number of busy servers by one, assuming that the number of users in the orbit does not change. This happens if an arriving user joins the service. In this case, the corresponding intensities are defined by the matrix $\mathrm{diag}\{q_1,q_2,\dots ,q_W\}{D}_1.$

The blocks $Q_{i,i}^{(n,n-1)},n=\overline{1,N},$ of the matrices $Q_{i,i}$ define the intensities of the event that leads to the decrease in the number of busy servers by one, provided that the number of users in the orbit does not change. This can happen in the case of a service completion in one of the busy servers. The matrix $n\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\}$ defines the corresponding intensities.

The blocks $Q_{i,i+1},i\ge 0,$ have form (2) and define the intensity of transitions that lead to an increase in the number of users in the orbit by one. They consist only of the non-zero diagonal blocks $Q_{i,i+1}^{(n,n)}$ due to the fact that an increase in the number of users in the orbit cannot lead to a change in the number of busy servers. The number of users in the orbit increases by one only when a new user joins it. The intensities of this event are defined by the matrix $p_1{D}_1$ if a new user arrives at the system when all servers are busy, and he/she decides to join the orbit or by the matrix $p_1(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\})D_1$ if an arriving user finds a free server but decides to postpone service due to the price dissatisfaction.

The blocks $Q_{i,i-1},i\ge 0,$ define the intensity of transitions that lead to a decrease in the number of users in the orbit by one and have structure (3). The decrease in the number of users in the orbit can result in the following:

(a) It can lead to an increase in the number of busy servers in the system (a user from the orbit makes a successful attempt and starts service). The corresponding blocks $Q_{i,i-1}^{(n,n+1)}$ are defined by the matrices ${\alpha }_i\mathrm{diag}\{q_1,q_2,\dots ,q_W\},n=\overline{1,N-1};$

(b) It may not change the number of busy servers in the system. The intensities of this event are defined by the blocks $Q_{i,i-1}^{(n,n)}$ that are given by the matrix $(1-p_2){\alpha }_i{I}_W$ if a user from the orbit makes an unsuccessful attempt to join service because all servers are busy and he/she leaves the system forever, as well as by the matrices $(1-p_2){\alpha }_i(I_W-\mathrm{diag}\{q_1,q_2,\dots ,q_W\}),n=\overline{0,N-1},$ if a user from the orbit finds a free server but decides to leave the system due to price dissatisfaction. □

4. Ergodicity Condition and Computation of Stationary Distribution

An important step in the analysis of any $MC$ with infinite state space is the derivation of conditions or criterion of existence of the stationary distribution of this $MC$ (ergodicity and non-ergodicity conditions). Such conditions for the $MC$ ${\xi }_t$ are given by the following statement.

Theorem 2.

If $p_2<1$ (the users in the orbit are not absolutely persistent), the $MC$ ${\xi }_t$ is ergodic for all system parameters.

If $p_2=1$, the sufficient condition for the ergodicity of the $MC$ ${\xi }_t$ is the fulfillment of the inequality

$$p_1\lambda <N\sum _{\nu =1}^W{\theta }_{\nu }{\mu }_{\nu }$$

(4)

and the sufficient condition for the non-ergodicity of the $MC$ ${\xi }_t$ is the fulfillment of the inequality

$$p_1\lambda >N\sum _{\nu =1}^W{\theta }_{\nu }{\mu }_{\nu }.$$

(5)

Proof. 

It is possible to check that the $MC$ ${\xi }_t$ belongs to the class of asymptotically Quasi-Toeplitz Markov chains ($AQTMC$), see [36]. In [36], wherein the ergodicity condition of the $AQTMC$ is expressed in terms of the matrices

$$Y_0=\underset{i\to \infty }{lim}{R}_i^{-1}{Q}_{i,i-1},Y_1=\underset{i\to \infty }{lim}{R}_i^{-1}{Q}_{i,i}+I,Y_2=\underset{i\to \infty }{lim}{R}_i^{-1}{Q}_{i,i+1},$$

where $R_i$ is a diagonal matrix with diagonal entries given by the modules of the corresponding entries of the matrix $Q_{i,i},i\ge 0.$ Then, according to the work of [36], the sufficient condition for the ergodicity of $AQTMC$s is the fulfillment of the inequality

$$\mathbf{y}{Y}_0\mathbf{e}>\mathbf{y}{Y}_2\mathbf{e}$$

(6)

and the sufficient condition for the non-ergodicity of the $AQTMC$s is the fulfillment of the inequality

$$\mathbf{y}{Y}_0\mathbf{e}<\mathbf{y}{Y}_2\mathbf{e}$$

(7)

where the vector $\mathbf{y}$ is the single solution of the equations

$$\mathbf{y}(Y_0+Y_1+Y_2)=\mathbf{y},\mathbf{y}\mathbf{e}=1.$$

(8)

First, we suppose that $p_2<1.$ In this case, it can be seen that for the system under consideration,

$$Y_0=\left(\begin{array}{ccccccc}\mathrm{\Phi }& \mathrm{\Psi }& O& O& \dots & O& O\\ O& \mathrm{\Phi }& \mathrm{\Psi }& O& \dots & O& O\\ O& O& \mathrm{\Phi }& \mathrm{\Psi }& \dots & O& O\\ ⋮& ⋮& ⋮& \ddots & \ddots & ⋮& ⋮\\ O& O& O& O& \dots & \mathrm{\Phi }& \mathrm{\Psi }\\ O& O& O& O& \dots & O& I_W\end{array}\right),Y_1=O,Y_2=O,$$

where

$$\mathrm{\Phi }=\mathrm{diag}\{{\displaystyle \frac{(1-p_2)(1-q_{\nu })}{1-p_2(1-q_{\nu })}},\nu =\overline{1,W}\},\mathrm{\Psi }=\mathrm{diag}\{{\displaystyle \frac{q_{\nu }}{1-p_2(1-q_{\nu })}},\nu =\overline{1,W}\}.$$

Taking into account this explicit form of the matrices $Y_0,Y_1,$ and $Y_2$ for the $MC$ ${\xi }_t$, it can be verified that the matrix $Y_0$ is a stochastic matrix, and inequality (7) takes the form $\mathbf{y}{Y}_0\mathbf{e}>0,$ where the vector $\mathbf{y}$ is a stochastic vector. So, it is obvious that inequality (7) is fulfilled for any system parameters.

Next, consider the case when $p_2=1.$ Then, the square matrices $Y_0,Y_1,$ and $Y_2$ of size $(N+1)W$ have the following forms:

$$Y_0=\left(\begin{array}{ccccccc}{O}_W& I_W& O& O& \dots & O& O\\ O& O& I_W& O& \dots & O& O\\ O& O& O& I_W& \dots & O& O\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ O& O& O& O& \dots & O& I_W\\ O& O& O& O& \dots & O& O_W\end{array}\right),$$

$$Y_1=\left(\begin{array}{cccccc}O& O& \dots & O& O& O\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ O& O& \dots & O& O& O\\ O& O& \dots & O& \mathrm{\Delta }& \mathrm{\Gamma }\end{array}\right),Y_2=\left(\begin{array}{cc}{O}_{NW}& O_{NW,W}\\ O_{W,NW}& p_1{\mathrm{\Omega }}^{-1}{D}_1\end{array}\right)$$

where

$$\mathrm{\Delta }={\mathrm{\Omega }}^{-1}N\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\},$$

$$\mathrm{\Gamma }={\mathrm{\Omega }}^{-1}(D_0+(1-p_1)D_1-N\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\})+I_W,$$

$$\mathrm{\Omega }={\mathrm{\Lambda }}_0+(1-p_1){\mathrm{\Lambda }}_1+N\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\}.$$

Here, ${\mathrm{\Lambda }}_0$ and ${\mathrm{\Lambda }}_1$ are the diagonal matrices with diagonal entries given by the modules of the corresponding entries of the matrices $-D_0$ and $D_1$, respectively.

Since the matrix $Y_0+Y_1+Y_2$ is reducible, based on the results from [36], ergodicity condition (6) can be rewritten as

$$\mathbf{x}{X}_0\mathbf{e}>\mathbf{x}{X}_2\mathbf{e}$$

(9)

where the vector $\mathbf{x}$ is the single solution of the equations

$$\mathbf{x}(X_0+X_1+X_2)=\mathbf{x},\mathbf{x}\mathbf{e}=1.$$

(10)

Here, the matrices $X_0,X_1$ and $X_2$ have the following forms:

$$X_0=\left(\begin{array}{cc}{O}_W& I_W\\ O_W& O_W\end{array}\right),X_1=\left(\begin{array}{cc}{O}_W& O_W\\ \mathrm{\Delta }& \mathrm{\Gamma }\end{array}\right),X_2=\left(\begin{array}{cc}{O}_W& O_W\\ O_W& p_1{\mathrm{\Omega }}^{-1}{D}_1\end{array}\right).$$

Substituting the vector $\mathbf{x}$ in the form $\mathbf{x}=({\mathbf{x}}^{\left(0\right)},{\mathbf{x}}^{\left(1\right)})$ into (10), we obtain that

$${\mathbf{x}}^{\left(0\right)}=N{\mathbf{x}}^{\left(1\right)}{\mathrm{\Omega }}^{-1}\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\}.$$

Hence, inequality (9) will be written in the form

$$N{\mathbf{x}}^{\left(1\right)}{\mathrm{\Omega }}^{-1}\mathrm{diag}\{{\mu }_1,{\mu }_2,\dots ,{\mu }_W\}\mathbf{e}>p_1{\mathbf{x}}^{\left(1\right)}{\mathrm{\Omega }}^{-1}{D}_1\mathbf{e},$$

(11)

and it follows from system (10) that

$${\mathbf{x}}^{\left(1\right)}{\mathrm{\Omega }}^{-1}(D_0+D_1)=\mathbf{0}.$$

Thus, the vector ${\mathbf{x}}^{\left(1\right)}{\mathrm{\Omega }}^{-1}$ coincides with the vector $\mathit{\theta }$ of stationary probabilities of the $MC$ ${\nu }_t$ up to a normalizing constant. By the direct substitution of this vector into (11) and using $\mathit{\theta }{D}_1\mathbf{e}=\lambda$, we are convinced of the validity of the theorem.

The sufficient condition for ergodicity is proven. The proof of the sufficient condition for the non-ergodicity is analogous. □

Remark 1.

Condition (4) is intuitively clear. The $MC$ ${\xi }_t$ is ergodic if the mean service rate of users (the right-hand side $N{\displaystyle \sum _{\nu =1}^W}{\theta }_{\nu }{\mu }_{\nu }$) exceeds the arrival intensity of users into the orbit (the left-hand side $p_1\lambda$) conditioned on the fact that the system is overloaded. Here, the average service rate of a permanently busy server is defined as ${\displaystyle \sum _{\nu =1}^W}{\theta }_{\nu }{\mu }_{\nu },$ since the service rate ${\mu }_{\nu }$ depends on the current state ν of the underlying process ${\nu }_t,t\ge 0.$

Remark 2.

One can see that the ergodicity condition does not contain the price coefficients. Thus, the pricing policy does not depend on the ergodicity of the system.

Let us assume that the ergodicity condition is satisfied; then, the stationary probabilities

$$\pi (i,n,\nu )=\underset{t\to \infty }{lim}P\{i_t=i,n_t=n,{\nu }_t=\nu \},i\ge 0,n=\overline{0,N},\nu =\overline{1,W},$$

exist. Let us form the row vectors of these probabilities as

$$\mathit{\pi }(i,n)=(\pi (i,n,1),\pi (i,n,2),\dots ,\pi (i,n,W)),n=\overline{0,N},$$

and ${\mathit{\pi }}_i=(\mathit{\pi }(i,0),\mathit{\pi }(i,1),\dots ,\mathit{\pi }(i,N)),i\ge 0.$

As is known, one can find the vectors of the stationary probabilities as a solution to the system of equilibrium equations as

$$({\mathit{\pi }}_0,{\mathit{\pi }}_1,{\mathit{\pi }}_2,\dots )Q=\mathbf{0},$$

$$({\mathit{\pi }}_0,{\mathit{\pi }}_1,{\mathit{\pi }}_2,\dots )\mathbf{e}=1.$$

The problem of solving this infinite system of equations is not trivial. In the majority of the papers devoted to the analysis of multi-server retrial queues, the authors applied a rough truncation of the system. This method is poor because the question about the proper truncation level is not answered. It is intuitively clear that the truncation level must be large to have a good quality of approximation. But if this level is large, the significant problems of solving the finite system of equations on a computer arise. Some authors use the soft truncation method offered in [71]. Soft truncation works better than rough truncation. However, the same problems (justification of the truncation level and solution of a large system of linear algebraic equations) with its application arise. The last, but not the least, is the following. The application of any approximate method is correct here only if the conditions for the existence of a solution to the infinite system are known and verified. Here, we derived such a condition for the considered queueing model. A numerically stable algorithm given in [57] may be recommended for solving the system of equilibrium equations.

5. Performance Characteristics

Formulas for computation of the main performance measures of the system and their brief explanations are given as follows.

• The average number of users residing in the orbit is

  $$L_{orbit}=\sum _{i=1}^{\infty }i{\mathit{\pi }}_i\mathbf{e}.$$

  (12)

  Proof. 

  Evidently, the values ${\mathit{\pi }}_i\mathbf{e},i\ge 0,$ define the marginal distribution of the number of users residing in the orbit at an arbitrary moment, and Formula (12) defines the mathematical expectation of the discrete random variable having such a distribution. □
• The average number of busy servers is

  $$N_{busy}=\sum _{i=0}^{\infty }\sum _{n=1}^{N}n\mathit{\pi }(i,n)\mathbf{e}.$$

  (13)

  Proof. 

  The values ${\displaystyle \sum _{i=0}^{\infty }}\mathit{\pi }(i,n)\mathbf{e},n=\overline{0,N}$ define the marginal distribution of the number of users receiving service in the system, and Formula (13) defines the mathematical expectation of the discrete random variable having such a distribution. □
• The average number of busy servers conditioned that the underlying process ${\nu }_t$ has the state $\nu$ is

  $$N_{busy-\nu }={\displaystyle \frac{1}{{\theta }_{\nu }}}\sum _{i=0}^{\infty }\sum _{n=1}^{N}n\pi (i,n,\nu ),\nu =\overline{1,W}.$$

  (14)

  Proof. 

  Here, ${\displaystyle \sum _{i=0}^{\infty }}\pi (i,n,\nu ),n=\overline{0,N},$ defines the joint distribution of the number of busy servers when the state of the underlying process of arrivals is equal to $\nu .$ The value ${\theta }_{\nu }$ is the stationary probability of the state $\nu$ of the underlying process of arrivals. Correspondingly, Formula (14) defines the computed conditional mean number of busy servers. □
• The average number of users in the system is

  $$L_{system}=\sum _{i=0}^{\infty }\sum _{n=0}^N(i+n)\mathit{\pi }(i,n)\mathbf{e}=L_{orbit}+N_{busy}.$$

  (15)

  Proof. 

  Formula (15) is evident because the average number of users in the system is the sum of the average numbers of users in the orbit and in service. □
• The probability that the system is empty at an arbitrary moment is

  $$P_{empty}=\mathit{\pi }(0,0)\mathbf{e}.$$

  (16)

  Proof. 

  Formula (16) is obvious because the emptiness of the system is equivalent to the absence of users in orbit and in service. □
• The probability that an arriving user finds all servers busy and permanently leaves the system is

  $$P_{loss-busy}^{ent}={\displaystyle \frac{1-p_1}{\lambda }}\sum _{i=0}^{\infty }\mathit{\pi }(i,N)D_1\mathbf{e}.$$

  (17)

  Proof. 

  Here, $(1-p_1)$ is the probability that the arriving user, who finds all servers busy, decides to abandon the system. The vector ${\displaystyle \sum _{i=0}^{\infty }}\mathit{\pi }(i,N)$ defines the distribution of the states of the underlying arrival process when all N servers are busy. The column vector ${\displaystyle \frac{1}{\lambda }}{D}_1\mathbf{e}$ defines the probabilities of a user arrival under the fixed values of the underlying process of arrivals; for details, see [29]. Because a user loss can occur, namely, due to this user arrival when all N servers are busy, we obtain Formula (17). □
• The probability that an arriving user finds an idle server but is not satisfied with the price and permanently leaves the system is

  $$P_{loss-price}^{ent}={\displaystyle \frac{1-p_1}{\lambda }}\sum _{i=0}^{\infty }\sum _{n=0}^{N-1}\mathit{\pi }(i,n)(I_W-\mathcal{Q})D_1\mathbf{e}$$

  (18)

  where $\mathcal{Q}=\mathrm{diag}\{q_1,q_2,\dots ,q_W\}.$

  The explanation of Formula (18) is similar to the proof of Formula (17). Only it is necessary to account for the fact that Formula (17) gives the loss probability of a user, which occurs when N servers are busy at the user arrival moment, while Formula (18) considers the scenario when the number of busy servers can be arbitrary from 0 to $N-1$, and the user loss happens due to his/her dissatisfaction with the offered price of service. Recall that a user is dissatisfied by the price with the probability $(1-q_{\nu })$ when the state of underlying arrival process is $\nu ,\nu =\overline{1,W}.$ This explains the presence of the matrix multiplier $(I_W-\mathcal{Q}).$
• The loss probability of a retrying user because all servers are busy at a retrial moment and the user decides not to return to the orbit is

  $$P_{loss-busy}^{from-orbit}={\displaystyle \frac{1-p_2}{\lambda }}\sum _{i=1}^{\infty }{\alpha }_i\mathit{\pi }(i,N)\mathbf{e}.$$

  (19)

  Proof. 

  This probability is calculated as the ratio of the users departure rate due to making a retrial when all servers are busy and users arrival rate. The departure rate is equal to $(1-p_2){\displaystyle \sum _{i=1}^{\infty }}{\alpha }_i\mathit{\pi }(i,N)\mathbf{e}$, while the arrival rate is $\lambda .$ As a result, we obtain Formula (19). □
• The loss probability of a user upon arrival is

  $$P_{loss}^{ent}=P_{loss-busy}^{ent}+P_{loss-price}^{ent}.$$

  (20)

  Proof. 

  Because the user loss upon arrival can occur due to the business of all servers or dissatisfaction with the offered price, Formula (20) is evident. □
• The probability of losing a user from the orbit due to price dissatisfaction is

  $$P_{loss-price}^{from-orbit}={\displaystyle \frac{1-p_2}{\lambda }}\sum _{i=0}^{\infty }\sum _{n=0}^{N-1}{\alpha }_i\mathit{\pi }(i,n)(I_W-\mathcal{Q})\mathbf{e}.$$

  (21)

  The explanation of Formula (21) easily follows from the proof of Formulas (18) and (20).
• The probability that a user goes to service immediately upon arrival is

  $$P_{to-service}^{ent}={\displaystyle \frac{1}{\lambda }}\sum _{i=0}^{\infty }\sum _{n=0}^{N-1}\mathit{\pi }(i,n)\mathcal{Q}{D}_1\mathbf{e}.$$

  (22)

  Proof. 

  An arbitrary user goes to service upon arrival if it arrives when the number of busy servers is less than N and the user is satisfied by the offered price. The diagonal entries $q_{\nu }$ of the diagonal matrix $\mathcal{Q}$ define the probabilities of the satisfaction by the price when the arrival occurs under the state $\nu$ of the arrival underlying process. □
• The probability that an arbitrary user makes a successful attempt from the orbit is

  $$P_{to-service}^{from-orbit}={\displaystyle \frac{1}{\lambda }}\sum _{i=0}^{\infty }\sum _{n=0}^{N-1}{\alpha }_i\mathit{\pi }(i,n)\mathcal{Q}\mathbf{e}.$$

  This probability is defined as the ratio of the rate of the successful attempts, which is given by ${\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{n=0}^{N-1}}{\alpha }_i\mathit{\pi }(i,n)\mathcal{Q}\mathbf{e}$ and the rate of arrivals $\lambda .$
• The intensity of the output flow of successfully serviced users is

  $${\lambda }_{out}=\sum _{i=0}^{\infty }\sum _{n=1}^N\sum _{\nu =1}^{W}n{\mu }_{\nu }\pi (i,n,\nu ).$$

  This formula obviously follows from the formula of total probability. Here, $n{\mu }_{\nu }$ is the rate of the output flow of successfully serviced users conditional on the number of busy servers being equal to n and the state of the underlying arrival process being $\nu ,$ while ${\displaystyle \sum _{i=0}^{\infty }}\pi (i,n,\nu )$ defines the probability of this condition fulfillment.
• The loss probability of an arbitrary user from the orbit is

  $$P_{loss}^{from-orbit}=P_{loss-busy}^{from-orbit}+P_{loss-price}^{from-orbit}.$$

  (23)

  This formula is clear because a user loss from the orbit happens if all servers are busy or the user is not satisfied by the price offered at a retrial moment.
• The loss probability of an arbitrary user is

  $$P_{loss}=1-{\displaystyle \frac{{\lambda }_{out}}{\lambda }}=P_{loss}^{from-orbit}+P_{loss}^{ent}.$$

  The existence of two different formulas for computation of the loss probability $P_{loss}$ is helpful for control of the accuracy of the derivation of the generator and the computation of the stationary probabilities.

6. Numerical Example

In this section, we present numerical results. Two goals of these examples are as follows. The first goal is to demonstrate the feasibility of the obtained results and the possibility of their computer realization for realistic values of parameters, in particular, the number N of cars operating in a considered cell of the transportation network. The second goal is to provide some insight into the behavior of the system and to study the impact of multiplying factors on the key system performance measures. The problem of optimal choice of these factors is considered.

Let us assume that the users enter the system according to the $MAP$ defined by the following matrices

$$D_0=\left(\begin{array}{ccc}-3& 0.0012& 0.001\\ 0.0025& -6& 0.003\\ 0.0021& 0.0063& -12\end{array}\right),D_1=\left(\begin{array}{ccc}2.9978& 0& 0\\ 0& 5.9945& 0\\ 0& 0& 11.9916\end{array}\right).$$

This $MAP$ has the rate $\lambda =5.47847$, and the coefficient of the correlation of successive inter-arrival times is equal to 0.190165. The coefficient of the variation is 1.61472. The invariant probability vector of the underlying process is $\mathit{\theta }=(0.517241,0.310345,0.172414).$

In the potential application to the analysis of a ride-hailing platform, these input data can be interpreted as follows. Let us consider the operation of the analyzed taxi service provider in a relatively small town. The fleet of active cars (providing service simultaneously) is 200. Let us choose a time unit of one minute. During operation of the system, there are three levels of user demand. For about 52 percent of the time, the demand is low. On average, three demands are generated per minute. During approximately 31 percent of the time, the demand is moderate. On average, six calls are generated by users per minute. During about 17 percent of the time, the demand is high. On average, 12 calls are generated by users per minute. The average durations of the journey are 10 min during the low-demand period, 14.3 min during the middle-demand period, and 20 min during the high-demand period. We suppose that service becomes slower during periods of middle and high demand because it is natural to suppose that the common traffic (beside a taxi) in the town is also higher during these periods, and therefore, the average speed of cars is smaller. The loads of the system during the different periods, calculated as the ratio of the arrival rate to the product of the number of servers by the corresponding service rate, are equal to 0.15, 0.4285, and 1.2, respectively. Note that the load of the system during the high-demand periods is greater than one, and the stationary value of the queue length is infinite. Therefore, application of various approximate methods for computing performance measures of the system via some kind of averaging of the values of these measures under the fixed demand level is not possible here.

The rest of the system parameters are chosen as follows. The number of servers is $N=200.$ The service intensities are equal to ${\mu }_1=0.1,$ ${\mu }_2=0.07,$ and ${\mu }_3=0.05.$

The total retrial rate from the orbit when i users stay there is defined as ${\alpha }_i=i\alpha ,i>0,$ where $\alpha =0.04.$ The probabilities $p_1$ and $p_2$ are assumed to be equal to 0.6 and 0.5, respectively.

The surge multiples (multiplying factors) under states 1, 2, and 3 of the underlying process of the $MAP$ are $c_1=1,$ $c_2,$ and $c_3,$ correspondingly, and the probabilities $q_{\nu },\nu =\overline{1,3},$ of joining the system depend on the multiplying factors as follows:

$$q_1=0.95,q_2={\displaystyle \frac{0.2}{\max \{0.8c_2,1\}}}+{\displaystyle \frac{0.75}{{\left(c_2\right)}^2}},q_3={\displaystyle \frac{0.35}{\max \{0.6c_3,1\}}}+{\displaystyle \frac{0.6}{{\left(c_3\right)}^2}}.$$

Note that the dependence of the probabilities of $q_2$ and $q_3$ of joining the system on the multiplying factors $c_2$ and $c_3$ have been chosen here based on common sense for illustrative purposes. These dependencies may be more complicated in a real-world system. In a real system, a service provider has statistics about the probability of trip refusal depending on cost coefficients, based on which he/she can approximate functions $q_{\nu }\left(c_{\nu }\right)$ using the standard methods.

To graphically illustrate the dependence of various performance characteristics of the system on the multiplying factors $c_2$ and $c_3,$ let us vary the values of these factors over the intervals $[1,3]$ and $[c_2,5],$ respectively, with a step of 0.1.

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 illustrate the dependence of the average number of users in the orbit $L_{orbit}$, the average number $N_{busy}$ of users in service, and the average number $N_{busy-\nu }$ of serviced users under the state $\nu$ of the underlying process of the $MAP$; $\nu =2,3,$ define the loss probabilities of an arbitrary user $P_{loss}^{ent}$ upon arrival and $P_{loss}^{from-orbit}$ from the orbit on the multiplying factors $c_2$ and $c_3$.

To calculate the values of the listed performance measures and build up the corresponding surfaces, the following steps were done. (i) The generator Q with the blocks defined by Formulas (1)–(3) was computed for any fixed set of the system parameters; (ii) the infinite system of equilibrium equations for the vectors ${\mathit{\pi }}_i,i\ge 0,$ was solved using the algorithm presented in [57]; Formulas (12)–(23) were used.

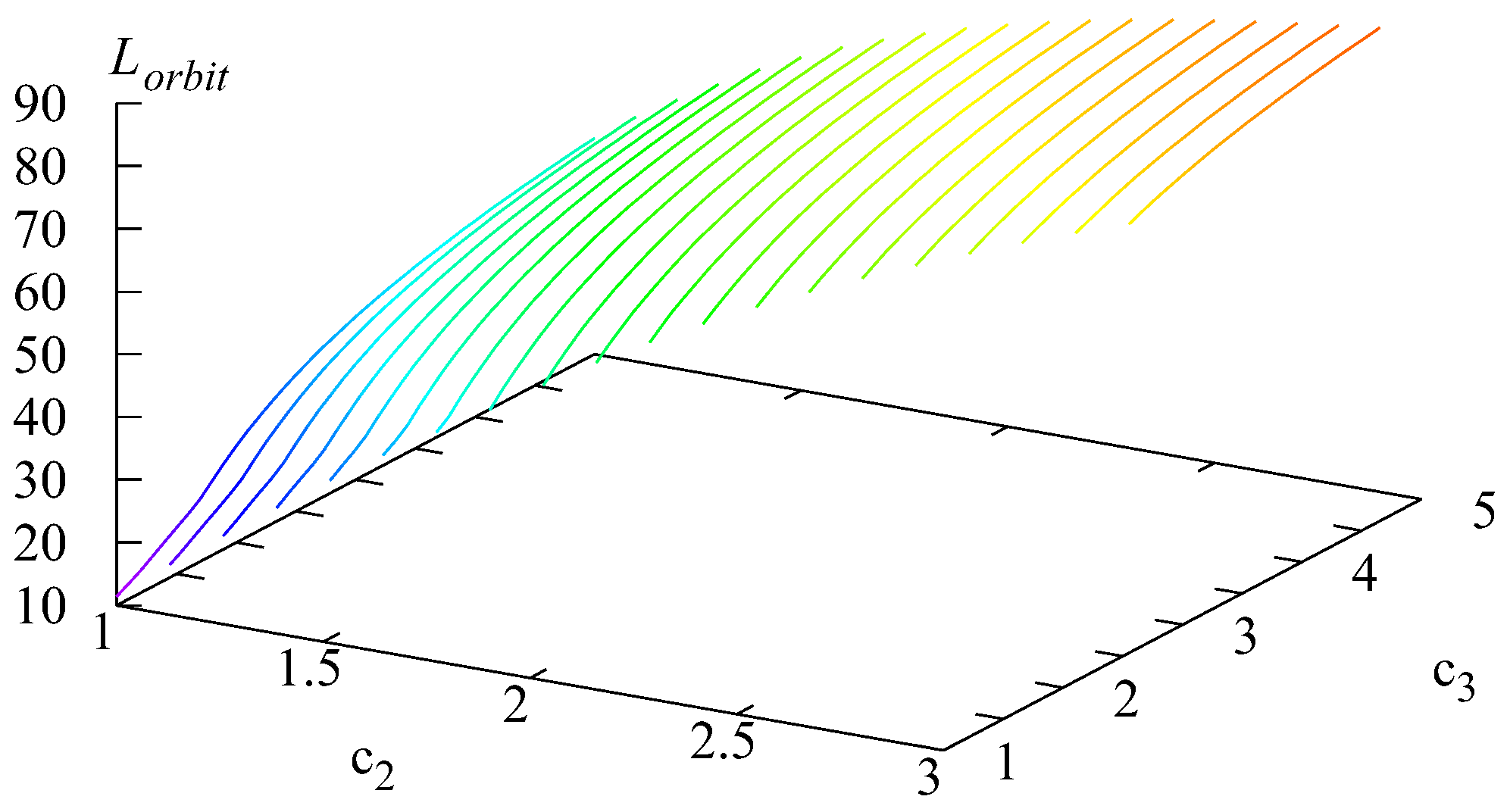
Figure 2 was built using Formula (12). As can be seen in the figure, the value of the average number of users in the orbit $L_{orbit}$ quickly grows with the increase in the multiplying factors $c_2$ and $c_3$. This result is understandable because the users prefer to wait for a while in the orbit for periods of low demand if the price of service at other periods becomes higher.

Figure 3 was built using Formula (13). As can be seen in the figure, the value of the average number $N_{busy}$ of users in service quickly grows with the decrease in the multiplying factors $c_2$ and $c_3$. When service at the periods of middle and high demand becomes cheaper, the users rarely postpone their service to periods of low demand. They start service without delay, and correspondingly, more servers are busy at an arbitrary moment.

Figure 4 was built using Formula (14) for $\nu =2.$ As can be seen in the figure, the value of the average number $N_{busy-2}$ of users in service conditional that the underlying process of arrival resides in the state 2 sharply increases with the decrease in surge factor $c_2.$ Dependence on surge factor $c_3$ is weak.

Figure 5 was built using Formula (14) for $\nu =3.$ As can be seen in the figure, the value of the average number $N_{busy-3}$ of users in service conditional that the underlying process of arrival resides in the state 3 sharply increases with the decrease in surge factor $c_3.$ The values of $N_{busy-3}$ are larger than the values of $N_{busy-2}$ due to two reasons. The first reason is that these values are the conditional average numbers. They are obtained as the joint mean values divided by the probability of condition. Recall that the probability that the underlying process of arrival resides in state 2 is essentially larger (0.31 vs. 0.17) than the probability that the underlying process of arrival resides in state 3. The second reason is as follows. It follows from the form of the matrix $D_1$ that the instantaneous user arrival rate is maximal, namely, during the stay of the underlying process of arrival in state 3. This causes the larger value of $N_{busy-3}$.

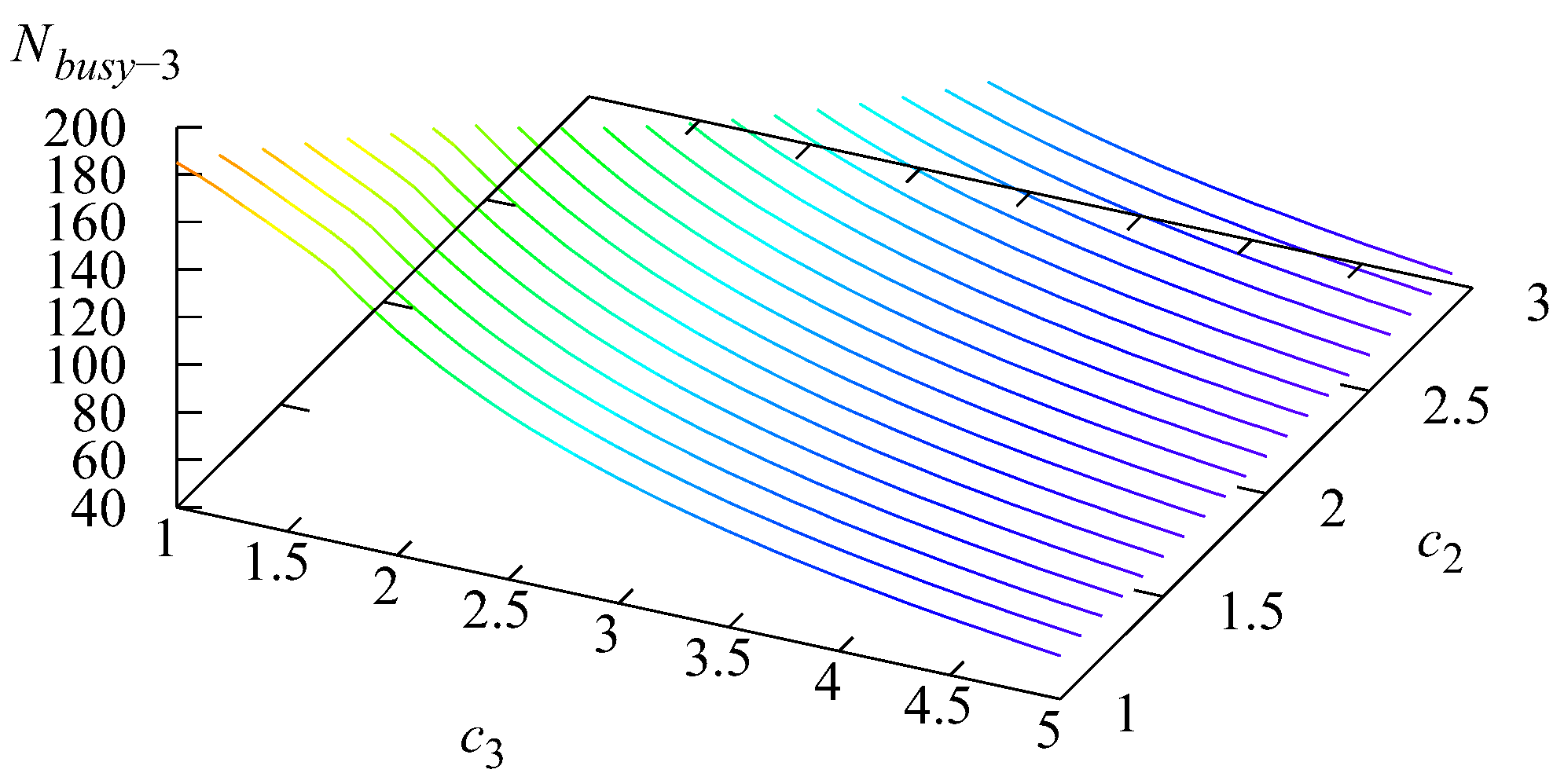
Figure 6 was built using Formula (20), and the probability used here is $P_{loss}^{ent}$. In turn, this probability is the sum of two probabilities: the probability of the loss because all servers are busy (defined by Formula (17)) and the probability of the loss due to the customer’s dissatisfaction with the offered price of service (defined by Formula (18)). An increase in surges $c_2$ and $c_3$ implies an increase in customer dissatisfaction (although it slightly decreases the probability that all servers are busy). This causes the increase in the probability $P_{loss}^{ent}$.

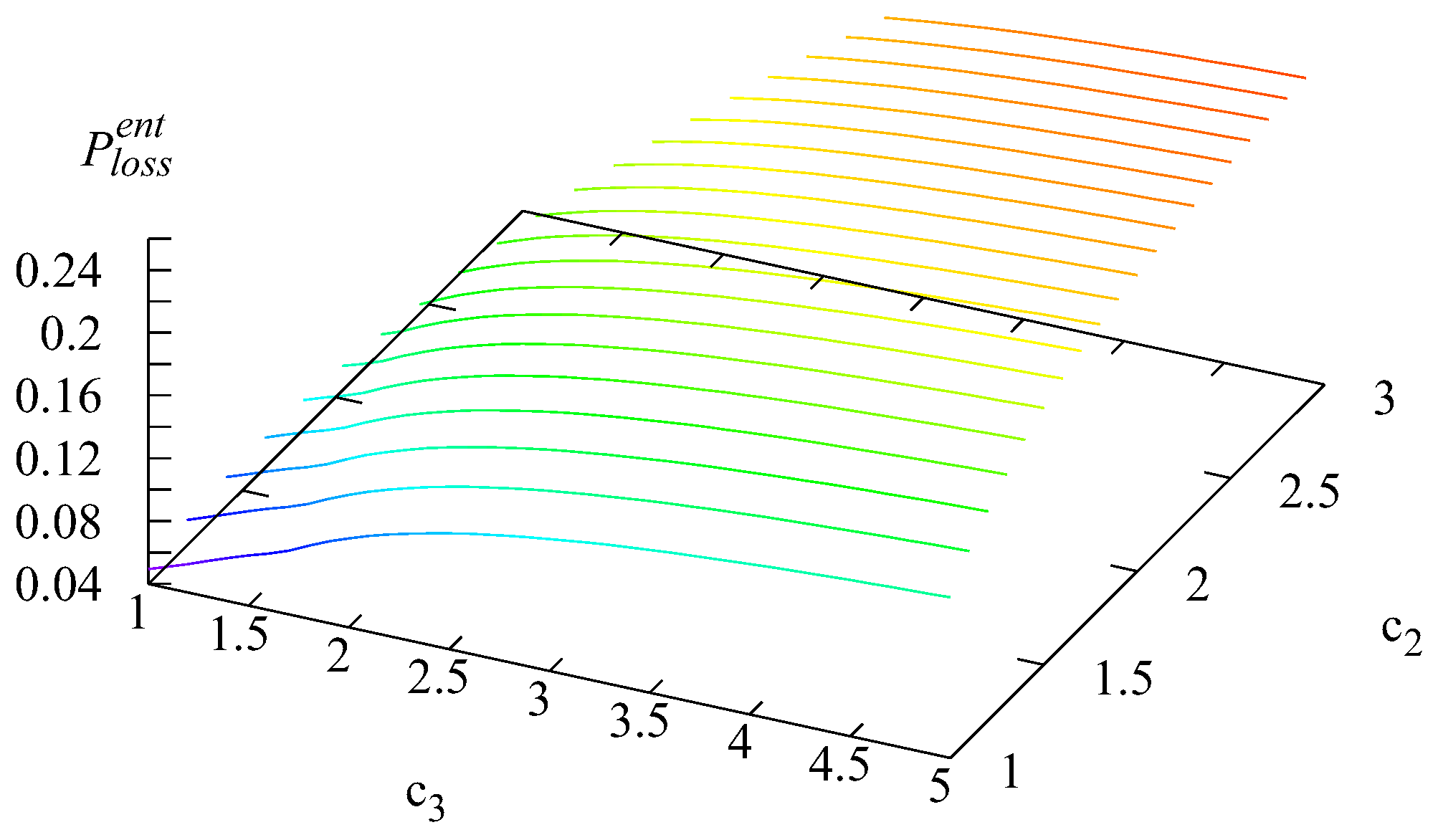
The reasons for the loss of users retrying from the orbit are the same as the reasons for the loss of new users. This implies the similarity of the shapes of the surfaces presented in Figure 6 and Figure 7, where the latter was built based on Formula (23), with the summands calculated using Formulas (19) and (21).

Summarizing the presented brief comments on the shapes of the surfaces presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, one can conclude that these figures confirm the intuitive expectation that the smaller values of multiplying factors $c_2$ and $c_3$ imply a higher occupancy of the servers, a smaller loss probability—especially due to the dissatisfaction with the offered price—and a smaller number of users staying in the orbit. During the stay of the underlying process in state 3, when the arrival rate is at its maximum, the servers are almost permanently busy if the multiplying factors $c_2$ and $c_3$ are small. When the multiplying factors increase, the number of busy servers decreases, while the number of users residing in orbit increases. The rates of these increases and decreases can be very high.

As is evident from the presented figures, the variation in the multiplying factors has an essential impact on the system performance measures, and the value of the presented analytical research consists of creating the possibility of exact quantitative characterization of the relatively qualitatively clear effects.

Having quantitatively confirmed the profound effect of the values of the multiplying factors $c_2$ and $c_3$ on the values of the performance measures of the system, let us briefly illustrate the possibility of using the obtained results for the optimal choice of these factors.

We assume that the quality of the system’s operation is defined by the following criterion defining the average revenue received during a unit of time:

$$E=E(c_2,c_3)=a\sum _{i=0}^{\infty }\sum _{n=0}^{N-1}\sum _{\nu =1}^W{c}_{\nu }{q}_{\nu }\left(c_{\nu }\right)(\pi (i,n,\nu ){\left(D_1\right)}_{\nu }\mathbf{e}+i\alpha )-b_1\lambda (P_{loss-busy}^{from-orbit}+P_{loss-busy}^{ent})$$

$$-b_2\lambda (P_{loss-price}^{from-orbit}+P_{loss-price}^{ent})$$

where a is the averaged base revenue obtained via the service of one user when the multiplying factors are not applied ($c_1=c_2=c_3=1$), $b_1$ is a charge paid by the system due to the loss of one user when all servers are busy, and $b_2$ is a charge paid by the system due to the loss of one user because of dissatisfaction with the offered price. The goal of the choice of the multiplying factors $c_2$ and $c_3$ is to guarantee the maximum revenue of the system.

The summand $a{\displaystyle \sum _{i=0}^{\infty }}{\displaystyle \sum _{n=0}^{N-1}}{\displaystyle \sum _{\nu =1}^W}{c}_{\nu }{q}_{\nu }\left(c_{\nu }\right)(\pi (i,n,\nu ){\left(D_1\right)}_{\nu }\mathbf{e}+i\alpha )$ in the formula for $E(c_2,c_3)$ defines the averaged price paid by an arbitrary admitted user.

It is worth noting that the values of the stationary probabilities $\pi (i,n,\nu )$ of the system states and loss probabilities appearing in the expression for $E(c_2,c_3)$ also depend on the multiplying factors $c_2$ and $c_3.$ It is impossible to evaluate the impact of the variation in the values of the surge factors $c_2$ and $c_3$ from intuitive reasoning. On the one hand, if these factors increase, the first summand should increase because these factors are the multipliers there. But on the other hand, the probabilities $q_{\nu }$ decrease with the growth of the factors $c_{\nu },\nu =\overline{2,W}.$ Also, the dynamics of the average number of users receiving service during a unit of time are not clear because the increase in the factors $c_{\nu }$ implies a higher value of probabilities of losses due to dissatisfaction with the price but a lower loss probability due to the business of all servers.

Thus, the problem of maximization of the implicitly defined function $E(c_2,c_3)$ has to be solved, under the fixed set of the system parameters, only numerically.

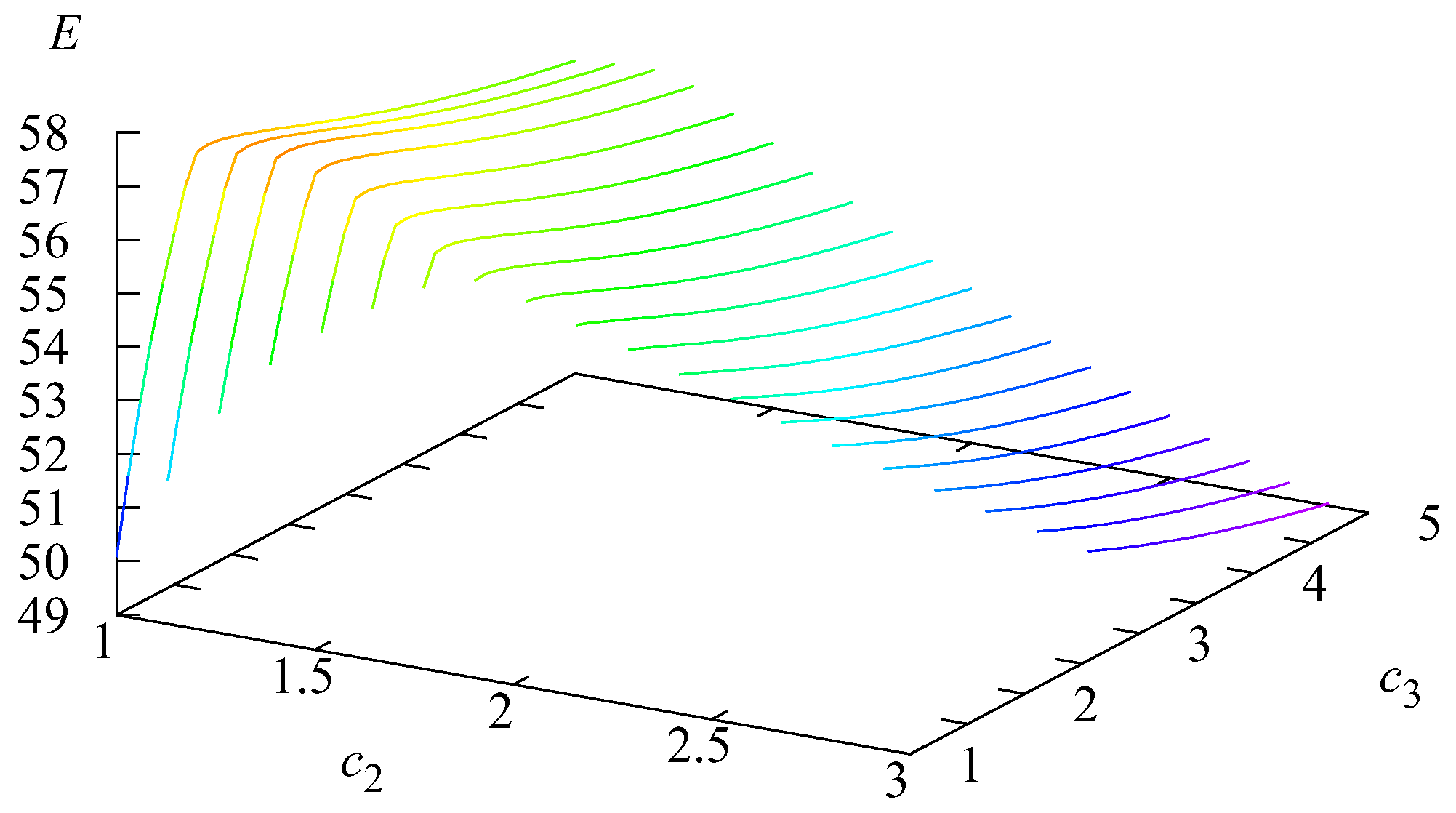
We fixed the following values of cost coefficients: $a=10,$ $b_1=5$, and $b_2=4.$ The dependence of the cost criterion $E(c_2,c_3)$ on the factors $c_2$ and $c_3$ is presented in Figure 8.

As can be seen from Figure 8, the value of the cost criterion is very sensitive with respect to variation in $c_2$ and $c_3.$ When both of these factors are small, the revenue from the system is low. The revenue essentially increases when these factors (and the average payment by each accepted user) increase. The revenue reaches a maximum and then starts decreasing because users begin preferring to postpone the service until the value of the multiplying factor drops or refuse service. This implies a decrease in revenue.

The optimal value 57.0183 of the cost criterion $E(c_2,c_3)$ is achieved when $c_2=1.2$ and $c_3=1.8.$ The value of $E(c_2,c_3)$ when $c_2=c_3=c_1=1,$ i.e., the dynamic pricing is not applied (flat price), is equal to 50.077. The value of $E(c_2,c_3)$ when the factors $c_2$ and $c_3$ admit the maximal values (greedy price) in the considered range are 3 and 5, respectively, is equal to 48.7961. Thus, the dynamic use of the optimal price policy increases the system revenue compared to the flat price and greedy price of 13.9 and 16.8 percent, respectively.

Let us mention that the problem of maximization of the function $E(c_2,c_3)$ is quite difficult. The main difficulty consists of the fact that this function includes the values of the stationary probabilities $\pi (i,n,\nu )$ and the four kinds of loss probabilities, for which the problem of computation is solved above. But, we did not solve the problem of computation of the derivatives of these probabilities with respect to the parameters $c_{\nu },\nu =\overline{1,W}.$ Therefore, many powerful methods of optimization cannot be applied here. However, the optimization can be more or less easily performed using a grid search (possibly with a more dense grid in the neighborhood of the point of maximum) or using one of the numerous existing so-called derivative-free algorithms; see, e.g., [72].

7. Conclusions

The generation of requests for service in modern real-world transportation, telecommunication, logistic systems, and others can be adequately described by the $MAP$. This allows for taking into account in analysis not only the mean arrival rate (as is possible under the use of the model of the stationary Poisson arrival process) but also higher moments and the coefficient of correlation of successive inter-arrival times. We proposed to link the mechanism of dynamic pricing for user service in queueing systems to the states of the underlying process of the $MAP$. We illustrated the possible application of this mechanism via its use for control of a multi-server retrial queueing system with dependence of the probability of an arbitrary user joining the system on the value of the offered multiplying factor (surge multiplier). The stationary characteristics of this system are computed. The proposed algorithm’s feasibility for computation and optimization goals has been numerically demonstrated. An example of the computation of the optimal values of the multiplying factors has been presented.

The suggested and analyzed mechanism of dynamic service pricing in this paper can be applied not only in the ride-hailing system analyzed here but also in many other queueing systems and networks (transportation, entertainment, retail, etc.) where the price of service can be dynamically changed, e.g., via the organization of various actions, promotions, special offers, etc., to attract more clients. The results of the presented analysis can be used for the optimal choice of the parameters of proposed discounts or promotions.

The results are planned to be extended in several directions, including cases when the dynamic pricing is applied to other types of queueing systems or queueing networks. The interesting case for analysis is when the number of active servers also depends on the current state of the underlying process of the $MAP$ (and, therefore, the value of the multiplying factor). Such a dependence on applications to modeling ride-hailing platforms is mentioned, e.g., in [73]. Some freelance drivers may prefer to work only when the surge multiplier is high. The consideration of heterogeneous users with different schemes of priorities and server reservations is of interest. The application of game theory is also a promising direction for further research.