A Novel Exponentiated Generalized Weibull Exponential Distribution: Properties, Estimation, and Regression Model
Abstract
1. Introduction
2. Exponentiated Generalized Weibull Exponential Distribution
- For , , , and , the E distribution with parameter is obtained.
- For and , the Weibull distribution with shape parameter c and a scale parameter is obtained.
- For , , and , the EE distribution in [33] with parameters is obtained.
- For and , the exponentiated Weibull distribution in [43] is obtained.
- For and , the EGE distribution in [37] with parameters is obtained.
- For and , the WE distribution in [24] with parameters is obtained.
- For in [44], the proposed EGWE is obtained.
3. Useful Representation
4. Statistical Properties
4.1. Quantile Function
4.2. Moments
4.3. Moment Generating Function
4.4. Incomplete Moments
4.5. Rényi Entropy
4.6. Order Statistics
5. Estimation of Parameters
6. Simulation Study
7. Applications
- The E distribution, with cdf.
- The EE distribution in [33], with cdf.
- The EGE distribution in [37], with cdf.
- The WE distribution (a member of the Weibull G family) in [24], with cdf.
- The BE distribution in [34], with cdf,.
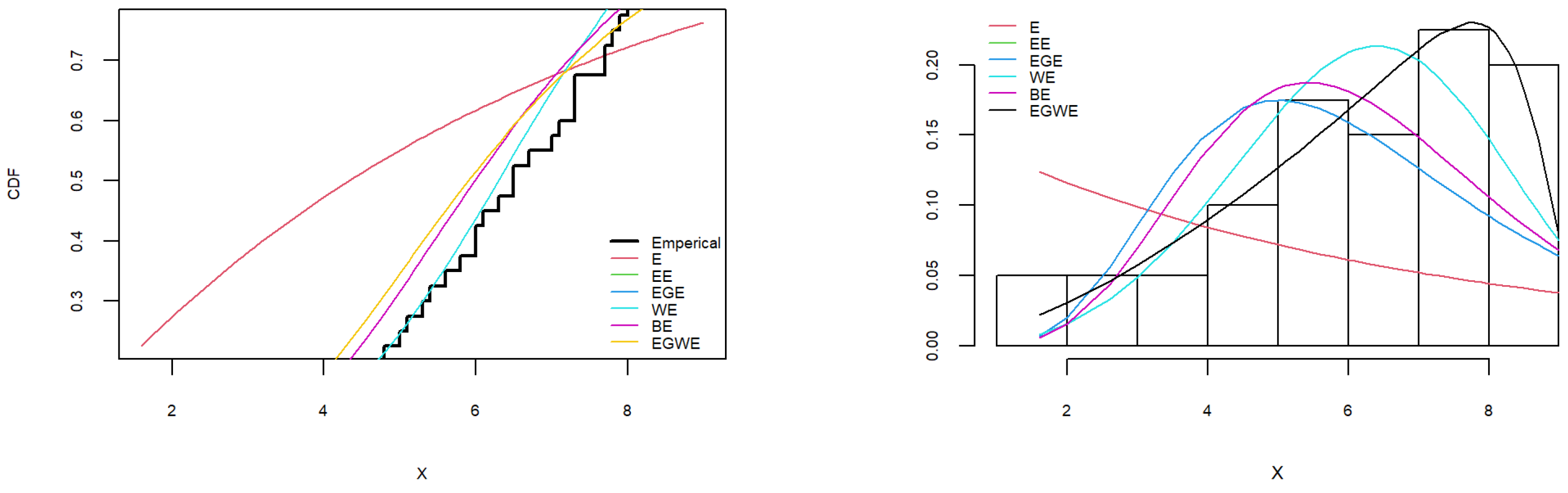
7.1. The First Dataset
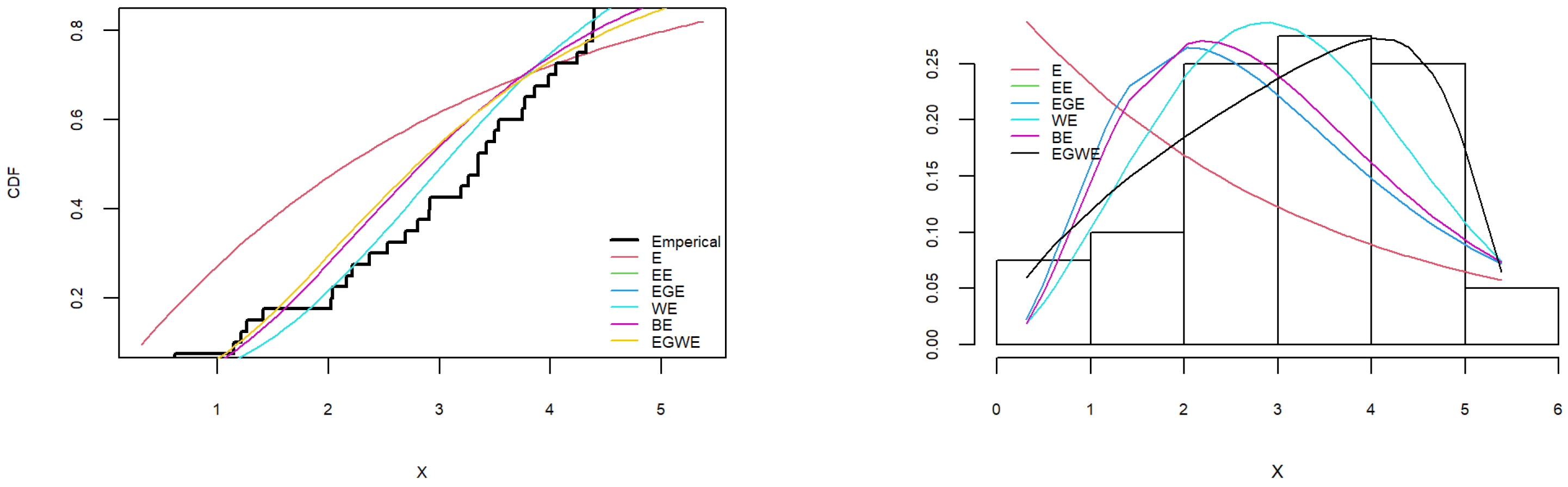
7.2. The Second Dataset
7.3. The Third Dataset
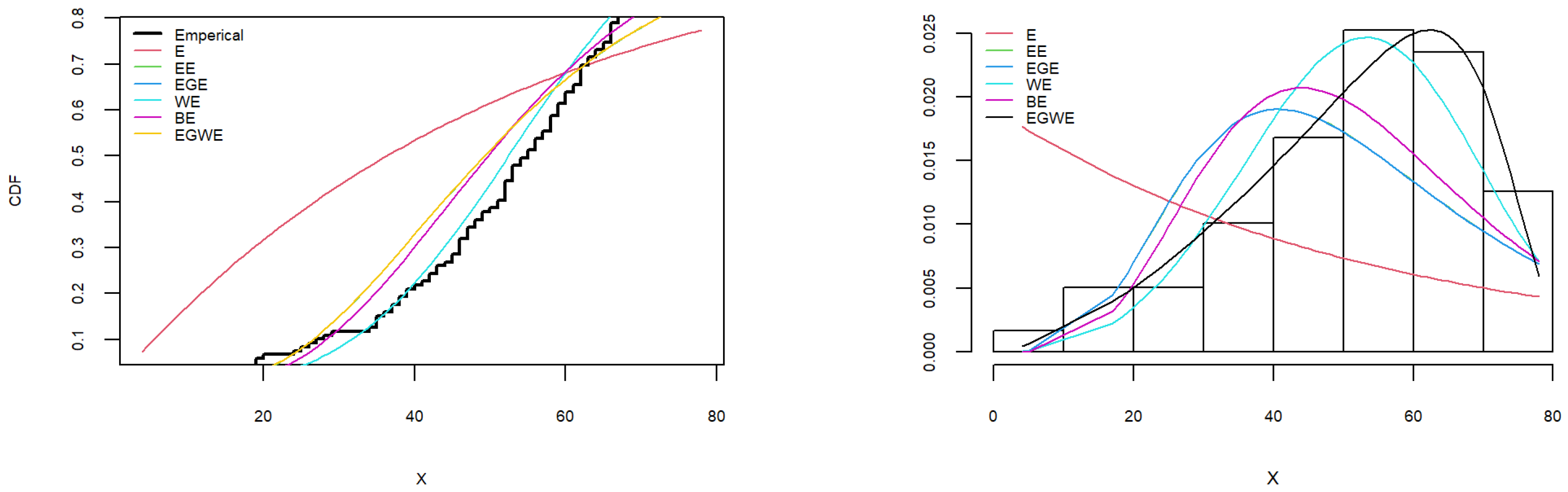
7.4. The Fourth Dataset
8. Exponentiated Generalized Weibull Exponential Distribution Regression Model
8.1. Application 1: Regression Model for Complete Sample
8.2. Application 2: Regression Model for Censored Sample
9. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| cdf | cumulative distribution function |
| probability density function | |
| RV | random variable |
| EGWE | exponentiated generalized Weibull exponential |
| RMSE | root mean squared error |
| EG | exponentiated generalized |
| MLE | maximum likelihood estimator |
| E | exponential |
| EE | exponentiated exponential |
| WE | Weibull exponential |
| BE | beta exponential |
| EGE | exponentiated generalized exponential |
| AIC | Akaike information criterion |
| AICc | corrected Akaike information criterion |
| K-S | Kolmogorov–Smirnov |
| LRT | likelihood ratio test |
| df | degrees of freedom |
| BWE | Beta Weibull exponential |
| KWE | Kumaraswamy Weibull exponential |
| EKW | Exponentiated Kumaraswamy Weibull References |
References
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling failure time data by Lehman alternatives. Commun. Stat.-Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Nassar, M.M.; Eissa, F.H. On the exponentiated Weibull distribution. Commun. Stat.-Theory Methods 2003, 32, 1317–1336. [Google Scholar] [CrossRef]
- Nadarajah, S.; Gupta, A.K. The exponentiated gamma distribution with application to drought data. Calcutta Stat. Assoc. Bull. 2007, 59, 29–54. [Google Scholar] [CrossRef]
- Salem, H.M. The exponentiated lomax distribution: Different estimation methods. Am. J. Appl. Math. Stat. 2014, 2, 364–368. [Google Scholar] [CrossRef]
- Dey, S.; Kumar, D.; Ramos, P.L.; Louzada, F. Exponentiated Chen distribution: Properties and estimation. Commun. Stat.-Simul. Comput. 2017, 46, 8118–8139. [Google Scholar] [CrossRef]
- Abd EL-Baset, A.A.; Ghazal, M. Exponentiated additive Weibull distribution. Reliab. Eng. Syst. Saf. 2020, 193, 106663. [Google Scholar] [CrossRef]
- Sharma, V.K.; Singh, S.V.; Shekhawat, K. Exponentiated Teissier distribution with increasing, decreasing and bathtub hazard functions. J. Appl. Stat. 2022, 49, 371–393. [Google Scholar] [CrossRef]
- Ferreira, A.A.; Cordeiro, G.M. The exponentiated power Ishita distribution: Properties, simulations, regression, and applications. Chil. J. Stat. (ChJS) 2023, 14, 65–81. [Google Scholar] [CrossRef]
- Lone, S.A.; Ramzan, Q.; AL-Essa, L.A. The exponentiated Ailamujia distribution: Properties and application. Alex. Eng. J. 2024, 108, 1–15. [Google Scholar] [CrossRef]
- Rahman, H. Exponentiated Arctan-X Family of Distribution: Properties, Simulation and Applications to Insurance Data. Thail. Stat. 2025, 23, 199–216. [Google Scholar]
- Lekhane, O.; Oluyede, B.; Gabaitiri, L.; Mabikwa, O.V. The Exponentiated-Gompertz-Marshall-Olkin-G Family of Distributions: Properties and Applications. Stat. Optim. Inf. Comput. 2025, 13, 1752–1788. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; da Cunha, D.C. The exponentiated generalized class of distributions. J. Data Sci. 2013, 11, 1–27. [Google Scholar] [CrossRef]
- Andrade, T.; Rodrigues, H.; Bourguignon, M.; Cordeiro, G. The exponentiated generalized Gumbel distribution. Rev. Colomb. Estad. 2015, 38, 123–143. [Google Scholar] [CrossRef]
- Abd-Elfattah, A.; Assar, S.; Abd-Elghaffar, H. Exponentiated Generalized Frechet Distribution. Int. J. Math. Anal. Appl. 2016, 3, 39–48. [Google Scholar]
- Rodrigues, J.; Percontini, A.; Hamedani, G. The exponentiated generalized Lindley distribution. Asian Res. J. Math. 2017, 5, 1–14. [Google Scholar] [CrossRef]
- Elgarhy, M.; ul Haq, M.A.; ul Ain, Q. Exponentiated generalized Kumaraswamy distribution with applications. Ann. Data Sci. 2018, 5, 273–292. [Google Scholar] [CrossRef]
- De Andrade, T.A.; Chakraborty, S.; Handique, L.; Gomes-Silva, F. The exponentiated generalized extended Gompertz distribution. J. Data Sci. 2019, 17, 299–330. [Google Scholar] [CrossRef]
- El-Morshedy, M.; El-Faheem, A.A.; Al-Bossly, A.; El-Dawoody, M. Exponentiated generalized inverted gompertz distribution: Properties and estimation methods with applications to symmetric and asymmetric data. Symmetry 2021, 13, 1868. [Google Scholar] [CrossRef]
- ElSherpieny, E.A.; Almetwally, E.M. The exponentiated generalized alpha power family of distribution: Properties and applications. Pak. J. Stat. Oper. Res. 2022, 18, 349–367. [Google Scholar] [CrossRef]
- Kpangay, M. On the exponentiated generalized exponentiated exponential distribution with properties and application. Int. J. Sci. Res. Eng. Develop. 2023, 6, 941–951. [Google Scholar]
- Altinisik, Y.; Çankaya, E. Exponentiated generalized Ramos-Louzada distribution with properties and applications. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2024, 73, 76–103. [Google Scholar] [CrossRef]
- Bashiru, S.O.; Isa, A.M.M.; Chinedu, A.K.; Ebele, O.H. Exponentiated Generalized Burr XII Distribution: Properties and Applications. J. R. Stat. Soc. Niger. Group (JRSS-NIG Group) 2024, 1, 1–18. [Google Scholar]
- Badr, M.M.; Darwish, J.A.; Alkhathaami, F. Modeling radiation and engineering data using the exponentiated generalized Topp-Leone exponential model. J. Radiat. Res. Appl. Sci. 2025, 18, 101287. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alzaatreh, A.; Mansoor, M.; Zubair, M. A new Weibull-G family of distributions. J. Stat. Comput. Simul. 2016, 86, 3191–3208. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Ghosh, I. On the Weibull-X family of distributions. J. Stat. Theory Appl. 2015, 14, 169–183. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Famoye, F.; Lee, C. Weibull-Pareto distribution and its applications. Commun. Stat.-Theory Methods 2013, 42, 1673–1691. [Google Scholar] [CrossRef]
- Ahmad, A.; Ahmad, S.; Ahmed, A. Characterization and Estimation of Weibull-Rayleigh distribution with Applications to life time data. Appl. Math. Inf. Sci. Lett. 2017, 5, 71–79. [Google Scholar] [CrossRef]
- Klakattawi, H.S. The Weibull-gamma distribution: Properties and applications. Entropy 2019, 21, 438. [Google Scholar] [CrossRef]
- Bilal, M.; Mohsin, M.; Aslam, M. Weibull-Exponential Distribution and Its Application in Monitoring Industrial Process. Math. Probl. Eng. 2021, 2021, 6650237. [Google Scholar] [CrossRef]
- Ünal, C.; Özel, G. A New Weibull-Lindley Distribution in Modelling Lifetime Data. Mugla J. Sci. Technol. 2022, 8, 9–15. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 362. [Google Scholar]
- Gupta, R.D.; Kundu, D. Exponentiated exponential family: An alternative to gamma and Weibull distributions. Biom. J. J. Math. Methods Biosci. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. The beta exponential distribution. Reliab. Eng. Syst. Saf. 2006, 91, 689–697. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized exponential distribution: Existing results and some recent developments. J. Stat. Plan. Inference 2007, 137, 3537–3547. [Google Scholar] [CrossRef]
- de Araujo Rodrigues, J.; Silva, A.P.C.M. The exponentiated Kumaraswamy-exponential distribution. Br. J. Appl. Sci. Technol. 2015, 10, 1–12. [Google Scholar] [CrossRef]
- Oguntunde, P.E.; Adejumo, A.O.; Adepoju, K.A. Assessing the flexibility of the exponentiated generalized exponential distribution. Assess. Flex. Exponentiated Gen. Exponential Distrib. 2016, 17, 49–57. [Google Scholar]
- Mahdavi, A.; Kundu, D. A new method for generating distributions with an application to exponential distribution. Commun. Stat.-Theory Methods 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- Al-Salafi, A.A.; Adham, S.A. Maximum Likelihood Estimation in the Odd Generalized Exponential-Exponential Distribution. Int. J. Contemp. Math. Sci. 2018, 13, 111–123. [Google Scholar] [CrossRef]
- Mansoor, M.; Tahir, M.; Cordeiro, G.M.; Provost, S.B.; Alzaatreh, A. The Marshall-Olkin logistic-exponential distribution. Commun. Stat.-Theory Methods 2019, 48, 220–234. [Google Scholar] [CrossRef]
- Afify, A.Z.; Mohamed, O.A. A new three-parameter exponential distribution with variable shapes for the hazard rate: Estimation and applications. Mathematics 2020, 8, 135. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Pal, M.; Ali, M.M.; Woo, J. Exponentiated weibull distribution. Statistica 2006, 66, 139–147. [Google Scholar]
- Abonongo, A.I.L.; Abonongo, J. Exponentiated generalized weibull exponential distribution: Properties, estimation and applications. Comput. J. Math. Stat. Sci. 2024, 3, 57–84. [Google Scholar] [CrossRef]
- Alshangiti, A.M.; Kayid, M.; Almulhim, M. Reliability analysis of extended generalized inverted exponential distribution with applications. J. Syst. Eng. Electron. 2016, 27, 484–492. [Google Scholar] [CrossRef]
- Oguntunde, P.E.; Adejumo, A.; Owoloko, E.A. On the exponentiated generalized inverse exponential distribution. In Proceedings of the World Congress on Engineering 2017 Vol I (WCE 2017), London, UK, 5–7 July 2017. [Google Scholar]
- Khan, M.S. Transmuted generalized inverted exponential distribution with application to reliability data. Thail. Stat. 2018, 16, 14–25. [Google Scholar]
- Pavlov, N.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Transmuted inverse exponential software reliability model. Int. J. Latest Res. Eng. Technol. 2018, 4, 1–6. [Google Scholar]
- Alshenawy, R.; Al-Alwan, A.; Almetwally, E.M.; Afify, A.Z.; Almongy, H.M. Progressive Type-II Censoring Schemes of Extended Odd Weibull Exponential Distribution with Applications in Medicine and Engineering. Mathematics 2020, 8, 1679. [Google Scholar] [CrossRef]
- Aldahlan, M.A.; Afify, A.Z. The Odd Exponentiated Half-Logistic Exponential Distribution: Estimation Methods and Application to Engineering Data. Mathematics 2020, 8, 1684. [Google Scholar] [CrossRef]
- Aldahlan, M.A.; Afify, A.Z. A new three-parameter exponential distribution with appli-cations in reliability and engineering. J. Nonlinear Sci. Appl. (JNSA) 2020, 13, 258–269. [Google Scholar] [CrossRef]
- Nadarajah, S.; Rocha, R. Newdistns: An R package for new families of distributions. J. Stat. Softw. 2016, 69, 1–32. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory, Budapest, Hungary, 2–8 September 1973; Petrov, B.N., Csaki, F., Eds.; pp. 267–281. [Google Scholar]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Proschan, F. Theoretical explanation of observed decreasing failure rate. Technometrics 2000, 42, 7–11. [Google Scholar] [CrossRef]
- Xu, K.; Xie, M.; Tang, L.C.; Ho, S. Application of neural networks in forecasting engine systems reliability. Appl. Soft Comput. 2003, 2, 255–268. [Google Scholar] [CrossRef]
- Abouammoh, A.; Ahmad, R.; Khalique, A. On new renewal better than used classes of life distributions. Stat. Probab. Lett. 2000, 48, 189–194. [Google Scholar] [CrossRef]
- Zamanah, E.; Nasiru, S.; Luguterah, A. Harmonic Mixture Weibull-G Family of Distributions: Properties, Regression and Applications to Medical Data. Comput. Math. Methods 2022, 2022, 2836545. [Google Scholar] [CrossRef]
- Eugene, N.; Lee, C.; Famoye, F. Beta-Normal Distribution and Its Applications. Commun. Stat.-Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de Castro, M. A New Family of Generalized Distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Barreto-Souza, W.; Cordeiro, G.M. The Exponentiated Kumaraswamy Distribution and Its Log-Transform. Braz. J. Probab. Stat. 2013, 27, 31–53. [Google Scholar] [CrossRef]
- Collett, D. Modelling Survival Data in Medical Research; Chapman and Hall/CRC: Boca Raton, FL, USA, 2023. [Google Scholar]
- Cox, D.R.; Snell, E.J. A general definition of residuals. J. R. Stat. Soc. Ser. B (Methodol.) 1968, 30, 248–265. [Google Scholar] [CrossRef]
- Nanga, S.; Nasiru, S.; Dioggban, J. Cosine Topp–Leone family of distributions: Properties and regression. Res. Math. 2023, 10, 2208935. [Google Scholar] [CrossRef]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data; Wiley Series in Probability and Mathematical Statistics; John Wiley &Sons: New York, NY, USA, 1980. [Google Scholar]
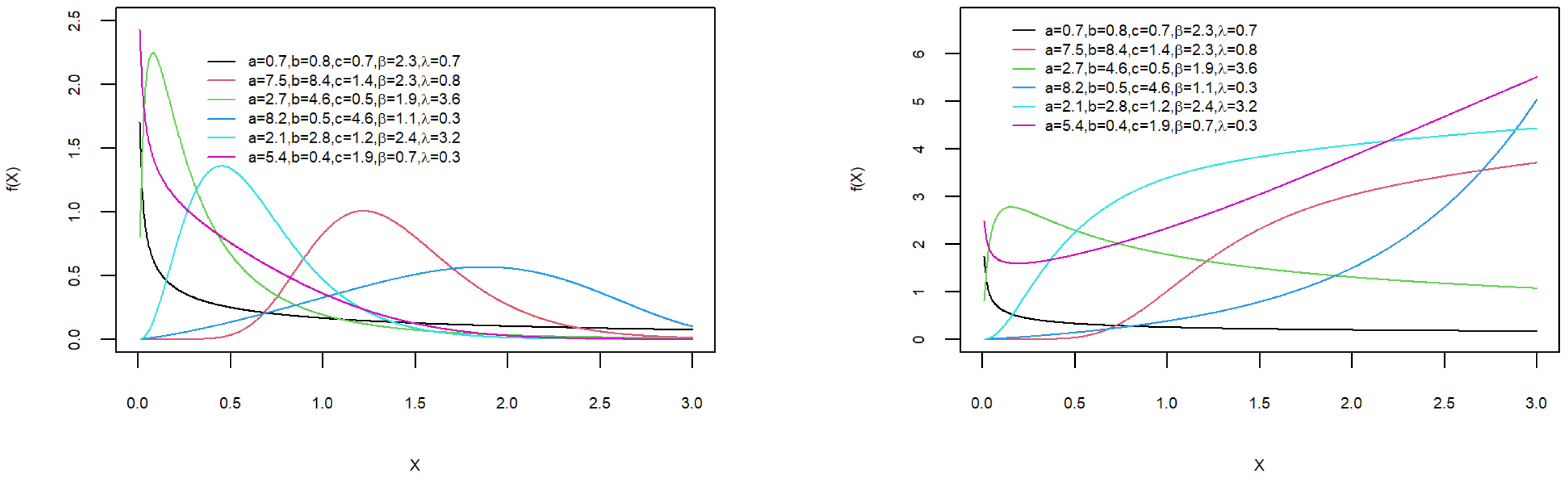



| a | b | c | Skewness | Kurtosis | ||
|---|---|---|---|---|---|---|
| 0.7 | 0.8 | 0.7 | 2.3 | 0.7 | 3.7943 | 25.2583 |
| 7.5 | 8.4 | 1.4 | 2.3 | 0.8 | 0.8497 | 4.2573 |
| 2.7 | 4.6 | 0.5 | 1.9 | 3.6 | 4.6672 | 46.7914 |
| 8.2 | 0.5 | 4.6 | 1.1 | 0.3 | −0.0896 | 2.4648 |
| 2.1 | 2.8 | 1.2 | 2.4 | 3.2 | 1.0775 | 4.5906 |
| 5.4 | 0.4 | 1.9 | 0.7 | 0.3 | 1.1459 | 4.1250 |
| Case I | Case II | Case III | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MLE | Bias | RMSE | MLE | Bias | RMSE | MLE | Bias | RMSE | ||
| a | 3.8304 | 0.5304 | 0.9561 | 5.6457 | 0.6457 | 1.2918 | 3.5945 | 0.1945 | 0.5675 | |
| b | 1.2520 | 0.6520 | 3.2481 | 3.5196 | 2.3196 | 10.5700 | 0.9861 | 0.5861 | 4.1433 | |
| c | 1.9426 | 0.8426 | 1.8225 | 1.5328 | 0.7328 | 1.7611 | 2.1497 | 0.8497 | 1.6991 | |
| 4.2165 | −0.0835 | 0.4208 | 2.3085 | −0.1915 | 0.4664 | 0.6906 | 0.1906 | 0.3922 | ||
| 3.5154 | 0.5154 | 1.0332 | 4.2455 | 0.6455 | 1.2440 | 1.4549 | 0.6549 | 1.1340 | ||
| a | 3.5934 | 0.2934 | 0.7838 | 5.3644 | 0.3644 | 1.0432 | 3.5533 | 0.1533 | 0.4868 | |
| b | 0.7486 | 0.1486 | 0.8655 | 1.9173 | 0.7173 | 3.7844 | 0.4952 | 0.0952 | 0.6847 | |
| c | 1.4530 | 0.3530 | 0.9739 | 1.0041 | 0.2041 | 0.6572 | 1.6703 | 0.3703 | 0.9592 | |
| 4.2923 | −0.0077 | 0.3547 | 2.4617 | −0.0383 | 0.4292 | 0.6531 | 0.1531 | 0.3878 | ||
| 3.3112 | 0.3112 | 0.7342 | 4.0611 | 0.4611 | 1.0468 | 1.1756 | 0.3756 | 0.8140 | ||
| a | 3.4483 | 0.1483 | 0.4988 | 5.1423 | 0.1423 | 0.6679 | 3.4810 | 0.0810 | 0.4048 | |
| b | 0.6550 | 0.0550 | 0.3769 | 1.3811 | 0.1811 | 0.9960 | 0.4289 | 0.0289 | 0.2320 | |
| c | 1.2349 | 0.1349 | 0.4669 | 0.8773 | 0.0773 | 0.2977 | 1.4695 | 0.1695 | 0.5617 | |
| 4.2895 | −0.0105 | 0.2869 | 2.4388 | −0.0612 | 0.2807 | 0.5728 | 0.0728 | 0.2754 | ||
| 3.1446 | 0.1446 | 0.5104 | 3.7813 | 0.1813 | 0.5648 | 0.9771 | 0.1771 | 0.5670 | ||
| a | 3.3228 | 0.0228 | 0.2089 | 5.0172 | 0.0172 | 0.3722 | 3.4401 | 0.0401 | 0.2055 | |
| b | 0.6053 | 0.0053 | 0.1153 | 1.2320 | 0.0320 | 0.2751 | 0.4035 | 0.0035 | 0.0775 | |
| c | 1.1229 | 0.0229 | 0.1509 | 0.8092 | 0.0092 | 0.1013 | 1.3313 | 0.0313 | 0.1907 | |
| 4.2895 | −0.0105 | 0.1518 | 2.4819 | −0.0181 | 0.1887 | 0.5304 | 0.0304 | 0.1719 | ||
| 3.0150 | 0.0150 | 0.1716 | 3.6317 | 0.0317 | 0.2190 | 0.8548 | 0.0548 | 0.2973 | ||
| Model | MLEs | ℓ | AIC | AICc | K-S | p-Value |
|---|---|---|---|---|---|---|
| E | −1038.2480 | 2078.4970 | 2078.5180 | 0.0845 | 0.1368 | |
| (0.0008) | ||||||
| EE | −1037.7510 | 2079.5030 | 2079.5670 | 0.0732 | 0.2654 | |
| (0.0869) (0.0010) | ||||||
| EGE | −1037.7500 | 2081.5000 | 2081.6300 | 0.0728 | 0.2722 | |
| (0.6170) (0.0867) | ||||||
| (0.0346) | ||||||
| WE | −1036.7520 | 2079.5050 | 2079.6350 | 0.0578 | 0.5555 | |
| (0.0505) (1.1443) | ||||||
| (0.0130) | ||||||
| BE | −1037.7390 | 2081.4770 | 2081.6080 | 0.0733 | 0.2653 | |
| (0.0868) (0.5976) | ||||||
| (0.0048) | ||||||
| EGWE | −1033.1490 | 2076.2980 | 2076.6280 | 0.0447 | 0.8473 | |
| (8.4796) (1.5611) | ||||||
| (0.1092) (17.1033) | ||||||
| (0.0466) |
| Model | MLEs | ℓ | AIC | AICc | K-S | p-Value |
|---|---|---|---|---|---|---|
| E | −113.3193 | 228.6385 | 228.7438 | 0.3631 | 0.0001 | |
| (0.0253) | ||||||
| EE | −90.1427 | 184.2853 | 184.6097 | 0.1542 | 0.2973 | |
| (2.8950) (0.0578) | ||||||
| EGE | −90.1427 | 186.2853 | 186.952 | 0.1542 | 0.2975 | |
| (11.4663) (2.8962) | ||||||
| (13.5817) | ||||||
| WE | −82.4753 | 170.9506 | 171.6172 | 0.1074 | 0.7458 | |
| (0.5175) (1.1286) | ||||||
| (0.0805) | ||||||
| BE | −87.5174 | 181.0347 | 181.7014 | 0.1269 | 0.5396 | |
| (1.7605) (11.9902) | ||||||
| (0.0718) | ||||||
| EGWE | −78.0985 | 166.197 | 167.9617 | 0.0666 | 0.9943 | |
| (0.0489) (0.0234) | ||||||
| (0.0466) (0.0450) | ||||||
| (0.0105) |
| Model | MLEs | ℓ | AIC | AICc | K-S | p-Value |
|---|---|---|---|---|---|---|
| E | −85.7781 | 173.5563 | 173.6616 | 0.3002 | 0.0015 | |
| (0.0503) | ||||||
| EE | −74.9624 | 153.9249 | 154.2492 | 0.1612 | 0.2494 | |
| (0.8757) (0.0910) | ||||||
| EGE | −74.9624 | 155.9249 | 156.5915 | 0.1612 | 0.2494 | |
| (24.3012) (0.8757) | ||||||
| (49.4421) | ||||||
| WE | −69.558 | 145.1159 | 145.7826 | 0.1184 | 0.6290 | |
| (0.3371) (13.2653) | ||||||
| (3.7702) | ||||||
| BE | −73.5721 | 153.1443 | 153.8109 | 0.1588 | 0.2657 | |
| (0.7364) (49.5981) | ||||||
| (0.2398) | ||||||
| EGWE | −64.9851 | 139.9701 | 141.7348 | 0.0617 | 0.9980 | |
| (0.1609) (0.0228) | ||||||
| (0.1060) (0.1852) | ||||||
| (0.0446) |
| Model | MLEs | ℓ | AIC | AICc | K-S | p-Value |
|---|---|---|---|---|---|---|
| E | −590.1748 | 1182.3500 | 1182.3840 | 0.3610 | 0 | |
| (0.0017) | ||||||
| EE | −530.9825 | 1065.9650 | 1066.0680 | 0.1607 | 0.0043 | |
| (1.1285) (0.0036) | ||||||
| EGE | −530.9824 | 1067.9650 | 1068.1730 | 0.1607 | 0.0043 | |
| (0.0473) (1.1269) | ||||||
| (0.1198) | ||||||
| WE | −502.8310 | 1011.6620 | 1011.8710 | 0.0854 | 0.3500 | |
| (0.2884) (0.7119) | ||||||
| (0.0054) | ||||||
| BE | −522.8252 | 1051.6500 | 1051.8590 | 0.1413 | 0.0173 | |
| (0.8673) (2.3122) | ||||||
| (0.0044) | ||||||
| EGWE | −492.0572 | 994.1143 | 994.6453 | 0.0446 | 0.9717 | |
| (0.0138) (0.0221) | ||||||
| (0.0153) (0.0147) | ||||||
| (0.0030) |
| Model | First Dataset | Second Dataset | Third Dataset | Fourth Dataset |
|---|---|---|---|---|
| E | ||||
| EE | ||||
| EGE | ||||
| WE |
| Dataset | Model | ℓ | AIC | AICc | K-S | p-Value |
|---|---|---|---|---|---|---|
| First dataset | EGWE | −1033.1490 | 2076.2980 | 2076.628 | 0.0447 | 0.8473 |
| BWE | −1033.1590 | 2076.3180 | 2076.647 | 0.0449 | 0.8434 | |
| KWE | −1033.2060 | 2076.4120 | 2076.7420 | 0.0469 | 0.8033 | |
| EKW | −1033.3820 | 2076.7650 | 2077.0940 | 0.0454 | 0.8336 | |
| Second dataset | EGWE | −78.0985 | 166.1970 | 167.9617 | 0.0666 | 0.9943 |
| BWE | −78.2736 | 166.5472 | 168.3119 | 0.0728 | 0.9839 | |
| KWE | −82.1965 | 174.3931 | 176.1578 | 0.1077 | 0.7418 | |
| EKW | −81.0747 | 172.1494 | 173.9141 | 0.0989 | 0.8285 | |
| Third dataset | EGWE | −64.9851 | 139.9701 | 141.7348 | 0.0617 | 0.9980 |
| BWE | −65.4759 | 140.9518 | 142.7165 | 0.0717 | 0.9863 | |
| KWE | −69.2655 | 148.5310 | 150.2957 | 0.1359 | 0.4514 | |
| EKW | 65.2224 | 140.4448 | 142.2095 | 0.0687 | 0.9916 | |
| Fourth dataset | EGWE | −492.0572 | 994.1143 | 994.6453 | 0.0446 | 0.9717 |
| BWE | −500.5021 | 1011.0040 | 1011.5350 | 0.0995 | 0.1897 | |
| KWE | −500.2737 | 1010.548 | 1011.0780 | 0.0868 | 0.3308 | |
| EKW | −504.3558 | 1018.7120 | 1019.2420 | 0.1183 | 0.0716 |
| Model | MLEs | ℓ | acAIC | AICc | K-S | p-Value |
|---|---|---|---|---|---|---|
| EGWE | −491.9093 | 995.8187 | 996.5687 | 0.0569 | 0.8352 | |
| (0.0140) (0.0216) | ||||||
| (0.0157) (0.0156) | ||||||
| (0.0253) (0.0272) |
| Model | MLEs | ℓ | AIC | AICc | K-S | p-Value |
|---|---|---|---|---|---|---|
| EGWE | −746.3648 | 1506.73 | 1505.376 | 0.0661 | 0.5870 | |
| (0.0047) (1.4239) | ||||||
| (0.1487) (0.0733) | ||||||
| (3.9221) (0.0118) (0.2323) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klakattawi, H.S. A Novel Exponentiated Generalized Weibull Exponential Distribution: Properties, Estimation, and Regression Model. Axioms 2025, 14, 706. https://doi.org/10.3390/axioms14090706
Klakattawi HS. A Novel Exponentiated Generalized Weibull Exponential Distribution: Properties, Estimation, and Regression Model. Axioms. 2025; 14(9):706. https://doi.org/10.3390/axioms14090706
Chicago/Turabian StyleKlakattawi, Hadeel S. 2025. "A Novel Exponentiated Generalized Weibull Exponential Distribution: Properties, Estimation, and Regression Model" Axioms 14, no. 9: 706. https://doi.org/10.3390/axioms14090706
APA StyleKlakattawi, H. S. (2025). A Novel Exponentiated Generalized Weibull Exponential Distribution: Properties, Estimation, and Regression Model. Axioms, 14(9), 706. https://doi.org/10.3390/axioms14090706






