A Note on Multi-Index Mittag-Leffler Functions and Parametric Laguerre-Type Exponentials

Abstract

This paper explores the eigenfunctions of specific Laguerre-type parametric operators to develop multi-parametric models, which are associated with a class of the generalized Mittag-Leffler type functions, for dynamical systems and population dynamics. By leveraging these multi-parametric approaches, we introduce new concepts in number theory, specifically those involving multi-parametric Bernoulli and Euler numbers, along with other related polynomials. Several numerical examples, which are generated by using the computer algebra program Mathematica© (Version 14.3), demonstrate the effectiveness of the models that we have presented and analyzed in this paper.

1. Introduction

The connection between Mittag-Leffler functions and hyper-Bessel functions has been highlighted in several papers (see, for example, [1,2,3,4,5,6]). Their importance in fractional calculus is clearly demonstrated in these and other papers. Several interesting applications using one-parameter Mittag-Leffler functions in the study of physical phenomena have recently been obtained in [7,8].

In this paper, we propose to show that a set of special multi-index Mittag-Leffler functions can be viewed as generalized exponentials with respect to suitable generalized Laguerre-type operators. The multi-index functions, which we consider here, are a very special case of those of the type given by

$$\begin{array}{c}\hfill {\displaystyle {\mathrm{E}}_{\left({\alpha }_i\right),\left({\beta }_i\right)}^r\left(t\right)=\sum _{k=0}^{\infty }\frac{t^k}{k!{\displaystyle \prod _{i=1}^r}\mathrm{\Gamma }({\alpha }_{i}k+{\beta }_i)}(r:\mathrm{positive}\mathrm{integer}),}\end{array}$$

(1)

which were considered by Paneva-Konovska (see [5,6]) by extending those studied by Prabhakar [9].

Assuming that ${\alpha }_i=1$ and ${\beta }_i=m_i+1$$(\forall i=1,2,\cdots ,r)$, with positive integers $m_i$, the above functions simply become of the following form:

$$\begin{array}{c}\hfill {\displaystyle {\mathrm{E}}_{\left(m_i\right)}^r\left(t\right)=\sum _{k=0}^{\infty }\frac{t^k}{k!{\displaystyle \prod _{i=1}^r}(k+m_i)!}.}\end{array}$$

(2)

In what follows, we will examine the Laguerre-type operators for the functions in (2), since similar results using fractional-type operators are more complex, as demonstrated in [10] with reference to population dynamics models.

2. Pseudo Versus True Exponential Functions

The pseudo-exponentials, which were considered by Mishra (see, for example, [11] (p. 168, Equation (5.11))) are defined as follows:

$$\begin{array}{c}\hfill {\displaystyle e_m\left(t\right)=\sum _{k=0}^{\infty }\frac{t^k}{k!(k+m)!}.}\end{array}$$

(3)

They satisfy the following property:

$$\begin{array}{c}\hfill D_t{e}_m\left(t\right)=e_{m+1}\left(t\right),\end{array}$$

which is similar to the exponential property but with the shifted parameter m.

Here, and what follows, we use the derivative symbol

$$D_t=D={\displaystyle \frac{d}{dt}}.$$

In fact, the functions in (3) are a special case of the generalized Mittag-Leffler function, which was studied by Prabhakar [9], in its following Laguerre-type version:

$${\displaystyle {}_L\mathrm{E}_{\alpha ,\beta }^{\gamma }\left(z\right)=\sum _{k=0}^{\infty }\frac{{\left(\gamma \right)}_k{z}^k}{{(k!)}^2\mathrm{\Gamma }(\alpha k+\beta )},}$$

where ${\left(\gamma \right)}_k$ denotes the Pochhammer symbol

$${\left(\gamma \right)}_0=1\mathrm{and}{\left(\gamma \right)}_k=\gamma (\gamma +1)(\gamma +2)\cdots (\gamma +k-1)={\displaystyle \frac{\mathrm{\Gamma }(\gamma +k)}{\mathrm{\Gamma }\left(\gamma \right)}},$$

since

$$e(z,m)={}_L\mathrm{E}_{1,m+1}^1\left(z\right).$$

We remark in passing that the functions in each of Equations (1)–(3), and indeed also many of those which were similarly considered in numerous studies of the Mittag-Leffler type functions (see, for details, [12]), are rather obvious special cases of the relatively more widely and more extensively studied Fox–Wright function ${}_p\mathrm{\Psi }_q$ with p numerator parameters and q denominator parameters (see [13,14,15]; see also [16] (p. 183)). As a matter of fact, in a recent survey-cum-expository paper [17], the interested reader will find a comprehensive and extensive analysis of various general families of Mittag-Leffler type functions and their associated operators of fractional calculus, some of which have their origin in the monumental works by Barnes [18] in 1906 and Wright [19] in 1940 (see also [20,21]). Some potentially useful developments, which concern the familiar Mittag-Leffler function itself (see [22]), may be found in (for example) [23,24,25].

It is worth noting here that the function in Equation (3) can easily be seen to behave like a true exponential function with respect to the Laguerre-type operator $DtD+mD$.

Indeed, the following result holds true.

Theorem 1. 

The function $e_m\left(t\right)$ defined in (3), with a positive integer $m,$ is an eigenfunction of the operator:

$$\begin{array}{c}\hfill DtD+mD,\end{array}$$

(4)

since, for every complex constant $a,$ it results

$$\begin{array}{c}\hfill (DtD+mD)a{e}_m\left(t\right)=a{e}_m\left(t\right).\end{array}$$

(5)

Proof. 

In fact, we have

$$\begin{array}{cc}\hfill & {\displaystyle (DtD+mD)\sum _{k=0}^{\infty }\frac{t^k}{k!(k+m)!}}\hfill \\ \hfill & {\displaystyle =Dt\sum _{k=1}^{\infty }\frac{t^{k-1}}{(k-1)!(k+m)!}+m\sum _{k=1}^{\infty }\frac{t^{k-1}}{(k-1)!(k+m)!}}\hfill \\ \hfill & {\displaystyle =D\sum _{k=0}^{\infty }\frac{t^{k+1}}{k!(k+m+1)!}+m\sum _{k=0}^{\infty }\frac{t^k}{k!(k+m+1)!}}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^{\infty }\frac{(k+1)t^k}{k!(k+m+1)!}+m\sum _{k=0}^{\infty }\frac{t^k}{k!(k+m+1)!}}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^{\infty }\frac{(k+m+1)t^k}{k!(k+m+1)!}}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^{\infty }\frac{t^k}{k!(k+m)!},}\hfill \end{array}$$

which evidently completes the proof of Theorem 1. □

For brevity, we use the following notations for the Laguerre-type operators:

$$D_L=DtD=D+t{D}^2\mathrm{and}{D}_{2L}=D+3t{D}^2+t^2{D}^3,$$

and, in general,

$$\begin{array}{cc}\hfill D_{nL}& :=Dt\cdots DtDtD\hfill \\ \hfill & =S(n+1,1)D+S(n+1,2)t{D}^2+\cdots +S(n+1,n+1)t^{n}D+t^{n+1},\hfill \end{array}$$

where $S(n,k)$ denote the Stirling numbers of the second kind, which are defined by the following generating functions:

$$z^n=\sum _{k=0}^{n}S(n,k)z(z-1)\cdots (z-k+1),$$

$${(e^z-1)}^k=k!\sum _{n=k}^{\infty }S(n,k){\displaystyle \frac{z^n}{n!}}$$

and

$${\left[(1-z)(1-2z)\cdots (1-kz)\right]}^{-1}=\sum _{n=k}^{\infty }S(n,k)z^{n-k}\left(\left|z\right|<{\displaystyle \frac{1}{k}}\right).$$

Using this notation, we now generalize the result of Theorem 1 to the case of r parameters, starting from the case $r=2$.

The Two-Parameter Case

We note that, upon putting $m=m_1$, the operator (4) becomes

$$D[tD+m_1],$$

and, by introducing a second parameter $m_2$, it can be iterated in the following form:

$$\begin{array}{cc}\hfill D[tD+m_1][tD+m_2]& =D[t{D}_{t}t{D}_t+(m_1+m_2)t{D}_t+m_1{m}_2]\hfill \\ \hfill & =D_{2L}+(m_1+m_2)D_L+m_1{m}_{2}D.\hfill \end{array}$$

The following result holds true.

Theorem 2. 

The function $e_{m_1,m_2}\left(t\right)$ defined by

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle e_{m_1,m_2}\left(t\right)=\sum _{k=0}^{\infty }\frac{t^k}{k!(k+m_1)!(k+m_2)!},}\hfill \end{array}\end{array}$$

(6)

where $m_1$ and $m_2$ are positive integers, is an eigenfunction of the operator:

$$\begin{array}{c}\hfill D_{2L}+(m_1+m_2)D_L+m_1{m}_{2}D,\end{array}$$

(7)

since, for every complex constant $a,$ it results

$$\begin{array}{c}\hfill [D_{2L}+(m_1+m_2)D_L+m_1{m}_{2}D]a{e}_{m_1,m_2}\left(t\right)=a{e}_{m_1,m_2}\left(t\right).\end{array}$$

(8)

Proof. 

The assertion of Theorem 2 follows by a direct computation, which is similar to that used in the proof of Theorem 1. And, indeed, it was validated by means of Mathematica© (Version 14.3). □

3. The General Case

The procedure used in the two-parameter case can be iterated in general by

$$\begin{array}{cc}\hfill & D[tD+m_1][tD+m_2]\cdots [tD+m_r]\hfill \\ \hfill & =D_{rL}+(m_1+m_2+\cdots +m_r)D_{(r-1)L}+\cdots +m_1{m}_2\cdots m_{r}D.\hfill \end{array}$$

Thus, we find a polynomial in the Laguerre-type operators whose coefficients are the elementary symmetric functions of the parameters, and the following result emerges, which extends those asserted by Theorems 1 and 2.

Theorem 3. 

The function $e_{m_1,m_2,\cdots ,m_r}\left(t\right)$ defined by

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle e_{m_1,m_2,\cdots ,m_r}\left(t\right)=\sum _{k=0}^{\infty }\frac{t^k}{k!{\displaystyle \prod _{i=1}^r}(k+m_i)!},}\hfill \end{array}\end{array}$$

(9)

where $m_1,$$m_2,$$\cdots ,m_r$ are positive integers, is an eigenfunction of the operator:

$$\begin{array}{c}\hfill c_r{D}_{rL}+c_{r-1}{D}_{(r-1)L}+c_{r-2}{D}_{(r-2)L}+\cdots +c_1{D}_L+c_{0}D,\end{array}$$

(10)

with

$$\begin{array}{c}\hfill c_h={\displaystyle \frac{1}{h!}}{\left.{\displaystyle \frac{d^h}{d{x}^h}{\displaystyle \prod _{i=1}^r}(x+m_i)}\right|}_{x=0}(h=0,1,\cdots ,r),\end{array}$$

(11)

that is,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle c_r=1,c_{r-1}=\sum _{i=1}^r{m}_i,c_{r-2}=\sum _{\begin{array}{c}i,j=1\\ i\ne j\end{array}}^r{m}_i{m}_j,}\\ {\displaystyle \phantom{1pt26pt}{c}_{r-3}=\sum _{\begin{array}{c}i,j,k=1\\ i\ne j\ne k\end{array}}^r{m}_i{m}_j{m}_k,\cdots ,c_0={\displaystyle \prod _{i=1}^r}{m}_i,}\end{array}\end{array}$$

since, for every complex constant $a,$ it results

$$\begin{array}{cc}\hfill & \left[c_r{D}_{rL}+c_{r-1}{D}_{(r-1)L}+c_{r-2}{D}_{(r-2)L}+\cdots +c_1{D}_L+c_{0}D\right]a{e}_{m_1,m_2,\cdots ,m_r}\left(t\right)\hfill \\ \hfill & =a{e}_{m_1,m_2,\cdots ,m_r}\left(t\right).\hfill \end{array}$$

(12)

Proof. 

The proof of Theorem 3 can be developed by appealing to the principle of mathematical induction. The relevant verification was obtained up to the order $r=4$, using Mathematica© (Version 14.3), and can be found in Appendix A at the end of this article. □

4. Applications and Extensions

Regarding the possible applications of the multi-parameter functions introduced in the previous sections, we would like to emphasize that, since the exponential function is commonly used to model various physical phenomena and to define sequences of polynomials and special numbers, the introduction of the various forms of the above-mentioned multi-parametric exponentials can possibly be exploited to extend these phenomena and mathematical entities. This has been performed in the recent articles in special cases where generalizations of population dynamics have been illustrated (see [10,26], and the references therein), as well as definitions of new examples of polynomials and special numbers, which are studied in (for example) [27,28].

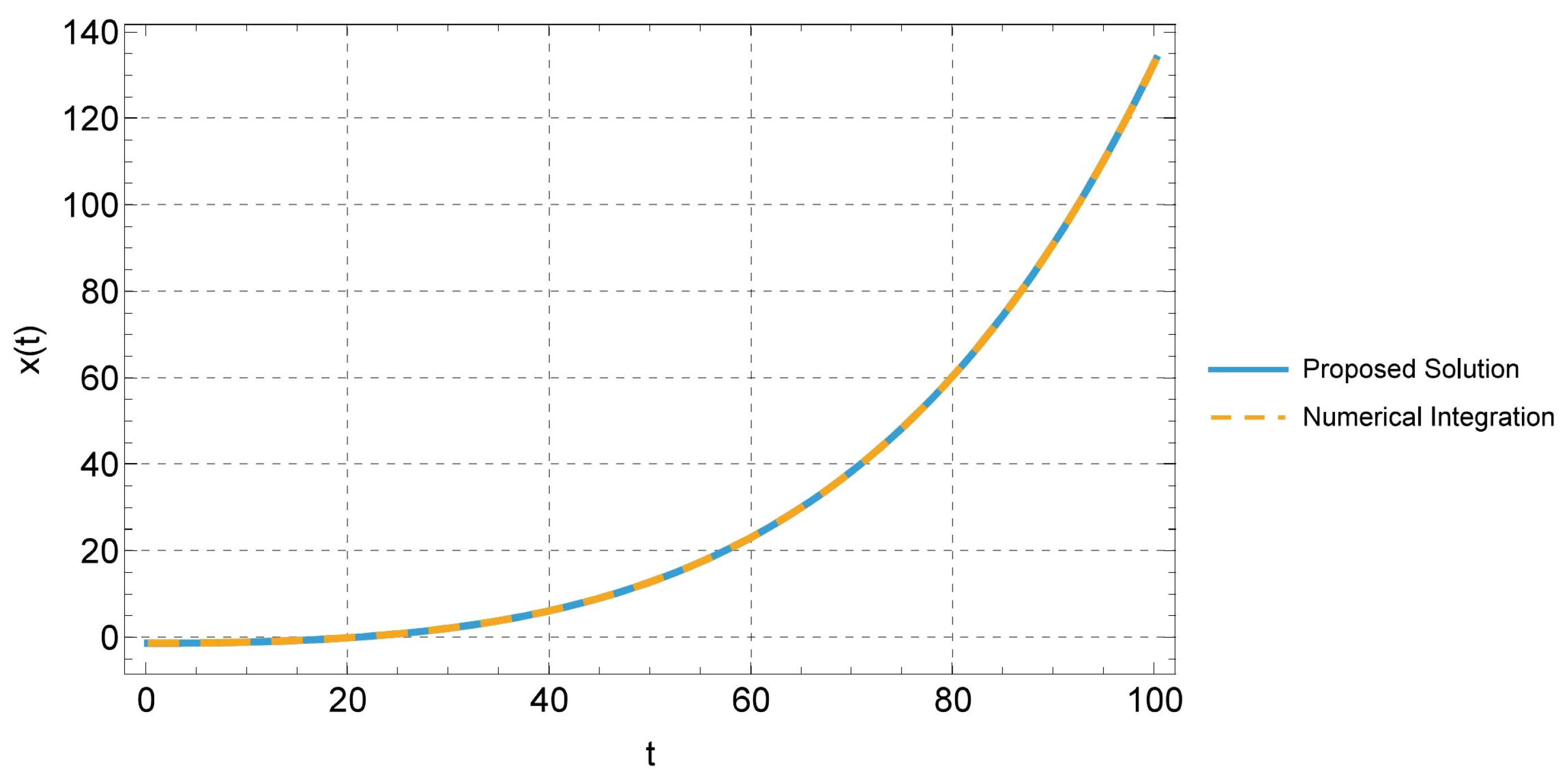
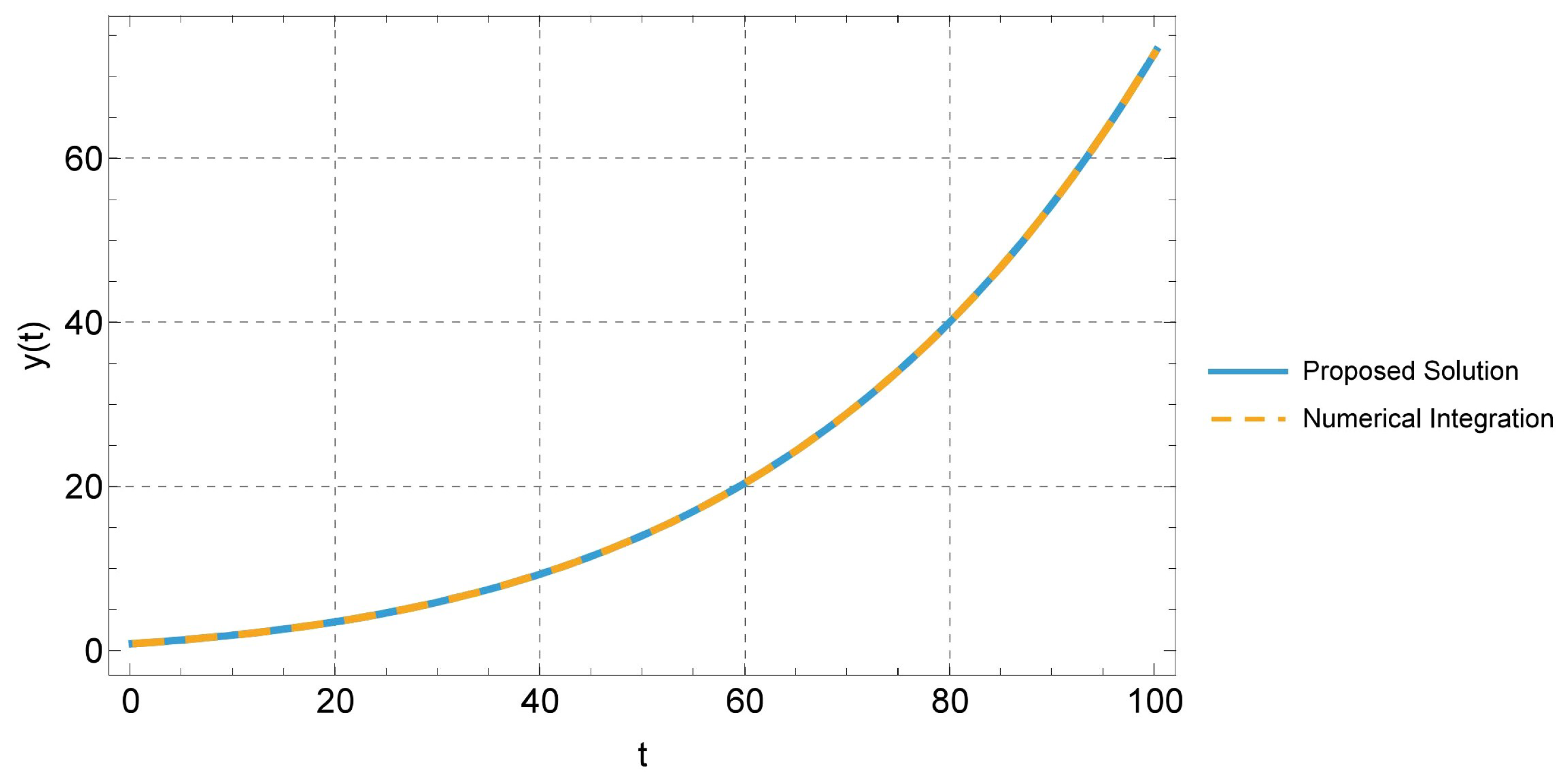
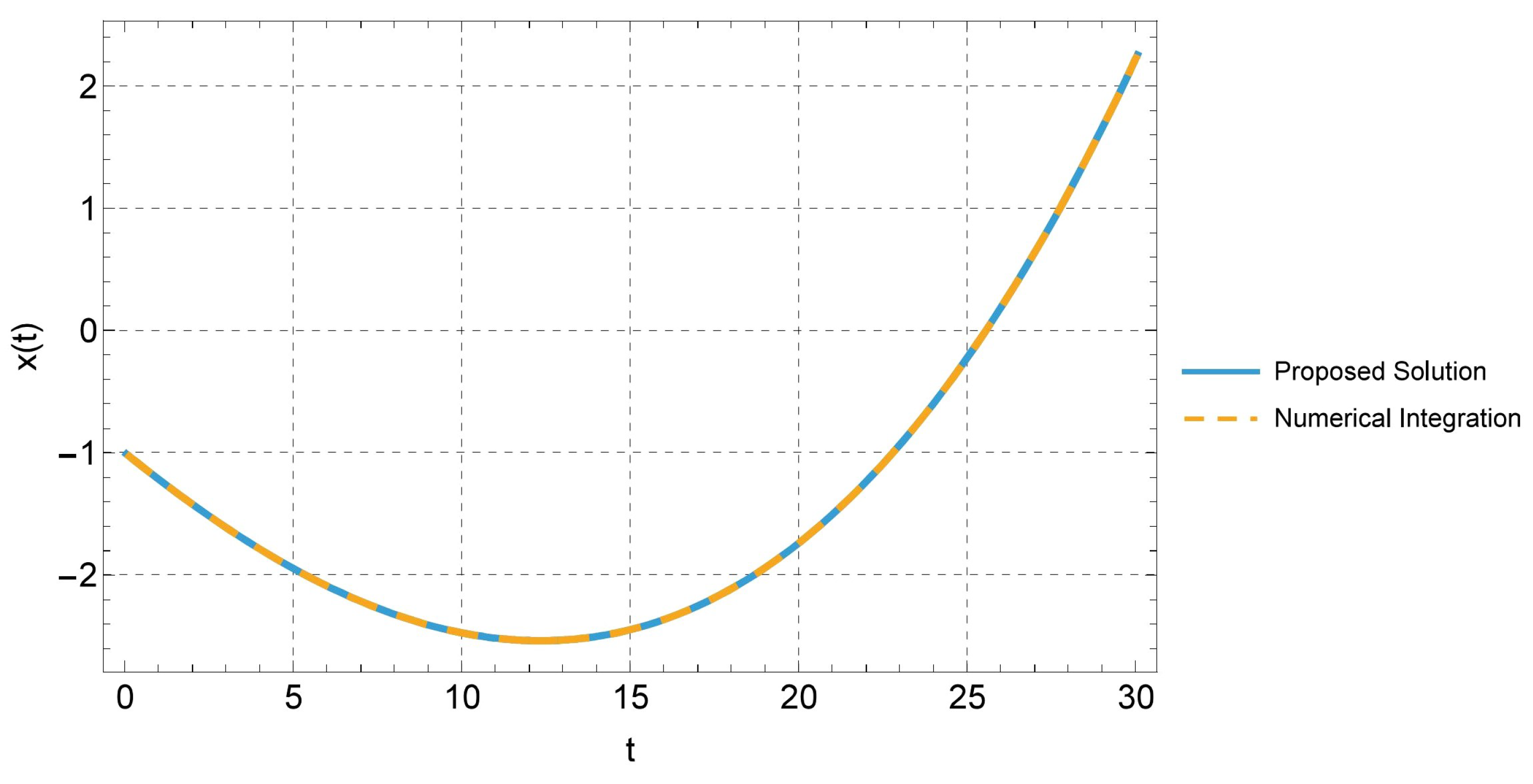
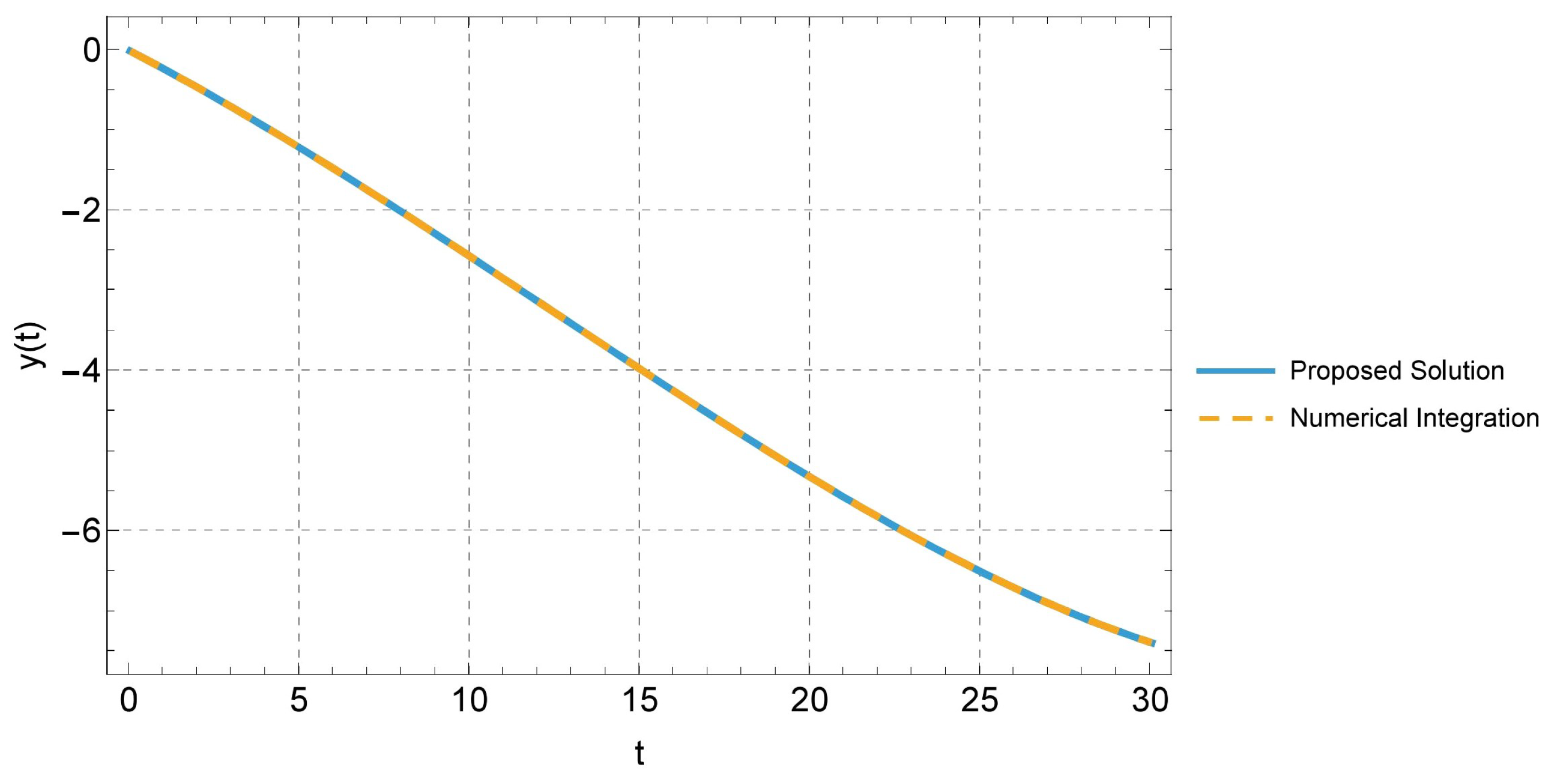
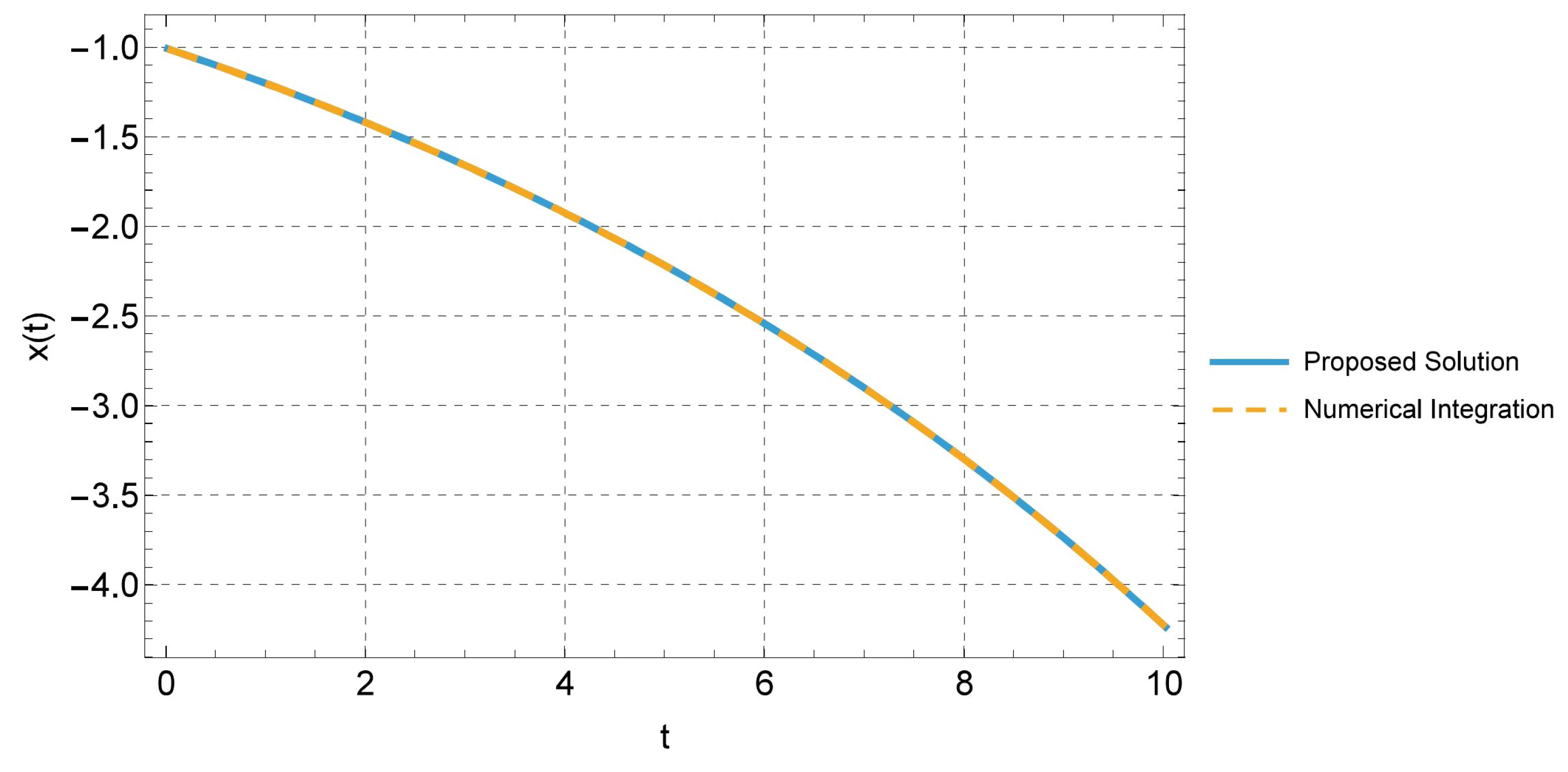
4.1. Multi-Parametric Linear Dynamical Systems

One of the standard applications of the exponential function is related to evolution problems. In this context, with reference to linear dynamical systems, an extension has already been made in [29], but broader generalizations can be obtained in the multi-parametric case. In order to be more precise, using the same technique applied in the above-cited recent work [29], it is possible to prove the following theorem.

Theorem 4. 

Let $\mathcal{A}={\mathcal{A}}_{r\times r}$ be an $r\times r$ non-singular complex matrix. Then the solution to the following Cauchy problem is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left[D_{rL}+(m_1+m_2+\cdots +m_r)D_{(r-1)L}+\cdots +m_1{m}_2\cdots m_{r}D\right]Z\left(t\right)=\mathcal{A}·Z\left(t\right)\hfill \\ Z\left(0\right)=Z_0,\hfill \\ Z^{\prime }\left(0\right)=C\mathcal{A}·Z_0=Z_0^{\prime },\hfill \\ ⋮\hfill \\ Z^{\left(r\right)}\left(0\right)=C{\mathcal{A}}^r·Z_0=Z_0^{\left(r\right)},\hfill \end{array}\right.\end{array}$$

(13)

with

$${\displaystyle C=\frac{1}{c_0+c_1+\cdots +c_r},}$$

is given by

$$\begin{array}{c}\hfill {\displaystyle Z\left(t\right)=\sum _{k=0}^{\infty }{t}^k\frac{{\displaystyle \prod _{i=1}^r}{m}_i!}{k!{\displaystyle \prod _{i=1}^r}(k+m_i)!}{\alpha }_k\left(\mathcal{A}\right)·Z_0,}\end{array}$$

(14)

where the coefficients satisfy the recursion formula:

$${\alpha }_k\left(\mathcal{A}\right)=\mathcal{A}{\alpha }_{k-1}\left(\mathcal{A}\right)and{\alpha }_0\left(\mathcal{A}\right)=\mathcal{I}.$$

Example 1. 

Let $r=2$, $m_1=3,m_2=2$, $\mathcal{A}=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$, $x_0=-1,$ and $y_0=1$. Then $c_1=6,c_2=5,c_3=1,$ and $C=1/12$.

Putting $Z\left(t\right)={\left(x\left(t\right),y\left(t\right)\right)}^T$, the components of the solution to the following Cauchy problem are

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left[D_{2L}+5D_L+6D\right]{\left(x\left(t\right),y\left(t\right)\right)}^T=\mathcal{A}·{\left(x\left(t\right),y\left(t\right)\right)}^T\hfill \\ Z\left(0\right)={(-1,1)}^T,\hfill \\ Z^{\prime }\left(0\right)={\displaystyle \frac{1}{12}}\mathcal{A}·Z_0=Z_0^{\prime },\hfill \\ Z^{\left(2\right)}\left(0\right)={\displaystyle \frac{1}{12}}{\mathcal{A}}^2·Z_0=Z_0^{\left(2\right)}\hfill \end{array}\right.\end{array}$$

and are represented in Figure 1 and Figure 2, where a comparison with the proposed method is shown.

Example 2. 

Let $r=3$, $m_1=1,m_2=2,m_3=2$,

$$\mathcal{A}=\left(\begin{array}{ccc}1& -2& -3\\ 2& 1& -2\\ 3& 2& 1\end{array}\right),$$

$x_0=-1,y_0=0,$ and $z_0=1$. Then $c_1=4,c_2=8,c_3=5,c_4=1,$ and $C=1/18$.

Putting $Z\left(t\right)={\left(x\left(t\right),y\left(t\right),z\left(t\right)\right)}^T$, the components of the solution to the following Cauchy problem are

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left[D_{3L}+5D_{2L}+8D_L+4D\right]{\left(x\left(t\right),y\left(t\right)\right)}^T=\mathcal{A}·{\left(x\left(t\right),y\left(t\right)\right)}^T\hfill \\ Z\left(0\right)={(-1,1)}^T,\hfill \\ Z^{\prime }\left(0\right)={\displaystyle \frac{1}{18}}\mathcal{A}·Z_0=Z_0^{\prime },\hfill \\ Z^{\left(2\right)}\left(0\right)={\displaystyle \frac{1}{18}}{\mathcal{A}}^2·Z_0=Z_0^{\left(2\right)},\hfill \\ Z^{\left(3\right)}\left(0\right)={\displaystyle \frac{1}{18}}{\mathcal{A}}^3·Z_0=Z_0^{\left(3\right)}\hfill \end{array}\right.\end{array}$$

and are represented in Figure 3, Figure 4 and Figure 5, where a comparison with the proposed method is shown.

4.2. Multi-Parametric Population Dynamics Models

Generalizing the results in [30], we consider a multi-parametric extension of the classical Malthus and Verhulst models. Further extensions to the minimum-threshold and Lotka–Volterra models will be considered elsewhere.

4.3. The Multi-Parametric Malthus Case

For example, the multi-parametric Malthus model can be written as follows (see, for details, [31]):

$$\begin{array}{c}\hfill \left[D_{rL}+(m_1+m_2+\cdots +m_r)D_{(r-1)L}+\cdots +m_1{m}_2\cdots m_{r}D\right]P\left(t\right)=RP\left(t\right),\end{array}$$

(15)

where R is a positive integer. Upon applying the following initial conditions:

$$\begin{array}{c}\hfill \begin{array}{c}P\left(0\right)=P_0,\hfill \\ P^{\prime }\left(0\right)=CR{P}_0=P_0^{\prime },\hfill \\ ⋮\hfill \\ P^{\left(r\right)}\left(0\right)=C{R}^r{P}_0=P_0^{\left(r\right)},\hfill \end{array}\end{array}$$

(16)

with

$${\displaystyle C=\frac{1}{c_0+c_1+\cdots +c_r},}$$

the solution is given by

$$\begin{array}{c}\hfill P\left(t\right)={\displaystyle \prod _{i=1}^r}{m}_i!e_{m_1,m_2,\cdots ,m_r}\left(Rt\right)P_0.\end{array}$$

(17)

Example 3. 

Let $r=3$, $m_1=1,m_2=2,m_3=3$, $P_0=x_0=1$, $R=3$. Then $c_1=6,c_2=11,c_3=6,c_4=1$, $C=1/34$.

The solution to the following Mathus problem

$$\begin{array}{c}\hfill \begin{array}{c}\left[D_{3L}+6D_{2L}+11D_L+6D\right]P\left(t\right)=3P\left(t\right)\hfill \\ P\left(0\right)=1,\hfill \\ P^{\prime }\left(0\right)={\displaystyle \frac{1}{8}},\hfill \\ P^{\prime \prime }\left(0\right)={\displaystyle \frac{9}{34}},\hfill \\ P^{\left(3\right)}\left(0\right)={\displaystyle \frac{27}{34}},\hfill \end{array}\end{array}$$

according to Equation (17), is given by

$$\begin{array}{c}\hfill {\displaystyle P\left(t\right)=12e_{1,2,3}\left(3t\right)=12\sum _{k=0}^{\infty }\frac{{\left(3t\right)}^k}{k!(k+1)!(k+2)!(k+3)!}.}\end{array}$$

The relevant graph is represented in Figure 6, where a comparison with the proposed solution is shown.

4.4. The Multi-Parametric Verhulst Case

We consider the following multi-parametric Verhulst model:

$$\begin{array}{cc}\hfill & \left[D_{rL}+(m_1+m_2+\cdots +m_r)D_{(r-1)L}+\cdots +m_1{m}_2\cdots m_{r}D\right]P\left(t\right)\hfill \\ \hfill & =RP\left(t\right)\left[1-{\displaystyle \frac{1}{K}}P\left(t\right)\right],\hfill \end{array}$$

(18)

where R is a positive constant, which is called the intrinsic growth rate, and K denotes the environmental capacity.

Upon applying the following initial conditions:

$$\begin{array}{c}\hfill \begin{array}{c}P\left(0\right)=P_0,\hfill \\ P^{\prime }\left(0\right)=CR{P}_0\left(1-{\displaystyle \frac{1}{K}}{P}_0\right)=P_0^{\prime },\hfill \\ ⋮\hfill \\ P^{\left(r\right)}\left(0\right)=C{R}^r{P}_0\left(1-{\displaystyle \frac{1}{K}}{P}_0\right)=P_0^{\left(r\right)},\hfill \end{array}\end{array}$$

(19)

with

$${\displaystyle C=\frac{1}{c_0+c_1+\cdots +c_r},}$$

the solution is given by

$$\begin{array}{c}\hfill {\displaystyle P\left(t\right)=\sum _{k=0}^{\infty }{a}_k\frac{t^k}{k!{\displaystyle \prod _{i=1}^r}(k+m_i)!},}\end{array}$$

(20)

where the coefficients $a_k$ satisfy the following recursion formula:

$$\begin{array}{c}\hfill a_0={\displaystyle \prod _{i=1}^r}{m}_i!P_0,\end{array}$$

and

$$\begin{array}{c}\hfill a_{k+1}=R\left({\displaystyle a_k-\frac{1}{K}\sum _{n=0}^k\frac{k!{\displaystyle \prod _{i=1}^r}(k+m_i)!a_n{a}_{k-n}}{n!{\displaystyle \prod _{i=1}^r}(n+m_i)!(k-n)!{\displaystyle \prod _{i=1}^r}(k-n+m_i)!}}\right).\end{array}$$

Example 4. 

Let $r=3$, $m_1=1,m_2=2,m_3=3$, $P_0=x_0=-1$, $R=3$, and $K=2$. Then $c_1=6,c_2=11,c_3=6,c_4=1,$ and $C=1/34$.

The solution to the following Mathus problem

$$\begin{array}{c}\hfill \begin{array}{c}\left[D_{3L}+6D_{2L}+11D_L+6D\right]P\left(t\right)=3P\left(t\right)\left(1-{\displaystyle \frac{1}{2}}P\left(t\right)\right)\hfill \\ P\left(0\right)=-1,\hfill \\ P^{\prime }\left(0\right)=-{\displaystyle \frac{1}{8}}\left(1+{\displaystyle \frac{1}{2}}\right)=-{\displaystyle \frac{3}{16}},\hfill \\ P^{\prime \prime }\left(0\right)=-{\displaystyle \frac{9}{34}}\left(1+{\displaystyle \frac{1}{2}}\right)=-{\displaystyle \frac{27}{8}},\hfill \\ P^{\left(3\right)}\left(0\right)=-{\displaystyle \frac{27}{34}}\left(1+{\displaystyle \frac{1}{2}}\right)=-{\displaystyle \frac{81}{68}},\hfill \end{array}\end{array}$$

according to Equation (21), is given by

$$\begin{array}{c}\hfill {\displaystyle P\left(t\right)=\sum _{k=0}^{\infty }{a}_k\frac{t^k}{k!(k+1)!(k+2)!(k+3)!},}\end{array}$$

where the coefficients $a_k$ satisfy the following recursion formula:

$$\begin{array}{c}\hfill a_0=-12,\end{array}$$

and

$$\begin{array}{c}\hfill a_{k+1}=R\left({\displaystyle a_k-\frac{1}{2}\sum _{n=0}^k\frac{k!(k+1)!(k+2)!(k+3)!a_n{a}_{k-n}}{n!(n+1)!(n+2)!(n+3)!(k-n)!(k-n+1)!(k-n+2)!(k-n+3)!}}\right).\end{array}$$

The relevant graph is represented in Figure 7, where a comparison with the proposed solution is shown below.

5. Further Applications

Extending the results that are shown in [27], one can consider the multi-parametric Bernoulli and Euler numbers and the related polynomials, starting from the following definitions:

•

Multi-parametric Bernoulli numbers:

$$\begin{array}{c}\hfill {\displaystyle \frac{t}{e_{m_1,m_2,\cdots ,m_r}\left(t\right)-1}=\sum _{n=0}^{\infty }{B}_{(m_1,m_2,\cdots ,m_r|n)}\frac{t^n}{n!}.}\end{array}$$

(21)

•

Multi-parametric Bernoulli polynomials:

$$\begin{array}{c}\hfill {\displaystyle \frac{t{e}_{m_1,m_2,\cdots ,m_r}\left(xt\right)}{e_{m_1,m_2,\cdots ,m_r}\left(t\right)-1}=\sum _{n=0}^{\infty }{B}_{(m_1,m_2,\cdots ,m_r|n)}\left(x\right)\frac{t^n}{n!}.}\end{array}$$

(22)

•

Multi-parametric Euler numbers:

$$\begin{array}{c}\hfill {\displaystyle \frac{2e_{m_1,m_2,\cdots ,m_r}\left(t\right)}{e_{m_1,m_2,\cdots ,m_r}\left(2t\right)+1}=\sum _{n=0}^{\infty }{E}_{(m_1,m_2,\cdots ,m_r|n)}\frac{t^n}{n!}.}\end{array}$$

(23)

•

Multi-parametric Euler polynomials:

$$\begin{array}{c}\hfill {\displaystyle \frac{2e_{m_1,m_2,\cdots ,m_r}\left(xt\right)}{e_{m_1,m_2,\cdots ,m_r}\left(t\right)+1}=\sum _{n=0}^{\infty }{E}_{(m_1,m_2,\cdots ,m_r|n)}\left(x\right)\frac{t^n}{n!}.}\end{array}$$

(24)

The Case of the Fractional Derivatives

Extensions of the above results deal with the use of fractional derivatives by introducing the multi-parametric fractional operators defined as follows:

$$\begin{array}{cc}\hfill & D_t^{\alpha }[t^{\alpha }{D}_t^{\alpha }+m_1][t^{\alpha }{D}_t^{\alpha }+m_2]\cdots [t^{\alpha }{D}_t^{\alpha }+m_r]\hfill \\ \hfill & =D_{rL}^{\alpha }+(m_1+m_2+\cdots +m_r)D_{(r-1)L}^{\alpha }+\cdots +m_1{m}_2\cdots m_r{D}^{\alpha }\left(D^{\alpha }:=D_t^{\alpha }\right).\hfill \end{array}$$

This is not a trivial topic, and it is not sufficient to change the factorials into their expressions using the familiar (Euler’s) Gamma function $\mathrm{\Gamma }(·)$, but it needs a deeper analysis. In addition to those that are extensively and comprehensively analyzed in the above-cited survey-cum-expository paper [17], the interested readers may find useful information in the vast literature on the various existing operators of fractional integrals and fractional derivatives (see, for example, [32,33,34,35,36,37]).

In forthcoming articles, some of the above-mentioned topics will be examined in detail. We choose to cite a number of potentially useful works on the hyper-Bessel type functions and the related operational calculus [38,39,40,41,42] as well as on mathematical biology (see, for example, [43,44,45]).

6. Conclusions

Here, in our present investigation, we have applied and exploited some multi-parametric forms of functions that behave as exponentials with respect to suitable Laguerre-type differential operators in order to introduce extensions of some classical mathematical models. In particular, we have introduced multi-parametric versions of linear dynamical systems and population dynamics models.

Multi-parametric extensions of classical entities from number theory, such as the Bernoulli and Euler numbers and the related generalized polynomial systems, have also been suggested herein.

Numerical verifications, which are constructed using the computer graphics program Mathematica© (Version 14.3), have been shown throughout our investigation.