1. Introduction
The boundary integral equation (BIE) method is a very powerful approach for the numerical solution of various boundary value problems (BVPs). The main advantage of the BIE method consists in the dimensionality decrease of the given differential problem: the BVP is reduced to the BIE, where the unknown function is defined only on the domain boundary [
1]. Clearly, the considered differential equation needs to have a fundamental solution and be homogeneous. For the numerical solution of such a BIE, effective numerical methods have been developed, for example, projection methods [
1].
In the case of non-stationary BVPs, there are additional difficulties caused by the presence of time as an independent variable. There are several ways to apply the BIE to such BVPs [
2]. One approach involves a fundamental solution of the time-dependent differential equation. Then, by a direct or indirect BIE method, the initial BVP can be reduced to a time-domain boundary integral equation. The numerical solution of such a BIE is more difficult than in the stationary case. The most popular method for time-domain boundary integral equations is the convolution quadrature method suggested by Christian Lubich in the 1980s [
3].
Another so-called two-step method consists of the semi-discretization of the given initial BVP with respect to the time variable. As a result, the set of stationary BVPs for elliptic equations is obtained. This time discretization can be achieved using approaches such as finite-difference approximations (e.g., the Rothe method [
4]) or integral transforms (e.g., the Laguerre transform [
5,
6], the Laplace transform [
7]). In the second step, which addresses the spatial variable, various techniques are available, including the BIE method. Two-step methods offer several advantages, such as dimension reduction and the avoidance of volume integrals. The finite-difference semi-discretization is the simplest approach, which gives the numerical solution in a fixed set of time moments. In the case of integral transforms, we have an approximation for an arbitrary time, but it is necessary to calculate the inverse transform numerically.
The application of the Laplace transform to time-dependent problems has a long history. It can be used in combination with the finite difference method [
8], finite element method [
9], boundary element method [
10,
11] and others. In the case of the parabolic initial BVP, stationary BVPs for the Helmholtz-type equations with complex parameters can be obtained. The inverse Laplace transform is defined as the Bromwich integral on the complex plane, and there are multiple numerical methods for its calculation (see [
7,
12,
13,
14,
15,
16,
17,
18,
19] and references therein).
In this paper, we use the two-step approach based on the Laplace transform and the BIE method to solve parabolic initial BVPs in 3D domains. To calculate the inverse transform, the sinc-quadrature rule suggested in [
13] is applied. This leads to a set of independent BVPs for the Helmholtz-type equation, which can be numerically solved in parallel. We consider the case of specific smooth surfaces, diffeomorphic to the unit sphere. It provides the possibility of applying effective numerical schemes for the received BIE. We apply the Nyström method based on the Wienert’s quadrature rules for the surface integrals [
20].
The main contribution of this work is reducing computational costs by selecting optimal values for the inverse Laplace transform’s contour parameters, decreasing the number of stationary BVPs due to the symmetry of the quadrature nodes and applying an efficient method for numerically solving the resulting BIEs.
The outline of the present work is as follows. In
Section 2, we apply the Laplace transform to the parabolic initial boundary value problem and describe the sinc quadrature for the numerical inverse transform. Two ideas for decreasing computational cost are presented in
Section 2.1 and
Section 2.2. In
Section 2.1, it is shown that due to a certain symmetry of the sinc-quadrature nodes, the number of stationary problems can be reduced almost twice. In
Section 2.2 reflects how the choice of integration contour in the complex plane influences the precision of the sinc quadrature. In
Section 3, we apply the indirect BIE method to stationary elliptic problems. The unknown solution is presented in the form of a double-layer potential, and a BIE of the second kind is obtained. Taking into account that the boundary surface is diffeomorphic to the unit sphere, we apply the Nyström method based on the Wienert’s quadrature rules.
Section 4 presents numerical examples to clarify our approach and its optimization.
Before closing this section, we formulate the problem to be studied. Let
be a simply connected region with a smooth boundary
. It is necessary to find function
, which satisfies the heat equation
the initial condition
and the Dirichlet boundary value condition
Assume that the given function
g is bounded and continuous and satisfies the compatibility condition
.
We consider surfaces
, diffeomorphic to the unit sphere
described by an analytic function
with a nonzero Jacobian
J.
2. Time Semi-Discretization via Laplace Transform
The Laplace transform of a function
is given by
The integral in (
4) is convergent for
, where
is the order of growth of function
, and
is an analytic function [
21].
For the known image
F, the original
f can be reconstructed by using the inverse Laplace transform, described by the Bromwich integral
where
C is a suitable integration contour (see [
7,
13,
14,
15,
16] and references therein).
A popular strategy to use the Laplace transform for the heat problems is as follows:
Apply the Laplace transform in time to the initial boundary value problem to obtain boundary value problems for the Helmholtz-type equations.
Build an effective solver for stationary problems.
Reconstruct time-domain solution via numerical inversion of the Laplace transform.
One approach to approximating the inverse Laplace transform was proposed in [
13]. If
F can be analytically continued to the set
, where
and there exists
such that
then to approximate the inverse Laplace transform of function
F, a quadrature formula is proposed based on the use of sinc quadrature for integral (
5) with a special integration contour (see
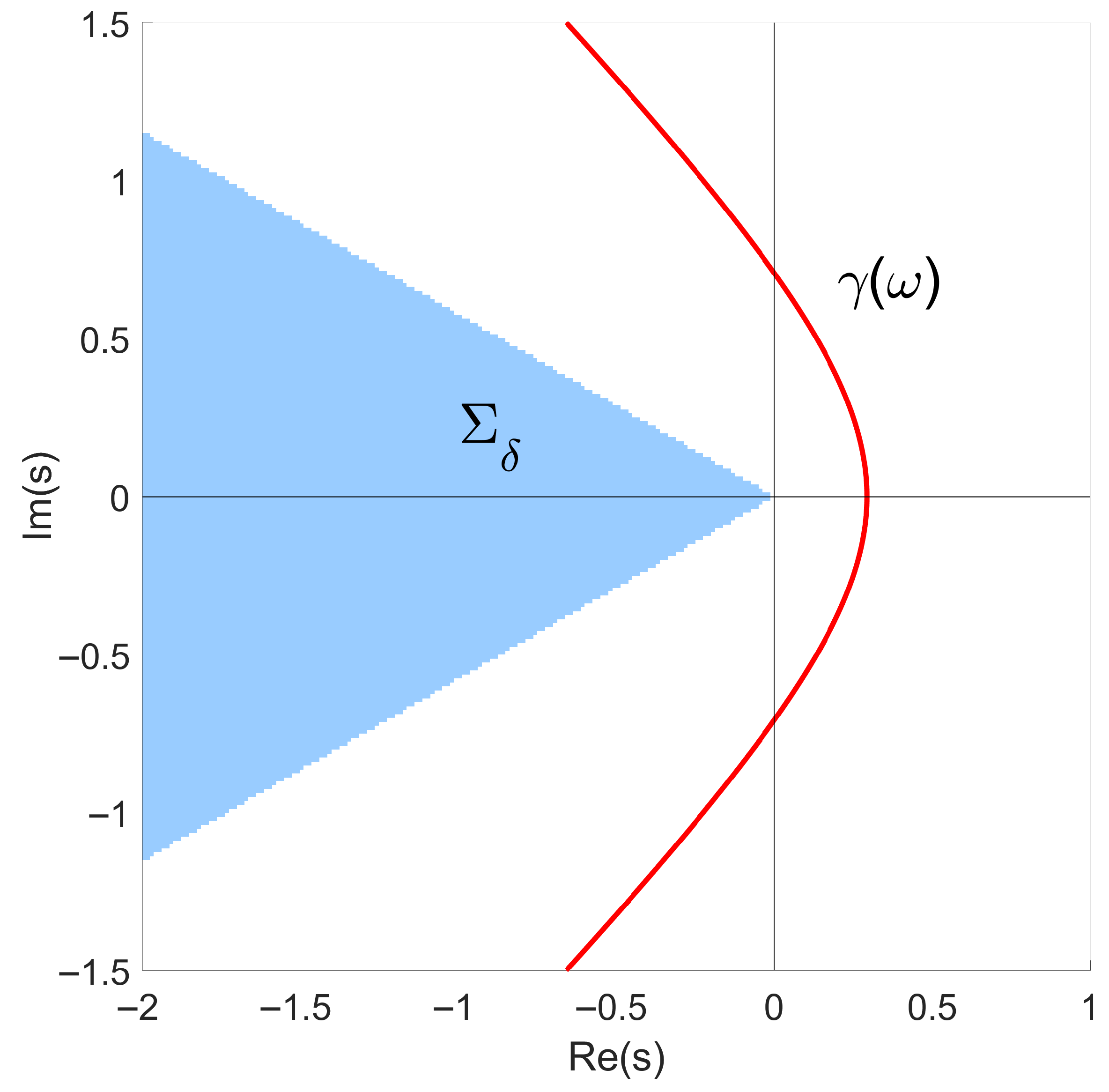
Figure 1)
Here,
,
are arbitrary parameters that define the geometry of contour (
6).
Using contour (
6) to parametrize integral (
5), we obtain
Let
,
,
,
. Integral (
7) can be approximated using the following quadrature formula [
13]
Let us denote
and
; then, we obtain
Note that when computing
for different values of
t, one can use the same set of values
. The approximation error of (
9) is shown to behave like
and is stable to the perturbations of
. This is especially important when values
are computed numerically [
13].
Since the solution of the non-stationary problem (
1)–(
3)
u is bounded with respect to the time variable, i.e., its order of growth is equal to 0, the Laplace transform with respect to time can be applied to both parts of Equation (
1). Taking into account property
[
21] and the zero initial condition, we obtain the following equation for the Laplace image
On the boundary of the domain, the function
satisfies the following condition
where
. Thus, for
we get a boundary value problem (
10) and (
11) for the Helmholtz equation with a complex wavenumber.
Applying the described approach for the inverse Laplace transform, in order to find an approximate solution of problem (
1)–(
3), it is necessary to compute
that is, to solve a set of
problems (
10) and (
11) for
Here,
. It is important to emphasize that problems (
12) and (
13) are independent of each other, enabling their parallel solution.
In [
7,
14], it was shown that the image of the solution to the heat problem
, as a function of the complex argument
s, could be analytically continued to the set
, and there existed a constant
such that
Thus, in our case, we can apply the approach from [
13] and use contour (
6) for any
and
.
Note that in order to solve problems (
12) and (
13), it is necessary to have boundary functions
, i.e., have the Laplace image
of the original boundary condition
g. If
is not available in a closed form, it can be approximated using various techniques, including using Laguerre polynomials or exponential sums’ expansions of the original function [
22,
23], approximation of the original function by rational functions [
24], applying quadrature rules to the Laplace transform integral [
25] and others. The approximation of
is beyond the scope of the current article, and we use examples of
g with a known Laplace transform for the numerical experiments.
Recalling problems (
12) and (
13) are 3D stationary boundary value problems, it is easy to see that solving them numerically may pose a significant computational effort. The main motivation for this article was to suggest certain ideas for decreasing the amount of computational work, as described further.
2.1. Reducing the Number of Stationary Problems
It is easy to notice that .
Then,
where
denotes the complex conjugate of z. We use the fact that
for any complex
z [
26].
Thus, quadrature nodes (
14) are pairwise conjugate, except for node
. This allows us to reduce the solution of the set of
stationary problems to
problems.
Theorem 1. Assume is a simply connected region with a smooth boundary Γ from , and complex-valued parameter . Let be a solution of the problem
- (a)
- (b)
- (c)
- (d)
Proof. Statement (d) follows directly from (b). Let us show that (c) follows from (a).
We denote
Then, (a) can be written as
Thus,
Then,
which proves statement (c). □
Corollary 1. Solutions of problems (
12)
and (
13)
with indices and j are complex conjugates Proof. Using the well-known fact that
(for real valued
[
26]), it is easy to see that the boundary conditions of the problems with indices
and
j are complex conjugates. Since
, it follows from Theorem 1 that the solutions of problems (
12) and (
13) with indices
and
j are also complex conjugates. □
Thus, it is sufficient to solve the stationary problems for indices , and the solutions for indices can be obtained automatically from the Corollary 1.
2.2. Integration Contour Parameters Optimization
As mentioned earlier, integration contour (
6) depends on parameters
and
.
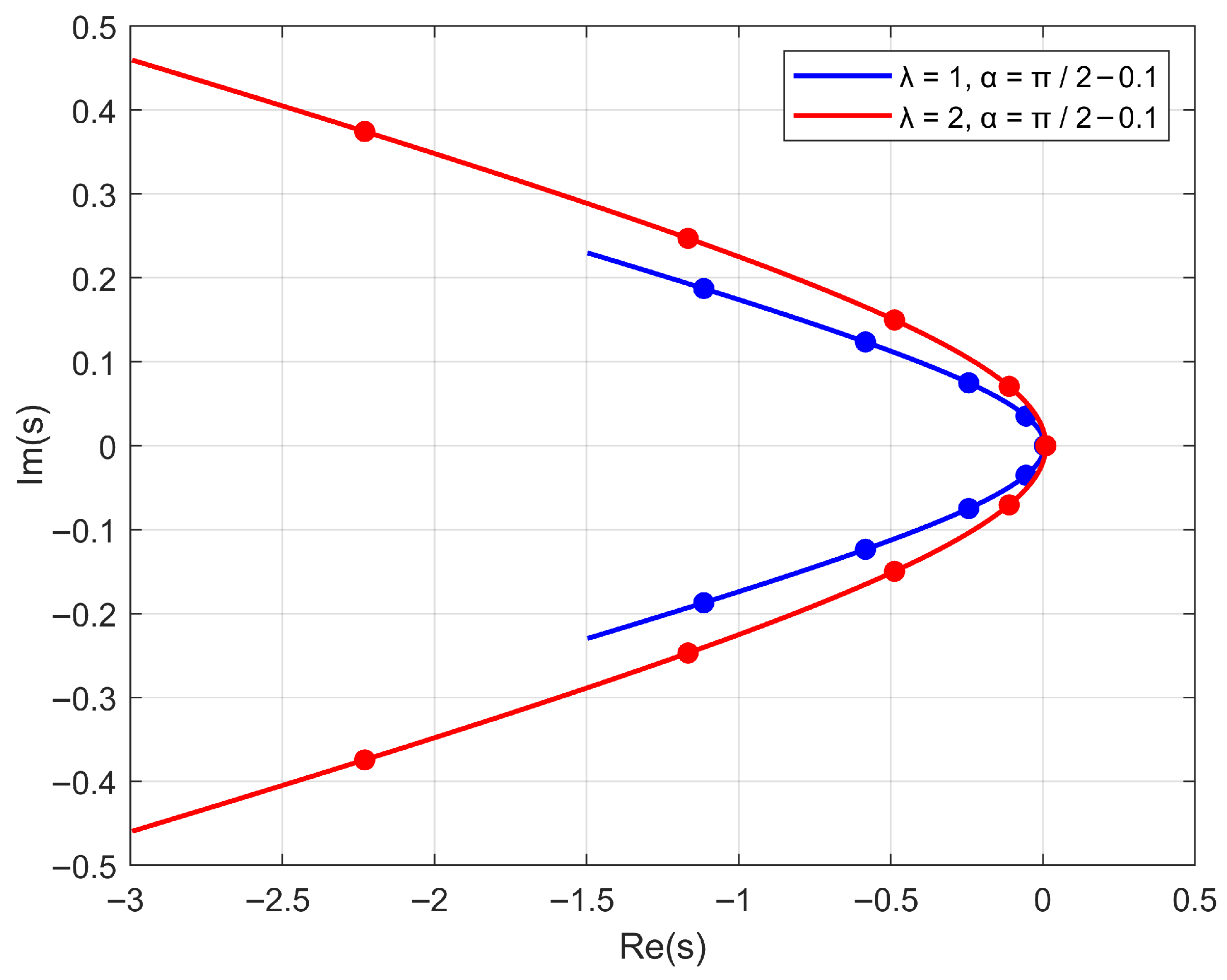
Figure 2 and
Figure 3 show the influence of parameters
and
on the shape of the contour and placement of the nodes for
.
Since the approximate solution of the 3D stationary problems requires a large number of computations, it makes sense to select parameters and in such a way as to reduce the expected error.
To find parameters
and
for which the error is minimized, we define search intervals for the optimal values of
and
and construct a uniform grid of test values for them:
We fix certain values of
t and
and select a Laplace transform pair of test functions
and
. It is natural to select
to be similar to the behavior of the boundary condition
g. Then, for each pair of values
, we compute the absolute or relative errors
and
of the numerical Laplace transform inversion (
9) for
and find the values
for which
The obtained contour parameters
are then used to define quadrature nodes
and solve
stationary problems. We do not provide an explicit recipe to define
and
. For
it seems natural to define
close to 0 and
close to
and thus “scan” most of the
interval. For
, it seems natural to define
close to 0, and it is empirically observed that increasing
prevents us from finding different
’s after certain values of
. This is intuitively supported by understanding that for large values of
, nodes
quickly start to extend far into the left half-plane and their contribution in sum (
9) becomes negligible.
3. Solver for Stationary Boundary Value Problems
In this section, we consider the numerical solution of the stationary problems (
12)–(
13). We apply the BIE method with later application of the Nyström method based on the quadrature rules for surface integrals proposed by Wienert [
20].
For brevity, we rewrite problems (
12) and (
13) as
The fundamental solution of Equation (
19) has the following form [
27]
Since
, it is known that under suitable assumptions on the boundary
and for sufficiently smooth boundary data
, the solution of the Dirichlet problem exists and is unique; see [
27] and references therein. The solution of (
19) can be written in the form of a double-layer potential
where
,
is the potential density, and
is the unit outward normal vector to
.
Potential (
22) is a solution of problems (
12) and (
13) if the density
is a solution of the Fredholm integral equation of the second kind
For any
, Equation (
23) has a unique solution
in
[
27].
Since
, we can obtain the parametrized integral equation on
where we denoted
and
Function
K is a weakly singular integral kernel that can be rewritten in the form
where
Note that due to the analyticity of
q, the well-posedness of (
23) also applies to (
24). In order to discretize (
24), we consider the quadrature rules proposed by Wienert [
20]. For a given space discretization parameter
, the following values are defined
where
are the zeros of the Legendre polynomials
[
28].
For a given function
, approximation
is defined as
where
, and by
we denote a scalar product of two vectors. Note that the poles are excluded from the continuity requirements, since values of the parametrized functions
at the poles may depend on the direction of approach (i.e., specific value of
) and may be not continuous at the poles.
For non-singular integrands, the following quadrature rule is suggested
For weakly singular integrands, the following quadrature rule can be used
where
and
Both quadratures are obtained by approximating the regular part of the integrand via approximation
and then using exact integration. According to results in [
20], these quadrature rules have super-algebraic or even exponential convergence order, depending on the smoothness of
f.
By simple substitution, the quadrature rule (
28) can be extended to a more general case
where
is usually a rotation, such that
, see [
20].
Applying (
29) to the integral in (
24), for
, we get an approximation equation
We observe that (
30) contains values of the density
in the rotated nodes
. In order to be able to construct a system of linear equations, we replace
with its approximation by
(
26)
Substituting (
31) back into (
30), we get
where
Collocating the Equation (
32) in the nodes
, we get a
system of linear equations for the unknown values
After solving (
33), the approximate solutions of problems (
19) and (
20) for parameter
can be found by applying the quadrature rule (
27) to (
22)
where
for the parameter value
.
Having solved a set of problems (
19) and (
20), we can construct the approximate solution of the original non-stationary problems (
1)–(
3)
As previously mentioned, the error rate of the numerical inversion of the Laplace transform behaves like
and is stable to perturbations of
values. In our case, these perturbations are created by the fact that
are approximated by
, which in practice exhibits a super-algebraic convergence rate for sufficiently smooth surfaces and boundary conditions. As result, when
and
N are selected in a balanced way, the overall error rate of the original non-stationary problem is super-algebraic, which is shown in the following numerical experiments.
5. Conclusions
In this article, an effective combination of the Laplace transform and boundary integral equation method for the numerical solution of the 3D initial boundary value problem for the heat equation was proposed and tested.
The optimization of the inverse Laplace transform integration contour parameters was shown to substantially decrease the approximation error, allowing for the reduction in the number of stationary BVPs to achieve a certain level of precision. Moreover, using observed and proven symmetry in the set of boundary value problems, computational work was further reduced by a factor of almost two. As mentioned in the article, due to the independence of the boundary value problems, the proposed approach is also suitable for parallel computing.
The stationary BVPs were solved using the indirect BIE method with application of the Nyström method based on the Wienert quadrature rules for the surface integrals.
The efficiency and feasibility of the suggested two-step approach were confirmed by a set of numerical experiments, testing time and space discretization methods separately and combined.
In future work, the presented approach will be tested with other methods for solving boundary value problems, as well as different equations or types of boundary conditions. Further research of the optimization techniques for the numerical Laplace transform inversion is planned. Another direction of research is to expand the domain types, consider doubly connected regions, etc. Additionally, the described approach will be used for the numerical solution of inverse problems, for example, the lateral Cauchy problem to reconstruct boundary data on part of the domain boundary.