Two Reducts of Basic Algebras

Abstract

This paper investigates the relationship between implication reducts and Sheffer stroke reducts in basic algebras. The study establishes a one-to-one correspondence between bounded Sheffer stroke basic algebras and strong implication basic algebras. Furthermore, it examines several key properties of compatible filters in Sheffer stroke basic algebras.

1. Introduction

The Sheffer stroke (also known as a NAND operation) was initially introduced by Sheffer [1], in order to obtain Boolean functions from a single binary operation. This operation holds a unique position in algebraic logic, due to its functional completeness—the remarkable ability to express all fundamental logical operations by itself without usage of any other logical connective; this property distinguishes it as a powerful tool for logical system representation. The Sheffer stroke is not only useful in Boolean algebra but also in other algebraic structures, helping us explore the connections between logic and algebra more deeply.

The study of Sheffer stroke operations in algebraic structures has attracted considerable attention in recent years. McCune et al. [2] demonstrated that the Sheffer stroke operation can be used to formulate a single equational axiom for Boolean algebras. This result was later extended by Chajda [3], who proved that an analogous axiomatization holds in lattices endowed with an antitone involution, particularly in ortholattices. Oner and Senturk [4] introduced the Sheffer stroke operation in basic algebras and established its connection to Boolean algebras. Subsequently, together with Saeid [5], they investigated congruence properties in Sheffer stroke basic algebras. Senturk [6] further constructed and analyzed three state operators on Sheffer stroke basic algebras. Molkhasi [7] proved that Lukasiewicz near-semi-rings are categorically equivalent to Sheffer stroke basic algebras with a least element 0. Meanwhile, the connection between Sheffer stroke operations and Hilbert algebras was first explored in [8] and extended in [9], leading to the emergence of Sheffer stroke Hilbert algebras as a distinct research area.

Implication algebras were initially introduced by Abbott in 1967 [10] for Boolean algebras. As a generalization, Abbot investigated orthoimplication algebra in [11] and Chajda, Halaš and Kühr introduced weak implication algebras as the implication reducts of MV-algebras [12]. To include these two implication algebras, the concept of implication basic algebras was proposed in [13]. Furthermore, for non-associative MV-algebras, the authors show that the correspondence between weak Sheffer stroke NMV-algebras and implication NMV-algebras is one-to-one in [14].

The study of algebraic reducts has deep roots in Mal’tsevs systematic development of algebraic structures [15], particularly his categorical treatment of derived operations. Building upon Plotkin’s subsequent unification of algebraic logic with computational structures [16], our investigation of Sheffer stroke versus implication reducts reveals new connections between these two fundamental representations of basic algebras.

In this work, we first discuss the relationship between Sheffer stroke basic algebras and implication basic algebras. We show that every Sheffer stroke basic algebra is an implication basic algebra, although the converse does not hold. Then, we focus on a special class of implicative basic algebras, which is called strong implication basic algebras, and we obtain a one-to-one correspondence between bounded Sheffer stroke basic algebras and strong implication basic algebras (cf. Theorem 1). We also show that the variety of Sheffer stroke basic algebras is weakly regular, congruence distributive and congruence 3-permutable (cf. Theorem 2). Finally, we use the ideal terms to characterize compatible filters of Sheffer stroke basic algebras (cf. Theorem 3).

2. Preliminaries

In this section, we present the fundamental concepts and key results concerning basic algebras and MV-algebras that will be utilized throughout this paper.

Definition 1

([17]). A basic algebra is an algebraic structure $\mathcal{B}=(B;\oplus ,\neg ,0)$ equipped with a binary operation ⊕ and a unary operation ¬ satisfying the following identities for all $x,y,z\in B$:

$$\begin{array}{ccc}(BA1)\hfill & \hfill & x\oplus 0=x;\hfill \\ (BA2)\hfill & \hfill & \neg \neg x=x;\hfill \\ (BA3)\hfill & \hfill & \neg (\neg x\oplus y)\oplus y=\neg (\neg y\oplus x)\oplus x;\hfill \\ (BA4)\hfill & \hfill & \neg (\neg (\neg (x\oplus y)\oplus y)\oplus z)\oplus (x\oplus z)=\neg 0.\hfill \end{array}$$

If B also satisfies $x\oplus y=y\oplus x$ then we call B a commutative basic algebra.

Defining $1=:\neg 0$, we obtain a partial order via

$$\begin{array}{c}\hfill x\le y\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\neg x\oplus y=1.\end{array}$$

(1)

Definition 2

([4] (p. 928, Def. 3.1)). A Sheffer stroke basic algebra means an algebra $(B;|)$ of type $(2)$ satisfying the following identities:

$$\begin{array}{c}(SH1)(x|(x|x))|(x|x)=x;\hfill \\ (SH2)(x|(y|y))|(y|y)=(y|(x|x))|(x|x);\hfill \\ (SH3)(((x|(y|y))|(y|y))|(z|z))|((x|(z|z))|(x|(z|z)))=x|(x|x).\hfill \end{array}$$

The relation between basic algebras and Sheffer stroke basic algebras was discussed in [4].

Lemma 1

([4] (p. 930, Thm. 3.4)). Every basic algebra $\mathcal{B}=(B;\oplus ,\neg ,0)$ admits a Sheffer stroke structure through the operation $x|y=\neg x\oplus \neg y$, making $(B;|)$ a Sheffer stroke basic algebra.

Remark 1.

In [4], the authors investigated a particular class of basic algebras $\mathcal{B}$ where each element x has a negation $\neg x$ that serves as its lattice complement in the induced lattice $\mathcal{L}(\mathcal{B})$, i.e., $x\oplus x=x.$

Lemma 2

([4] (p. 932, Thm. 3.4)). A Sheffer Stroke basic algebra $(B;|)$ with the least element 0 can be converted into a basic algebra $\mathcal{B}=(B;\oplus ,\neg ,0)$ with $x\oplus y:=(x|(0|0))|(y|y)$ and $\neg x:=x|0|0$.

Some properties of Sheffer stroke basic algebras in [4] are listed as follows.

Lemma 3.

Let $(B,|)$ be a Sheffer stroke basic algebra. Then,

(i) According to [4] (p. 928, Lem. 3.2), $x|(x|x)=1,x|(1|1)=1,1|(x|x)=x,$ where 1 is an algebraic constant element in $B.$

(ii) According to [4] (p. 931, Lem. 3.5), there is a partial order on B defined by

$$x\le yif and only ifx|(y|y)=1,$$

such that 1 is the largest element. Moreover, we have $z\le x|(z|z)$ and $x\le y$ implies $y|(z|z)\le x|(z|z)$ for all $x,y,z\in B.$

Remark 2.

If $(B;|)$ admits a least element 0, we speak of a Sheffer stroke basic algebra with 0. For a Sheffer stroke basic algebra with 0 and 1, we call it a bounded Sheffer stroke basic algebra. Obviously, $0|(x|x)=1.$

Lemma 4

([4] (p. 933, Lem. 3.13)). In a bounded Sheffer stroke basic algebra B, $0|0=1$ and $x|1=x|x$ for every $x\in B.$

Proposition 1.

Let $(B;|)$ be a bounded Sheffer stroke basic algebra. Then, $x|(0|0)=x|x$ and $(x|x)|(x|x)=x$ for every $x\in B.$

Proof. 

Applying Lemma 4 yields $x|(0|0)=x|x$ directly. By Lemma 3 (i) and Remark 2, we have $(x|x)|(x|x)=(x|(0|0))|(0|0)=(0|(x|x))|(x|x)=1|(x|x)=x.$ □

Definition 3

([13] (p. 23, Def. 1)). An algebra $(B;\circ )$ is called an implication basic algebra if it satisfies the following identities:

$$\begin{array}{c}(I1)(x\circ x)\circ x=x;\hfill \\ (I2)(x\circ y)\circ y=(y\circ x)\circ x;\hfill \\ (I3)(((x\circ y)\circ y)\circ z)\circ (x\circ z)=x\circ x.\hfill \end{array}$$

If $(B;\circ )$ admits a least element 0, we speak of an implication basic algebra with 0.

In [13], the authors examined the correspondence between basic algebras and implication basic algebras.

Lemma 5

([13] (p. 24, Thm. 2)). Let $\mathcal{B}=(B;\oplus ,\neg ,0)$ be a basic algebra. Define $x\circ y=\neg x\oplus y.$ Then, $(B;\circ )$ is a implication basic algebra.

Lemma 6

([13] (p. 27, Thm. 6)). Let $(B;\circ )$ be an implication basic algebra with least element 0. Put $x\oplus y=(x\circ 0)\circ y$ and $\neg x=x\circ 0$. Then, $\mathcal{B}=(B;\oplus ,\neg ,0)$ forms a basic algebra and $x\circ y=\neg x\oplus y$.

We recall some properties of implication basic algebras in [13].

Lemma 7.

Let $(B;\circ )$ be an implication basic algebra. Then,

(i) According to [13] (p. 23, Lem. 2), $0\circ x=1,1\circ x=x,x\circ 1=x\circ x=1$, where 1 is an algebraic constant element.

(ii) According to [13] (p. 25, Lem. 3), there is a partial order on B defined by

$$x\le yifandonlyifx\circ y=1$$

for all $x,y\in B$, such that 1 is the greatest element.

Next, we will recall some results about MV-algebras. The introduction of MV-algebras by Chang [18] is well-known, as they were originally developed to establish the completeness of a particular axiomatic system for multiple-valued reasoning. Recall that an MV-algebra is a system $(M;\oplus ,\neg ,0)$ satisfying the following:

$$\begin{array}{ccc}\hfill & \hfill & (M,\oplus ,0)isacommutativemonoid;\hfill \\ \hfill & \hfill & x\oplus 1=1(where1:=\neg 0);\hfill \\ \hfill & \hfill & \neg \neg x=x;\hfill \\ \hfill & \hfill & \neg (\neg x\oplus y)\oplus y=\neg (\neg y\oplus x)\oplus x.\hfill \end{array}$$

The relation ≤ given by $x\le y\iff \neg x\oplus y=1$ is a partial order. It is straightforward to verify that conditions (BA1)–(BA4) in Definition 2 are satisfied in any MV-algebra, showing that every MV-algebra is indeed a basic algebra.

However, as demonstrated by Botur and Halaš in [19], the associativity of the binary operation in MV-algebras can lead to significant problems in certain applications, particularly in expert systems and artificial intelligence more broadly. These concerns prompted the introduction and study of so-called non-associative MV-algebras.

Definition 4

([20]). A non-associative MV-algebra (abbreviated as NMV-algebra) is an algebraic structure $M=(M;\oplus ,\neg ,0)$, where ⊕ is a binary operation and ¬ is a unary operation, satisfying the following identities:

$$\begin{array}{ccc}\hfill & \hfill & x\oplus y=y\oplus x;\hfill \\ \hfill & \hfill & x\oplus 0=x;\hfill \\ \hfill & \hfill & x\oplus 1=1(where1:=\neg 0);\hfill \\ \hfill & \hfill & \neg \neg x=x;\hfill \\ \hfill & \hfill & \neg (\neg x\oplus y)\oplus y=\neg (\neg y\oplus x)\oplus x;\hfill \\ \hfill & \hfill & \neg x\oplus (x\oplus y)=1;\hfill \\ \hfill & \hfill & x\oplus (\neg (\neg (\neg (x\oplus y)\oplus y)\oplus z)\oplus z)=1.\hfill \end{array}$$

Remark 3.

In [20], the authors’ definition of non-associative MV-algebras does not simply remove associativity from standard MV-algebras (which would disrupt the partial order relation). Rather, they substitute the associativity condition with the last two axioms that preserve the partial order structure. In this way, it not natural to obtain the relation between NMV-algebras and commutative basic algebras. So, Zhang [21] introduced and characterized a special class of NMV-algebras, termed strong NMV-algebra, which is defined as NMV-algebra $(M,\oplus ,\neg ,0)$ satisfying the following identity:

$$x\oplus (y\oplus z)=1ifandonlyif(x\oplus y)\oplus z$$

for all $x,y,z\in M$. He demonstrated that strong NMV-algebras are equivalent to commutative basic algebras.

Some results on implication NMV-algebras and Sheffer stroke NMV-algebras are presented below.

Definition 5

([14]). A non-empty groupoid $(M;\circ )$ is called an implication NMV-algebra if it satisfies the following identities:

$$\begin{array}{ccc}\hfill & \hfill & x\circ x=y\circ y;\hfill \\ \hfill & \hfill & x\oplus 1=1(where1:=\neg 0);\hfill \\ \hfill & \hfill & 1\circ x=x;\hfill \\ \hfill & \hfill & (x\circ y)\circ y=(y\circ x)\circ x;\hfill \\ \hfill & \hfill & x\circ (y\circ x)=1;\hfill \\ \hfill & \hfill & x\circ ((((x\circ y)\circ y)\circ z)\circ z))=1.\hfill \end{array}$$

Every NMV-algebra naturally induces an implication NMV-algebra through the operation defined by $x\circ y:=\neg x\oplus y$. Conversely, an implication NMV-algebra with 0 satisfying the identity $x\circ y=\neg y\circ \neg x$ can be endowed with an NMV-algebra structure by defining $x\oplus y:=\neg x\circ y.$ Furthermore, the authors also established a one-to-one correspondence between strong Sheffer stroke NMV-algebras and NMV-algebras.

As established in [14], any NMV-algebra can be viewed as a strong Sheffer stroke NMV-algebra by defining the Sheffer stroke operation as $x|y:=\neg x\oplus \neg y$. Conversely, every strong Sheffer stroke NMV-algebra admits an NMV-algebra structure by defining $x\oplus y:=\neg x\circ y,\neg x:=x|1$ and $0:=1|1$.

Definition 6

([14]). An algebraic structure $(M;|,1)$ of type (2, 0) is said to be a strong Sheffer stroke NMV-algebra if the following identities hold:

$$\begin{array}{ccc}\hfill & \hfill & x|y=y|x;\hfill \\ \hfill & \hfill & x|0=1;\hfill \\ \hfill & \hfill & (x|1)|1=x;\hfill \\ \hfill & \hfill & ((x|1)|y)|y=((y|1)|x)|x;\hfill \\ \hfill & \hfill & (x|1)|((x|y)|1)=1;\hfill \\ \hfill & \hfill & x|((((x|y)|y)|z)|z)|1)=1.\hfill \end{array}$$

The authors in [14] also investigate the relation between implication NMV-algebras and Sheffer stroke NMV-algebras by modifying some axioms in Definition 7 to define a weak Sheffer stroke NMV-algebra.

Definition 7

([14]). A weak Sheffer stroke NMV-algebra is defined as a (2, 0)-algebra $(M;|,1)$ satisfying the following conditions:

$$\begin{array}{ccc}\hfill & \hfill & (x|1)|1=x;\hfill \\ \hfill & \hfill & x|(x|1)=1;\hfill \\ \hfill & \hfill & x|(1|1)=1;\hfill \\ \hfill & \hfill & (1|1)|x=1;\hfill \\ \hfill & \hfill & 1|x=x|1;\hfill \\ \hfill & \hfill & ((x|1)|y)|y=((y|1)|x)|x;\hfill \\ \hfill & \hfill & (x|1)|((y|x)|1)=1;\hfill \\ \hfill & \hfill & x|((((x|y)|y)|z)|z)|1)=1.\hfill \end{array}$$

Proposition 2

([14] (p. 3944, Thm. 4.8)). Let $\mathit{M}=(M;\circ ,0)$ be an implication NMV-algebra with 0 and define $x|y:=x\circ \neg y$ for all $x,y\in M$. Then, $W(\mathit{M})=(M;|,1)$ is a weak Sheffer stroke NMV-algebra. Conversely, let $\mathit{S}=(M;|,1)$ be a weak Sheffer stroke NMV-algebra and put $x\circ y:=x|(y|1),0:=1|1$ for all $x,y\in M.$ Then, $I(\mathit{S})=(M;\circ ,0)$ is an implication NMV-algebra with 0. The correspondence is one-to-one.

3. Sheffer Stroke Basic Algebras and Implication Basic Algebras

It is well-established in the literature that every non-associative strong MV-algebra forms a commutative basic algebra. Furthermore, as demonstrated in [14], there exists a one-to-one correspondence between weak Sheffer stroke NMV-algebras and implication NMV-algebras with 0. Motivated by these results, we investigate an analogous relationship between Sheffer stroke basic algebras and implication basic algebras. Our main results establish that every Sheffer stroke basic algebra can be viewed as an implication basic algebra, whereas the converse assertion is not valid. Then, we introduce strong implication basic algebras and show that their relation with bounded Sheffer stroke basic algebras is one-to-one.

Proposition 3.

Let $(B;|)$ be a Sheffer stroke basic algebra. Then, $(B;\circ )$ is an implication basic algebra with $x\circ y:=x|(y|y)$ for each $x,y\in B$.

Proof. 

By Lemma 3 $(i)$, $x|(x|x)=1$ and $1(x|x)=x$, a direct verification shows that B fulfills condition (I1) $(x\circ y)\circ y=x.$

The validity of (I2) $(x\circ y)\circ y=(y\circ x)\circ x$ and (I3) $(((x\circ y)\circ y)\circ z)\circ (x\circ z)=x\circ x$ in B follows immediately from (SH2) and (SH3)in Definition 2. □

Conversely, we give an example to show that an implication basic algebra may be not a Sheffer stroke basic algebra.

Example 1

([22] (p. 144, Ex. 3.7)). An implication basic algebra $B=\{0,a,b,c,d,1\}$ with the following Hasse diagram and operation ∘ is given by Table 1.

Table 1. Operation ∘ of Example 1.

∘	0	a	b	c	d	1
0	1	1	1	1	1	1
a	c	1	d	c	1	1
b	d	d	1	1	1	1
c	a	a	c	1	d	1
d	b	d	d	c	1	1
1	0	a	b	c	d	1

Table 1. Operation ∘ of Example 1.

∘	0	a	b	c	d	1
0	1	1	1	1	1	1
a	c	1	d	c	1	1
b	d	d	1	1	1	1
c	a	a	c	1	d	1
d	b	d	d	c	1	1
1	0	a	b	c	d	1

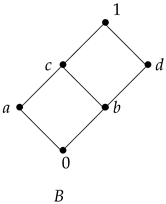
By Lemma 6, $(B,\oplus ,\neg ,0)$ is a basic algebra, where $x\oplus y=(x\circ 0)\circ y$ and $\neg x=x\circ 0$. However, $b\oplus b=d\ne b$, which means B is not a Sheffer stroke basic algebra (

Table 2. Operation ⊕ of Example 1.

⊕	0	a	b	c	d	1
0	0	a	b	c	d	1
a	a	a	c	1	d	1
b	b	d	d	c	1	1
c	c	1	d	c	1	1
d	d	d	1	1	1	1
1	1	1	1	1	1	1

).

We construct a concrete algebraic structure that simultaneously admits both implication basic algebra and Sheffer stroke basic algebra structures.

Example 2. 

Consider a basic algebra $M=\{0,a,b,c,d,1\}$ with the following Hasse diagram and the operation ⊕ being given by Table 3:

Table 3. Operation ⊕ and ¬ of Example 2.

⊕	0	a	b	c	d	1
0	0	a	b	c	d	1
a	a	a	b	1	c	1
b	b	a	b	1	1	1
c	c	1	1	c	d	1
d	d	b	1	c	d	1
1	1	1	1	1	1	1
¬	0	a	b	c	d	1
	1	c	d	a	b	0

Table 3. Operation ⊕ and ¬ of Example 2.

⊕	0	a	b	c	d	1
0	0	a	b	c	d	1
a	a	a	b	1	c	1
b	b	a	b	1	1	1
c	c	1	1	c	d	1
d	d	b	1	c	d	1
1	1	1	1	1	1	1
¬	0	a	b	c	d	1
	1	c	d	a	b	0

Define the implication operation $x\circ y:=\neg x\oplus y$. Then, by Lemma 5 the algebra $(M;\circ )$ forms an implication basic algebra, with the complete operation table for ∘ given in

Table 4. Operation ∘ of Example 2.

∘	0	a	b	c	d	1
0	1	1	1	1	1	1
a	c	1	1	c	d	1
b	d	b	1	c	d	1
c	a	a	b	1	c	1
d	b	a	b	1	1	1
1	0	a	b	c	d	1

.

For all $x,y\in M$, put $x|y:=x\circ (y\circ 0)$. Then, M equipped with this operation forms a Sheffer stroke basic algebra, as verified by the operation | given by

Table 5. Operation | of Example 2.

|	0	a	b	c	d	1
0	1	1	1	1	1	1
a	1	c	c	1	1	c
b	1	c	d	1	1	d
c	1	1	1	a	b	a
d	1	1	1	b	b	b
1	1	c	d	a	b	0

.

We can also provide another way to show that M can be converted into a Sheffer stroke basic algebra. Since M is a basic algebra satisfying $x\oplus x=x$ for each $x\in O_6$ by Table 1 then it is also a Sheffer stroke basic algebra by Lemma 1 with $x{|}_{2}y=\neg x\oplus \neg y.$ It is easily proved that | coincides with ${|}_2$, since ${x|y=x\circ (y\circ 0)=\neg x\oplus (y\circ 0)=\neg x\oplus \neg y=x|}_{2}y.$

By Example 2, if we want to obtain the one-to-one correspondence between a Sheffer stroke operation and an implication operation on basic algebras then we need to consider the relations between basic algebras. Therefore, we focus on a special class of implicative basic algebras with 0 that satisfy $x\circ (x\circ 0)=x\circ 0$, which we call strong implication basic algebras.

Definition 8.

A strong implication basic algebra $(B;\circ )$ is an implication basic algebra with the least element 0 satisfying $x\circ (x\circ 0)=x\circ 0$ for all $x\in B$.

In what follows, we establish a correspondence between strong implication basic algebras and bounded Sheffer stroke basic algebras.

Proposition 4.

A bounded Sheffer stroke basic algebra $\mathbf{S}=(B;|)$ can be converted into a strong implication basic algebra $\mathcal{I}(\mathbf{S})=(B;\circ ,0)$ via defining $x\circ y=x|(y|y)$ for all $x,y\in B$.

Proof. 

By Proposition 3, $(B;\circ )$ is an implication basic algebra. Furthermore, we have $x\circ (x\circ 0)=x|((x|(0|0)|(x|(0|0)))=x|((x|x)|(x|x))=x|x=x|(0|0)=x\circ 0$ by Proposition 1. So, $(A,\circ )$ is a strong implication basic algebra. □

Conversely:

Proposition 5.

A strong implication basic algebra $\mathbf{I}=(B;\circ )$ induces a bounded Sheffer basic algebra $\mathcal{S}(\mathbf{I})=(B;|)$ with defining $x|y=x\circ (y\circ 0)$ for all $x,y\in B$.

Proof. 

By Lemma 7 (i), we obtain $x|x=x\circ (x\circ 0)=x\circ 0$ and $x|(y|y)=x\circ ((y|y)\circ 0)=x\circ ((y\circ 0)\circ 0)=x\circ ((0\circ y)\circ y)=x\circ (1\circ y)=x\circ y$. Then, $(x|(x|x))|(x|x)=(x|(x|x))\circ ((x\circ 0)\circ 0)=(x\circ x)\circ x=1\circ x=x$, which shows that (SH1) holds in $B.$ We can also obtain $(x|(y|y))|(y|y)=(x|(y|y))\circ ((y\circ 0)\circ 0)=(x|(y|y))\circ y=(x\circ y)\circ y=(y\circ x)\circ x=(y\circ ((x\circ 0)\circ 0))\circ ((x\circ 0)\circ 0)=(y\circ ((x|x)\circ 0)\circ ((x\circ (x\circ 0))\circ 0)=(y|(x|x))|(x|x).$ So, B satisfies (SH2). By (I3) in Definition 3, $(((x|(y|y))|(y|y))|(z|z))|((x|(z|z))|(x|(z|z)))=(((x\circ y)\circ y)\circ z)\circ (x\circ z)=x\circ x=x|(x|x),$ which means that (SH3) holds in $B.$

Furthermore, we have $x|(1|1)=x\circ 1=1$ and $0|(x|x)=0\circ x=1$ for every $x\in B$, which means $0\le x\le 1$. So, $(B;|)$ is a bounded Sheffer basic algebra. □

Theorem 1.

$\mathcal{I}\mathcal{S}(\mathbf{I})=\mathbf{I}$ and $\mathcal{S}\mathcal{I}(\mathbf{S})=\mathbf{S}$, where $\mathbf{I}=(B;\circ )$ is a strong implication basic algebra and $\mathbf{S}=(B;|)$ is a bounded Sheffer basic algebra.

Proof. 

Since $\mathbf{I}=(B;\circ )$ is a strong implication basic algebra, by Proposition 5, $\mathcal{S}(\mathbf{I})=(B;|)$ is a Sheffer stroke basic algebra where $x|y=x\circ (y\circ 0)$ for all $x,y\in B.$ By Proposition 4, $(\mathcal{I}\mathcal{S}(\mathbf{I}),{\circ }_1)$ is a strong implication basic algebra, where $x{\circ }_{1}y=x|(y|y).$ So, $x{\circ }_{1}y=x|(y|y)=x\circ ((y|y)\circ 0)=x\circ ((y\circ (y\circ 0))\circ 0)=x\circ ((y\circ 0)\circ 0)=x\circ y,$ i.e., $\mathcal{I}\mathcal{S}(\mathbf{I})=\mathbf{I}.$ We denote, respectively, the partial order in $(B;\circ )$ by ≤ and the partial order in $(\mathcal{I}\mathcal{S}(\mathbf{I}),{\circ }_1)$ by ${\le }_1$; it is obvious that ≤ coincides with ${\le }_1.$ For every $x,y\in (B,\circ )$, we know that $x\le y$ is equivalent to $x\circ y=1$. Then, $x{\circ }_{1}y=x\circ y=1$; this shows that $x{\le }_{1}y$.

Conversely, we put $x\circ y=x|(y|y)$ for all $x,y\in B,$ where $\mathbf{S}=(B;|)$ is a bounded Sheffer basic algebra. Then, by Proposition 4, $\mathcal{I}(\mathbf{S})$ is a strong implication basic algebra. By Proposition 5, we obtain $\mathcal{S}\mathcal{I}(\mathbf{S})=(B;{|}_1)$, which is a bounded Sheffer stroke basic algebra with operation ${|}_1$ defined by ${x|}_{1}y=x\circ (y\circ 0).$ According to Proposition 1, we obtain ${x|}_{1}y=x\circ (y\circ 0)=x|((y\circ 0)|(y\circ 0))=x|((y|(0|0))|(y|(0|0)))=x|((y|y)|(y|y))=x|y,$ i.e., $\mathcal{S}\mathcal{I}(\mathbf{S})=\mathbf{S}$. We denote the partial order in $(B;|)$ by ${\le }^{\prime }$ and the partial order in $\mathcal{S}\mathcal{I}(\mathbf{S})=(B;{|}_1)$ by ${\le }_1^{\prime }$, respectively; it is obvious that ${\le }^{\prime }$ coincides with ${\le }_1^{\prime }.$ Since $x{\le }^{\prime }y\iff x{|(y|y)=1\iff x|}_1(y{|}_{1}y)=1\iff x{\le }_1^{\prime }y$ for every $x,y\in B.$ □

We give an example to illustrate Theorem 1.

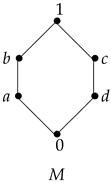
Example 3.

Consider an implication basic algebra $N=\{0,a,b,1\}$ with the least element 0 whose Hasse diagram and the operation ∘ are given in the following (Figure 1 and

Table 6. Operation ∘ of Example 3.

∘	0	a	b	1
0	1	1	1	1
a	b	1	b	1
b	a	a	1	1
1	0	a	b	1

).

A straightforward verification demonstrates that $(B,\circ )$ is a strong implication basic algebra. We define $x|y=x\circ (y\circ 0).$ Then, $(B,|)$ is a bounded Sheffer stroke basic algebra by Proposition 5, and the operation | is given by

Table 7. Operation | of Example 3.

|	0	a	b	1
0	1	1	1	1
a	1	b	1	b
b	1	1	a	a
1	1	b	a	0

.

Next, we put $x{\circ }_{1}y=x|(y|y).$ Then, by Proposition 4 we obtain $(B,{\circ }_1)$, which is an implication basic algebra with the operation ${\circ }_1$ given by

Table 8. Operation ${\circ }_1$ of Example 3.

${\circ }_1$	0	a	b	1
0	1	1	1	1
a	b	1	b	1
b	a	a	1	1
1	0	a	b	1

. It is clear that ${\circ }_1$ is coincident with ∘ and that $(B,{\circ }_1)$ is a strong implication basic algebra.

4. Some Results of Congruences and Filters of Sheffer Stroke Basic Algebras

Based on the relationship between a Sheffer stroke basic algebra and an implication basic algebra according to Proposition 3, we derive analogous results concerning congruences and filters of Sheffer stroke basic algebras that parallel those in implication basic algebras.

Definition 9

([5]). An equivalence relation Θ on a Sheffer stroke basic algebra B is called congruence if it satisfies the following conditions:

$$\begin{array}{cc}(x,y)\in \mathsf{\Theta }\Rightarrow (x|(z|z),y|(z|z))\in \mathsf{\Theta },\hfill & (R)\\ (x,y)\in \mathsf{\Theta }\Rightarrow ((x|x)|z,(y|y)|z)\in \mathsf{\Theta }\hfill & (L)\end{array}$$

for all $x,y,z\in B.$

Let $Con(B)$ denote the congruence lattice of B. For any congruence $\mathsf{\Theta }\in Con(B)$ and elements $x,y\in B$, the equivalence $(x,y)\in \mathsf{\Theta }$ implies the equality of congruence classes ${\left[x\right]}_{\mathsf{\Theta }}={\left[y\right]}_{\mathsf{\Theta }}$.

Next, we recall some basic concepts, all from [23]. Let A be an algebra with a constant 1, $R_1,R_2,R_3\in ConA;$ then, A is $weakly regular$ if ${\left[1\right]}_{R_1}={\left[1\right]}_{R_2}$ implies $R_1=R_2.$ A is $distributive at$ 1 if ${\left[1\right]}_{R_1\wedge (R_2\vee R_3)}={\left[1\right]}_{(R_1\wedge R_2)\vee (R_1\wedge R_3)}.$ A is congruence 3-permutable if $R_1\circ R_2\circ R_1=R_2\circ R_1\circ R_2$. A is $congruence distributive$ if $R_1\wedge (R_2\vee R_3)=(R_1\wedge R_2)\vee (R_1\wedge R_3).$

Evidently, from the weak regularity and distributivity at 1 of an algebra A with constant 1 the congruence distributivity of A follows immediately.

Some characterizations of the above-mentioned concepts of an algebra A that is a variety are also given in [23]: A variety V with a constant 1 is said to be $weakly regular$ if there exists a finite system of binary terms $t_i(x,y)(i=1,2,n)$, such that $t_i(x,y)=1\iff x=y;$ V is $distributive at$ 1 if there exists a binary term $t(x,y)$, such that $t(x,x)=t(1,x)=1$ and $t(x,1)=x;$ V is congruence 3-permutable if there exist two ternary terms $t_1(x,y,z)$ and $t_2(x,y,z)$ satisfying $t_1(x,z,z)=x,t_2(x,x,z)=z,t_1(x,x,z)=t_2(x,z,z).$

We denote the variety of Sheffer stroke basic algebras by $\mathcal{SSB}.$ We establish the following result:

Theorem 2.

The variety $\mathcal{SSB}$ is weakly regular, congruence distributive and congruence 3-permutable.

Proof. 

Let $n=2$ and define the binary terms $t_1(x,y):=x|(y|y),t_2(x,y):=y|(x|x).$ By Lemma 3 (i), we have $t_1(x,x)=t_2(x,x)=x|(x|x)=1$. Conversely, if $t_1(x,y)=t_2(x,y)=1$ then Lemma 3 (i) implies $x\le y$ and $y\le x$; hence, $x=y$. This shows that $\mathcal{SSB}$ is weakly regular. Furthermore, taking $t(x,y):=y|(x|x),$ Lemma 3 (i) yields $t(x,x)=x|(x|x)=1$, $t(1,x)=1|(x|x)=1$ and $t(x,1)=x|(1|1)=x$. Consequently, $\mathcal{SSB}$ is distributive at 1 and, therefore, congruence distributive.

Consider the ternary terms $t_1(x,y,z):=(z|(y|y))|(x|x)$ and $t_2(x,y,z):=(x|(y|y))|(z|z).$ By Lemma 3 (i), we obtain $t_1(x,z,z)=(z|(z|z))|(x|x)=1|(x|x)=x$, $t_2(x,x,z)=(x|(x|x))|(z|z)=1|(z|z)=z$ and $t_1(x,x,z)=(z|(x|x))|(x|x)=(x|(z|z))|(z|z)=t_2(x,z,z)$ by Definition 2 (SH2). Thus, $\mathcal{SSB}$ is congruence 3-permutable. □

In what follows, we will use ideal terms to characterize compatible filters of Sheffer stroke basic algebras. Recall that an ideal term [23] on an algebra $\mathcal{A}$ with a constant 1 is a term $t(x_1,\dots ,x_m,y_1,\dots ,y_n)$, such that the identity $t(x_1,\dots ,x_m,1,\dots ,1)=1$ holds on $\mathcal{A}$. For non-empty subsets $M,N$, $M\subseteq N$ of A, we say M is closed under the ideal term t if $t(x_1,\dots ,x_m,y_1,\dots ,y_n)\in M$ for all $x_1,\dots ,x_m\in M$ and $y_1,\dots ,y_n\in N.$ The definition of compatible filters of Sheffer stroke basic algebras and their relation with congruence relation are given as follows.

Definition 10

([5]). A subset F of a Sheffer stroke basic algebra A is said to be a compatible filter if $1\in F$ and for all $x,y,z\in A$:

$$\begin{array}{c}(FSH1)x\in Fandx|(y|y)\in Fimpliesy\in F,\hfill \\ (FSH2)Ifx|(y|y)\in Fandy|(x|x)=1,then(y|(z|z))|((x|(z|z))|(x|(z|z)))\in F,\hfill \\ (FSH3)Ifx|(y|y)\in Fandy|(x|x)\in F,then(z|(x|x))|((z|(y|y))|(z|(y|y)))\in F.\hfill \end{array}$$

Proposition 6

([5]). For any compatible filter F of a Sheffer stroke basic algebra B, the binary relation $\mathsf{\Theta }(F)$ defined by

$$(x,y)\in \mathsf{\Theta }(F)\iff x|(y|y)\in F,y|(x|x)\in F$$

being a congruence relation on A. Moreover, ${\left[1\right]}_{\mathsf{\Theta }(F)}=F.$

In what follows, we present our main result characterizing compatible filters through ideal terms.

Theorem 3.

A subset F with 1 in a Sheffer stroke basic algebra $B=(B;|)$ is a compatible filter if and only if it is closed under the following four ideal terms:

$$\begin{array}{l}{t}_1(x,y_1,y_2)=(y_1|((y_2|(x|x))|(y_2|(x|x))))|(x|x);\\ t_2(x_1,x_2,x_3,y)=(((y|(x_1|x_1))|(x_2|x_2))|(x_3|x_3))|(((x_1|(x_2|x_2))|(x_3|x_3))|\\ ((x_1|(x_2|x_2))|(x_3|x_3)));\\ t_3(x_1,x_2,x_3,y)=(x_1|((x_2|(y|(x_3|x_3))|(y|(x_3|x_3))|(x_2|(y|(x_3|x_3))|(y|(x_3|\\ x_3))))|(x_2|(y|(x_3|x_3))|(y|(x_3|x_3))|(x_2|(y|(x_3|x_3))|(y|(x_3|x_3))))))|((x_1|(((x_2|(x_3|\\ x_3)))|(x_2|(x_3|x_3))))|(x_1|(((x_2|(x_3|x_3)))|(x_2|(x_3|x_3)))));\\ t_4(x_1,x_2,y_1,y_2)=((y_1|(x_1|x_1))|(x_2|x_2))|((x_1|((y_2|(x_2|x_2))|(y_2|(x_2|x_2))))|\\ (x_1|((y_2|(x_2|x_2))|(y_2|(x_2|x_2))))).\end{array}$$

Proof. 

By Proposition 6, for any compatible filter F of B, the relation $\mathsf{\Theta }(F)$ is a congruence on B and ${\left[1\right]}_{\mathsf{\Theta }(F)}=F$. For all $y_1,y_2\in F$ and $x\in A,$ we have

$$\begin{array}{cc}\hfill & (y_1|((y_2|(x|x))|(y_2|(x|x))))|(x|x)\mathsf{\Theta }(1|((1|(x|x))|(1|(x|x))))|(x|x)\hfill \\ \hfill =& (1|(x|x))|(x|x)=x|(x|x)=1.\hfill \end{array}$$

Then, $t_1(x,y_1,y_2)\in F.$

If $y\in F,x_1,x_2,x_3\in B$ then

$$\begin{array}{cc}\hfill & (((y|(x_1|x_1))|(x_2|x_2))|(x_3|x_3))\mathsf{\Theta }(((1|(x_1|x_1))|(x_2|x_2))|(x_3|x_3))\hfill \\ \hfill =& (x_1|(x_2|x_2))|(x_3|x_3).\hfill \end{array}$$

Since $(x_1|(x_2|x_2))|(x_3|x_3)|((x_1|(x_2|x_2))|(x_3|x_3)|(x_1|(x_2|x_2))|(x_3|x_3))=1,$ we obtain $t_2(x_1,x_2,x_3,y)\in F.$ Similarly, if $y\in F,x_1,x_2,x_3\in B$ then it follows that $t_3(x_1,x_2,x_3,y)\in F$, and if $y_1,y_2\in F$ and $x_1,x_2\in A$ then $t_4(x_1,x_2,y_1,y_2)\in F.$

Conversely, if $x\in F$ and $x|(y|y)\in F$ then

$$\begin{array}{cc}\hfill t_1(y,x|(y|y),x)=& ((x|(y|y))|((x|(y|y))|(x|(y|y))))|(y|y)\hfill \\ \hfill & =1|(y|y)=y\in F.\hfill \end{array}$$

So, we verify that F satisfies (FSH1).

Assume that $x|(y|y)\in F$ and $y|(x|x)=1;$ then,

$$\begin{array}{cc}\hfill & (y|(z|z))|((x|(z|z))|(x|(z|z)))\hfill \\ \hfill =& 1|((y|(z|z))|((x|(z|z))|(x|(z|z)))|(y|(z|z))|((x|(z|z))|(x|(z|z))))\hfill \end{array}$$

Substitute 1 by $((x|(z|z))|((x|(z|z))|(x|(z|z))))$ and then substitute the first x by $(x|(y|y))|(y|y),$ since $(x|(y|y))|(y|y)=(y|(x|x))|(x|x)=1|(x|x)=x$ by Lemma 3 (i) and (SH2); so, we obtain $(y|(z|z))|((x|(z|z))|(x|(z|z)))=t_2(y,z,x|(z|z),x|(y|y))\in F$, which means that F satisfies (FSH2).

If $x|(y|y),y|(x|x)\in F$ then denote $(x|(y|y))|(y|y)=(y|(x|x))|(x|x)$ by ∆; then,

$$\begin{array}{cc}\hfill & (z|(x|x))|((z|(∆|∆)|(z|(∆|∆))\hfill \\ \hfill =& ((1|(z|z))|(x|x))|((z|(∆|∆)|(z|(∆|∆))\hfill \\ \hfill =& t_4(z,x,1,y|(x|x))\in F.\hfill \end{array}$$

Denote $((z|(x|x))|((z|(y|y))|(z|(y|y))))$ by ∇; then,

$$t_4(z,x,1,y|(x|x))|(\nabla |\nabla )=t_3(z|(x|x),z,y,x|(y|y))\in F.$$

Together with (FSH1), we have $(z|(x|x))|((z|(y|y))|(z|(y|y)))\in F$, which shows that F satisfies (FSH3). So, F is a compatible filter of $A.$ □

As an immediate consequence, we have the following result.

Corollary 1

([5] (p. 224, Thm. 3.30)). Let Θ be a congruence of a Sheffer stroke basic algebra A; then, ${\left[1\right]}_{\mathsf{\Theta }}$ is a compatible filter of $A.$

Proof. 

By the proof of Theorem 3, when $\mathsf{\Theta }$ is a congruence of A, ${\left[1\right]}_{\mathsf{\Theta }}$ is closed under the ideal items $t_1,t_2,t_3,t_4;$ then, it is a compatible filter. □

Remark 4.

This proof is different from that in [5].