Dynamic Analysis and Application of 6D Multistable Memristive Chaotic System with Wide Range of Hyperchaotic States
Abstract
1. Introduction
- (1)
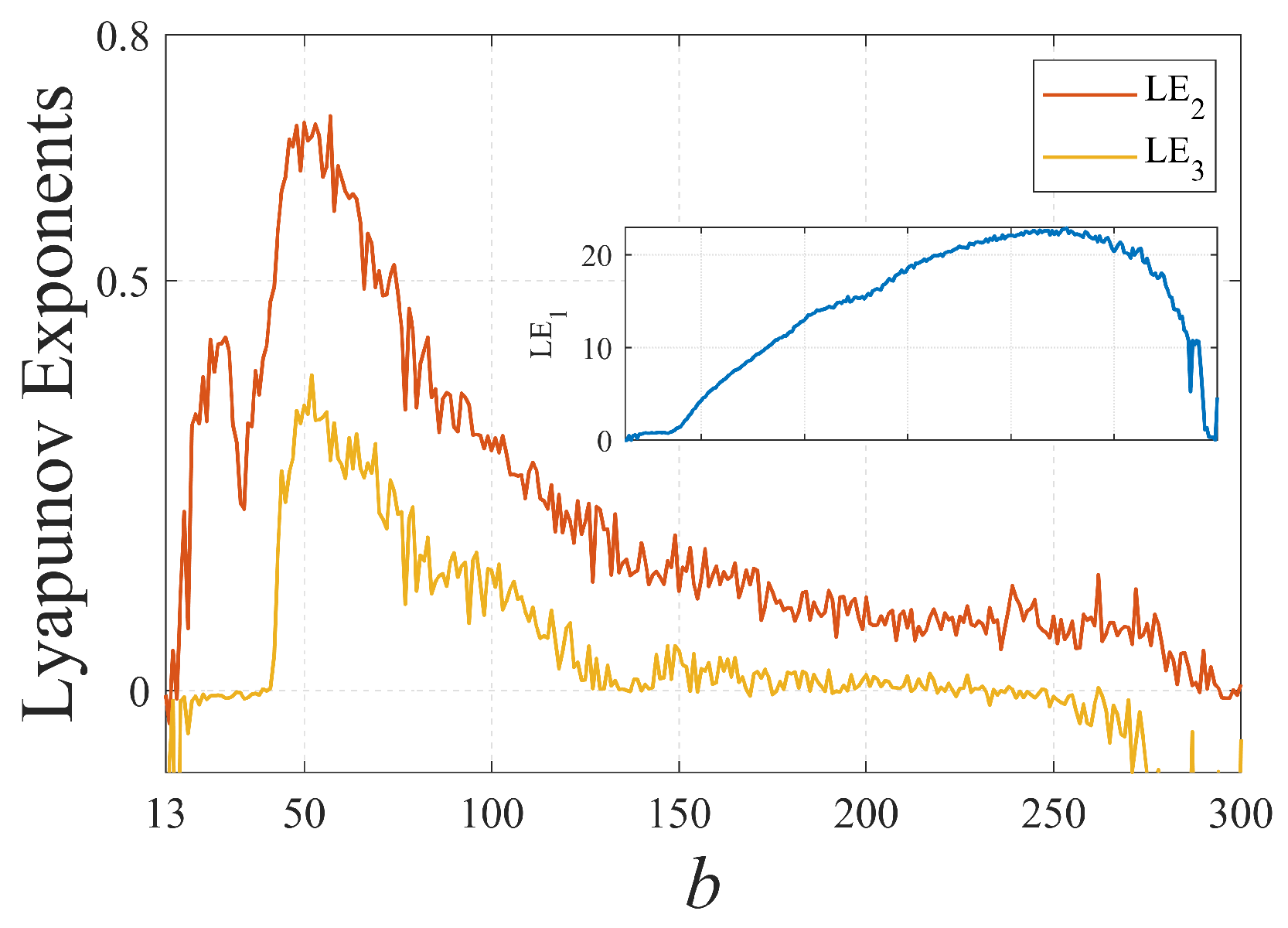
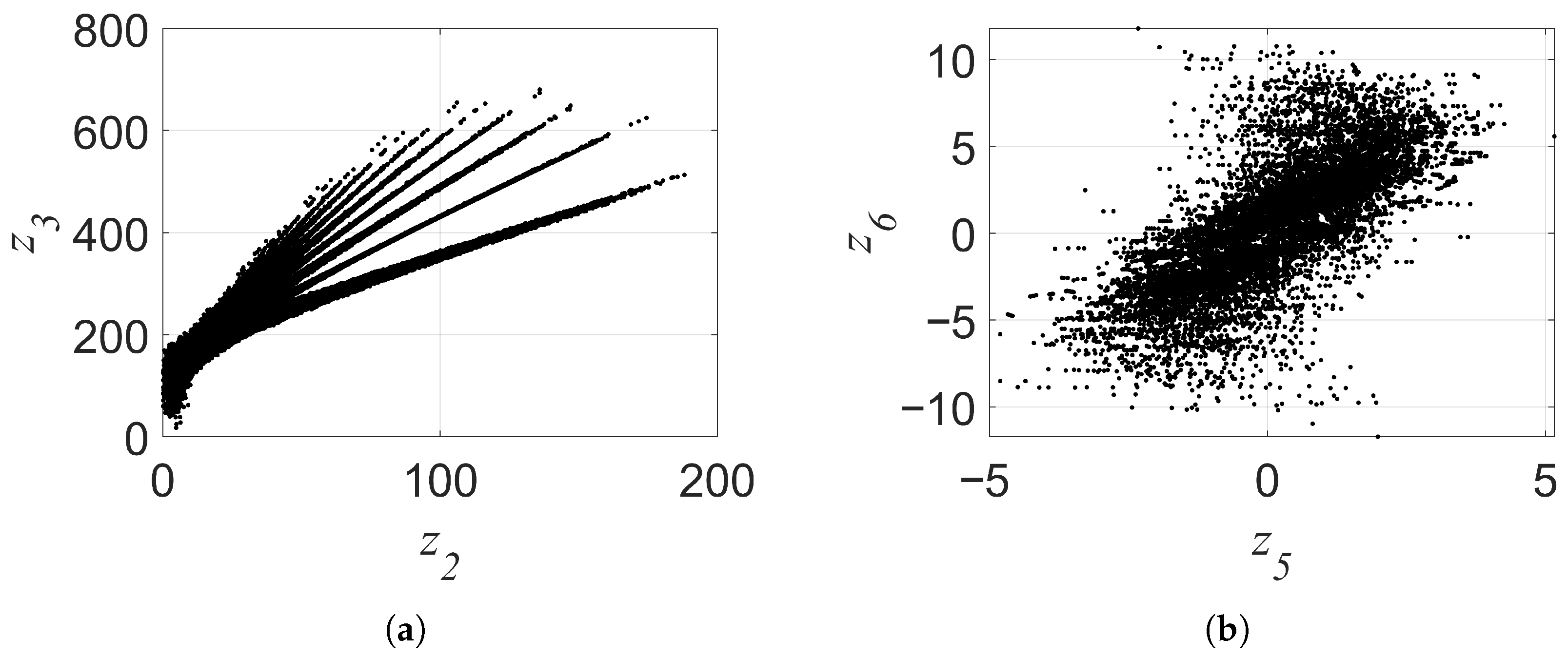
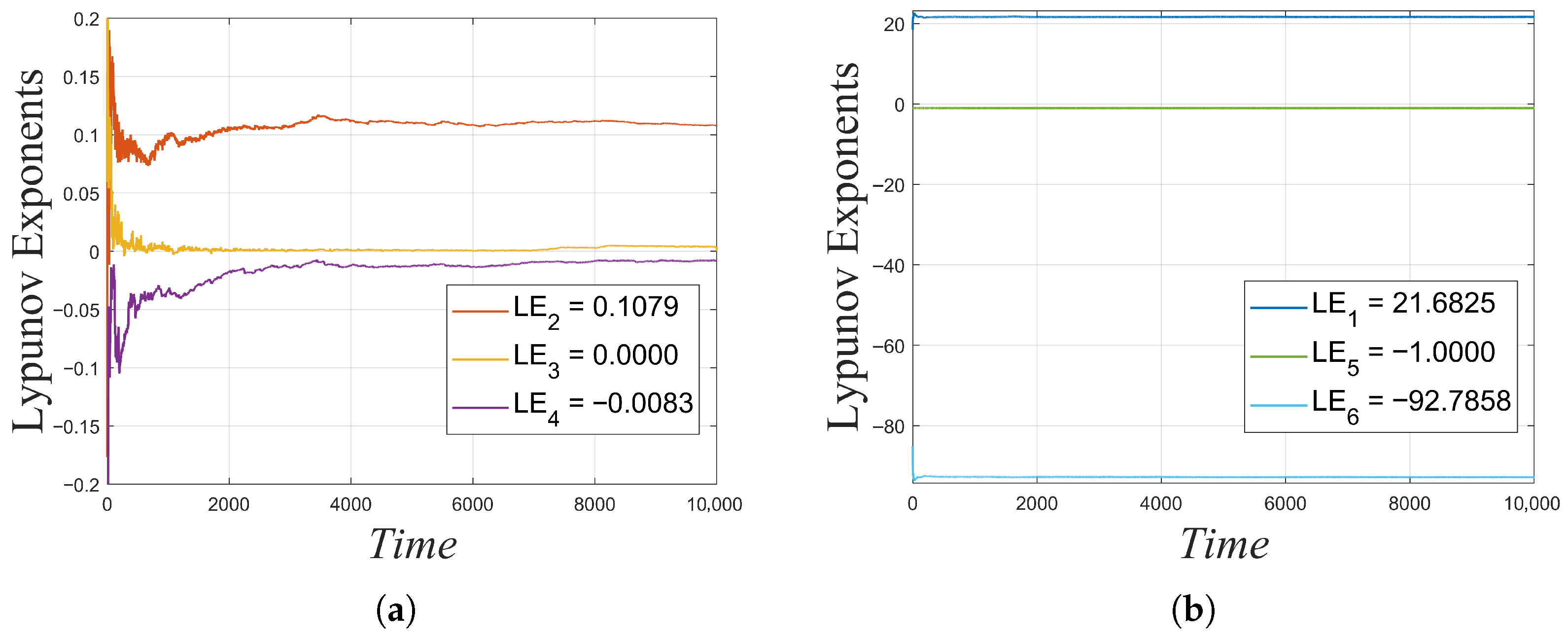
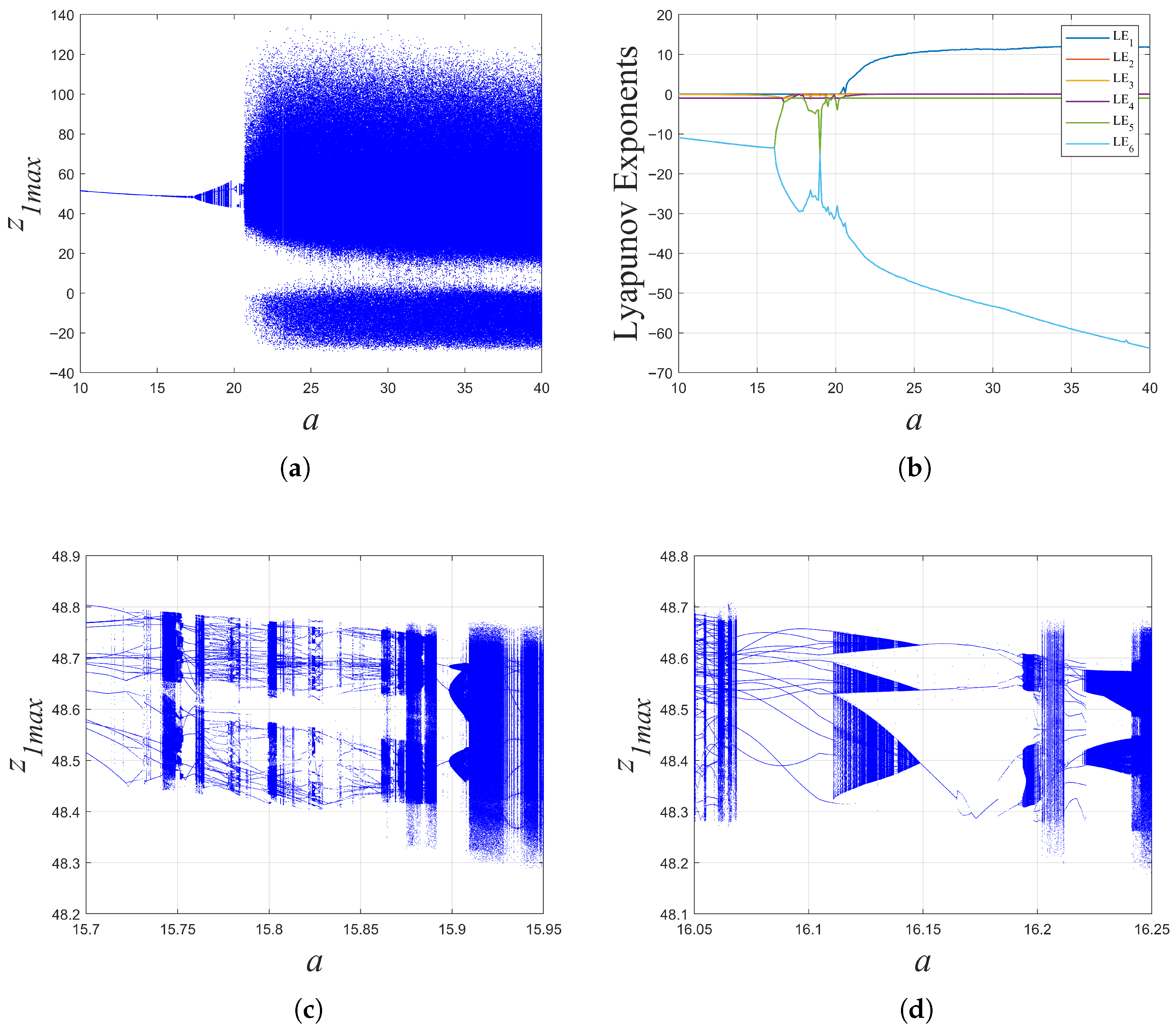
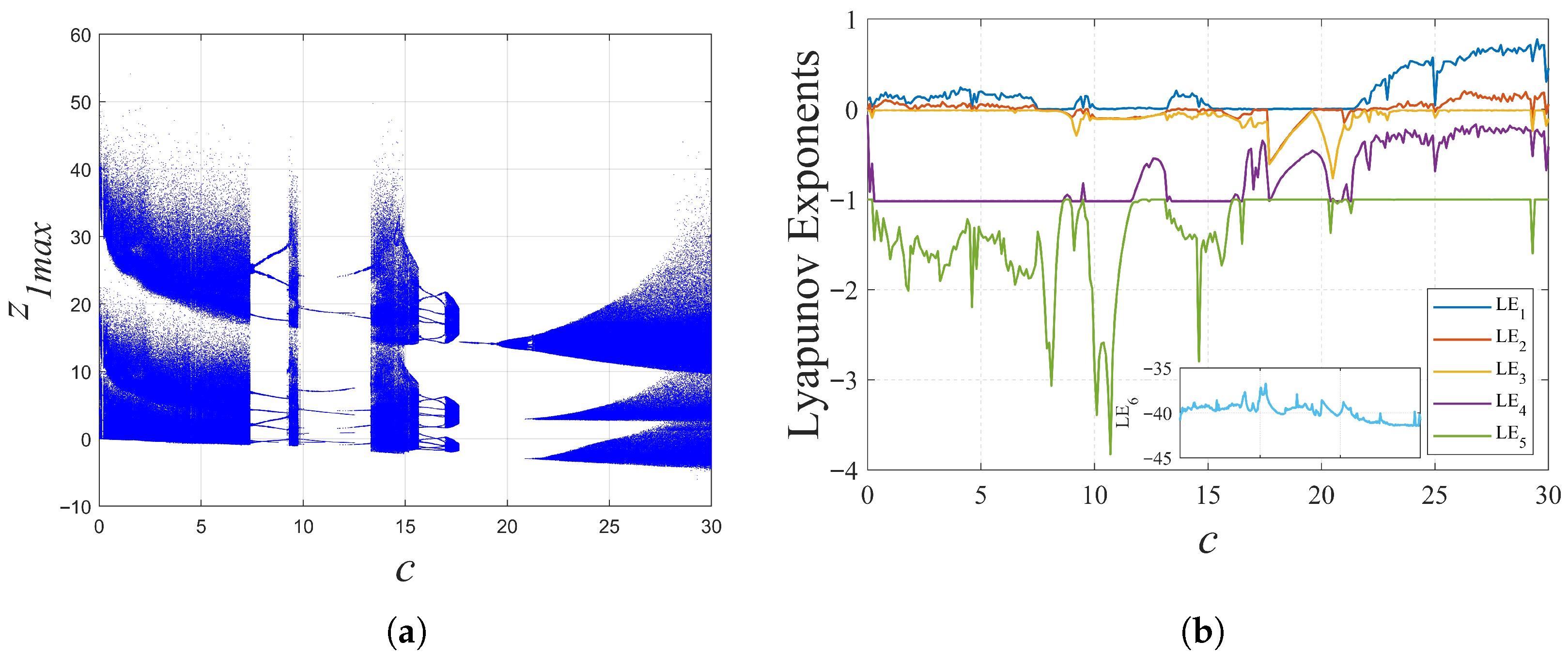
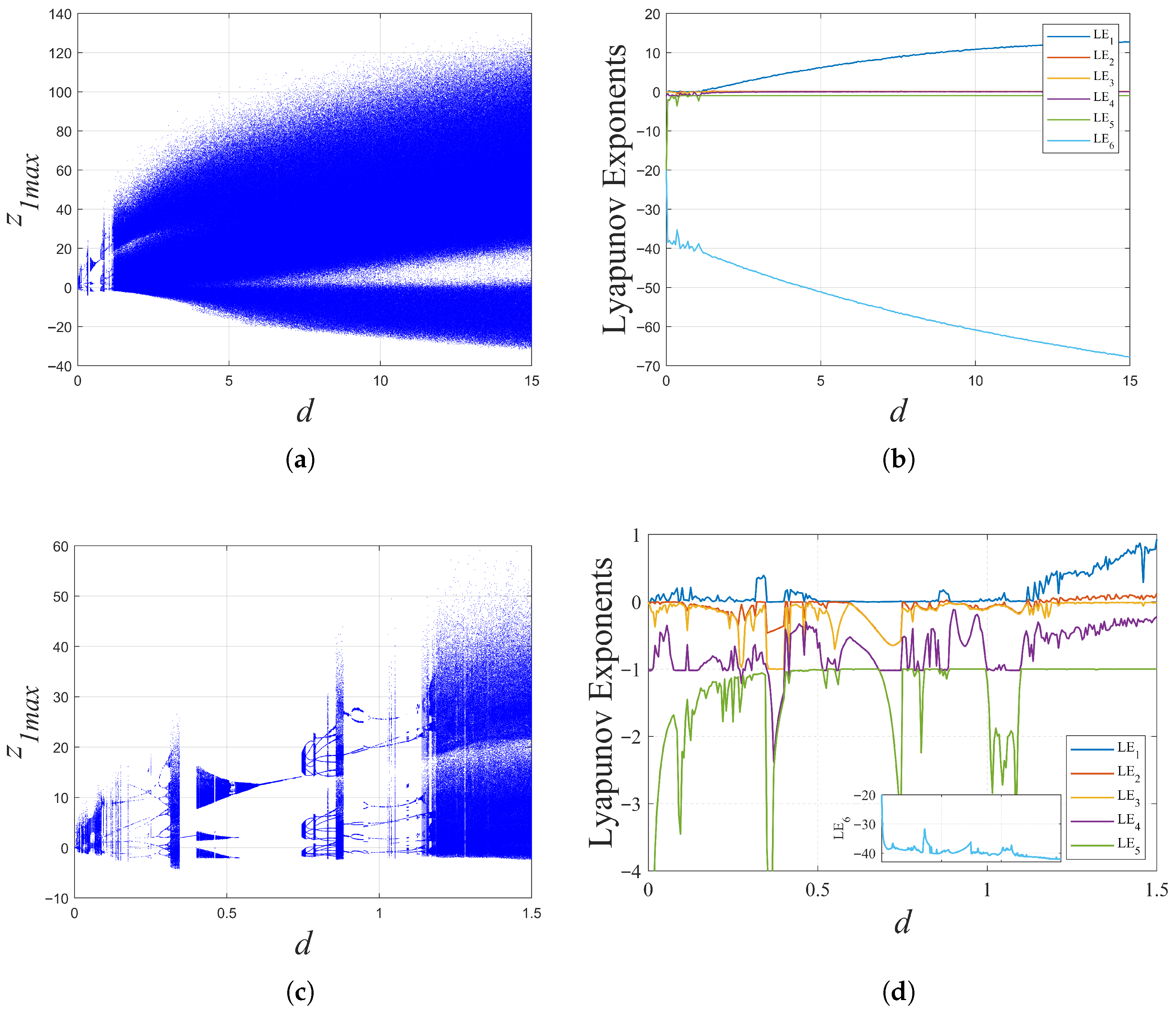
- A novel, 6D, MMHS architecture was developed, with its hyperchaotic characteristics rigorously verified through the analysis of the Lyapunov exponent spectrum and the quantification of the Kaplan–Yorke dimension. Under specific parameters, the 6D MMHS exhibits either two positive Lyapunov exponents with the maximum exceeding 21 or three positive Lyapunov exponents with the maximum exceeding 4. By analyzing the Lyapunov exponents and Kaplan–Yorke dimension when the parameter b was within a wide range of , its hyperchaotic characteristics over the wide range were verified.
- (2)
- Multistability mechanisms were analytically established through invariance analysis of state variables under specific coordinate transformations. Offset boosting control was successfully implemented via strategic modulation of the fifth state variable ().
- (3)
- By discretizing the 6D MMHS and performing numerical simulation on an FPGA, the experimental results showed that the attractor on the oscilloscope closely resembled the software simulation results.
- (4)
- An image encryption scheme derived from the 6D MMHS was proposed, with its cryptographic security systematically evaluated through statistical and differential analyses.
2. A 6D, Multistable, Memristive, Hyperchaotic System
2.1. Mathematical Description of the New System
- Peak MLE: within ;
- Maximum Kaplan–Yorke dimension: .

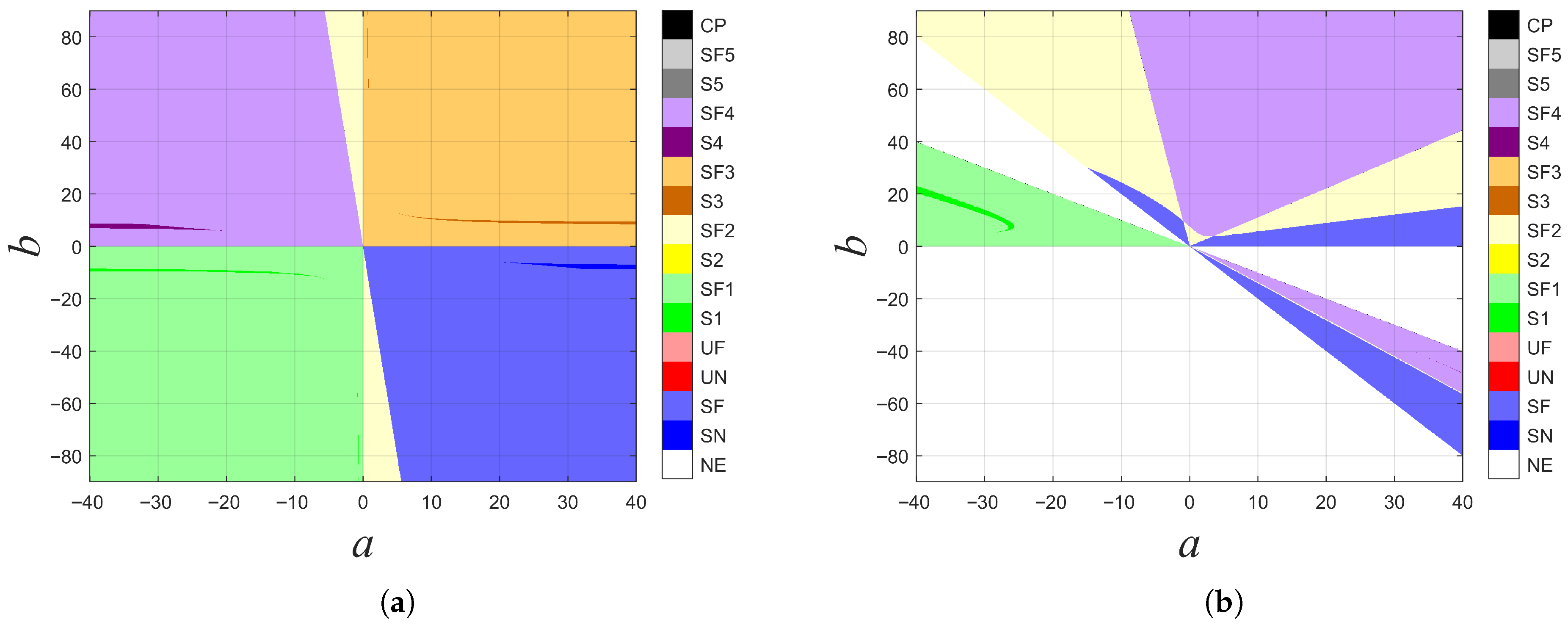
2.2. Equilibrium Point and Stability
- Stable Node (SN, dark blue regions): All eigenvalues of the Jacobian matrix had negative real parts and were purely real. Trajectories in the phase space exhibited exponential convergence along a six-dimensional stable manifold without oscillation.
- Stable Focus (SF, light blue regions): All eigenvalues had negative real parts but contained complex conjugate pairs. Trajectories displayed spiral convergence with damped oscillatory characteristics.
- Unstable Node (UN, dark red regions): All eigenvalues had positive real parts and were purely real. Trajectories diverged exponentially along a six-dimensional, unstable manifold.
- Unstable Focus (UF, light red regions): All eigenvalues had positive real parts but contained complex conjugate pairs. Trajectories exhibited diverging spiral patterns with amplifying oscillations.
- Saddle Point with (S1, dark green regions): Featured one eigenvalue with a positive real part (one-dimensional unstable manifold) and five eigenvalues with negative real parts (five-dimensional stable manifold), all real. Trajectories diverged along one dimension while converging along five dimensions.
- Saddle-Focus with (SF1, light green regions): Contained one real eigenvalue with a positive real part (one-dimensional unstable manifold) and complex conjugate pairs with negative real parts (five-dimensional stable manifold with spiral convergence).
- Saddle Point with (S2, bright yellow regions): Two real eigenvalues with positive real parts (two-dimensional unstable manifold) and four real eigenvalues with negative real parts (four-dimensional stable manifold).
- Saddle-Focus with (SF2, light yellow regions): The two-dimensional unstable manifold or four-dimensional stable manifold contained complex eigenvalues, inducing spiral motion in corresponding subspaces.
- Saddle Point with (S3, orange regions): Three real eigenvalues with positive real parts (three-dimensional unstable manifold) and three real eigenvalues with negative real parts (three-dimensional stable manifold).
- Saddle-Focus with (SF3, light orange regions): The three-dimensional unstable manifold or stable manifold contained complex eigenvalues. This configuration could induce chaos when satisfying Shilnikov conditions.
- Saddle Point with (S4, purple regions): Four real eigenvalues with positive real parts (four-dimensional unstable manifold) and two real eigenvalues with negative real parts (two-dimensional stable manifold).
- Saddle-Focus with (SF4, pale purple regions): The four-dimensional unstable manifold or two-dimensional stable manifold contained complex eigenvalues, forming a high-dimensional spiral saddle structure.
- Saddle Point with (S5, dark gray regions): Five real eigenvalues with positive real parts (five-dimensional unstable manifold) and one real eigenvalue with negative real part (one-dimensional stable manifold).
- Saddle-Focus with (SF5, light gray regions): The five-dimensional unstable manifold contained complex eigenvalues, producing spiral divergence within strongly repulsive domains.
- Critical Point (CP, black regions): At least one eigenvalue had a real part approaching zero, corresponding to bifurcation points (e.g., Hopf bifurcation, fold bifurcation).
- Non-existent (NE, white regions): Exclusive to , undefined when or (i.e., when did not exist in the set of real numbers.). Under these conditions, the system possessed only the equilibrium point.
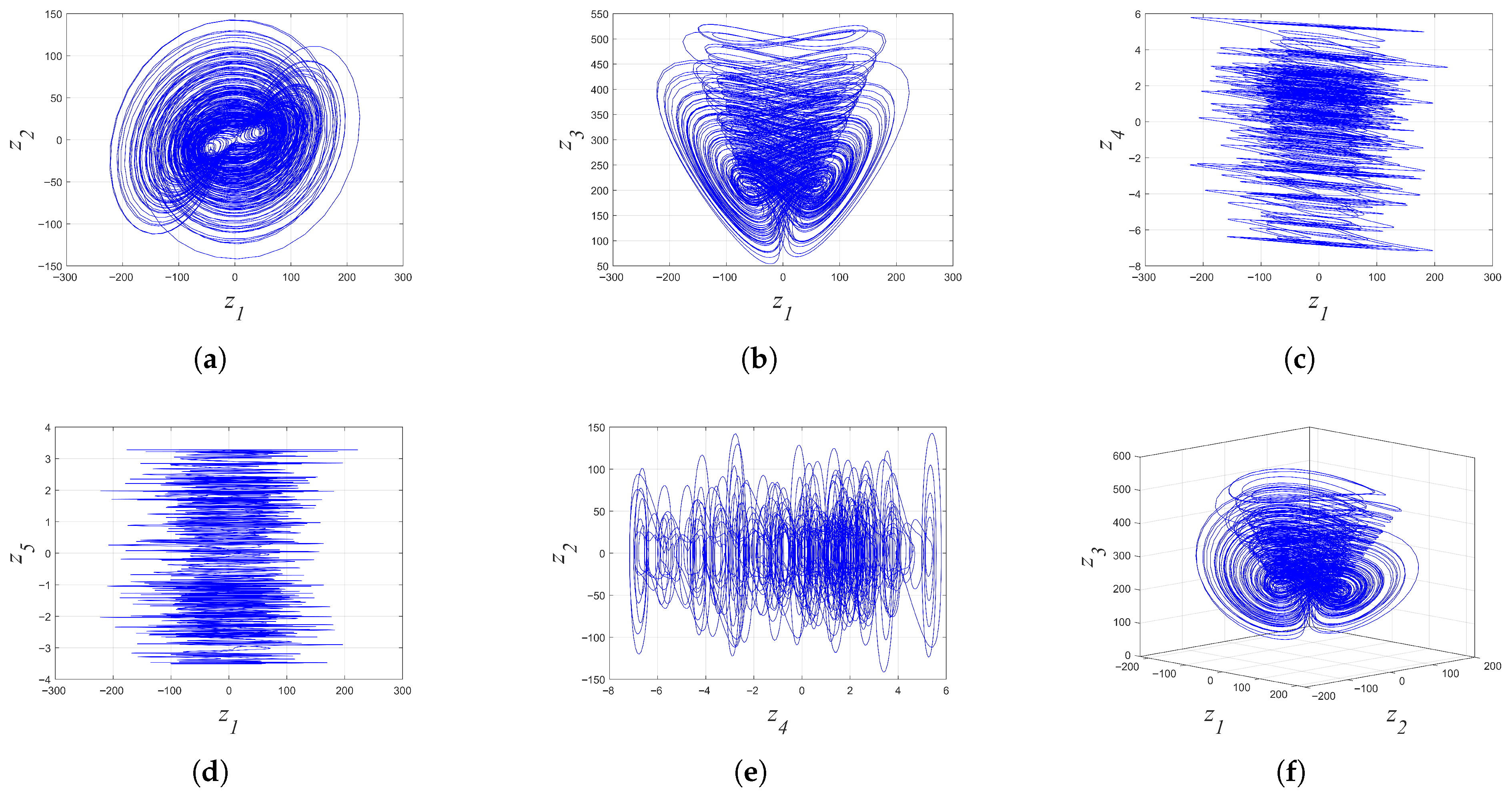
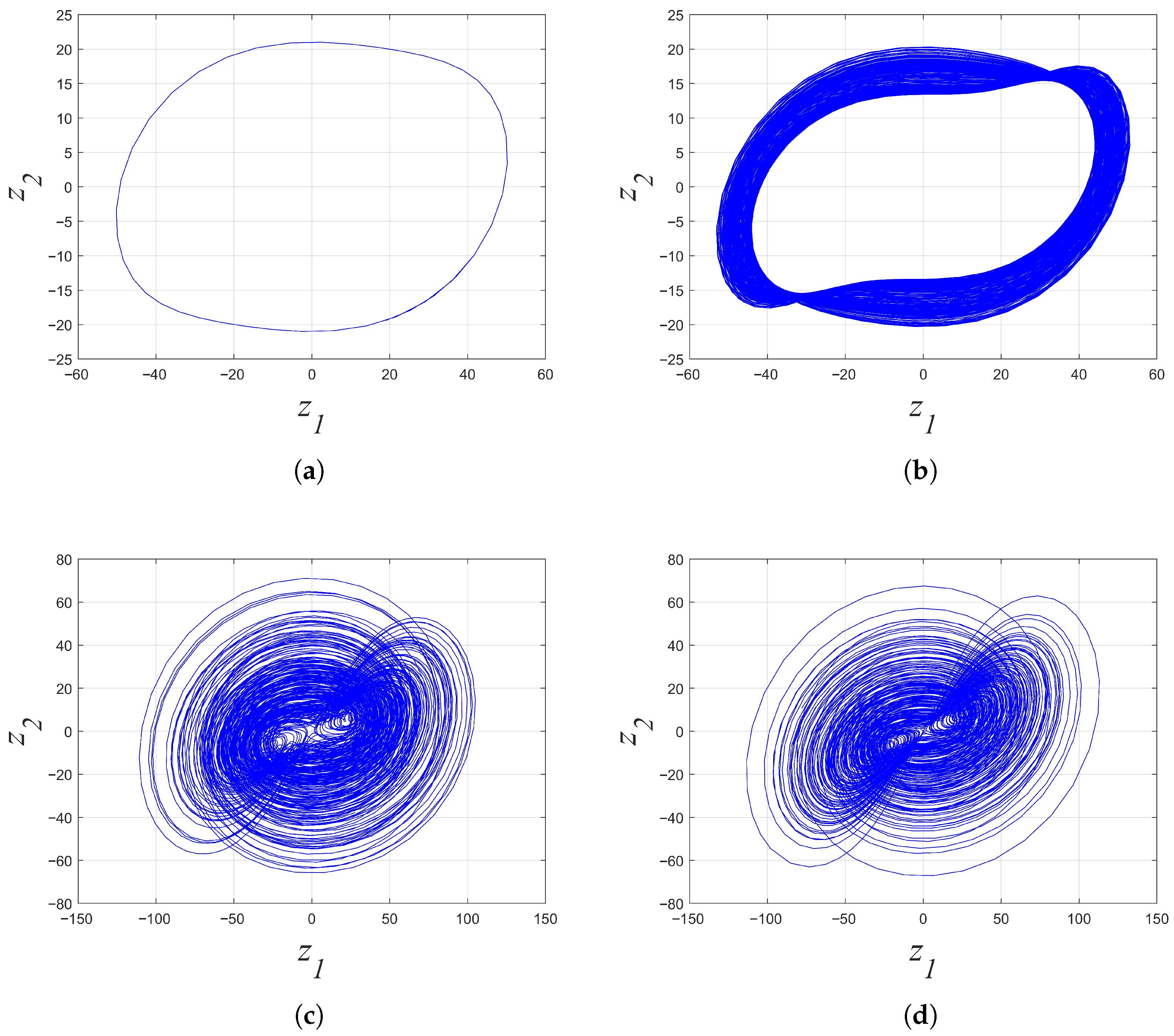
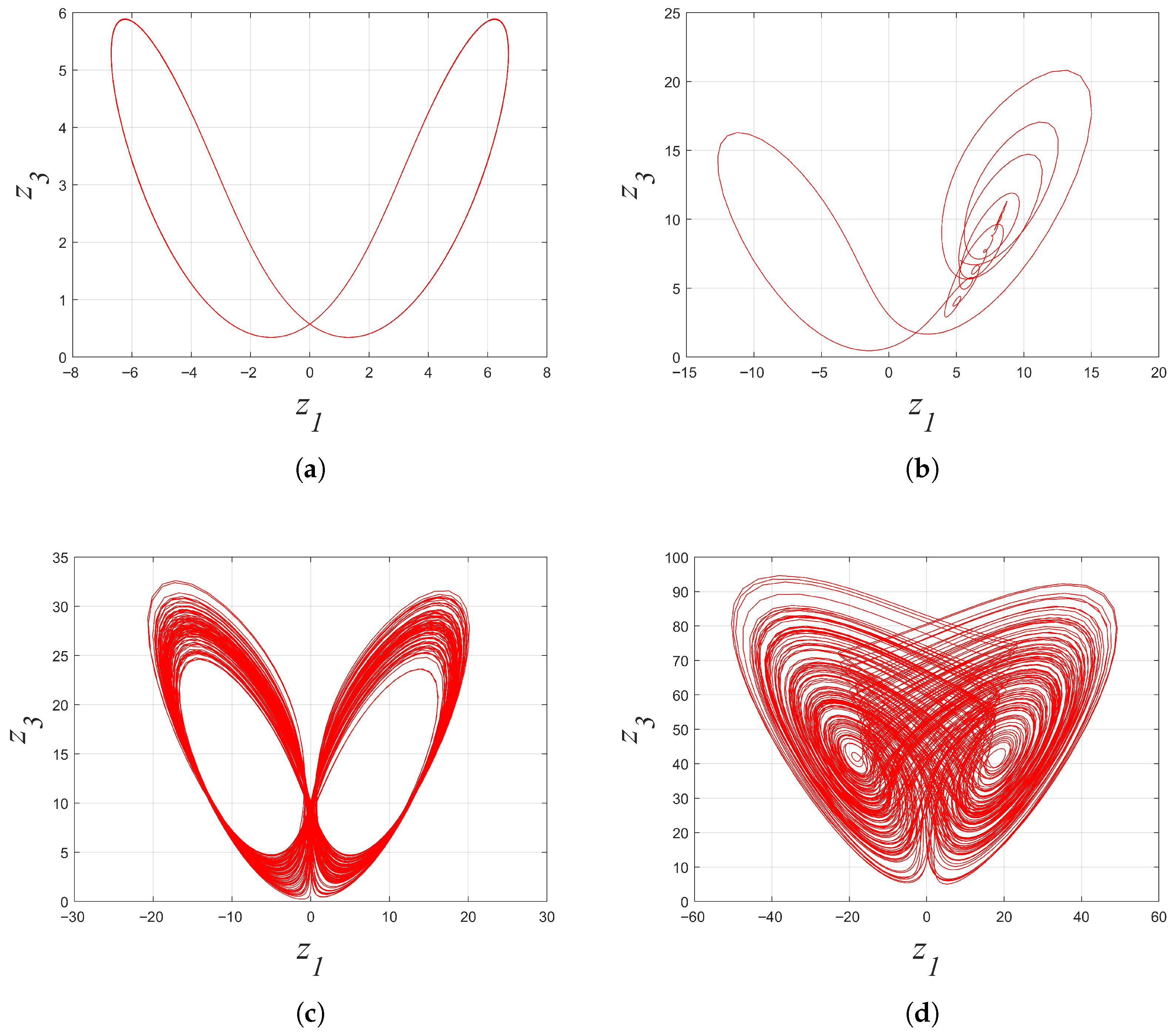
2.3. Dynamical Behavior When System Parameters Changed
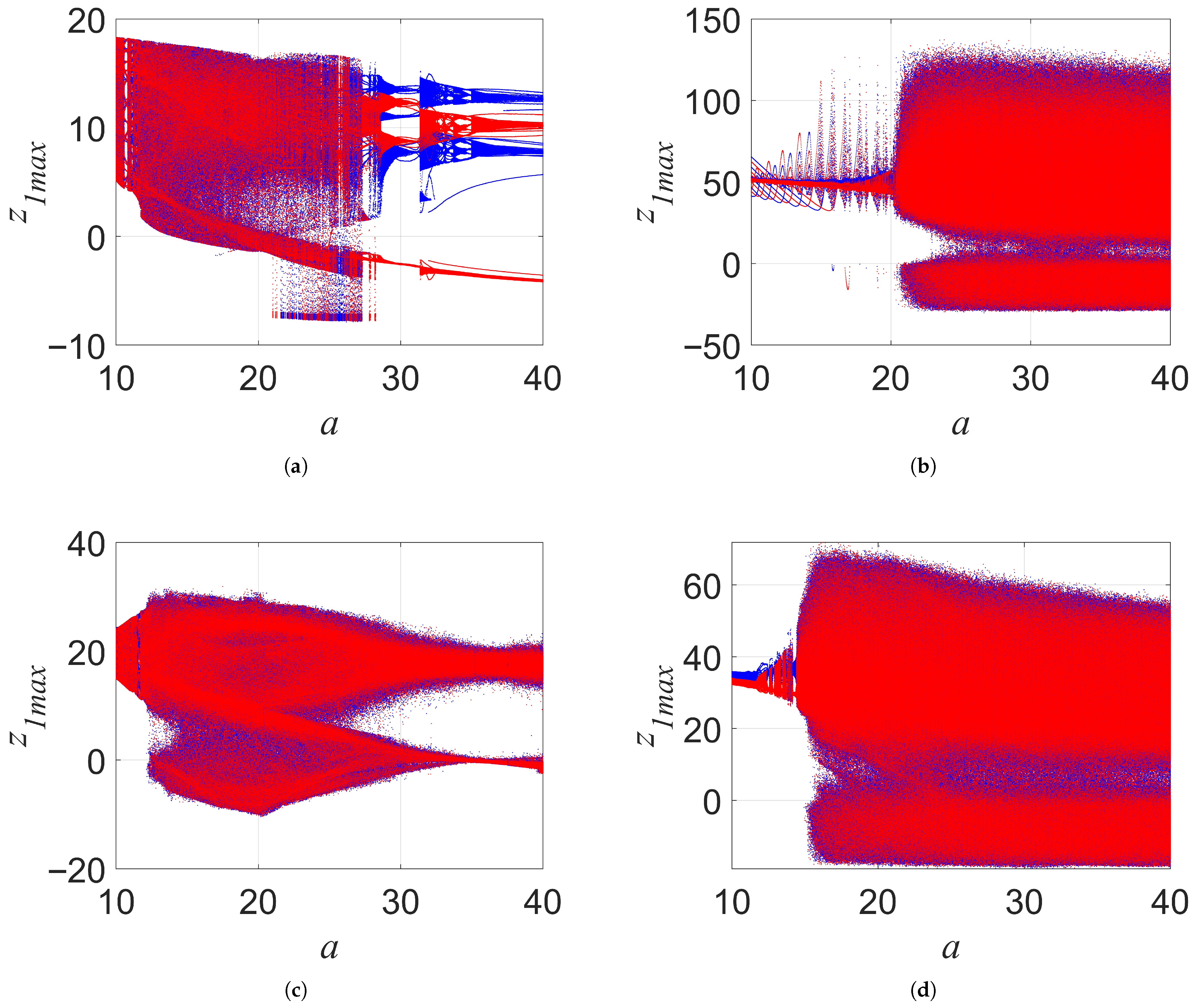
2.3.1. When a and b Changed
2.3.2. When c and d Changed
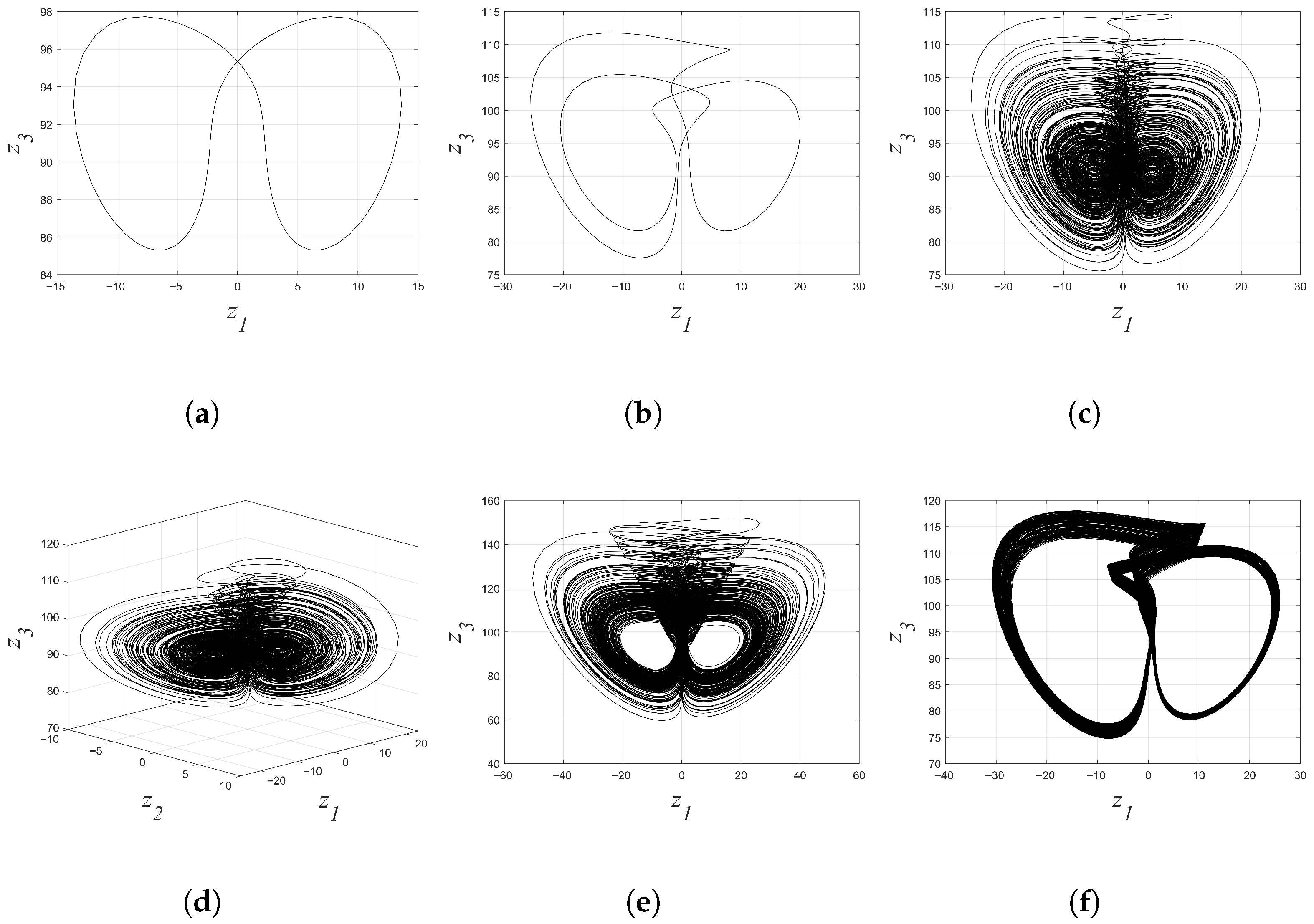
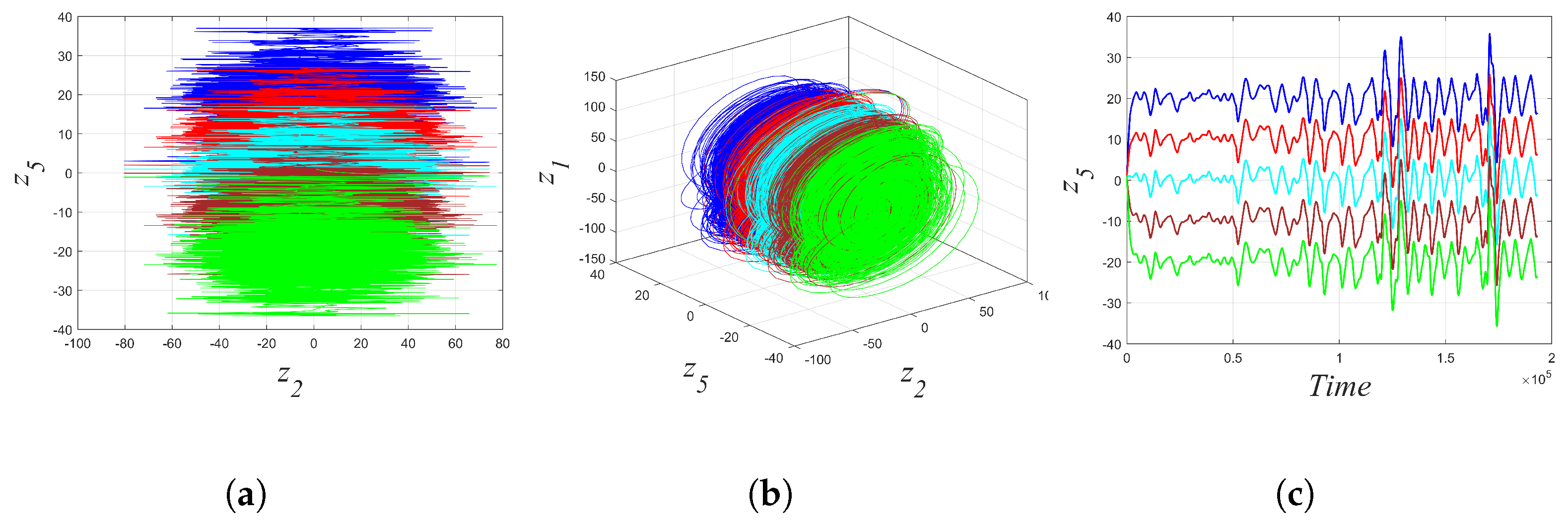
2.3.3. Multistability and Coexistence of Attractors

2.3.4. Offset Boosting Control
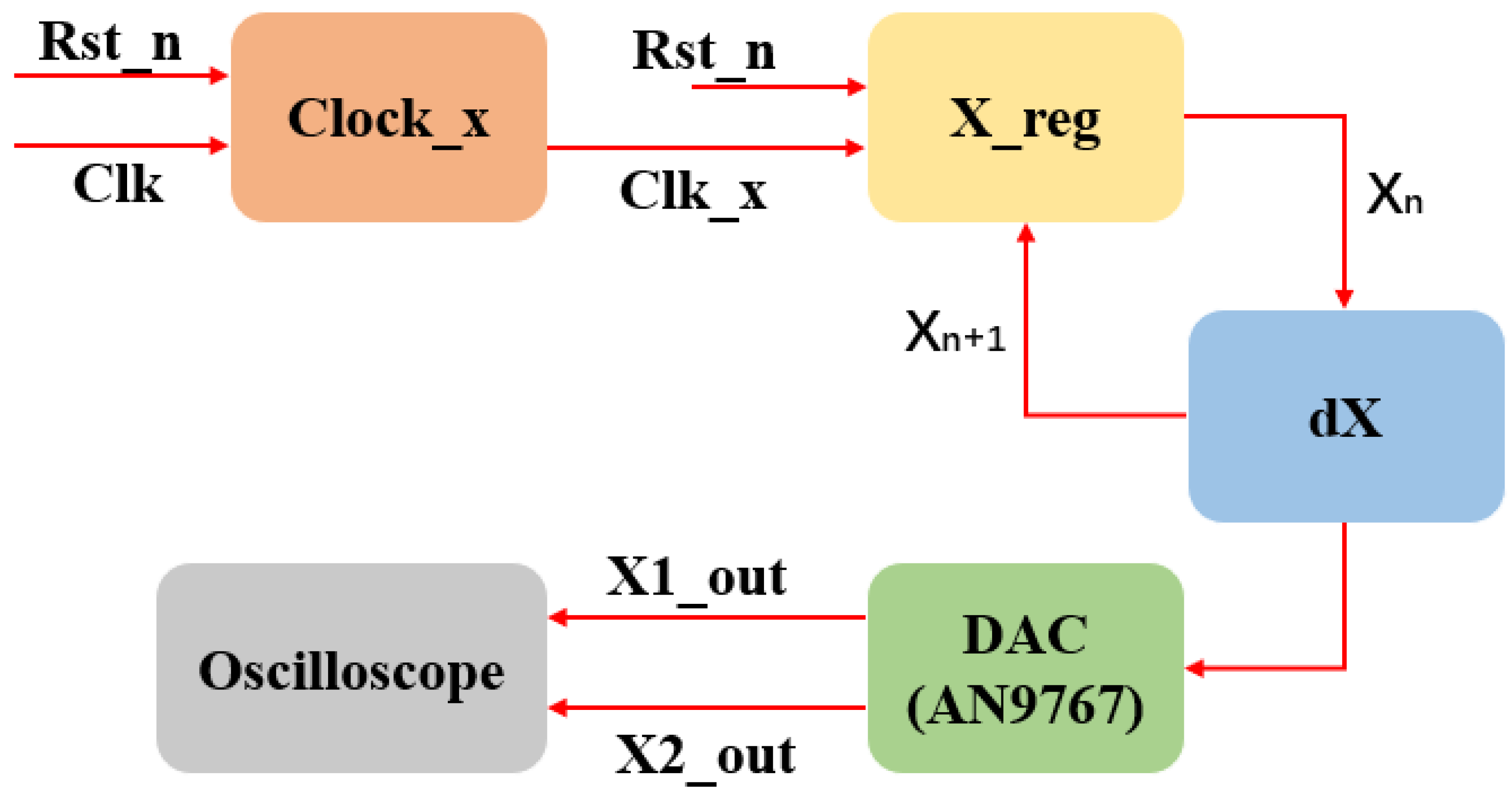
3. FPGA Implementation
4. Image Encryption
4.1. Image Encryption Process
- Let .
- Here, represents the summation of a vector. If , , or is obtained, the position of the corresponding remains unchanged.
- If , , or is obtained, the position of the corresponding remains unchanged. After the above operations, matrix D is transformed into matrix E.
4.2. Performance and Security Analysis
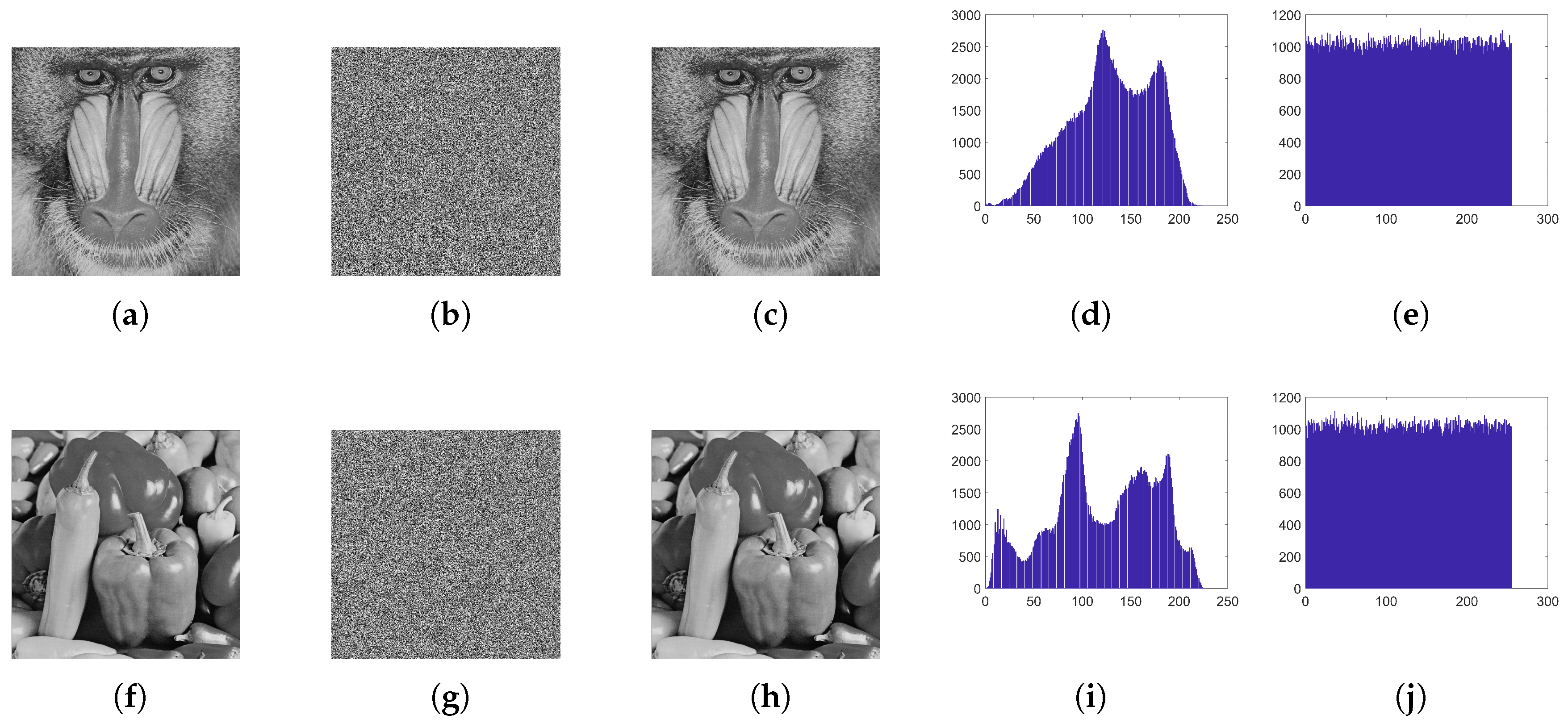
4.2.1. Histogram Analysis
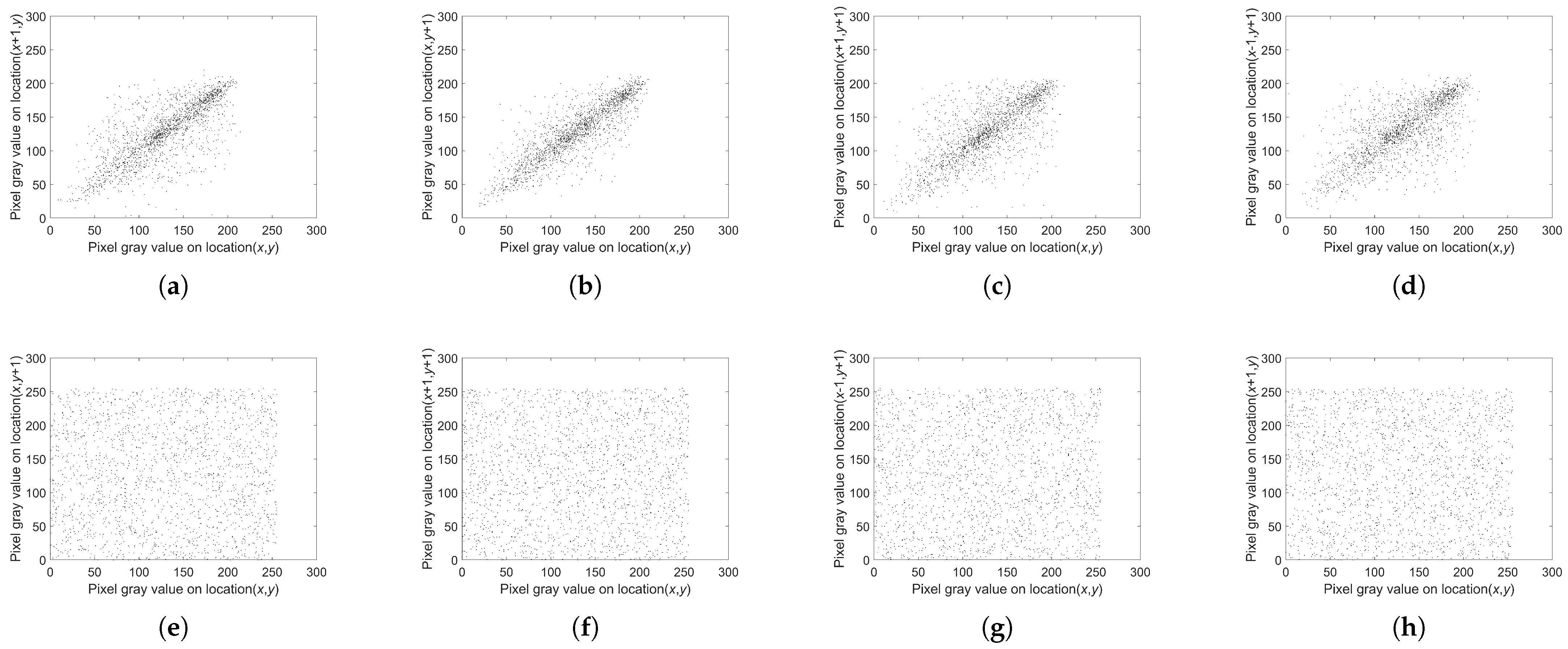
4.2.2. Correlation Analysis of Adjacent Pixels
4.2.3. Information Entropy
4.2.4. Key Sensitivity Analysis
4.2.5. Plain Image Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Zhu, J.; Jin, J.; Chen, C.; Wu, L.; Lu, M.; Ouyang, A. A New-Type Zeroing Neural Network Model and Its Application in Dynamic Cryptography. IEEE Trans. Emerg. Top. Comput. Intell. 2025, 9, 176–191. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Sun, Y.; Yang, G. Memristive multi-wing chaotic Hopfield neural network for LiDAR data security. Nonlinear Dyn. 2025, 113, 17161–17176. [Google Scholar] [CrossRef]
- Tan, F.; Zhou, L.; Zong, G.; Wang, Z.; Zhuang, G.; Shangguan, X. Fixed Time Control for Interlayer Synchronism under DDMNNs and Application in Secure Communication. IEEE Trans. Autom. Sci. Eng. 2025, 22, 10827–10834. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, K.; Tan, F.; Zhang, H.; Li, C. Synchronization for security communication of multi-delay MNNs under uncertain parameters identification: An adaptive time-controllable approach. Nonlinear Dyn. 2025, 113, 13507–135221. [Google Scholar] [CrossRef]
- Hua, C.; Cao, X.; Liao, B. Real-Time Solutions for Dynamic Complex Matrix Inversion and Chaotic Control Using ODE-Based Neural Computing Methods. Comput. Intell. 2025, 41, e70042. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Ouyang, A.; Yu, F.; Liu, H. A time-varying fuzzy parameter zeroing neural network for the synchronization of chaotic systems. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 364–376. [Google Scholar] [CrossRef]
- Hong, Q.; Jiang, H.; Xiao, P.; Du, S.; Li, T. A Parallel Computing Scheme Utilizing Memristor Crossbars for Fast Corner Detection and Rotation Invariance in the ORB Algorithm. IEEE Trans. Comput. 2025, 74, 996–1010. [Google Scholar] [CrossRef]
- Xu, Q.; Ding, X.; Chen, B.; Parastesh, F.; Ho-Ching Iu, H.; Wang, N. A Universal Configuration Framework for Mem-Element-Emulator-Based Bionic Firing Circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4120–4130. [Google Scholar] [CrossRef]
- Xiao, P.; Fang, J.; Wei, Z.; Dong, Y.; Du, S.; Wen, S.; Hong, Q. A Riccati Matrix Equation Solver Design Based Neurodynamics Method and Its Application. IEEE Trans. Autom. Sci. Eng. 2025, 22, 15163–15176. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, S.; Su, D.; Wu, Y.; Gracia, Y.M.; Yin, H. Dynamic Analysis and Implementation of FPGA for a New 4D Fractional-Order Memristive Hopfield Neural Network. Fractal Fract. 2025, 9, 115. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Deng, Q. Discrete-time fractional-order local active memristor-based Hopfield neural network and its FPGA implementation. Chaos Solitons Fractals 2025, 193, 116053. [Google Scholar] [CrossRef]
- Yu, F.; He, S.; Yao, W.; Cai, S.; Xu, Q. Bursting Firings in Memristive Hopffeld Neural Network with Image Encryption and Hardware Implementation. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2025, 1–13. [Google Scholar] [CrossRef]
- Jin, J.; Wu, M.; Ouyang, A.; Li, K.; Chen, C. A Novel Dynamic Hill Cipher and Its Applications on Medical IoT. IEEE Internet Things J. 2025, 12, 14297–14308. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Z.; Iu, H.H.C.; Ding, S.; Mou, J.; Erkan, U.; Toktas, A.; Li, Q.; Wang, C.; Cao, Y. A Parallel Color Image Encryption Algorithm Based on a 2D Logistic-Rulkov Neuron Map. IEEE Internet Things J. 2025, 12, 18115–18124. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting Newly Designed Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Yang, G. Chaotic Dynamics of Memristor-Coupled Tabu Learning Neuronal Network. Int. J. Bifurc. Chaos 2025, 35, 2550053. [Google Scholar] [CrossRef]
- Xiang, Q.; Gong, H.; Hua, C. A new discrete-time denoising complex neurodynamics applied to dynamic complex generalized inverse matrices. J. Supercomput. 2025, 81, 159. [Google Scholar] [CrossRef]
- Lin, H.; Deng, X.; Yu, F.; Sun, Y. Diversified Butterfly Attractors of Memristive HNN With Two Memristive Systems and Application in IoMT for Privacy Protection. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2025, 44, 304–316. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Yang, G.; Luo, D. Discrete Memristive Delay Feedback Rulkov Neuron Model: Chaotic Dynamics, Hardware Implementation and Application in Secure Communication. IEEE Internet Things J. 2025, 12, 25559–25567. [Google Scholar] [CrossRef]
- Gao, S.; Iu, H.H.C.; Erkan, U.; Simsek, C.; Toktas, A.; Cao, Y.; Wu, R.; Mou, J.; Li, Q.; Wang, C. A 3D Memristive Cubic Map with Dual Discrete Memristors: Design, Implementation, and Application in Image Encryption. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 7706–7718. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Sun, Y.; Yang, G. Discrete Memristive Conservative Chaotic Map: Dynamics, Hardware Implementation, and Application in Secure Communication. IEEE Trans. Cybern. 2025, 55, 3926–3934. [Google Scholar] [CrossRef]
- Yu, F.; Tan, B.; He, T.; He, S.; Huang, Y.; Cai, S.; Lin, H. A Wide-Range Adjustable Conservative Memristive Hyperchaotic System with Transient Quasi-Periodic Characteristics and Encryption Application. Mathematics 2025, 13, 726. [Google Scholar] [CrossRef]
- Huang, L.L.; Ma, Y.H.; Li, C. Characteristic analysis of 5D symmetric Hamiltonian conservative hyperchaotic system with hidden multiple stability. Chin. Phys. B 2024, 33, 010503. [Google Scholar] [CrossRef]
- Yuan, Y.; Yu, F.; Tan, B.; Huang, Y.; Yao, W.; Cai, S.; Lin, H. A class of n-D Hamiltonian conservative chaotic systems with three-terminal memristor: Modeling, dynamical analysis, and FPGA implementation. Chaos 2025, 35, 013121. [Google Scholar] [CrossRef] [PubMed]
- Lai, Q.; Liu, Y.; Fortuna, L. Dynamical Analysis and Fixed-Time Synchronization for Secure Communication of Hidden Multiscroll Memristive Chaotic System. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4665–4675. [Google Scholar] [CrossRef]
- Xin, Z.J.; Lai, Q. Dynamical investigation and encryption application of a new multiscroll memristive chaotic system with rich offset boosting features. Chaos Solitons Fractals 2024, 181, 114696. [Google Scholar] [CrossRef]
- Shen, Y.; Li, Y.; Li, W.; Yao, Q.; Gao, H. Extremely multi-stable grid-scroll memristive chaotic system with omni-directional extended attractors and application of weak signal detection. Chaos Solitons Fractals 2025, 190, 115791. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Chen, G. Design and performance analysis of discrete memristive hyperchaotic systems with stuffed cube attractors and ultraboosting behaviors. IEEE Trans. Ind. Electron. 2024, 71, 7819–7828. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Woźniak, M. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Yu, F.; Su, D.; He, S.; Wu, Y.; Zhang, S.; Yin, H. Resonant tunneling diode cellular neural network with memristor coupling and its application in police forensic digital image protection. Chin. Phys. B 2025, 34, 050502. [Google Scholar] [CrossRef]
- Deshpande, A.S.; Daftardar-Gejji, V. Enhancing the security of image communication with a new hyper-chaotic system. Phys. Scr. 2024, 99, 115234. [Google Scholar] [CrossRef]
- Nabil, H.; Tayeb, H. A secure communication scheme based on generalized modified projective synchronization of a new 4-D fractional-order hyperchaotic system. Phys. Scr. 2024, 99, 095203. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, Y.; Luo, X.; Gou, X.; Xu, B.; Tang, S. n-Dimensional Hyperchaotic Discrete Maps With Desired Positive Lyapunov Exponents and Its Application in Secure Communication. IEEE Trans. Ind. Electron. 2024, 72, 6412–6421. [Google Scholar] [CrossRef]
- Benkouider, K.; Sambas, A.; Bonny, T.; Al Nassan, W.; Moghrabi, I.A.; Sulaiman, I.M.; Hassan, B.A.; Mamat, M. A comprehensive study of the novel 4D hyperchaotic system with self-exited multistability and application in the voice encryption. Sci. Rep. 2024, 14, 12993. [Google Scholar] [CrossRef]
- Zhang, J.; Bi, J.; Hou, J.; Xie, Q. Dynamical analysis, circuit realization, and applications of 4D hyperchaotic systems with bursty oscillations and infinite attractor coexistence. J. Supercomput. 2024, 80, 8767–8800. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, H.; Ho-Ching Iu, H.; Erkan, U.; Toktas, A. Novel n-Dimensional Nondegenerate Discrete Hyperchaotic Map With Any Desired Lyapunov Exponents. IEEE Internet Things J. 2025, 12, 9082–9090. [Google Scholar] [CrossRef]
- Kopp, M.; Samuilik, I. A New 6D Two-wing Hyperhaotic System: Dynamical Analysis, Circuit Design, and Sinchronization. Chaos Theory Appl. 2024, 6, 273–283. [Google Scholar] [CrossRef]
- Yu, F.; Wu, C.; Xu, S.; Yao, W.; Xu, C.; Cai, S.; Wang, C. Color video encryption transmission in IoT based on memristive hopfield neural network. Signal Image Video Process. 2025, 19, 77. [Google Scholar] [CrossRef]
- Peng, Y.; Li, M.; Li, Z.; Ma, M.; Wang, M.; He, S. What is the impact of discrete memristor on the performance of neural network: A research on discrete memristor-based BP neural network. Neural Netw. 2025, 185, 107213. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Zhang, Y.; Cao, Y. A New Hyperchaotic Map Based on Discrete Memristor and Meminductor: Dynamics Analysis, Encryption Application, and DSP Implementation. IEEE Trans. Ind. Electron. 2024, 71, 5094–5104. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Wang, C.; Li, Y. Dynamic analysis and field-programmable gate array implementation of a 5D fractional-order memristive hyperchaotic system with multiple coexisting attractors. Fractal Fract. 2024, 8, 271. [Google Scholar] [CrossRef]
- Hassan, A.; Zhou, L. A novel 6D four-wing memristive hyperchaotic system: Generalized fixed-time synchronization and its application in secure image encryption. Chaos Solitons Fractals 2025, 192, 115986. [Google Scholar] [CrossRef]
- Wan, Q.; Yang, Q.; Liu, T.; Chen, C.; Shen, K. Single direction, grid and spatial multi-scroll attractors in Hopfield neural network with the variable number memristive self-connected synapses. Chaos Solitons Fractals 2024, 189, 115584. [Google Scholar] [CrossRef]
- Wang, M.; Ding, J.; Li, J.; He, S.; Zhang, X.; Iu, H.H.C.; Li, Z. A novel multistable chaotic system with 2 m-scroll attractor and its application. Eur. Phys. J. Plus 2024, 139, 64. [Google Scholar] [CrossRef]
- Zhang, S.; Peng, X.; Wang, X.; Chen, C.; Zeng, Z. A Novel Memristive Multiscroll Multistable Neural Network With Application to Secure Medical Image Communication. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 1774–1786. [Google Scholar] [CrossRef]
- Yuan, Z.; Wu, Y.; Ou, C.; Zhong, P.; Zhao, X.; Ma, M. Dynamical behavior of SW-SW neural networks. Chinese J. Phys. 2025, 94, 108–120. [Google Scholar] [CrossRef]
- Lai, Q.; Liu, Y.; Chen, Z. Multiscroll chaos and extreme multistability of memristive chaotic system with application to image encryption. J. Vib. Eng. Technol. 2024, 12, 3487–3505. [Google Scholar] [CrossRef]
- Maazouz, M.; Toubal, A.; Bengherbia, B.; Houhou, O.; Batel, N. FPGA implementation of a chaos-based image encryption algorithm. J. King Saud-Univ.-Comput. Inf. Sci. 2022, 34, 9926–9941. [Google Scholar] [CrossRef]
- Pan, G.; Li, C.; Liu, W.; Xue, Y.; Qi, X. Countless coexisting chaotic attractors: From system construction to FPGA-based observation. Chaos Solitons Fractals 2025, 198, 116610. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, J. A dynamic information flow control framework for hyperchaos in complex-variable systems and FPGA-based applications. Chaos Solitons Fractals 2025, 199, 116858. [Google Scholar] [CrossRef]
- Chua, L. Everything You Wish to Know About Memristors But Are Afraid to Ask. Radioengineering 2015, 24, 319–368. [Google Scholar] [CrossRef]
- Chua, L. If it’s pinched it’s a memristor. Semicond. Sci. Technol. 2014, 29, 104001. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 2003, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L. Resistance switching memories are memristors. In Handbook of Memristor Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 197–230. [Google Scholar]
- Benkouider, K.; Vaidyanathan, S.; Sambas, A.; Tlelo-Cuautle, E.; Abd El-Latif, A.A.; Abd-El-Atty, B.; Bermudez-Marquez, C.F.; Sulaiman, I.M.; Awwal, A.M.; Kumam, P. A new 5-D multistable hyperchaotic system with three positive Lyapunov exponents: Bifurcation analysis, circuit design, FPGA realization and image encryption. IEEE Access 2022, 10, 90111–90132. [Google Scholar] [CrossRef]
- Wang, J.; Yu, W.; Wang, J.; Zhao, Y.; Zhang, J.; Jiang, D. A new six-dimensional hyperchaotic system and its secure communication circuit implementation. Int. J. Circuit Theory Appl. 2019, 47, 702–717. [Google Scholar] [CrossRef]
- Sabaghian, A.; Balochian, S.; Yaghoobi, M. Synchronisation of 6D hyper-chaotic system with unknown parameters in the presence of disturbance and parametric uncertainty with unknown bounds. Connect. Sci. 2020, 32, 362–383. [Google Scholar] [CrossRef]
- Kopp, M.; Kopp, A. A New 6D Chaotic Generator: Computer Modelling and Circuit Design. Int. J. Eng. Technol. Innov. 2022, 12, 288–307. [Google Scholar] [CrossRef]
- Das, B.D.C.; Patra, A.; Saha, A.; Sikder, S.S. Secured communication of multiple compressed infrared images using 6D hyper-chaotic encryption. J. Opt. 2024, 53, 4202–4214. [Google Scholar] [CrossRef]
- AL-Azzawi, S.F.; Al-Obeidi, A.S. Chaos synchronization in a new 6D hyperchaotic system with self-excited attractors and seventeen terms. Asian-Eur. J. Math. 2021, 14, 2150085. [Google Scholar] [CrossRef]
- Benkouider, K.; Bouden, T.; Yalcin, M.E.; Vaidyanathan, S. A new family of 5D, 6D, 7D and 8D hyperchaotic systems from the 4D hyperchaotic Vaidyanathan system, the dynamic analysis of the 8D hyperchaotic system with six positive Lyapunov exponents and an application to secure communication design. Int. J. Model. Identif. Control 2020, 35, 241–257. [Google Scholar] [CrossRef]
- Yang, J.; Feng, Z.; Liu, Z. A new five-dimensional hyperchaotic system with six coexisting attractors. Qual. Theory Dyn. Syst. 2021, 20, 1–31. [Google Scholar] [CrossRef]
- Ojoniyi, O.S.; Njah, A.N. A 5D hyperchaotic Sprott B system with coexisting hidden attractors. Chaos Solitons Fractals 2016, 87, 172–181. [Google Scholar] [CrossRef]
- Bao, B.; Jiang, T.; Xu, Q.; Chen, M.; Wu, H.; Hu, Y. Coexisting infinitely many attractors in active band-pass filter-based memristive circuit. Nonlinear Dyn. 2016, 86, 1711–1723. [Google Scholar] [CrossRef]
- Jia, H.; Shi, W.; Wang, L.; Qi, G. Energy analysis of Sprott-A system and generation of a new Hamiltonian conservative chaotic system with coexisting hidden attractors. Chaos Solitons Fractals 2020, 133, 109635. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Ahmed, M. Analysis of chaotic and hyperchaotic conservative complex nonlinear systems. Miskolc Math. Notes 2017, 18, 315–326. [Google Scholar] [CrossRef]
- Brandon, J. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Wiggins, S., Ed.; DM98.00; Springer: Berlin/Heidelberg, Germany, 1990; p. 672. ISBN 3-540-9703-7. [Google Scholar]
- Kuznetsov, Y.A.; Kuznetsov, I.A.; Kuznetsov, Y. Elements of Applied Bifurcation Theory; Springer: Berlin/Heidelberg, Germany, 1998; Volume 112. [Google Scholar]
- Kuznetsov, Y.A. Elements of applied bifurcation theory. Appl. Math. Sci. 2004, 288, 715–730. [Google Scholar]
- Golubitsky, M.; Stewart, I. The Symmetry Perspective; Birkhäuser: Basel, Switzerland, 2002. [Google Scholar]
- Ashwin, P.; Orosz, G.; Borresen, J. Heteroclinic Switching in Coupled Oscillator Networks: Dynamics on Odd Graphs; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lai, Q.; Lai, C.; Zhang, H.; Li, C. Hidden coexisting hyperchaos of new memristive neuron model and its application in image encryption. Chaos Solitons Fractals 2022, 158, 112017. [Google Scholar] [CrossRef]
- Lai, Q.; Lai, C.; Kuate, P.D.K.; Li, C.; He, S. Chaos in a simplest cyclic memristive neural network. Int. J. Bifurc. Chaos 2022, 32, 2250042. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kamdem Kuate, P.D. Modelling and circuit realisation of a new no-equilibrium chaotic system with hidden attractor and coexisting attractors. Electron. Lett. 2020, 56, 1044–1046. [Google Scholar] [CrossRef]
- Hu, J.; Rao, S.; Zhu, M.; Huang, J.; Wang, J.; Wang, J. SRCC: Sub-RTT Congestion Control for Lossless Datacenter Networks. IEEE Trans. Ind. Inform. 2025, 21, 2799–2808. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Li, D.; Wang, J.; Wang, J. Crack segmentation network via difference convolution-based encoder and hybrid CNN-Mamba multi-scale attention. Pattern Recognit. 2025, 167, 111723. [Google Scholar] [CrossRef]
- Hu, J.; He, Y.; Luo, W.; Huang, J.; Wang, J. Enhancing Load Balancing with In-Network Recirculation to Prevent Packet Reordering in Lossless Data Centers. IEEE/ACM Trans. Netw. 2024, 32, 4114–4127. [Google Scholar] [CrossRef]
- Badshah, A.; Daud, A.; Alharbey, R.; Banjar, A.; Bukhari, A.; Alshemaimri, B. Big data applications: Overview, challenges and future. Artif. Intell. Rev. 2024, 57, 290. [Google Scholar] [CrossRef]
- Hu, J.; Huang, J.; Li, Z.; Li, Y.; Rao, S.; Jiang, W.; Chen, K.; Wang, J.; He, T. Proactive Transport with High Link Utilization Using Opportunistic Packets in Cloud Data Centers. IEEE Trans. Mob. Comput. 2025, 1–16. [Google Scholar] [CrossRef]
- Feng, W.; Yang, J.; Zhao, X.; Qin, Z.; Zhang, J.; Zhu, Z.; Wen, H.; Qian, K. A novel multi-channel image encryption algorithm leveraging pixel reorganization and hyperchaotic maps. Mathematics 2024, 12, 3917. [Google Scholar] [CrossRef]
- Ning, Y.; Jin, J.; Li, Z.; Chen, C.; Ouyang, A. A Time-varying Hill Cipher for Dynamic Image Cryptography. Tsinghua Sci. Technol. 2025. [Google Scholar] [CrossRef]
- Kumar, M.; Mohapatra, R.N.; Agarwal, S.; Sathish, G.; Raw, S.N. A new RGB image encryption using generalized Vigenere-type table over symmetric group associated with virtual planet domain. Multimed. Tools Appl. 2019, 78, 10227–10263. [Google Scholar] [CrossRef]
- Doubla, I.S.; Njitacke, Z.T.; Ekonde, S.; Tsafack, N.; Nkapkop, J.D.D.; Kengne, J. Multistability and circuit implementation of tabu learning two-neuron model: Application to secure biomedical images in IoMT. Neural Comput. Appl. 2021, 33, 14945–14973. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zheng, J.; Wang, X.; Zeng, Z.; Peng, X. Generating any number of initial offset-boosted coexisting Chua’s double-scroll attractors via piecewise-nonlinear memristor. IEEE Trans. Ind. Electron. 2021, 69, 7202–7212. [Google Scholar] [CrossRef]





| Dimension | Paper | |||||||
|---|---|---|---|---|---|---|---|---|
| 6D | 0.799484 | 0.295845 | 0 | −0.407744 | −0.659364 | −14.69188 | 5.00192 | Ref. [57] |
| 6D | 1.0529 | 0.6213 | 0.0342 | 0 | −13.7815 | −15.2637 | 4.12396 | Ref. [58] |
| 6D | 0.0988591 | 0.0109865 | −0.544226 | −1.00557 | −1.15581 | −1.77091 | 2.20184 | Ref. [59] |
| 6D | 1.0639 | 0.60107 | 0.0431 | 0 | −13.8708 | −15.1728 | 4.1231 | Ref. [60] |
| 6D | 4.1306 | 0.4936 | −0.0033 | −3.5059 | −14.8197 | −99.6187 | 4.07523769 | Ref. [43] |
| 6D | 0.653 | 0.326 | 0.000 | 1.558 | −4.419 | −12.676 | 4.574 | Ref. [61] |
| 6D | 1.462 | 0.1433 | 0.0725 | 0.0449 | 0 | −12.0700 | 5.1427 | Ref. [62] |
| 5D | 6.053 | 0.028 | 0.000 | −4.747 | −46.214 | / | 4.029 | Ref. [63] |
| 5D | 12.659 | 0.055 | 0.024 | 0 | −67.701 | / | 4.189 | Ref. [56] |
| 6D | 21.6825 | 0.1079 | 0 | −0.0083 | −1.0000 | −92.7858 | 5.224 | Section 2.1 |
| 6D | 4.4553 | 0.1681 | 0.1006 | 0 | −1.0000 | −56.7186 | 5.066 | Section 2.3.3 |
| Dimension | Interval Length of Chaotic State | Paper |
|---|---|---|
| 5D | Less than 100 | Ref. [64] |
| 4D | Less than 6 | Ref. [65] |
| 4D | Less than 10 | Ref. [66] |
| 4D | Less than 50 | Ref. [67] |
| 6D | [13, 300] | This paper |
| Resource Type | Used | Available | Utilization (%) |
|---|---|---|---|
| LUT | 5304 | 53,200 | 9.97 |
| LUTRAM | 376 | 17,400 | 2.16 |
| Flip-Flop (FF) | 9978 | 106,400 | 9.38 |
| DSP48E | 82 | 220 | 37.27 |
| IO | 34 | 125 | 27.20 |
| BUFG | 1 | 32 | 3.13 |
| Index | Plain Image | Cipher Image | ||
|---|---|---|---|---|
| result | Baboon | Peppers | Baboon | Peppers |
| 235.2344 | 226.2598 | |||
| Image | Horizontal | Vertical | Main Diagonal | Anti-Diagonal |
|---|---|---|---|---|
| Plain Image | 0.749483 | 0.862469 | 0.740462 | 0.706836 |
| Cipher image | −0.03479 | −0.034369 | 0.005658 | 0.001927 |
| Index | Plain Image | Cipher Image | ||||
|---|---|---|---|---|---|---|
| result | Lena | Baboon | Peppers | Lena | Baboon | Peppers |
| 7.4451 | 7.3583 | 7.5937 | 7.9992 | 7.9994 | 7.9993 | |
| Image | Plain | Cipher | Ref. [83] | Ref. [84] | Ref. [85] |
|---|---|---|---|---|---|
| Information entropy | 7.3538 | 7.9994 | 7.991 | 7.906 | 7.740 |
| Index | Theoretical Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NPCR | 99.611 | 99.6081 | 99.6082 | 99.6085 | 99.6118 | 99.6094 | 99.6101 | 99.6097 | 99.6107 | 99.6094 |
| UACI | 33.4608 | 33.4625 | 33.4657 | 33.469 | 33.4538 | 33.4645 | 33.4651 | 33.4624 | 33.4661 | 33.4635 |
| Index | Lena | Baboon | Pepper | Theoretical Value |
|---|---|---|---|---|
| NPCR | 99.6106 | 99.6094 | 99.6095 | 99.6094 |
| UACI | 33.4567 | 33.4659 | 33.4629 | 33.4635 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Gracia, Y.M.; Guo, R.; Ying, Z.; Xu, J.; Yao, W.; Jin, J.; Lin, H. Dynamic Analysis and Application of 6D Multistable Memristive Chaotic System with Wide Range of Hyperchaotic States. Axioms 2025, 14, 638. https://doi.org/10.3390/axioms14080638
Yu F, Gracia YM, Guo R, Ying Z, Xu J, Yao W, Jin J, Lin H. Dynamic Analysis and Application of 6D Multistable Memristive Chaotic System with Wide Range of Hyperchaotic States. Axioms. 2025; 14(8):638. https://doi.org/10.3390/axioms14080638
Chicago/Turabian StyleYu, Fei, Yumba Musoya Gracia, Rongyao Guo, Zhijie Ying, Jiarong Xu, Wei Yao, Jie Jin, and Hairong Lin. 2025. "Dynamic Analysis and Application of 6D Multistable Memristive Chaotic System with Wide Range of Hyperchaotic States" Axioms 14, no. 8: 638. https://doi.org/10.3390/axioms14080638
APA StyleYu, F., Gracia, Y. M., Guo, R., Ying, Z., Xu, J., Yao, W., Jin, J., & Lin, H. (2025). Dynamic Analysis and Application of 6D Multistable Memristive Chaotic System with Wide Range of Hyperchaotic States. Axioms, 14(8), 638. https://doi.org/10.3390/axioms14080638










