Bipartite Synchronization of Cooperation–Competition Neural Networks Using Asynchronous Sampling Scheme
Abstract
1. Introduction
- (1)
- (2)
- Unlike existing works [9,10,11,12], we consider the asynchronous sampling scheme in the presence of deception attacks. Using the characteristics of an asynchronous sampling scheme, we constructed a class of associated loop functionals that can fully utilize the state information at each node’s sampling instants.
2. Discussion
3. Preliminaries and Problem Formulation
- (1)
- If , .
- (2)
- If , .
4. Main Results
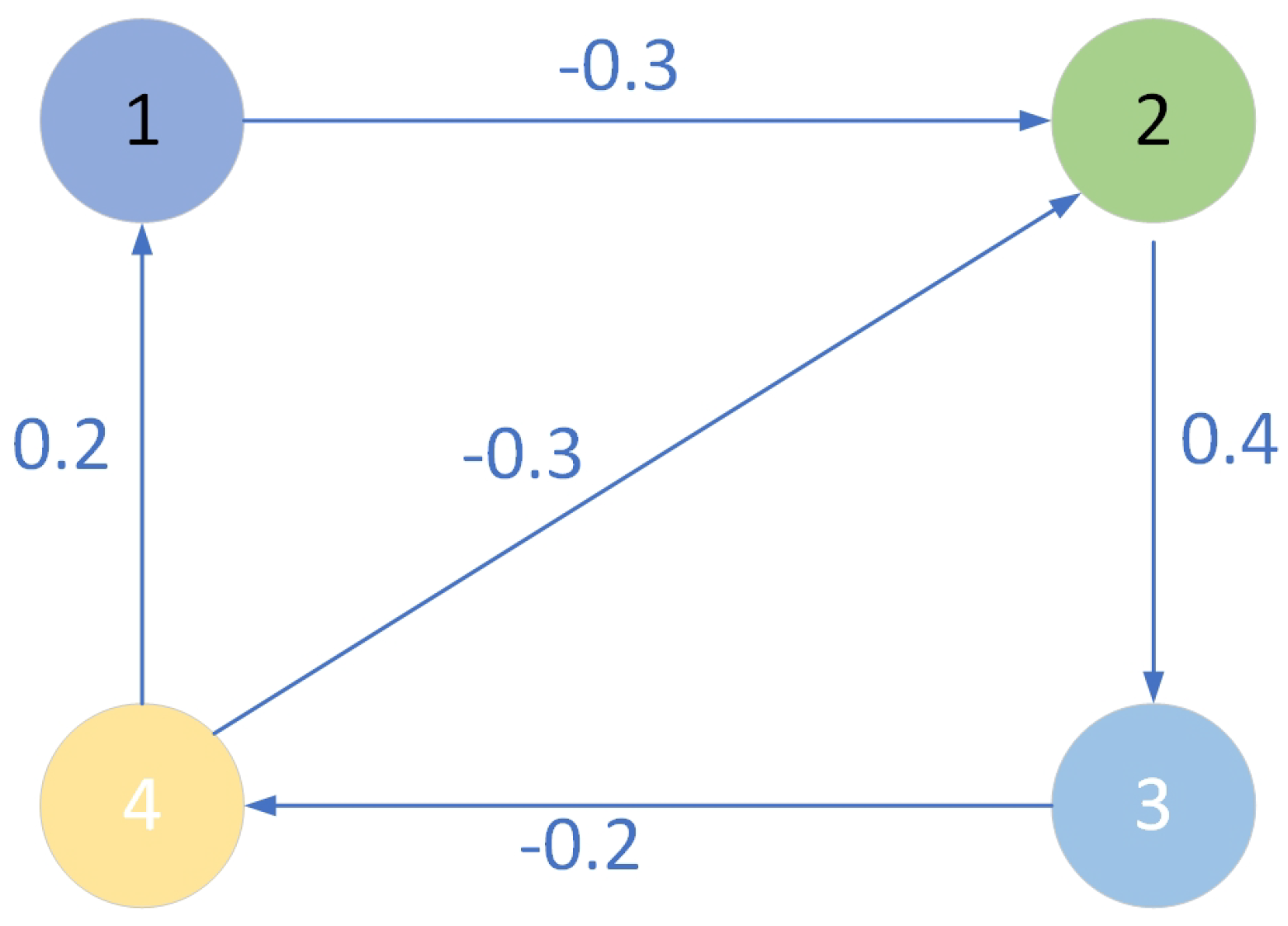
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCNNs | Cooperation–competition neural networks; |
| LMI | Linear matrix inequality. |
References
- Wu, Z.; Li, Q.; He, B. Practical vertical federated learning with unsupervised representation learning. IEEE Trans. Big Data 2022, 10, 864–878. [Google Scholar] [CrossRef]
- Huang, W.; Wang, D.; Ouyang, X.; Wan, J.; Liu, J.; Li, T. Multimodal federated learning: Concept, methods, applications and future directions. Inf. Fusion 2024, 112, 102576. [Google Scholar] [CrossRef]
- Guo, D.; Liu, Z.; Li, R. RegraphGAN: A graph generative adversarial network model for dynamic network anomaly detection. Neural Netw. 2023, 166, 273–285. [Google Scholar] [CrossRef]
- Xue, L.; Wu, H.; Zheng, H.; He, Z. Control chart pattern recognition for imbalanced data based on multi-feature fusion using convolutional neural network. Comput. Ind. Eng. 2023, 182, 109410. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Wang, Z.; Liang, H. Mode-dependent stochastic synchronization for Markovian coupled neural networks with time-varying mode-delays. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2621–2634. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Wang, Z.; Chen, Y.; Yi, X. State estimation for coupled stochastic complex networks with periodical communication protocol and intermittent nonlinearity switching. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1414–1425. [Google Scholar] [CrossRef]
- Liu, F.; Song, Q.; Wen, G.; Lu, J.; Cao, J. Bipartite synchronization of Lur’e network under signed digraph. Int. J. Robust Nonlinear Control 2018, 28, 6087–6105. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, Y.; Li, L.; Xu, X.; Yang, R. Bipartite consensus for second-order multi-agent systems with external disturbances via constraint data-sampled impulsive method. Commun. Nonlinear Sci. Numer. Simul. 2022, 109, 106314. [Google Scholar] [CrossRef]
- Chi, X.; Liu, X.; Jia, X. Multi-rate sampled-data observer-based networked load frequency control for multi-area interconnected power systems under multiple cyber-attacks. J. Frankl. Inst. 2025, 362, 107427. [Google Scholar] [CrossRef]
- He, Y.; Zhu, D.; Chen, C.; Wang, Y. Data-driven control of singularly perturbed hybrid systems with multi-rate sampling. ISA Trans. 2024, 148, 490–499. [Google Scholar] [CrossRef]
- Chi, X.; Jia, X.; Cheng, F.; Fan, M. Networked H∞ filtering for Takagi–Sugeno fuzzy systems under multi-output multi-rate sampling. J. Frankl. Inst. 2019, 356, 3661–3691. [Google Scholar] [CrossRef]
- Park, J.; Park, P. An improved stability criterion for linear systems with multi-rate sampled data. Nonlinear Anal. Hybrid Syst. 2020, 38, 100947. [Google Scholar] [CrossRef]
- Chang, Q.; Park, J.H.; Yang, Y. The optimization of control parameters: Finite-time bipartite synchronization of memristive neural networks with multiple time delays via saturation function. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7861–7872. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, Y.; Huang, P.; Chen, G. Appointed-time and attack-free bipartite synchronization of generic linear multiagent systems over directed switching networks. IEEE Trans. Autom. Control 2022, 67, 4498–4513. [Google Scholar] [CrossRef]
- Li, N.; Zheng, W.X. Bipartite synchronization of multiple memristor-based neural networks with antagonistic interactions. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1642–1653. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, X. Prescribed-time synchronization of Kuramoto oscillators over undirected network. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3041–3045. [Google Scholar] [CrossRef]
- Akhmet, M.; Başkan, K.; Yeşil, C. Markovian noise-induced delta synchronization approach for Hindmarsh–Rose model. Chaos Solitons Fractals 2024, 185, 115155. [Google Scholar] [CrossRef]
- Matusik, R.; Michalak, A.; Nowakowski, A. Fixed-time anti-synchronization for reaction-diffusion neural networks. Comput. Math. Appl. 2024, 173, 19–32. [Google Scholar] [CrossRef]
- Feng, H.; Wu, Z.; Zhang, X.; Xiao, Z.; Zhang, M.; Tao, J. Secure adaptive event-triggered anti-synchronization for BAM neural networks with energy-limited DoS attacks. Inf. Sci. 2024, 670, 120594. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, C.; Yu, J. Bipartite leaderless synchronization of fractional-order coupled neural networks via edge-based adaptive pinning control. J. Frankl. Inst. 2024, 361, 1303–1317. [Google Scholar] [CrossRef]
- Li, N.; Cao, J.; Wang, F. Bipartite secure synchronization criteria for coupled quaternion-valued neural networks with signed graph. Neural Netw. 2024, 180, 106717. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; He, X.; Wen, S. Bipartite synchronization of signed Lur’e network via quantized control. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2475–2479. [Google Scholar]
- Yang, D.; Wang, H.; Ren, G.; Yu, Y.; Zhang, X.L. Exponential bipartite synchronization of distributed-order multilayer neural networks with antagonistic interactions via aperiodic intermittent control. Commun. Nonlinear Sci. Numer. Simul. 2025, 147, 108820. [Google Scholar] [CrossRef]
- Liu, X.; Qin, P. Parameter estimation and model-free multi-innovation adaptive control algorithms. Int. J. Control. Autom. Syst. 2024, 22, 3509–3524. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Lü, J.; Lu, J.A. Further on Synchronization of Dynamical Networks Via Adaptive Intermittent Control. IEEE Trans. Autom. Control 2024, 69, 7216–7222. [Google Scholar] [CrossRef]
- Wang, L.; Qi, R.; Jiang, B. Adaptive fault-tolerant optimal control for hypersonic vehicles with state constrains based on adaptive dynamic programming. J. Frankl. Inst. 2024, 361, 106833. [Google Scholar] [CrossRef]
- Zhang, S.; Ding, X.; Lu, J.; Lou, J.; Liu, Y. Output-feedback stabilization of probabilistic Boolean control networks. Nonlinear Anal. Hybrid Syst. 2024, 53, 101505. [Google Scholar] [CrossRef]
- Liang, H.; Chen, L.; Pan, Y.; Lam, H.K. Fuzzy-based robust precision consensus tracking for uncertain networked systems with cooperative–antagonistic interactions. IEEE Trans. Fuzzy Syst. 2022, 31, 1362–1376. [Google Scholar] [CrossRef]
- Park, P.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Shi, Y.; Wei, Z. Bipartite Synchronization of Cooperation–Competition Neural Networks Using Asynchronous Sampling Scheme. Axioms 2025, 14, 625. https://doi.org/10.3390/axioms14080625
Fan S, Shi Y, Wei Z. Bipartite Synchronization of Cooperation–Competition Neural Networks Using Asynchronous Sampling Scheme. Axioms. 2025; 14(8):625. https://doi.org/10.3390/axioms14080625
Chicago/Turabian StyleFan, Shuxian, Yongjie Shi, and Zhongliang Wei. 2025. "Bipartite Synchronization of Cooperation–Competition Neural Networks Using Asynchronous Sampling Scheme" Axioms 14, no. 8: 625. https://doi.org/10.3390/axioms14080625
APA StyleFan, S., Shi, Y., & Wei, Z. (2025). Bipartite Synchronization of Cooperation–Competition Neural Networks Using Asynchronous Sampling Scheme. Axioms, 14(8), 625. https://doi.org/10.3390/axioms14080625




