On Factorable Surfaces of Finite Chen Type in the Lorentz–Heisenberg Space ${\mathbb{H}}_3$

Abstract

This paper is about a problem at the intersection of differential geometry, spectral analysis and the theory of manifolds. The study of finite-type subvarieties was initiated by Chen in the 1970s, with the aim of obtaining improved estimates for the mean total curvature of compact subvarieties in Euclidean space. The concept of a finite-type subvariety naturally extends that of a minimal subvariety or surface, the latter being closely related to variational calculus. In this work, we classify factorable surfaces in the Lorentz–Heisenberg space ${\mathbb{H}}_3$, equipped with a flat metric satisfying ${\Delta }^I{r}_i={\lambda }_i{r}_i$, which satisfies algebraic equations involving coordinate functions and the Laplacian operator with respect to the surface’s first fundamental form.

1. Introduction

Research on finite-type submanifolds began in the 1970s with the work of Chen [1], who posed the problem of classifying finite-type surfaces in a three-dimensional Euclidean space ${\mathbb{E}}^3$. In the mid-1980s, the concept of the finite type was extended to include any function defined on a submanifold of a Euclidean or pseudo-Euclidean space. The notion of finite-type surfaces was first explored in 1966 by Takahashi [2].

In recent years, significant progress has been made in the study of finite-type surfaces. Yoon [3] classified coordinate finite-type translation surfaces in a three-dimensional Galilean space. Medjahdi and Zoubir [4] classified affine factorable surfaces in a three-dimensional simply isotropic space, demonstrating that these surfaces satisfy specific algebraic equations involving their coordinate functions and the Laplacian operator with respect to the first and second fundamental forms. In [5], Medjati et al. proved that translation surfaces satisfy the conditions $\Delta r_i={\lambda }_i{r}_i$, $i=1,2,3$, ${\lambda }_i\in \mathbb{R}$, if and only if they have zero mean curvature.

In [6] the authors showed that in a modulo automorphism of the Lie algebra, the 3-dimensional Lorentz Heisenberg group ${\mathbb{H}}_3$ has the following classes of left-invariant Lorentz metrics:

$$\begin{array}{ccc}\hfill g_1& =& -d{x}^2+d{y}^2+{(xdy+dz)}^2,\hfill \\ \hfill g_2& =& d{x}^2+d{y}^2-{(xdy+dz)}^2,\hfill \\ \hfill g_3& =& d{x}^2+{(xdy+dz)}^2-{\left[\left(1-x\right)dy-dz\right]}^2.\hfill \end{array}$$

They showed that the metrics $g_1,g_2,g_3$ are non-isometric and that $g_3$ is flat. The Laplacian $\Delta$ on $M^2$ is given by (see [1])

$$\Delta ={\displaystyle \frac{-1}{\sqrt{\left|D\right|}}}\sum _{ij}{\displaystyle \frac{\partial }{\partial x^i}}\left(\sqrt{\left|D\right|}{g}^{ij}{\displaystyle \frac{\partial }{\partial x^j}}\right),$$

(1)

where $G=\left(g_{ij}\right)$ denotes the induced metric tensor on $M^2$, with inverse metric $G^{-1}=\left(g^{ij}\right)$ and determinant $D=detG$. We define (see [7])

$$\Delta r=(\Delta r_1,\Delta r_2,\Delta r_3),$$

(2)

where $r=r(x,y)=(r_1(x,y),r_2(x,y),r_3(x,y))$ is a $C^2$ function. The Heisenberg space, equipped with a flat Lorentzian metric, shares properties with Minkowski space (see [8]). However, it is well known that the Laplacian of the position vector of a surface in a pseudo-Euclidean space is twice the mean curvature vector [1]. Specifically, the Beltrami formula in $({\mathbb{H}}_3,g_3)$ is

$$\Delta r=2\hslash ,$$

(3)

where $\Delta$ denotes the Laplacian of the surface and ℏ is the mean curvature vector field of any surface $M^2$ in $({\mathbb{H}}_3,g_3).$

Let $r:$$M^2⟶$${\mathbb{H}}_3$ be an isometric immersion of surface in ${\mathbb{H}}_3$. Then r is said to be a semi-Riemannian surface in ${\mathbb{H}}_3$ if the induced metric on $M^2$ is non-degenerate. In that case this metric is Riemannian or Lorentzian and the surface is said to be spacelike or timelike, respectively. In this paper, we classify some types of spacelike translation surfaces of ${\mathbb{H}}_3$ endowed with a flat metric $g_3$ under the condition

$$\Delta r_i={\lambda }_i{r}_i,{\lambda }_i\in \mathbb{R},i=1,2,3.$$

(4)

Related work on surfaces in Euclidean 3-space satisfying similar spectral conditions on the coordinate functions includes the classification of conchoidal surfaces by Bulca Sokur and Dirim [9], where the authors obtained classification results for surfaces under the condition $\Delta x_i={\lambda }_i{x}_i$. Their approach, focusing on the radius function and the Laplacian with respect to the first fundamental form, complements and motivates our investigation in the Lorentz Heisenberg space setting.

2. The Beltrami Formula

Let $M^2$ be a surface in the Lorentz–Heisenberg 3-space ${\mathbb{H}}_3$ which represents the graph of the function $z=f(x,y)$, parameterized by

$$\begin{array}{cccc}& \begin{array}{c}r:U\subset {\mathbb{R}}^2\\ (x,y)\end{array}& \begin{array}{c}⟶\\ ⟼\end{array}& \begin{array}{c}{\mathbb{H}}_3\\ \left(x,y,f\left(x,y\right)\right)\end{array}\end{array}$$

where $r(x,y)=(x,y,f(x,y\left)\right)$ is the position vector. Hence,

$$\begin{array}{ccc}\hfill r_x& =& (1,0,f_x)={\partial }_x+f_x{\partial }_z\hfill \\ \hfill r_y& =& (0,1,f_y)={\partial }_y+f_y{\partial }_z\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}& & \begin{array}{c}{r}_x=e_1+f_x{e}_2-f_x{e}_3\end{array}\hfill \\ & & \begin{array}{c}{r}_y=\left(x+f_y\right)e_2+\left(1-x-f_y\right)e_3\end{array}\hfill \end{array}$$

(5)

The first fundamental form I and second fundamental form $II$ of the surface $M^2$ are given by

$$\begin{array}{ccc}\hfill I& =& Ed{x}^2+2Fdxdy+Gd{y}^2\hfill \\ \hfill II& =& Ld{x}^2+2Mdxdy+Nd{y}^2\hfill \end{array}$$

with

$$\begin{array}{c}E=g_3\left(r_x,r_x\right)=1,F=g_3\left(r_x,r_y\right)=f_x,G=g_3\left(r_y,r_y\right)=\left(2f_y+2x-1\right).\end{array}$$

And

$$L=g_3\left({\nabla }_{r_x}{r}_x,\aleph \right),M=g_3\left({\nabla }_{r_x}{r}_y,\aleph \right),N=g_3\left({\nabla }_{r_y}{r}_y,\aleph \right),$$

where ℵ is a unit normal vector field on $M^2$ that satisfies the following system:

$$\left\{\begin{array}{c}{g}_3\left(r_x,\aleph \right)=0,\\ g_3\left(r_y,\aleph \right)=0,\\ g_3\left(\aleph ,\aleph \right)=-1.\end{array}\right.$$

and so,

$$\begin{array}{ccc}& & \begin{array}{c}{\nabla }_{r_x}{r}_x=f_{xx}{e}_2-f_{xx}{e}_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_x}{r}_y=\left(f_{xy}+1\right)e_2-\left(f_{xy}+1\right)e_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_y}{r}_y=-e_1+f_{yy}{e}_2-f_{yy}{e}_3.\end{array}\hfill \end{array}$$

(6)

The normal vector is then given by

$$\begin{array}{ccc}\hfill \aleph & =& {\displaystyle \frac{(-f_x,\left(1-x-f_y\right),\left(x+f_y\right))}{W}}\hfill \\ & =& {\displaystyle \frac{-f_x}{W}}{e}_1+{\displaystyle \frac{\left(1-x-f_y\right)}{W}}{e}_2+{\displaystyle \frac{\left(x+f_y\right)}{W}}{e}_3,\hfill \end{array}$$

with

$$W=\sqrt{|EG-F^2|}=\sqrt{|2\left(f_y+x\right)-1-f_x^2|}.$$

Therefore

$$\begin{array}{ccc}L={\displaystyle \frac{1}{W}}{f}_{xx},& M={\displaystyle \frac{1}{W}}\left(1+f_{xy}\right),& N={\displaystyle \frac{1}{W}}\left(f_x+f_{yy}\right),\end{array}$$

and the mean curvature of the surface $M^2$ is given by the formula

$$\begin{array}{c}\hfill H={\displaystyle \frac{EN+GL-2FM}{2\left(EG-F^2\right)}}.\end{array}$$

So the mean curvature of the surface $M^2$ parameterized by $\left(x,y,f\left(x,y\right)\right)$ is given by

$$H={\displaystyle \frac{1}{2W^3}}\left[f_{yy}+\left(2\left(f_y+x\right)-1\right)f_{xx}-2f_x{f}_{xy}-f_x\right].$$

(7)

By (1), the Laplacian operator $\Delta$ of $M^2$ can be expressed as

$$\begin{array}{c}\Delta =-{\displaystyle \frac{1}{W^2}}\left[\left(2\left(f_y+x\right)-1\right){\displaystyle \frac{{\partial }^2}{\partial x^2}}-2f_x{\displaystyle \frac{{\partial }^2}{\partial x\partial y}}+{\displaystyle \frac{{\partial }^2}{\partial y^2}}\right]\\ -\left({\displaystyle \frac{2f_x}{W}}H+{\displaystyle \frac{1}{W^2}}\right){\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{2}{W}}H{\displaystyle \frac{\partial }{\partial y}}.\end{array}$$

(8)

By a direct computation, the Laplacian $\Delta r$ of r, using Equations (5)–(7), is given by

$${\Delta }^{I}r=-{\displaystyle \frac{2f_x}{W}}H{e}_1+{\displaystyle \frac{2\left(1-f_y-x\right)}{W}}H{e}_2+{\displaystyle \frac{2\left(f_y+x\right)}{W}}H{e}_3$$

(9)

$${\Delta }^{I}r=2H\aleph .$$

(10)

The mean curvature vector field ℏ is given by the formula

$$\begin{array}{ccc}\hfill \hslash & =& H\aleph ,\hfill \end{array}$$

with:

$${\Delta }^{I}r=2\hslash$$

(11)

So we have the following result:

Theorem 1.

A Beltrami formula in $({\mathbb{H}}_3,g_3)$ is given by the following:

$${\Delta }^{I}r=2\hslash$$

(12)

where Δ is the Laplacian of the surface and ℏ is the mean curvature vector field of $M^2.$

Remark 1.

The surface $M^2$ has zero mean curvature in ${\mathbb{H}}_3$ if and only if its coordinate functions are harmonic.

3. Factorable Surfaces in $({\mathbb{H}}_3,g_3)$

A surface $M^2$ in the Lorentz–Heisenberg space ${\mathbb{H}}_3$ is called a factorable surface if it can be parameterized as follows:

$$r(x,y)=(x,y,f(x\left)g\right(y\left)\right),$$

(13)

or

$$r(x,z)=(x,f(x\left)h\right(z),z),$$

(14)

or

$$r(y,z)=\left(g\right(y\left)h\right(z),y,z),$$

(15)

where f, g, and h are smooth functions of a single variable on ${\mathbb{H}}_3$. Surfaces defined by (13)–(15) are referred to as factorable surfaces of the first, second, and third type, respectively. Factorable surfaces in Euclidean space, pseudo-Euclidean space, and the Heisenberg group have been investigated in [10,11,12]. We now examine the properties of each type of factorable surface in ${\mathbb{H}}_3$:

3.1. The First Type of Factorable Surfaces

Consider a factorable surface $M^2$ parameterized by (13). The basis of the tangent space $T_p{M}^2$ at point p in $M^2$ is given by

$$\begin{array}{ccc}\hfill r_x& =& (1,0,f_{x}g)={\partial }_x+f_{x}g{\partial }_z,\hfill \\ \hfill r_y& =& (0,1,f{g}_y)={\partial }_y+f{g}_y{\partial }_z.\hfill \end{array}$$

(16)

Equivalently,

$$r_x=e_1+f_{x}g{e}_2-f_{x}g{e}_3,r_y=\left(x+f{g}_y\right)e_2+\left(1-x-f{g}_y\right)e_3.$$

(17)

A pseudo-orthonormal basis for the corresponding Lie algebra can be expressed as

$$B=\left\{e_1={\displaystyle \frac{\partial }{\partial x}},e_2={\displaystyle \frac{\partial }{\partial y}}+(1-x){\displaystyle \frac{\partial }{\partial z}},e_3={\displaystyle \frac{\partial }{\partial y}}-x{\displaystyle \frac{\partial }{\partial z}}\right\}.$$

The characterizing properties of this algebra are the following commutation relations:

$$\left[e_2,e_3\right]=0,\left[e_3,e_1\right]=e_2-e_3,\left[e_2,e_1\right]=e_2-e_3,$$

with

$$g_3\left(e_1,e_1\right)=1,g_3\left(e_2,e_2\right)=1,g_3\left(e_3,e_3\right)=-1.$$

The coefficients of the first and second fundamental forms are

$$\begin{array}{c}E=g_3\left(r_x,r_x\right)=1,F=g_3\left(r_x,r_y\right)=f_{x}g,G=g_3\left(r_y,r_y\right)=2(x+f{g}_y)-1,\end{array}$$

(18)

and

$$L=g_3\left({\nabla }_{r_x}{r}_x,\aleph \right),M=g_3\left({\nabla }_{r_x}{r}_y,\aleph \right),N=g_3\left({\nabla }_{r_y}{r}_y,\aleph \right),$$

(19)

where ℵ is a unit vector field normal on $M^2$, satisfying

$$\left\{\begin{array}{c}{g}_3\left(r_x,\aleph \right)=0,\\ g_3\left(r_y,\aleph \right)=0,\\ g_3\left(\aleph ,\aleph \right)=-1.\end{array}\right.$$

(20)

Therefore,

$$\begin{array}{ccc}& & \begin{array}{c}{\nabla }_{r_x}{r}_x=f_{xx}g{e}_2-f_{xx}g{e}_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_x}{r}_y=\left(1+f_x{g}_y\right)e_2-\left(1+f_x{g}_y\right)e_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_y}{r}_y=-e_1+f{g}_{yy}{e}_2-f{g}_{yy}{e}_3.\end{array}\hfill \end{array}$$

(21)

ℵ represents the unit vector field normal on $M^2$ and is given by

$$\aleph =-{\displaystyle \frac{f_{x}g}{W}}{e}_1+{\displaystyle \frac{\left(1-x-f{g}_y\right)}{W}}{e}_2+{\displaystyle \frac{\left(x+f{g}_y\right)}{W}}{e}_3,$$

(22)

where

$$W=\sqrt{\left|EG-F^2\right|}=\sqrt{|2(x+f{g}_y)-1-{\left(f_{x}g\right)}^2|}.$$

(23)

Hence,

$$\begin{array}{c}L={\displaystyle \frac{f_{xx}g}{W}},M={\displaystyle \frac{1+f_x{g}_y}{W}},N={\displaystyle \frac{f_{x}g+f{g}_{yy}}{W}}\end{array}$$

(24)

The mean curvature vector field ℏ is given by

$$\hslash =H\aleph ,$$

where the mean curvature H of the surface $M^2$ is

$$H={\displaystyle \frac{EN+GL-2FM}{2\left(EG-F^2\right)}}.$$

(25)

For the surface $M^2$ parameterized by $r(x,y)=(x,y,f(x\left)g\right(y\left)\right)$, the mean curvature is expressed as

$$H={\displaystyle \frac{1}{2W^3}}\left[f{g}_{yy}+(2(x+f{g}_y)-1)f_{xx}g-f_{x}g\left(1+2f_x{g}_y\right)\right].$$

(26)

3.2. The Second Type of Factorable Surfaces

Consider a factorable surface $M^2$ parameterized by (14). The basis of the tangent space $T_p{M}^2$ is given by

$$\begin{array}{ccc}\hfill r_x& =& (1,f_{x}h,0)={\partial }_x+f_{x}h{\partial }_y,\hfill \\ \hfill r_z& =& (0,f{h}_z,1)=f{h}_z{\partial }_y+{\partial }_z.\hfill \end{array}$$

(27)

Equivalently,

$$r_x=e_1+x{f}_{x}h{e}_2+\left(1-x\right)f_{x}h{e}_3,r_z=\left(xf{h}_z+1\right)e_2+\left[f{h}_z\left(1-x\right)-1\right]e_3.$$

(28)

The coefficients of the first fundamental form are

$$\begin{array}{ccc}E=1+\left(2x-1\right){\left(f_x\right)}^2{h}^2,& F=\left[\left(2x-1\right)f{h}_z+1\right]f_{x}h,& G=\left[2+\left(2x-1\right)f{h}_z\right]f{h}_z,\end{array}$$

(29)

We have

$$\begin{array}{ccc}& & \begin{array}{c}{\nabla }_{r_x}{r}_x=-{\left(f_x\right)}^2{\left(g\right)}^2{e}_1+\left(2f_x+x{f}_{xx}\right)g{e}_2+\left[-2f_x+\left(1-x\right)f_{xx}\right]g{e}_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_x}{r}_z=-fg{f}_x{g}_z{e}_1+\left(f+x{f}_x\right)g_z{e}_2+\left(-f+\left(1-x\right)f_x\right)e_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_z}{r}_z=-{\left(f\right)}^2{\left(g_z\right)}^2{e}_1+xf{g}_{zz}{e}_2+\left(1-x\right)f{g}_{zz}{e}_3.\end{array}\hfill \end{array}$$

(30)

ℵ represents the unit vector field normal on $M^2$ and is given by

$$\aleph ={\displaystyle \frac{f_{x}h}{W}}{e}_1+{\displaystyle \frac{f{h}_z\left(1-x\right)-1}{W}}{e}_2+{\displaystyle \frac{xf{h}_z+1}{W}}{e}_3,$$

(31)

where $W=\sqrt{|\left[2+\left(2x-1\right)f{h}_z\right]f{h}_z-{\left(f_x\right)}^2{\left(h\right)}^2|},$ and satisfies

$$\left\{\begin{array}{c}{g}_3\left(r_x,\aleph \right)=0,\\ g_3\left(r_z,\aleph \right)=0,\\ g_3\left(\aleph ,\aleph \right)=-1.\end{array}\right.$$

(32)

The coefficients of the second fundamental form of $M^2$ are

$$\begin{array}{cc}\hfill L& ={\displaystyle \frac{-{\left(f_x\right)}^3{h}^3+2fh{f}_x{h}_z-h{f}_{xx}}{W}},\hfill \\ \hfill M& ={\displaystyle \frac{-{\left(f_x\right)}^2{h}^{2}f{h}_z+f^2{\left(h_z\right)}^2-f_x{h}_z}{W}},\hfill \\ \hfill N& ={\displaystyle \frac{-f_{x}h{f}^2{\left(h_z\right)}^2-f{h}_{zz}}{W}}.\hfill \end{array}$$

(33)

Following analogous steps to the previous case, the mean curvature H for this second type of factorable surface is

$$\begin{array}{cc}\hfill H={\displaystyle \frac{1}{2W^3}}[& -f^2{f}_{x}h{h}_z^2+f{h}_{zz}+2f{f}_{xx}h{h}_z-2f_x^{2}h{h}_z\hfill \\ \hfill & +(2x-1)\left(f{f}_x^2{h}^2{h}_{zz}+f^2{f}_{xx}h{h}_z^2-2f{f}_x^{2}h{h}_z^2\right)].\hfill \end{array}$$

(34)

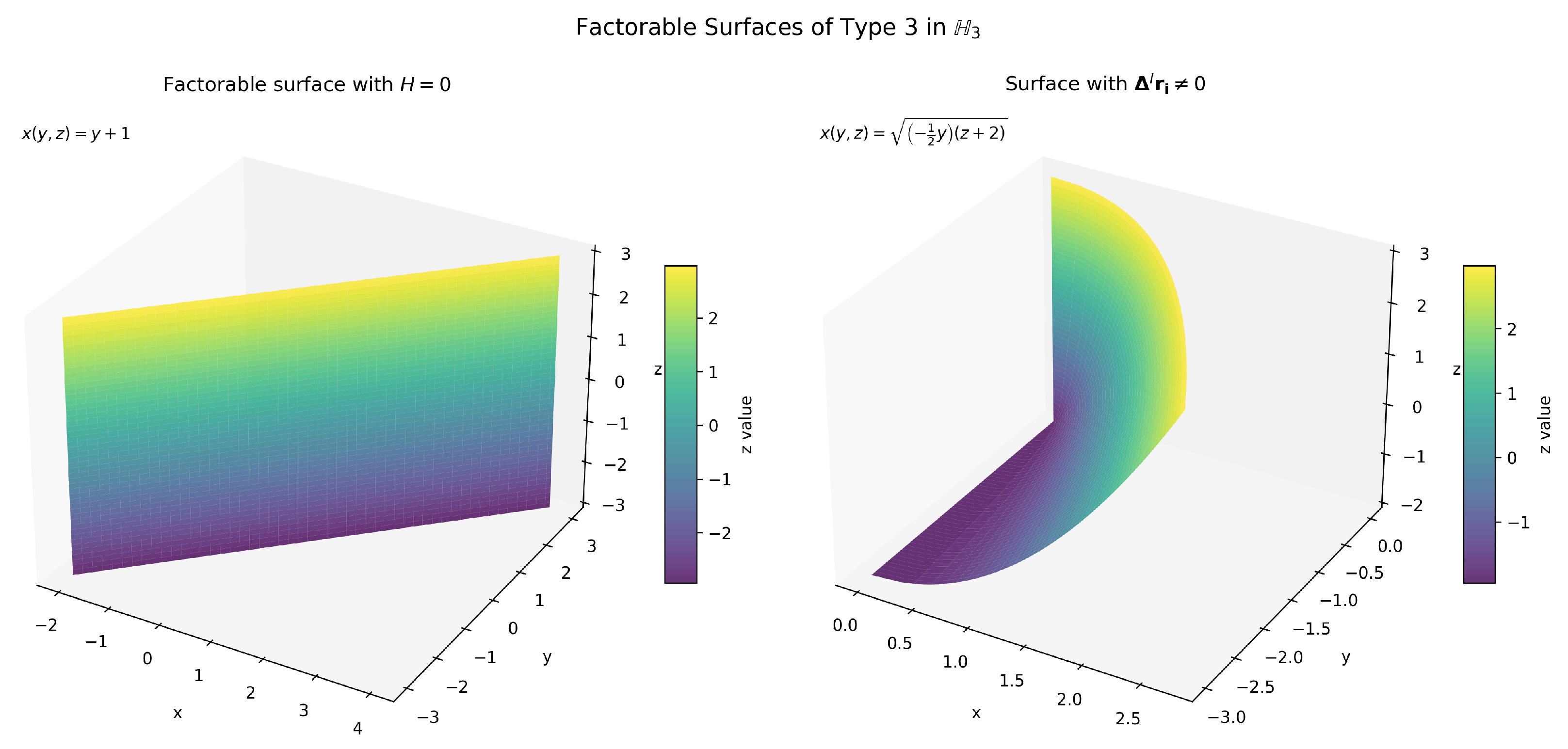
3.3. The Third Type of Factorable Surfaces

Consider a factorable surface $M^2$ parameterized by (15). The basis of the tangent space $T_p{M}^2$ is given by

$$\begin{array}{ccc}\hfill r_y& =& (g_{y}h,1,0)=g_{y}h{\partial }_x+{\partial }_y,\hfill \\ \hfill r_z& =& (g{h}_z,0,1)=g{h}_z{\partial }_x+{\partial }_z.\hfill \end{array}$$

(35)

Equivalently,

$$r_y=g_{y}h{e}_1+gh{e}_2+\left(1-gh\right)e_3,r_z=g{h}_z{e}_1+e_2-e_3,$$

(36)

The coefficients of the first fundamental form are

$$\begin{array}{c}E=g_3\left(r_y,r_y\right)={\left(g_y\right)}^2{h}^2+2gh-1,F=g_3\left(r_y,r_z\right)=gh{g}_y{h}_z+1,\\ G=g_3\left(r_z,r_z\right)=g^2{\left(h_z\right)}^2.\end{array}$$

(37)

The covariant derivatives are

$$\begin{array}{ccc}& & \begin{array}{c}{\nabla }_{r_y}{r}_y=\left(h{g}_{yy}-1\right)e_1+2g_{y}h{e}_2-2g_{y}h{e}_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_y}{r}_z=g_y{h}_z{e}_1+g{h}_z{e}_2-g{h}_z{e}_3,\end{array}\hfill \\ & & \begin{array}{c}{\nabla }_{r_z}{r}_z=g{h}_{zz}{e}_1.\end{array}\hfill \end{array}$$

(38)

ℵ represents the unit vector field normal on $M^2$ and is given by

$$\aleph ={\displaystyle \frac{1}{W}}{e}_1+{\displaystyle \frac{\left(g^2{h}_z-g_y\right)h-g{h}_z}{W}}{e}_2-{\displaystyle \frac{\left(g^2{h}_z-g_y\right)h}{W}}{e}_3,$$

(39)

where $W=\sqrt{|\left[2gh\left(g^2{h}_z-g_y\right)-g^2{h}_z\right]h_z-1|}$ and satisfies

$$g_3\left(r_y,\aleph \right)=0,g_3\left(r_z,\aleph \right)=0,g_3\left(\aleph ,\aleph \right)=-1.$$

The coefficients of the second fundamental form of $M^2$ are

$$\begin{array}{c}L={\displaystyle \frac{h{g}_{yy}-2gh{g}_y{h}_z-1}{W}},M={\displaystyle \frac{g_y{h}_z-g^2{\left(h_z\right)}^2}{W}},N={\displaystyle \frac{g{h}_{zz}}{W}}.\end{array}$$

(40)

Following the same steps as for the previous types, the mean curvature H for this third type of factorable surface is

$$H={\displaystyle \frac{\left({\left(g_y\right)}^2{h}^2+2gh-1\right)g{h}_{zz}+g^2{\left(h_z\right)}^{2}h{g}_{yy}+\left(g^2-2gh{\left(g_y\right)}^2\right){\left(h_z\right)}^2-2g_y{h}_z}{2W^3}}.$$

(41)

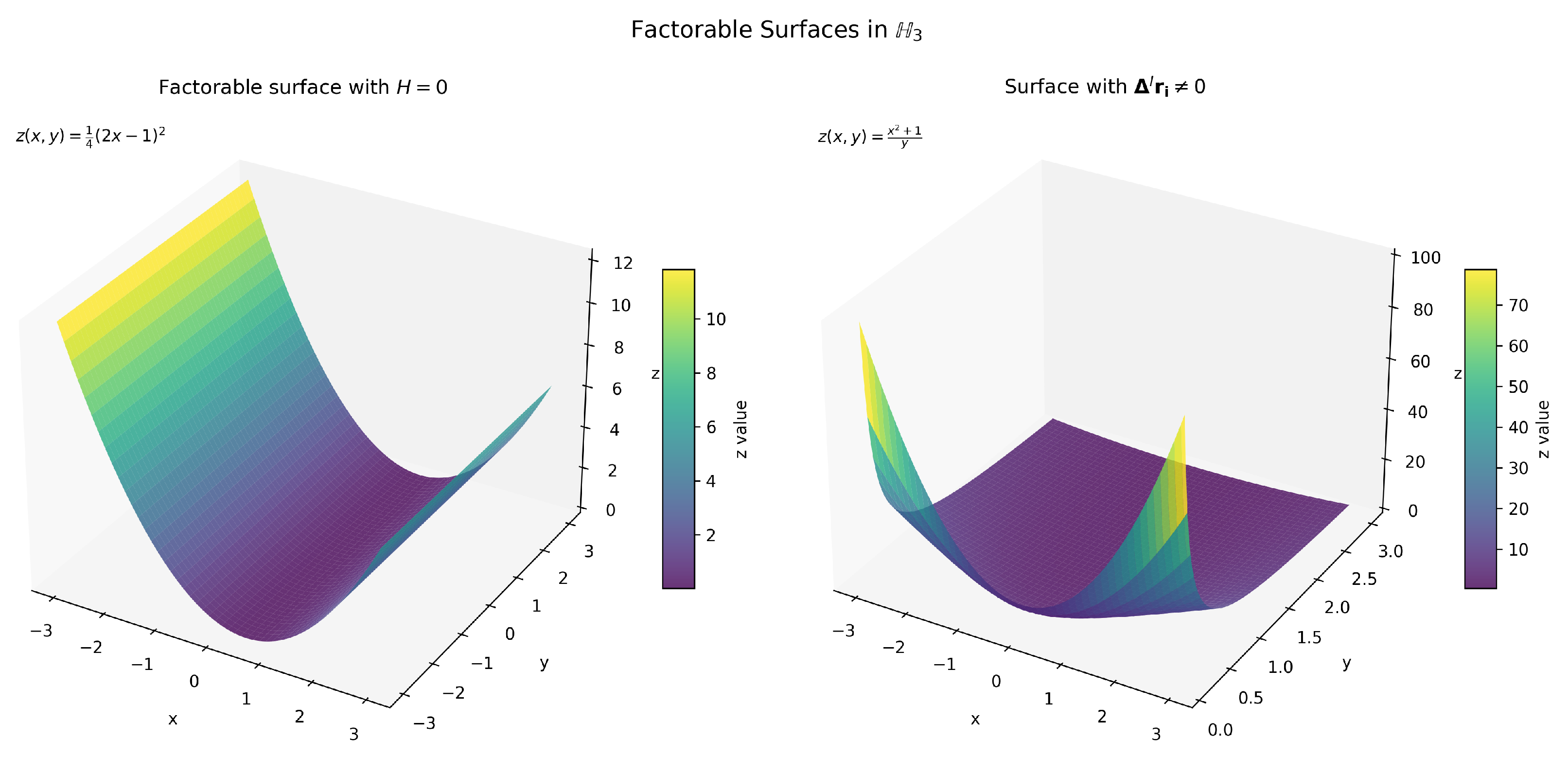
4. Factorable Surfaces of the First Type Satisfying ${\Delta }^I{r}_i={\lambda }_i{r}_i$

In this section, we classify factorable surfaces in ${\mathbb{H}}_3$ parameterized by (13) that satisfy the equation

$${\Delta }^I{r}_i={\lambda }_i{r}_i,$$

(42)

where ${\lambda }_i\in \mathbb{R}$, $i=1,2,3$ and

$${\Delta }^{I}r=\left({\Delta }^I{r}_1,{\Delta }^I{r}_2,{\Delta }^I{r}_3\right),$$

(43)

where

$$r_1=x,r_2=y,r_3=f\left(x\right)g\left(y\right).$$

(44)

From (1) and (18), we derive the Laplacian operator on $M^2$ to be

$${\Delta }^{I}r=-{\displaystyle \frac{2f_{x}gH}{W}}{e}_1+{\displaystyle \frac{2\left(1-x-f{g}_y\right)H}{W}}{e}_2+{\displaystyle \frac{2\left(x+f{g}_y\right)H}{W}}{e}_3.$$

(45)

Next, we assume $M^2$ to satisfy the condition (42). From (13) and (45), we obtain the following system of ordinary differential equations (ODEs):

$$-{\displaystyle \frac{2f_{x}gH}{W}}={\lambda }_{1}x,$$

(46)

$${\displaystyle \frac{2\left(1-x-f{g}_y\right)}{W}}H=xy{\lambda }_2+{\lambda }_{3}fg,$$

(47)

$${\displaystyle \frac{2\left(x+f{g}_y\right)}{W}}H=\left(1-x\right)y{\lambda }_2-{\lambda }_{3}fg.$$

(48)

Hence, the classification problem for factorable surfaces $M^2,$ satisfying condition (42) reduces to integrating the system of ODEs given by (46)–(48). In what follows, we analyze this system by considering different cases for the constants ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$. Using (46)–(48), we obtain

$${\displaystyle \frac{2}{W}}H(1-f_{x}g)={\lambda }_{1}x+{\lambda }_{2}y.$$

(49)

We consider two cases based on the values of ${\lambda }_1$ and ${\lambda }_2$

Case A: 

If ${\lambda }_1={\lambda }_2=0$, then $H=0$, and the surface $M^2$ is minimal. From (26), a sufficient condition for this is

$$f{g}_{yy}+\left[2(x+f{g}_y)-1\right]f_{xx}g-f_{x}g\left(1+2f_x{g}_y\right)=0.$$

(50)

This leads to the following sub-cases:

Case A.1: 

If $f_x=0$, then $f=d_0\ne 0$. Substituting into (50), we obtain $g_{yy}=0$, so $g=c_{0}y+c_1$. Thus, the surface $M^2$ is parameterized as

$$r\left(x,y\right)=(x,y,d_0(c_{0}y+c_1)),$$

where $c_1\in \mathbb{R},$ and $d_0,c_0\in {\mathbb{R}}^{*}.$

Case A.2: 

If $g_y=0$, then $g=c_2\ne 0$. From (50), we derive

$$\left(2x-1\right)f_{xx}=f_x.$$

(51)

Solving (51) yields

$$f={\displaystyle \frac{c_3}{4}}{\left(2x-1\right)}^2+c_4.$$

(52)

Thus, the surface $M^2$ is parameterized as

$$r\left(x,y\right)=(x,y,{\displaystyle \frac{c_5}{4}}{\left(2x-1\right)}^2+c_6),$$

where $c_5,c_6\in \mathbb{R}$ and $c_5\ne 0.$

Case A.3: 

If $f_{xx}=0$, then $f=c_{7}x+c_8$, where $c_7\ne 0$. Substituting into (50), we obtain

$$\left(c_{7}x+c_8\right)g_{yy}-c_{7}g\left(1+2a{g}_x\right)=0.$$

(53)

We consider two sub-cases:

Case A.3.1: 

$g_{yy}=0$

$$c_{7}g\left(1+2c_7{g}_x\right)=0,$$

(54)

Since $c_7\ne 0$ and $g\ne 0$, this implies

$$g_x=-{\displaystyle \frac{1}{2c_7}},$$

(55)

thus

$$g=-{\displaystyle \frac{1}{2c_7}}y+c_9,$$

(56)

Therefore, the surface $M^2$ is parameterized as

$$r\left(x,y\right)=(x,y,(-{\displaystyle \frac{1}{2c_7}}y+c_9)\left(c_{7}x+c_8\right)),$$

where $c_8,c_9\in \mathbb{R}$ and $c_7\in {\mathbb{R}}^{*}.$

Case A.3.2: 

$g_{yy}\ne 0$

$${\displaystyle \frac{g\left(1+2c_7{g}_x\right)}{g_{yy}}}={\displaystyle \frac{\left(c_{7}x+c_8\right)}{c_7}}.$$

(57)

The left-hand side of (57) is a function of y, while the right-hand side is a function of x. This leads to contradiction.

Case A-4: 

If $g_{yy}=0,$ so $(g=c_{8}y+c_9$ with $c_8\ne 0),$ Then, Formulas (50) and (22) become

$$\left[2(x+c_{8}f)-1\right]f_{xx}-f_x\left(1+2c_8{f}_x\right)=0,$$

(58)

$$\aleph =-{\displaystyle \frac{f_x\left(c_{8}y+c_9\right)}{W}}{e}_1+{\displaystyle \frac{\left(1-x-c_{8}f\right)}{W}}{e}_2+{\displaystyle \frac{\left(x+c_{8}f\right)}{W}}{e}_3.$$

(59)

Let us put

$$\mathbb{F}={\displaystyle \frac{1+2c_8{f}_x}{c_{8}y+c_9}}{e}_1-f_{xx}{e}_2-f_{xx}{e}_3,$$

(60)

by (58)–(60), we can easily check that (50) is verified if and only if $g_3\left(\mathbb{F},\aleph \right)=0.$ Therefore, we have $\mathbb{F}=0$ or $\mathbb{F}\in T_p{M}^2.$

Case A.4.1: 

If $\mathbb{F}=0,$ from (60) we have

$$f_x=-{\displaystyle \frac{1}{2c_8}},$$

(61)

then

$$f=-{\displaystyle \frac{1}{2c_8}}x+c_{10},$$

(62)

therefore, we obtain the same parameterization as in Case A.3.1:

Case A.4.2: 

If $\mathbb{F}\in T_p{M}^2$, which implies that there exists $\eta ,\mu \in \mathbb{R},$ such that

$$\mathbb{F}=\eta r_x+\mu r_y.$$

(63)

then, from (17) and (60), we obtain the following system of ODEs:

$${\displaystyle \frac{1+2c_8{f}_x}{c_{8}y+c_9}}=\eta ,$$

(64)

$$-f_{xx}=\eta f_x\left(c_{8}y+c_9\right)+\mu \left(x+c_{8}f\right),$$

(65)

$$-f_{xx}=-\eta f\left(c_{8}y+c_9\right)+\mu \left(1-x-c_{8}f\right).$$

(66)

Case A.4.2.1: 

If $\eta =\mu =0,$ this is Case A.4.1, where $\mathbb{F}=0.$

Case A.4.2.2: 

If $\eta =0$ and $\mu \ne 0,$ then the following system of ODEs is obtained:

$$2c_8{f}_x=-1,$$

(67)

$$-f_{xx}=\mu \left(x+c_{8}f\right),$$

(68)

$$-f_{xx}=\mu \left(1-x-c_{8}f\right).$$

(69)

From (67) we have $f=-{\displaystyle \frac{1}{2c_8}}x+c_{10}$. Substituting this into (69) and (68) yields

$$\mu \left(x+c_{8}f\right)=0,$$

(70)

$$\mu \left(1-x-c_{8}f\right)=0.$$

(71)

Adding (70) and (71) yields $\mu =0$, which leads to a contradiction.

Case A.4.2.3: 

If $\eta \ne 0,$ from (64), we obtain

$$2d{f}_x=\eta \left(c_{8}y+c_9\right)-1.$$

(72)

Since the right-hand side of (72) depends on y while the left-hand side depends only on x or is constant, we reach a contradiction.

Case A-5: 

If $f_{xx}{g}_{yy}\ne 0,$ we put

$$\mathbb{G}=\left(1+2f_x{g}_y\right)e_1-\left(f_{xx}g-f{g}_{yy}\right)e_2-\left(f_{xx}g+f{g}_{yy}\right)e_3,$$

(73)

from (73), (50) and (17), we can easily check that (50) is verified if and only if $g_3\left(\mathbb{G},\aleph \right)=0.$ Therefore, we have $\mathbb{G}=0$ or $\mathbb{G}\in T_p{M}^2.$

Case A.5.1: 

If $\mathbb{G}=0,$ from (73) we have

$$f_x=-{\displaystyle \frac{1}{2g_y}}.$$

(74)

Since the left side of (74) is a function of x and the right side is a function of y, both sides have to be equal to a non-zero constant, which means

$$f_x=\beta =-{\displaystyle \frac{1}{2g_y}}.$$

(75)

then $f_{xx}=0,$ which is not possible.

Case A.5.2: 

If $\mathbb{G}\in T_p{M}^2$, which implies that there exist $\eta ,\mu \in \mathbb{R},$ such that

$$\mathbb{G}=\eta r_x+\mu r_y,$$

(76)

then, from (17) and (73), we obtain the following system of ODEs:

$$1+2f_x{g}_y=\eta ,$$

(77)

$$-\left(f_{xx}g-f{g}_{yy}\right)=\eta f_{x}g+\mu \left(x+f{g}_y\right),$$

(78)

$$-\left(f_{xx}g+f{g}_{yy}\right)=-\eta f_{x}g+\mu \left(1-x-f{g}_y\right).$$

(79)

Case A.5.2.1: 

If $\eta =\mu =0,$ this is Case A.5.1, where $\mathbb{G}=0.$

Case A.5.2.2: 

If $\eta =0$ and $\mu \ne 0,$ from (77), we have

$$2f_x=-{\displaystyle \frac{1}{g_y}},$$

(80)

and we obtain the same case as Case A.5.1.

Case A.5.2.3: 

If $\eta \ne 0,$ from (77) we obtain

$$f_x={\displaystyle \frac{\eta -1}{2g_y}}.$$

(81)

then $g_{yy}=0,$ which is impossible.

Case B: 

Let ${\lambda }_2\ne 0$; the last equation in (49) becomes

$$(1-f_{x}g)\left[f{g}_{yy}+\left(2(x+f{g}_y)-1\right)f_{xx}g-f_{x}g\left(1+2f_x{g}_y\right)\right]=({\lambda }_{1}x+{\lambda }_{2}y)W^4.$$

(82)

To find solutions to Equation (82), we distinguish two cases based on the values of ${\lambda }_1$:

Case B.1: 

Let ${\lambda }_1=0$, the last equation in (82) becomes

$$(1-f_{x}g)\left[f{g}_{yy}+(2(x+f{g}_y)-1)f_{xx}g-f_{x}g\left(1+2f_x{g}_y\right)\right]={\lambda }_{2}y{\left[2(x+f{g}_y)-1-{\left(f_{x}g\right)}^2\right]}^2.$$

We will now look at the following sub-cases:

Case B.1.1: 

If $f_x=0,f=\alpha$ we have

$$\alpha g_{yy}={\lambda }_{2}y{\left[2(x+\alpha g_y)-1\right]}^2.$$

After simplifying, we find

$${\left({\displaystyle \frac{\alpha g_{yy}}{{\lambda }_{2}y}}\right)}^{{\displaystyle \frac{1}{2}}}-2\alpha g_y=2x-1$$

Since the equation g has a variable y that is independent of x, we get a contradiction.

Case B.1.2: 

If $f_{xx}=0$, $f_x=a$, and $f\left(x\right)=ax+a_0$, where a is not zero, then we have

$$(1-ag)\left[f{g}_{yy}-ag\left(1+2a{g}_y\right)\right]={\lambda }_{2}y{\left[2(x+f{g}_y)-1-{\left(ag\right)}^2\right]}^2.$$

(83)

Taking the partial derivative of (83) with respect to x twice yields

$$g_y=-{\displaystyle \frac{1}{a}},$$

from which the general solution to the equation is

$$g\left(y\right)=-{\displaystyle \frac{1}{a}}y+a_1.$$

Case B.1.3: 

If $g_y=0,g=\beta$ we have

$$(1-f_x\beta )\left[(2x-1)f_{xx}\beta -f_x\beta \right]={\lambda }_{2}y{\left[2x-1-{\left(f_x\beta \right)}^2\right]}^2,$$

$${\displaystyle \frac{(1-f_x\beta )\left[(2x-1)f_{xx}\beta -f_x\beta \right]}{{\left[2x-1-{\left(f_x\beta \right)}^2\right]}^2}}={\lambda }_{2}y,$$

Since the equation f has a variable x that is independent of y, we get a contradiction.

Case B.1.4 

If $g_{yy}=0,g_y={\beta }_0$ and $g\left(y\right)={\beta }_{0}y$ where ${\beta }_0$ is not zero, then we have

$$(1-f_{x}g)\left[(2(x+f{\beta }_0)-1)f_{xx}g-f_{x}g\left(1+2f_x{\beta }_0\right)\right]={\lambda }_{2}y{\left[2(x+f{\beta }_0)-1-{\left(f_{x}g\right)}^2\right]}^2,$$

(84)

so

$${\beta }_0(1-{\beta }_{0}y{f}_x)\left[(2(x+f{\beta }_0)-1)f_{xx}-f_x\left(1+2f_x{\beta }_0\right)\right]={\lambda }_2{\left[2(x+f{\beta }_0)-1-{\left({\beta }_{0}y{f}_x\right)}^2\right]}^2,$$

(85)

Taking the partial derivative of (85) with respect to y twice yields

$$-4{\lambda }_2{\left({\beta }_0{f}_x\right)}^2(2(x+f{\beta }_0)-1)+12{\lambda }_2{\left({\beta }_0{f}_x\right)}^4{y}^2=0,$$

(86)

We have to consider two cases.

Case B.1.4.1 

If $f_x=0$, $f\left(x\right)=c$, where $c\in {\mathbb{R}}^{*}.$

Case B.1.4.2. 

If $f_x\ne 0$, we find a contradiction.

Case B.2: 

Let ${\lambda }_1\ne 0$. Using (46)–(48), we obtain

$${\lambda }_{2}y{f}_{x}g+{\lambda }_{1}x=0.$$

(87)

The last equation in (87) becomes

$${\displaystyle \frac{{\lambda }_2}{{\lambda }_1}}yg={\displaystyle \frac{x}{f_x}}.$$

(88)

Since the left side of (88) is a function of x and the right side is a function of y, both sides have to be equal to a non-zero constant, i.e.,

$${\displaystyle \frac{{\lambda }_2}{{\lambda }_1}}yg=d={\displaystyle \frac{x}{f_x}}.$$

(89)

Therefore, we find the solutions of Equation (89):

$$g\left(y\right)={\displaystyle \frac{d_1}{y}},\mathrm{and}f\left(x\right)=d_2{x}^2+d_3.$$

(90)

where $d_1={\displaystyle \frac{d{\lambda }_1}{{\lambda }_2}},$$d_2={\displaystyle \frac{1}{d}}$ and $d\in {\mathbb{R}}^{*}.$

Therefore, we have the following result:

Theorem 2.

The factorable surfaces $M^2$ of type 1 satisfying the condition ${\Delta }^I{r}_i={\lambda }_i{r}_i$, where ${\lambda }_i\in \mathbb{R}$, in the Lorentz–Heisenberg space are congruent to an open part of the surfaces:

1. 

$M^2$ has zero mean curvature.

• $M^2$ is a part of a plane in ${\mathbb{H}}_3$ and parameterized by $r\left(x,y\right)=(x,y,d_0(c_{0}y+c_1)).$
• $M^2$ is parameterized by $r\left(x,y\right)=(x,y,{\displaystyle \frac{c_5}{4}}{\left(2x-1\right)}^2+c_6).$
• $M^2$ is parameterized by $r\left(x,y\right)=(x,y,(-{\displaystyle \frac{1}{2c_7}}y+c_9)\left(c_{7}x+c_8\right)).$

where $d_0,c_i\in \mathbb{R},i\in \left\{0,1,5,6,7,8,9\right\}$ and $d_0,c_0,c_5,c_7\ne 0.$

2. 

$M^2$ is parameterized by $r\left(x,y\right)=(x,y,(ax+a_0)(-{\displaystyle \frac{1}{a}}y+a_1)).$

3. 

$M^2$ is parameterized by $r\left(x,y\right)=(x,y,\left({\displaystyle \frac{d_0}{y}}\right)(d_1{x}^2+d_2).$

where $a,a_i,d,d_i\in \mathbb{R},i\in \left\{0,1,2\right\},d_1={\displaystyle \frac{d{\lambda }_1}{{\lambda }_2}},$ and ${\lambda }_1,{\lambda }_2,a,d,d_0,d_1\ne 0.$

Example 1.

1. 

Consider factorable surfaces of type 1 in ${\mathbb{H}}_3$ with ${\Delta }^I{r}_i=0$ given by

$$z(x,y)={\displaystyle \frac{1}{4}}{\left(2x-1\right)}^2,x\in [-3,3].$$

2. 

Consider factorable surfaces of type 1 in ${\mathbb{H}}_3$ with ${\Delta }^I{r}_i\ne 0$ given by

$$z\left(x,y\right)=\left(x^2+1\right)\left({\displaystyle \frac{1}{y}}\right).$$

Figure 1 contrasts these geometrically distinct surfaces: one exhibiting perfect translational symmetry, and the other displaying asymptotic singularity.

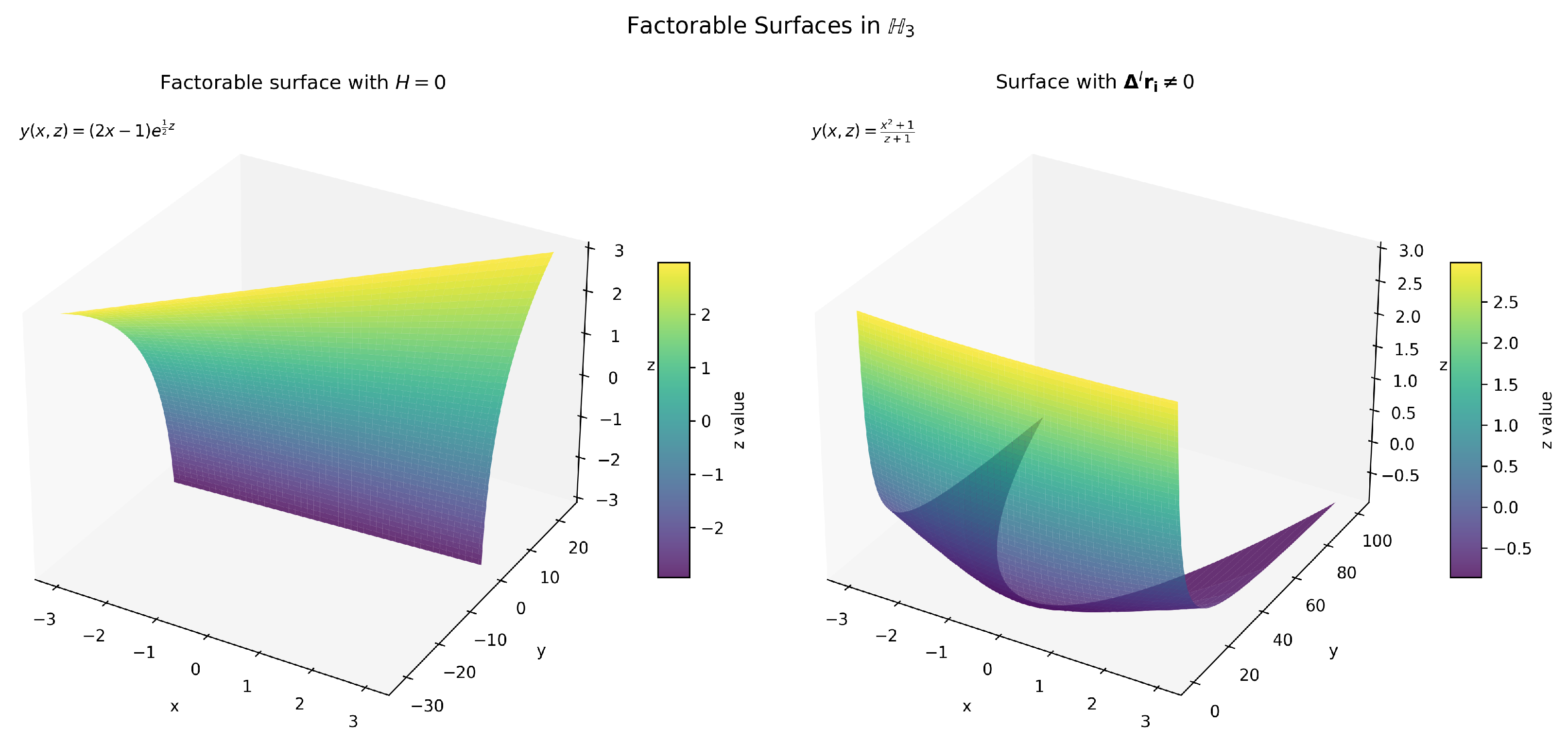
5. Factorable Surfaces of the Second Type Satisfying ${\Delta }^I{r}_i={\lambda }_i{r}_i$

In this section we classify factorable surfaces given by (14) in ${\mathbb{H}}^3$ satisfying the equation

$${\Delta }^I{r}_i={\lambda }_i{r}_i,$$

(91)

where ${\lambda }_i\in \mathbb{R}$, $i=1,2,3$ and

$${\Delta }^{I}r=\left({\Delta }^I{r}_1,{\Delta }^I{r}_2,{\Delta }^I{r}_3\right),$$

(92)

where

$$r_1=x,r_2=f\left(x\right)h\left(z\right),r_3=z.$$

(93)

Using (1) and (29), a direct calculation yields the Laplacian operator on $M^2$ in the form

$${\Delta }^{I}r={\displaystyle \frac{2f_{x}h}{W}}H{e}_1+{\displaystyle \frac{2\left[f{h}_z\left(1-x\right)-1\right]}{W}}H{e}_2+{\displaystyle \frac{2\left(xf{h}_z+1\right)}{W}}H{e}_3.$$

(94)

Assuming that $M^2$ satisfies (91), we derive from (14) and (95) the following system of ODEs:

$${\displaystyle \frac{2f_{x}h}{W}}H={\lambda }_{1}x,$$

(95)

$${\displaystyle \frac{2\left[f{h}_z\left(1-x\right)-1\right]}{W}}H=\left(x{\lambda }_{2}fh+{\lambda }_{3}z\right),$$

(96)

$${\displaystyle \frac{2\left(xf{h}_z+1\right)}{W}}H=\left(1-x\right).{\lambda }_{2}fh-{\lambda }_{3}z$$

(97)

Applying algebraic methods similar to those used for surfaces of the first type, we analyze this system based on the values of the constants ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$. By combining (96) and (97), we obtain

$${\displaystyle \frac{2f_{x}h}{W}}H={\lambda }_{1}x,$$

(98)

$${\displaystyle \frac{2h_z}{W}}H={\lambda }_{2}h.$$

(99)

We now consider all possible cases for values of ${\lambda }_i,i=1,2,3.$

Case C: 

If ${\lambda }_1={\lambda }_2=0$, we consider condition $f_x=h_z=0$, which implies that f and h are constant. This leads to a contradiction ($W=0$), implying $H=0$. Therefore, the surface $M^2$ is minimal. From Equation (34), we obtain

$$\begin{array}{cc}\hfill & -f^2{f}_{x}h{h}_z^2+f{h}_{zz}+2f{f}_{xx}h{h}_z-2f_x^{2}h{h}_z\hfill \\ \hfill & +(2x-1)\left(f{f}_x^2{h}^2{h}_{zz}+f^2{f}_{xx}h{h}_z^2-2f{f}_x^{2}h{h}_z^2\right)=0.\hfill \end{array}$$

(100)

We now examine the following sub-cases:

Case C.1. 

When $f_x{h}_z=0$, we consider two distinct possibilities.

Case C.1.1. 

If $f_x=0,$ so $(f=a\ne 0),$ from (100) we have

$$a{h}_{zz}=0,$$

(101)

then $h=cz+d,$ which gives the surface $M^2$ parameterized as

$$r(x,z)=(x,a\left(cz+d\right),z),$$

(102)

Case C.1.2. 

If $h_z=0,$ so $(h=c\ne 0),$ then Equation (100) is trivially satisfied for all smooth functions $f.$ Hence, we obtain

$$r(x,z)=(x,cf\left(x\right),z),$$

Case C.2. 

If $f_x\ne 0,$ so $(f=ax+b$ with $a\ne 0),$ then, Equation (100) becomes

$$\begin{array}{c}\left(2x-1\right)[-{\left(a\right)}^2\left(ax+b\right){\left(h\right)}^2{h}_{zz}+2a{\left(ax+b\right)}^2{\left(h\right)}^2{h}_z]+\\ +a{\left(ax+b\right)}^{2}h{\left(h_z\right)}^2-\left(ax+b\right)h_{zz}+2{\left(a\right)}^{2}h{h}_z=0,\end{array}$$

(103)

taking the partial derivative of (103) three times with respect to x gives

$${\left(h\right)}^2{h}_z=0,$$

(104)

thus $h_z=0,$ which is a particular case of Case C.1.2.

Case C.3. 

If $h_{zz}=0,$ so $(h=cz+d$ with $c\ne 0),$ then, from (100) we obtain

$$\begin{array}{c}\left(2x-1\right)[-c{\left(f\right)}^2{f}_{xx}+2\left(cz+d\right){\left(f\right)}^2{f}^{\prime }]+\\ +c{\left(f\right)}^2{f}_x-2f{f}_{xx}+2{\left(f_x\right)}^2=0,\end{array}$$

(105)

Taking the partial derivative of (105) with respect to z gives

$$c\left(2x-1\right){\left(f\right)}^2{f}_x=0,$$

(106)

thus $f_x=0,$ which is a particular case of Case C.1.1.

Case C.4. 

If $f_{xx}{h}_{zz}\ne 0$, we put

$$\Re ={\Re }_1{e}_1+{\Re }_2{e}_2+{\Re }_3{e}_3,$$

(107)

where

$${\Re }_1={\left(f\right)}^2{\left(h_z\right)}^2-\left(2x-1\right)f{f}_{x}h{h}_{zz}+2f_x{h}_z-4fh,$$

(108)

$${\Re }_2=f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2-{\displaystyle \frac{h_{zz}}{h_z}},$$

(109)

$${\Re }_3=f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2+{\displaystyle \frac{h_{zz}}{h_z}},$$

(110)

from (107), (100) and (31), we can easily check that (100) is verified if and only if $g_3\left(\Re ,\aleph \right)=0.$

Therefore, we have $\Re =0$ or $\Re \in T_p{M}^2.$

Case C.4.1. 

Substituting (109) into (110) yields $h_{zz}=0$, which contradicts the assumption that $h_{zz}\ne 0$.

Case C.4.2. 

If ℜ ∈ $T_p{M}^2$, which implies that there exist $\eta ,\mu \in \mathbb{R},$ such that

$$\Re =\eta r_x+\mu r_y.$$

(111)

From (28) and (107), we obtain the following system of ODEs:

$${\left(f\right)}^2{\left(h_z\right)}^2-\left(2x-1\right)f{f}_{x}h{h}_{zz}+2f_x{h}_z-4fh=\eta ,$$

(112)

$$f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2-{\displaystyle \frac{h_{zz}}{h_z}}=\eta x{f}_{x}h+\mu \left(xf{h}_z+1\right),$$

(113)

$$f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2+{\displaystyle \frac{h_{zz}}{h_z}}=\eta \left(1-x\right)f_{x}h+\mu \left[f{h}_z\left(1-x\right)-1\right].$$

(114)

Case C.4.2.1. 

If $\eta =\mu =0,$ this reduces to Case C.4.1, where $\Re =0$, which is not possible.

Case C.4.2.2. 

If $\eta =0$ and $\mu \ne 0,$ we obtain the following system of ODEs:

$${\left(f\right)}^2{\left(h_z\right)}^2-\left(2x-1\right)f{f}_{x}h{h}_{zz}+2f_x{h}_z-4fh=0,$$

(115)

$$f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2-{\displaystyle \frac{h_{zz}}{h_z}}=\mu \left(xf{h}_z+1\right),$$

(116)

$$f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2+{\displaystyle \frac{h_{zz}}{h_z}}=\mu \left[f{h}_z\left(1-x\right)-1\right].$$

(117)

Combining Equations (116) and (117) yields

$$2f_{xx}h{h}_z-4f_x{\left(h\right)}^2=\mu h_z,$$

(118)

Taking the partial derivative of (118) with respect to x gives

$${\displaystyle \frac{f_{xxx}}{f_{xx}}}=2{\displaystyle \frac{h}{h_z}}.$$

(119)

Since both sides must equal a non-zero constant, let

$${\displaystyle \frac{f_{xxx}}{f_{xx}}}=\beta =2{\displaystyle \frac{h}{h_z}},$$

(120)

then $h_z={\displaystyle \frac{2}{\beta }}h,$ and substituting this in (118), we get

$$2\left(f_{xx}-f_x\beta \right)={\displaystyle \frac{\mu }{h}}$$

(121)

Taking the partial derivative of (118) with respect to z gives $\mu h_z=0$. Thus this case is not possible.

Case C.4.3. 

If $\eta \ne 0$ and $\mu =0,$ we obtain the following system of ODEs:

$${\left(f\right)}^2{\left(h_z\right)}^2-\left(2x-1\right),f{f}_{x}h{h}_{zz}+2f_x{h}_z-4fh=\eta$$

(122)

$$f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2-{\displaystyle \frac{h_{zz}}{h_z}}=\eta x{f}_{x}h,$$

(123)

$$f{f}_{xx}h{h}_z-2f{f}_x{\left(h\right)}^2+{\displaystyle \frac{h_{zz}}{h_z}}=\eta \left(1-x\right)f_{x}h.$$

(124)

Combining (123) with (124) yields

$$2f{f}_{xx}{h}_z-4f{f}_{x}h=\eta f_x,$$

(125)

and taking the partial derivative of (125) with respect to z gives

$${\displaystyle \frac{f_{xx}}{f_x}}=2{\displaystyle \frac{h_z}{h_{zz}}}$$

(126)

Both sides have to equal a non-zero constant, namely

$${\displaystyle \frac{f_{xx}}{f_x}}=\lambda =2{\displaystyle \frac{h_z}{h_{zz}}},$$

(127)

then $f_{xx}=\lambda f_x,$ and substituting this in (125), we get

$$2\left[\lambda h^{\prime }-2h\right]={\displaystyle \frac{\eta }{f}}$$

(128)

Taking the partial derivative of (125) with respect to x gives $\eta f_x=0$, which is not possible.

Case C.4.4. 

If $\eta \ne 0$ and $\mu \ne 0$, combining Equations (113) and (114) yields

$$2{\displaystyle \frac{h_{zz}}{h_z}}=\eta \left(1-2x\right)f_{x}h+\mu \left[f{h}_z\left(1-2x\right)-2\right]$$

(129)

Taking the partial derivative of (129) with respect to x gives

$$\eta \left[-2f_x+\left(1-2x\right)f_{xx}\right]h-\mu \left[2f-\left(1-2x\right)f_x\right]h_z=0.$$

(130)

Case C.4.4.1. 

If $f_x={\displaystyle \frac{2f}{1-2x}},$ then on one hand we have

$$f_{xx}={\displaystyle \frac{2f_x\left(1-2x\right)+4f}{{\left(1-2x\right)}^2}},$$

(131)

and on the other hand, from (130), we have

$$f_{xx}={\displaystyle \frac{2f_x}{\left(1-2x\right)}}$$

(132)

Substituting (132) in (131), we get $f\left(x\right)=0$, which is not possible.

Case C.4.4.2. 

If $f_x\ne {\displaystyle \frac{2f}{1-2x}}$, from (128) we obtain

$$\eta {\displaystyle \frac{\left[-2f_x+\left(1-2x\right)f_{xx}\right]}{\left[2f-\left(1-2x\right)f_x\right]}}=\mu {\displaystyle \frac{h_z}{h}}.$$

(133)

The right-hand side of (133) depends on z, while the left-hand side is either constant or depends on x. For the equation to hold, both sides must equal the same non-zero constant; thus,

$$\eta {\displaystyle \frac{\left[-2f_x+\left(1-2x\right)f_{xx}\right]}{\left[2f-\left(1-2x\right)f_x\right]}}=\delta =\mu {\displaystyle \frac{h_z}{h}},$$

(134)

then we get

$${\displaystyle \frac{h_z}{h}}={\displaystyle \frac{\delta }{\mu }}.$$

(135)

Solving (135) gives

$$h=d{e}^{{\displaystyle \frac{\delta }{\mu }}z},$$

(136)

where $d\ne 0$. Substituting (135) with $h_z$ and $h_{zz}$ into (136), we get

$${\left(f\right)}^2{\left(h_z\right)}^2-\left(2x-1\right)f{f}_{x}h{h}_{zz}+2f_x{h}_z-4fh=\eta ,$$

(137)

$${\delta }^2{d}^2\left[{\left(f\right)}^2-\left(2x-1\right)f{f}_x\right]e^{2{\displaystyle \frac{\delta }{\mu }}z}+2d\mu \left[\delta f_x-2\mu f\right]e^{{\displaystyle \frac{\delta }{\mu }}z}=\eta {\mu }^2$$

(138)

Taking the partial derivative of (138) with respect to z, we obtain

$${\delta }^{2}d\left[{\left(f\right)}^2-\left(2x-1\right)f{f}_x\right]e^{{\displaystyle \frac{\delta }{\mu }}z}+\mu \left[\delta f_x-2\mu f\right]=0$$

(139)

Taking the partial derivative of (139) with respect to z, we derive

$${\displaystyle \frac{f_x}{f}}={\displaystyle \frac{1}{2x-1}}.$$

(140)

Solving (140) yields

$$f=a\left(2x-1\right),$$

(141)

which gives the surface $M^2$ parameterized as

$$r(x,z)=(x,ad\left(2x-1\right)e^{{\displaystyle \frac{\delta }{\mu }}z},z).$$

Case D: 

For ${\lambda }_1\ne 0$ or ${\lambda }_2\ne 0$, we find $H\ne 0$. We distinguish the following cases:

Case D-1. 

${\lambda }_1=0$ and ${\lambda }_2\ne 0$. Thus, $f\left(x\right)=c_0$, where $c_0\in {\mathbb{R}}^{*}$. Substituting into (99), we obtain

$${\displaystyle \frac{c{h}_z{h}_{zz}}{{\left(\left[2+\left(2x-1\right)c{h}_z\right]c{h}_z\right)}^2}}={\lambda }_{2}h.$$

(142)

Rewriting (142), we derive the following polynomial equation in x:

$$\left(4c_0^2{h}_z^2\right)x^2+4c_0{h}_z\left(2-c_0{h}_z\right)x+{\left(2-c_0{h}_z\right)}^2-{\displaystyle \frac{h_{zz}}{{\lambda }_2{c}_{0}h{h}_z}}=0.$$

(143)

For this to hold for all x, the coefficients must vanish:

$$4c_0^2{h}_z^2=0,2-c_0{h}_z=0,{\left(2-c_0{h}_z\right)}^2-{\displaystyle \frac{h_{zz}}{{\lambda }_2{c}_{0}h{h}_z}}=0.$$

(144)

The first condition implies $h_z=0$, which contradicts the second condition ($2-c_0{h}_z=0$). Thus, this case is impossible.

Case D-2. 

${\lambda }_2=0$ and ${\lambda }_1\ne 0$. Then we have $h_z=0.$ We find $h\left(z\right)=c_1,$ where $c_1\in {\mathbb{R}}^{*}.$ Then we have $H=0,$ which gives a contradiction.

Case D-3. 

Let ${\lambda }_1\ne 0$ and ${\lambda }_2\ne 0$. By combining Equations (99) and (98), we obtain

$${\displaystyle \frac{{\lambda }_2}{{\lambda }_1}}{\displaystyle \frac{f_x}{x}}=\mu \mathrm{and}{\displaystyle \frac{h_z}{h^2}}=\mu ,\mathrm{where}\mu \in {\mathbb{R}}^{*}.$$

(145)

Integration of the two equations into (145) leads to $f\left(x\right)=c_2{x}^2+c_3,$ and $h\left(z\right)=-{\left(\mu z+c_4\right)}^{-1},$ where $c_2=\mu {\displaystyle \frac{{\lambda }_1}{{\lambda }_2}},c_3,c_4\in \mathbb{R}$.

This leads to the following theorem:

Theorem 3.

The factorable surfaces $M^2$ of type 2 satisfying the condition ${\Delta }^I{r}_i={\lambda }_i{r}_i$, where ${\lambda }_i\in \mathbb{R}$, in the Lorentz–Heisenberg space are congruent to an open part of the surfaces:

1. 

$M^2$ has zero mean curvature.

(a) 

$M^2$ is parameterized by $r(x,z)=(x,cf\left(x\right),z).$

(b) 

$M^2$ is parameterized by $r(x,z)=(x,ad(2x-1)e^{{\displaystyle \frac{\delta }{\mu }}z},z).$

2. 

$M^2$ is parameterized by $r(x,z)=(x,\left(c_2{x}^2+c_3\right){\left(\mu z+c_4\right)}^{-1},z)$,

where $\mu ,c_i\in \mathbb{R}$, $i\in \left\{0,\dots ,4\right\},c_2=\mu {\displaystyle \frac{{\lambda }_1}{{\lambda }_2}},$ and ${\lambda }_1,{\lambda }_2,\mu ,c_0,c_2\ne 0.$

Example 2.

1. 

Consider factorable surfaces of type 2 in ${\mathbb{H}}_3$ with ${\Delta }^I{r}_i=0$ given by

$$y(x,z)=\left(2x-1\right)e^{{\displaystyle \frac{1}{2}}z},x,z\in [-3;3].$$

2. 

Consider factorable surfaces of type 2 in ${\mathbb{H}}_3$ with ${\Delta }^I{r}_i\ne 0$ given by

$$y\left(x,z\right)=\left(x^2+1\right){\left(z+1\right)}^{-1},x\in [-3;3],z\in [-0,5;3].$$

As visualized in Figure 2, these surfaces exhibit strikingly different geometric behaviors despite their similar factorable structure.

6. Factorable Surfaces of the Third Type Satisfying ${\Delta }^I{r}_i={\lambda }_i{r}_i$

In this section, we classify a factorable surface given by (15) in ${\mathbb{H}}^3$ satisfying the equation

$${\Delta }^I{r}_i={\lambda }_i{r}_i,$$

(146)

where ${\lambda }_i\in \mathbb{R}$, $i=1,2,3$ and

$${\Delta }^{I}r=\left({\Delta }^I{r}_1,{\Delta }^I{r}_2,{\Delta }^I{r}_3\right),$$

(147)

where

$$r_1=g\left(y\right)h\left(z\right),r_2=y,r_3=z.$$

(148)

Using (1) and (18), a direct computation yields the Laplacian operator on $M^2$ as

$${\Delta }^{I}r={\displaystyle \frac{2}{W}}H{e}_1+{\displaystyle \frac{2\left[\left(g^2{h}_z-g_y\right)h-g{h}_z\right]}{W}}H{e}_2-{\displaystyle \frac{2\left(g^2{h}_z-g_y\right)h}{W}}H{e}_3.$$

(149)

Assuming $M^2$ satisfies (91), we derive from (15) and (149) the following system of ODEs:

$${\displaystyle \frac{2}{W}}H={\lambda }_{1}gh,$$

(150)

$${\displaystyle \frac{2\left(g^2{h}_z-g_y\right)h-2g{h}_z}{W}}H=gh{\lambda }_{2}y+{\lambda }_{3}z,$$

(151)

$$-{\displaystyle \frac{2\left(g^2{h}_z-g_y\right)h}{W}}H=\left(1-gh\right){\lambda }_{2}y-{\lambda }_{3}z.$$

(152)

We analyze this system based on the values of the constants ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$, considering two cases depending on the value of ${\lambda }_1$.

Case E: 

Let ${\lambda }_1=0$. From (150), we obtain $H=0$. Thus, the surface $M^2$ is minimal and from (41), we get

$$\begin{array}{c}[{\left(g_y\right)}^2{h}^2+2gh-1]g{h}_{zz}+g^2{g}_{yy}h{\left(h_z\right)}^2\\ +[g^2-2g{\left(g_y\right)}^{2}h]{\left(h_z\right)}^2-2g_y{h}_z=0,\end{array}$$

(153)

so we consider the following sub-cases:

Case E-1: 

If $g_y=0,$ so $(g=a\ne 0),$ then Equations (153) and (39) become

$$\left(2ah-1\right)h_{zz}+a{\left(h_z\right)}^2=0,$$

(154)

and

$$\mathbb{N}={\displaystyle \frac{1}{W}}{e}_1+{\displaystyle \frac{a^{2}h{h}_z-a{h}_z}{W}}{e}_2-{\displaystyle \frac{a^{2}h{h}_z}{W}}{e}_3,$$

(155)

we put

$$\mathbb{Y}=\left(2ah-1\right)h_{zz}{e}_1-h_z{e}_2+h_z{e}_3,$$

(156)

from (154)–(156), we can easily check that the surface $M^2$ is minimal if and only if $g_3\left(\mathbb{Y},\mathbb{N}\right)=0.$ Therefore we have $\mathbb{Y}=0$ or $\mathbb{Y}$ ∈ $T_p{M}^2.$

Case E.1.1. 

If $\mathbb{Y}=0,$ from (156), there exist $d\in \mathbb{R}$ such that $h=d,$ then the surface $M^2$ is parameterized as

$$r\left(y,z\right)=(ad,y,z),$$

Case E.1.2. 

If $\mathbb{Y}$ ∈ $T_p{M}^2$, which implies that there exist $\eta ,\mu \in \mathbb{R},$ such that

$$\mathbb{Y}=\eta r_y+\mu r_z,$$

(157)

then, from (36) and (157), we obtain the following system of ODEs:

$$\left(2ah-1\right)h_{zz}=\mu a{h}_z,$$

(158)

$$-h_z=\eta ah+\mu ,$$

(159)

$$h_z=\eta \left(1-ah\right)-\mu .$$

(160)

Case E.1.2.1. 

If $\eta =\mu =0,$ this is Case E.1.1, where $\mathbb{Y}=0.$

Case E.1.2.2. 

If $\eta =0$ and $\mu \ne 0,$ we have

$$\left(2ah-1\right)h_{zz}=\mu a{h}_z,$$

(161)

$$h_z=-\mu ,$$

(162)

therefore $h_{zz}=0$ and from (161), we obtain $\mu =0,$ which is a contradiction.

Case E.1.2.3. 

If $\eta \ne 0$, substituting (159) into (160) yields $\eta =0$, resulting in a contradiction.

Case E-2: 

If $h_z=0,$ $(h=c\ne 0),$ so Equation (153) is trivially satisfied for all smooth functions $y,$ and we have

$$r\left(y,z\right)=(cg\left(y\right),y,z).$$

Case E-3: 

If $g_{yy}=0,$ so $(g=ay+b$ with $a\ne 0),$ then, Equations (153) and (39) become

$$\begin{array}{c}[{\left(a\right)}^2{h}^2+2\left(ay+b\right)h-1]\left(ay+b\right)h_{zz}+\\ +[{\left(ay+b\right)}^2-2{\left(a\right)}^2\left(ay+b\right)h]{\left(h_z\right)}^2-2a{h}_z=0,\end{array}$$

(163)

$$\aleph ={\displaystyle \frac{1}{W}}{e}_1+{\displaystyle \frac{[{\left(ay+b\right)}^2{h}_z-a]h-\left(ay+b\right)h_z}{W}}{e}_2-{\displaystyle \frac{[{\left(ay+b\right)}^2{h}_z-a]h}{W}}{e}_3,$$

(164)

taking the partial derivative of (163) twice with respect to y gives

$$2h{h}_{zz}+{\left(h_z\right)}^2=0,$$

(165)

we put

$$\mathbb{X}=2h{h}_{zz}{e}_1-{\displaystyle \frac{h_z}{ay+b}}{e}_2+{\displaystyle \frac{h_z}{ay+b}}{e}_3,$$

(166)

from (164)–(166), we can easily check that the surface $M^2$ is minimal if and only if $g_3\left(\mathbb{X},\aleph \right)=0.$ Therefore we have $\mathbb{X}=0$ or $\mathbb{X}$∈ $T_p{M}^2.$

Case E.3.1. 

If $\mathbb{X}=0,$ from (166), there exist $d\in \mathbb{R}$ such that $w=d,$ then the surface $M^2$ parameterized as

$$r\left(y,z\right)=(\left(ay+b\right)d,y,z).$$

Case E.3.2. 

If $\mathbb{X}$ ∈ $T_p{M}^2,$ which implies that there exist $\eta ,\mu \in \mathbb{R},$ such that

$$\mathbb{X}=\eta s_y+\mu s_z,$$

(167)

then, from (36) and (167), we obtain the following system of ODEs:

$$2h{h}_{zz}=\eta ah+\mu \left(ay+b\right)h_z,$$

(168)

$$-{\displaystyle \frac{h_z}{ay+b}}=\eta \left(ay+b\right)h+\mu ,$$

(169)

$${\displaystyle \frac{h_z}{ay+b}}=\eta \left(1-\left(ay+b\right)h\right)-\mu ,$$

(170)

Case E.3.2.1. 

If $\eta =\mu =0,$ this is Case E.3.1, where $\mathbb{X}=0.$

Case E.3.2.2. 

If $\eta =0$ and $\mu \ne 0,$ from (170) we obtain

$$h_z=-\mu \left(ay+b\right).$$

(171)

The right-hand side of (171) is a function of y, whereas the left-hand side is either a constant or a function of z. This leads to a contradiction.

Case E.3.2.3. 

If $\eta \ne 0,$ Equations (169) and (169) yield

$$\eta =0,$$

(172)

leading to a contradiction.

Case E.3.4. 

If $h_{zz}=0,$ $(h=cz+d$ with $c\ne 0),$ then Equations (153) and (39) give

$$g^2{g}_{yy}\left(cz+d\right){\left(c\right)}^2+[g^2-2y{\left(g_y\right)}^2\left(cz+d\right)]{\left(c\right)}^2-2g_{y}c=0,$$

(173)

$$\aleph ={\displaystyle \frac{1}{W}}{e}_1+{\displaystyle \frac{\left(g^{2}c-g_y\right)\left(cz+d\right)-cg}{W}}{e}_2-{\displaystyle \frac{\left(c{g}^2-g_y\right)\left(cz+d\right)}{W}}{e}_3,$$

(174)

taking the partial derivative of (173) with respect to z gives

$$g{g}_{yy}-2{\left(g_y\right)}^2=0,$$

(175)

we put

$$\mathbb{U}=-2c{\left(g_y\right)}^2{e}_1-g_{yy}{e}_2+g_{yy}{e}_3,$$

(176)

from (174)–(176), we can easily check that the surface $M^2$ is minimal if and only if $g_3\left(\mathbb{U},\aleph \right)=0.$ Therefore we have $\mathbb{U}=0$ or $\mathbb{U}$ ∈ $T_p{M}^2.$

Case E.4.1. 

If $\mathbb{U}=0,$ from (176) we have $g_y=0,$ this is the (Case E.1.).

Case E.4.2. 

If $\mathbb{U}$ ∈ $T_p{M}^2$, which implies that there exist $\eta ,\mu \in \mathbb{R},$ such that

$$\mathbb{U}=\eta r_y+\mu r_z$$

(177)

then, from (36) and (176), we obtain the following system of ODEs:

$$-2c{\left(g_y\right)}^2=\eta g_y\left(cz+d\right)+\mu cg,$$

(178)

$$-g_{yy}=\eta g\left(cz+d\right)+\mu ,$$

(179)

$$g_{yy}=\eta \left(1-g\left(cz+d\right)\right)-\mu .$$

(180)

Case E.4.2.1. 

If $\eta =\mu =0,$ this is Case E.4.1, where $\mathbb{U}=0.$

Case E.4.2.2. 

If $\eta =0$ and $\mu \ne 0,$ from (178) and (179), we obtain

$$-2{\left(g_y\right)}^2=\mu g,$$

(181)

$$g_{yy}=-\mu ,$$

(182)

taking the partial derivative of (181) with respect to y gives

$$-4g_y{g}_{yy}=\mu g_y.$$

(183)

If $g_y=0$, we recover Case E.1. Otherwise, substituting (182) into (183) yields $\mu =0$, leading to a contradiction.

Case E.4.2.3. 

If $\eta \ne 0,$ combining Equations (179) and (180) yields $\eta =0,$ leading to a contradiction.

Case E.5. 

$g_{yy}{h}_{zz}\ne 0.$ If we take

$$\mathbb{V}={\mathbb{V}}_1{e}_1+{\mathbb{V}}_2{e}_2+{\mathbb{V}}_3{e}_3,$$

(184)

such that

$${\mathbb{V}}_1=[{\left(g_y\right)}^2{h}^2+2gh-1]g{h}_{zz}-2g_y{h}_z,$$

(185)

$${\mathbb{V}}_2=[2{\left(g_y\right)}^{2}h-y]h_z-g{g}_{yy}h{h}_z,$$

(186)

$${\mathbb{V}}_3=g{g}_{yy}h{h}_z+[g-2{\left(g_y\right)}^{2}h]h_z,$$

(187)

from (39), (153) and (184), the surface $M^2$ is minimal if and only if $g_3\left(\mathbb{V},\aleph \right)=0.$ Therefore we have $\mathbb{V}=0$ or $\mathbb{V}$$\in T_p{M}^2.$

Case E.5.1. 

If $\mathbb{V}=0,$ Equation (186) becomes

$${\displaystyle \frac{2{\left(g_y\right)}^2-g{g}_{yy}}{g}}={\displaystyle \frac{1}{h}}.$$

(188)

The right side in (188) is either a function of z while the other side is a constant or a function of $y;$ both sides have to equal a non-zero constant, namely

$${\displaystyle \frac{2{\left(g_y\right)}^2-g{g}_{yy}}{g}}=\alpha ={\displaystyle \frac{1}{h}},$$

(189)

therefore $h_z=0$, leading to a contradiction.

Case E.5.2. 

If $\mathbb{V}$ ∈ $T_p{M}^2,$ which implies that there exist $\eta ,\mu \in \mathbb{R},$ such that

$$\mathbb{V}=\eta r_y+\mu r_z$$

(190)

then, from (36) and (190), we obtain the following system of ODEs:

$$[{\left(g_y\right)}^2{h}^2+2gh-1]g{h}_{zz}-2g_y{h}_z=\eta g_{y}h+\mu g{h}_z,$$

(191)

$$[2{\left(g_y\right)}^{2}h-g]h_z-g{g}_{yy}h{h}_z=\eta gh+\mu ,$$

(192)

$$g{g}_{yy}h{h}_z+[g-2{\left(g_y\right)}^{2}h]h_z=\eta \left(1-gh\right)-\mu .$$

(193)

Case E.5.2.1. 

If $\eta =0$ and $\mu \ne 0,$ from (192), we obtain

$$[2{\left(g_y\right)}^{2}h-g]h_z-g{g}_{yy}h{h}_z=\mu$$

(194)

Taking the partial derivative of (194) with respect to y gives

$${\displaystyle \frac{\left(3g_y{g}_{yy}-g{g}_{yyy}\right)}{v^{\prime }}}={\displaystyle \frac{1}{h}}.$$

(195)

Since the left-hand side of the equation is a function of y and the right-hand side is a function of z, both sides must equal a non-zero constant, such that

$${\displaystyle \frac{\left(3g_y{g}_{yy}-g{g}_{yyy}\right)}{g_y}}=\gamma ={\displaystyle \frac{1}{h}},$$

(196)

therefore $h_z=0$, this leads to a contradiction.

Case E.5.2.2. 

If $\eta \ne 0,$ combining Equations (192) and (193) yields $\eta =0$, leading to a contradiction.

Case F. 

Let ${\lambda }_1\ne 0$, then we have $H\ne 0.$ Combining Equations (150)–(152), we have

$${\lambda }_1{g}^{2}h{h}_z+{\lambda }_{2}y=0.$$

(197)

We discuss two sub-cases based on the values of ${\lambda }_2.$

Case F.1. 

Let ${\lambda }_2=0$, then we have $h_z=0.$ This solution gives a contradiction.

Case F.2. 

Let ${\lambda }_2\ne 0$. From (197) we have

$$-{\displaystyle \frac{{\lambda }_1}{{\lambda }_2}}{\displaystyle \frac{g^2}{y}}={\displaystyle \frac{1}{h{h}_z}}.$$

(198)

Since the left side of (198) is a function of y and the right side is a function of z, both sides have to be equal to a non-zero constant, that is

$$-{\displaystyle \frac{{\lambda }_1}{{\lambda }_2}}{\displaystyle \frac{g^2}{y}}=\alpha ={\displaystyle \frac{1}{h{h}_z}},\mathrm{where}\alpha \in {\mathbb{R}}^{*}.$$

(199)

Solving (199), we obtain

$$g\left(y\right)=\sqrt{{\displaystyle \frac{-\alpha {\lambda }_2}{{\lambda }_1}}y},\mathrm{and}h\left(z\right)=\sqrt{{\displaystyle \frac{2}{\alpha }}z+2{\alpha }_0},$$

(200)

where ${\displaystyle \frac{-\alpha {\lambda }_2}{{\lambda }_1}}y>0,$${\displaystyle \frac{2}{\alpha }}z+2{\alpha }_0>0$ and ${\alpha }_0\in \mathbb{R}.$

Theorem 4.

The factorable surfaces $M^2$ of type 3 satisfying the condition ${\Delta }^I{r}_i={\lambda }_i{r}_i$ where ${\lambda }_i\in \mathbb{R}$, in the Lorentz–Heisenberg space are congruent to an open part of the surfaces:

1. 

$M^2$ has zero mean curvature.

(a) 

$M^2$ is parameterized by $r\left(y,z\right)=(ad,y,z).$

(b) 

$M^2$ is parameterized by $r\left(y,z\right)=(cg\left(y\right),y,z)$.

(c) 

$M^2$ is parameterized by $r\left(y,z\right)=(\left(ay+b\right)d,y,z).$

2. 

$M^2$ is parameterized by $r\left(y,z\right)=\sqrt{\left({\displaystyle \frac{-\alpha {\lambda }_2}{{\lambda }_1}}y\right)\left({\displaystyle \frac{2}{\alpha }}z+2{\alpha }_0\right)}$.

where $\alpha ,{\alpha }_0\in \mathbb{R}$, ${\lambda }_1,{\lambda }_2$$\in \mathbb{R}-\left\{0\right\}$ and $\alpha \ne 0.$

Example 3 (Type 3 Factorable Surfaces in ${\mathbb{H}}_3$).

This example provides two classes of type 3 factorable surfaces in the Lorentz–Heisenberg group:

1. 

A minimal surface (${\Delta }^I{r}_i=0$) with linear dependence on y:

$$x(y,z)=y+1,y,z\in [-3,3].$$

2. 

A surface with non-vanishing ${\Delta }^I{r}_i$ exhibiting square-root dependence:

$$x(y,z)=\sqrt{-{\displaystyle \frac{1}{2}}y(z+2)},y\in [-3,0],z\in [-2,3].$$

Figure 3 illustrates the striking geometric contrast between these surfaces, with the minimal case showing planar behavior while the second case displays curved characteristics.

The visual comparison in Figure 3 reveals how the minimality condition affects surface geometry, with the right panel’s curvature arising from the non-linear coordinate dependence.

Figure 3. Factorable surfaces in ${\mathbb{H}}_3$. (Left): Planar minimal surface $x(y,z)=y+1$ with zero mean curvature; (Right): Curved surface $x(y,z)=\sqrt{-{\displaystyle \frac{1}{2}}y(z+2)}$ with non-zero ${\Delta }^I{r}_i$.

Figure 3. Factorable surfaces in ${\mathbb{H}}_3$. (Left): Planar minimal surface $x(y,z)=y+1$ with zero mean curvature; (Right): Curved surface $x(y,z)=\sqrt{-{\displaystyle \frac{1}{2}}y(z+2)}$ with non-zero ${\Delta }^I{r}_i$.

7. Conclusions

We have investigated factorable surfaces in the Lorentz–Heisenberg space ${\mathbb{H}}_3$ with a flat metric, considering three distinct parameterizations involving smooth functions of a single variable. By analyzing surfaces that admit finite-type immersions, characterized by the Laplace–Beltrami operator acting on the position vector field, we extended the notion of minimal surfaces in this geometric setting. Our results contribute to a deeper understanding of the interplay between factorable surfaces, finite-type conditions, and differential operators in Lorentz–Heisenberg geometry. This work opens new directions for further research on the classification of finite-type surfaces and their geometric properties in similar pseudo-Riemannian spaces.