Rotational Influence on Wave Propagation in Semiconductor Nanostructure Thermoelastic Solid with Ramp-Type Heat Source and Two-Temperature Theory

Abstract

This study investigates the influence of rotation on wave propagation in a semiconducting nanostructure thermoelastic solid subjected to a ramp-type heat source within a two-temperature model. The thermoelastic interactions are modeled using the two-temperature theory, which distinguishes between conductive and thermodynamic temperatures, providing a more accurate description of thermal and mechanical responses in semiconductor materials. The effects of rotation, ramp-type heating, and semiconductor properties on elastic wave propagation are analyzed theoretically. Governing equations are formulated and solved analytically, with numerical simulations illustrating the variations in thermal and elastic wave behavior. The key findings highlight the significant impact of rotation, nonlocal parameters $e_{0}a$, and time derivative fractional order (FO) $\alpha$ on physical quantities, offering insights into the thermoelastic performance of semiconductor nanostructures under dynamic thermal loads. A comparison is made with the previous results to show the impact of the external parameters on the propagation phenomenon. The numerical results show that increasing the rotation rate $\mathsf{\Omega }=5$ causes a phase lag of approximately 22% in thermal and elastic wave peaks. When the thermoelectric coupling parameter ${\mathsf{\epsilon }}_3$ is increased from $-0.8\times {10}^{-42}$ to $1.2\times {10}^{-42}$. The temperature amplitude rises by 17%, while the carrier density peak increases by over 25%. For nonlocal parameter values $\mathsf{\epsilon }=0.3\to 0.6$, high-frequency stress oscillations are damped by more than 35%. The results contribute to the understanding of wave propagation in advanced semiconductor materials, with potential applications in microelectronics, optoelectronics, and nanoscale thermal management.

1. Introduction

The thermoelastic behavior of semiconductor nanostructures under dynamic thermal and mechanical loads has garnered significant attention due to its implications for microelectronics, optoelectronics, and nanoscale energy transport. This study examines the coupled effects of rotation, ramp-type heat sources, and two-temperature thermodynamics on wave propagation in semiconducting thermoelastic solids, addressing a critical gap in the understanding of transient thermo-mechanical interactions in rotating nanostructures. Unlike classical thermoelasticity, the two-temperature model (TTM) decouples the conductive temperature from the thermodynamic temperature, enabling a more accurate description of thermal wave propagation in semiconductors, where nonlocal effects dominate at nanoscales. The inclusion of rotation introduces Coriolis and centrifugal forces, which modify elastic wave characteristics (e.g., phase velocity, attenuation) and thermal diffusion patterns, while the ramp-type heat source—a time-dependent thermal load—mimics realistic laser heating or pulsed thermal excitation scenarios. By formulating the governing equations within the TTM framework and solving them analytically/numerically, this work elucidates how rotation alters thermoelastic energy dissipation, wave dispersion, and temperature gradients in semiconductor nanomaterials. The results provide foundational insights for designing rotating semiconductor devices (e.g., MEMS sensors, nanogenerators) subjected to abrupt thermal loads, where conventional single-temperature models fail to capture experimental observations. Interactions between thermal fields, elastic fields, and semiconducting fields have recently received increased attention due to their practical applications in fields as varied as geophysics, geology, acoustics, engineering, and aerospace. Several articles have investigated the role of nanostructure in the thermoelasticity of materials. Tang et al. [1] present a new constitutive equation for thermoelasticity in crystals and demonstrate its accuracy through calculations on copper and graphene. Micropolar thermoelastic solids are included in the entropy production inequality by Dost and Tabarrok [2], who demonstrate that the energy equation takes on a hyperbolic shape and displays wave characteristics. Kim et al. [3] show that embedding ErAs nano islands in In/sub 0.53/Ga/sub 0.47/As decreases heat conductivity below the alloy limit and boosts thermoelectric figure of merit. This may be due to the nano islands scattering mid- to long-wavelength phonons. Nowacki [4] discusses the propagation of surfaces of discontinuity in thermoelastic solids, including weak and strong thermoelastic waves of different orders.

To take into consideration the consequences of nonlocal behavior in heat conduction, the field of solid mechanics known as nonlocal thermoelasticity was developed. Nonlocal thermoelasticity takes into account the nonlocal character of heat transport at tiny scales, in contrast to standard heat conduction theories based on Fourier’s equation. According to Fourier’s law, which governs classical heat conduction, the heat flux at any given site is directly proportional to the local temperature gradient. However, at very small scales, nonlocal interactions between surrounding atoms or molecules allow for thermal transfer to occur.

Nonlocal thermoelasticity has gained significant attention in recent years due to the development of nanotechnology and miniaturization of devices, where heat transfer at small scales becomes crucial. It is also relevant in materials with highly heterogeneous microstructures, such as composites or porous media, where the traditional local heat transfer models fail to capture accurately the thermal behavior. The nonlocal theory of heat conduction considers the integral form of Fourier’s law, where the heat flux is expressed as an integral of the temperature gradient over a certain range. The range of integration, known as the nonlocal length scale, represents the characteristic distance over which the heat transfer occurs nonlocally. This nonlocal length scale can be determined experimentally or through theoretical approaches, such as molecular dynamics simulations or statistical mechanics.

Nonlocal thermoelasticity has been extensively studied in various applications, including heat conduction in nanowires, thin films, and biological systems. It has also found application in the analysis of microscale electronic devices, such as transistors and integrated circuits, where the accurate prediction of the temperature distribution and heat dissipation is crucial for device performance and reliability.

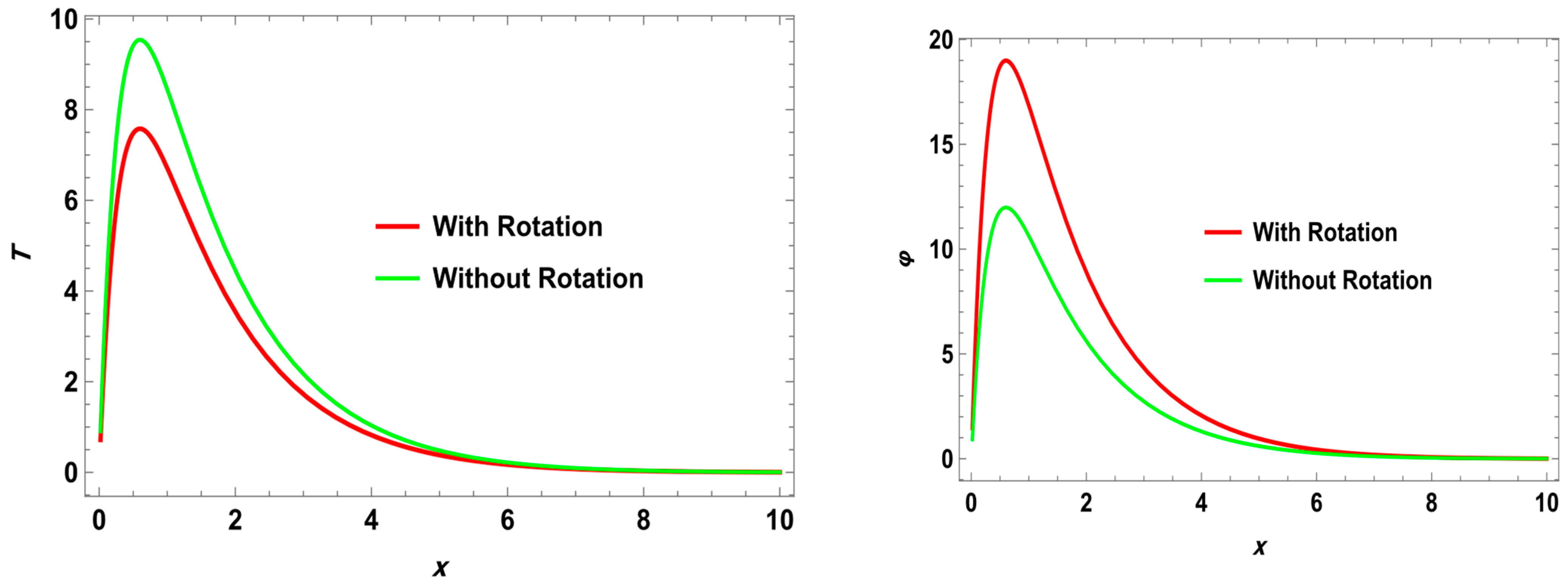
In thermoelasticity, the concept of rotation with nonlocal effects refers to the consideration of the rotational displacement field and the incorporation of nonlocal effects in the analysis of thermomechanical behavior. Thermoelasticity deals with the coupling between thermal and mechanical phenomena in solids, where temperature changes induce mechanical deformations and vice versa. Traditionally, in classical elasticity, the displacement field is described by the translation of material points without considering rotation. However, in certain cases, rotations of material elements cannot be neglected, especially in small-scale structures or when dealing with non-homogeneous materials. The consideration of rotation in thermoelasticity allows for a more accurate description of the deformation behavior, particularly in cases where the rotation field significantly influences the thermomechanical response. Nonlocal effects in thermoelasticity refer to the incorporation of nonlocal operators or integral formulations to model the dependence of the deformation field on the behavior of neighboring material points. Nonlocal operators take into account the spatial variations in the deformation field and provide a means to capture the effects of long-range interactions between material points, which are often ignored in classical elasticity.

The study of rotation with nonlocal effects in thermoelasticity is an active area of research, with applications in various fields such as micro- and nano-electromechanical systems, materials science, and biomechanics. Researchers are investigating the theoretical foundations, mathematical modeling, numerical methods, and experimental validations of these concepts.

Thermoelasticity relies heavily on rotation. Several investigations have looked into what happens to thermoelastic materials when they are rotated. For an isotropic elastic material at two temperatures, El-Sapa et al. [5] constructed a generalized micropolar thermo-visco-elasticity model, taking rotation and viscosity into account. Considering the influence of rotation, Mashat et al. [6] proposed a model for generalized thermoelasticity with phase-lags in an orthotropic body including a spherical cavity. Using Lord–Shulman’s theory and the classical dynamically linked theory, for a homogeneous isotropic elastic half-space solid, Sarkar [7] studied the effects of rotation on the equations of generalized thermoelasticity. Abo-Dahab used multiple thermoelastic theories to examine how rotation affects a generalized thermoelastic half-space with diffusion, electromagnetic field, and gravity field [8]. Lotfy et al. [9] investigated the effect of rotation on the thermoelastic half-space using the theory of two-temperature generalized thermoelasticity. Sharma et al. [10] investigated plane wave reflection in the generalized thermoelastic half-plane, considering rotation and starting stress. In the presence of rotation and “initial stress in thermoelasticity”, the reflection coefficient was found.

The thermoelastic effects of rotation and magnetic field have been the subject of several articles. Four distinct theories, namely the coupled theory (CT), the Lord–Schulman (LS) theory, the Green–Lindsay (GL) theory, and the Green–Naghdi (GN) theory, have been examined to comprehend the impact of rotation and magnetic field on the generalized thermoelasticity equations for a uniform isotropic elastic half-space [11]. The impact of diffusion in gaps in an extended thermoelastic half-space subjected to a magnetic field, gravity field, and rotation is modeled mathematically in [8]. Transient waves from a line heat source have been investigated in a rotating half-space fiber-reinforced thermoelastic medium [12]. This study investigates the influence of magnetic field and rotation on a two-dimensional problem of fiber-reinforced thermoelasticity in a homogeneous isotropic elastic half-space by the application of normal mode analysis [13]. Harmonic wave propagation in a rotating nonlinear magneto-thermoelastic medium has been simulated using homotopy perturbation and variational iteration [14].

The effects of rotation and magnetic fields on nonlocal thermoelasticity have been the subject of numerous papers. The effects of a rotating magnetic field on the free oscillations of an elastic hollow sphere were studied by Bayones et al. [15]. Both the magnetic field and the rotation were shown to have significant effects on the wave dispersion curves. Al-Basyouni and Mahmoud [16] discussed the effect of the magnetic field, initial stress, rotation, and nonhomogeneity on stresses in orthotropic material. The planar strain two-temperature problem in a semiconducting medium was studied by Abo-dahab and Lotfy [17] using photothermal theory. Using nonlocal modified couple stress theory and generalized thermoelastic theory, Yahya et al. [18] studied thermoelastic rotating nanobeams subjected to periodic pulse heating. Liu et al. [19] investigated the photothermal phenomenon: extended ideas for thermophysical property characterization. Different field variables were tested for their sensitivity to rotation and pair stress. This body of research, taken as a whole, sheds light on how rotation and magnetic field affect nonlocal thermoelastic behavior. The photothermal phenomena were the subject of research in [19]: expanded ideas for characterizing thermophysical qualities. The wave propagation in thermoelastic via semiconductor nanostructure by a ramp heat source was studied by Abo-Dahab et al. [20]. Mondal and Sur [21] discussed the photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Ezzat [22] studied hyperbolic thermal–plasma wave propagation in a semiconductor of organic material. Ezzat [23] investigated a novel model of fractional thermal and plasma transfer within a non-metallic plate. Hirdes and Honig’s method for numerically inverting Laplace transforms was explored in [24]. El-Sapa et al. [25] examined the effect of moisture diffusivity on the photothermal excitation process in semiconductor materials. The authors of [26] investigated the photothermal excitation mechanism in a magneto-thermoelastic medium using hyperbolic two-temperature theory. One-dimensional applications of fractional generalized thermoelasticity related to two relaxation durations were described by Hamza et al. The authors of [27,28] highlighted the fractional derivative heat transport and nonlocal theory of thermoelastic materials with voids. Functionally graded (FG) magneto-photo-thermoelastic semiconductor materials using hyperbolic two-temperature theory were examined by Saeed et al. [29].

Recent studies from 2024 also continue to advance this field. For example, Marin and Abbas [30] extended thermoelastic void models with fractional operators; Lotfy et al. [31] examined noise-influenced photoacoustic wave interactions; and Saeed et al. [29] developed magneto-photothermal models in FG semiconductors under stochastic excitation.

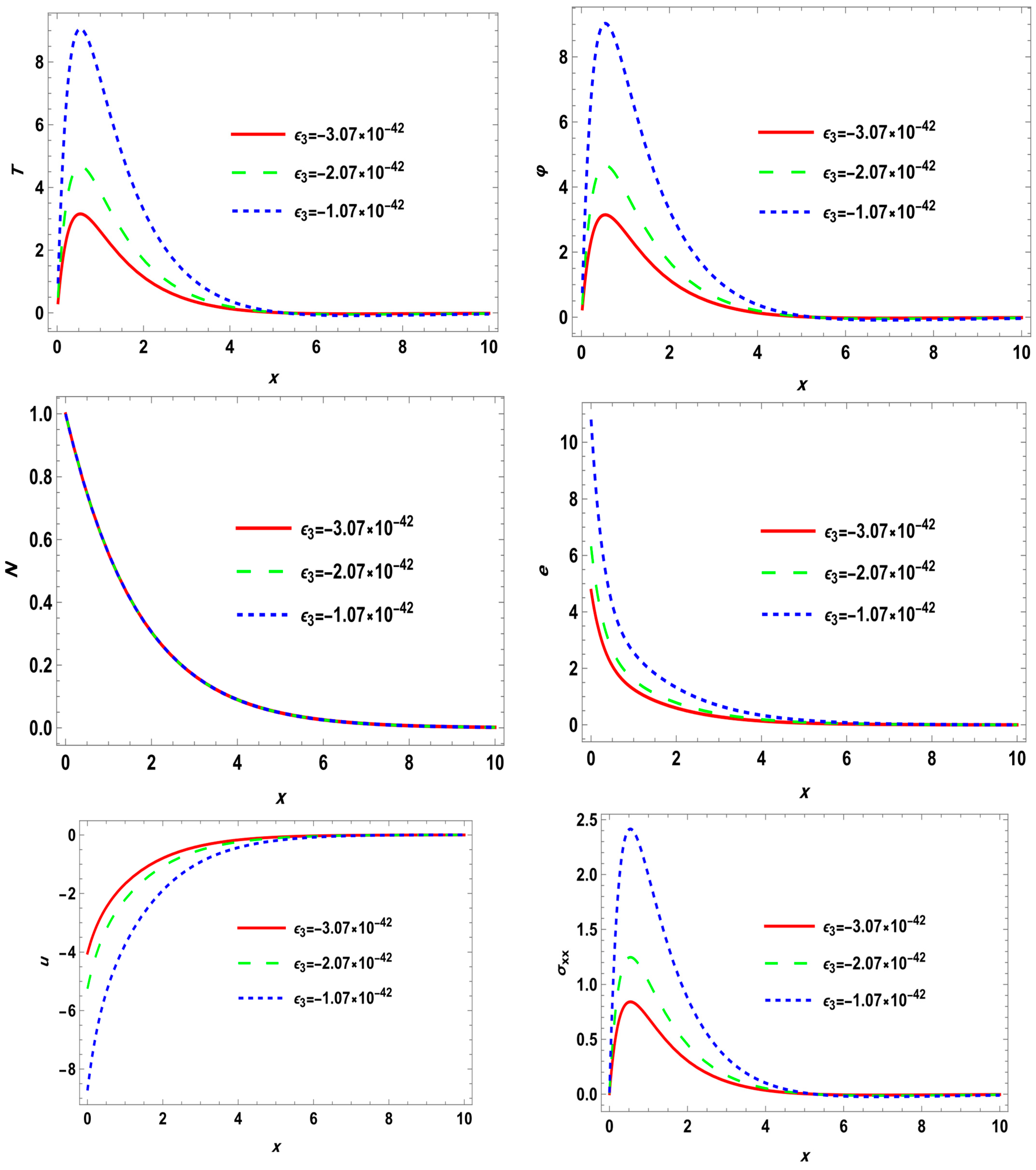
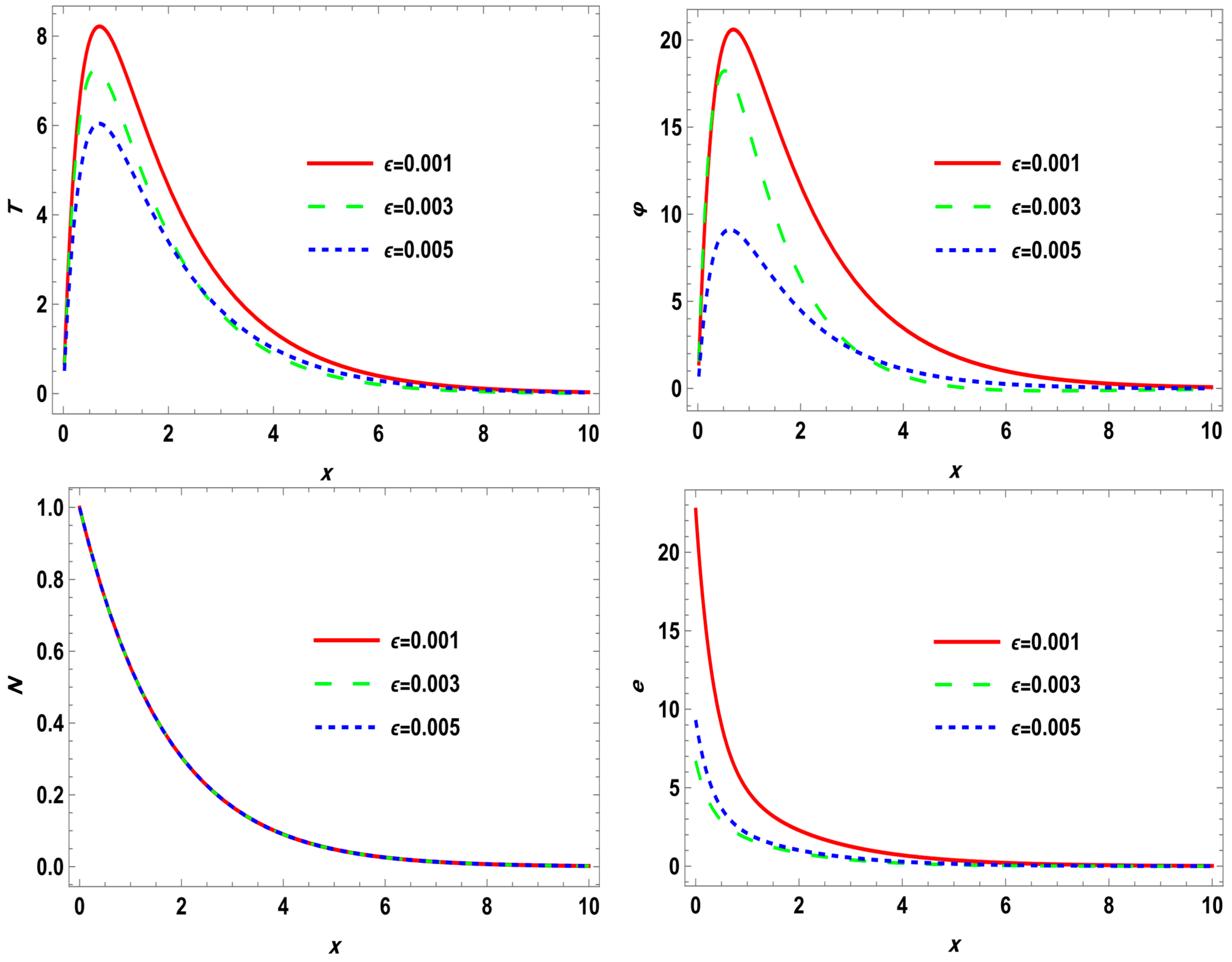
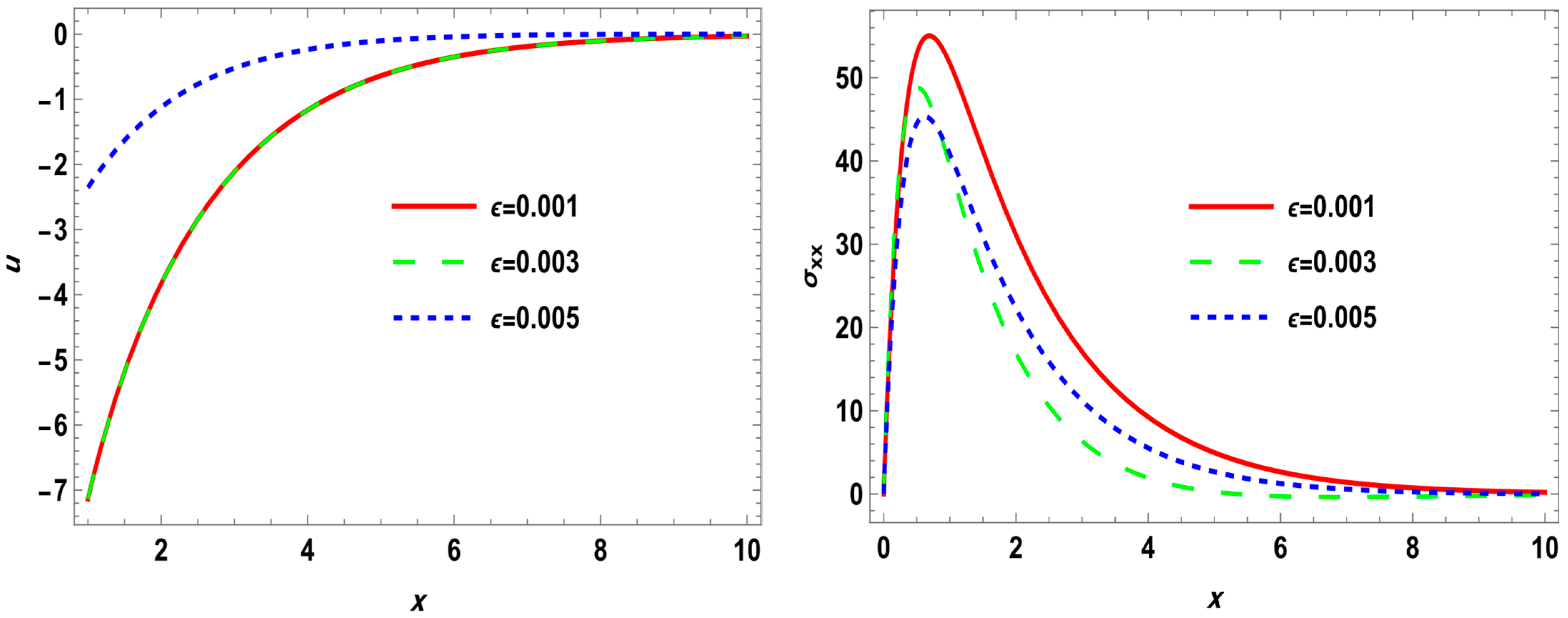
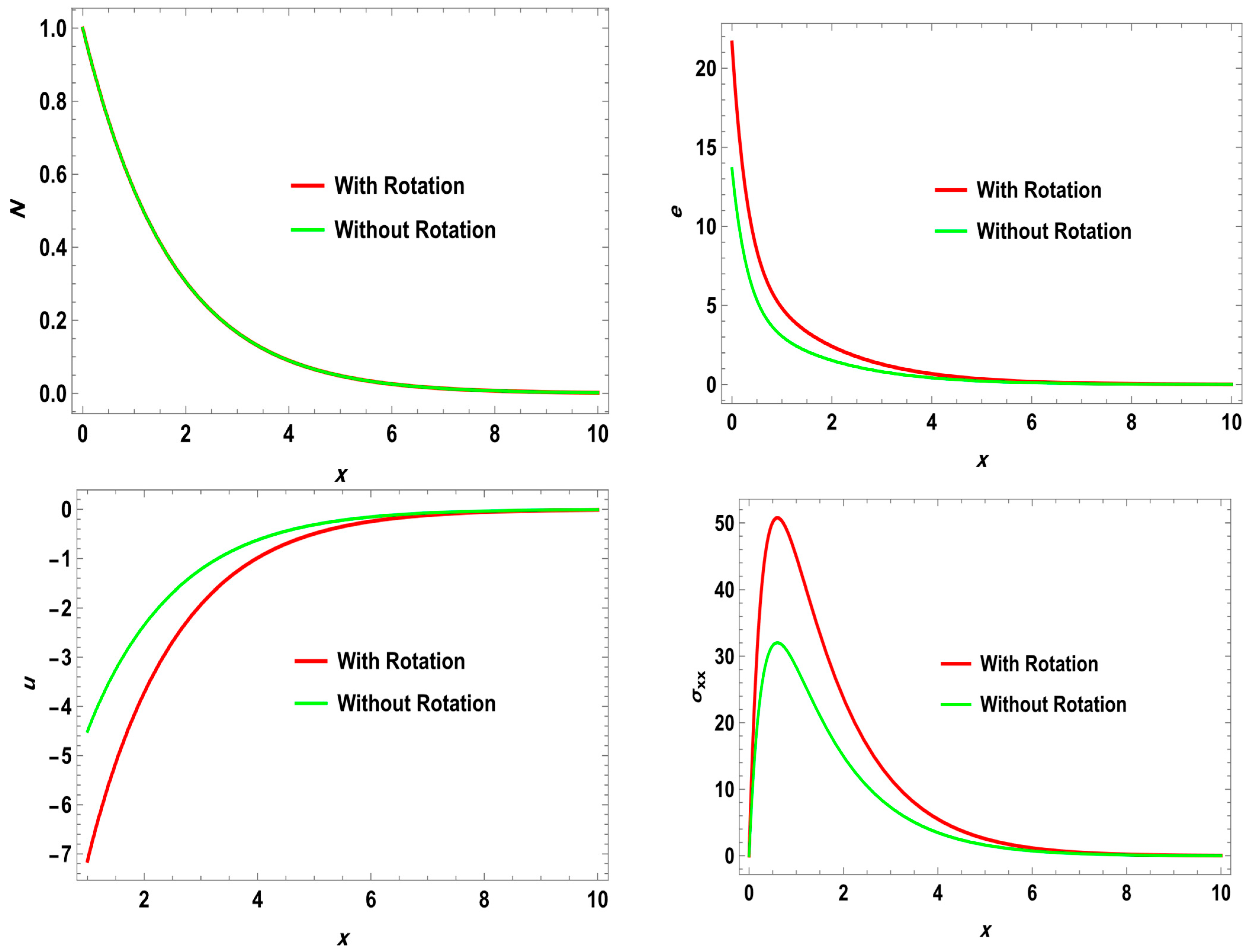
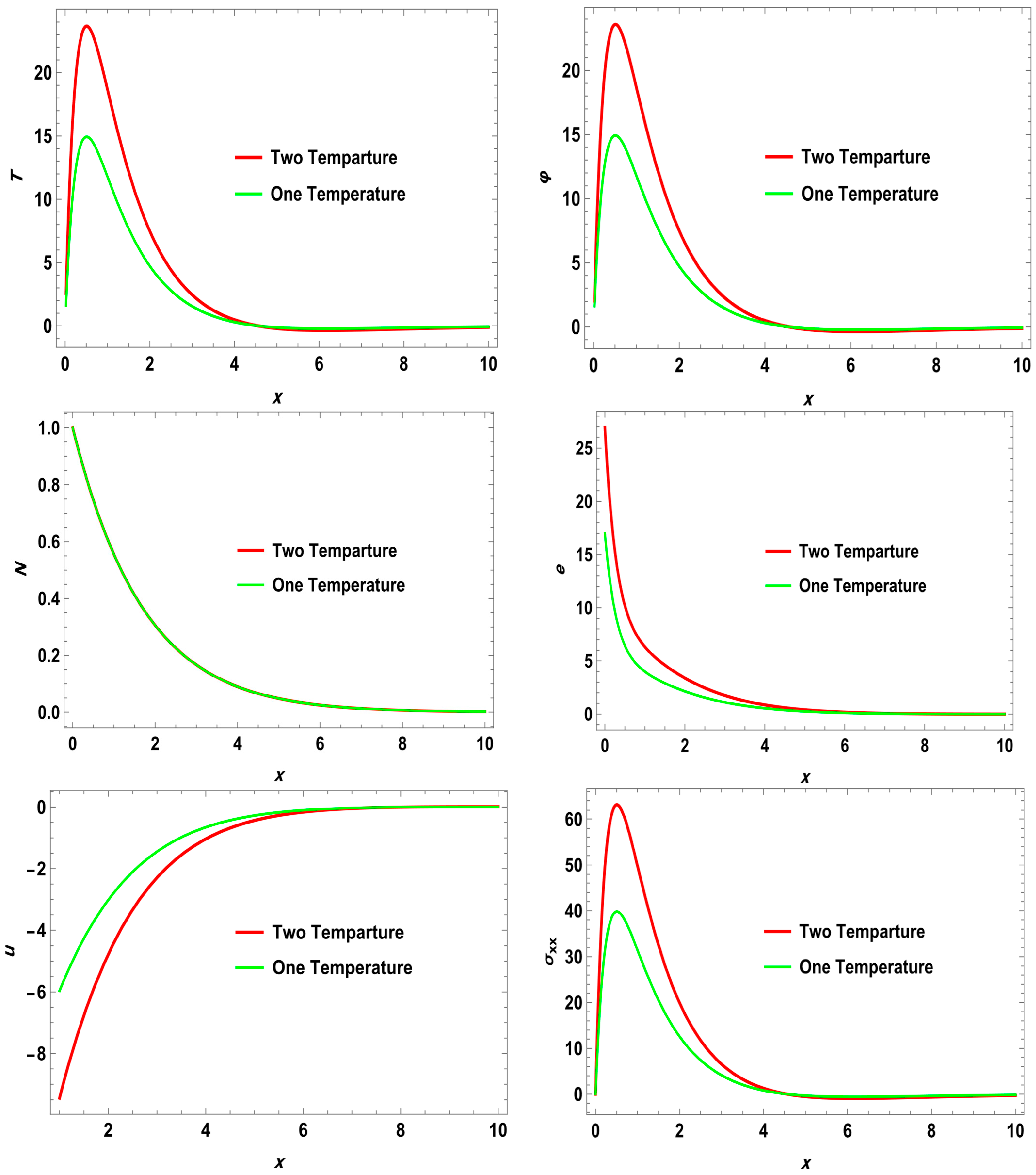
In this article, the rotational and ramp-type heat source on wave propagation in a semiconductor nanostructure thermoelastic solid is studied. A generalized thermoelastic theory, along with coupled nonlocal elastic theory, is formulated as a mathematical model representing the phenomena. Incorporating a ramp-type heat equation of fractional order allows us to point out the influence of temperature on wave motion. The decomposition method is used to separate the governing equations into their longitudinal and transverse parts. It is obvious that one longitudinal P-type and secondary shear S-type three waves are propagating through the medium. For a given material, analytical results for the reflection coefficient of each of the transmitted waves are computed numerically and then displayed graphically. The influence of rotation, nonlocal parameters $e_{0}a$, and time derivative fractional order (FO) $\alpha$ is also discussed.

Although significant efforts have been made to model thermoelastic wave propagation in semiconducting media under various conditions—such as rotation [9], photothermal excitation [20], fractional derivatives [27], and two-temperature frameworks [26]—most existing studies consider these effects in isolation or limited combinations. For example, Lotfy et al. [9] examined rotational effects using two-temperature thermoelasticity but without ramp-type or fractional heating, while Abo-Dahab et al. [20] studied ramp-type photothermal heating in semiconductors but excluded rotation and nonlocal elasticity.

The present study distinguishes itself by integrating four key mechanisms—(i) mechanical rotation, (ii) ramp-type heat input modeled using fractional derivatives, (iii) the two-temperature theory, and (iv) nonlocal thermoelasticity—within a unified analytical framework. This comprehensive formulation enables us to investigate the intricate coupling between thermal, elastic, and electronic fields under realistic nanoscale conditions, including Coriolis and centrifugal forces, phase-lag heat conduction, and long-range atomic interactions. To the best of our knowledge, this is the first work to explore these combined effects analytically using Laplace–Fourier inversion techniques for semiconductor nanostructures. As such, our model offers enhanced predictive capabilities for next-generation optoelectronic and microelectromechanical (MEMS) devices subjected to dynamic multi-physical loads.

While our earlier studies have addressed some individual aspects (e.g., rotation or ramp heating), the present work is the first to combine all of the following mechanisms: (i) mechanical rotation with Coriolis effects, (ii) fractional-order ramp-type heating, (iii) nonlocal thermoelasticity, and (iv) the two-temperature model. This unified framework allows us to reveal emergent interactions between thermal, mechanical, and plasma fields not captured in any prior work. No previous study, including those by the authors, has treated this specific configuration analytically using Laplace–Fourier techniques.

2. Basic Equations

Assume that the medium being analyzed is uniformly rotating; in this case, the angular velocity is $\underset{¯}{\mathsf{\Omega }}=\mathsf{\Omega }\underset{¯}{n},$ and $\underset{¯}{n}$ is a unit vector explaining the direction of the rotation axis. The equation of motion in the rotating reference frame contains two supplementary terms:

(1) Centripetal acceleration, $\underset{¯}{\mathsf{\Omega }}\mathrm{x}(\underset{¯}{\mathsf{\Omega }}\mathrm{x}\underset{¯}{\mathrm{u}})$ due to time-varying motion only.

(2) The acceleration of Coriolis $2\underset{¯}{\mathsf{\Omega }}\mathrm{x}\underset{¯}{\dot{u}}$, where $\underset{¯}{u}$ is the displacement vector.

In a problem that involves only one dimension, every variable is solely dependent on coordinate x and time t. We considered the angular velocity as $\underset{¯}{\mathsf{\Omega }}=(0,\mathsf{\Omega },0)$. On the other hand, when there is no rotation, these terms are absent in the medium.

Consider the transport mechanism of plasma in a semiconductor nanostructure medium, the time derivative fractional-order thermoelastic model, and the equation of motion. By applying the principle of nonlocal theory, quantity $e_{0}a$ is brought in, where $e_0$ describes the nonlocal effect, and $a$ is the material characteristic length. Semiconductor and isotropic media are under consideration. The carrier density N ($\overrightarrow{r}$, t), temperature distribution T ($\overrightarrow{r}$, t), and elastic displacement u ($\overrightarrow{r}$, t) are the main variable quantities. The equation of motion for a plasma wave that is subject to hydrostatic initial stress without body force is determined. In this analysis, the plasma transport equation with a new model under two-temperature theory [22] and the heat conduction model [14] is as follows:

$$\left(\mu \right)u_{i,jj}+\left(\lambda +\mu \right)u_{j,ij}-{\beta }_T{\mathrm{T}}_{,i}-{\delta }_n{N}_{,i}=\rho \left(1-{\epsilon }^2{\nabla }^2\right)\left\{{\ddot{u}}_i+{\left\{\underset{¯}{\mathsf{\Omega }}\mathrm{x}(\underset{¯}{\mathsf{\Omega }}\mathrm{x}\underset{¯}{u})\right\}}_i+{(2\underset{¯}{\mathsf{\Omega }}\mathrm{x}\underset{¯}{\dot{\mathrm{u}}})}_i\right\}$$

(1)

$${\displaystyle \frac{\partial N}{\partial t}}=D_E{N}_{,ii}-{\displaystyle \frac{N}{\tau }}+\kappa T$$

(2)

$$K^{*}{\phi }_{,ii}+K{\displaystyle \frac{{{\tau }_{\mathrm{T}}}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}{\dot{\phi }}_{,ii}+(K+K^{*}{\displaystyle \frac{{{\tau }_{\upsilon }}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}){\dot{\phi }}_{,ii}=\left(1+{\displaystyle \frac{{{\tau }_q}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}+{\displaystyle \frac{{{\tau }_q}^{2\alpha }}{(2\alpha )!}}{\displaystyle \frac{{\partial }^{2\alpha }}{\partial t^{2\alpha }}}\right)\left(\rho C_e\ddot{T}+{\beta }_T{\mathrm{T}}_0{\ddot{u}}_{i,i}\right)+{\displaystyle \frac{E_{g}N}{\tau }}$$

(3)

The fractional-order time derivative α appearing in Equation (3) accounts for non-Fourier, memory-dependent heat conduction, especially relevant at micro- and nanoscales. Physically, α  <  1 reflects subdiffusive thermal behavior, where the energy carriers (e.g., phonons, hot electrons) experience scattering, trapping, or delayed release during transport. Such behavior is often observed in semiconductor heterostructures, amorphous systems, or nano-layered materials. An experimental estimation of α can be achieved via ultrafast thermoreflectance measurements or by the inverse modeling of time-domain photothermal response curves (see Ezzat [22] and Liu et al. [19]).

The displacement and strain tensor equation looks like this:

$${\epsilon }_{ij}={\displaystyle \frac{1}{2}}(u_{i,j}+u_{j,i})$$

(4)

In a thermoelastic, isotropic, semiconducting medium, the stress–strain relationship is written as follows:

$${{\sigma }_{ij}}^L=\lambda u_{k,k}{\delta }_{ij}+\mu (u_{i,j}+u_{j,i})-({\beta }_T\mathrm{T}+{\delta }_{n}N){\delta }_{ij}.$$

(5)

Here is an expression for the connection between local and nonlocal theories of stress:

$$\left(1-{\epsilon }^2{\nabla }^2\right){\sigma }_{kl}={\sigma }_{kl}^L$$

(6)

where ${\sigma }_{kl}^L$ represents the Cauchy’s stress tensor at any point of the body, and ${\sigma }_{kl}$ is the nonlocal stress tensor at the reference point. By contrasting the formulas for wave frequencies in the nonlocal model with those in the Born–Karman model of lattice dynamics, the correctness of Equation (6) has been demonstrated, ${\delta }_{ij}$ which is the Kronecker delta. $T(r,t)$ is the temperature, $N(r,t)$ is the carrier density, $u(r,t)$ is the displacement distribution, $r$ indicates the position vector, $D_E$ represents carrier diffusion coefficients, $\rho$ is the density, $\tau$ is the photo-generated carrier lifetime, and $c_e,k$ represent the coefficients of specific heat and thermal conductivity, respectively. $\lambda ,\mu$ are Lame elastic constants, and $E_g$ is the energy gap of the semiconductor parameter. ${\beta }_T=(3\lambda +2\mu ){\alpha }_T$ is the volume thermal expansion. ${\alpha }_T$ is the coefficient of linear thermal expansion. ${\delta }_n=(3\lambda +2\mu )d_n\mathrm{where}{d}_n$ is the coefficient of electronic deformation, $\kappa ={\displaystyle \frac{\partial N_0}{\partial T}}{\displaystyle \frac{T}{\tau }}$ is the coupling parameter for thermal activation, and $N_0$ is the carrier concentration at the equilibrium position. The boundary conditions for the elastic surfaces of the semiconductor $x=\pm 1$ (taken as a rod) under electrical short (closed circuit) and stress loads are isothermal and are governed when the boundary conditions on the surface are thermally insulated.

The relation between heat conduction and dynamical heat takes the form

$$\varphi -T=a{\nabla }^2\varphi$$

(7)

where $a$ > 0 is the two-temperature parameter (Youssef [32]).

The constitutive law of the theory of generalized thermoelasticity takes the following form:

$${\mathsf{\sigma }}_{\mathrm{xx}}=(2\mu +\lambda ){\displaystyle \frac{\partial u}{\partial x}}+\lambda {\displaystyle \frac{\partial w}{\partial z}}-(3\lambda +2\mu )({\alpha }_{T}T+d_{n}N)$$

(8)

We can define the physical quantities in one dimension (1D) using the following expressions:

$$\rho \left(1-{\epsilon }^2{\displaystyle \frac{{\partial }^2}{\partial x^2}}\right)\left({\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}-{\mathsf{\Omega }}^{2}u\right)=(2\mu +\lambda -p){\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-{\beta }_T{\displaystyle \frac{\partial T}{\partial x}}-{\delta }_n{\displaystyle \frac{\partial N}{\partial x}}$$

(9)

$${\displaystyle \frac{\partial N}{\partial t}}=D_E{\displaystyle \frac{{\partial }^{2}N}{\partial x^2}}-{\displaystyle \frac{N}{\tau }}+\kappa T$$

(10)

$$\begin{array}{l}\left[k^{*}(1+{\displaystyle \frac{{{\tau }_{\upsilon }}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}})+k({\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{{{\tau }_{\mathrm{T}}}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha +1}}{\partial t^{\alpha +1}}})\right]\left({\displaystyle \frac{{\partial }^2\phi }{\partial x^2}}\right)\\ =\left(1+{\displaystyle \frac{{{\tau }_q}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}+{\displaystyle \frac{{{\tau }_q}^{2\alpha }}{(2\alpha )!}}{\displaystyle \frac{{\partial }^{2\alpha }}{\partial t^{2\alpha }}}\right)\left(\rho C_e{\displaystyle \frac{{\partial }^{2}T}{\partial t^2}}+{\beta }_T{\mathrm{T}}_0({\displaystyle \frac{{\partial }^{3}u}{\partial x\partial t^2}})\right)+{\displaystyle \frac{E_{g}N}{\tau }}\end{array}$$

(11)

$$\phi -T=a{\displaystyle \frac{{\partial }^2\phi }{\partial x^2}}$$

(12)

The following constitutive equation in 1D takes the form

$${\sigma }_{xx}=(2\mu +\lambda ){\displaystyle \frac{\partial u}{\partial x}}-({\beta }_{T}T+{\delta }_{n}N)=\sigma$$

(13)

3. Mathematical Formulation of the Problem

To make it simpler, new simplified variables are introduced that have no units associated with them.

$$\begin{array}{c}(x^{\prime },u^{\prime })={\displaystyle \frac{(x,u)}{C_T{t}^{*}}},((T^{\prime },{\phi }^{\prime }),N^{\prime })={\displaystyle \frac{({\beta }_T(T,\phi ),{\delta }_{n}N)}{2\mu +\lambda }},{\sigma }^{\prime }={\displaystyle \frac{\sigma }{\mu }},e^{\prime }=e,\left(t^{\prime },{{\tau }^{\prime }}_{\nu },{{\tau }_q}^{\prime }\right)={\displaystyle \frac{\left(t,{\tau }_{\nu },{\tau }_q\right)}{t^{*}}}\\ {\left(e_{0}a\right)}^{\prime }={\displaystyle \frac{e_{0}a}{C_T{t}^{*}}},C_T^2={\displaystyle \frac{(\lambda +2\mu )}{\rho }},C_L^2={\displaystyle \frac{\mu }{\rho }},t^{*}={\displaystyle \frac{k}{\rho C_e{C}_T^2}},{\mathsf{\Omega }}^{\prime }=t^{*}\mathsf{\Omega }\end{array}$$

(14)

In Equations (9)–(13), the dashes are omitted for convenience. Using Equation (14), we define the strain as $e=u_x$ and we get:

$$(\alpha {\nabla }^2-{\displaystyle \frac{{\partial }^2}{\partial t^2}}-{\mathsf{\Omega }}^2)e-{\nabla }^{2}T-{\nabla }^{2}N=0$$

(15)

$$({\nabla }^2-{\alpha }_1-{\alpha }_2{\displaystyle \frac{\partial }{\partial t}})N+{\epsilon }_{3}T=0$$

(16)

$$\left[{\beta }_0(1+{\displaystyle \frac{{{\tau }_{\upsilon }}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}})+({\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{{{\tau }_{\mathrm{T}}}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha +1}}{\partial t^{\alpha +1}}})\right]\left({\displaystyle \frac{{\partial }^{2}T}{\partial x^2}}\right)-\left(1+{\displaystyle \frac{{{\tau }_q}^{\alpha }}{\alpha !}}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}+{\displaystyle \frac{{{\tau }_q}^{2\alpha }}{(2\alpha )!}}{\displaystyle \frac{{\partial }^{2\alpha }}{\partial t^{2\alpha }}}\right)\left({\displaystyle \frac{{\partial }^{2}T}{\partial t^2}}-\left({\beta }_1{\displaystyle \frac{{\partial }^{2}e}{\partial t^2}}\right)\right)-{\beta }_{2}N=0$$

(17)

$$\phi -T=a_1{\nabla }^2\phi$$

(18)

The stress component in one dimension appears in the non-dimensional form in the following way:

$${\mathsf{\sigma }}_{xx}={\beta }_3\left(e-(T+N)\right)=\mathsf{\sigma }$$

(19)

where

$$\begin{array}{c}{\alpha }^{\ast }=1+{\displaystyle \frac{C_T^2{\epsilon }^2}{t^{\ast 2}}},{\alpha }_1={\displaystyle \frac{k{t}^{*}}{D_E\rho \tau C_e}},{\alpha }_2={\displaystyle \frac{k}{D_E\rho C_e}},{\epsilon }_3={\displaystyle \frac{d_{n}k\kappa t^{*}}{{\alpha }_T\rho C_e{D}_E}},{\delta }_n=(2\mu +3\lambda )d_n,\\ t^{*}={\displaystyle \frac{k}{\rho C_e{C}_T^2}},{\beta }_0={\displaystyle \frac{K^{*}}{\rho C_e{C}_T^2}},{\beta }_1={\displaystyle \frac{{{\beta }_T}^2{T}_0}{\rho C_e(2\mu +\lambda )}},{\beta }_2={\displaystyle \frac{E_g{\beta }_T{w}^{*}}{\tau \rho C_e{\delta }_n}},{\beta }^2={\displaystyle \frac{C_T^2}{C_L^2}},{\beta }_3={\displaystyle \frac{2\mu +\lambda }{\mu }},\\ C_T^2={\displaystyle \frac{2\mu +\lambda }{\rho }},C_L^2={\displaystyle \frac{\mu }{\rho }},a_1={\displaystyle \frac{a}{C_T^2{t}^{\ast 2}}}\end{array}$$

Parameter ${\epsilon }_3$ can be called the thermoelectric coupling parameter.

This study integrates several coupled physical fields—thermal, mechanical, electronic, and rotational—within a unified framework to model wave propagation in semiconducting nanostructures. These fields interact as follows:

• Thermal field: Governed by a fractional-order, two-temperature model that separates the thermodynamic and conductive temperatures, capturing microscale thermal inertia and heat transport.
• Mechanical field: Governed by displacement and stress equations accounting for rotation-induced Coriolis and centrifugal forces, affecting phase velocity and energy dissipation.
• Electronic field: Represented by plasma carrier density evolution, influenced by temperature gradients, recombination rates, and diffusion coefficients.
• Nonlocal effects: Introduced through integral operators in the constitutive laws, representing long-range interatomic interactions essential at the nanoscale.
• Thermoelectric coupling: Encapsulated via a coupling parameter, ${\mathsf{\epsilon }}_3$, linking thermal activation with carrier transport and mechanical deformation.

These fields are interdependent. For example, a ramp-type heat source alters the conductive temperature, which in turn modifies the stress and carrier density profiles due to the thermoelectric coupling. Meanwhile, rotational effects introduce asymmetries and dispersion, altering the propagation characteristics of all wave types (P-wave, S-wave, and thermal wave). The two-temperature framework further enriches the model by resolving the divergence between energy transport and entropy production at nanoscale time scales.

To solve the problem analytically, one might consider the following initial conditions that possess homogeneity qualities, which can be expressed as follows:

$$\begin{array}{c}{\left.T(x,t)\right|}_{t=0}={\left.{\displaystyle \frac{\partial T(x,t)}{\partial t}}\right|}_{t=0}=0,{\left.\phi (x,t)\right|}_{t=0}={\left.{\displaystyle \frac{\partial \phi (x,t)}{\partial t}}\right|}_{t=0}=0,{\left.\sigma (x,t)\right|}_{t=0}={\left.{\displaystyle \frac{\partial \sigma (x,t)}{\partial t}}\right|}_{t=0}=0,\\ {\left.N(x,t)\right|}_{t=0}={\left.{\displaystyle \frac{\partial N(x,t)}{\partial t}}\right|}_{t=0}=0,{\left.u(x,t)\right|}_{t=0}={\left.{\displaystyle \frac{\partial u(x,t)}{\partial t}}\right|}_{t=0}=0,{\left.e(x,t)\right|}_{t=0}={\left.{\displaystyle \frac{\partial e(x,t)}{\partial t}}\right|}_{t=0}=0\end{array}$$

(20)

4. Solution of the Problem

Employing the Laplace Transform Method for any function $\Theta (x,t)$ as follows

$$L(\Theta (x,t))=\overline{\Theta }(x,s)={\displaystyle \underset{0}{\overset{\infty }{\int }}\Theta (x,t)\exp (-st)}dt$$

(21)

from (20) into four Equations (15)–(18) yields the following:

$$({\alpha }^{\ast }{D}^2-{\alpha }_3)\overline{e}-D^2\overline{T}-D^2\overline{N}=0$$

(22)

$$(D^2-{\alpha }_4)\overline{N}+{\epsilon }_3\overline{T}=0$$

(23)

$$\left(D^2-D_{\alpha }\right)\overline{T}-C_{\alpha }\overline{e}-E_{\alpha }\overline{N}=0$$

(24)

$$\left(1-a_1{D}^2\right)\overline{\phi }-\overline{T}=0$$

(25)

$${\overline{\mathsf{\sigma }}}_{xx}={\beta }_3\left(\overline{e}-(\overline{T}+\overline{N})\right)$$

(26)

where $D={\displaystyle \frac{d}{dx}}$, ${\alpha }_3=(\alpha +s^2+{\mathsf{\Omega }}^2)$, ${\alpha }_4={\alpha }_1+{\alpha }_{2}s$, $D_{\alpha }={\displaystyle \frac{B_{\alpha }}{A_{\alpha }}}$, $E_{\alpha }={\displaystyle \frac{s^2{\beta }_2}{A_{\alpha }}},$ $C_{\alpha }={\displaystyle \frac{{\beta }_1{B}_{\alpha }}{A_{\alpha }}},$ $A_{\alpha }={\beta }_0(1+s^{\alpha }{\displaystyle \frac{{{\tau }_{\upsilon }}^{\alpha }}{\alpha !}})+(s+s^{\alpha +1}{\displaystyle \frac{{{\tau }_{\mathrm{T}}}^{\alpha }}{\alpha !}})$, and $B_{\alpha }=\left(s^2+s^{\alpha +2}{\displaystyle \frac{{{\tau }_q}^{\alpha }}{\alpha !}}+s^{2\alpha +2}{\displaystyle \frac{{{\tau }_q}^{2\alpha }}{(2\alpha )!}}\right)$.

Eliminating $\overline{T},\overline{N},\overline{\phi },\mathrm{and}\overline{e}$ between Equations (22)–(25) yields

$$D^6-{\Theta }_1{D}^4+{\Theta }_2{D}^2-{\Theta }_3)\left\{\overline{N},\overline{\phi },\overline{T},\overline{e}\right\}(x,s)=0$$

(27)

where

$$\left.\begin{array}{l}{\Theta }_1=-{\displaystyle \frac{1}{{\alpha }^{\ast }}}\left\{\left(-C_{\alpha }-{\alpha }^{\ast }{D}_{\alpha }-{\alpha }_3-{\alpha }^{\ast }{\alpha }_4\right)\right\}\\ {\Theta }_2={\displaystyle \frac{\left\{\left(D_{\alpha }{\alpha }_3+C_{\alpha }{\alpha }_4+{\alpha }^{\ast }{D}_{\alpha }{\alpha }_4+{\alpha }_3{\alpha }_4+C_{\alpha }{\epsilon }_3+{\alpha }^{\ast }{\mathrm{e}}_{\alpha }{\epsilon }_3\right)\right\}}{{\alpha }^{\ast }}},\\ {\Theta }_3=-{\displaystyle \frac{\left\{-D_{\alpha }{\alpha }_3{\alpha }_4-{\mathrm{E}}_{\alpha }{\alpha }_3{\epsilon }_3\right\}}{{\alpha }^{\ast }}},\end{array}\right\}$$

(28)

Using the factorization method, the main ordinary differential equation, Equation (27), was solved as follows.

$$\left(D^2-k_1^2\right)\left(D^2-k_2^2\right)\left(D^2-k_3^2\right)\{\overline{T},\overline{\phi },\overline{e},\overline{N}\}(x,s)=0$$

(29)

where $k_i^2(i=1,2,3)$ represents the roots, which may be taken in the positive real part when $x\to \infty$. The solution of Equation (ODE) (29) takes the following form:

$$\overline{T}(x,s)={\displaystyle \sum _{i=1}^3{D}_i}(s)e^{-k_{i}x}$$

(30)

The other quantities’ solutions can also be stated as

$$\overline{N}(x,s)={\displaystyle \sum _{i=1}^3{D_i}^{\prime }}(s)e^{-k_{i}x}={\displaystyle \sum _{i=1}^3{H}_{1i}{D}_i(s)}{e}^{-k_{i}x}$$

(31)

$$\overline{e}(x,s)={\displaystyle \sum _{i=1}^3{D_i}^{″}}(s)\exp (-k_{i}x)={\displaystyle \sum _{i=1}^3{H}_{2i}{D}_i}(s)\exp (-k_{i}x)$$

(32)

$$\overline{\sigma }(x,s)={\displaystyle \sum _{i=1}^3{D_i}^{‴}}(s)\exp (-k_{i}x)={\displaystyle \sum _{i=1}^3{H}_{3i}{D}_i}(s)\exp (-k_{i}x)$$

(33)

$$\overline{\phi }(x,s)={\displaystyle \sum _{i=1}^3{D_i}^{(4)}}(s)\exp (-k_{i}x)={\displaystyle \sum _{i=1}^3{H}_{4i}{D}_i}(s)\exp (-k_{i}x)$$

(34)

where $D_i,{D_i}^{\prime },{D^{″}}_i,{D_i}^{‴},$ and ${D_i}^{(4)},i=1,2,3$ are parameters depending on parameter $s$. The relationship between $D_i,{D_i}^{\prime },{D^{″}}_i,{D_i}^{‴},$ and ${D_i}^{(4)}$ can be obtained when utilizing the primary Formulas (19)–(23), which describe the subsequent correlation:

$$\begin{array}{c}{H}_{1i}={\displaystyle \frac{-{\epsilon }_3}{{m_i}^2-{\alpha }_4}},H_{2i}={\displaystyle \frac{m_i^2-D_{\alpha }-H_{1i}{\mathrm{e}}_{\alpha }}{C_{\alpha }}},H_{3i}={\beta }_3\left(H_{2i}-(1+H_{1i})\right),\\ H_{4i}=-{\displaystyle \frac{1}{-1+{m_i}^2{a}_1}}\end{array}$$

The above equations provide a solution for Laplace’s main variable transforms in the domain of $D_i(s)$. These parameters can be determined from the given boundary conditions.

5. Boundary Conditions

To specify certain parameters $D_i(s)$, suppose that an elastic semiconductor material is subjected to different mechanical, plasma, and thermal loads on its external surface. In all scenarios, the Laplace transforms are utilized.

(I) The free surface is subjected to thermal shock and acts as the isothermal boundary condition for a thermally isolated system when $x=0$:

$$\overline{T}(0,s)=T_{0}Z(s)$$

(35)

Therefore,

$${\displaystyle \sum _{n=1}^3{D}_i}(s)={\displaystyle \frac{T_0}{s}}$$

(36)

(II) Laplace transformation used to analyze free-surface mechanical normal stress components when $x=0$ results in

$${\overline{\sigma }}_{xx}(0,s)=0$$

(37)

Therefore,

$${\displaystyle \sum _{i=1}^3\left\{B_3\left(H_{2i}-(1+H_{1i})\right)\right\}\left(D_i\right)}=0$$

(38)

(III) When the diffusion of carrier density and the photo-generation during recombination processes are being transported, the plasma boundary condition at the free surface $x=0$ can be expressed differently by using the Laplace transform. Here, the plasma condition takes the following form:

$$\overline{N}(0,s)={\displaystyle \frac{\mathsf{ƛ}}{D_e}}\overline{R}(s)$$

(39)

In contrast, we found this connection:

$${\displaystyle \sum _{i=1}^3{H}_{1i}}{D}_i(x,s)={\displaystyle \frac{\mathsf{ƛ}}{s{D}_e}}$$

(40)

The equations above use symbols $Z(s)$ and $R(s)$ that indicate the Heaviside unit step function, with a chosen constant represented by the symbol $\mathsf{ƛ}$. We can obtain the unknown parameters $D_i$ by solving these equations in terms of the parameters.

For the simulations, the ramp-type thermal input is defined in the time domain as

$$Z(t)=\left\{\begin{array}{ll}Ht,\hfill & 0\le t\le t_r\hfill \\ H{t}_r,\hfill & t>t_r\hfill \end{array}\right.$$

where $\mathrm{H}$ is the heating rate and $\mathrm{t}\mathrm{r}$ is the ramp duration. Its Laplace transform is

$$Z(s)={\displaystyle \frac{H}{s^2}}(1-e^{-s{t}_r})$$

The photo-generation boundary function $\mathrm{R}\left(\mathrm{t}\right)$ is modeled as exponential saturation:

$$R(t)=N_0(1-e^{-\gamma t})\mathrm{With}\mathrm{the}\mathrm{Laplace}\mathrm{transform}:R(s)={\displaystyle \frac{N_0\gamma }{s(s+\gamma )}}$$

It is important to note that the boundary conditions employed in this study are idealized as homogeneous (zero displacement, zero stress, thermally insulated or isothermal), which simplifies the mathematical formulation and facilitates analytical tractability. However, in practical applications—such as laser-irradiated semiconductor wafers, MEMS devices, or photothermal imaging systems—inhomogeneous or mixed boundary conditions (e.g., convective heat loss, applied surface tractions, or time-dependent thermal pulses) are more representative of realistic environments. While the current model captures the fundamental behavior of wave propagation and field interactions under ideal constraints, deviations from real-world setups may arise, particularly near surfaces or interfaces. These differences could manifest in altered amplitude, phase shifts, or localized field enhancements. Future work may extend this model to incorporate more complex and physically relevant boundary conditions, such as Robin-type thermal conditions, nonlinear mechanical constraints, or spatially varying plasma boundary terms, thereby enhancing predictive accuracy and practical applicability.

6. Transforming the Fourier–Laplace Transforms in Reverse

Laplace transform inversion can be used to derive the dimensionless physical fields in the time domain. The Laplace transform in this scenario can be approximated numerically using techniques like the Riemann sum [24].

In the Laplace domain, the inverse of any function $\overline{\Theta }(x,s)$ can be obtained as follows:

$$\Theta (x,t^{\prime })=L^{-1}\{\overline{\Theta }(x,s)\}={\displaystyle \frac{1}{2\pi i}}{\displaystyle {\int }_{n-i\infty }^{n+i\infty }\exp (s{t}^{\prime })}\overline{\Theta }(x,s)ds$$

(41)

In the case of $s=n+i{\rm M}$($n,{\rm M}\in R$), the inverted Equation (38) can be rewritten as

$$\Theta (x,t^{\prime })={\displaystyle \frac{\exp (n{t}^{\prime })}{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\exp (i\beta t)}\overline{\Theta }(x,n+i\beta )d\beta$$

(42)

Using the Fourier series, we expand the function $\Theta (x,t^{\prime })$ in the closed interval $\left[0,2t^{\prime }\right]$ to get the next relationship:

$$\Theta (x,t^{\prime })={\displaystyle \frac{e^{n{t}^{\prime }}}{t^{\prime }}}\left[{\displaystyle \frac{1}{2}}\overline{\Theta }(x,n)+Re{\displaystyle \sum _{k=1}^N\overline{\Theta }(x,n+\frac{ik\pi }{t^{\prime }}){(-1)}^n}\right]$$

(43)

where $i$ and $Re$ represent the imaginary unit and the real part, respectively. In this case, sufficient $N$ can be chosen freely as a large integer and can be selected in the notation $n{t}^{\prime }\approx 4.7$; see Appendix A [24].

7. Numerical Results and Discussion

In this section, we will introduce numerical data to analyze the suggested photo-thermoelasticity model. Temperature, displacement, carrier intensity, and nonlocal thermal stress are all accounted for in this model. In addition, we will contrast our findings with those of earlier studies. The following physical coefficients have been considered for this study, assuming that the main material being examined is silicon (Si). Simulation software, like Mathematica 13.2, is employed to plot physical fields using SI units and symbols. Paraphrased

Table 1. Physical constants of Si, Ge, and Cu materials.

Name (Unit)	Symbol	Si
Lamé’s constants $(\mathrm{N}/{\mathrm{m}}^3)$	$\lambda$, $\mu$	$6.4\times {10}^{10}$, $6.5\times {10}^{10}$
Absolute temperature ($\mathrm{K}$)	$T_0$	$800$
Density $(\mathrm{k}\mathrm{g}/{\mathrm{m}}^3)$	$\rho$	$2330$
The photo-generated carrier lifetime $\left(\mathrm{s}\right)$	$\tau$	$5\times {10}^{-5}$
The energy gap ($\mathrm{e}\mathrm{V})$	$E_g$	$1.11$
The carrier diffusion coefficient $({\mathrm{m}}^2/\mathrm{s})$	$D_E$	$2.5\times {10}^{-3}$
The coefficient of linear thermal expansion $\left({\mathrm{K}}^{-1}\right)$	${\alpha }_t$	$4.14\times {10}^{-6}$
The coefficient of electronic deformation $\left({\mathrm{m}}^3\right)$	$d_n$	$-9\times {10}^{-31}$
The thermal conductivity of the sample $\left(\mathrm{W}{\mathrm{m}}^{-1}{\mathrm{K}}^{-1}\right)$	$k$	$150$
Specific heat at constant strain $\left({\displaystyle \frac{\mathrm{J}}{\mathrm{k}\mathrm{g}\mathrm{K}}}\right)$	$C_e$	$695$
The recombination velocities $({\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}$)	$s$	$2$

displays the physical constants specific to semiconductor materials, including silicon (Si), germanium (Ge), and copper, as referred to in the given references [25,26,27,28].

7.1. The Influence of the Thermoelectric Coupling Parameter

Figure 1 explores the influence of varying the thermoelectric coupling parameter ${\mathsf{\epsilon }}_3$, which appears in the constitutive relation linking thermal, elastic, and electronic fields. Physically, ${\mathsf{\epsilon }}_3$ models how heat-induced excitation generates or modulates electronic carriers. Temperature ($\mathrm{T}$) shows a significant rise in peak magnitude with more negative ε₃ values. This suggests that increased coupling enhances energy conversion from heat to carrier motion, thereby raising internal thermal energy. Carrier density ($\mathrm{N}$) also peaks higher and decays more slowly, indicating prolonged plasma activity due to stronger electron–phonon interactions. Displacement ($\mathrm{u}$) exhibits more oscillations but with increasing attenuation, highlighting greater internal damping induced by stronger thermoelectric feedback. Stress ($\mathsf{\sigma }$) distributions become broader and less sharp, with small phase delays. This reflects additional strain caused by thermally activated carriers. This behavior underscores the essential role of ε₃ in photothermal systems, where light or heat generates carriers and impacts mechanical behavior. In practical semiconductor devices, this governs thermoelastic actuation, optoelectronic conversion, and MEMS heat sensors.

7.2. Influence of Nonlocal Parameter

Figure 2 highlights how nonlocal effects—characterized by parameter ε—modify field behavior. Nonlocality arises due to long-range interactions, modeled here by integral operators in the stress–strain relationships. All fields (T, u, N, and σ) show amplitude reduction as ε increases. Temperature (T) curves flatten out, indicating heat diffusion is smoothed spatially rather than being steeply localized. Displacement (u) and stress (σ) show damped oscillations with smoother wavefronts, demonstrating the suppression of sharp mechanical transitions. Carrier density (N) becomes more uniform across space, as long-range interactions reduce spatial variance. Physically, this behavior is consistent with nanoscale materials, where classical local theories break down, and atomistic interactions affect heat and momentum transfer over extended domains. This has relevance in nanoelectronics, graphene composites, and heat-conductive polymers.

7.3. Influence of Rotation

Here, the medium is subjected to rotation with angular velocity Ω = 5. The rotational effects are introduced through the Coriolis and centrifugal terms in the equations of motion. Temperature (T) waves are delayed and broadened due to Coriolis-induced transport distortion, suggesting reduced effective diffusivity. Displacement (u) exhibits a phase shift and reduced amplitude due to inertial resistance from rotation. Carrier density (N) shows a flatter peak, indicating centrifugal dispersion of carriers. Stress (σ) distributions become asymmetric, with wave crests distorted by rotational momentum (Figure 3). These behaviors confirm that rotation introduces gyroscopic effects, altering wave speed and directionality. This is critical for rotating microdevices, gyroscopes, and disk-based thermal storage systems, where angular momentum affects thermal and elastic performance.

7.4. Influence of Two-Temperature Theory

The two-temperature theory (TTM) introduces decoupling between conductive temperature (φ) and thermodynamic temperature (T) (Figure 4). Parameter a₁ governs the rate of energy exchange between them. As a₁ increases, a larger gap forms between φ and T. This reflects the delay in thermal energy flow, especially under rapid heating. Stress (σ) and displacement (u) are highly sensitive to this divergence, showing amplified values due to delayed feedback between temperature and deformation. Carrier density (N) is moderately affected, as photo-generation is governed by φ, but recombination dynamics depend on T. This behavior is especially important in ultrafast laser heating, photothermal imaging, and optical switching, where heat carriers (phonons and electrons) operate on different time scales, making TTM indispensable.

7.5. Three-Dimensional Graphs

The final Figure 5a,b present three-dimensional plots of the physical fields as functions of space and time, under the effect of rotation (Ω = 5). The temperature (T) surface shows curved wavefronts, distorted by rotation-induced dispersion. Carrier density (N) exhibits non-monotonic decay, with initial sharp peaks followed by recombination flattening. Displacement (u) and stress (σ) exhibit saddle-like structures, where curvature results from Coriolis-induced phase rotation. These 3D plots validate the efficacy of Laplace–Fourier inversion in resolving field transients across multiple coupled domains. They also demonstrate the combined effects of rotation, nonlocality, and TTM on multi-physics wave behavior.

While no direct experimental datasets exist for the combined configuration studied here, our results are qualitatively consistent with previous findings. For example, Lotfy et al. [9] observed rotational-induced phase shifts and energy dissipation in two-temperature media, and Abo-Dahab et al. [20] confirmed non-uniform carrier excitation under ramp-type photothermal heating. Our model generalizes these individual findings into a unified system, producing similar wave dispersion and damping behavior. These comparisons reinforce the validity of our extended formulation. Although the present model does not explicitly include micropolar rotations, the nonlocal elasticity and fractional-order heat conduction inherently capture microstructural interaction effects, which influence wavefront smoothness and energy dispersion. These features act similarly to micropolar terms by regularizing stress gradients and preventing singularities at discontinuities. The model supports both harmonic wave propagation (shown in Figure 1, Figure 2, Figure 3 and Figure 4) and the suppression of strong discontinuities, thus offering insight into the propagation regularities of both sharp and smooth wavefronts in advanced thermoelastic media.

In general, Figure 1 and Figure 2 collectively illustrate how thermoelectric coupling (${\mathsf{\epsilon }}_3$) and nonlocality (ε) influence the physical response of the medium. While Figure 1 highlights the amplification of thermal and carrier responses due to stronger thermoelectric feedback, Figure 2 demonstrates how increasing nonlocal effects act to smooth and attenuate these sharp responses revealing a competing interaction between energy concentration and spatial diffusion mechanisms.

Extending this analysis, Figure 3 focuses on the effect of mechanical rotation (Ω). Compared to previous figures, the thermal and mechanical fields now exhibit additional phase lags and directional asymmetry due to Coriolis forces. This shift in waveform characteristics complements the behaviors seen in Figure 1 and Figure 2, confirming that rotational effects further modulate the energy distribution initiated by thermal and plasma excitations. Figure 4 turns attention to the influence of the two-temperature parameter (${\mathrm{a}}_1$). When compared to Figure 1, Figure 2 and Figure 3, the two-temperature mechanism appears to amplify energy storage while decoupling heat conduction from the mechanical response, an effect critical in ultrafast thermal systems. To synthesize these spatial and temporal dynamics, Figure 5 presents contour plots of all four physical fields under simultaneous effects of rotation and coupling. These visuals display the combined wave dispersion, gradient smoothing, and delayed field evolution, offering a comprehensive spatial–temporal picture of the system behavior under multi-physical excitation.

8. Conclusions

This study comprehensively investigates the influence of rotation, nonlocal effects, and thermoelectric coupling on wave propagation in semiconductor nanostructures under a two-temperature thermoelastic framework, employing a fractional-order ramp-type heat source. The analytical and numerical results reveal that rotation (Ω) significantly alters wave characteristics through Coriolis and centrifugal forces, introducing phase shifts and dispersion in displacement, stress, and thermal fields, which are critical for applications in rotating MEMS/NEMS devices. The thermoelectric coupling parameter (ε₃) amplifies thermoelastic–plasma interactions, leading to enhanced energy dissipation and distinct peaks in temperature and carrier density distributions, particularly in materials like silicon. Nonlocal effects dampen high-frequency oscillations, validating the necessity of nonlocal theory for accurate nanoscale modeling, where classical Fourier-based approaches fall short. The two-temperature model (TTM) further resolves the gap between conductive and thermodynamic temperatures, providing a more precise description of thermal inertia in ultrafast heating scenarios, essential for laser-based and photothermal applications. The 3D visualizations of field distributions underscore the complex interplay of these factors, demonstrating how rotational dispersion and nonlocal damping shape wavefronts in transient regimes. These findings advance the understanding of multi-physical interactions in semiconductor nanostructures, offering practical insights for optimizing thermal management, wave control, and device performance in microelectronics, optoelectronics, and nanoscale energy systems. Future work could extend this model to anisotropic or functionally graded materials and experimental validation to further refine predictive capabilities for next-generation semiconductor technologies.