The Effects of the Weak Allee Effect and Disease on the Dynamics of a Predator–Prey System: Stability and Bifurcation Properties
Abstract
1. Introduction
2. Mathematical Model Formulation
- Assuming that there is no predator in the system, the dynamics of the prey population is described by the logistic equation, i.e., , where r is the intrinsic growth rate and K is the environmental carrying capacity.
- In the presence of disease, we divide the prey population into two subclasses and use S and I to represent susceptible prey and infected prey, respectively.
- The disease transmission is confined to the prey population. Infected prey dies before attaining reproductive capability and cannot recover from the infection.
- The predator only captures the diseased prey, because the activity of the diseased prey may be weakened, and it is easy to be captured.
3. Dynamics of the Model
3.1. Equilibrium Existence
- Trivial equilibrium , which always exists.
- Axial equilibrium , which always exists.
- Planar equilibrium exists when , with its components as , .
- a.
- Model (1) does not have a coexistence equilibrium if and only if one of the following conditions holds:
- (a)
- ;
- (b)
- and ;
- b.
- If conditionsand hold, thenhas exactly one real positive root. Therefore, the model has one coexistence equilibrium .
- c.
- If conditions and are satisfied, then has two real positive roots. Therefore, the model has two coexistence equilibria and .
3.2. Local Stability Analysis
- a.
- is a saddle node.
- b.
- is locally asymptotically stable if . Otherwise, it is unstable.
- c.
- If and are satisfied, then is locally asymptotically stable; conversely, it is unstable.
- a.
- If holds, then the unique coexistence equilibrium is stable; otherwise, it is unstable.
- b.
- If holds, then the coexistence equilibria and are both locally asymptotically stable.
- c.
- If holds, then the coexistence equilibrium is stable, while remains unstable.
- Case (1)
- Case (2)
3.3. Bifurcation Analysis
3.3.1. Transcritical Bifurcation
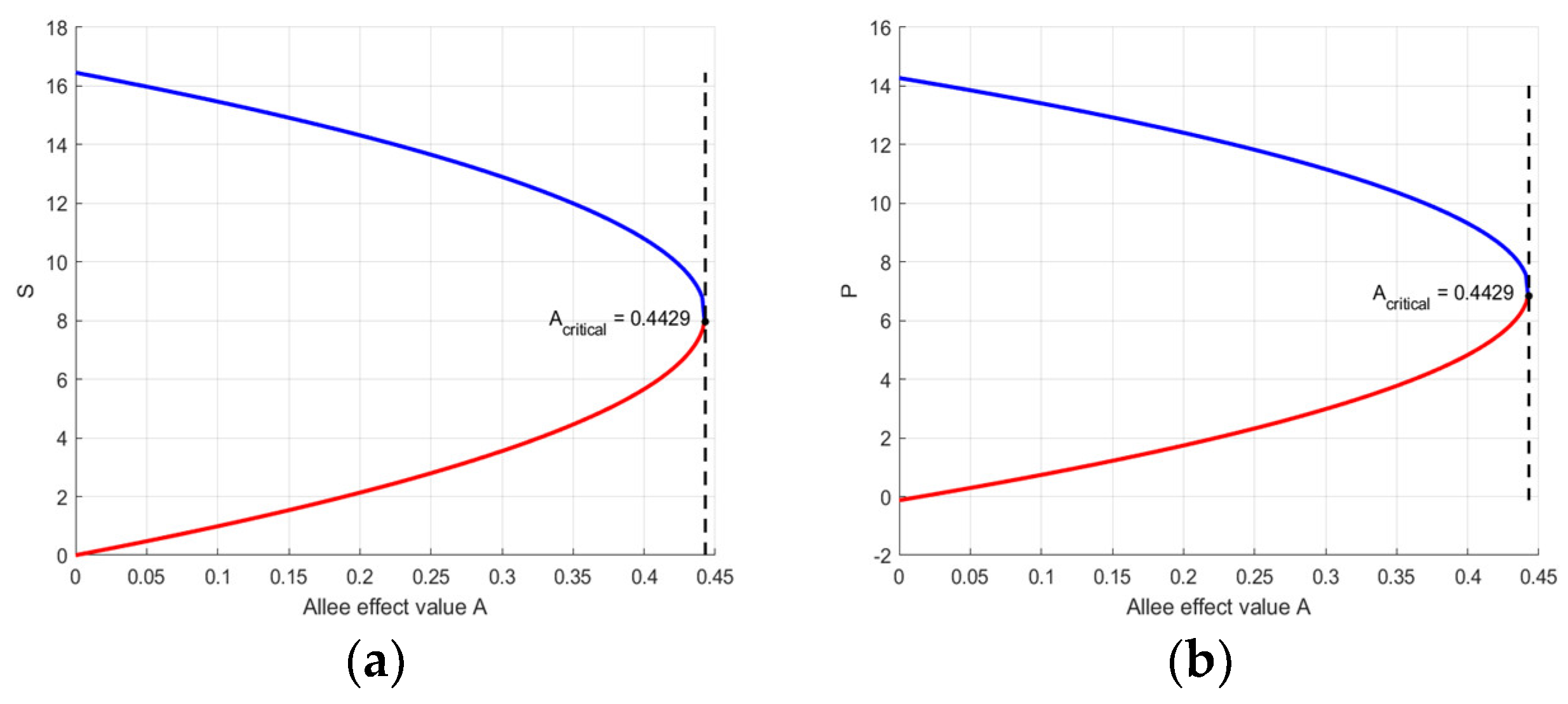
3.3.2. Saddle-Node Bifurcation
3.3.3. Hopf Bifurcation
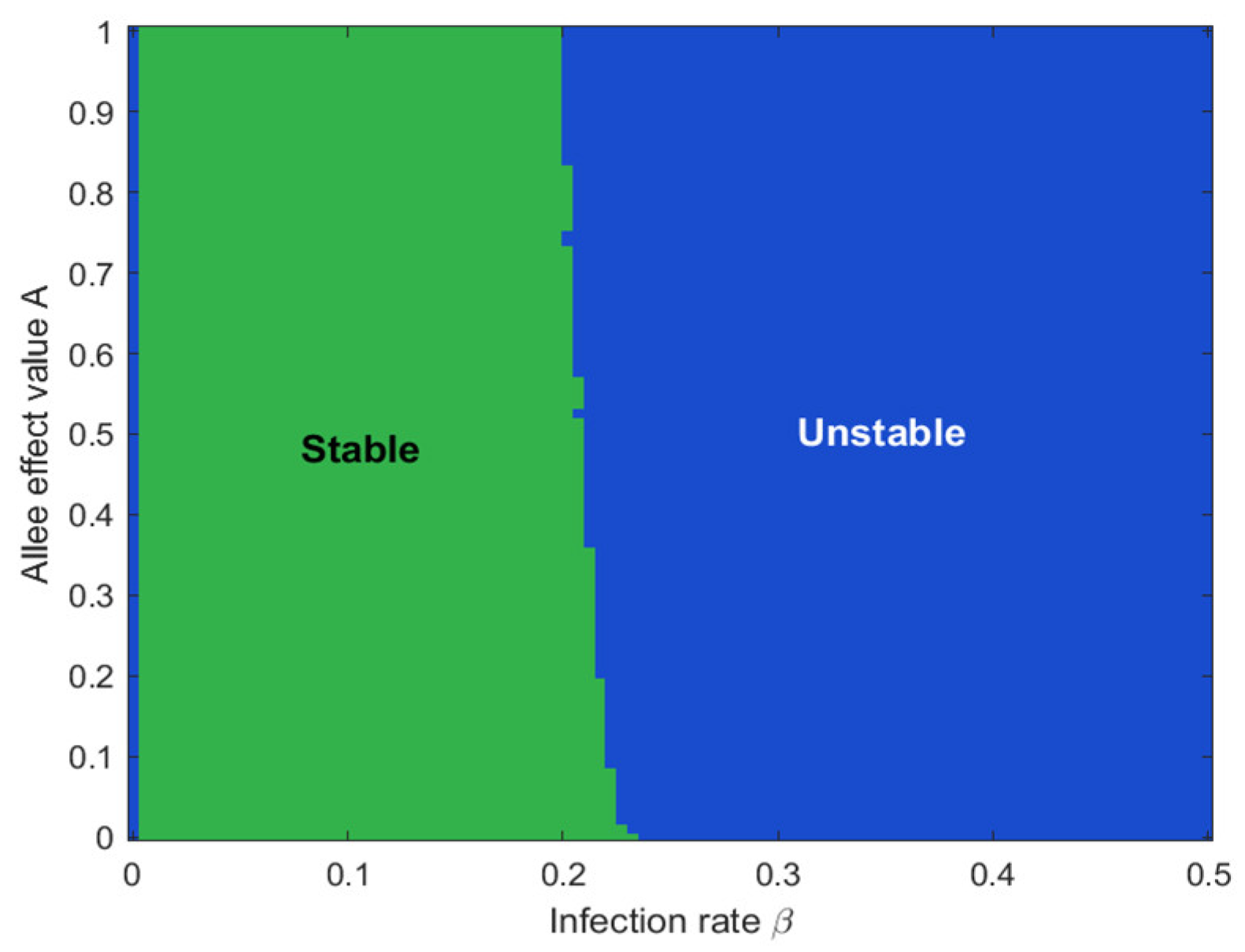
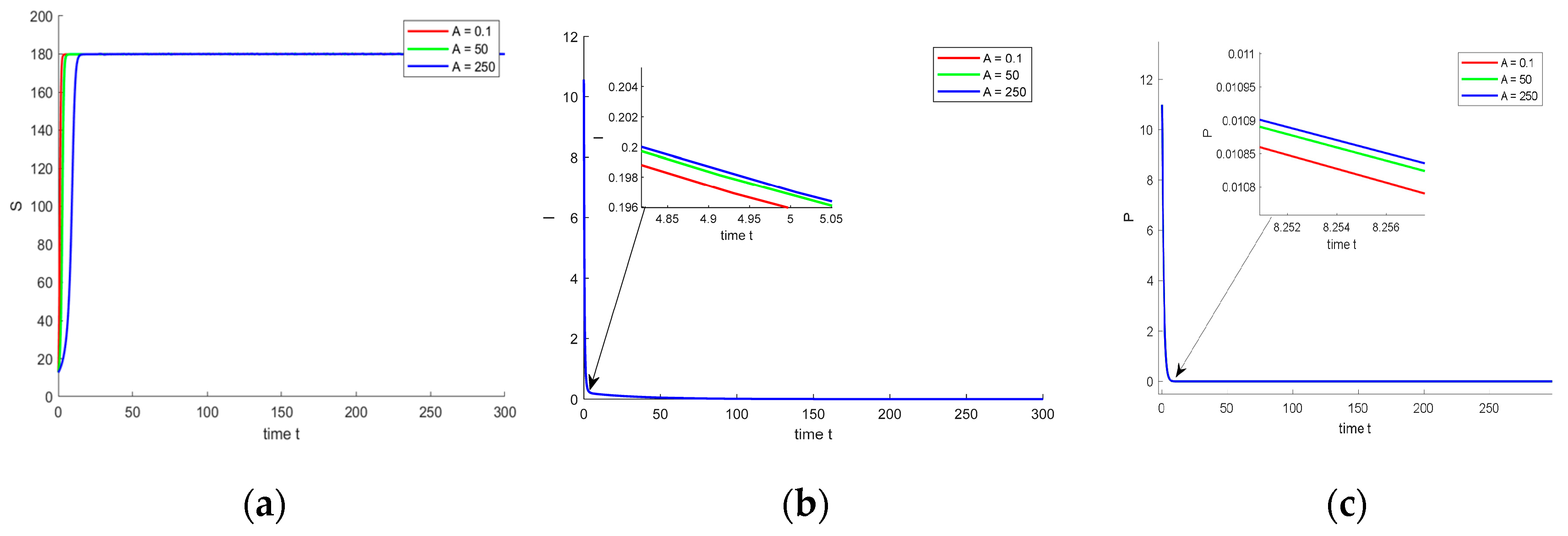
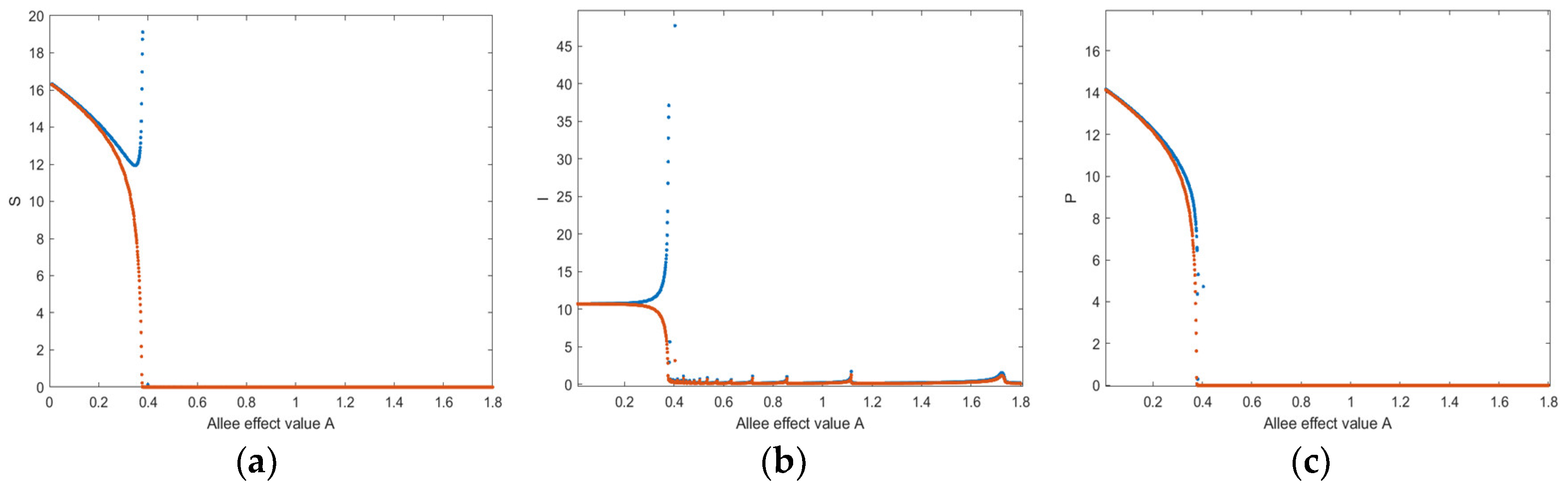
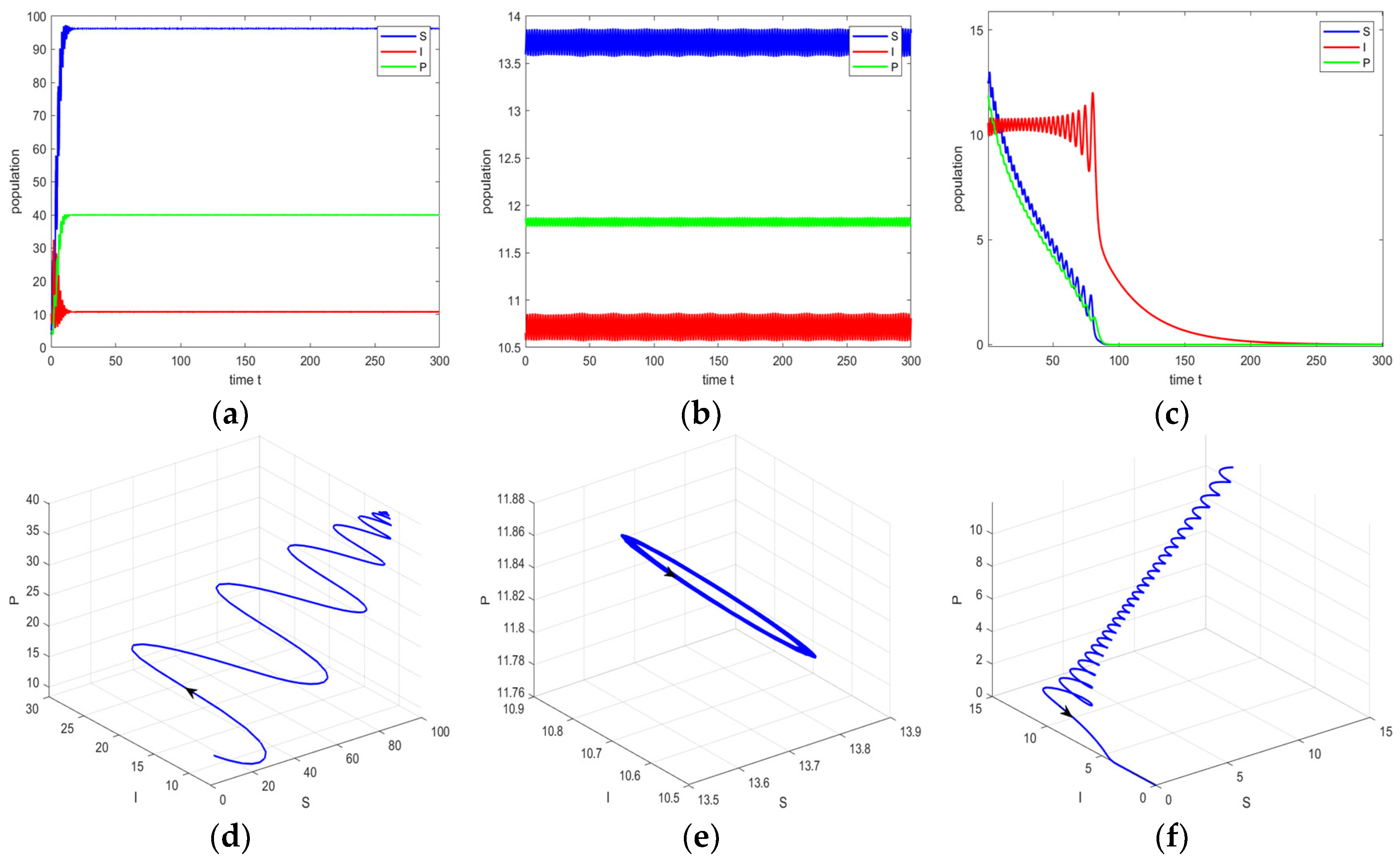
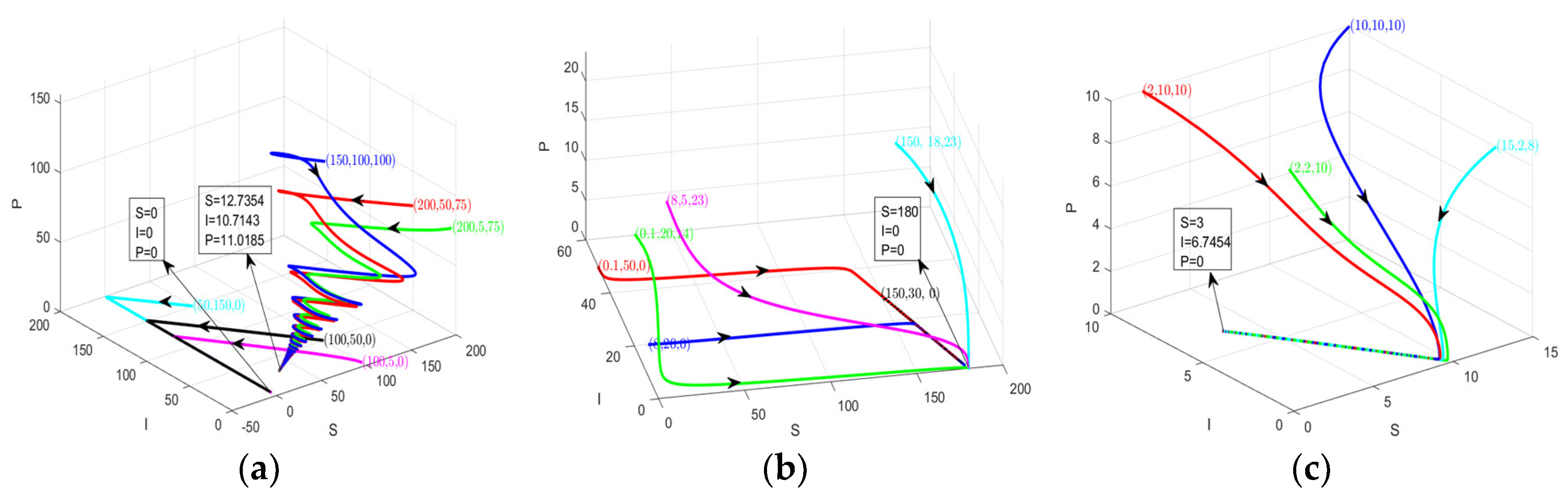
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, C. Protecting Endangered Animal Species. Animals 2024, 14, 2644. [Google Scholar] [CrossRef]
- Lotka, A.J. Elements of Physical Biology; Williams & Wilkins: Baltimore, MD, USA, 1925. [Google Scholar]
- Lotka, A.J. Fluctuations in the abundance of a species considered mathematically. Nature 1927, 119, 12. [Google Scholar] [CrossRef]
- Hadeler, K.P.; Freedman, H.I. Predator–prey population with parasite infection. J. Math. Biol. 1989, 27, 609–631. [Google Scholar] [CrossRef] [PubMed]
- Venturino, E. Epidemics in predator-prey models: Disease in the predators. Math. Med. Biol. 2002, 19, 185–205. [Google Scholar] [CrossRef]
- May, R.M.; Anderson, R.M. Population biology of infectious diseases: Part II. Nature 1979, 280, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Allee, W.C. Animal Aggregations: A Study in General Sociology; University of Chicago Press: Chicago, IL, USA, 1931. [Google Scholar]
- Wei, C.; Chen, L. Periodic solution and heteroclinic bifurcation in a predator–prey system with Allee effect and impulsive harvesting. Nonlinear Dyn. 2014, 76, 1109–1117. [Google Scholar] [CrossRef]
- Biswas, S.; Sasmal, S.K.; Samanta, S.; Saifuddin, M.; Pal, N.; Chattopadhyay, J. Optimal harvesting and complex dynamics in a delayed eco-epidemiological model with weak Allee effects. Nonlinear Dyn. 2017, 87, 1553–1573. [Google Scholar] [CrossRef]
- Samanta, S.; Sen, P. Multistability and Chaos in the Eco-epidemiological System with Allee Effect. Differ. Equ. Dyn. Syst. 2024, 33, 1–24. [Google Scholar] [CrossRef]
- Shaikh, A.A.; Das, H. An eco-epidemic predator–prey model with Allee effect in prey. Int. J. Bifurc. Chaos 2020, 30, 2050194. [Google Scholar] [CrossRef]
- Ye, Y.; Liu, H.; Wei, Y.M.; Ma, M.; Zhang, K. Dynamic study of a predator-prey model with weak Allee effect and delay. Adv. Math. Phys. 2019, 2019, 7296461. [Google Scholar] [CrossRef]
- Li, D.; Liu, H.; Zhang, H.; Ma, M.; Ye, Y.; Wei, Y.M. Bifurcation Analysis in a Predator-Prey Model with an Allee Effect and a Delayed Mechanism. Acta Math. Sci. 2023, 43, 1415–1438. [Google Scholar] [CrossRef]
- Celik, C.; Duman, O. Allee effect in a discrete-time predator–prey system. Chaos Solitons Fractals 2009, 40, 1956–1962. [Google Scholar] [CrossRef]
- Javaid, Y.; Jawad, S.; Ahmed, R.; Ali, A.H.; Rashwani, B. Dynamic complexity of a discretized predator-prey system with Allee effect and herd behaviour. Appl. Math. Sci. Eng. 2024, 32, 2420953. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z.; Li, Z. The Impact of Allee Effect on a Leslie–Gower Predator–Prey Model with Hunting Cooperation. Qual. Theory Dyn. Syst. 2024, 23, 88. [Google Scholar] [CrossRef]
- Din, Q. Controlling chaos in a discrete-time prey-predator model with Allee effects. Int. J. Dyn. Control 2018, 6, 858–872. [Google Scholar] [CrossRef]
- Berec, L.; Angulo, E.; Courchamp, F. Multiple Allee effects and population management. Trends Ecol. Evol. 2007, 22, 185–191. [Google Scholar] [CrossRef]
- Møller, A.P.; Legendre, S. Allee effect, sexual selection and demographic stochasticity. Oikos 2001, 92, 27–34. [Google Scholar] [CrossRef]
- Courchamp, F.; Macdonald, D.W. Crucial importance of pack size in the African wild dog Lycaon pictus. In Animal Conservation Forum; Cambridge University Press: Cambridge, IL, USA, 2001; Volume 4, pp. 169–174. [Google Scholar]
- Avilés, L.; Tufino, P. Colony size and individual fitness in the social spider Anelosimus eximius. Am. Nat. 1998, 152, 403–418. [Google Scholar] [CrossRef][Green Version]
- Mooring, M.S.; Fitzpatrick, T.A.; Nishihira, T.T.; Reisig, D.D. Vigilance, predation risk, and the Allee effect in desert bighorn sheep. J. Wildl. Manag. 2004, 68, 519–532. [Google Scholar] [CrossRef]
- Courchamp, F.; Berec, L.; Gascoigne, J. Allee Effects in Ecology and Conservation; OUP Oxford: Oxford, UK, 2008. [Google Scholar]
- Gascoigne, J.; Lipcius, R.N. Allee effects in marine systems. Mar. Ecol. Prog. Ser. 2004, 269, 49–59. [Google Scholar] [CrossRef]
- Berec, L. Mate search and mate-finding Allee effect: On modeling mating in sex-structured population models. Theor. Ecol. 2018, 11, 225–244. [Google Scholar] [CrossRef]
- Wang, L.; Qiu, Z.; Feng, T.; Kang, Y. An eco-epidemiological model with social predation subject to a component Allee effect. Appl. Math. Model. 2022, 101, 111–131. [Google Scholar] [CrossRef]
- Burrows, R.; Hofer, H.; East, M.L. Population dynamics, intervention and survival in African wild dogs (Lycaon pictus). Proc. R. Soc. Lond. Ser. B Biol. Sci. 1995, 262, 235–245. [Google Scholar]
- Courchamp, F.; Clutton-Brock, T.; Grenfell, B. Multipack dynamics and the Allee effect in the African wild dog, Lycaon pictus. In Animal Conservation Forum; Cambridge University Press: Cambridge, IL, USA, 2000; Volume 3, pp. 277–285. [Google Scholar]
- Gabera, T.; Widowati, R.H. The impact of ecological mechanisms on stability in an eco-epidemiological model: Allee effect and prey refuge. Comput. Res. Model. 2025, 17, 139–169. [Google Scholar]
- Angulo, E.; Roemer, G.W.; Berec, L.; Gascoigne, J.; Courchamp, F. Double Allee effects and extinction in the island fox. Conserv. Biol. 2007, 21, 1082–1091. [Google Scholar] [CrossRef]
- Clifford, D.L.; Mazet, J.A.K.; Dubovi, E.J.; Garcelon, D.K.; Coonan, T.J.; Conrad, P.A.; Munson, L. Pathogen exposure in endangered island fox (Urocyon littoralis) populations: Implications for conservation management. Biol. Conserv. 2006, 131, 230–243. [Google Scholar] [CrossRef]
- Saifuddin, M.; Biswas, S.; Samanta, S.; Sarkar, S.; Chattopadhyay, J. Complex dynamics of an eco-epidemiological model with different competition coefficients and weak Allee in the predator. Chaos Solitons Fractals 2016, 91, 270–285. [Google Scholar] [CrossRef]
- Sasmal, S.K. Population dynamics with multiple Allee effects induced by fear factors—A mathematical study on prey-predator interactions. Appl. Math. Model. 2018, 64, 1–14. [Google Scholar] [CrossRef]
- Kumar, B.; Sinha, R.K. Dynamics of an eco-epidemic model with Allee effect in prey and disease in predator. Comput. Math. Biophys. 2023, 11, 20230108. [Google Scholar] [CrossRef]
- Ghosh, S.; Mukherjee, C.; Panigrahi, G.; Biswas, S. Dynamics of alternative food and allee effect in an eco-epidemiological system with disease in predator. Nonlinear Stud. 2023, 30, 1025. [Google Scholar]
- Nath, B.; Kumar, V.; Kumari, N.; Pada Das, K.; Maiti, S. A study of chaos and its possible control in an eco-epidemiological model with alternative food source in predator and weak allee effect in prey species. Nonlinear Stud. 2020, 27, 725. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Liu, H.; Ye, J.; Ma, G.; Wei, Y. The Effects of the Weak Allee Effect and Disease on the Dynamics of a Predator–Prey System: Stability and Bifurcation Properties. Axioms 2025, 14, 531. https://doi.org/10.3390/axioms14070531
Dong Y, Liu H, Ye J, Ma G, Wei Y. The Effects of the Weak Allee Effect and Disease on the Dynamics of a Predator–Prey System: Stability and Bifurcation Properties. Axioms. 2025; 14(7):531. https://doi.org/10.3390/axioms14070531
Chicago/Turabian StyleDong, Yurong, Hua Liu, Jianhua Ye, Gang Ma, and Yumei Wei. 2025. "The Effects of the Weak Allee Effect and Disease on the Dynamics of a Predator–Prey System: Stability and Bifurcation Properties" Axioms 14, no. 7: 531. https://doi.org/10.3390/axioms14070531
APA StyleDong, Y., Liu, H., Ye, J., Ma, G., & Wei, Y. (2025). The Effects of the Weak Allee Effect and Disease on the Dynamics of a Predator–Prey System: Stability and Bifurcation Properties. Axioms, 14(7), 531. https://doi.org/10.3390/axioms14070531





