RegCGAN: Resampling with Regularized CGAN for Imbalanced Big Data Problem

Abstract

We consider the imbalanced data problem involving a new class of resampling-based models for classification. These models are variants of the conditional generative adversarial networks. An entropy regularization approach (RegCGAN) is employed to implement the corresponding imbalanced data learning. Its basic framework is introduced. Theoretical and simulation-based analyses are performed to demonstrate the existence and uniqueness of RegCGAN’s equilibrium point, and RegCGAN has excellent minority class prediction ability. We apply the results to two synthetically constructed and a real imbalanced dataset.

1. Introduction

Extensive array of practical tasks, from credit card fraud detection to bioinformatics, face the persistent challenge of imbalanced class distributions. Standard learning algorithms often perform poorly on imbalanced large-scale datasets, as they tend to prioritize majority class accuracy to minimize overall training error. This results in a noticeable decline in accuracy, most significantly for the minority class. In real-world applications, misclassifying minority class samples often incurs greater costs than errors related to majority instances. Thus, imbalance-handling techniques focus on improving minority class accuracy to boost model performance in skewed datasets. Various approaches to handling class imbalance have been identified in the literature [1], where artificial data can be directly generated by applying generative models that learn the distribution of the minority class. Generative adversarial networks (GANs) represent a novel class of generative models that leverage neural networks to learn data distributions [2], particularly in synthesizing photorealistic images [3,4,5,6] and learning meaningful data representations [7,8,9], which has led to their widespread adoption across various domains [9,10,11,12,13].

The GAN architecture is modeled as a minimax game involving two players, where the generator G transforms random noise z into fake data, and the discriminator D distinguishes between real and synthetic inputs. The generator attempts to produce outputs that the discriminator cannot distinguish from real data, and this competition is formally defined as follows:

$$\underset{G}{\min }\underset{D}{\max }U(G,D)=E_{x\sim f\left(x\right)}[lnD\left(x\right)]+E_{z\sim f_z\left(z\right)}[ln(1-D\left(G\left(z\right)\right)].$$

(1)

Here, $f\left(x\right)$ refers to the true data distribution, and $f_z\left(z\right)$ corresponds to the prior over the noise variable z. From a theoretical perspective, this adversarial setup between the generator and discriminator is adequate for enabling unsupervised learning. Under the assumption of nonparametric models, once equilibrium is achieved, the distribution generated by G aligns with that of the real data.

Although unsupervised GANs show great potential, the learned representations often underperform in downstream tasks such as classification and disentangled conditional generation, which are highly relevant in practice [14,15,16,17,18,19,20]. Unsupervised deep generative models typically yield fewer discriminative representations than those learned by supervised DNNs, leading to suboptimal predictive performance [21]. In addition, learning disentangled representations that correspond to interpretable physical factors and generating data samples conditioned on these factors remains a difficult challenge in unsupervised settings and largely relies on model inductive biases [22].

One intuitive approach to overcome these limitations is to introduce label information into the GAN framework [23,24,25,26,27,28]. Shrivastava et al. [29] trained a conditional GAN on unlabeled data to generate alternative versions of given real images. Conditional GANs (cGANs) extend the original GAN framework by incorporating external information into the generator’s input during training. Douzas and Bacao [30] applied cGANs to binary-class imbalanced datasets, where the conditioning information was provided by the class labels.

In general, GANs have demonstrated effectiveness not only in generating realistic samples but also in semi-supervised learning (SSL). Within the same two-player game framework, CatGAN [24] extends the original GAN by incorporating a classification–discriminative network and a novel objective function. However, existing GAN-based approaches for SSL face two main challenges: (1) The generator and discriminator (which also serves as a classifier) often fail to reach an optimal balance simultaneously. (2) The generator lacks the ability to control the semantic content of the generated samples.

According to [31], these challenges stem from the inherent limitations of a two-player architecture, where the discriminator is required to perform two conflicting roles—distinguishing fake samples and predicting class labels. Regarding challenge (2), disentangling meaningful factors (such as object labels) from latent representations with limited supervision remains a fundamental issue in SSL.

To tackle these issues, ref. [31] introduced a versatile game-theoretic model for joint classification and conditional generation tasks. Their model introduces three networks and explicitly considers a real data-label joint distribution and two conditional distributions output by the networks. This multi-network setup allows for better control over both classification and generation tasks.

It is important to note, however, that such SSL-oriented network architectures are not directly applicable to our problem, as they typically assume a balanced class distribution across categories. This paper targets the analysis and processing of imbalanced big data. We aim to develop novel resampling-based inference methods and theoretical frameworks grounded in deep learning, thereby offering new statistical support for both the advancement of big data technologies and their practical applications across industries.

In Section 2, we first describe a regularized CGAN model, as well as the generative resampling approach. Moreover, we provide the theoretical analysis of RegCGAN under nonparametric assumptions. Section 3 reviews the existing literature relevant to RegCGAN. In Section 4, we describe the applications of the RegCGAN to a real SVHN dataset and the synthetically imbalanced variants of well-refined datasets, CIFAR-10 and CIFAR-100. Finally, Section 5 concludes the paper by summarizing the key findings and outlining possible avenues for future work.

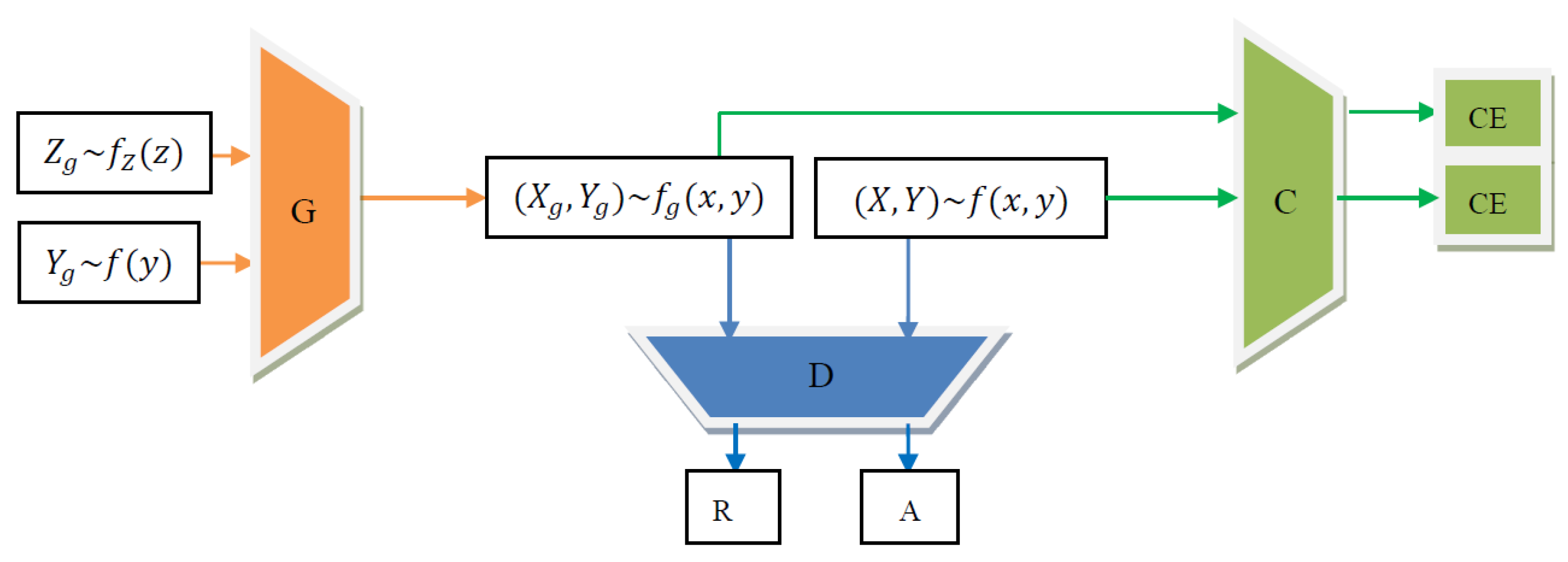
2. Methodology

In this section, we build upon the main model by combining the conditional generative adversarial network (CGAN) framework by incorporating a cross-entropy loss term, resulting in a classification-oriented network called RegCGAN (regularized CGAN). The model addresses the shortcomings of traditional generative methods on imbalanced data by directly optimizing classification performance.

2.1. Resampling Model for Imbalanced Data

RegCGAN is capable of fully and effectively utilizing all available information in imbalanced big data while addressing both theoretical and practical challenges. Specifically, we investigate the convergence properties of the generator and classifier in this newly proposed resampling-based model, as well as the robustness of the training algorithm and its applicability in real-world scenarios.

The architecture of the proposed model is as follows: RegCGAN is composed of three core modules: $\left(a\right)$ A classifier C serves as the primary objective of the model. It approximates the conditional distribution $f_c\left(y\right|x)\approx f\left(y\right|x)$, aiming to optimize classification performance. $\left(b\right)$ A generator G conditioned on class labels approximates the conditional distribution $f_g\left(y\right|x)\approx f\left(y\right|x)$ from the complementary direction. By generating auxiliary samples, it helps mitigate the class imbalance problem. $\left(c\right)$ A discriminator D determines whether a data pair $(x,y)$ comes from the real joint distribution $f(x,y)$ or is generated synthetically.

RegCGAN aims to attain distributional alignment by guiding the generator and classifier to produce the distribution that matches the real data distribution. This alignment allows the model to effectively overcome the limitations posed by imbalanced datasets.

More specifically, we train the generator with the dual guidance of both the classifier—driven by prediction accuracy—and the discriminator. This approach ensures that the generated samples are not only realistic but also beneficial for the classification task. Under the model architecture illustrated in Figure 1, we consider the following utility function:

$$\begin{array}{cc}\hfill {\displaystyle \underset{C,G}{\min }}{\displaystyle \underset{D}{\max }}U(C,G,D)& =E_{(x,y)\sim f(x,y)}[lnD(x,y)]+E_{(z,y)\sim f_Z\left(z\right)f\left(y\right)}[ln(1-D(G(y,z),y))]\hfill \\ & +E_{(x,y)\sim f(x,y)}[-ln{f}_c\left(y\right|x)]+\alpha E_{(z,y)\sim f_Z\left(z\right)f\left(y\right)}[-ln{f}_c\left(y\right|G(y,z))]\hfill \\ & =E_{(x,y)\sim f(x,y)}[lnD(x,y)]+E_{(x,y)\sim f_g(x,y)}[ln(1-D(x,y))]\hfill \\ & +E_{(x,y)\sim f(x,y)}[-ln{f}_c\left(y\right|x)]+\alpha E_{(x,y)\sim f_g(x,y)}[-ln{f}_c\left(y\right|x)]\hfill \end{array}$$

(2)

where the sum of the first two terms corresponds to the utility function of the standard CGAN, denoted as follows:

$$V(G,D)=E_{(x,y)\sim f(x,y)}[lnD(x,y)]+E_{(x,y)\sim f_g(x,y)}[ln(1-D(x,y))]$$

(3)

Among the latter two terms, the first is denoted as $L_C=E_{(x,y)\sim f(x,y)}[-ln{f}_c\left(y\right|x)]$, representing the cross-entropy loss of the classifier C on real data. The second is denoted as $L_G=E_{(x,y)\sim f_g(x,y)}[-ln{f}_c\left(y\right|x)]$, which corresponds to the cross-entropy loss of the classifier C on the generated data. We fixed the entropy regularization coefficient $\alpha \in (0,1)$ at $1/2$ to focus on the balanced setting throughout this study. In the study, $\alpha$ was fixed at $1/2$ based on both empirical observations and theoretical considerations. Specifically, our theoretical analysis established that for any $\alpha \in (0,1)$, the training process of RegCGAN was guaranteed to converge. This provides a general foundation for choosing $\alpha$ within this interval without compromising theoretical soundness.

With respect to the model depicted in Figure 1 and the utility function defined in Equation (2), this section focuses on the following key aspects:

• The equilibrium point in RegCGAN is demonstrated to exist and be unique;
• The minority class prediction capability of RegCGAN: specifically, we study whether the generator can accurately produce resampled data that follow the minority class distribution, and whether the classifier—trained using the utility function in Equation (2)—can, with the aid of the generator, effectively improve the prediction accuracy for the minority class while making full use of the information contained in the entire dataset.

2.2. Theoretical Analysis

In this subsection, a rigorous theoretical investigation of RegCGAN is carried out under nonparametric assumptions in this subsection. Analogous to the original GAN framework, we present the following lemma regarding the behavior of RegCGAN.

Lemma 1 ([2]).

Given a fixed generator G, the optimal solution for the discriminator D under the objective $V(G,D)$ is

$$D_G^{\ast }(x,y)={\displaystyle \frac{f(x,y)}{f(x,y)+f_g(x,y)}}.$$

(4)

Proof. 

With G fixed, the objective function $V(G,D)$ is reformulated as

$$\begin{array}{c}\hfill V(G,D)={\displaystyle \int }{\displaystyle \int }f(x,y)lnD(x,y)dydx+{\displaystyle \int }{\displaystyle \int }{f}_g(x,y)ln(1-D(x,y))dydz\\ \hfill ={\displaystyle \int }{\displaystyle \int }f(x,y)lnD(x,y)dydx+f_g(x,y)log(1-D(x,y))dydx.\end{array}$$

Under the nonparametric setting, that is, for any given $(x,y)$, the discriminator $D(x,y)$ is allowed to take arbitrary values. To maximize the integrand in the objective function $V(G,D)$

$$h\left(D\right)=f(x,y)lnD(x,y)+f_g(x,y)log(1-D(x,y))$$

for any fixed $(x,y)$, it suffices that $D(x,y)$ satisfies the following equation:

$${\displaystyle \frac{dh\left(D\right)}{dD}}=0$$

It is straightforward to verify that the solution to this equation is $D(x,y)={\displaystyle \frac{f(x,y)}{p(x,y)+f_g(x,y)}}$. The second derivative $h^{″}\left(D\right)=-{\displaystyle \frac{f(x,y)}{D^2}}-{\displaystyle \frac{f_g(x,y)}{{(1-D)}^2}}$ is negative, which proves that it is a maximum. □

Lemma 2 ([2]).

$V(G,D)$ reaches its global minimum precisely when the generated distribution $f_g(x,y)$ matches the real distribution $f(x,y)$.

Proof. 

Given $D_G^{\ast }(x,y)$, we can obtain from Lemma 1 that

$$\begin{array}{cc}\hfill \underset{D}{\max }V(G,D)& =V(G,D^{\ast })\hfill \\ & ={\displaystyle \int \int }f(x,y)ln{\displaystyle \frac{f(x,y)}{f(x,y)+f_g(x,y)}}dydx+{\displaystyle \int \int }{f}_g(x,y)log{\displaystyle \frac{f_g(x,y)}{f(x,y)+f_g(x,y)}}dydx.\hfill \end{array}$$

Noting that the $V(G,D^{\ast })$ can be rewritten as

$$\begin{array}{c}\hfill V(G,D^{\ast })=-ln4+2{\mathbb{D}}_{JS}(f(x,y)\left|\right|f_g(x,y)),\end{array}$$

(5)

where ${\mathbb{D}}_{JS}$ is the Jensen–Shannon divergence, which is always non-negative, and the unique optimum is achieved if and only if $f(x,y)=f_g(x,y)$. □

Theorem 1.

The equilibrium of $U(C,G,D)$ is achieved if and only if the joint distributions satisfy $f(x,y)=f_g(x,y)=f_c(x,y)$.

Proof. 

Based on the defined Equations (2) and (3),

$$U(C,G,D)=V(G,D)+L_C+\alpha L_G$$

where

$$L_C=E_{(x,y)\sim f(x,y)}[-ln{f}_c\left(y\right|x)]={\mathbb{D}}_{KL}(f(x,y)||f_c(x,y))+{\mathbb{H}}_f\left(y\right|x).$$

where ${\mathbb{D}}_{KL}$ denotes the KL divergence, and $\mathbb{H}$ is the conditional entropy. It is important to note that the second term in the above expression is independent of $C,G,D$, and hence the objective $L_C$ reaches its minimum when the KL divergence ${\mathbb{D}}_{KL}\left(f(x,y)\right|f_c(x,y))$ is minimized, attaining zero only if $f(x,y)$ matches $f_c(x,y)$. Similarly, $L_G$ reaches its minimum if and only if $f_g(x,y)=f_c(x,y)$. □

Noting that $L_C+\alpha L_G$ depends only on the pair $(C,G)$, and that

$$\underset{D}{\max }U(C,G,D)=\underset{D}{\max }V(G,D)+L_C+\alpha L_G$$

it follows from Lemma 2 and the non-negativity of $L_C+\alpha L_G$ that the global minimum of the objective is attained if and only if $f(x,y)=f_g(x,y)=f_c(x,y)$. This completes the proof.

Theorem 1 demonstrates that, under the proposed model framework, RegCGAN can theoretically guarantee the optimality of the resulting classifier C.

2.3. Optimization

RegCGAN decouples the hypothesis spaces of the discriminator and classifier, allowing for the integration of recent innovations from supervised learning and GAN research, such as advanced architectures and loss designs. Algorithm 1 demonstrates the overall training pipeline.

Algorithm 1 Minibatch Minibatch SGD training of RegCGAN.

1: for all numbers of training iterations do 2:  Generate a minibatch of $m_g$ synthetic samples $(x_g,y_g)\sim f_g(x,y)$ and $m_d$ real labeled samples $(x,y)\sim f(x,y)$; 3:  Update D by performing stochastic gradient ascent as defined in Equation (2): $${\nabla }_{{\theta }_d}\left[{\displaystyle \frac{1}{m_d}}\sum _{(x_d,y_d)}lnD(x_d,y_d)+{\displaystyle \frac{1}{m_g}}\sum _{(x_g,y_g)}ln(1-D(x_g,y_g))\right]$$ 4:  Update C performing stochastic gradient ascent as defined in Equation (2): $${\nabla }_{{\theta }_c}\left[-{\displaystyle \frac{1}{m_d}}\sum _{(x_d,y_d)}ln{f}_c\left(y_d\right|x_d)-\alpha {\displaystyle \frac{1}{m_g}}\sum _{(x_g,y_g)}ln{f}_c\left(y_g\right|x_g)\right].$$ 5:  Update G performing stochastic gradient ascent as defined in Equation (2): $${\nabla }_{{\theta }_g}\left[{\displaystyle \frac{1}{m_g}}\sum _{(x_g,y_g)}ln(1-D(x_g,y_g))\right]$$ 6: end for

3. Related Work

Learning from minority classes is often crucial, as they may correspond to rare but significant events [32], or because collecting such data is expensive and challenging [33]. Most machine learning algorithms are designed to optimize predictive accuracy and generalization performance. However, this inductive bias can become problematic when dealing with imbalanced datasets [34].

Firstly, when model training is driven by maximizing overall accuracy, it tends to favor the majority class, as it dominates the dataset. Secondly, decision rules targeting the minority (positive) class are usually highly specific with limited coverage, making them more likely to be rejected in favor of broader rules that classify the majority (negative) class. In practice, differentiating between noise and minority class samples is challenging, often causing classifiers to ignore or incorrectly label minority instances. Numerous strategies have been proposed to address the challenge of class imbalance, applicable to both standard learning models and ensemble frameworks [35,36,37]. These methods are generally divided into three main categories:

• Supervised Learning: The majority of existing research addresses class imbalance within the supervised learning framework. These approaches are generally grouped into three categories: $\left(a\right)$ Sampling-based data-level methods mitigate class imbalance by modifying the training dataset. These are considered external strategies [38,39,40,41,42]. $\left(b\right)$ Algorithm-level strategies adapt or redesign learning algorithms to emphasize the minority class, making them internal methods that integrate imbalance awareness directly into the learning process [43,44,45]. $\left(c\right)$ Cost-sensitive methods assign higher penalties to errors involving minority class instances. These techniques can be applied at the data level, algorithm level, or both, with the goal of reducing high-cost misclassifications [46,47,48,49,50]. However, none of these approaches can be directly applied to unsupervised scenarios, as they inherently depend on class labels or prediction outputs tied to labels. Recent studies have also revealed that the feature extractor (backbone) and the classifier can be trained separately [51,52], inspiring new strategies such as imbalance-aware pre-training and later fine-tuning for target tasks.
• Self-Supervised Learning: The exploration of self-supervised learning on naturally imbalanced datasets was initiated by [53]. Their findings suggest that pre-training with self-supervised tasks, such as image rotation [54] or contrastive learning methods like MoCo [55], consistently improves performance over direct end-to-end training. This implies a regularizing effect that leads to a more balanced feature representation. Subsequent studies [56,57] further validate the advantage of contrastive learning in mitigating data imbalance while also pointing out that it does not completely resolve the issue.
• Active Learning: In conventional machine learning, active learning has been widely studied as an effective approach to data-efficient sampling, with techniques including information-theoretic approaches [58], ensemble-based strategies [59,60], and uncertainty sampling [61,62]. A recent study [63] addressed the challenge of imbalanced seed data in active learning by introducing a model-aware K-center sampling strategy, a unified sampling framework designed to enhance learning efficiency in such settings.

One key benefit of data-level approaches is their flexibility, as they can be applied regardless of the specific classifier being used. Additionally, data-level techniques allow for preprocessing datasets in advance, enabling the reuse of the same processed data across multiple classifiers, thereby eliminating the need for repeated preparation. Various data rebalancing strategies can be employed during preprocessing, which generally fall into three categories: undersampling, oversampling, and hybrid approaches. We also observe that recent concurrent studies [64,65,66] propose domain-specific techniques, including the use of energy functionals and finite element method (FEM) frameworks for defect detection, as well as fuzzy divergence-based methods for quantifying classifier uncertainty and confidence in decision-making. Incorporating such techniques into RegCGAN may, in principle, lead to improved performance, and we consider this a promising direction for future exploration.

4. Application

Open-world data typically exhibit a long-tail distribution, which exacerbates class imbalance in supervised and semi-supervised learning. This work addresses this issue through RegCGAN, a unified resampling approach that improves classification performance by separating the generator from the classifier. In this section, we are interested in uncovering differences in the classification accuracy between the RegCGAN-based resampling model and the original conventional convolutional neural networks without resampling.

4.1. Setting

On the one hand, this study creates artificially imbalanced versions of standard benchmark datasets such as CIFAR-10 and CIFAR-100. In exactly the same way as [67], we consider two types of imbalance: (a) long-tailed distribution (see Figure 2); (b) step distribution (see Figure 3).

On the other hand, as an application, we consider Street View House Numbers (SVHN) which consists of images extracted from Google Street View [68].

GAN training is often time-consuming, as it involves repeated adversarial updates between the generator and discriminator to reach convergence. To accelerate training speed, researchers often explore approaches such as employing more efficient optimization algorithms and reducing network complexity. In the simulated experiments described in this section, we adopted a pre-trained model strategy to enhance training efficiency. Specifically, for the RegCGAN model on the CIFAR10 dataset, we conducted approximately 30,000 iterations, requiring about 75 h of training on an NVIDIA P100 GPU with Adam optimizer, which was applied to all three networks All networks utilized ReLU activation functions, with batch size configured as 100. The learning rates for the classifier, generator, and discriminator were set to 0.003, 0.0001, and 0.0001, respectively, while their network architectures employed CNN and ResNet frameworks. Figure 4 illustrates the training learning curve of RegCGAN.

In our empirical experiments on the SVHN dataset, the experimental configuration for RegCGAN training remained fundamentally consistent with the simulated experiments, with the notable exception of extending the iteration count to 40,000 for this particular dataset. This study used balanced accuracy to assess image classification performance [69].

4.2. Experimental Results

This section introduces a CNN baseline for validating the performance of RegCGAN. A comparative simulation study was conducted employing RegCGAN alongside the baseline CNN model on both the original CIFAR10 dataset and its imbalanced variant. The model efficacy was evaluated through prediction accuracy rates, with the comparative results presented in the table below.

As indicated in

Table 1. Prediction accuracy (%) for CIFAR-10.

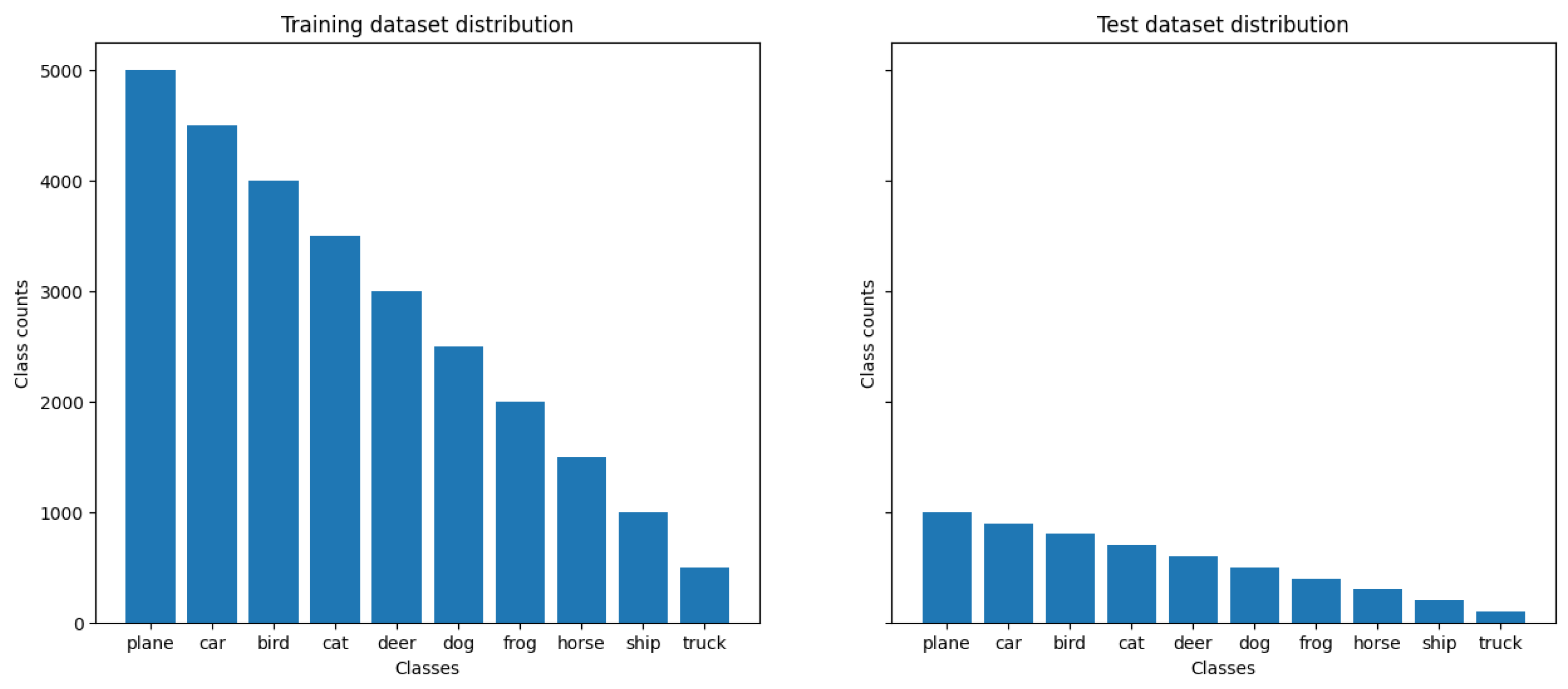
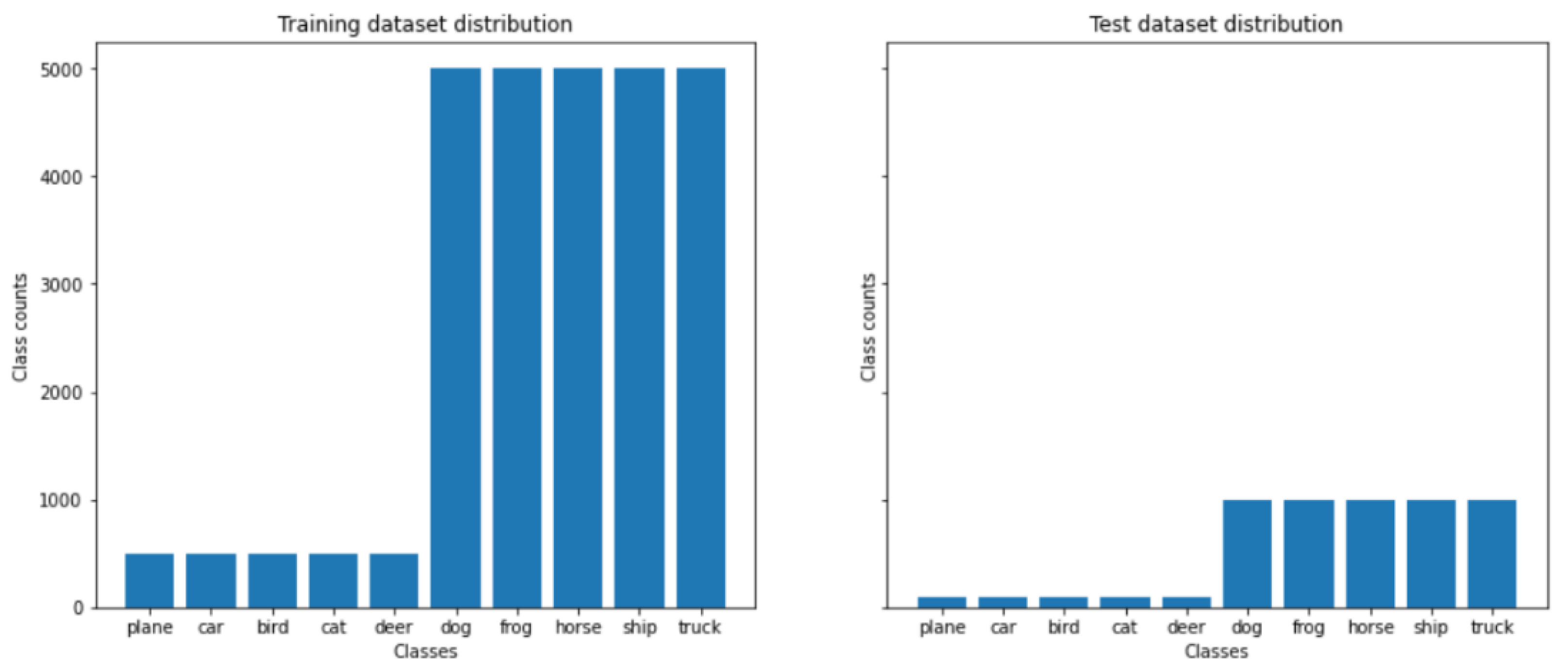
Model	Balanced Data	Long-Tailed Data	Step Data
CNN	71.75	69.80	71.13
RegCGAN	80.93	81.60	86.38

, the CNN performs poorly regardless of whether the dataset is balanced or imbalanced. Unlike baseline models, RegCGAN enhances prediction accuracy by using generative resampling of minority samples during training, which helps the classifier better capture their feature representations.

Compared to the CIFAR-10 dataset, the most significant difference in the CIFAR-100 dataset lies in its larger number of categories—100 in total. Similar to the experimental results on CIFAR-10, the classifier incorporating RegCGAN achieves substantially higher prediction accuracy than the baseline CNN model under both balanced and imbalanced data settings. Specifically, the prediction accuracies of the baseline CNN model are 40.08% and 41.26% for the balanced and imbalanced datasets, respectively; in contrast, the classifier enhanced with RegCGAN achieves prediction accuracies of 49.35% and 56.09%, respectively.

On the other hand, Figure 5 shows the CIFAR-100 images generated by the RegCGAN model: the left panel corresponds to iteration 3000, while the right panel represents outputs at iteration 30,000. As training progressed, the quality of generated images improved significantly, becoming increasingly similar to real images.

4.3. Empirical Results

SVHN consists of images sourced from Google Street View [68] and exhibits an inherently long-tailed distribution. In this subsection, RegCGAN is applied to the real-world imbalanced dataset SVHN. The results show that the proposed model achieves a prediction accuracy of 92.54%, outperforming both the standard convolutional neural network and the residual network. This further demonstrates the effectiveness of the model in addressing imbalanced data problems. Detailed results are presented in

Table 2. Prediction accuracy (%) for SVHN.

Model	CNN	Resnet34	RegCGAN
accuracy	89.30	90.68	92.54

.

5. Conclusions and Discussion

A generative resampling method was introduced in this study to address the widespread problem of data imbalance prevalent in real-world applications. Leveraging the conditional GAN structure, we proposed RegCGAN to improve accuracy in classification tasks. A theoretical investigation was carried out to verify that RegCGAN uses a unique and well-defined optimal classifier. The results on both synthetic and real imbalanced datasets show that the generator accurately models the minority class distribution during resampling. The classifier trained with the proposed utility function, aided by the generator, significantly improves the prediction accuracy for minority classes while effectively leveraging information from the entire dataset.

In many real-world scenarios, labeled data are scarce or entirely unavailable [63,70], and the data distribution in the open world is highly diverse, often characterized by long-tail patterns [71,72]. As a result, semi-supervised and unsupervised learning methods under imbalanced conditions emerge as important directions for future research. To illustrate how our framework could be extended, we take semi-supervised learning as an example and propose a simple idea for its potential adaptation.

We adopt a minor assumption in semi-supervised learning that the marginal input distribution is easy to sample from the marginal distribution $f\left(x\right)$. In this scenario, after a sample x is drawn from $f\left(x\right)$, the discriminator C produces a fake label y given x following the conditional distribution $f_c\left(y\right|x)$. As a result, the fake input-label pair is a sample from the joint distribution $f_c(x,y)=f\left(x\right)f_c\left(y\right|x)$. For the semi-supervised learning task, in view of Equation (2), we consider the following utility function:

$$\begin{array}{cc}\hfill {\displaystyle \underset{C,G}{\min }}{\displaystyle \underset{D}{\max }}\tilde{U}(C,G,D)& =U(C,G,D)+E_{(x,y)\sim f_c(x,y)}[ln(1-D(x,y))]\hfill \\ & =E_{(x,y)\sim f(x,y)}[lnD(x,y)]+E_{(x,y)\sim f_g(x,y)}[ln(1-D(x,y))]\hfill \\ & +E_{(x,y)\sim f(x,y)}[-ln{f}_c\left(y\right|x)]+\alpha E_{(x,y)\sim f_g(x,y)}[-ln{f}_c\left(y\right|x)]\hfill \\ & +E_{(x,y)\sim f_c(x,y)}[ln(1-D(x,y))].\hfill \end{array}$$

The remaining procedure follows a similar implementation to that of the RegCGAN algorithm. In fact, a valuable direction for future work would be to provide theoretical foundations and empirical analyses analogous to those conducted for RegCGAN.