On the Bifurcation Behavior of Decoupled Systems of Difference Equations

Abstract

This paper, we study systems of difference equations numerically and theoretically. These systems have been examined by many researchers. We focus on their general forms and limits. We consider different orders of difference systems. In certain cases, we use a computer in order to verify the summation laws that we encountered. We consider a system with two parameters. For certain values of the parameters, we determine the explicit form of the solution and show that the limit of this sequence tends to zero. We show that for the values of a parameter between 0 and 1, the limit of the sequence is a nonzero value, while for the values greater than 1, the limit of the sequence becomes zero.

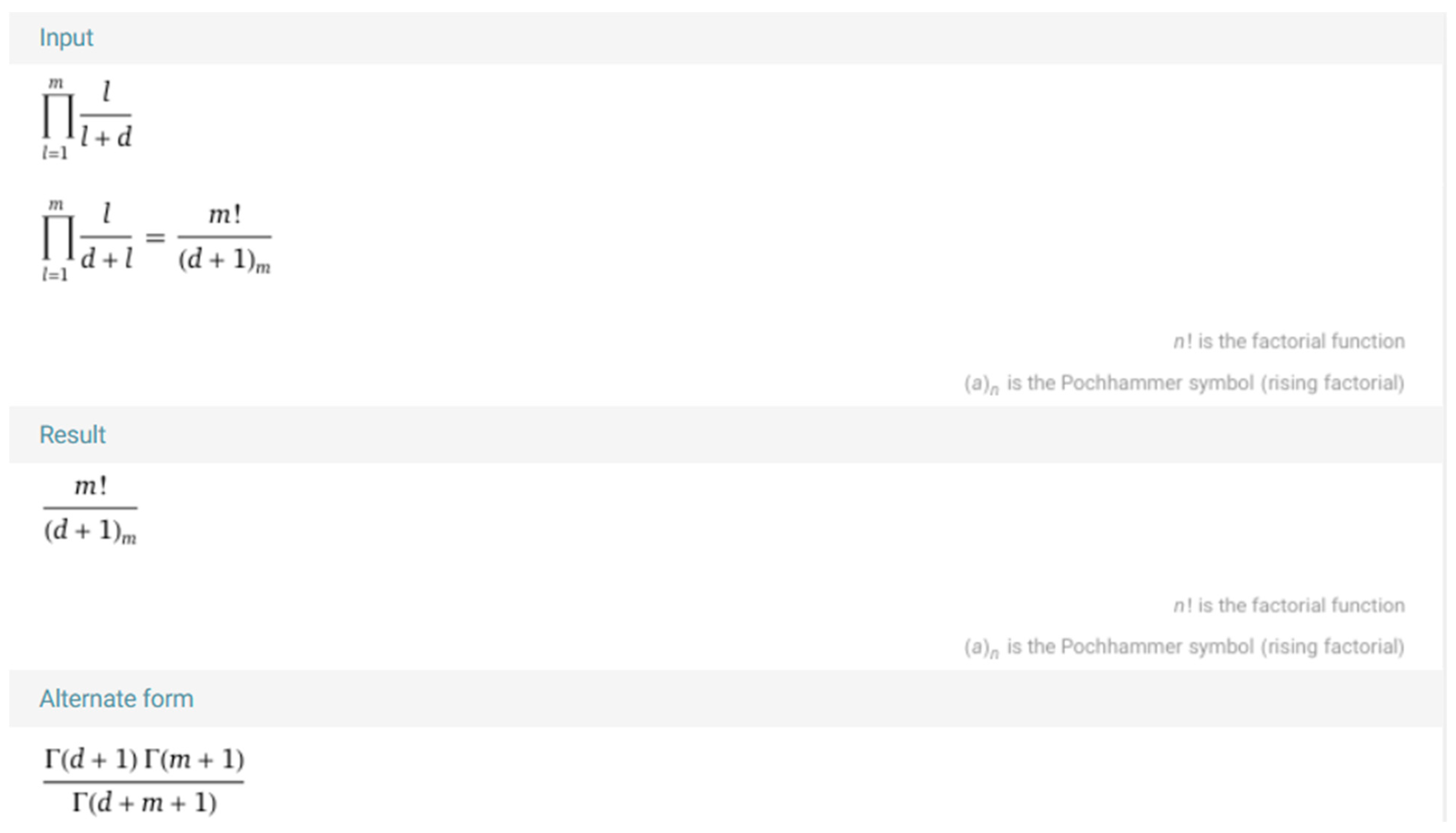
1. Introduction

The purpose of this paper is to explicate the behaviors of difference equation systems, which are called rational systems. Many students wrote their master thesis in this topic as we see in [1,2,3,4,5]. Al-ashhab supervised them and published many papers about this topic as we see in [6,7,8]. This topic is extensively covered in the existing literature, e.g., in [9,10,11,12,13], and we also refer to authoritative surveys [14,15,16,17,18,19] for further illumination. The machinery of rational difference appears naturally in the form of discrete analogues and numerical solutions of differential equations. Although the results of this paper are interesting in the theoretical sense, they are also applicable to practical problems in applied science, for example, in biology, ecology, and physics.

The values of most economic variables are given as a sequence of values observed at discrete time intervals or periods. These sequences are often specified by recursion with some initial elements. But it is preferable to know a rule in the form of an equation for the n-th element to calculate the values of the sequence elements. The recursive rule of a sequence represents a difference equation, and the functional notation for the n-th element can be obtained by solving this difference equation (see [20]). Many formulas used in financial mathematics can be derived from the recursive rules between two consecutive elements, which are modeled by difference equations of the first order. This includes, for example, simple and compound interest calculations, the present and future value of annuity, and loan amortization. In detail, we present some results from the references.

In [8], Al-Ashhab and Hasan consider the following system of equations:

$$x_{n+1}={\displaystyle \frac{x_{n-1}}{x_{n-1}+r}}, y_{n+1}={\displaystyle \frac{x_n{y}_{n-1}}{x_n{y}_{n-1}+r}}$$

(1)

Suppose that $r=1$ for any positive real initial values:

$$x_0=b, x_{-1}=c, y_0=a, \mathrm{a}\mathrm{n}\mathrm{d} y_{-1}=d.$$

They prove that the solution is

$$x_{2k}={\displaystyle \frac{b}{G\left(b,k\right)}}, x_{2k+1}={\displaystyle \frac{c}{G(c,k+1)}},$$

$$y_{2k}=a{\left(a+\left(aU\left(k,{\displaystyle \frac{1}{c}}\right)+\Gamma {\left({\displaystyle \frac{1+c}{c}}\right)}^{-1}\right)\Gamma \left(k+{\displaystyle \frac{1+c}{c}}\right)\right)}^{-1},$$

$$y_{2k+1}=db{\left(db+\left(dbU\left(k,{\displaystyle \frac{1}{c}}\right)+\Gamma {\left({\displaystyle \frac{1+b}{b}}\right)}^{-1}\right)\Gamma \left(k+{\displaystyle \frac{1+b}{b}}\right)\right)}^{-1}.$$

Now, suppose that $r=-1$ for any positive initial values:

$$x_0=b\ne 1, x_{-1}=c, y_0=a, \mathrm{a}\mathrm{n}\mathrm{d} y_{-1}=d.$$

In this case, the solution is

$$x_{2k}=1, x_{2k+1}={\displaystyle \frac{1}{b-1}}$$

$$y_{2k}=\left\{\begin{array}{c}a{c}^k{\left(Y^l-{\displaystyle \frac{acY}{v}}\left(Y^l-c^{2l}\right)\right)}^{-1}\mathrm{i}\mathrm{f} k=2l\\ a{c}^k{\left(a{c}^k-{\displaystyle \frac{ac}{v}}\left(c{Y}^2\left)\right(Y^l-c^{2l}\right)\right)}^{-1} \mathrm{i}\mathrm{f} k=2l+1\end{array}\right.$$

$$y_{2k+1}=\left\{\begin{array}{c}d{b}^{k+1}{\left(d{b}^{k}Z-{\displaystyle \frac{dZ}{W}}\left(b^2{Z}^l-b^{2l}+Z^l\right)\right)}^{-1}\mathrm{i}\mathrm{f} k=2l\\ d{b}^{k+1}{\left(d{b}^{k}Z+{\displaystyle \frac{d{\left(bZ\right)}^2}{W}}(Z^l-b^{2l}-Z^{l+1})\right)}^{-1} \mathrm{i}\mathrm{f} k=2l+1\end{array}\right.$$

$$V=c^2-c+1, W=b^2-b+1, Y=c-1 \mathrm{a}\mathrm{n}\mathrm{d} Z=b-1.$$

Al-Ashhab [7] considers the following case:

$$x_{n+1}={\displaystyle \frac{x_{n-1}}{x_{n-1}+r}}, y_{n+1}={\displaystyle \frac{y_{n-1}}{x_n{y}_{n-1}+r}}$$

(2)

$$x_0=b, x_{-1}=c, y_0=a, \mathrm{a}\mathrm{n}\mathrm{d} y_{-1}=d.$$

He proves that if $r=1,$ the general form of the solution for $k=1,2,\dots$ is:

$$x_{2k}={\displaystyle \frac{b}{1+kb}}, x_{2k+1}={\displaystyle \frac{c}{1+\left(k+1\right)c}},$$

$$y_{2k+1}={\left(\Psi \left(\mathrm{k}+{\displaystyle \frac{1+b}{b}}\right)-\Psi \left({\displaystyle \frac{1+b}{b}}\right)+b+{\displaystyle \frac{1}{d}}\right)}^{-1},$$

$$y_{2k}={\left(\Psi \left(\mathrm{k}+{\displaystyle \frac{1+c}{c}}\right)-\Psi \left({\displaystyle \frac{1+c}{c}}\right)+{\displaystyle \frac{1}{a}}\right)}^{-1},$$

where the symbol $\Psi$ denotes the Psi (digamma) function. Furthermore, Yacoub (see [8]) considers the following system:

$$x_{n+1}={\displaystyle \frac{x_{n-1}}{x_n+r}}, y_{n+1}={\displaystyle \frac{y_n}{x_{n-1}{y}_{n-1}+r}}$$

(3)

He calculates the system for $r=1$ with one vanishing initial value. For example,

$$x_{-1}=a, x_0=0, y_{-1}=b, y_0=d.$$

It is proven that the general solution when $n=0,1,2,\dots$ is as follows:

$$x_{2n}=0, y_{2n}={\displaystyle \frac{d}{ab+(n-1)ad+1}}, x_{2n+1}=a, y_{2n+1}={\displaystyle \frac{d}{ab+nad+1}}$$

Thus, the general solution converges to zero under the assumption that a$,b,d>0$. In [10], Ibrahim considers

$$x_{n+1}={\displaystyle \frac{x_{n-1}}{x_{n-1}+r}}, y_{n+1}={\displaystyle \frac{x_n{y}_{n-1}}{x_n{y}_{n-1}+r}}$$

(4)

where $r$ is a fixed real number. He takes the following as the initial values:

$$x_0=b, x_{-1}=c, y_0=a, y_{-1}=d.$$

The general solution of System (4) for $k=2,3,4,$… is as follows:

$$x_{2k}={\displaystyle \frac{b}{G(b,k)}}, x_{2k+1}={\displaystyle \frac{c}{G(c,k+1)}},$$

$$y_{2k}={\displaystyle \frac{a{c}^k}{a{c}^k+a{\sum }_{i=2}^k{c}^{k-i+1}{r}^{i-1}{\prod }_{j=0}^{i-2}G\left(c,k-j\right)+r^k{\prod }_{j=0}^{k-1}G\left(c,k-j\right)}},$$

$$y_{2k+1}={\displaystyle \frac{d{b}^{k+1}}{d{b}^{k+1}+db{\sum }_{i=2}^k{b}^{k-i+1}{r}^{i-1}{\prod }_{j=0}^{i-2}G\left(b,k-j\right)+r^k{\prod }_{j=0}^{k-1}G\left(b,k-j\right)}}.$$

It is proven that if $r=2$ and $a$ and $d$ are positive real numbers, the solution for System (4) with the initial values

$$x_0=x_{-1}=-1, y_0=a \mathrm{a}\mathrm{n}\mathrm{d} y_{-1}=d,$$

is

$$x_{2k}=x_{2k+1}=-1, y_{2k+2}={\displaystyle \frac{{\left(-1\right)}^{k+1}3a}{a\left(5{\left(-1\right)}^{k+1}+2^{k+1}\right)+{3\ast 2}^{k+1}}},$$

$$y_{2k+1}={\displaystyle \frac{{(-1)}^{k+1}3d}{d\left({\left(-1\right)}^{k+1}-2^{k+1}\right)+3\ast 2^{k+1}}}.$$

for $k=$ 0, 1, 2, ….

In some cases, a rational difference equation has a periodic solution, as in [9]. For example, consider the following equation:

$$y_{n+1}={\displaystyle \frac{y_n}{y_{n-1}}}.$$

If we take the initial values $y_{-1}=a$ and $y_0=c$, we obtain the following for $n=0,1,2,\dots$:

$${y_{6n}=c, y}_{6n+1}={\displaystyle \frac{c}{a}},{ y}_{6n+2}={\displaystyle \frac{1}{a}},$$

$$y_{6n+3}={\displaystyle \frac{1}{c}}, y_{6n+4}={\displaystyle \frac{a}{c}}, y_{6n+5}=a.$$

In this paper, our goal is to present sequences of solutions for two crucial cases. The first case is System (7), illustrated in detail in the Section 2:

$$y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+r}},{ y}_0=c, x_n={\displaystyle \frac{1}{G\left(n\right)}},$$

where $G\left(n\right)=\alpha \left(n+1\right)$ and a $\alpha \ne 0$. We prove that the limit of this sequence under such conditions tends towards zero. In the second case, we consider System (10) (see Section 2):

$$x_n={\displaystyle \frac{1}{\alpha }}{\displaystyle \frac{n+1+d}{n+1}}, y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+1}}, y_0=c,$$

We show that if $\alpha \ge 1,$ the sequence converges to zero. However, when $\alpha <1,$ this system tends towards a non-zero value.

2. Main Results

Above, we saw that the limit of systems of difference equations was solved for both variables simultaneously. We now seek a generalization of these systems by considering the sequence for the first variable given as

$$x_n={\displaystyle \frac{1}{G\left(n\right)}},$$

where $G\left(n\right)$ is a nonzero sequence, which we determine later. We seek a solution for the sequence

$$y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+r}}, y_0=c$$

(5)

where $y_n$ is bounded in certain cases because when $x_n{y}_n$ and $r$ have the same sign, the absolute value of the numerator will be less than the absolute value of the denominator. Thus, $1\ge \left|y_n\right|.$ We consider a trivial case, namely, $G\left(n\right)=1$ and $r=0$, then $x_n=y_n=1$. Hence, the solution of System (5) converges to one. In this paper, we will treat nontrivial cases in which we encounter other limits of the sequence, like zero and nonzero values.

We first derive the general formula. We find that the following is true by definition:

$$y_1={\displaystyle \frac{\frac{1}{G\left(0\right)}c}{\frac{1}{G\left(0\right)}c+r}}={\displaystyle \frac{c}{c+rG\left(0\right)}}={\displaystyle \frac{c}{P\left(1\right)}} , y_2={\displaystyle \frac{x_1{y}_1}{x_1{y}_1+r}}={\displaystyle \frac{\frac{1}{G\left(1\right)}\frac{c}{P\left(1\right)}}{\frac{1}{G\left(1\right)}\frac{c}{P\left(1\right)}+r}}={\displaystyle \frac{c}{c+rG\left(1\right)P\left(1\right)}}={\displaystyle \frac{c}{P\left(2\right)}},$$

$$y_3={\displaystyle \frac{\frac{1}{G\left(2\right)}\frac{c}{P\left(2\right)}}{\frac{1}{G\left(2\right)}\frac{c}{P\left(2\right)}+r}}={\displaystyle \frac{c}{P\left(3\right)}}, P\left(3\right)=c+rG\left(2\right)P\left(2\right)=c+crG\left(2\right)+r^{2}G\left(1\right)G\left(2\right)P\left(1\right).$$

In general, we obtain

$$P\left(n\right)=c+rG\left(n-1\right)P\left(n-1\right), y_n={\displaystyle \frac{c}{P\left(n\right)}} \mathrm{f}\mathrm{o}\mathrm{r} n=1,2,\dots$$

(6)

In general, the following holds when n = 3, 4, 5, …:

$$\begin{array}{c}P\left(n\right)=c+c{\sum }_{m=2}^{n-1}{r}^{m-1}{\prod }_{l=m}^{n-1}G\left(l\right)+r^{n-1}P\left(1\right)=\\ {\prod }_{l=1}^{n-1}G\left(l\right)\left(c{\sum }_{m=2}^n{\displaystyle \frac{r^{n-m}}{{\prod }_{l=1}^{m-1}G\left(l\right)}}+r^{n-1}P\left(1\right)\right).\end{array}$$

We use the notation

$$B\left(m,n\right)={\prod }_{l=m}^{n}G\left(l\right).$$

Hence,

$$P\left(n\right)=B(1,n-1)\left(c{\sum }_{m=2}^n{\displaystyle \frac{r^{n-m}}{B(1,m-1)}}+r^{n-1}P\left(1\right)\right).$$

We define the function $W\left(.,.,.\right)$ as follows

$$W\left(r,q,n\right)={\displaystyle \frac{(1-r)(1-r^{q+1})\Gamma (q+1)}{r^{q+1}}}-{\displaystyle \frac{{\left(1-r\right)}^n\Gamma \left(q+n\right){}_{2}F_1\left(1,q+n;n,1-r\right)}{\Gamma \left(n\right)}}$$

where ${}_{2}F_1$ is the hypergeometric function. Using Mathematica (online), we obtain the following formula

$${\sum }_{m=2}^{n-1}{\displaystyle \frac{u^m\Gamma (w+m)}{\left(m-1\right)!}}={\sum }_{m=2}^{n-1}{\displaystyle \frac{u^m\Gamma (w+m)}{\Gamma \left(m\right)}}=W\left(1-u,w,n\right)$$

To see how this works, we visited the website of Wolframalpha (https://www.wolframalpha.com, accessed on 15 May 2025) and entered

sum (u^{^k∗}Γ(k + w))/Γ(k), k = 2 to n − 1

in the input cell. Then, by pressing the ENTER tab, we saw on the Figure 1.

We use the notation

$$R\left(u,d,n\right)={\sum }_{m=1}^{n-1}{\displaystyle \frac{u^m\Gamma (d+m)}{\Gamma \left(m\right)}}=W\left(1-u,d,n\right)+u\Gamma (d+1)$$

and consider two cases for the sequence. We first choose the following form of the function G:

$$G\left(l\right)=\alpha (l+1), \alpha \ne 0.$$

Thus,

$$B\left(0,m-1\right)={\prod }_{l=0}^{m-1}G\left(l\right)={\prod }_{l=0}^{m-1}\alpha (l+1)={\alpha }^{m}m! ,$$

$$B\left(1,m-1\right)={\displaystyle \frac{B\left(0,m-1\right)}{G\left(0\right)}}={\displaystyle \frac{1}{\alpha }}B\left(0,m-1\right)=m!{\alpha }^{m-1} .$$

We can now study the first case, namely, the system

$$x_n={\displaystyle \frac{1}{\alpha (n+1)}},{ y}_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+r}},{ y}_0=c$$

(7)

Hence, using Mathematica (online), we obtain

$$\begin{array}{c}P\left(n\right)=r^{n-1}B\left(1,n-1\right)\left(c{\sum }_{m=2}^n{\displaystyle \frac{{{(r}^{-1})}^{m-1}}{B\left(1,m-1\right)}}+P\left(1\right)\right)=\\ r^{n-1}B\left(1,n-1\right)\left(c{\sum }_{m=2}^n{\displaystyle \frac{{{(r}^{-1})}^{m-1}}{m!{\alpha }^{m-1}}}+P\left(1\right)\right)=\\ {\sum }_{m=2}^n{\displaystyle \frac{{{(r}^{-1})}^{m-1}}{m!{\alpha }^{m-1}}}={\sum }_{m=2}^n{\displaystyle \frac{b^{m-1}}{m!}}={\displaystyle \frac{e^b\Gamma \left(n+1,b\right)-(b+1)\Gamma \left(n+1\right)}{b\Gamma \left(n+1\right)}}\end{array}$$

where ${b=\left(r\alpha \right)}^{-1}$ and $\Gamma \left(m+1,1\right)$ is the incomplete gamma function. Thus, we obtain the following form for $P\left(n\right):$

$$\begin{array}{c}P\left(n\right)=b^{1-n}n!\left({\displaystyle \frac{e^b\Gamma \left(n+1,b\right)-\left(b+1\right)\Gamma \left(n+1\right)}{b{c}^{-1}\Gamma \left(n+1\right)}}+\left(c+b^{-1}\right)\right)=\\ {\displaystyle \frac{c}{b^n}}\left(e^b\Gamma \left(n+1,b\right)-\left(b+1\right)\Gamma \left(n+1\right)+b+c^{-1}\right)\end{array}$$

(8)

Since $y_n={\displaystyle \frac{c}{P\left(n\right)}}$, $y_n$ is the reciprocal of

$${\displaystyle \frac{1}{b^n}}\left(e^b\Gamma \left(n+1,b\right)-\left(b+1\right)\Gamma \left(n+1\right)+b+c^{-1}\right).$$

Now, we investigate the limit of the sequence. We consider the case in which $b=1$. In this case, the function $e\Gamma \left(m+1,1\right)-2\Gamma \left(m+1\right)$ increases without bounds in m. Further, $y_n$ is the reciprocal of $e\Gamma \left(n+1,1\right)-2\Gamma \left(n+1\right)+1+c^{-1}$, i.e.,

$$y_n={\displaystyle \frac{c}{ce\Gamma \left(n+1,1\right)-2c\Gamma \left(n+1\right)+c+1}}$$

Proposition 1.

Let $\alpha , c,$ and r be positive real numbers. If $r={\alpha }^{-1}$, we conclude for System (7) that the limit of the system is zero.

Proof. 

It is clear that $x_n$ converges at 0 as n tends to infinity, by definition. The solution of the system $y_n$ is the reciprocal of a quantity growing in magnitude to infinity, as we calculated. □

For example, the system with the values $\alpha =2,c=1,$ and $d=4$ is

$$x_n={\displaystyle \frac{1}{2(n+1)}} , y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+\frac{1}{2}}},{ y}_0=1$$

(9)

We obtain the following values for $y_n$: 1, 1, ${\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}},{\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{65}},{\displaystyle \frac{1}{326}},{\displaystyle \frac{1}{1957}},\dots$ Using Excel, we generated some remaining values when n is greater than 7, which we list in

Table 1. Values of System (9).

n	x	y
8	0.055555556	9.124 × 10−6
9	0.05	1.01378 × 10−6
10	0.045454545	1.01378 × 10−7
11	0.041666667	9.21616 × 10−9
12	0.038461538	7.68013 × 10−10
13	0.035714286	5.90779 × 10−11
14	0.033333333	4.21985 × 10−12
15	0.03125	2.81323 × 10−13
16	0.029411765	1.75827 × 10−14
17	0.027777778	1.03428 × 10−15
18	0.026315789	5.74599 × 10−17
19	0.025	3.0242 × 10−18

.

In some cases, we can modify the assumptions of the proposition and use the following reasoning in the previous proof: First, we ensure that the property (the terms $y_n$ are less than one) holds and the terms $x_n$ go to zero, so the limit of the numerator is zero while the limit of the denominator is nonzero. For example, if $\alpha ,c,r>0,$ then the terms $x_n$ and $y_n$ are positive. Thus, the limit of System (7) is zero.

We consider the second case in two propositions. Here, we deal with the situation in which one parameter is greater and less than one.

$$r=1, G\left(l\right)={\displaystyle \frac{\alpha (l+1)}{l+1+d}}, d\ne 0,-1,-2,\dots$$

We consider the following system:

$$x_n={\displaystyle \frac{1}{\alpha }}{\displaystyle \frac{n+1+d}{n+1}}, y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+1}} ,{ y}_0=c, \alpha >1$$

(10)

where $\alpha$ and d are fixed real numbers. By using Mathematica, we know that

$$B\left(0,m-1\right)={\prod }_{l=0}^{m-1}G\left(l\right)={\prod }_{l=0}^{m-1}{\displaystyle \frac{\alpha (l+1)}{l+1+d}}={\alpha }^m{\prod }_{l=1}^m{\displaystyle \frac{l}{l+d}}={\alpha }^m{\displaystyle \frac{\Gamma (d+1)}{\Gamma (d+m+1)}}m!.$$

This can be established by visiting the website of Wolframalpha using the link: https://www.wolframalpha.com/input?i2d=true&i=Product%5BDivide%5Bl%2Cl%2Bd%5D%2C%7Bl%2C1%2Cm%7D%5D (accessed on 15 May 2025).

By pressing on the “=” bottom (compute input), we obtained Figure 2.

Hence, we obtain

$$B\left(1,m-1\right)={\displaystyle \frac{B\left(0,m-1\right)}{G\left(0\right)}}={\displaystyle \frac{1+d}{\alpha }}B\left(0,m-1\right)={\displaystyle \frac{\left(1+d\right)m!{\alpha }^{m-1}\Gamma (d+1)}{\Gamma (d+m+1)}}={\displaystyle \frac{m!{\alpha }^{m-1}\Gamma (d+2)}{\Gamma (d+m+1)}},$$

$${\sum }_{m=2}^n{\displaystyle \frac{1}{B\left(1,m-1\right)}}={\sum }_{m=2}^n{\displaystyle \frac{\Gamma \left(d+m+1\right)}{m!{\alpha }^{m-1}\Gamma \left(d+2\right)}}={\displaystyle \frac{{\alpha }^2}{\Gamma \left(d+2\right)}}{\sum }_{m=3}^{n+1}{\displaystyle \frac{\Gamma \left(d+m\right)}{{\alpha }^m\left(m-1\right)!}}=$$

$$\begin{array}{c}{\displaystyle \frac{{\alpha }^2}{\Gamma \left(d+2\right)}}\left({\sum }_{m=1}^{n+1}{\displaystyle \frac{\Gamma (d+m)}{{\alpha }^m\left(m-1\right)!}}-{\displaystyle \frac{\Gamma \left(d+1\right)}{\alpha }}-{\displaystyle \frac{\Gamma \left(d+2\right)}{{\alpha }^2}}\right)=\\ {\displaystyle \frac{{\alpha }^2}{\Gamma \left(d+2\right)}}\left[R\left({\alpha }^{-1},d,n+2\right)-{\displaystyle \frac{\Gamma \left(d+1\right)}{\alpha }}-{\displaystyle \frac{\Gamma \left(d+2\right)}{{\alpha }^2}}\right]=\\ {\displaystyle \frac{{\alpha }^{2}R\left({\alpha }^{-1},d,n+2\right)}{\Gamma \left(d+2\right)}}-{\displaystyle \frac{\alpha }{d+1}}-1.\end{array}$$

We then obtain the following form:

$$\begin{array}{c}P\left(n\right)=B\left(1,n-1\right)\left(c{\sum }_{m=2}^n{\displaystyle \frac{1}{B\left(1,m-1\right)}}+P\left(1\right)\right)=\\ {\alpha }^{n-1}{\displaystyle \frac{\Gamma (d+2)}{\Gamma (d+n+1)}}n!\left({\displaystyle \frac{{\alpha }^{2}cR\left({\alpha }^{-1},d,n+2\right)}{\Gamma \left(d+2\right)}}-{\displaystyle \frac{\alpha c}{d+1}}-c+c+G\left(0\right)\right)=\\ {\alpha }^{n-1}{\displaystyle \frac{\Gamma (d+2)}{\Gamma (d+n+1)}}n!\left({\displaystyle \frac{{\alpha }^{2}cR\left({\alpha }^{-1},d,n+2\right)}{\Gamma \left(d+2\right)}}+{\displaystyle \frac{\alpha (1-c)}{d+1}}\right)={\alpha }^{n}n!{\displaystyle \frac{\alpha cR\left({\alpha }^{-1},d,n+2\right)+(1-c)\Gamma (d+1)}{\Gamma (d+n+1)}}.\end{array}$$

In general, we will obtain

$$y_n={\displaystyle \frac{c}{P\left(n\right)}}={\displaystyle \frac{c\Gamma (n+d+1)}{{\alpha }^n\Gamma (n+1)\left(\alpha cR\left({\alpha }^{-1},d,n+2\right)+(1-c)\Gamma (d+1)\right)}}.$$

In other words, $y_n$ is the reciprocal of

$${\displaystyle \frac{{\alpha }^n\Gamma \left(n+1\right)}{c\Gamma \left(n+d+1\right)}}(\alpha cR\left({\alpha }^{-1},d,n+2\right)+\left(1-c\right)\Gamma \left(d+1\right)).$$

Proposition 2.

Let $\alpha$ and $c$ be positive real numbers, with $\alpha >1$. Assume that 0 < d < $\alpha -1$. The general solution of System (10) satisfies

$$\underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{y}_n=0 , \underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{x}_n={\displaystyle \frac{1}{\alpha }}.$$

Proof. 

We know that

$$\begin{array}{c}R\left({\alpha }^{-1},d,n+2\right)=W\left({1-\alpha }^{-1},d,n+2\right)+{\alpha }^{-1}\Gamma \left(d+1\right)=\\ {\alpha }^{-1}{\displaystyle \frac{(1-{({1-\alpha }^{-1})}^{d+1})\Gamma (d+1)}{{({1-\alpha }^{-1})}^{d+1}}}+{\alpha }^{-1}\Gamma \left(d+1\right)-{\displaystyle \frac{{\left({\alpha }^{-1}\right)}^{n+2}\Gamma \left(d+n+2\right)}{\Gamma \left(n+2\right)}}{F}_1^2\left(1,d+n+2;n+2;{\alpha }^{-1}\right)=\\ {\displaystyle \frac{{\alpha }^{-1}\Gamma (d+1)}{{({1-\alpha }^{-1})}^{d+1}}}-{\displaystyle \frac{{\left({\alpha }^{-1}\right)}^{n+2}\Gamma \left(d+n+2\right)}{\Gamma \left(n+2\right)}}{F}_1^2\left(1,d+n+2;n+2;{\alpha }^{-1}\right),\\ \alpha cR\left({\alpha }^{-1},d,n+2\right)+\left(1-c\right)\Gamma \left(d+1\right)={\displaystyle \frac{c\Gamma (d+1)}{{({1-\alpha }^{-1})}^{d+1}}}+\left(1-c\right)\Gamma \left(d+1\right)-\\ {\displaystyle \frac{{\alpha c\left({\alpha }^{-1}\right)}^{n+2}\Gamma \left(d+n+2\right)}{\Gamma \left(n+2\right)}}{F}_1^2\left(1,d+n+2;n+2;{\alpha }^{-1}\right).\end{array}$$

We create two parts

$${\displaystyle \frac{{\alpha }^n\Gamma \left(n+1\right)}{c\Gamma \left(n+1+d\right)}}\left(\alpha cR\left({\alpha }^{-1},d,n+2\right)+\left(1-c\right)\Gamma \left(d+1\right)\right)=S_1-S_2,$$

$$S_1={\displaystyle \frac{\Gamma (d+1)}{c}}{\displaystyle \frac{c+(1-c){({1-\alpha }^{-1})}^{d+1}}{{({1-\alpha }^{-1})}^{d+1}}}{\displaystyle \frac{{\alpha }^n\Gamma \left(n+1\right)}{\Gamma \left(d+n+1\right)}},$$

$$S_2={\displaystyle \frac{{\alpha }^{n+1}{\left({\alpha }^{-1}\right)}^{n+2}\Gamma (n+1)\Gamma (d+n+2)F_1^2(1,d+n+2;n+2,{\alpha }^{-1})}{\Gamma (n+2)\Gamma (d+n+1)}}={\displaystyle \frac{d+n+1}{\alpha \left(n+1\right)}}{}_{2}F_1(1,d+n+2;n+2;{\alpha }^{-1}).$$

We then consider the function

$${}_{2}F_1\left(1,d+m+2;m+2;{\alpha }^{-1}\right)={\sum }_{n=0}^{\infty }{\displaystyle \frac{\Gamma (m+n+2+d)\Gamma (m+2)}{{\alpha }^n\Gamma (m+2+d)\Gamma (m+n+2)}},$$

$${\displaystyle \frac{\Gamma (m+n+2+d)\Gamma (m+2)}{\Gamma (m+2+d)\Gamma (m+n+2)}}={\displaystyle \frac{\Gamma (m+2)}{\Gamma (m+2+d)}}{\displaystyle \frac{\Gamma (m+n+2+d)}{\Gamma (m+n+2)}},$$

$${\displaystyle \frac{\Gamma (m+n+2+d)}{\Gamma (m+n+2)}}={\displaystyle \frac{(m+n+1+d)\Gamma (m+n+1+d)}{(m+n+1)\Gamma (m+n+1)}}={\displaystyle \frac{(m+n+1+d)(m+n+d)\Gamma (m+n+d)}{(m+n+1)(m+n)\Gamma (m+n)}}.$$

And so on:

$${\sum }_{n=0}^{\infty }{\displaystyle \frac{\Gamma (m+n+2+d)\Gamma (m+2)}{{\alpha }^n\Gamma (m+2+d)\Gamma (m+n+2)}}=1+{\sum }_{n=1}^{\infty }{\alpha }^{-n}{\prod }_{k=0}^{n-1}{\displaystyle \frac{m+n+d+1-k}{m+n+1-k}}.$$

Since $0 < d < \alpha -1$ and m > 2, k = 0, …, $n-1$,

$$0<{\displaystyle \frac{m+n+d+1-k}{m+n+1-k}}=1+{\displaystyle \frac{d}{m+n+1-k}}<1+d,$$

$$1+{\sum }_{n=1}^{\infty }{\alpha }^{-n}{\prod }_{k=0}^{n-1}{\displaystyle \frac{m+n+d+1-k}{m+n+1-k}}<1+{\sum }_{n=1}^{\infty }{\alpha }^{-n}{\prod }_{k=0}^{n-1}\left(1+d\right)={\sum }_{n=0}^{\infty }{\left({\displaystyle \frac{1+d}{\alpha }}\right)}^n={\displaystyle \frac{\alpha }{\alpha -d-1}}.$$

Thus,

$$0<F_1^2\left(1,d+n+2;n+2;{\alpha }^{-1}\right)<{\displaystyle \frac{\alpha }{\alpha -d-1}}.$$

For example,

$${}_{2}F_1\left(1,5;4;{\displaystyle \frac{1}{2}}\right)=1.44<{\displaystyle \frac{4}{4-1-1}}, {}_{2}F_1\left(1,25;23;{\displaystyle \frac{1}{5}}\right)=1.28<{\displaystyle \frac{5}{5-2-1}}.$$

Since d > 0, we obtain the following for n = 3, 4, …:

$${\displaystyle \frac{d+n+1}{\alpha (n+1)}}={\displaystyle \frac{d}{\alpha (n+1)}}+{\displaystyle \frac{n+1}{\alpha (n+1)}}<{\displaystyle \frac{d+1}{\alpha }}, 0<S_2<{\displaystyle \frac{d+1}{\alpha -d-1}} .$$

We turn our attention to $S_1$:

$$\begin{array}{c}{\displaystyle \frac{{\alpha }^n\Gamma \left(n+1\right)}{\Gamma \left(n+1+d\right)}}={\alpha }^n{\displaystyle \frac{n\Gamma \left(n\right)}{(n+d)\Gamma \left(n+d\right)}}={\alpha }^n{\displaystyle \frac{n(n-1)\Gamma \left(n-1\right)}{(n+2)(n-1+2)\Gamma \left(n-1+d\right)}}= \dots =\\ {\alpha }^n{\displaystyle \frac{n\left(n-1\right)\left(n-2\right)\dots \Gamma \left(1\right)}{\left(n+d\right)\left(n-1+d\right)\dots \Gamma \left(1\right)}}={\alpha }^n{\displaystyle \frac{n}{n+d}}{\displaystyle \frac{n-1}{n-1+d}}\dots {\displaystyle \frac{1}{1+d}}>{\displaystyle \frac{{\alpha }^n}{{\left(1+d\right)}^n}}.\end{array}$$

Since $0 < d < \alpha -1,$ we conclude that

$$\underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\alpha }^n\Gamma \left(n+1\right)}{\Gamma \left(n+1+d\right)}}=\infty .$$

Now, since $c, d > 0,$ and $\alpha >1$,

$$\left({\left({1-\alpha }^{-1}\right)}^{d+1}-1\right)c<0<{\left({1-\alpha }^{-1}\right)}^{d+1}.$$

So, we can conclude from these computations that

$${\displaystyle \frac{\Gamma (d+1)}{c}}{\displaystyle \frac{c+(1-c){({1-\alpha }^{-1})}^{d+1}}{{({1-\alpha }^{-1})}^{d+1}}}={\displaystyle \frac{\Gamma (d+1)}{c}}{\displaystyle \frac{{\left({1-\alpha }^{-1}\right)}^{d+1}-\left({\left({1-\alpha }^{-1}\right)}^{d+1}-1\right)c}{{({1-\alpha }^{-1})}^{d+1}}}>0,$$

$$\underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{S}_1=\underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{\Gamma (d+1)}{c}}{\displaystyle \frac{c+(1-c){({1-\alpha }^{-1})}^{d+1}}{{({1-\alpha }^{-1})}^{d+1}}}{\displaystyle \frac{{\alpha }^n\Gamma \left(n+1\right)}{\Gamma \left(d+n+1\right)}}=\infty , {\underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}y}_n=0$$

□

For example, for a system with the values $a=2, c=1,$ and $d=4$, we consider that

$$x_n={\displaystyle \frac{n+5}{2n+2}}, y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+1}}, y_0=1$$

(11)

Using Excel, we calculated the first terms of the sequence, which are listed in

Table 2. Values of System (11).

n	x	y
0	2.5	1
1	1.5	0.714285714
2	1.166667	0.517241379
3	1	0.376344086
4	0.9	0.2734375
5	0.833333	0.197492163
6	0.785714	0.141318977
7	0.75	0.099939431
8	0.722222	0.069728131
9	0.7	0.047944746
10	0.681818	0.032471535
11	0.666667	0.021660134
12	0.653846	0.014234541
13	0.642857	0.009221375
14	0.633333	0.005893092
15	0.625	0.003718414
16	0.617647	0.00231862
17	0.611111	0.001430041
18	0.605263	0.000873151
19	0.6	0.000528207
29	0.566667	2.38186 × 10−6
39	0.55	7.01505 × 10−9

.

Now, let us study the case in which $0 < \alpha <1$. We change the notations so that $\lambda$ is the reciprocal of $\alpha$. In other words, we now study the system

$$x_n=\lambda {\displaystyle \frac{n+1+d}{n+1}}, y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+1}}, y_0=c, \lambda >1$$

(12)

In the same manner, we conclude that $y_n$ is the reciprocal of

$${\displaystyle \frac{\Gamma \left(n+1\right)}{c{\lambda }^n\Gamma \left(n+d+1\right)}}({\displaystyle \frac{c}{\lambda }}R\left(\lambda ,d,n+2\right)+\left(1-c\right)\Gamma \left(d+1\right)),$$

where

$$R\left(\lambda ,d,m\right)={\sum }_{j=1}^{m-1}{\displaystyle \frac{{\lambda }^j\Gamma \left(d+j\right)}{\Gamma \left(j\right)}}.$$

According to the previous formulas,

$$\begin{array}{c}R\left(\lambda ,d,m\right)=\lambda {\displaystyle \frac{\left(1-{\left(1-\lambda \right)}^{d+1}\right)\Gamma \left(d+1\right)}{{\left(1-\lambda \right)}^{d+1}}}+\lambda \Gamma \left(d+1\right)-{\displaystyle \frac{{\lambda }^m\Gamma \left(d+m\right)}{\Gamma \left(m\right)}}{}_{2}F_1\left(1,d+m;m;\lambda \right)=\\ {\displaystyle \frac{\lambda \Gamma (d+1)}{{(1-\lambda )}^{d+1}}}-{\displaystyle \frac{{\lambda }^m\Gamma \left(d+m\right)}{\Gamma \left(m\right)}}{}_{2}F_1\left(1,d+m;m,\lambda \right)\end{array}$$

But we now have negative values for the hypergeometric function. For example,

$${}_{2}F_1\left(1,9;5;3\right)=-{\displaystyle \frac{433}{2240}}.$$

In fact, we tested the value of ${}_{2}F_1\left(1,d+n;n,x\right)$ for d = 1, 2, 3, and 4 by using Mathematica online as we did previously, and we concluded that

$${}_{2}F_1\left(1,d+n;n;x\right)={\displaystyle \frac{n^d{(x-1)}^d+a_1{n}^{d-1}+\dots +a_d}{n\left(n+1\right)\left(n+2\right)\dots \left(n+d-1\right)(1-x)({x-1)}^d}},$$

where $a_1,\dots ,a_d$ are constants. For example,

$${}_{2}F_1\left(1,2+n;n;x\right)={\displaystyle \frac{n^2{(x-1)}^2+\left(1-x^2\right)n+2x}{n\left(n+1\right)(1-x){(x-1)}^2}}.$$

We calculate the following expressions as indicated:

$$\begin{array}{c}{\lambda }^{-1}cR\left(\lambda ,d,m\right)+\left(1-c\right)\Gamma \left(d+1\right)=\\ {\displaystyle \frac{c+\left(1-c\right){(1-\lambda )}^{d+1}}{{(1-\lambda )}^{d+1}}}\Gamma \left(d+1\right)-{\displaystyle \frac{{c\lambda }^{m-1}\Gamma \left(d+m\right)}{\Gamma \left(m\right)}}{}_{2}F_1\left(1,d+m;m;\lambda \right),\\ {\displaystyle \frac{\Gamma \left(m-1\right)}{c{\lambda }^{m-2}\Gamma \left(m-1+d\right)}}\left({\lambda }^{-1}cR\left(\lambda ,d,m\right)+\left(1-c\right)\Gamma \left(d+1\right)\right)=S_1-S_2,\end{array}$$

where

$$S_1={\displaystyle \frac{\Gamma (d+1)}{c}}{\displaystyle \frac{c+(1-c){(1-\lambda )}^{d+1}}{{(1-\lambda )}^{d+1}}}{\displaystyle \frac{\Gamma \left(m-1\right)}{{\lambda }^{m-2}\Gamma \left(d+m-1\right)}},$$

$$S_2=\lambda {\displaystyle \frac{\Gamma (m-1)\Gamma (d+m)F_1^2(1,d+m;m,\lambda )}{\Gamma \left(m\right)\Gamma (d+m-1)}}=\lambda {\displaystyle \frac{d+m-1}{m-1}}{}_{2}F^1(1,d+m;m;\lambda ).$$

Therefore,

$$\underset{m\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{S}_2={\displaystyle \frac{\lambda }{1-\lambda }}.$$

We can now turn our attention to $S_1$. Since the gamma function increases at the interval (1.46, ∞), we obtain the following for m = 3, 4, …:

$$0<{\displaystyle \frac{\Gamma \left(m-1\right)}{{\lambda }^{m-2}\Gamma \left(d+m-1\right)}}<{\displaystyle \frac{1}{{\lambda }^{m-2}}}.$$

In the case that $\lambda >1$ and $c>0$, we conclude that

$$\underset{m\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{\Gamma \left(m-1\right)}{{\lambda }^{m-2}\Gamma \left(d+m-1\right)}}=0, \underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{S}_1=0,$$

$$\underset{m\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{\Gamma \left(m-1\right)}{c{\lambda }^{m-2}\Gamma \left(m-1+d\right)}}\left({\lambda }^{-1}cR\left(\lambda ,d,m\right)+\left(1-c\right)\Gamma \left(d+1\right)\right)={\displaystyle \frac{\lambda }{\lambda -1}}.$$

Proposition 3.

Let $\lambda$ and $c$ be positive real numbers, with $\lambda >1$. Then, for the solution of System (12), we have

$$\underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{y}_n={\displaystyle \frac{\lambda -1}{\lambda }}, \underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{x}_n=\lambda .$$

We reformulate the result as follows: Let $\lambda$ and $c$ be positive real numbers, with $0<\alpha <1$. Then, for the solution of System (10), we have

$$\underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{x}_n={\displaystyle \frac{1}{\alpha }}, \underset{n\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{y}_n=1-\alpha .$$

For example, the system with the values $\lambda =3,c=8,$ and $d=4$ is

$$x_n={\displaystyle \frac{3n+15}{n+1}}, y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+1}},{ y}_0=8$$

(13)

We then obtain

$$\begin{array}{c}{x}_0=15, x_1={\displaystyle \frac{18}{2}}=9, x_2={\displaystyle \frac{21}{3}}=7{, x_3={\displaystyle \frac{24}{4}}=6,{ x}_4={\displaystyle \frac{27}{5}}, y}_0=8, y_1={\displaystyle \frac{120}{121}},\\ y_2={\displaystyle \frac{\frac{9\ast 120}{9\ast 120+1}}{\frac{9\ast 120}{9\ast 120}+1}}={\displaystyle \frac{\frac{1080}{121}}{\frac{1080}{121}+1}}={\displaystyle \frac{1080}{1201}}, y_3={\displaystyle \frac{7\ast 9\ast 120}{7\ast 9\ast 120+1201}}={\displaystyle \frac{7560}{7560+1201}}={\displaystyle \frac{7560}{8761}},\\ y_4={\displaystyle \frac{\mathrm{45,360}}{\mathrm{45,360}+8761}}={\displaystyle \frac{\mathrm{45,360}}{\mathrm{54,121}}}=0.83812, y_5={\displaystyle \frac{\frac{27}{5}\ast \frac{\mathrm{45,360}}{\mathrm{54,121}}}{\frac{27}{5}\ast \frac{\mathrm{45,360}}{\mathrm{54,121}}+1}}={\displaystyle \frac{\mathrm{244,944}}{\mathrm{299,065}}}=0.81903.\end{array}$$

Using Excel, we calculated some other terms of the sequence, which are listed in

Table 3. Values of System (13).

n	x	y
6	4.714285714	0.803735435
7	4.5	0.791189817
8	4.333333333	0.780718786
9	4.2	0.77185174
10	4.090909091	0.764249764
11	4	0.757662488
12	3.923076923	0.751901055
13	3.857142857	0.746820424
14	3.8	0.74230743
15	3.75	0.738272531
16	3.705882353	0.734643979
17	3.666666667	0.731363631
18	3.631578947	0.728383883
19	3.6	0.725665394

:

We notice that ${\displaystyle \frac{\lambda -1}{\lambda }}={\displaystyle \frac{2}{3}}=0.666667$. It is clear that the sequence is decreasing and that two-thirds is the lower limit. To be precise, using Mathematica, we conclude that the exact value of the solution is

$$y_{n+1}={\displaystyle \frac{4(n+1)(n+2)(n+3)(n+4)3^n}{(2n\left(n\left(n\left(n+8\right)+26\right)+34\right)+33)3^{n+1}-87}},$$

and we see immediately that two-thirds is the limit.

We can now study the system in the remaining case, which is $\lambda =\alpha =1$, i.e.,

$$x_n={\displaystyle \frac{n+1+d}{n+1}}, y_{n+1}={\displaystyle \frac{x_n{y}_n}{x_n{y}_n+1}},{ y}_0=c.$$

(14)

This is a simple case. We state the result in a separate proposition.

Proposition 4.

Assume that $d > 0$. Then, the general solution of System (14) converges to zero.

Proof. 

Of course, $y_n$ is the reciprocal of

$${\displaystyle \frac{\Gamma \left(n+1\right)}{c\Gamma \left(n+d+1\right)}}(cR\left(1,d,n+2\right)+\left(1-c\right)\Gamma \left(d+1\right)),$$

where

$$R\left(1,d,m\right)={\sum }_{j=1}^{m-1}{\displaystyle \frac{\Gamma \left(d+j\right)}{\Gamma \left(j\right)}}$$

Using Mathematica (online) as we did previously,

$$R\left(1,d,m\right)={\displaystyle \frac{\left(m-1\right)\Gamma \left(d+m\right)}{(d+1)\Gamma \left(m\right)}}$$

In other words, $y_n$ is the reciprocal of

$${\displaystyle \frac{\Gamma \left(n+1\right)}{c\Gamma \left(n+d+1\right)}}\left(c{\displaystyle \frac{\left(n+1\right)\Gamma \left(d+n+2\right)}{\left(d+1\right)\Gamma \left(n+2\right)}}+\left(1-c\right)\Gamma \left(d+1\right)\right)=\left({\displaystyle \frac{d+n+1}{d+1}}+{\displaystyle \frac{(1-c)\Gamma \left(d+1\right)}{c}}{\displaystyle \frac{\Gamma \left(n+1\right)}{\Gamma \left(n+d+1\right)}}\right)$$

Since $d>0$, the limit of this quantity is infinity, the sequence converges to zero for all real values of c. □

3. Conclusions

We have determined the limits of some sequences without determining the explicit formulas of the solutions, which might be not easily expressible in closed form. We encountered many formulas, which were provided by the software program Mathematica. Yet there are still cases to be studied in the future. We studied special cases due to the lack of formulas of summation in some cases.