A Novel Approach to Strengthening Cryptography Using RSA, Efficient Domination and Fuzzy Logic

Abstract

A secured communications system is a structure or infrastructure that is intended to ensure the confidentiality, integrity, and authenticity of data being exchanged between entities. Such systems use various security technologies to guarantee that communications are not tampered with, read, or accessed by unauthorized parties. The intractability of factoring huge composite numbers is a prerequisite for RSA’s security. With big enough key sizes, it is still computationally infeasible for attackers to defeat RSA encryption with today’s technology. Efficient domination is an idea based on graph theory, specifically in the investigation of domination in graphs. Although it has many applications in problems in computation, it is only for cryptography in contexts involving efficient algorithms, combinatorial structures, and optimization for security that it finds uses. This idea provides minimal redundancy in domination, similar to the optimization of resources in a cryptographic scenario. In this work, we concentrate on enhancing the complexity of secure systems using a mathematical model that is based on fuzzy graph networks. The suggested model combines efficient domination, the RSA algorithm, and triangular fuzzy membership functions. By integrating these optimized parameters, we construct a very secure mathematical fuzzy graph network that can efficiently protect secret information.

1. Introduction

Fuzzy graph networks merge fuzzy set theory and graph theory and offer a mechanism to model imprecision, vagueness, and uncertainty in systems and relations. Fuzzy graph networks increasingly find application in cryptography because they can deal with ambiguity and allow flexible solutions for security issues. Fuzzy graph networks are graphs whose nodes and edges possess fuzzy attributes that define uncertain or imprecise relationships between entities. A fuzzy graph is represented by $\mathbb{G}$ = ($\mathbb{V}$, υ, ω), where υ is a mapping from $\mathbb{V}$ into [0, 1], a membership function representing the extent of participation of a vertex, and ω is a mapping from $\mathbb{V}$ × $\mathbb{V}$ into [0, 1], a relation showing the extent of the relationship (edge weight) between two vertices.

If every vertex in the graph is either in the subset or adjacent to at least one vertex in the subset, the subset is known as a dominating set in graph theory. A dominating set in a graph that has the further requirement that just one vertex in the dominating set dominates every vertex in the graph is called an efficient dominating set, often referred to as a perfect dominating set. This ensures that domination is not redundant and is therefore an “efficient” solution. Vertex set $\mathbb{D}$ is a subset of $\mathbb{V}$ of $\mathbb{G}$ = ($\mathbb{V}$, υ, ω) and is a dominating set if, for each vertex ${\mathfrak{x}}_1$ in $\mathbb{V}$ − $\mathbb{D}$, the following condition is met: (i) υ(${\mathfrak{x}}_1$) > 0 and the vertex ${\mathfrak{x}}_1$ is in $\mathbb{D}$, or (ii) ${\mathfrak{x}}_1$ is adjacent to vertex ${\mathfrak{x}}_2$ in $\mathbb{D}$, with ω(${\mathfrak{x}}_1,{\mathfrak{x}}_2$) > 0. The edge (${\mathfrak{x}}_1,{\mathfrak{x}}_2$) connects to ${\mathfrak{x}}_2$ in $\mathbb{D}$ and contains a positive membership value. A fuzzy graph network ($\mathfrak{F}\mathfrak{G}\mathfrak{N})$ is a graph network if it satisfies ω(${\mathfrak{x}}_1,{\mathfrak{x}}_2$) $\le$ min($\upsilon \left({\mathfrak{x}}_1\right),\upsilon ({\mathfrak{x}}_2))$ for every (${\mathfrak{x}}_1,{\mathfrak{x}}_2$) in $\mathbb{V}$. A fuzzy graph network is said to be a strong fuzzy graph network (${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}})$ if ω(${\mathfrak{x}}_1,{\mathfrak{x}}_2$) $=$ min($\upsilon \left({\mathfrak{x}}_1\right),\upsilon ({\mathfrak{x}}_2))$ for every (${\mathfrak{x}}_1,{\mathfrak{x}}_2$) in $\mathbb{V}.$

To define the notion of uncertainty in practical situations, Zadeh presented a mathematical theory in 1965 [1]. This was the start of fuzzy graph theory and research on certain kinds of connected graph theoretical structures. Research by Bondy and U.S.R. Murthy delved into graph theory and its diverse applications [2]. Ore [3] studied dominance in graph structures. Haynes et al. [4] initiated research on paired domination. Biggs [5] and Kulli [6] contributed prominently to the theoretical part of domination in graphs. Kulli and Janakiram [7] worked on split domination, whereas Kulli and Patwari [8] worked on graph domination in general. Cockayne and Hedetniemi [9] first proposed the independent domination numbers in graphs. Meenakshi and Baskar Babujee [10] extended the idea of paired equitable domination. Kwon et al. [11] were involved in classifying efficiently dominant sets of circular graphs with a degree of 5. Somasundram A and Somasundram S studied domination and total domination in fuzzy graphs [12]. Nagoorkani and chandrasekaran [13] studied domination in fuzzy graphs. Atanassov [14] laid the basis for intuitionistic fuzzy graphs (IFGs) and intuitionistic fuzzy relations. Enrico Enriquez [15] researched domination in fuzzy directed graphs, while Atanassov worked on intuitionistic fuzzy graphs and their relational structures. Karunambigai et al. later examined a certain subtype of IFGs, as characterized by Shannon and Atanassov [16].

Pius et al. [17] proposed a cryptographic method to encrypt sensitive information to solve data privacy in fuzzy graph theory. Wang et al. [18] gave a more concise derivation for matrix extension by extending the extended visual Cryptography Scheme to encrypt several color pictures with significant shares. Also, the authors proposed new applications for these tagged structures and cryptography to optimize the graph features, particularly in networks that require high efficiency and interconnectedness. The paper presented a mathematical framework and outlined its applications in network security. The work was subsequently followed up by Meenakshi et al. [19] and later generalized to hypergraphs [20]. Wu et al. [21] suggested a security model based on hypergraph structures to model and handle security mechanisms over multiple layers in optical networks. Finally, in [22,23,24,25,26], the authors discussed various types and applications of fuzzy graphs.

Motivation and Novelty

Although many studies have considered fuzzy-logic-based cryptographic systems, most of them consider fuzzy authentication, threshold schemes, or standard fuzzy set uses without incorporating essential structural graph theoretic features. Fuzzy and intuitionistic fuzzy graphs have been considered for modeling uncertainty in networks in previous research, and RSA is a well-established encryption technique. The integration of fuzzy domination principles with traditional cryptographic methods is still unexplored. The innovation of this research is the integration of efficient domination in fuzzy graph networks with RSA cryptosystem, a layered encryption mechanism that increases security through mathematical complexity and structural optimization. In contrast to traditional hybrid cryptosystems, which tend to merge fuzzy logic concepts with encryption schemes, our approach embeds data within fuzzy graph structures that are controlled by effective dominating sets, minimizing redundancy and maximizing control in secure communication. In addition, the employment of triangular fuzzy membership functions and strong fuzzy graph networks in the cryptographic process introduces a new paradigm for handling uncertainty and vagueness in encryption methods. This integrated framework not only enhances encryption but also confers a structural advantage in secure key distribution and decryption, hence presenting a marked improvement over earlier methods.

For the sake of clarity, a list of all symbols and notations employed in this paper is given in

Table 1. Glossary.

Symbol	Description
$\mathbb{G}$ = ($\mathbb{V}$, $\upsilon$, ω)	Fuzzy graph, where $\mathbb{V}$ is the vertex set.
$\upsilon$(${\mathfrak{x}}_i$)	Fuzzy membership value of vertex ${\mathfrak{x}}_i$, where υ: $\mathbb{V}$→[0, 1].
$\omega$(${\mathfrak{x}}_i,{\mathfrak{x}}_j)$	Fuzzy membership (edge weight) between vertices ${\mathfrak{x}}_i\mathrm{and} {\mathfrak{x}}_j$, where $\omega$: $\mathbb{V}$ × $\mathbb{V}$→[0, 1].
$\mathbb{D}$ ⊆ $\mathbb{V}$	Dominating set in fuzzy graph.
${\mathfrak{M}}_1$, ${\mathfrak{M}}_2,\dots ,{\mathfrak{M}}_k$	Components split from plaintext.
${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$, ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$, …, ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}r$	Sub networks constructed from each component after encryption process.
$x_{11},x_{12},\dots ,x_{1i}$	Vertices in the sub network 1, typically used to denote neighbors or elements in subset relations.
$\mathfrak{F}\mathfrak{G}\mathfrak{N}$	Fuzzy graph network.
${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$	Strong fuzzy graph network.
$\mathbb{e},\mathbb{n}$	RSA encryption exponent and modulus, respectively.
$\mathbb{d}$	RSA decryption exponent.
$\mathcal{N}\mathcal{P}\mathcal{L}$	Numerical plaintext message.
$\mathbb{C}$	Cipher text obtained after encryption.
${\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,\dots ,{\mathcal{a}}_r$	Efficient dominating nodes of complex network.
${\mathcal{p}}_{11},{\mathcal{p}}_{12},\dots ,{\mathcal{p}}_{1r}$	Neighboring vertices of efficient dominating nodes.
${\mathfrak{F}}_{11},{\mathfrak{F}}_{12}{,\mathfrak{F}}_{13},\dots ,{\mathfrak{F}}_{1r}$	Node membership values of sub network.
${\mathfrak{P}}_{11},$${\mathfrak{P}}_{12},\dots {,\mathfrak{P}}_{1n}$	Prime numbers chosen for RSA encryption.
$<\mathbb{r},\mathbb{s},\mathbb{t}>$	Triangular fuzzy numbers.
${\mathsf{\Psi }(\mathfrak{F}}_r)$	Membership values of triangular fuzzy number.

.

Section 2 describes how a fuzzy graph network can be constructed using an efficient dominating set, RSA algorithm, and triangular fuzzy membership function. Section 3, Section 4 and Section 5 present the encryption and decryption algorithms of the designed cryptosystem. Section 6 presents the cryptosystem through an example that explains how to obtain the cipher graph and plaintext of the secret data. Section 7 provides a comparative study of various cryptographic methods against the proposed one. Section 8, Section 9 and Section 10 present the flowchart of the proposed cryptosystem and possible vector attacks and Section 11 presents the conclusion.

2. Proposed Cryptosystem

The proposed system consists of (i) the numerical plaintext, (ii) cipher graph, (iii) encryption algorithm, (iv) decryption algorithm and (v) key.

(i)

Numerical plaintext: This is the original, readable, and unencrypted data or message. It is what is fed into an encryption procedure, which scrambles it to make it unreadable in the form of a cipher graph to secure its confidentiality. In this cryptosystem, the numerical plaintext is the non-negative composite number.

(ii)

Cipher graph: This is the encrypted, non-readable data resulting from plaintext having an encryption algorithm applied to it. It is meant to safeguard the original information against unauthorized parties, so its confidentiality can be guaranteed during storage or transmission. In this study, the cipher graph is a fuzzy graph network, and it is denoted by ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$.

(iii)

Encryption algorithm: This is a mathematical operation to convert plaintext (readable data) into a cipher graph (unreadable data) in order to maintain its confidentiality and security. This algorithm, along with a cryptographic key, specifies how the conversion is performed. In this cryptosystem, the encryption algorithm is constructed based on RSA, efficient domination and the triangular fuzzy membership function.

(iv)

Decryption algorithm: This is an algorithmic process applied to decrypt data that have been encrypted back to their original readable form. It is the inverse of encryption and needs the proper cryptographic key in order to execute the conversion.

(v)

Key: This is a piece of information, often a string of characters, used in conjunction with an encryption or decryption algorithm to secure and unlock data. Keys are a fundamental component of cryptographic systems, determining how data are encrypted or decrypted. The keys used in this methodology are (i) finding efficient dominating nodes in the cipher graph represented as ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ (key 1), (ii) finding the range of triangular fuzzy triplets (key 2) and (iii) RSA private key $\mathbb{d}$. The decryption process is performed by applying these keys to access the numerical plaintext.

3. Construction of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$

Step 1: Let the numerical plain text $\mathcal{N}\mathcal{P}\mathcal{L}$ be

$$x_{11}{x}_{12}{x}_{13}\dots x_{1i_1}/x_{21}{x}_{22}{x}_{23}\dots x_{2i_2}/x_{31}{x}_{32}{x}_{33}\dots x_{3i_3}//x_{(r-1)1}{x}_{(r-1)2}\dots x_{(r-1)i_{(r-1)}}/x_{r1}{x}_{r2}\dots x_{r{i}_r},$$

where k and $\mathcal{i}$_r are positive integers.

Partition the $\mathcal{N}\mathcal{P}\mathcal{L}$ as

$${\mathfrak{M}}_1=x_{11}{x}_{12}{x}_{13}\dots x_{1i_1},{\mathfrak{M}}_2=x_{21}{x}_{22}{x}_{23}\dots x_{2i_2},{\mathfrak{M}}_3=x_{31}{x}_{32}{x}_{23}\dots x_{2i_2},\dots ,{\mathfrak{M}}_{(r-1)}=x_{(r-1)1}{x}_{(r-1)2}\dots x_{(r-1)i_{(r-1)}},{\mathfrak{M}}_r=x_{r1}{x}_{r2}\dots x_{r{i}_r}.$$

Step 2: Using ${\mathfrak{M}}_1=x_{11}{x}_{12}{x}_{13}\dots x_{1i_1}$, the first sub network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$ is constructed. By using the RSA algorithm, find the encrypted message that says ${\mathbb{C}}_1\equiv {{\mathfrak{M}}_1}^{{\mathbb{e}}_1}$ $(\mathrm{m}\mathrm{o}\mathrm{d}{\mathfrak{N}}_1)$, which corresponds to ${\mathfrak{M}}_1$. Convert ${\mathbb{C}}_1$ into a triangular fuzzy number and let it be ${\mathfrak{F}}_1$. Let ${\mathfrak{F}}_1={\mathfrak{F}}_{11}+{\mathfrak{F}}_{12}+{\mathfrak{F}}_{13}+\dots +{\mathfrak{F}}_{1{\mathrm{i}}_1}$.

Step 3: Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$ (Figure 1) be ${\mathcal{a}}_1,{\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},\dots ,{\mathcal{p}}_{1{\mathrm{i}}_1}$ such that the distance between ${\mathcal{a}}_1$ and ${\mathcal{p}}_{1{\breve{\mathcal{k}}}_1}=1$, where $1\le {\breve{\mathcal{k}}}_1\le {\mathcal{i}}_1$. Regarding the node membership value ($\mathbb{N}\mathbb{M}\mathbb{V}),$ the $\mathbb{N}\mathbb{M}\mathbb{V}$ values of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$ ${\mathcal{a}}_1,{\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},\dots ,{\mathcal{p}}_{1{\mathrm{i}}_1}$ are given by ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11},{\mathfrak{F}}_{12}{,\mathfrak{F}}_{13},\dots ,{\mathfrak{F}}_{1{\mathrm{i}}_1}$, respectively. The edge membership values $(\mathbb{E}\mathbb{M}\mathbb{V})$ are $\mathbb{E}\mathbb{M}\mathbb{V}$ $({\mathcal{a}}_1,{\mathcal{p}}_{11})=\mathrm{m}\mathrm{i}\mathrm{n}$ $({\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11}),{\mathbb{E}\mathbb{M}\mathbb{V}({\mathcal{a}}_1,\mathcal{p}}_{12})=\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{12}\right),\mathbb{E}\mathbb{M}\mathbb{V}\left({\mathcal{a}}_1,{\mathcal{p}}_{13}\right)=\mathrm{m}\mathrm{i}\mathrm{n}({\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{13}),\dots ,$ and $\mathbb{E}\mathbb{M}\mathbb{V}{(\mathcal{a}}_1,{\mathcal{p}}_{1{\mathrm{i}}_1})$ $=$ min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{1{\mathrm{i}}_1})$, respectively.

Step 4: Using ${\mathfrak{M}}_2=x_{21}{x}_{22}{x}_{23}\dots x_{2i_2}$, the second sub network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$ is constructed. By using the RSA algorithm, find the encrypted message that says ${\mathbb{C}}_2\equiv {{\mathfrak{M}}_2}^{{\mathbb{e}}_2}$ $(\mathrm{m}\mathrm{o}\mathrm{d}{\mathfrak{N}}_2)$, which corresponds to ${\mathfrak{M}}_2$. Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$ be ${{\mathcal{a}}_2,\mathcal{p}}_{21},{\mathcal{p}}_{22},{\mathcal{p}}_{23},\dots ,{\mathcal{p}}_{2{\mathrm{i}}_2}$ such that the distance between ${\mathcal{a}}_2$ and ${\mathcal{p}}_{2{\mathrm{k}}_2}$ is equal to 1, where $1\le {\breve{\mathcal{k}}}_2\le {\mathcal{i}}_2$. The $\mathbb{N}\mathbb{M}\mathbb{V}\mathrm{s}$ of ${{\mathcal{a}}_2,\mathcal{p}}_{21},{\mathcal{p}}_{22},{\mathcal{p}}_{23},\dots ,{\mathcal{p}}_{2{\mathrm{i}}_2}$ are ${\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{21},{\mathfrak{F}}_{22}{,\mathfrak{F}}_{23},\dots ,{\mathfrak{F}}_{2{\mathrm{i}}_2}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ of $\left({\mathcal{a}}_2,{\mathcal{p}}_{21}\right)=\mathrm{m}\mathrm{i}\mathrm{n}({\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{21}),$ $\mathbb{E}\mathbb{M}\mathbb{V}({\mathcal{a}}_2,{\mathcal{p}}_{22})$ = min (${\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{22}),\mathbb{E}\mathbb{M}\mathbb{V}({\mathcal{a}}_2,{\mathcal{p}}_{23})$ = min (${\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{23})$, …, and $\mathbb{E}\mathbb{M}\mathbb{V}{(\mathcal{a}}_2,{\mathcal{p}}_{2{\mathrm{i}}_2})$ = min (${\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{2{\mathrm{i}}_2})$, respectively.

Step 5: Continuing this until the last step, construct rth sub network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}\mathrm{r}$. Using $x_{r1}{x}_{r2}\dots x_{r{i}_r}$, rth sub network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}\mathrm{r}$ is constructed. By using the RSA algorithm, find the encrypted message and let it be ${\mathbb{C}}_{\mathrm{r}}\equiv {{\mathfrak{M}}_{\mathrm{r}}}^{{\mathbb{e}}_r}(\mathrm{m}\mathrm{o}\mathrm{d}{\mathfrak{N}}_{\mathrm{r}})$, which corresponds to ${\mathfrak{M}}_{\mathrm{r}}$. Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}\mathrm{r}$ be ${\mathcal{a}}_{\mathrm{r}},{\mathcal{p}}_{\mathrm{r}1},{\mathcal{p}}_{\mathrm{r}2},{\mathcal{p}}_{\mathrm{r}3},\dots ,{\mathcal{p}}_{\mathrm{r}{\mathrm{i}}_{\mathrm{r}}}$ such that the distance between ${\mathcal{a}}_{\mathrm{r}}$ and ${\mathcal{p}}_{\mathrm{r}\mathrm{k}}$ = 1, where $1\le {\breve{\mathcal{k}}}_{\mathrm{r}}\le {\mathcal{i}}_{\mathrm{r}}.$ The $\mathbb{N}\mathbb{M}\mathbb{V}\mathrm{s}$ of ${\mathcal{a}}_{\mathrm{r}},{\mathcal{p}}_{\mathrm{r}1},{\mathcal{p}}_{\mathrm{r}2},{\mathcal{p}}_{\mathrm{r}3},\dots ,{\mathcal{p}}_{\mathrm{r}{\mathrm{i}}_{\mathrm{r}}}$ are ${{\mathfrak{F}}_{{\mathrm{r}}_{\mathcal{a}}},\mathfrak{F}}_{\mathrm{r}1},{\mathfrak{F}}_{\mathrm{r}2}{,\mathfrak{F}}_{\mathrm{r}3},\dots ,{\mathfrak{F}}_{\mathrm{r}{\mathrm{i}}_{\mathrm{r}}}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}{(\mathcal{a}}_{\mathrm{r}},{\mathcal{p}}_{\mathrm{r}1})$ = min (${\mathfrak{F}}_{{\mathrm{r}}_{\mathcal{a}}},{\mathfrak{F}}_{\mathrm{r}1}),\mathbb{E}\mathbb{M}\mathbb{V}$ ${(\mathcal{a}}_{\mathrm{r}},{\mathcal{p}}_{\mathrm{r}2})$ = min (${\mathfrak{F}}_{{\mathrm{r}}_{\mathcal{a}}},{\mathfrak{F}}_{\mathrm{r}2}),\mathbb{E}\mathbb{M}\mathbb{V}$ ${(\mathcal{a}}_{\mathrm{r}},{\mathcal{p}}_{\mathrm{r}3})$ = min (${\mathfrak{F}}_{{\mathrm{r}}_{\mathcal{a}}},{\mathfrak{F}}_{\mathrm{r}3})$, …, and $\mathbb{E}\mathbb{M}\mathbb{V}$ ${(\mathcal{a}}_{\mathrm{r}},{\mathcal{p}}_{\mathrm{r}\mathrm{i}\mathrm{r}})$ = min (${\mathfrak{F}}_{{\mathrm{r}}_{\mathcal{a}}},{\mathfrak{F}}_{\mathrm{r}\mathrm{i}\mathrm{r}})$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ of the rest of the constructed edges is established according to the definition of $\mathfrak{F}\mathfrak{G}.$

Step 6: Let ${\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,\dots ,{\mathcal{a}}_{\mathrm{r}}$ be the nodes of the efficient dominating set, which has $\mathbb{N}\mathbb{M}\mathbb{V}\mathrm{s}$ that are ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{2_{\mathcal{a}}}{,\mathfrak{F}}_{3_{\mathcal{a}}},\dots {,\mathfrak{F}}_{{\mathrm{r}}_{\mathcal{a}}}.$ Construct network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ using ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2,\dots ,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}\mathrm{r}$ as follows. The node set of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is $\mathfrak{V}\left({\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}\right)=\{{\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,\dots ,{\mathcal{a}}_{\mathrm{r}}\}\bigcup \{{\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},\dots ,{\mathcal{p}}_{\mathrm{r}{\breve{\mathcal{k}}}_{\mathrm{r}}}\}$ where $1\le {\breve{\mathcal{k}}}_1\le {\mathcal{i}}_1,1\le {\breve{\mathcal{k}}}_2\le {\mathcal{i}}_2,1\le {\breve{\mathcal{k}}}_3\le {\mathcal{i}}_3,\dots ,1\le {\breve{\mathcal{k}}}_{\mathrm{r}}\le {\mathcal{i}}_{\mathrm{r}}.$ The number of nodes present in ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is r + ${\mathcal{i}}_1$ + ${\mathcal{i}}_2$ + ${\mathcal{i}}_3$ + … + ${\mathcal{i}}_{\mathrm{r}}.$ The minimum number of edges required for ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is calculated as follows.

Step 7: Define ${\mathcal{E}}_1=\{{(\mathcal{p}}_{1{\breve{\mathcal{k}}}_1}{,\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}){,(\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}{\mathcal{p}}_{3{\breve{\mathcal{k}}}_3}),{(\mathcal{p}}_{3{\breve{\mathcal{k}}}_3,},{\mathcal{p}}_{4{\breve{\mathcal{k}}}_4}),\dots ,{(\mathcal{p}}_{\left(\mathrm{r}-2\right){\breve{\mathcal{k}}}_{\left(\mathrm{r}-2\right)}}),{(\mathcal{p}}_{(\mathrm{r}-1){\breve{\mathcal{k}}}_{(\mathrm{r}-1)}})\}$ for only one $1\le {\breve{\mathcal{k}}}_1\le {\mathcal{i}}_1,1\le {\breve{\mathcal{k}}}_2\le {\mathcal{i}}_2,1\le {\breve{\mathcal{k}}}_3\le {\mathcal{i}}_3,\dots ;1\le {\breve{\mathcal{k}}}_{\mathrm{r}-1}\le {\mathcal{i}}_{\mathrm{r}-1}.$ ${\mathcal{E}}_2=\{{(\mathcal{a}}_1{,\mathcal{p}}_{1{\breve{\mathcal{k}}}_1}){,(\mathcal{a}}_2{,\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}),{(\mathcal{a}}_3{,\mathcal{p}}_{3{\breve{\mathcal{k}}}_3}),\dots ,{(\mathcal{a}}_{\mathrm{r}}{,\mathcal{p}}_{\mathrm{r}{\breve{\mathcal{k}}}_{\mathrm{r}}})\}$ where $1\le {\breve{\mathcal{k}}}_1\le {\mathcal{i}}_1,1\le {\breve{\mathcal{k}}}_2\le {\mathcal{i}}_2,1\le {\breve{\mathcal{k}}}_3\le {\mathcal{i}}_3,\dots ,1\le {\breve{\mathcal{k}}}_{\mathrm{r}}\le {\mathcal{i}}_{\mathrm{r}}$. The minimum number of edges required for ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is ${\mathcal{E}}_{\left(\mathrm{M}\mathrm{i}\mathrm{n}\right)}$ = ${\mathcal{E}}_1\cup {\mathcal{E}}_2$.

Step 8: The maximum number of edges required for ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is ${\mathcal{E}}_{\left(\mathrm{M}\mathrm{a}\mathrm{x}\right)}$ = (r + ${\mathcal{i}}_1$ + ${\mathcal{i}}_2$ + ${\mathcal{i}}_3$ + … + ${\mathcal{i}}_{\mathrm{r}}){\mathcal{C}}_2-\{({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_2),({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_3),({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_4),\dots ,({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_{\mathrm{r}}) \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1\le {\breve{\mathcal{k}}}_1\le {\mathcal{i}}_1,$ $({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_1),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_3),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_4),\dots ,({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_{\mathrm{r}}), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1\le {\breve{\mathcal{k}}}_2\le {\mathcal{i}}_2,$ $({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_1),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_2),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_4), \dots ,{(\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_{\mathrm{r}}), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1\le {\breve{\mathcal{k}}}_3\le {\mathcal{i}}_3,\dots ,$ $({\mathcal{p}}_{\left(\mathrm{r}-1\right){\breve{\mathcal{k}}}_{\left(\mathrm{r}-1\right)}},{\mathcal{a}}_1),({\mathcal{p}}_{\left(\mathrm{r}-1\right){\breve{\mathcal{k}}}_{\left(\mathrm{r}-1\right)}},{\mathcal{a}}_2),({\mathcal{p}}_{\left(\mathrm{r}-1\right){\breve{\mathcal{k}}}_{\left(\mathrm{r}-1\right)}},{\mathcal{a}}_3),\dots ,{(\mathcal{p}}_{\left(\mathrm{r}-1\right){\breve{\mathcal{k}}}_{\left(\mathrm{r}-1\right)}},{\mathcal{a}}_{\mathrm{r}}), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1\le {\breve{\mathcal{k}}}_{\left(\mathrm{r}-1\right)}\le {\mathcal{i}}_{\left(\mathrm{r}-1\right)}, \mathrm{a}\mathrm{n}\mathrm{d} ({\mathcal{p}}_{\mathrm{r}{\breve{\mathcal{k}}}_{\mathrm{r}}},{\mathcal{a}}_1),({\mathcal{p}}_{\mathrm{r}{\breve{\mathcal{k}}}_{\mathrm{r}}},{\mathcal{a}}_2),({\mathcal{p}}_{\mathrm{r}{\breve{\mathcal{k}}}_{\mathrm{r}}},{\mathcal{a}}_4),\dots ,{(\mathcal{p}}_{\mathrm{r}{\breve{\mathcal{k}}}_{\mathrm{r}}},{\mathcal{a}}_{\mathrm{r}}),$ where $1\le {\breve{\mathcal{k}}}_{\mathrm{r}}\le {\mathcal{i}}_{\mathrm{r}}$}.

4. Encryption Procedure

Input: $\mathcal{N}\mathcal{P}\mathcal{L}:$ $x_{11}{x}_{12}{x}_{13}\dots x_{1i_1}{x}_{21}{x}_{22}{x}_{23}\dots x_{2i_2}\dots x_{r1}{x}_{r2}\dots x_{r{i}_r}$ where $\mathcal{N}\mathcal{P}\mathcal{L}>0$.

Output: Cipher graph ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$.

Step 1: Let the numerical plaintext $\mathcal{N}\mathcal{P}\mathcal{L}$ be $x_{11}{x}_{12}{x}_{13}\dots x_{1i_1}/x_{21}{x}_{22}{x}_{23}\dots x_{2i_2}/\dots /x_{r1}{x}_{r2}\dots x_{r{i}_r},$ where k and i_r are positive integers.

Partition the $\mathcal{N}\mathcal{P}\mathcal{L}$ as ${\mathfrak{M}}_1=x_{11}{x}_{12}{x}_{13}\dots x_{1i_1}$, ${\mathfrak{M}}_2=x_{21}{x}_{22}{x}_{23}\dots x_{2i_2}$, ${\mathfrak{M}}_3=x_{31}{x}_{32}{x}_{33}\dots x_{3i_3}$, …, and ${\mathfrak{M}}_r=x_{r1}{x}_{r2}\dots x_{r{i}_r}.$ Using ${\mathfrak{M}}_1=x_{11}{x}_{12}{x}_{13}\dots x_{1i_1}$, the first sub network is constructed.

Step 2: For ${\mathfrak{M}}_1$, choose ${\mathfrak{P}}_{11},$ ${\mathfrak{P}}_{12},{\mathfrak{P}}_{13},\dots {,\mathfrak{P}}_{{1l}_1}$, (where l < i) and all are prime numbers (if preferred, choose the number ${\mathfrak{P}}_{{1s}_1}$, where $1\le s_1\le l_1,$ and it may be one digit or two digits or something else).

For ${\mathfrak{M}}_2$, choose ${\mathfrak{P}}_{21},$ ${\mathfrak{P}}_{22},{\mathfrak{P}}_{23},\dots {,\mathfrak{P}}_{{2l}_2}$, (where l < i) and all are prime numbers (if preferred, choose the number ${\mathfrak{P}}_{{2s}_2}$, where $1\le s_2\le l_2,$ and it may be one digit or two digits or something else). Proceeding to ${\mathfrak{M}}_k,$ choose ${\mathfrak{P}}_{r1},$ ${\mathfrak{P}}_{r2},{\mathfrak{P}}_{r3},\dots {,\mathfrak{P}}_{{rl}_r}$, (where l < i) and all are prime numbers (if preferred, choose the number ${\mathfrak{P}}_{{rs}_r}$, where $1\le s_r\le l_r,$ and it may be one digit or two digits or something else).

Step 3: Let ${\mathfrak{N}}_1=$ ${\mathfrak{P}}_{11} \ast$ ${\mathfrak{P}}_{12}\ast \dots \ast {\mathfrak{P}}_{{1l}_1}$, such that ${\mathfrak{N}}_1>{\mathfrak{M}}_1$. Let ${\xi }_1\left({\mathfrak{N}}_1\right)=$ ${(\mathfrak{P}}_{11}-1) \ast$ ${(\mathfrak{P}}_{12}-1)\ast \dots \ast {(\mathfrak{P}}_{{1l}_1}-1)$. By using the RSA algorithm, find suitable ${\mathbb{e}}_1$ and ${\mathbb{d}}_1$ such that ${\mathbb{d}}_1\ast {\mathbb{e}}_1$, which is congruent to 1 mod $({\xi }_1\left({\mathfrak{N}}_1\right))$. Compute the encrypted message ${\mathbb{C}}_1\equiv {{\mathfrak{M}}_1}^{{\mathbb{e}}_1}(mod{\mathfrak{N}}_1)$, which corresponds to ${\mathfrak{M}}_1$. Let ${\mathfrak{N}}_2=$ ${\mathfrak{P}}_{21} \ast$ ${\mathfrak{P}}_{22}\ast \dots \ast {\mathfrak{P}}_{{2l}_2}$, such that ${\mathfrak{N}}_2>{\mathfrak{M}}_2$. Let ${\xi }_1\left({\mathfrak{N}}_2\right)=$ ${(\mathfrak{P}}_{21}-1) \ast$ ${(\mathfrak{P}}_{22}-1)\ast \dots \ast {(\mathfrak{P}}_{{2l}_2}-1)$. By using the RSA algorithm, find suitable ${\mathbb{e}}_2$ and ${\mathbb{d}}_2$ such that ${\mathbb{d}}_2\ast {\mathbb{e}}_2$ $\equiv 1$ mod (${\xi }_1\left({\mathfrak{N}}_2\right))$.

Compute the encrypted message ${\mathbb{C}}_2\equiv {{\mathfrak{M}}_2}^{{\mathbb{e}}_2} (mod {\mathfrak{N}}_2)$, which corresponds to ${\mathfrak{M}}_2$. Continue this until the last value is calculated.

Let ${\mathfrak{N}}_k=$ ${\mathfrak{P}}_{r1} \ast$ ${\mathfrak{P}}_{r2}\ast \dots \ast {\mathfrak{P}}_{{rl}_r}$, such that ${\mathfrak{N}}_k>{\mathfrak{M}}_k$. Let ${\xi }_1\left({\mathfrak{N}}_k\right)=$ ${(\mathfrak{P}}_{r1}-1) \ast$ ${(\mathfrak{P}}_{r2}-1)\ast \dots \ast {(\mathfrak{P}}_{{rl}_r}-1)$. By using the RSA algorithm, find suitable ${\mathbb{e}}_k$ and ${\mathbb{d}}_k$ such that ${\mathbb{d}}_k\ast {\mathbb{e}}_k\equiv 1$ mod (${\xi }_1\left({\mathfrak{N}}_k\right))$. Compute the encrypted message ${\mathbb{C}}_k\equiv {{\mathfrak{M}}_k}^{{\mathbb{e}}_k}$ $\left(mod{\mathfrak{N}}_k\right).$

Step 4: Using triangular fuzzy membership functions, convert ${\mathbb{C}}_1$ into a triangular fuzzy number, say ${\mathfrak{F}}_1$. Then, the fuzzy number $\mathsf{\Psi }\left({\mathfrak{F}}_1\right)$ is as follows:

$$\mathsf{\Psi }({\mathfrak{F}}_1) = \left\{\begin{array}{c}\begin{array}{c}0 if {\mathbb{x}}_1<{\mathbb{r}}_1\\ {\displaystyle \frac{{\mathbb{x}}_1-{\mathbb{r}}_1}{{\mathbb{s}}_1-{\mathbb{r}}_1 }} if r\le {\mathbb{x}}_1\le {\mathbb{s}}_1\\ {\displaystyle \frac{{\mathbb{t}}_1-{\mathbb{x}}_1}{{\mathbb{t}}_1-{\mathbb{s}}_1}} if {\mathbb{s}}_1\le {\mathbb{x}}_1\le {\mathbb{t}}_1\end{array}\\ 0 if {\mathbb{x}}_1>{\mathbb{t}}_1.\end{array}\right.$$

Let ${\mathfrak{F}}_1={\mathfrak{F}}_{11}+{\mathfrak{F}}_{12}+{\mathfrak{F}}_{13}+\dots +{\mathfrak{F}}_{1i_1}.$ Using triangular fuzzy membership functions, convert ${\mathbb{C}}_2$ into a triangular fuzzy number, say ${\mathfrak{F}}_2$. Let ${\mathfrak{F}}_2 = {\mathfrak{F}}_{21}+{\mathfrak{F}}_{22}+{\mathfrak{F}}_{23}+\dots +{\mathfrak{F}}_{2i_2}$. Continuing this until the last value is calculated, using triangular fuzzy membership functions, convert ${\mathbb{C}}_k$ into a triangular fuzzy number, say ${\mathfrak{F}}_k$. Let ${\mathfrak{F}}_r = {\mathfrak{F}}_{r1}+{\mathfrak{F}}_{r2}+{\mathfrak{F}}_{r3}+\dots +{\mathfrak{F}}_{r{i}_r}$.

Step 5: Fuzzy graph sub network construction ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$: Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$ be ${\mathcal{a}}_1,{\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},{\mathcal{p}}_{14},{\mathcal{p}}_{15},{\mathcal{p}}_{16}$ such that distance between ${\mathcal{a}}_1$ and ${\mathcal{p}}_{1{\breve{\mathcal{k}}}_1}=1,$ where $1\le {\breve{\mathcal{k}}}_1\le {\mathcal{i}}_1$. The $\mathbb{N}\mathbb{M}\mathbb{V}s$ of ${\mathcal{a}}_1,{\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},{\mathcal{p}}_{14},{\mathcal{p}}_{15},{\mathcal{p}}_{16}$ are given by ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11},$ ${\mathfrak{F}}_{12}{,\mathfrak{F}}_{13},\dots ,{\mathfrak{F}}_{1i_1}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ $({\mathcal{a}}_1,{\mathcal{p}}_{11})$ = min(${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11}),$ ${\mathbb{E}\mathbb{M}\mathbb{V}({\mathcal{a}}_1,\mathcal{p}}_{12})$ = min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{12}),\mathrm{a}\mathrm{n}\mathrm{d} \mathbb{E}\mathbb{M}\mathbb{V}\left({\mathcal{a}}_1,{\mathcal{p}}_{13}\right)=$ min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{13}),\dots ,$ and the $\mathbb{E}\mathbb{M}\mathbb{V}$ of ${\mathcal{a}}_1$ and ${\mathcal{p}}_{1i_1}$ is a minimum of ${{(a}_1,\mathcal{p}}_{1i_1})$, where $1\le k_2\le i_2.$

Fuzzy graph sub network construction ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$: Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$ be ${\mathcal{a}}_2,{\mathcal{p}}_{21},{\mathcal{p}}_{22},{\mathcal{p}}_{23},\dots ,{\mathcal{p}}_{2i_2}$ such that the distance between ${\mathcal{a}}_2$ and ${\mathcal{p}}_{2k_2}=1,$ where $1\le k_2\le i_2.$ The $\mathbb{N}\mathbb{M}\mathbb{V}s$ of ${{\mathcal{a}}_2,\mathcal{p}}_{21},{\mathcal{p}}_{22},{\mathcal{p}}_{23},\dots ,{\mathcal{p}}_{2i_2}$ are ${\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{21},{\mathfrak{F}}_{22}{,\mathfrak{F}}_{23},\dots ,{\mathfrak{F}}_{2i_2}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ of ${\mathcal{a}}_2$ and ${\mathcal{p}}_{2k_2}$ is a minimum of (${\mathcal{a}}_2$,${\mathcal{p}}_{2k_2}),\dots , \mathrm{a}\mathrm{n}\mathrm{d}$ the $\mathbb{E}\mathbb{M}\mathbb{V}$ of ${\mathcal{a}}_2$ and ${\mathcal{p}}_{2i_2}$ is a minimum of (${\mathcal{a}}_2,$ ${\mathcal{p}}_{2i_2})$, where $1\le k_2\le i_2.$

Fuzzy graph sub network construction ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}r$: Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}r$ be ${\mathcal{a}}_r,{\mathcal{p}}_{r1},{\mathcal{p}}_{r2},{\mathcal{p}}_{r3},\dots ,{\mathcal{p}}_{r{i}_r}$ such that the distance between ${\mathcal{a}}_r$ and ${\mathcal{p}}_{r{i}_r}$ = 1, where $1\le k_r\le i_r.$ The $\mathbb{N}\mathbb{M}\mathbb{V}s$ of ${\mathcal{a}}_r,{\mathcal{p}}_{r1},{\mathcal{p}}_{r2},{\mathcal{p}}_{r3},\dots ,{\mathcal{p}}_{r{i}_r}$ are ${{\mathfrak{F}}_{r_{\mathcal{a}}},\mathfrak{F}}_{r1},{\mathfrak{F}}_{r2}{,\mathfrak{F}}_{r3},\dots ,{\mathfrak{F}}_{r{i}_r}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}s$ of ${\mathcal{a}}_r$ and ${\mathcal{p}}_{r{i}_r}$ are a minimum of (${\mathcal{a}}_r$,${\mathcal{p}}_{r{i}_r}$), where $1\le i_r\le k_r.$ The $\mathbb{E}\mathbb{M}\mathbb{V}$s of the rest of the constructed edges follow the definition of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}.$ The nodes ${\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,\dots ,{\mathcal{a}}_r$ are the centers of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1,$ ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$, …${,\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}r$. They are members of the efficient dominating set $\mathbb{E}\mathbb{D}\mathbb{S}$ of the ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}.$

End

5. Decryption Procedure

Input: Cipher graph ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$.

Output: $x_{11}{x}_{12}{x}_{13}\dots x_{1r}{x}_{21}{x}_{22}{x}_{23}\dots x_{2r}{x}_{31}{x}_{32}{x}_{33}\dots x_{3r}{x}_{41}{x}_{42}{x}_{43}\dots x_{4r}{x}_{r1}{x}_{r2}\dots x_{rr}$.

Begin

Step 1: Determine the $\mathbb{E}\mathbb{D}\mathbb{S}$ ${\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,\dots ,{\mathcal{a}}_r$ of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$, whose $\mathbb{N}\mathbb{M}\mathbb{V}\mathrm{s}$ are denoted by ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{2_{\mathcal{a}}}{\mathfrak{F}}_{3_{\mathcal{a}}},\dots ,{\mathfrak{F}}_{r_{\mathcal{a}}}$.

Step 2: Let the membership values of triangular fuzzy number of ${\mathbb{C}}_1,$ ${\mathbb{C}}_2$, ${\mathbb{C}}_3$, ${\mathbb{C}}_4,{\dots ,\mathbb{C}}_r$ be ${\mathsf{\Psi }(\mathfrak{F}}_1)$, ${\mathsf{\Psi }(\mathfrak{F}}_2),$ ${\mathsf{\Psi }(\mathfrak{F}}_3)$, $\dots$, ${\mathsf{\Psi }(\mathfrak{F}}_r)$ and its triplet parameters are given as $<{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>$, $<{\mathbb{r}}_2,{\mathbb{s}}_2,{\mathbb{t}}_2>,<{\mathbb{r}}_3,{\mathbb{s}}_3,{\mathbb{t}}_3>,\dots ,<{\mathbb{r}}_r,{\mathbb{s}}_r,{\mathbb{t}}_r>$, respectively.

Step 3: Let the triangular fuzzy number of ${\mathbb{C}}_1$ be $<{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>$ and its range be ${\mathbb{s}}_1-{\mathbb{r}}_1={\mathcal{R}}_1$, meaning ${\mathbb{r}}_1={\mathbb{s}}_1{-\{\mathcal{R}}_1\ast {\mathsf{\Psi }(\mathfrak{F}}_1)\},$ and likewise, find ${\mathbb{t}}_1$. Continue this for ${\mathbb{C}}_r,$ whose triangular triplets are $<{\mathbb{r}}_r,{\mathbb{s}}_r,{\mathbb{t}}_r>$ and its range is ${\mathbb{s}}_r-{\mathbb{r}}_r={\mathcal{R}}_r$, meaning ${\mathbb{r}}_r={\mathbb{s}}_r{-\mathcal{R}}_r\ast {\mathsf{\Psi }(\mathfrak{F}}_r),$ and likewise, find ${\mathbb{t}}_r$. Similarly, find the values of ${\mathbb{s}}_2,{\mathbb{s}}_3,\dots ,{\mathbb{s}}_{\mathrm{r}}$ from ${\mathfrak{F}}_2$,${\mathfrak{F}}_3,\dots ,{\mathfrak{F}}_{\mathrm{r}}$, respectively.

Step 4: By using the RSA algorithm, obtain ${\mathfrak{M}}_1$ while decrypting ${\mathbb{s}}_1$ using ${\mathfrak{M}}_1\equiv {{\mathbb{C}}_1}^{{\mathbb{d}}_1}$ (mod ${\mathfrak{N}}_1)$. Obtain ${\mathfrak{M}}_2$ while decrypting ${\mathbb{s}}_2$ using ${\mathfrak{M}}_2\equiv {{\mathbb{C}}_2}^{{\mathbb{d}}_2}$ (mod ${\mathfrak{N}}_2)$ and continue this until the last value is obtained, and obtain ${\mathfrak{M}}_r$ while decrypting ${\mathbb{s}}_r$ using ${\mathfrak{M}}_{\mathrm{r}}\equiv {{\mathbb{C}}_{\mathrm{r}}}^{{\mathbb{d}}_{\mathrm{r}}}$ (mod ${\mathfrak{N}}_{\mathrm{r}})$.

Step 5: Concatenate the values ${\mathfrak{M}}_1{\mathfrak{M}}_2{\mathfrak{M}}_3\dots {\mathfrak{M}}_r$, which gives the $\mathcal{N}\mathcal{P}\mathcal{L}$.

6. Illustration

Step 1: Let the numerical plaintext $\mathcal{N}\mathcal{P}\mathcal{L} x_{11}{x}_{12}{x}_{13}\dots x_{18}{x}_{21}{x}_{22}{x}_{23}\dots x_{28}{x}_{31}{x}_{32}{x}_{33}\dots x_{36}{x}_{41}{x}_{42}{x}_{43}\dots x_{49}{x}_{51}{x}_{52}\dots x_{55}$ be 11,985,920/21,450,625/245,394/149,528,879/77,343.

Divide the $\mathcal{N}\mathcal{P}\mathcal{L}$ into components ${\mathfrak{M}}_1$,${\mathfrak{M}}_2,{\mathfrak{M}}_3,{\mathfrak{M}}_4,{\mathrm{a}\mathrm{n}\mathrm{d} \mathfrak{M}}_5$.

Let ${\mathfrak{M}}_1=x_{11}{x}_{12}{x}_{13}\dots x_{18}=$ 11,985,920, ${\mathfrak{M}}_2={\mathcal{x}}_{21}{\mathcal{x}}_{22}{\mathcal{x}}_{23}\dots {\mathcal{x}}_{28}=$ 21,450,625, ${\mathfrak{M}}_3=$ 245,394, ${\mathfrak{M}}_4=$ 149,528,879, and ${\mathfrak{M}}_5=$ 77,343.

Step 2: Using ${\mathfrak{M}}_1=x_{11}{x}_{12}{x}_{13}\dots x_{18}$, the first sub network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$ is constructed. An illustration of $\mathfrak{F}\mathfrak{G}\mathfrak{N}1$ is given in Figure 2. Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$ be ${\mathcal{a}}_1,$ ${\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},\dots ,{\mathcal{p}}_{16}$ such that the distance between ${\mathcal{a}}_1$ and ${\mathcal{p}}_{1{\breve{\mathcal{k}}}_1}=1$, where $1\le {\breve{\mathcal{k}}}_1\le 6$.

Let $\mathbb{G}$ = ($\mathbb{V}$, υ, ω) be a graph. Subset $\mathbb{D}\subseteq \mathbb{V}$ is an efficient dominating set if $\forall \mathcal{v}\in \mathbb{V}$, |{$\mathcal{u}\in \mathbb{D}$|$\mathcal{v}\in \mathcal{N}\left[\mathcal{u}\right]|=1,$ where $\mathcal{N}\left[\mathcal{u}\right]$ denotes the neighboring vertices of $\mathcal{u}$. The $\mathbb{N}\mathbb{M}\mathbb{V}s$ of ${\mathcal{a}}_1,{\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},\dots ,{\mathcal{p}}_{16}$ are given by ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11},{\mathfrak{F}}_{12}{,\mathfrak{F}}_{13},\dots ,{\mathfrak{F}}_{16}$ respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ of $\left({\mathcal{a}}_1,{\mathcal{p}}_{11}\right)=$ min ${(\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11}), {\mathbb{E}\mathbb{M}\mathbb{V} \mathrm{o}\mathrm{f} ({\mathcal{a}}_1,\mathcal{p}}_{12})=\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{12}\right),$ $\mathbb{E}\mathbb{M}\mathbb{V}$ of $\left({\mathcal{a}}_1,{\mathcal{p}}_{13}\right)=$ min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{13})$,…, and $\mathbb{E}\mathbb{M}\mathbb{V} \mathrm{o}\mathrm{f} {(\mathcal{a}}_1,{\mathcal{p}}_{16})$ $=$ min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{16})$, respectively.

Step 3: Using ${\mathfrak{M}}_2=x_{21}{x}_{22}{x}_{23}\dots x_{28}$, the second sub network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$ is constructed. Let the nodes of the ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2$ be ${{\mathcal{a}}_2,\mathcal{p}}_{21},{\mathcal{p}}_{22},{\mathcal{p}}_{23},\dots ,{\mathcal{p}}_{26}$ such that the distance between ${\mathcal{a}}_2$ and ${\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}=1$, where $1\le {\breve{\mathcal{k}}}_2\le 6.$ The $\mathbb{N}\mathbb{M}\mathbb{V}s$ of ${{\mathcal{a}}_2,\mathcal{p}}_{21},{\mathcal{p}}_{22},{\mathcal{p}}_{23},\dots ,{\mathcal{p}}_{26}$ are ${\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{21},{\mathfrak{F}}_{22}{,\mathfrak{F}}_{23},\dots ,{\mathfrak{F}}_{26}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ of ${(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{21})$ = min ${(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{21}),\mathbb{E}\mathbb{M}\mathbb{V}$ of ${(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{22})$ = ${\mathrm{m}\mathrm{i}\mathrm{n}(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{22}),\mathbb{E}\mathbb{M}\mathbb{V}$ of ${(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{23})$ = ${\mathrm{m}\mathrm{i}\mathrm{n}(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{23})$, …, and $\mathbb{E}\mathbb{M}\mathbb{V}$ of ${(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{26})$ = ${\mathrm{m}\mathrm{i}\mathrm{n}(\mathfrak{F}}_{2_{\mathcal{a}}},{\mathfrak{F}}_{26})$, respectively.

Step 4: Similarly, construct ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}3, {\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}4,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}5$. Using $x_{51}{x}_{52}\dots x_{55}$, the fifth sub network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}5$ is constructed. Let the nodes of $\mathfrak{F}{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}5$ be ${\mathcal{a}}_5,{\mathcal{p}}_{51},$ ${\mathcal{p}}_{52},{\mathcal{p}}_{53},\dots ,{\mathcal{p}}_{55}$ such that the distance between ${\mathcal{a}}_5$ and ${\mathcal{p}}_{55}=1$, where $1\le {\breve{\mathcal{k}}}_5\le {\mathcal{i}}_5.$ The $\mathbb{N}\mathbb{M}\mathbb{V}s$ of ${\mathcal{a}}_5,{\mathcal{p}}_{51},{\mathcal{p}}_{52},{\mathcal{p}}_{53},\dots ,{\mathcal{p}}_{55}$ are ${{\mathfrak{F}}_{5_{\mathcal{a}}},\mathfrak{F}}_{51},{\mathfrak{F}}_{52}{,\mathfrak{F}}_{53}{,\mathfrak{F}}_{53},{\mathfrak{F}}_{55}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ of ${(\mathfrak{F}}_{5_{\mathcal{a}}},{\mathcal{p}}_{51})$ = $\mathrm{m}\mathrm{i}\mathrm{n}{(\mathfrak{F}}_{5_{\mathcal{a}}},{\mathcal{p}}_{51}),\mathbb{E}\mathbb{M}\mathbb{V}$ of ${(\mathfrak{F}}_{5_{\mathcal{a}}},{\mathcal{p}}_{52})$ = min ${(\mathfrak{F}}_{5_{\mathcal{a}}},{\mathcal{p}}_{52}),\mathbb{E}\mathbb{M}\mathbb{V}$ of ${(\mathfrak{F}}_5,{\mathcal{p}}_{53})$ = min ${(\mathfrak{F}}_{5_{\mathcal{a}}},{\mathcal{p}}_{53})$, …, and $\mathbb{E}\mathbb{M}\mathbb{V} \mathrm{o}\mathrm{f} {(\mathfrak{F}}_{5_{\mathcal{a}}},{\mathfrak{F}}_{r5})$ = ${\mathrm{m}\mathrm{i}\mathrm{n}(\mathfrak{F}}_{5_{\mathcal{a}}},{\mathcal{p}}_{55})$, respectively.

Step 5: The $\mathbb{E}\mathbb{M}\mathbb{V}$ of the rest of the constructed edges follows the definition of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}.$Let ${\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,\dots ,{\mathcal{a}}_5$ be the nodes of the efficient dominating set, which have $\mathbb{N}\mathbb{M}\mathbb{V}’\mathrm{s}$ that are ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{2_{\mathcal{a}}}{\mathfrak{F}}_{3_{\mathcal{a}}},\dots ,{\mathfrak{F}}_{5_{\mathcal{a}}}$. Construct the network ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ using ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2,\dots ,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}5$ as follows. The node set of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is $\mathfrak{V}\left({\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}\right)=\{{\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,{\mathcal{a}}_4,{\mathcal{a}}_5\}\bigcup \{{\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},$${\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{p}}_{5{\breve{\mathcal{k}}}_5}\}$ where $1\le {\breve{\mathcal{k}}}_1\le 6,1\le {\breve{\mathcal{k}}}_2\le 6,1\le {\breve{\mathcal{k}}}_3\le 7,1\le {\breve{\mathcal{k}}}_4\le 5,1\le {\breve{\mathcal{k}}}_5\le 5.$ The number of nodes present in ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is $5$ + $6$ + $6$ + $7$ + $5$ + $5=34$. The minimum number of edges required for ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is calculated as follows.

Define ${\mathcal{E}}_1=\{{(\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}{\mathcal{p}}_{3{\breve{\mathcal{k}}}_3}),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_{3,}},{\mathcal{p}}_{4{\breve{\mathcal{k}}}_4}),\dots ,({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{p}}_{5{\breve{\mathcal{k}}}_5})\}$ for only one $1\le {\breve{\mathcal{k}}}_1\le 6,1\le {\breve{\mathcal{k}}}_2\le 6,1\le {\breve{\mathcal{k}}}_3\le 7,1\le {\breve{\mathcal{k}}}_4\le 5,1\le {\breve{\mathcal{k}}}_5\le 5.$ ${\mathcal{E}}_2=\{{(\mathcal{a}}_1{,\mathcal{p}}_{1{\breve{\mathcal{k}}}_1}){,(\mathcal{a}}_2{,\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}),{(\mathcal{a}}_3{,\mathcal{p}}_{3{\breve{\mathcal{k}}}_3}),\dots ,{(\mathcal{a}}_r{,\mathcal{p}}_{r{\breve{\mathcal{k}}}_r})\}$ where $1\le {\breve{\mathcal{k}}}_1\le 6,1\le {\breve{\mathcal{k}}}_2\le 6,1\le {\breve{\mathcal{k}}}_3\le 7,1\le {\breve{\mathcal{k}}}_4\le 5,1\le {\breve{\mathcal{k}}}_5\le 5.$

The minimum number of edges required for ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is ${\mathcal{E}}_{\left(Min\right)}$ = ${\mathcal{E}}_1 \cup {\mathcal{E}}_2$.

Step 6: The maximum number of edges required for ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$ is ${\mathcal{E}}_{\left(Max\right)}$ = ($5$ + $6$ + $6$ + $7$ + $5$ + $5)C_2 -$ $\{({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_2),({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_3),({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_4),\dots ,({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_5),$ where $1\le {\breve{\mathcal{k}}}_1\le 6$, $({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_1),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_3),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_4),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_5), \mathrm{where} 1 \le {\breve{\mathcal{k}}}_2\le 6$, $({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_1),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_2),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_4),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_5), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1 \le {\breve{\mathcal{k}}}_3\le 7$, $({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_1),({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_2),({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_3),({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_5), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1 \le {\breve{\mathcal{k}}}_4\le 5$, and $({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_1),({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_2),({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_3),({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_4)$, $\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1 \le {\breve{\mathcal{k}}}_5\le 5\}$.

(i)

Encryption Algorithm

Input: Numerical plaintext

$x_{11}{x}_{12}{x}_{13}\dots x_{18}{x}_{21}{x}_{22}{x}_{23}\dots x_{28}{x}_{31}{x}_{32}{x}_{33}\dots x_{36}{x}_{41}{x}_{42}{x}_{43}\dots x_{49}$$x_{51}{x}_{52}\dots x_{55}$, which are all positive integers.

Output: Cipher graph ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}.$

Begin

Step 1: Let the numerical plaintext $\mathcal{N}\mathcal{P}\mathcal{L}$ be 11,985,920/21,450,625/245,394/149,528,879/77,343. Divide the $\mathcal{N}\mathcal{P}\mathcal{L}$ into components ${{\mathfrak{M}}_1,\mathfrak{M}}_2, {\mathfrak{M}}_3,{\mathfrak{M}}_4,{\mathfrak{M}}_5$, respectively, where ${\mathfrak{M}}_1=$ 11,985,920, ${\mathfrak{M}}_2=$ 21,450,625, ${\mathfrak{M}}_3=$ 245,394, ${\mathfrak{M}}_4=$ 149,528,879, and ${\mathfrak{M}}_5=$ 77,343.

Step 2: Consider ${\mathfrak{M}}_1=$11,985,920. ${\mathfrak{M}}_1$ is encrypted using the RSA algorithm. Let us consider the prime numbers ${\mathfrak{P}}_{11}=$53,${\mathfrak{P}}_{12}=59, {\mathfrak{P}}_{13}=79, \mathrm{a}\mathrm{n}\mathrm{d} {\mathfrak{P}}_{14}=89$(it may be two digits or three digits). ${\mathfrak{N}}_1=$ ${\mathfrak{P}}_{11} \ast$ ${\mathfrak{P}}_{12}\ast {\mathfrak{P}}_{12}\ast {\mathfrak{P}}_{14}$ = 21,985,937, such that ${\mathfrak{N}}_1>{\mathfrak{M}}_1.$

Step 3: Let the function ${\xi }_1\left({\mathfrak{N}}_1\right)=$ ${(\mathfrak{P}}_{11}-1)\ast$ ${(\mathfrak{P}}_{12}-1)\ast {(\mathfrak{P}}_{13}-1)\ast {(\mathfrak{P}}_{14}-1) =$$52 \ast 58\ast 78\ast 88=$ $\mathrm{20,701,824}.$

Step 4: Find suitable ${\mathbb{e}}_1$ and ${\mathbb{d}}_{1 }$ such that ${\mathbb{d}}_1 \ast {\mathbb{e}}_1$, which is congruent to 1 mod $({\xi }_1\left({\mathfrak{N}}_1\right))$, and find the encrypted message that says ${\mathfrak{M}}_1\equiv {{\mathbb{C}}_1}^{{\mathbb{d}}_1}$ (mod ${\mathfrak{N}}_1)$, which corresponds to ${\mathfrak{M}}_1$. Find a suitable ${\mathbb{e}}_1$, where $1<{\mathbb{e}}_1<{\xi }_1\left({\mathfrak{N}}_1\right)$ such that gcd(${\mathbb{e}}_1,{\xi }_1\left({\mathfrak{N}}_1\right))$=$1$. Let ${\mathbb{e}}_1=\mathrm{65,537}.$

Step 5: Find ${\mathbb{d}}_1,$ such that ${\mathbb{d}}_1\ast {\mathbb{e}}_1\equiv 1$ mod (${\xi }_1\left({\mathfrak{N}}_1\right)).{\mathbb{d}}_1$ = 8,606,465. Now, let the cipher integer ${\mathbb{C}}_1={{\mathfrak{M}}_1}^{{\mathbb{e}}_1}$ mod ${\mathfrak{N}}_1=$ 7,517,755.

Step 6: Convert ${\mathbb{C}}_1$ into a triangular fuzzy number, say ${\mathfrak{F}}_1 = <{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>$, and let its range be ${\mathbb{s}}_1-{\mathbb{r}}_1={\mathcal{R}}_1$, meaning ${\mathbb{r}}_1={\mathbb{s}}_1{-\{\mathcal{R}}_1\ast {\mathsf{\Psi }(\mathfrak{F}}_1)\},$ and likewise, find ${\mathbb{t}}_1$. For the $\mathbb{x}$ value, choose any number between $<{\mathbb{r}}_1,{\mathbb{t}}_1>$ and then the fuzzy number.

Step 7: Let the triangular fuzzy number of ${\mathbb{C}}_1$ be $<{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>$ and its range be ${\mathbb{s}}_1-{\mathbb{r}}_1={\mathcal{R}}_1$, meaning ${\mathbb{r}}_1={\mathbb{s}}_1{-\{\mathcal{R}}_1\ast {\mathsf{\Psi }(\mathfrak{F}}_1)\},$ and likewise, find ${\mathbb{t}}_1$. Let ${\mathfrak{F}}_1={\mathfrak{F}}_{11}+{\mathfrak{F}}_{12}+{\mathfrak{F}}_{13}+\dots +{\mathfrak{F}}_{16}$. Convert the cipher integer to TFNs $<{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>$. For the $\mathbb{x}$ value, choose any number between $<{\mathbb{r}}_1,{\mathbb{t}}_1>$. Then, the fuzzy number $\mathsf{\Psi }({\mathfrak{F}}_1)$ is as follows:

$$\mathsf{\Psi }({\mathfrak{F}}_1)=\left\{\begin{array}{c}\begin{array}{c}0 if {\mathbb{x}}_1<{\mathbb{r}}_1\\ {\displaystyle \frac{{\mathbb{x}}_1-{\mathbb{r}}_1}{{\mathbb{s}}_1-{\mathbb{r}}_1 }} if r\le {\mathbb{x}}_1\le {\mathbb{s}}_1\\ {\displaystyle \frac{{\mathbb{t}}_1-{\mathbb{x}}_1}{{\mathbb{t}}_1-{\mathbb{s}}_1}} if {\mathbb{s}}_1\le {\mathbb{x}}_1\le {\mathbb{t}}_1\end{array}\\ 0 if {\mathbb{x}}_1>{\mathbb{t}}_1.\end{array}\right.$$

Here, the cipher graph ${\mathbb{C}}_1=$ 7,517,755 is given as $<{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>,$ where ${\mathbb{r}}_1=\mathrm{7,492,212},$ ${\mathbb{s}}_1=$ 7,517,755 and ${\mathbb{t}}_1=\mathrm{7,543,298}$ and its range is ${\mathcal{R}}_1=\mathrm{25,543}$.

Let ${\mathbb{x}}_1=\mathrm{7,519,755}.$ $\mathsf{\Psi }\left({\mathfrak{F}}_1\right)={\displaystyle \frac{{\mathbb{t}}_1-{\mathbb{x}}_1}{{\mathbb{t}}_1-{\mathbb{s}}_1}}\because {\mathbb{s}}_1\le {\mathbb{x}}_1\le {\mathbb{t}}_1$

$$\mathsf{\Psi }\left({\mathfrak{F}}_1\right)=0.92$$

Step 8: Now, $\mathsf{\Psi }\left({\mathfrak{F}}_1\right)$ is split into six parts and assigned as a membership value for the vertices of the network, as in

Table 2. $\mathbb{N}\mathbb{M}\mathbb{V}$ of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$.

Nodes	$\mathbb{N}\mathbb{M}\mathbb{V}$	Nodes	$\mathbb{N}\mathbb{M}\mathbb{V}$	Nodes	$\mathbb{N}\mathbb{M}\mathbb{V}$	Nodes	$\mathbb{N}\mathbb{M}\mathbb{V}$	Nodes	$\mathbb{N}\mathbb{M}\mathbb{V}$
${\mathcal{a}}_1$	0.1	${\mathcal{a}}_2$	0.02	${\mathcal{a}}_3$	0.01	${\mathcal{p}}_{37}$	0.026	${\mathcal{a}}_5$	0.01
${\mathcal{p}}_{11}$	0.1536	${\mathcal{p}}_{21}$	0.2013	${\mathcal{p}}_{31}$	0.015	${\mathcal{a}}_4$	0.01	${\mathcal{p}}_{51}$	0.026
${\mathcal{p}}_{12}$	0.1536	${\mathcal{p}}_{22}$	0.031	${\mathcal{p}}_{32}$	0.002	${\mathcal{p}}_{41}$	0.0998	${\mathcal{p}}_{52}$	0.026
${\mathcal{p}}_{13}$	0.1532	${\mathcal{p}}_{23}$	0.031	${\mathcal{p}}_{33}$	0.0084	${\mathcal{p}}_{42}$	0.12475	${\mathcal{p}}_{53}$	0.0193
${\mathcal{p}}_{14}$	0.1532	${\mathcal{p}}_{24}$	0.0372	${\mathcal{p}}_{34}$	0.0105	${\mathcal{p}}_{43}$	0.1663	${\mathcal{p}}_{54}$	0.0193
${\mathcal{p}}_{15}$	0.1021	${\mathcal{p}}_{25}$	0.0465	${\mathcal{p}}_{35}$	0.0042	${\mathcal{p}}_{44}$	0.3036	${\mathcal{p}}_{55}$	0.0386
${\mathcal{p}}_{16}$	0.2043	${\mathcal{p}}_{26}$	0.025	${\mathcal{p}}_{36}$	0.026	${\mathcal{p}}_{45}$	0.3036

. ${\mathfrak{F}}_1=0.1536+0.1536+0.1532+0.1532+0.1021+0.2043$.

Step 9: Let the nodes of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1$ be ${\mathcal{a}}_1,{\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},{\mathcal{p}}_{14},{\mathcal{p}}_{15},{\mathcal{p}}_{16}$ such that the distance between ${\mathcal{a}}_1$ and ${\mathcal{p}}_{1{\breve{\mathcal{k}}}_1}$ is equal to 1, where $1\le {\breve{\mathcal{k}}}_1\le {\mathcal{i}}_1$. The $\mathbb{N}\mathbb{M}\mathbb{V}s$ of ${\mathcal{a}}_1,{\mathcal{p}}_{11},{\mathcal{p}}_{12},{\mathcal{p}}_{13},{\mathcal{p}}_{14},{\mathcal{p}}_{15},{\mathcal{p}}_{16}$ are given by ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11},{\mathfrak{F}}_{12}{,\mathfrak{F}}_{13},\dots ,{\mathfrak{F}}_{1i_1}$, respectively. The $\mathbb{E}\mathbb{M}\mathbb{V}$ of $({\mathcal{a}}_1,{\mathcal{p}}_{11})$ = min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{11}),{ \mathbb{E}\mathbb{M}\mathbb{V} \mathrm{o}\mathrm{f} ({\mathcal{a}}_1,\mathcal{p}}_{12})$ = min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{12}),\mathbb{E}\mathbb{M}\mathbb{V}$ of $\left({\mathcal{a}}_1,{\mathcal{p}}_{13}\right)=$ min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{13})$, …, and $\mathbb{E}\mathbb{M}\mathbb{V} \mathrm{o}\mathrm{f} {(\mathcal{a}}_1,{\mathcal{p}}_{16})$ = min (${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{16})$, respectively, as in

Table 3. $\mathbb{E}\mathbb{M}\mathbb{V}$ for ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$.

Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$	Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$	Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$	Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$
${\mathcal{a}}_1{\mathcal{p}}_{11}$	0.1536	${\mathcal{a}}_2{\mathcal{p}}_{21}$	0.02	${\mathcal{a}}_3{\mathcal{p}}_{31}$	0.015	${\mathcal{a}}_4{\mathcal{p}}_{41}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{12}$	0.1536	${\mathcal{a}}_2{\mathcal{p}}_{22}$	0.02	${\mathcal{a}}_3{\mathcal{p}}_{32}$	0.002	${\mathcal{a}}_4{\mathcal{p}}_{42}$	0.01
${{\mathcal{a}}_1\mathcal{p}}_{13}$	0.1532	${\mathcal{a}}_2{\mathcal{p}}_{23}$	0.02	${{\mathcal{a}}_3\mathcal{p}}_{33}$	0.0084	${\mathcal{a}}_4{\mathcal{p}}_{43}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{14}$	0.1532	${\mathcal{a}}_2{\mathcal{p}}_{24}$	0.02	${{\mathcal{a}}_3\mathcal{p}}_{34}$	0.0105	${\mathcal{a}}_4{\mathcal{p}}_{44}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{15}$	0.1021	${\mathcal{a}}_2{\mathcal{p}}_{25}$	0.02	${\mathcal{a}}_3{\mathcal{p}}_{35}$	0.0042	${\mathcal{a}}_4{\mathcal{p}}_{45}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{16}$	0.1	${\mathcal{a}}_2{\mathcal{p}}_{26}$	0.025	${\mathcal{a}}_3{\mathcal{p}}_{36}$	0.01	${\mathcal{p}}_{44}{\mathcal{p}}_{53}$	0.018
${\mathcal{p}}_{12}{\mathcal{p}}_{26}$	0.011	${\mathcal{p}}_{23}{\mathcal{p}}_{31}$	0.010	${\mathcal{p}}_{35}{\mathcal{p}}_{42}$	0.0020	${\mathcal{a}}_5{\mathcal{p}}_{51}$	0.01
${\mathcal{a}}_5{\mathcal{p}}_{52}$	0.01	${\mathcal{a}}_5{\mathcal{p}}_{53}$	0.0193	${{\mathcal{a}}_5\mathcal{p}}_{54}$	0.0193	${\mathcal{a}}_5{\mathcal{p}}_{55}$	0.01

.

Step 10: Similarly, construct ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}3,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}4,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}5$ from ${\mathfrak{M}}_2=$ 21,450,625, ${\mathfrak{M}}_3=$245,394, ${\mathfrak{M}}_4=$ 149,528,879, and ${\mathfrak{M}}_5=$77,343, respectively.

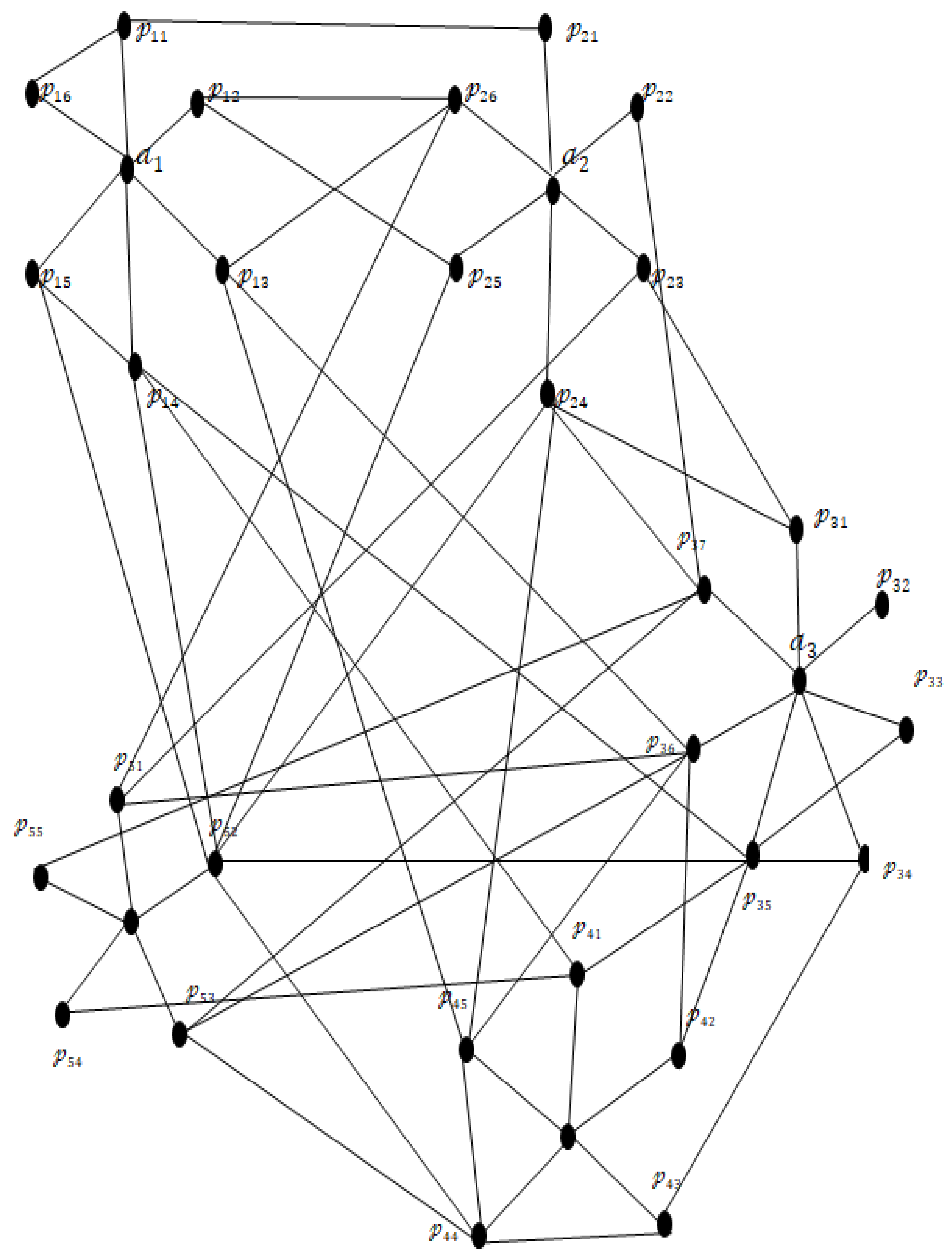
Step 11: Now, the networks ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}1,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}2,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}3,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}4,{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}5$ are connected using edges from set ${\mathcal{E}}_1 \mathrm{t}\mathrm{o} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{h}\mathrm{e}$network $\mathfrak{F}\mathfrak{G}\mathfrak{N}$ (Figure 3), where ${\mathcal{E}}_1=\{{(\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2}{\mathcal{p}}_{3{\breve{\mathcal{k}}}_3}),{(\mathcal{p}}_{3{\breve{\mathcal{k}}}_3,}{,\mathcal{p}}_{4{\breve{\mathcal{k}}}_4}) ,{(\mathcal{p}}_{4{\breve{\mathcal{k}}}_4,}{,\mathcal{p}}_{5{\breve{\mathcal{k}}}_5}) \}$ for only one $1\le {\breve{\mathcal{k}}}_1\le 6, 1\le {\breve{\mathcal{k}}}_2\le 6, 1\le {\breve{\mathcal{k}}}_3\le 7, 1\le {\breve{\mathcal{k}}}_4\le 5, 1\le {\breve{\mathcal{k}}}_5\le 5.$The $\mathbb{E}\mathbb{M}\mathbb{V}$ of the above constructed edges follows from the definition of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}.$ Let ${\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,{\mathcal{a}}_4, {\mathcal{a}}_5$ be the nodes of the $\mathbb{E}\mathbb{D}\mathbb{S}$, which have $\mathbb{N}\mathbb{M}\mathbb{V}$s ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{2_{\mathcal{a}}}{\mathfrak{F}}_{3_{\mathcal{a}}},{\mathfrak{F}}_{4_{\mathcal{a}}},{\mathfrak{F}}_{5_{\mathcal{a}}}.$

Step 12: The network is expanded by adding additional edges, as in Figure 4, while adhering to the given constraints, resulting in a moderately connected structure as in

Table 4. $\mathbb{E}\mathbb{M}\mathbb{V}$ for constructing network with moderate number of edges.

Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$	Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$	Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$	Edges	$\mathbb{E}\mathbb{M}\mathbb{V}$
${\mathcal{a}}_1{\mathcal{p}}_{11}$	0.1536	${\mathcal{a}}_2{\mathcal{p}}_{21}$	0.02	${\mathcal{a}}_3{\mathcal{p}}_{31}$	0.015	${\mathcal{a}}_4{\mathcal{p}}_{41}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{12}$	0.1536	${\mathcal{a}}_2{\mathcal{p}}_{22}$	0.02	${\mathcal{a}}_3{\mathcal{p}}_{32}$	0.002	${\mathcal{a}}_4{\mathcal{p}}_{42}$	0.01
${{\mathcal{a}}_1\mathcal{p}}_{13}$	0.1532	${\mathcal{a}}_2{\mathcal{p}}_{23}$	0.02	${{\mathcal{a}}_3\mathcal{p}}_{33}$	0.0084	${\mathcal{a}}_4{\mathcal{p}}_{43}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{14}$	0.1532	${\mathcal{a}}_2{\mathcal{p}}_{24}$	0.02	${{\mathcal{a}}_3\mathcal{p}}_{34}$	0.0105	${\mathcal{a}}_4{\mathcal{p}}_{44}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{15}$	0.1021	${\mathcal{a}}_2{\mathcal{p}}_{25}$	0.02	${\mathcal{a}}_3{\mathcal{p}}_{35}$	0.0042	${\mathcal{a}}_4{\mathcal{p}}_{45}$	0.01
${\mathcal{a}}_1{\mathcal{p}}_{16}$	0.1	${\mathcal{a}}_2{\mathcal{p}}_{26}$	0.025	${\mathcal{a}}_3{\mathcal{p}}_{36}$	0.01	${\mathcal{p}}_{44}{\mathcal{p}}_{53}$	0.018
${\mathcal{p}}_{12}{\mathcal{p}}_{26}$	0.011	${\mathcal{p}}_{23}{\mathcal{p}}_{31}$	0.010	${\mathcal{p}}_{35}{\mathcal{p}}_{42}$	0.0020	${\mathcal{a}}_5{\mathcal{p}}_{51}$	0.01
${\mathcal{a}}_5{\mathcal{p}}_{52}$	0.01	${\mathcal{a}}_5{\mathcal{p}}_{53}$	0.0193	${{\mathcal{a}}_5\mathcal{p}}_{54}$	0.0193	${\mathcal{a}}_5{\mathcal{p}}_{55}$	0.01
${\mathcal{p}}_{11}{\mathcal{p}}_{12}$	0.1530	${\mathcal{p}}_{14}{\mathcal{p}}_{41}$	0.09	${\mathcal{p}}_{37}{\mathcal{p}}_{52}$	0.02	${\mathcal{p}}_{51}{\mathcal{p}}_{55}$	0.02
${\mathcal{p}}_{16}{\mathcal{p}}_{15}$	0.101	${\mathcal{p}}_{14}{\mathcal{p}}_{52}$	0.02	${\mathcal{p}}_{36}{\mathcal{p}}_{42}$	0.01	${\mathcal{p}}_{44}{\mathcal{p}}_{53}$	0.01
${\mathcal{p}}_{21}{\mathcal{p}}_{22}$	0.03	${\mathcal{p}}_{13}{\mathcal{p}}_{45}$	0.143	${\mathcal{p}}_{43}{\mathcal{p}}_{44}$	0.16	${\mathcal{p}}_{32}{\mathcal{p}}_{33}$	0.001
${\mathcal{p}}_{25}{\mathcal{p}}_{52}$	0.02	${\mathcal{p}}_{13}{\mathcal{p}}_{36}$	0.02	${\mathcal{p}}_{23}{\mathcal{p}}_{31}$	0.02	${\mathcal{p}}_{23}{\mathcal{p}}_{45}$	0.02

.

Step 13: The maximum number of edges required for $\mathfrak{F}\mathfrak{G}\mathfrak{N}$ is ${\mathcal{E}}_{\left(Max\right)}$ = ($5$ + $6$ + $6$ + $7$ + $5$ + $5$)C₂ − {$({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_2),({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_3),({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_4),({\mathcal{p}}_{1{\breve{\mathcal{k}}}_1},{\mathcal{a}}_5),$ where $1\le {\breve{\mathcal{k}}}_1\le 6$, $({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_1),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_3),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_4),({\mathcal{p}}_{2{\breve{\mathcal{k}}}_2},{\mathcal{a}}_5), \mathrm{where} 1 \le {\breve{\mathcal{k}}}_2\le 6$, $({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_1),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_2),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_4),({\mathcal{p}}_{3{\breve{\mathcal{k}}}_3},{\mathcal{a}}_5), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1 \le {\breve{\mathcal{k}}}_3\le 7$, $({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_1),({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_2),({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_4),({\mathcal{p}}_{4{\breve{\mathcal{k}}}_4},{\mathcal{a}}_5), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1 \le {\breve{\mathcal{k}}}_4\le 5$, and $({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_1),({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_2),({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_4),({\mathcal{p}}_{5{\breve{\mathcal{k}}}_5},{\mathcal{a}}_5)$, $\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 1 \le {\breve{\mathcal{k}}}_5\le 5\}$.

This is shown in ${{\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}}_{\left(Max\right)},$ Figure 5.

End.

(ii)

Decryption Algorithm

Input: Cipher graph ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$.

Output: $x_{11}{x}_{12}{x}_{13}\dots x_{18}{x}_{21}{x}_{22}{x}_{23}\dots x_{28}{x}_{31}{x}_{32}{x}_{33}\dots x_{36}{x}_{41}{x}_{42}{x}_{43}\dots x_{49}{x}_{51}{x}_{52}\dots x_{55}$.

Begin

Step 1: Determine the $\mathbb{E}\mathbb{D}\mathbb{S}$ ${\mathcal{a}}_1,{\mathcal{a}}_2,{\mathcal{a}}_3,\dots ,{\mathcal{a}}_5$ of ${\mathfrak{F}\mathfrak{G}\mathfrak{N}}_{\mathfrak{s}}$. whose $\mathbb{N}\mathbb{M}\mathbb{V}\mathrm{s}$ are denoted by ${\mathfrak{F}}_{1_{\mathcal{a}}},{\mathfrak{F}}_{2_{\mathcal{a}}}{\mathfrak{F}}_{3_{\mathcal{a}}},\dots ,{\mathfrak{F}}_{5_{\mathcal{a}}}.$

Step 2: Let the membership values of the triangular fuzzy number of ${\mathbb{C}}_1,$ ${\mathbb{C}}_2$,${\mathbb{C}}_3,$ ${\mathbb{C}}_4, {\mathrm{a}\mathrm{n}\mathrm{d} \mathbb{C}}_5$ be ${\mathsf{\Psi }(\mathfrak{F}}_1)$, ${\mathsf{\Psi }(\mathfrak{F}}_2),$ ${\mathsf{\Psi }(\mathfrak{F}}_3)$,${\mathsf{\Psi }(\mathfrak{F}}_4)$,$\mathrm{a}\mathrm{n}\mathrm{d} {\mathsf{\Psi }(\mathfrak{F}}_5)$ and its triplet parameters are given as $<{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>$, $<{\mathbb{r}}_2,{\mathbb{s}}_2,{\mathbb{t}}_2>,<{\mathbb{r}}_3,{\mathbb{s}}_3,{\mathbb{t}}_3>,<{\mathbb{r}}_4,{\mathbb{s}}_4,{\mathbb{t}}_4> , \mathrm{a}\mathrm{n}\mathrm{d} <{\mathbb{r}}_5,{\mathbb{s}}_5,{\mathbb{t}}_5>$, respectively.

Step 3: Let the triangular fuzzy number of ${\mathbb{C}}_1$ be $<{\mathbb{r}}_1,{\mathbb{s}}_1,{\mathbb{t}}_1>$ and its range be ${\mathbb{s}}_1-{\mathbb{r}}_1={\mathcal{R}}_1$, meaning ${\mathbb{r}}_1={\mathbb{s}}_1{-\{\mathcal{R}}_1\ast {\mathsf{\Psi }(\mathfrak{F}}_1)\},$ and likewise, find ${\mathbb{t}}_1$.

$$\mathsf{\Psi }{(\mathbb{x}}_1)={\displaystyle \frac{{\mathfrak{F}}_1\times {\mathcal{R}}_1}{{\mathbb{t}}_1-{\mathbb{s}}_1}} \mathrm{where} {\mathbb{t}}_1-{\mathbb{s}}_1={\mathcal{R}}_1$$

$$\mathrm{7,543,298}-{\mathbb{s}}_1=\mathrm{25,543}, {\mathbb{s}}_1=\mathrm{7,517,755}$$

Similarly, find the values of ${\mathbb{s}}_2,{\mathbb{s}}_3,{\mathbb{s}}_4,{\mathbb{s}}_5$ from ${\mathfrak{F}}_2$,${\mathfrak{F}}_3,{\mathfrak{F}}_4,{\mathfrak{F}}_5$, respectively.

Step 4: By using the RSA algorithm, obtain ${\mathfrak{M}}_1$ while decrypting ${\mathbb{s}}_1$ using ${\mathfrak{M}}_1\equiv {{\mathbb{C}}_1}^{{\mathbb{d}}_1}$ (mod ${\mathfrak{N}}_1)$.

$${\mathfrak{M}}_1\equiv {\mathrm{7,517,755}}^{\mathrm{8,606,465}}(\mathrm{mod} \mathrm{21,985,937})=\mathrm{11,985,920}.$$

Likewise, obtain ${\mathfrak{M}}_2$ while decrypting ${\mathbb{s}}_2$ using ${\mathfrak{M}}_2\equiv {{\mathbb{C}}_2}^{{\mathbb{d}}_2}$ (mod ${\mathfrak{N}}_2)$ and continue this until the last value is obtained, and obtain ${\mathfrak{M}}_5$ while decrypting ${\mathbb{s}}_5$ using ${\mathfrak{M}}_5\equiv {{\mathbb{C}}_5}^{{\mathbb{d}}_5}$ (mod ${\mathfrak{N}}_5)$.

Step 5: Concatenate values ${\mathfrak{M}}_1{\mathfrak{M}}_2{\mathfrak{M}}_3\dots {\mathfrak{M}}_5$ to obtain the $\mathcal{N}\mathcal{P}\mathcal{L}$.

$$\mathrm{11,985,920}/\mathrm{21,450,625}/\mathrm{245,394}/\mathrm{149,528,879}/7734$$

7. Comparative Study

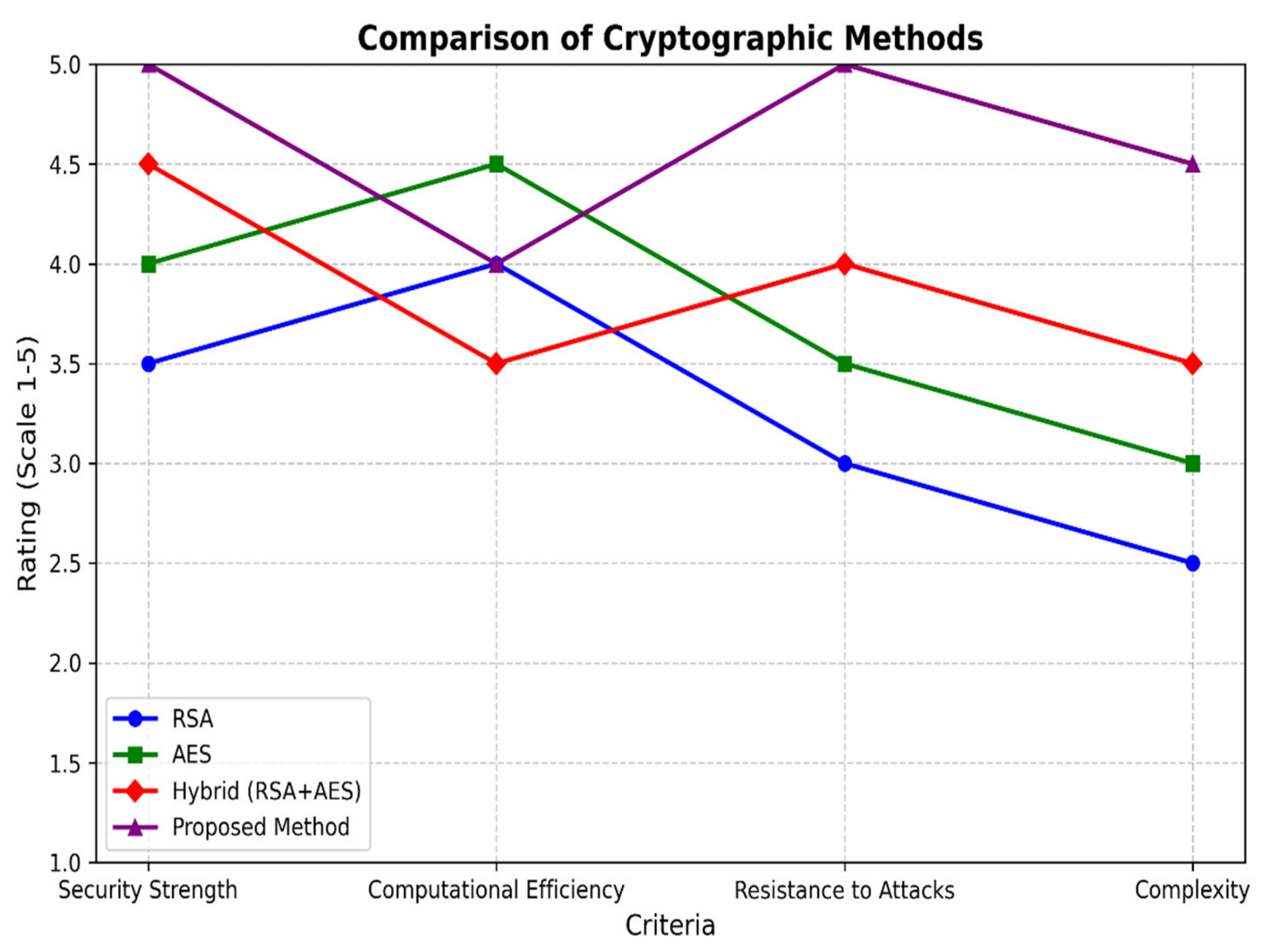
Cryptographic encryption methods are essential to protect data from unauthorized access. Conventional techniques like RSA and AES have been extensively employed, while hybrid techniques use more than one encryption method for better security. This research compares the available methods with the new encryption method proposed in this research, using the RSA algorithm, fuzzy logic, and graph-based transformations to offer a highly secure and efficient cryptographic system. The encryption techniques are assessed on the basis of the following four crucial criteria’s namely security strength, computational efficiency, resistance to attacks and complexity. The comparative assessment, as represented in the graph (Figure 6) and

Table 5. Comparative analysis of cryptographic methods.

Method	Mathematical Importance	Security Level	Computational Complexity	Attack Resistance	Use Case
RSA	Based on number theory, modular arithmetic, prime factorization problem	Moderate–High	High (especially with large keys)	Vulnerable to quantum attacks	Secure messaging, digital signatures
AES	Relies on substitution–permutation networks, algebra over finite fields (GF(28))	High	Low	Strong against classical and quantum attacks (symmetric)	Real-time data encryption, IoT, file systems
Hybrid (RSA + AES)	Merges number theory (RSA) with block cipher algebra (AES)	Very High	Medium–High	Strong (combines advantages)	Key exchange + data encryption (e.g., HTTPS)
Proposed Method	Combines RSA (number theory), fuzzy logic (membership theory), graph theory (domination, topology)	Very High	High–Very High	Very strong (due to added fuzzy and graph complexity)	Highly confidential transmissions, layered security

, reflects the following:

⮚

RSA Encryption: Though popular, RSA has less security and resistance to attacks but it is computationally intensive.

⮚

AES Encryption: It offers greater security and efficiency than RSA and is thus best for rapid encryption but vulnerable to quantum attacks.

⮚

Hybrid (RSA + AES): It provides a well-balanced trade-off between efficiency and security, improving resistance against attacks.

⮚

Proposed Method: It outperforms all other current methods, with better security and attack resistance without compromising computational efficiency. Fuzzy logic combined with graph-based encryption provides a greater level of complexity, and therefore, decryption is very difficult for an unauthorized user.

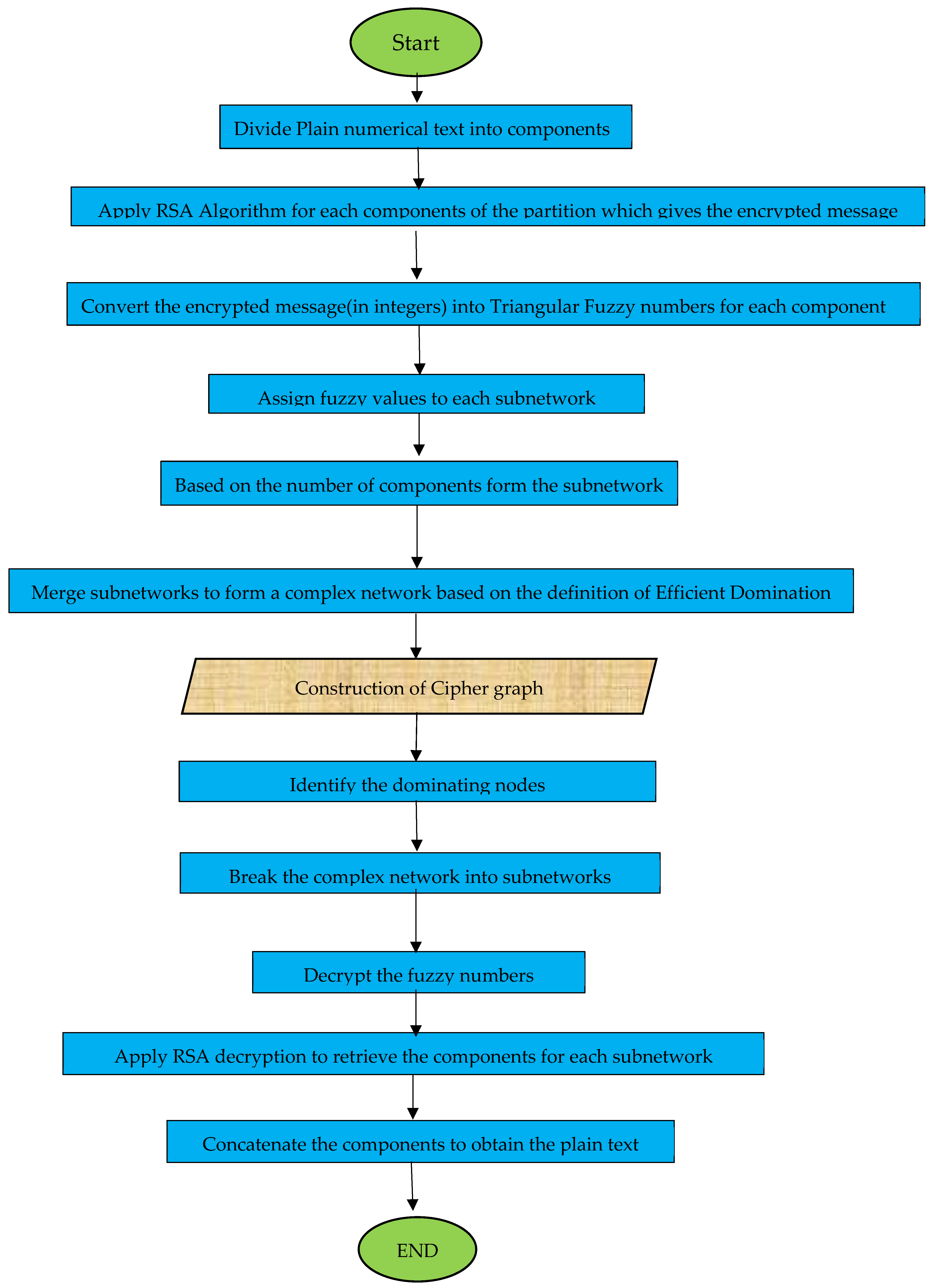
8. Flowchart

This workplan outlines a multi layer encryption process where a very large numerical plaintext is encrypted in structured steps and then converted into a complex fuzzy graph network. A flowchart is essential to visualize each stage from plaintext to ciphertext and finally back to plaintext in decryption. The flowchart is given in Figure 7.

9. Applications in Secure Cloud Storage and Access Control

Cloud computing has emerged as the core infrastructure for the storage of data and delivery of services, but the open and distributed nature of cloud computing poses great challenges to security-sensitive information. Classical security systems tend to bank on static access control and binary authentication, which can be inadequate to manage the dynamic and contextual nature of user access in today’s cloud computing environment. The fuzzy graph-based model proposed here overcomes these shortcomings by combining RSA encryption, effective domination in graph theory, and fuzzy logic to create an adaptive and robust security system.

How the Working Model Operates in a Cloud Scenario:

(i)

RSA for Data Privacy and Authentication: The entire sensitive information kept in the cloud is encrypted with the help of RSA, so even if storage is hacked, the data cannot be read without the private key. RSA also facilitates secure key exchange and digital signatures, enabling both cloud service providers and users to authenticate each other.

(ii)

Efficient Domination for Fine-Tuned Access Control Structures: The cloud infrastructure can be modeled as a graph in which the nodes are either users, devices, or access points and the edges are communication or control relationships. Using efficient domination, the system is able to determine a minimum subset of key control points (dominating nodes) that are capable of monitoring and controlling access across the network. This minimizes redundancy, decreases overhead, and provides efficient monitoring and policy enforcement.

(iii)

Fuzzy Logic for Context-Aware Access Decisions: In contrast to static access control systems, the fuzzy logic module presents triangular fuzzy membership functions to analyze contextual variables such as the following: access time (e.g., working hours vs. non-working hours), geography (e.g., familiar vs. unfamiliar IPs), user activity (e.g., frequent vs. suspicious usage) and device trust level (e.g., personal vs. public device).

Given these fuzzy inputs, the system allocates access permissions on a graded basis (e.g., full access, reduced access, or denial), enhancing flexibility without sacrificing security.

Advantages of the Model in Cloud Environments

(i)

Dynamic Access Control: Access decisions are taken dynamically according to contextual information, enhancing responsiveness to threats or anomalies.

(ii)

Resource Optimization: Efficient domination decreases the workload by minimizing the nodes that need to actively control access and security enforcement.

(iii)

Greater Resilience: The hybrid model incorporates additional layers of security—cryptographic strength provided by RSA, structural optimization by graph theory, and flexibility by fuzzy logic.

(iv)

Improved User Experience: Legitimate users stand less chance of denial of access because of strict rules since the fuzzy system checks intent and context more astutely.

This model demonstrates that the suggested fuzzy graph network model provides a big improvement over standard access control and encryption methods used in cloud computing. It can provide both secure protection of information and intelligent management of access and is particularly best suited for conditions where flexibility, scalability, and real-time decisions are needed.

10. Possible Attack Vectors of the Proposed Model

Although the model proposed here is an innovative blend of RSA, efficient domination, and fuzzy logic used to improve security, it is important to keep in mind possible attack surfaces that could threaten system integrity. The detection of these vulnerabilities aids in making the model more resilient and consistent with typical threat models used in cryptography.

• Chosen-Cipher Text Attack: An attacker presents a decryption oracle with random cipher texts to obtain respective plaintexts, potentially exposing patterns or secret keys.
• Graph Theoretic Structural Attacks: Efficient domination determines key nodes in a graph. If the attacker can determine and take out these dominating nodes, they can potentially achieve higher-level access or interfere with communication channels.
• Fuzzy Inference Manipulation: Attackers can take advantage of the fuzzy logic layer by providing specially designed input values to control decision outputs (e.g., gain unauthorized access via marginal input conditions).

11. Conclusions

This research provides a solid mathematical framework for the protection of communication systems by combining fuzzy graph networks, efficient domination, and RSA. The suggested model increases security using the intractability of the prime factorization in RSA and improving resource consumption with efficient domination within fuzzy graphs. Through the addition of triangular fuzzy membership functions, the system provides an extra level of complexity to unauthorized decryption, rendering it very difficult. Hence, this approach guarantees a very secure and computation-friendly cryptographic form, reinforcing the confidentiality and integrity of data within contemporary networks of communication.

Key Takeaways

• The model merges RSA, fuzzy logic, and graph theory for better security.
• It incorporates efficient domination in fuzzy graphs for additional structural complexity.
• It scales well with key size and sub-network design.
• It is most appropriate for high-security data transmissions.
• It is no longer quantum-resistant, but additional layers provide added protection.
• It is flexible for future expansion with post-quantum methods.