On the Dynamics of Some Three-Dimensional Systems of Difference Equations
Abstract
1. Introduction
2. The Main Results
2.1. The First Case
2.2. The Second Case
2.3. The Third Case
2.4. The Fourth Case
2.5. The Fifth Case
2.6. The Sixth Case
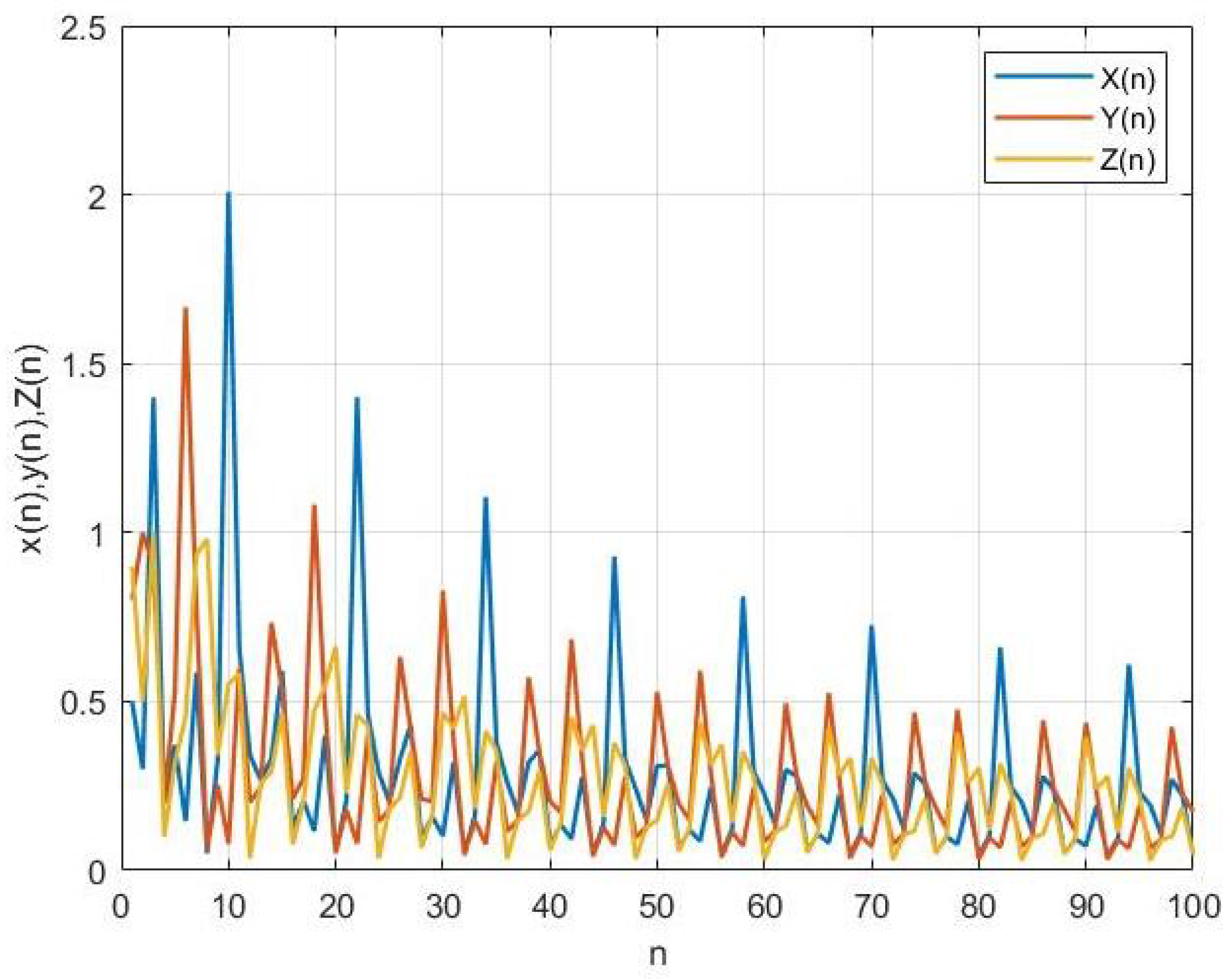
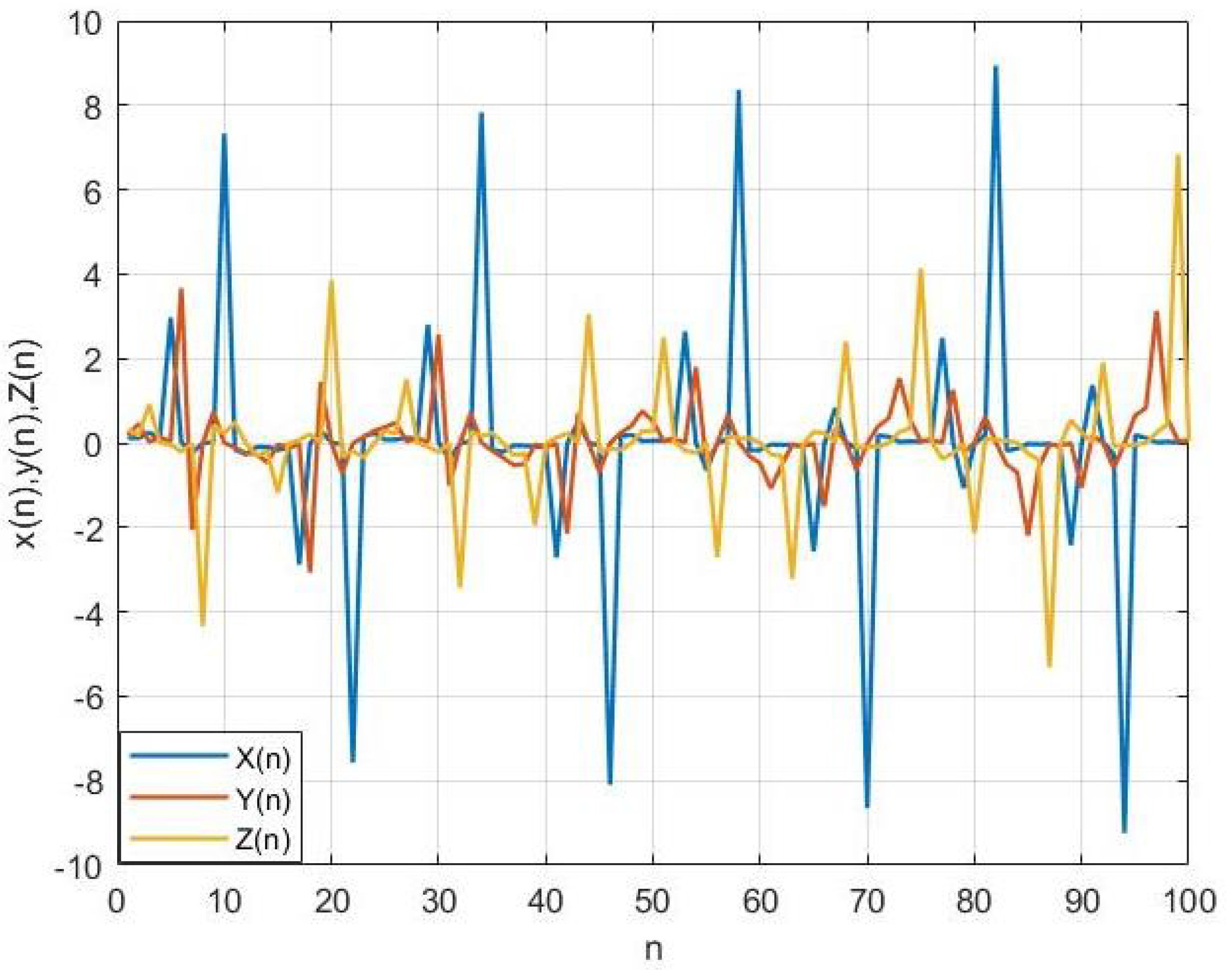
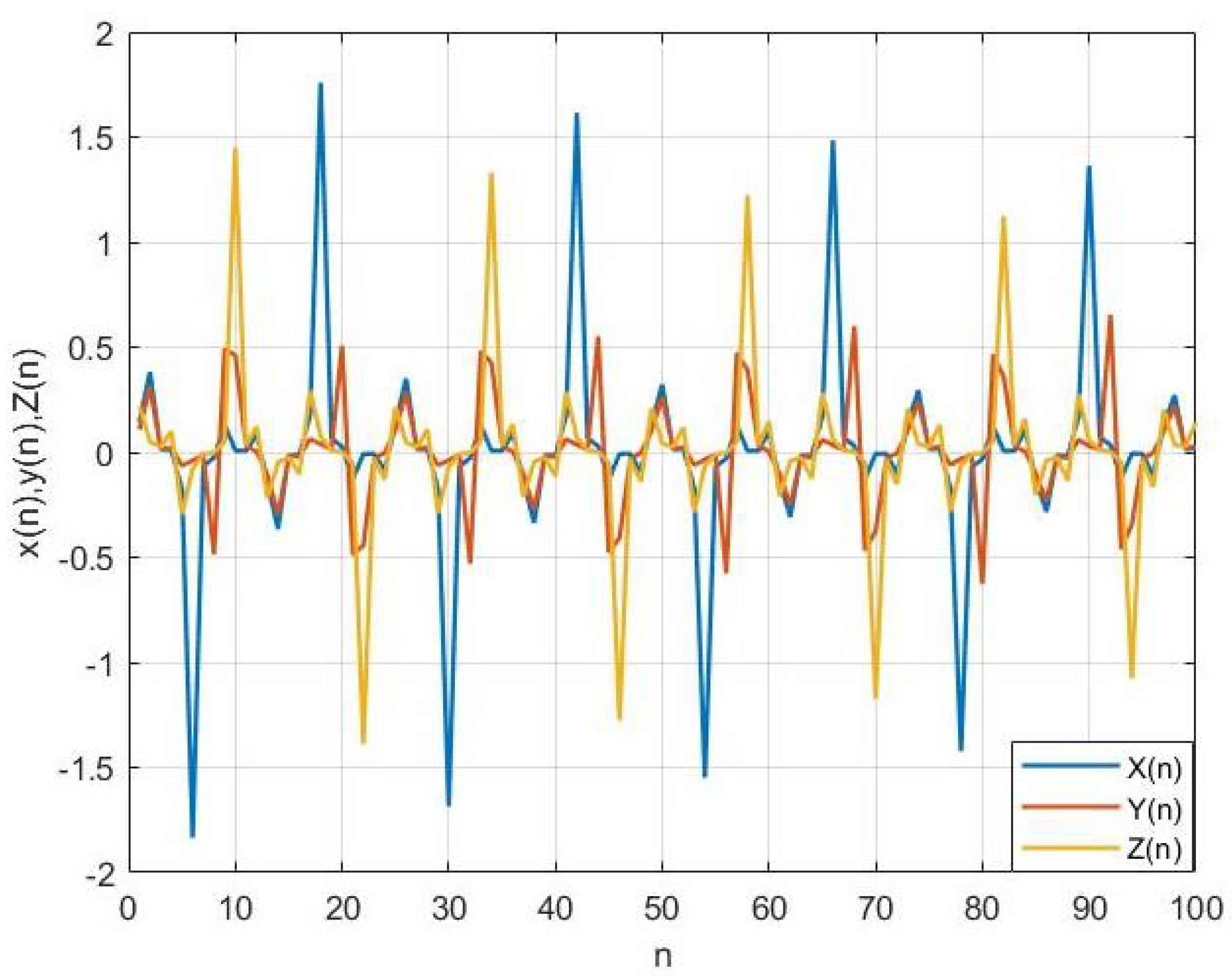
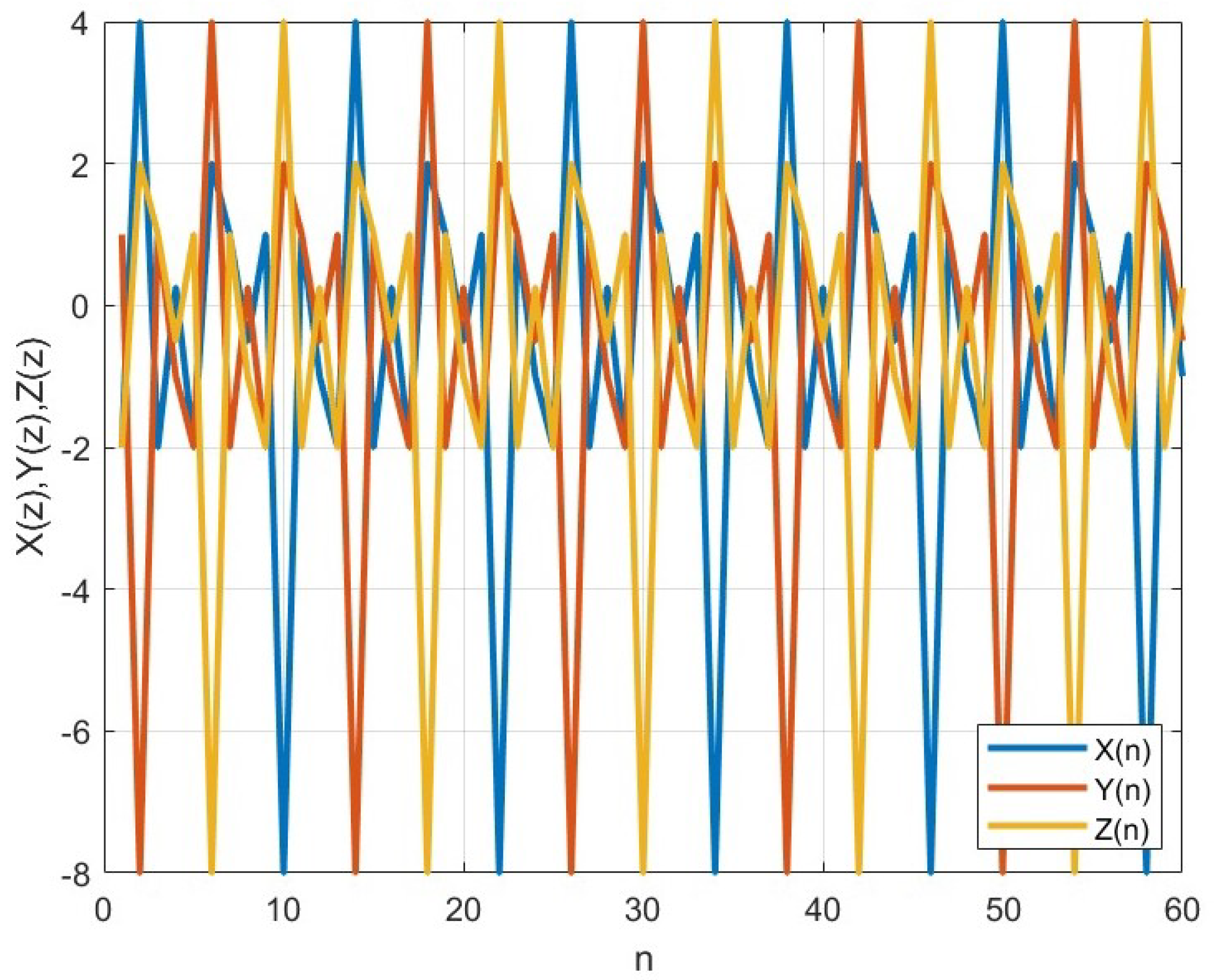
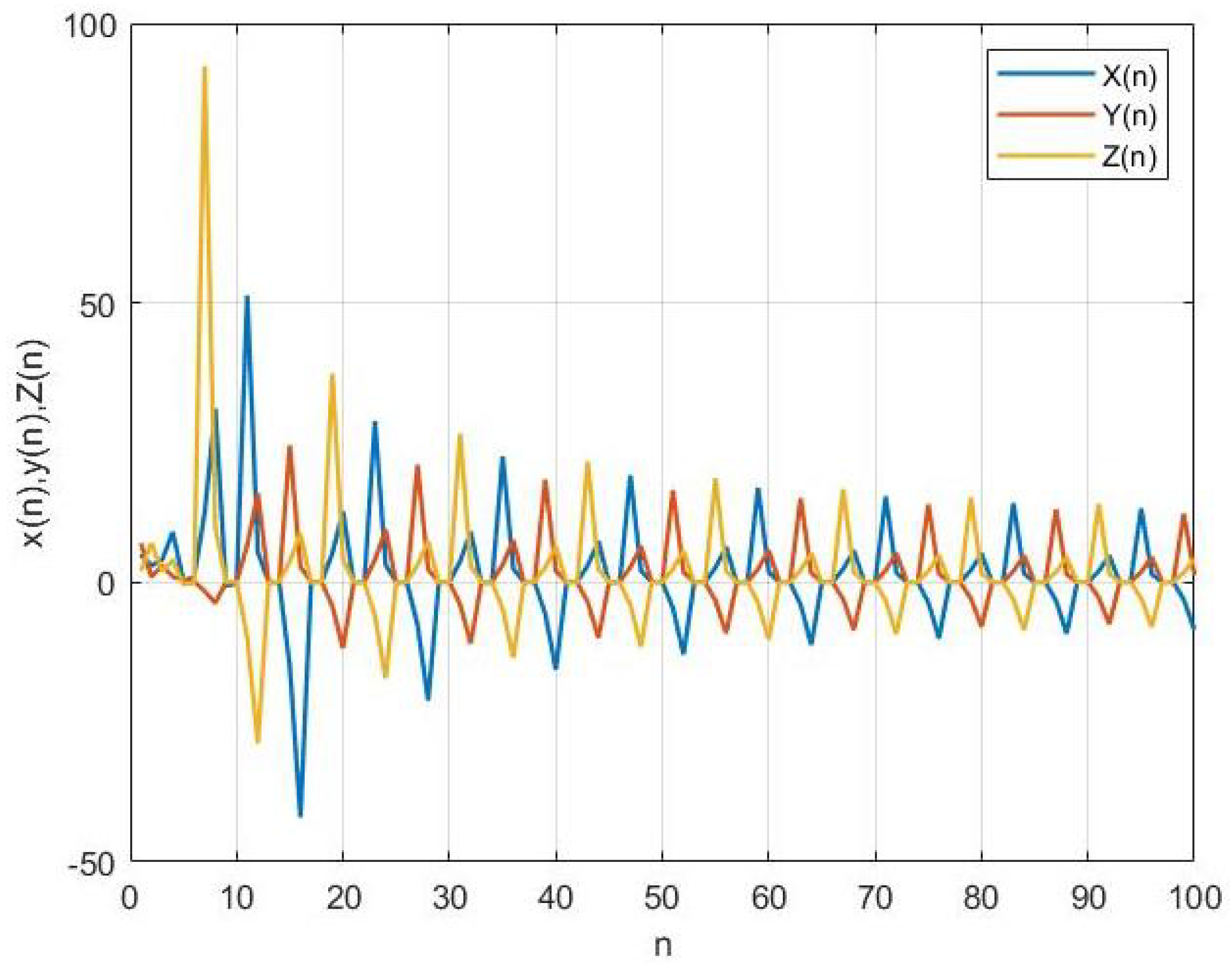
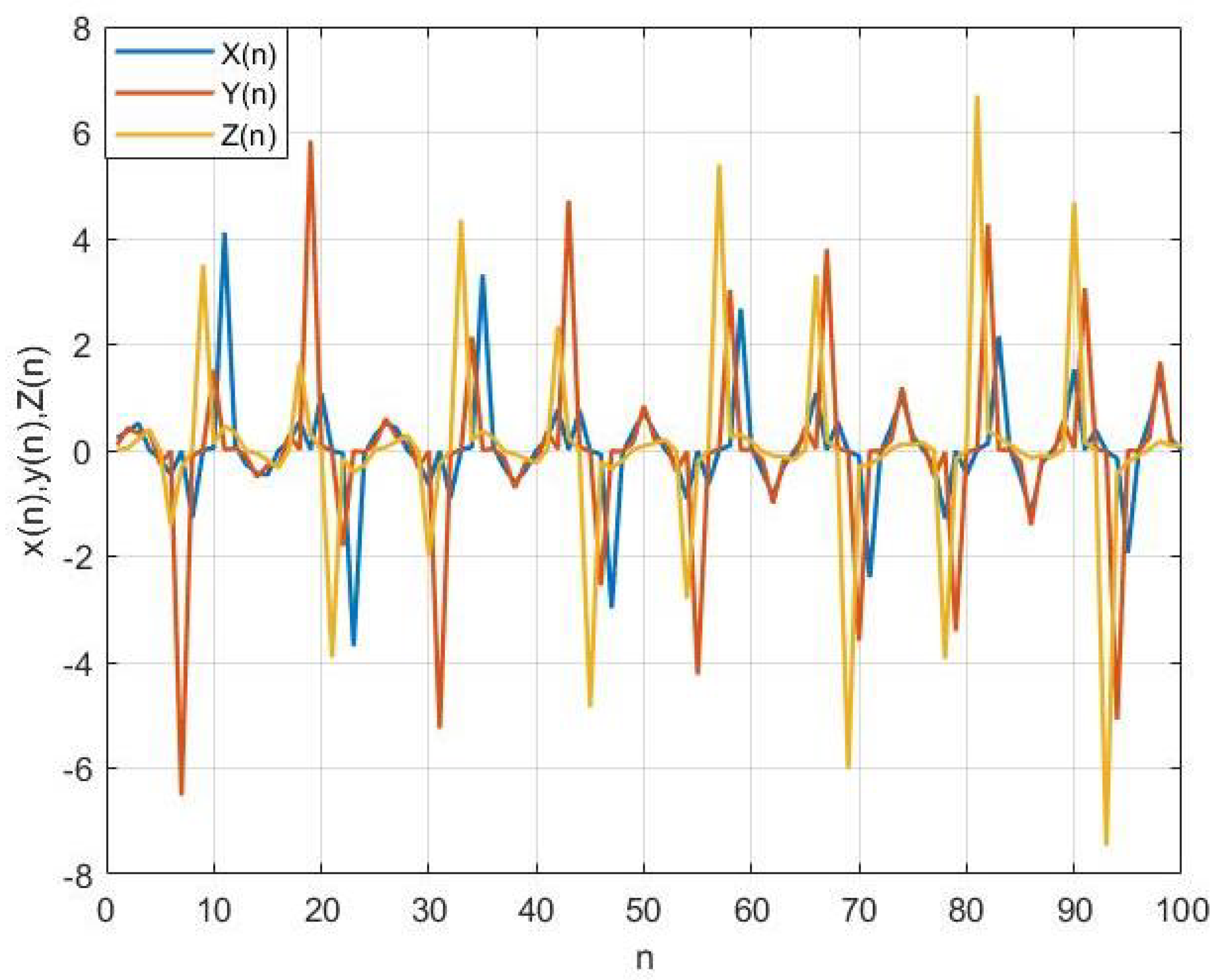
3. Numerical Simulations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 3
Appendix B. Proof of Theorem 5
References
- Althagafi, H. Dynamics of difference systems: A mathematical study with applications to neural systems. AIMS Math. 2025, 10, 2869–2890. [Google Scholar] [CrossRef]
- Alharbi, T.D.; Hasan, M.R. On the Dynamics of Some Higher-Order Nonlinear Difference Equations. Mathematics 2024, 12, 3810. [Google Scholar] [CrossRef]
- Ahlbrandt, C.D.; Peterson, A.C. Discrete Hamiltonian Systems: Difference Equations, Continued Fractions, and Riccati Equations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Khan, A.Q.; Ayesha, Y.; Alsaadi, A. Discrete Hepatitis C virus model with local dynamics, chaos and bifurcations. AIMS Math. 2024, 9, 28643–28670. [Google Scholar] [CrossRef]
- Lei, C.; Han, X. Codimension-two bifurcation analysis of a discrete predator–prey system with fear effect and Allee effect. Nonlinear Anal. Model. Control. 2025, 30, 386–404. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Alshareef, A.; Alzahrani, F. Qualitative behavior and solution of a system of three-dimensional rational difference equations. Math. Methods Appl. Sci. 2022, 45, 5456–5470. [Google Scholar] [CrossRef]
- Gümüş, M.; Abo-Zeid, R. Qualitative study of a third order rational system of difference equations. Math. Moravica 2021, 25, 81–97. [Google Scholar] [CrossRef]
- El-Dessoky, M.M.; Elsayed, E.M.; Elabbasy, E.M.; Asiri, A. Expressions of The Solutions of Some Systems of Difference Equations. J. Comput. Anal. Appl. 2019, 27, 1161–1172. [Google Scholar]
- Halim, Y. Global Character of Systems of Rational Difference Equations. Electron. J. Math. Anal. Appl. 2015, 3, 204–214. [Google Scholar]
- Elsayed, E.M.; Al-Juaid, J.G.; Malaikah, H. On the Solutions of Systems of Rational Difference Equations. J. Progress. Res. Math. 2022, 9, 1987–1997. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Al-Juaid, J.G. The Form of Solutions and Periodic Nature for Some System of Difference Equations. Fundam. J. Math. Appl. 2023, 6, 24–34. [Google Scholar] [CrossRef]
- Alharbi, T.D.; Elsayed, E.M. The solution expressions and the periodicity solutions of some nonlinear discrete systems. Pan-Am. J. Math. 2023, 2, 3. [Google Scholar] [CrossRef] [PubMed]
- Kara, M. Solvability of a Three-Dimensional System of Nonlinear Difference Equations. Math. Sci. Appl. E-Notes 2022, 10, 1–15. [Google Scholar] [CrossRef]
- Khaliq, A.; Ibrahim, F.T.; Alotaibi, A.M.; Shoaib, M.; El-Moneam, M. Dynamical Analysis of Discrete-Time Two-Predators One-Prey Lotka–Volterra Model. Mathematics 2022, 10, 4015. [Google Scholar] [CrossRef]
- Taskara, N.; Buyuk, H. On The Solutions of Three-Dimensional Difference Equation Systems Via Pell Numbers. Eur. J. Sci. TechnoL. 2022, 34, 433–440. [Google Scholar] [CrossRef]
- Almatra, M.B.; Elsayed, E.M. Solutions And Formulae For Some Systems Of Difference Equations. MathLAB J. 2018, 1. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; Society for Industrial and Applied Mathematics: Montreal, QC, Canada, 2005; pp. 40–41. [Google Scholar]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Kluwer Academic Publishers: London, UK; Springer: New York, NY, USA, 1993. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, T.D.; AL-Juaid, J.G. On the Dynamics of Some Three-Dimensional Systems of Difference Equations. Axioms 2025, 14, 371. https://doi.org/10.3390/axioms14050371
Alharbi TD, AL-Juaid JG. On the Dynamics of Some Three-Dimensional Systems of Difference Equations. Axioms. 2025; 14(5):371. https://doi.org/10.3390/axioms14050371
Chicago/Turabian StyleAlharbi, Turki D., and Jawharah G. AL-Juaid. 2025. "On the Dynamics of Some Three-Dimensional Systems of Difference Equations" Axioms 14, no. 5: 371. https://doi.org/10.3390/axioms14050371
APA StyleAlharbi, T. D., & AL-Juaid, J. G. (2025). On the Dynamics of Some Three-Dimensional Systems of Difference Equations. Axioms, 14(5), 371. https://doi.org/10.3390/axioms14050371





