1. Introduction
This paper considers only undirected and simple graphs. A graph G has a -partition into if its vertex set can be partitioned into k sets where is an empty set or the induced subgraph is in a family of graphs for each . This concept generalizes a notion of proper k-vertex coloring (when each family consists of edgeless graphs). Other widely studied families consist of graphs with no edges, graphs with maximum degree at most d, forests with maximum degree at most and forests without restricted degree. Such families are denoted by and , respectively.
Naturally, vertex partition has been investigated in planar graphs with specific girths.
It was shown that every planar graph has an
-partition [FCT], a
-partition [
1], an
-partition [
2], and a
-partition [
3].
For each planar graph with girth 4, it was shown that this graph has an
-partition [
4] and a
-partition [
5].
For each planar graph with girth 5, it was shown that this graph has a
-partition [
6] and a
-partition [
7,
8]. With an additional condition that this graph has no adjacent 5-cycles, then it has a
-partition [
9].
For each planar graph with girth 6, it was shown that this graph has a
-partition [
10],
-partition [
11], a
-partition [
12], and a
-partition [
13].
For each planar graph with girth 7, it was shown that this graph has an
-partition [
10] and a
-partition [
14].
For each planar graph with girth 8, it was shown that this graph has an
-partition [
10] and an
-partition [
14].
For each planar graph with girth 10, it was shown that this graph has an
-partition [
14] and an
-partition [
14].
Some results presented in the list above may be redundant since we can partition a forest into two independent sets, whereas is a subfamily of However, for chronological clarity, earlier results for -partitions are presented.
The search for sufficient conditions for an
-partition of planar graphs has gained attention since Chartrand and Kronk [
15] provided an example of a planar graph without such partition.
Additionally, exploring conditions for an
-partition is also of particular interest since it may require stronger conditions than that of an
-partition. For example, since every planar graph with girth 4 is 3-degenerate, it has an
-partition. However, Montassier and Ochem [
16] constructed, for each
and
, a planar graph with girth 4 having no
-partitions. As a result, an existence of
-partition cannot guarantee to be strengthened into any
-partition.
To further study planar graphs of girth
an
-partition (where the condition of bounded degree of one family is relaxed to be unbounded) was considered instead. Dross et al. [
5] showed that every planar graph of girth 4 has an
-partition when
The case for
is still open. Note that the case
, if positive, will imply Grötzsch’s result [
4] (an
-partition). Now, Feghali and Šámal [
17] answer the following question for
Apart from girth, certain conditions related to cycles have been explored. Sittitrai and Nakprasit [
18] proved that every planar graph with neither 4- nor 5-cycles admits both a
-partition and a
-partition. Later, Cho et al. [
19] strengthened the result by establishing an
-partition.
Several results concerning planar graphs neither 4- nor 6-cycles are as follows. Wang and Chen [
20] showed that such a graph admits an
-partition if it also has no 8-cycles, while Kang et al. [
21] showed a similar result if it has no 9-cycles. Liu and Yu [
22] improved both results by establishing an
-partition for such graphs.
Without additional requirements, Nakprasit et al. [
23] showed that every planar graph with neither 4- nor 6-cycles has a
-partition. Recently, Hu and Huang [
24] improved the result into an (
)-partition. Furthermore, Wang and Xu [
25] proved that every planar graph with neither 4- nor 6-cycles has a
-partition. Furthermore, Huang et al. and Sittitrai et al. [
26,
27] independently improved the result in the following theorem.
Theorem 1 ([
26,
27])
. Every planar graph with neither 4- nor 6-cycles has an ()-partition. Another condition for a planar graph to have an ()-partition was provided by Liu and Wang as follows.
Theorem 2 ([
28])
. Every planar graph with neither 3-cycles nor chordal 6-cycles has an ()-partition. The following theorem, which is the main result of this work, can be shown to imply Theorems 1 and 2.
Theorem 3. If a planar graph G satisfies the following conditions: (i) none of its 3-faces is adjacent to a -face, and (ii) none of its 4-faces is adjacent to a -face, then it has an ()-partition.
We organize this paper as follows. In
Section 2, we investigate configurations of the minimal counterexample to the main theorem. In
Section 3, we employ a discharging method, with the knowledge of configurations, to prove the main theorem. In
Section 4, we discuss the implications of the main result, including Theorems 1 and 2. Additionally, we propose a conjecture related to partitioning planar graphs with neither 4- nor 6-cycles.
2. Structures of Minimal Counterexamples
We use the following notation in this paper. A k-vertex, -vertex, and -vertex is a vertex of degree k, at least k, and at most k, respectively. We also have a similar notation for faces. A k-neighbor of v is a vertex with degree k adjacent to v.
Let denote the boundary walk of a face f. A vertex v and a face f are incident if v is on The degree of a face denoted by is the number of the boundary walk of a face If a vertex v is not incident to a face f but is adjacent to a 3-vertex u on then f is a pendent face of a vertex v and v is a pendent neighbor of u (with respect to f).
We use to denote the number of incident i-faces of a vertex v, and use to denote the number of pendent i-faces of a vertex v. We use in the previous notation when considering -faces.
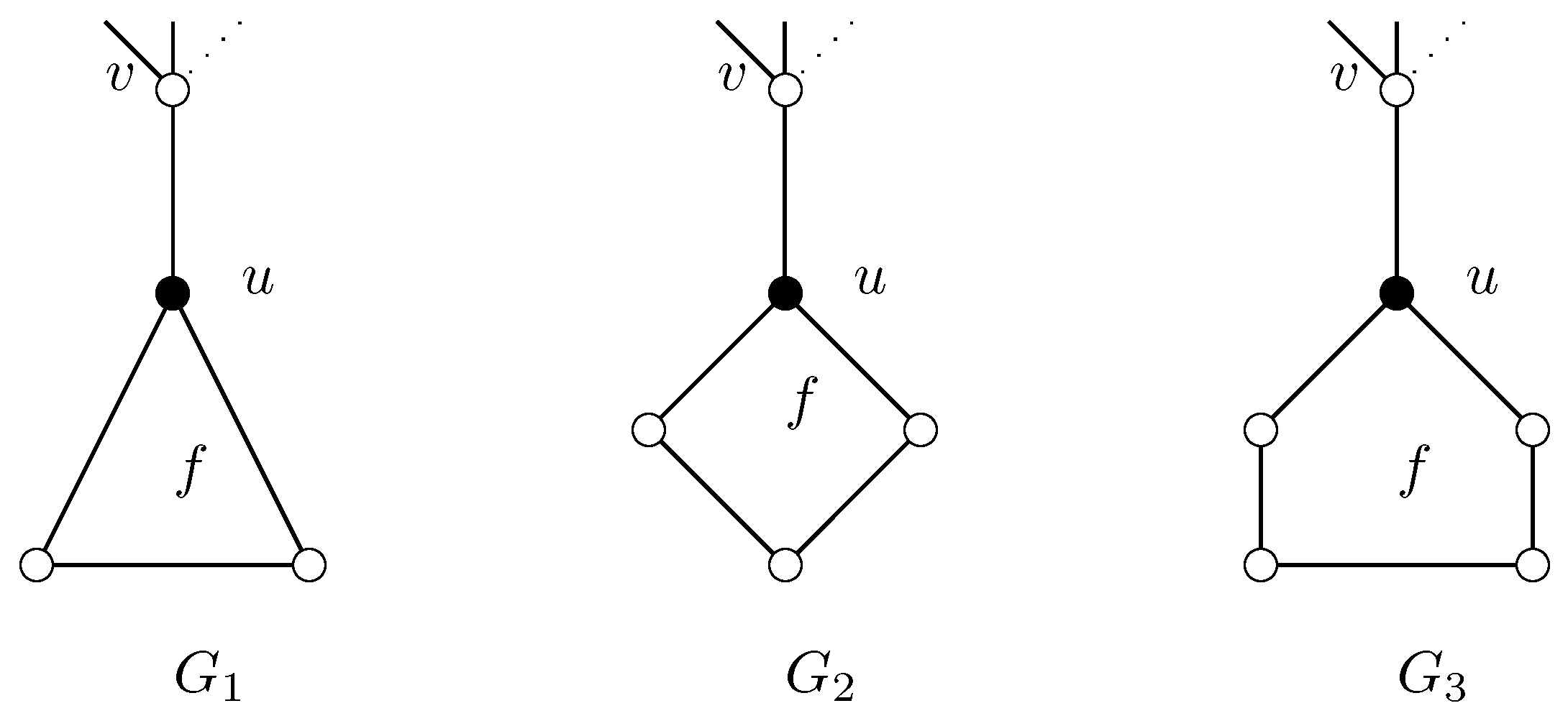
A 3-vertex
u incident to a
k-face
f for
is a
terrible 3-vertex (see
Figure 1) of
f if
u has a pendent
-neighbor with respect to
A 3-face
f is a
poor 3-face (see
Figure 2) if
f is incident to two terrible 3-vertices.
Suppose is a (not necessarily proper) subgraph of G, and is partitioned into and . If a vertex u in () is a neighbor of v (where v may be not in , then we call u a -neighbor of v. Furthermore, v is called -saturated if and v has at least two -neighbors.
Conditions (i) and (ii) in Theorem 3 are not considered in the next three lemmas. The only assumption in those lemmas is that a planar graph G is a minimal graph (subject to the number of vertices and edges) without an ()-partition. In contrast, Lemma 4 is only concerned with Conditions (i) and (ii).
Lemma 1. If G is a minimal graph without an ()-partition, then each vertex in G is a -vertex.
Proof. We show the contradiction only for the case of a 2-vertex u in G, as the remaining case is more straightforward. By minimality, has an ()-partition into and .
Let v and w are two adjacent vertices of If or , then G has an ()-partition into and , a contradiction. If , then G has an ()-partition into and a contradiction. □
Lemma 2. If G has an ()-partition into and then we can assume that (i) each 3-vertex in is not -saturated, and (ii) each 2-vertex is in but has no -neighbors, or is in with at most one -neighbor.
Proof. Assume G has an ()-partition into and (i) We can reduce the 3-vertices in that are -saturated as follows. If v is a -vertex that is -saturated, then v has at most one -neighbor. Consequently, G has an ()-partition into and with a decreasing number of -vertices that is -saturated. The process can be continued until each 3-vertex is not -saturated.
(ii) We say that a 2-vertex v has the undesired property if v is in and has a -neighbor, or is in and has two -neighbors. From the process above, each 2-vertex in has at most one -neighbor.
Consider a 2-vertex v in with one -neighbor and one -neighbor, say u. We obtain a new ()-partition of G as follows. If u is a 2-vertex with one -neighbor, then we have a new ()-partition into and , otherwise we have a new ()-partition into and . In either case, G has a new ()-partition with the reduced number of undesired 2-vertices.
Consider a 2-vertex v in with two -neighbors. Then, G has a new ()-partition into and with the reduced number of undesired 2-vertices.
Continue this process until we have no undesired 2-vertices. Note that each -vertex in still is not -saturated by this process. Thus, the proof is complete. □
Lemma 3. A planar graph G which is a minimal graph without an ()-partition has the following properties.
- (i)
Each 3-vertex is adjacent to a -vertex.
- (ii)
Each 5-vertex is not incident to a poor 3-face.
- (iii)
Each 6-vertex is incident to at most one poor 3-face.
Proof. (i) Suppose to the contrary that a 3-vertex v is adjacent to three -vertices. By minimality, has an ()-partition into and .
If v has no -neighbors, then G has an ()-partition into and If v has at least two -neighbors, then G has an ()-partition into and
It remains to consider that v has exactly one -neighbor u. By Lemma 2, u is not -saturated. Consequently, G has an ()-partition into and This contradiction completes the proof.
(ii) Suppose to the contrary that a poor 3-face f is incident to a 5-vertex v. Let From the definition, and are terrible 3-vertices with pendent -neighbors, say and , respectively.
Consider with an ()-partition into and Note that each of v, , and is a -vertex in By Lemma 2, each of them is not -saturated.
If or is in , then G has an ()-partition into and a contradiction.
If and are in , then G has an ()-partition into and since v is not -saturated, a contradiction.
If and are in , then G has an ()-partition into and a contradiction.
If is in and is in , then G has an ()-partition into and a contradiction.
If and are in , then G has an ()-partition into and since is not -saturated, a contradiction.
(iii) Suppose to the contrary that v is incident to two poor 3-faces with the boundary walks and From the definition, is a terrible 3-vertices with pendent -neighbors, say , for .
Consider with an ()-partition into and Note that or v, where is a -vertex in . By Lemma 2, these vertices are not -saturated. Additionally, if then it has no -neighbors.
We show that we can extend an ()-partition to G as follows.
If and are in then G has an ()-partition of G into and .
If v and are in while and are in , then G has an ()-partition of G into and .
If v is in while and are in , then G has an ()-partition of G into and .
If and are in while v is in , then G has an ()-partition of G into and .
If is in while and are in , then G has an ()-partition of G into and .
If and are in then G has an ()-partition of G into and .
Each of the remaining cases is symmetric to one of the previous cases. Thus, G has an ()-partition. This contradiction completes the proof. □
Lemma 4. If G satisfies Conditions (i) and (ii) in Theorem 3, then each k-vertex v has bounds on and as follows.
- (i)
.
- (ii)
- (iii)
.
- (iv)
.
Proof. Let be the neighbors of a k-vertex
Define the following sets: A: = the set of where and v share the same incident -face.
B: = the set of where v is a pendent neighbor of with regard to a -face.
C: = the set of where and v share the same incident 5-face.
D: = the set of where v is a pendent neighbor of with regard to a 5-face.
The following properties arise directly from the definitions of the four sets and Condition (ii) of G which states that none of its 4-faces is adjacent to a -face.
Property (a): The sets and D are mutually disjoint.
Property (b): If , then is incident to exactly one 4-face of v. On the other hand, a 4-face of v is incident to two neighbors of Thus,
Property (c): Since a 5-face incident to v is also incident to two neighbors of v, it follows that when .
From Properties (a) and (b), we deduce that
The inequalities imply (i), (iii), and (iv), as well as the first two cases of (ii), immediately.
It follows from Property (c) that the second inequality becomes strict when . This implies the last case of (ii) to complete the proof. □
3. Proof of Theorem 3
Suppose
G is a minimal counterexample to the theorem. The discharging process is defined as follows. The initial charge of a vertex
v is given by
and the initial charge of a face
f is given by
. By Euler’s formula
and the Handshaking Lemma, we obtain that
Now, we establish a new charge for each by redistributing charge from one element to another. The total sum of the new charge remains If, after the redistribution, the final charge satisfies for all , we obtain a contradiction, thereby completing the proof.
Let represent the charge transferred from a vertex v to both an incident face and a pendent face x. Similarly, let represent the charge transferred from a face f to an incident vertex y.
The rules for discharging these charges are articulated as follows.
- (R1)
Let v be a 3-vertex.
if x is its incident 3-face.
- (R2)
Let v be a 4-vertex.
- (R3)
Let v be a -vertex.
- (R4)
Let f be a -face.
if y is its incident 3-vertex that is also incident to a 3-face.
To complete the proof, we need to show that the resulting for each . It is clear that when z is a 3-vertex not incident to any 3-faces or when z is a 6-face.
CASE 1: Let v be a 3-vertex incident to a 3-face.
Recall Condition (i) of G that none of its 3-faces is adjacent to a -face. It follows that v is incident to two -faces and one 3-face. Consequently, by (R1) and (R4).
CASE 2: Let v be a 4-vertex.
By (R2), v loses charge . Using Lemmas 4 (i) and (ii), we consider the following subcases:
- -
If , then . Thus,
- -
If , then . Thus,
- -
If , then . Thus,
CASE 3: Let v be a -vertex and .
By Lemmas 4 (ii) and (iv), we have
and
Thus,
by (R3) and the fact that
.
CASE 4: Let v be a 5-vertex with .
By Lemma 3 (ii),
v is not incident to any poor 3-face. Consequently,
v gives a charge at most
to each incident
-face. By (R3), we have the final charge of
v as
CASE 4.1: Suppose .
By Lemma 4, we obtain
and
. Also,
. Substituting these into the equation for
, we obtain
CASE 4.2: Suppose .
By Lemma 4, we obtain
,
, and
. Substituting these into the equation for
, we obtain
CASE 5: Let v be a 6-vertex with .
By Lemma 3 (iii), v is incident to at most one poor 3-face. We only need to consider the case where v incident to exactly one poor 3-face, denoted by f. In this case, v gives a charge of to the 3-face f, and to the other -faces.
By (R3), we calculate
as follows:
CASE 5.1: Suppose .
By Lemmas 4 (iii) and (iv), we have
It follows from a calculation in
CASE 4.1 that
CASE 5.2: Let .
It follows from a calculation in
CASE 4.2 that
CASE 6: Let v be a -vertex with .
Then
v transfers at most
of its charge to each incident
-face. By (R3), we compute
as follows:
CASE 6.1: Suppose .
By Lemmas 4 (iii) and (iv), we have
. It follows from a calculation in
CASE 4.1 that
- -
If
v is a 7-vertex, then
and
. Thus,
- -
If
v is an
-vertex, then we use
to obtain
CASE 6.2: Suppose .
By Lemma 4, we have
,
, and
. It follows from a calculation in
CASE 4.2 that
CASE 7: Let f be a 3-face.
If f is incident to a terrible 3-vertex, then it must also be incident to a -vertex, according to Lemma 3 (i). As a result, f can have at most two incident terrible 3-vertices.
Let k be the number of incident non-terrible 3-vertices of
If f has no incident terrible 3-vertices, then by (R1), (R2), and (R3).
If f has exactly one incident terrible 3-vertex, then by (R1), (R2), and (R3).
If f has two incident terrible 3-vertices, then by (R1) and (R3).
CASE 8: Let f be a 4-face. We use Lemma 3 (i) to obtain the following results. If f has no incident -vertices, then f has four non-terrible 3-vertices. If f has exactly one incident 4-vertex, then f has three non-terrible 3-vertices. Thus, by (R3).
If f has an incident -vertex, then f has at least one non-terrible 3-vertex by Lemma 3 (i). Thus by (R3).
If f has at least two incident -vertices, then by (R2) and (R3).
CASE 9: Let f be a 5-face.
If f has no incident -vertices, then f has five non-terrible 3-vertices by Lemma 3 (i). Thus, by (R3).
If f has exactly one incident -vertex, then f has at least two non-terrible 3-vertices by Lemma 3 (i). Thus by (R2) and (R3).
If f has at least two incident -vertices, then by (R2) and (R3).
CASE 10: Let f be a -face.
Note that a 7-face is incident to at most six 3-vertices that are also incident to a 3-face; otherwise, there are two adjacent 3-faces, which contradicts Condition (i) of G.
By (R4), if f is a 7-face, and if f is a -face.
From all the cases considered, we obtain a contradiction. This completes the proof.
4. Concluding Remarks and Open Problem
Before we show that our main result in Theorem 3 implies Theorems 1 and 2, two following lemmas are required.
Lemma 5. Let G be a graph with no chordal -cycles where G has no -vertices. Given f and g are adjacent faces in G, the following statements hold.
- (i)
If f is a 3-face, then g is not an m-face where .
- (ii)
If f is a 4-face, then g is not an m-face where .
Proof. (i) Suppose to the contrary that f is a 3-face and g is -face.
- -
Let be bounded by one cycle (a -cycle).
If and share exactly two vertices, then is a ()-cycle with a chord where , a contradiction.
If and share exactly three vertices, then is a -cycle with a chord where , a contradiction.
- -
Let be bounded by at least two cycles. Since G has no 2-vertices, we only consider the case g is a 6-face where is intersecting two 3-cycles and .
If and share exactly two vertices, then or is a 4-cycle with a chord, a contradiction.
If and share exactly three vertices, then or . Consequently, G contains a 2-vertex, a contradiction.
(ii) Suppose to the contrary that f is a 4-face and g is -face. Note that is bounded by one cycle (a -cycle).
If and share exactly two vertices, then is a ()-cycle with a chord where , a contradiction.
If and share at least three vertices, then let and . By symmetry, we only consider the case where If , then is a 2-vertex which contradicts Lemma 1, otherwise is a -cycle with a chord which is also a contradiction. □
Lemma 6. Let G be a graph with neither 4-cycles nor 6-cycles where G has no -vertices. If f and g are adjacent faces in G where f is a 3-face, then g is not an m-face where .
Proof. Suppose to the contrary that f is a 3-face and g is -face.
- -
Let be bounded by one cycle (a -cycle).
From the condition of G, we assume . Consider , we have G contains a 4-cycle if and share exactly two vertices, and G contains a 2-vertex if and share exactly three vertices, a contradiction.
Consider , we have G contains a 6-cycle if and share exactly two vertices, and G contains a 4-cycle if and share exactly three vertices, a contradiction.
- -
Let be bounded by at least two cycles. By Lemma 1, we only consider the case that g is a 6-face where is intersecting two 3-cycles and .
If and share exactly two vertices, then or is a 4-cycle, a contradiction.
If and share exactly three vertices, then or . Consequently, G has a 2-vertex. □
Now, we are in a position to show that our main result in Theorem 3 implies Theorems 1 and 2.
Theorem 4. Every planar graph (i) with no chordal -cycles, or (ii) with neither 4- nor 6-cycles, has an ()-partition.
Proof. Suppose to the contrary that there exists a minimal counterexample G. By Lemma 3 (i), G has no -vertices.
- (i)
Suppose G has no chordal -cycles. By Lemma 5, none of its 3-faces is adjacent to a -face, and none of its 4-faces is adjacent to a -face. It follows from Theorem 3 that G has an ()-partition.
- (ii)
Suppose G has neither 4- nor 6-cycles. By Lemma 6, none of its 3-faces is adjacent to a -face. Since G has no 4-cycles, it has no 4-faces. It follows from Theorem 3 that G has an ()-partition.
Thus, a minimal counterexample does not exist. This completes the proof. □
Note that Theorem 4 (i) implies Theorem 2, while Theorem 4 (ii) is exactly Theorem 1. Apart from the latter result, it is shown by Kang et al. [
29] that each planar graph with neither 4- nor 6-cycles also has an
-partition. Motivated by these results, we propose the following conjecture.
Problem 1. Every planar graph with neither 4- nor 6-cycles has an -partition.
It is worth noting that vertex partition problems have broad applications in various domains. For instance, they play a key role in frequency assignment for wireless networks and in the design of fault-tolerant networks, where partitioning helps to minimize interference and maintain functionality under failures. Moreover, planar graphs themselves are widely used to model real-world structures such as circuit layouts, traffic systems, and geographic networks.