Abstract
In this survey, we provide an overview of category theory-derived machine learning from four mainstream perspectives: gradient-based learning, probability-based learning, invariance and equivalence-based learning, and topos-based learning. For the first three topics, we primarily review research in the past five years, updating and expanding on the previous survey by Shiebler et al. The fourth topic, which delves into higher category theory, particularly topos theory, is surveyed for the first time in this paper. In certain machine learning methods, the compositionality of functors plays a vital role, prompting the development of specific categorical frameworks. However, when considering how the global properties of a network reflect in local structures and how geometric properties and semantics are expressed with logic, the topos structure becomes particularly significant and profound.
Keywords:
machine learning; category theory; topos theory; gradient-based learning; categorical probability; Bayesian learning; functorial manifold learning; persistent homology MSC:
68T01; 68-02; 18A99; 18C10
1. Introduction and Background
In recent years, there has been an increasing amount of research involving category theory in machine learning. This survey primarily reviews recent research on the integration of category theory in various machine learning paradigms. Roughly, we divide this research into two main directions:
- Studies on specific categorical frameworks corresponding to specific machine learning methods. Backpropagation is formalized within Cartesian differential categories, structuring gradient-based learning. Probabilistic models, including Bayesian inference, are studied in Markov categories, capturing stochastic dependencies. Clustering algorithms are analyzed in the category of metric spaces, providing a structured view of similarity-based learning.
- Methodological approaches that explore the potential applications of category theory to various aspects of machine learning from a broad mathematical perspective. For example, research has examined how topoi capture the internal properties of neural networks, how 2-categories formalize component compositions in learning models, and how toposes and stacks provide structured frameworks for encoding learning dynamics and invariances.
We begin by introducing the key terms category theory, functoriality, and topos for readers who may not be familiar with these mathematical concepts. Category theory is a branch of mathematics that provides a unifying framework for describing mathematical structures and their relationships in an abstract manner. Mathematical domains such as algebra, topology, and logic can all be described within this framework. A fundamental concept in category theory, functoriality, refers to a method of mapping one category to another. It provides a systematic way to translate concepts and results from one mathematical context to another, enabling the study of similarities and connections across different areas of mathematics. As a higher-order category, a topos behaves like the category of sets in that it supports operations such as taking limits, colimits, and exponentials, and it also has an internal logic (often intuitionistic rather than classical). Topoi are used in fields such as logic, geometry, and computer science, particularly in areas like type theory and the semantics of programming languages, where they provide a versatile and abstract framework for representing data structures and reasoning about computations. We provide the specific definitions as follows.
Definition 1
(Category Theory). A category consists of objects and morphisms (also called arrows) between these objects, satisfying two key properties: associativity (the composition of morphisms is associative) and identity (each object has an identity morphism that acts as a neutral element under composition).
Definition 2
(Functor). A functor is a structure-preserving map between categories that assigns to each object in one category an object in another category, and to each morphism in the first category a morphism in the second, while preserving the composition of morphisms and identity morphisms.
Definition 3
(Topos). A topos is a category that generalizes the category of sets and is equipped with additional logical and topological structures. It serves as a generalized space where various mathematical concepts can be interpreted.
Our framework, shown in Figure 1, structures category-derived learning into two levels. Low-order category theory provides functorial frameworks, where components—defined with their own inputs, outputs, and parameters—are composed using functors. This modular perspective parallels programming languages and has influenced approaches in gradient-based learning, Bayesian learning, and functorial manifold learning for invariance and equivalence. High-order category theory captures global properties relevant to learning. For instance, coarse-graining and refinement can be structured using sites on networks, and constructive frameworks like stacks may offer further insights.
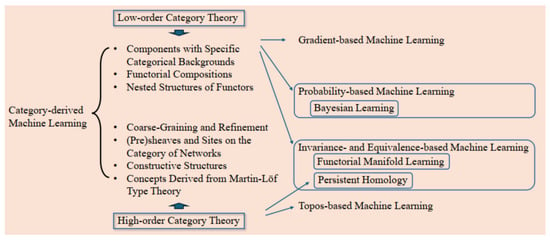
Figure 1.
Category-derived machine learning framework.
For the first direction, the survey by Shiebler et al. [1] provided a detailed overview of the main results up to 2021. In this survey, we complement their survey by including more recent results from 2021 to the present. Additionally, we introduce some other branches beyond these mainstream results. The second direction, high-order category theory-derived learnings, which is not covered in Shiebler et al.’s survey, is emphasized in this survey, and explores causality by leveraging the rich structures of sheaves and presheaves. These constructs effectively capture local–global relationships in datasets, such as the impact of local interventions on global outcomes. Furthermore, the internal logic of a topos provides a robust foundation for reasoning about counterfactuals and interventions, both of which are central to causal inference. For example, a systematic framework based on functor composition provides a robust design-oriented approach and effectively encodes ‘parallelism’ by describing independent processes. However, it struggles to fully encode ‘concurrency’, where events can be both ‘fired’ and ‘enabled’ at the same time, and to model the dynamic state transitions of these events. On the other hand, a topos, with its inherent (co)sheaf structures, naturally accommodates graph-like networks. When applied in this context, it implicitly supports a Petri net structure, which excels at capturing the dynamic activation and interactions of events, including concurrency and state changes [2]. The comparison between our work and Shiebler et al.’s is summarized in Table 1.

Table 1.
Comparison between Shiebler et al. [1] (2021) and this survey.
Next, we provide practical examples illustrating the benefits of incorporating topos theory into machine learning.
- Example 1. Dimensionality Reduction: Traditional methods risk information loss. Topos theory leverages its algebraic properties and thus enables dimensionality reduction while preserving structural integrity and extracting key features.
- Example 2. Interpretability of Machine Learning Models: Deep learning models are often ‘black boxes’. Topos theory provides logical reasoning to interpret internal structures, outputs, and emergent phenomena in large-scale models.
- Example 3. Dynamic Data Analysis: Traditional static analysis struggles with evolving data. Topos theory naturally captures temporal changes and local–global relationships.
The diagram in Figure 2 illustrates category-theoretic machine learning as a unifying framework, integrating gradient-based, probability-based, invariance and equivalence-based, and topos-based learning, each of which will be introduced in subsequent sections. Gradient-based learning interacts bidirectionally with probability-based learning, where optimization techniques such as gradient descent refine probabilistic models, and probability distributions enhance optimization efficiency. Probability-based learning further connects to manifold learning and clustering, generalizing probabilistic measures to structured geometric representations. Invariance and equivalence-based learning builds on these foundations, incorporating persistent homology to capture topological invariants and structural consistency. Topos-based learning extends categorical structures to higher-order logic, providing a framework to analyze compositional relationships and logical inference in neural networks. This integrated framework emphasizes structured learning, ensuring coherence across different learning paradigms.
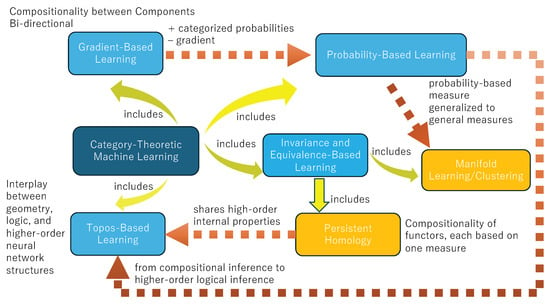
Figure 2.
Category-theoretic machine learning framework.
The following develops a categorical and topos-theoretic approach to machine learning, structured as follows:
- In gradient-based learning, we introduce base categories, functors, and the structure of compositional optimization.
- In probability-based learning, we present categorical probability models, Bayesian inference, and probabilistic programming.
- In invariance and equivalence-based learning, we explore categorical clustering, manifold learning, and persistent homology.
- In topos-based learning, we apply sheaf and stack structures to machine learning, building on Lafforgue’s reports.
- Finally, we discuss applications and future directions, covering frustrated AI systems, categorical modeling, and emerging challenges.
In the following, we generally use a sans serif font to represent categories and a bold font to represent functors, though we may occasionally emphasize sheaves/toposes with different fonts.
2. Developments in Gradient-Based Learning
The primary objective of integrating concepts from category theory into concrete, modularizable learning processes or methods is to leverage compositionality, enabling existing processes to be represented through graphical (diagrammatic) representations and calculus, where the modular design facilitates replacements of individual components. For existing methods, in [3], the author listed different gradient descent optimization algorithms and compared their behavior. The categorical approach, on the other hand, highlights their similarities and integrates different algorithms/optimizers into a common framework within the learning process. We summarized the differences and characteristics of gradient descent optimizers within a categorical framework in Table 2. In [4], the authors developed categorical frameworks focused on the most classical and straightforward gradient-based learning methods, demonstrating the variations achievable through the composition of the categorical components they defined. Specifically, the graphical representation, semantic properties, and diagrammatic reasoning—key aspects of category theory—are regarded as a rigorous semantic foundation for learning. They also facilitate the construction of scalable deep learning systems through compositionality.

Table 2.
Comparison of gradient descent optimizers in a categorical framework.
In this section, we aim to explain how (low-order) category semantics are applied to understand the fundamental structures of gradient-based learning, which is a core component of the deep learning paradigm. The mainstream approach is to decompose learning into independent components: the parameter component, the bidirectional dataflow component, and the differentiation component. These components, especially the bidirectional components—lenses and optics—are widely applied in other categorical frameworks of machine learning. After introducing the basic framework, we will present related research in Section 2.3.
Shiebler et al. [1] provided an overview of the fundamental structures in their survey. However, their definitions and explanations may be quite challenging for general readers without a mathematical background. Therefore, we briefly outline the most commonly used concepts in a more accessible manner.To technically introduce the critical parametric lens structure in this work, we begin by outlining the three key characteristics of gradient-based learning identified in [4,5]. Each characteristic motivates a specific categorical construction, respectively.
These concepts are summarized in Table 3. It provides the key characteristics of neural network learning and their categorical constructions. Parametricity is represented by Para, which captures parameterized mappings in supervised learning. Bidirectionality, modeled by Lens, describes the forward and backward flow of information, essential for backpropagation. Differentiation, expressed using CRDC, formalizes loss function optimization by differentiating parameters to minimize loss. These constructions provide a categorical perspective on neural network structures and learning dynamics.

Table 3.
Summary of the key characteristics in gradient-based learning with corresponding construction.
These basic settings can be extended or modified to accommodate various learning tasks, methods, or datasets. For example, bicategory- and actegory-based approaches adapt to different objects (e.g., polynomial circuits) or methodologies (e.g., Bayesian learning using Grothendieck lenses instead of standard functors). The Cartesian property of the background category enables duality, particularly through products and coproducts. Works like [6,7] extend this framework with dual components, introducing concepts such as parametrized/coparametrized morphisms and algebra/coalgebra. These enrichments integrate diverse networks (e.g., GCNNs, GANs) into a unified framework, while the Cartesian structure also allows Lawvere theory to model algebraic structures within the base category.
In complex network architectures, gradient-based composition alone is insufficient because it lacks structural constraints to ensure semantic consistency, logical validity, and global coherence. Therefore, topos-based learning provides a solution by introducing sheaf and stack structures, which enforce hierarchical dependencies and maintain local–global consistency. Additionally, subobject classifiers and fibered categories regulate module composition, preventing information distortion. Homotopy theory and categorical invariants further enable scalable modeling, preserving structural integrity across expanding architectures. Thus, topos theory extends compositional optimization, ensuring interpretable, adaptable, and logically consistent AI systems.
Now we give the definitions of these functors and categories in order.
2.1. Fundamental Components: The Base Categories and Functors
Definition 4
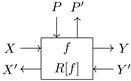
(Functor [4]). Let be a strict symmetric monoidal category. The mapping by results in a category with the following structure:
- Objects: the objects of .
- Morphisms: pairs of the form , representing a map from the input A to the output B, with P being an object of and .
- Compositions of morphisms: the composition of morphisms and is given by the pair .
- Identity: The identity endomorphism on A is the pair . ( due to the strict monoidal property.)
Every parametric morphism has a horizontal, but also a vertical component, emphasized by its string diagram representation
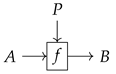
In supervised parameter learning, the update of parameters is formulated as 2-morphisms in , called reparameterizations. A reparameterization from is a morphism in such that the diagram
 commutes in , yielding a new map . Following the authors, we write for the reparameterization of f with , as shown in this string diagram representation
commutes in , yielding a new map . Following the authors, we write for the reparameterization of f with , as shown in this string diagram representation
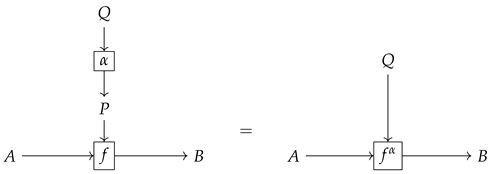 where = . In this context, based on the vertical morphism setting, Para(C) can be viewed as a bicategory with models as its 1-morphisms associating inputs and outputs, and with reparameterizations as its 2-morphisms associating models.
where = . In this context, based on the vertical morphism setting, Para(C) can be viewed as a bicategory with models as its 1-morphisms associating inputs and outputs, and with reparameterizations as its 2-morphisms associating models.

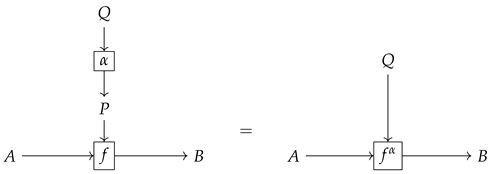
The following construction facilitates bidirectional data transmission.
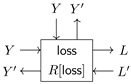
Definition 5
(Functor [4]). For any Cartesian category , the mapping of functor results in the category with the following data:
- Objects are pairs of objects in .
- A morphism from to consists of a pair of morphisms in , denoted as , as illustrated inwhere f:A → B is called the get or forward part of the lens and fr:A × B′ → A′ is called the put or backwards part of the lens. The inside construction is illustrated as in
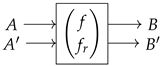
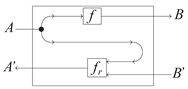
- The composition of and is given by get and put . The graphical notation is
- The identity on is the pair .
Definition 6
(Cartesian left additive category [8]). A Cartesian left additive category is both a Cartesian category and a left additive category. A Cartesian category is specified by four components: binary products ×, projection maps , pairing operation , and a terminal object. A left additive category is defined by commutative monoid hom-sets, an addition operation +, zero maps 0, with compositions on the left that are compatible with the addition operation. The compatibility in is reflected in the fact that the projection maps of as a Cartesian category are additive.
Definition 7
(Cartesian differential category [8]). A Cartesian differential category is a Cartesian left additive category with a differential combinator D, with which the inference rule is given by:
, which satisfies the eight axioms listed in [8], is called the derivative of f.
We highlight the Chain Rule of Derivative axiom in particular which defines the differential operation on composite maps: .
Definition 8
(Cartesian reverse differential category (CRDC), first introduced by [8] and first applied to the context of machine learning and automatic differentiation by [9]). A Cartesian reverse differential category is a Cartesian left additive category with a reverse differential combinator R, with which the inference rule is given by:
where satisfying the eight axioms listed in [9] is called the reverse derivative of f. And we would highlight the Reverse Chain Rule of Derivative axiom in particular which defines the differential operation on composite maps.
A more straightforward relationship between the forward and reverse derivatives in standard computations, in terms of function approximations, is as follows:
The correspondence between the forward and reverse derivatives is as follows:
The structure integrates seamlessly with the reverse differential combinator R of CRDC. Specifically, the pair forms a morphism in when is a CRDC. In the context of learning, functions as a backward map, enabling the ‘learning’ of f. The type assignment for conceals essential distinctions: takes a tangent vector (corresponding to the gradient descent algorithm) at B and outputs one at A. Since on the side, both outputs and inputs are different from those on the f side, the diagram representation is revised as follows.
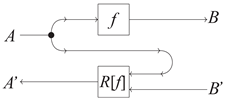

The fundamental category where gradient-based learning takes place is the composite of the and constructions given the base CRDC .
2.2. Composition of Components
This section highlights principal results from Deep Learning with Parametric Lenses [5], which describes parametric lenses as homogeneous components functioning in the gradient-based learning process.
For the most basic situation, they discussed a typical supervised learning scenario and its categorization. It involves finding a parametrized model f with parameters , which are updated step by step until certain requirements are met. The gradient-based updating algorithm, referred to as the optimizer, updates these parameters iteratively based on a loss map and is controlled by a learning rate . The authors of [5] emphasize that each component, including the model, loss map, optimizer, and learning rate, can vary independently but are uniformly formalized as parametric lenses. Their pictorial definitions and types are summarized in Table 4. It summarizes the following key components in categorical supervised learning using parametric lenses.

Table 4.
Summary of key components at work in the learning process: parametric lenses [5].
- Model: A parameterized function maps inputs to outputs, with reparameterization enabling parameter updates.
- Loss Map: Computes error; its reverse map aids in gradient-based updates.
- Gradient Descent: Iteratively updates parameters using gradient information.
- Optimizer: Includes basic and stateful variants, the latter incorporating memory for adaptive updates.
- Learning Rate: A scalar controlling update step size.
- Corner Structure: Ensures compatibility between learning components.
This formalism unifies learning processes into a modular and compositional framework. Moreover, can be introduced as the base category for the learning of digital circuits (as inputs) involved in the same framework [10].
In Ref. [5], the authors present a comprehensive framework of parametric lenses, which can accommodate a wide range of variations, including different models (such as linear-bias-activation neural networks, Boolean circuits [11], and polynomial circuits), loss functions (such as mean squared error and Softmax cross-entropy), and gradient update algorithms. These algorithms include well-known optimizers like momentum, Nesterov momentum, and Adaptive Moment Estimation (ADAM), all of which are captured within the parametric lens framework.
The stateful parameter update proposed by the authors involves selecting an object S (the state object) and a lens . In the momentum variant of gradient descent, the previous change is tracked and used to adjust the current parameter. Specifically, the authors set , fix some , and define the momentum lens , where and , with . This formulation reduces to standard gradient descent when .
For Nesterov momentum, the authors use the momentum from previous updates to modify the input parameter supplied to the network. This behavior can be precisely captured by a small variation of the lens from the momentum case. Again, they set , fix some , and define the Nesterov momentum lens by and as in the previous case.
Additionally, the authors discuss Adaptive Moment Estimation (ADAM), a method that computes adaptive learning rates for each parameter by storing exponentially decaying averages of past gradients (m) and squared gradients (v). For fixed , , and , Adam is given by , with the lens whose get part is and the put part is , where , , and , .
Thus, the parametric lens framework introduced by the authors provides a unified approach to modeling different optimization algorithms, each with its own distinctive characteristics. The pictorial definitions of parametric lenses rely on three types of interfaces: inputs, outputs, and parameters, which serve as the foundation of the component-based approach.
The composition of learning components can be viewed as a ‘plugging’ operation in graphical lens descriptions. A model represents a parametric lens, while the gradient descent optimizer G updates parameters by adjusting their values. By connecting G to through their shared interface , the model undergoes reparameterization via G. This process discards backward wires and , resulting in another parametric lens of type .
This modular approach integrates the components in Table 4 to construct a gradient-based learning system for the following two case studies (Figure 3 and Figure 4).
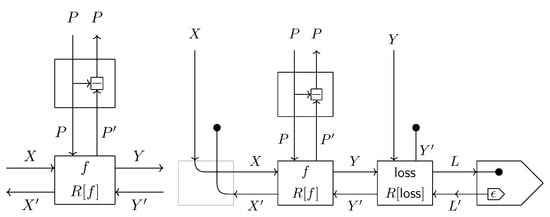
Figure 3.
Model reparameterized by basic gradient descent (left, adapted from Figure 4 in [5]) and a full picture of an end-to-end supervised learning process (right, adapted from Equation (5.1) in [5]).

Figure 4.
Deep dreaming as a parametric lens, adapted from Equation (4.3) in [5].
- Case Study 1. Supervised Learning: In the former, fixing the optimizer enables parameter learning as a morphism in , yielding a lens of type , where ‘get’ is the identity morphism and ‘put’ maps inputs to updated parameters. The following formulas can summarize the learning process.where
- * Updates of parameters for the network provided by the state and step size
- * Predicted output of the network
- * Difference between prediction and true value
- * Updates of parameters and input
- Case Study 2: DeepDream framework: This utilizes the parameters p of a trained classifier network to generate or amplify specific features and shapes of a given type b in the input a. This enables the network to enhance selected features in an image. The corresponding categorical framework formalizes how the gradient descent lens connects to the input, facilitating structured image modification to elicit a specific interpretation. The system learns a morphism in from to , with the parameter space . This defines a lens of type , where the ‘get’ function is trivial, and the ‘put’ function maps to . The learning process follows the formulas below.where
- * The updated input provided by the state and step size
- * Prediction of the network
- * Changes in prediction and true value
- * Changes in parameters and input
Notably, the authors also illustrated the component-based approach that covers the iterative process, which is a parametric morphism (Figure in [4], page 20).

As another case study, a notable practical implementation of category theory in gradient-based learning is the ‘numeric-optics-python’ library, which applies categorical concepts such as lenses and reverse derivatives to neural network construction and optimization [12]. This library follows a compositional approach, allowing neural network architectures to be systematically assembled from primitive categorical components. Its framework enhances modularity and interpretability while remaining compatible with conventional deep learning frameworks. The library includes practical experiments on standard machine learning benchmarks, such as Iris and MNIST, demonstrating its effectiveness in real-world tasks. Additionally, equivalent implementations using Keras provide a direct comparison, highlighting its capability to integrate categorical methods into existing gradient-based optimization pipelines. By leveraging categorical optics and functorial differentiation, this case study exemplifies how category theory can improve the structure, modularity, and interpretability of gradient-based learning models, paving the way for more compositional and mathematically grounded machine learning frameworks. Building upon [4,5], data-parallel algorithms have been explored in string diagrams which efficiently compute symbolic representations of gradient-based learners based on reverse derivatives [13]. Based on these efficient algorithms, several Python implementations [14,15,16] have been released. These implementations are characterized by their speed, data-parallel capabilities, and GPU compatibility; they require minimal primitives/dependencies and are straightforward to implement correctly.
2.3. Other Related Research
The categorical framework for gradient-based learning, introduced by Cruttwell et al. [4] and refined in later works [5,17,18], builds on foundational research by Fong et al. [19,20]. Initially developed for supervised learning, it later incorporated probabilistic learning to handle uncertainty [7,21].
Cruttwell et al. emphasized the compositional nature of learning processes, unifying models, optimizers, and loss functions as parametric lenses. This abstraction enables a modular and integrable system where components interact through functorial compositions, visually represented using graphical notation. The resulting open system structure aligns with frameworks like open Petri nets, ensuring flexibility in learning model design.
An extension of lenses is ‘optics’. They correspond to the case where learning processes do not involve the ‘differentiation’, thus not requiring the Cartesian property of the background category. While the base category still needs to permit parallel composition of processes, it then degenerates to a monoidal structure [7,20].
In [22], the authors discuss aggregating data in a database using optics structures. They also consider the category Poly, which is closely related to machine learning in (analog) circuit designs [10,23]. Another work, [24], demonstrates that servers with composability can also be abstracted using the lenses structure.
In [25], the higher categorical (2-categorical) properties of optics are specifically mentioned for programming their internal setups. Specifically, the internal configuration of optics is described by the 2-cells. From another viewpoint, the 2-cells encapsulate homotopical properties, which are often considered as the internal semantics of a categorical system. This aligns with the topos-based research of [26]. Some contents were also mentioned in [27].
In [28], game theory factors are also integrated into this categorical framework, focusing more on the feedback mechanism rather than the learning algorithm. We consider combining their ideas with reinforcement learning [29] (see the next paragraph) as an interesting direction, with existing instances provided in [30].
A critical example is that, instead of lenses, optics are used for composing the Bayesian learning process [31]. We will introduce this work in detail in the next section. Because decisions are made based on policies and Bayesian inference, they introduced the concept of ‘actegory’ to express actions on categories, which is also related to the monoidal structure (Cartesian categories are a specific type of monoidal category with additional structures, such as symmetric tensor products and projection maps). Moreover, a similar structure is employed in [29], where the component-compositional framework is expanded to reinforcement learning. They demonstrated how to fit several major algorithms of reinforcement learning into the framework of categorical parametrized bidirectional processes, where the available actions of a reinforcement learning agent depend on the current state of the Markov chain. In [32], the authors considered how to specify constraints in a top-down manner and implementations in a bottom-up manner together. This approach introduces algebraic structures to play the role of ‘action’, or more precisely, the invariance or equivariance under action. In this context, they chose to introduce the monad structure and employ monad algebra homomorphisms to describe equivariance. An important instance of their framework is geometric deep learning, where the main objective is to find neural network layers that are monad algebra homomorphisms of monads associated with group actions. It is worth noting that this structure is further related to the ‘sheaf action’ in [26].
When this framework is further expanded to learning on manifolds, where a point has additional data (in its tangent space), reverse differential categories considering only the data themselves are not sufficient. Ref. [18] extended the base category to reverse tangent categories, i.e., categories with an involution operation for their differential bundles.
Other research applying category theory to gradient-based learning includes [33]. This work primarily serves programming languages with expressive features. The authors built their results on the original automatic differentiation algorithm, considering it as a homomorphic (structure-preserving) functor from the syntax of its source programming language to the syntax of its target language. This approach is extensible to higher-order primitives, such as map operations over constructive data structures. Consequently, they can use automatic differentiation to build instances such as differential and algebraic equation solvers.
Some studies, such as [13,34,35], have also provided comprehensive ideas on the compositional, graphical, and symbolic properties of categorical learning in neural circuit diagrams and deep learning. Their work also discussed related semantics.
3. Developments in Probability-Based Learning
Probability plays a key role in machine learning, particularly in probabilistic modeling, Bayesian inference, and generative models. Many machine learning tasks can be framed as optimization problems, where the objective is to minimize a loss function. Effective problem-solving in this context requires a careful consideration of dataset origins and limitations, such as biases and data quality. In probabilistic approaches, uncertainty is modeled through probability theory and Bayesian inference, converting supervised learning into a problem of approximating distributions over outputs.
In category theory, stochastic behavior is studied in categories like Markov categories and categories of stochastic maps (e.g., , ), where morphisms represent probabilistic transitions, modeling the evolution of uncertainty over time.
Here is an overview of key probability types relevant to ML:
- Empirical Probability: Defined as the ratio of event occurrences to total observations. In the context of category theory, empirical probability is represented in three distinct ways: first, as a functor mapping observations A to distributions ; second, through the Giry monad, which captures finite measures; and third, within the framework of measure-theoretic probability, where categories such as formalize measurable spaces and measurable functions.
- Theoretical Probability: Defined as the ratio of favorable outcomes to possible outcomes. Within category theory, theoretical probability is modeled using the Giry monad to represent probability distributions, and categories like to formalize measurable spaces and functions. Furthermore, monoidal categories provide a structured framework for combining distributions, facilitating the modeling of probabilistic processes in machine learning.
- Joint Probability: Joint probability, , quantifies the likelihood of two events occurring together. In category theory, it is modeled using the copying structure in Markov categories or the tensor product in monoidal categories.
- Conditional Probability and Bayes’ Theorem in Machine Learning: Conditional probability plays a fundamental role in probabilistic reasoning, allowing the update of beliefs based on new information. In machine learning, it is widely used in probabilistic models such as Bayesian networks and hidden Markov models. The joint probability of two events can be expressed as:which forms the basis for sequential decision-making and inference in learning algorithms.A direct application of conditional probability is Bayes’ Theorem, which updates the probability of a hypothesis given new evidence, is as follows:This theorem is crucial in Bayesian inference, widely applied in generative models, reinforcement learning, and uncertainty quantification.In category-theoretic terms, probabilistic transitions can be modeled using Markov categories, where conditional dependencies are naturally represented. However, for practical machine learning applications, the focus remains on efficient approximation techniques, such as variational inference (VI) and Monte Carlo methods (MCMC), to handle complex distributions.
Statistics forms the backbone of machine learning, offering essential methodologies for data analysis, interpretation, and inference. In particular, the applications in ML include: Poisson processes, martingales, probability metrics, empirical processes, Vapnik-Chervonenkis (VC) theory, large deviations, the exponential family, and simulation techniques like Markov Chain Monte Carlo. We specifically highlight that the field of algebraic geometry is also closely related to statistical methods in machine learning [36]. Statistical methods in machine learning are broadly classified into two key areas:
- Descriptive Statistics: This summarizes data characteristics through measures such as central tendency, dispersion, and visualization techniques, offering insights into distribution patterns and trends.
- Inferential Statistics—This uses sample data to estimate population parameters, facilitating hypothesis testing, interval estimation, and predictive modeling.
3.1. Categorical Background of Probability and Statistics Learning
In machine learning, predefined datasets are commonly used to formulate optimization problems. Effectively addressing these problems requires a thorough understanding of the data’s provenance, biases, and inherent limitations. Understanding the data distribution is crucial for machine learning. Random uncertainties are modeled using probability theory and Bayesian inference, enabling the shift from function approximation to distribution approximation in supervised learning. This transition effectively addresses aleatoric uncertainty, which cannot be reduced by simply increasing the dataset size.
Category theory is a powerful framework for analyzing and interpreting randomness within various models, connecting probability, statistics, and information theory. This approach offers a solid foundation for developing robust and widely applicable learning models.
A significant advancement in this field is the formal categorization of the Bayesian learning framework. Bayesian learning combines prior knowledge with observational data to refine model parameters. The prior distribution represents beliefs before observing data, while the posterior distribution updates these beliefs by incorporating new evidence. Bayes’ rule derives the posterior distribution from the prior and likelihood, ensuring parameter estimates align with observed data. Bayesian methods not only provide optimal parameter estimates but also quantify uncertainty through the posterior, which captures both data variability and inherent randomness. This makes Bayesian learning a robust and adaptive framework for model development. Category-theoretic approaches to probability theory provide an abstract and unifying framework, which can be broadly summarized as follows:
- Categorization of traditional probability theory structures: Constructs like probability spaces and integration can be categorized using structures such as the Giry monad, which maps measurable spaces to probability measures, preserving the measurable structure. These frameworks formalize relationships between spaces and probability measures, enabling compositional probabilistic models.
- Categorization of synthetic probability and statistical concepts: Some axioms and structures are seen as ‘fundamental’ in probabilistic logic, which derive inference processes. Measure-theoretic models serve as concrete instances of these abstract frameworks. Markov categories are used to represent stochastic maps, conditional probabilities, and compositional reasoning in probabilistic systems.
Early categorical frameworks formalized probability measures. Lawvere [37] and Giry [38] introduced a categorical perspective on probability measures. Ref. [39] focused on the resulting ultrafilter monad, a structure derived when the probability monad is induced from a functor without an adjoint, known as the codensity monad. They demonstrated that an ultrafilter monad on a set can be interpreted as a functional mapping subsets to the two-element set, satisfying properties of finitely additive probability measures. Ref. [40] later generalized this framework, describing such a probability measure as a weakly averaging, affine measurable functional mapping into [0, 1]. Probability measures on a space were shown to constitute elements of a submonad of the Giry monad.
Working with real-world datasets, where discreteness plays a crucial role, brings deeper significance. Ref. [41] shows that the Giry monad can be restricted to countable measurable spaces with discrete -algebras, yielding a restricted Giry functor from the codensity monad. This suggests that natural numbers N are ’sufficient’ for such applications. Here, standard measurable spaces are replaced by Polish spaces, a class that has not been fully explored in categorical probability-related machine learning.
The Giry monad structure has been applied in many areas, such as [42], where stochastic automata are built as algebras on the monoid and Giry monads. This survey emphasizes the categorical approach to Bayesian Networks [21], Bayesian reasoning, and inference [43,44] using the Giry monad. To illustrate how the measure-theoretic perspective is incorporated into probabilistic inference in machine learning, we summarize the role of the Giry monad in Table 5.

Table 5.
Role of the Giry monad in probabilistic inference for machine learning.
Markov categories, which represent ‘randomness’ through random functions, offer a unique synthetic approach to understanding probability. The first research on Markov categories goes back to Lawvere [37] and Chentsov [45]. Related studies involve early synthetics research [46,47,48] and the specialization of Markov categories with restrictions by Kallenberg [49], Fritz [50,51,52,53,54,54], and Sabok [55], among others. Markov categories’ advantage lies in their graphical calculus, which simplifies translating diagram-based operations into programming languages [31,55,56].
Category theory’s application in Probabilistic Machine Learning aims to elucidate properties and facilitate data updating, especially for probability distributions and uncertainty inference. Key steps include formalizing random variables, modeling learning processes in a categorical framework, and establishing principles for probabilistic reasoning. For instance, random variables are treated as morphisms in a category, and learning processes as functors between categories of data and models. Bayesian machine learning uses categorical methods for both parametric and nonparametric reasoning on function spaces, representing priors, likelihoods, and posteriors with categorical structures. These frameworks enable compositional reasoning, where probabilistic updates are modeled compositionally, especially in supervised learning. Categorical Bayesian probability formalizes prior knowledge and belief updates based on data.
The categorical approach to probabilistic modeling provides practical advantages, simplifying proofs, complementing measure-theoretic methods, and intuitively representing complex probabilistic relationships. For example, Markov categories offer a framework for reasoning about stochastic processes, conditional probability, and independence. Research includes contributions by [1,21,31,43,44], among others. Experimental studies, such as [57], showcase the use of categorical theories in automatic inference systems [58,59,60], demonstrating their practical value in machine learning.
3.2. Preliminaries and Notions
In this section, we introduce key preliminaries and notions relevant to the research.
In traditional probability theory, a measurable space consists of a set X equipped with a -algebra , which defines a structured way to determine which subsets of X can be assigned probabilities. A function between measurable spaces is called measurable if it preserves this structure. A measure space extends this by introducing a measure , a function that assigns a non-negative value to each set in , following certain consistency rules such as countable additivity. When the total measure is normalized to one, the space is called a probability space, commonly used in probabilistic modeling.
While these classical structures provide a foundation for probability theory, they are not always well-suited for representing function spaces in machine learning, leading to the exploration of alternative frameworks such as quasi-Borel spaces, which define measurability in terms of random variables rather than -algebras. Probabilistic learning algorithms rely on distributions defined over a fixed global sample space, focusing on random variables that are characterized by predefined spaces. In probabilistic programming, reasoning often necessitates the Cartesian closed property. However, , the category of measurable spaces, is not Cartesian closed because measurable functions between measurable spaces may not preserve measurability. To overcome this limitation, two main approaches have been proposed. The first involves augmenting with various monoidal products, thus enabling probabilistic reasoning and compositionality within the existing framework [43]. The second approach generalizes measurable spaces to categories that are inherently Cartesian closed, such as quasi-Borel spaces (QBSs) [61].
Definition 9
(Quasi-Borel space [61]). A quasi-Borel space is a pair where X is a set and is a collection of ‘measurable’ maps from some standard Borel space B to X, satisfying the following conditions:
- 1.
- For every , the map defined byis in .
- 2.
- If are in , then any measurable function such that is also in .
- 3.
- contains all constant functions.
A fundamental issue with the category of measurable spaces is that it is not Cartesian closed, meaning function spaces do not always inherit a measurable structure, which complicates higher-order probabilistic reasoning. QBS addresses this by defining measurability in terms of random variables rather than -algebras, ensuring that function spaces remain well-structured. The lack of Cartesian closure in arises because function spaces do not naturally inherit a measurable structure, disrupting composability in probabilistic inference. In contrast, QBS ensures well-defined function spaces: according to Proposition 15 in [61], an adjunction between and establishes a natural framework where function spaces exist consistently. Moreover, Example 12 in [61] illustrates two ways to equip a set X with a quasi-Borel structure, demonstrating its adaptability for probabilistic models. Additionally, QBS is inherently compatible with probability measures, as it seamlessly integrates with them, preserving the structure necessary for probabilistic reasoning.
Definition 10
([61] Probability measure on QBS). A probability measure on a quasi-Borel space is a pair of and a probability measure μ on .
The key operations, such as pushforward and integration, are also well-defined in QBS, ensuring the preservation of probabilistic structures. Furthermore, in applications to Probabilistic Machine Learning, QBS facilitates structured reasoning in Bayesian inference, stochastic maps, and probabilistic programming, offering a compositional framework for complex models.
In conclusion, quasi-Borel spaces restore Cartesian closure, making them a powerful tool for structuring higher-order probabilistic computations in machine learning while ensuring compatibility with traditional probability theory.
Definition 11
(Stochastic process). A stochastic process is defined as a collection of random variables defined on a common probability space , where Ω is a sample space, is a σ-algebra, and is a probability measure; and the random variables, indexed by some set T, all take values in the same mathematical space S, which must be measurable with respect to some σ-algebra .
Definition 12
(Stochastic Process [62]). A stochastic process is a collection of random variables defined on a common probability space , where:
- Ω is the sample space;
- is a σ-algebra of subsets of Ω;
- is a probability measure on .
Each random variable is indexed by and takes values in a measurable space , where S is the state space and is a σ-algebra on S.
Definition 13
(Stochastic Map [62]). Let X and Y be sets. A stochastic map (also known as a stochastic matrix in the finite case) from X to Y is a function that represents the conditional probability of transitioning from to . It satisfies the following properties:
- 1.
- Non-negativity: for all and .
- 2.
- Finiteness: For each , the number of nonzero probabilities is finite.
- 3.
- Normalization: For each , the transition probabilities sum to one:
A stochastic map models uncertainty by specifying probabilistic transitions between states rather than deterministic ones. In machine learning, it plays a fundamental role in Markov decision processes (MDPs), reinforcement learning, and probabilistic graphical models. Specifically:
- In Markov chains, a stochastic map describes the transition probabilities between states, forming the basis for modeling sequential dependencies.
- In reinforcement learning, policy functions and transition models are often represented as stochastic maps, capturing the inherent randomness in environment dynamics.
- In probabilistic inference, stochastic maps define the conditional distributions in Bayesian networks and hidden Markov models.
Definition 14
(Stochastic Kernel [62]). A stochastic kernel (or probability kernel) from a measurable space to another measurable space is a function satisfying:
- 1.
- Probability Measure Condition: For each , the function is a probability measure on , meaning:
- 2.
- Measurability Condition: For each , the function is -measurable.
A stochastic kernel generalizes a stochastic map to continuous spaces by allowing probabilistic transitions between arbitrary measurable subsets of Y rather than just discrete points. It is a crucial tool in:
- Bayesian learning: Modeling posterior distributions in Bayesian inference.
- Sequential decision-making: Representing transition dynamics in stochastic control and reinforcement learning.
- Variational inference: Defining probability measures in stochastic optimization and Monte Carlo methods.
In machine learning, stochastic maps and stochastic kernels enable structured uncertainty modeling, facilitating robust decision-making under probabilistic assumptions.
Using stochastic kernels and Markov kernels, we can define the following categories commonly used in categorical probabilistic learning research, where these kernels serve as morphisms (See Table 6).

Table 6.
Categories in categorical probabilistic learning.
The categorization of probability-based learning processes involves using the following monads to handle probabilistic measures (Definitions in [46,63]).
As mentioned earlier, Markov categories are categories where morphisms encode ‘randomness’. In categorical probability-based learning, a Markov category background is necessary to describe Bayesian inversion, stochastic dependencies, and the interplay between randomness and determinism.
Definition 15
(Markov Category [53]). A Markov category is a symmetric monoidal category in which every object is equipped with a commutative comonoid structure, consisting of:
- A comultiplication map ;
- A counit map .
These maps must satisfy coherence laws with the monoidal structure. Additionally, the counit map del must be natural with respect to every morphism f.
Next, some commonly used probabilistic monads in this context are listed in Table 7.

Table 7.
Summary of probabilistic monads in measurable spaces.
One of the most common ways to construct a Markov category is by constructing it as a Kleisli category, which involves adding a commutative monad structure to a base category. In the following, we introduce a typical example: the Giry monad on . The Kleisli morphisms of the Giry monad on (and related subcategories) are Markov kernels. Therefore, its Kleisli category is the category , which is an essential example of a Markov category.
Definition 16
(Kleisli Category [64]). Given a monad on a category , the Kleisli category associated with is defined as follows:
- Objects: The objects of are the same as the objects of .
- Morphisms: For objects , the morphisms in are given by:where denotes the set of morphisms in from A to .
- Composition: For and , their composition in is defined as:where is the functorial action of , and is the monad multiplication.
- Identity: For each object , the identity morphism is given by the unit of the monad.
To generalize, given a distribution monad where:
The corresponding Kleisli category (a monad structure in addition to a base category, with morphisms like ) can describe the probability distribution of one object associated with another, forming a Markov category. Hence, once there is a probability distribution, there is a natural corresponding Markov category.
Next, we introduce another commonly used distribution monad in probability-based learning.
Definition 17
(Bayesian Inverse (Posterior Distribution) [62]). Let be a Markov kernel from a measurable space to a measurable space , and let π be a prior probability measure on X. The Bayesian inverse or posterior distribution is a Markov kernel defined for and measurable sets by:
provided that .
Here:
- represents the probability density or likelihood of y given x;
- is the marginal probability of y under the prior π;
- is a probability measure on , representing the conditional distribution of x given y (the posterior distribution).
Finally, the concept of entropy is introduced to measure the information (uncertainty) in probability distributions.
Definition 18
(Entropy [65]). The entropy of a random variable X quantifies the uncertainty or information content associated with its probability distribution. It is defined as follows:
- Discrete Case: If X is a discrete random variable with a probability mass function defined on a finite set , the entropy is given by:where the base of the logarithm determines the unit of entropy.
- Continuous Case: If X is a continuous random variable with a probability density function defined on a support set , the entropy , also referred to as differential entropy, is given by:
The discrete entropy is always non-negative, whereas the continuous entropy can take negative values due to the use of densities. In both cases, measures the average uncertainty or surprise in the random variable X.
3.3. Framework of Categorical Bayesian Learning
In the work of Kamiya et al. [31], the authors introduced a categorical framework for Bayesian inference and learning. Their methodology is mainly based on the ideas from [4,19], with relevant concepts from Markov categories introduced to formalize the entire framework. The key ideas can be summarized as two points:
- The combination of Bayesian inference and backpropagation induces the Bayesian inverse.
- The gradient-based learning process is further formalized as a functor .
As a result, they found Bayesian learning to be the simplest case of the learning paradigm described in [4]. The authors also constructed a categorical formulation for batch Bayesian updating and sequential Bayesian updating and verified the consistency of these two in a special case.
3.3.1. Probability Model
The basic idea of their work is to model the relationship between two random variables using conditional probabilities . Unlike gradient-based learning methods, Bayesian machine learning updates the prior distribution on using Bayes’ theorem. The posterior distribution is defined by the following formula, up to a normalization constant:
This approach is fundamental to Bayesian machine learning, as it leverages Bayes’ theorem to update parameter distributions rather than settling on fixed values. By focusing on these distributions instead of fixed estimates, the Bayesian framework enhances its ability to manage data uncertainty, thereby improving model generalization.
The model from [4] as a function f with inputs, outputs, and parameters, is adjusted to the following model: For the input data and parameters, the data parallelism and data fusion are much more complicated when they are distributions. Therefore, the following conceptions (such as joint distribution, disintegration, conditional distribution) become necessary.
- A morphism in a Markov category can be viewed as a probability distribution on X. A morphism is called a channel.
- Given a pair and , a state on can be defined as the following diagram, referred to as the jointification of f and .
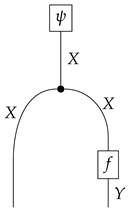
- Let be a joint state. A disintegration of consists of a channel and a state such that the following diagram commutes. If every joint state in a category allows for decomposition, then the category is said to allow for conditional distribution.
- Let be a Markov category. If for every morphism , there exists a morphism such that the following commutative diagram holds, then is said to have conditional distribution (i.e., X can be factored out as a premise for Y).

- Equivalence of Channels: Let be a state on the object . Let be morphisms in . f is said to be almost everywhere equal to g if the following commutative diagram holds. If is a state and is the corresponding marginal distribution, and are channels such that and both form decompositions with respect to , then f is almost everywhere equal to g with respect to .
- Bayesian Inverse: Let be a state on . Let be a channel. The Bayesian inverse of f with respect to is a channel . If a Bayesian inverse exists for every state and channel f, then is said to support Bayesian inverses. This definition can be rephrased using the concept of decomposition. The Bayesian inverse can be obtained by decomposing the joint distribution which results from integrating over , where f is a channel. The Bayesian inverse is not necessarily unique. However, if and are Bayesian inverses of a channel with respect to the state , then is almost everywhere equal to .
As an example, in , corresponds to a probability distribution on . The decomposition of is given by the related conditional distribution and the state obtained by marginalizing y in . Define the conditional distribution such that, if is non-zero, then
If , then define as an arbitrary distribution on Y. This can also be discussed in the subcategory , where objects are Borel spaces.
However, in order to ensure that the composition of Bayesian inverses is strict (to define a functor similar to gradient learning functors), equivalent channels are no longer used, and instead, the category (abbreviated to in some references) is used (based on the following propositions).
- If a category admits conditional probabilities, it is causal. However, the converse does not hold.
- The categories and are both causal.
- If is causal, then (or written as ) is symmetric monoidal.
3.3.2. Introduction of Functor
The concept of parameterized functions has a natural expression in the categorification of machine learning models: the functor. By modifying the functor in gradient learning algorithms, the objective here is to understand conditional distributions between random variables or morphisms within a Markov category that satisfies certain constraints. In this context, a parameterized function is used to model the conditional distribution , and the learning algorithm updates using a given training set. In a Markov category, the type of the parameter need not be the same as the type of the variable. By leveraging the concept of actegories (categories with an action), parameters are considered to act on the model.
Definition 19
(Actegory [66]). Let be a monoidal category, and let be a category.
- is called an -actegory if there exists a strong monoidal functor , where is the category of endofunctors on , with composition as the monoidal operation. For and , the action is denoted by .
- is called a right -actegory if it is an -actegory and is equipped with a natural isomorphism:where is a monoidal category, and κ satisfies the coherence conditions.
- If is a right -actegory, the following natural isomorphisms must exist:called the mixed associator , andcalled the mixed interchanger.
The structure of is then adjusted as follows. Let be a symmetric monoidal category and be an -actegory. becomes a 2-category, which is defined as follows:
- Objects: The objects of .
- 1-morphism: in consists of a pair , where and is a morphism in .
- Composition of 1-morphisms: Let and . The composition is the morphism in given by:
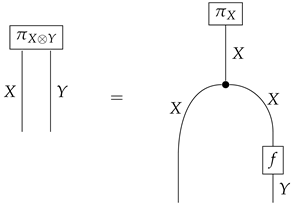
- 2-morphism: Let . A 2-morphism is given by a morphism such that the following diagram commutes:
- Identity morphisms and composition: These in the category inherit from the identity morphisms and composition in .
defines a pseudomonad on the category of -actegories (consider the monoidal structure of the endofunctor category, which can be composed with itself multiple times—a multi-parameter setting). In particular, if there is a functor , one can obtain a related functor:
3.3.3. The Final Combination: Functor
The ultimate goal is to synthesize the entire Bayesian process into a functor , so that its construction can capture the characteristics of Bayesian learning. Beyond the aforementioned functor, a reverse feedback mechanism (lenses) needs to be incorporated. In this context, to maintain the characteristics of an actegory, Grothendieck Lenses are used in the construction.
Here is the text extracted from the image:
Definition 20
(Grothendieck Lenses [64]). Let be a (pseudo)functor, and let denote the total category arising from the Grothendieck construction of . The category of Grothendieck lenses (or category of -lenses) is defined as follows:
- Objects: Pairs , where and .
- Morphisms: A morphism consists of a pair , where:
- 1.
- is a morphism in ;
- 2.
- is a morphism in .
- Hom-Sets: The Hom-set is given by the dependent sum:
Let be a Markov category with conditional probabilities (i.e., indicating that there are Bayesian inverses in ). Bayesian inverses are typically defined up to an equivalence relation. Observing the category , Bayesian inverses define a symmetric monoidal dagger functor.
The gradient learning functor is defined based on a functor , where is a Cartesian reverse differential category. In the context of Bayesian learning, this structure is reflected through the construction of Bayesian inverses and generalized lenses. Therefore, the goal is to define a functor , where is the -Lens associated with the functor , where is the category of small categories.
The entire construction of is as follows.
- Define the functor : given , let .
- Define as the lens corresponding to the functor with objects and morphisms as follows.
- Objects: For , where and .
- Morphisms: A morphism is given by a morphism in and a morphism in .
- Combining with reverse derivatives, define the functor : given , let . If is a morphism in , thenis defined as the pair , where is the Bayesian inverse of f with respect to the state on X.
- Let and be Markov categories, with being causal. Assume is a symmetric monoidal -actegory consistent with . Then is a symmetric monoidal category. The categories and are -actegories. is a functor that, when applied to , yields:If is a symmetric monoidal category, then a -actegory allows a canonical functor , where . The functor is the unit of the pseudomonad defined by . Thus, we obtain the following diagram:

- Define the functor .
The functor does not include updates or shifts like the gradient learning functor. This is because the nature of Bayesian learning is relatively simplified; here, parameter updates correspond to obtaining the posterior distribution using the prior and likelihood, rather than as a result of optimization relative to a loss function.
The method of using the posterior distribution for prediction can be formalized within the category, i.e., by considering the following composition:
3.4. Other Related Research
3.4.1. Categorical Probability Framework and Bayesian Inference
Fritz et al. [53] developed a categorical framework for probability theory, which underpins many modern approaches in probability-based machine learning. By utilizing concepts such as the Giry monad and Markov categories, this framework bridges classical probability theory and categorical structures. Similar models, such as those in [31,43,59], further refine this connection, emphasizing coherence and adaptability.
A primary application of this framework is Bayesian inference, where log-linear models are used to express relationships and conditional independencies in multivariate categorical data. Categorical-from-binary models enable efficient Bayesian analysis of generalized linear models, particularly in cases with numerous categories. These models simplify computations, reducing the complexity of encoding and manipulating the data. Bayesian methods, including conjugate priors, asymmetric hyperparameters, and MCMC techniques, are seamlessly integrated, facilitating efficient inference while preserving compatibility with categorical structures. For instance, MCMC procedures can be interpreted as morphisms within Markov categories, aligning with the stochastic transitions inherent in probabilistic systems.
Probability measures within this framework are viewed as weakly averaging affine measurable functionals that preserve limits, forming a submonad of the double dualization monad on the measurable space category . This submonad is isomorphic to the Giry monad [54], reinforcing its classical applicability. Moreover, the Giry monad serves as a formal bridge for describing and manipulating probability measures.
Beyond classical probability, this framework accommodates generalized models, including fuzzy probability theories. By modeling probability measures using enriched categories and submonads, it provides a flexible approach to handle uncertainty across diverse contexts. This adaptability positions the framework for integration with future models that deal with imprecision or ambiguity in data.
3.4.2. Generalized Models and Probabilistic Programming
Baez et al. [67] first discussed the connection between categorical perspectives and statistical field theories, including quantum mechanics and quantum field theory in their Euclidean form. They identified a similarity to nonparametric Bayesian approaches and explored the construction of probability theory using a monad. This construction aligns with the Bayesian perspective of distributions over distributions, such as Dirichlet processes. In [68], the authors highlighted that in statistical learning theory, the richness of the hypothesis space is determined not by the number of parameters but by the VC-dimension, which measures falsifiability. Thus, the introduction of logical classification, such as topos structure, is natural in this context.
Further research emphasizes the role of syntax in machine learning, particularly in fields like natural language processing. Syntax ensures the preservation of structural and relational properties during data encoding. Categorical methods, through a functorial framework, offer robustness in both maintaining structural consistency and clarifying data relationship propagation [69,70].
To address this challenge, [70] introduced a classification pseudodistance, derived from the softmax function, to transform datasets into generalized metric spaces. This approach quantifies structural differences and facilitates syntax-based comparisons while preserving relational information.
At the application level, Bayesian synthesis advances probabilistic programming by efficiently managing uncertainty in complex statistical models. Central to this approach are Bayesian networks, which represent dependency structures using directed acyclic graphs. They simplify joint distribution representation and enable efficient inference by extracting conditional independence relationships, reducing computational complexity. Additionally, Markovian stochastic processes in probabilistic graphical models support scalable inference [59].
Another key component is probabilistic couplings, based on Strassen’s theorem [71], which enable coupling between distributions without requiring a bijection between sampling spaces. This enhances the expressivity of probabilistic programs. Lastly, Bayesian lenses simplify Bayesian updating, analogous to automatic differentiation in numerical computation, offering flexibility and adaptability in probabilistic programming languages [60].
3.4.3. Applications and Advanced Techniques in Categorical Structures
The synthetic approach to probability, focusing on relationships between probabilistic objects rather than their concrete definitions, offers a robust foundation for probability and statistics within the framework of Markov categories. By abstracting away from specific representations, it emphasizes the compositional and structural properties of probabilistic systems, facilitating the development of fundamental results, such as zero-one laws, that describe extreme probabilistic behaviors [52]. This framework also enhances probabilistic programming, particularly in languages like Stan and WebPPL, through Bayesian synthesis. Bayesian synthesis supports both soft constraints—allowing flexible regularization or partial observations—and exact conditioning, ensuring strict conformity to observed data. This dual capability enables precise and adaptable statistical modeling, with semantic analyses in Gaussian probabilistic languages demonstrating the operation of Bayesian synthesis within the structured framework of Markov categories.
Shiebler et al. [1] offer a categorical perspective on causality, covering key components such as causal independence, conditionals, and intervention effects. This perspective leverages the abstraction and compositionality of category theory to model and infer causal relationships. In the Bayesian framework for causal inference, the potential outcomes approach addresses causal estimands, identification assumptions, Bayesian estimation, and sensitivity analysis. Tools such as propensity scores, identifiability techniques, and prior selection are integral to robust causal modeling. A formal graphical framework, grounded in monoidal categories and causal theories, introduces algebraic structures that enhance our understanding of causal relationships. Monoidal categories represent independent or parallel processes using tensor products, while causal theories formalize their interactions. Markov categories, in particular, offer a compositional framework for reasoning about random mappings and noisy processing units [72,73]. Objects in Markov categories represent spaces of possible states, and morphisms act as channels that may introduce noise, enabling precise interpretations of causal relationships [1].
String diagrams serve as powerful tools for visualizing and analyzing causal models. These diagrams align with morphisms in Markov categories when decomposed according to the specifications of the causal model. For instance, the decomposition of a string diagram might represent a causal system where variables influence each other through noisy channels, reflecting probabilistic dependencies. This compatibility highlights the deep connection between causal structures and probabilistic relationships [74]. Key concepts, such as second-order stochastic dominance and the Blackwell-Sherman-Stein Theorem, further refine our understanding of causal inference [53]. In this categorical framework, causal models abstractly represent causal independence, conditionals, and intervention effects, moving beyond model-specific methods like structural equation models or causal Bayesian networks. Instead, causal models are formalized as probabilistic interpretations of string diagrams, with equivalence established through natural transformations between functors, known as abstractions and equivalences. This abstraction enables a more general and unified understanding of causality, providing a principled foundation for reasoning about causal relationships and intervention effects.
In [57], the integration of categorical structures such as symmetric monoidal categories and operads with amortized variational inference is explored within frameworks like DisCoPyro. Symmetric monoidal categories enable modeling of compositional processes, while operads formalize hierarchical and modular structures. These structures align naturally with the iterative and modular nature of variational inference frameworks. This integration demonstrates how Markov categories bridge abstract mathematical foundations and practical machine learning applications, enhancing both the efficiency and expressiveness of Bayesian models. By leveraging categorical methods, it is possible to construct models for parametric and nonparametric Bayesian reasoning on function spaces, such as Gaussian processes, and to define inference maps analytically within symmetric monoidal weakly closed categories. These developments highlight the potential of Markov categories to provide a unified and robust foundation for supervised learning and general stochastic processes.
From an algebraic perspective, Ref. [75] introduces the concepts of categoroid and functoroid to characterize universal properties of conditional independence. Categoroids extend traditional categories to account for probabilistic structures, while functoroids generalize functors to capture relationships of conditional independence. As previously mentioned, research on quasi-Borel spaces, which are cartesian closed, supports higher-order functions and continuous distributions, providing a robust framework for probabilistic reasoning [60]. This approach aligns with the Curry-Howard isomorphism, providing a universal representation for finite discrete distributions. The integration of these advanced techniques facilitates the development of sophisticated models and inference algorithms for probabilistic queries and assigning probabilities to complex events [72].
For applications, Ref. [76] employed the monad structure to perform automatic differentiation in reverse mode for statically typed functions containing multiple trainable variables.
4. Developments in Invariance and Equivalence-Based Learning
In machine learning, invariance and equivalence are key concepts, ensuring models produce consistent results under transformations like image splitting, zooming, or rotation. These transformations often reflect the geometric structure of data, viewed as lying on a manifold. Similarly, analyzing how shared network components affect data or how semantics evolve during training is essential for understanding equivalence. Despite their differences, these concepts all relate to forms of invariance or equivalence.
Category theory offers two main approaches to studying these concepts. The first uses functors, which map between categories while preserving structural relationships. This method is straightforward, computationally efficient, and practical. The second approach involves higher-order categories—such as topoi, stacks, or infinity categories—to capture complex relationships and multi-scale dependencies. While powerful, these methods are computationally intensive and harder to implement. The following sections will explore both approaches and their relevance to machine learning. We briefly introduce common homological methodologies, focusing on:
- Shiebler’s work [77,78], which leverages functorial constructions;
- Other functorial construction-based methods.;
- Persistent homology approaches for analyzing topological features in data [79,80].
Before delving into the details, we compare traditional invariant learning methods with a novel categorical approach, highlighting differences in theoretical formulation and computational complexity.
Traditional methods rely on explicitly defining transformation groups (e.g., rotations, translations) to ensure model invariance. CNNs, for example, use shared filters to achieve translation invariance. However, extending this approach to other symmetries, like rotation or scaling, requires additional layers or data augmentations, increasing computational overhead and design complexity. The categorical approach abstracts these transformations using category theory. Instead of manually applying transformations, data points and their transformations are represented as objects and morphisms within a category. Functors and natural transformations capture relationships between these objects, enabling the model to generalize beyond predefined transformations. This abstraction simplifies handling complex symmetries without needing specific modifications.
One may think of a practical example, such as image recognition, while reading the section. A traditional CNN processes image data using convolutional filters that slide across the image, detecting features invariant to spatial translations. However, making the model invariant to rotations or scaling requires additional mechanisms, increasing complexity. Instead of applying transformations directly, transformations like translation, rotation, and scaling are represented as morphisms between image objects. A functor captures how these transformations relate, enabling the model to generalize across different symmetries without additional layers. The categorical approach offers greater flexibility and efficiency by abstracting transformations through functors and morphisms, reducing the need for explicit definitions and enhancing scalability for complex data and symmetries.
4.1. Functorial Constructions and Properties
The thesis [81] explores the compositional and functorial structure of machine learning systems, focusing on how assumptions, problems, and models interact and adapt to change. It addresses two key questions: How does a model’s structure reflect its training dataset? Can common structures underlie seemingly different machine learning systems?
Shiebler [77] models hierarchical overlapping clustering algorithms as functors factoring through a category of simplicial complexes. He defines a pair of adjoint functors that link simplicial complexes with clustering algorithm outputs. In [78], he characterizes manifold learning algorithms as functors mapping metric spaces to optimization objectives, building on hierarchical clustering functors. This approach proves refinement bounds and organizes manifold learning algorithms into a hierarchy based on their equivariants. By projecting these algorithms along specific criteria, new manifold learning algorithms can be derived.
In this section, we mainly introduce algorithms that extract structure from unlabeled data, i.e., unsupervised learning. Studying these algorithms’ properties helps people understand how they separate signals from noise, focusing on the invariant and equivariant properties of the functors.
- Clustering: A clustering algorithm takes a finite metric space and assigns each point in the space to a cluster.
- Manifold Learning: Manifold learning algorithms, such as Isomap, Metric Multidimensional Scaling, and UMAP, construct -embeddings for the points in X, which are interpreted as coordinates for the support . These techniques are based on the assumption that this support can be well-approximated with a manifold.
In the following, we first introduce the fundamental notions and then delve into the core ideas.
4.1.1. Preliminaries and Notions
In many learning systems, especially manifold learning, a dataset is represented as a finite set of points. Simultaneously, invariance and equivariance are expressed as ‘keeping the distances between points’. Uber-metric spaces allow for infinite distances and non-identical points with zero distance.
Definition 21
(Finite Uber-Metric Space and the Category [82]). A finite uber-metric space is a pair , where:
- X is a finite set,
- is a function satisfying the following properties:
- 1.
- Identity: for all ,
- 2.
- Symmetry: for all ,
- 3.
- Triangle Inequality: for all .
A map between two uber-metric spaces and is called non-expansive if:
The category consists of:
- Objects: Finite uber-metric spaces;
- Morphisms: Non-expansive maps between uber-metric spaces.
To structure the locals on a manifold and to relate those locals with common topological structures, such as simplices, the following notions are necessary.
Definition 22
(Non-Nested Flag Cover [77]). Let X be a set. A non-nested flag cover of X is a collection of subsets of X satisfying the following conditions:
- Non-Nestedness: If and , then .
- Flag Property: The simplicial complex associated with , defined by:is a flag complex. This means that every set of vertices in that are pairwise connected by edges spans a simplex in .
Definition 23
(Refinement preserving and the category [77]). A map is refinement preserving if for any set S in , there exists some set in such that . Non-nested flag covers form the category with refinement-preserving functions as the morphisms.
For example, consider the tuples and as objects in . The function is a morphism between them.
An overlapping clustering algorithm can be described as a functor as follows. The details will be provided in the next subsection.
Definition 24
(Flat Clustering Functor [77]). A flat clustering functor is a functor that satisfies the following properties:
- Identity on Underlying Sets: For each object , the underlying set of is X.
- Preservation of Structure: maps morphisms (non-expansive maps) in to morphisms in , preserving the clustering structure.
Compared to non-overlapping clustering, overlapping clustering algorithms allow elements to belong to multiple clusters, preserving more information about the original space.
Definition 25
(Finite Simplicial Complex [83]). A finite simplicial complex is a collection of finite subsets of a set X (called the vertex set) that satisfies the following properties:
- Closure under Subsets: If and , then .
- Finiteness: is a finite collection of finite sets.
The elements of are called simplices. An n-element set in is called an n-simplex, and the elements of X are called the vertices of . The set of all 0-simplices (single-element subsets of X) forms the vertex set, denoted X.
For example, given a graph G with vertex set X, the collection of cliques in G forms a simplicial complex, called a flag complex. Another example is the Vietoris–Rips complex:
Definition 26
(Vietoris–Rips Complex [84]). Given a finite metric space and a parameter , the Vietoris–Rips complex is a simplicial complex defined as follows:
- The vertices of are the elements of X.
- A subset forms a simplex in if and only if for all .
A sequence of parameters induces a filtration on these complexes, where .
Definition 27
(Simplicial map and the category [77]). A map is a simplicial map if whenever the vertices span an n-simplex in , the vertices span an m-simplex in for . The category with finite simplicial complexes as objects and simplicial maps as morphisms is denoted .
The subsets of a non-nested flag cover form a simplicial complex, and the maximal simplices of constitute a non-nested cover. More precisely, they give rise to adjoint functors and . Hence, these two functors describe how to transform between simplicial complexes and non-nested flag covers. The connected components functor is used when the connected components of form a non-nested flag cover.
A functor maps to a complex whose simplices are sets such that for some choice of .
The category is denoted by , in which objects are and morphisms are defined by the relation ≥.
The following definition is essential for categorizing fuzzy classification, which groups elements into fuzzy sets based on membership functions determined by the truth value of a fuzzy propositional function.
Definition 28
(Fibered fuzzy simplicial complex and the category [77]). A fibered fuzzy simplicial complex is a functor , where the vertex set of the simplicial complex is the same for all . Fibered fuzzy simplicial complexes form the category . The morphisms are natural transformations μ such that each component for is a simplicial map.
Definition 29
(Functor [77]). The functor maps an uber-metric space to a fuzzy simplicial complex whose simplices are the sets such that .
4.1.2. Functorial Manifold Learning
Shiebler’s research focuses on clustering methods, particularly classifying clustering algorithms using manifold learning techniques. Manifold learning reduces high-dimensional data by embedding them into a lower-dimensional space while preserving their geometric structure. This process mitigates the curse of dimensionality, enabling clustering algorithms to identify patterns more effectively than when applied to the original data.
Consider a common setup in manifold learning: a finite metric space is sampled from a larger space according to a probability measure . The goal of manifold learning is to construct -embeddings for the points in X, which are interpreted as coordinates for the support of . Given an uber-metric space , where , the goal is to find an real-valued matrix A in . For example, in Metric Multidimensional Scaling, the main objective is to find a matrix that minimizes .
Given a loss function that accepts n embeddings in and outputs a real value, and a set of constraints , a manifold learning optimization problem aims to find the matrix that minimizes subject to . To summarize, a manifold learning problem is a function that maps a pseudo-metric space to a pairwise embedding optimization problem in the form of . The optimization is to minimalize . The invariance here lies on the following: If a manifold learning problem maps an isometric quasi-metric space to an embedding optimization problem with the same solution set, it is called isometrically invariant. The output of an isometrically invariant manifold learning algorithm does not depend on the ordering of elements from X. This specific kind of manifold learning problem can be factorized by hierarchical clustering. Namely, given any isometrically invariant manifold learning problem , there exists a manifold learning problem , where is an overlapping hierarchical clustering problem, and is a function that maps the output of to an embedding optimization problem, such that in any quasi-metric space , the solution spaces of the images of and are identical.
The categorization of Problem is as follows.
Definition 30
(Category of manifold learning optimization problems [78]). The categorization of a problem , denoted , is specified as follows.
- Objects: Tuples , where n is a natural number and is a real-valued function that satisfies for or .
- Morphisms: when for all and .
Given a choice of m, the object in is viewed as a pairwise embedding optimization problem. To complete the categorization, a category is defined as a pullback of and (see the diagram; is a forgetful functor that maps to n.), where the objects are tuples , and whenever and for any and .
In particular, in the case of the metric multidimensional embedding optimization problem , where , each object corresponds to the pairwise embedding optimization problem , where .
Then, manifold learning algorithms can be represented as functors . This gives rise to the category , where the objects are these functors that commute with the forgetful functor mapping to n, and the morphisms are natural transformations.
Definition 31
(-manifold learning functor [78]). Given the subcategories of and of , the composition is called a -manifold learning functor if:
- is a hierarchical -clustering functor;
- maps a fuzzy, non-nested flag cover with vertex set X to some with cardinality .
There are two notable hierarchical clustering functors, single linkage and maximal linkage , since they represent two extremes, respectively. By leveraging functoriality and Definition 31, the authors concluded that all non-trivial clustering algorithms exist on a spectrum between maximal and single linkage to gain a similar insight of manifold learning.
Specifically, if is a -manifold learning functor, then the inequality holds, up to a rescaling factor. There are many manifold learning functors that lie between these extremes. For any functor and a sequence of clustering functors , one obtains .
Definition 32
(Functor [78]). The functor maps the fuzzy, non-nested flag cover to , where n is the cardinality of the vertex set of and are defined as follows:
For example, Laplacian Eigenmaps can be expressed as the composition .
Definition 33
(Functor [78]). The functor maps the fuzzy, non-nested flag cover to , where n is the cardinality of the vertex set of , and are defined as follows:
The algorithm is not functorial over because may contain positive terms while may contain negative terms. However, it is functorial over since increases and decreases as the distance increases in . The Metric Multidimensional Scaling (MMDS) algorithm is thus defined as . In this case, the loss function is .
is the composition of five functors, where the first four constitute a -hierarchical clustering algorithm. Specifically, these functors are:
- : Constructs a local metric space around each point in X;
- : Converts each local metric space into a fuzzy simplicial complex;
- : Takes a fuzzy union of these fuzzy simplicial complexes;
- : Converts the resulting fuzzy simplicial complex into a fuzzy non-nested flag cover;
- : Constructs a loss function based on this cover.
Since does not preserve non-expansiveness, UMAP is not functorial over .
The functorial perspective on manifold learning offers a natural framework for generating new manifold learning algorithms by recombining the components of existing algorithms. For example, swapping with allows the definition of a metric multidimensional scaling-like manifold learning functor , which encourages chained embeddings.
In [81] Shiebler demonstrates how this new perspective can help improve the performance of manifold learning algorithms with certain task. The task involves DNA recombination, where the goal is to match a mutated DNA sequence back to its original form. To accomplish this, random DNA sequences are generated and then mutated to create mutation lists. Each list starts with an original DNA sequence and ends with a final mutated sequence. These mutated sequences are placed into a metric space, and a manifold learning algorithm is employed to build embeddings for each sequence. The embeddings help measure the distance between the sequences, enabling the identification of the closest match to the original sequence. A key technique used in this task is , which clusters sequences in the same mutation list by mapping them to a loss function. The scaling algorithm ensures that sequences connected by mutations are embedded closer together in the metric space. This method outperforms traditional multidimensional scaling by better preserving the relationships among sequences in the mutation lists. The algorithm’s effectiveness is demonstrated in experimental results, confirming its ability to recognize and cluster sequences accurately.
As research in this direction has advanced (most will be mentioned in Section 4.3), several open problems remain to be solved:
- Developing more robust theories regarding the resistance of various types of unsupervised and supervised algorithms to noise;
- Exploring the possibility of imposing stricter bounds on the stability of our results by shifting from a finite-dimensional space to a distributional perspective, potentially incorporating concepts such as surrogate loss functions and divergence measures.
4.1.3. Functorial Clustering
Clustering algorithms have been widely studied in data mining and machine learning, with applications including summarization, learning, image segmentation, and market segmentation. There are various methods for clustering, categorized based on the types of clusters obtained. In [85], the following classifications are mentioned:
- Disjoint clustering: When an element belongs to only one cluster, e.g., clustering by content .
- Fuzzy clustering: An element can belong to all clusters, but with a certain degree of membership, e.g., clustering within a color range.
- Overlapping clustering: An element can belong to multiple clusters, e.g., people who like Eastern and Western cuisines.
Another way to classify clustering is into independent and non-independent clustering. Independent clustering does not allow overlaps, while non-independent clustering does. Independent clustering uses the internal classification similarity matrix (also called semi-supervised learning), while external classification relies on labels. Internal classification can be divided into hierarchical clustering and planning clustering. Hierarchical clustering further splits clusters based on similarity and uses a parameter to determine the number of clusters.
These algorithms are effective for clustering documents with implicit subtopics, dense graphs, subgraphs, center-based methods, density, target functions, and tree structures, enabling modern algorithms to perform repetitive identification and prediction tasks.
In [77], Shiebler introduced a framework where hierarchical overlapping clustering algorithms are modeled as functors decomposing through simplicial complexes. He defined a pair of adjoint functors that map between simplicial complexes and clustering outputs. Maximal and single linkage clustering were presented as compositions of flagification and connected components functors with the finite singular set functor. He also showed that maximal linkage refines all other hierarchical overlapping clustering functors, which can further refine single linkage.
The main problem addressed was as follows: Given a finite dataset X sampled from a larger space with a probability measure , clustering algorithms must group points in while preserving the input structure. By modeling these algorithms as functors, Shiebler ensured they preserve injectivity, homogeneity, and composability. This approach identifies algorithmic commonalities, extends algorithms while maintaining functoriality, and detects modifications that break functoriality.
Earlier work by Carlsson et al. [86] used a functorial description to show that non-nested clustering algorithms can be combined through single linkage, creating a framework for generating clustering algorithms. In [77], Shiebler advanced this work in several key aspects.
As mentioned in the preliminaries, there exists a pair of adjoint functors between the category of non-nested flag covers (which define topology and metrics based on graph-like structures) and the category of fibered fuzzy simplicial complexes (which capture the information of fuzzy classification): and . The topological refinement process, known as flagification, is thus represented by the functor , which converts any fuzzy simplicial complex into a fuzzy simplicial flag complex. The flagification process is completed by the functor. This allows for the integration of any general cover at any local into the maximal cover at that local, which corresponds to the class in the classification.
In earlier research, Spivak and McInnes [87,88] introduced the adjoint functors and , which operate similarly to the realization functor and the singular set functor in algebraic topology, facilitating the conversion between fuzzy simplicial sets and uber-metric spaces. Under the framework introduced in [77], these functors can be further decomposed into more fundamental functors. First, the following functor is needed.
Definition 34
(Functor [77]). The functor is defined as follows.
- For objects: A finite uber-metric space is sent to a fibered fuzzy simplicial complex , where for , is a simplicial complex whose 0-simplices are X, and the 1-simplices satisfy for . has no n-simplices for .
- For morphisms: A map is sent to a natural transformation between the two fibered fuzzy simplicial complexes , where the distribution at α is given by f.
The use of a negative logarithmic function (in for ) is justified because is a monotonic decreasing function from to . If , then the strength of the simplex in is 1, and as approaches zero, the strength of the simplex approaches 1. For , if an n-simplex exists in , then it certainly exists in . Within , the largest for which the fibered fuzzy simplicial complex has the strength is 1. Functor is then decomposed as .
For , is a flag complex, where the set forms a simplex if the pairwise distances between the points in the set are all less than or equal to . That is, corresponds to a Vietoris–Rips complex.
Definition 35
(Functor [77]). Its adjunct, the functor is then defined as follows.
- For objects: The vertex set X of is mapped to , where .
- For morphisms: sends a natural transformation to the function f defined by μ on the vertex sets of and (the function must be non-expansive because for all , if , then must be in or ).
Note that is an uber-metric space, where the distance between points and is determined by the strength of the 1-simplex connecting them.
A nested clustering algorithm accepts a finite uber-metric space and returns a non-nested flag cover of X. Therefore, the following clustering functors are needed. Here, we suppose that is the metric space where the distance between any two elements is . Other algorithms, such as extrapolative clustering methods, can also be concluded into this framework with a slight modification.
- Flat Clustering Functor: A functor , which is constant on the underlying set.
- Non-trivial Flat Clustering Functor: is a flat clustering functor, where there exists a clustering parameter such that for any is a single simplex containing two points, and for any , is a pair of two simplices. The clustering parameter is the upper bound on the distance at which the clustering functor identifies two points as belonging to the same simplex.
To capture data structure at different scales, one needs to consider the hierarchical clustering functors, defined as follows [77].
- A functor is defined such that for any , is a flat clustering functor.
- Non-trivial hierarchical clustering functor : A hierarchical clustering functor where for all , is a flat clustering functor with clustering parameter .
Under this framework, the hierarchical clustering functor is further specified with the functor .
Definition 36
(Hierarchical clustering functor [77]). The category has objects that are functors such that is a fibered fuzzy simplicial complex, and morphisms are natural transformations. A hierarchical clustering functor is a flat clustering functor at each .
Examples of non-trivial hierarchical clustering functors include single linkage and maximum linkage. See [77].
- Single Linkage : The points lie in the same cluster with strength at least a if there exists a sequence of points such that .
- Maximum Linkage : The points lie in the same cluster with strength at least a if the largest pairwise distance between them is no larger than .
Thus, and become non-trivial hierarchical clustering functors. Single linkage clustering always results in a partition of X, whereas maximal linkage clustering does not. The hierarchical clustering obtained from maximal linkage can reconstruct an uber-metric space. It can be proven that there exists an adjunction .
A case study (see [81]) on implementing multiparameter flattening explores an approach to aggregate results from hierarchical clustering across different hyperparameter values, eliminating the need for manual parameter selection. The proposed multiparameter flattening algorithm uses Monte Carlo sampling to collect cluster partitions across a range of parameters and applies a binary integer program to determine the optimal flattened partition. Evaluated on Fashion MNIST and 20 Newsgroups, the method outperformed manually chosen hyperparameters, improving clustering accuracy 91.2 percent of the time for Fashion MNIST and 76.8 percent for 20 Newsgroups. These results highlight its effectiveness over traditional approaches by preserving structural information across scales, making it a valuable tool for unsupervised learning tasks like data visualization and preprocessing. The method provides a robust alternative to single-parameter clustering, especially when the best parameter varies across data samples.
4.2. Persistent Homology
Topology plays a key role in machine learning, particularly in data analysis, feature extraction, dimensionality reduction, network design, and optimization. Topological Data Analysis (TDA) lies at the core of these applications, using topology to study data shape and connectivity, especially in high-dimensional spaces where traditional methods fall short. Techniques like Betti numbers and persistent homology (PH) help identify patterns and structures within data. PH conducts multi-scale analyses of data shapes, using persistence diagrams to represent features like holes, voids, and connected components. These insights are crucial for tasks such as classification, clustering, image processing, and bioinformatics, as they reveal the intrinsic structure of data, enhancing machine learning performance.
The construction of PH originates from algebraic topology and provides stable, computable, and topologically meaningful invariants for geometrical datasets such as graphs and point clouds. A classical example of PH encodes the topological features of sublevel sets of a function on a topological space X, such as a graph or a point cloud.
Theoretically, the research object of PH is sequences of linear maps between vector spaces:
PH focuses on identifying which vectors remain non-zero over multiple iterations, termed persistence modules. In ML, usually, these vector spaces are homology groups of topological spaces , which form a sequence:
The basic category employed in these studies is , defined as follows.
Definition 37
(Persistence module and its category [79]). A persistence module V is a functor from the poset to the category of vector spaces over k. A morphism between two persistence modules is a natural transformation between functors. The category of persistence modules is then denoted by , which is an abelian category admitting pointwise kernels, cokernels, images, and direct sums.
The goal is to identify the homology cycles that persist across multiple iterations. The main theorem in PH, the algebraic stability theorem, is applied to analyze noise in data [89]. Most of the early mathematical results were detailed in [79], with critical contributions including [90,91,92,93]. Additionally, some research is associated with quiver representation theory, which can be considered a ‘weak’ version of category theory.
A key concept in topological data analysis is the persistence barcode, an algebraic invariant that represents the stability of topological features in a filtration. It consists of intervals on the extended real line, each indicating the lifespan of a feature within a filtration of point clouds, graphs, functions, or complexes. Longer intervals signify robust features, while shorter ones often indicate noise, making the barcode a complete invariant of the filtration [90].
The differentiability of the persistence map is crucial for applying optimization methods like Newton–Raphson. For example, [94] introduced an algorithmic framework that scales efficiently with increasing data size and dimensionality.
In [95], the author summarizes previous findings and explores new theoretical aspects of PH for data analysis, focusing on its differentiability and discriminative power. Key contributions include:
- Defining differentiability and derivatives within the infinite-dimensional and singular category of barcodes , enabling PH-based gradient-descent optimization [96].
- Introducing Extended Persistent Homology (EPH) and applying it to machine learning, using the Laplacian operator for graph dataset classification [97].
- Analyzing the fiber of the persistence map from filter functions on a simplicial complex to . By applying increasing homeomorphisms of , they showed the fiber forms a polyhedral complex and established a functorial relationship from barcodes to polyhedral complexes [98].
- Developing an algorithm to compute the polyhedral complex forming the fiber for arbitrary simplicial complexes K. enabling homology computations and fiber statistics [99].
Jardine [100,101] studies Vietoris–Rips and Lesnick complexes from a homotopic perspective, representing them as homotopy types via posets of simplices and viewing them as functors on a parameter space. Using the category of space systems, they establish a partial homotopy theory with controlled equivalences, proving that branch point maps from dataset inclusions are controlled homotopy equivalences. Ref. [102] introduces an algorithm to compute the path category (fundamental category) of finite oriented simplicial complexes and proves a stability theorem, including a specific stability result for path categories.
Ref. [80] systematically reviews PH and its use in supervised and unsupervised models, highlighting three challenges: data representation, distance metrics, and feature extraction. It outlines four key steps in PH-based machine learning: simplicial complex construction, PH analysis, feature extraction, and machine learning.
Ref. [103] explores topological data analysis (TDA), including PH and Mapper, in studying neural networks and datasets. It reviews recent articles (Appendix A) across four areas: network structure, input/output spaces, internal representations, and training dynamics. Applications include regularization, pruning, adversarial detection, model selection, accuracy prediction, and assessing generative models. The paper also discusses challenges and future directions.
The effectiveness of persistent homology (PH) and the specific topological or geometric information it captures remain unclear. Ref. [104] investigates this using synthetic point clouds in and , showing that PH can identify holes, curvature, and convexity, even with limited data, noise, and low computational resources. These insights could enhance deep learning models by integrating PH features, kernels, or priors [105,106].
The thesis by [107] explores more refined persistent invariants, extending beyond the usual persistent objects from persistent homology by replacing the homology functor with homotopy group functors, the cohomology ring functor, or the functor of taking chain complexes.
There is also some work on -algebra or -coalgebra structures in persistent homology or persistent cohomology, as seen in [108,109].
4.3. Other Related Research
Ref. [110] redefines neural architecture selection by linking data complexity to a network’s ability to generalize. Using algebraic topology to measure data complexity, they show that a network’s capacity to represent a dataset’s topological complexity limits its generalization. Their analysis reveals topological phase transitions at different dataset complexities, offering insights into selecting fully-connected neural networks. Unlike traditional approaches focusing on depth, width, or Neural Architecture Search (NAS)—which finds optimal but hard-to-interpret architectures—they propose data-first architecture selection. This approach selects architectures based on the true data distribution, emphasizing networks that are expressive and properly regularized for a given dataset. By measuring data complexity, one can match a dataset with a suitable architecture, streamlining the selection process.
Ref. [111] measures neural network expressive power using the topology of decision boundaries. By sampling networks of varying depth, width, and size, they show that expressive power depends on architecture properties. Given a neural architecture with n parameters, its decision boundaries correspond to points in . Persistent homology is used to quantify the topological complexity of these boundaries.
Ref. [112] explores normalizing flows, generative models that map complex distributions to simpler ones using bijective functions. They are applied in variational inference, density estimation, and tasks like speech and image generation.
Ref. [113] unifies causal inference and reinforcement learning (RL) using simplicial objects , where higher-order objects induce symmetries that explain DAG model equivalences. Structure discovery is framed as a Kan extension problem of ‘filling horns’ in simplicial complexes, similar to [114].
Ref. [115] introduces GAIA, a generative AI model using simplicial complexes, with parameter updates guided by lifting diagrams. Applications are detailed in [116].
Ref. [117] presents UCLA (Universal Causality Layered Architecture), with four layers: (1) causal interventions as higher-order categories, (2) categorical causal models, (3) data layer mapping objects to instances, and (4) homotopy layer using colimits for abstraction. Functors between layers, defined via Yoneda Lemma, create a Grothendieck category that integrates models with data. Causal inference between layers is modeled as a lifting problem.
Ref. [118] explores homotopical equivalences between DAGs using posets and finite Alexandroff topologies, while [119] applies causal homology to spacetime in quantum research.
5. Developments in Topos-Based Learning
One of the key challenges in conventional low-order categorical frameworks is their limited capacity to capture global properties in machine learning models. These frameworks often rely on base categories with specific morphisms or functors, limiting their ability to model complex structural relationships across multiple scales and to capture properties that emerge at a global level. In contrast, topos theory provides a more flexible and expressive approach by generalizing the concept of ‘space’ and incorporating high-order categorical structures. Recent works, including those by Lafforgue [120], Caramello [121], and Belfiore et al. [26], have demonstrated that topoi can serve as abstract frameworks for reasoning about deep learning architectures, particularly by enabling a logical and geometric representation of transformations within neural networks.
Some emerging ideas in machine learning can be examined from various categorical perspectives. Employing low-order categorical structures, such as specific base categories with topmost bi-morphisms, or high-order categorical frameworks, such as (co)sheaves and topoi, represents different ways to model the structural relationships inherent in machine learning. For example, in the following discussion, we introduce Lafforgue’s report, which proposes using geometric morphisms between topoi to transfer and constrain similar structures in data and information. These geometric morphisms not only connect different topological or algebraic contexts through their associated topoi but also serve as a geometric model of the ‘coarse-graining’ process and its reverse, ‘refinement’. This is particularly significant from a logical perspective, as geometric morphisms effectively model the evolution of data and relationships across different layers or scales. From a practical perspective, we summarized the applications of topos theory in machine learning in Table 8.

Table 8.
Applications of topos theory in machine learning.
A topos can be considered a category consisting of spaces that possess specific properties, where each space locally resembles a given reference space. The categorical structure makes it analogous to the category of sets, which means many operations allowed in —such as taking products, limits, and exponential objects—are also permissible in a topos. Neural networks can be considered as systems for transmitting and composing data through edges, with additional processing applied as needed. Existing data can be readily duplicated and combined with other data in a form similar to tensors.
The topos structure is particularly effective in representing geometric properties through logic since the internal logic of topoi is an intuitionistic higher-order logic. Additionally, algebraic structures can be incorporated as invariances maintained by geometric morphisms. In this section, we aim to introduce recent advancements in the application of topos theory to machine learning.
The research in this direction can be divided into two types based on whether semantics correspond to intuitionistic logic, a key aspect when analyzing neural networks as structured learning systems. Since information flow in neural networks resembles a language, semantics naturally align with type theory, providing a categorical foundation for machine learning architectures. Earlier works like [123,124] developed type systems and integrated lexical meaning theory into compositional semantics, while [125,126,127] categorically interpret axiomatic semantics, modeling inference and learning transformations in topoi, where constructive higher-order logic translates into function types. Ref. [128] introduces an ontological hierarchy relevant to machine learning. First, hierarchical structures in language composition align with neural network architectures, as confirmed through corpora experiments. Second, Ref. [129] highlights a key gap in topos-theoretic ML frameworks: ontological concepts (strongly-typed ontology) and logical concepts (relations between types) remain unclearly separated, limiting the full integration of semantic structures in learning models.
In addition, Ref. [130] links ontological perspectives to topoi, suggesting ways to integrate ontological and logical concepts in topos-based machine learning and explores parallels between Turing machines and topoi for potential applications in learning networks. Focusing on space-like properties of topoi (from (co)sheaves) can enhance network performance. While [131] interprets logic through topology, topos-theoretic ML instead translates topology into logic. Ref. [132] introduces the topos of noise, offering insights for statistical machine learning.
In the following sections, we will systematically introduce the main research in this direction.
5.1. The Reports of Laurent Lafforgue
Laurent Lafforgue’s work explores the application of Grothendieck topos theory in AI, particularly for artificial neural networks. Topos theory, as a framework for geometric logic, translates invariance and equivariance properties in neural networks into logical expressions, enhancing interpretability and learning mechanisms. Key ideas in topos-theoretic machine learning include:
- Emergence and Invariance: Higher-order categories and geometric logic model emergent behavior and preserved properties in neural networks.
- Geometric Representation: Data spaces can be modeled as geometric objects, capturing structural evolution beyond linear representations.
- Local-to-Global Analysis: Topos-theoretic spaces enable local properties to determine global learning behavior.
- Categories and Generic Models: A mathematical theory derived from a neural network framework in logic can be effectively expressed using a category with suitable properties and a generic model, which acts as a functor.
- Logical Foundations: Axiomatic structures in category theory provide a formal basis for machine learning transformations.
- Theory Mappings: Functors between categories of models facilitate structured transformations across learning paradigms.
- Classifying Topos: A universal framework encoding neural network properties via categorical semantics.
This approach bridges geometry, logic, and learning, offering a structured mathematical foundation for machine learning architectures.
Several key category-theoretic concepts play a foundational role in applying topos theory to machine learning. Sieves and Grothendieck topologies provide a formal framework for defining coverings, extending the notion of topological spaces to more abstract settings, which is essential for structuring data relationships in learning models. Sites generalize topological spaces, enabling flexible representations of structured information, while Grothendieck topoi provide a rich framework for generalizing geometric and logical concepts, allowing global reasoning from local structures. Classifying topoi serve as universal spaces encoding geometric and logical properties of neural network architectures, while geometric morphisms ensure structural consistency across different learning models. These concepts establish a rigorous mathematical foundation for compositional, interpretable, and structured learning frameworks, making category-theoretic approaches highly relevant to modern machine learning research.
The Idea in the Reports of Laurent Lafforgue
The reports by Laurent Lafforgue [120,133] explore how topos theory provides a structured mathematical framework for machine learning. The core idea is that objects in a category, such as images belonging to the same class in a dataset, should be described using a unified language based on consistent rules and symbols. This structured language helps capture common patterns and properties among elements while allowing flexibility to differentiate finer details. For instance, in an image-classification task, all cat images might belong to the same category, but their relative positions and orientations vary. To describe these variations, additional grammatical rules are introduced, formalizing geometric properties using structured axioms and deduction rules. These rules allow the development of first-order geometric theories, which systematically define how data elements relate to each other.
Mathematically, a geometric theory defines a set of models that adhere to its constraints. These models are organized into a category , capturing how different machine learning structures conform to topos-based interpretations. The Grothendieck topos provides a global perspective, allowing local properties of data to be extended and reasoned about in a structured way. In this framework, information flows from local constraints to global structures, making it useful for understanding how neural network features generalize.
A key feature of this approach is its ability to link local and global properties using sheaf theory. A sheaf can be thought of as a structured way to organize and retrieve information based on different perspectives. The function acts as a mapping tool, translating global models into local interpretations, ensuring that learning remains consistent across different contexts. Additionally, transformations between different parameter spaces (e.g., changing input distributions or retraining models on new datasets) can be expressed using morphisms. These transformations allow models to adapt to new data environments, helping to establish a formal way to reason about model transferability and adaptation.
The classifying topos serves as a universal semantic space for models of a theory , containing a universal model that can be translated into different topoi via geometric morphisms. This ensures a consistent representation of -models across different mathematical contexts.
A subtopos represents a refined version of a topos, directly linked to quotient theories, where additional constraints shape model behavior. The hierarchy of subtopoi reflects different levels of abstraction in knowledge, with operations like unions, intersections, and differences describing relationships between structured learning environments.
In this framework, real-world elements such as data structures, learning rules, and concepts are modeled as topoi, each with known and unknown attributes. The categories encode structured knowledge and map to topoi via functors, enabling the transfer, refinement, and extension of learning models.
Two key operations facilitate knowledge representation:
- The naming functor assigns structured labels to objects, creating a unified vocabulary.
- The partial knowledge functor encodes what is currently known and how it evolves.
These functors induce structured transformations between learning models, enabling adaptation and generalization. This framework provides a mathematically grounded way to model learning dynamics, representation refinement, and information transfer using topos theory.
In syntactic learning and formalized inductive reasoning, the partial knowledge functor maps structured knowledge into a topos . This mapping establishes relationships between different learning models, provided that the underlying theory follows a structured extrapolation principle. Formally, this can be expressed as:
Information extraction is modeled using topos morphisms. The naming functor associates knowledge structures with a quotient theory , which provides a precise way to describe a category within the theory . Information extraction is then represented as a topos morphism , mapping a collection of structured elements into a refined framework .
This process can be decomposed into simpler steps through a sequence of intermediate transformations:
where each transformation gradually refines the conceptual structure, ensuring that new information is integrated while preserving existing knowledge.
In this context:
- Each topos represents a structured knowledge space, capturing relationships between learning components.
- Topos morphisms track how information evolves, refining knowledge across different layers of abstraction.
- Hierarchical decomposition enables a systematic approach to integrating localized details into broader learning architectures.
This study highlights how topos theory provides a mathematical foundation for structuring and analyzing complex information across different domains. By modeling data elements as topoi and organizing them through quotient theories and subtopoi, a hierarchical framework for representing both known and unknown properties in machine learning was created.
5.2. Artificial Neural Networks: Corresponding Topos and Stack
A key contribution in 2021 by Laurent Lafforgue’s team, including Jean-Claude Belfiore and Daniel Bennequin [26,134], introduced stack structures in artificial neural networks. Their work applied topos theory to better understand deep neural networks (DNNs) and extend this framework to other AI models. The goal was to explain emergent reasoning capabilities within neural networks, often seen as a ‘black box’. To achieve this, they used categorical logic, built on the topos-stacks framework, to integrate logic, topology, and algebra in machine learning. While Martin–Löf Type Theory (MLTT) provides a foundation for structured reasoning, their approach extends beyond MLTT, leveraging hierarchical and semantic representations in topos theory to model complex learning processes, such as multi-modal learning, compositional reasoning, and knowledge transfer.
A core challenge in AI is that:
- DNNs excel at pattern recognition but lack structured reasoning.
- Bayesian models are good at probabilistic inference but do not support logical deduction.
- Human-like intelligence requires both statistical learning and logical inference.
By integrating categorical logic, this approach aims to combine the strengths of neural networks and symbolic reasoning, making AI models more interpretable, modular, and generalizable. The topos-stacks framework provides a systematic way to model information flow, allowing neural networks to capture geometric and logical structures in data and improve explainability and adaptability.
Specifically, their topos-based approach has strong potential in AI, including:
- Explainable AI: Making neural networks more interpretable by modeling learning as logical transformations.
- Transfer and Compositional Learning: Enabling modular knowledge transfer between tasks.
- Hierarchical and Multi-Agent Learning: Encoding layered decision-making in AI systems.
- AI for Scientific Discovery: Applying topos-based representations in physics-inspired machine learning.
- Symbolic-Neural Hybrid Models: Bridging deep learning and structured reasoning for more robust AI.
As outlined by Laurent Lafforgue [120], topoi on generalized topological spaces provide a robust geometric and logical foundation for AI. Their work also connects to intuitionistic and contextual inference, relevant to AI decision-making under uncertainty. The stack framework extends the versatility of AI models by incorporating hierarchical learning representations, enabling more structured, context-aware processing. Additionally, by applying topos theory and categorical logic to AI, their approach offers a new perspective on neural networks, particularly in explainability, modularity, and structured inference. The topos-stacks framework provides a foundation for more interpretable, adaptable, and mathematically grounded AI models.
- Key Concepts and Their Role: Several fundamental mathematical structures are central to understanding the topos-theoretic approach to machine learning. While detailed definitions are omitted, we highlight the key ideas and their relevance to our discussion.
- Groupoids and Stacks: Groupoids represent structures where every morphism is invertible, capturing symmetries and equivalences. Stacks extend this idea by formalizing hierarchical relationships between objects in a categorical framework. These notions are useful in modeling invariance and modularity in deep learning architectures.
- Grothendieck Construction and Fibrations: The Grothendieck construction provides a systematic way to transition between category-valued functors and structured categories, particularly in the study of fibration structures. This is instrumental in understanding hierarchical feature representations in neural networks.
- Type Theory and Logical Structures: Type theory provides a formal language for structuring logical reasoning. Within categorical semantics, type-theoretic frameworks are used to interpret neural network functions as structured logical operations, enhancing explainability and compositional learning.
- Locally Cartesian Closed Categories and Model Categories: These structures support flexible transformations between logical and geometric representations of learning processes. They facilitate the integration of homotopy-theoretic ideas with machine learning, particularly in capturing topological invariants of learned representations.
- Sheaves, Cosheaves, and Invariance Principles: Sheaf-theoretic techniques allow for local-to-global reasoning, enabling structured information flow in learning systems. Cosheaves, in contrast, provide a dual perspective that is valuable for understanding distributed representations and signal propagation in neural networks.
By leveraging these categorical structures, the work establishes a mathematical framework for deep learning that unifies statistical inference, logical reasoning, and geometric representation. The subsequent sections will introduce and develop these ideas in the context of topos-based learning methodologies.
Topoi and Stacks of Deep Neural Networks
The study by [26] demonstrates that deep neural networks (DNNs) can be naturally viewed as objects within a Grothendieck topos, where learning processes are represented as morphism flows. This approach strengthens the connection between neural networks and category theory. Their methodology begins by constructing a base category that encodes the network’s graph structure using a freely generated category. The learning process is then decomposed into fundamental components, each of which can be implemented independently or in combination. These components are represented as functors that map the base category to well-known categories such as sets (), groupoids (), or small categories (). When the target category is , reversing the category direction transforms these functors into presheaves, providing a structured representation of learning dynamics. The main results can be summarized as follows:
- Deep Neural Networks as Topos Objects: Every artificial deep neural network (DNN) can be represented as an object within a standard Grothendieck topos, where the learning process corresponds to morphism flows, building on ideas introduced in the reports of Laurent [120,133].
- Invariant Network Structures: Patterns in neural networks, such as CNNs and LSTMs, correspond to Giraud’s stack structures, supporting generalization under specific constraints.
- Artificial Languages and Logic: Learning representations are structured along the fibers of stacks, incorporating different types of logic (intuitionistic, classical, linear) to enable formal reasoning.
- Semantic Functions in Networks: Neural network functions act as semantic functions, encoding and processing structured information, leading to meaningful outputs.
- Entropy and Semantic Information: Entropy measures the distribution of semantic information within the network, providing insights into how knowledge is processed and retained.
- Geometric Semantics and Invariance: Geometric fibrant objects in Quillen’s closed model categories help classify semantics, particularly through homotopy invariants that capture structural consistency.
- Type-Theoretic Learning Structures: Intensional Martin–Löf Type Theory (MLTT) structures geometric objects and their relationships, offering a constructive reasoning framework.
- Information Flow and Derivators: Grothendieck derivators analyze how information is stored and exchanged within the categorical framework.
Correspondence between Deep Neural Networks and Grothendieck Topos: The study by [120,133] establishes that deep neural networks (DNNs) can be represented as objects within a Grothendieck topos, where learning processes are modeled as morphism flows. The framework begins by interpreting the network as a directed graph , where layers and connections form a structured path. Feedforward and feedback mechanisms correspond to a partial order ≤ and its opposite, reflecting the hierarchical nature of neural computation(see the following diagram).
For a simple chain-like network, the learning process is described using two covariant functors: the feedforward functor and the weight functor . Here, is a freely generated category, incorporating all possible directed paths without additional constraints. Each layer corresponds to a set of neuron activities , while connections are represented by functions , parameterized by learned weights . Similarly, the weights are structured as a functor , where corresponds to the set of all weights from layer k onward, forming a hierarchical structure.
To extend this categorical model into a topos framework, the opposite category is introduced. The functors , , and are then reformulated as presheaves on , turning them into objects within the topos . This structure naturally aligns with multi-layer perceptrons, capturing the hierarchical propagation of information. A key feature of this framework is its ability to describe learning dynamics within the topos. The subobject represents the learned weights, forming a projection from the terminal object 1. This projection models how different weight configurations define substructures within the network, guiding inference and optimization.
For chain-like networks, the subobject classifier provides an internal logic, refining the learning process layer by layer. This progression models the increasing certainty of the network’s predictions as it processes input data through successive layers. For more complex architectures, such as RNNs, LSTMs, and GRUs, additional modifications to are required, such as duplicating nodes to accommodate memory mechanisms. Regardless of the network structure, the presheaf framework ensures a consistent representation of learning dynamics, making it applicable across various architectures. In supervised learning, the backpropagation algorithm is formalized as a flow of natural transformations of the functor , adjusting the weight space iteratively.
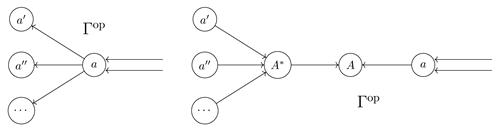

Supervised learning optimizes an energy function F, with gradients computed as
where transforms gradient information, and represents the weight space over the network graph . The gradient
captures how weight variations affect the expected energy , with directed paths determining neuron interactions. Learning dynamics are structured using the presheaf , where neuron activations and weight updates follow hierarchical mappings. Initial states define the topos structure, guiding information propagation. The layer encodes weight configurations for deep and recurrent neural networks. Classifying topoi provide a structured framework for semantic inference in machine learning. As shown in [135], topoi model learning processes using directed graphs and morphisms, organizing computational flow. Ref. [121] further explores how topos fragments, structured via graph-based representations, capture semantic and computational principles.
Topos structures have been used to model information flow in wireless and biological networks [136]. Key insights include:
- Local–Global Coherence: Topos theory formalizes how local interactions in a network lead to global coherence, explaining structured information flow.
- Structured Node Representation: Nodes act as both receivers and transmitters. The Grothendieck construction models their internal structure, associating fibers with a base category. This extends to stacks (2-sheaves) [26], capturing hierarchical dependencies in complex networks.
The Stack of DNNs The study in [26] explores the stack structure in DNNs using a topos-theoretic framework. It examines the network structure () and learning constraints (), shaped by geometric and semantic invariants [121]. In DNNs, extracted invariants must be preserved across layers, as seen in CNNs, where group actions G ensure consistent transformations. The study highlights that such invariants should be analyzed within the stack (2-sheaf) framework.
A key approach represents network transformations as contravariant functors mapping the network category to the topos of G-sets . This setup captures symmetry and equivariance in learning. The algebraic structure on these functors, along with equivariant transformations, defines a topos , providing a categorical framework for modeling invariants.
In this framework:
- A fibration encodes fibered categories satisfying stack axioms.
- The topos of sheaves is equivalent to , forming a classifying topos.
Beyond topos structures, groupoid theory provides a logical model for network transformations and invariants. Presheaves on groupoids form Boolean topoi, where the network’s logic aligns with Boolean algebras. In CNNs, irreducible linear representations describe invariant subspaces, ensuring transformation consistency. Additionally, intuitionistic logic (e.g., Heyting algebras) models uncertainty within classifying topoi. This insight links groupoid stacks with internal groupoids, formalized via the Grothendieck construction. Here, stacks correspond to strict 2-functors mapping the category into the 2-category . The equivariant structure of neural networks is captured through fibered categories. Given two sheaves , their interaction follows a commutative diagram:

This generalizes group equivariance, modeling network transformations as morphisms in stacks. The stack-theoretic approach thus provides a unified categorical framework for symmetry, equivariance, and invariance in machine learning.
The goal is to identify the subobject classifier in this framework. For each object U in , the sheaf forms a small category, and functors define a local classifying topos . Natural transformations describe subobjects of , encoding the logical structure of learning. A presheaf A is given by . Whether the pullback functor is geometric determines if satisfies the stack property, ensuring consistency in learning.
Two functors govern information flow in neural networks:
- (feedforward propagation).
- (feedback propagation).
These functors form a duality (), propagating logical formulas and truth values across layers [26], ensuring that:
As the logical interpretation in learning, this framework connects category theory to neural networks:
- Type-Theoretic Structure: Network operations are represented as types (presheaves) on a stack’s fibers, capturing the logical rules of learning.
- Semantic Refinement Across Layers: Deeper layers refine their understanding of inputs, aligning with the hierarchical nature of feature extraction in DNNs.
Logical Structures and Neural Networks The internal logic of a category is structured as follows:
- Types: Objects in .
- Contexts: Slice categories .
- Propositions: -truncated objects in .
- Proofs: Generalized elements of propositions.
A theory consists of axioms and derivable proofs. In a topos , logical concepts such as types, variables, and truth values are interpreted as categorical structures, ensuring compatibility of logical operations.
Semantic Interpretation in Neural Networks: DNNs require semantic consistency across layers. Modeled as a dynamic object X in a classifying topos , learning propagates through:
- Feedforward transformation: .
- Feedback transformation: .
Each layer interprets logic via a presheaf L, with theory sets . The function maps data to a consistent set of propositions, refining semantics at deeper layers.
By integrating logic, category theory, and machine learning, this framework enhances interpretability and semantic consistency in deep learning. Supporting results are provided in [137].
Experimental Insights from [137] and Machine Learning Implications: Experiments show that internal layers of deep neural networks (DNNs) progressively interpret the output layer’s structure, with backward propagation () transmitting semantic information. This provides a systematic method to analyze how neurons encode and propagate logical relationships. In their experiments, a metric is introduced to quantify information transfer:
Higher values indicate better semantic consistency between input features and learned representations.
Additionally, experiments reveal that certain subsets of weights in the parameter space evolve robustly from to , acting as structurally stable components. Targeting these subsets for stabilization could enhance learning efficiency, generalization, and robustness, benefiting applications such as transfer learning and continual learning.
- Model Category and M-L Type Theory in DNNs: Homotopy theory provides a structured way to study transformations between neural network mappings. In model categories, weak equivalences capture essential features of learning, allowing homotopies between mappings to be explicitly observed. This perspective aligns with Quillen’s model theory, where fibrations and cofibrations ensure structural consistency in DNNs.
This study focuses on DNN architectures, where stack structures emerge naturally. The fibers of these stacks are groupoids, forming a Quillen closed model category. This setting connects homotopy theory to Martin–Löf type theory (M-L theory), supporting logical reasoning in neural networks.
- The category of stacks (groupoid stacks) corresponds to the category . Within the groupoid fibration, stacks are fibrant objects, and weak equivalences define homotopy relations, linking them to M-L type theory.
- This result extends to general stack categories, connecting Quillen models with intensional M-L theory and Voevodsky’s homotopy type theory.
- The primary categories studied include (groupoids) and (small categories). In , fibrations lift isomorphisms, cofibrations are injective functors, and weak equivalences correspond to categorical equivalences.
- Given the hierarchical structure of DNNs, a poset representing layers induces a fibration , providing a structured context for M-L type theory.
- Types in this framework are defined as fibrations, supporting logical operations such as conjunction, disjunction, implication, negation, and quantification.
- The M-L structure over DNNs associates contexts and types with geometric fibrations in the 2-category of contravariant functors , ensuring a well-defined internal logic.
- Similar principles apply to groupoids, allowing M-L theory to define language and semantics for neural networks, aligning machine learning with structured categorical reasoning.
This approach integrates type theory and categorical semantics, using categorical logic to model learning processes. Previously, machine learning had not explored pre-stack and pre-sheaf semantics, making this study the first to introduce these methods. This framework enhances DNNs by aligning their internal representations with formal logical structures, bridging machine learning with programming semantics.
- Dynamics and Homology in Deep Neural Networks In supervised and reinforcement learning, network decisions rely on structured information flow. The dynamic object represents network activity, guiding decision-making based on learned semantic structures. The key challenge is understanding how the entire deep neural network (DNN) contributes to output decisions. This is achieved by encoding output propositions into truth values and expanding the network’s structure accordingly.
Network decision-making follows category-theoretic approximations. The subset of activities confirming an output proposition is described via Kan extensions, leading to global invariants given by cohomology . Forward propagation corresponds to computing limits of , while backpropagation refines semantic representation. Stacks and costacks in the network are modeled in the classifying topos, linking homology and homotopy invariants to semantic information. This framework supports:
- Direct representation of semantic content (first level).
- Higher-order structures capturing evolving theories (second level).
Information processing between layers must ensure effective semantic communication. Existing results relate to Shannon entropy, where entropy in Bayesian networks corresponds to first-order cohomology . In higher homotopy settings, mutual information extends to higher-dimensional cocycles.
Topos semantics also formalizes probability propagation. Marginalization corresponds to covariant functors, mapping transformations between layers. These transformations align with fiber transitions in stacked DNNs, supporting contextual reasoning. To refine this structure, the presheaf within the stack encodes logical relations. Theories are interpreted using sheaf and cosheaf structures, with monoids defining homotopy-invariant semantic information. Heyting algebras introduce logical order in layers, structuring conditioning as monoid actions.
Two primary models emerge in Bayesian-inspired semantics:
- Random variables in a layer correspond to logical propositions, enabling measurement.
- Layers represent gerbe objects, modeling dynamic semantic transformations across feedforward and feedback loops.
Semantic information quantifies fuzziness in propositions, using homology-based 0-cochains to assess uncertainty. Cohomology of categorical neurons evaluates how information evolves across layers. Moreover, the interaction of monoid actions with logical propositions formalizes information propagation. The mutual information formula:
describes how conditions shape semantic knowledge.
This study further explores the linguistic structure of information using Galois groups, fundamental groups of information spaces, and stability of information transport. The introduction of a 3-category of DNNs provides a higher-order formalization, ensuring network robustness across varying inputs.
In conclusion, Ref. [26] provides a groundbreaking framework that integrates topos theory, type theory, and categorical semantics to analyze and interpret the dynamics and semantic structures of Deep Neural Networks (DNNs). It introduces novel applications of homology, cohomology, and presheaf-based semantics to model information flow, invariance, and logical operations within DNNs. By extending these ideas to higher categorical structures and incorporating concepts like Galois actions and internal invariants, the work offers a robust mathematical foundation for understanding and enhancing the learning processes of neural networks.
5.3. Other Related Works
The compositional categorical structure discussed in Section 2 closely aligns with topos theory. As shown in [27], the map in can be naturally interpreted in terms of dynamical systems, specifically as generalized Moore machines. Consequently, the derived category , equipped with a coalgebraic structure, forms a topos for dynamical systems on any . This structure provides a powerful framework where logical propositions can be expressed and manipulated in its internal language.
In [122], transformer networks are examined as a unique case compared to other architectures like convolutional and recurrent neural networks. While these architectures are embedded within a pre-topos of piecewise-linear functions, transformer networks reside in their topos completion, enabling higher-order reasoning. This advancement builds on the concept of ‘corresponding to a geometric model’ introduced in [120] and leverages the foundational categorical framework detailed in [4].
Further contributions to semantic investigation include the extended fibered algebraic semantics for first-order logic presented in [138], and the relative topos theory framework developed in [139], which generalizes the construction of sheaf topoi on locales. These results provide critical insights into the relationships between Grothendieck topoi and elementary topoi, forming a robust mathematical foundation for exploring semantics in categorical and logical contexts.
Several application-oriented results have been reported in the literature, highlighting the integration of semantic frameworks with advanced mathematical and communication theories:
- Ref. [140] leveraged the logical programming language ProbLog to unify semantic information and communication by integrating technical communication (TC) and semantic communication (SC) through the use of internal logics. This approach demonstrates how logical programming can bridge semantic and technical paradigms to enhance communication systems.
- Ref. [141] examined semantic communication in AI applications, focusing on causal representation learning and its implications for reasoning-driven semantic communication networks. The authors proposed a comprehensive set of key performance indicators (KPIs) and metrics to evaluate semantic communication systems and demonstrated their scalability to large-scale networks, thereby establishing a framework for designing efficient, learning-oriented semantic communication networks.
- Ref. [142] explored the mathematical underpinnings of statistical systems by representing them as partially ordered sets (posets) and expressing their phases as invariants of these representations. By employing homological algebra, the authors developed a methodology to compute these phases, offering a robust framework for analyzing the structural and statistical properties of such systems.
5.4. Case Study: Frustrated Systems in AI and Topos-Theoretic Approaches
There are several notable case studies and experimental results in this direction. Here, we present the findings from [143] as an example. The focus, frustrated systems, emerge in various AI and computational settings where conflicting constraints hinder convergence to a single optimal state. These include:
- Neural Networks: In deep learning, conflicting weight updates can create local minima, complicating optimization.
- Optimization Problems: Problems like the traveling salesman problem and graph coloring exhibit frustration due to multiple competing constraints.
- Quantum Computing: Quantum error correction and superposition management rely on coherent state transitions, which can be modeled using topos structures.
Main challenges in frustrated systems include:
- Difficulty in Finding Global Optima: Local minima hinder effective optimization.
- High Computational Complexity: Navigating rugged optimization landscapes requires extensive computation.
- Sensitivity to Perturbations: Small changes can lead to instability in model performance.
- Long Relaxation Times: Convergence to stable states can be slow in complex AI systems.
To address these challenges, topos theory provides a mathematical framework to manage complexity and maintain coherence by:
- Formalizing Learning Architectures: Representing training processes as morphisms within a topos.
- Enhancing Optimization: Providing structured methods to escape local minima.
- Ensuring Stability and Robustness: Using categorical structures to generalize across learning conditions.
As a result, the following applications in AI and quantum computing align well with topos-based methodologies.
- Neural Networks: Regularization techniques and structured weight updates reduce the risk of local minima.
- Quantum Algorithms: Error correction and coherence management benefit from topos-theoretic representations.
- Reinforcement Learning: Managing the exploration-exploitation tradeoff through categorical methods.
- Hybrid Approaches: Combining topos theory with traditional optimization techniques for enhanced performance.
5.5. Outlook and Future Directions
Topos theory has emerged as a powerful mathematical framework for understanding machine learning through categorical semantics, hierarchical structures, and logical reasoning. By modeling realistic elements as topoi and utilizing quotient theories and subtopoi, this study integrates semantic content into a structured categorical framework. The representation of each realistic element as a topos encapsulates both known and unknown properties, enabling a categorical formulation of information refinement and structural transformations. This provides a systematic approach to decomposing localized information and integrating it into broader frameworks, offering deeper insights into complex learning systems.
In this direction, open problems arising from existing research ideas include extending the application of topos theory in machine learning to develop more interpretable, structured, and theoretically grounded AI models. Furthermore, exploring higher-order learning structures, semantic communication, and compositional invariance principles could provide foundational insights for next-generation AI architectures. To conclude, we outline the open research directions in Table 9.

Table 9.
Open problems and future directions in topos-based machine learning.
Additionally, from a practical perspective, several applied research directions emerge:
- Robustness in Adversarial Learning: Investigating topos-theoretic invariances to develop models that are more resistant to adversarial perturbations.
- Explainability in Deep Learning: Using internal logic of topoi to formalize explainability in black-box models such as transformers and generative AI.
- Multi-Agent and Federated Learning: Applying categorical compositionality to improve information sharing and coordination between decentralized models.
- Efficient Knowledge Transfer in Pretrained Models: Leveraging geometric morphisms to enhance the transferability of representations across different tasks.
- Topos-Based Optimization Frameworks: Exploring higher categorical structures in optimization, potentially improving convergence and stability in gradient-based learning.
6. Conclusions
In this survey, we reviewed recent advancements in category-theoretical and topos-theoretical frameworks within machine learning, categorizing the studies into four main directions: gradient-based learning, probability-based learning, invariance- and equivariance-based learning, and topos-based learning. The primary research in gradient- and probability-based learning shares compositional frameworks, while probability-based and invariance- and equivariance-based learning often draw upon overlapping foundational categories, typically involving similar metric or algebraic structures. In contrast, topos-based learning introduces a distinct perspective, emphasizing global versus local structures rather than focusing solely on the functoriality of basic compositional components. Nonetheless, it integrates homotopical and homological viewpoints, establishing partial alignment with invariance- and equivariance-based learning.
This survey aims to outline potential future directions in ‘categorical machine learning’. A key consideration for future research is to further investigate how structural properties preserved across system components and semantic integration within frameworks can be effectively leveraged to advance machine learning methodologies.
Author Contributions
Conceptualization, Y.J.; Supervision, Y.J.; Surveying, Y.J., G.P., Z.Y. and T.C.; writing—review and editing, Y.J. (Section 1, Section 5 and Section 6), G.P. (Section 3), Z.Y. (Section 4), T.C. (Section 2); funding acquisition, Y.J. and G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the JSPS KAKENHI Grant (No. JP22K13951) and the Doctoral Science Foundation of XiChang University (No. YBZ202206).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors appreciate Wei Ke at Macao Polytechnic University for his critical review of this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shiebler, D.; Gavranović, B.; Wilson, P. Category Theory in Machine Learning. arXiv 2021, arXiv:2106.07032. [Google Scholar]
- Lu, X.; Tang, Z. Causal Network Condensation. arXiv 2022, arXiv:2112.15515. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2017, arXiv:1609.04747. [Google Scholar]
- Cruttwell, G.S.H.; Gavranovic, B.; Ghani, N.; Wilson, P.; Zanasi, F. Categorical Foundations of Gradient-Based Learning. In Programming Languages and Systems; Sergey, I., Ed.; Springer: Cham, Switzerland, 2022; pp. 1–28. [Google Scholar]
- Cruttwell, G.S.H.; Gavranovic, B.; Ghani, N.; Wilson, P.; Zanasi, F. Deep Learning with Parametric Lenses. arXiv 2024, arXiv:2404.00408. [Google Scholar]
- Capucci, M.; Gavranović, B.; Hedges, J.; Rischel, E.F. Towards Foundations of Categorical Cybernetics. Electron. Proc. Theor. Comput. Sci. 2022, 372, 235–248. [Google Scholar] [CrossRef]
- Gavranović, B. Fundamental Components of Deep Learning: A category-theoretic approach. arXiv 2024, arXiv:2403.13001. [Google Scholar]
- Blute, R.F.; Cockett, J.R.B.; Seely, R.A. Cartesian differential categories. Theory Appl. Categ. 2009, 22, 622–672. [Google Scholar]
- Cockett, R.; Cruttwell, G.; Gallagher, J.; Lemay, J.S.P.; MacAdam, B.; Plotkin, G.; Pronk, D. Reverse derivative categories. arXiv 2019, arXiv:1910.07065. [Google Scholar]
- Wilson, P.W. Category-Theoretic Data Structures and Algorithms for Learning Polynomial Circuits. Ph.D. Thesis, University of Southampton, Southampton, UK, 2023. [Google Scholar]
- Wilson, P.; Zanasi, F. Reverse Derivative Ascent: A Categorical Approach to Learning Boolean Circuits. Electron. Proc. Theor. Comput. Sci. 2021, 333, 247–260. [Google Scholar] [CrossRef]
- Statusfailed. Numeric Optics: A Python Library for Constructing and Training Neural Networks Based on Lenses and Reverse Derivatives; Online Resource. 2025. Available online: https://github.com/statusfailed/numeric-optics-python (accessed on 20 February 2025).
- Wilson, P.; Zanasi, F. Data-Parallel Algorithms for String Diagrams. arXiv 2023, arXiv:2305.01041. [Google Scholar]
- Wilson, P. Yarrow Diagrams: String Diagrams for the Working Programmer. 2023. Available online: https://github.com/yarrow-id/diagrams (accessed on 23 August 2024).
- Wilson, P. Yarrow-polycirc: Differentiable IR for Zero-Knowledge Machine Learning. 2023. Available online: https://github.com/yarrow-id/polycirc (accessed on 23 August 2024).
- Wilson, P. Catgrad: A Categorical Deep Learning Compiler. 2024. Available online: https://github.com/statusfailed/catgrad (accessed on 23 August 2024).
- Cruttwell, G.; Gallagher, J.; Lemay, J.S.P.; Pronk, D. Monoidal reverse differential categories. Math. Struct. Comput. Sci. 2022, 32, 1313–1363. [Google Scholar] [CrossRef]
- Cruttwell, G.; Lemay, J.S.P. Reverse Tangent Categories. arXiv 2023, arXiv:2308.01131. [Google Scholar]
- Fong, B.; Spivak, D.I.; Tuyéras, R. Backprop as Functor: A Compositional Perspective on Supervised Learning. In Proceedings of the 34th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS 2019), Vancouver, BC, Canada, 24–27 June 2019; IEEE: New York, NY, USA, 2019; pp. 1–13. [Google Scholar] [CrossRef]
- Fong, B.; Johnson, M. Lenses and Learners. arXiv 2019, arXiv:1903.03671. [Google Scholar]
- Fong, B. Causal Theories: A Categorical Perspective on Bayesian Networks. arXiv 2013, arXiv:1301.6201. [Google Scholar]
- Spivak, D.I. Functorial aggregation. arXiv 2023, arXiv:2111.10968. [Google Scholar] [CrossRef]
- Ghica, D.R.; Kaye, G.; Sprunger, D. A Fully Compositional Theory of Sequential Digital Circuits: Denotational, Operational and Algebraic Semantics. arXiv 2024, arXiv:2201.10456. [Google Scholar]
- Videla, A.; Capucci, M. Lenses for Composable Servers. arXiv 2022, arXiv:2203.15633. [Google Scholar]
- Gavranović, B. Space-time tradeoffs of lenses and optics via higher category theory. arXiv 2022, arXiv:2209.09351. [Google Scholar]
- Belfiore, J.C.; Bennequin, D. Topos and Stacks of Deep Neural Networks. arXiv 2022, arXiv:2106.14587. [Google Scholar]
- Spivak, D.I. Learners’ languages. Electron. Proc. Theor. Comput. Sci. 2022, 372, 14–28. [Google Scholar] [CrossRef]
- Capucci, M. Diegetic Representation of Feedback in Open Games. Electron. Proc. Theor. Comput. Sci. 2023, 380, 145–158. [Google Scholar] [CrossRef]
- Hedges, J.; Sakamoto, R.R. Reinforcement Learning in Categorical Cybernetics. arXiv 2024, arXiv:2404.02688. [Google Scholar]
- Lanctot, M.; Lockhart, E.; Lespiau, J.B.; Zambaldi, V.; Upadhyay, S.; Pérolat, J.; Srinivasan, S.; Timbers, F.; Tuyls, K.; Omidshafiei, S.; et al. OpenSpiel: A Framework for Reinforcement Learning in Games. arXiv 2020, arXiv:1908.09453. [Google Scholar]
- Kamiya, K.; Welliaveetil, J. A category theory framework for Bayesian learning. arXiv 2021, arXiv:2111.14293. [Google Scholar]
- Gavranović, B.; Lessard, P.; Dudzik, A.J.; Von Glehn, T.; Madeira Araújo, J.A.G.; Veličković, P. Position: Categorical Deep Learning is an Algebraic Theory of All Architectures. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; Salakhutdinov, R., Kolter, Z., Heller, K., Weller, A., Oliver, N., Scarlett, J., Berkenkamp, F., Eds.; Proceedings of Machine Learning Research, Volume 235. PMLR: Cambridge, MA, USA, 2024; pp. 15209–15241. [Google Scholar]
- Vákár, M.; Smeding, T. CHAD: Combinatory Homomorphic Automatic Differentiation. ACM Trans. Program. Lang. Syst. 2022, 44, 1–49. [Google Scholar] [CrossRef]
- Abbott, V. Neural Circuit Diagrams: Robust Diagrams for the Communication, Implementation, and Analysis of Deep Learning Architectures. arXiv 2024, arXiv:2402.05424. [Google Scholar]
- Abbott, V.; Zardini, G. Functor String Diagrams: A Novel Approach to Flexible Diagrams for Applied Category Theory. arXiv 2024, arXiv:2404.00249. [Google Scholar]
- Hauenstein, J.D.; He, Y.H.; Kotsireas, I.; Mehta, D.; Tang, T. Special issue on Algebraic Geometry and Machine Learning. J. Symb. Comput. 2023, 118, 93–94. [Google Scholar] [CrossRef]
- Lawvere, F.W. The Category of Probabilistic Mappings—With Applications to Stochastic Processes, Statistics, and Pattern Recognition. Semin. Handout Notes 1962. Unpublished. [Google Scholar]
- Giry, M. A categorical approach to probability theory. In Categorical Aspects of Topology and Analysis; Banaschewski, B., Ed.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 68–85. [Google Scholar]
- Leinster, T. Codensity and the ultrafilter monad. arXiv 2013, arXiv:1209.3606. [Google Scholar]
- Sturtz, K. Categorical Probability Theory. arXiv 2015, arXiv:1406.6030. [Google Scholar]
- Belle, R.V. Probability Monads as Codensity Monads. Theory Appl. Categ. 2021, 38, 811–842. [Google Scholar]
- Burroni, E. Distributive laws. Applications to stochastic automata. (Lois distributives. Applications aux automates stochastiques.). Theory Appl. Categ. 2009, 22, 199–221. [Google Scholar]
- Culbertson, J.; Sturtz, K. Bayesian machine learning via category theory. arXiv 2013, arXiv:1312.1445. [Google Scholar]
- Culbertson, J.; Sturtz, K. A categorical foundation for Bayesian probability. Appl. Categ. Struct. 2014, 22, 647–662. [Google Scholar] [CrossRef]
- Chentsov, N.N. Categories of mathematical statistics. Uspekhi Mat. Nauk 1965, 20, 194–195. [Google Scholar]
- Giry, M. A categorical approach to probability theory. In Proceedings of the 1982 International Conference on Category Theory, Dundee, Scotland, 29 March–2 April 1982. [Google Scholar]
- Golubtsov, P.V. Axiomatic description of categories of information transformers. Probl. Peredachi Informatsii 1999, 35, 80–98. [Google Scholar]
- Golubtsov, P.V. Monoidal Kleisli category as a background for information transformers theory. Inf. Process. 2002, 2, 62–84. [Google Scholar]
- Kallenberg, O. Random Measures, Theory and Applications; Springer: Cham, Switzerland, 2017; Volume 1. [Google Scholar]
- Fritz, T.; Perrone, P. Bimonoidal Structure of Probability Monads. In Proceedings of the 2018 Symposium on Logic in Computer Science, Oxford, UK, 9–12 July 2018. [Google Scholar]
- Fritz, T. A synthetic approach to Markov kernels, conditional independence and theorems on sufficient statistics. Adv. Math. 2020, 370, 107239. [Google Scholar] [CrossRef]
- Fritz, T.; Rischel, E.F. Infinite Products and Zero-One Laws in Categorical Probability. Compositionality 2020, 2, 13509. [Google Scholar] [CrossRef]
- Fritz, T.; Gonda, T.; Perrone, P.; Fjeldgren Rischel, E. Representable Markov categories and comparison of statistical experiments in categorical probability. Theor. Comput. Sci. 2023, 961, 113896. [Google Scholar] [CrossRef]
- Fritz, T.; Gadducci, F.; Perrone, P.; Trotta, D. Weakly Markov Categories and Weakly Affine Monads. arXiv 2023, arXiv:2303.14049. [Google Scholar]
- Sabok, M.; Staton, S.; Stein, D.; Wolman, M. Probabilistic programming semantics for name generation. Proc. ACM Program. Lang. 2021, 5, 1–29. [Google Scholar] [CrossRef]
- Moggi, E. Computational Lambda-Calculus and Monads; Laboratory for Foundations of Computer Science, Department of Computer Science, University of Edinburgh: Edinburgh, UK, 1988. [Google Scholar]
- Sennesh, E.; Xu, T.; Maruyama, Y. Computing with Categories in Machine Learning. arXiv 2023, arXiv:2303.04156. [Google Scholar]
- Ambrogioni, L.; Lin, K.; Fertig, E.; Vikram, S.; Hinne, M.; Moore, D.; van Gerven, M. Automatic structured variational inference. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual, 13–15 April 2021; pp. 676–684. [Google Scholar]
- Meulen, F.; Schauer, M. Automatic Backward Filtering Forward Guiding for Markov processes and graphical models. arXiv 2020, arXiv:2010.03509. [Google Scholar]
- Braithwaite, D.; Hedges, J. Dependent Bayesian Lenses: Categories of Bidirectional Markov Kernels with Canonical Bayesian Inversion. arXiv 2022, arXiv:2209.14728. [Google Scholar]
- Heunen, C.; Kammar, O.; Staton, S.; Yang, H. A convenient category for higher-order probability theory. In Proceedings of the IEEE 2017 32nd Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), Reykjavik, Iceland, 20–23 June 2017; pp. 1–12. [Google Scholar]
- Kallenberg, O. Foundations of Modern Probability, 2nd ed.; Probability and Its Applications; Springer: New York, NY, USA, 2002. [Google Scholar]
- Villani, C. Optimal Transport: Old and New. In Grundlehren der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 2009; Volume 338. [Google Scholar]
- Lane, S.M. Categories for the Working Mathematician, 2nd ed.; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1998; Volume 5. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Etingof, P.; Gelaki, S.; Nikshych, D.; Ostrik, V. Tensor Categories; Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2015; Volume 205. [Google Scholar]
- Schreiber, U.; Leinster, T.; Baez, J. The n-Category Café, September 2006. Available online: https://golem.ph.utexas.edu/category/2006/09/index.shtml (accessed on 23 August 2024).
- Corfield, D.; Schölkopf, B.; Vapnik, V. Falsificationism and statistical learning theory: Comparing the Popper and Vapnik-Chervonenkis dimensions. J. Gen. Philos. Sci. 2009, 40, 51–58. [Google Scholar] [CrossRef]
- Bradley, T.D.; Terilla, J.; Vlassopoulos, Y. An enriched category theory of language: From syntax to semantics. La Mat. 2022, 1, 551–580. [Google Scholar] [CrossRef]
- Fabregat-Hernández, A.; Palanca, J.; Botti, V. Exploring explainable AI: Category theory insights into machine learning algorithms. Mach. Learn. Sci. Technol. 2023, 4, 045061. [Google Scholar] [CrossRef]
- Alejandro Aguirre, G.B.L.B.; Bizjak, A.; Gaboardi, M.; Garg, D. Relational Reasoning for Markov Chains in a Probabilistic Guarded Lambda Calculus. In Proceedings of the European Symposium on Programming, Thessaloniki, Greece, 16–19 April 2018. [Google Scholar]
- Schauer, M.; Meulen, F. Compositionality in algorithms for smoothing. In Proceedings of the 2023 International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Fritz, T.; Klingler, A. The d-separation criterion in Categorical Probability. J. Mach. Learn. Res. 2022, 24, 1–49. [Google Scholar]
- Perrone, P. Markov Categories and Entropy. IEEE Trans. Inf. Theory 2024, 70, 1671–1692. [Google Scholar] [CrossRef]
- Mahadevan, S. Categoroids: Universal Conditional Independence. arXiv 2022, arXiv:2208.11077. [Google Scholar]
- Yang, B.; Marisa, Z.Z.K.; Shi, K. Monadic Deep Learning. arXiv 2023, arXiv:2307.12187. [Google Scholar]
- Shiebler, D. Functorial Clustering via Simplicial Complexes. In Proceedings of the NeurIPS 2020 Workshop on Topological Data Analysis and Beyond, Online, 11 December 2020. [Google Scholar]
- Shiebler, D. Functorial Manifold Learning. Electron. Proc. Theor. Comput. Sci. 2022, 372, 1–13. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Persistent homology-a survey. Contemp. Math. 2008, 453, 257–282. [Google Scholar]
- Pun, C.S.; Xia, K.; Lee, S.X. Persistent-Homology-based Machine Learning and its Applications—A Survey. arXiv 2018, arXiv:1811.00252. [Google Scholar] [CrossRef]
- Shiebler, D. Compositionality and Functorial Invariants in Machine Learning. Ph.D. Thesis, University of Oxford, Oxford, UK, 2023. [Google Scholar]
- Kelly, G.M. Basic Concepts of Enriched Category Theory; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1982; Volume 64. [Google Scholar]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Edelsbrunner, H.; Harer, J.L. Computational Topology: An Introduction; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Carlsson, G.E.; Mémoli, F. Classifying Clustering Schemes. Found. Comput. Math. 2010, 13, 221–252. [Google Scholar] [CrossRef]
- Spivak, D.I. Metric Realization of Fuzzy Simplicial Sets; Online Resource; Self-Published Notes. Available online: https://dspivak.net/metric_realization090922.pdf (accessed on 23 August 2024).
- McInnes, L. Topological methods for unsupervised learning. In Proceedings of the Geometric Science of Information: 4th International Conference, GSI 2019, Toulouse, France, 27–29 August 2019; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2019; pp. 343–350. [Google Scholar]
- Chazal, F.; Cohen-Steiner, D.; Glisse, M.; Guibas, L.J.; Oudot, S.Y. Proximity of persistence modules and their diagrams. In Proceedings of the Twenty-Fifth Annual Symposium on Computational Geometry, Aarhus, Denmark, 8–10 June 2009; pp. 237–246. [Google Scholar]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Morozov, D. Persistent Homology: Theory and Practice; Technical Report; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2012. [Google Scholar]
- Huber, S. Persistent homology in data science. In Proceedings of the Data Science—Analytics and Applications: 3rd International Data Science Conference–iDSC2020, Vienna, Austria, 13 May 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 81–88. [Google Scholar]
- Dłotko, P.; Wagner, H. Computing homology and persistent homology using iterated Morse decomposition. arXiv 2012, arXiv:1210.1429. [Google Scholar]
- Gameiro, M.; Hiraoka, Y.; Obayashi, I. Continuation of point clouds via persistence diagrams. Phys. D Nonlinear Phenom. 2016, 334, 118–132. [Google Scholar] [CrossRef]
- Leygonie, J. Differential and fiber of persistent homology. Ph.D. Thesis, University of Oxford, Oxford, UK, 2022. [Google Scholar]
- Leygonie, J.; Oudot, S.; Tillmann, U. A Framework for Differential Calculus on Persistence Barcodes. Found. Comput. Math. 2019, 22, 1069–1131. [Google Scholar] [CrossRef]
- Yim, K.M.; Leygonie, J. Optimization of Spectral Wavelets for Persistence-Based Graph Classification. Front. Appl. Math. Stat. 2021, 7, 651467. [Google Scholar] [CrossRef]
- Leygonie, J.; Tillmann, U. The fiber of persistent homology for simplicial complexes. J. Pure Appl. Algebra 2021, 226, 107099. [Google Scholar] [CrossRef]
- Leygonie, J.; Henselman-Petrusek, G. Algorithmic reconstruction of the fiber of persistent homology on cell complexes. J. Appl. Comput. Topol. 2024, 226, 2015–2049. [Google Scholar] [CrossRef]
- Jardine, J.F. Data and homotopy types. arXiv 2019, arXiv:1908.06323. [Google Scholar]
- Jardine, J.F. Persistent homotopy theory. arXiv 2020, arXiv:2002.10013. [Google Scholar]
- Jardine, J.F. Directed Persistence. 2020. Available online: https://www.math.uwo.ca/faculty/jardine/preprints/fund-cat03.pdf (accessed on 23 August 2024).
- Ballester, R.; Casacuberta, C.; Escalera, S. Topological Data Analysis for Neural Network Analysis: A Comprehensive Survey. arXiv 2024, arXiv:2312.05840. [Google Scholar]
- Turkevs, R.; Montúfar, G.; Otter, N. On the effectiveness of persistent homology. Adv. Neural Inf. Process. Syst. 2022, 35, 35432–35448. [Google Scholar]
- Zhao, Q.; Ye, Z.; Chen, C.; Wang, Y. Persistence Enhanced Graph Neural Network. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020. [Google Scholar]
- Solomon, E.; Wagner, A.; Bendich, P. From Geometry to Topology: Inverse Theorems for Distributed Persistence. In Proceedings of the 38th International Symposium on Computational Geometry (SoCG 2022), Berlin, Germany, 7–10 June 2022; Leibniz International Proceedings in Informatics (LIPIcs). Goaoc, X., Kerber, M., Eds.; Dagstuhl: Berlin, Germany, 2022; Volume 224, pp. 61:1–61:16. [Google Scholar]
- Zhou, L. Beyond Persistent Homology: More Discriminative Persistent Invariants. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2023. [Google Scholar]
- Belchí, F.; Murillo, A. A∞-persistence. Appl. Algebra Eng. Commun. Comput. 2014, 26, 121–139. [Google Scholar] [CrossRef][Green Version]
- Herscovich, E. A higher homotopic extension of persistent (co)homology. J. Homotopy Relat. Struct. 2014, 13, 599–633. [Google Scholar] [CrossRef]
- Guss, W.H.; Salakhutdinov, R. On Characterizing the Capacity of Neural Networks using Algebraic Topology. arXiv 2018, arXiv:1802.04443. [Google Scholar]
- Petri, G.; Leitão, A. On the topological expressive power of neural networks. In Proceedings of the Topological Data Analysis and Beyond Workshop at the 34th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Walton, S. Isomorphism, Normalizing Flows, and Density Estimation: Preserving Relationships Between Data; Technical Report; University of Oregon, Computer and Information Sciences Department. 2023. Available online: https://www.cs.uoregon.edu/Reports/AREA-202307-Walton.pdf (accessed on 4 July 2024).
- Mahadevan, S. Unifying causal inference and reinforcement learning using higher-order category theory. arXiv 2022, arXiv:2209.06262. [Google Scholar]
- Shiebler, D. Kan Extensions in Data Science and Machine Learning. arXiv 2022, arXiv:2203.09018. [Google Scholar]
- Mahadevan, S. GAIA: Categorical Foundations of Generative AI. arXiv 2024, arXiv:2402.18732. [Google Scholar]
- Mahadevan, S. Empowering Manufacturing: Generative AI Revolutionizes ERP Application. Int. J. Innov. Sci. Res. 2024, 9, 593–595. [Google Scholar] [CrossRef]
- Sridhar, M. Universal Causality. Entropy 2023, 25, 574. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, S. Causal Homotopy. arXiv 2021, arXiv:2112.01847. [Google Scholar]
- Morales-Álvarez, P.; Sánchez, M. A note on the causal homotopy classes of a globally hyperbolic spacetime. Class. Quantum Gravity 2015, 32, 197001. [Google Scholar] [CrossRef]
- Lafforgue, L. Some Possible Roles for AI of Grothendieck Topos Theory; Technical Report. 2022. Available online: https://www.laurentlafforgue.org/Expose_Lafforgue_topos_AI_ETH_sept_2022.pdf (accessed on 23 August 2024).
- Caramello, O. Grothendieck Toposes as Unifying ‘Bridges’: A Mathematical Morphogenesis. In Objects, Structures, and Logics: FilMat Studies in the Philosophy of Mathematics; Springer International Publishing: Cham, Switzerland, 2022; pp. 233–255. [Google Scholar]
- Villani, M.J.; McBurney, P. The Topos of Transformer Networks. arXiv 2024, arXiv:2403.18415. [Google Scholar]
- Asher, N. Lexical Meaning in Context: A Web of Words; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Márta Abrusán, N.A.; de Cruys, T.V. Content vs. function words: The view from distributional semantics. Zas Pap. Linguist. 2018, 60, 1–21. [Google Scholar] [CrossRef]
- Yasuo Kawahara, H.F.; Mori, M. Categorical representation theorems of fuzzy relations. Inf. Sci. 1999, 119, 235–251. [Google Scholar] [CrossRef]
- Hyland, J.M.E.; Pitts, A.M. The theory of constructions: Categorical semantics and topos-theoretic models. Contemp. Math. 1989, 92, 137–199. [Google Scholar]
- Katsumata, S.Y.; Rival, X.; Dubut, J. A categorical framework for program semantics and semantic abstraction. Electron. Notes Theor. Inform. Comput. 2023, 3, 11-1–11-18. [Google Scholar] [CrossRef]
- Babonnaud, W. A topos-based approach to building language ontologies. In Proceedings of the Formal Grammar: 24th International Conference, FG 2019, Riga, Latvia, 11 August 2019; Proceedings 24. Springer: Berlin/Heidelberg, Germany, 2019; pp. 18–34. [Google Scholar]
- Saba, W.S. Logical Semantics and Commonsense Knowledge: Where Did we Go Wrong, and How to Go Forward, Again. arXiv 2018, arXiv:1808.01741. [Google Scholar]
- Tasić, M. On the knowability of the world: From intuition to turing machines and topos theory. Biocosmol.-Neo-Aristot. 2014, 4, 87–114. [Google Scholar]
- Awodey, S.; Kishida, K. Topological Semantics for First-Order Modal Logic; Online Resource. 2006. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=17cc1aa99e748fddc31320de1409efa78991b913 (accessed on 12 August 2024).
- Wilkins, I. Topos of Noise. Angelaki 2023, 28, 144–162. [Google Scholar] [CrossRef]
- Lafforgue, L. Some Sketches for a Topos-Theoretic AI; Technical Report. 2024. Available online: https://bm2l.github.io/projects/lafforgue/ (accessed on 5 August 2024).
- Bennequin, D.; Belfiore, J.C. Mathematics for AI: Categories, Toposes, Types. In Mathematics for Future Computing and Communications; Cambridge University Press: Cambridge, UK, 2021; pp. 98–132. [Google Scholar]
- Caramello, O.; Lafforgue, L. Ontologies, knowledge representations and Grothendieck toposes. In Proceedings of the Invited Talk to Semantics Workshop, Lagrange Center, Huawei, Paris, France, 3–4 February 2022. [Google Scholar]
- Hmamouche, Y.; Benjillali, M.; Saoudi, S.; Yanikomeroglu, H.; Renzo, M.D. New Trends in Stochastic Geometry for Wireless Networks: A Tutorial and Survey. Proc. IEEE 2021, 109, 1200–1252. [Google Scholar] [CrossRef]
- Belfiore, J.C.; Bennequin, D.; Giraud, X. Logical Information Cells I. arXiv 2021, arXiv:2108.04751. [Google Scholar]
- Bloomfield, C.; Maruyama, Y. Fibered universal algebra for first-order logics. J. Pure Appl. Algebra 2024, 228, 107415. [Google Scholar] [CrossRef]
- Caramello, O. Fibred sites and existential toposes. arXiv 2022, arXiv:2212.11693. [Google Scholar]
- Choi, J.; Loke, S.W.; Park, J. A Unified Approach to Semantic Information and Communication Based on Probabilistic Logic. IEEE Access 2022, 10, 129806–129822. [Google Scholar] [CrossRef]
- Chaccour, C.; Saad, W.; Debbah, M.; Han, Z.; Poor, H.V. Less Data, More Knowledge: Building Next Generation Semantic Communication Networks. IEEE Commun. Surv. Tutorials 2024, 27, 37–76. [Google Scholar] [CrossRef]
- Sergeant-Perthuis, G. Compositional statistical mechanics, entropy and variational inference. In Proceedings of the Twelfth Symposium on Compositional Structures (SYCO 12), Birmingham, UK, 15–16 April 2024. [Google Scholar]
- Youvan, D. Modeling Frustrated Systems within the Topos of Artificial Intelligence: Achieving Coherent Outputs through Categorical and Logical Structures; Online Resource. 2023. Available online: https://www.researchgate.net/publication/381656591_Modeling_Frustrated_Systems_within_the_Topos_of_Artificial_Intelligence_Achieving_Coherent_Outputs_through_Categorical_and_Logical_Structures?channel=doi&linkId=667962688408575b8384bdb4&showFulltext=true (accessed on 6 August 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).