The Sombor Index (Coindex) and Lanzhou Index (Coindex) of Some Graphs

Abstract

In this paper, motivated by the recently introduced topological indices—the Sombor index, Sombor coindex, and Lanzhou index, we define a new index—the Lanzhou coindex of a graph. Furthermore, we investigate the Sombor index (coindex) and the Lanzhou index (coindex) of tadpole graphs, wheel graphs, and two-dimensional grid graphs, as well as their paraline graphs.

1. Introduction

Throughout the paper we consider simple, finite, and connected graphs. Let G be a graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$ where $\left|V\right(G\left)\right|=n$. The degree of a vertex u is the number of its neighbors in the graph G that is denoted by $d\left(v\right)$ for short. The complement of a graph G is the graph $\overline{G}$ with vertex set $V\left(\overline{G}\right)=V\left(G\right)$ where two vertices of G are adjacent if and only if they are not adjacent in G. We denote the path graph, cycle graph, and complete graph with n vertices by $P_n$, $C_n$ and $K_n$, respectively.

Topological indices serve as valuable tools in the study of molecular graphs, offering a quantitative approach to analyze and characterize their structures and properties. In 1970 [1], the first Zagreb index was defined by

$$M_1\left(G\right)=\sum _{uv\in E\left(G\right)}[d\left(u\right)+d\left(v\right)].$$

There is significant interest in the subdivision of graphs related to Zagreb indices [2]. By recognizing the contribution of both adjacent and non-adjacent vertex pairs, we can achieve a more comprehensive understanding of graph properties when calculating the Zagreb coindex for subdivision graphs [3,4]. In [5], Došlić defined the first Zagreb coindex as

$${\overline{M}}_1\left(G\right)=\sum _{uv\notin E\left(G\right)}[d\left(u\right)+d\left(v\right)].$$

The forgotten index was defined to enhance the applicability of the first Zagreb index, offering a new perspective and improving the understanding of molecular properties in physico-chemical contexts [6]

$$F\left(G\right)=\sum _{uv\in E\left(G\right)}[d^2\left(u\right)+d^2\left(v\right)].$$

The recently introduced Sombor index and Lanzhou index have captured the attention of researchers in mathematical chemistry. Their properties have been thoroughly investigated, highlighting their potential as valuable tools for analyzing and understanding molecular structures and properties. The Sombor index [7] and Lanzhou index [8] are defined by

$$SO\left(G\right)=\sum _{uv\in E\left(G\right)}\sqrt{d^2\left(u\right)+d^2\left(v\right)}$$

and

$$Lz\left(G\right)=(n-1)M_1\left(G\right)-F\left(G\right)=\sum _{u\in V\left(G\right)}{d}^2\left(u\right)[(n-1)-d\left(u\right)]=\sum _{u\in V\left(G\right)}{d}^2\left(u\right)\overline{d\left(u\right)},$$

respectively. Here, $M_1\left(G\right)$ is the first Zagreb index, $F\left(G\right)$ is the forgotten index, and $\overline{d\left(u\right)}$ represents the degree of vertex u in the complement of G.

In what follows, we need another expression for the Lanzhou index, namely,

$$Lz\left(G\right)=\sum _{uv\in E\left(G\right)}[(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))].$$

In 2021 [7,9], Gutman characterized the minimal and maximal Sombor index with simple graphs, connected simple graphs, and trees. In [10], Cruz et al. determined the extremal graph of the Sombor index for chemical graphs and trees, and also for hexagonal systems. Moreover, extremal values of the Sombor index for both unicyclic and bicyclic graphs were investigated in [11]. Fang et al. studied the extremal graph of the Sombor index for graphs with fixed clique number, fixed chromatic number, and fixed number of pendant vertices in [12]. Almire et al. [13] studied the Sombor index of some chemical graphs.

To demonstrate the application of the Sombor index, we provide concrete examples below. For more details, we refer the reader to [7].

Example 1

([7]). (i) $SO\left(K_n\right)={\displaystyle \frac{n{(n-1)}^2}{\sqrt{2}}}$.

(ii) $SO\left(C_n\right)=2\sqrt{2}n$.

(iii) For $n\ge 3$, $SO\left(P_n\right)=2\sqrt{2}(n-3)+2\sqrt{5}$.

At present, there are some research results on the Lanzhou index. In [8], Vukicevic et al. determined extremal graphs, trees, and restricted trees. In [14], the lower bound for the Lanzhou index of trees was determined based on their order, as well as their maximum and second maximum degrees, and extremal trees were also characterized. In [15], the unicyclic chemical graphs with the maximum and minimum Lanzhou indices were determined. In [16], several known classes of hexagonal systems were studied and the Lanzhou index of trees with some given diameters were obtained. Moreover, Cartesian product graphs and Nordhaus Gaddum-type results of this index were obtained.

We present some examples of the Lanzhou index. For more details, we refer the reader to [8].

Example 2

([8]). (i) $Lz\left(K_n\right)=0$.

(ii) $Lz\left(C_n\right)=4n(n-3)$.

(iii) For $n\ge 3$, $Lz\left(P_n\right)=2(n-2)(2n-5)$.

Motivated by the Sombor index, in [17], the Sombor coindex of a graph G was defined as

$$\overline{SO}\left(G\right)=\sum _{uv\notin E\left(G\right)}\sqrt{d^2\left(u\right)+d^2\left(v\right)}=\sum _{uv\in E\left(\overline{G}\right)}\sqrt{d^2\left(u\right)+d^2\left(v\right).}$$

The Sombor coindex is defined by considering analogous contributions from the pairs of non-adjacent vertices, thereby capturing and quantifying the potential impact of distant vertex pairs within the graph. It should be noted that the defining sums run over $E\left(\overline{G}\right)$ in the definition the of Sombor coindex of G, but the degrees of the vertices are with respect to G [17]. Therefore, it is not equal to the Sombor index of $\overline{G}$. In [17], the authors gave some properties of the Sombor coindex and its associations with the Zagreb indices, the Sombor index, the forgotten coindex, and various other crucial graph parameters. Additionally, they determined the bounds of the Sombor coindex for certain graph operations and calculated the Sombor coindex for specific chemical graphs as a practical application.

Example 3

([17]). (i) $\overline{SO}\left(K_n\right)=0$.

(ii) $\overline{SO}\left(C_n\right)=\sqrt{2}n(n-3)$.

(iii) For $n\ge 3$, $\overline{SO}\left(P_n\right)=\sqrt{2}[(n-4)(n-3)+1]+2\sqrt{5}(n-3)$.

The Sombor coindex, with its distinctive definition method, offers us invaluable inspiration for defining the Lanzhou coindex. We define the Lanzhou coindex of a graph G as

$$\begin{array}{cc}\hfill \overline{Lz}\left(G\right)& =\sum _{uv\notin E\left(G\right)}[(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]\hfill \\ \hfill & =\sum _{uv\in E\left(\overline{G}\right)}[(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))].\hfill \end{array}$$

Accordingly, the defining sums run over $E\left(\overline{G}\right)$ in the definition of the Lanzhou coindex of G, but the degrees of the vertices are with respect to G. Therefore, it is not equal to the Lanzhou index of $\overline{G}$ .

We provide some examples of the Lanzhou coindex.

Example 4.

For graphs $K_n$, $C_n$ and $P_n$, we have

(i) $\overline{Lz}\left(K_n\right)=0$.

(ii) $\overline{Lz}\left(C_n\right)=2n{(n-3)}^2$.

(iii) For $n\ge 3$, $\overline{Lz}\left(P_n\right)=4{(n-2)}^2(n-1)$.

To provide a clearer comparison between the Sombor index (coindex) and Lanzhou index (coindex), we present the following table (Table 1).

Table 1. The values of four indices for graphs $K_n$, $C_n$, and $P_n$.

Class of Graph	Sombor Index	Sombor Coindex	Lanzhou Index	Lanzhou Coindex
$K_n$	${\displaystyle \frac{n{(n-1)}^2}{\sqrt{2}}}$	0	0	0
$C_n$	$2\sqrt{2}n$	$\sqrt{2}n(n-3)$	$4n(n-3)$	$2n{(n-3)}^2$
$P_n(n\ge 3)$	$2\sqrt{2}(n-3)+2\sqrt{5}$	$\sqrt{2}[(n-4)(n-3)+1]+2\sqrt{5}(n-3)$	$2(n-2)(2n-5)$	$4{(n-2)}^2(n-1)$

Motivated by results on the topological index that was recently introduced, we consider the Sombor index (coindex) and Lanzhou index (coindex) of graphs in this paper. To state our results, we give some definitions of graphs.

Let $S\left(G\right)$ denote the subdivision graph of G in which each edge of G is replaced by a path $P_2$.

Let $L\left(G\right)$ denote the line graph of G whose vertex set is the edge set of G, and two vertices of $L\left(G\right)$ are adjacent if and only if the corresponding edges in G are adjacent.

Let $PL\left(G\right)$ denote the paraline graph of graph G that is a line graph of the subdivision graph $S\left(G\right)$.

Let $T_{n,k}$ denote a tadpole graph which consists of a cycle of order n and a path of length k attached to one vertex of the cycle $C_n$; see Figure 1.

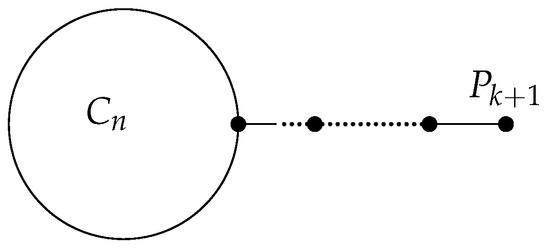
Figure 1. The graph $T_{n,k}$.

Let $W_{n+1}$ denote the wheel graph of order $n+1$ where each vertex in cycle $C_n$ is connected to one other vertex, for example, $W_7$, depicted in Figure 2.

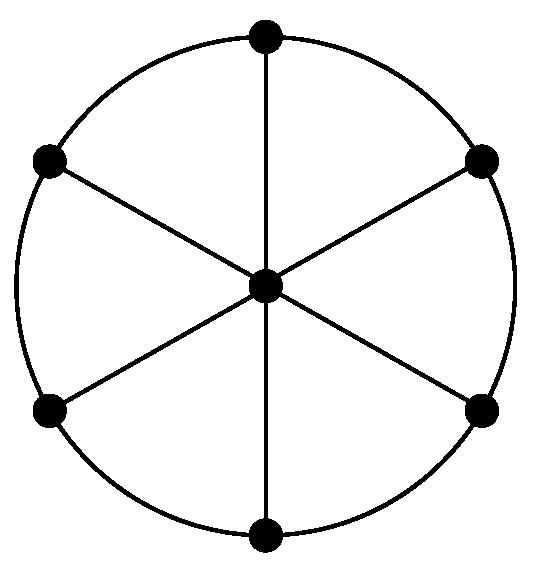
Figure 2. The graph $W_7$.

The Cartesian product $G_1\square G_2$ of graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ is a simple graph where $V(G_1\square G_2)=V_1\times V_2$, $E(G_1\square G_2)=\{(x_1,y_1)(x_2,y_2):x_1=y_1$ and $x_2{y}_2\in E\left(G_2\right)$ or $x_2=y_2$ and $x_1{y}_1\in E\left(G_1\right)\}$.

Let $G_{n,m}$ denote the two-dimensional grid graph that is a Cartesian product of $P_n$ and $P_m$. The “grid graph” is a specific grid-like structure in graph theory, such as a two-dimensional grid graph $G_{n,m}$ with n rows and m columns, for example, the grid graph $G_{4,6}$ depicted in Figure 3. It is easy to obtain from the properties of the Cartesian product of the graph that $\left|V\right(G_{n,m}\left)\right|=mn$ and $|E\left(G_{n,m}\right)|=m(n-1)+n(m-1)=2mn-n-m$.

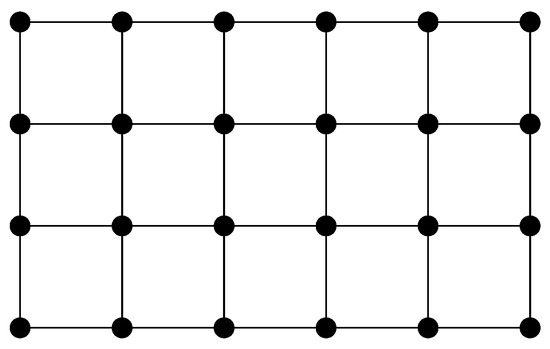
Figure 3. The graph $G_{4,6}$.

Almire et al. determined the Sombor index of $T_{n,k}$, $W_{n+1}$, and $G_{n,m}$ as follows:

Theorem 1

([13]). (i) $SO\left(T_{n,k}\right)=2\sqrt{2}(n+k-4)+3\sqrt{13}+\sqrt{5}$.

(ii) $SO\left(W_{n+1}\right)=3\sqrt{2}n+n\sqrt{9+n^2}(n\ge 3)$.

(iii) $SO\left(G_{n,m}\right)=2\sqrt{2}(4mn-7n-7m+6)+10(m+n-4)+8\sqrt{13}(m,n\ge 3)$.

In this paper, we determine the Sombor coindex and Lanzhou index (coindex) of graphs $T_{n,k}$, $W_{n+1}$, and $G_{n,m}$, and investigate the Sombor index (coindex) and Lanzhou index (coindex) of their paraline graphs. For more notations, one may refer to [18].

2. Results for the Lanzhou Index and Sombor Index

We study the Lanzhou index of graphs $T_{n,k}$, $W_{n+1}$ and $G_{n,m}$, and the Sombor index and Lanzhou index of their paraline graphs in this section. Moreover, we give results concerning the relationship between the Lanzhou index of a graph G and its subdivision graph, as well as between the subdivision graph of a graph G and its paraline graph.

Theorem 2.

Let $T_{n,k}$, $W_{n+1}$, and $G_{n,m}$ be a tadpole graph, a wheel graph and a two-dimensional grid graph. Then,

(i) $Lz\left(T_{n,k}\right)=2(2n^2-5n-7)+k(8n-11)+4k^2+k$.

(ii) $Lz\left(W_{n+1}\right)=9n(n-3)$.

(iii) $Lz\left(G_{n,m}\right)=16m^2{n}^2-72mn-14m^{2}n-14m{n}^2+88m+88n-80$.

Proof. 

In graph $T_{n,k}$, $(n-1)+(k-1)$ vertices have a degree of 2, one vertex has a degree of 1, and one vertex has a degree of 3. By calculation, we have $Lz\left(T_{n,k}\right)=2(2n^2-5n-7)+k(8n-11)+4k^2+k$.

In graph $W_{n+1}$, there are n vertices with a degree of 3 and one vertex with a degree of n. By calculation, we have $Lz\left(W_{n+1}\right)=9n(n-3)$.

Clearly, $\left|V\right(G_{n,m}\left)\right|=mn$; $G_{n,m}$ consists of 2-degree, 3-degree, and 4-degree vertices. The degree of four corner vertices is 2, which contribute to the Lanzhou index of grid graph being $4\times 2^2(mn-3)$. There are $2(m-2)+2(n-2)$ vertices with a degree of 3, which contribute to the Lanzhou index of grid graph being $[2(m-2)+2(n-2)]\times 3^2(mn-4)$. The remaining 4-degree vertices contribute to $(mn-2m-2n+4)\times 4^2(mn-5)$. Therefore, by calculation, we have $Lz\left(G_{n,m}\right)=16m^2{n}^2-72mn-14m^{2}n-14m{n}^2+88m+88n-80$. □

Theorem 3.

Let $PL\left(T_{n,k}\right)$ be a paraline graph of a tadpole graph. Then,

(i) $Lz\left(PL\left(T_{n,k}\right)\right)=8n^2+8kn-24k-12n-62$.

(ii) $SO\left(PL\left(T_{n,k}\right)\right)=4\sqrt{2}(k+n)+3\sqrt{13}-3\sqrt{2}+\sqrt{5}$.

Proof. 

Clearly, $|E\left(S\left(T_{n,k}\right)\right)|=2(n+k)$, and therefore $|V\left(PL\left(T_{n,k}\right)\right)|=2(n+k)$. Among these vertices, $2n+2k-4$ vertices have a degree of 2, three vertices have a degree of 3, and one vertex has a degree of 1. Therefore, by calculation we have

$$Lz\left(PL\left(T_{n,k}\right)\right)=8n^2+8kn-24k-12n-62.$$

There is a path of length $2k-1$ in the paraline graph $PL\left(T_{n,k}\right)$. Let $u_1$ be a vertex of degree 3 that is adjacent to this path. So, the value $\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}$ of this path is $4\sqrt{2}k-6\sqrt{2}+\sqrt{5}+\sqrt{13}$.

Let $u_2$ and $u_3$ be the neighbors of $u_1$ where $d\left(u_2\right)=d\left(u_3\right)=3$. The vertices $u_2$ and $u_3$ are adjacent to two 3-degree vertices and one 2-degree vertex. The vertex $u_1$ has two 3-degree neighbors and one 2-degree neighbor in the path. So, the value $\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}$ of the vertices $u_1$, $u_2$, and $u_3$ in $L[S\left(C_n\right)+e]$ is $9\sqrt{2}+2\sqrt{13}$.

The remaining $2n-3$ vertices are adjacent to 2-degree vertices and one 3-degree vertex. So, the value $\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}$ of these $2n-3$ vertices is $2\sqrt{2}(2n-3)$. Hence, summing up all the numbers, the Sombor index of the paraline graph of the tadpole graph is

$$SO\left(PL\left(T_{n,k}\right)\right)=4\sqrt{2}(k+n)+3\sqrt{13}-3\sqrt{2}+\sqrt{5}.$$

□

Theorem 4.

Let $PL\left(W_{n+1}\right)$ be a paraline graph of a wheel graph. Then,

(i) $Lz\left(PL\left(W_{n+1}\right)\right)=3n^4-n^3+108n^2-108n$.

(ii)$SO\left(PL\left(W_{n+1}\right)\right)=n[{\displaystyle \frac{\sqrt{2}}{2}}n(n-1)+\sqrt{n^2+9}+12\sqrt{2}]$.

Proof. 

The paraline graph $PL\left(W_{n+1}\right)$ has $4n$ vertices, among which $3n$ vertices have a degree of 3 and the other n vertices have a degree of n. So, $Lz\left(PL\left(W_{n+1}\right)\right)=3n^4-n^3+108n^2-108n$.

The paraline graph $PL\left(W_{n+1}\right)$ has ${\displaystyle \frac{n^2+9n}{2}}$ edges. Among these, there are $4n$ edges are connected to two vertices of a degree of 3, n edges are incident with a vertex of a degree of 3 and a vertex of a degree of n, and ${\displaystyle \frac{n(n-1)}{2}}$ edges are connected to two vertices of a degree of n. Thus,

$$\begin{array}{cc}\hfill SO\left(PL\left(W_{n+1}\right)\right)& =4n\sqrt{3^2+3^2}+n\sqrt{n^2+9}+{\displaystyle \frac{n(n-1)}{2}}\sqrt{n^2+n^2}\hfill \\ \hfill & =n[{\displaystyle \frac{\sqrt{2}}{2}}n(n-1)+\sqrt{n^2+9}+12\sqrt{2}].\hfill \end{array}$$

□

In the two-dimensional grid graph, each vertex has a degree of at most 4, the corner vertices have a degree of 2, the degree of the center vertex is 4, and the remaining vertices have a degree of 3. After determining the degree of each vertex in the graph and in its complement graph, the Sombor index and Lanzhou index can be calculated by the formula. However, the specific calculation process is relatively complex and requires a careful analysis of the structure of the two-dimensional grid graph and its paraline graph; see Figure 4.

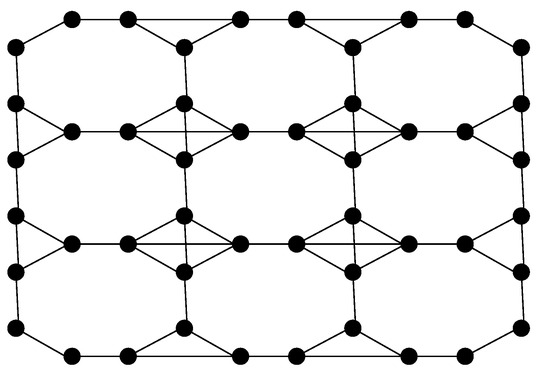
Figure 4. The graph $PL\left(G_{4,4}\right)$.

Theorem 5.

Let $PL\left(G_{n,m}\right)$ be a paraline graph of a two-dimensional grid graph. Then,

$$\begin{array}{cc}\hfill \left(i\right)Lz\left(PL\left(G_{n,m}\right)\right)& =256m^2{n}^2-424m^{2}n+148m^2-424m{n}^2+264mn+280m+148n^2\hfill \\ \hfill & +280n-512.\hfill \\ \hfill \left(ii\right)SO\left(PL\left(G_{n,m}\right)\right)& =32\sqrt{2}mn+40mn-44\sqrt{2}m-35m-44\sqrt{2}n-35n+18\sqrt{13}\hfill \\ \hfill & +44\sqrt{2}+20.\hfill \end{array}$$

Proof. 

Since the graph $G_{n,m}$ has $nm$ vertices and $n(m-1)+m(n-1)$ edges, its subdivision graph has $2\left[n\right(m-1)+m(n-1\left)\right]$ edges. Furthermore, the paraline graph of $G_{n,m}$ has $2\left[n\right(m-1)+m(n-1\left)\right]=4mn-2n-2m$ vertices. Among them, there are eight 2-degree vertices, $6(n-2)+6(m-2)$ vertices have a degree of 3, and the remaining $4mn-8m-8n+16$ vertices have a degree of 4. Therefore, we have

$$\begin{array}{cc}\hfill Lz\left(PL\left(G_{n,m}\right)\right)& =8\times 2^2(4mn-2n-2m-3)+3^2\times (6n+6m-24)(4mn-2n-2m-4)\hfill \\ \hfill & +4^2\times (4mn-8n-8m+16)(4mn-2n-2m-5)\hfill \\ \hfill & =256m^2{n}^2-424m^{2}n+148m^2-424m{n}^2+264mn+280m\hfill \\ \hfill & +148n^2+280n-512.\hfill \end{array}$$

From the above analysis, we can obtain that $\left|E\right(PL\left(G_{n,m}\right)\left)\right|=8mn-7n-7m+4$. In these edges, there are four edges incident with two 2-degree vertices, and eight edges incident with a 2-degree vertex and a 3-degree vertex. There are $8n+8m-36$ edges connecting two 3-degree vertices, $8mn-17n-17m+36$ edges connecting two 4-degree vertices, and the remaining $2n+2m-8$ edges connect a 3-degree vertex and a 4-degree vertex. Hence, we have

$$\begin{array}{cc}\hfill SO\left(PL\left(G_{n,m}\right)\right)& =\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}=4\sqrt{2^2+2^2}+8\sqrt{2^2+3^2}+(8n+8m-36)\sqrt{3^2+3^2}\hfill \\ \hfill & +\sqrt{4^2+4^2}(8mn-17n-17m+36)+\sqrt{3^2+4^2}(2n+2m-8)\hfill \\ \hfill & =32\sqrt{2}mn+40mn-44\sqrt{2}m-35m-44\sqrt{2}n-35n+18\sqrt{13}+44\sqrt{2}+20.\hfill \end{array}$$

□

By observing, we find the relationships between Lanzhou index of a graph G and its subdivision graph, as well as the subdivision graph of a graph G and its paraline graph, as follows.

Proposition 1.

Let S be the subdivision graph of graph G. Then,

$$Lz\left(S\right)=Lz\left(G\right)+4\sum _{uv\in E\left(G\right)}(n-3).$$

Proof. 

Let $V\left(S\right)$ be a vertex set of the subdivision graph of graph G. Then, $V\left(S\right)=V\left(G\right)\cup E\left(G\right)$. And $\left|E\right(G\left)\right|$ is the number of additional vertices inserted to each edge of graph G. Then, all additional vertices are of a degree of 2. Therefore,

$$Lz\left(S\right)=\sum _{u\in V\left(G\right)}{d}^2\left(u\right)\overline{d\left(u\right)}+\sum _{uv\in E\left(G\right)}{2}^2(n-3)=Lz\left(G\right)+4\sum _{uv\in E\left(G\right)}(n-3).$$

□

Proposition 2.

Let S be the subdivision graph of graph G, and let $PL$ be the paraline graph of graph S. Then,

$$Lz\left(PL\right)=[(n-1)M_1\left(G\right)-Lz\left(S\right)+4\sum _{uv\in E\left(G\right)}(n-3)]\sum _{u\in V\left(G\right)}\overline{d\left(u\right)}$$

Proof. 

Let $V\left(S\right)$ be a vertex set of the subdivision graph of graph G. Then, $V\left(S\right)=V\left(G\right)\cup E\left(G\right)$. And $\left|E\right(G\left)\right|$ is the number of additional vertices inserted to each edge of graph G. Then, all additional vertices are of a degree of 2. Therefore,

$$Lz\left(S\right)=\sum _{u\in V\left(G\right)}{d}^2\left(u\right)\overline{d\left(u\right)}+\sum _{uv\in E\left(G\right)}{2}^2(n-3)=Lz\left(G\right)+4\sum _{uv\in E\left(G\right)}(n-3).$$

□

3. Results for the Sombor Coindex and Lanzhou Coindex

We calculate the Sombor coindex and Lanzhou coindex of graphs $T_{n,k}$, $W_{n+1}$, and $G_{n,m}$, as well as their paraline graphs, in this section.

Theorem 6.

The Sombor coindex and Lanzhou coindex of graph $T_{n,k}$ are

(i) $\overline{SO}\left(T_{n,k}\right)=\sqrt{2}[k^2+k(2n-7)+(n-7)n+14]+\sqrt{13}(k+n-5)+\sqrt{5}(k+n-5)+\sqrt{10}$.

(ii) $\overline{Lz}\left(T_{n,k}\right)=2k^{2}n-6k^2+4k{n}^2-18kn+16k+2n^3-12n^2+12n+36$.

Proof. 

In the complement of graph $T_{n,k}$, there are 1 edge connecting a 1-degree vertex and a 3-degree vertex, and $n+k-3$ edges connecting a 2-degree vertex and a 3-degree vertex. There are $n+k-3$ edges connecting a 1-degree vertex and a 2-degree vertex, and ${\displaystyle \frac{1}{2}}(k^2+2kn-7k+n^2-7n+14)$ edges connecting two 2-degree vertices. Thus, by the definitions of the Sombor coindex and Lanzhou coindex, we have

$$\begin{array}{cc}\hfill \overline{SO}\left(T_{n,k}\right)& =\sum _{uv\in E\left(\overline{G}\right)}\sqrt{d^2\left(u\right)+d^2\left(v\right)}=\sqrt{1^2+3^2}+(n+k-5)\sqrt{2^2+3^2}\hfill \\ \hfill & +(n+k-3)\sqrt{1^2+2^2}+{\displaystyle \frac{1}{2}}(k^2+2kn-7k+n^2-7n+14)\sqrt{2^2+2^2}\hfill \\ \hfill & =\sqrt{2}[k^2+k(2n-7)+(n-7)n+14]+\sqrt{13}(k+n-5)+\sqrt{5}(k+n-5)+\sqrt{10}.\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \overline{Lz}\left(T_{n,k}\right)& =\sum _{uv\in E\left(\overline{G}\right)}[(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]=[(n-1)(1+3)-(1+9)]\hfill \\ \hfill & +(n+k-5)\left[\right(n-1\left)\right(3+2)-(9+4\left)\right]+(n+k-3)\left[\right(n-1\left)\right(2+1)-(4+1\left)\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}(k^2+2kn-7k+n^2-7n+14)[(n-1)(2+2)-(4+4)]\hfill \\ \hfill & =2k^{2}n-6k^2+4k{n}^2-18kn+16k+2n^3-12n^2+12n+16.\hfill \end{array}$$

□

Theorem 7.

The Sombor coindex and Lanzhou coindex of graph $W_{n+1}$ are

(i) $\overline{SO}\left(W_{n+1}\right)={\displaystyle \frac{3\sqrt{2}n(n-3)}{2}}$.

(ii) $\overline{Lz}\left(W_{n+1}\right)=3n{(n-3)}^2$.

Proof. 

Clearly, $\left|V\right(W_{n+1}\left)\right|=n+1$ and $\left|E\right(W_{n+1}\left)\right|=2n$. Therefore, there are ${\displaystyle \frac{n(n-3)}{2}}$ edges in its complement and each of them is incident with two 3-degree vertices in graph $W_{n+1}$. Thus, by the definition of the Sombor coindex and Lanzhou coindex, we have these results. □

Theorem 8.

The Sombor coindex and Lanzhou coindex of graph $G_{n,m}$ are

$$\begin{array}{cc}\hfill \left(i\right)\overline{SO}\left(G_{n,m}\right)& =2m^2[\sqrt{2}{n}^2+(5-4\sqrt{2})n+7\sqrt{2}-10]\hfill \\ \hfill & +m[(10-8\sqrt{2})n^2+2(-40+17\sqrt{2}+4\sqrt{5})n+8\sqrt{13}-16\sqrt{5}-65\sqrt{2}+110]\hfill \\ \hfill & +(14\sqrt{2}-20)n^2+(110-65\sqrt{2}-16\sqrt{5}+8\sqrt{13})n\hfill \\ \hfill & +4(-30+33\sqrt{2}+8\sqrt{5}-10\sqrt{13}).\hfill \\ \hfill \left(ii\right)\overline{Lz}\left(G_{n,m}\right)& =4m^2{n}^3-22m^2{n}^2+16m^{2}n-2m{n}^3-4m{n}^2+108mn-104m\hfill \\ \hfill & +16n^2-112n+88.\hfill \end{array}$$

Proof. 

Clearly, $\left|V\right(G_{n,m}\left)\right|=mn$ and $\left|E\right(G_{n,m}\left)\right|=2nm-n-m$. Therefore, there are ${\displaystyle \frac{1}{2}}(m^2{n}^2-5mn+2m+2n)$ edges in its complement. In these edges, there are just 6 edges incident with two 2-degree vertices, $8(n+m-5)$ edges incident with a 2-degree vertex and a 3-degree vertex, and $4mn-8m-8n+16$ edges incident with a 2-degree vertex and a 4-degree vertex. There are $2m^2+4mn-19m+2n^2-19n+48$ edges connecting two 3-degree vertices, $2m^{2}n-4m^2+2m{n}^2-16mn+22m-4n^2+22n-24$ edges connecting a 3-degree vertex and a 4-degree vertex, and ${\displaystyle \frac{1}{2}}(m^2{n}^2-4m^{2}n+4m^2-4m{n}^2+11mn-4m+4n^2-4n-12)$ connecting two 4-degree vertices. Hence, we have

$$\begin{array}{cc}\hfill \overline{SO}\left(G_{n,m}\right)& =\sum _{uv\in E\left(\overline{G}\right)}\sqrt{d^2\left(u\right)+d^2\left(v\right)}=6\sqrt{2^2+2^2}+8(n+m-5)\sqrt{2^2+3^2}\hfill \\ \hfill & +(4mn-8m-8n+16)\sqrt{2^2+4^2}\hfill \\ \hfill & +(2m^2+4mn-19m+2n^2-19n+48)\sqrt{3^2+3^2}\hfill \\ \hfill & +(2m^{2}n-4m^2+2m{n}^2-16mn+22m-4n^2+22n-24)\sqrt{3^2+4^2}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}(m^2{n}^2-4m^{2}n+4m^2-4m{n}^2+11mn-4m+4n^2-4n-12)\sqrt{4^2+4^2}\hfill \\ \hfill & =2m^2[\sqrt{2}{n}^2+(5-4\sqrt{2})n+7\sqrt{2}-10]\hfill \\ \hfill & +m[(10-8\sqrt{2})n^2+2(-40+17\sqrt{2}+4\sqrt{5})n+8\sqrt{13}-16\sqrt{5}-65\sqrt{2}+110]\hfill \\ \hfill & +(14\sqrt{2}-20)n^2+(110-65\sqrt{2}-16\sqrt{5}+8\sqrt{13})n\hfill \\ \hfill & +4(-30+33\sqrt{2}+8\sqrt{5}-10\sqrt{13}).\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \overline{Lz}\left(G_{n,m}\right)& =\sum _{uv\in E\left(\overline{G}\right)}[(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right)]=6(4n-12)\hfill \\ \hfill & +8(n+m-5)(5n-18)+(4mn-8m-8n+16)(6n-26)\hfill \\ \hfill & +(2m^2+4mn-19m+2n^2-19n+48)(6n-24)\hfill \\ \hfill & +(2m^{2}n-4m^2+2m{n}^2-16mn+22m-4n^2+22n-24)(7n-32)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}(m^2{n}^2-4m^{2}n+4m^2-4m{n}^2+11mn-4m+4n^2-4n-12)(8n-40)\hfill \\ \hfill & =4m^2{n}^3-22m^2{n}^2+16m^{2}n-2m{n}^3-4m{n}^2+108mn-104m+16n^2-112n+88.\hfill \end{array}$$

□

Theorem 9.

The Sombor coindex of the paraline graph of a tadpole graph is

$$\overline{SO}\left(PL\left(T_{n,k}\right)\right)=\left\{\begin{array}{c}4\sqrt{2}{(n+k)}^2+6\sqrt{13}(n-k)+2\sqrt{5}(n+k-1)+\sqrt{2}(16-22k-14n)\hfill \\ -15\sqrt{13}+3(\sqrt{10}-\sqrt{5}),whenk>1.\hfill \\ 2\sqrt{2}(2n^2-3n+2)+2\sqrt{13}(3n+2k-6)+8\sqrt{2}(kn-n-k)\hfill \\ +2\sqrt{5}n+2\sqrt{5}(\sqrt{2}-1),whenk=1.\hfill \end{array}\right.$$

(1)

Proof. 

The paraline graph $PL\left(T_{n,k}\right)$ has three 3-degree vertices, $u_1$, $u_2$, and $u_3$. In these vertices, $u_1$ is adjacent to a path of length $2k-1$. Furthermore, $u_1$ is non-adjacent to a pendant vertex and $2k-3$ vertices, each with a degree of 2. Then, the vertices in $N\left(u_1\right)$ are non-adjacent to a pendant vertex and $2(k-2)$ vertices of a degree of 2. So, the value $\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}$ of $u_1$ with regard to the path is $4\sqrt{2}{k}^2+(2\sqrt{13}-14\sqrt{2}+2\sqrt{5})k-3\sqrt{13}+\sqrt{10}+12\sqrt{2}-3\sqrt{5}$ for $k>1$. This value will be 0 for $k=1$, since $u_1$ is adjacent to a path $P_1$.

The vertices $u_2$ and $u_3$ are non-adjacent to a pendant vertex and $2(n+k)-5$ vertices, each with a degree of 2. The vertex $u_1$ is non-adjacent to $2(n-1)$ vertices in $L\left[S(C_n+e)\right]$, in which e is the edge adjacent to the subdivision of $C_n$, each with a degree of 2. Hence, the value $\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}$ of these 3 vertices is $2\sqrt{13}(3n+2k)-12\sqrt{13}+2\sqrt{10}$. Moreover, the $2(n-1)$ vertices mentioned above are non-adjacent with the path of length $2k-1$. So, the value $\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}$ of this path is $2(n-1)[4\sqrt{2}(k-1)+\sqrt{5}]$.

Among these $2(n-1)$ vertices mentioned above, $2(n-2)$ vertices with a degree of 2 are non-adjacent to $2n-5$ vertices with a degree of 2. The remaining two vertices that are adjacent with $u_2$ and $u_3$ are non-adjacent to $2(n-2)$ vertices in $L\left[S(C_n+e)\right]$, in which e is the edge adjacent to the subdivision of $C_n$, each with a degree of 2. So, the value $\sum \sqrt{d^2\left(u\right)+d^2\left(v\right)}$ of $2(n-1)$ vertices is $2\sqrt{2}(n^2-3n-2)$.

When we sum these up together, we obtain the Sombor coindex of $PL\left(T_{n,k}\right)$, which is

$\overline{SO}\left(PL\left(T_{n,k}\right)\right)=4\sqrt{2}{(n+k)}^2+6\sqrt{13}(n-k)+2\sqrt{5}(n+k-1)+\sqrt{2}(16-22k-14n)-15\sqrt{13}+3(\sqrt{10}-\sqrt{5})$ when $k>1$. $\overline{SO}\left(PL\left(T_{n,k}\right)\right)=2\sqrt{2}(2n^2-3n+2)+2\sqrt{13}(3n+2k-6)+8\sqrt{2}(kn-n-k)+2\sqrt{5}n+2\sqrt{5}(\sqrt{2}-1)$, when $k=1$. □

Theorem 10.

The Lanzhou coindex of $PL\left(T_{n,k}\right)$ is

$$\overline{Lz}\left(PL\left(T_{n,k}\right)\right)=\left\{\begin{array}{cc}8k^2(n-3)+2k[n(8n-27)-2]+n^{2}8(n-2)-89n+190,\hfill & whenk>1.\hfill \\ n^2(16k+8n-16)-(44k+90)n-24k+180,\hfill & whenk=1.\hfill \end{array}\right.$$

(2)

Proof. 

The paraline graph $PL\left(T_{n,k}\right)$ has three 3-degree vertices which we denote by $u_1$, $u_2$, and $u_3$. Among them, $u_1$ is adjacent to a path and non-adjacent to 1 pendant vertex and $2k-3$ vertices with a degree of 2. Thus, the vertices in $N\left(u_1\right)$ are non-adjacent to 1 pendant vertex and $2k-4$ vertices with a degree of 2. Hence, for $k>1$, we have $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]=8k^{2}n-24k^2-10kn+20k+n+10$. For $k=1$, $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]=0$, since $u_1$ is adjacent to $P_1$.

The vertices $u_2$ and $u_3$ are non-adjacent to 1 pendant vertex and $2(n+k)-5$ vertices, each with a degree of 2. The vertex $u_1$ is non-adjacent to $2(n-1)$ vertices in $L\left[S(C_n+e)\right]$, in which e is the edge adjacent to the subdivision of $C_n$, each with a degree of 2. So, the value $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]$ of these three vertices is $k(20n-72)+n(30n-160)+188$ .

Furthermore, the $2(n-1)$ vertices mentioned above are non-adjacent to the path. So, the value $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]$ of these $2(n-1)$ vertices with regard to the path is $2(n-1)(8kn-24k-5n+16)$.

Among the $2(n-1)$ vertices mentioned above, $2(n-2)$ vertices with a degree of 2 are non-adjacent to $2n-5$ vertices, each with a degree of 2. The remaining two vertices that are adjacent with $u_2$ and $u_3$ are non-adjacent to $2(n-2)$ vertices in $L\left[S(C_n+e)\right]$, in which e is the edge adjacent to the subdivision of $C_n$, each with a degree of 2. So, the value $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]$ of these vertices is $4(n-3)(n-2)(2n+1)$. Adding all these together, the Lanzhou coindex of $PL\left(T_{n,k}\right)$ is $8k^2(n-3)+2k(n(8n-27)-2)+n^{2}8(n-2)-89n+190$, for $k>1$, and $n^2(16k+8n-16)-(44k+90)n-24k+180$, for $k=1$.

□

Theorem 11.

Let $PL\left(W_{n+1}\right)$ be a paraline graph of a wheel graph. Then,

(i) $\overline{Lz}\left(PL\left(W_{n+1}\right)\right)=62n^3-240n^2+288n$.

(ii) $\overline{SO}\left(PL\left(W_{n+1}\right)\right)=n[(3n-1)\sqrt{n^2+9}+18\sqrt{2}n-33\sqrt{2}]$.

Proof. 

Clearly, $\left|V\right(PL\left(W_{n+1}\right)\left)\right|=4n$. Among these vertices, $2n$ vertices with a degree of 3, and they are non-adjacent to $3n-4$ vertices, each with a degree of 3, and n vertices, each with a degree of n. So, the value $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]$ of these vertices is $36n^3-192n^2+192n$.

Another n vertices, each having a degree of 3, are non-adjacent to $3n-3$ vertices, each with a degree of 3, and $n-1$ vertices, each with a degree of n. So, the value of $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]$ of these n vertices is $20n^3-104n^2+84n$.

All n vertices, each with a degree of n, are non-adjacent to $3n-1$ vertices, each with a degree of 3. So, the value of $\sum [(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]$ of these vertices is $6n^3-38n^2+12n$.

Hence, adding all these together, $\overline{Lz}\left(PL\left(W_{n+1}\right)\right)=62n^3-240n^2+288n$. In the same way, the Sombor coindex of a paraline graph of a wheel graph is $\overline{SO}\left(PL\left(W_{n+1}\right)\right)=n[(3n-1)\sqrt{n^2+9}+18\sqrt{2}n-33\sqrt{2}]$.

□

At last, we calculate the Lanzhou index and Sombor index of the paraline graph of a two-dimensional grid graph $PL\left(G_{n,m}\right)$.

Theorem 12.

For the paraline graph of a grid graph $PL\left(G_{n,m}\right)$, we have:

$$\begin{array}{cc}\hfill \left(i\right)\overline{Lz}\left(PL\left(G_{n,m}\right)\right)& =4m^2(16n^3-102n^2+135n-44)+m(-88n^3+1731n^2-5736n-352)\hfill \\ \hfill & +4n(7n^2-26n-108)+592.\hfill \\ \hfill \left(ii\right)\overline{SO}\left(PL\left(G_{n,m}\right)\right)& =32\sqrt{2}{m}^2{n}^2+(120-128\sqrt{2})(m^{2}n+m{n}^2)\hfill \\ \hfill & +(64\sqrt{5}+580\sqrt{2}+960)mn+(182\sqrt{2}-240)(m^2+n^2)\hfill \\ \hfill & +(48\sqrt{13}-128\sqrt{5}-893\sqrt{2}+1430)(m+n)\hfill \\ \hfill & +1392\sqrt{2}+256\sqrt{5}-200\sqrt{13}-1880.\hfill \end{array}$$

Proof. 

By the definition of the paraline graph, graph $PL\left(G_{n,m}\right)$ has $4mn-2n-2m$ vertices and $8mn-7n-7m+4$ edges. Thus, its complement has $2(4m^2{n}^2-4m^{2}n+m^2-4m{n}^2-3mn+4m+n^2+4n-2)$ edges. Among them, there are 24 edges between two 2-degree vertices, $48m+48n-200$ edges between a 2-degree vertex and a 3-degree vertex, and $32mn-64m-64n+128$ edges between a 2-degree vertex and a 4-degree vertex. There are $18m^2+36mn-155m+18n^2-155n+336$ edges connecting two 3-degree vertices, $24m^{2}n+24m{n}^2-48m^2-48n^2-192mn+286m+286n-376$ edges connecting a 3-degree vertex and a 4-degree vertex, and $8m^2{n}^2-32m^{2}n-32m{n}^2+32m^2+32n^2+118mn-107n-107m+84$ edges connecting two 4-degree vertices. Hence, we have

$$\begin{array}{cc}\hfill \overline{Lz}\left(PL\left(G_{n,m}\right)\right)& =\sum _{uv\in E\left(\overline{G}\right)}[(n-1)(d\left(u\right)+d\left(v\right))-(d^2\left(u\right)+d^2\left(v\right))]=24(4n-12)\hfill \\ \hfill & +(48m+48n-200)(5n-18)+(32mn-64m-64n+128)(6n-26)\hfill \\ \hfill & +(18m^2+36mn-155m+18n^2-155n+336)(6n-24)\hfill \\ \hfill & +(24m^{2}n+24m{n}^2-48m^2-48n^2-192mn+286m+286n-376)(7n-32)\hfill \\ \hfill & +(8m^2{n}^2-32m^{2}n-32m{n}^2+32m^2+32n^2+118mn-107n-107m\hfill \\ \hfill & +84\left)\right(8n-40)\hfill \\ \hfill & =4m^2(16n^3-102n^2+135n-44)+m(-88n^3+1731n^2-5736n-352)\hfill \\ \hfill & +4n(7n^2-26n-108)+592.\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \overline{SO}\left(PL\left(G_{n,m}\right)\right)& =\sum _{uv\in E\left(\overline{G}\right)}\sqrt{d^2\left(u\right)+d^2\left(v\right)}=24\sqrt{2^2+2^2}+(48m+48n-200)\sqrt{2^2+3^2}\hfill \\ \hfill & +(32mn-64m-64n+128)\sqrt{2^2+4^2}\hfill \\ \hfill & +(18m^2+36mn-155m+18n^2-155n+336)\sqrt{3^2+3^2}\hfill \\ \hfill & +(24m^{2}n+24m{n}^2-48m^2-48n^2-192mn+286m+286n-376)\sqrt{3^2+4^2}\hfill \\ \hfill & +[2mn(4mn+16m+16n+59)+32(m^2+n^2)-107(m+n)+84]\sqrt{4^2+4^2}\hfill \\ \hfill & =32\sqrt{2}{m}^2{n}^2+(120-128\sqrt{2})(m^{2}n+m{n}^2)\hfill \\ \hfill & +(64\sqrt{5}+580\sqrt{2}+960)mn+(182\sqrt{2}-240)(m^2+n^2)\hfill \\ \hfill & +(48\sqrt{13}-128\sqrt{5}-893\sqrt{2}+1430)(m+n)\hfill \\ \hfill & +1392\sqrt{2}+256\sqrt{5}-200\sqrt{13}-1880.\hfill \end{array}$$

□

4. Conclusions

In this paper, we define a new index, the Lanzhou coindex, and investigate the Sombor index (coindex) and Lanzhou index (coindex) for some graphs, including tadpole graphs, wheel graphs, and two-dimensional grid graphs, and their paraline graphs. Moreover, we explore the relationships between the Lanzhou index of a graph G and its subdivision graph, and further investigate the relationships between the subdivision graph of a graph G and its paraline graph. This paper enriches the research results on the Sombor index (coindex) and Lanzhou index. Furthermore, future research could explore these indices in important yet understudied graph classes, which will constitute a key focus of our upcoming investigations. Additionally, a critical future task involves the systematic examination of the newly proposed Lanzhou coindex—including its mathematical relationships with the Lanzhou index, the Sombor index, the Zagreb indices, the forgotten coindex, and other significant graph-theoretic parameters.