A Study on the Existence of Fixed Point Results for Some Fuzzy Contractions in Fuzzy Metric Spaces with Application

Abstract

In this manuscript, we analyze fuzzy-fixed-point results for fuzzy-mappings under some fuzzy contraction conditions in the setting of a complete fuzzy metric space. Fuzzy-fixed-point techniques are used in mathematical modeling to solve problems where traditional methods fail due to imprecise or uncertain data. To obtain fuzzy-fixed-points, different contraction conditions are implemented in a fuzzy context. To emphasize the impact of our research, we have furnished several intriguing examples. Applications are also incorporated to furnish the results. Previous results are given as corollaries from the relevant research. Our results extend and combine many results that exist in a significant area of related research.

1. Introduction

The concept of fuzzy-sets was initiated by Zadeh [1] in 1965. This groundbreaking concept challenged the traditional binary logic of true and false by introducing the notion of partial membership, which states that elements can belong to a set to varying degrees. Fuzzy-set theory introduced a new realm of possibilities in various fields, including artificial intelligence, decision-making, control systems, and pattern recognition. Numerous examples emerged highlighting how uncertainty in systems often possesses a fuzziness distinct from unpredictable randomness. To capture this nuance, non-stationary fuzzy systems, modeled by fuzzy processes, were proposed as a natural extension of traditional fuzzy systems in the time domain. Comprehensive analysis across various mathematical and scientific disciplines has shed light on the distinctive capacity of fuzzy processes to model and handle non-stationary uncertainty in dynamical systems. For the latest literature, see, for example [2] and the references therein.

The best conditions for approximating the solutions of linear and nonlinear operator equations are provided by fixed-point results in the study of mathematical analysis [3]. Analysis, topology, and geometry are all wonderfully integrated in the theory itself [4]. The theory of fixed points is a highly useful and significant instrument for the investigation of nonlinear problems [5]. Consequently, it can be noted that fixed-point techniques have been used in a variety of domains, including physics, game theory, biology, chemistry, economics, and engineering. The definition of a fuzzy metric space with the help of a continuous triangular norm (t-norm) was given by Kramosil and Michalek [6] in 1975, which was modified by George and Veeramani [7] to generate a Hausdorff topology induced by fuzzy metrics. Grabiec [8] explained the completeness of the fuzzy metric space and extended the Banach contraction theorem to complete the fuzzy metric space. After that, many fixed-point results were established by many researchers in the fuzzy metric space and its generalizations; for example, see [9,10,11,12,13,14,15,16,17,18,19] and the references therein. An essential component of metric geometry is the Hausdorff metric space [20], which provides a flexible framework for measuring the separation and difference between subsets of metric spaces. Therefore, Hausdorff metric spaces have a wide range of applications. A study of fixed points for multivalued mappings was basically proposed by von Neumann. The notion of fuzzy-mapping was first introduced in 1981 by Heilpern [21], allowing for mappings between fuzzy sets, as an extension of a classical mapping. He established a fixed-point theorem for fuzzy contraction mappings, which is a generalization of the fixed-point theorem for the multivalued mapping of Nadler’s contractive principle [22]. Afterwards, many authors (for example, see [15,18,23,24,25] and the references therein) derived and calculated the existence of the fixed points and common fixed points of fuzzy-mappings. The concepts of different types of fuzzy metric space have accelerated research in fuzzy-fixed-point theorems, highlighting the broad applications of fuzzy set, rough set, soft set, and intuitionistic set theories in decision-making, modeling, pattern classification, and other areas [2].

Taking motivation from the above series of studies, we present fixed-point results for some fuzzy contractions in fuzzy metric spaces with applications. Our work is the extension of some existing results in the literature, where we also give definitions for upper and lower semi-continuity in the fuzzy sense. Using these definitions, we prove Theorem 1 as the generalization of the result proved in [10] for fuzzy-mapping. Theorem 2 is the extension of the result proved in [26] by using fuzzy sets for multivalued mappings. In this theorem, we use fuzzy-mappings, which were defined by Heilpern [21], to find the fuzzy-fixed-point in the framework of the fuzzy metric space defined by George and Veeramani [7] in association with the Hausdorff fuzzy metric defined by [20]. Theorems 3–6 are extensions of the results proved in [15] for some other similar contractions. Examples are also incorporated to verify and validate the results obtained. Previous findings are presented as the corollaries of the established results. Applications are incorporated as well.

The structure of this article is as follows: We present some necessary preliminaries in Section 2. The main results are presented in Section 3. To prove these results, we define the concepts of upper semi-continuity and lower semi-continuity for fuzzy-mappings. The applications of the main results are presented in Section 3.1. These results are summarized in Section 4.

2. Preliminaries

In this section, fundamental concepts are presented, with the goal of providing a thorough understanding to the readers of the basic definitions, examples, and lemmas required for a good understanding of our presented results. These essential elements were drawn from previously published research articles, and they are all included in the provided material. It must be noted that throughout this article, we denote $K_{\mathsf{\ell }}(\Delta )$ for the set of all compact sets in the universal set $\Delta .$

Definition 1

([15]). In the fuzzy theory, the fuzzy-sets ℏ of the universal set Δ are defined by a function, ${\mu }_{\hslash }:\Delta \to [0,1]$, called the membership function of $\hslash ,$ where

$$\begin{array}{cc}\hfill & {\mu }_{\hslash }\left(\sigma \right)=0if\sigma isnotin\hslash ;\hfill \\ \hfill & {\mu }_{\hslash }\left(\sigma \right)=1if\sigma istotallyin\hslash ;\hfill \\ \hfill & 0<{\mu }_{\hslash }\left(\sigma \right)<1if\sigma ispartiallyin\hslash .\hfill \end{array}$$

The α-cut of fuzzy sets, ℏ, is denoted by ${[\hslash ]}_{\alpha }$ and is defined as

$${[\hslash ]}_{\alpha }=\{\sigma \in \Delta :\hslash \left(\sigma \right)\ge \alpha \}where\alpha \in [0,1].$$

The set of all fuzzy sets in Δ will be denoted by $\mathsf{Ϝ}(\Delta )$.

Example 1.

Consider a nonempty set, $\Gamma =[0,100]$, and two mappings, Φ and Ψ, defined below:

$$\Phi \left(\sigma \right)=\left\{\begin{array}{cc}1\hfill & \mathit{if}0\le \sigma \le 30\hfill \\ {\displaystyle \frac{(60-\sigma )}{30}}\hfill & \mathit{if}30<\sigma <60\hfill \\ 0\hfill & \mathit{if}\sigma \ge 60\hfill \end{array}\right.$$

and

$$\Psi \left(\sigma \right)=\left\{\begin{array}{cc}0\hfill & \mathit{if}0\le \sigma \le 45\hfill \\ {\displaystyle \frac{(\sigma -45)}{25}}\hfill & \mathit{if}45<\sigma <70\hfill \\ 1\hfill & \mathit{if}\sigma \ge 60.\hfill \end{array}\right.$$

Clearly, $\Phi$ and $\Psi$ are fuzzy sets on $\Gamma$.

Example 2.

Consider that $\Lambda =[0,10].$ Define two fuzzy sets, K and L, on Λ, as below:

$$K\left(\mu \right)=\left\{\begin{array}{cc}1-{\displaystyle \frac{\left|\mu -3\right|}{2}},\hfill & \mathit{when}1\le \mu \le 5\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

and

$$L\left(\mu \right)=\left\{\begin{array}{ll}1-{\displaystyle \frac{\left|\mu -3\right|}{2}},& \mathit{when}2\le \mu \le 6\\ 0& \mathit{otherwise}.\end{array}\right.$$

Graphs of the fuzzy sets K and L are shown in Figure 1.

Definition 2

([15]). A function, $\ast :[0,1]\times [0,1]\to [0,1]$, is known as a continuous triangular norm (t-norm), if the following conditions are fulfilled for all $\theta ,\kappa ,\lambda ,\nu \in [0,1];$

(1) 

Symmetry: $\theta \ast \kappa =\kappa \ast \theta ;$

(2) 

Monotonicity: $\theta \ast \kappa \le \lambda \ast \nu ,if\theta \le \lambda$ and $\kappa \le \nu ;$

(3) 

Associativity: $(\theta \ast (\kappa \ast \lambda \left)\right)=\left(\right(\theta \ast \kappa )\ast \lambda );$

(4) 

Boundary conditions: $1\ast \theta =\theta .$

Three basic t-norms are as follows:

(1) 

Lukasiewicz t-norm: $\theta {\ast }_L\lambda$ = $max\{\theta +\lambda -1,0\};$

(2) 

Product t-norm: $\theta {\ast }_p\lambda$ = $\theta \lambda ;$

(3) 

Minimum t-norm: that is, $\theta {\ast }_M\lambda$ = $min\{\theta ,\lambda \}.$

Definition 3

([8]). The triplet $(\Delta ,\mathsf{\ell },\ast )$ is a fuzzy metric space if Δ is a nonempty set and ℓ, a fuzzy set on $\Delta \times \Delta \times [0,\infty )$, satisfies the following conditions, $\forall \varphi ,\phi ,\omega \in \Delta$ and $k,t\ge 0:$

(ℓ1) 

$\mathsf{\ell }(\varphi ,\phi ,t)>0;$

(ℓ2) 

$\mathsf{\ell }(\varphi ,\phi ,t$) =1 iff $\varphi =\phi ;$

(ℓ3) 

$\mathsf{\ell }(\varphi ,\phi ,t)$ = $\mathsf{\ell }(\phi ,\varphi ,t);$

(ℓ4) 

$\mathsf{\ell }(\varphi ,\phi ,t)$$\ast \mathsf{\ell }(\phi ,\omega ,k)\le \mathsf{\ell }(\varphi ,\omega ,t+k);$

(ℓ5) 

$\mathsf{\ell }(\varphi ,\phi ,.)$ $:[0,\infty )$ $\to [0,1]$ is continuous.

Example 3.

Consider a complete metric space, $(\Delta ,d)$. Define ℓ: ${\Delta }^2\times [0,\infty )\to [0,1]$ as $\mathsf{\ell }(\sigma ,\eta ,t)={\displaystyle \frac{t}{t+d(\sigma ,\eta )}}$ for all $\sigma ,\eta \in \Delta$ and $t>0$ and define $\sigma \ast \eta =\sigma \eta (or\sigma \ast \eta =min\{\eta ,\sigma \left\}\right)$∀$\sigma ,\eta \in [0,1]$; then, $(\Delta ,\mathsf{\ell },\ast )$ is a fuzzy metric space on Δ.

Example 4.

Consider a complete metric space, $(\Delta ,d)$, and a continuous increasing function, g: ${\mathbb{R}}^{+}\to [0,\infty )$.

• Define $\mathsf{\ell }:{\Delta }^2\times [0,\infty )\to [0,1]$ as $\mathsf{\ell }(\sigma ,\eta ,t)$ = $e^{(-{\displaystyle \frac{d(\sigma ,\eta )}{g\left(t\right)}})}$ for all $\sigma ,\eta \in \Delta$ and $t>0$; then, $(\Delta ,\mathsf{\ell },\ast )$ is a fuzzy metric space on Δ with the product t-norm ∗.

Definition 4

([15]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a fuzzy metric space. A sequence, $\left\{{\sigma }_n\right\}$, in Δ is said to be convergent to a point, $q\in \Delta$, if ${lim}_{n\to \infty }\mathsf{\ell }({\sigma }_n,q,t)=1$ for all $t>0$.

Definition 5

([15]). A sequence, $\left\{{\sigma }_n\right\}$, in the fuzzy metric space $(\Gamma ,\Lambda ,\ast )$ is called a Cauchy sequence if $\Lambda ({\sigma }_n,{\sigma }_{n+m},t)\to 1$, as $n\to \infty$ for every $m\in \mathbb{N}$ and $t>0$.

Definition 6

([15]). A fuzzy metric space is called complete if every Cauchy sequence in it is convergent.

Definition 7

([15]). A fuzzy metric space in which every sequence has a convergent subsequence is said to be compact.

Definition 8

([20]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a fuzzy metric space. The Hausdorff fuzzy metric $H_{\mathsf{\ell }}$: $K_{\mathsf{\ell }}(\Delta )\times K_{\mathsf{\ell }}(\Delta )\to \mathbb{R}$ is defined as

• $H_{\mathsf{\ell }}(A,B,t)$ = min $\{{inf}_{\sigma \in A}({sup}_{\eta \in B}\mathsf{\ell }(\sigma ,\eta ,t)),{inf}_{\eta \in B}({sup}_{\sigma \in A}\mathsf{\ell }(\sigma ,\eta ,t))\}$
• where A, B $\in K_{\mathsf{\ell }}(\Delta )$ and $t>0$.

  $$\mathsf{\ell }(\sigma ,A,t)=sup\{\mathsf{\ell }(\sigma ,\rho ,t):\rho \in A\}.$$

Definition 9

([15]). Let Y be a metric space and Δ be any nonempty set. A mapping, f: $\Delta \to \mathsf{Ϝ}\left(Y\right)$, is called a fuzzy-mapping. For convenience, we denote the α-cut set of $f\left(\sigma \right)$ by ${\left[f\sigma \right]}_{\alpha }$ instead of ${\left[f\left(\sigma \right)\right]}_{\alpha }$.

Example 5.

Consider a mapping, $T:X\to \mathsf{Ϝ}\left(Y\right)$, where $X=[-6,6]$ and $Y=[-10,10]$. Define T as

$$T(x,y)={\displaystyle \frac{(se{c}^{2}x+ta{n}^{2}y)}{30}}.$$

Clearly, T is a fuzzy-mapping. The functional values $T(x,y)$ are shown in Figure 2.

Example 6.

Consider a mapping, $T:X\to \mathsf{Ϝ}\left(Y\right)$, where $X=[-1,1]$ and $Y=[-4,4]$. Define T as

$$T(x,y)=e^{\left({\displaystyle \frac{y^{-3}-x^{-2}}{10}}\right)}.$$

Clearly, T is a fuzzy-mapping. The functional values $T(x,y)$ are shown in Figure 3.

Definition 10

([15]). Any point, $q\in \Delta$, is called a fuzzy-fixed-point of f: $\Delta \to \mathsf{Ϝ}(\Delta )$ if there is $\alpha \in (0,1]$, such that $q\in {\left[fq\right]}_{\alpha }$.

Definition 11

([10]). A mapping, f: $\Delta \to \mathbb{R}$, is called upper semi-continuous, if for any sequence of $\left\{{\sigma }_n\right\}\subset \Delta$ and $\sigma \in \Delta$, $\left\{{\sigma }_n\right\}\to \sigma$, $f\left(\sigma \right)\ge {lim\; sup}_{n\to \infty }f\left({\sigma }_n\right)$ is implied.

Definition 12

([10]). A mapping, f: $\Delta \to \mathbb{R}$, is known as lower semi-continuous, if for any $\left\{{\sigma }_n\right\}\subset \Delta$ and $\sigma \in \Delta ,\left\{{\sigma }_n\right\}\to \sigma$, $f\left(\sigma \right)\le {lim\; inf}_{n\to \infty }f\left({\sigma }_n\right)$ is implied.

Definition 13

([11]). Consider that $\varpi =\{\lambda$: $[0,1]\to [0,1]\}$ is a collection of all continuous functions such that $\lambda \left(1\right)=1,$ $\lambda \left(0\right)=0,$ and $\lambda \left(\iota \right)>\iota$ for all $0<\iota <1.$

Lemma 1

([15]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a fuzzy metric space. For all $\sigma ,\eta \in \Delta$, ℓ$(\sigma ,\eta ,t)$, is a non-decreasing function.

Lemma 2

([15]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a fuzzy metric space. Then, for each $\sigma \in \Delta$, $B\in K_{\mathsf{\ell }}(\Delta )$, and for $t>0$, there exists ${\eta }_0\in B$, such that

$$\mathsf{\ell }(\sigma ,{\eta }_0,t)=\mathsf{\ell }(\sigma ,B,t).$$

Lemma 3

([20]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space, such that $(K_{\mathsf{\ell }}(\Delta ),H_{\mathsf{\ell }},\ast )$ is a Hausdroff fuzzy metric space on $K_{\mathsf{\ell }}(\Delta )$. Then, for all $M,N\in K_{\mathsf{\ell }}(\Delta )$, for $i\in M$, and for $t>0$, there exists $j_i\in N$, which satisfies

$$\mathsf{\ell }(i,N,t)=\mathsf{\ell }(i,j_i,t).$$

Then, $H_{\mathsf{\ell }}(M,N,t)\le \mathsf{\ell }(i,j_i,t).$

Lemma 4

([15]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space; if there exists $\alpha \in (0,1)$ such that $\mathsf{\ell }(\sigma ,\eta ,\alpha t)\ge \mathsf{\ell }(\sigma ,\eta ,\alpha )$ for all $\sigma ,\eta ,\in \Delta$ and $t\in [0,\infty )$, then $\sigma =\eta .$

Lemma 5

([10]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a fuzzy metric space satisfying

$$\underset{n\to \infty }{lim}{\ast }_{i=n}^{\infty }\mathsf{\ell }(\sigma ,\eta ,t{h}^i)=1$$

(1)

for each $\sigma ,\eta \in \Delta ,$ $t>0$ and $h>1$; suppose that $\left\{{\sigma }_n\right\}$ is a sequence in Δ that satisfies

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},kt)\ge \mathsf{\ell }({\sigma }_{n-1},{\sigma }_n,t),$$

for all $n\in \mathbb{N}$ and $0<k<1.$ Then, $\left\{{\sigma }_n\right\}$ is a Cauchy sequence.

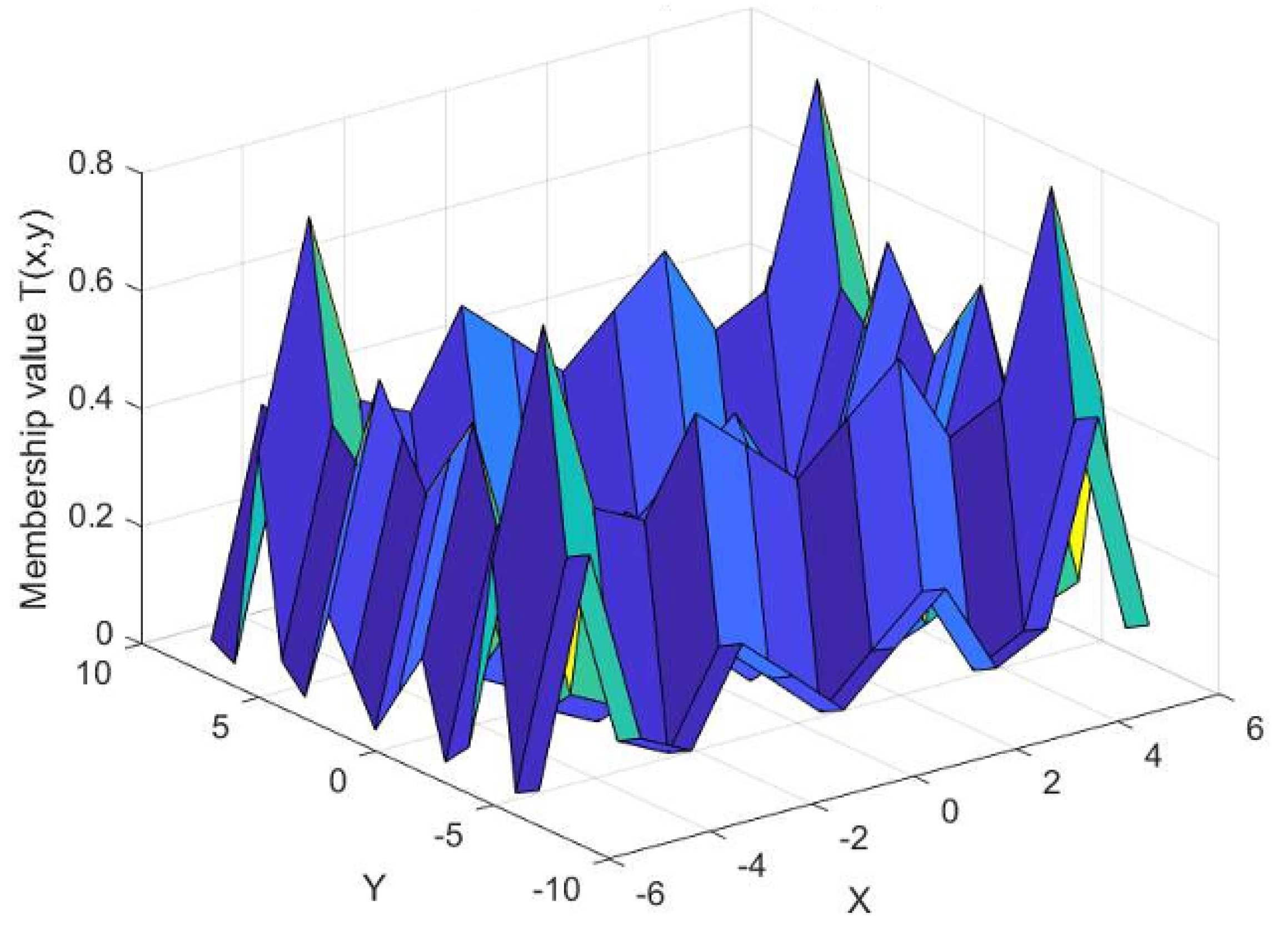
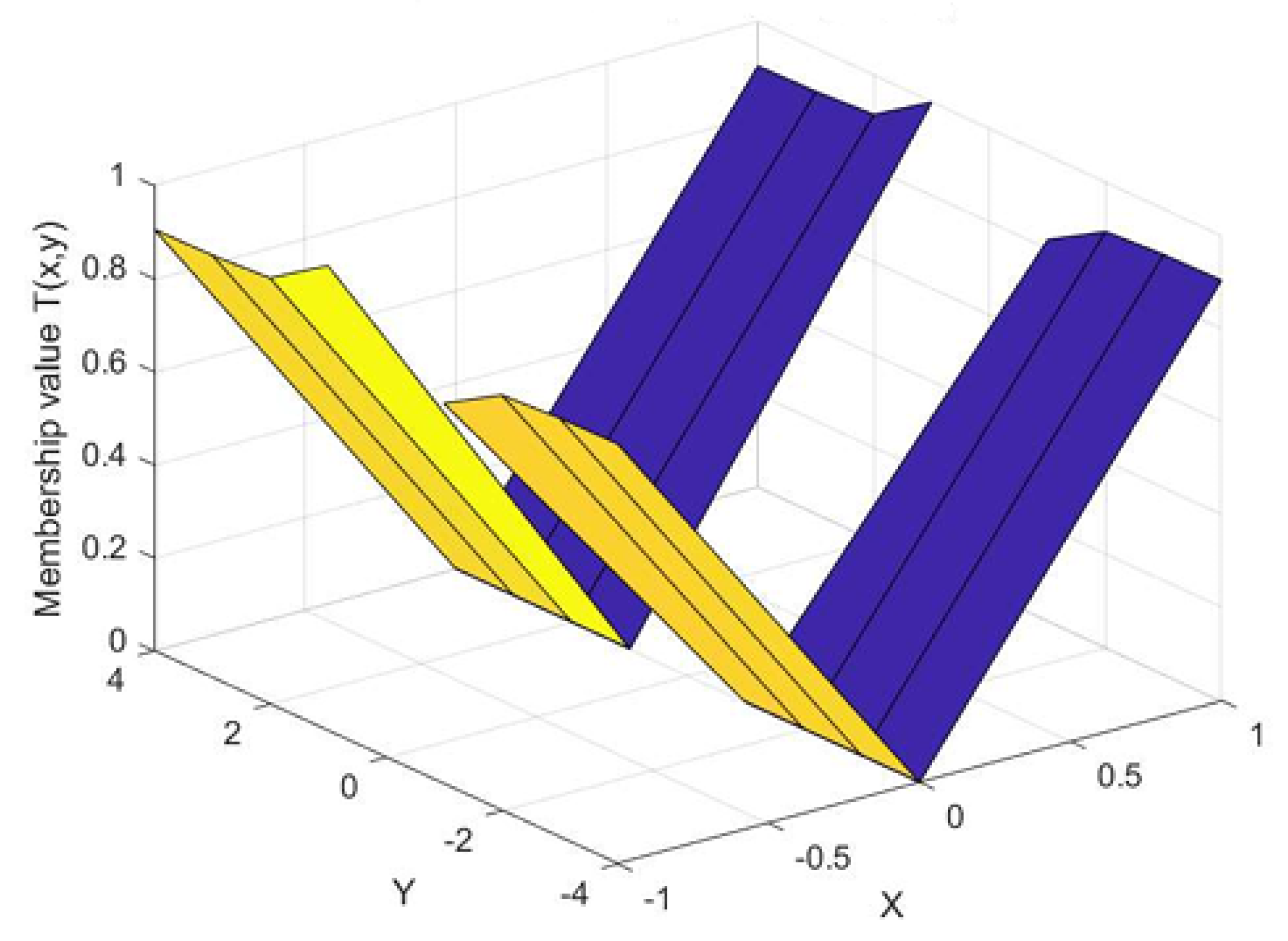
3. Fuzzy-Fixed-Points for Fuzzy Contractions

In this section, we establish the new generalized theorem as a consequence of the analysis of fuzzy-fixed-point results for fuzzy-mappings under certain contraction conditions. We show that there exist fixed points in the framework of complete fuzzy metric spaces if the mappings defined on it are fuzzy and furnish this concept with interesting examples. First, we define the concepts of upper semi-continuity and lower semi-continuity for fuzzy-mappings. It is significant to remark that these concepts in the fuzzy sense have not been explored before in the existing literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30].

Definition 14.

A fuzzy-mapping, T: $\Delta \to \mathsf{Ϝ}(\Delta )$, is known as upper semi-continous if for a sequence, $\sigma \in \Delta$, and a neighborhood, C, of ${\left[T\left(\sigma \right)\right]}_{\alpha },$ there is a neighborhood, D, of σ, such that for any $\eta \in D,$ we obtain ${\left[T\left(\eta \right)\right]}_{\alpha }\subset C.$ A fuzzy-mapping, T: $\Delta \to \mathsf{Ϝ}(\Delta )$, is said to be lower semi-continuous, if for any sequence, $\sigma \in \Delta$, and a neighborhood, C, $C\cap {\left[T\left(\sigma \right)\right]}_{\alpha }\ne \varphi ,$ and there is a neighborhood, D, of σ, such that for any $\eta \in D,$ we have ${\left[T\left(\eta \right)\right]}_{\alpha }\cap C\ne \varphi$.

Definition 15.

Let T: $\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping. Define $f\left(\sigma \right)=\mathsf{\ell }(\sigma ,{\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},t)$ where $t>0.$ For $p\in (0,1),$ define a set

$${\kappa }_p^{\sigma }=\{\eta \in {\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)}:\mathsf{\ell }(\sigma ,\eta ,t)\ge \mathsf{\ell }(\sigma ,{\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},pt)\}.$$

Theorem 1.

Consider a complete fuzzy metric space, $(\Delta ,\mathsf{\ell },\ast )$, and a fuzzy-mapping, T: $\Delta \to \mathsf{Ϝ}(\Delta )$, such that ${\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)}\in K_{\mathsf{\ell }}(\Delta )$. If there exists a constant, $k\in (0,1)$, for any $\sigma \in \Delta$ there is $\eta \in {\kappa }_p^{\sigma }$, satisfying

$$\mathsf{\ell }(\eta ,{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},kt)\ge \mathsf{\ell }(\sigma ,\eta ,t),$$

(2)

for $t>0.$ Assume that $(\Delta ,\mathsf{\ell },\ast )$ satisfies $\left(1\right)$ for some ${\sigma }_0$ in $\Delta ;$ then, T has a fuzzy-fixed-point provided $k<p$ and f is upper semi-continuous.

Proof. 

We know that ${\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)}\in K_{\mathsf{\ell }}(\Delta )$ by using Lemma 2 and that ${\kappa }_p^{\sigma }$ is nonempty for any $\sigma \in \Delta$ and $P\in (0,1).$ Let $\sigma \in \Delta$ be arbitrary; there exists ${\sigma }_1\in {\kappa }_p^{{\sigma }_0}$, satisfying

$$\mathsf{\ell }({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_T\left({\sigma }_1\right)},kt)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,t),$$

and for ${\sigma }_1\in \Delta ,$ there exists ${\sigma }_2\in {\kappa }_p^{{\sigma }_1}$, satisfying

$$\mathsf{\ell }({\sigma }_2,{\left[T{\sigma }_2\right]}_{{\alpha }_T\left({\sigma }_2\right)},kt)\ge \mathsf{\ell }({\sigma }_1,{\sigma }_2,t).$$

Consequently, we obtain a sequence, $\left\{{\sigma }_n\right\}$, in $\Delta$, such that ${\sigma }_{n+1}\in {\kappa }_p^{{\sigma }_n}$, satisfying

$$\mathsf{\ell }({\sigma }_{n+1},{\left[T{\sigma }_{n+1}\right]}_{{\alpha }_T\left({\sigma }_{n+1}\right)},kt)\ge \mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},t).$$

(3)

On the other hand, ${\sigma }_{n+1}\in {\kappa }_p^{{\sigma }_n}$ gives

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},t)\ge \mathsf{\ell }({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},pt).$$

(4)

From (3) and (4), we obtain

$$\mathsf{\ell }({\sigma }_{n+1},{\left[T{\sigma }_{n+1}\right]}_{{\alpha }_T\left({\sigma }_{n+1}\right)},kt)\ge \mathsf{\ell }({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},pt).$$

$$\mathsf{\ell }({\sigma }_{n+1},{\left[T{\sigma }_{n+1}\right]}_{{\alpha }_T\left({\sigma }_{n+1}\right)},t)\ge \mathsf{\ell }({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},{\displaystyle \frac{p}{k}}t).$$

(5)

Consider that $\beta ={\displaystyle \frac{k}{p}}$; then, from (5), we obtain

$$\mathsf{\ell }({\sigma }_{n+1},{\left[T{\sigma }_{n+1}\right]}_{{\alpha }_T\left({\sigma }_{n+1}\right)},t)\ge \mathsf{\ell }({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},{\displaystyle \frac{t}{\beta }}).$$

Now, we have

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},t)\ge \mathsf{\ell }({\sigma }_{n-1},{\sigma }_n,{\displaystyle \frac{t}{\beta }})\ge \mathsf{\ell }({\sigma }_{n-2},{\sigma }_{n-1},{\displaystyle \frac{t}{\beta .\beta }})\ge \dots \ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{{\beta }^n}})$$

(6)

for all $n\in \mathbb{N}$ and $0<\beta <1.$ We choose the constant $s>1$ such that $\beta s<1$, then ${\displaystyle \frac{1}{s}}<1$ and ${\sum }_{i=n}^{\infty }{\displaystyle \frac{1}{s^i}}<1,$ that is, ${\sum }_{i=0}^{m-1}{\displaystyle \frac{1}{s^i}}<1,$ and we have

$$t[{\displaystyle \frac{1}{s^n}}+{\displaystyle \frac{1}{s^{n+1}}}+\dots +{\displaystyle \frac{1}{s^{m-2}}}+{\displaystyle \frac{1}{s^{m-1}}}]<t,$$

for all $m>n$ and $h>1$. Also, we have

$$\mathsf{\ell }({\sigma }_n,{\sigma }_m,t)\ge \mathsf{\ell }({\sigma }_n,{\sigma }_m,t({\displaystyle \frac{1}{s^n}}+{\displaystyle \frac{1}{s^{n+1}}}+\dots +{\displaystyle \frac{1}{s^{m-2}}}+{\displaystyle \frac{1}{s^{m-1}}})$$

$$\ge \mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},{\displaystyle \frac{t}{s^n}})\ast \mathsf{\ell }({\sigma }_{n+1},{\sigma }_{n+2},{\displaystyle \frac{t}{s^{n+1}}})\ast \dots \ast \mathsf{\ell }({\sigma }_{m-1},{\sigma }_m,{\displaystyle \frac{t}{s^{m-1}}})$$

This implies that

$$\mathsf{\ell }({\sigma }_n,{\sigma }_m,t)\ge [\mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{{\left(\beta s\right)}^n}})\ast \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{{\left(\beta s\right)}^{n+1}}})\ast \dots \ast \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{{\left(\beta s\right)}^{m-1}}})]$$

$$\mathsf{\ell }({\sigma }_n,{\sigma }_m,t)\ge \ast i_{i=n}^{\infty }[\mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{{\left(\beta s\right)}^i}})].$$

(7)

Then, by using Lemma 5, we obtain

$$\underset{m,n\to \infty }{lim}\mathsf{\ell }({\sigma }_n,{\sigma }_m,t)=1.$$

Thus, $\left\{{\sigma }_n\right\}$ is a Cauchy sequence in $\Delta$. Since $\Delta$ is complete, there exists $q\in \Delta$, such that ${lim}_{n\to \infty }{\sigma }_n=q.$

From (3) and (4), it is clear that $f\left({\sigma }_n\right)=\mathsf{\ell }({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},t)$ is increasing and hence converges to 1. Since f is upper semi-continuous, we have

$$1=\underset{n\to \infty }{lim\; sup}f\left({\sigma }_n\right)\le f\left(q\right)\le 1.$$

This implies that $f\left(q\right)=1$, so $\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)=1.$

$$\Rightarrow q\in {\left[Tq\right]}_{{\alpha }_T\left(q\right)}.$$

Thus, q is a fuzzy-fixed-point of $T.$ □

Example 7.

Let $(\Delta ,d)$ be a complete metric space and $t>0$ and Δ = $[0,\infty )$ for all $\sigma ,\eta \in \Delta ,$ where t is a fixed constant in $[0,\infty )$.

Define a function, $\mathsf{\ell }:{\Delta }^2\times [0,\infty )\to [0,1]$, as

$$\mathsf{\ell }(\sigma ,\eta ,t)={\displaystyle \frac{t}{t+d(\sigma ,\eta )}},$$

where $d(\sigma ,\eta )$ = $|\sigma -\eta |$ for all $\sigma ,\eta \in$ $\Delta$ and $t>0.$ Then, $(\Delta ,\mathsf{\ell },\ast )$ is a fuzzy metric space. We define fuzzing mapping such that

$$T:\Delta \to \mathsf{Ϝ}(\Delta )$$

as

$$T\left(\sigma \right)\left(t\right)=\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & \mathit{if}0\le t\le {\displaystyle \frac{\sigma }{3^n}},\hfill \\ 0,\hfill & \mathit{if}{\displaystyle \frac{\sigma }{3^n}}\le t<\infty .\hfill \end{array}$$

For $\alpha ={\displaystyle \frac{1}{2}}$,

$${\left[T\sigma \right]}_{{\displaystyle \frac{1}{2}}}=\{t:T\sigma \left(t\right)\ge {\displaystyle \frac{1}{2}}\}=[0,{\displaystyle \frac{\sigma }{3^n}}],$$

$${\left[T\eta \right]}_{{\displaystyle \frac{1}{2}}}=\{t:T\eta \left(t\right)\ge {\displaystyle \frac{1}{2}}\}=[0,{\displaystyle \frac{\eta }{3^n}}].$$

Since, ${lim}_{n\to \infty }{\ast }_{i=n}^{\infty }\mathsf{\ell }(\sigma ,\eta ,t{h}^i)=1,$ and

$$\underset{n\to \infty }{lim}{\ast }_{i=n}^{\infty }{\displaystyle \frac{t{h}^i}{t{h}^i+\frac{\eta }{3^n}}}=1,$$

which implies that T satisfies $\left(1\right)$. Moreover,

$$H_{\mathsf{\ell }}({\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},kt)={\displaystyle \frac{kt}{kt+H({\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)})}}.$$

On the other hand,

$$f\left(\sigma \right)=\mathsf{\ell }(\sigma ,{\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},t)={\displaystyle \frac{t}{t+d(\sigma ,{\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)})}}\le 1$$

is continuous. Similarly, we have

$$\mathsf{\ell }(\eta ,{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},t)={\displaystyle \frac{t}{t+d(\eta ,{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)})}}\le 1.$$

Thus, all the conditions of Theorem 1 are satisfied. So, T has a fuzzy-fixed-point in a fuzzy metric space.

Corollary 1

([27]). Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space. Suppose that T: $\Delta \to \mathsf{Ϝ}(\Delta )$ is a fuzzy-mapping, such that ${\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)}\in K_{\mathsf{\ell }}(\Delta )$.

$$H_{\mathsf{\ell }}({\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},kt)\ge \mathsf{\ell }(\sigma ,\eta ,t),$$

(8)

for each $\sigma ,\eta \in \Delta ,$ $0<k<1$ and $t>0$. Furthermore, assume that $(\Delta ,\mathsf{\ell },\ast )$ satisfies (1) for some ${\sigma }_0$ and ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_T\left({\sigma }_0\right)}$. Then, T has a fuzzy-fixed-point.

Proof. 

Let T satisfy the conditions of Theorem 1 above, and if f is upper semi-continuous, then from (8), for any $\sigma \in \Delta ,$ $\eta \in {\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},$ we obtain

$$\mathsf{\ell }(\eta ,{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},kt)\ge H_{\mathsf{\ell }}({\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},kt)\ge \mathsf{\ell }(\sigma ,\eta ,t).$$

□

Theorem 2.

Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space, where $\ast =min\{{\sigma }_1,{\sigma }_2\}$ and $\mathsf{\ell }(\sigma ,\eta ,.)$ is strictly increasing and

$$\underset{t\to \infty }{lim}\mathsf{\ell }(\sigma ,\eta ,t)=1\forall ,\sigma ,\eta \in \Delta .$$

(9)

Let M: $\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping such that ${\left[M\sigma \right]}_{{\alpha }_M\left(\sigma \right)},{\left[M\eta \right]}_{{\alpha }_M\left(\eta \right)}\in K_{\mathsf{\ell }}(\Delta )$, which satisfies the given contraction condition

$$H_{\mathsf{\ell }}({\left[M\sigma \right]}_{{\alpha }_M\left(\sigma \right)},{\left[M\eta \right]}_{{\alpha }_M\left(\eta \right)},kt)\ge \mathsf{\ell }(\sigma ,{\left[M\sigma \right]}_{{\alpha }_M\left(\sigma \right)},t)\ast \mathsf{\ell }(\eta ,{\left[M\eta \right]}_{{\alpha }_M\left(\eta \right)},t),$$

(10)

for all $\sigma ,\eta \in \Delta ,$ where $t\ge 0$ and $0<k<1$; then, there will be a fuzzy-fixed-point of M.

Proof. 

Let ${\sigma }_0\in \Delta$, and then ${\left[M{\sigma }_0\right]}_{{\alpha }_M\left({\sigma }_0\right)}\ne \varphi \in K_{\mathsf{\ell }}(\Delta )$, and then there exists ${\sigma }_1\in {\left[M{\sigma }_0\right]}_{{\alpha }_M\left({\sigma }_0\right)}$; similarly, ${\left[M{\sigma }_1\right]}_{{\alpha }_M\left({\sigma }_1\right)}\ne \varphi \in K_{\mathsf{\ell }}(\Delta )$, and then there exists ${\sigma }_2\in {\left[M{\sigma }_1\right]}_{{\alpha }_M\left({\sigma }_1\right)}$.

By using Lemma 3, we have

$$\mathsf{\ell }({\sigma }_1,{\sigma }_2,t)\ge H_{\mathsf{\ell }}({\left[M{\sigma }_0\right]}_{{\alpha }_M\left({\sigma }_0\right)},{\left[M{\sigma }_1\right]}_{{\alpha }_M\left({\sigma }_1\right)},t).$$

By using (10), we have

$$\mathsf{\ell }({\sigma }_1,{\sigma }_2,t)\ge \mathsf{\ell }({\sigma }_0,{\left[M{\sigma }_0\right]}_{{\alpha }_M\left({\sigma }_0\right)},{\displaystyle \frac{t}{k}})\ast \mathsf{\ell }({\sigma }_1,{\left[M{\sigma }_1\right]}_{{\alpha }_M\left({\sigma }_1\right)},{\displaystyle \frac{t}{k}}),$$

$$\mathsf{\ell }({\sigma }_1,{\sigma }_2,t)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k}})\ast \mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}}).$$

We know that $\mathsf{\ell }(\sigma ,\eta ,t)$ is strictly increasing in terms of variable t, so we can write

$$\mathsf{\ell }({\sigma }_1,{\sigma }_2,t)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k}}).$$

Again, we have

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge H_{\mathsf{\ell }}({\left[M{\sigma }_1\right]}_{{\alpha }_M\left({\sigma }_1\right)},{\left[M{\sigma }_2\right]}_{{\alpha }_M\left({\sigma }_2\right)},t).$$

By using (10), we have

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mathsf{\ell }({\sigma }_1,{\left[M{\sigma }_1\right]}_{{\alpha }_M\left({\sigma }_1\right)},{\displaystyle \frac{t}{k}})\ast \mathsf{\ell }({\sigma }_2,{\left[M{\sigma }_2\right]}_{{\alpha }_M\left({\sigma }_2\right)},{\displaystyle \frac{t}{k}}),$$

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}})\ast \mathsf{\ell }({\sigma }_2,{\sigma }_3,{\displaystyle \frac{t}{k}}).$$

We know that $\mathsf{\ell }(\sigma ,\eta ,t)$ is strictly increasing in terms of variable t, so we can write

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}})\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}}).$$

In this way, we obtain

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},t)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^n}}).$$

(11)

Let $m,n\in \mathbb{N}$ such that m = n + p.

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)\ge \mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},{\displaystyle \frac{t}{p}})\ast \dots \ast \mathsf{\ell }({\sigma }_{n+p-1},{\sigma }_{n+p},{\displaystyle \frac{t}{p}}),p-times.$$

By using (11), we have

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{p{k}^n}})\ast \dots \ast \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{p{k}^{n+p-1}}}).$$

Now, we take ${lim}_{n\to \infty }$ by using (9) and by using the definition of the fuzzy metric space:

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)\ge 1\ast 1\ast 1\dots \ast 1.$$

$$\Rightarrow \mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)\ge 1.$$

$$\Rightarrow \mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)=1.$$

Thus, $\left\{{\sigma }_n\right\}$ is a Cauchy sequence in $\Delta$. According to the completeness of $\Delta$, there exists a point, q, in $\Delta$, such that ${\sigma }_n\to q$.

Now, we have

$$\mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)\ge \mathsf{\ell }(\xi ,{\sigma }_{n+1},(1-k)t)\ast \mathsf{\ell }({\sigma }_{n+1},{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t),$$

$$\mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)\ge \mathsf{\ell }(\xi ,{\sigma }_{n+1},(1-k)t)\ast H_{\mathsf{\ell }}({\left[M{\sigma }_n\right]}_{{\alpha }_M\left({\sigma }_n\right)},{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t),$$

$$\mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)\ge \mathsf{\ell }(\xi ,{\sigma }_{n+1},(1-k)t)\ast \mathsf{\ell }({\sigma }_n,{\left[M{\sigma }_n\right]}_{{\alpha }_M\left({\sigma }_n\right)},{\displaystyle \frac{t}{k}})\ast \mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},{\displaystyle \frac{t}{k}}).$$

If $n\to \infty ,$ then ${\sigma }_n\to \xi ,{\sigma }_{n+1}\to \xi$.

$$\mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)\ge \mathsf{\ell }(\xi ,\xi ,(1-k)t)\ast \mathsf{\ell }(\xi ,{\sigma }_{n+1},{\displaystyle \frac{t}{k}})\ast \mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},{\displaystyle \frac{t}{k}}),$$

$$\mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)\ge \mathsf{\ell }(\xi ,\xi ,(1-k)t)\ast \mathsf{\ell }(\xi ,\xi ,{\displaystyle \frac{t}{k}})\ast \mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},{\displaystyle \frac{t}{k}}).$$

According to the definition of the fuzzy metric space, ${lim}_{t\to \infty }\mathsf{\ell }(\sigma ,y,t)=1$ $t>0$ iff $\sigma =y$.

$$\mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)\ge 1\ast 1\ast \mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},{\displaystyle \frac{t}{k}}).$$

We know that $\mathsf{\ell }(\sigma ,\eta ,t)$ is strictly increasing in terms of variable t:

$$\Rightarrow \mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)\ge 1$$

$$\Rightarrow \mathsf{\ell }(\xi ,{\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)},t)=1$$

$$\Rightarrow \xi \in {\left[M\xi \right]}_{{\alpha }_M\left(\xi \right)}$$

Thus, $\xi$ is a fuzzy-fixed-point of $M.$ □

Example 8.

Let $\Delta =[0,\infty ]$ be a complete metric space with the metric d defined as $d(\sigma ,\eta )=|\sigma -\eta |$ and g: ${\mathbb{R}}^{+}\to [0,\infty )$ be an increasing continuous function. We define a map, $\mathsf{\ell }:{\Delta }^2\times (0,\infty )\to [0,1]$, as

$$\mathsf{\ell }(\sigma ,\eta ,t)=e^{(-{\displaystyle \frac{d(\sigma ,\eta )}{g\left(t\right)}})}$$

$t>0$ for all $\sigma ,\eta \in \Delta$. Then, $(\Delta ,\mathsf{\ell },\ast )$ is a fuzzy metric space on Δ, where ∗ is the product t-norm.

We define a mapping

$$M:\Delta \to \mathsf{Ϝ}(\Delta )$$

$$M\left(\sigma \right)\left(t\right)=\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & \mathit{if}0\le t\le 3\sigma \hfill \\ {\displaystyle \frac{1}{3}},\hfill & \mathit{if}3\sigma <t<4\sigma \hfill \\ 0,\hfill & \mathit{if}4\sigma \le t<\infty .\hfill \end{array}$$

For $\alpha ={\displaystyle \frac{1}{2}}$,

$${\left[M\sigma \right]}_{{\displaystyle \frac{1}{2}}}=\{t:M\sigma \left(t\right)\ge {\displaystyle \frac{1}{2}}\}=[0,3\sigma ]$$

$${\left[M\eta \right]}_{{\displaystyle \frac{1}{2}}}=\{t:M\eta \left(t\right)\ge {\displaystyle \frac{1}{2}}\}=[0,3\eta ].$$

All the conditions of Theorem 2 are satisfied. So, M has a fuzzy-fixed-point in the fuzzy metric space Δ.

Theorem 3.

Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space and T: $\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping satisfying these conditions.

$$\underset{t\to \infty }{lim}\mathsf{\ell }(\sigma ,\eta ,t)=1,$$

(12)

$$H_{\mathsf{\ell }}({\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},kt)\ge \mu (\sigma ,\eta ,t),$$

(13)

where $\mu (\sigma ,\eta ,t)=min\left\{\mathsf{\ell }(\sigma ,\eta ,t),\mathsf{\ell }(\sigma ,{\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},t),\mathsf{\ell }(\eta ,{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},t)\right\}$ for all $\sigma ,\eta \in \Delta ,$ $\alpha \in (0,1]$, $k\in (0,1)$ and ${\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)}\in K_{\mathsf{\ell }}(\Delta )$. Then, T has a fuzzy-fixed-point.

Proof. 

Let ${\sigma }_0\in \Delta$; ${\left[T{\sigma }_0\right]}_{{\alpha }_T\left({\sigma }_0\right)}\ne \varphi$ and belongs to $K_{\mathsf{\ell }}(\Delta )$, so there exists ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_T\left({\sigma }_o\right)}$. Similarly, we have ${\sigma }_2\in {\left[T{\sigma }_1\right]}_{{\alpha }_T\left({\sigma }_1\right)}.$ By using Lemma 3, we have

$$\mathsf{\ell }({\sigma }_1,{\sigma }_2,t)\ge H_{\mathsf{\ell }}({\left[T{\sigma }_0\right]}_{{\alpha }_T\left({\sigma }_0\right)},{\left[T{\sigma }_1\right]}_{{\alpha }_T\left({\sigma }_1\right)},t).$$

(14)

We can write

$${\sigma }_{n+1}\in {\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)}\forall n\in \mathbb{N}\cup \left\{0\right\}.$$

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},t)\ge H_{\mathsf{\ell }}({\left[T{\sigma }_{n-1}\right]}_{{\alpha }_T\left({\sigma }_{n-1}\right)},{\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},t).$$

(15)

Now, we have

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge H_{\mathsf{\ell }}({\left[T{\sigma }_1\right]}_{{\alpha }_T\left({\sigma }_1\right)},{\left[T{\sigma }_2\right]}_{{\alpha }_T\left({\sigma }_2\right)},t).$$

(16)

By using (13), we have

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mu ({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}}),$$

(17)

where

$$\begin{array}{cc}\hfill \mu ({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}})=& min\{\mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}}),\mathsf{\ell }({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_T\left({\sigma }_1\right)},{\displaystyle \frac{t}{k}}),\mathsf{\ell }({\sigma }_2,{\left[T{\sigma }_2\right]}_{{\alpha }_T\left({\sigma }_2\right)},{\displaystyle \frac{t}{k}})\}\hfill \\ \hfill =& min\{\mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}}),\mathsf{\ell }({\sigma }_2,{\sigma }_3,{\displaystyle \frac{t}{k}})\}.\hfill \end{array}$$

If

$$\mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}})\ge \mathsf{\ell }({\sigma }_2,{\sigma }_3,{\displaystyle \frac{t}{k}})$$

then by using (17), we have

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mathsf{\ell }({\sigma }_2,{\sigma }_3,{\displaystyle \frac{t}{k}}).$$

So, according to Lemma 4, there is nothing left to prove. If

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,{\displaystyle \frac{t}{k}})\ge \mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}}),$$

then by using Lemma 3, we have

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k}}).$$

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge H_{\mathsf{\ell }}({\left[T{\sigma }_0\right]}_{{\alpha }_T\left({\sigma }_0\right)},{\left[T{\sigma }_1\right]}_{{\alpha }_T\left({\sigma }_1\right)},{\displaystyle \frac{t}{k}}).$$

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mu ({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}}).$$

(18)

Now, we know that

$$\begin{array}{cc}\hfill \mu ({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}})=& min\{\mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}}),\mathsf{\ell }({\sigma }_0,{\left[T{\sigma }_0\right]}_{{\alpha }_T\left({\sigma }_0\right)},{\displaystyle \frac{t}{k^2}}),\mathsf{\ell }({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_T\left({\sigma }_1\right)},{\displaystyle \frac{t}{k^2}})\}\hfill \\ \hfill =& min\{\mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}}),\mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k^2}})\}.\hfill \end{array}$$

If

$$\mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}})\ge \mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k^2}}),$$

then by using Lemma 4, there is nothing left to prove. If

$$\mathsf{\ell }({\sigma }_1,{\sigma }_2,{\displaystyle \frac{t}{k^2}})\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}}),$$

then by using (18),

$$\mathsf{\ell }({\sigma }_2,{\sigma }_3,t)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^2}}).$$

Consequently, we obtain

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},t)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{k^n}}).$$

(19)

Let $m,n\in \mathbb{N}$ such that m = n + p; then,

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)\ge \mathsf{\ell }({\sigma }_n,{\sigma }_{n+1},{\displaystyle \frac{t}{p}})\ast ...\ast \mathsf{\ell }({\sigma }_{n+p-1},{\sigma }_{n+p},{\displaystyle \frac{t}{p}}),p-times$$

By using (19), we have

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)\ge \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{p{k}^n}})\ast ...\ast \mathsf{\ell }({\sigma }_0,{\sigma }_1,{\displaystyle \frac{t}{p{k}^{n+p-1}}}).$$

Now, by taking $n\to \infty$ as well as using (12) and the definition of the fuzzy metric space, we have

$$\mathsf{\ell }({\sigma }_n,{\sigma }_{n+p},t)=1.$$

Thus, $\left\{{\sigma }_n\right\}$ is a Cauchy sequence in $\Delta$. According to the completeness of $\Delta$, we can find a point, q, in $\Delta$, such that ${\sigma }_n\to q.$ Now, we have

$$\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\ge \mathsf{\ell }(q,{\sigma }_{n+1},(1-k)t)\ast \mathsf{\ell }({\sigma }_{n+1},{\left[Tq\right]}_{{\alpha }_T\left(q\right)},kt)$$

$$\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\ge \mathsf{\ell }(q,{\sigma }_{n+1},(1-k)t)\ast H_{\mathsf{\ell }}({\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},{\left[Tq\right]}_{{\alpha }_T\left(q\right)},kt)$$

$$\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\ge \mathsf{\ell }(q,{\sigma }_{n+1},(1-k)t)\ast \mu ({\sigma }_n,q,t),$$

(20)

where

$$\begin{array}{cc}\hfill \mu ({\sigma }_n,q,t)=& min\{\mathsf{\ell }({\sigma }_n,q,t),\mathsf{\ell }({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_T\left({\sigma }_n\right)},t),\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\}.\hfill \end{array}$$

In the limiting case ${\sigma }_n\to q$,

$$\mu (q,q,t)=min\{\mathsf{\ell }(q,q,t),\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t),\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\}$$

$$\mu (q,q,t)=min\{\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\}.$$

If $\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\ge 1$, then we obtain our desired result. If $\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\le 1$, then by using (20), we obtain

$$\mathsf{\ell }(q,{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)\ge \mathsf{\ell }(q,{\sigma }_{n+1},(1-k)t)\ast \mathsf{\ell }({\sigma }_{n+1},{\left[Tq\right]}_{{\alpha }_T\left(q\right)},t)$$

$$q\in {\left[Tq\right]}_{{\alpha }_T\left(q\right)},asn\to \infty .$$

Thus, q is a fuzzy-fixed-point of $T.$ □

Corollary 2.

Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space and T: $\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping satisfying these conditions.

$$\left(a\right)\underset{t\to \infty }{lim}\mathsf{\ell }(\sigma ,\eta ,t)=1,$$

$$\left(b\right)H_{\mathsf{\ell }}({\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)},kt)\ge \mathsf{\ell }(\sigma ,\eta ,t),$$

for all $\sigma ,\eta \in \Delta$ $\alpha \in (0,1]$ and $k\in (0,1)$, such that ${\left[T\sigma \right]}_{{\alpha }_T\left(\sigma \right)},{\left[T\eta \right]}_{{\alpha }_T\left(\eta \right)}\in K_{\mathsf{\ell }}(\Delta )$. Then, T has a fuzzy-fixed-point.

Theorem 4.

Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space and $T:\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping satisfying these conditions.

$$\left(a\right)\underset{t\to \infty }{lim}\mathsf{\ell }(m,n,t)=1,$$

$$\left(b\right)H_{\mathsf{\ell }}({\left[Tm\right]}_{{\alpha }_T\left(m\right)},{\left[Tn\right]}_{{\alpha }_T\left(n\right)},kt)\ge \lambda \left\{\mu (m,n,t)\right\},$$

where

$$\mu (m,n,t)=min\{\mathsf{\ell }(m,n,t),\mathsf{\ell }(m,{\left[Tm\right]}_{{\alpha }_T\left(m\right)},t),\mathsf{\ell }(n,{\left[Tn\right]}_{{\alpha }_T\left(n\right)},t)\}$$

for all $m,n\in \Delta$ $\alpha \in (0,1],$ $k\in (0,1)$ and $\lambda \in \varpi$, such that ${\left[Tm\right]}_{{\alpha }_T\left(m\right)},{\left[Tn\right]}_{{\alpha }_T\left(n\right)}\in K_{\mathsf{\ell }}(\Delta )$. Then, T has a fuzzy-fixed-point.

Proof. 

Using Definition 13, we obtain $\lambda \left(\iota \right)>\iota$ for all $0<\iota <1.$

Thus, we have

$$H_{\mathsf{\ell }}({\left[Tm\right]}_{{\alpha }_T\left(m\right)},{\left[Tn\right]}_{{\alpha }_T\left(n\right)},kt)\ge \lambda \left\{\mu (m,n,t)\right\}\ge \mu (m,n,t)$$

Now, using Theorem 3, we obtain the desired result. □

Corollary 3.

Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space and T: $\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping satisfying these conditions.

$$\left(a\right)\underset{t\to \infty }{lim}\mathsf{\ell }(m,n,t)=1,$$

$$\left(b\right)H_{\mathsf{\ell }}({\left[Tm\right]}_{{\alpha }_T\left(m\right)},{\left[Tn\right]}_{{\alpha }_T\left(n\right)},kt)\ge \lambda \mathsf{\ell }((m,n,t),$$

for all $m,n\in \Delta$ $\alpha \in (0,1],$ $k\in (0,1)$ and $\lambda \in \varpi$, such that ${\left[Tm\right]}_{{\alpha }_T\left(m\right)},{\left[Tn\right]}_{{\alpha }_T\left(m\right)}\in K_{\mathsf{\ell }}(\Delta )$. Then, T has a fuzzy-fixed-point.

3.1. Applications

Let us define a function, $\theta :[0,\infty )\to [0,\infty )$, as

$$\theta \left(\beta \right)={\int }_0^{\beta }\varphi \left(\beta \right)d\beta$$

and as a non-decreasing and continuous function. Moreover, for each $\beta >0$, $\varphi \left(\beta \right)>0.$ Also, $\varphi \left(\beta \right)=0$ if and only if $\beta =0.$

Theorem 5.

Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space and T: $\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping satisfying the following conditions

$$\underset{t\to \infty }{lim}\mathsf{\ell }(m,n,t)=1,$$

and

$${\int }_0^{H_{\mathsf{\ell }}({\left[Tm\right]}_{{\alpha }_T\left(m\right)},{\left[Tn\right]}_{{\alpha }_T\left(n\right)},kt)}\varphi \left(\beta \right)d\beta \ge {\int }_0^{\mu (m,n,t)}\varphi \left(\beta \right)d\beta ,$$

where

$$\mu (m,n,t)=min\{\mathsf{\ell }(m,n,t),\mathsf{\ell }(m,{\left[Tm\right]}_{{\alpha }_T\left(m\right)},t),\mathsf{\ell }(n,{\left[Tn\right]}_{{\alpha }_T\left(n\right)},t)\},$$

for all $m,n\in \Delta$, $\varphi \left(\beta \right)\in [0,\infty )$, $\alpha \in (0,1]$, and $k\in (0,1)$, such that ${\left[Tm\right]}_{{\alpha }_T\left(m\right)},$ ${\left[Tn\right]}_{{\alpha }_T\left(n\right)}\in K_{\mathsf{\ell }}(\Delta )$. Then, T has a fuzzy-fixed-point.

Proof. 

Let us take $\varphi \left(\beta \right)=1$; by using Theorem 3, we obtain the desired result. □

Theorem 6.

Let $(\Delta ,\mathsf{\ell },\ast )$ be a complete fuzzy metric space and T: $\Delta \to \mathsf{Ϝ}(\Delta )$ be a fuzzy-mapping satisfying the following conditions:

$$\underset{t\to \infty }{lim}\mathsf{\ell }(m,n,t)=1,$$

and

$${\int }_0^{H_{\mathsf{\ell }}({\left[Tm\right]}_{{\alpha }_T\left(m\right)},{\left[Tn\right]}_{{\alpha }_T\left(n\right)},kt)}\varphi \left(\beta \right)d\beta \ge \lambda \left\{{\int }_0^{\mu (m,n,t)}\varphi \left(\beta \right)d\beta \right\},$$

where

$$\mu (m,n,t)=min\{\mathsf{\ell }(m,n,t),\mathsf{\ell }(m,{\left[Tm\right]}_{{\alpha }_T\left(m\right)},t),\mathsf{\ell }(n,{\left[Tn\right]}_{{\alpha }_T\left(n\right)},t)\}$$

for all $m,n\in \Delta$, $\varphi \left(\beta \right)\in [0,\infty )$, $\lambda \in \varpi$, $\alpha \in (0,1]$, and $k\in (0,1)$, such that ${\left[Tm\right]}_{{\alpha }_T\left(m\right)},$ ${\left[Tn\right]}_{{\alpha }_T\left(n\right)}\in K_{\mathsf{\ell }}(\Delta )$. Then, T has a fuzzy-fixed-point.

Proof. 

Using Definition 13, we obtain $\lambda \left(\iota \right)>\iota$ for all $0<\iota <1.$ Taking $\varphi \left(\beta \right)=1$ and using Theorem 3, we obtain the desired result. □

4. Conclusions

Fixed-point theory, acknowledged for its versatility in numerous mathematical realms, provides crucial methods for validating both the existence and uniqueness of solutions. In our study, we investigated the fixed-point theorem for fuzzy-mappings under various fuzzy contractive conditions in the context of complete fuzzy metric spaces. Moreover, we supported our results with examples and demonstrated their applicability across various contraction methods. These results have significant implications for theoretical research and practical applications in diverse fields, including fuzzy logic, decision theory, and fixed-point theory. The established theorems provide a solid foundation for further advancements in the study of fuzzy metric spaces and their extensions. By applying the concepts of multivalued mappings to the framework of fuzzy-mappings in fuzzy metric spaces, the outcome of this paper advances fixed-point theory and serves as a foundation for further study. Specifically, this paper’s findings can be applied to a broad variety of contexts, including fuzzy b-metric spaces, L-fuzzy sets, linear matrix inequality techniques [28], and fuzzy difference equations [29]. These existence results are expected to offer a conducive framework for approximating additional operator equations in applied science, thereby advancing current research efforts. We anticipate that our research will contribute significantly to the field.