On the Global Dynamics of a Fourth-Order Riccati-Type Exponential Fuzzy Difference Equation
Abstract
1. Introduction and Motivation
2. Preliminaries
- (i)
- **Normality:** There exists some such that .
- (ii)
- **Fuzzy Convexity:** For all and ,
- (iii)
- **Upper Semicontinuity:** The function u is upper semicontinuous on .
- (iv)
- **Compact Support:** The support of u, denoted asis a compact set.
- (i)
- The function is LC (i.e., left-continuous) on , RC (i.e., right-continuous) at 0, bounded, and non-decreasing.
- (ii)
- The function is LC (i.e., left-continuous) on , RC (i.e., right-continuous) at 0, bounded, and non-increasing.
- (iii)
- .
- (i)
- for .
- (ii)
- for .
- (iii)
- for .
- (iv)
- (v)
- for .
- (i)
- is a closed for any .
- (ii)
- If and , then .
- (iii)
- If we compute the convergence rate for any sequence from below to 0, we have .
- (iv)
- If we compute the convergence rate for any sequence from above to 0, we have .
- Persists if there exists such that ;
- Is bounded if there exists such that ;
- If , then the function is bounded and persists s.t .
- (1)
- The parametric shapes of that function are
- (2)
- The functions and are taken as continuous functions if for every , there exists s.twith , and for every , there exists such thatwith .
3. Main Results
- (i)
- (ii)
- System , where for , has a unique +ve equilibrium point (EP).andwhich shows that the given equation is stable asymptotically.
- Consider the following systems:for . Now,Let be a +ve fuzzy solution of (6), and for . Now, from (29), we havefor .Now, from (33) and (35), if , thenGiven that , , , , , and are all left-continuous, it follows from (34) that and are also left-continuous.
- Now, from (35), we have
From (39), and , and it is clear thatFrom (34), (38), and (40), it is clear that there exists that satisfiesLet us assume that (6) has another +ve EP with which satisfieswhereFor , we have and . Consequently, it follows that , confirming that x is the unique equilibrium point of (6).- Now, from (37), we have
- Now, if (29) is true, then
for .□
4. Numerical Simulation
5. Conclusions
- Managing the computational complexity of higher-order equations involving exponential terms and fuzzy parameters.
- Designing efficient numerical methods to verify theoretical results, especially for large initial conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dubois, D.; Prade, H. Possibility Theory: An Approach to Computerized Processing of Uncertainty; Plenum Publishing Corporation: New York, NY, USA, 1988. [Google Scholar]
- Din, Q. Global stability of a population model. Chaos Solitons Fractals 2014, 59, 119–128. [Google Scholar] [CrossRef]
- Din, Q.; Khan, K.; Nosheen, A. Stability Analysis of a System of Exponential Difference Equations. Discret. Dyn. Nat. Soc. 2014, 2014, 375890. [Google Scholar] [CrossRef]
- Din, Q. Asymptotic Behavior of a Second-Order Fuzzy Rational Difference Equation. J. Discret. Math. 2015, 2015, 524931. [Google Scholar] [CrossRef]
- Kalabušić, S.; Kulenović, M.; Pilav, E. Dynamics of a two-dimensional system of rational difference equations of Leslie–Gower type. Adv. Differ. Equ. 2011, 2011, 29. [Google Scholar] [CrossRef]
- Deeba, E.; de Korvin, A.; Koh, E. A fuzzy difference equation with an application. J. Differ. Equ. Appl. 1996, 2, 365–374. [Google Scholar] [CrossRef]
- Deeba, E.; de Korvin, A. Analysis by fuzzy difference equations of a model of CO2 level in the blood. Appl. Math. Lett. 1999, 12, 33–40. [Google Scholar] [CrossRef]
- Mondal, S.; Vishwakarma, D.; Saha, A. Solution of Second Order Linear Fuzzy Difference Equation by Lagrange’s Multiplier Method. J. Soft Comput. Appl. 2016, 2016, 11–27. [Google Scholar] [CrossRef][Green Version]
- Khastan, A. Fuzzy Logistic Difference Equation. Iran. J. Fuzzy Syst. 2018, 15, 55–66. [Google Scholar] [CrossRef]
- Papaschinopoulos, G.; Papadopoulos, B. On the fuzzy difference equation xn+1 = A + B/xn. Soft Comput. 2002, 6, 456–461. [Google Scholar] [CrossRef]
- Papaschinopoulos, G.; Papadopoulos, B. On the fuzzy difference equation xn+1 = a + xn/xn−m. Fuzzy Sets Syst. 2002, 129, 73–81. [Google Scholar] [CrossRef]
- Memarbashi, R.; Ghasemabadi, A. Fuzzy difference equations of Volterra type. Int. J. Nonlinear Anal. Appl. 2013, 4, 74–78. [Google Scholar] [CrossRef]
- Stefanidou, G.; Papaschinopoulos, G.; Schinas, C. On an Exponential-Type Fuzzy Difference Equation. Adv. Differ. Equ. 2010, 2010, 196920. [Google Scholar] [CrossRef]
- Sun, T.; Su, G.; Qin, B. On the fuzzy difference equation xn = F(xn−1, xn−k). Fuzzy Sets Syst. 2020, 387, 81–88. [Google Scholar] [CrossRef]
- Wang, C.; Su, X.; Liu, P.; Hu, X.; Li, R. On the dynamics of a five-order fuzzy difference equation. J. Nonlinear Sci. Appl. 2017, 10, 3303–3319. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.; Luo, Z. Dynamical behavior of a third-order rational fuzzy difference equation. Adv. Differ. Equ. 2015, 2015, 108. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.; Liao, D. Behavior of Solutions to a Fuzzy Nonlinear Difference Equation. Iran. J. Fuzzy Syst. 2012, 9, 1–12. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.; Liao, D. On first order fuzzy Ricatti difference equation. Inf. Sci. 2014, 270, 226–236. [Google Scholar] [CrossRef]
- Stefanini, L. A generalization of Hukuhara difference and division for interval and fuzzy arithmetic. Fuzzy Sets Syst. 2010, 161, 1564–1584. [Google Scholar] [CrossRef]
- Khastan, A.; Alijani, Z. On the New Solutions to the Fuzzy Difference Equation xn+1 = A + B/xn. Fuzzy Sets Syst. 2019, 358, 64–83. [Google Scholar] [CrossRef]
- Khastan, A. New solutions for first order linear fuzzy difference equations. J. Comput. Appl. Math. 2017, 312, 156–166. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, F.; Zhong, X. On discrete time Beverton–Holt population model with fuzzy environment. Math. Biosci. Eng. 2019, 16, 1471–1488. [Google Scholar] [CrossRef] [PubMed]
- Papaschinopoulos, G.; Stefanidou, G. Boundedness and asymptotic behavior of the solutions of a fuzzy difference equation. Fuzzy Sets Syst. 2003, 140, 523–539. [Google Scholar] [CrossRef]
- Yalçınkaya, İ.; Tollu, D.T.; Khastan, A.; Ahmad, H.; Botmart, T. Qualitative behavior of a higher-order fuzzy difference equation. AIMS Math. 2023, 8, 6309–6322. [Google Scholar] [CrossRef]
- Han, C.; Li, L.; Su, G.; Sun, T. Dynamical behaviors of a k-order fuzzy difference equation. Open Math. 2022, 20, 391–403. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, W.; Lin, F.; Li, D. On dynamic behavior of second-order exponential-type fuzzy difference equation. Fuzzy Sets Syst. 2021, 419, 169–187. [Google Scholar] [CrossRef]
- Atpinar, S.; Yazlik, Y. Qualitative behavior of exponential type of fuzzy difference equations system. J. Appl. Math. Comput 2023, 69, 4135–4162. [Google Scholar] [CrossRef]
- Bede, B. Mathematics of Fuzzy Sets and Fuzzy Logic; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Alamin, A.; Mondal, S.; Alam, S.; Goswami, A. Solution and stability analysis of non-homogeneous difference equation followed by real life application in fuzzy environment. Sadhana 2020, 45, 185. [Google Scholar] [CrossRef]
- Kocic, V.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Springer Science+Business Media: Dordrecht, The Netherlands, 1993. [Google Scholar] [CrossRef]
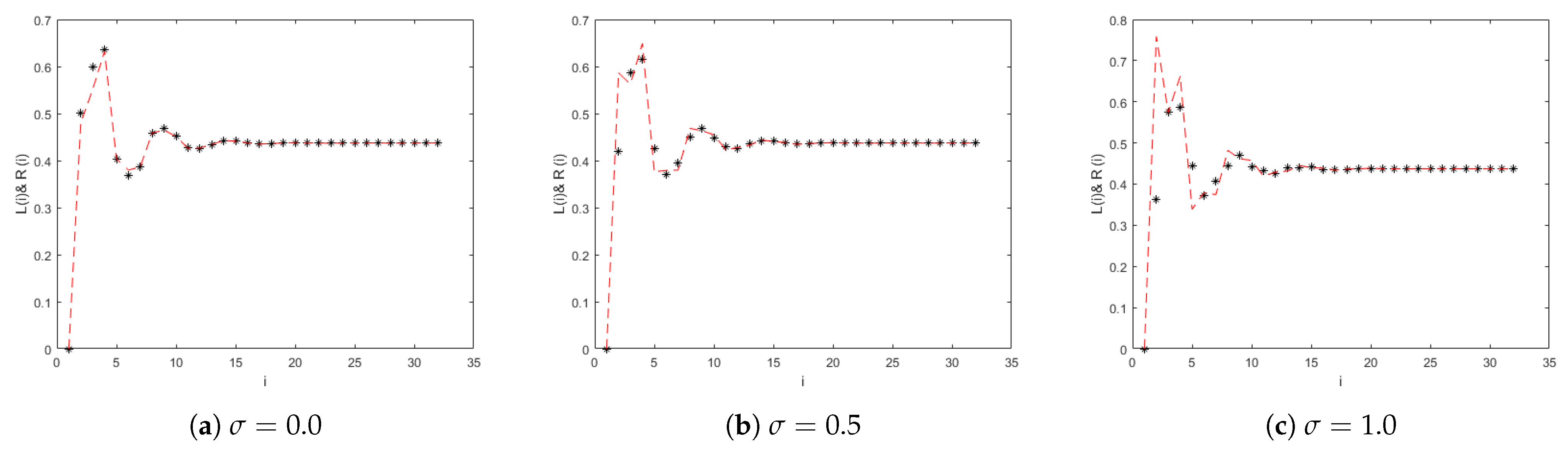

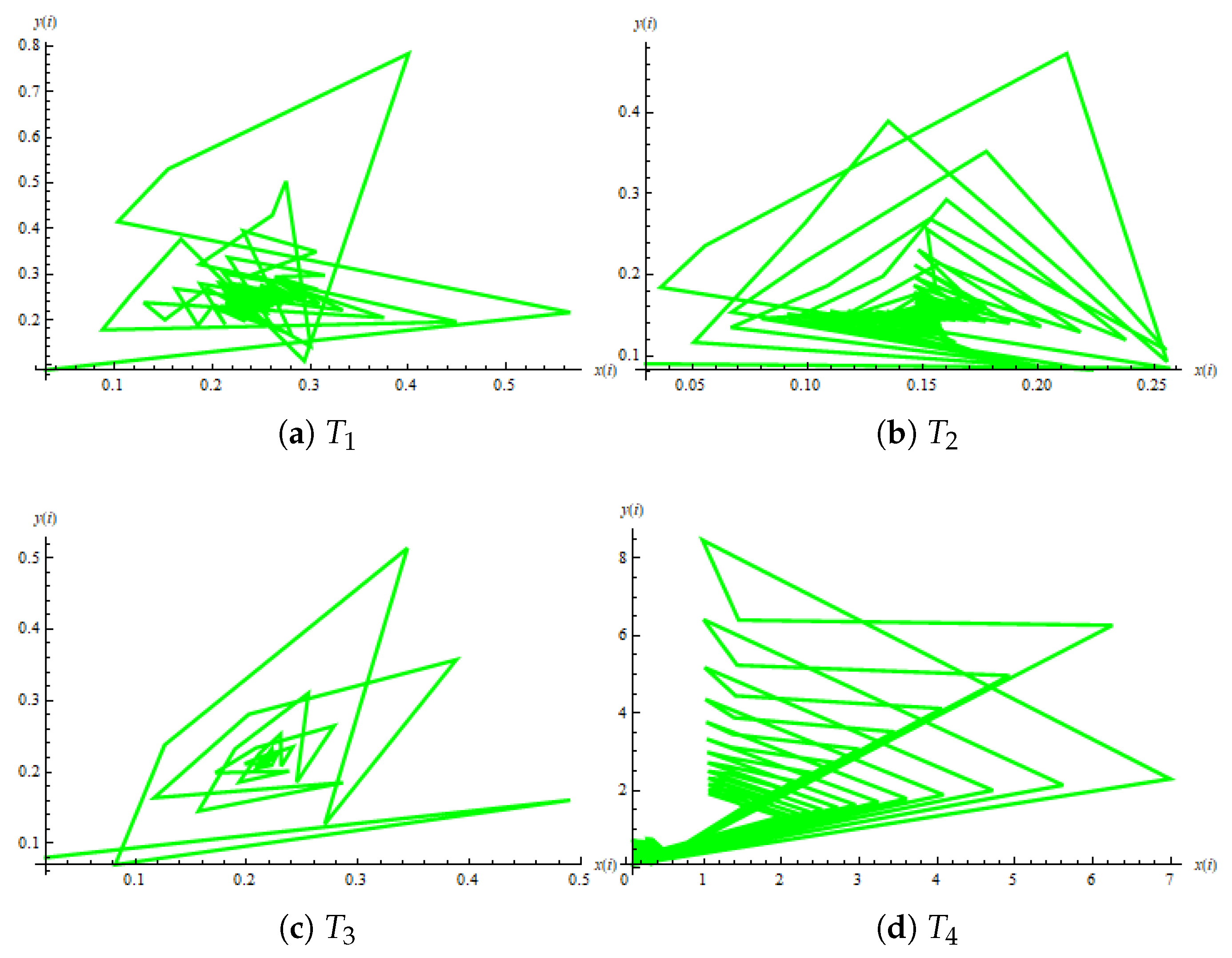
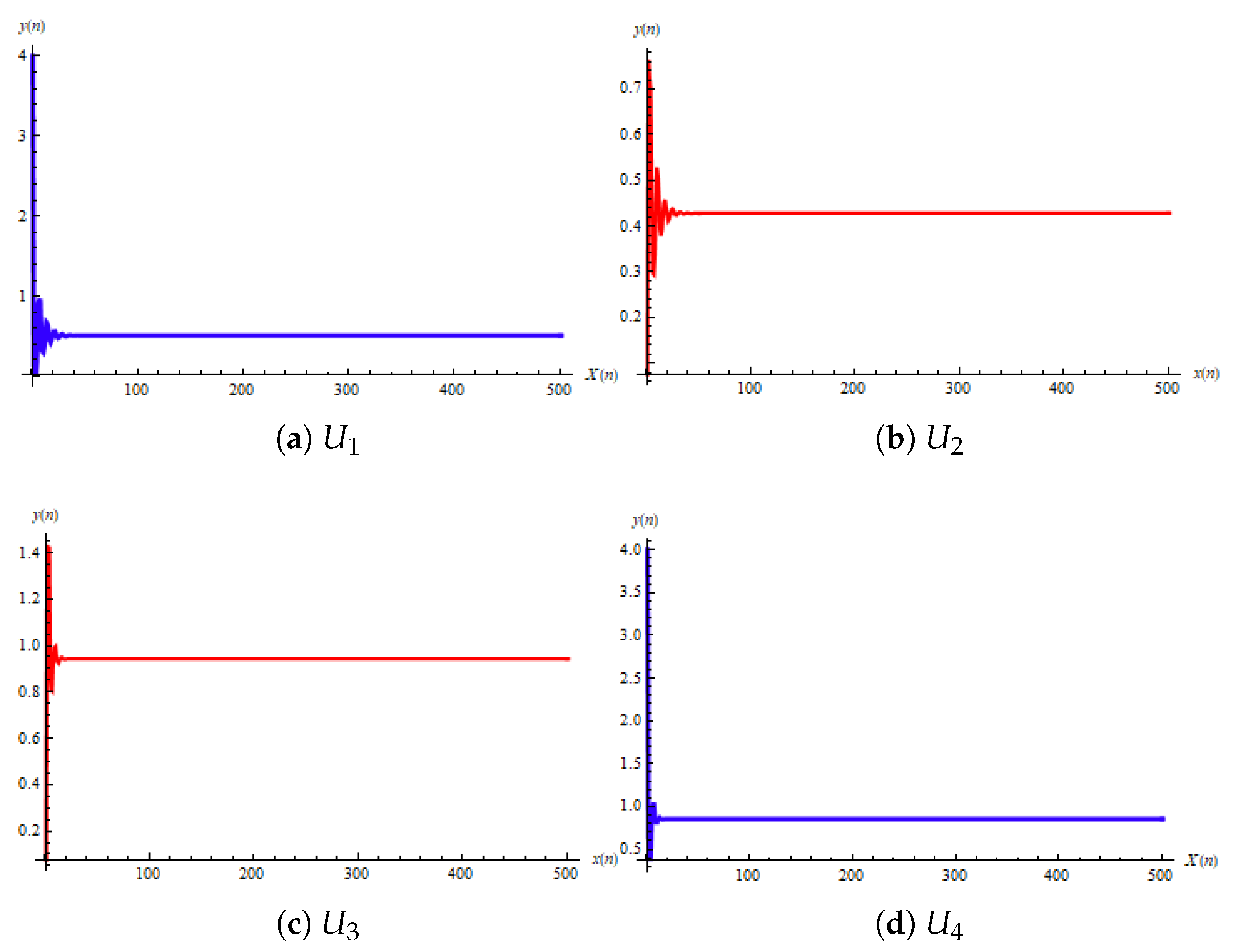
| Parameters (D, E, F) | Equilibrium Point | Trajectory |
|---|---|---|
| , , | ||
| , , | ||
| , , | ||
| , , |
| Parameters (D, E, F) | Equilibrium Point | Trajectory |
|---|---|---|
| , , | ||
| , , | ||
| 12, 15, 18 | ||
| 20, , 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tassaddiq, A.; Tanveer, M.; Usman, M.; Almutairi, D.K.; Alharbi, R. On the Global Dynamics of a Fourth-Order Riccati-Type Exponential Fuzzy Difference Equation. Axioms 2025, 14, 118. https://doi.org/10.3390/axioms14020118
Tassaddiq A, Tanveer M, Usman M, Almutairi DK, Alharbi R. On the Global Dynamics of a Fourth-Order Riccati-Type Exponential Fuzzy Difference Equation. Axioms. 2025; 14(2):118. https://doi.org/10.3390/axioms14020118
Chicago/Turabian StyleTassaddiq, Asifa, Muhammad Tanveer, Muhammad Usman, Dalal Khalid Almutairi, and Rabab Alharbi. 2025. "On the Global Dynamics of a Fourth-Order Riccati-Type Exponential Fuzzy Difference Equation" Axioms 14, no. 2: 118. https://doi.org/10.3390/axioms14020118
APA StyleTassaddiq, A., Tanveer, M., Usman, M., Almutairi, D. K., & Alharbi, R. (2025). On the Global Dynamics of a Fourth-Order Riccati-Type Exponential Fuzzy Difference Equation. Axioms, 14(2), 118. https://doi.org/10.3390/axioms14020118






