Orthogonal Polynomials on Radial Rays in the Complex Plane: Construction, Properties and Applications

Abstract

Orthogonal polynomials on radial rays in the complex plane were introduced and studied intensively in several papers almost three decades ago. This paper presents an account of such kinds of orthogonality in the complex plane, as well as a number of new results and examples. In addition to several types of standard orthogonality, the concept of orthogonality on arbitrary radial rays is introduced, some or all of which may be infinite. A general method for numerical constructing, the so-called discretized Stieltjes–Gautschi procedure, is described and several interesting examples are presented. The main properties, zero distribution and some applications are also given. Special attention is paid to completely symmetric cases. Recurrence relations for such kinds of orthogonal polynomials and their zero distribution, as well as a connection with the standard polynomials orthogonal on the real line, are derived, including the corresponding linear differential equation of the second order. Finally, some applications in physics and electrostatics are mentioned.

1. Introduction

Orthogonal polynomial sequences play a fundamental role in mathematics (approximation theory, Fourier series, numerical analysis, special functions, etc.), and also in many other computational and applied sciences, physics, chemistry, engineering, etc. In this paper, we give an account on polynomials that are orthogonal on the radial rays in the complex plane, as well as some new results and examples for such kinds of orthogonal polynomials. We introduced and studied such polynomials in several papers [1,2,3,4,5], including an electrostatic interpretation of their zeros in the case of the generalized Gegenbauer polynomials, assuming a logarithmic potential [6]. Polynomials that are orthogonal on radial rays were mentioned in the book [7] (p. 111). An extended Dunkl oscillator model based on our generalized Hermite polynomials on radial rays [1,2] was discussed very recently by Bouzeffour [8] (see also [9]). Also, we mention here the references [10,11], which may have some connection to our results.

This paper is organized as follows. In Section 2, we present some basic facts from the standard theory of orthogonality on the real line, necessary for the development of orthogonality on the radial rays in the complex plane, while in Section 3, we very briefly mention some classes of orthogonal polynomials in the complex plane. Orthogonal polynomials on the radial rays are presented in Section 4, including the existence and uniqueness of such polynomials, the general distribution of their zeros and some interesting examples. The numerical construction of this class of orthogonal polynomials is presented in Section 5. In particular, the cases on finite and infinite radial rays are considered, as well as the cases with Jacobi weight functions on equidistant rays. An approach, called the discretized Stieltjes–Gautschi procedure, has been developed as the main method for the numerical construction of orthogonal polynomials on arbitrary radial rays and with arbitrary weight functions. The fully symmetric cases of orthogonal polynomials on radial rays and their zero distributions are studied in Section 6. In particular, the cases with Jacobi and Legendre weight functions on $[0,1]$ and generalized Laguerre and Hermite weights on $[0,+\infty )$, as well as their connection with the standard orthogonal polynomials on the real line, are discussed, including differential equations. Finally, in Section 7, some applications in physics and electrostatics are considered.

2. Orthogonal Polynomials on the Real Line

Orthogonal polynomials on the real line $\mathbb{R}$, related to the inner product

$$(p,q)={\int }_{\mathbb{R}}p\left(t\right)q\left(t\right)\mathrm{d}\mu \left(t\right)\left(p,q\in L^2(\mathbb{R};\mathrm{d}\mu )\right),$$

(1)

are the most important in applications. Here, $\mathrm{d}\mu$ is a positive measure on $\mathbb{R}$, with finite or unbounded support, for which all moments ${\mu }_k={\int }_{\mathbb{R}}{t}^k\mathrm{d}\mu \left(t\right)$, $k\ge 0$ exist and are finite, and ${\mu }_0>0$ (cf. [12,13]). If we work with complex polynomials (polynomials with complex coefficients ), then the second component $q\left(t\right)$ in (1) should be conjugated, i.e., $\overline{q\left(t\right)}$.

An interesting class of the measures are those when $\mu$ is an absolutely continuous function. Then, ${\mu }^{\prime }\left(t\right)=w\left(t\right)$ is a weight function, which is non-negative and measurable in Lebesgue’s sense for which all moments exist and ${\mu }_0>0$.

Because of the property $(tp,q)=(p,tq)$, the orthogonal polynomials ${\pi }_k\left(t\right)$ on $\mathbb{R}$ satisfy a three-term recurrence relation of the form

$${\pi }_{k+1}\left(t\right)=(t-{\alpha }_k){\pi }_k\left(t\right)-{\beta }_k{\pi }_{k-1}\left(t\right),k=0,1,2\dots ,$$

(2)

with ${\pi }_0\left(t\right)=1$ and ${\pi }_{-1}\left(t\right)=0$. The recursion coefficients ${\alpha }_k$ and ${\beta }_k$ in (2) can be expressed over the inner product as

$${\alpha }_k={\displaystyle \frac{(t{\pi }_k,{\pi }_k)}{({\pi }_k,{\pi }_k)}}(k\ge 0),{\beta }_k={\displaystyle \frac{({\pi }_k,{\pi }_k)}{({\pi }_{k-1},{\pi }_{k-1})}}(k\ge 1),$$

and they depend on the weight function w (in general, on the measure $\mathrm{d}\mu$). The coefficient ${\beta }_0$, which is multiplied by ${\pi }_{-1}\left(t\right)=0$ in (2), can be arbitrary, but usually, it is convenient to take ${\beta }_0={\mu }_0$. In this case, we have $\parallel {\pi }_k{\parallel }^2=({\pi }_k,{\pi }_k)={\beta }_0{\beta }_1\cdots {\beta }_k$.

Alternatively, these recursion coefficients can be expressed in terms of the Hankel determinants

$${\alpha }_k={\displaystyle \frac{{\Delta }_{k+1}^{\prime }}{{\Delta }_{k+1}}}-{\displaystyle \frac{{\Delta }_k^{\prime }}{{\Delta }_k}}(k\ge 0),{\beta }_k={\displaystyle \frac{{\Delta }_{k-1}{\Delta }_{k+1}}{{\Delta }_k^2}}(k\ge 1),$$

where

$${\Delta }_k=\left|\begin{array}{cccc}{\mu }_0& {\mu }_1& \cdots & {\mu }_{k-1}\\ {\mu }_1& {\mu }_2& \cdots & {\mu }_k\\ ⋮& & & \\ {\mu }_{k-1}& {\mu }_k& \cdots & {\mu }_{2k-2}\end{array}\right|\mathrm{and}{\Delta }_k^{\prime }=\left|\begin{array}{ccccc}{\mu }_0& {\mu }_1& \cdots & {\mu }_{k-2}& {\mu }_k\\ {\mu }_1& {\mu }_2& \cdots & {\mu }_{k-1}& {\mu }_{k+1}\\ ⋮& & & \\ {\mu }_{k-1}& {\mu }_k& \cdots & {\mu }_{2k-3}& {\mu }_{2k-1}\end{array}\right|.$$

The polynomials ${\pi }_k\left(t\right)$ and $k\ge 1$, which are orthogonal with respect to the inner product (1), have only real zeros, are mutually different and are located in the support of the measure $\mathrm{d}\mu$. Moreover, the zeros of two consecutive polynomials, $p_k\left(t\right)$ and $p_{k+1}\left(t\right)$, interlace, i.e.,

$${\tau }_1^{(k+1)}<{\tau }_1^{\left(k\right)}<{\tau }_2^{(k+1)}<{\tau }_2^{\left(k\right)}<\cdots <{\tau }_k^{(k+1)}<{\tau }_k^{\left(k\right)}<{\tau }_{k+1}^{(k+1)},$$

where ${\tau }_1^{\left(k\right)}<{\tau }_2^{\left(k\right)}<\cdots <{\tau }_k^{\left(k\right)}$ denotes the zeros of ${\pi }_k\left(t\right)$ in increasing order (see [13], pp. 99–101).

The zeros of the orthogonal polynomials ${\pi }_n\left(t\right)$, in notation ${\tau }_k^{\left(n\right)}$, $k=1,2,\dots ,n$, play an important role in the Gauss quadrature formula related to the measure $\mathrm{d}\mu$. Namely, for each $n\in \mathbb{N}$, there exists the n-point Gauss formula

$${\int }_{\mathbb{R}}f\left(t\right)\mathrm{d}\mu \left(t\right)=\sum _{k=1}^n{A}_k^{\left(n\right)}f\left({\tau }_k^{\left(n\right)}\right)+R_n\left(f\right),$$

(3)

which is exact for all algebraic polynomials of degree at most $2n-1$, i.e., $R_n\left(f\right)=0$ for each $f\in {\mathcal{P}}_{2n-1}$ ($\mathcal{P}$ denotes the space of all algebraic polynomials, and ${\mathcal{P}}_m$ is its subspace of polynomials of degree at most m). Thus, there is a deep connection between the Gauss quadrature Formula (3) and the orthogonal polynomial sequence $\left\{{\pi }_n\left(t\right)\right\}$. The quadrature nodes ${\tau }_k^{\left(n\right)}$, $k=1,2,\dots ,n$, are zeros of the polynomial ${\pi }_n\left(t\right)$, i.e., the eigenvalues of the symmetric tridiagonal Jacobi matrix

$$J_n\left(\mathrm{d}\mu \right)=\left[\begin{array}{ccccc}{\alpha }_0& \sqrt{{\beta }_1}& & & \mathbf{O}\\ \sqrt{{\beta }_1}& {\alpha }_1& \sqrt{{\beta }_2}\\ & \sqrt{{\beta }_2}& {\alpha }_2& \ddots \\ & & \ddots & \ddots & \sqrt{{\beta }_{n-1}}\\ \mathbf{O}& & & \sqrt{{\beta }_{n-1}}& {\alpha }_{n-1}\end{array}\right],$$

(4)

while the weight coefficients in the quadrature rule (3) are given by $A_k^{\left(n\right)}={\beta }_0{v}_{k,1}^2$, $k=1,2,\dots ,n$, where $v_{k,1}$ is the first component of the (normalized) eigenvector ${\mathbf{v}}_k$, corresponding to the eigenvalue ${\tau }_k^{\left(n\right)}$, with Euclidean norm equal to unity (${\mathbf{v}}_k^T{\mathbf{v}}_k=1$).

The Golub–Welsch procedure [14] is one of standard methods for solving this eigenvalue problem. Thus, the knowledge of the coefficients ${\alpha }_k$ and ${\beta }_k$ in the three-term recurrence relation (2) is of exceptional importance. Unfortunately, only for certain narrow classes of orthogonal polynomials are these coefficients known in the explicit form, including classical orthogonal polynomials, which can be classified as follows:

• The Jacobi polynomials, with the weight $w\left(t\right)=v^{\alpha ,\beta }\left(t\right)={(1-t)}^{\alpha }{(1+t)}^{\beta }$$(\alpha ,\beta >-1)$ on the finite interval $(-1,1)$;
• The generalized Laguerre polynomials, with the weight $w\left(t\right)=t^{\alpha }{\mathrm{e}}^{-t}$$(\alpha >-1)$ on $(0,\infty )$;
• The Hermite polynomials, with the weight function $w\left(t\right)={\mathrm{e}}^{-t^2}$ on $(-\infty ,\infty )$.

There are several characterizations of the classical orthogonal polynomials (cf. [15,16,17]). Orthogonal polynomials for which the recursion coefficients are not known in explicit form are known as strongly non-classical polynomials ([13], p. 159), and they must be constructed numerically, but such a construction is usually an ill-conditioned process. Because of this, the use of strongly non-classical polynomials has long been limited.

Four decades ago, Walter Gautschi developed the so-called constructive theory of orthogonal polynomials on $\mathbb{R}$ for numerical generating orthogonal polynomials with respect to an arbitrary measure (see [18,19] and the book [12]). Three approaches for generating recursion coefficients were developed: the method of modified moments as a generalization of the classical Chebyshev method of moments, the discretized Stieltjes–Gautschi procedure, and the Lanczos algorithm. This constructive theory opened the door for extensive computational work on orthogonal polynomials, many applications, as well as further development of the theory of orthogonality in different directions (s and $\sigma$-orthogonality [20,21,22,23], Sobolev type of orthogonality, multiple orthogonality [24], etc.).

Recently, however, there has been substantial progress in computer architecture (arithmetic of variable precision), as well as progress in symbolic calculations. These advances enabled the direct generation of recurrence coefficients in the relation (2), using only the original Chebyshev method of moments, but with an arithmetic of sufficiently high precision, which avoids the ill-conditioning of the numerical process. The corresponding symbolic/variable-precision software for orthogonal polynomials and quadrature formulae is now available: Gautschi’s Matlab package SOPQ and our Mathematica package OrthogonalPolynomials (see [25,26]), which are freely downloadable from the website (Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade, Serbia): http://www.mi.sanu.ac.rs/~gvm/.

3. Orthogonal Polynomials in the Complex Plane

Beside the orthogonality on the real line, there are several concepts of orthogonality in the complex plane. In the next subsections, we mention some of these concepts.

3.1. Orthogonal Polynomials on the Unit Circle

This kind of orthogonality on the unit circle was introduced and studied by Szegő [27,28] and Smirnov [29,30]. A more general case was considered by Achieser and Kreĭn [31], Geronimus [32,33], etc. (for details see the books [34,35,36]). The inner product is defined by

$$(p,q)={\int }_0^{2\pi }p\left({\mathrm{e}}^{\mathrm{i}\theta }\right)\overline{q\left({\mathrm{e}}^{\mathrm{i}\theta }\right)}\mathrm{d}\mu \left(\theta \right),$$

where $\mathrm{d}\mu \left(\theta \right)$ is a finite positive measure on the interval $[0,2\pi ]$ whose support is an infinite set. This inner product does not have the property $(zp,q)=(p,zq)$, so that the three-term recurrence relation like (2) does not exist! But, $(zp,zq)=(p,q)$, which is important in proving that all zeros of the corresponding orthogonal polynomials ${\varphi }_k\left(z\right)$ are inside the unit circle $|z|=1$.

This kind of polynomials has many applications in digital filters, image processing, scattering theory, control theory, etc.

Similarly, orthogonal polynomials on a rectifiable curve or arc lying in the complex plane can be studied (cf. [34,37]), as well as ones related to the inner product defined by double integrals.

3.2. Orthogonal Polynomials on the Semicircle

In [38], we introduced and studied orthogonal polynomials on the semicircle with respect to the quasi-inner product given by

$$⟨p,q⟩={\int }_0^{\pi }p\left({\mathrm{e}}^{\mathrm{i}\theta }\right)q\left({\mathrm{e}}^{\mathrm{i}\theta }\right)\mathrm{d}\theta (p,q\in \mathcal{P}),$$

where the second factor is not conjugated, so that this product is not Hermitian, but it has the property $(zp,q)=(p,zq)$. This means that the corresponding monic orthogonal polynomials satisfy the three-term recurrence relation like (2). This kind of orthogonality was later generalized, together with W. Gautschi and H. Landau [39], using the weight function w on the open interval $(-1,1)$, with possible singularities at $\pm 1$, and which can be extended to a holomorphic function $w\left(z\right)$ in the half disc $D_{+}=\{z\in \mathbb{C}:|z|<1,\mathrm{Im}z>0\}$. This generalized quasi-inner product is given by

$$⟨p,q⟩={\int }_0^{\pi }p\left({\mathrm{e}}^{\mathrm{i}\theta }\right)q\left({\mathrm{e}}^{\mathrm{i}\theta }\right)w\left({\mathrm{e}}^{\mathrm{i}\theta }\right)\mathrm{d}\theta (p,q\in \mathcal{P}).$$

The corresponding (monic) orthogonal polynomials ${\pi }_k$ with respect to this inner product exist uniquely under the mild restriction $\mathrm{Re}{\mu }_0=\mathrm{Re}{\int }_0^{\pi }w\left({\mathrm{e}}^{\mathrm{i}\theta }\right)\mathrm{d}\theta \ne 0$ (see [39]). A detailed study of these polynomials (recurrence relation, zeros, differential equation, etc.), as well as some applications in numerical integration and numerical differentiation were given in several works [40,41,42,43,44], including, also, a general concept of orthogonality with respect to a complex moment functional $\mathcal{L}\left[z^k\right]={\mu }_k=⟨1,z^k⟩={\int }_0^{\pi }{\mathrm{e}}^{\mathrm{i}k\theta }w\left({\mathrm{e}}^{\mathrm{i}\theta }\right)\mathrm{d}\theta$ (cf. [45]) when k runs over ${\mathbb{N}}_0$ or $\mathbb{Z}$.

4. Orthogonal Polynomials on Radial Rays

We consider $M(\in \mathbb{N})$ radial rays ${\ell }_s$, given by complex points $z_s=a_s{\epsilon }_s\in \mathbb{C}$, $a_s>0$, ${\epsilon }_s={\mathrm{e}}^{\mathrm{i}{\theta }_s}$, $s=1,2,\dots ,M$, with different arguments ${\theta }_s$, $0\le {\theta }_1<{\theta }_2<\cdots <{\theta }_M<2\pi$. Some of $a_s$ (or all) can be ∞. The case $M=6$, with $z_5=\infty$, is shown in Figure 1.

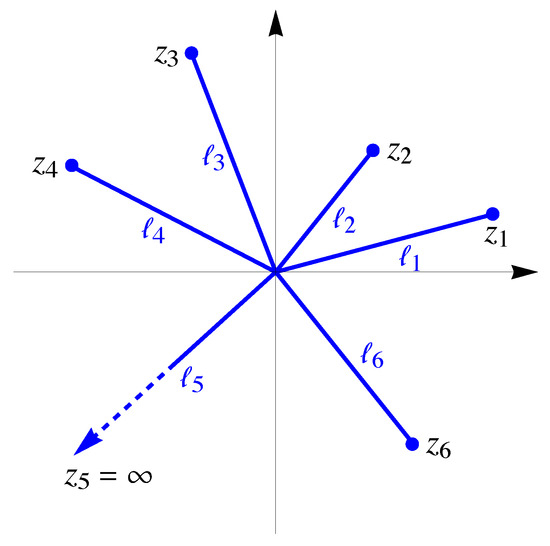
Figure 1. The rays in the complex plane (case with $M=6$).

We now define an inner product $(p,q)$ over all radial rays ${\ell }_s$, which connects the origin $z=0$ and the points $z_s$, $s=1,2,\dots ,M$, in the following way:

$$(p,q)=\sum _{s=1}^M{\mathrm{e}}^{-\mathrm{i}{\theta }_s}{\int }_{{\ell }_s}p\left(z\right)\overline{q\left(z\right)}|w_s\left(z\right)|\mathrm{d}z(p,q\in \mathcal{P}),$$

(5)

where $z\mapsto w_s\left(z\right)$ are suitable complex (weight) functions on the radial rays ${\ell }_s$, respectively. Here, we suppose that the functions

$$x\mapsto {\omega }_s\left(x\right)=|w_s\left(x{\epsilon }_s\right)|=|w_s\left(z\right)|(z\in {\ell }_s,s=1,\dots ,M)$$

are weight functions on $(0,a_s)$, i.e., they are non-negative on $(0,a_s)$ and ${\int }_0^{a_s}{\omega }_s\left(x\right)\mathrm{d}x>0$. In the case $a_s=+\infty$, it is required that all moments exist and are finite.

As we can see, this inner product (5) can also be expressed in the form

$$(p,q)=\sum _{s=1}^M{\int }_0^{a_s}p\left(x{\epsilon }_s\right)\overline{q\left(x{\epsilon }_s\right)}{\omega }_s\left(x\right)\mathrm{d}x.$$

(6)

Remark 1. 

Without loss of generality, we can assume that ${\theta }_1=0$.

Remark 2. 

In a simple case when $M=2$, ${\theta }_1=0$ and ${\theta }_2=\pi$, (6) becomes

$$(p,q)={\int }_0^{a_1}p\left(x\right)\overline{q\left(x\right)}{\omega }_1\left(x\right)\mathrm{d}x+{\int }_0^{a_2}p(-x)\overline{q(-x)}{\omega }_2\left(x\right)\mathrm{d}x,$$

i.e.,

$$(p,q)={\int }_a^{b}p\left(x\right)\overline{q\left(x\right)}\omega \left(x\right)\mathrm{d}x(p,q\in \mathcal{P}),$$

where $a=-a_2$, $b=a_1$, and 

$$\omega \left(x\right)=\left\{\begin{array}{cc}{\omega }_1\left(x\right),\hfill & 0<x<b,\hfill \\ {\omega }_2(-x),\hfill & a<x<0,\hfill \end{array}\right.$$

which means that it reduces to the case of polynomials orthogonal to $(a,b)$ by the weight functionx $\mapsto \omega \left(x\right)$.

By the characteristic function of a set L, defined by

$$\chi (L;z)=\left\{\begin{array}{cc}1,\hfill & z\in L,\hfill \\ 0,\hfill & z\notin L,\hfill \end{array}\right.$$

and taking $L={\ell }_1\cup {\ell }_2\cup \cdots \cup {\ell }_M$, the inner product (5) reduces to a standard form

$$(p,q)={\int }_{L}p\left(z\right)\overline{q\left(z\right)}\mathrm{d}\mu \left(z\right)(p,q\in \mathcal{P}),$$

(7)

with the measure

$$\mathrm{d}\mu \left(z\right)=\left\{\sum _{s=1}^M{\epsilon }_s^{-1}|w_s\left(z\right)|\chi ({\ell }_s;z)\right\}\mathrm{d}z.$$

(8)

4.1. Existence and Uniqueness of Polynomials Orthogonal on the Radial Rays

Consider again the inner product defined by (6). As we can see, $(p,q)=\overline{(q,p)}$ and

$${\parallel p\parallel }^2=(p,p)=\sum _{s=1}^M{\int }_0^{a_s}{|p\left(x{\epsilon }_s\right)|}^2{\omega }_s\left(x\right)\mathrm{d}x>0,$$

except $p\left(z\right)\equiv 0$. The corresponding moments are given by

$${\mu }_{k,j}=(z^k,z^j)=\sum _{s=1}^M{\epsilon }_s^{k-j}{\int }_0^{a_s}{x}^{k+j}{\omega }_s\left(x\right)\mathrm{d}x(k,j>0).$$

(9)

Let ${\mu }_k^{\left(s\right)}$ denote the single moments (of order k), which correspond to the weight functions $x\mapsto {\omega }_s\left(x\right)$ on the rays ${\ell }_s$, i.e., 

$${\mu }_k^{\left(s\right)}={\int }_0^{a_s}{x}^k{\omega }_s\left(x\right)\mathrm{d}x,s=1,\dots ,M,$$

and then,

$${\mu }_{k,j}=\sum _{s=1}^M{\mathrm{e}}^{\mathrm{i}(k-j){\theta }_s}{\mu }_{k+j}^{\left(s\right)},k,j\ge 0.$$

(10)

Since ${\mu }_k^{\left(s\right)}>0$ for each $k\ge 0$, from (10), we can conclude that

$${\overline{\mu }}_{j,k}={\mu }_{k,j}\mathrm{and}{\mu }_{k,k}=\sum _{s=1}^M{\mu }_{2k}^{\left(s\right)}>0(k,j\ge 0).$$

(11)

Now, we use the so-called Gram matrix of order n, constructed by the moments (9), i.e., (10),

$$G_n=\left[\begin{array}{cccc}{\mu }_{0,0}& {\mu }_{0,1}& \cdots & {\mu }_{0,n-1}\\ {\mu }_{1,0}& {\mu }_{1,1}& \cdots & {\mu }_{1,n-1}\\ ⋮& ⋮\\ {\mu }_{n-1,0}& {\mu }_{n-1,1}& \cdots & {\mu }_{n-1,n-1}\end{array}\right],n\ge 1.$$

According to (11), the matrix $G_n$ is Hermitian ($G_n=G_n^{*}=\overline{G_n^T}$ ) and non-singular, i.e., ${\Delta }_n=det{G}_n\ne 0$, because the system of functions $\{1,z,z^2,\dots ,z^{n-1}\}$ is linearly independent. Moreover, the Gram matrix is also positive-definite, which means that the moment determinant ${\Delta }_n=det{G}_n>0$. Formally, we introduce ${\Delta }_0=1$.

The existence of a sequence of orthogonal polynomials $\left\{{\pi }_n\left(z\right)\right\}$ is ensured by the following result:

Theorem 1. 

For each $n\ge 0$, the monic polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{+\infty }$, with respect to the inner product (6), exist uniquely. Their determinant representation is given by

$${\pi }_n\left(z\right)={\displaystyle \frac{1}{{\Delta }_n}}\left|\begin{array}{ccccc}{\mu }_{0,0}& {\mu }_{0,1}& \cdots & {\mu }_{0,n-1}& 1\\ {\mu }_{1,0}& {\mu }_{1,1}& \cdots & {\mu }_{1,n-1}& z\\ ⋮\\ {\mu }_{n-1,0}& {\mu }_{n-1,1}& \cdots & {\mu }_{n-1,n-1}& z^{n-1}\\ {\mu }_{n0}& {\mu }_{n1}& \cdots & {\mu }_{n,n-1}& z^n\end{array}\right|,n\ge 1,$$

(12)

as well as the norm of polynomials:

$$\parallel {\pi }_n\parallel =\sqrt{{\displaystyle \frac{{\Delta }_{n+1}}{{\Delta }_n}}},n\ge 0.$$

(13)

Proof. 

Let us denote the monic polynomial of order n, from the sequence $\left\{{\pi }_n\left(z\right)\right\}$, by 

$${\pi }_n\left(z\right)=\sum _{\nu =0}^n{\alpha }_{\nu }^{\left(n\right)}{z}^{\nu },{\alpha }_n^{\left(n\right)}=1,$$

and consider the orthogonality conditions

$$({\pi }_n,z^k)=\sum _{\nu =0}^n{\alpha }_{\nu }^{\left(n\right)}(z^{\nu },z^k)=\sum _{\nu =0}^n{\alpha }_{\nu }^{\left(n\right)}{\mu }_{\nu ,k}={\parallel {\pi }_n\parallel }^2{\delta }_{nk},k\le n,$$

where ${\delta }_{nk}$ is Kronecker’s delta. These conditions give the following system of equations:

$$\left[\begin{array}{cccc}{\mu }_{0,0}& {\mu }_{0,1}& \cdots & {\mu }_{0,n}\\ {\mu }_{1,0}& {\mu }_{1,1}& \cdots & {\mu }_{1,n}\\ ⋮\\ {\mu }_{n,0}& {\mu }_{n,1}& \cdots & {\mu }_{n,n}\end{array}\right]·\left[\begin{array}{c}{\alpha }_0^{\left(n\right)}\\ {\alpha }_1^{\left(n\right)}\\ ⋮\\ {\alpha }_n^{\left(n\right)}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ⋮\\ \parallel {\pi }_n{\parallel }^2\end{array}\right].$$

(14)

Since ${\Delta }_{n+1}>0$, the system (14) has a unique solution for the coefficients ${\alpha }_{\nu }^{\left(n\right)}$, $\nu =0,1,\dots ,n$. Notice that the leading coefficient ${\alpha }_n^{\left(n\right)}$ is given by ${\alpha }_n^{\left(n\right)}={\parallel {\pi }_n\parallel }^2{\Delta }_n/{\Delta }_{n+1}=1$, according to (13).

Similar to the proof for orthonormal polynomials (cf. [13], Thm. 2.1.1), we prove the equality (12) for monic polynomials, which are orthogonal with respect to the inner product (6).    □

Now, we prove an important extremal property of polynomials orthogonal on the radial rays. With ${\widehat{\mathcal{P}}}_n(\in {\mathcal{P}}_n)$, we denote the subspace of all monic polynomials of degree n and consider the following extremal problem:

$$\underset{P\in {\widehat{\mathcal{P}}}_n}{inf}\sum _{s=1}^M{\int }_0^{a_s}{|P\left(x{\epsilon }_s\right)|}^2{\omega }_s\left(x\right)\mathrm{d}x.$$

(15)

Theorem 2. 

For each $P\in {\widehat{\mathcal{P}}}_n$, we have

$${\parallel P\parallel }^2=\sum _{s=1}^M{\int }_0^{a_s}|P\left(x{\epsilon }_s\right){|}^2{\omega }_s\left(x\right)\mathrm{d}x\ge {\parallel {\pi }_n\parallel }^2,$$

(16)

where ${\left\{{\pi }_k\right\}}_{k=0}^{+\infty }$ is the sequence of monic orthogonal polynomials on M radial rays with respect to the inner product (6).

Proof. 

Let $P\in {\widehat{\mathcal{P}}}_n$. Then, $P\left(z\right)$ can be expressed in the form

$$P\left(z\right)=\sum _{k=0}^n{c}_k{\pi }_k\left(z\right),$$

where $c_k=(P,{\pi }_k)/{\parallel {\pi }_k\parallel }^2$, $k=0,1,\dots ,n$, and $c_n=1$. Since

$${\parallel P\parallel }^2=\sum _{k=0}^n|c_k{|}^2\parallel {\pi }_k{\parallel }^2\ge {\parallel {\pi }_n\parallel }^2,$$

we obtain (16), with equality if and only if $P\left(z\right)={\pi }_n\left(z\right)$.    □

According to (15) and (16), we conclude that the best $L^2$-approximation of the monomial $z\mapsto z^{n+1}$, with respect to the norm $\parallel p\parallel =\sqrt{(p,p)}$, in the space of polynomials of lower degree ${\mathcal{P}}_n$, i.e.,

$$\underset{p\in {\mathcal{P}}_n}{inf}\parallel z^{n+1}-p\left(z\right)\parallel =\parallel {\pi }_{n+1}\parallel ,$$

is given by $p\left(z\right)=p^{*}\left(z\right)=z^{n+1}-{\pi }_{n+1}\left(z\right)$. The problem of $L^2$-approximation of functions will not be treated in this paper.

4.2. General Distribution of Zeros of Orthogonal Polynomials on the Radial Rays

Let ${\pi }_n\left(z\right)$ be monic polynomials orthogonal with respect to the inner product $(p,q)={\int }_{L}p\left(z\right)\overline{q\left(z\right)}\mathrm{d}\mu \left(z\right)$, where the measure is given by (8), i.e.,

$$\mathrm{d}\mu \left(z\right)=\left\{\sum _{s=1}^M{\epsilon }_s^{-1}|w_s\left(z\right)|\chi ({\ell }_s;z)\right\}\mathrm{d}z.$$

Let $\mathrm{Co}\left(A\right)$ be the smallest convex set containing A, known as the convex hull of a set $A\in \mathbb{C}$, and let the support of the measure $\mathrm{d}\mu \left(z\right)$ be denoted by $S=\mathrm{supp}\left(\mathrm{d}\mu \right)$. Since $S\subset L={\ell }_1\cup {\ell }_2\cup \cdots \cup {\ell }_M$, using a result of Fejér, we can state the following theorems (cf. Saff [46,47]).

Theorem 3. 

All the zeros ${\zeta }_1,\dots ,{\zeta }_n$ of the orthogonal polynomial ${\pi }_n\left(z\right)$ lie in the convex hull of the rays $L={\ell }_1\cup {\ell }_2\cup \cdots \cup {\ell }_M$.

Furthermore, an improvement can be also performed.

Theorem 4. 

If the support of the measure, $\mathrm{Co}\left(\mathrm{supp}\right(\mathrm{d}\mu \left)\right)$, is not a line segment, then all the zeros of the polynomial ${\pi }_n\left(z\right)$ are in the interior of $\mathrm{Co}\left(\mathrm{supp}\right(\mathrm{d}\mu \left)\right)\subset \mathrm{Co}\left(L\right)$.

4.3. Some Examples

Using the previous “determinant approach”, here, we give a few simple examples of polynomials orthogonal on the radial rays, including the distribution of their zeros.

Example 1. 

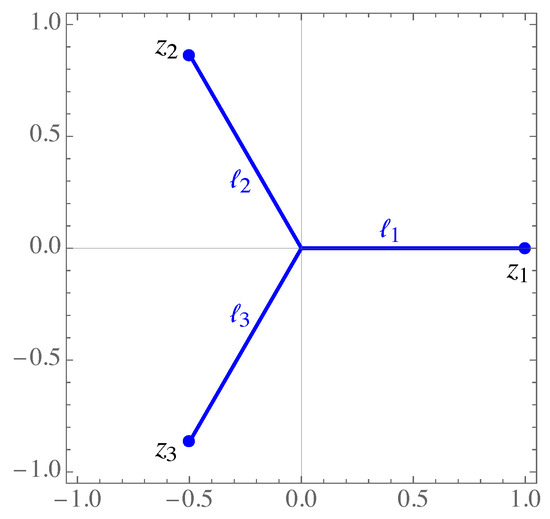
We consider the case with thee unit rays ($M=3$, $a_s=1$, $s=1,2,3$), with ${\theta }_1=0$, ${\theta }_2=2\pi /3$, ${\theta }_3=4\pi /3$, and the Legendre weight on the rays ${\omega }_s\left(x\right)=1$, $s=1,2,3$ (see Figure 2).

Figure 2. Three rays ${\ell }_1$, ${\ell }_2$ and ${\ell }_3$ in the complex plane, given by the complex points $z_s={\mathrm{e}}^{2\mathrm{i}(s-1)\pi /3}$, $s=1,2,3$.

The moments (10) are

$${\mu }_{k,j}=(z^k,z^j)={\displaystyle \frac{1}{k+j+1}}\left(1+{\mathrm{e}}^{\mathrm{i}2\pi (k-j)/3}+{\mathrm{e}}^{\mathrm{i}4\pi (k-j)/3}\right),k,j\ge 0,$$

so that, for example, for $n=10$, we obtain the symmetric matrix

$$G_{10}=\left[\begin{array}{cccccccccc}3& 0& 0& {\displaystyle \frac{3}{4}}& 0& 0& {\displaystyle \frac{3}{7}}& 0& 0& {\displaystyle \frac{3}{10}}\\ 0& 1& 0& 0& {\displaystyle \frac{1}{2}}& 0& 0& {\displaystyle \frac{1}{3}}& 0& 0\\ 0& 0& {\displaystyle \frac{3}{5}}& 0& 0& {\displaystyle \frac{3}{8}}& 0& 0& {\displaystyle \frac{3}{11}}& 0\\ {\displaystyle \frac{3}{4}}& 0& 0& {\displaystyle \frac{3}{7}}& 0& 0& {\displaystyle \frac{3}{10}}& 0& 0& {\displaystyle \frac{3}{13}}\\ 0& {\displaystyle \frac{1}{2}}& 0& 0& {\displaystyle \frac{1}{3}}& 0& 0& {\displaystyle \frac{1}{4}}& 0& 0\\ 0& 0& {\displaystyle \frac{3}{8}}& 0& 0& {\displaystyle \frac{3}{11}}& 0& 0& {\displaystyle \frac{3}{14}}& 0\\ {\displaystyle \frac{3}{7}}& 0& 0& {\displaystyle \frac{3}{10}}& 0& 0& {\displaystyle \frac{3}{13}}& 0& 0& {\displaystyle \frac{3}{16}}\\ 0& {\displaystyle \frac{1}{3}}& 0& 0& {\displaystyle \frac{1}{4}}& 0& 0& {\displaystyle \frac{1}{5}}& 0& 0\\ 0& 0& {\displaystyle \frac{3}{11}}& 0& 0& {\displaystyle \frac{3}{14}}& 0& 0& {\displaystyle \frac{3}{17}}& 0\\ {\displaystyle \frac{3}{10}}& 0& 0& {\displaystyle \frac{3}{13}}& 0& 0& {\displaystyle \frac{3}{16}}& 0& 0& {\displaystyle \frac{3}{19}}\end{array}\right].$$

The determinants ${\Delta }_n=det{G}_n$ are

$$\begin{array}{cc}\hfill {\Delta }_0& =1,{\Delta }_1=3,{\Delta }_2=3,{\Delta }_3={\displaystyle \frac{9}{5}},{\Delta }_4={\displaystyle \frac{243}{560}},{\Delta }_5={\displaystyle \frac{81}{2240}},{\Delta }_6={\displaystyle \frac{2187}{1576960}},\hfill \\ \hfill {\Delta }_7& ={\displaystyle \frac{531441}{25113088000}},{\Delta }_8={\displaystyle \frac{59049}{502261760000}},{\Delta }_9={\displaystyle \frac{14348907}{50624469575680000}},etc.,\hfill \end{array}$$

as well as the corresponding orthogonal polynomials, with respect to the inner product (12):

$$\begin{array}{cc}\hfill {\pi }_0\left(z\right)& =1,{\pi }_1\left(z\right)=z,{\pi }_2\left(z\right)=z^2,{\pi }_3\left(z\right)=z^3-{\displaystyle \frac{1}{4}},{\pi }_4\left(z\right)=z^4-{\displaystyle \frac{1}{2}}z,\hfill \\ \hfill {\pi }_5\left(z\right)& =z^5-{\displaystyle \frac{5}{8}}{z}^2,{\pi }_6\left(z\right)=z^6-{\displaystyle \frac{4}{5}}{z}^3+{\displaystyle \frac{2}{35}},{\pi }_7\left(x\right)=z^7-z^4+{\displaystyle \frac{1}{6}}z,\hfill \\ \hfill {\pi }_8\left(z\right)& =z^8-{\displaystyle \frac{8}{7}}{z}^5+{\displaystyle \frac{20}{77}}{z}^2,{\pi }_9\left(z\right)=z^9-{\displaystyle \frac{21}{16}}{z}^6+{\displaystyle \frac{21}{52}}{z}^3-{\displaystyle \frac{7}{520}},\hfill \\ \hfill {\pi }_{10}\left(z\right)& =z^{10}-{\displaystyle \frac{3}{2}}{z}^7+{\displaystyle \frac{3}{5}}{z}^4-{\displaystyle \frac{1}{20}}z,{\pi }_{11}\left(z\right)=z^{11}-{\displaystyle \frac{33}{20}}{z}^8+{\displaystyle \frac{66}{85}}{z}^5-{\displaystyle \frac{11}{119}}{z}^2,etc.\hfill \end{array}$$

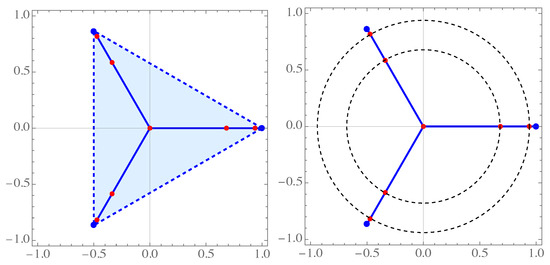
Zeros of the polynomial ${\pi }_8\left(z\right)$ are presented in Figure 3. According to Theorem 4, these zeros lie in the convex hull of the rays $L={\ell }_1\cup {\ell }_2\cup {\ell }_3$ (see Figure 3, left).

Figure 3. Zeros of ${\pi }_8\left(z\right)$ ($M=3$), with the Legendre weight $\omega \left(x\right)=1$, lie in the convex hull of the rays (left) and on the concentric circles (right).

Notice that ${\pi }_8\left(z\right)=z^2\left(z^6-{\displaystyle \frac{88}{77}}{z}^3+{\displaystyle \frac{20}{77}}\right)$, so that we can calculate its zeros in the explicit form. Indeed, ${\zeta }_1={\zeta }_2=0$ (double zero), and other six zeros are solutions of the equations

$$z^3={\displaystyle \frac{2}{77}}\left(22-3\sqrt{11}\right)=r_1^{3}and{z}^3={\displaystyle \frac{2}{77}}\left(22+3\sqrt{11}\right)=r_2^3,$$

where $r_1\approx 0.678959$ and $r_2=\approx 0.939729$. Thus,

$${\zeta }_3=r_1,{\zeta }_4=r_1{\mathrm{e}}^{2\mathrm{i}\pi /3},{\zeta }_5=r_1{\mathrm{e}}^{4\mathrm{i}\pi /3},{\zeta }_6=r_2,{\zeta }_7=r_2{\mathrm{e}}^{2\mathrm{i}\pi /3},{\zeta }_8=r_2{\mathrm{e}}^{4\mathrm{i}\pi /3}.$$

As we can see, all zeros also lie on the concentric circles with radii $r_1$ and $r_2$. This property will be analyzed in the sequel.

Example 2. (i) An interesting inner product is

$$(p,q)={\int }_0^1\left[p\left(x\right)\overline{q\left(x\right)}+p\left(\mathrm{i}x\right)\overline{q\left(\mathrm{i}x\right)}+p(-x)\overline{q(-x)}+p(-\mathrm{i}x)\overline{q(-\mathrm{i}x)}\right]\mathrm{d}x,$$

(17)

with the same (Legendre) weight function on all the rays. It is a case with four unit rays ($M=4$), equidistantly distributed: ${\theta }_s=(s-1)\mathrm{i}\pi /2$, $a_s=1$, $s=1,2,3,4$.

Since ${\mu }_k^{\left(4\right)}={\int }_0^1{x}^k\mathrm{d}x=1/(k+1)$, the moments (10) are

$${\mu }_{k,j}={\displaystyle \frac{1}{k+j+1}}\sum _{s=1}^4{\mathrm{e}}^{\mathrm{i}(s-1)(k-j)\pi /2}={\displaystyle \frac{1+{\mathrm{i}}^{k-j}}{k+j+1}}\left(1+{(-1)}^{k-j}\right),$$

i.e.,

$${\mu }_{k,j}=\left\{\begin{array}{cc}{\displaystyle \frac{4}{k+j+1}},\hfill & j\equiv k\left(\mathrm{mod}4\right),\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

so that, e.g., for $n=8$, we have

$$G_8=\left[\begin{array}{cccccccc}4& 0& 0& 0& {\displaystyle \frac{4}{5}}& 0& 0& 0\\ 0& {\displaystyle \frac{4}{3}}& 0& 0& 0& {\displaystyle \frac{4}{7}}& 0& 0\\ 0& 0& {\displaystyle \frac{4}{5}}& 0& 0& 0& {\displaystyle \frac{4}{9}}& 0\\ 0& 0& 0& {\displaystyle \frac{4}{7}}& 0& 0& 0& {\displaystyle \frac{4}{11}}\\ {\displaystyle \frac{4}{5}}& 0& 0& 0& {\displaystyle \frac{4}{9}}& 0& 0& 0\\ 0& {\displaystyle \frac{4}{7}}& 0& 0& 0& {\displaystyle \frac{4}{11}}& 0& 0\\ 0& 0& {\displaystyle \frac{4}{9}}& 0& 0& 0& {\displaystyle \frac{4}{13}}& 0\\ 0& 0& 0& {\displaystyle \frac{4}{11}}& 0& 0& 0& {\displaystyle \frac{4}{15}}\end{array}\right].$$

As we can see, this matrix is symmetric. The corresponding determinants ${\Delta }_n=det{G}_n$ are

$$\begin{array}{cc}\hfill {\Delta }_0& =1,{\Delta }_1=4,{\Delta }_2={\displaystyle \frac{16}{3}},{\Delta }_3={\displaystyle \frac{64}{15}},{\Delta }_4={\displaystyle \frac{256}{105}},{\Delta }_5={\displaystyle \frac{16384}{23625}},\hfill \\ \hfill {\Delta }_6& ={\displaystyle \frac{1048576}{12733875}},{\Delta }_7={\displaystyle \frac{67108864}{13408770375}},{\Delta }_8={\displaystyle \frac{4294967296}{24336918230625}},\hfill \end{array}$$

so that the orthogonal polynomials with respect to the inner product (17) are

$$\begin{array}{cc}\hfill {\pi }_0\left(z\right)& =1,{\pi }_1\left(z\right)=z,{\pi }_2\left(z\right)=z^2,{\pi }_3\left(z\right)=z^3,{\pi }_4\left(z\right)=z^4-{\displaystyle \frac{1}{5}},\hfill \\ \hfill {\pi }_5\left(z\right)& =z^5-{\displaystyle \frac{3}{7}}z,{\pi }_6\left(z\right)=z^6-{\displaystyle \frac{5}{9}}{z}^2,{\pi }_7\left(z\right)=z^7-{\displaystyle \frac{7}{11}}{z}^3,{\pi }_8\left(z\right)=z^8-{\displaystyle \frac{10}{13}}{z}^4+{\displaystyle \frac{5}{117}},\hfill \end{array}$$

etc. In the sequel, in Remark 5, we present a simple way for calculating this sequence of orthogonal polynomials.

These polynomials are discussed in detail in [2]. Their zeros are simple and located symmetrically on the radial rays, with the possible exception a zero of order $\nu (\in \{1,2,3\left\}\right)$ at the origin $z=0$.

(ii) Similarly, introducing an inner product with the weight function $\omega \left(x\right)=x^2{(1-x^4)}^{1/2}$, instead of Legendre’s $\omega \left(x\right)=1$ as in (17), we have

$${\mu }_k^{\left(4\right)}={\int }_0^1{x}^{k+2}{(1-x^4)}^{1/2}\mathrm{d}x={\displaystyle \frac{\sqrt{\pi }\mathsf{\Gamma }\left(\frac{k+3}{4}\right)}{8\mathsf{\Gamma }\left(\frac{k+9}{4}\right)}},k\ge 0.$$

In the same way, after much calculation, we obtain the corresponding orthogonal polynomials:

$$\begin{array}{cc}\hfill {\pi }_0\left(z\right)& =1,{\pi }_1\left(z\right)=z,{\pi }_2\left(z\right)=z^2,{\pi }_3\left(z\right)=z^3,{\pi }_4\left(z\right)=z^4-{\displaystyle \frac{1}{3}},\hfill \\ \hfill {\pi }_5\left(z\right)& =z^5-{\displaystyle \frac{5}{11}}z,{\pi }_6\left(z\right)=z^6-{\displaystyle \frac{7}{13}}{z}^2,{\pi }_7\left(z\right)=z^7-{\displaystyle \frac{3}{5}}{z}^3,{\pi }_8\left(z\right)=z^8-{\displaystyle \frac{14}{17}}{z}^4+{\displaystyle \frac{21}{221}},\hfill \end{array}$$

etc.

Example 3. 

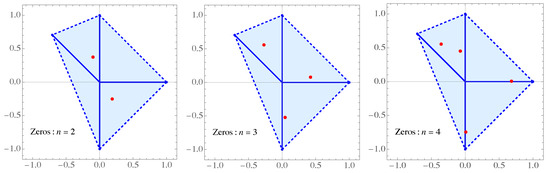
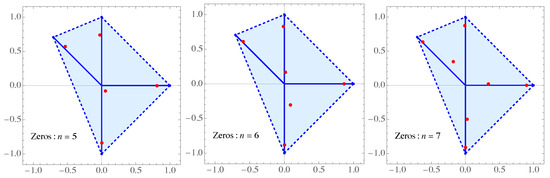
We consider the case with four unit rays ($M=4$, $a_s=1$, $s=1,2,3,4$), with ${\theta }_1=0$, ${\theta }_2=\pi /2$, ${\theta }_3=3\pi /4$, ${\theta }_4=3\pi /2$ and the Legendre weight on the rays ${\omega }_s\left(x\right)=1$, $s=1,2,3,4$.

Since ${\mu }_k^{\left(4\right)}={\int }_0^1{x}^k\mathrm{d}x=1/(k+1)$, the moments (10) are

$${\mu }_{k,j}={\displaystyle \frac{1}{k+j+1}}\left(1+{\mathrm{e}}^{\mathrm{i}(k-j)\pi /2}+{\mathrm{e}}^{\mathrm{i}(k-j)3\pi /4}+{\mathrm{e}}^{\mathrm{i}(k-j)3\pi /2}\right),k,j\ge 0.$$

For example, for $n=5$, we have

$$G_5=\left[\begin{array}{ccccc}4& {\displaystyle \frac{1}{2}}\left(1+{\mathrm{e}}^{-{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)& -{\displaystyle \frac{1-\mathrm{i}}{3}}& {\displaystyle \frac{1}{4}}\left(1+{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{i}\pi }{4}}}\right)& {\displaystyle \frac{2}{5}}\\ {\displaystyle \frac{1}{2}}\left(1+{\mathrm{e}}^{{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)& {\displaystyle \frac{4}{3}}& {\displaystyle \frac{1}{4}}\left(1+{\mathrm{e}}^{-{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)& -{\displaystyle \frac{1-\mathrm{i}}{5}}& {\displaystyle \frac{1}{6}}\left(1+{\mathrm{e}}^{-{\displaystyle \frac{\mathrm{i}\pi }{4}}}\right)\\ -{\displaystyle \frac{1+\mathrm{i}}{3}}& {\displaystyle \frac{1}{4}}\left(1+{\mathrm{e}}^{{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)& {\displaystyle \frac{4}{5}}& {\displaystyle \frac{1}{6}}\left(1+{\mathrm{e}}^{-{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)& -{\displaystyle \frac{1-\mathrm{i}}{7}}\\ {\displaystyle \frac{1}{4}}\left(1+{\mathrm{e}}^{{\displaystyle \frac{\mathrm{i}\pi }{4}}}\right)& -{\displaystyle \frac{1+\mathrm{i}}{5}}& {\displaystyle \frac{1}{6}}\left(1+{\mathrm{e}}^{{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)& {\displaystyle \frac{4}{7}}& {\displaystyle \frac{1}{8}}\left(1+{\mathrm{e}}^{-{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)\\ {\displaystyle \frac{2}{5}}& {\displaystyle \frac{1}{6}}\left(1+{\mathrm{e}}^{{\displaystyle \frac{\mathrm{i}\pi }{4}}}\right)& -{\displaystyle \frac{1+\mathrm{i}}{7}}& {\displaystyle \frac{1}{8}}\left(1+{\mathrm{e}}^{{\displaystyle \frac{3\mathrm{i}\pi }{4}}}\right)& {\displaystyle \frac{4}{9}}\end{array}\right],$$

while for ${\Delta }_n=det{G}_n$, we can calculate

$$\begin{array}{cc}\hfill {\Delta }_0& =1,{\Delta }_1=4,{\Delta }_2={\displaystyle \frac{58+3\sqrt{2}}{12}},{\Delta }_3={\displaystyle \frac{1658+243\sqrt{2}}{540}},\hfill \\ \hfill {\Delta }_4& ={\displaystyle \frac{3238241+1019800\sqrt{2}}{3024000}},{\Delta }_5={\displaystyle \frac{6319849979+3000852550\sqrt{2}}{33339600000}},\hfill \end{array}$$

so that

$$\begin{array}{cc}\hfill {\pi }_0\left(z\right)& =1,{\pi }_1\left(z\right)=z-{\displaystyle \frac{1}{16}}\left(2-\sqrt{2}+\mathrm{i}\sqrt{2}\right),\hfill \\ \hfill {\pi }_2\left(z\right)& =z^2-{\displaystyle \frac{424-195\sqrt{2}+\mathrm{i}(46+113\sqrt{2})}{1673}}z+{\displaystyle \frac{2432-645\sqrt{2}+\mathrm{i}(1280+453\sqrt{2})}{20076}},\hfill \end{array}$$

etc., with norms, according to (13),

$$\parallel {\pi }_0\parallel =2,\parallel {\pi }_1\parallel ={\displaystyle \frac{1}{4}}\sqrt{{\displaystyle \frac{58+3\sqrt{2}}{3}}},\parallel {\pi }_2\parallel ={\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{47353+4560\sqrt{2}}{8365}}},etc.$$

The zeros of polynomials ${\pi }_n\left(z\right)$ for $n=2,3,\dots ,7$ are presented in Figure 4 and Figure 5.

Figure 4. Zeros of the orthogonal polynomials ${\pi }_n\left(z\right)$ for $n=2,3,4$ in Example 3.

Figure 5. Zeros of the orthogonal polynomials ${\pi }_n\left(z\right)$ for $n=5,6,7$ in Example 3.

Example 4. 

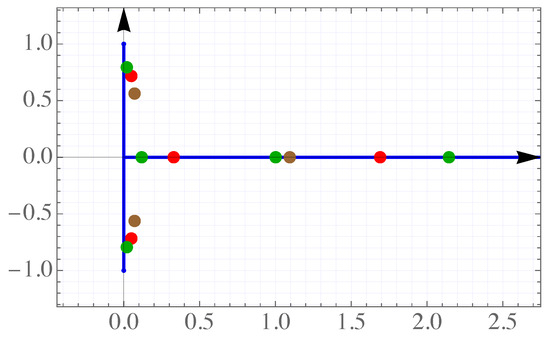
Consider now a case with three rays $M=3$, given by $a_1=+\infty$, $a_2=a^3=1$, with ${\theta }_1=0$, ${\theta }_2=\pi /2$, ${\theta }_3=3\pi /2$ and the weight functions on the rays ${\omega }_1\left(x\right)=exp(-x^2)$ and ${\omega }_2\left(x\right)={\omega }_3\left(x\right)=1$.

Since the inner product is defined by

$$(p,q)={\int }_0^{+\infty }p\left(x\right)\overline{q\left(x\right)}{\mathrm{e}}^{-x^2}\mathrm{d}x+{\int }_0^1\left[p\left(\mathrm{i}x\right)\overline{q\left(\mathrm{i}x\right)}+p\left(-\mathrm{i}x\right)\overline{q\left(-\mathrm{i}x\right)}\right]\mathrm{d}x,$$

(18)

the moments are

$$(z^k,z^j)={\displaystyle \frac{1}{2}}\mathsf{\Gamma }\left({\displaystyle \frac{1}{2}}(j+k+1)\right)+{\displaystyle \frac{{(-\mathrm{i})}^{k-j}+{\left(\mathrm{i}\right)}^{k-j}}{j+k+1}},k,j\ge 0,$$

so that the corresponding orthogonal polynomials are

$$\begin{array}{cc}\hfill {\pi }_0\left(z\right)& =1,{\pi }_1\left(z\right)=z-{\displaystyle \frac{1}{4+\sqrt{\pi }}},\hfill \\ \hfill {\pi }_2\left(z\right)& =z^2-{\displaystyle \frac{32+3\sqrt{\pi }}{26+20\sqrt{\pi }+3\pi }}z+{\displaystyle \frac{100-9\pi }{6\left(26+20\sqrt{\pi }+3\pi \right)}},\hfill \\ \hfill {\pi }_3\left(z\right)& =z^3-{\displaystyle \frac{3}{2A}}\left(5656+1104\sqrt{\pi }+135\pi \right)z^2\hfill \\ \hfill & +{\displaystyle \frac{3}{10A}}\left(25088+7722\sqrt{\pi }-6210\pi -675{\pi }^{3/2}\right)z+{\displaystyle \frac{3}{A}}(1125\pi -26384),\dots ,\hfill \end{array}$$

where $A=-3008+3675\sqrt{\pi }+1746\pi +135{\pi }^{3/2}$.

These three rays and zeros of polynomials ${\pi }_k\left(z\right)$, where $k=3,4,5$, are presented in Figure 6.

Figure 6. Zeros of the orthogonal polynomials ${\pi }_3\left(z\right)$ (brown), ${\pi }_4\left(z\right)$ (red) and ${\pi }_5\left(z\right)$ (green) in Example 4.

5. Numerical Construction of Orthogonal Polynomials Related to the Inner Product (6)

In this section, we describe a much better and simpler numerical method for constructing orthogonal polynomials on arbitrary radial rays.

Let ${\pi }_k\left(z\right)$$(k\in {\mathbb{N}}_0)$ be monic orthogonal polynomials related to the inner product (6), i.e., (7). Since ${\pi }_0\left(z\right)=1$ and the polynomial ${\pi }_k\left(z\right)-z{\pi }_{k-1}\left(z\right)$$(k\ge 1)$ is of degree at most $k-1$, then for each $k\in \mathbb{N}$, it can be expressed in the form

$${\pi }_k\left(z\right)-z{\pi }_{k-1}\left(z\right)=\sum _{j=0}^{k-1}{\beta }_{kj}{\pi }_j\left(z\right),$$

(19)

i.e.,

$$\left.\begin{array}{cc}\hfill {\pi }_1\left(z\right)& =z{\pi }_0\left(z\right)+{\beta }_{10}{\pi }_0\left(z\right),\hfill \\ \hfill {\pi }_2\left(z\right)& =z{\pi }_1\left(z\right)+{\beta }_{20}{\pi }_0\left(z\right)+{\beta }_{21}{\pi }_1\left(z\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\pi }_n\left(z\right)& =z{\pi }_{n-1}\left(z\right)+{\beta }_{n0}{\pi }_0\left(z\right)+{\beta }_{n1}{\pi }_1\left(z\right)+\cdots +{\beta }_{n,n-1}{\pi }_{n-1}\left(z\right),\hfill \end{array}\right\}$$

(20)

where ${\beta }_{kj}$$(j=0,1,\dots ,k-1;k=1,\dots ,n)$ are some constants. If, for a fixed $n\in \mathbb{N}$, we introduce two n-dimensional vectors

$${\mathbf{q}}_n\left(z\right)={\left[{\pi }_0\left(z\right){\pi }_1\left(z\right)\dots {\pi }_{n-1}\left(z\right)\right]}^T\mathrm{and}{\mathbf{e}}_n={[00\dots 01]}^T,$$

as well as the following lower (unreduced) n-order Hessenberg matrix:

$$B_n=\left[\begin{array}{ccccc}{\beta }_{10}& -1& 0& \cdots & 0\\ {\beta }_{20}& {\beta }_{21}& -1& \cdots & 0\\ ⋮& ⋮& & \ddots & \\ {\beta }_{n-1,0}& {\beta }_{n-1,1}& & \ddots & -1\\ {\beta }_{n,0}& {\beta }_{n,1}& & \cdots & {\beta }_{n,n-1}\end{array}\right],$$

then the system of equalities (20) can be expressed in the matrix form

$${\pi }_n\left(z\right){\mathbf{e}}_n=z{\mathbf{q}}_n\left(z\right)+B_n{\mathbf{q}}_n\left(z\right).$$

(21)

Now, we state an important result on the determinant form of the monic orthogonal polynomials ${\pi }_n\left(z\right)$ and their zeros.

Theorem 5. 

The monic orthogonal polynomials ${\pi }_n\left(z\right)$ can be expressed in the following determinant form:

$${\pi }_n\left(z\right)=det(z{I}_n+B_n),$$

(22)

where $I_n$ is the $n\times n$ identity matrix. Moreover, ${\zeta }_j\equiv {\zeta }_j^{\left(n\right)}$, $j=1,\dots ,n$, are zeros of this polynomial ${\pi }_n\left(z\right)$ if and only if they are eigenvalues of the Hessenberg matrix $-B_n$.

Proof. 

Let ${\zeta }_j\equiv {\zeta }_j^{\left(n\right)}$, $j=1,\dots ,n$, be zeros of the polynomial ${\pi }_n\left(z\right)$. Taking z in (21) to be any of ${\zeta }_j$$(j=1,\dots ,n)$, then the matrix relation (21) reduces to the eigenvalue problem

$$-B_n{\mathbf{q}}_n\left(z\right)=z{\mathbf{q}}_n\left(z\right)$$

for the the Hessenberg matrix $-B_n$, where ${\zeta }_1$, …, ${\zeta }_n$ are eigenvalues of the matrix $-B_n$, and  ${\mathbf{q}}_n\left({\zeta }_1\right)$, …, ${\mathbf{q}}_n\left({\zeta }_n\right)$ are the corresponding eigenvectors.

From (21), i.e., ${\pi }_n\left(z\right){\mathbf{e}}_n=(z{I}_n+B_n){\mathbf{q}}_n\left(z\right)$, we conclude that ${\zeta }_j$, $j=1,2,\dots ,n$, are zeros of the polynomial ${\pi }_n\left(z\right)$ if and only if they are the eigenvalues of the matrix $-B_n$. Evidently, (22) is true.    □

For computing zeros of ${\pi }_n\left(z\right)$ as the eigenvalues of the square matrix $-B_n(=$ m), we use the Mathematica command Eigenvalues[m].

Using the relation (19) and orthogonality of the polynomials ${\pi }_n$ from 

$$({\pi }_k,{\pi }_m)=(z{\pi }_{k-1},{\pi }_m)+\sum _{j=0}^{k-1}{\beta }_{kj}({\pi }_j,{\pi }_m),0\le m\le k-1,$$

for $m=j$, we obtain

$${\beta }_{kj}=-{\displaystyle \frac{(z{\pi }_{k-1},{\pi }_j)}{({\pi }_j,{\pi }_j)}}(0\le j\le k-1;k\in \mathbb{N}).$$

(23)

Now, we have the problem of how to numerically compute these coefficients.

5.1. Case When All $a_s$ Are Finite

The inner product (6), in this case, can be transformed to M integrals over $(0,1)$, with respect to the weight functions ${\mathsf{\Omega }}_s\left(t\right)={\omega }_s\left(a_{s}t\right)$, $s=1,2,\dots ,M$. Namely,

$$(p,q)=\sum _{s=1}^M{\int }_0^1{a}_{s}p\left(a_s{\epsilon }_{s}t\right)\overline{q\left(a_s{\epsilon }_{s}t\right)}{\mathsf{\Omega }}_s\left(t\right)\mathrm{d}t.$$

(24)

Since we have M integrals with the weight functions ${\mathsf{\Omega }}_s\left(t\right)$, $s=1,\dots ,M$, it is enough to apply the n-point quadrature rules of Gaussian type, with respect to the weight functions (i.e., with respect to the measures $\mathrm{d}{\mu }_s\left(t\right)={\mathsf{\Omega }}_s\left(t\right)\mathrm{d}t$, $s=1,\dots ,M$),

$${\int }_0^1\varphi \left(t\right){\mathsf{\Omega }}_s\left(t\right)\mathrm{d}t=\sum _{\nu =1}^n{A}_{\nu }^{(n,s)}\varphi \left({\tau }_{\nu }^{(n,s)}\right)+R_{n,s}\left(\varphi \right),s=1,\dots ,M,$$

(25)

where ${\tau }_{\nu }^{(n,s)}$ and $A_{\nu }^{(n,s)}$, $\nu =1,\dots ,n$, are the corresponding nodes and weight coefficients of these quadratures (see (3)).

The construction of these quadrature parameters (with respect to the weight functions ${\mathsf{\Omega }}_s\left(t\right)$) can be performed by using our Mathematica package OrthogonalPolynomials (see [25,26]). Since each of quadratures in (25) has the maximal degree of precision $2n-1$, i.e., $R_{n,s}\left(\varphi \right)=0$ for each $\varphi \in {\mathcal{P}}_{2n-1}$, we conclude that the inner product (24) can be calculated exactly as

$$(p,q)=\sum _{s=1}^M{a}_s\sum _{\nu =1}^n{A}_{\nu }^{(n,s)}p\left(a_s{\epsilon }_s{\tau }_{\nu }^{(n,s)}\right)\overline{q\left(a_s{\epsilon }_s{\tau }_{\nu }^{(n,s)}\right)}.$$

(26)

Since for each $j\le k-1$ and $k\le n$, the maximal degree of polynomials in the inner product $(z{\pi }_{k-1},{\pi }_j)$ in the numerator of (23) is

$$d_{max}=deg\left(z{\pi }_{k-1}\right)+deg\left({\pi }_j\right)=1+(k-1)+j=k+j\le 2k-1\le 2n-1,$$

it is absolutely sufficient to take n nodes in the quadrature formulas (25).

Thus, in this way, all the elements ${\beta }_{kj}$ of the Hessenberg matrix $B_n$ can be accurately computed, except for rounding errors.

5.2. Cases When Some of $a_s$ (or All) Are Infinity

In these cases, we should take the corresponding n-point quadrature rules of Gaussian type over $(0,+\infty )$. For example, in the case considered in Example 4, for the first integral in the inner product (18), we can use the one-sided Gauss–Hermite quadrature formula:

$${\int }_0^{+\infty }f\left(t\right){\mathrm{e}}^{-t^2}\mathrm{d}t=\sum _{\nu =1}^n{A}_{\nu }^{\left(n\right)}f\left({\tau }_{\nu }^{\left(n\right)}\right)+R_n\left(f\right),$$

(27)

where ${\tau }_{\nu }^{\left(n\right)}$ and $A_{\nu }^{\left(n\right)}$, $\nu =1,\dots ,n$, are the corresponding nodes and weight coefficients. Since the moments for this weight function are ${\mu }_k={\displaystyle \frac{1}{2}}\mathsf{\Gamma }\left({\displaystyle \frac{1+k}{2}}\right)$, $k\in {\mathbb{N}}_0$, the recurrence coefficients in the relation (2) (i.e., in the Jacobi matrix (4)), as well as the quadrature parameters in (27), can be calculated by our Mathematica package OrthogonalPolynomials (see [26], p. 176). Therefore, only the knowledge of the moments of the weight function is required.

5.3. Discretized Stieltjes–Gautschi Procedure

The main problem is how to numerically calculate the elements of the Hessenberg matrix $B_n$ in an efficient way. Our proposal to solve this problem is to use a kind of Stieltjes procedure, which we call the discretized Stieltjes–Gautschi procedure ([13], pp. 162–166). Namely, we apply Formula (23) for recurrence coefficients ${\beta }_{kj}$, with the inner products in a discretized form, in tandem with the basic linear relations (19), i.e., (20).

Since ${\pi }_0\left(z\right)=1$, we can compute ${\beta }_{10}$ from (23). Having obtained ${\beta }_{10}$, we then use the first relation in (20) to compute ${\pi }_1\left(z\right)$ for all $\left\{a_s{\epsilon }_s{\tau }_{\nu }^{(n,s)}\right\}$ to obtain its values needed to reapply (23) with $k=2$. This yields ${\beta }_{20}$ and ${\beta }_{21}$, which in turn can be used in (20) to obtain the corresponding values of ${\pi }_2\left(z\right)$ needed to return to (23) for computing ${\beta }_{30}$, ${\beta }_{31}$ and ${\beta }_{32}$. Thus, in this way, alternating between (23) and (20), we can ‘bootstrap’ ourselves up to any desired order n.

In a numerical implementation of the previous procedure, it is very convenient to use Wolfram (Mathematica) or Matlab.

As we have seen, a good way of discretizing the original measures on the radial rays can be obtained by applying suitable quadrature formulae to the corresponding integrals like (26) or (27).

In the general (asymmetric) cases, we have to use the discretized Stieltjes–Gautschi procedure as a basic method in numerical construction.

5.4. Jacobi Weight Functions on the Equidistant Rays

We now consider an important case with M equidistant points on the unit circle in the complex plane, $z_s={\epsilon }_s={\mathrm{e}}^{\mathrm{i}2\pi (s-1)/M}\in \mathbb{C}$, $s=1,\dots ,M$, but with different Jacobi weight functions on the rays, when

$$(p,q)=\sum _{s=1}^M{\int }_0^{1}p\left({\epsilon }_{s}x\right)\overline{q\left({\epsilon }_{s}x\right)}{\omega }_s\left(x\right)\mathrm{d}x,$$

(28)

where ${\omega }_s\left(x\right)={(1-x)}^{{\alpha }_s}{x}^{{\beta }_s}$, with ${\alpha }_s,{\beta }_s>-1$, $s=1,2,\dots ,M$.

In this case, we can successfully apply the discretized Stieltjes–Gautschi procedure, with discretization using Gauss–Jacobi quadratures, to construct the corresponding orthogonal polynomials on the radial rays. Namely, for $t=2x-1$,

$$\omega \left(x\right)\mathrm{d}x={(1-x)}^{\alpha }{x}^{\beta }\mathrm{d}x={\displaystyle \frac{1}{2^{\alpha +\beta +1}}}{(1-t)}^{\alpha }{(1+t)}^{\beta }\mathrm{d}t,$$

so that the weights of the integrals in (28) reduce to the Jacobi weights on $(-1,1)$. For calculating these integrals (28) on $(0,1)$, we simply apply the standard Gauss–Jacobi quadrature formula:

$${\int }_0^{1}f\left(t\right)\omega \left(x\right)\mathrm{d}x\approx {\displaystyle \frac{1}{2^{\alpha +\beta +1}}}\sum _{\nu =1}^n{A}_{n,\nu }^{(\alpha ,\beta )}f\left({\displaystyle \frac{1}{2}}\left(1+{\tau }_{n,\nu }^{(\alpha ,\beta )}\right)\right),$$

(29)

where ${\tau }_{n,\nu }^{(\alpha ,\beta )}$ and $A_{n,\nu }^{(\alpha ,\beta )}$, $\nu =1,\dots ,n$, are nodes and weights of the n-point Gauss–Jacobi quadrature formula, with respect to the Jacobi weight $v^{\alpha ,\beta }\left(t\right)={(1-t)}^{\alpha }{(1+t)}^{\beta }$, $\alpha ,\beta >-1$. These parameters are connected with the symmetric tridiagonal Jacobi matrix (4), via the Golub–Welsch algorithm [14], which is realized in our software OrthogonalPolynomials (see [25,26]) as

<< orthogonalPolynomials‘

{nodes, weights} =

  aGaussianNodesWeights[n,{aJacobi,alpha,beta},

   WorkingPrecision -> WP,Precision ->PR];

thereby giving, e.g., WorkingPrecision->40 and requiring Precision->30, if we need parameters with the relative errors about ${10}^{-30}$.

Below, we give a few examples.

Example 5. 

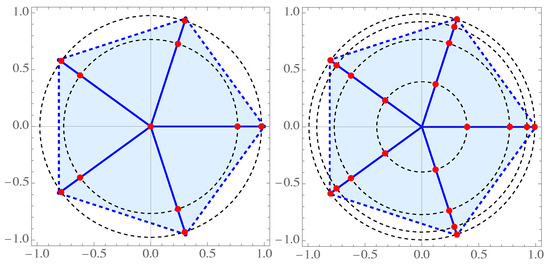
Let M be the number of unit rays and n be the degree of the orthogonal polynomial $z\mapsto {\pi }_n\left(z\right)$ related to the inner product (28) with the same weight function $x\mapsto \omega \left(x\right)$ on all rays. In this example we consider two cases.

(i) Chebyshev case of the first kind, when $\omega \left(x\right)=1/\sqrt{x(1-x)}$, with $M=5$ rays. Using the discretized Stieltjes–Gautschi procedure, we obtain the corresponding polynomials:

$$\begin{array}{cc}\hfill {\pi }_k\left(z\right)& =z^k(k=0,1,2,3,4),{\pi }_5\left(z\right)=z^5-{\displaystyle \frac{63}{256}},{\pi }_6\left(z\right)=z^6-{\displaystyle \frac{143}{256}}z,\hfill \\ \hfill {\pi }_7\left(z\right)& =z^7-{\displaystyle \frac{2431}{3584}}{z}^2,{\pi }_8\left(z\right)=z^8-{\displaystyle \frac{4199}{5632}}{z}^3,{\pi }_9\left(z\right)=z^9-{\displaystyle \frac{260015}{329472}}{z}^4,\hfill \\ \hfill {\pi }_{10}\left(z\right)& =z^{10}-{\displaystyle \frac{3392469}{3880064}}{z}^5+{\displaystyle \frac{309677219}{7946371072}},\hfill \\ \hfill {\pi }_{11}\left(z\right)& =z^{11}-{\displaystyle \frac{196707247}{189709312}}{z}^6+{\displaystyle \frac{3348446513}{22414884864}}z,\hfill \end{array}$$

etc.

In Figure 7, we present zeros of ${\pi }_{12}\left(z\right)$ and ${\pi }_{20}\left(z\right)$. In the first case, ten zeros are on the five rays while two concentric circles and one double zero is at the origin, whereas in the second case, all twenty zeros lie on the five rays and the four concentric circles (see Theorem 9 in the sequel).

Figure 7. Zeros of polynomials of degree $n=12$ (left) and $n=20$ (right) for Chebyshev weight of the first kind on $M=5$ rays.

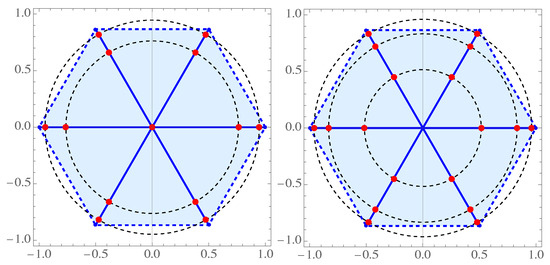
(ii) Chebyshev case of the second kind $\omega \left(x\right)=\sqrt{x(1-x)}$, with $M=6$ rays.

As in (i), we obtain the following polynomials:

$$\begin{array}{cc}\hfill {\pi }_k\left(z\right)& =z^k(k=0,1,2,3,4,5),{\pi }_6\left(z\right)=z^6-{\displaystyle \frac{429}{4096}},{\pi }_7\left(z\right)=z^7-{\displaystyle \frac{2431}{10240}}z,\hfill \\ \hfill {\pi }_8\left(z\right)& =z^8-{\displaystyle \frac{4199}{12288}}{z}^2,{\pi }_9\left(z\right)=z^9-{\displaystyle \frac{185725}{439296}}{z}^3,{\pi }_{10}\left(z\right)=z^{10}-{\displaystyle \frac{570285}{1171456}}{z}^4,\hfill \\ \hfill {\pi }_{11}\left(z\right)& =z^{11}-{\displaystyle \frac{3411705}{6336512}}{z}^5,{\pi }_{12}\left(z\right)=z^{12}-{\displaystyle \frac{724279545}{1144543232}}{z}^6+{\displaystyle \frac{103127749255}{4688049078272}},\hfill \end{array}$$

etc.

In Figure 8, we present zeros of ${\pi }_{15}\left(z\right)$ and ${\pi }_{18}\left(z\right)$. Figure 8 (left) shows twelve zeros on six rays, and two concentric circles and one triple zero at the origin, while the Figure 8 (right) displays eighteen zeros on three concentric circles and six rays.

Figure 8. Zeros of polynomials of degree $n=15$ (left) and $n=18$ (right) for Chebyshev weight of the second kind on $M=6$ rays.

Example 6. 

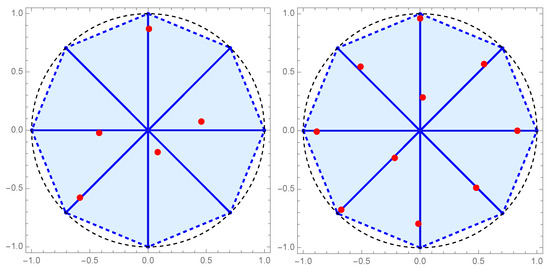
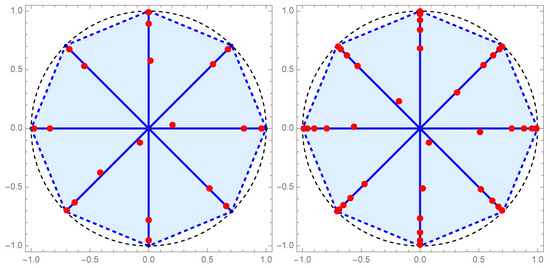
Here, we consider eight rays ($M=8$) and the inner product (28), with eight different Jacobi weights on $(0,1)$:

$$\left\{\sqrt{x(1-x)},\sqrt{{\displaystyle \frac{1-x}{x}}},\sqrt{{\displaystyle \frac{x}{1-x}}},x\sqrt{1-x},\sqrt{x},{\displaystyle \frac{\sqrt[4]{x}}{\sqrt{1-x}}},{\displaystyle \frac{\sqrt{1-x}}{x^{3/4}}},\sqrt{x}(1-x)\right\}.$$

Using the discretized Stieltjes–Gautschi procedure, we calculate $B_{60}$, so that we are now able to construct all polynomials ${\pi }_n\left(z\right)$ for $n\le 60$ and determine their zeros by solving the eigenvalue problem for the Hessenberg matrix $-B_n$.

To save space, we now only mention the matrix $B_3$, whose elements are given with only a few decimal digits:

$$B_3=\left[\begin{array}{ccc}\hfill 0.0837609-0.0100600\mathrm{i}& -1.000000\hfill & \phantom{-}0\hfill \\ \hfill 0.0871212-0.1071982\mathrm{i}& \phantom{-}0.181465-0.088039\mathrm{i}\hfill & -1.000000\hfill \\ \hfill -0.0245078+0.0774873\mathrm{i}& \phantom{-}0.154522-0.172507\mathrm{i}\hfill & \phantom{-}0.119911-0.0610793\mathrm{i}\hfill \end{array}\right].$$

The first five orthogonal polynomials are

$$\begin{array}{cc}\hfill {\pi }_0\left(z\right)& =1,{\pi }_1\left(z\right)=z+(0.0837609-0.0100600\mathrm{i}),\hfill \\ \hfill {\pi }_2\left(z\right)& =z^2+(0.265225-0.098099\mathrm{i})z+(0.101435-0.116398\mathrm{i}),\hfill \\ \hfill {\pi }_3\left(z\right)& =z^3+(0.385137-0.159178\mathrm{i})z^2+(0.281769-0.316868\mathrm{i})z\hfill \\ \hfill & -(0.0082466-0.0413304\mathrm{i}),\hfill \\ \hfill {\pi }_4\left(z\right)& =z^4+(0.404671-0.165400\mathrm{i})z^3+(0.318252-0.388245\mathrm{i})z^2\hfill \\ \hfill & -(0.0479628-0.1086000\mathrm{i})z-(0.0301391-0.0021550\mathrm{i}),\hfill \\ \hfill {\pi }_5\left(z\right)& =z^5+(0.454259-0.154317\mathrm{i})z^4+(0.291573-0.439576\mathrm{i})z^3\hfill \\ \hfill & -(0.083702-0.122281\mathrm{i})z^2-(0.1066780-0.0425364\mathrm{i})z\hfill \\ \hfill & -(0.0051564-0.0284693\mathrm{i}).\hfill \end{array}$$

The zeros of the polynomials ${\pi }_5\left(z\right)$, ${\pi }_{10}\left(z\right)$, ${\pi }_{20}\left(z\right)$ and ${\pi }_{40}\left(z\right)$ are presented in Figure 9 and Figure 10. We notice that as the degree of the orthogonal polynomial increases, we have a buildup of zeros towards the ends of the radial rays.

Figure 9. Zeros of ${\pi }_5\left(z\right)$ (left) and ${\pi }_{10}\left(z\right)$ (right) in Example 6.

Figure 10. Zeros of ${\pi }_{20}\left(z\right)$ (left) and ${\pi }_{40}\left(z\right)$ (right) in Example 6.

6. Symmetric Cases of Orthogonal Polynomials on the Radial Rays

In some special cases, it is possible to find the moment determinants in an explicit form. Then, we can obtain the corresponding orthogonal polynomials, as well as some other properties of these orthogonal polynomials, including recurrence relations, zero distribution, or even an electrostatic interpretation of their zeros (see [6]).

6.1. Symmetrical Case of Equal Rays, Equidistantly Spaced and with the Same Weight Function

Consider the symmetric case with $a_s=a>0$, ${\theta }_s=2\pi (s-1)/M$, $s=1,\dots ,M$, with the same weight function on the rays

$$|w_s\left(x{\epsilon }_s\right)|=|w_s\left(z\right)|=\omega \left(x\right)(z\in {\ell }_s,s=1,\dots ,M).$$

Some of such cases are presented in Examples 1 and 2, with Legendre weight $\omega \left(x\right)=1$ on $[0,1]$, except Example 2 (ii), where we used $\omega \left(x\right)=x^2{(1-x^4)}^{1/2}$ on $[0,1]$.

The inner product, in this case, becomes

$$(p,q)=\sum _{s=1}^M{\int }_0^{a}p\left(x{\epsilon }_s\right)\overline{q\left(x{\epsilon }_s\right)}\omega \left(x\right)\mathrm{d}x,$$

(30)

and the moments are given by (see also (9))

$${\mu }_{k,j}=(z^k,z^j)=\left(\sum _{s=1}^M{\epsilon }_s^{k-j}\right){\int }_0^a{x}^{k+j}\omega \left(x\right)\mathrm{d}x.$$

Note that ${\epsilon }_s^M=1$ and $(z^{M}p,q)=(p,z^{M}q)$. As in [2], we obtain that

$${\mu }_{k,j}=\left\{\begin{array}{cc}{\displaystyle M{\int }_0^a{x}^{k+j}\omega \left(x\right)\mathrm{d}x},\hfill & j\equiv k\left(\mathrm{mod}M\right),\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(31)

as well as the following result (see [3]).

Theorem 6. 

The monic orthogonal polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{+\infty }$, related to the inner product (30), satisfy the recurrence relation

$${\pi }_{n+M}\left(z\right)=(z^M-{\alpha }_n){\pi }_n\left(z\right)-{\beta }_n{\pi }_{n-M}\left(z\right),n\ge 0,$$

(32)

with ${\pi }_n\left(z\right)=z^n$, $n=0,1,\dots ,M-1$, and ${\pi }_n\left(z\right)=0$ for $n<0$. The recursion coefficients in (32) are given by

$${\alpha }_n={\displaystyle \frac{(z^M{\pi }_n,{\pi }_n)}{({\pi }_n,{\pi }_n)}}(n\ge 0),{\beta }_n={\displaystyle \frac{({\pi }_n,{\pi }_n)}{({\pi }_{n-M},{\pi }_{n-M})}}(n\ge M).$$

In the case of an even number of rays $M=2m$, the previous result can be simplified (see [2]). Notice that, in that case, for the inner product, we have $(z^{m}p,q)=(p,z^{m}q)$.

Theorem 7. 

Let $M=2m$ in the inner product (30). The monic polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{+\infty }$ satisfy the recurrence relation

$${\pi }_{n+m}\left(z\right)=z^m{\pi }_n\left(z\right)-b_n{\pi }_{n-m}\left(z\right),n\ge m,$$

(33)

with ${\pi }_n\left(z\right)=z^n$ for $n=0,1,\dots ,2m-1$. The coefficient $b_n$ in (33) is given by

$$b_n={\displaystyle \frac{({\pi }_n,z^m{\pi }_{n-m})}{({\pi }_{n-m},{\pi }_{n-m})}}={\displaystyle \frac{\parallel {\pi }_n{\parallel }^2}{\parallel {\pi }_{n-m}{\parallel }^2}}(n\ge m).$$

Because ${\pi }_n\left(z\right)=0$ for $n<0$, the coefficients $b_n$ are arbitrary for $n\le m-1$, and we can take, e.g., $b_n=0$ for $0\le n\le m-1$.

Remark 3. 

There is a connection between the recurrence relations (33) and (32). Namely, using (33), one can obtain the recurrence relation

$${\pi }_{n+2m}\left(z\right)=\left[z^{2m}-(b_n+b_{n+m})\right]{\pi }_n\left(z\right)-b_n{b}_{n-m}{\pi }_{n-2m}\left(z\right),$$

i.e., (32), where $2m=M$ and

$${\alpha }_n=b_n+b_{n+m},{\beta }_n=b_n{b}_{n-m}.$$

We return again to the general case. For $n=Mk+\nu$, where $k=[n/M]$ and $\nu \in \{0,1,\dots ,M-1\}$, we see that (32) reduces to

$${\pi }_{M(k+1)+\nu }\left(z\right)=\left(z^M-{\alpha }_{Mk+\nu }\right){\pi }_{Mk+\nu }\left(z\right)-{\beta }_{Mk+\nu }{\pi }_{M(k-1)+\nu },k\ge 0,$$

(34)

so that, for $k=0,1,2,\dots$ and $\nu =0,1,\dots ,M-1$, we have

$$\begin{array}{cc}\hfill {\pi }_{M+\nu }\left(z\right)& =(z^M-{\alpha }_{\nu }){\pi }_{\nu }\left(z\right)=z^{M+\nu }-{\alpha }_{\nu }{z}^{\nu },\hfill \\ \hfill {\pi }_{2M+\nu }\left(z\right)& =(z^M-{\alpha }_{M+\nu }){\pi }_{M+\nu }\left(z\right)-{\beta }_{M+\nu }{\pi }_{\nu }\left(z\right)\hfill \\ \hfill & =z^{2M+\nu }-({\alpha }_{\nu }+{\alpha }_{M+\nu })z^{M+\nu }+({\alpha }_{\nu }{\alpha }_{M+\nu }-{\beta }_{M+\nu })z^{\nu },\hfill \\ \hfill {\pi }_{3M+\nu }\left(z\right)& =(z^M-{\alpha }_{2M+\nu }){\pi }_{2M+\nu }\left(z\right)-{\beta }_{2M+\nu }{\pi }_{M+\nu }\left(z\right),\hfill \\ \hfill & =z^{3M+\nu }-\left({\alpha }_{\nu }+{\alpha }_{M+\nu }+{\alpha }_{2M+\nu }\right)z^{2M+\nu }\hfill \\ \hfill & +\left({\alpha }_{\nu }{\alpha }_{M+\nu }+{\alpha }_{\nu }{\alpha }_{2M+\nu }+{\alpha }_{M+\nu }{\alpha }_{2M+\nu }-{\beta }_{M+\nu }-{\beta }_{2M+\nu }\right)z^{M+\nu }\hfill \\ \hfill & -\left({\alpha }_{\nu }{\alpha }_{M+\nu }{\alpha }_{2M+\nu }-{\alpha }_{2M+\nu }{\beta }_{M+\nu }-{\alpha }_{\nu }{\beta }_{2M+\nu }\right)z^{\nu },\hfill \end{array}$$

etc. We can conclude that the monic polynomials ${\pi }_n\left(z\right)={\pi }_{Mk+\nu }\left(z\right)$ can be expressed in the following form, with the real coefficients:

$${\pi }_n\left(z\right)={\pi }_{Mk+\nu }\left(z\right)=z^{\nu }\sum _{j=0}^k{c}_j^{\left(n\right)}{z}^{Mj},c_k^{\left(n\right)}=1,$$

where $k=[n/M]$ and $\nu \in \{0,1,\dots ,M-1\}$. Thus, we have the following representation:

$${\pi }_{Mk+\nu }\left(z\right)=z^{\nu }{q}_k^{\left(\nu \right)}\left(z^M\right),\nu =0,1,\dots ,M-1,$$

(35)

where $q_k^{\left(\nu \right)}\left(t\right)$, $\nu =0,1,\dots ,M-1$, are monic polynomials of the degree k. Putting (35) in (34), we obtain

$$z^{\nu }{q}_{k+1}^{\left(\nu \right)}\left(z^M\right)=\left(z^M-{\alpha }_{Mk+\nu }\right)z^{\nu }{q}_k^{\left(\nu \right)}\left(z^M\right)-{\beta }_{Mk+\nu }{z}^{\nu }{q}_{k-1}^{\left(\nu \right)}\left(z^M\right),$$

i.e., the following result (see [3]).

Theorem 8. 

For each $\nu =0,1,\dots ,M-1$, the monic polynomials $q_k^{\left(\nu \right)}\left(t\right)$ satisfy the three-term recurrence relations

$$q_{k+1}^{\left(\nu \right)}\left(t\right)=\left(t-a_k^{\left(\nu \right)}\right)q_k^{\left(\nu \right)}\left(t\right)-b_k^{\left(\nu \right)}{q}_{k-1}^{\left(\nu \right)}\left(t\right),k=0,1,\dots ,$$

(36)

with $q_0^{\left(\nu \right)}\left(t\right)=1$, $q_{-1}^{\left(\nu \right)}\left(t\right)=0$, where $a_k^{\left(\nu \right)}={\alpha }_n$ and $b_k^{\left(\nu \right)}={\beta }_n$ for $n=Mk+\nu$, $k=[n/M]$, and $n\in {\mathbb{N}}_0$. Moreover, these polynomials are orthogonal on $(0,a^M)$ with respect to the weight function

$$w_{\nu }\left(t\right)=t^{(2\nu +1)/M-1}\omega \left(t^{1/M}\right),$$

where $\omega \left(x\right)$ is the weight function in the inner product (30).

The second part of this theorem can be proven by using the equality

$$({\pi }_{Mk+\nu },{\pi }_{Mj+\nu })={\int }_0^{a^M}{q}_k^{\left(\nu \right)}\left(t\right)\overline{q_j^{\left(\nu \right)}\left(t\right)}{t}^{(2\nu +1)/M-1}\omega \left(t^{1/M}\right)\mathrm{d}t={\delta }_{k,j}{\parallel {\pi }_{Mk+\nu }\parallel }^2,$$

obtained by (30) and (35) and the change in variables $t=x^M$. Defining

$${(p,q)}_{\nu }:={\int }_0^{a^M}p\left(t\right)\overline{q\left(t\right)}{w}_{\nu }\left(t\right)\mathrm{d}t\mathrm{and}{\parallel p\parallel }_{\nu }=\sqrt{{(p,p)}_{\nu }},$$

we conclude that $\parallel {\pi }_{Mj+\nu }\parallel ={\parallel q_j^{\left(\nu \right)}\parallel }_{\nu }$. As we mentioned in Section 2, the coefficient $b_0^{\left(\nu \right)}$ can be arbitrary, but it is convenient to take

$$b_0^{\left(\nu \right)}={\int }_0^{a^M}{w}_{\nu }\left(t\right)\mathrm{d}t={\int }_0^{a^M}{t}^{(2\nu +1)/M-1}\omega \left(t^{1/M}\right)\mathrm{d}t,\nu =0,1,\dots ,M-1,$$

so that we have

$$\parallel {\pi }_{Mj+\nu }{\parallel }^2={\parallel q_j^{\left(\nu \right)}\parallel }_{\nu }^2=b_0^{\left(\nu \right)}{b}_1^{\left(\nu \right)}\cdots b_j^{\left(\nu \right)}={\beta }_{\nu }{\beta }_{M+\nu }\cdots {\beta }_{Mj+\nu }.$$

Notice that $a_j^{\left(\nu \right)}={\alpha }_{Mj+\nu }$ and $b_j^{\left(\nu \right)}={\beta }_{Mj+\nu }$, as well as

$${\displaystyle \frac{\parallel q_{j+1}^{\left(\nu \right)}{\parallel }_{\nu }}{\parallel q_j^{\left(\nu \right)}{\parallel }_{\nu }}}={\displaystyle \frac{\parallel {\pi }_{M(j+1)+\nu }\parallel }{\parallel {\pi }_{Mj+\nu }\parallel }}=\sqrt{b_{j+1}^{\left(\nu \right)}}=\sqrt{{\beta }_{M(j+1)+\nu }}.$$

If we write the recurrence relation (36) with the index j instead of k, the corresponding recurrence relation for orthonormal polynomials ${\widehat{q}}_j^{\left(\nu \right)}\left(t\right)\left(=q_j^{\left(\nu \right)}\left(t\right)/\parallel q_j^{\left(\nu \right)}\parallel \right)$ is

$$t{\widehat{q}}_j^{\left(\nu \right)}\left(t\right)=\sqrt{{\beta }_{Mj+\nu }}{\widehat{q}}_{j-1}^{\left(\nu \right)}\left(t\right)+{\alpha }_{Mj+\nu }{\widehat{q}}_j^{\left(\nu \right)}\left(t\right)+\sqrt{{\beta }_{M(j+1)+\nu }}{\widehat{q}}_{j+1}^{\left(\nu \right)}\left(t\right),j=0,1,\dots .$$

Taking $j=0,1,\dots ,k-1$ in this relation, for a fixed $\nu \in \{0,1,\dots ,M-1\}$, we obtain the following matrix relation:

$$t{\mathbf{q}}_k^{(\nu ,M)}=J_k^{(\nu ,M)}{\mathbf{q}}_k^{(\nu ,M)}+\sqrt{{\beta }_{Mk+\nu }}{\widehat{q}}_k^{\left(\nu \right)}\left(t\right){\mathbf{e}}_k,$$

where ${\mathbf{q}}_k^{(\nu ,M)}={[{\widehat{q}}_0^{\left(\nu \right)}\left(t\right){\widehat{q}}_1^{\left(\nu \right)}\left(t\right)\cdots {\widehat{q}}_{k-1}^{\left(\nu \right)}\left(t\right)]}^T$ and $J_k^{(\nu ,M)}$ is the symmetric tridiagonal Jacobi matrix given by

$$J_k^{(\nu ,M)}=\left[\begin{array}{ccccc}{\alpha }_{\nu }& \sqrt{{\beta }_{M+\nu }}& & & \mathrm{O}\\ \sqrt{{\beta }_{M+\nu }}& {\alpha }_{M+\nu }& \sqrt{{\beta }_{2M+\nu }}\\ & \sqrt{{\beta }_{2M+\nu }}& {\alpha }_{2M+\nu }& \ddots \\ & & \ddots & \ddots & \sqrt{{\beta }_{(k-1)M+\nu }}\\ \mathrm{O}& & & \sqrt{{\beta }_{(k-1)M+\nu }}& {\alpha }_{(k-1)M+\nu }\end{array}\right].$$

(37)

It is clear that ${\widehat{q}}_k^{\left(\nu \right)}\left(t\right)=0$ if and only if $t{\mathbf{q}}_k^{(\nu ,M)}=J_k^{(\nu ,M)}{\mathbf{q}}_k^{(\nu ,M)}$, i.e., the zeros of ${\widehat{q}}_k^{\left(\nu \right)}\left(t\right)$ are the same as the eigenvalues of the Jacobi matrix $J_k^{(\nu ,M)}$. Also, $q_k^{\left(\nu \right)}\left(t\right)=det\left(t{I}_k-J_k^{(\nu ,M)}\right)$, where $I_k$ is the identity matrix of order k.

6.2. Zero Distribution

The following theorem gives the zero distribution of the polynomials ${\pi }_n\left(z\right)$.

Theorem 9. 

All zeros of the orthogonal polynomials ${\pi }_n\left(z\right)$, $n\ge 1$, related to the inner product (30), are simple and lie on the radial rays, with the possible exception of a multiple zero at the origin $z=0$ of the order ν if $n\equiv \nu (modM)$.

Let ${\tau }_j^{(k,\nu )}$, $j=1,2,\dots ,k$, denote the zeros of the polynomial $q_k^{\left(\nu \right)}\left(t\right)$, defined in (35), in an increasing order, i.e.,

$$0<{\tau }_1^{(k,\nu )}<{\tau }_2^{(k,\nu )}<\cdots <{\tau }_k^{(k,\nu )}.$$

These zeros can be easily calculated using the Golub–Welsch algorithm [14], implemented in our Mathematica package OrthogonalPolynomials (see [25,26]).

Then, each zero ${\tau }_j^{(k,\nu )}$ generates M zeros

$${\zeta }_{j,s}^{(k,\nu )}=\sqrt[M]{{\tau }_j^{(k,\nu )}}{\mathrm{e}}^{\mathrm{i}2\pi (s-1)/M},s=1,2,\dots ,M,$$

of the polynomial ${\pi }_n\left(z\right)$. On each ray, we have

$$0<|{\zeta }_{1,s}^{(k,\nu )}|<|{\zeta }_{2,s}^{(k,\nu )}|<\cdots <|z_{k,s}^{(k,\nu )}|,s=1,2\dots ,M.$$

If $n=Mk+\nu$, where $k=[n/M]$ and $0<\nu \le M-1$, then there exists one zero of ${\pi }_n\left(z\right)$ of order $\nu$ at the origin $z=0$.

6.3. Legendre Weight on $[0,1]$

Let $\omega \left(x\right)={(1-x)}^{\alpha }{x}^{\beta }$ be a Jacobi weight on the interval $[0,1]$, where $\alpha ,\beta >-1$. Suppose that this weight is on all rays, i.e., the inner product (30), in the form

$$(p,q)=\sum _{s=1}^M{\int }_0^{1}p\left(x{\epsilon }_s\right)\overline{q\left(x{\epsilon }_s\right)}{(1-x)}^{\alpha }{x}^{\beta }\mathrm{d}x.$$

(38)

Then, the moments (39) become

$${\mu }_{k,j}=\left\{\begin{array}{cc}{\displaystyle M{\int }_0^1{x}^{k+j+\beta }{(1-x)}^{\alpha }\mathrm{d}x},\hfill & j\equiv k\left(\mathrm{mod}M\right),\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(39)

i.e.,

$${\mu }_{k,j}={\displaystyle \frac{\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(j+k+\beta +1)}{\mathsf{\Gamma }(j+k+\alpha +\beta +2)}},j\equiv k\left(\mathrm{mod}M\right)$$

and ${\mu }_{k,j}=0$ in other cases. In fact, this is a special case of the general one considered earlier in Section 5.4. Here, we study Legendre’s case ($\alpha =\beta =0$) in particular, for which we can obtain some analytical results.

Thus, we take $\omega \left(x\right)=1$ and the moments (39) become

$${\mu }_{k,m}=(z^k,z^m)=\left\{\begin{array}{cc}{\displaystyle \frac{M}{1+k+m}},\hfill & m\equiv k\left(\mathrm{mod}M\right),\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

i.e., for $k=Mi+\nu$ and $m=Mj+\nu$,

$${\mu }_{Mi+\nu ,Mj+\nu }={\displaystyle \frac{M}{M(i+j)+2\nu +1}},0\le \nu \le M-1,i,j\ge 0.$$

In this case, the corresponding moment determinants can be evaluated as (see [3,5])

$$\begin{array}{cc}\hfill {\Delta }_{Mk}& =E_k^{\left(0\right)}{E}_k^{\left(1\right)}\cdots E_k^{(M-1)},\hfill \\ \hfill {\Delta }_{Mk+\nu }& =\prod _{i=0}^{\nu -1}{E}_{k+1}^{\left(i\right)}\prod _{j=\nu }^{M-1}{E}_k^{\left(j\right)},0<\nu <M,\hfill \end{array}$$

where $E_0^{\left(\nu \right)}=1$ and

$$E_k^{\left(\nu \right)}=\left|\begin{array}{cccc}{\mu }_{\nu ,\nu }& {\mu }_{M+\nu ,\nu }& \cdots & {\mu }_{M(k-1)+\nu ,\nu }\\ {\mu }_{\nu ,M+\nu }& {\mu }_{M+\nu ,M+\nu }& \cdots & {\mu }_{M(k-1)+\nu ,M+\nu }\\ ⋮& & & \\ {\mu }_{\nu ,M(k-1)+\nu }& {\mu }_{M+\nu ,M(k-1)+\nu }& \cdots & {\mu }_{M(k-1)+\nu ,M(k-1)+\nu }\end{array}\right|.$$

Lemma 1. 

The value of $E_k^{\left(\nu \right)}$ is

$$E_k^{\left(\nu \right)}=M^{k^2}{\displaystyle \frac{{[0!1!\cdots (k-1)!]}^2}{{\displaystyle \prod _{i,j=0}^{k-1}}[M(i+j)+2\nu +1]}}.$$

Using Theorem 1 and the previous lemma, we can calculate the norm $\parallel {\pi }_n\parallel$ of the orthogonal polynomial in this symmetric case, when $n=Mk+\nu$, $k=[n/M]$ and $\nu \in \{0,1,\dots ,M-1\}$, because (see Equation (13))

$$\parallel {\pi }_n{\parallel }^2={\displaystyle \frac{{\Delta }_{n+1}}{{\Delta }_n}}={\displaystyle \frac{E_{k+1}^{\left(\nu \right)}}{E_k^{\left(\nu \right)}}},n=Mk+\nu .$$

Theorem 10. 

We have

$$\parallel {\pi }_{Mk+\nu }{\parallel }^2=\left\{\begin{array}{cc}{\displaystyle \frac{M}{2\nu +1}},\hfill & k=0,\hfill \\ {\displaystyle \frac{M}{2Mk+2\nu +1}}{\left({\displaystyle \prod _{j=k}^{2k-1}}{\displaystyle \frac{M(j-k+1)}{Mj+2\nu +1}}\right)}^2,\hfill & k\ge 1,\hfill \end{array}\right.$$

where $0\le \nu \le M-1$.

Using these explicit expressions, we can state the following corollary of Theorem 6, for the Legendre weight:

Corollary 1. 

Let $n=Mk+\nu$, $k=[n/M]$ and $\nu \in \{0,1,\dots ,M-1\}$. The monic orthogonal polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{+\infty }$, with respect to the inner product (30), with $\omega \left(x\right)=1$, satisfy the recurrence relation (32), where

$$\begin{array}{cc}\hfill {\alpha }_n& ={\displaystyle \frac{2{\left(Mk\right)}^2+(2\nu +1)[(2k-1)M+2\nu +1]}{\left[\right(2k-1)M+2\nu +1]\left[\right(2k+1)M+2\nu +1]}},\hfill \\ \hfill {\beta }_n& ={\displaystyle \frac{{\left(Mk\right)}^2{[(k-1)M+2\nu +1]}^2}{[2(k-1)M+2\nu +1]{[(2k-1)M+2\nu +1]}^2[2Mk+2\nu +1]}},\hfill \end{array}$$

except $n=1$, when ${\alpha }_1=3/(3+M)$.

Example 7. 

Recurrence coefficients ${\alpha }_n$ and ${\beta }_n$ in (32) for polynomials from Example 1 ($M=3$), regarding Corollary 1, are

$$\begin{array}{cc}\hfill {\left\{{\alpha }_n\right\}}_{n=0}^{\infty }& =\left\{{\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{2}},{\displaystyle \frac{5}{8}},{\displaystyle \frac{11}{20}},{\displaystyle \frac{1}{2}},{\displaystyle \frac{29}{56}},{\displaystyle \frac{41}{80}},{\displaystyle \frac{1}{2}},{\displaystyle \frac{71}{140}},{\displaystyle \frac{89}{176}},{\displaystyle \frac{1}{2}},{\displaystyle \frac{131}{260}},{\displaystyle \frac{155}{308}},{\displaystyle \frac{1}{2}},{\displaystyle \frac{209}{416}},{\displaystyle \frac{239}{476}},\dots \right\},\hfill \\ \hfill {\left\{{\beta }_n\right\}}_{n=0}^{\infty }& =\left\{0,0,0,{\displaystyle \frac{9}{112}},{\displaystyle \frac{1}{12}},{\displaystyle \frac{45}{704}},{\displaystyle \frac{144}{2275}},{\displaystyle \frac{1}{15}},{\displaystyle \frac{576}{9163}},{\displaystyle \frac{3969}{63232}},{\displaystyle \frac{9}{140}},{\displaystyle \frac{9801}{156400}},{\displaystyle \frac{144}{2299}},\dots \right\}.\hfill \end{array}$$

Consider now an interesting simple case when $M=4$ (even number of rays $2m=4$) and inner product is given by (17), as in Example 2. Then, Theorem 7 reduces to the following result (see [2]):

Corollary 2. 

The sequence of monic orthogonal polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{+\infty }$, related to the inner product (17), satisfies the recurrence relation

$${\pi }_{n+2}\left(z\right)=z^2{\pi }_n\left(z\right)-b_n{\pi }_{n-2}\left(z\right),n\ge 2,$$

with ${\pi }_n\left(z\right)=z^n$, $n=0,1,2,3$, where

$$b_{4k+\nu }=\left\{\begin{array}{cc}{\displaystyle \frac{16k^2}{(8k+2\nu -3)(8k+2\nu +1)}}\hfill & if\nu =0,1,\hfill \\ {\displaystyle \frac{{(4k+2\nu -3)}^2}{(8k+2\nu -3)(8k+2\nu +1)}}\hfill & if\nu =2,3.\hfill \end{array}\right.$$

In this simple symmetric case $(M=4)$, with inner product given in Example 2 (i) by (17), the extremal problem from Theorem 2 reduces to the following (see [48]):

Corollary 3. 

For each $P\in {\widehat{\mathcal{P}}}_n$, where $n=4k+\nu$, $k=[n/4]$, and $\nu \in \{0,1,2,3\}$, we have

$${\int }_0^1\left({|P\left(x\right)|}^2+{|P\left(\mathrm{i}x\right)|}^2+{|P(-x)|}^2+{|P(-\mathrm{i}x)|}^2\right)\mathrm{d}x\ge K_n,$$

where

$$K_n={\displaystyle \frac{4}{2n+1}}{\left(\prod _{j=k}^{2k-1}{\displaystyle \frac{4(j-k+1)}{4j+2\nu +1}}\right)}^2,n\ge 4,$$

and $K_n=4/(2n+1)$ for $0\le n\le 3$.

Here, we used Theorem 10 for $M=4$.

6.4. An Analog of the Jacobi Polynomials (M—Generalized Gegenbauer Polynomials)

We consider a symmetric case of M unit rays, equidistantly spaced (${\epsilon }_s={\mathrm{e}}^{\mathrm{i}2\pi (s-1)/M}\in \mathbb{C}$, $s=1,\dots ,M$), with the same weight function on the rays:

$$\omega \left(x\right)={(1-x^M)}^{\alpha }{x}^{M\gamma },\alpha >-1,\gamma >-{\displaystyle \frac{1}{M}}.$$

(40)

The inner product is given by

$$(p,q)=\sum _{s=1}^M{\int }_0^{1}p\left(x{\epsilon }_s\right)\overline{q\left(x{\epsilon }_s\right)}\omega \left(x\right)\mathrm{d}x.$$

(41)

Let $p_k^{(\alpha ,\beta )}\left(t\right)$ be the monic Jacobi polynomial on $[0,1]$, orthogonal with respect to the weight function ${(1-t)}^{\alpha }{t}^{\beta }$$(\alpha ,\beta >-1)$. It is connected to the standard monic Jacobi polynomial ${\widehat{P}}_k^{(\alpha ,\beta )}\left(x\right)$ on $[-1,1]$ as

$$p_k^{(\alpha ,\beta )}\left(t\right)={\displaystyle \frac{1}{2^k}}{\widehat{P}}_k^{(\alpha ,\beta )}(2t-1).$$

Using the three-term recurrence relation for ${\widehat{P}}_k^{(\alpha ,\beta )}\left(x\right)$ (cf. [13], p. 132), we obtain the corresponding recurrence relation for the polynomial $p_k^{(\alpha ,\beta )}\left(t\right)$,

$$p_{k+1}^{(\alpha ,\beta )}\left(t\right)=\left(t-{\displaystyle \frac{1+{\alpha }_k}{2}}\right)p_k^{(\alpha ,\beta )}\left(t\right)-{\beta }_k{p}_{k-1}^{(\alpha ,\beta )}\left(t\right),k\ge 0,$$

where

$${\alpha }_k={\displaystyle \frac{{\beta }^2-{\alpha }^2}{(2k+\alpha +\beta )(2k+\alpha +\beta )}}(k\ge 0,\mathrm{except}{\alpha }_0=-\alpha \mathrm{if}\alpha +\beta =0)$$

and

$${\beta }_k={\displaystyle \frac{k(k+\alpha )(k+\beta )(k+\alpha +\beta )}{{(2k+\alpha +\beta )}^2\left({(2k+\alpha +\beta )}^2-1\right)}}(k\ge 1,\mathrm{except}{\beta }_1=-2\alpha (\alpha +1)\mathrm{if}\alpha +\beta =-1).$$

According to Theorems 6 and 8, we can prove the following result:

Theorem 11. 

The monic polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{+\infty }$, orthogonal with respect to the inner product (41), with the weight function (40), satisfy the recurrence relation of the form (32), and can be expressed in the form

$${\pi }_{Mk+\nu }\left(z\right)=z^{\nu }{p}_k^{(\alpha ,{\beta }_{\nu })}\left(z^M\right)=2^{-k}{z}^{\nu }{\widehat{P}}_k^{(\alpha ,{\beta }_{\nu })}\left(2z^M-1\right),\nu =0,1,\dots ,M-1,$$

(42)

where $k=[n/M]$ and

$${\beta }_{\nu }=\gamma -1+{\displaystyle \frac{2\nu +1}{M}},\nu =0,1,\dots ,M-1.$$

Remark 4. 

The case when $M=2m$ was considered in [2].

Remark 5. 

As we can see, from (40) and (41) for $\alpha =\gamma =0$, we obtain the monic orthogonal polynomials in Legendre case (cf. Section 6.3):

$${\pi }_{Mk+\nu }\left(z\right)=2^{-k}{z}^{\nu }{\widehat{P}}_k^{(0,{\beta }_{\nu })}\left(2z^M-1\right),\nu =0,1,\dots ,M-1,$$

where $k=[n/M]$ and ${\beta }_{\nu }=(2\nu -M+1)/M$.

For $M=4$, it reduces to ${\pi }_{4k+\nu }\left(z\right)=2^{-k}{z}^{\nu }{\widehat{P}}_k^{(0,(2\nu -3)/4)}\left(2z^4-1\right)$, where $k=[n/4]$ and $\nu \in \{0,1,2,3\}$.

Since the leading coefficient in the standard Jacobi polynomial $P_n^{(\alpha ,\beta )}\left(z\right)=k_n{z}^n+\cdots$ is given by $k_n={(n+\alpha +\beta +1)}_n/(2^{n}n!)$ (cf. [13], p. 132), for generating, e.g., the first 12 (monic) orthogonal polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{11}$, only one command in the Wolfram (Mathematica) 14.1 is enough:

Flatten[Table[(k!/Pochhammer[(4k+2v+1)/4,k])z^v

   JacobiP[k,0,(2v-3)/4,2z^4-1],{k,0,2},{v,0,3}]]//Simplify  

Note that these polynomials for $n\le 8$ were calculated by the complicated “determinant approach” in Example 2 (i).

Remark 6. 

Taking $M=2$, the weight function (40) becomes $\omega \left(x\right)=x^{2\gamma }{(1-x^2)}^{\alpha }$, where $\alpha >-1$ and $\gamma >-1/2$. Since it can be written in the form $\omega \left(x\right)={|x|}^{2\gamma }{(1-x^2)}^{\alpha }$, as well as the inner product (41),

$$(p,q)={\int }_0^1\left[p\left(x\right)\overline{q\left(x\right)}+p(-x)\overline{q(-x)}\right]\omega \left(x\right)\mathrm{d}x={\int }_{-1}^{1}p\left(x\right)\overline{q\left(x\right)}\omega \left(x\right)\mathrm{d}x,$$

we conclude that the orthogonal polynomials ${\pi }_{2k+\nu }\left(z\right)=2^{-k}{z}^{\nu }{\widehat{P}}_k^{(\alpha ,\gamma -1/2+\nu )}\left(2z^2-1\right)$, where $k=[n/2]$ and $\nu \in \{0,1\}$, in this case are, in fact, the generalized Gegenbauer polynomials introduced in 1953 by Laščenov [49] (cf. Chihara ([45], pp. 155–156) and Mastroianni and Milovanović ([13], p. 147). This is the reason we refer the polynomials (42) as the M-generalized Gegenbauer polynomials.

6.5. Some Analogs of the Generalized Laguerre (M-Generalized Hermite Polynomials)

We now consider a symmetric case of M infinity rays, equidistantly spaced as in Section 6.4, with the same weight function on the rays

$$\omega \left(x\right)=x^{M\gamma }{\mathrm{e}}^{-x^M},\gamma >-{\displaystyle \frac{1}{M}},$$

(43)

and the inner product given by

$$(p,q)=\sum _{s=1}^M{\int }_0^{+\infty }p\left(x{\epsilon }_s\right)\overline{q\left(x{\epsilon }_s\right)}\omega \left(x\right)\mathrm{d}x,$$

(44)

with ${\widehat{L}}_k^{\left(\alpha \right)}\left(t\right)$ denoting the monic generalized orthogonal Laguerre polynomials related to the weight function $t^{\alpha }{\mathrm{e}}^{-t}$ on $(0,+\infty )$. Such polynomials satisfy the three-term recurrence relation: ([13], p. 141)

$${\widehat{L}}_{k+1}^{\left(\alpha \right)}\left(t\right)=\left[t-(2k+\alpha +1)\right]{\widehat{L}}_k^{\left(\alpha \right)}\left(t\right)-k(k+\alpha ){\widehat{L}}_{k-1}^{\left(\alpha \right)}\left(t\right),k\ge 0.$$

Using Theorems 6 and 8, we can prove the following result:

Theorem 12. 

The monic orthogonal polynomials ${\left\{{\pi }_n\left(z\right)\right\}}_{n=0}^{+\infty }$, related to the inner product (44), with the weight function (43), satisfy the recurrence relation of the form (32), and can be expressed in the form

$${\pi }_n\left(z\right)={\pi }_{Mk+\nu }\left(z\right)=z^{\nu }{\widehat{L}}_k^{\left({\alpha }_{\nu }\right)}\left(z^M\right),k=\left[{\displaystyle \frac{n}{M}}\right],\nu =0,1,\dots ,M-1;k=0,1,\dots ,$$

where

$${\alpha }_{\nu }=\gamma -1+{\displaystyle \frac{2\nu +1}{M}},\nu =0,1,\dots ,M-1.$$

Remark 7. 

The case when $M=2m$ was considered in [1,2]. Then, according to Theorem 7, the polynomials ${\pi }_n\left(z\right)$, $n=2mk+\nu$, satisfy (33), where for $k\ge 1$,

$$b_{2mk+\nu }=\left\{\begin{array}{cc}k+1+{\alpha }_{\nu }\hfill & 0\le \nu \le m-1,\hfill \\ k\hfill & m\le \nu \le 2m-1.\hfill \end{array}\right.$$

6.6. Differential Equation

In the completely symmetric case, with M rays, using (35), we can prove the following result (cf. [3]).

Theorem 13. 

If polynomials $q_k^{\left(\nu \right)}\left(t\right)$, $\nu =0,1,\dots ,M-1$, defined in (35), satisfy linear differential equations of the second order of the form

$$p^{\left(\nu \right)}\left(t\right)y^{\prime \prime }+q^{\left(\nu \right)}\left(t\right)y^{\prime }+r^{\left(\nu \right)}(t,k)y=0,$$

then the monic orthogonal polynomial ${\pi }_n\left(z\right)\equiv {\pi }_{Mk+\nu }\left(z\right)$ satisfies the following second-order linear differential equation:

$$z^2{P}^{\left(\nu \right)}\left(z\right)Y^{\prime \prime }+z{Q}^{\left(\nu \right)}\left(z\right)Y^{\prime }+R^{\left(\nu \right)}(z,n)Y=0,$$

where

$$\begin{array}{cc}\hfill P^{\left(\nu \right)}\left(z\right)& =p^{\left(\nu \right)}\left(z^M\right),\hfill \\ \hfill Q^{\left(\nu \right)}\left(z\right)& =M{q}^{\left(\nu \right)}\left(z^M\right)z^M-(M+2\nu -1)p^{\left(\nu \right)}\left(z^M\right),\hfill \\ \hfill R^{\left(\nu \right)}(z,n)& =M^2{r}^{\left(\nu \right)}\left(z^M,(n-\nu )/M\right)z^{2M}-\nu M{q}^{\left(\nu \right)}\left(z^M\right)z^M+\nu (\nu +M)p^{\left(\nu \right)}\left(z^M\right).\hfill \end{array}$$

Starting from the Jacobi differential equation for ${\widehat{P}}_k^{(\alpha ,{\beta }_{\nu })}\left(t\right)$ (cf. [50], p. 781)

$$(1-x^2)y^{\prime \prime }+[{\beta }_{\nu }-\alpha -(\alpha +{\beta }_{\nu }+2)x]y^{\prime }+k(k+\alpha +{\beta }_{\nu }+1)y=0,$$

i.e., from the corresponding equation for polynomials $p_k^{(\alpha ,{\beta }_{\nu })}\left(t\right)$ orthogonal on $(0,1)$,

$$t(1-t)y^{\prime \prime }+\left[\gamma +{\displaystyle \frac{2\nu +1}{M}}-t\left(\alpha +\gamma +1+{\displaystyle \frac{2\nu +1}{M}}\right)\right]y^{\prime }+k\left(k+\alpha +\gamma +{\displaystyle \frac{2\nu +1}{M}}\right)y=0,$$

and Theorem 13, we conclude that the monic polynomials ${\pi }_n\left(z\right)\equiv {\pi }_{Mn+\nu }\left(z\right)$ from Theorem 12 satisfy the second-order linear differential equation:

$$\begin{array}{ccc}\hfill & & z^2(1-z^M)Y^{\prime \prime }-z\left[\left(M(\alpha +\gamma )+2\right)z^M-2-M(\gamma -1)\right]Y^{\prime }\hfill \\ & & +\left[n\left(n+1+M(\alpha +\gamma )\right)z^M-\nu \left(\nu +1+M(\gamma -1)\right)\right]Y=0.\hfill \end{array}$$

(45)

A similar result can be obtained for orthogonal polynomials from Theorem 12 (see [1]).

7. Applications

In this section, we mention some applications of our orthogonal polynomials on the radial rays.

7.1. A Physical Problem Connected to a Non-Linear Diffusion Equation

In several problems in fluid mechanics, the equations for the dispersion of a buoyant contaminant can be approximated by the Erdogan–Chatwin equation [51]:

$${\partial }_{t}c={\partial }_z\left\{\left[D_0+{\left({\partial }_{z}c\right)}^2{D}_2\right]{\partial }_{z}c\right\},$$

(46)

where $D_0$ is the dispersion coefficient. The increased dispersion rate associated with buoyancy-driven currents is represented by the coefficient $D_2$ (cf. [52,53]). Equation (46) was also derived by other authors, but for some other physical problems.

Analytic expressions for the similarity solutions of the previous equation were derived by Smith [52], in the case when $D_0=0$ (the limit of strong non-linearity), i.e., for

$${\partial }_{t}c=D_2{\partial }_y\left[{\left({\partial }_{y}c\right)}^3\right],$$

both for a concentration jump and for a finite discharge. He also studied the asymptotic stability of the obtained solutions and showed that for the finite discharge, it involves a sequence of orthogonal polynomials $\left\{Y_n\left(z\right)\right\}$, which satisfy the following second-order ordinary differential equation:

$$(1-z^4)Y^{\prime \prime }-6z^3{Y}^{\prime }+n(n+5)z^{2}Y=0,$$

(47)

and the degree n is restricted to the values $0,1,4,5,8,9,\dots$. The first few polynomials were listed in [52]:

$$1,z,1-3z^4,z-{\displaystyle \frac{11}{5}}{z}^5,1-{\displaystyle \frac{26}{3}}{z}^4+{\displaystyle \frac{221}{21}}{z}^8.$$

However, it is easy to see that these polynomials, more precisely their monic versions, form a subsequence of our polynomials considered in Example 2 (ii), with the inner product

$$(p,q)={\int }_0^1\left[p\left(x\right)\overline{q\left(x\right)}+p\left(\mathrm{i}x\right)\overline{q\left(\mathrm{i}x\right)}+p(-x)\overline{q(-x)}+p(-\mathrm{i}x)\overline{q(-\mathrm{i}x)}\right]x^2{(1-x^4)}^{1/2}\mathrm{d}x.$$

According to Section 6.4, these polynomials are exactly 4-generalized Gegenbauer polynomials with respect to the weight function (40), with the parameters $M=4$ and $\alpha =\gamma =1/2$, i.e.,

$${\pi }_n\left(z\right)={\pi }_{4k+\nu }\left(z\right)=2^{-k}{z}^{\nu }{\widehat{P}}_k^{(1/2,(2\nu -1)/4)}\left(2z^4-1\right),n=0,1,2,\dots ,$$

(48)

where $k=[n/4]$ and $\nu \in \{0,1,2,3\}$. They satisfy the second-order linear differential Equation (45), which in this particular case becomes

$$(1-z^4)Y^{\prime \prime }-6z^3{Y}^{\prime }+\left[n(n+5)z^2-\nu (\nu -1)z^{-2}\right]Y=0,$$

where $n=4k+\nu$, $\nu \in \{0,1,2,3\}$. Evidently, for $n=4k$$(\nu =0)$ and $n=4k+1$$(\nu =1)$, this equation reduces to the Smith Equation (47).

Thus, the complete system of these orthogonal polynomials is given by (48). Beside the first nine polynomials, given in Example 2 (ii), here, we list the next six polynomials (up to $n\le 14$):

$$\begin{array}{cc}\hfill {\pi }_9\left(z\right)& =z^9-{\displaystyle \frac{18}{19}}{z}^5+{\displaystyle \frac{3}{19}}z,{\pi }_{10}\left(z\right)=z^{10}-{\displaystyle \frac{22}{21}}{z}^6+{\displaystyle \frac{11}{51}}{z}^2,\hfill \\ \hfill {\pi }_{11}\left(z\right)& =z^{11}-{\displaystyle \frac{26}{23}}{z}^7+{\displaystyle \frac{117}{437}}{z}^3,{\pi }_{12}\left(z\right)=z^{12}-{\displaystyle \frac{33}{25}}{z}^8+{\displaystyle \frac{11}{25}}{z}^4-{\displaystyle \frac{11}{425}},\hfill \\ \hfill {\pi }_{13}\left(z\right)& =z^{13}-{\displaystyle \frac{13}{9}}{z}^9+{\displaystyle \frac{13}{23}}{z}^5-{\displaystyle \frac{65}{1311}}z,{\pi }_{14}\left(z\right)=z^{14}-{\displaystyle \frac{45}{29}}{z}^{10}+{\displaystyle \frac{99}{145}}{z}^6-{\displaystyle \frac{11}{145}}{z}^2.\hfill \end{array}$$

7.2. Electrostatic Interpretation of the Zeros of Orthogonal Polynomials ${\pi }_n\left(z\right)$

As an application of our polynomials ${\pi }_n\left(z\right)$, orthogonal on the symmetric radial rays in the complex plane, we give an electrostatic interpretation of their zeros. We mention that the first electrostatic interpretation for the zeros of Jacobi polynomials was given in 1885 by Stieltjes [54,55], who studied an electrostatic problem with particles of positive charge p and q placed at the points $x=1$ and $x=-1$, respectively, and with n unit charges placed on the interval $(-1,1)$ at the points $x_s$, $s=1,\dots ,n$. Assuming a logarithmic potential, Stieltjes showed that the electrostatic equilibrium occurs when $x_s$, $s=1,\dots ,n$, are zeros of the Jacobi polynomial $P_n^{(\alpha ,\beta )}\left(x\right)$, where the parameters $\alpha$ and $\beta$ take values $2p-1$ and $2q-1$, respectively. In this case, the energy of this electrostatic system, defined by the Hamiltonian

$$H(x_1,x_2,\dots ,x_n)=-\sum _{k=1}^n\left(log{(1-x_k)}^p+log{(1+x_k)}^q\right)-\sum _{1\le k<j\le n}log|x_k-x_j|,$$

reaches its minimum. Indeed, this is a unique global minimum of $H(x_1,x_2,\dots ,x_n)$ (see Szegő [34], p. 140). There are several results on the similar electrostatic problems (cf. [34,56,57,58,59,60,61,62,63,64,65,66,67]). Recently, Johnson and Simanek [68] used classical Jacobi polynomials to identify the equilibrium configurations of charged particles confined to the unit circle. Their result unifies the theorems from [56]. Generally speaking, problems related to the distribution of zeros of polynomials and their electrostatic meaning have been and remain very topical from Stieltjes to the present day (cf. [69]).

Here, we consider a symmetric electrostatic problem with M positive charges of the same strength q, placed at the fixed points $z_s={\epsilon }_s=exp\left(2\mathrm{i}\pi (s-1)/M\right)$, $s=1,2,\dots ,M$, and a charge of strength p$(>-(M-1)/2)$ at the point $z=0$, as well as n positive free unit charges, positioned at the points ${\zeta }_1$, ${\zeta }_2$, …, ${\zeta }_n$. Assuming a logarithmic potential, it is interesting to find the positions of these n points, so that this electrostatic system is in equilibrium.

As in [5,6], we are interested only in a solution with rotational symmetry. Denoting $(z-{\zeta }_1)(z-{\zeta }_2)\cdots (z-{\zeta }_n)={\pi }_n\left(z\right)$, with $n=Mk+\nu$, $k=[n/M]$, and using the approach of equilibrium conditions from [6], we arrive at the differential equation

$$\begin{array}{ccc}& & z^2(1-z^M){\pi }_n^{\prime \prime }\left(z\right)+2\left[p-(Mq+p)z^M\right]z{\pi }_n^{\prime }\left(z\right)\hfill \\ & & +\left\{n\left[n-1+2(Mq+p)\right]z^M-\nu (\nu +2p-1)\right\}{\pi }_n\left(z\right)=0.\hfill \end{array}$$

Comparing this equation with (45), we find that

$$\alpha =2q-1\mathrm{and}\gamma =1+{\displaystyle \frac{2}{M}}(p-1),$$

as well as ${\beta }_{\nu }=(2p+2\nu -1)/M$, so that the following result holds.

Theorem 14. 

The previous electrostatic system is in equilibrium if the points ${\zeta }_s$, $s=1,\dots ,n$, are zeros of the polynomial ${\pi }_n\left(z\right)$, orthogonal with respect to (41), with

$$\omega \left(x\right)={(1-x^M)}^{2q-1}{x}^{M+2(p-1)}.$$

(49)

This monic polynomial ${\pi }_n\left(z\right)$, where $n=Mk+\nu$ and $k=[n/M]$, can be expressed in terms of the monic Jacobi polynomials as ${\pi }_n\left(z\right)=2^{-k}{z}^{\nu }{\widehat{P}}_k^{(2q-1,(2p+2\nu -1)/M)}(2z^M-1)$.

Finally, we mention a recent contribution by Bouzeffour [8], who used M-generalized Hermite polynomials on radial rays from Section 6.5. Taking the case of even rays $M=2m$ and writing the inner product (44) in the simpler form

$$(p,q)=\sum _{s=1}^m{\int }_{\mathbb{R}}p\left(x{\epsilon }_s\right)\overline{q\left(x{\epsilon }_s\right)}{|x|}^{2m\gamma }{\mathrm{e}}^{-x^{2m}}\mathrm{d}x,$$

with the generalized Hermite weight on $\mathbb{R}$, Bouzeffour [8] introduced a new model of the extended Dunkl oscillator. In addition, he also considered the so-called Supersymmetric Quesne–Dunkl Quantum Mechanics (SSQM) on Radial Lines [9]. Otherwise, Supersymmetric Quantum Mechanics has emerged as a powerful framework for uncovering symmetries between bosonic and fermionic systems.

8. Concluding Remarks

The main concept on orthogonal polynomials on the radial rays is presented, including existence and uniqueness, a general method for constructing (the so-called Stieltjes–Gautschi procedure), the main properties of such polynomials, as well as some applications.

Special attention is paid to completely symmetric cases, i.e., when the rays are distributed equidistant in the complex plane, with equal lengths and the same weights on the rays. A recurrence relation for these polynomials, a connection with standard polynomials orthogonal on the real line and a differential equation are derived. It is shown that their zeros are simple and distributed symmetrically on the radial rays, with the possible exception of a multiple zero at the origin. In a symmetric radial ray scenario, using the corresponding differential equations, a few applications are given.