On the Asymptotic Expansions of the (p,k)-Analogues of the Gamma Function and Associated Functions

Abstract

General asymptotic expansion of the $(p,k)$-gamma function is obtained and various approaches to this expansion are studied. The numerical precision of the derived asymptotic formulas is shown and compared. Results are applied to the analogues of digamma and polygamma functions, and asymptotic expansion of the quotient of two $(p,k)$-gamma functions is also derived and analyzed. Various examples and application to the k-Pochhammer symbol are presented.

1. Introduction

The classical gamma function $\mathrm{\Gamma }\left(x\right)$ is usually defined for real $x>0$ in the following way:

$$\mathrm{\Gamma }\left(x\right)=\underset{n\to \infty }{lim}{\displaystyle \frac{n!n^x}{x(x+1)\cdots (x+n)}}={\int }_0^{\infty }{t}^{x-1}{e}^{-t}dt.$$

The quotient above is called the p-analogue or the p-deformation of the gamma function, that is

$${\mathrm{\Gamma }}_p\left(x\right)={\displaystyle \frac{p!p^x}{x(x+1)\cdots (x+p)}}={\int }_0^p{t}^{x-1}{\left(1-{\displaystyle \frac{t}{p}}\right)}^{p}dt,$$

where $p\in \mathbb{N}$ and obviously ${lim}_{p\to \infty }{\mathrm{\Gamma }}_p\left(x\right)=\mathrm{\Gamma }\left(x\right)$. For the rising factorial that appears in the denominator, we often use the Pochhammer symbol, denoted by

$${\left(x\right)}_n=x(x+1)\cdots (x+n-1)={\displaystyle \frac{\mathrm{\Gamma }(x+n)}{\mathrm{\Gamma }\left(x\right)}}.$$

(1)

In [1], the authors introduced a generalization of the Pochhammer symbol

$${\left(x\right)}_{n,k}=x(x+k)(x+2k)\cdots (x+(n-1)k),$$

(2)

which appears in various settings, such as the combination of creation and annihilation operators [2,3] and the perturbation computation of Feynman integrals [4]. Motivated by this, they also defined the k-analogue of the gamma function ${\mathrm{\Gamma }}_k\left(x\right)$ for real $k>0$ and $x>0$ as

$${\mathrm{\Gamma }}_k\left(x\right)=\underset{n\to \infty }{lim}{\displaystyle \frac{n!k^n{\left(nk\right)}^{\frac{x}{k}-1}}{x(x+k)\cdots (x+(n-1\left)k\right)}}.$$

(3)

Of course, ${lim}_{k\to 1}{\mathrm{\Gamma }}_k\left(x\right)=\mathrm{\Gamma }\left(x\right)$, and we can easily derive a direct relation to the standard gamma function:

$${\mathrm{\Gamma }}_k\left(x\right)=k^{{\displaystyle \frac{x}{k}}-1}\mathrm{\Gamma }\left(\frac{x}{k}\right).$$

(4)

Applying (4), the properties of k-gamma and related functions are easily transferred from the standard gamma function. Note that ${\mathrm{\Gamma }}_k\left(k\right)=1$ and the following recursive property holds,

$${\mathrm{\Gamma }}_k(x+k)=x{\mathrm{\Gamma }}_k\left(x\right),$$

which leads to the k-factorial function for $x\in \mathbb{N}$. Hence, the k-Pochhammer symbol can be written through the quotient of the k-gamma functions as

$${\left(x\right)}_{n,k}=x(x+k)(x+2k)\cdots (x+(n-1)k)={\displaystyle \frac{{\mathrm{\Gamma }}_k(x+nk)}{{\mathrm{\Gamma }}_k\left(x\right)}},$$

(5)

which corresponds nicely to the standard relation (1).

Note that introducing the k-analogue is not as significant for mathematical purposes as for practical ones because it has a diverse application and simplifies notation and calculation. For example, the authors in [5] used k-gamma for combinatorial analysis in view of applications in statistics, and the authors in [6] used such functions while solving the Schrödinger equation for harmonium and related models in view of important applications in quantum chemistry. Also, it is interesting that the k-gamma function and related k-Pochhammer symbol have a significant role in fractional calculus, see [7] and the papers cited therein.

Most recently in [8], the authors combined the p and k analogues of the gamma function and defined the $(p,k)$-gamma function for $p\in \mathbb{N}$ and real $k>0$ and $x>0$ in the following way:

$${\mathrm{\Gamma }}_{p,k}\left(x\right)={\displaystyle \frac{(p+1)!k^{p+1}{\left(pk\right)}^{\frac{x}{k}-1}}{x(x+k)\cdots (x+pk)}}.$$

(6)

It is clear that ${\mathrm{\Gamma }}_{p,k}$ yields a commutative diagram with other definitions of the gamma function:

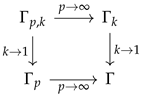
Over the last few years, various properties and many inequalities related to $(p,k)$-gamma and other associated functions have been studied, see [8,9,10,11,12,13,14,15,16].

The asymptotic behavior of the factorial function, and consequently of the gamma function, has been studied for centuries. The famous Stirling asymptotic formula

$$n!\sim \sqrt{2\pi n}{\left({\displaystyle \frac{n}{e}}\right)}^n,n\to \infty ,$$

is a shortening of asymptotic expansion according to Barnes [17]

$$log\mathrm{\Gamma }(x+t)\sim {\displaystyle \frac{1}{2}}log2\pi +\left(x+t-{\displaystyle \frac{1}{2}}\right)logx-x+\sum _{n=1}^{\infty }{\displaystyle \frac{{(-1)}^{n+1}{B}_{n+1}\left(t\right)}{n(n+1)x^n}},x\to \infty .$$

(7)

Here, $t=1$ leads to the formula for the factorial function, but parameter t is introduced in the general expansion of the gamma function, since it appears naturally as a variable in Bernoulli polynomials $B_n\left(t\right)$ in the coefficients of this expansion. It also easily yields expansions with shifted variables, which give better precision. In a series of papers, many other Stirling-type asymptotic expansions for the gamma function were obtained, and their numerical precision was compared; for an overview, see [18].

Asymptotic analysis of the gamma function is an important tool in the application of special functions, but has not been studied for the $(p,k)$-analogues in the existing literature and papers. Therefore, the main aim of this paper is to obtain asymptotic expansions for the $(p,k)$-gamma function and other $(p,k)$-analogues of functions related to gamma, namely the digamma function, the polygamma functions, and the quotient of two gamma functions, which will be discussed in the last section. Algorithms for calculating coefficients in these expansions will be derived and some examples will be presented, namely the expansion for the k-Pochhammer symbol. In the fourth section, the numerical precision of the derived asymptotic formulas for the $(p,k)$-gamma function is shown and compared.

2. Asymptotic Expansion of $(\mathit{p},\mathit{k})$-Gamma Function

In this section, we will derive the main Stirling-type expansion (7) of the $(p,k)$-gamma function, but let us start with the asymptotic expansion of the k-gamma function, which is useful to have as a separate result.

In [1], the authors deduced only the beginning of the asymptotic formula for the k-gamma function in the form

$${\mathrm{\Gamma }}_k(x+1)\sim \sqrt{{\displaystyle \frac{2\pi }{kx}}}{x}^{{\displaystyle \frac{x+1}{k}}}{e}^{-{\displaystyle \frac{x}{k}}},x\to \infty ,$$

(8)

but they did not present the general expansion nor the expression for the coefficients. Note that for the k-gamma function, it is more natural to introduce parameter t in the form ${\mathrm{\Gamma }}_k(x+kt)$. This leads to the Bernoulli polynomials $B_n\left(t\right)$ in the same form as in the original expansion (7), but this will also yield a direct connection to the k-Pochhammer symbol because of relation (5). The final result is in the next proposition, which can be easily obtained by taking the logarithm of (4) and applying expansion (7), so we will leave out the details.

Proposition 1.

The logarithm of the k-gamma function has the following asymptotic expansions as $x\to \infty$:

$$log{\mathrm{\Gamma }}_k(x+kt)\sim {\displaystyle \frac{1}{2}}log{\displaystyle \frac{2\pi }{k}}+\left({\displaystyle \frac{x}{k}}+t-{\displaystyle \frac{1}{2}}\right)logx-{\displaystyle \frac{x}{k}}+\sum _{n=1}^{\infty }{\displaystyle \frac{{(-1)}^{n+1}{k}^n{B}_{n+1}\left(t\right)}{n(n+1)x^n}}.$$

(9)

Note that for $t=0$, we obtain Bernoulli numbers $B_n=B_n\left(0\right)$. For example, the first few terms in the asymptotic expansion for $k=2$, which leads to the double factorial function, are as follows:

$${\mathrm{\Gamma }}_2\left(x\right)\sim \sqrt{{\displaystyle \frac{\pi }{x}}{\left({\displaystyle \frac{x}{e}}\right)}^x}exp\left({\displaystyle \frac{1}{6x}}-{\displaystyle \frac{1}{45x^3}}+{\displaystyle \frac{8}{315x^5}}-{\displaystyle \frac{8}{105x^7}}+\cdots \right),x\to \infty .$$

(10)

For the asymptotic expansion of ${\mathrm{\Gamma }}_{p,k}$, parameter t will be introduced in the same way as for ${\mathrm{\Gamma }}_k$, that is, as $x+kt$, to preserve the properties of Bernoulli polynomials. In the next theorem, we will present the $(p,k)$-analogue of expansion (7).

Theorem 1.

The logarithm of the $(p,k)$-gamma function has the following asymptotic expansion as $x\to \infty$:

$$\begin{array}{cc}\hfill log{\mathrm{\Gamma }}_{p,k}(x+kt)\sim & log(p+1)!+\left({\displaystyle \frac{x}{k}}+t-1\right)logpk+(p+1)log{\displaystyle \frac{k}{x}}+\hfill \\ \hfill & +\sum _{n=1}^{\infty }{(-k)}^n{\displaystyle \frac{B_{n+1}(t+p+1)-B_{n+1}\left(t\right)}{n(n+1)}}{x}^{-n}.\hfill \end{array}$$

(11)

Proof. 

By applying (5), ${\mathrm{\Gamma }}_{p,k}$ can be written through the quotient of k-gamma functions in the following way

$${\mathrm{\Gamma }}_{p,k}\left(x\right)={\displaystyle \frac{(p+1)!k^{p+1}{\left(pk\right)}^{\frac{x}{k}-1}}{{\left(x\right)}_{p+1,k}}}=(p+1)!k^{p+1}{\left(pk\right)}^{{\displaystyle \frac{x}{k}}-1}{\displaystyle \frac{{\mathrm{\Gamma }}_k\left(x\right)}{{\mathrm{\Gamma }}_k(x+(p+1)k)}}.$$

(12)

Now, by taking the logarithm of (12), it follows that

$$\begin{array}{cc}\hfill log{\mathrm{\Gamma }}_{p,k}(x+kt)=& log(p+1)!+\left({\displaystyle \frac{x}{k}}+t-1\right)logpk+(p+1)logk+\hfill \\ \hfill & +log{\mathrm{\Gamma }}_k(x+kt)-log{\mathrm{\Gamma }}_k(x+(t+p+1)k),\hfill \end{array}$$

(13)

and finally we apply (9) from Proposition 1. □

Here, it is worthy to mention that Bernoulli polynomials satisfy nicely the property

$$B_{n+1}(s+1)-B_{n+1}\left(s\right)=(n+1)s^n.$$

Hence, the quotient appearing in the coefficients of (11) can be calculated as follows:

$${\displaystyle \frac{B_{n+1}(t+p+1)-B_{n+1}\left(t\right)}{n+1}}=\sum _{j=0}^p{(t+j)}^n=\sum _{j=0}^p\sum _{i=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{i}}\right)t^i{j}^{n-i}.$$

(14)

Here are the first few terms in the $(p,k)$-analogue of Stirling asymptotic expansion for $t=0$ as $x\to \infty$:

$${\mathrm{\Gamma }}_{p,k}\left(x\right)\sim (p+1)!{\left(pk\right)}^{{\displaystyle \frac{x}{k}}-1}{\left({\displaystyle \frac{k}{x}}\right)}^{p+1}exp\left({\displaystyle \frac{k{c}_1\left(p\right)}{x}}+{\displaystyle \frac{k^2{c}_2\left(p\right)}{x^2}}-{\displaystyle \frac{k^3{c}_3\left(p\right)}{x^3}}+{\displaystyle \frac{k^4{c}_4\left(p\right)}{x^4}}+\cdots \right),$$

(15)

where

$$\begin{array}{cc}\hfill c_1\left(p\right)& =-{\displaystyle \frac{1}{2}}p(p+1),\hfill \\ \hfill c_2\left(p\right)& ={\displaystyle \frac{1}{12}}p(p+1)(2p+1),\hfill \\ \hfill c_3\left(p\right)& =-{\displaystyle \frac{1}{12}}{p}^2{(p+1)}^2,\hfill \\ \hfill c_4\left(p\right)& ={\displaystyle \frac{1}{120}}p(p+1)(2p+1)(p^2+3p-1).\hfill \end{array}$$

Note that in this case, the coefficients are directly connected to the known formulas for the sum of powers of the first p natural numbers. In the fourth section, we will discuss the numerical precision of this expansion for various values of p and k.

Recall that the classical digamma and polygamma functions are defined as derivatives of the logarithm of the gamma function. Analogously, we can define the $(p,k)$-digamma and $(p,k)$-polygamma functions as

$${\psi }_{p,k}^{\left(i\right)}\left(x\right)={\displaystyle \frac{d^i}{d{x}^i}}log{\mathrm{\Gamma }}_{p,k}\left(x\right).$$

Recently, many monotonicity properties and inequalities related to the $(p,k)$-digamma and polygamma functions have been studied by various authors, see [8,10,11,13,14,15,16].

The digamma function has the following known asymptotic expansion, see [17]:

$$\psi (x+t)\sim logx+\sum _{n=1}^{\infty }{\displaystyle \frac{{(-1)}^{n-1}{B}_n\left(t\right)}{n}}{x}^{-n},x\to \infty .$$

(16)

Similarly, by differentiating (11), we can obtain asymptotic expansions of the $(p,k)$-analogues of the digamma and polygamma functions.

Corollary 1.

${\psi }_{p,k}\left(x\right)$ has the following asymptotic expansion as $x\to \infty$:

$${\psi }_{p,k}(x+kt)\sim {\displaystyle \frac{1}{k}}log\left(px\right)+{\displaystyle \frac{1}{k}}\sum _{n=1}^{\infty }{(-k)}^n{\displaystyle \frac{B_n(t+p+1)-B_n\left(t\right)}{n}}{x}^{-n},$$

For the $(p,k)$-polygamma function, the following asymptotic expansion is valid as $x\to \infty$:

$${\psi }_{p,k}^{\left(i\right)}(x+kt)\sim {\displaystyle \frac{{(-1)}^{i-1}(i-1)!}{k{x}^i}}-{\displaystyle \frac{1}{k^i}}\sum _{n=i}^{\infty }{(-k)}^{n}n!{\displaystyle \frac{B_{n-i+1}(t+p+1)-B_{n-i+1}\left(t\right)}{(n-i)!x^{n+1}}}.$$

Again, the difference in Bernoulli polynomials in the coefficients of these expansions can be calculated through sum (14). For example, the first few terms in the expansion of ${\psi }_{p,k}$ for $t=0$ are exactly formulas for the sum of powers of the first p natural numbers. As $x\to \infty$, we have

$${\psi }_{p,k}\left(x\right)\sim {\displaystyle \frac{1}{k}}logpx-{\displaystyle \frac{p+1}{x}}+{\displaystyle \frac{kp(p+1)}{2x^2}}-{\displaystyle \frac{k^{2}p(p+1)(2p+1)}{6x^3}}+{\displaystyle \frac{k^3{p}^2{(p+1)}^2}{4x^4}}+\cdots$$

3. Related Asymptotic Expansions of $(\mathit{p},\mathit{k})$-Gamma Function

In this section, we will deal with the asymptotic expansions of the gamma function, which do not involve the exponential function like classical Stirling expansion (15). These expansions are in fact generalizations of the Laplace expansion for the factorial function:

$$n!\sim \sqrt{2\pi n}{\left({\displaystyle \frac{n}{e}}\right)}^n\left(1+{\displaystyle \frac{1}{12n}}+{\displaystyle \frac{1}{288n^2}}-{\displaystyle \frac{139}{51840n^3}}+\cdots \right),n\to \infty .$$

Such an approach was studied by the authors in [19], and they presented the general expansion for $m>0$ as $x\to \infty$:

$$log\mathrm{\Gamma }(x+t)\sim (x+t-\frac{1}{2})logx-x+\frac{1}{2}log\left(2\pi \right)+{\displaystyle \frac{1}{m}}log\left(\sum _{n=0}^{\infty }{P}_n\left(t\right)x^{-n}\right),$$

(17)

where polynomials $P_n\left(t\right)$ are defined by $P_0\left(t\right)=1$ and by the simple recursive formula

$$P_n\left(t\right)={\displaystyle \frac{m}{n}}\sum _{i=1}^n{\displaystyle \frac{{(-1)}^{i+1}{B}_{i+1}\left(t\right)}{i+1}}{P}_{n-i}\left(t\right),n\ge 1.$$

(18)

Many known asymptotic formulas are specific cases of this expansion for various choices of parameter m; for example, $m=1$ gives the Laplace formula and $m=6$ leads to the famous Ramanujan formula. For a complete review and comparison of these expansions, see [18].

However, to obtain the $(p,k)$-analogue of expansion (17), we cannot simply use the same method as in Theorem 1. In this case, we need additional manipulations with asymptotic power series, but this has already been carried out for the quotient of two gamma functions.

The ratio in the form

$${\displaystyle \frac{\mathrm{\Gamma }(x+t)}{\mathrm{\Gamma }(x+s)}}$$

(19)

has been studied by many authors in the past decades. Many monotonicity properties and inequalities concerning this quotient have been obtained, namely for the Wallis ratio ${\displaystyle \frac{\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n+\frac{1}{2})}}$, which comes from the famous Wallis formula for number $\pi$. For an extensive overview of this topic, see [20]. In [21], the authors derived the asymptotic expansion of this quotient in the form

$${\displaystyle \frac{\mathrm{\Gamma }(x+t)}{\mathrm{\Gamma }(x+s)}}\sim x^{t-s}{\left(\sum _{n=0}^{\infty }{P}_n(t,s)x^{-n}\right)}^{\frac{1}{m}},x\to \infty ,$$

(20)

where polynomials $P_n(t,s)$ are defined by $P_0(t,s)=1$ and the recursive relation

$$P_n(t,s)={\displaystyle \frac{m}{n}}\sum _{k=1}^n{(-1)}^{k+1}{\displaystyle \frac{B_{k+1}\left(t\right)-B_{k+1}\left(s\right)}{k+1}}{P}_{n-k}(t,s),n\ge 1.$$

(21)

Similarly as for the gamma function, parameter $m>0$ was introduced to generalize known approximation formulas for the Wallis ratio, and the authors showed that choice $m={\displaystyle \frac{1}{t-s}}$ is more natural than the classical approach $m=1$ by Tricomy-Erdely (1951) [17]. We will use this result to obtain the following expansion.

Theorem 2.

The logarithm of the $(p,k)$-gamma function has the following asymptotic expansion for $m>0$ when $x\to \infty$:

$$log{\mathrm{\Gamma }}_{p,k}(x+kt)\sim log(p+1)!+({\displaystyle \frac{x}{k}}+t-1)logpk+(p+1)log{\displaystyle \frac{k}{x}}+{\displaystyle \frac{1}{m}}log\sum _{n=0}^{\infty }{\displaystyle \frac{k^n{Q}_n(t,p)}{x^n}},$$

(22)

where the polynomials $Q_n(t,p)$ are defined by $Q_0(t,p)=1$ and the recursive relation

$$Q_n(t,p)={\displaystyle \frac{m}{n}}\sum _{j=1}^n{(-1)}^j{\displaystyle \frac{B_{j+1}(t+p+1)-B_{j+1}\left(t\right)}{j+1}}{Q}_{n-j}(t,p),n\ge 1.$$

(23)

Proof. 

In (12), we connected the $(p,k)$-gamma function with the quotient of two k-gamma functions, but using (4), we further have

$${\displaystyle \frac{{\mathrm{\Gamma }}_k\left(x\right)}{{\mathrm{\Gamma }}_k(x+(p+1)k)}}={\displaystyle \frac{k^{\frac{x}{k}-1}\mathrm{\Gamma }\left(\frac{x}{k}\right)}{k^{\frac{x}{k}+p}\mathrm{\Gamma }(\frac{x}{k}+p+1)}}=k^{-p-1}{\displaystyle \frac{\mathrm{\Gamma }\left(\frac{x}{k}\right)}{\mathrm{\Gamma }(\frac{x}{k}+p+1)}}.$$

This leads to

$$\begin{array}{cc}\hfill log{\mathrm{\Gamma }}_{p,k}(x+kt)=& log(p+1)!+\left({\displaystyle \frac{x}{k}}+t-1\right)logpk+(p+1)logk+\hfill \\ \hfill & +log{\displaystyle \frac{\mathrm{\Gamma }(\frac{x}{k}+t)}{\mathrm{\Gamma }(\frac{x}{k}+t+p+1)}},x\to \infty .\hfill \end{array}$$

(24)

and we can apply (20) with $s=t+p+1$. □

Similarly as in the previous section, the quotient of Bernoulli polynomials appearing in (23) can be calculated by (14).

Let us show an example for $t=0$ and $m=1$, that is, the $(p,k)$-analogue of Laplace asymptotic expansion, as $x\to \infty$:

$${\mathrm{\Gamma }}_{p,k}\left(x\right)\sim (p+1)!{\left(pk\right)}^{{\displaystyle \frac{x}{k}}-1}{\left({\displaystyle \frac{k}{x}}\right)}^{p+1}\left(1+{\displaystyle \frac{k{q}_1\left(p\right)}{x}}+{\displaystyle \frac{k^2{q}_2\left(p\right)}{x^2}}+{\displaystyle \frac{k^3{q}_3\left(p\right)}{x^3}}+\cdots \right)$$

where the first few polynomials $q_n\left(p\right)$ are as follows:

$$\begin{array}{cc}\hfill q_1\left(p\right)& =-{\displaystyle \frac{1}{2}}p(p+1),\hfill \\ \hfill q_2\left(p\right)& ={\displaystyle \frac{1}{24}}p(p+1)(p+2)(3p+1),\hfill \\ \hfill q_3\left(p\right)& =-{\displaystyle \frac{1}{48}}{p}^2{(p+1)}^2(p+2)(p+3).\hfill \end{array}$$

However, as we have already mentioned, the most natural choice for the parameter m is $1/(t-s)$, which in our case is $m=1/(p+1)$. Then, we have the following asymptotic expansion when $x\to \infty$:

$${\mathrm{\Gamma }}_{p,k}\left(x\right)\sim (p+1)!{\left(pk\right)}^{{\displaystyle \frac{x}{k}}-1}{\left({\displaystyle \frac{k}{x}}+{\displaystyle \frac{k^2{q}_1\left(p\right)}{x^2}}+{\displaystyle \frac{k^3{q}_2\left(p\right)}{x^3}}+{\displaystyle \frac{k^4{q}_3\left(p\right)}{x^4}}+\cdots \right)}^{p+1},$$

(25)

where the first few coefficients are obviously simpler than before,

$$\begin{array}{cc}\hfill q_1\left(p\right)& =-{\displaystyle \frac{p}{2}},\hfill \\ \hfill q_2\left(p\right)& ={\displaystyle \frac{1}{24}}p(7p+2),\hfill \\ \hfill q_3\left(p\right)& =-{\displaystyle \frac{1}{16}}{p}^2(3p+2).\hfill \end{array}$$

It is common in the literature to study asymptotic expansions through shifted variables. For example, De Moivre’s ’n-half’ formula follows from (17) for $x=n+{\displaystyle \frac{1}{2}}$ and $t={\displaystyle \frac{1}{2}}$ with $m=1$:

$$n!\sim \sqrt{2\pi }{\left({\displaystyle \frac{n+\frac{1}{2}}{e}}\right)}^{n+{\displaystyle \frac{1}{2}}}\left(1-{\displaystyle \frac{1}{24(n+\frac{1}{2})}}+{\displaystyle \frac{1}{1152{(n+\frac{1}{2})}^2}}+\cdots \right),n\to \infty .$$

(26)

Shifted formulas provide a much better numerical approximation of the gamma function than original formulas, see [18] for details.

Hence, we will derive the $(p,k)$-analogue of the ’n-half’ formula. The next expansion follows from (22), with $x+{\displaystyle \frac{1}{2}}k$, $t=-{\displaystyle \frac{1}{2}}$ and $m=1$ as $x\to \infty$:

$${\mathrm{\Gamma }}_{p,k}\left(x\right)\sim (p+1)!{\left(pk\right)}^{{\displaystyle \frac{x}{k}}-1}{\left({\displaystyle \frac{k}{x+\frac{1}{2}k}}\right)}^{p+1}\left(1+{\displaystyle \frac{k{s}_1\left(p\right)}{x+\frac{1}{2}k}}+{\displaystyle \frac{k^2{s}_2\left(p\right)}{{(x+\frac{1}{2}k)}^2}}+{\displaystyle \frac{k^3{s}_3\left(p\right)}{{(x+\frac{1}{2}k)}^3}}+\cdots \right),$$

where

$$\begin{array}{cc}\hfill s_1\left(p\right)& =-{\displaystyle \frac{1}{2}}(p^2-1),\hfill \\ \hfill s_2\left(p\right)& ={\displaystyle \frac{1}{24}}(p^2+3p+2)(3p^2-5p+3),\hfill \\ \hfill s_3\left(p\right)& =-{\displaystyle \frac{1}{48}}(p^2-1)(p^2+5p+6)(p^2-p+1),\hfill \end{array}$$

and for $m=1/(p+1)$ we again have a simpler expansion as $x\to \infty$:

$${\mathrm{\Gamma }}_{p,k}\left(x\right)\sim (p+1)!{\left(pk\right)}^{{\displaystyle \frac{x}{k}}-1}{\left({\displaystyle \frac{k}{x+\frac{1}{2}k}}-{\displaystyle \frac{k^2(p-1)}{2{(x+\frac{1}{2}k)}^2}}+{\displaystyle \frac{k^3(7p^2-10p+6)}{24{(x+\frac{1}{2}k)}^3}}+\cdots \right)}^{p+1}.$$

However, there is an even more natural shift for this type of asymptotic expansion. Recall that the $(p,k)$-gamma function (12) is directly connected with the quotient of gamma functions. The authors in [21] proved that polynomials $P_n(t,s)$ in expansion (20) can be expressed through the intrinsic variables $\alpha ={\displaystyle \frac{t+s-1}{2}},\beta ={\displaystyle \frac{1-{(t-s)}^2}{4}}$ and that the most natural shift for the quotient of gamma functions is $x+\alpha$. Then, all odd coefficients in the expansion are equal to zero. In our case, variable $\alpha$ is equal to $\alpha ={\displaystyle \frac{p}{2}}$. Hence, from (22), taking $t=-{\displaystyle \frac{1}{2}}p$ and $m=1/(p+1)$, the following expansion holds true when $x\to \infty$:

$${\mathrm{\Gamma }}_{p,k}\left(x\right)\sim (p+1)!{\left(pk\right)}^{{\displaystyle \frac{x}{k}}-1}{\left({\displaystyle \frac{k}{x+\frac{1}{2}pk}}-{\displaystyle \frac{k^3{r}_2\left(p\right)}{{(x+\frac{1}{2}pk)}^3}}+{\displaystyle \frac{k^5{r}_4\left(p\right)}{{(x+\frac{1}{2}pk)}^5}}+\cdots \right)}^{p+1},$$

(27)

where

$$\begin{array}{cc}\hfill r_2\left(p\right)& ={\displaystyle \frac{1}{24}}p(p+2),\hfill \\ \hfill r_4\left(p\right)& ={\displaystyle \frac{1}{5760}}p(p+2)(23p^2+46p-24).\hfill \end{array}$$

4. Numerical Precision of the Asymptotic Formulas

We will now check the numerical precision of the asymptotic formulas for the $(p,k)$-analogues of the gamma function. Namely, we will compare the Stirling-type formula (15) with the exponential function, the Laplace-type formula (25) with the natural choice of parameter $m=p+1$, and the shifted ’half’ formula (27), which only has even coefficients in its expansion.

Numerical precision will be expressed through the number of exact decimal digits (EDDs), which are defined by

$$\mathrm{EDD}\left(x\right)=-{log}_{10}\left|1-{\displaystyle \frac{\mathrm{formula}\left(\mathrm{x}\right)}{\mathrm{exact}\left(\mathrm{x}\right)}}\right|$$

for some values of variable x. Since we analyze asymptotic formulas for $x\to \infty$, only big values of x will be considered. In the following tables, the $\left(n\right)$-th column is the EDDs of the approximation formula (in the given row) using the series up to the n-th coefficient. All the calculations were carried out with Mathematica. Here, it is worthy to note that Bernoulli polynomials are implemented in most software packages, but nevertheless they can also be manually implemented by various efficient algorithms from the standard literature, e.g., [17], or in our case by the sum of powers from formula (14).

We will start with the EDDs for relatively small values of p and k, shown in

Table 1. Precision of the $(p,k)$-asymptotic formulas for $p=10$ and $k=1$.

Formula	x	(2)	(3)	(4)	(5)	(6)	(7)	(8)
(15)	100	3.0	4.2	5.4	6.5	7.6	8.7	9.8
(25)	100	2.7	3.8	4.9	6.0	7.1	8.2	9.3
(27)	100	5.3		8.1		10.9		13.7
(15)	1000	6.0	8.2	10.3	12.5	14.6	16.7	18.8
(25)	1000	5.7	7.8	9.9	12.0	14.1	16.2	18.3
(27)	1000	9.2		14.0		18.8		23.5
(15)	10000	9.0	12.2	15.4	18.5	21.6	24.7	27.8
(25)	10000	8.7	11.8	14.9	18.0	21.1	24.2	27.3
(27)	10000	13.2		20.0		26.8		33.5

. Obviously, formulas are more accurate for larger values of x and when taking more terms in their expansion. We can see that the shifted formula (27) gives much better precision than the other formulas.

In

Table 2. Precision of the $(p,k)$-asymptotic formulas for $p=100$ and $k=1$.

Formula	x	(2)	(3)	(4)	(5)	(6)	(7)	(8)
(15)	1000	2.1	3.3	4.5	5.6	6.8	7.9	9.0
(25)	1000	1.7	2.9	4.0	5.2	6.3	7.4	8.4
(27)	1000	4.5		7.4		10.2		13.0
(15)	10000	5.1	7.3	9.5	11.6	13.7	15.8	17.9
(25)	10000	4.7	6.9	9.0	11.1	13.3	15.3	17.4
(27)	10000	8.4		13.3		18.1		22.9

, we have the EDDs for bigger values of p and small k. The formulas are noticeably less accurate than for small values of p and practically not useful for lower values of x.

Finally, in

Table 3. Precision of the $(p,k)$-asymptotic formulas for $p=10$ and $k=100$.

Formula	x	(2)	(3)	(4)	(5)	(6)	(7)	(8)
(15)	10000	3.0	4.2	5.4	6.5	7.6	8.7	9.8
(25)	10000	2.7	3.8	4.9	6.0	7.1	8.2	9.3
(27)	10000	5.3		8.1		10.9		13.7
(15)	100000	6.0	8.2	10.3	12.5	14.6	16.7	18.8
(25)	100000	5.7	7.8	9.9	12.0	14.1	16.2	18.3
(27)	100000	9.2		14.0		18.8		23.5

, we have smaller values of p and greater values of k. Here, we need even greater values of variable x to achieve precision comparable to previous two cases. Such behavior of the formulas comes directly from the definition of the $(p,k)$-gamma function.

As expected, when p and k become greater, the formulas are less accurate, that is, they become better only with more terms in the expansion and for greater values of x. Because of this, asymptotic formulas are not practical for p and k, with both having big values, so we will skip that case. We can conclude that Stirling-type expansion (15) is better than (25), but formula (27) with shifted variables overpowers both of them and has the best precision with fewer terms in the expansion in all the presented cases. This coincides with approximation formulas for the classical gamma function, see [18].

5. Asymptotic Expansions of the Ratio of $(\mathit{p},\mathit{k})$-Gamma Functions

In the last section, we will study the $(p,k)$-analogue of the ratio of two gamma functions. In a recent paper [11], the authors studied such a quotient of two $(p,k)$-gamma functions and established various related inequalities, particularly for the quotient in the form

$${\displaystyle \frac{{\mathrm{\Gamma }}_{p,k}(x+k)}{{\mathrm{\Gamma }}_{p,k}(x+\frac{1}{2}k)}},$$

(28)

which is the $(p,k)$-analogue of the Wallis ratio mentioned before. We will now present the analogue of the asymptotic expansion (20).

Theorem 3.

The quotient of two $(p,k)$-gamma functions has the following asymptotic expansion as $x\to \infty$:

$${\displaystyle \frac{{\mathrm{\Gamma }}_{p,k}(x+kt)}{{\mathrm{\Gamma }}_{p,k}(x+ks)}}\sim {\left(pk\right)}^{t-s}{\left(\sum _{n=0}^{\infty }{k}^n{Q}_n(t,s,p)x^{-n}\right)}^{\frac{1}{m}},$$

(29)

where polynomials $Q_n(t,s,p)$ are defined by $Q_0(t,s,p)=1$ and for $n\ge 1$

$$Q_n(t,s,p)={\displaystyle \frac{m}{n}}\sum _{j=1}^n{(-1)}^j{\displaystyle \frac{B_{j+1}(t+p+1)-B_{j+1}\left(t\right)+B_{j+1}\left(s\right)-B_{j+1}(s+p+1)}{j+1}}{Q}_{n-j}(t,s,p).$$

Proof. 

Applying (12) and (4), we obtain

$${\displaystyle \frac{{\mathrm{\Gamma }}_{p,k}(x+kt)}{{\mathrm{\Gamma }}_{p,k}(x+ks)}}={\left(pk\right)}^{t-s}{\displaystyle \frac{\mathrm{\Gamma }(\frac{x}{k}+t)}{\mathrm{\Gamma }(\frac{x}{k}+s)}}{\displaystyle \frac{\mathrm{\Gamma }(\frac{x}{k}+s+p+1)}{\mathrm{\Gamma }(\frac{x}{k}+t+p+1)}}$$

Here, we cannot simply use (20), but we can apply the result from [22] concerning multiple quotients of gamma functions. The authors showed that for $t-s=v-u$, the following expansion holds

$${\displaystyle \frac{\mathrm{\Gamma }(x+t)}{\mathrm{\Gamma }(x+s)}}{\displaystyle \frac{\mathrm{\Gamma }(x+u)}{\mathrm{\Gamma }(x+v)}}\sim {\left(\sum _{n=0}^{\infty }{P}_n(t,s,u,v)x^{-n}\right)}^{\frac{1}{m}},x\to \infty ,$$

(30)

where polynomials $P_n$ are defined recursively by $P_n(t,s,u,v)=1$ and

$$P_n(t,s,u,v)={\displaystyle \frac{m}{n}}\sum _{j=1}^n{(-1)}^{j+1}{\displaystyle \frac{B_{j+1}\left(t\right)-B_{j+1}\left(s\right)+B_{j+1}\left(u\right)-B_{j+1}\left(v\right)}{j+1}}{P}_{n-j}(t,s,u,v).$$

Hence, in our case $u=s+p+1$, $v=t+p+1$ and the theorem follows. □

Let us show an example of this expansion for the quotient (28) studied in recent papers. In this case, we have $t=1$, $s={\displaystyle \frac{1}{2}}$, and we will take natural choice $m=2$:

$${\displaystyle \frac{{\mathrm{\Gamma }}_{p,k}(x+k)}{{\mathrm{\Gamma }}_{p,k}(x+\frac{1}{2}k)}}\sim \sqrt{pk+{\displaystyle \frac{p{k}^2{q}_1\left(p\right)}{x}}+{\displaystyle \frac{p{k}^3{q}_2\left(p\right)}{x^2}}+{\displaystyle \frac{p{k}^4{q}_3\left(p\right)}{x^3}}+\cdots },x\to \infty ,$$

where

$$\begin{array}{cc}\hfill q_1\left(p\right)& =-(p+1),\hfill \\ \hfill q_2\left(p\right)& ={\displaystyle \frac{1}{4}}(p+1)(4p+5),\hfill \\ \hfill q_3\left(p\right)& =-{\displaystyle \frac{1}{2}}{(p+1)}^2(3+2p).\hfill \end{array}$$

There is another useful application of the expansion (20). Recall that the k-Pochhammer symbol is directly connected to the quotient of gamma functions:

$${\left(x\right)}_{t,k}={\displaystyle \frac{{\mathrm{\Gamma }}_k(x+kt)}{{\mathrm{\Gamma }}_k\left(x\right)}}=k^t{\displaystyle \frac{\mathrm{\Gamma }(\frac{x}{k}+t)}{\mathrm{\Gamma }\left(\frac{x}{k}\right)}}.$$

(31)

We can now easily derive the asymptotic expansion of the k-Pochhammer symbol taking $s=0$ in (20). We will use the natural choice $m=1/t$, which leads to

$${\left(x\right)}_{t,k}\sim {\left(x+k{p}_1\left(t\right)+{\displaystyle \frac{k^2{p}_2\left(t\right)}{x}}+{\displaystyle \frac{k^3{p}_3\left(t\right)}{x^2}}+{\displaystyle \frac{k^4{p}_4\left(t\right)}{x^3}}+\cdots \right)}^t,x\to \infty .$$

(32)

Polynomials $p_n\left(t\right)$ are calculated by (21), and the first few are as follows:

$$\begin{array}{cc}\hfill p_1\left(t\right)& ={\displaystyle \frac{1}{2}}(t-1),\hfill \\ \hfill p_2\left(t\right)& =-{\displaystyle \frac{1}{24}}(t^2-1),\hfill \\ \hfill p_3\left(t\right)& ={\displaystyle \frac{1}{48}}(t^2-1)(t-1),\hfill \\ \hfill p_4\left(t\right)& =-{\displaystyle \frac{1}{5760}}(t^2-1)(73t^2-120t+23).\hfill \end{array}$$

As discussed before, polynomials $p_n\left(t\right)$ can be expressed through intrinsic variables $\alpha ={\displaystyle \frac{t-1}{2}}$ and $\beta ={\displaystyle \frac{{(1-t)}^2}{4}}$, and then better formulas can be obtained through shifted variable $x+\alpha$. When we apply this to our case, we have

$${\displaystyle \frac{{\mathrm{\Gamma }}_k(x+kt)}{{\mathrm{\Gamma }}_k\left(x\right)}}\sim {\left(x+k\alpha +{\displaystyle \frac{k^2{r}_2\left(\beta \right)}{x+k\alpha }}+{\displaystyle \frac{k^4{r}_4\left(\beta \right)}{{(x+k\alpha )}^3}}+{\displaystyle \frac{k^6{r}_6\left(\beta \right)}{{(x+k\alpha )}^5}}+\cdots \right)}^t,x\to \infty ,$$

(33)

where

$$\begin{array}{cc}\hfill r_2\left(\beta \right)& ={\displaystyle \frac{1}{6}}\beta ,\hfill \\ \hfill r_4\left(\beta \right)& =-{\displaystyle \frac{13}{360}}{\beta }^2-{\displaystyle \frac{1}{60}}\beta ,\hfill \\ \hfill r_6\left(\beta \right)& ={\displaystyle \frac{737}{45360}}{\beta }^3+{\displaystyle \frac{53}{2520}}{\beta }^2+{\displaystyle \frac{1}{126}}\beta .\hfill \end{array}$$

Polynomials $r_{2n}\left(\beta \right)$ can be efficiently calculated by the recursive relation given by the authors in [21].

Finally, applying (29) we can derive the $(p,k)$-analogue of the quotient (31) connected to the k-Pochhammer symbol. Now, we have $s=0$, and for a natural choice $m=1/t$ it follows that

$${\displaystyle \frac{{\mathrm{\Gamma }}_{p,k}(x+kt)}{{\mathrm{\Gamma }}_{p,k}\left(x\right)}}\sim {\left({\displaystyle \frac{pk}{x}}+{\displaystyle \frac{p{k}^2{q}_1(t,p)}{x^2}}+{\displaystyle \frac{p{k}^3{q}_2(t,p)}{x^3}}+{\displaystyle \frac{p{k}^4{q}_3(t,p)}{x^4}}+\cdots \right)}^t,x\to \infty ,$$

where the first few polynomials $q_n(t,p)$ are as follows:

$$\begin{array}{cc}\hfill q_1(t,p)& =-(1+p),\hfill \\ \hfill q_2(t,p)& ={\displaystyle \frac{1}{2}}(1+p)(1+2p+t),\hfill \\ \hfill q_3(t,p)& =-{\displaystyle \frac{1}{6}}(1+p)(1+6p+3t+6pt+6p^2+2t^2).\hfill \end{array}$$

Of course, the quotient appearing in the coefficients (29) can be calculated through sums (14), and it can be expressed through intrinsic variables $\alpha$ and $\beta$, as mentioned before. In papers [21,22], various asymptotic expansions of the Wallis quotient were studied and efficient algorithms for calculating coefficients in such expansions were derived. They can also be applied to the quotient of $(p,k)$-gamma functions in a same way as the results above, which we leave to the interested reader.

6. Conclusions

In this paper, the asymptotic behavior of the $(p,k)$-analogue of the gamma function was studied and discussed. The general asymptotic expansion for the $(p,k)$-gamma function ${\mathrm{\Gamma }}_{p,k}\left(x\right)$, as $x\to \infty$, was obtained and applied to the $(p,k)$-analogues of functions related to gamma, namely the digamma function, polygamma functions, and the quotient of two gamma functions. Algorithms for calculating coefficients in these expansions were derived, and also some examples of expansions were presented. The numerical precision of the obtained asymptotic formulas was discussed and it was shown that the shifted formulas give better numerical results. Obtained expansions have potential in application to various areas from fractional analysis and statistics to quantum chemistry.