Abstract
The red palm weevil (Rhynchophorus ferrugineus) is a highly destructive pest, causing severe damage to palm trees and significantly reducing their productivity. This paper aims to develop and analyze a mathematical model that captures the interactions between palm trees, Rhynchophorus ferrugineus, and entomopathogenic nematodes as a means of integrated control. We identify the equilibrium points of the system and perform a stability analysis to assess the system’s behavior. Additionally, we design a linear quadratic regulator (LQR) to limit the spread of the red palm weevil within a locally linearized framework. The feedback control law, which is both straightforward and immediately implementable, is employed to avoid the need for complex cost calculations, thus simplifying the solution to the optimal control problem. Numerical simulations demonstrate that the proposed control strategy is effective in reducing the number of infected palm trees. The results indicate that increasing the population of entomopathogenic nematodes can significantly decrease the red palm weevil population, offering a promising approach to mitigating this pest’s impact.
Keywords:
optimal control; Rhynchophorus ferrugineus; local stability; red palm weevil; linear quadratic regulator MSC:
37N25; 92B99; 49N10
1. Introduction
The red palm weevil was first documented in South Asia, with initial reports of its discovery published in India in 1891. It was later identified as a serious pest of coconut palms in 1906 and date palms in 1917 [1,2]. The weevil then began to spread, particularly westward, reaching the Middle East by the end of the last century and expanding to the Maghreb, southern Europe, and eventually northern Europe at the start of this century. Its range extended as far west as the Caribbean Islands and as far east as Japan [2].
In the Gulf region, the insect appeared in the mid-1980s in the United Arab Emirates and subsequently spread to neighboring countries, first being recorded in the Kingdom of Saudi Arabia in 1987 [3,4]. Over the past thirty years, its threat has increased, affecting many palm plantations worldwide [5,6]. If control measures against the red palm weevil are not implemented on infected trees, the palm will die within six months to a year due to the destruction of its internal trunk tissues [7].
The method involves fumigating the infected palm trunk with aluminum phosphide tablets, which react with atmospheric humidity to release toxic phosphine gas, killing all stages of the insect inside the trunk without leaving any residue [8]. Due to its superior effectiveness, this pesticide has been approved in Saudi Arabia to combat the weevil [9,10,11]. Another approach to controlling the red palm weevil involves scraping the infested site, tracing the insect’s tunnels, and eliminating all stages within the trunk to ensure complete removal. After scraping, the affected area is sprayed with an approved insecticide, and the cavities are sealed with clay [12,13,14,15,16].
The use of entomopathogenic nematodes offers a promising, environmentally friendly method for controlling the spread of RPW. Ongoing research and field trials are focused on improving its application and effectiveness in integrated pest management programs [16,17]. Mathematical models are valuable tools for describing and analyzing various phenomena in the fields of industry, medicine, and agriculture. They can help in understanding how the red palm weevil spreads and identifying the best methods to combat and eliminate it. Recently, several mathematical models addressing the red palm weevil have emerged [18,19,20,21,22,23].
Recently, several studies [20,21,22] have investigated mathematical models for RPW control using chemical injections, the sterile insect technique, and pheromone traps. Solano Rojas et al. [23] proposed a dynamic model for controlling the red palm weevil and concluded that in the optimal control model for red palm weevil larvae, the application of chemical control measures can significantly reduce the initial larval peak. Alnafisah et al. [24] developed a mathematical model for the optimal chemical control of the red palm weevil by applying Pontryagin’s maximum principle. They demonstrated that implementing optimal control strategies effectively reduces the populations of larvae and pupae, thereby aiding in the management of mature stages of the RPW insect. To the best of our knowledge, previous mathematical models have not considered the impact of nematodes that cause insect diseases in controlling the spread of the red palm weevil. This paper addresses that gap. Additionally, the Pontryagin maximum principle was employed in prior studies [23,24]. Recently, numerous studies have started to incorporate linear feedback control in epidemic models [25,26,27,28,29,30]. Linear feedback control in biological models typically represents how a biological system regulates itself to maintain stability or achieve a desired state. In ecological models, linear feedback can represent factors that regulate population sizes, such as predation, competition, or disease [25,27]. For instance, in a predator–prey model, the growth rate of the prey population might decrease as the predator population increases, which is a form of negative feedback. According to [30], the linear feedback control can be implemented in real time since the control action depends on the current state of the system. The control law is straightforward and can be implemented immediately, whereas the Pontryagin maximum principle generally requires solving a two-point boundary value problem, which is computationally intensive and not always feasible for real-time applications [31,32,33,34]. This paper aims to apply a linear quadratic regulator (LQR) to the red palm weevil (RPW) model and examine the effect of nematodes as natural enemies on RPW.
In Section 2 of this paper, the mathematical model of the red palm weevil (RPW) (Rhynchophorus ferrugineus) is introduced, and the conditions for the stability of the RPW model are derived. Section 3 presents the optimal control method using a linear quadratic regulator (LQR) to achieve optimal feedback control. In Section 4, numerical simulations are conducted to verify the theoretical results. Section 5 presents the conclusions of this study.
2. Mathematical Formulation
Following [18,19,20], the mathematical model describing the potential interactions between palm trees, the red palm weevil, and entomopathogenic nematodes are represented by the following four differential equations:
The population density of susceptible palm trees is represented by . These trees grow at an intrinsic rate r and, in the absence of the red palm weevil, reach a carrying capacity denoted by k. The infection rate of these susceptible palm trees by the red palm weevil is assumed to be . The population density of infected palm trees is denoted by , and these trees face a mortality rate due to infestation by the red palm weevil. The recovery rate of infected palm trees as a result of aluminum phosphide fumigation is assumed to be . The population density of red palm weevil larvae is represented by , with their population increasing at a rate due to the hatching of eggs. The predation intensity between the larvae and entomopathogenic nematodes is denoted by , while the larvae mortality rate is represented by . The rate of predation by larvae on the interior of the infected palm trunk is assumed to be . Finally, the population density of entomopathogenic nematodes is denoted by , and their mortality rate is assumed to be . Table 1 presents the parameters of system (1).

Table 1.
Parameters and Description.
Positivity and Boundedness
In this section, we demonstrate that our model is well posed. To establish the well posedness, we prove that all solutions to the system (1) with positive initial conditions remain positive for all . Additionally, we show that the solutions are bounded for all within the positive region W, which represents the biologically feasible region. Thus, the model is biologically meaningful.
Theorem 1.
For positive initial conditions, every solution of the red palm weevil model (1) remains positive for all .
Proof.
Given that the initial conditions are non-negative, the first equation of the red palm weevil system (1) yields
Thus,
Applying the initial condition implies that
Similarly, it can be shown that
Thus, according to [44], the solution of the red palm weevil system (1) remains positive for all . □
Theorem 2.
The solutions of the red palm weevil system (1) in are uniformly bounded.
Proof.
By adding the first and second equations in the RPW system (1), we obtain
Therefore,
By applying the comparison theorem for differential inequalities established by Birkhoff and Rota [44,45,46], we obtain Consequently, x and y are bounded. The third and fourth equations of model (1) can be written in the following Kolmogorov-type system:
and then,
for , , where the subscripts indicate partial derivatives. According to [47], z and w are bounded, which completes the proof. □
3. Model Analysis
3.1. Equilibrium Points
is the extinction equilibrium point. This point refers to a situation where the population reaches zero over time, meaning that the species has become extinct. The weevil-free equilibrium represents a state where the weevil is absent from the population. Understanding this equilibrium is crucial for evaluating the potential success of weevil eradication efforts and the stability of a population without the weevil. The palm tree extinction equilibrium point and the infected palm tree extinction equilibrium point exist if , while the weevil–extinction equilibrium point exists if . The nematode-free equilibrium point exists if and . The coexistence point represents a state where multiple populations coexist in a steady-state without any of them going extinct. This point exists if and .
3.2. Basic Reproduction Number
The basic reproduction number, generally denoted by , is defined as the number of new infections generated by a single infected individual. It is computed using the next-generation matrix technique [48,49]. To determine , we focus on the second and third equations of model (1), which represent the infected compartments, and use them to construct the matrices and , as follows:
The Jacobian matrices of and at are given by
The basic reproduction number for system (1) is defined as the spectral radius of the matrix [48,49]. It is expressed as follows:
3.3. Stability of the RPW System
The Jacobian matrix of the RPW system (1) is
- The eigenvalues of at the extinction equilibrium point are , , , ; thus, is always unstable. Therefore, the entire population cannot become extinct at the same time.
- The eigenvalues of at the weevil-free equilibrium point are , , , and ; thus, is locally stable if and .
- One of the eigenvalues of is positive; so, , the palm tree extinction equilibrium point, is unstable.
- The eigenvalues of the Jacobian matrix at the infected palm tree extinction equilibrium point are , , , and . Therefore, is unstable.
Theorem 3.
The weevil–extinction equilibrium point is locally stable if .
Proof.
The eigenvalues of the Jacobian matrix are and . The other two eigenvalues are the roots of the quadratic equation where and due to . Therefore, the condition for the local stability of the equilibrium point is which corresponds to . □
Theorem 4.
The nematode-free equilibrium point is locally stable if
Proof.
The characteristic polynomial of at is where , and One can note that and . if and
It follows that is stable if . □
Theorem 5.
The coexistence equilibrium point , if it exists, is locally stable.
Proof.
The characteristic polynomial of at is as follows:
where
Also,
It follows that the roots of (5) have negative real parts, and therefore, is locally stable. □
Theorem 6.
The weevil-free equilibrium point is globally stable if and .
Proof.
Consider the following positive definite Lyapunov function . Taking the time derivative of along the solution of the red palm weevil system (1), we obtain
Thus, if and , then the weevil-free equilibrium point is globally asymptotically stable according to LaSalle’s invariant principle [50].
□
In the next theorem, we focus on the global stability of the coexistence equilibrium point of the red palm weevil model (1) with .
Theorem 7.
The coexistence equilibrium point , if it exists, is globally asymptotically stable.
Proof.
Consider the following positive definite Lyapunov function
Taking the time derivative of along the solution of the red palm weevil system (1), we obtain
Therefore, by LaSalle’s invariant principle [50], is globally asymptotically stable.
□
This section investigates the occurrence of forward bifurcation in the RPW model (1). To achieve this, we utilize the Castillo-Chavez and Song approach described in [51]. In exploring this phenomenon, we use as the bifurcation parameter and assume , leading to the following equation:
Theorem 8.
The system (1) undergoes a forward bifurcation at when (i.e., at ) provided that
Proof.
Using a theorem by Chavez and Song [51], let , and With the vector notation , the RPW system (1) can be written as follows:
The Jacobian matrix of (6) evaluated at the weevil-free equilibrium point with is
Following [52], it can be observed that the Jacobian of the linearized RPW system has a simple zero eigenvalue, while all other eigenvalues have negative real parts. As a result, the dynamics of the transformed system near are studied using central manifold theory [51]. It can be shown that the matrix has a right eigenvector, denoted by , and a left eigenvector, denoted by , where and Substituting the vectors w and v into the expression
gives and As a result, when , the red palm weevil system (6) at experiences forward bifurcation. According to [52], in forward bifurcation, when an unstable weevil-free equilibrium point coexists with a stable endemic equilibrium point. This indicates that the red palm weevil spreads when and dies out when [52]. In the red palm weevil model (1), represents a critical threshold. If exceeds 1, the infestation may lead to an outbreak. However, if is kept below 1, the spread of the infestation can be controlled or eliminated. Therefore, managing the value of (e.g., through interventions such as aluminum phosphide fumigation) is essential for controlling the spread of the red palm weevil. □
4. Model Analysis Optimization of the Biological Control
In this section, following [25,26,27,28,29,30], we apply optimal control theory to design a feedback law aimed at stabilizing the equilibrium point or maintaining the red palm weevil population below the economic threshold where it cannot harm palm trees. Using the linear quadratic regulator (LQR) theory, one can derive a state-dependent feedback control law that can be implemented in the original nonlinear system. In the next section, we will begin with the theoretical basis of the optimal control method, and we will first begin by deducing the algebraic Riccati equation (ARE). Consider the performance index
where is positive definite and are symmetric positive semidefinite matrices. The objective is to minimize J subject to
According to [53], the solution can be obtained by introducing the following augmented cost function:
Applying the total variation of in Equation (9) results in the following:
By applying integration in parts, the total variation in Equation (10) can be simplified as follows:
Following [53], minimizing J requires that each variation term in Equation (11) be set to zero for an optimal control solution. This leads to the following:
Due to the linearity of the dynamics, we can assume that , and this can be substituted into Equation (12) to derive the following:
The transpose of Equation (15) is given as follows:
From Equation (13), we obtain
By eliminating the terminal cost and taking , the algebraic Riccati equation (ARE) is obtained as follows:
In the following portion, we will stabilize the red palm weevil system under the condition that the density of infected palm trees does not reach the critical value , ensuring that remains below . Thus, the RPW system (1) with control is expressed as follows:
The control function U in Equation (20) is composed of two components: . Here, represents a constant control that keeps the RPW larvae population at the target pest density level , which is below the critical value that stabilizes the system. The second component, u, is a feedback control that stabilizes the ecosystem at the desired steady state. U represents the procedure for the chemical control of the red palm weevil, such as fumigation with aluminum phosphide, which causes the infected palm trees to move to the group of susceptible palm trees . According to (20), the desired coexistence steady state of the RPW model with control satisfies
From the system (21), we obtain the following values:
Introducing the following variables:
The vector is given by
According to [25,26,27,54,55], the following theorem can be used to obtain the feedback control u.
Theorem 9.
If there exist constant matrices Q and R that are positive definite and Q-symmetric, such that the function
is positive definite, then the linear feedback control is optimal. In order to transfer the nonlinear system (20) from an initial state to a final state minimizing the functional
where P is the symmetric and positive definite matrix, is the solution of the matrix algebraic Riccati equation below:
The following theorem establishes the positive definiteness of the function in the neighborhood of the origin for the system (24).
Theorem 10.
For the two matrices
the function defined by is positive definite at the neighborhood of .
Proof.
The first-order partial derivatives are as follows:
It is obvious that One can thus compute the Hessian of at as
This implies that is positive definite, making the origin a strict local minimum point of the function and ensuring that remains positive definite in the neighborhood of the origin. □
5. Numerical Simulations
To illustrate the interactions between red palms, Rhynchophorus ferrugineus, and entomopathogenic nematodes, we utilize the parameter values provided in Table 1.
We aim to stabilize the system (20) at the desired steady state, with . Using (22), one can obtain , , , and . The matrix A has the following form:
with eigenvalues Choosing
By applying the MATLAB command LQR to solve the algebraic Riccati equation (Equation (26)), we obtain
The optimal strategy U can also be calculated as follows:
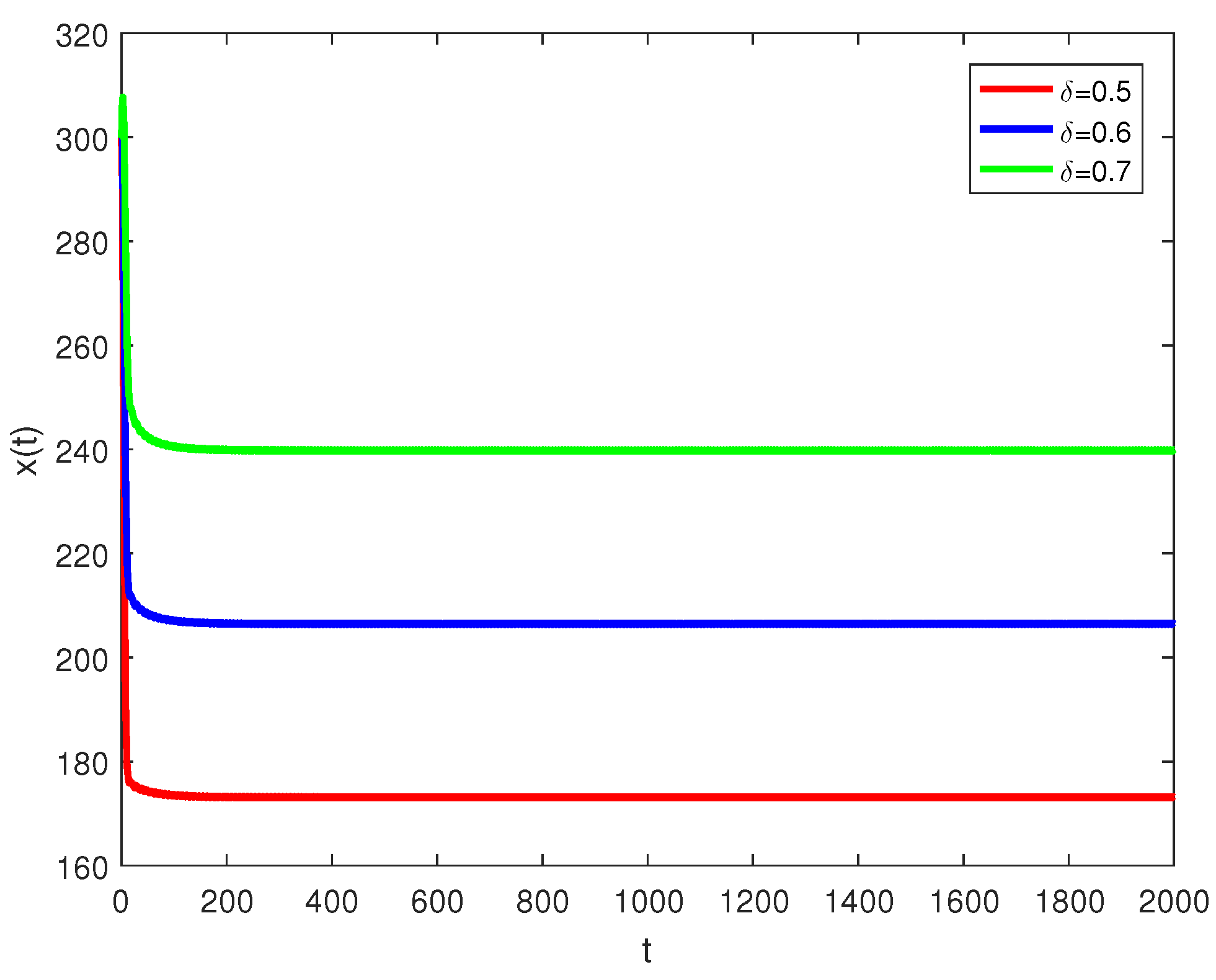
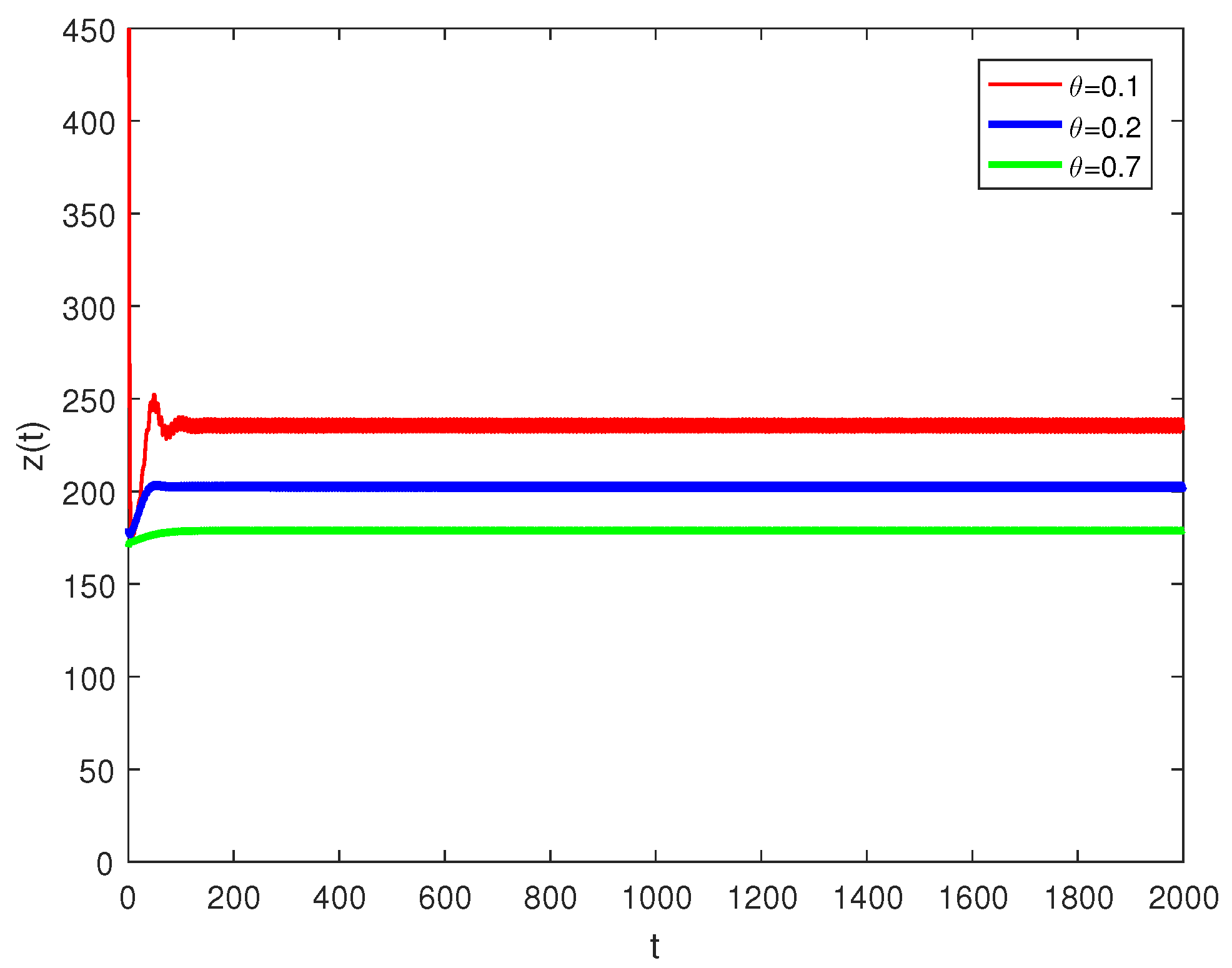
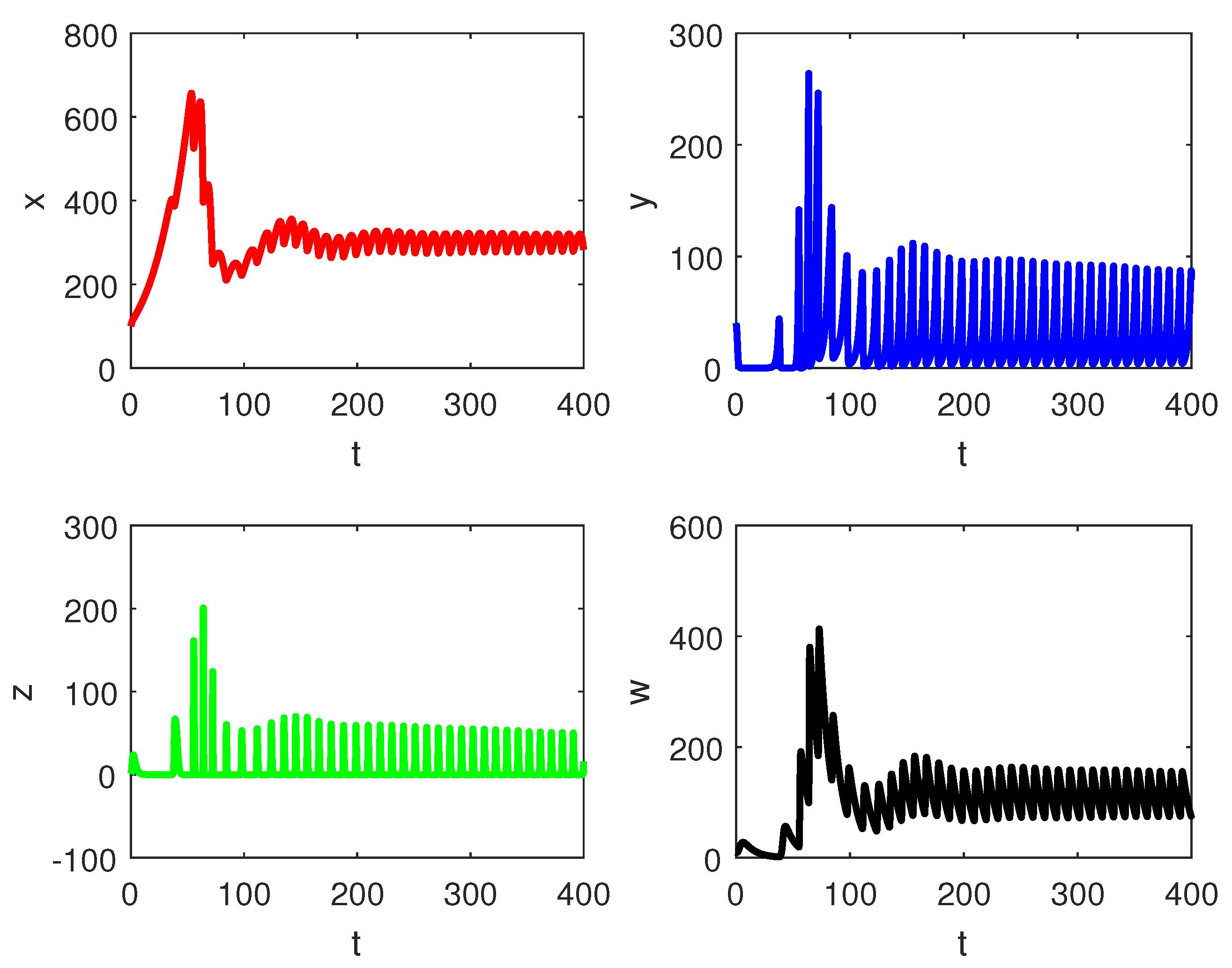
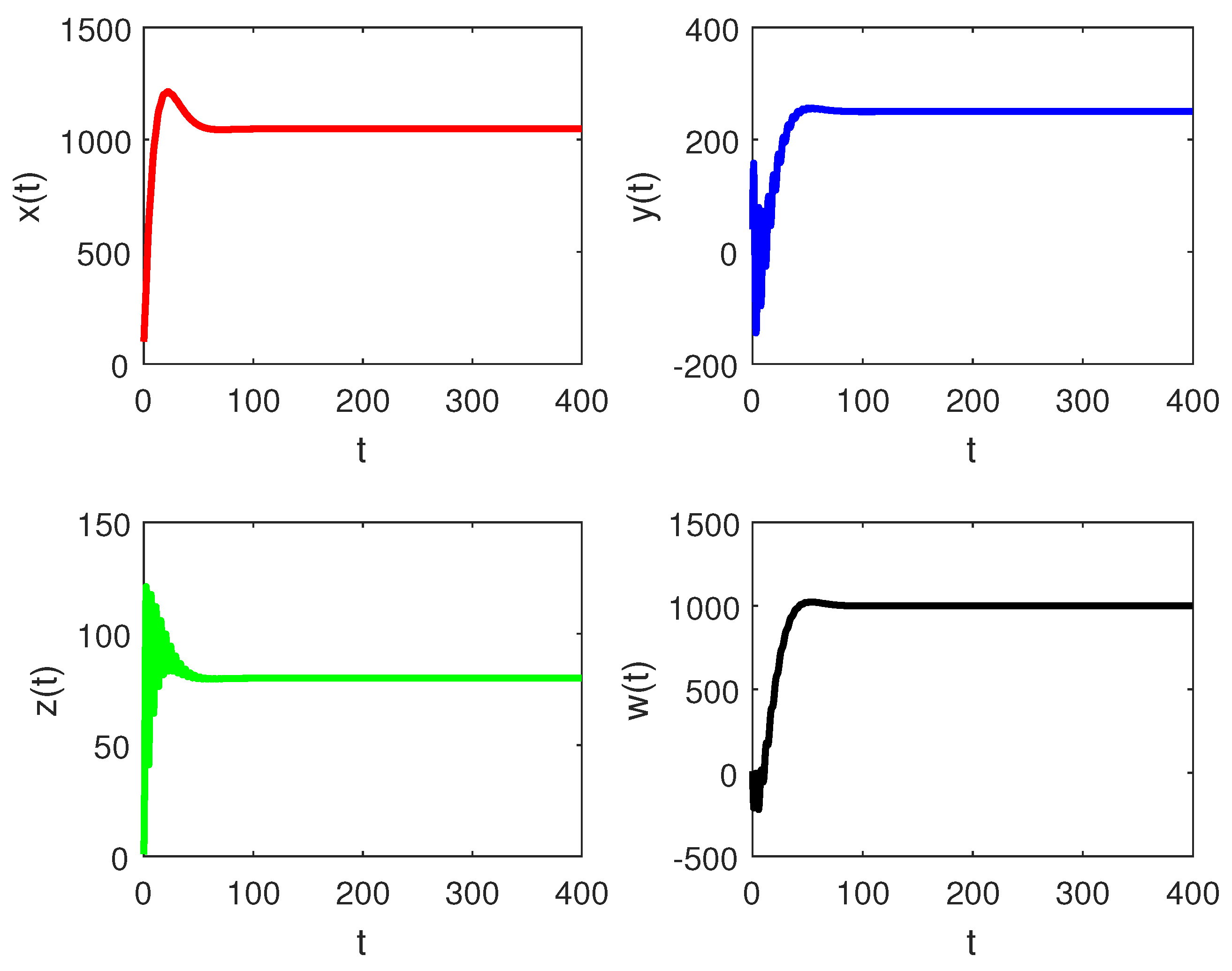
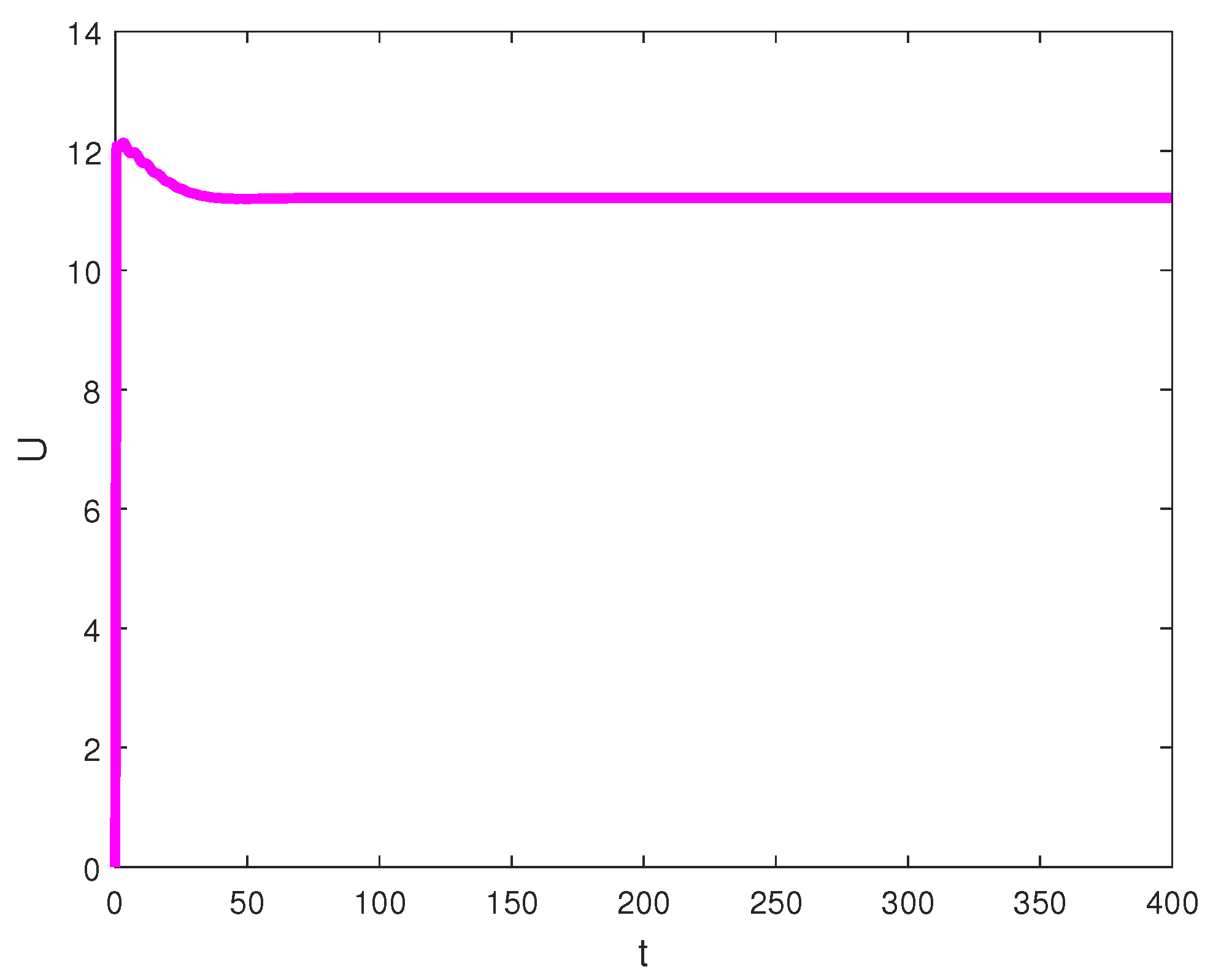
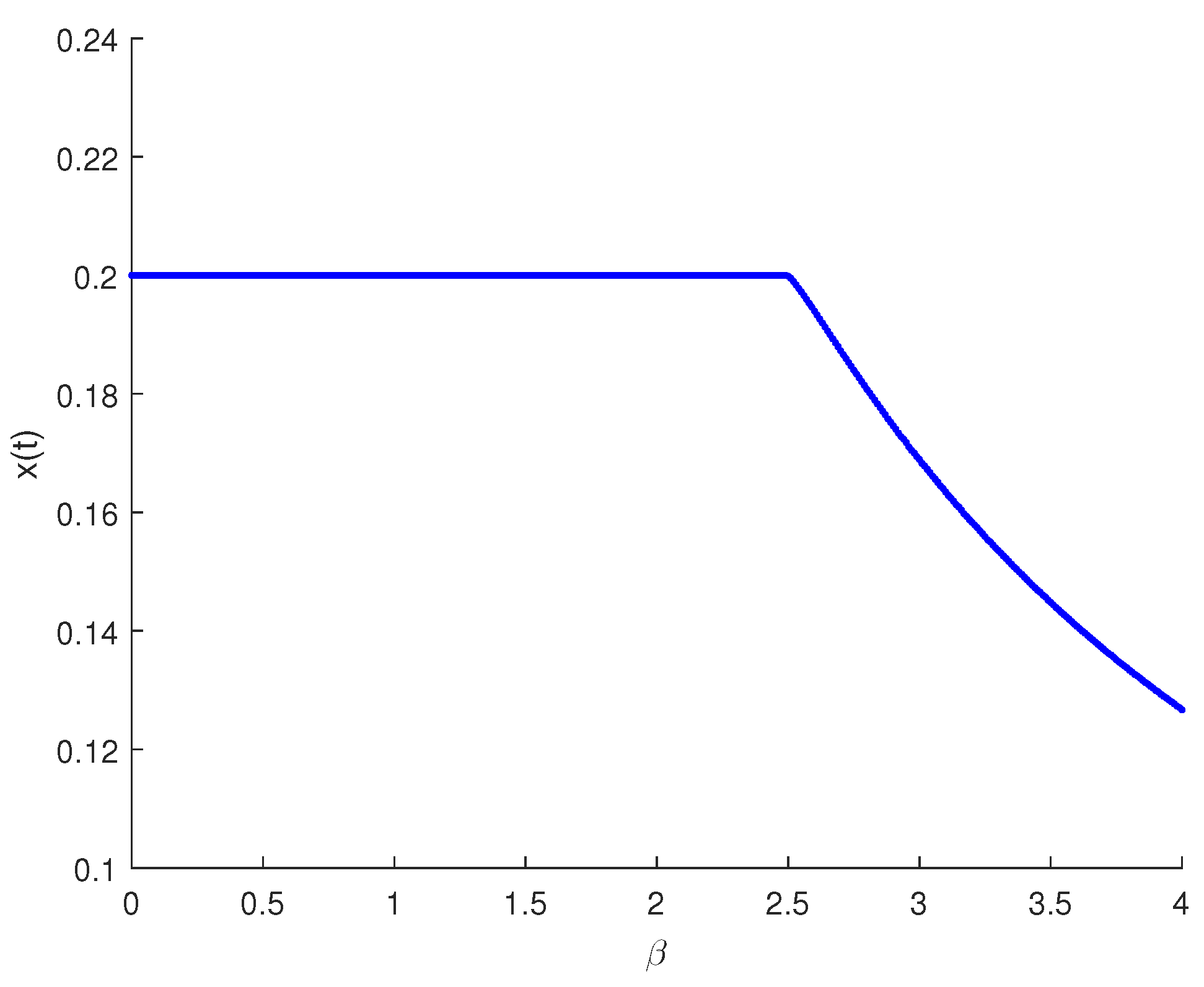
Figure 1 demonstrates that the fumigation parameter influences the population density of susceptible palm trees, . It is evident from the figure that increases as increases, indicating that the dynamics of RPW can be effectively controlled using the aluminum phosphide fumigation method. When the evaporation rate of aluminum phosphide fumigation increased from to , the population density of susceptible palm trees increased by . Further increasing the evaporation rate to led to a increase in the population density of susceptible palm trees. Figure 2 illustrates the effect of the recovery rate of infected palm trees, , due to predation between larvae and entomopathogenic nematodes. The figure shows that the density of red palm weevil larvae decreases as increases. An increase in from to resulted in a decrease in the density of red palm weevil larvae. This suggests that entomopathogenic nematodes can effectively control the spread of the red palm weevil, thereby reducing its associated risks. Figure 3 indicates the variational curves of and without control when , while Figure 4 indicates the dynamic of system (20) with the effect of feedback control. This indicates that the linear feedback optimal control can stabilize the system. To drive the trajectory of the RPW model (20) to the desired steady state , the optimal control (32) is designed as shown in Figure 5. According to Theorems 5 and 7, if the coexistence of equilibrium point exists, it is globally asymptotically stable, and the system (1) does not undergo a Hopf bifurcation. When and , Figure 6 indicates the occurrence of a forward bifurcation at , as stated in Theorem 8. For , the weevil-free equilibrium is locally asymptotically stable. When , the equilibrium point is locally asymptotically stable. In this case, the equilibrium points and do not exist because . A critical insight from the forward bifurcation diagrams in Figure 6 is the clear threshold (typically ) that determines whether the red palm weevil infestation will die out or persist. Agricultural interventions aim to reduce below this critical point, which could be achieved through strategies such as biological control, pheromone trapping or chemical insecticides.
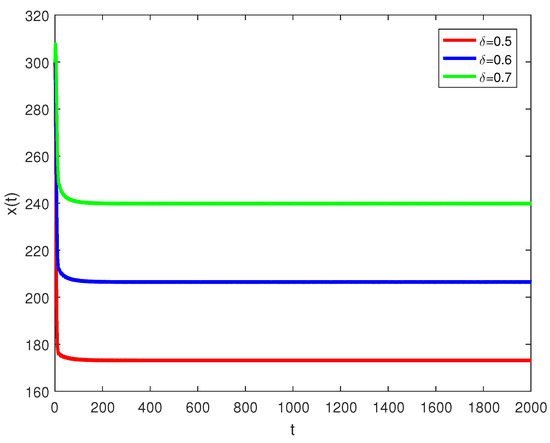
Figure 1.
Susceptible palm trees for different values of .
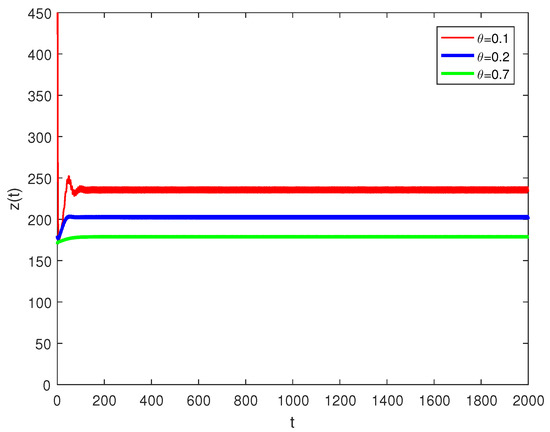
Figure 2.
Larvae population for different values of .
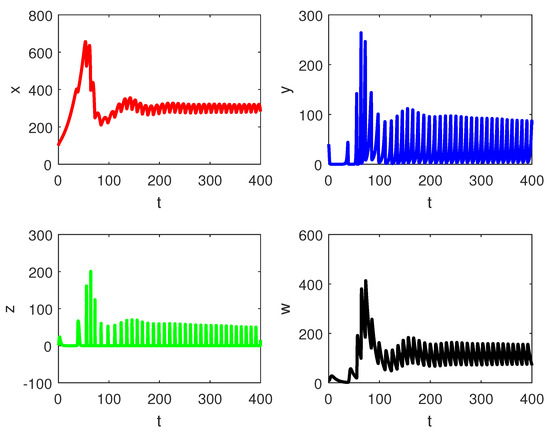
Figure 3.
Variational curves of and without control when .
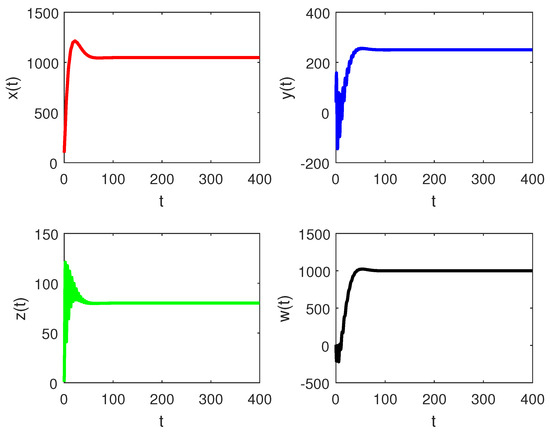
Figure 4.
Variational curves of and with control when .
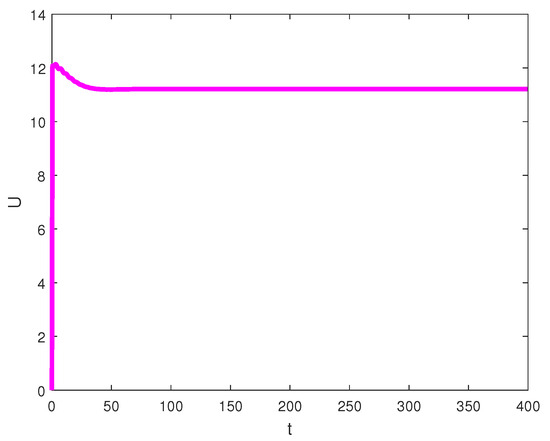
Figure 5.
Dynamics of the optimal control strategy U.
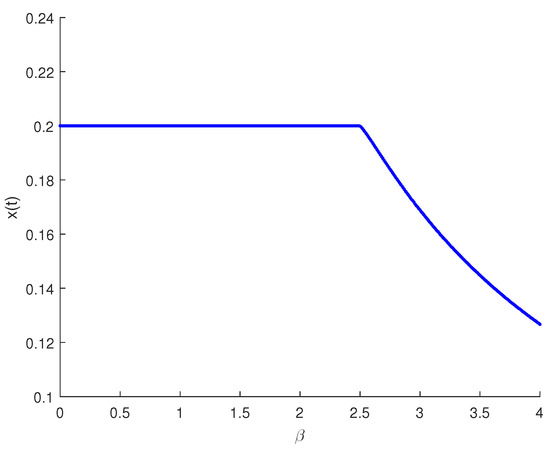
Figure 6.
Forward bifurcation of the red palm weevil model (1) with respect to .
6. Discussion and Conclusions
We have developed a mathematical model to describe the potential interactions between palm trees, the red palm weevil (Rhynchophorus ferrugineus), and entomopathogenic nematodes. The model incorporates a biological control function representing the introduction of pathogenic nematode populations into a palm plantation. A dynamical analysis of the RPW model is discussed both analytically and numerically.
An optimal control problem aimed at limiting the spread of the red palm weevil is solved within a locally linearized context. A linear feedback control strategy, based on optimal control theory, is proposed to demonstrate how entomopathogenic nematodes should be introduced into the environment to stabilize the number of infected palm trees at a level . This strategy helps to keep the red palm weevil under control and prevent its spread to surrounding areas.
Based on the numerical results, it can be concluded that the aluminum phosphide fumigation method effectively reduces the spread of the red palm weevil (RPW). Increasing the fumigation intensity leads to more susceptible palm trees and fewer infected ones. When the evaporation rate of aluminum phosphide fumigation increased from to , the population density of susceptible palm trees rose by . Further increasing the evaporation rate to resulted in a increase in the population density of susceptible palm trees. This indicates that aluminum phosphide fumigation is an effective method for controlling the RPW, and this protocol is currently used in the KSA to manage the pest.
Forward bifurcation diagrams offer valuable insights into the dynamics of red palm weevil infestations, helping to predict whether control measures will be successful in reducing or eradicating the pest population. By understanding how the system transitions between weevil-free and infested states as changes, agricultural experts and policymakers can better design and implement strategies to protect palm trees. These diagrams highlight the importance of sustained, coordinated efforts in pest management and illustrate the long-term economic and ecological impacts of failing to control RPW populations.
This study can be expanded by applying the linear quadratic regulator (LQR) to the stochastic red palm weevil model instead of the deterministic one. Additionally, it can be assumed that the larval stage harvests the internal tissues of date palm trees according to the second type of Holling’s functional response, as indicated by experimental studies on date palm pests [56,57]. A more comprehensive mathematical model that accounts for the different stages of the red palm weevil life cycle could also be explored in future research.
Author Contributions
Conceptualization, Z.A. and M.E.-S.; Methodology, A.A. and M.E.-S.; Software, M.E.-S.; Visualization, Z.A. and A.A.; Writing—original draft, M.E.-S.; Writing—review and editing, Z.A., A.A. and M.E.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0922.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the existing affiliation information. This change does not affect the scientific content of the article.
References
- Aldawood, A.; Rasool, K. Rearing optimization of red palm weevil: Rhynchophorus ferrugineus (Coleoptera: Curculionidae) on date palm: Phoenix dactylifera. Fla. Entomol. 2011, 94, 756. [Google Scholar] [CrossRef]
- Abdel-Banat, B.; El-Shafie, H. Management of the Red Palm Weevil in Date Palm Plantations in Al-Ahsa Oasis of Saudi Arabia. Plant Health Cases 2023, 2023, phcs20230001. [Google Scholar] [CrossRef]
- Seman-Kamarulzaman, A.F.; Pariamiskal, F.A.; Azidi, A.N.; Hassan, M. A Review on Digestive System of Rhynchophorus ferrugineus as Potential Target to Develop Control Strategies. Insects 2023, 14, 506. [Google Scholar] [CrossRef] [PubMed]
- Hoddle, M.S.; Antony, B.; El-Shafie, H.A.; Chamorro, M.L.; Milosavljević, I.; Löhr, B.; Faleiro, J.R. Taxonomy, Biology, Symbionts, Omics, and Management of Rhynchophorus Palm Weevils (Coleoptera: Curculionidae: Dryophthorinae). Annu. Rev. Entomol. 2024, 69, 455–479. [Google Scholar] [CrossRef] [PubMed]
- Manee, M.M.; Alqahtani, F.H.; Al-Shomrani, B.M.; El-Shafie, H.A.; Dias, G.B. Omics in the Red Palm Weevil Rhynchophorus ferrugineus (Olivier) (Coleoptera: Curculionidae): A Bridge to the Pest. Insects 2023, 14, 255. [Google Scholar] [CrossRef]
- Al-Khayri, J. Date palm Phoenix dactylifera micropropagation. In Protocols for Micropropagation of Woody Trees and Fruits; Springer: Berlin/Heidelberg, Germany, 2007; pp. 509–526. [Google Scholar]
- Eldin, H.A.; Waleed, K.; Samir, M.; Tarek, M.; Sobeah, H.; Salam, M.A. A survey on detection of Red Palm Weevil inside palm trees: Challenges and applications. In Proceedings of the 9th International Conference on Software and Information Engineering, Cairo, Egypt, 11–13 November 2020; pp. 119–125. [Google Scholar]
- Mashal, M.M.; Obeidat, B.F. The efficacy assessment of emamectin benzoate using micro injection system to control red palm weevil. Heliyon 2019, 5, e01833. [Google Scholar] [CrossRef]
- Refaat, E.S.M.; El Shazly, M.; El Deeb, M.; Eliwa, A. Study the effect of mechanical injection technique on controlling red palm weevil. Zagazig J. Agric. Res. 2017, 44, 1889–1900. [Google Scholar]
- Abbas, M.S.T. IPM of the red palm weevil, Rhynchophorus ferrugineus. In Integrated Management of Arthropod Pests and Insect Borne Diseases; Springer: Berlin/Heidelberg, Germany, 2010; pp. 209–233. [Google Scholar]
- Chihaoui-Meridja, S.; Harbi, A.; Abbes, K.; Chaabane, H.; La Pergola, A.; Chermiti, B.; Suma, P. Systematicity, persistence and efficacy of selected insecticides used in endotherapy to control the red palm weevil Rhynchophorus ferrugineus (Olivier, 1790) on Phoenix canariensis. Phytoparasitica 2020, 48, 75–85. [Google Scholar] [CrossRef]
- El-Juhany, L.I. Degradation of date palm trees and date production in Arab countries: Causes and potential rehabilitation. Aust. J. Basic Appl. Sci. 2010, 4, 3998–4010. [Google Scholar]
- Hoddle, M.; Al-Abbad, A.H.; El-Shafie, H.; Faleiro, J.; Sallam, A.; Hoddle, C. Assessing the impact of areawide pheromone trapping, pesticide applications, and eradication of infested date palms for Rhynchophorus ferrugineus (Coleoptera: Curculionidae) management in Al Ghowaybah, Saudi Arabia. Crop Prot. 2013, 53, 152–160. [Google Scholar] [CrossRef]
- Milosavljević, I.; El-Shafie, H.A.; Faleiro, J.R.; Hoddle, C.D.; Lewis, M.; Hoddle, M.S. Palmageddon: The wasting of ornamental palms by invasive palm weevils, Rhynchophorus spp. J. Pest Sci. 2019, 92, 143–156. [Google Scholar] [CrossRef]
- Sarwar, M. Biological control of red palm weevil Rhynchophorus Ferrugineus (Coleoptera: Curculionidae) by the natural enemies. Int. J. Res. Biol. Pharm. 2016, 2, 22–35. [Google Scholar]
- El Sadawy, H.A.; Namaky, A.H.E.; Al Omari, F.; Bahareth, O.M. Susceptibility of Rhynchophorus Ferrugineus (Olivier) (Coleoptera: Curculionidae) to entomopathogenic nematodes with regard to its immune response. Biol. Control 2020, 148, 104308. [Google Scholar] [CrossRef]
- Rehman, G.; Mamoon-ur Rashid, M. Evaluation of entomopathogenic nematodes against red palm weevil, Rhynchophorus ferrugineus (Olivier) (Coleoptera: Curculionidae). Insects 2022, 13, 733. [Google Scholar] [CrossRef]
- El-Shahed, M.; Al-Dubiban, A.M. Mathematical Modelling of Lesser Date Moth Using Sex Pheromone Traps and Natural Enemies. Math. Probl. Eng. 2021, 2021, 8835321. [Google Scholar] [CrossRef]
- El-Shahed, M.; Al-Dububan, A.M. Deterministic and Stochastic Fractional Order Model for Lesser Date Moth. Comput. Syst. Sci. Eng. 2022, 40, 749–764. [Google Scholar] [CrossRef]
- El-Shahed, M.; Al-Nujiban, A.; Abdel-Baky, N.F. Stochastic Modelling of Red Palm Weevil Using Chemical Injection and Pheromone Traps. Axioms 2022, 11, 334. [Google Scholar] [CrossRef]
- Ben Dhahbi, A.; Chargui, Y.; Boulaaras, S.M.; Ben Khalifa, S. A one-sided competition mathematical model for the sterile insect technique. Complexity 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Ben Dhahbi, A.; Chargui, Y.; Boulaaras, S.M.; Ben Khalifa, S.; Koko, W.; Alresheedi, F. Mathematical modelling of the sterile insect technique using different release strategies. Math. Probl. Eng. 2020, 2020, 8896566. [Google Scholar] [CrossRef]
- Solano-Rojas, Y.; Gámez, M.; López, I.; Garay, J.; Varga, Z.; Cabello, T. Conservation Strategy for Palm Groves: Optimal Chemical Control Model for Red Palm Weevil, Rhynchophorus ferrugineus. Agronomy 2021, 11, 920. [Google Scholar] [CrossRef]
- Alnafisah, Y.; El-Shahed, M. Optimal control of red palm weevil model incorporating sterile insect technique, mechanical injection, and pheromone traps. Alex. Eng. J. 2024, 93, 382–391. [Google Scholar] [CrossRef]
- Gulati, P.; Chauhan, S.; Mubayi, A.; Singh, T.; Rana, P. Dynamical analysis, optimum control and pattern formation in the biological pest (EFSB) control model. Chaos Solitons Fractals 2021, 147, 110920. [Google Scholar] [CrossRef]
- Barik, M.; Chauhan, S.; Misra, O.P.; Bhatia, S.K. Optimal control using linear feedback control and neutralizing antibodies for an HIV model with dynamical analysis. J. Appl. Math. Comput. 2022, 68, 4361–4389. [Google Scholar] [CrossRef]
- Molter, A.; Bezerra, J.I.; Rafikova, E.; Nava, D.E.; Rafikov, M. Dynamics and biological control of the sugarcane borer with two parasitoids. Ecol. Model. 2023, 481, 110371. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Gabrielli, F. State Feedback as a Strategy for Control and Analysis of COVID-19. arXiv 2024, arXiv:2405.17735. [Google Scholar]
- Farman, M.; Saleem, M.U.; Tabassum, M.F.; Ahmad, A.; Ahmad, M.O. A linear control of composite model for glucose insulin glucagon pump. Ain Shams Eng. J. 2019, 10, 867. [Google Scholar] [CrossRef]
- Di Giamberardino, P.; Iacoviello, D. A linear quadratic regulator for nonlinear SIRC epidemic model. In Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 733–738. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Anderson, B.D.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Courier Corporation: Washington, DC, USA, 2007. [Google Scholar]
- Bernstein, D.S. Nonquadratic cost and nonlinear feedback control. Int. J. Robust Nonlinear Control. 1993, 3, 211–229. [Google Scholar] [CrossRef]
- Asri, S.; Rodrigues, L. Data-Driven LQR using Reinforcement Learning and Quadratic Neural Networks. arXiv 2023, arXiv:2311.10235. [Google Scholar]
- Ismail, A.I.; Hassaballa, A.A.; Almadini, A.M.; Daffalla, S. Analyzing the Spatial Correspondence between Different Date Fruit Cultivars and Farms’ Cultivated Areas, Case Study: Al-Ahsa Oasis, Kingdom of Saudi Arabia. Appl. Sci. 2022, 12, 5728. [Google Scholar] [CrossRef]
- Ali-Bob, M. Management of the red palm weevil Rhynchophorus ferrugineus (Olivier) using sustainable options in Saudi Arabia. Arab. J. Plant Prot. 2019, 37, 2019. [Google Scholar] [CrossRef]
- Abbas, M.K.; Hou, Y.; Wu, S.Y.; Batt, M.A. Evaluation of some control methods against the red palm weevil, Rhynchophorus ferrugineus Olivier (Coleoptera: Curculionidae) infesting date palm trees. Menoufia J. Plant Prot. 2024, 9, 223–229. [Google Scholar] [CrossRef]
- Fenton, A.; Norman, R.; Fairbairn, J.P.; Hudson, P.J. Modelling the efficacy of entomopathogenic nematodes in the regulation of invertebrate pests in glasshouse crops. J. Appl. Ecol. 2000, 37, 309–320. [Google Scholar] [CrossRef]
- Mohanny, K.M.; Mohamed, G.S.; Abdo, O.M. Laboratory study of life table and demographic parameters of Red Palm Weevil (Rhynchophorus ferrugineus, Coleoptera: Dryophthoridae) on sugarcane slices. SVU-Int. J. Agric. Sci. 2020, 2, 93–103. [Google Scholar] [CrossRef]
- Mehdi, M.Z.; Wakil, W.; Jan, H.; Raza, M.M.; Shah, Q.; Zia-ul-Haq, M. Evaluation of entomopathogenic nematode and fungi alone and their combination against red palm weevil, Rhynchophorus ferrugineus (Olivier). J. Entomol. Zool. Stud. 2018, 6, 2038–2042. [Google Scholar]
- Alwaneen, W.S.; Wakil, W.; Kavallieratos, N.G.; Qayyum, M.A.; Tahir, M.; Rasool, K.G.; Husain, M.; Aldawood, A.S.; Shapiro-Ilan, D. Efficacy and persistence of entomopathogenic fungi against Rhynchophorus ferrugineus on date palm: Host to host transmission. Agronomy 2024, 14, 642. [Google Scholar] [CrossRef]
- Fenton, A.; Norman, R.; Fairbairn, J.P.; Hudson, P.J. Evaluating the efficacy of entomopathogenic nematodes for the biological control of crop pests: A nonequilibrium approach. Am. Nat. 2001, 158, 408–425. [Google Scholar] [CrossRef]
- Mushanyu, J.; Chazuka, Z.; Mudzingwa, F.; Ogbogbo, C. Modelling the impact of detection on COVID-19 transmission dynamics in Ghana. RMS Res. Math. Stat. 2021, 8, 1953722. [Google Scholar] [CrossRef]
- Gatyeni, S.P.; Chirove, F.; Nyabadza, F. Modelling the potential impact of stigma on the transmission dynamics of COVID-19 in South Africa. Mathematics 2022, 10, 3253. [Google Scholar] [CrossRef]
- Birkhoff, G.; Rota, G. Ordinary Differential Equation; John Wiley and Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Hassan, K.; Mustafa, A.; Hama, M. An Eco-Epidemiological Model Incorporating Harvesting Factors. Symmetry 2021, 13, 2179. [Google Scholar] [CrossRef]
- Brauer, F. Boundedness of solutions of predator-prey systems. Theor. Popul. Biol. 1979, 15, 268–273. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- La Salle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.P.; Santra, P.K.; Mahapatra, G.S. Global stability and analysing the sensitivity of parameters of a multiple-susceptible population model of SARS-CoV-2 emphasising vaccination drive. Math. Comput. Simul. 2023, 203, 741–766. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Rafikov, M.; de Holanda Limeira, E. Mathematical modelling of the biological pest control of the sugarcane borer. Int. J. Comput. Math. 2012, 89, 390–401. [Google Scholar] [CrossRef]
- Rafikov, M.; Silveira, J.C. On dynamical behavior of the sugarcane borer–Parasitoid agroecosystem. Ecol. Complex. 2014, 18, 67–73. [Google Scholar] [CrossRef]
- Shehab, B.; Ammr, M. THE INFLUENCE OF PREY AND PREDATOR DENSITY ON THE PREDACIOUS BEHAVIOR OF Chrysoperla mutata (MACLACHLAN) LARVAE FEEDING ON DUBAS NYMPHS Ommatissus lybicus DEBERG. Iraqi J. Sci. 2008, 49, 40–49. [Google Scholar]
- Al-Rawy, M.A.; Hamad, B.S.; Abdullatif, A.M. Factors affecting the effectiveness of Chrysoperla mutata (McL.) larvae feeding on dubas nymphs Ommatissus lybicus DeBerg. J. Educ. Sci. Stud. 2013, 1, 387–398. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).