Some Statistical and Direct Approximation Properties for a New Form of the Generalization of q-Bernstein Operators with the Parameter λ
Abstract
1. Introduction
2. Auxiliary Results
3. Statistical Approximation
4. Direct Estimate
- ,
- ,
- .
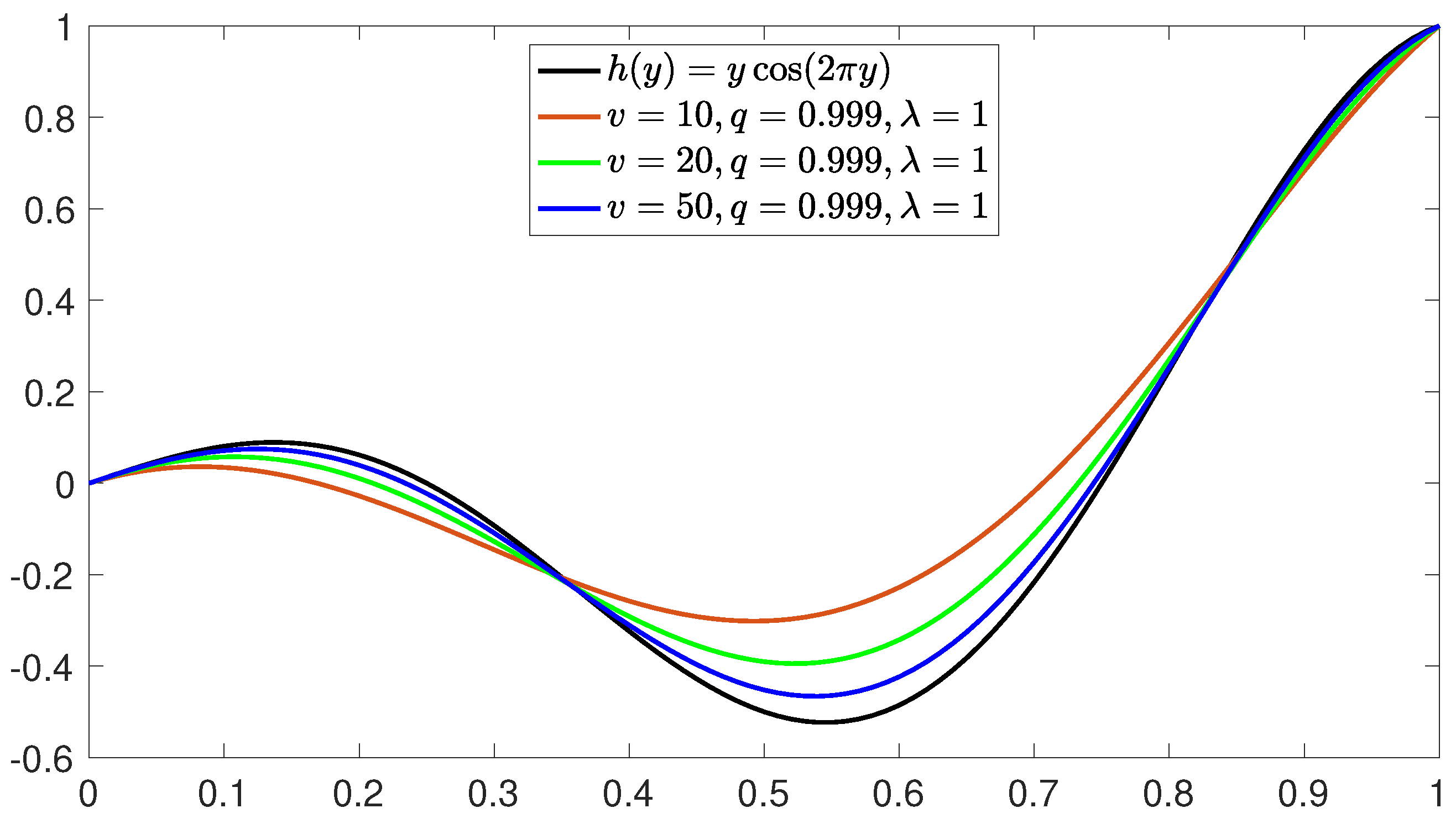
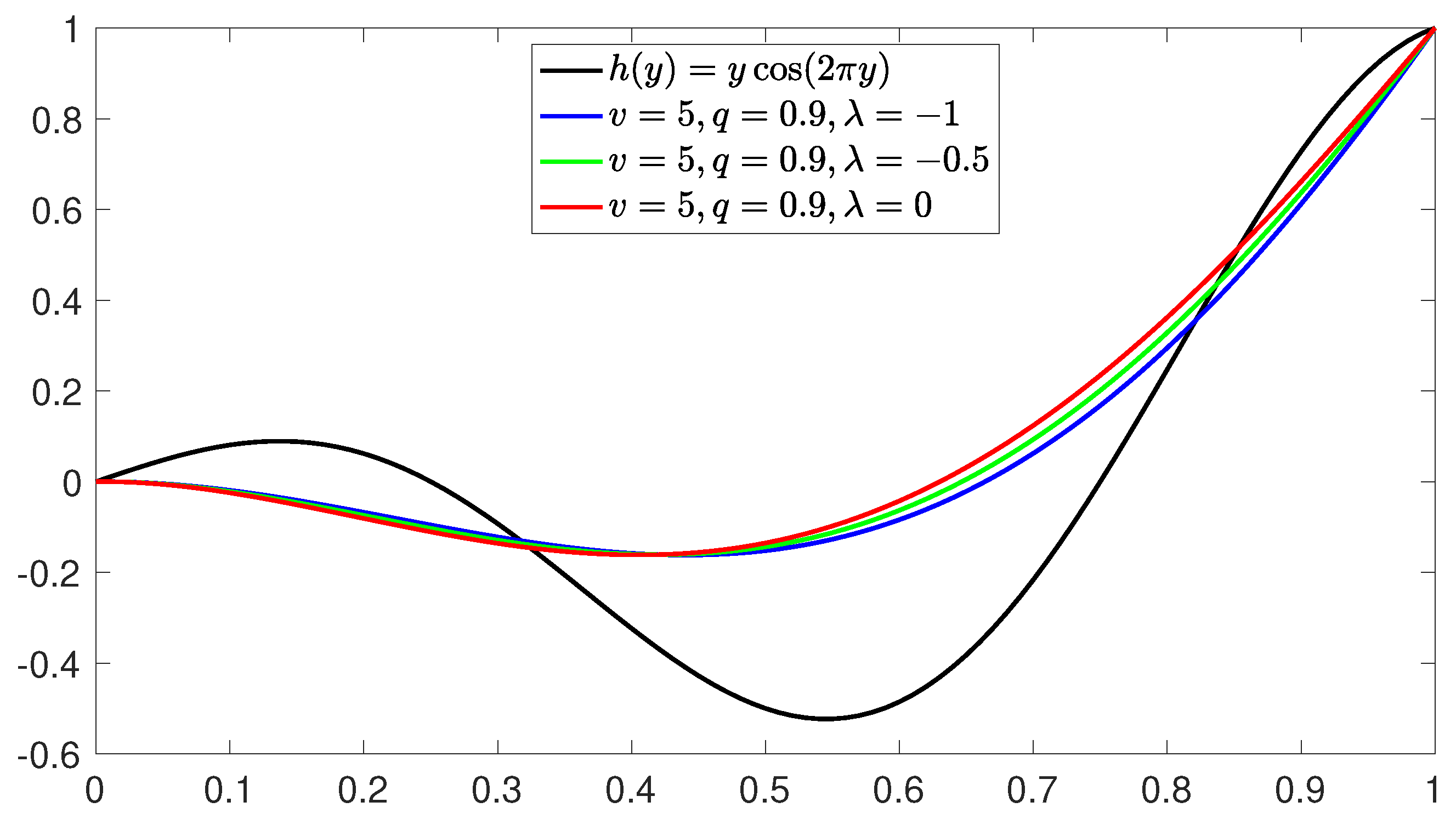
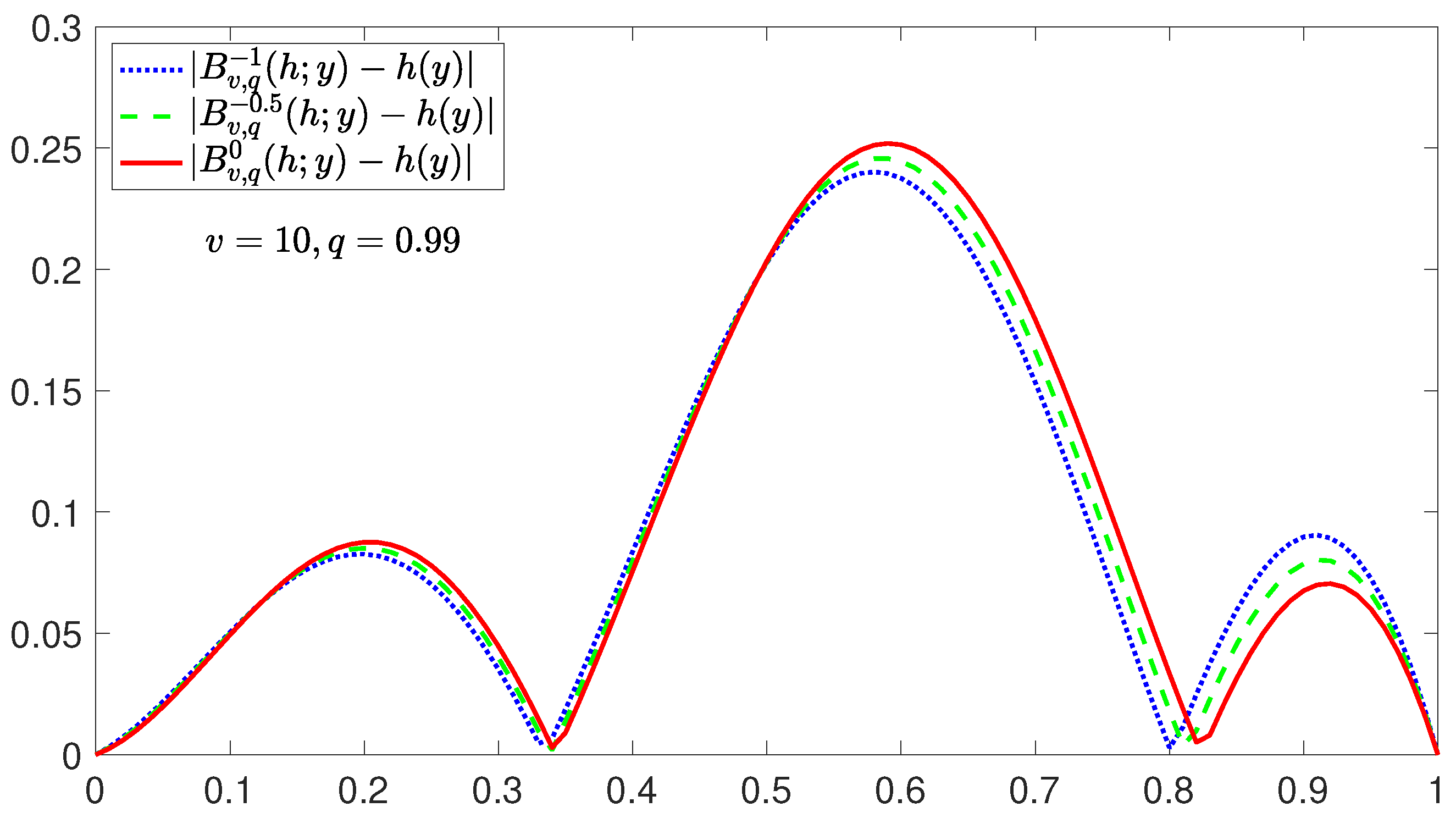
5. Numerical Example
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Braha, N.L.; Mansour, T.; Mursaleen, M.; Acar, T. Convergence of λ-Bernstein operators via power series summability method. J. Appl. Math. Comput. 2021, 65, 125–146. [Google Scholar] [CrossRef]
- Bodur, M.; Manav, N.; Tasdelen, F. Approximation properties of λ-Bernstein-kantorovich-stancu operators. Math. Slovaca 2022, 72, 141–152. [Google Scholar] [CrossRef]
- Hamal, H.; Sabancigil, P. Kantorovich Type Generalization of Bernstein Type Rational Functions Based on (p, q)-Integers. Symmetry 2022, 14, 1054. [Google Scholar] [CrossRef]
- Özkan, E.Y.; Aksoy, G. On a New Generalization of Bernstein-type Rational Functions and Its Approximation. Mathematics 2022, 10, 973. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Cheng, W.-T.; Zhang, W.-H.; Ye, P.-X. Approximation Properties of the Blending-type Bernstein–Durrmeyer Operators. Axioms 2023, 12, 5. [Google Scholar] [CrossRef]
- Acu, A.M.; Mutlu, G.; Çekim, B.; Yazıcı, S. A new representation and shape-preserving properties of perturbed Bernstein operators. Math. Methods Appl. Sci. 2024, 47, 5–14. [Google Scholar] [CrossRef]
- Lipi, K.; Deo, N. λ-Bernstein Operators Based on Pólya Distribution. Numer. Funct. Anal. Optim. 2023, 44, 529–544. [Google Scholar] [CrossRef]
- Aslan, R. Approximation properties of univariate and bivariate new class λ-Bernstein–Kantorovich operators and its associated GBS operators. Comput. Appl. Math. 2023, 42, 34. [Google Scholar] [CrossRef]
- Yilmaz, Ö.G.; Ostrovska, S.; Turan, M. The continuity in q of the Lupaş q-analogues of the Bernstein operators. J. Math. Anal. Appl. 2024, 529, 126842. [Google Scholar] [CrossRef]
- Lupaş, A. A q-analogue of the Bernstein operator. In Seminar on Numerical and Statistical Calculus; University of Cluj-Napoca: Cluj-Napoca, Romania, 1987; Volume 9. [Google Scholar]
- Phillips, G.M. Bernstein polynomials based on the q-integers. Ann. Numer. Math. 1997, 4, 511–518. [Google Scholar]
- Ostrovska, S. q-Bernstein polynomials and their iterates. J. Approx. Theory 2003, 123, 232–255. [Google Scholar] [CrossRef]
- Ostrovska, S. On the improvement of analytic properties under the limit q-Bernstein operator. J. Approx. Theory 2006, 138, 37–53. [Google Scholar] [CrossRef][Green Version]
- Ostrovska, S. On the Lupaş q-analogue of the Bernstein operator. Rocky Mt. J. Math. 2006, 36, 1615–1629. [Google Scholar] [CrossRef]
- Dalmanoglu, Ö.; Doğru, O. On statistical approximation properties of Kantorovich type q-Bernstein operators. Math. Comput. Model. 2010, 52, 760–771. [Google Scholar] [CrossRef]
- Agrawal, P.N.; Finta, Z.; Kumar, A.S. Bernstein-Schurer-Kantorovich operators based on q-integers. Appl. Math. Comput. 2015, 256, 222–231. [Google Scholar] [CrossRef]
- Mursaleen, M.; Khan, F.; Khan, A. Approximation properties for King’s type modified q-Bernstein-Kantorovich operators. Math. Methods Appl. Sci. 2015, 36, 1178–1197. [Google Scholar] [CrossRef]
- Cai, Q.-B.; Cheng, W.-T. Convergence of λ-Bernstein operators based on (p, q)-integers. J. Inequalities Appl. 2020, 2020, 35. [Google Scholar] [CrossRef]
- Khan, A.; Mansoori, M.S.; Khan, K.; Mursaleen, M. Phillips-type q-Bernstein Operators on Triangles. J. Funct. Spaces 2021, 2021, 6637893. [Google Scholar] [CrossRef]
- Cai, Q.-B.; Aslan, R. Note on a new construction of Kantorovich form q-Bernstein operators related to shape parameter λ. Comput. Model. Eng. Sci. 2022, 130, 1479–1493. [Google Scholar] [CrossRef]
- Cheng, W.-T.; Nasiruzzaman, M.; Mohiuddine, S.A. Stancu-type Generalized q-Bernstein–Kantorovich Operators Involving Bézier Bases. Mathematics 2022, 10, 2057. [Google Scholar] [CrossRef]
- Su, L.-T.; Aslan, R.; Zheng, F.-S.; Mursaleen, M. On the Durrmeyer variant of q-Bernstein operators based on the shape parameter λ. J. Inequalities Appl. 2023, 2023, 56. [Google Scholar] [CrossRef]
- Sabancıgil, P. Genuine q-Stancu-Bernstein–Durrmeyer Operators. Symmetry 2023, 15, 437. [Google Scholar] [CrossRef]
- Gupta, V. Some approximation properties of q-Durrmeyer operators. Appl. Math. Comput. 2008, 197, 172–178. [Google Scholar] [CrossRef]
- Gupta, V.; Wang, H. The rate of convergence of q-Durrmeyer operators for 0 < q < 1. Math. Methods Appl. Sci. 2008, 31, 1946–1955. [Google Scholar]
- Gupta, V.; Finta, Z. On certain q-Durrmeyer type operators. Appl. Math. Comput. 2009, 209, 415–420. [Google Scholar] [CrossRef]
- Dinlemez, Ü.; Yüksel, İ. Voronovskaja Type Approximation Theorem For q-Szász-Beta-Stancu Type Operators. Gazi Univ. J. Sci. 2016, 29, 115–122. [Google Scholar]
- Yüksel, İ.; Dinlemez, Ü. Weighted Approximation by the q-Szász-Schurer-Beta Type Operators. Gazi Univ. J. Sci. 2015, 28, 231–238. [Google Scholar]
- Yüksel, İ.; Dinlemez, Ü.; Altın, B. Approximation by q-Baskakov–Durrmeyer Type Operators of Two Variables. In Computational Analysis: AMAT, Ankara, May 2015 Selected Contributions; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 195–209. [Google Scholar]
- Doğru, O.; İçöz, G.; Kanat, K. On the Rates of Convergence of the q-Lupaş-Stancu Operators. Filomat 2016, 30, 1151–1160. [Google Scholar] [CrossRef]
- Cai, Q.-B.; Zeng, X.M.; Cui, Z. Approximation properties of the modification of Kantorovich type q-Szász operators. J. Comput. Anal. Appl. 2013, 15, 176–187. [Google Scholar]
- Cai, Q.-B. Approximation properties of the modification of q-Stancu-Beta operators which preserve x2. J. Inequalities Appl. 2014, 2014, 505. [Google Scholar] [CrossRef][Green Version]
- Ulusoy, G.; Acar, T. q-Voronovskaya type theorems for q-Baskakov operators. Math. Methods Appl. Sci. 2016, 39, 3391–3401. [Google Scholar] [CrossRef]
- Khan, K.; Lobiyal, D.K.; Kılıcman, A. Bézier curves and surfaces based on modified Bernstein polynomials. Azerb. J. Math. 2019, 9, 3–21. [Google Scholar]
- Farin, G. Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Sederberg, T.W. Computer Aided Geometric Design 2012. Available online: https://scholarsarchive.byu.edu/facpub/1/ (accessed on 1 September 2021).
- Farouki, R.T. The Bernstein polynomial basis: A centennial retrospective. Comput. Aided Geometr. Design 2012, 29, 379–419. [Google Scholar] [CrossRef]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series, Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 1990; Volume 35. [Google Scholar]
- Kac, V.G.; Cheung, P. Quantum Calculus, Universitext; Springer: New York, NY, USA, 2002. [Google Scholar]
- Zhou, G.; Chen, S.; Zhao, G. Approximation properties of a new kind of λ-Bernstein operators. 2024; in press. [Google Scholar]
- Niven, I.; Zuckerman, H.S.; Montgomery, H. An Introduction to the Theory of Numbers, 5th ed.; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Gadjiev, A.D.; Orhan, C. Some approximation theorem via statistical convergence. Rocky Mt. J. Math. 2002, 32, 129–138. [Google Scholar] [CrossRef]
- De Vore, R.A.; Lorentz, G.G. Constructive Approximation; Springer: Berlin, Germany, 1993. [Google Scholar]
| q | |||||
|---|---|---|---|---|---|
| 0.242074235 | 0.242921216 | 0.243768198 | 0.244615179 | 0.245462161 | |
| 0.146636656 | 0.147073061 | 0.147581795 | 0.14809053 | 0.148599265 | |
| 0.074389442 | 0.074658736 | 0.07492803 | 0.075197324 | 0.075466618 | |
| 0.066814352 | 0.067069407 | 0.067324461 | 0.067579516 | 0.06783457 | |
| 0.06108183 | 0.061325904 | 0.061569978 | 0.061814053 | 0.062058127 | |
| 0.059833655 | 0.060075309 | 0.060316963 | 0.060558617 | 0.060800271 | |
| 0.059709692 | 0.059951105 | 0.060192518 | 0.060433931 | 0.060675344 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.-T.; Kangal, E.; Kantar, Ü.D.; Cai, Q.-B. Some Statistical and Direct Approximation Properties for a New Form of the Generalization of q-Bernstein Operators with the Parameter λ. Axioms 2024, 13, 485. https://doi.org/10.3390/axioms13070485
Su L-T, Kangal E, Kantar ÜD, Cai Q-B. Some Statistical and Direct Approximation Properties for a New Form of the Generalization of q-Bernstein Operators with the Parameter λ. Axioms. 2024; 13(7):485. https://doi.org/10.3390/axioms13070485
Chicago/Turabian StyleSu, Lian-Ta, Esma Kangal, Ülkü Dinlemez Kantar, and Qing-Bo Cai. 2024. "Some Statistical and Direct Approximation Properties for a New Form of the Generalization of q-Bernstein Operators with the Parameter λ" Axioms 13, no. 7: 485. https://doi.org/10.3390/axioms13070485
APA StyleSu, L.-T., Kangal, E., Kantar, Ü. D., & Cai, Q.-B. (2024). Some Statistical and Direct Approximation Properties for a New Form of the Generalization of q-Bernstein Operators with the Parameter λ. Axioms, 13(7), 485. https://doi.org/10.3390/axioms13070485






