A Reduced-Dimension Weighted Explicit Finite Difference Method Based on the Proper Orthogonal Decomposition Technique for the Space-Fractional Diffusion Equation

Abstract

A kind of reduced-dimension method based on a weighted explicit finite difference scheme and the proper orthogonal decomposition (POD) technique for diffusion equations with Riemann–Liouville fractional derivatives in space are discussed. The constructed approximation method written in matrix form can not only ensure a sufficient accuracy order but also reduce the degrees of freedom, decrease storage requirements, and accelerate the computation rate. Uniqueness, stabilization, and error estimation are demonstrated by matrix analysis. The procedural steps of the POD algorithm, which reduces dimensionality, are outlined. Numerical simulations to assess the viability and effectiveness of the reduced-dimension weighted explicit finite difference method are given. A comparison between the reduced-dimension method and the classical weighted explicit finite difference scheme is presented, including the error in the $L_2$ norm, the accuracy order, and the CPU time.

1. Introduction

The initial boundary value problems addressed here are as follows:

$$\left\{\begin{array}{cc}{\displaystyle \frac{\partial u(x,t)}{\partial t}}=d\left(x\right){\displaystyle \frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}}+f(x,t),\hfill & x\in [a,b],t\in (0,T],\hfill \\ u(a,t)=u(b,t)=0,\hfill & t\in (0,T],\hfill \\ u(x,0)={\varphi }_0\left(x\right),\hfill & x\in [a,b],\hfill \end{array}\right.$$

(1)

where $d\left(x\right)$ represents the diffusion coefficient, T is the final time, and $f(x,t)$ denotes the source term. ${\varphi }_0\left(x\right)$ is the initial value, which is sufficiently smooth. The term $\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}$ is used to represent the Riemann–Liouville fractional derivative, which has the following definition:

$${\displaystyle \frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}}=\left\{\begin{array}{c}\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\Gamma (2-\alpha )}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}{\int }_0^x{\displaystyle \frac{u(\zeta ,t)d\zeta }{{(x-\zeta )}^{\alpha -1}}},}& 1<\alpha <2,\\ \\ {\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}},& \alpha =2,\end{array}\hfill \end{array}\right.$$

in which $\alpha$ represents the order of the equation, and $1<\alpha ⩽2$ (see [1,2]).

Fractional calculus emerges as an indispensable mathematical instrument for elucidating a spectrum of phenomena encountered in scientific and engineering disciplines [3,4,5,6,7]. Within this versatile framework, one of the key applications is the depiction of subdiffusion and superdiffusion [8,9,10]. The fractional diffusion equation’s importance and use in various fields have garnered significant interest. However, the complexity of fractional diffusion equations typically makes it difficult to obtain solutions that are precisely accurate. Consequently, it becomes necessary for us to utilize numerical approaches to obtain numerical solutions to these equations. As we know, there exist challenges in the numerical approximation of fractional derivatives because of their lack of the advantageous properties that classical approximation operators possess. So, many researchers keep working hard on constructing approximate formulas for fractional derivatives. And, during the preceding decades, there has been notable progress, for example, the finite difference method [1,2,11,12]. Utilizing the traditional Grünwald–Letnikov technique for discretizing the Riemann–Liouville fractional derivative [3], first-order accuracy was obtained; however, the technique is unstable in time-dependent contexts. Meerschaert and Tadjeran [1] proposed the shifted Grünwald–Letnikov formula to approximate the fractional advection–dispersion flow equation, ensuring stability. Wang et al. [13] approximated the space-fractional diffusion equation by weighting the Grünwald–Letnikov formula and shifting Grünwald–Letnikov formula. Savović et al. [14] studied radon diffusion in soil and air, deriving the solution of the correlation diffusion equation using the explicit finite difference method. They compared the results of the two-medium model (soil–air) with those of the simplified single-medium model (soil). Savović et al. [15] used the explicit finite difference method (EFDM) and a physical information neural network (PINN) to study Burgers’ equation. Although the method above performs well, it contains too many degrees of freedom for practical calculations. Therefore, a significant problem is how to simplify computations, reduce computational and storage requirements, and slow the accumulation of truncation errors during the calculation process, all while ensuring that the numerical solution maintains sufficient precision. A possible solution to achieve these goals is to construct a kind of reduced-dimension method.

A wealth of numerical evidence demonstrates the efficacy of the POD technique as a potential and practical reduced-dimension method that can reduce the unknowns of the numerical models, slow down the accumulation of round-off errors, minimize CPU running time, and enhance computational efficiency to some extent [16,17,18]. The POD method has been applied in many fields, including but not limited to turbulence analysis [19,20,21], principal component analysis [22], sample identification for statistics [23], atmospheric modeling [24], geophysics [25], and so on. In particular, the POD dimension reduction technique is commonly integrated with many classical numerical methods to develop different reduced-dimension models, including POD finite volume element models [26], the mixed finite element method based on the POD technique [27,28], the space–time POD element method [29,30], reduced-dimension spectral methods [31,32], and difference methods combined with the POD method [33,34,35,36], etc. These reduced-dimension schemes have achieved a lot of meaningful results.

However, to our knowledge, there have been no reports about a reduced-dimension weighted finite difference scheme for the space-fractional diffusion equation established by the POD method. Therefore, this is our main purpose in this paper. To achieve this, we have developed a reduced-dimension model for space-fractional diffusion equations by combining the weighted finite difference scheme and the POD method. The weighted explicit finite difference form is given and written in matrix form. Additionally, the uniqueness of the solution with this method is proven. Based on the classical difference method with the matrix form, a reduced-dimension weighted explicit finite difference method is obtained by selecting suitable samples, establishing a snapshot matrix, and constructing a POD basis. Uniqueness, stability, and error estimations are presented through matrix analysis. Numerical simulations for assessing the viability and efficiency of the reduced-dimension weighted explicit finite difference method are provided. A comparison between the reduced-dimension method and the classical weighted explicit finite difference scheme is presented, including the error in the $L_2$ norm, the accuracy order, and the CPU time. The results demonstrate that the POD reduced-dimension weighted explicit finite difference scheme can ensure precision while saving CPU computation time and improving computing efficiency.

The paper is structured as follows. In Section 2, we present a matrix formulation of the weighted explicit finite difference scheme for the space-fractional diffusion equation and demonstrate the uniqueness of its solutions. Furthermore, Section 3 describes the creation of POD bases and the establishment of a reduced-dimension weighted explicit finite difference scheme using POD techniques. In Section 4, the uniqueness, stabilization, and error estimates of the reduced-dimension weighted explicit finite difference solutions are provided, and the implementation steps of the POD reduced-dimension method are described. For the purpose of verifying the constructed scheme’s efficiency and feasibility, numerical simulations are presented in Section 5. Finally, Section 6 provides the main conclusions.

2. The Weighted Explicit Finite Difference Scheme for the Space-Fractional Diffusion Equation

To establish the weighted explicit finite difference scheme for problem (1), the discretized space and time variables are given. The time is divided as $0⩽t_0⩽t_1⩽t_2⩽\cdots ⩽t_N⩽T$. Let $\tau =\frac{T}{N}$ denote the time step, $t_n=n\tau$ $(n=0,1,2,\cdots ,N)$. And, let $x_i(i=0,1,2,\cdots ,M)$ be space mesh nodes, with the equivalent step length $h=\frac{b-a}{M}$, and $x_i=a+ih$ for $i=0,1,2,\cdots ,M$.

We define the grid function as

$$u_i^n=u(x_i,t_n),d_i=d\left(x_i\right),f_i^n=f(x_i,t_n),for0⩽i⩽M,0⩽n⩽N.$$

Before constructing the weighted explicit finite difference method, we first define the Grünwald–Letnikov formula for $\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}$:

$$\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}=\frac{1}{\Gamma (-\alpha )}\underset{M\to \infty }{\lim }\frac{1}{h^{\alpha }}\sum _{k=0}^M\frac{\Gamma (k-\alpha )}{\Gamma (k+1)}u(x-kh,t).$$

(2)

Next, we define the right-shifted Grünwald–Letnikov formula for $\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}$ [1]:

$$\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}=\frac{1}{\Gamma (-\alpha )}\underset{M\to \infty }{\lim }\frac{1}{h^{\alpha }}\sum _{k=0}^M\frac{\Gamma (k-\alpha )}{\Gamma (k+1)}u(x-(k-1)h,t),$$

(3)

where M is a positive integer, and $\Gamma (·)$ denotes the Gamma function [3] defined by the integral.

$$\Gamma \left(z\right)={\int }_0^{\infty }{e}^{-t}{t}^{z-1}dt,Re\left(z\right)>0.$$

We rewrite Equations (2) and (3) as follows, respectively:

$$\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}=\underset{h\to 0}{\lim }\frac{1}{h^{\alpha }}\sum _{k=0}^M{\omega }_k^{\left(\alpha \right)}u(x-kh,t)+\mathit{O}(\tau +h),$$

(4)

$$\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}=\underset{h\to 0}{\lim }\frac{1}{h^{\alpha }}\sum _{k=0}^M{\omega }_k^{\left(\alpha \right)}u(x-(k-1)h,t)+\mathit{O}(\tau +h).$$

(5)

The ‘normalized’ Grünwald weight is defined by

$${\omega }_k^{\left(\alpha \right)}=\frac{\Gamma (k-\alpha )}{\Gamma (-\alpha )\Gamma (k+1)}={(-1)}^k\left(\begin{array}{c}\alpha \\ k\end{array}\right),\left(\begin{array}{c}\alpha \\ k\end{array}\right)=\frac{\alpha (\alpha -1)\cdots (\alpha -k+1)}{k!},\forall k⩾2,$$

(6)

in which $\left(\begin{array}{c}\alpha \\ k\end{array}\right)$ represents a binomial coefficient.

The coefficient ${\omega }_k^{\left(\alpha \right)}$, which is the coefficient of the power series of the function ${(1-z)}^{\alpha }$, is determined by just the order $\alpha$ and the index k:

$${(1-z)}^{\alpha }=\sum _{k=0}^{\infty }{(-1)}^k\left(\begin{array}{c}\alpha \\ k\end{array}\right)z^k=\sum _{k=0}^{\infty }{\omega }_k^{\left(\alpha \right)}{z}^k,-1<z⩽1.$$

The following is their recurrence relationship:

$${\omega }_0^{\left(\alpha \right)}=1,{\omega }_k^{\left(\alpha \right)}=\left(1-\frac{\alpha +1}{k}\right){\omega }_{k-1}^{\left(\alpha \right)},k=1,2,\cdots .$$

Lemma 1

([37]). When $1<\alpha <2$, the coefficient $\left\{{\omega }_k^{\left(\alpha \right)}\right\}$ in Equation (6) satisfies the properties below:

$$\begin{array}{cc}\hfill & {\omega }_0^{\left(\alpha \right)}=1,{\omega }_1^{\left(\alpha \right)}=-\alpha ,{\omega }_2^{\left(\alpha \right)}>{\omega }_3^{\left(\alpha \right)}>\cdots >0,\hfill \\ \hfill & \sum _{k=0}^{\infty }{\omega }_k^{\left(\alpha \right)}=0,\sum _{k=0}^m{\omega }_k^{\left(\alpha \right)}<0,m⩾1.\hfill \end{array}$$

(7)

The following difference quotient can be applied to approximate the derivative of (1):

$$\frac{\partial u}{\partial t}{|}_{(x_i,t_n)}={\displaystyle \frac{u_i^n-u_i^{n-1}}{\tau }}+\mathit{O}\left(\tau \right).$$

(8)

By combining Equations (4) and (5), we obtain the finite difference equation as follows:

$$\frac{u_i^n-u_i^{n-1}}{\tau }=\frac{d_i}{h^{\alpha }}\sum _{k=0}^i{\omega }_k^{\left(\alpha \right)}{u}_{i-k}^{n-1}+f_i^{n-1}+\mathit{O}(\tau +h),$$

(9)

$$\frac{u_i^n-u_i^{n-1}}{\tau }=\frac{d_i}{h^{\alpha }}\sum _{k=0}^i{\omega }_k^{\left(\alpha \right)}{u}_{i-k+1}^{n-1}+f_i^{n-1}+\mathit{O}(\tau +h).$$

(10)

Equations (9) and (10) possess only first-order precision in both time and space [1]. To achieve higher precision in space, we can employ a weighted approach with the Grünwald–Letnikov formula and the right-shifted Grünwald–Letnikov formula:

$$\frac{\partial u^{\alpha }(x,t)}{\partial x^{\alpha }}=\frac{1}{h^{\alpha }}\left\{(1-ϵ)\sum _{k=0}^i{\omega }_k^{\left(\alpha \right)}{u}_{i-k}^{n-1}+ϵ\sum _{k=0}^{i+1}{\omega }_k^{\left(\alpha \right)}{u}_{i-k+1}^{n-1}\right\}+\mathit{O}\left(h^2\right).$$

(11)

Therefore, the weighted explicit finite difference scheme for initial boundary value problems (1) can be obtained:

$$\left\{\begin{array}{c}\frac{u_i^n-u_i^{n-1}}{\tau }={\displaystyle \frac{d_i}{h^{\alpha }}}\left\{(1-ϵ)\sum _{k=0}^i{\omega }_k^{\left(\alpha \right)}{u}_{i-k}^{n-1}+ϵ\sum _{k=0}^{i+1}{\omega }_k^{\left(\alpha \right)}{u}_{i-k+1}^{n-1}\right\}+f_i^{n-1}+\mathit{O}(\tau +h^2),\hfill \\ 1⩽i⩽M-1,1⩽n⩽N,\hfill \\ u_i^0={\varphi }_0\left(x_i\right),1⩽i⩽M-1,\hfill \\ u_0^n=u_{M,}^n=0,0⩽n⩽N,\hfill \end{array}\right.$$

(12)

in which $0<ϵ<1$ is a weight parameter. In this article, we take the weight parameter as $ϵ={\displaystyle \frac{\alpha }{2}}$.

Let $B_i$ be defined as $B_i={\displaystyle \frac{d_i\tau }{h^{\alpha }}}$ with the condition that $B_i⩾0$. Equation (12) can then be rewritten as follows:

$$\left\{\begin{array}{cc}\hfill & u_i^n=u_i^{n-1}+B_i\left\{(1-ϵ)\sum _{k=0}^i{\omega }_k^{\left(\alpha \right)}{u}_{i-k}^{n-1}+ϵ\sum _{k=0}^{i+1}{\omega }_k^{\left(\alpha \right)}{u}_{i-k+1}^{n-1}\right\}+\tau f_i^{n-1}+\mathit{O}(\tau +h^2),\hfill \\ \hfill & 1⩽i⩽M-1,1⩽n⩽N,\hfill \\ \hfill & u_i^0={\varphi }_0\left(x_i\right),1⩽i⩽M-1,\hfill \\ \hfill & u_0^n=u_{M,}^n=0,0⩽n⩽N.\hfill \end{array}\right.$$

(13)

Furthermore, the matrix form of the weighted explicit finite difference scheme (13) can be rewritten as follows:

$${\mathit{U}}^n={\mathit{AU}}^{n-1}+\tau {\mathit{F}}^{n-1},$$

(14)

in which the factor

$$\begin{array}{cc}\hfill & {\mathit{U}}^n={\left[u_1^n,u_2^n,\cdots ,u_{M-1}^n\right]}^T,\hfill \\ \hfill & {\mathit{F}}^{n-1}={\left[f_1^{n-1},f_2^{n-1},\cdots ,f_{M-1}^{n-1}\right]}^T,\hfill \\ \hfill & \mathit{A}={\left(A_{ij}\right)}_{(M-1)\times (M-1)}.\hfill \end{array}$$

(15)

The element $A_{ij}$ in matrix $\mathit{A}$ for $i=1,2,\cdots ,M-1$ and $j=1,2,\cdots ,M-1$ are defined as follows (note that the values of ${\omega }_0^{\left(\alpha \right)}$ and ${\omega }_1^{\left(\alpha \right)}$ are given in Lemma 1):

$$A_{ij}=\left\{\begin{array}{c}\begin{array}{ll} 0,& \mathrm{when}\mathrm{j}⩾\mathrm{i}+2,\\ B_iϵ{\omega }_0^{\left(\alpha \right)},& \mathrm{when}\mathrm{j}=\mathrm{i}+1,\\ 1+B_i(1-ϵ){\omega }_0^{\left(\alpha \right)}+B_iϵ{\omega }_1^{\left(\alpha \right)},& \mathrm{when}\mathrm{j}=\mathrm{i},\\ B_i(1-ϵ){\omega }_1^{\left(\alpha \right)}+B_iϵ{\omega }_2^{\left(\alpha \right)},& \mathrm{when}\mathrm{j}=\mathrm{i}-1,\\ B_i(1-ϵ){\omega }_{i-j}^{\left(\alpha \right)}+B_iϵ{\omega }_{i-j+1}^{\left(\alpha \right)},& \mathrm{when}\mathrm{j}⩽\mathrm{i}-2.\end{array}\hfill \end{array}\right.$$

(16)

Theorem 1.

The weighted explicit finite difference scheme (12) has a unique solution.

Proof of Theorem 1. 

Assuming that $v_i^n$ is another solution of Equation (12) and defining $z_i^n=u_i^n-v_i^n$, we obtain

$$\left\{\begin{array}{c}{z}_i^n=z_i^{n-1}+\frac{d_i}{h^{\alpha }}\left\{(1-ϵ)\sum _{k=0}^i{\omega }_k^{\left(\alpha \right)}{z}_{i-k}^{n-1}+ϵ\sum _{k=0}^{i+1}{\omega }_k^{\left(\alpha \right)}{z}_{i-k+1}^{n-1}\right\},\hfill \\ 1⩽i⩽M-1,1⩽n⩽N,\hfill \\ z_i^0=0,1⩽i⩽M-1,\hfill \\ z_0^n=0,z_{M,}^n=0,0⩽n⩽N.\hfill \end{array}\right.$$

(17)

Let $\parallel z^n{\parallel }_{\infty }=\left|z_{i_n}^n\right|$, where $i_n\in \{1,2,\cdots ,M-1\}$. In the above equation, setting $i=i_n$, taking the absolute value on both sides and then applying the triangle inequality, we obtain the following result:

$$\begin{array}{cc}\hfill \parallel z^n{\parallel }_{\infty }& =\left|z_{i_n}^{n-1}+\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}{z}_{i_n-k}^{n-1}+\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}{z}_{i_n-k+1}^{n-1}\right|\hfill \\ \hfill & ⩽\left|z_{i_n}^{n-1}\right|+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|\left|z_{i_n-k}^{n-1}\right|+\left|\frac{d_i\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\left|z_{i_n-k+1}^{n-1}\right|\hfill \\ \hfill & ⩽\parallel z^{n-1}{\parallel }_{\infty }+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|\parallel z^{n-1}{\parallel }_{\infty }+\left|\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|{\parallel z^{n-1}\parallel }_{\infty }\hfill \\ \hfill & ⩽\left(1+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|+\left|\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\right){\parallel z^{n-1}\parallel }_{\infty },\hfill \\ \hfill & 1⩽i⩽M-1,1⩽n⩽N.\hfill \end{array}$$

(18)

For $n=1$, Equation (18) can be written as follows:

$${\parallel z^1\parallel }_{\infty }⩽\left(1+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|+\left|\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\right){\parallel z^0\parallel }_{\infty }.$$

Similarly, for $n=2$, we obtain

$$\begin{array}{cc}\hfill \parallel z^2{\parallel }_{\infty }& ⩽\left(1+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|+\left|\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\right){\parallel z^1\parallel }_{\infty }\hfill \\ \hfill & ⩽{\left(1+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|+\left|\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\right)}^2{\parallel z^0\parallel }_{\infty },\hfill \end{array}$$

and by the principle of induction, we obtain

$$\begin{array}{cc}\hfill \parallel z^n{\parallel }_{\infty }& ⩽\left(1+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|+\left|\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\right){\parallel z^{n-1}\parallel }_{\infty }\hfill \\ \hfill & ⩽{\left(1+\left|\frac{d_{i_n}\tau }{h^{\alpha }}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|+\left|\frac{d_{i_n}\tau }{h^{\alpha }}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\right)}^n{\parallel z^0\parallel }_{\infty }.\hfill \end{array}$$

Due to $\tau =\mathit{O}\left(h^2\right)$, the equation can be rewritten as follows:

$$\begin{array}{cc}\hfill \parallel z^n{\parallel }_{\infty }& ⩽\left[1+{\tau }^{2-\alpha }{\left(\left|d_{i_n}(1-ϵ)\sum _{\begin{array}{c}k=0\end{array}}^{i_n}{\omega }_k^{\left(\alpha \right)}\right|+\left|d_{i_n}ϵ\sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}{\omega }_k^{\left(\alpha \right)}\right|\right)}^n\right]{\parallel z^0\parallel }_{\infty }\hfill \\ \hfill & ⩽e^{n{\tau }^{2-\alpha }\gamma }\parallel z^0{\parallel }_{\infty }⩽e^{n\tau \gamma }{\parallel z^0\parallel }_{\infty }\hfill \\ \hfill & ⩽e^{T\gamma }\parallel z^0{\parallel }_{\infty }⩽c{\parallel z^0\parallel }_{\infty },\hfill \end{array}$$

where $\gamma =\left|d_{i_n}(1-ϵ){\displaystyle \sum _{\begin{array}{c}k=0\end{array}}^{i_n}}{\omega }_k^{\left(\alpha \right)}\right|+\left|d_{i_n}ϵ{\displaystyle \sum _{\begin{array}{c}k=0\end{array}}^{i_n+1}}{\omega }_k^{\left(\alpha \right)}\right|$.

Owing to $z^0=0$, it follows that ${\parallel z^n\parallel }_{\infty }=0$, which implies $u_i^n=v_i^n$. Consequently, the finite difference scheme (12) has a unique solution, thereby proving the conclusion of Theorem 1. □

The stabilization and convergence of the set of solutions ${\left\{{\mathit{U}}^n\right\}}_{n=1}^N$ were proved in Theorems 2.2 and 2.3, as referenced in [13].

Theorem 2.

Given $ϵ=\frac{\alpha }{2}$ and the condition $1+B_i(1-ϵ)-B_iϵ\alpha >0$, the series of solutions ${\left\{{\mathit{U}}^n\right\}}_{n=1}^N$ for the weighted explicit finite difference scheme (14) is stabilized and converges. Furthermore, the error estimates between this series and the analytical solution vector $\mathit{U}\left(t_n\right)={[u(x_1,t_n),u(x_2,t_n),\cdots ,u(x_{M-1},t_n)]}^T$ for $n=1,2,\cdots ,N$, produced by the space-fractional diffusion Equation (1), are denoted as follows.

$${∥\mathit{U}\left(t_n\right)-{\mathit{U}}^n∥}_2⩽\mathit{O}(\tau ,h^2),n=1,2,\cdots ,N.$$

(19)

Remark 1.

The series of solutions ${\left\{{\mathit{U}}^n\right\}}_{n=1}^N$ for the weighted explicit finite difference scheme can be obtained in vector format by providing the space step h, time step τ, coefficients $d\left(x\right)$, initial values ${\varphi }_0\left(x\right)$, and parameters ϵ. From this series, we select the first S $(S\ll N)$ as a group of snapshots.

3. The Establishment of a Reduced-Dimension Scheme for the Space-Fractional Diffusion Equation

As we know, the matrix $\mathit{A}$ is $(M-1)\times (M-1)$, and there are $(M-1)$ unknowns in Equation (14) when solving the equations obtained from the weighted explicit finite difference scheme. When M is larger, it can significantly limit the computation speed in practical implementation. To enhance the efficiency of computation and simplify the procedure, in this section, we construct a reduced-dimension model of the weighted explicit finite difference scheme based on the POD method.

3.1. Construction of POD Base

Firstly, we compute the first $S(S\ll N,\mathrm{for}\mathrm{example},S=20\mathrm{based}\mathrm{on}\mathrm{experience})$ solution vectors ${\mathit{U}}^n=\{u_i^k\mid 1⩽i⩽M-1,1⩽k⩽S$, $S\ll N\left\}\right(n=1,2,\cdots ,N)$ in the weighted explicit finite difference scheme as snapshots. Then, we establish an $(M-1)\times S$ snapshot matrix $\mathit{C}$:

$$\mathit{C}={\left[\begin{array}{cccc}{\mathit{U}}_1^1& {\mathit{U}}_1^2& \cdots & {\mathit{U}}_1^S\\ {\mathit{U}}_2^1& {\mathit{U}}_2^2& \cdots & {\mathit{U}}_2^S\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{U}}_{M-1}^1& {\mathit{U}}_{M-1}^2& \cdots & {\mathit{U}}_{M-1}^S\end{array}\right]}_{(M-1)\times S}.$$

(20)

Subsequently, the snapshot matrix $\mathit{C}$ undergoes factorization via the technique of singular value decomposition, that is,

$$\mathit{C}=\mathit{P}\left(\begin{array}{cc}\sum _{s\times s}& {\mathbf{0}}_{s\times (S-s)}\\ {\mathbf{0}}_{(M-1-s)\times s}& {\mathbf{0}}_{(M-1-l)\times (S-s)}\end{array}\right){\mathit{Q}}^T,$$

(21)

in which the diagonal matrix ${\sum }_{s\times s}=diag\{{\varsigma }_1,{\varsigma }_2,\cdots ,{\varsigma }_s\}$ is made up of the singular values of $\mathit{C}$ sorted in descending order, that is, ${\varsigma }_1⩾{\varsigma }_2⩾\cdots ⩾{\varsigma }_s>0$. Matrix $\mathit{P}=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\cdots ,{\mathit{\phi }}_{M-1})$ is an $(M-1)\times (M-1)$ orthogonal matrix whose column vectors are the orthonormal eigenvectors corresponding to ${\mathit{CC}}^T$. Similarly, matrix $\mathit{Q}$, which is an $S\times S$ orthogonal matrix, is defined as $({\psi }_1,{\psi }_2,\cdots ,{\psi }_S)$. The column vectors of matrix $\mathit{Q}$ are the orthonormal eigenvectors that correspond to ${\mathit{C}}^T\mathit{C}$. The symbol $\mathbf{0}$ denotes the zero vector [17].

Take

$${\mathit{C}}_{\mathit{q}}=\mathit{P}\left(\begin{array}{cc}\sum _{q\times q}& {\mathbf{0}}_{q\times (S-q)}\\ {\mathbf{0}}_{(M-1-q)\times q}& {\mathbf{0}}_{(M-1-q)\times (S-q)}\end{array}\right){\mathit{Q}}^T,$$

(22)

where the diagonal matrix is ${\sum }_{q\times q}=diag\{{\varsigma }_1,{\varsigma }_2,\cdots ,{\varsigma }_q\}$, which is made up of the diagonal matrix ${\sum }_{s\times s}$ in $\mathit{C}$’s first q positive singular values.

Lemma 2.

Let $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\cdots ,{\mathit{\phi }}_q)$ be composed of $\mathit{P}=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\cdots ,{\mathit{\phi }}_{M-1})$’s first q eigenvectors. Then, it holds that

$${\mathit{C}}_{\mathit{q}}=\sum _{i=1}^q{\varsigma }_i{\mathit{\phi }}_j{\mathit{\psi }}_i^T=\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{C}.$$

(23)

The proof of Lemma 2 has been shown in Lemma 1.2.2 of reference [17].

Consequently, based on the relationship between matrix norms and the spectral radius [38], it follows that

$$\underset{rank\left(\mathit{D}\right)⩽q}{\min }{∥\mathit{C}-\mathit{D}∥}_2={∥\mathit{C}-{\mathit{C}}_q∥}_2={∥\mathit{C}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{C}∥}_2=\sqrt{{\gamma }_{q+1}},$$

(24)

where $\sqrt{{\gamma }_{q+1}}={\varsigma }_{q+1}$.

Moreover, assuming that the S column vector of $\mathit{C}$ is represented by ${\mathit{U}}^n=(u_1^n,u_2^n,$$\cdots ,u_{M-1}^n{)}^T$, ($n=1,2,\cdots ,S$), the following results are obtained:

$$\begin{array}{cc}{∥{\mathit{U}}^n-{\mathit{U}}_q^n∥}_2\hfill & ={∥(\mathit{C}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{C}){\epsilon }^n∥}_2\hfill \\ \hfill & ⩽{∥(\mathit{C}-\mathbf{\Phi }{\mathbf{\Phi }}^T\mathit{C})∥}_2{∥{\epsilon }^n∥}_2=\sqrt{{\gamma }_{q+1}},n=1,2,\cdots ,S.\hfill \end{array}$$

(25)

In this context, ${\displaystyle {\mathit{U}}_q^n=\sum _{j=1}^q({\mathit{\phi }}_j,{\mathit{U}}^n){\mathit{\phi }}_j}$ denotes the projection of ${\mathit{U}}^n$ onto $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\cdots ,{\mathit{\phi }}_q)$, $({\mathit{\phi }}_j,{\mathit{U}}^n)$ represents the inner product between ${\mathit{\phi }}_j$ and ${\mathit{U}}^n$, and ${\epsilon }^n$ is an S-dimensional unit vector with the nth component 1 ($1⩽n⩽S$). Inequality $\left(25\right)$ indicates that the error between ${\mathit{U}}_q^n$ and ${\mathit{U}}^n$ is no greater than $\sqrt{{\gamma }_{q+1}}$. Consequently, ${\mathit{U}}_q^n$ represents the best approximation of ${\mathit{U}}^n$, and $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\cdots ,{\mathit{\phi }}_q)(1⩽q⩽s)$ constitutes the optimal POD basis for $\mathit{C}$.

Remark 2.

The S order of matrix ${\mathit{C}}^T\mathit{C}$ is significantly smaller than the $M-1$ order of matrix $\mathit{C}{\mathit{C}}^T$, indicating that the number of snapshots S is far less than the number of space nodes $M-1$. However, their positive eigenvalues ${\gamma }_i={\varsigma }_i^2$ ($i=1,2,\cdots ,s$) are identical. Therefore, we calculate the first q positive eigenvalues ${\gamma }_i$ (for $i=1,2,\cdots ,q$) and the corresponding eigenvectors ${\psi }_i$ (for $i=1,2,\cdots ,q$) of matrix ${\mathit{C}}^T\mathit{C}$. Then, utilizing the formula ${\mathit{\phi }}_i=\mathit{C}{\mathit{\psi }}_i/\sqrt{{\gamma }_i}$ (for $i=1,2,\cdots ,q$), we compute the positive eigenvalues ${\gamma }_i$ (for $i=1,2,\cdots ,q$) of matrix $\mathit{C}{\mathit{C}}^T$, which corresponds to the eigenvectors ${\mathit{\phi }}_i$ (for $i=1,2,\cdots ,q$). By doing so, we gain access to a set of POD bases $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\cdots ,{\mathit{\phi }}_q)$ (with $q\ll s⩽S\ll N$, typically choosing $q=5\sim 8$).

3.2. The Establishment of the Reduced-Dimension Scheme Based on POD

The first $S(S\ll N)$ reduced-dimension weighted explicit finite difference solutions, ${\mathit{U}}_q^n=\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}^n=:\mathbf{\Phi }{\mathit{\theta }}^n(1⩽n⩽S)$, are found in Section 3.1, where ${\mathit{U}}_q^n={\left(u_{q,1}^n,u_{q,2}^n,\cdots ,u_{q,M-1}^n\right)}^T$ and ${\mathit{\theta }}^n={\left({\theta }_1^n,{\theta }_2^n,\cdots ,{\theta }_q^n\right)}^T$. And, we replace ${\mathit{U}}^n$ in Equation $\left(14\right)$ with ${\mathit{U}}_q^n=\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}^n(S+1⩽n⩽N)$ and ${\mathit{U}}_q^n=\mathbf{\Phi }{\mathit{\theta }}^n(S+1⩽n⩽N)$. Then, we can obtain the reduced-dimension weighted explicit finite difference scheme for the space-fractional diffusion equation as follows:

$$\left\{\begin{array}{c}\hfill \begin{array}{cc}\mathbf{\Phi }{\mathit{\theta }}^n=\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}^n,& 1⩽n⩽S,\\ \mathbf{\Phi }{\mathit{\theta }}^n=\mathit{A}\mathbf{\Phi }{\mathit{\theta }}^{n-1}+\tau {\mathit{F}}^{n-1},& S+1⩽n⩽N,\\ {\mathit{U}}_q^n=\mathbf{\Phi }{\mathit{\theta }}^n,& 1⩽n⩽N,\end{array}\end{array}\right.$$

(26)

in which ${\mathit{U}}^n(n=1,2,\cdots ,S)$ is the solution coefficient vectors for the first S columns of Equation (14). The definition of matrix $\mathit{A}$ is given in Equations (15) and (16). We multiply both sides of Equation (26) by ${\mathbf{\Phi }}^T$. Based on the orthonormality of the POD bases, we obtain the reduced-dimension weighted explicit finite difference scheme of unknown vectors ${\mathit{\theta }}^n$ as follows:

$$\left\{\begin{array}{c}\hfill \begin{array}{cc}{\mathit{\theta }}^n={\mathbf{\Phi }}^T{\mathit{U}}^n,& 1⩽n⩽S,\\ {\mathit{\theta }}^n={\mathbf{\Phi }}^T\mathit{A}\mathbf{\Phi }{\mathit{\theta }}^{n-1}+\tau {\mathbf{\Phi }}^T{\mathit{F}}^{n-1},& S+1⩽n⩽N,\\ {\mathit{U}}_q^n=\mathbf{\Phi }{\mathit{\theta }}^n,& 1⩽n⩽N.\end{array}\end{array}\right.$$

(27)

Remark 3.

It is observed that scheme (14) contains $M-1$ unknowns at each time node, whereas scheme (27) has only q unknowns at the same time node $(q\ll M-1)$. As a result, we can see that the reduced-dimension weighted explicit finite difference scheme (27) contains very few degrees of freedom, considerably reduces the CPU running time, and delays the accumulation of computation errors.

4. The Uniqueness, Stabilization, and Error Estimates for the Reduced-Dimension Weighted Explicit Finite Difference Solutions and the Algorithmic Process of the POD Technique

4.1. The Uniqueness, Stabilization, and Error Estimates for the Reduced-Dimension Weighted Explicit Finite Difference Solutions

Before providing the error estimates for the reduced-dimension weighted explicit finite difference solutions, we first give the following norm estimation ${\parallel ·\parallel }_2$ of matrix $\mathit{A}$:

Lemma 3.

According to Lemma 1, $B_i>0$, when $1+B_i\left(1-ϵ\right)-B_iϵ\alpha >0$, we have

$${\parallel \mathit{A}\parallel }_2⩽\sqrt{M-1}.$$

(28)

Proof. 

when $1+B_i\left(1-ϵ\right)-B_iϵ\alpha >0$, we have

$$\begin{array}{cc}{\displaystyle \sum _{k=1}^{M-1}\left|A_{i,k}\right|}\hfill & {\displaystyle =B_iϵ{\omega }_0^{\left(\alpha \right)}+1+B_i\left(1-ϵ\right){\omega }_0^{\left(\alpha \right)}+B_iϵ{\omega }_1^{\left(\alpha \right)}+B_i\left(1-ϵ\right)\sum _{k=1}^{M-1}{\omega }_k^{\left(\alpha \right)}+B_iϵ\sum _{k=2}^M{\omega }_k^{\left(\alpha \right)}}\hfill \\ \hfill & {\displaystyle =1+B_i\left(1-ϵ\right)\sum _{k=0}^{M-1}{\omega }_k^{\left(\alpha \right)}+B_iϵ\sum _{k=0}^M{\omega }_k^{\left(\alpha \right)}}\hfill \\ \hfill & ⩽1,\hfill \end{array}$$

and thus, ${\displaystyle {\parallel \mathit{A}\parallel }_{\infty }=\underset{1⩽i⩽M-1}{max}\sum _{k=1}^{M-1}\left|A_{i,k}\right|⩽1}$.

On the basis of the relation $\frac{1}{\sqrt{n}}{∥\mathit{A}∥}_{\infty }⩽{∥\mathit{A}∥}_2⩽\sqrt{n}{∥\mathit{A}∥}_{\infty }$, where n represents the dimension of matrix $\mathit{A}$ (see [39]), we obtain

$${∥\mathit{A}∥}_2⩽\sqrt{M-1}.$$

□

Thus, the uniqueness, stabilization, and error estimates of the weighted explicit finite difference solutions are stated in the following theorem.

Theorem 3.

Under the same conditions as Theorem 2, the set of solutions ${\left\{{\mathit{U}}_q^n\right\}}_{n=1}^N$ for the reduced-dimension weighted explicit finite difference scheme (27) is unique, stable, and has the following error estimate with respect to the set of solutions ${\left\{{\mathit{U}}^n\right\}}_{n=1}^N$ for the weighted explicit finite difference scheme (14):

$${∥{\mathit{U}}^n-{\mathit{U}}_q^n∥}_2⩽E\left(n\right)\sqrt{{\gamma }_{q+1}},n=1,2,\cdots ,N.$$

(29)

Furthermore, the error between the exact solutions $\mathit{U}\left(t_n\right)=[u(x_1,t_n),u(x_2,t_n),\cdots$, $u(x_{M-1},$$t_n{\left)\right]}^T$ $(n=1,2,\cdots ,N)$ of Equation (1) and the set of solutions ${\left\{{\mathit{U}}_q^n\right\}}_{n=1}^N$ for the reduced-dimension weighted explicit finite difference scheme (27) satisfies the following error estimate:

$${∥\mathit{U}\left(t_n\right)-{\mathit{U}}_q^n∥}_2⩽\mathit{O}\left(\tau +h^2+E\left(n\right)\sqrt{{\gamma }_{q+1}}\right),n=1,2,\cdots ,N,$$

(30)

where $E\left(n\right)=1\left(0⩽n⩽S\right)$ and $E\left(n\right)={\left(\sqrt{M-1}\right)}^{n-S}\left(S+1⩽n⩽N\right)$.

Proof of Theorem 3. 

(1)

The uniqueness of the reduced-dimension weighted explicit finite difference solutions for Equation (27)

First, it is established that the set of solutions ${\left\{{\mathit{U}}^n\right\}}_{n=1}^S$, obtained from Equation (14), is unique. Consequently, this ensures that the set of solutions ${\left\{{\mathit{U}}_q^n\right\}}_{n=1}^S$, obtained from Equation (27), is unique as well.

For $S+1⩽n⩽N$, and ${\mathit{U}}_q^n=\mathbf{\Phi }{\mathit{\theta }}^n$, the reduced-dimension weighted explicit finite difference scheme (26) can be reformulated into the following equation:

$${\mathit{U}}_q^n=\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}^n,S+1⩽n⩽N,$$

(31)

$${\mathit{U}}_q^n={\mathit{AU}}_q^{n-1}+\tau {\mathit{F}}^{n-1},S+1⩽n⩽N.$$

(32)

Since Equations (31) and (32) have the same form as (14) when $S+1⩽n⩽N$, and given that Equation (14) possesses a unique set of solutions ${\left\{{\mathit{U}}^n\right\}}_{n=S+1}^N$, it follows that Equations (31) and (32) also possess a unique set of solutions ${\left\{{\mathit{U}}_q^n\right\}}_{n=S+1}^N$.

(2)

The stability of the reduced-dimension weighted explicit finite difference solutions for (27)

When $1⩽n⩽S$, because of the orthonormality of the vectors in $\mathbf{\Phi }$, we have

$${∥{\mathit{U}}_q^n∥}_2={∥\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}^n∥}_2⩽c{\parallel {\mathit{U}}^n\parallel }_2.$$

(33)

Due to the stability of the set of solutions ${\left\{{\mathit{U}}^n\right\}}_{n=1}^N$ established in Theorem (2), we can infer that the set of solutions ${\left\{{\mathit{U}}_q^n\right\}}_{n=1}^N$ also exhibits stability.

Therefore, utilizing the Cauchy–Schwarz inequality, from (32), we obtain

$${\parallel {\mathit{U}}_q^n\parallel }_2⩽{\parallel \mathit{A}\parallel }_2\parallel {\mathit{U}}_q^{n-1}{\parallel }_2+\tau {\parallel {\mathit{F}}^{n-1}\parallel }_2,S+1⩽n⩽N.$$

(34)

According to Lemma 3 and scheme (14), we have

$$\begin{array}{cc}\hfill \parallel {\mathit{U}}^n{\parallel }_2& ⩽{\parallel \mathit{A}\parallel }_2\parallel {\mathit{U}}^{n-1}{\parallel }_2+\tau {\parallel {\mathit{F}}^{n-1}\parallel }_2\hfill \\ \hfill & ⩽\sqrt{M-1}\parallel {\mathit{U}}^{n-1}{\parallel }_2+\tau {\parallel {\mathit{F}}^{n-1}\parallel }_2\hfill \\ \hfill & ⩽{\left(\sqrt{M-1}\right)}^n\parallel {\mathit{U}}^0{\parallel }_2+\tau \sum _{i=1}^n{\parallel {\mathit{F}}^{i-1}\parallel }_2⩽c,1⩽n⩽N.\hfill \end{array}$$

(35)

From (34), using (33) and (35), we obtain the following result:

$$\begin{array}{cc}\hfill \parallel {\mathit{U}}_q^n{\parallel }_2& ⩽{\left(\sqrt{M-1}\right)}^{n-S}\parallel {\mathit{U}}_q^S{\parallel }_2+\tau \sum _{i=S+1}^n{\parallel {\mathit{F}}^{i-1}\parallel }_2\hfill \\ \hfill & ⩽c\parallel {\mathit{U}}^S{\parallel }_2+\tau \sum _{i=S+1}^n{\parallel {\mathit{F}}^{i-1}\parallel }_2\hfill \\ \hfill & ⩽c\left(\parallel {\mathit{U}}^0{\parallel }_2+\tau \sum _{i=1}^n{\parallel {\mathit{F}}^{i-1}\parallel }_2\right)⩽c,S+1⩽n⩽N.\hfill \end{array}$$

(36)

This means that ${\left\{{\mathit{U}}_q^n\right\}}_{n=S+1}^N$ is also stable. Thus, the set of reduced-dimension weighted explicit finite difference solutions ${\left\{{\mathit{U}}_q^n\right\}}_{n=1}^N$ for Equation (27) is stable.

(3)

The error estimates of the reduced-dimension weighted explicit finite difference solutions

When $n=1,2,\cdots ,S$, the following error estimate can be derived from Equation (25):

$${∥{\mathit{U}}^n-{\mathit{U}}_q^n∥}_2={∥{\mathit{U}}^n-\mathbf{\Phi }{\mathbf{\Phi }}^T{\mathit{U}}^n∥}_2⩽\sqrt{{\gamma }_{q+1}},1⩽n⩽S.$$

(37)

Subtracting Equation (32) from Equation (14) and then computing the norm, we have

$${∥{\mathit{U}}^n-{\mathit{U}}_q^n∥}_2⩽{∥\mathit{A}∥}_2{∥{\mathit{U}}^{n-1}-{\mathit{U}}_q^{n-1}∥}_2.$$

(38)

From inequality (38), we obtain the following result:

$$\begin{array}{cc}\hfill & {∥{\mathit{U}}^{S+1}-{\mathit{U}}_q^{S+1}∥}_2⩽{∥\mathit{A}∥}_2{∥{\mathit{U}}^S-{\mathit{U}}_q^S∥}_2,\hfill \\ \hfill & {∥{\mathit{U}}^{S+2}-{\mathit{U}}_q^{S+2}∥}_2⩽{∥\mathit{A}∥}_2{∥{\mathit{U}}^{S+1}-{\mathit{U}}_q^{S+1}∥}_2⩽{∥\mathit{A}∥}_2^2{∥{\mathit{U}}^S-{\mathit{U}}_q^S∥}_2,\hfill \\ \hfill & ⋮\hfill \\ \hfill & {∥{\mathit{U}}^n-{\mathit{U}}_q^n∥}_2⩽{∥\mathit{A}∥}_2{∥{\mathit{U}}^{n-1}-{\mathit{U}}_q^{n-1}∥}_2⩽{∥\mathit{A}∥}_2^{n-S}{∥{\mathit{U}}^S-{\mathit{U}}_q^S∥}_2.\hfill \end{array}$$

(39)

According to Lemma 3 and Equation (37), we deduce the following:

$$\begin{array}{cc}{∥{\mathit{U}}^n-{\mathit{U}}_q^n∥}_2\hfill & ⩽{∥\mathit{A}∥}_2^{n-S}\sqrt{{\gamma }_{q+1}}\hfill \\ \hfill & ⩽{\left(\sqrt{M-1}\right)}^{n-S}\sqrt{{\gamma }_{q+1}},n=S+1,S+2,\cdots ,N.\hfill \end{array}$$

(40)

That is,

$${∥{\mathit{U}}^n-{\mathit{U}}_q^n∥}_2⩽E\left(n\right)\sqrt{{\gamma }_{q+1}},n=S+1,S+2,\cdots ,N,$$

(41)

where $E\left(n\right)={\left(\sqrt{M-1}\right)}^{n-S}\left(S+1⩽n⩽N\right)$. Furthermore, utilizing Theorem 2 and inequality (41), we derive the following conclusion:

$${∥\mathit{U}(x_i,t_n)-{\mathit{U}}_q^n∥}_2⩽\mathit{O}\left(\tau +h^2+{\left(\sqrt{M-1}\right)}^{n-S}\sqrt{{\gamma }_{q+1}}\right).$$

(42)

The conclusion of Theorem 3 is proven.

□

Remark 4.

It is evident that the error factor $E\left(n\right)\sqrt{{\gamma }_{q+1}}$ is produced by the reduced dimension for the weighted explicit finite difference scheme via the POD technique. This factor serves as a recommendation for choosing the number q of POD basis vectors; that is, if we choose the number q of POD basis vectors to satisfy $E\left(n\right)\sqrt{{\gamma }_{q+1}}<\tau +h^2$, we can obtain reduced-dimension solutions with the desired accuracy. Many numerical studies have suggested that the eigenvalues ${\gamma }_i(i=1,2,\cdots ,s)$ commonly decrease rapidly to near zero. Generally, when $q=5\sim 8$, $\sqrt{{\gamma }_{q+1}}$ is already minimum and satisfies $E\left(n\right)\sqrt{{\gamma }_{q+1}}⩽\tau +h^2$.

4.2. The Implementation of the Algorithm of the POD Reduced-Dimension Technique

The algorithmic process for implementing the reduced-dimension weighted explicit finite difference scheme of Equation (1) consists of the following five steps.

• Step 1. Take the first S weighted explicit finite difference solutions for the weighted explicit finite difference scheme as snapshots ${\mathit{U}}^i$ $(i=1,2,\cdots ,S,\mathrm{generally}S=20)$:

  $${\mathit{U}}^n={\mathit{AU}}^{n-1}+\tau {\mathit{F}}^{n-1},n=1,2,\cdots ,S,$$

  satisfying the following initial value conditions:

  $${\mathit{U}}^0={[u_1^0,u_2^0,\cdots ,u_{M-1}^0]}^T,u_i^0={\varphi }_0(a+ih),i=1,2,\cdots ,M-1.$$
  Subsequently, we construct the snapshot matrix $\mathit{C}$.
• Step 2. For the singular value decomposition for the snapshot matrix $\mathit{C}$, find the eigenvalues ${\gamma }_1⩾{\gamma }_2⩾\cdots ⩾{\gamma }_s>0$ (s = rankC) and eigenvectors ${\mathit{\psi }}_j$ $(j=1,2,\cdots ,S)$ of matrix ${\mathit{C}}^T\mathit{C}$.
• Step 3. According to the inequality $\sqrt{{\gamma }_{q+1}}⩽\mathit{O}\left(\tau +h^2\right)$, determine the number $q(q⩽s)$ of POD bases. In addition, create the POD base $\mathbf{\Phi }=({\mathit{\phi }}_1,{\mathit{\phi }}_2,\cdots ,{\mathit{\phi }}_q)$ (where ${\mathit{\phi }}_i=\mathit{C}{\mathit{\psi }}_i/\sqrt{{\gamma }_i}$ ($i=1,2,\cdots ,q$)) utilizing the approach shown in Section 3.1.
• Step 4. Obtain the reduced-dimension solution vectors ${\mathit{U}}_q^n={[u_{q,1}^n,u_{q,2}^n,\cdots ,u_{q,M-1}^n]}^T$ by solving the reduced-dimension weighted explicit finite difference scheme:

  $$\left\{\begin{array}{c}\hfill \begin{array}{cc}{\mathit{\theta }}^n={\mathbf{\Phi }}^T{\mathit{U}}^n,& 1⩽n⩽S,\\ {\mathit{\theta }}^n={\mathbf{\Phi }}^T\mathit{A}\mathbf{\Phi }{\mathit{\theta }}^{n-1}+\tau {\mathbf{\Phi }}^T{\mathit{F}}^{n-1},& S+1⩽n⩽N,\\ {\mathit{U}}_q^n=\mathbf{\Phi }{\mathit{\theta }}^n,& 1⩽n⩽N,\end{array}\end{array}\right.$$

  which contains only $q(\mathrm{usually}q=5\sim 8)$ unknowns.
• Step 5. The calculation is completed when the error is satisfied. Otherwise, select ${\mathit{U}}^1={\mathit{U}}_q^{n(n-S)},{\mathit{U}}^2={\mathit{U}}_q^{n(n-S+1)},\cdots ,{\mathit{U}}^S={\mathit{U}}_q^{n(n-1)}$, update the POD bases as needed, and return to step 2.

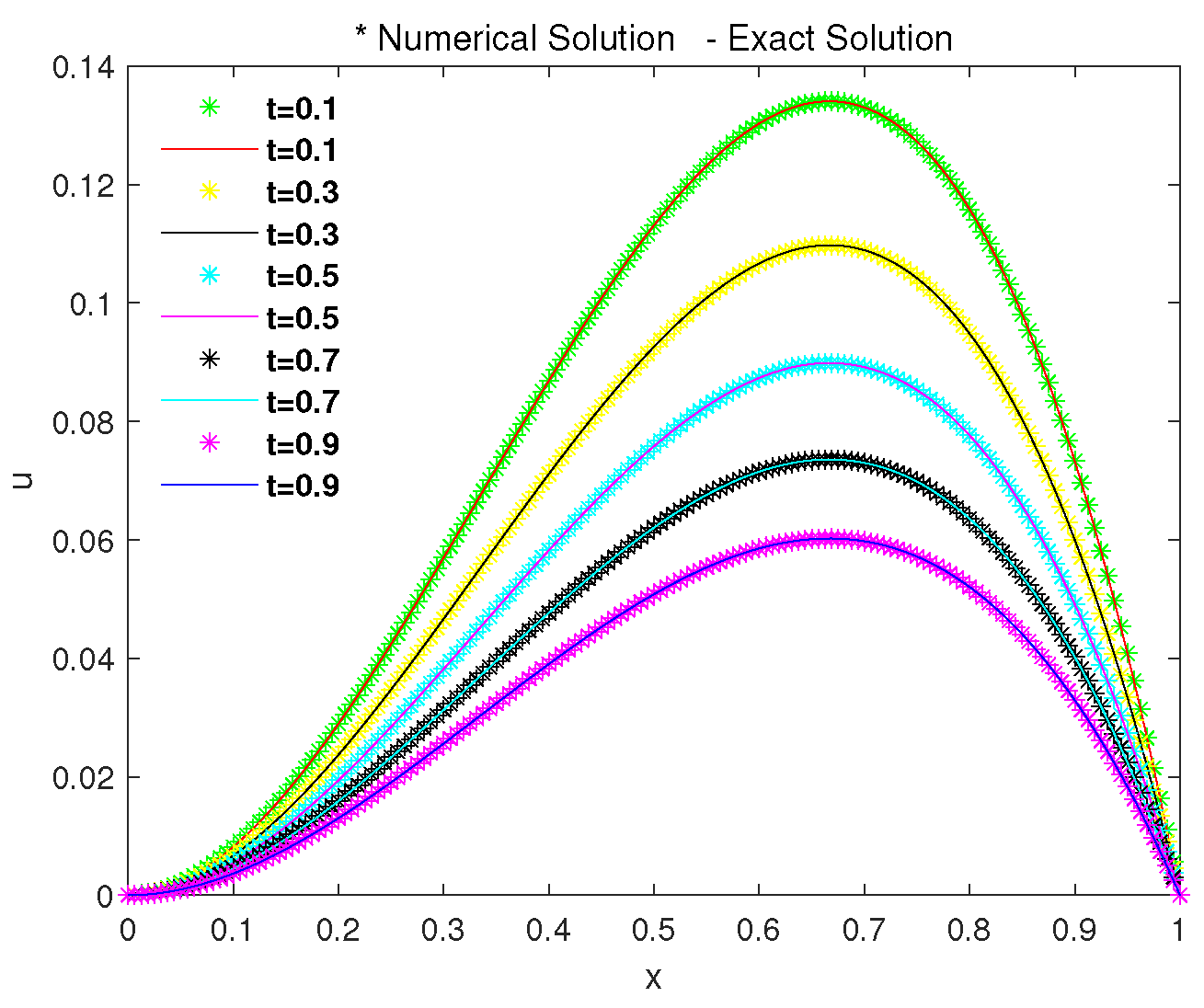
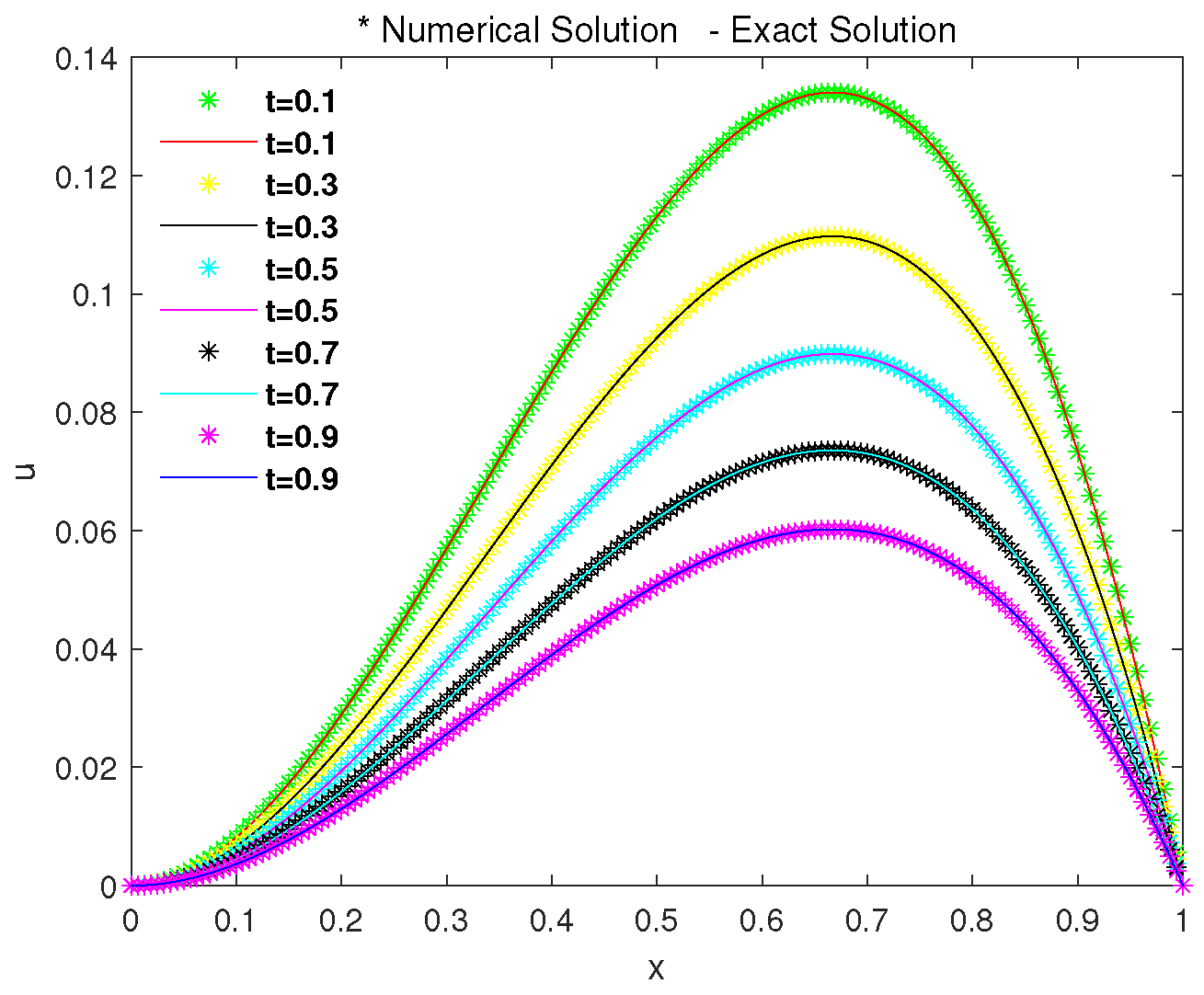
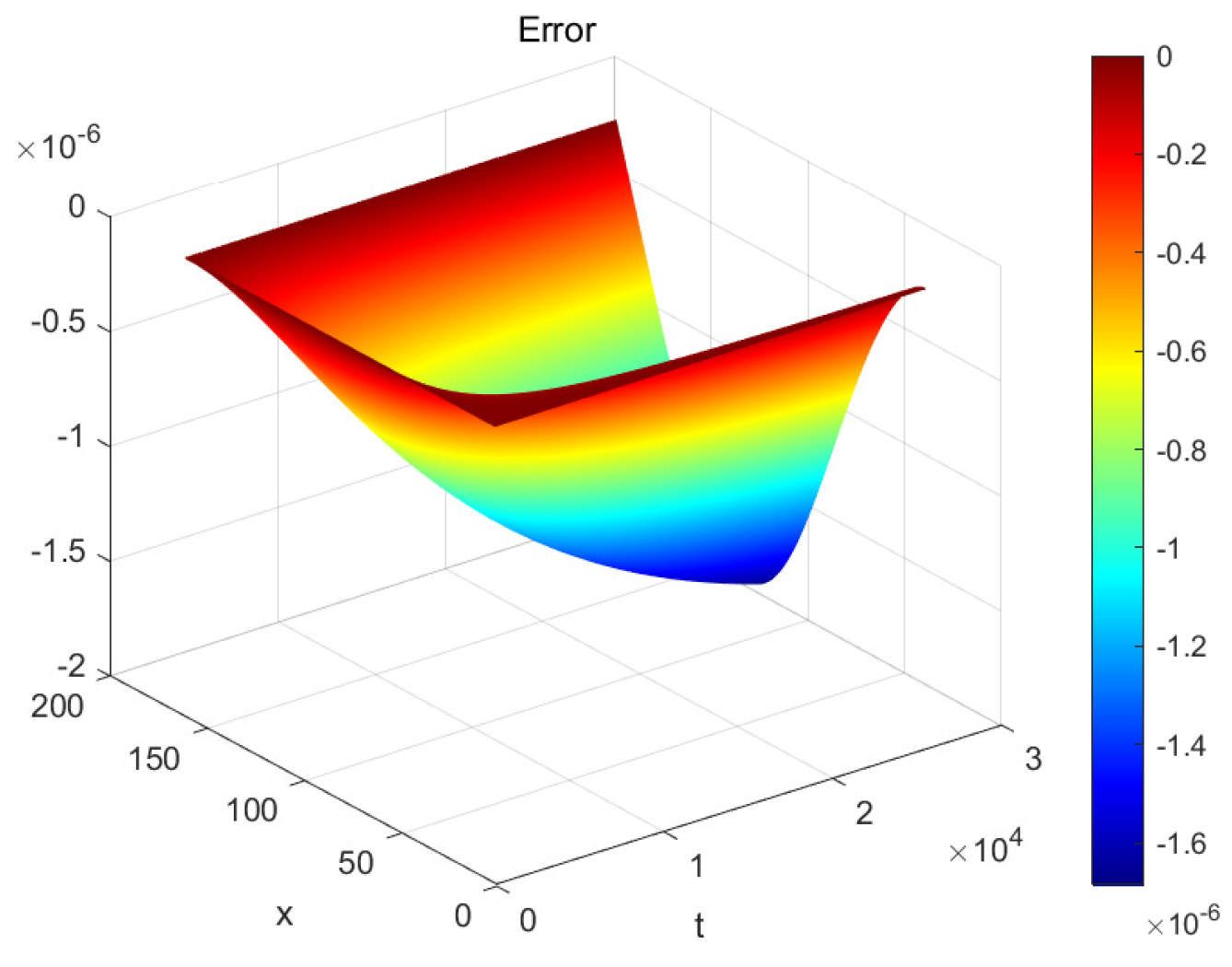
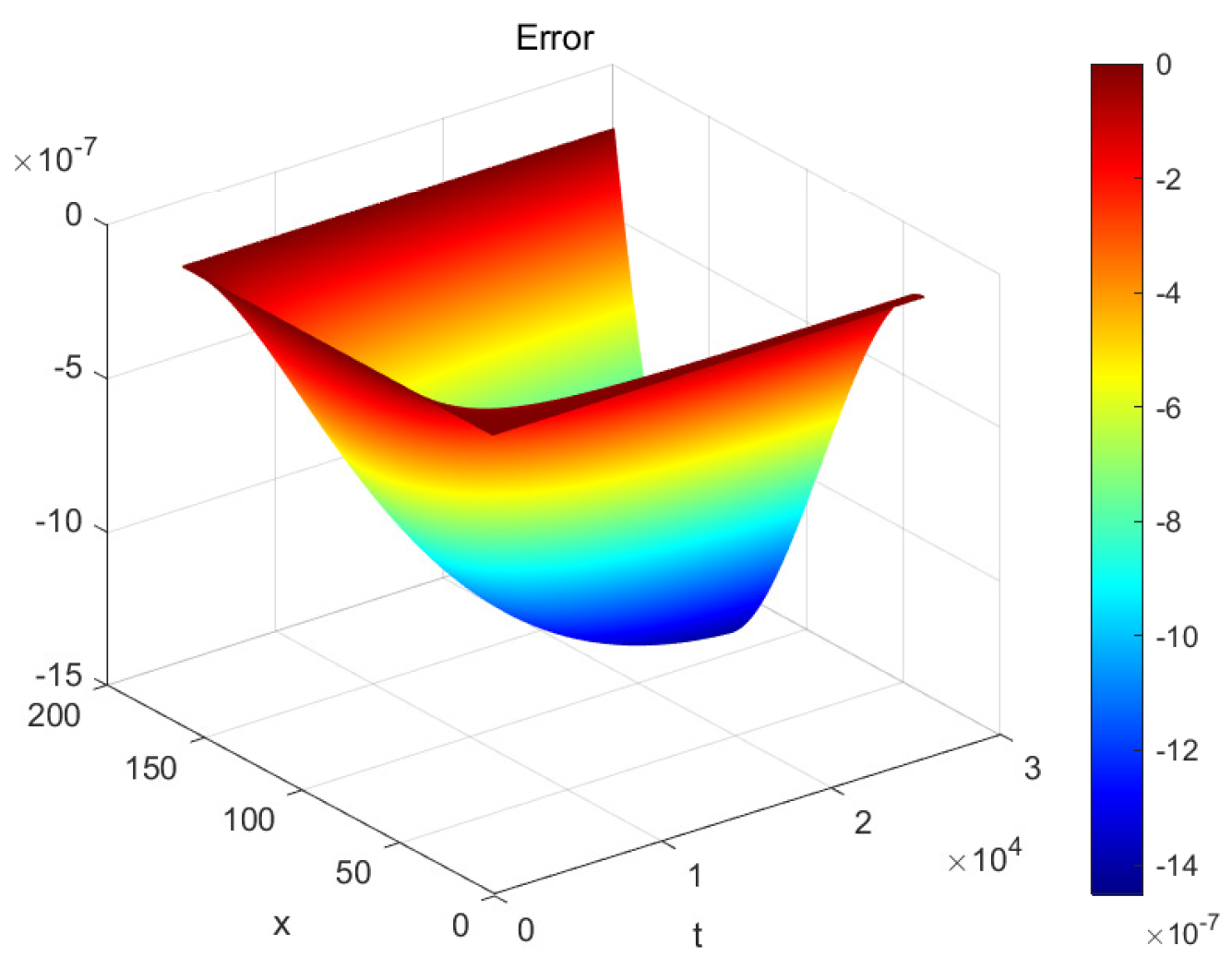
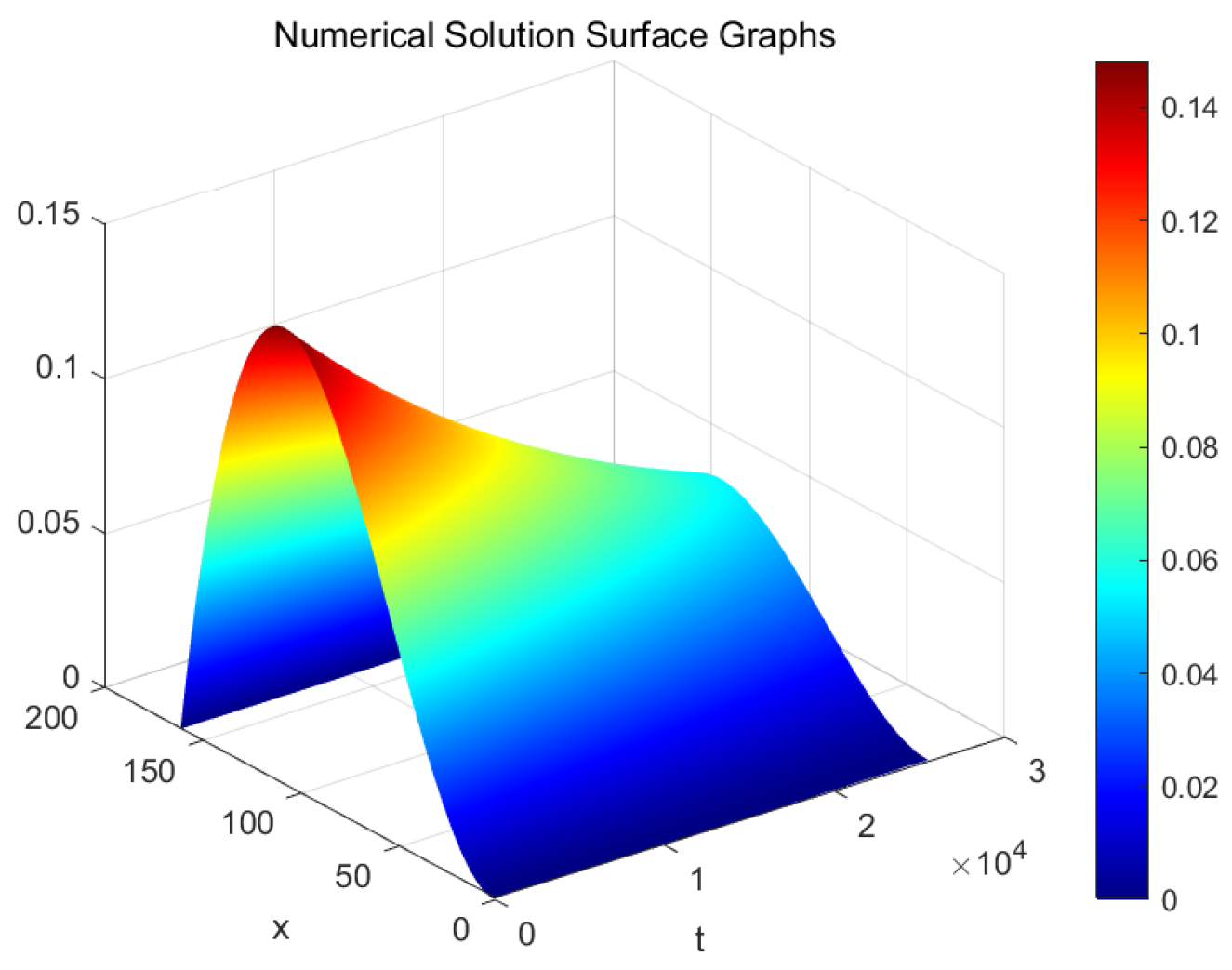
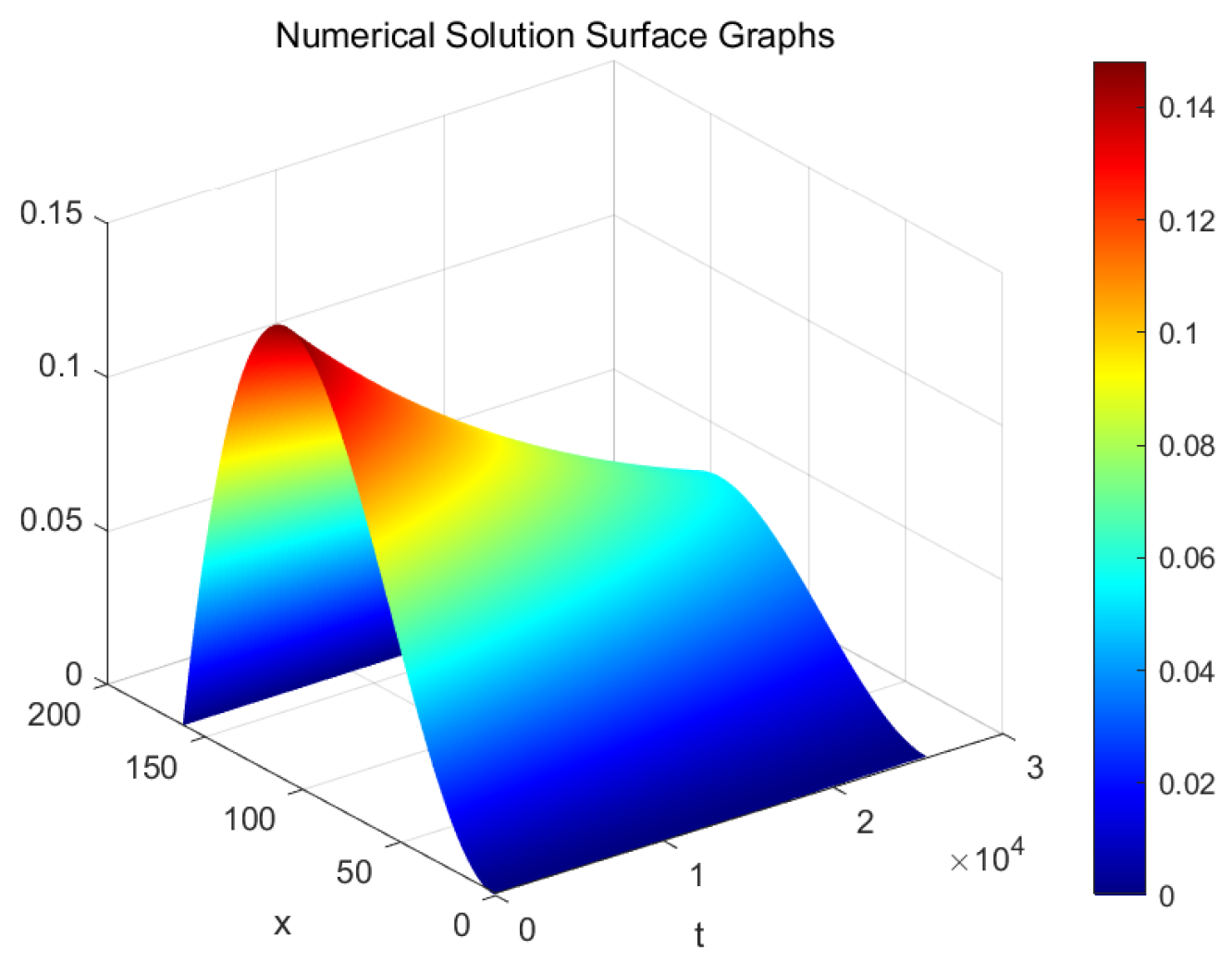
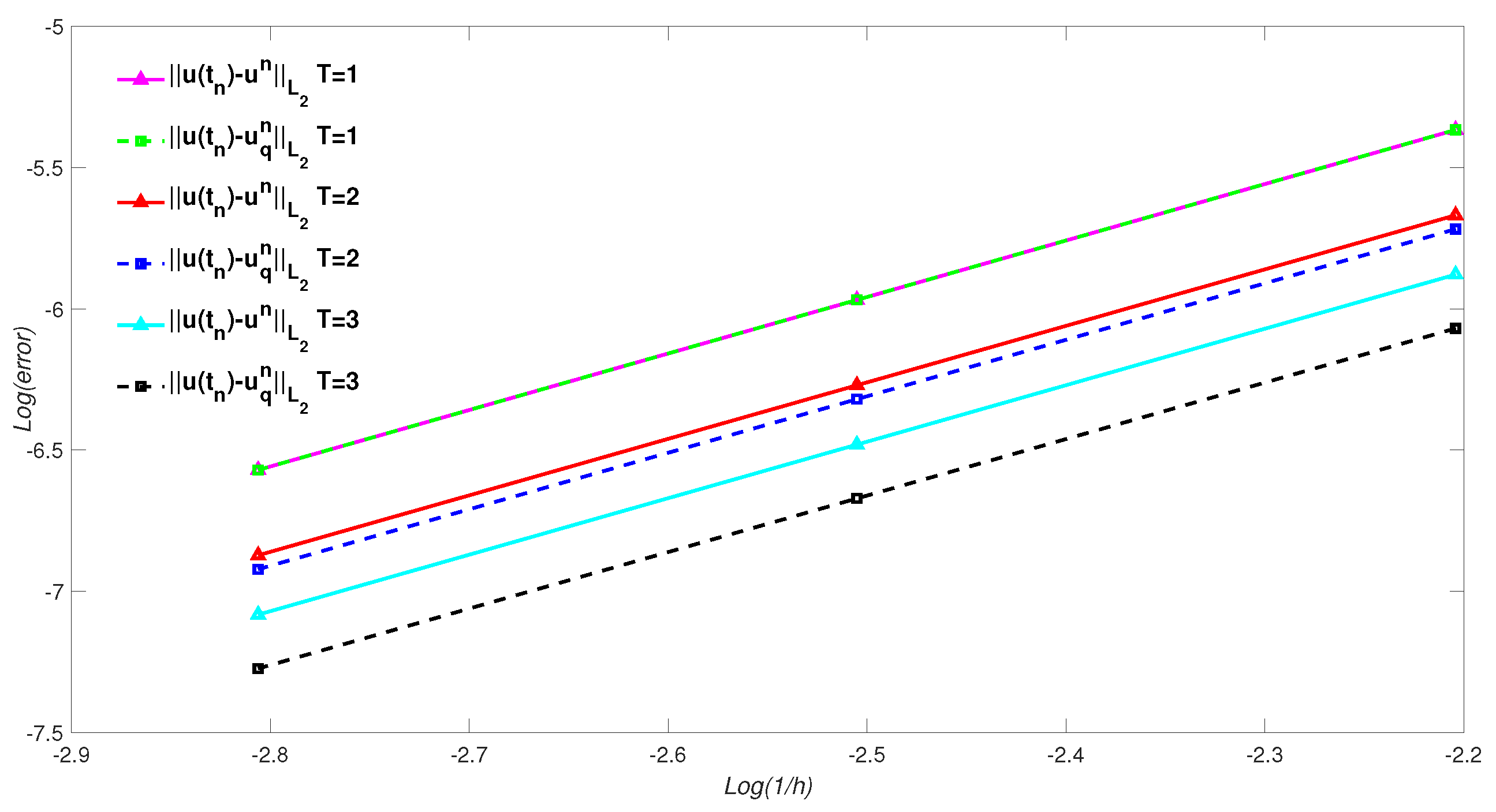
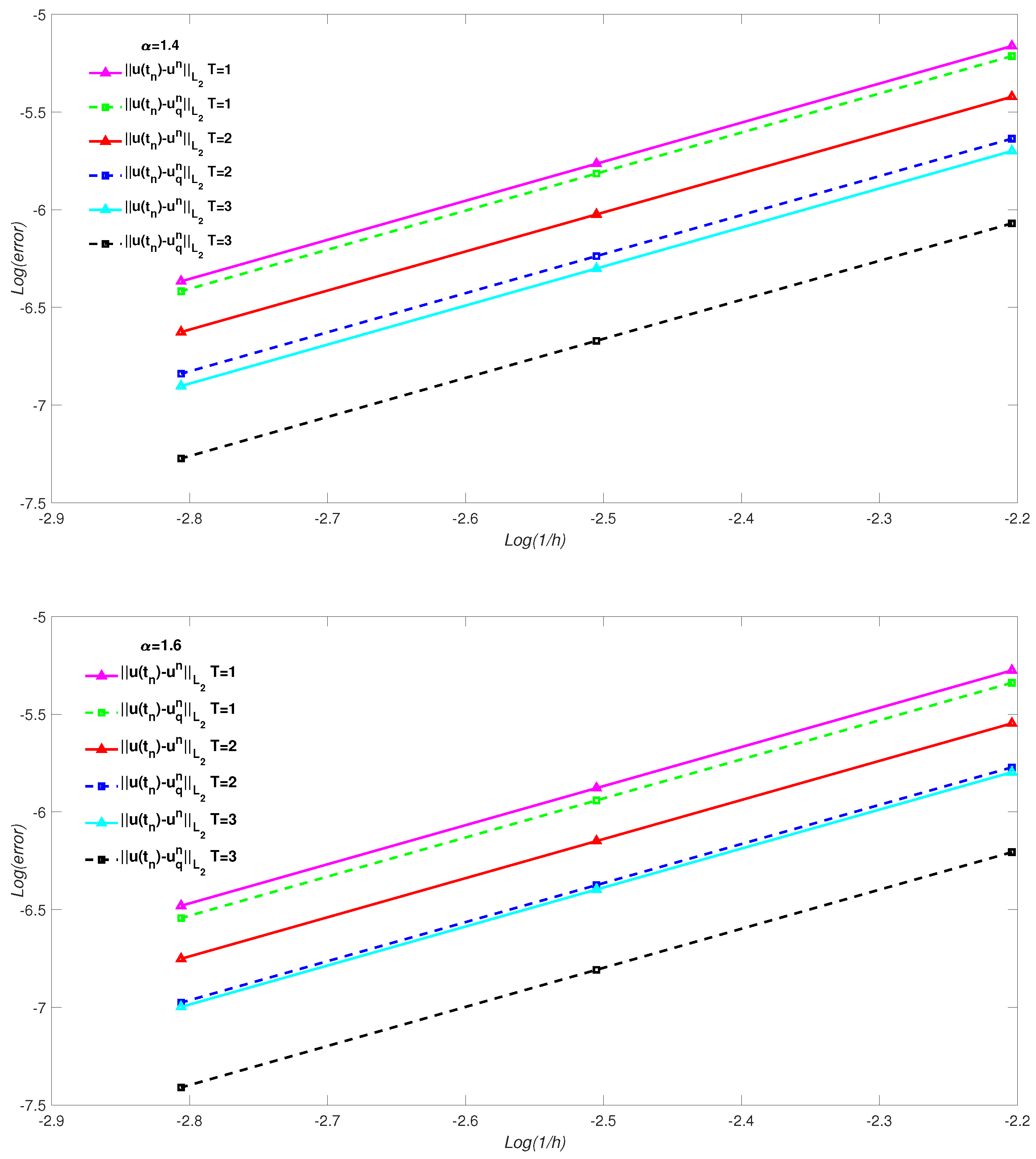
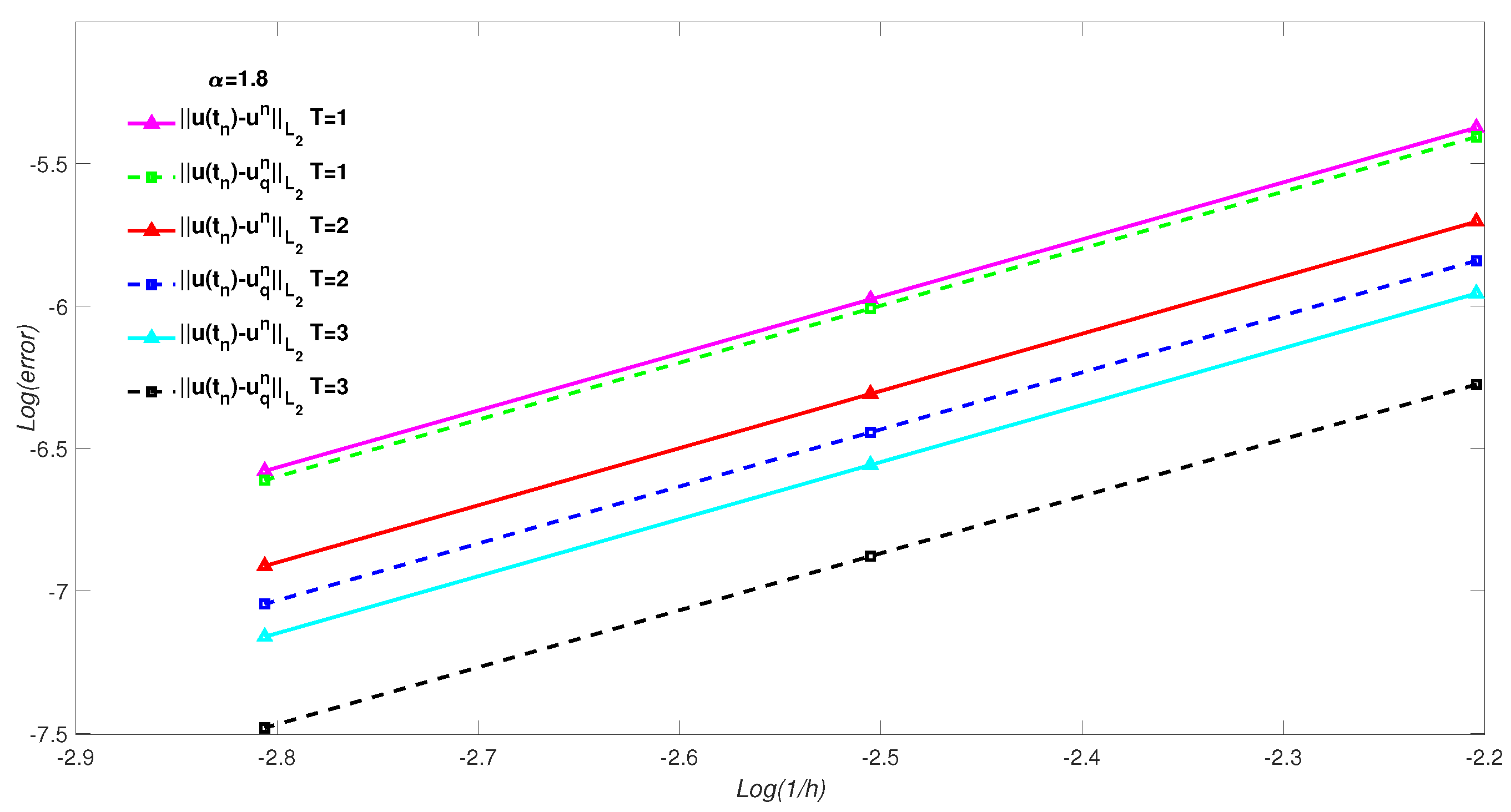
5. Numerical Simulation

To demonstrate the practicality and effectiveness of the dimension-reduced weighted finite difference approach on space-fractional diffusion equations, we examine two such diffusion issues.

Example 1.

Consider the following initial boundary value problems:

$$\left\{\begin{array}{cc}\frac{\partial u(x,t)}{\partial t}=d\left(x\right)\frac{{\partial }^{\alpha }u(x,t)}{\partial x^{\alpha }}+f(x,t),\hfill & x\in [0,1],t\in (0,T],\hfill \\ u(x,0)=(1-x)x^2,\hfill & x\in [0,1],\hfill \\ u(0,t)=u(1,t)=0,\hfill & t\in (0,T],\hfill \end{array}\right.$$

(43)

in which the diffusion coefficient $d\left(x\right)=\frac{\Gamma \left(2.2\right)}{6}{x}^{2.8}$ is fixed, and the exact solution is $u(x,t)=(1-x)e^{-t}{x}^2$.

The source term for the space-fractional diffusion equation is presented as follows:

$$f(x,t)=-e^{-t}{x}^2(1-x)-\frac{\Gamma \left(2.2\right)}{6}{x}^{2.8}{e}^{-t}\left(\frac{\Gamma \left(3\right)}{\Gamma (3-\alpha )}{x}^{2-\alpha }-\frac{\Gamma \left(4\right)}{\Gamma (4-\alpha )}{x}^{3-\alpha }\right),$$

which uses the specific formula

$$\frac{{\partial }^{\alpha }}{\partial x^{\alpha }}\left[x^{\beta }\right]=\frac{\Gamma (\beta +1)}{\Gamma (\beta +1-\alpha )}{x}^{\beta -\alpha }.$$

(44)

Setting the space step size to $h=\frac{1}{160}$, the time step size to $\tau =\frac{1}{\mathrm{25,600}}$, and $\alpha =1.8$, Figure 1 shows the comparison between the exact solution (line) and the numerical solution (star) of the weighted explicit finite difference method at $T=1$ (where $t=0.1$ to $t=0.9$ with an interval of $0.2$). Figure 2 shows a comparison between the analytical solution (line) and the numerical solution (star) of the reduced-dimension weighted explicit finite difference method for Equation (45). In Figure 1 and Figure 2, it can be observed that the numerical solution of Equation (45) is in good agreement with the analytical solution, which further demonstrates the effectiveness of the method.

Figure 3 and Figure 4 present the three-dimensional error figures for the two schemes. Figure 5 and Figure 6, respectively, illustrate surface graphs representing the relationship between the numerical solution and the space–time axis for the two methods. Furthermore, Figure 3 and Figure 4 demonstrate that the error between the exact solution and the numerical solutions for both the POD reduced-dimension weighted explicit finite difference method and the weighted explicit finite difference method can reach ${10}^{-6}$ when the space step size is $h=\frac{1}{160}$, the time step size is $\tau =h^2$, and $\alpha =1.8$. This observation is consistent with the numerical results presented in

Table 1. Comparison of POD method and finite difference method when $T=1$.

		Weighted Explicit Method			POD Method
$\mathbf{h}$	$\mathbf{\tau }$	$\mathbf{\parallel }\mathbf{u}\mathbf{\left(}{\mathbf{t}}_{\mathbf{n}}\mathbf{\right)}\mathbf{-}{\mathbf{u}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)	$\mathbf{\parallel }\mathbf{u}\left({\mathbf{t}}_{\mathbf{n}}\right)\mathbf{-}{\mathbf{u}}_{\mathbf{q}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)
${\displaystyle \frac{1}{160}}$	${\displaystyle \frac{1}{\mathrm{25,600}}}$	4.3029 × 10−6	–	1.0	4.3043 × 10−6	–	0.1
${\displaystyle \frac{1}{320}}$	${\displaystyle \frac{1}{\mathrm{102,400}}}$	1.0757 × 10−6	2.0000	7.6	1.0760 × 10−6	2.0001	1.0
${\displaystyle \frac{1}{640}}$	${\displaystyle \frac{1}{\mathrm{409,600}}}$	2.6892 × 10−7	2.0000	76.0	2.6899 × 10−7	2.0001	7.1

.

To verify that the reduced-dimension weighted explicit finite difference method ensures sufficient accuracy, reduces degrees of freedom, saves CPU computation time, and improves computational efficiency, we next analyze the error, convergence order, and CPU running time of Equation (45) at $T=1$, $T=2$, and $T=3$.

Since the error order is $\mathit{O}\left(\tau +h^2\right)$, the relationship $\tau =h^2$ is exploited in the calculation to compensate for the errors caused by the discrete time and space directions. For this purpose, the time step size is set to $\tau =h^2$, and the space grid parameter h takes the values $\frac{1}{160}$, $\frac{1}{320}$, and $\frac{1}{640}$. Table 1 gives the errors, convergence orders, and CPU running time (in seconds) of $\parallel u\left(t_n\right)-u^n\parallel$ and $\parallel u\left(t_n\right)-u_q^n\parallel$ in the $L_2$ norm for the weighted explicit finite difference approach and the reduced-dimension weighted explicit finite difference method, with a final time of $T=1$ and a parameter value of $\alpha =1.8$. The convergence rates of $|u\left(t_n\right)-u^n|$ and $|u\left(t_n\right)-u_q^n|$, as shown in Table 1, are nearly at the second order under the $L_2$ norm. Notably, the reduced-dimension weighted explicit finite difference method, which uses only six degrees of freedom at each time node, demonstrates a significant advantage in terms of computational efficiency. Furthermore, Table 1 also shows that the CPU running time for the weighted explicit finite difference method is 10 times that of the POD reduced-dimension weighted explicit finite difference method.

Building on the findings in Table 1,

Table 2. Comparison of POD method and finite difference method when $T=2$.

		Weighted Explicit Method			POD Method
$\mathbf{h}$	$\mathbf{\tau }$	$\mathbf{\parallel }\mathbf{u}\mathbf{\left(}{\mathbf{t}}_{\mathbf{n}}\mathbf{\right)}\mathbf{-}{\mathbf{u}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)	$\mathbf{\parallel }\mathbf{u}\left({\mathbf{t}}_{\mathbf{n}}\right)\mathbf{-}{\mathbf{u}}_{\mathbf{q}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)
${\displaystyle \frac{1}{160}}$	${\displaystyle \frac{1}{\mathrm{25,600}}}$	2.1459 × 10−6	–	1.9	1.9156 × 10−6	–	0.2
${\displaystyle \frac{1}{320}}$	${\displaystyle \frac{1}{\mathrm{102,400}}}$	5.3644 × 10−7	2.0001	21.0	4.7887 × 10−7	2.0001	1.9
${\displaystyle \frac{1}{640}}$	${\displaystyle \frac{1}{\mathrm{409,600}}}$	1.3411 × 10−7	2.0000	155.5	1.1970 × 10−7	2.0002	15.2

and

Table 3. Comparison of POD method and finite difference method when $T=3$.

		Weighted Explicit Method			POD Method
$\mathbf{h}$	$\mathbf{\tau }$	$\mathbf{\parallel }\mathbf{u}\mathbf{\left(}{\mathbf{t}}_{\mathbf{n}}\mathbf{\right)}\mathbf{-}{\mathbf{u}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)	$\mathbf{\parallel }\mathbf{u}\left({\mathbf{t}}_{\mathbf{n}}\right)\mathbf{-}{\mathbf{u}}_{\mathbf{q}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)
${\displaystyle \frac{1}{160}}$	${\displaystyle \frac{1}{\mathrm{25,600}}}$	1.3229 × 10−6	–	2.9	8.5270 × 10−7	–	0.3
${\displaystyle \frac{1}{320}}$	${\displaystyle \frac{1}{\mathrm{102,400}}}$	3.3069 × 10−7	2.0002	31.0	2.1315 × 10−7	2.0002	2.9
${\displaystyle \frac{1}{640}}$	${\displaystyle \frac{1}{\mathrm{409,600}}}$	8.2668 × 10−8	2.0001	354.1	5.3279 × 10−8	2.0002	20.6

extend the analysis to different final times, $T=2$ and $T=3$, respectively. They provide a detailed comparison of the errors, convergence rates, and CPU running times for both the weighted explicit finite difference method and the reduced-dimension weighted explicit finite difference method. Importantly, Table 3 indicates that the CPU running time for the weighted explicit finite difference method ranges from 10 to 17 times that of the POD reduced-dimension method. Furthermore, when the space step size is $h=\frac{1}{640}$, the numerical errors are consistent with theoretical calculations, both attaining an accuracy of $\mathit{O}\left({10}^{-8}\right)$. Nearly second-order convergence rates can also be observed in Table 3. These tables provide a comprehensive comparison of the errors, convergence rates, and CPU running times for both the weighted explicit finite difference method and the reduced-dimension variant. The results further substantiate the efficiency and accuracy of the reduced-dimension method.

Continuing the analysis, when the space step size h decreases, the convergence rate of errors $\parallel u\left(t_n\right)-u^n\parallel$ and $\parallel u\left(t_n\right)-u_q^n\parallel$, as indicated in

Table 4. Comparison of POD method and finite difference method.

T	$\mathit{\alpha }$	h	Weighted Explicit Method			POD Method
			$\mathbf{\parallel }\mathbf{u}\mathbf{\left(}{\mathbf{t}}_{\mathbf{n}}\mathbf{\right)}\mathbf{-}{\mathbf{u}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)	$\mathbf{\parallel }\mathbf{u}\left({\mathbf{t}}_{\mathbf{n}}\right)\mathbf{-}{\mathbf{u}}_{\mathbf{q}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)
1	1.1	${\displaystyle \frac{1}{160}}$	5.4838 × 10−6	–	1.0	5.3392 × 10−6	–	0.1
		${\displaystyle \frac{1}{320}}$	1.3709 × 10−6	2.0000	8.1	1.3348 × 10−6	2.0000	1.0
		${\displaystyle \frac{1}{640}}$	3.4273 × 10−7	2.0000	69.4	3.3369 × 10−7	2.0000	7.2
	1.4	${\displaystyle \frac{1}{160}}$	4.9449 × 10−6	–	1.0	5.0093 × 10−6	–	0.1
		${\displaystyle \frac{1}{320}}$	1.2362 × 10−6	2.0001	8.2	1.2523 × 10−6	2.0001	1.0
		${\displaystyle \frac{1}{640}}$	3.0904 × 10−7	2.0000	69.8	3.1304 × 10−7	2.0001	7.3
2	1.1	${\displaystyle \frac{1}{160}}$	3.6151 × 10−6	–	2.1	2.3787 × 10−6	–	0.2
		${\displaystyle \frac{1}{320}}$	9.0376 × 10−7	2.0000	16.3	5.9458 × 10−7	2.0002	2.0
		${\displaystyle \frac{1}{640}}$	2.2594 × 10−7	2.0000	101.1	1.4864 × 10−7	2.0001	14.5
	1.4	${\displaystyle \frac{1}{160}}$	2.8961 × 10−6	–	2.1	2.9586 × 10−6	–	0.2
		${\displaystyle \frac{1}{320}}$	7.2397 × 10−7	2.0001	16.9	7.3957 × 10−7	2.0002	2.0
		${\displaystyle \frac{1}{640}}$	1.8099 × 10−7	2.0001	142.6	1.8487 × 10−7	2.0002	15.6
3	1.1	${\displaystyle \frac{1}{160}}$	2.8208 × 10−6	–	3.1	2.9038 × 10−6	–	0.6
		${\displaystyle \frac{1}{320}}$	7.0518 × 10−7	2.0000	25.4	7.2592 × 10−7	2.0001	3.3
		${\displaystyle \frac{1}{640}}$	1.7630 × 10−7	2.0000	213.1	1.8147 × 10−7	2.0001	21.7
	1.4	${\displaystyle \frac{1}{160}}$	2.0562 × 10−6	–	3.1	1.8928 × 10−6	–	0.6
		${\displaystyle \frac{1}{320}}$	5.1399 × 10−7	2.0002	25.4	4.7311 × 10−7	2.0003	3.3
		${\displaystyle \frac{1}{640}}$	1.2849 × 10−7	2.0001	217.2	1.1826 × 10−7	2.0002	21.9

, approaches the second order for an $\alpha$ value of $1.4$ or $1.6$ and a T of 1, 2, or 3. Moreover, the CPU running time for the reduced-dimension weighted explicit finite difference method is observed to be faster than that for the traditional weighted explicit finite difference approach.

Therefore, based on the data presented in Table 1, Table 2, Table 3 and Table 4, the numerical errors are in line with theoretical expectations, regardless of the specific value chosen for $\alpha$ within the tested range ($1<\alpha <2$). Moreover, these results highlight the proposed scheme’s capability to ensure sufficient accuracy while reducing degrees of freedom, saving CPU computation time, and enhancing computational efficiency. Additionally, Figure 7 visually presents a comparison of the errors between the two methods when $\alpha =1.8$, further illustrating the validity of the reduced-dimension method.

Example 2.

Consider the following initial boundary value problems:

$$\left\{\begin{array}{cc}\frac{\partial u(x,t)}{\partial t}=d\left(x\right)\frac{{\partial }^{\alpha }u(x,t)}{\partial x^{\alpha }}+f(x,t),\hfill & x\in [0,1],t\in (0,T],\hfill \\ u(x,0)=(1-x)x^2,\hfill & x\in [0,1],\hfill \\ u(0,t)=u(1,t)=0,\hfill & t\in (0,T],\hfill \end{array}\right.$$

(45)

in which the diffusion coefficient is $d\left(x\right)=\Gamma (4-\alpha )x^{\alpha }$ and the exact solution is the same as in Example 1.

According to Formula (44), the following source term can be obtained:

$$f(x,t)=-e^{-t}{x}^2(1-x)-e^{-t}\left(\frac{\Gamma (4-\alpha )\Gamma \left(3\right)}{\Gamma (3-\alpha )}{x}^2-\Gamma \left(4\right)x^3\right).$$

In

Table 5. Comparison of POD method and finite difference method.

T	$\mathit{\alpha }$	h	Weighted Explicit Method			POD Method
			$\mathbf{\parallel }\mathbf{u}\mathbf{\left(}{\mathbf{t}}_{\mathbf{n}}\mathbf{\right)}\mathbf{-}{\mathbf{u}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)	$\mathbf{\parallel }\mathbf{u}\left({\mathbf{t}}_{\mathbf{n}}\right)\mathbf{-}{\mathbf{u}}_{\mathbf{q}}^{\mathbf{n}}{\mathbf{\parallel }}_{{\mathbf{L}}_{\mathbf{2}}}$	Order	CPU (s)
1	1.4	${\displaystyle \frac{1}{160}}$	6.8788 × 10−6	–	0.7	6.1104 × 10−6	–	0.1
		${\displaystyle \frac{1}{320}}$	1.7190 × 10−6	2.0006	5.3	1.5305 × 10−6	1.9973	1.0
		${\displaystyle \frac{1}{640}}$	4.2966 × 10−7	2.0003	60.4	3.8254 × 10−7	2.0003	7.0
	1.6	${\displaystyle \frac{1}{160}}$	5.3011 × 10−6	–	0.7	4.5807 × 10−6	–	0.1
		${\displaystyle \frac{1}{320}}$	1.3241 × 10−6	2.0013	5.3	1.1451 × 10−6	2.0002	1.0
		${\displaystyle \frac{1}{640}}$	3.3086 × 10−7	2.0007	67.2	2.8623 × 10−7	2.0002	7.0
	1.8	${\displaystyle \frac{1}{160}}$	4.2201 × 10−6	–	0.7	3.9155 × 10−6	–	0.1
		${\displaystyle \frac{1}{320}}$	1.0545 × 10−6	2.0007	5.3	9.7882 × 10−7	2.0001	1.0
		${\displaystyle \frac{1}{640}}$	2.6359 × 10−7	2.0002	63.7	2.4470 × 10−7	2.0000	7.3
2	1.4	${\displaystyle \frac{1}{160}}$	3.7828 × 10−6	–	1.3	2.3088 × 10−6	–	0.2
		${\displaystyle \frac{1}{320}}$	9.4569 × 10−7	2.0000	10.7	5.7863 × 10−7	1.9964	1.9
		${\displaystyle \frac{1}{640}}$	2.3643 × 10−7	2.0000	101.0	1.4463 × 10−7	2.0003	15.2
	1.6	${\displaystyle \frac{1}{160}}$	2.8401 × 10−6	–	1.4	1.6910 × 10−6	–	0.2
		${\displaystyle \frac{1}{320}}$	7.0916 × 10−7	2.0018	14.0	4.2271 × 10−7	2.0001	1.9
		${\displaystyle \frac{1}{640}}$	1.7712 × 10−7	2.0014	135.8	1.0567 × 10−7	2.0002	15.4
	1.8	${\displaystyle \frac{1}{160}}$	1.9753 × 10−6	–	1.4	1.4409 × 10−6	–	0.2
		${\displaystyle \frac{1}{320}}$	4.9137 × 10−7	2.0072	15.1	3.6020 × 10−7	2.0001	2.0
		${\displaystyle \frac{1}{640}}$	1.2240 × 10−7	2.0053	118.4	9.0048 × 10−8	2.0000	15.5
3	1.4	${\displaystyle \frac{1}{160}}$	1.9961 × 10−6	–	2.0	8.5087 × 10−7	–	0.6
		${\displaystyle \frac{1}{320}}$	4.9988 × 10−7	1.9976	16.3	2.1321 × 10−7	1.9966	3.5
		${\displaystyle \frac{1}{640}}$	1.2511 × 10−7	1.9984	166.5	5.3292 × 10−8	2.0003	22.3
	1.6	${\displaystyle \frac{1}{160}}$	1.5963 × 10−6	–	2.1	6.2218 × 10−7	–	0.6
		${\displaystyle \frac{1}{320}}$	4.0070 × 10−7	1.9942	25.5	1.5552 × 10−7	2.0003	3.5
		${\displaystyle \frac{1}{640}}$	1.0040 × 10−7	1.9968	189.4	3.8874 × 10−8	2.0002	22.8
	1.8	${\displaystyle \frac{1}{160}}$	1.1056 × 10−6	–	2.1	5.3008 × 10−7	–	0.7
		${\displaystyle \frac{1}{320}}$	2.7683 × 10−7	1.9978	17.6	1.3251 × 10−7	2.0001	3.5
		${\displaystyle \frac{1}{640}}$	6.9101 × 10−8	2.0022	216.5	3.3127 × 10−8	2.0000	22.9

, with a time step of $\tau =h^2$ and various space meshes of $\frac{1}{160}$, $\frac{1}{320}$, and $\frac{1}{640}$, the orders of convergence for $\parallel u\left(t_n\right)-u^n\parallel$ and $\parallel u\left(t_n\right)-u_q^n\parallel$ are observed to be close to 2. The observed convergence is in line with theoretical projections. Additionally, we present the CPU running time results for both methods, corresponding to different $\alpha$ values of $1.4$, $1.6$, and $1.8$ and for the final time T of 1, 2, and 3. The numerical results for the CPU running time confirm the effectiveness of the reduced-dimension weighted explicit finite difference method. Furthermore, Figure 8 provides a more intuitive comparison of the error estimates between the two methods under various conditions. Specifically, it illustrates the error estimates for different values of $\alpha$ (1.4, 1.6, and 1.8) and final times T (1, 2, and 3).

6. Conclusions

In this paper, we investigate a reduced-dimension weighted explicit finite difference scheme for the space-fractional diffusion equation. The weighted explicit finite difference scheme for the space-fractional diffusion equation is first presented and formulated into a matrix form. In addition, the uniqueness of the weighted explicit finite difference solutions is demonstrated. Subsequently, the POD technique is utilized to establish the matrix form of the reduced-dimension weighted explicit finite difference method, and the implementation steps of the algorithm of the POD reduced-dimension technique are described. We discuss the uniqueness, stability, and error estimation of the solutions.

Numerical simulations were conducted to substantiate the analysis’s correctness and to compare the POD method with the original weighted explicit finite difference scheme. The results indicate that the proposed POD scheme ensures sufficient precision while reducing the degrees of freedom, conserving CPU computation time, and enhancing computational efficiency. Consequently, the reduced-dimension method, leveraging the POD technique, shows promise for broader applications. This approach is potentially applicable to solving other complex partial differential equations in two or higher dimensions.