Visualization of Isometric Deformations of Helicoidal CMC Surfaces

Abstract

Helicoidal surfaces of constant mean curvature were fully described by do Carmo and Dajczer. However, the obtained parameterizations are given in terms of somewhat complicated integrals, and as a consequence, not many examples of such surfaces are visualized. In this paper, by using these methods in some particular cases, we provide several interesting visualizations involving these surfaces, mostly as an isometric deformation of a rotational surface. We also give interpretations of some older results involving helicoidal surfaces, motivated by the work carried out by Malkowsky and Veličković. All of the graphics in this paper were created in Wolfram Mathematica.

1. Introduction

Surfaces in the Euclidean three-dimensional space that satisfy particularly nice properties regarding their intrinsic or extrinsic curvatures have always been of interest. Surfaces with the constant mean curvature (CMC) H are a natural generalization of the minimal surfaces, where $H=0$. While the minimal surfaces are those that minimize area with some fixed boundary, and may be regarded as those that correspond to zero pressure difference, a proper CMC surface corresponds to a non-zero pressure difference, and as such, has wide applications in physics, chemistry, engineering, and architecture, in particular for air-supported constructions. Surfaces that are moreover invariant for some group of transformations, as rotational surfaces and their generalization, helicoidal surfaces, are, may also be applied in engineering design and computer graphics.

The rotational surfaces with constant mean curvature (CMC) are well known and were first described by Delauney; see [1]. The notion of helicoidal surfaces has also been known for a long time. They represent a natural generalization of rotational surfaces and they are, roughly speaking, generated by simultaneously rotating and translating a regular planar curve (called a profile curve) around a fixed line (called an axis) that lies in that given plane, in such a manner that the speed of translation is proportional to the angular velocity of rotation (such motion is called a screw motion). It is, therefore, quite interesting that the classification of the helicoidal CMC surfaces with non-zero mean curvature was given almost 150 years later, by Do Carmo and Dajczer in [2]. Moreover, using their approach, the minimal helicoidal surfaces were given in [3]. Interestingly, to obtain the classification in [2], the authors used Bour’s theorem [4], which proves that for any helicoidal surface, regardless of the mean curvature, there exists a two-parameter family of helicoidal surfaces which are mutually isometric to it and containing a rotational surface as a special case of a helicoidal surface. Further, the authors used the existence of such Bour’s families to extrapolate, in a effective and clever manner, the CMC helicoidal surfaces by showing that for any such surface, there exists a family of CMC helicoidal surfaces isometric to it, all with the same mean curvature.

However, as a result, these surfaces are described in terms of somewhat complicated integrals, involving functions which are mostly arbitrary, with a few additional properties, such as smoothness, for instance. As an immediate practical consequence, it turns out that not many examples of such surfaces are yet visualized. In this paper, we use the methods given in [2]. Particular calculations, which straightforwardly follow [2], were performed in [5]. However, the aim was to present the examples of such CMC surfaces obtained in different moments of a certain isometric deformation of rotational surfaces, by using the family parameter as time. This imposed the condition to present the expressions in order to depend smoothly over the parameter and, further, in some of the expressions, taking some of the terms with both positive and negative sign. Moreover, for particular choices of the constant $B_0$ defining the family, we provide a visualization of examples of such CMC helicoidal families and present here their elements at particular moments.

In this paper, we choose the $O_z$-axis for the axis of helicoidal motion, and as we will focus on regular surfaces, the profile curve will be a regular curve

$$\left(x\right(r),0,z(r\left)\right),r\in (a,b),$$

where $x\left(r\right)$ is a positive function. If we introduce a value $h\ge 0$ (called pitch) that represents the height difference between any point and its image after screw motion in a unit of time, we see that we can formally define the screw motion of a profile curve by

$$\left[\begin{array}{c}x\left(r\right)\\ 0\\ z\left(r\right)\end{array}\right]\to \left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\left(r\right)\\ 0\\ z\left(r\right)\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ h\theta \end{array}\right].$$

Therefore, a helicoidal surface of the pitch h is given in its parametric form by:

$$H(r,\theta ):=\left(x\right(r)cos\theta ,x(r)sin\theta ,z(r)+h\theta ),(r,\theta )\in (a,b)\times \mathbf{R}.$$

(1)

In particular, the curves of the form $r=const$ are called the helices on $H(r,\theta )$. Obviously, for $h=0$, we obtain rotational surfaces.

2. Delauney’s Surfaces

En route to classification of helicoidal CMC surfaces, the first step was to describe rotational CMC surfaces (also known as the Delauney surfaces). Kenmotsu in [6] approached the problem by deriving the equation for mean curvature of a rotational surface, that, in general, is not constant. If we assume that the profile curve of a rotational surface is a naturally parameterized $C^2$-curve

$$\left(x\right(s),0,z(s\left)\right),s\in (a,b)$$

where $x\left(s\right)>0$, we obtain a differential equation whose mean curvature $H\left(s\right)$ must satisfy:

$$2x\left(s\right)H\left(s\right)-z^{\prime }\left(s\right)+x\left(s\right)x^{″}\left(s\right)z^{\prime }\left(s\right)-x\left(s\right)x^{\prime }\left(s\right)z^{″}\left(s\right)=0.$$

Multiplying the previous equation with $x^{\prime }$ and $z^{\prime }$, respectively, along with the fact that the profile curve is parameterized by a natural parameter, yields the following equations:

$$\left\{\begin{array}{c}2x{x}^{\prime }H\left(s\right)-\underset{{\left(x{z}^{\prime }\right)}^{\prime }}{\underbrace{x^{\prime }{z}^{\prime }-x{z}^{″}}}=0,\hfill \\ 2xH\left(s\right)z^{\prime }+\underset{{\left(x{x}^{\prime }\right)}^{\prime }}{\underbrace{x{x}^{″}+{\left(x^{\prime }\right)}^2}}-1=0,\hfill \end{array}\right.$$

which combined produce the following ODE:

$$2H\left(s\right)(x{z}^{\prime }-x{x}^{\prime })+{(x{x}^{\prime }+x{z}^{\prime })}^{\prime }-1=0.$$

(2)

If we define the following complex function $f\left(s\right):=x{x}^{\prime }+ix{z}^{\prime }$, Equation (2) becomes a first-order linear ODE

$$f^{\prime }\left(s\right)-2iH\left(s\right)f\left(s\right)-1=0,$$

which is easily solvable and gives us the three-parameter family of profile curves for a rotational surface with mean curvature $H\left(s\right)$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}X(s;H\left(s\right),c_1,c_2,c_3)\hfill & :=(\sqrt{{(F\left(s\right)-c_2)}^2+{(G\left(s\right)+c_1)}^2},0,\hfill \\ & {\int }_0^s\frac{(G\left(t\right)+c_1)F^{\prime }\left(t\right)-(F\left(t\right)-c_2)G^{\prime }\left(t\right)}{\sqrt{{(F\left(s\right)-c_2)}^2+{(G\left(s\right)+c_1)}^2}}dt+c_3),s\in (a,b),\hfill \end{array}\right.\end{array}$$

(3)

where the functions $F\left(s\right)$ and $G\left(s\right)$ are defined as:

$$\left\{\begin{array}{c}F\left(s\right):={\int }_0^{s}sin\left(2{\int }_0^{t}H\left(u\right)du\right)dt\hfill \\ G\left(s\right):={\int }_0^{s}cos\left(2{\int }_0^{t}H\left(u\right)du\right)dt.\hfill \end{array}\right.$$

Firstly, we wish to see what are the minimal rotational surfaces, that is, what happens when $H\left(s\right)$ is equal to zero. In that case, the aforementioned three-parameter family comes down to

$$\left(\sqrt{c_2^2+{(s+c_1)}^2},0,{\int }_0^s\frac{c_2}{\sqrt{c_2^2+{(t+c_1)}^2}}dt+c_3\right),$$

(4)

and that is a part of a plane (for $c_2=0$), or a catenoid. In the remaining cases, by properly choosing the sign of the normal vector field, we may assume that $H\left(s\right)=H>0$. If we introduce a positive constant $B_0=2H{c}_1$ and apply adequate translations, the profile curve (4) becomes

$$\left(\frac{1}{2H}\sqrt{1+2B_{0}sin\left(2Hs\right)+B_0^2},0,{\int }_0^s\frac{1+B_{0}sin\left(2Ht\right)}{\sqrt{1+2B_{0}sin\left(2Ht\right)+B_0^2}}dt\right).$$

In [6], it was shown that possible rotational surfaces that can be generated by these profile curves are:

• Cylindrical surfaces, for $B_0=0$.
• Spherical surfaces, for $B_0=1$.
• Parts of an unduloid, for $B_0\in (0,1)$.
• Parts of a nodoid, for $B_0\in (1,+\infty )$.

All of the previous observations are summarized in the following theorem:

Theorem 1.

(Delauney) Rotational surfaces with the constant non-zero mean curvature are cylindrical or spherical surfaces or parts of an unduloid or a nodoid. Only minimal rotational surfaces are parts of planes and catenoids.

Remark 1.

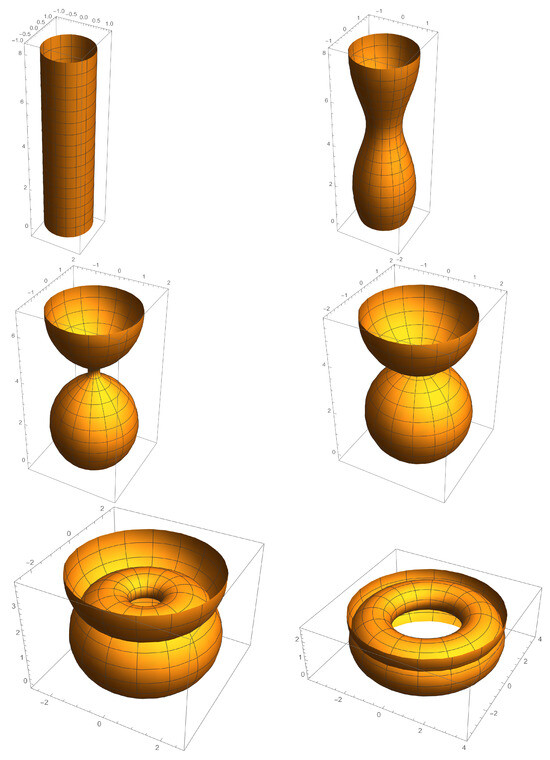
One way of visualizing non-minimal Delauney surfaces is through a deformation with a fixed mean curvature, where we interpret the parameter $B_0$ as time, and through its continuous movement we obtain all of the non-minimal Delauney surfaces with a fixed mean curvature H.

We may demonstrate the previous considerations for the Delauney surfaces of mean curvature $H=\frac{1}{2}$ and $s\in (0,8)$; see Figure 1.

Figure 1. Deformation of Delauney’s surfaces, all with the same constant mean curvature $H=\frac{1}{2}$. The starting point of the deformation is a cylinder at moment $B_0=0$. Following Delauney’s surfaces are an unduloid at the moment $B_0=0.3$, an unduloid at the moment $B_0=0.8$, a sphere(s) at the moment $B_0=1$, a nodoid at the moment $B_0=1.5$, and a nodoid at the moment $B_0=2.6$.

3. Visualization of Bour’s Theorems

In this section, we focus on two older claims related to helicoidal surfaces, the latter of which represented a starting point in the paper [2] en route to fully classifying helicoidal CMC surfaces and giving their global parameterization. Since we consider proper helicoidal surfaces of the pitch $h_0\ge 0$, by possible reparameterization, we may take it that they are locally given by

$$H(r,\theta ):=(rcos\theta ,rsin\theta ,\lambda \left(r\right)+h_0\theta ),(r,\theta )\in (0,a)\times (0,2\pi ).$$

(5)

Now, we recall the statement of Bour’s theorem. Having in mind that our main goal here is to construct and visualize new examples of CMC helicoidal surfaces, we present here a proof in more detail, following proofs given in [2,7,8].

Theorem 2.

(a) (Bour’s theorem) Each helicoidal surface (5) is isometric to some rotational surface. The listed isometry maps helices of the helicoidal surface to parallels of the rotational surface. (b) (Bour’s family) Each helicoidal surface (5) is a member of a two-parameter family of helicoidal surfaces that are all mutually locally isometric.

Proof. 

(a) Via direct computation, we see that the first fundamental form of the helicoidal surface $H(r,\theta )$ is equal to:

$$d{s}^2=(1+{\left({\lambda }^{\prime }\left(r\right)\right)}^2)d{r}^2+2h_0{\lambda }^{\prime }\left(r\right)drd\theta +(r^2+h_0^2)d{\theta }^2.$$

(6)

Firstly, we regard the reparameterization

$$\begin{array}{c}\hfill (\overline{r},\overline{\theta }):=\Psi (r,\theta )=\left({\Psi }_1(r,\theta ),{\Psi }_2(r,\theta )\right):=\left(r,\theta +\int \frac{h_0{\lambda }^{\prime }\left(r\right)}{r^2+{h_0}^2}dr\right).\end{array}$$

(7)

Its first fundamental form is:

$$d{s}^2=\left(1+\frac{{\overline{r}}^2{\left({\lambda }^{\prime }\left(\overline{r}\right)\right)}^2}{{\overline{r}}^2+{h_0}^2}\right)d{\overline{r}}^2+({\overline{r}}^2+{h_0}^2)d{\overline{\theta }}^2.$$

Further, we may introduce another reparameterization with parameters $r_1$ and ${\theta }_1$ in the following manner:

$$\begin{array}{c}\hfill (r_1,{\theta }_1):=\Phi (\overline{r},\overline{\theta })=\left(\int \sqrt{1+\frac{{\overline{r}}^2{\left({\lambda }^{\prime }\left(\overline{r}\right)\right)}^2}{{\overline{r}}^2+{h_0}^2}}d\overline{r},\overline{\theta }\right).\end{array}$$

(8)

It is clear that we have transformed parameter domain $(0,a)\times (0,2\pi )$ of $H(r,\theta )$ onto the domain $\Phi \circ \Psi \left(\right(0,a)\times (0,2\pi \left)\right)$, which is of the form $I_1\times I_2$, where $I_1$ and $I_2$ are open intervals on the real line. Now, the first fundamental form of the helicoidal surface has the following form:

$$d{s}^2=d{r}_1^2+({\overline{r}}^2+{h_0}^2)d{\theta }_1^2.$$

(9)

Let us now observe rotational surfaces given parameterically by

$$R(u,v):=(ucosv,usinv,\varphi \left(u\right)),u\in J,v\in I_2,$$

(10)

where J is an open subinterval of $(0,+\infty )$. The first fundamental form of $R(u,v)$ is

$$d{s}^2=(1+{\left({\varphi }^{\prime }\left(u\right)\right)}^2)d{u}^2+u^{2}d{v}^2.$$

(11)

Let us consider the transformation given by

$$\left\{\begin{array}{cc}u\hfill & =\sqrt{{\overline{r}}^2+h_0^2}=\sqrt{r^2+{h_0}^2},\hfill \\ v\hfill & =\overline{\theta }=\theta +\int \frac{h_0{\lambda }^{\prime }\left(r\right)}{r^2+{h_0}^2}dr.\hfill \end{array}\right.$$

(12)

Straightforwardly, we have that

$$\begin{array}{cc}\hfill \frac{d{r}_1}{du}& =\frac{dr}{du}\sqrt{1+\frac{r^2{\left({\lambda }^{\prime }\left(r\right)\right)}^2}{r^2+h_0^2}}=\sqrt{1+{\left({\lambda }^{\prime }\left(r\right)\right)}^2+\frac{h_0^2}{r^2}}\ge 1.\hfill \end{array}$$

Hence, there exist a differentiable function $\varphi$ such that $\frac{d{r}_1}{du}=\sqrt{1+{\left(\frac{d\varphi }{du}\right)}^2}$. Then, $\varphi$ is given by

$$\begin{array}{cc}\hfill \varphi \left(u\right)& =\int {\varphi }^{\prime }\left(u\right)du=\int \sqrt{\frac{d{r}_1^2}{d{u}^2}-1}du=\int \sqrt{d{r}_1^2-d{u}^2}\hfill \\ \hfill & =\int \sqrt{1+\frac{r^2{\left({\lambda }^{\prime }\left(r\right)\right)}^2}{r^2+{h_0}^2}-\frac{r^2}{r^2+{h_0}^2}}dr=\int \sqrt{\frac{{h_0}^2+r^2{\left({\lambda }^{\prime }\left(r\right)\right)}^2}{r^2+{h_0}^2}}dr.\hfill \end{array}$$

Now, the reparameterization is of the form

$$\left\{\begin{array}{cc}{r}_1\hfill & ={\int }_0^u\sqrt{1+({\varphi }^{\prime }{\left(t\right)}^2})dt,\hfill \\ {\theta }_1\hfill & =v\hfill \end{array}\right.$$

(13)

and, moreover, the function $g\left(u\right):={\int }_0^u\sqrt{1+({\varphi }^{\prime }{\left(t\right)}^2})dt$ maps J to $I_1$. Therefore, by taking such a function $\varphi$ into (10), we straightforwardly conclude that the given reparametrizations of $H(r,\theta )$ and $R(u,v)$ have the first fundamental forms that coincide, and further, the rotatational surface (10) is locally isometric to the helicoidal surface (5).

We note that the obtained rotational surface $R(r,\theta )$ is parameterized in the following way:

$$\left\{\begin{array}{c}x=\sqrt{r^2+{h_0}^2}cos\left(\theta +\int \frac{h_0{\lambda }^{\prime }\left(r\right)}{r^2+{h_0}^2}dr\right),\hfill \\ y=\sqrt{r^2+{h_0}^2}sin\left(\theta +\int \frac{h_0{\lambda }^{\prime }\left(r\right)}{r^2+{h_0}^2}dr\right),\hfill \\ z=\int \sqrt{\frac{{h_0}^2+r^2{\left({\lambda }^{\prime }\left(r\right)\right)}^2}{r^2+{h_0}^2}}dr.\hfill \end{array}\right.$$

(14)

As the helices on the helicoidal surfaces are curves given by $r=r_0=const$, which further implies that ${\lambda }^{\prime }\left(r\right)=0$, we obtain that the image of the helix on $H(r,\theta )$, with $r=r_0$ will be the circle of radius $\sqrt{r_0^2+{h_0}^2}$, with the height $h_{0}arsinh\left(\frac{r_0}{h_0}\right)$, i.e., a parallel on the rotational surface. Let us rewrite the first fundamental form (6) of $H(r,\theta )$:

$$\begin{array}{cc}\hfill d{s}^2& =\left(1+\frac{{\left({\lambda }^{\prime }\left(r\right)\right)}^2)(r^2+h_0^2)}{(r^2+h_0^2)}\right)d{r}^2+2h_0{\lambda }^{\prime }\left(r\right)drd\theta +(r^2+h_0^2)d{\theta }^2\hfill \\ \hfill & =\left(1+\frac{r^2\left({\lambda }^{\prime }{\left(r\right)}^2\right)}{(r^2+h_0^2)}\right)d{r}^2+(r^2+h_0^2){\left(d\theta +\frac{{\lambda }^{\prime }\left(r\right)h_0}{r^2+h_0^2}dr\right)}^2.\hfill \end{array}$$

By taking so-called natural parameters of the helicoidal surface, defined as:

$$\left\{\begin{array}{c}\sigma =\sigma (r,\theta ):=\int \sqrt{1+\frac{{\left({\lambda }^{\prime }\left(r\right)\right)}^2{r}^2}{(r^2+h_0^2)}}dr\hfill \\ \tau =\tau (r,\theta ):=\theta +h_0\int \frac{{\lambda }^{\prime }\left(r\right)}{r^2+h_0^2}dr\hfill \end{array}\right.$$

(15)

we obtain:

$$d{s}^2=d{\sigma }^2+U{\left(\sigma \right)}^{2}d{\tau }^2,$$

(16)

where the positive function $U\left(\sigma \right)$ is given by $U\left(\sigma \right):=\sqrt{r^2+h_0^2}$. Note that the parameter $\sigma$ is independent of $\theta$.

Now, let us consider an arbitrary positive function $U\left(\sigma \right)$ and an arbitrary real number $h\ge 0$. We want to construct functions r, $\lambda$, and $\theta$ depending on variables $\sigma$ and $\tau$, which satisfy the following equations:

$$\left\{\begin{array}{c}d{\sigma }^2=d{r}^2+\frac{r^2}{r^2+h^2}d{\lambda }^2\hfill \\ U\left(\sigma \right)d\tau =\pm \sqrt{r^2+h^2}(d\theta +\frac{h}{r^2+h^2}d\lambda ).\hfill \end{array}\right.$$

(17)

Clearly, such functions r and $\lambda$ will not depend on $\tau$. By dividing the second equation in (17) with $\sqrt{r^2+h^2}$, we obtain the following PDE:

$$d\theta =\pm \frac{U\left(\sigma \right)}{\sqrt{r^2+h^2}}d\tau -\frac{h}{r^2+h^2}d\lambda =\pm \frac{U\left(\sigma \right)}{\sqrt{r^2+h^2}}d\tau -\frac{h}{r^2+h^2}\frac{d\lambda }{d\sigma }d\sigma .$$

Comparing the previous equation with differential $d\theta =\frac{d\theta }{d\sigma }d\sigma +\frac{d\theta }{d\tau }d\tau$ yields the system:

$$\frac{d\theta }{d\sigma }=-\frac{h}{r^2+h^2}\frac{d\lambda }{d\sigma }\frac{d\theta }{d\tau }=\pm \frac{U\left(\sigma \right)}{\sqrt{r^2+h^2}}.$$

(18)

As the right-hand side of the first equation in (18) is independent of $\tau$, we have that $\frac{{\partial }^2\theta }{\partial \sigma \partial \tau }=0$, and moreover,

$$\frac{\partial }{\partial \sigma }\left(\pm \frac{U\left(\sigma \right)}{\sqrt{r^2+h^2}}\right)=0,$$

(19)

and since $U\left(\sigma \right)\ne 0$, there is a positive constant m such that:

$$\frac{U\left(\sigma \right)}{\sqrt{r^2+h^2}}=\frac{1}{m}\ne 0.$$

(20)

Note that this assumption automatically implies that $U\left(\sigma \right)$ is an increasing function.

From (20), we see that

$$m^2{\left(U\left(\sigma \right)\right)}^2=r^2+h^2$$

(21)

which determines the function $r\left(\sigma \right)$. Moreover, by differentiating this equation, we obtain

$$2m^{2}U\left(\sigma \right)\frac{dU}{d\sigma }=2r\frac{dr}{d\sigma }.$$

Note that from (15), it follows that $\frac{dr}{d\sigma }>0$, and further, from (3), we have $r\left(\sigma \right)>0$. By taking the square of (3) and by substituting $r^2$ from (21), we obtain the following ODE:

$${\left(\frac{dr}{d\sigma }\right)}^2=\frac{m^4{\left(U\left(\sigma \right)\right)}^2}{m^2{\left(U\left(\sigma \right)\right)}^2-h^2}{\left(\frac{dU}{d\sigma }\right)}^2.$$

(22)

Further, we have:

$$\begin{array}{cc}\hfill d{\lambda }^2& =\frac{r^2+h^2}{r^2}(d{\sigma }^2-d{r}^2)=\frac{m^2{\left(U\left(\sigma \right)\right)}^2}{m^2{\left(U\left(\sigma \right)\right)}^2-h^2}\left(1-{\left(\frac{dr}{d\sigma }\right)}^2\right)d{\sigma }^2\hfill \\ \hfill & =\frac{m^2{\left(U\left(\sigma \right)\right)}^2}{{(m^2{\left(U\left(\sigma \right)\right)}^2-h^2)}^2}\left(m^2{\left(U\left(\sigma \right)\right)}^2-h^2-m^4{\left(U\left(\sigma \right)\right)}^2{\left(\frac{dU}{d\sigma }\right)}^2\right)d{\sigma }^2,\hfill \end{array}$$

which determines the function $\lambda \left(\sigma \right)$.

Finally, the second equation in (17) transforms to:

$$d\theta =\pm \frac{1}{m}d\tau -\frac{h}{r^2+h^2}d\lambda .$$

Hence, we obtain:

$$\left\{\begin{array}{cc}r\left(\sigma \right)=\hfill & \sqrt{m^2{\left(U\left(\sigma \right)\right)}^2-h^2},\hfill \\ \theta (\sigma ,\tau )=\hfill & ϵ\frac{\tau }{m}-{ϵ}_{\lambda }\frac{h}{m}\int \frac{\sqrt{m^2{\left(U\left(\sigma \right)\right)}^2\left(1-m^2{\left(\frac{dU}{d\sigma }\right)}^2\right)-h^2}}{U\left(\sigma \right)(m^2{\left(U\left(\sigma \right)\right)}^2-h^2)}d\sigma ,\hfill \\ \lambda \left(\sigma \right)=\hfill & {ϵ}_{\lambda }\int \frac{mU\left(\sigma \right)}{m^2{\left(U\left(\sigma \right)\right)}^2-h^2}\sqrt{m^2{\left(U\left(\sigma \right)\right)}^2\left(1-m^2{\left(\frac{dU}{d\sigma }\right)}^2\right)-h^2}d\sigma ,\hfill \end{array}\right.$$

(23)

where $ϵ,{ϵ}_{\lambda }\in \{-1,1\}$.

Now, let $U\left(\sigma \right)$ be any particular increasing positive function. Let us consider the family of helicoidal surfaces $\left[U\right]$ that we obtain by substituting (23) into (5), for an arbitrary pitch $h\ge 0$ and a positive constant m:

$$X(h,m)(\sigma ,\tau ):=\left(r\right(\sigma )cos\theta (\sigma ,\tau ),r(\sigma )sin\theta (\sigma ,\tau ),\lambda (\sigma )+h\theta (\sigma ,\tau \left)\right).$$

(24)

Since $\mathrm{sgn}\frac{dr}{d\sigma }=1$, we have ${ϵ}_{\lambda }=\mathrm{sgn}\frac{d\lambda }{dr}\mathrm{sgn}\frac{dr}{d\sigma }=\mathrm{sgn}\frac{d\lambda }{dr},$ where, of course, $\mathrm{sgn}\frac{d\lambda }{dr}$ determines if $\lambda \left(r\right)$ in (5) is a locally increasing or decreasing function. By taking the isometry $J:(x,y,z)\mapsto (x,-y,-z)$ of the space ${\mathbf{R}}^3$, we obtain that $J\left(X\right)$ is determined by functions $\tilde{r}=r$, $\tilde{\theta }=-\theta$, and $\tilde{\lambda }=-\lambda$, such that $\frac{\tilde{\lambda }}{d\sigma }=-\frac{d\lambda }{d\sigma }$, so we may take it that ${ϵ}_{\lambda }=1$.

The local coordinate vector fields of $X\left(m\right)(\sigma ,\tau )$ are given by:

$$\begin{array}{cc}\hfill X{(h,m)}_{\sigma }& =(r^{\prime }cos\theta -rsin\theta \frac{d\theta }{d\sigma },r^{\prime }sin\theta +rcos\frac{d\theta }{d\sigma },{\lambda }^{\prime }+h\frac{d\theta }{d\sigma }),\hfill \\ \hfill X{(h,m)}_{\tau }& =\frac{d\theta }{d\tau }(-rsin\theta ,rcos\theta ,h),\hfill \end{array}$$

so the coefficients of the first fundamental form of $X(h,m)(\sigma ,\tau )$ are:

$$\begin{array}{cc}\hfill E& ={\left(r^{\prime }\right)}^2+{\left({\lambda }^{\prime }\right)}^2-(r^2+h^2){\left(\frac{d\theta }{d\sigma }\right)}^2={\left(r^{\prime }\right)}^2+\frac{r^2{\left({\lambda }^{\prime }\right)}^2}{r^2+h^2}\hfill \\ \hfill & =\frac{m^4{\left(U\left(\sigma \right)\right)}^2\left(U^{\prime }{\left(\sigma \right)}^2\right)}{m^2{\left(U\left(\sigma \right)\right)}^2-h^2}+\frac{r^2-m^4{\left(U\left(\sigma \right)\right)}^2{\left(U^{\prime }\left(\sigma \right)\right)}^2}{r^2}=1,\hfill \\ \hfill F& =\frac{d\theta }{d\tau }(r^2\frac{d\theta }{d\sigma }+h({\lambda }^{\prime }+h\frac{d\theta }{d\sigma }))=\frac{d\theta }{d\tau }(\frac{d\theta }{d\sigma }(h^2+r^2)+h{\lambda }^{\prime })=\frac{d\theta }{d\tau }(-h{\lambda }^{\prime }+h{\lambda }^{\prime })=0,\hfill \\ \hfill G& ={\left(\frac{d\theta }{d\tau }\right)}^2(r^2+h^2)={\left(U\left(\sigma \right)\right)}^2.\hfill \end{array}$$

We deduce that all elements of the family $\left[U\right]$ have the same first fundamental form given by (16), and therefore, the helicoidal surface $H(r,\theta )$ (which is also an element of this family, for $m=1$ and $h=h_0$) is locally isometric to any element of $\left[U\right]$, which proves the statement. □

Remark 2.

By straightforward computation, we obtain the unit normal vector field, as well as the coefficients of the second fundamental form for elements of Bour’s family $\left[U\right]$:

$$\begin{array}{cc}\hfill n(h,m)(\sigma ,\tau )& =\frac{1}{mU}(h{r}^{\prime }sin\theta -{\lambda }^{\prime }rcos\theta ,-{\lambda }^{\prime }rsin\theta -h{r}^{\prime }cos\theta ,r{r}^{\prime }),\hfill \\ \hfill e& =\frac{-m^4{\left(U\left(\sigma \right)\right)}^3{U}^{″}\left(\sigma \right)+h^2}{m^2{\left(U\left(\sigma \right)\right)}^2\sqrt{m^2{\left(U\left(\sigma \right)\right)}^2(1-m^2{\left(U^{\prime }\left(\sigma \right)\right)}^2)-h^2}},\hfill \\ \hfill f& =-ϵ\frac{h}{m^{2}U\left(\sigma \right)},\hfill \\ \hfill g& =\frac{r^2{\lambda }^{\prime }{\left(\frac{d\theta }{d\tau }\right)}^2}{mU\left(\sigma \right)}=\frac{\sqrt{m^2{\left(U\left(\sigma \right)\right)}^2(1-m^2{\left(\frac{dU}{d\sigma }\right)}^2)-h^2}}{m^2}.\hfill \end{array}$$

(25)

Note that, although the metrics of the elements of Bour’s family are independent of the parameters m and h, the second fundamental form, and hence, the mean curvature, is not.

We may also ask the question of the regularity of elements in a Bour’s family. We note that $n(h,m)=0$ for $r^{\prime }={\lambda }^{\prime }=0$ or $r=0$. In both cases, $r^{\prime }=0$, meaning that (5) is not a parameterization of a surface. Recall that we obtained the parameterization (5) by excluding from our consideration the case of the cylindrical surfaces, which may be included through the limit process, which we will see later.

Example 1.

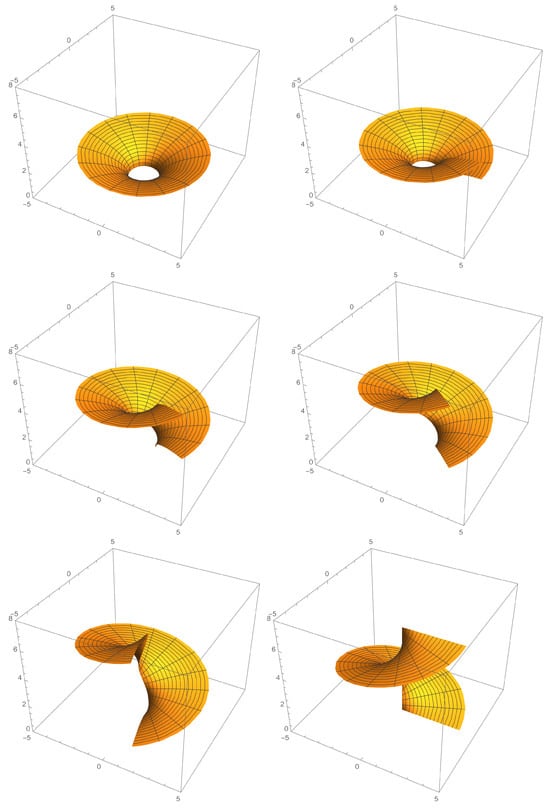
Let us regard the right helicoid, given by

$$H(r,\theta )=(rcos\theta ,rsin\theta ,\theta ),(r,\theta )\in (0,4)\times (0,2\pi ),$$

By taking this parameterization into (14), we obtain that, via Bour’s isometry, it is isometric to the catenoid, as a rotational surface

$$R(r,\theta )=\left(\sqrt{r^2+1}cos\theta ,\sqrt{r^2+1}sin\theta ,arsinhr\right).$$

Note that the right helicoid is already parameterized by natural parameters and that its metric is induced by the function $U\left(\sigma \right)=\sqrt{{\sigma }^2+1}$. By setting $m=1$ and after integration in (23), we see that for any $h\in [0,1)$, we have:

$$\begin{array}{cc}\hfill r\left(\sigma \right)& =\sqrt{{\sigma }^2+1-h^2},\hfill \\ \hfill \theta (\sigma ,\tau )& =\tau -arctan\left(\frac{h\sigma }{\sqrt{1-h^2}\sqrt{1+{\sigma }^2}}\right),\hfill \\ \hfill \lambda \left(\sigma \right)& =\sqrt{1-h^2}arsinh\sigma +harctan\left(\frac{h\sigma }{\sqrt{1-h^2}\sqrt{1+{\sigma }^2}}\right).\hfill \end{array}$$

By interpreting the pitch of the family’s element as time, we may obtain another isometric deformation of the right helicoid to the catenoid; see Figure 2.

Figure 2. Isometric deformation of right helicoid’s Bour’s family. The starting point of the deformation is a catenoid at the moment $h=0$ followed by helicoidal surfaces at moments $h=0.2$, $h=0.5$, $h=0.7$, $h=0.95$ and, in conclusion, the right helicoid at the moment $h=1$.

The examples of the rotational surfaces corresponding to particular helicoidal surfaces via Bour’s isometry are given in the Figure 3 and Figure 4.

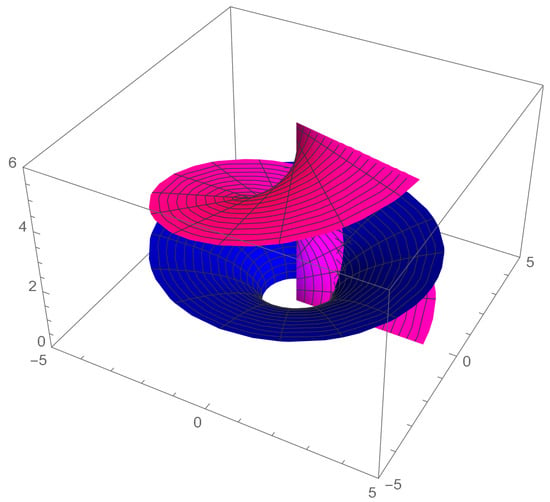
Figure 3. Right helicoid and catenoid are isometric via Bour’s isometry.

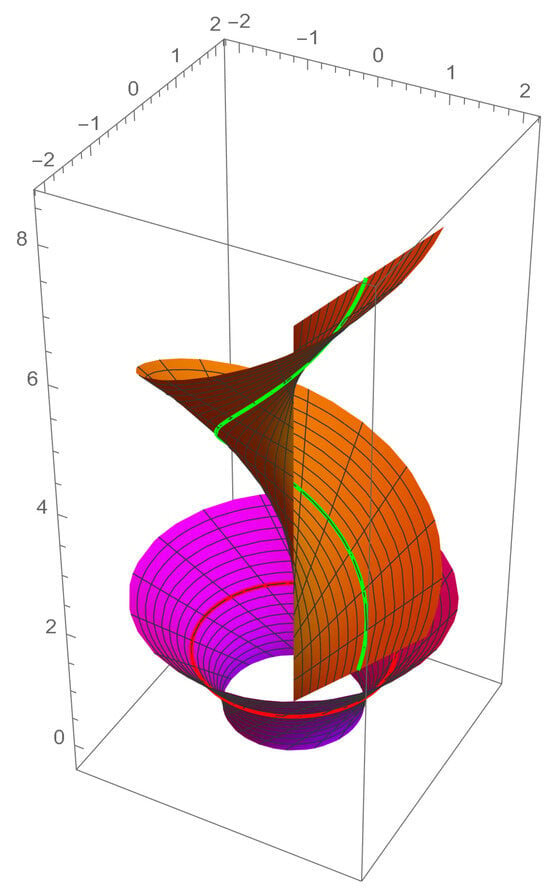
Figure 4. Helicoidal surface $H(r,\theta )$ for $\lambda \left(r\right)=r$ and $h_0=1$, where $(r,\theta )\in (0,2)\times (0,2\pi )$ and the rotational surface isometric to it via Bour’s isometry. Helix $r=1$ and its image via Bour’s isometry are highlighted.

4. Helicoidal CMC Surfaces

Although the elements of Bour’s family in general do not have the same, let alone constant, mean curvature, the main benefit of the existence of Bour’s family is in effective extrapolation of helicoidal CMC surfaces from it. Since we know the coefficients of the first and the second fundamental form of the Bour’s family elements, the next claim follows directly.

Theorem 3.

The helicoidal surface of Bour’s family $\left[U\right]$, with the pitch h and constant m, has a constant mean curvature H if and only if it satisfies the following ODE:

$$-2H\sqrt{m^2{\left(U\left(\sigma \right)\right)}^2(1-m^2{\left(U^{\prime }\left(\sigma \right)\right)}^2)-h^2}=m^{2}U\left(\sigma \right)U^{″}\left(\sigma \right)-1+m^2{\left(U^{\prime }\left(\sigma \right)\right)}^2.$$

(26)

For non-negative functions,

$$x\left(\sigma \right):=mU\left(\sigma \right),y\left(\sigma \right):=\sqrt{{\left(x\left(\sigma \right)\right)}^2-{\left(x\left(\sigma \right)\right)}^2{\left(x^{\prime }\left(\sigma \right)\right)}^2-h^2},$$

(27)

Equation (26) reduces to:

$$\begin{array}{c}\hfill -2Hy\left(\sigma \right)=x\left(\sigma \right)x^{″}\left(\sigma \right)-1+{\left(x^{\prime }\left(\sigma \right)\right)}^2.\end{array}$$

By differentiating the second equation in (27), we obtain that $\frac{y}{x}\frac{dy}{dx}=1-{\left(\frac{dx}{d\sigma }\right)}^2-x{x}^{\prime \prime }$, which further reduces (26) to $y=0$ or $2Hxdx=dy$ with the solution

$$y=H{x}^2+a,y\ge 0,a\in \mathbf{R}.$$

(28)

Let us find minimal helicoidal surfaces. From $H=0$, we obtain that $y=a,a\ge 0$. From (27), we have

$$m^{2}U\left(\sigma \right)U^{\prime }\left(\sigma \right)=\sqrt{m^2{\left(U\left(\sigma \right)\right)}^2-a^2-h^2}.$$

(29)

By substituting $f\left(\sigma \right):=m^2{\left(U\left(\sigma \right)\right)}^2-a^2-h^2$, we straightforwardly obtain $f\left(\sigma \right)={(\sigma +D)}^2,D\in \mathbf{R}$ and by possible translation in the domain of $\sigma$, we may take $D=0$.

Now, by taking (23), we see that in the case of $a=0$, we obtain helicoids

$$X(\sigma ,\tau )=\left(\sigma cos\left(\frac{ϵ\tau }{m}\right),\sigma sin\left(\frac{ϵ\tau }{m}\right),ϵh\frac{\tau }{m}\right).$$

(30)

In the case that $a\ne 0$, we obtain that $r\left(\sigma \right)=\sqrt{{\sigma }^2+a^2}$ and up to a constant

$$\begin{array}{ccc}\hfill \lambda \left(\sigma \right)& =& aln(\sigma +\sqrt{{\sigma }^2+h^2+a^2})+harctan\left(\frac{h\sigma }{a\sqrt{{\sigma }^2+h^2+a^2}}\right),\hfill \\ \hfill \theta (\sigma ,\tau )& =& ϵ\frac{\tau }{m}-arctan\left(\frac{h\sigma }{a\sqrt{{\sigma }^2+h^2+a^2}}\right).\hfill \end{array}$$

Hence, we obtain the surfaces

$$\begin{array}{cc}\hfill X(\sigma ,\tau )& =(\frac{a\sqrt{{\sigma }^2+h^2+a^2}cos\frac{ϵ\tau }{m}+h\sigma sin\frac{ϵ\tau }{m}}{\sqrt{a^2+h^2}},\frac{a\sqrt{{\sigma }^2+h^2+a^2}sin\frac{ϵ\tau }{m}-h\sigma cos\frac{ϵ\tau }{m}}{\sqrt{a^2+h^2}},\\ & \frac{ϵh\tau }{m}+aln(\sigma +\sqrt{{\sigma }^2+h^2+a^2}));\end{array}$$

see also [3].

We restrain now to the case where $H\ne 0$. Inputting (28) into (27) gives us an ODE for the function $x\left(\sigma \right)$:

$${(H{x}^2+a)}^2=x^2-x^2{\left(x^{\prime }\right)}^2-h^2.$$

Substitution of $z\left(\sigma \right):={\left(x\left(\sigma \right)\right)}^2$ and the fact that $x\left(\sigma \right)$ is positive and increasing reduce it to an easily solvable separable first-order ODE:

$$z^{\prime }=2\sqrt{-H^2{z}^2+(1-2aH)z-a^2-h^2}.$$

(31)

A necessary condition for the solvability of the previous ODE is a strict negativity of the discriminant of the quadratic trinomial by z on the right side, which reduces to

$$1-4aH-4H^2{h}^2>0.$$

(32)

A direct integration of the latter equation yields:

$$\begin{array}{cc}\hfill \sigma +c& =\frac{1}{2}\int \frac{dz}{\sqrt{-(H^2{z}^2+(2aH-1)z)-(a^2+h^2)}}\hfill \\ \hfill & =\frac{\left|H\right|}{\sqrt{1-4aH-4H^2{h}^2}}\int {\left(1-{\left(\frac{2H^{2}z+2aH-1}{\sqrt{1-4aH-4H^2{h}^2}}\right)}^2\right)}^{-\frac{1}{2}}dz.\hfill \end{array}$$

so we obtain, up to a constant:

$$\sigma =\frac{1}{2\left|H\right|}arcsin\left(\frac{2H^{2}z+2aH-1}{\sqrt{1-4aH-4H^2{h}^2}}\right).$$

(33)

For the sake of brevity, we may now introduce a strictly positive constant

$$\begin{array}{c}\hfill B:=\sqrt{1-4aH-4H^2{h}^2}.\end{array}$$

(34)

Replacing z with $m^2{\left(U\left(\sigma \right)\right)}^2$ in (33) provides the following expression for $U\left(\sigma \right)$ dependent on a, m, and h:

$${\left(U\left(\sigma \right)\right)}^2=\frac{1-2aH+Bsin\left(2\right|H\left|\sigma \right)}{2m^2{H}^2},U\left(\sigma \right)U^{\prime }\left(\sigma \right)=\frac{B}{2m^2\left|H\right|}cos\left(2\right|H\left|\sigma \right),$$

(35)

and since from (34), we have that $2aH=\frac{1}{2}(1-B^2-4H^2{h}^2)$, we straightforwardly obtain from (23):

$$\begin{array}{cc}\hfill r\left(\sigma \right)& =\frac{1}{2\left|H\right|}\sqrt{1+2Bsin\left(2\right|H\left|\sigma \right)+B^2},\hfill \\ \hfill \theta (\sigma ,\tau )& =ϵ\frac{\tau }{m}-4H^{2}h\int \frac{|1+Bsin(2\left|H\right|\sigma \left)\right|}{\sqrt{1+B^2+2Bsin\left(2\right|H\left|\sigma \right)+4H^2{h}^2}(1+2Bsin(2\left|H\right|\sigma )+B^2)}d\sigma ,\hfill \\ \hfill \lambda \left(\sigma \right)& =\int \frac{|1+Bsin(2\left|H\right|\sigma \left)\right|\sqrt{1+B^2+2Bsin\left(2\right|H\left|\sigma \right)+4H^2{h}^2}}{1+2Bsin\left(2\right|H\left|\sigma \right)+B^2}d\sigma .\hfill \end{array}$$

Remark 3.

Note that in the limit case when B goes to zero, we obtain that $r\left(\sigma \right)=\frac{1}{2H}=const.$, i.e., the surface is a cylinder. Hence, the cylinder and its Bour’s family may be considered as a limit case of Bour’s theorem.

Note that, by allowing h to take negative values, we may take it that $ϵ=1$.

Previous calculations as well as the following version of the theorem by Lawson and the preceding lemma had the key role in the classification of helicoidal CMC surfaces in the paper [2].

Theorem 4.

(Lawson) Let simply connected CMC surface M be given by immersion $f:\Omega \to {\mathbf{R}}^3$, where $\Omega \subset {\mathbf{R}}^2$ is a domain. Then, there exists a differentiable $2\pi -$ periodic family of surfaces $f_{\varphi }:\Omega \to {\mathbf{R}}^3$, $\varphi \in [0,2\pi ]$ all of which are isometric to M and all with the same mean curvature as M, where $f_0=f$. Also, the family in question is unique up to an isometry of Euclidean space ${\mathbf{R}}^3$.

The proof of the previous claim can be found in [9], where it is stated in a more general form than required here.

Let $a,h$, and m be defined in terms of new parameters $a_0$ and $\varphi$ and $H\ne 0$, with the condition that $4a_{0}H>-1$, in the following way:

$$\left\{\begin{array}{c}a:=-\frac{a_{0}cos\varphi }{1+2a_{0}H(1-cos\varphi )},\hfill \\ h:=\frac{a_{0}sin\varphi }{1+2a_{0}H(1-cos\varphi )},\hfill \\ m:=\sqrt{\frac{1}{1+2a_{0}H(1-cos\varphi )}}.\hfill \end{array}\right.$$

(36)

Then, from the expression for B, we straightforwardly obtain:

$$B(a_0,\varphi )=\frac{\sqrt{1+4a_{0}H}}{1+2a_{0}H(1-cos\varphi )}.$$

(37)

For the particular values $a=-a_0$, $h=0$, and $m=1$, i.e., $\varphi =0$ in (36), we obtain a Delauney’s surface with the constant mean curvature $H\ne 0$ that belongs to the Bour’s family $\left[U\right](a,h,m)$, which we shall denote by $R\left(a_0\right)$.

Lemma 1.

Let $a_0\in \mathbf{R}$ and $\varphi \in [0,2\pi ]$ be arbitrary and a, h, and m be defined by (36). Then: (a) For every $\varphi \in [0,2\pi ]$

$$U(a,h,m)=U(-a_0,0,1),$$

(38)

that is, for every Delauney’s surface $R\left(a_0\right)$ defined by (23), there exists a one-parameter family of helicoidal $CMC$ surfaces, all with the same mean curvature H, and that family is exactly the Lawson family of the surface $R\left(a_0\right)$. (b) For an arbitrary helicoidal $CMC$ surface M generated by (23), there exists a Delauney surface $R\left(a_0\right)$ and a real number $\varphi \in [0,2\pi ]$ such that M is an element of the Lawson family of the surface $R\left(a_0\right)$.

Proof. 

(a) Straightforwardly from (35) and by using (37), we get:

$$\begin{array}{c}\hfill U^2(a,h,m)=\frac{1+2a_{0}H+\sqrt{1+4a_{0}H}sin\left(2\right|H\left|\sigma \right)}{2H^2}=U^2(-a_0,0,1),\end{array}$$

so (38) is valid. By continuous transformation of $\varphi \in [0,2\pi ]$ in (36), we obtain a family of helicoidal surfaces with the same constant mean curvature H, all isometric to $R\left(a_0\right)$ and including $R\left(a_0\right)$. From the uniqueness of the Lawson family of the surface $R\left(a_0\right)$, we see that this part of the claim is true. (b) We now start with an arbitrary helicoidal CMC surface with the mean curvature H. It is an element of some Bour’s family $\overline{\left[U\right]}(\overline{a},\overline{h},\overline{m}).$ The goal is to find a Delauney surface $R\left(a_0\right)$ with the mean curvature H and an isometric deformation such that the helicoidal surface we started with is generated, at some moment $\varphi \in [0,2\pi ]$ of that deformation. In other words, we want to express $\varphi$ and $a_0$ in terms of $\overline{a}$, $\overline{h}$, and $\overline{m}$. Coefficients of the second fundamental form of the helicoidal surfaces $U[\overline{a},\overline{h},\overline{m}]$ are

$$\left\{\begin{array}{cc}e=\hfill & \frac{1}{x^{2}y}(h^2-x^3{x}^{″})=H-\frac{\overline{a}}{{\overline{m}}^2{\overline{U}}^2},\hfill \\ f=\hfill & -\frac{\overline{h}}{{\overline{m}}^2\overline{U}},\hfill \\ g=\hfill & \frac{1}{{\overline{m}}^2}(\overline{a}+H{\overline{m}}^2{\overline{U}}^2)=\frac{\overline{a}}{{\overline{m}}^2}+H{\overline{U}}^2.\hfill \end{array}\right.$$

(39)

The metric of the surface $R\left(a_0\right)$ is induced by $U(-a_0,0,1)$, such that $U=\overline{U}$, because all surfaces that appear during isometric deformation must have the same metric. Let $e_0$, $f_0=0$ and $g_0$ be the coefficients of the second fundamental form of $R\left(a_0\right)$. Reparameterization $d\sigma =Udp$ reduces its first fundamental form (16) to

$$d{s}^2=U^2(d{p}^2+d{\tau }^2),$$

so the surface is parameterized by isothermal parameters. From the Lawson theorem, we obtain the family corresponding to $R\left(a_0\right)$ that depends on $a_0$ and $\varphi \in [0,2\pi ]$. Straightforwardly, the coefficients of the second fundamental form of its elements are:

$$\left\{\begin{array}{cc}e=\hfill & H+cos\varphi (e_0-H),\hfill \\ f=\hfill & \frac{U}{2}sin\varphi (\frac{g_0}{U^2}-e_0),\hfill \\ g=\hfill & H{U}^2+cos\varphi (g_0-H{U}^2).\hfill \end{array}\right.$$

(40)

By comparing (40) and (39) and since all elements of the family are isometric, i.e., $U=\overline{U}$, we obtain

$$\begin{array}{cc}\hfill e_0=& -\frac{\overline{a}}{U^2{\overline{m}}^{2}cos\varphi }+H,\hfill \\ \hfill g_0=& H{U}^2+\frac{\overline{a}}{{\overline{m}}^{2}cos\varphi },\hfill \\ \hfill \overline{h}=& -\frac{{\overline{m}}^2{U}^2}{2}sin\varphi (\underset{2\frac{\overline{a}}{{\overline{m}}^2{U}^{2}cos\varphi }}{\underbrace{\frac{g_0}{U^2}-e_0}})=-\overline{a}\frac{sin\varphi }{cos\varphi }.\hfill \end{array}$$

Now, let us regard the Delauney’s surface $R\left(a_0\right)$ which is obtained in Lawson’s isometric deformation for $\varphi =0$, with $\overline{a}=-a_0$, $h=0$, and $\overline{m}=1$. From (36), we further obtain that:

$$\overline{a}=-a_{0}cos\varphi {\overline{m}}^2.$$

Now, if we take $\varphi$ and $a_0$ as

$$\left\{\begin{array}{cc}\overline{h}\hfill & =-\overline{a}\frac{sin\varphi }{cos\varphi },\hfill \\ a_0\hfill & =-\frac{\overline{a}}{cos\varphi {\overline{m}}^2},\hfill \end{array}\right.$$

(41)

a straightforward computation shows that for $a_0$, $\varphi$, $\overline{a}$, $\overline{h}$, and $\overline{m}$, the relations (36) are satisfied.

Hence, if we take $a:=\overline{a}$, $h:=\overline{h}$, and $m:=\overline{m}$, we obtain the Lawson’s family of helicoidal $CMC$ surfaces with the mean curvature $H\ne 0$ whose starting point is the Delauney’s surface $R\left(a_0\right)$, where $a_0$ is defined as (41), which ends the proof. □

Let $B_0$ be the value of B at the moment $\varphi =0$:

$$B_0:=\sqrt{1+4a_{0}H}.$$

(42)

Then, (36) and(37) reduce to:

$$\begin{array}{cc}\hfill m^2& =\frac{1}{1+2H\frac{\left(B_0^2-1\right)(1-cos\varphi )}{4H}}=\frac{2}{2+\left(B_0^2-1\right)(1-cos\varphi )},\hfill \\ \hfill h& =\frac{\left(B_0^2-1\right)sin\varphi }{4H+2H\left(B_0^2-1\right)(1-cos\varphi )},\hfill \\ \hfill B& =\frac{2B_0}{2+\left(B_0^2-1\right)(1-cos\varphi )}.\hfill \end{array}$$

(43)

We noted that in the each Bour’s family $\left[U\right](a,m,h)$, there exists one Delauney’s surface which we may deform isometrically to a helicoidal surface by fixing $m=1$ and varying the pitch h. Previous claims prove that via isometric deformation of the Delauney’s surface $R\left(a_0\right)$ through the Lawson’s family, we obtain helicoidal CMC surfaces that share the same mean curvature with the original Delauney’s surface. Moreover, for any mean curvature $H\ne 0$, a helicoidal CMC surface of that curvature is generated by an isometric deformation of some Delauney’s surface of the same mean curvature.

By taking unduloids, nodoids, and as a boundary case, a cylinder with a fixed mean curvature $H\ne 0$, we may regard parameter $\varphi \in [0,2\pi ]$ as the time, for particular choices of the constant $B_0$ in (43), and continuously shift it, which provides us with interesting examples of helicoidal CMC surfaces, all with the same mean curvature H; see Figure 5, Figure 6, Figure 7 and Figure 8. The isometric deformation in the case of a sphere would be of no interest, as it stays in the same position, the starting sphere for every moment $\varphi \in [0,2\pi ]$.

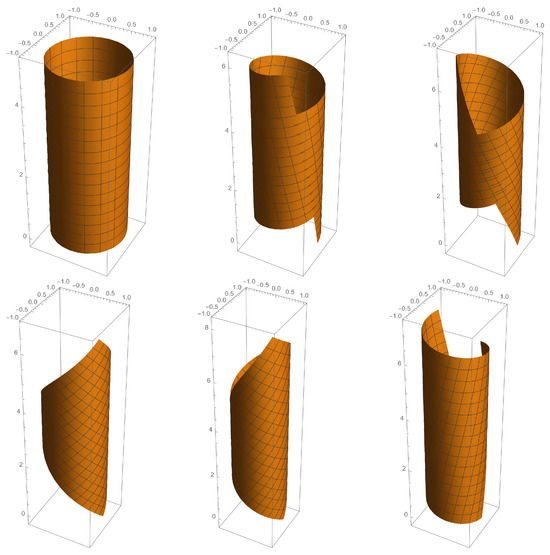
Figure 5. We consider the case of the cylinder as the limit case where $4a_{0}H=-1$. The figure shows the isometric deformation of the cylindric surface $R(-0.5)$ with the mean curvature $H=\frac{1}{2}$, for $(\sigma ,\tau )\in (0,5)\times (0,2\pi )$. Other moments of deformation shown in the figure are at $\varphi =\frac{15\pi }{8}$, $\varphi =\frac{7\pi }{4}$, $\varphi =\frac{3\pi }{2}$, $\varphi =\frac{11\pi }{8}$, and $\varphi =\frac{9\pi }{8}$, respectively.

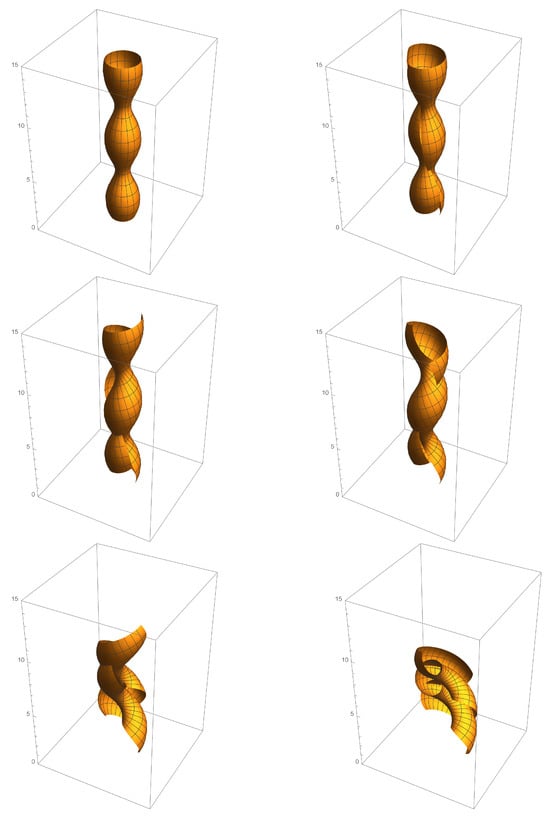
Figure 6. Isometric deformation of the unduloid $R(-0.42)$ with $H=\frac{1}{2}$, for $(\sigma ,\tau )\in (0,15)\times (0,2\pi )$. Other moments of the deformation shown in the figure are at $\varphi =\frac{15\pi }{8}$, $\varphi =\frac{7\pi }{4}$, $\varphi =\frac{13\pi }{8}$, $\varphi =\frac{11\pi }{8}$, and $\varphi =\frac{5\pi }{4}$, respectively.

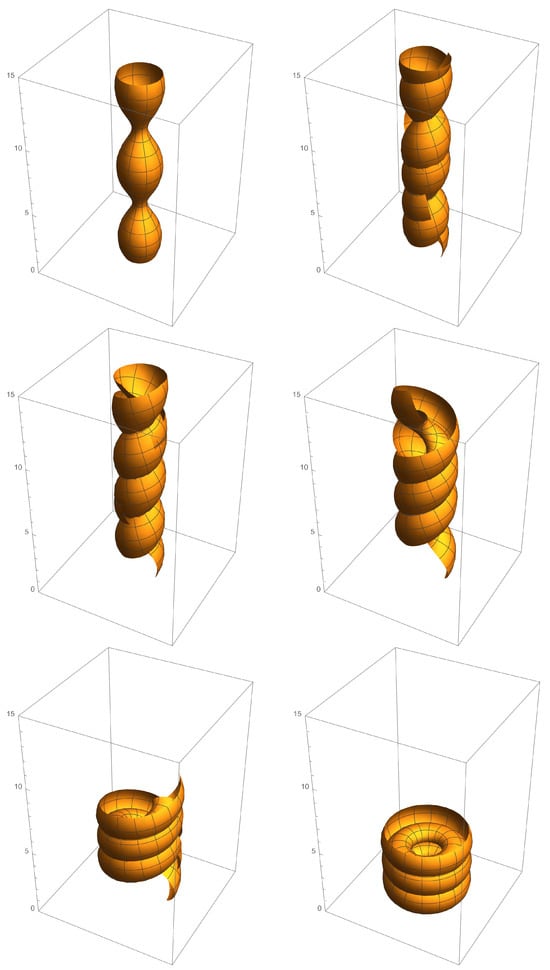
Figure 7. Isometric deformation of the unduloid $R(-0.375)$ with the mean curvature $H=\frac{1}{2}$, parameterized by $(\sigma ,\tau )\in (0,15)\times (0,4\pi )$. Other moments of the deformation shown in figure are at $\varphi =\frac{7\pi }{4}$, $\varphi =\frac{13\pi }{8}$, $\varphi =\frac{11\pi }{8}$, $\varphi =\frac{9\pi }{8}$ and $\varphi =\pi$, respectively.

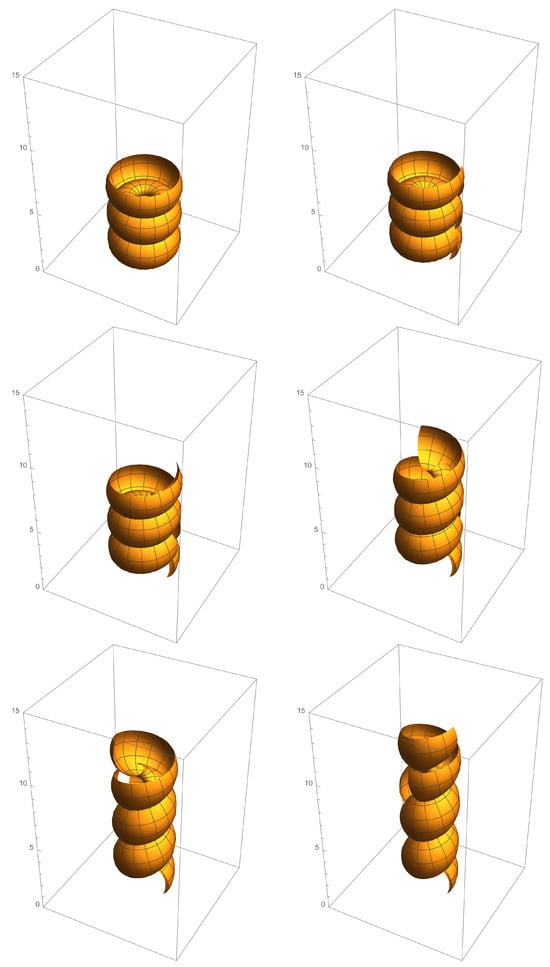
Figure 8. Isometric deformation of the nodoid $R\left(0.625\right)$ with the mean curvature $H=\frac{1}{2}$, for $(\sigma ,\tau )\in (0,15)\times (0,2\pi )$. Other moments of the deformation showed in figure are at $\varphi =\frac{\pi }{16}$, $\varphi =\frac{\pi }{8}$, $\varphi =\frac{\pi }{4}$, $\varphi =\frac{3\pi }{8}$ and $\varphi =\frac{\pi }{2}$, respectively.

For further applications of this topic, specifically in the area of computer graphics, it is of interest to fully describe the algorithmic manner in which helicoidal CMC surfaces are generated through the deformation of Delauney’s surfaces (that is, how Figure 5, Figure 6, Figure 7 and Figure 8 are created and how many similar figures may be created).

We start with a fixed mean curvature H and (23) and the Delauney surfaces of that mean curvature which we want to deform (with parameter $B_0$, i.e., $a_0$ via (42)). By continuous movement of parameter $\varphi$ from 0 to $2\pi$ (which continuously changes parameters m, B, and h in formulas (43)) and substituting those values into (24), we obtain new helicoidal surfaces, all with the same mean curvature H. In the images in this paper, we have restricted ourselves to choices $ϵ={ϵ}_{\lambda }=1$ in (23) and to the time intervals for $\varphi$ where the pitch h is positive, albeit the images in the time interval for $\varphi$ where the pitch h is negative are basically the same up to an isometry of ${\mathbf{R}}^3$.

It would be of interest to see if it is possible to visualize these deformations through real-time animations in some programs, but major problems we encounter here lie in the great time consumption even for creating one surface (frame in the moment of time $\varphi$), which arises due to the complexity of the integrals from definitions of functions $\theta (\sigma ,\tau )$ and $\lambda \left(\sigma \right)$ as well as singularities in parameterizations which may occur for certain values of $\varphi$ in certain cases, as described in [2]. So at the moment, we find that the best way of visualizing these deformations is through the frame-by-frame method, as described here, and we provide Mathematica codes (the link to the codes is here: https://github.com/Fica991/Visualisation-of-isometric-deformations-of-helicoidal-CMC-surfaces-Mathematica-codes (accessed on 1 July 2024)) for all the figures in this paper.