Remark on Intuitionistic Fuzzy Temporal Modal Topological Structures

Abstract

In a series of papers, we have discussed the concept of a modal topological structure modified, extended and illustrated by examples from intuitionistic fuzzy sets. Here, the concept of a temporal modal topological structure is introduced and illustrated with four different intuitionistic fuzzy temporal modal topological structures. These structures are based on intuitionistic fuzzy topological, temporal and modal operators. They are extensions of the temporal topological structures as well as of the modal topological structures.

1. Introduction

In the middle of 2022, the author introduced the idea of Modal Topological Structure (MTS) in [1] and illustrated it with Intuitionistic Fuzzy MTSs (IFMTSs). This idea was based on Kazimierz Kuratowski’s definitions of topological structures in [2] (see also [3,4,5]). In a series of papers by the author, different examples of IFMTSs were introduced.

By the end of 2022, the idea for MTS (and, respectively, for IFMTS) was modified by changing the modal operators with temporal ones in [6]; as a result, the concept of a Temporal Topological Structure (TTS) was developed and respectively illustrated with examples of Intuitionistic Fuzzy Temporal Topological Structures (IFTTSs).

As mentioned in [6], the first time the concept of a “temporal topology” was used was probably in Robin Le Poidevin’s paper [7], while the concept of a temporal intuitionistic fuzzy topology in Šostak’s sense was discussed by Fatih Kutlu and Tunay Bilgin in [8,9,10]. Other results in the area of intuitionistic fuzzy topology are described in [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. More precisely, in [11], a standard IF-topological structure was described for the first time; in [12,13,14,15,20,24,25], some types of IF-topological spaces were discussed; and in [16,17,19,21,26], some properties of these spaces (e.g., compactness, connectedness, and others) were studied. The category of IF-topological space was further introduced in [18], with the properties of the mappings over IF topological spaces elaborated in [22,23] and IF-metric spaces introduced in [27].

In Section 2 of the present paper, the ideas of MTS (respectively, IFMTS) and TTS (respectively, IFTTS) are united by defining the concept of a Temporal Modal Topological Structure (TMTS), which is illustrated with four Intuitionistic Fuzzy Temporal Modal Topological Structures (IFTMTSs). This is the first time that these structures have been reported to simultaneously contain three different types of intuitionistic fuzzy operators, namely, topological, temporal, and modal.

In Section 3, the idea of TMTS (respectively, IFTMTS) is extended to multi-Temporal Modal Topological Structure (multi-TMTS) featuring some temporal operators that satisfy an additional condition, and is illustrated with some Intuitionistic Fuzzy multi-Temporal Modal Topological Structures (IF-multi-TMTSs).

In the Conclusion, some potential applications of the new objects and ideas are described, paving the way to the future development of the present research.

The reader can find all the necessary definitions in [1,6,28]. For clarity of the exposition, we walk through only some of the most basic definitions.

Definition 1

(Closure type). Let us consider a set X with a minimal subset $O^{\ast }$ and the set of all its subsets $\mathcal{P}(X)$. We say that the operator $\mathcal{Z}:\mathcal{P}(X)\to \mathcal{P}(X)$ from topological, modal, or temporal type is of closure type ($cl$-type) if, for each set $A\in \mathcal{P}(X)$, we have

$$A\subseteq \mathcal{Z}(A),\mathcal{Z}(O^{\ast })=O^{\ast }.$$

Definition 2

(Interior type). Under the same suppositions for the set X with a minimal subset $O^{\ast }$ and the set of all its subsets $\mathcal{P}(X)$, we say that the operator $\mathcal{Z}:\mathcal{P}(X)\to \mathcal{P}(X)$ from topological, modal, or temporal type is of interior type ($in$-type) if

$$\mathcal{Z}(A)\subseteq A,\mathcal{Z}(X)=X.$$

Thus, the topological, temporal, and modal operators $\mathcal{C},{\mathcal{C}}^{\ast }$, and ◊ (“Possibility”) from [1,6] are of $cl$-type, while the operators $\mathcal{I},{\mathcal{I}}^{\ast }$, and □ (“Necessity”) are of $in$-type.

In this paper, the definitions related to the concept of topological structure are discussed in two aspects: general and particular. The general aspect is based on an arbitrarily fixed set X, while the particular aspect is related to intuitionistic fuzziness. To distinguish the particular case from the general, the adopted denotation of the universal set for the particular case is E.

2. Four Intuitionistic Fuzzy Temporal Modal Topological Structures

Let us consider a fixed set X over which the standard set-theoretical operation “negation” (¬) is defined. Following [6], we assume that we have two operations, $\Delta ,\nabla :\mathcal{P}(X)\times \mathcal{P}(X)\to \mathcal{P}(X)$, defined in such a way that for every two sets $A,B\in \mathcal{P}(X)$ we have

$$\begin{array}{cc}\hfill A\nabla B& =\neg (\neg A\Delta \neg B),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill A\Delta B& =\neg (\neg A\nabla \neg B).\hfill \end{array}$$

(2)

Let the operation $\Delta$ generate the $cl$-topological operator $\mathcal{O}$ and let the operation ∇ generate the $in$-topological operator $\mathcal{Q}$. For example, if operation $\Delta$ is the operation “union” (∪), then operator $\mathcal{O}$ is the $cl$-topological operator $\mathcal{C}$, the $cl$-modal operator ◊, or the $cl$-intuitionistic fuzzy temporal operator ${\mathcal{C}}^{\ast }$; if operation ∇ is the operation “intersection” (∩), then operator $\mathcal{Q}$ is the $in$-topological operator $\mathcal{I}$, the $in$-modal operator □, or the $in$-intuitionistic fuzzy temporal operator ${\mathcal{I}}^{\ast }$.

It must be mentioned here that many operations that do not satisfy Equalities (1) and (2) are defined over the Intuitionistic Fuzzy Sets (IFSs; see, e.g., [28]). However, some of these satisfy the following modifications of (1) and (2) for every two IFSs $A,B$:

$$\begin{array}{cc}\hfill \neg \neg A\nabla \neg \neg B& =\neg (\neg A\Delta \neg B),\hfill \\ \hfill \neg \neg A\Delta \neg \neg B& =\neg (\neg A\nabla \neg B).\hfill \end{array}$$

In this case, the well-known equality $\neg \neg A=A$ is not necessarily valid for each IFS A as well. As discussed in [28], this is an additional argument for applying the name “intuitionistic” to the IFSs. In the present research, no such operations are used.

By analogy with (1) and (2), it is assumed that for each set A, we have

$$\begin{array}{cc}\hfill \mathcal{Q}(A)& =\neg (\mathcal{O}(\neg A)),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathcal{O}(A)& =\neg (\mathcal{Q}(\neg A)).\hfill \end{array}$$

(4)

Now, following [2], we assume that the $cl$-operators satisfy the following conditions:

C1

$\mathcal{O}(A\Delta B)=\mathcal{O}(A)\Delta \mathcal{O}(B)$,

C2

$A\subseteq \mathcal{O}(A),$

C3

$\mathcal{O}(\mathcal{O}(A))=\mathcal{O}(A)$,

C4

$\mathcal{O}(O^{\ast })=O^{\ast }$

and that the $in$-operators satisfy the conditions

I1

$\mathcal{Q}(A\Delta B)=\mathcal{Q}(A)\Delta \mathcal{Q}(B)$,

I2

$\mathcal{Q}(A)\subseteq A,$

I3

$\mathcal{Q}(\mathcal{Q}(A))=\mathcal{Q}(A)$,

I4

$\mathcal{Q}(X)=X.$

In [1], two groups of C-conditions are used, namely, for the (intuitionistic fuzzy topological) operator $\mathcal{C}$ and the (intuitionistic fuzzy modal) operator ◊; likewise, two groups of I-conditions, for the (intuitionistic fuzzy topological) operator $\mathcal{I}$ and for the (intuitionistic fuzzy modal) operator □, are used.

In [6], two groups of C-conditions are used, for the operator $\mathcal{C}$ and the (intuitionistic fuzzy temporal topological) operator ${\mathcal{C}}^{\ast }$; two groups of I-conditions are employed as well: one for the operator $\mathcal{I}$, and one for the operator ${\mathcal{I}}^{\ast }$. One C-group and one I-group are used when working with the operators $\mathcal{C}$ and ${\mathcal{I}}^{\ast }$; analogously, one I-group and one C-group are used when working with the operators $\mathcal{I}$ and ${\mathcal{C}}^{\ast }$. To denote the use of $cl$-topological and $cl$-temporal topological operators for a structure, we use the record “$cl$-$cl$”, and write “$cl$-$in$” to indicate the use of $cl$-topological and $in$-temporal-topological operators for a structure. For the two other remaining cases, we write “$in$-$cl$” and “$in$-$in$”, respectively. Thus, for the sake of simplicity, we use the following two notations below: $\alpha ,\beta$, where each of them—in this order—denotes the type of the operator, namely, closure type or interior type (formally, $\alpha ,\beta \in \{cl,in\}$, where the first symbol defines the topological aspect of the structure and the second symbol $\beta$ defines the temporal aspect of the structure). Thus, when we use the denotation “$\alpha$-$\beta$-structure” it is defined by the $\alpha$-topological operator and the $\beta$-temporal operator, for four combinations altogether.

In any case, we have the eight conditions from Kuratowski’s type C1–C4 and/or I1–I4, and add to them the following ninth supplemental condition:

$$\begin{array}{c}\hfill \mathcal{Z}(\mathcal{Y}(A))=\mathcal{Y}(\mathcal{Z}(A)).\end{array}$$

(5)

Here, $\mathcal{Y}$ and $\mathcal{Z}$ are two operators from different types (either topological and modal or topological and temporal-topological types).

In general, the TTS over the set X is denoted by $\langle \mathcal{P}(X),\mathcal{O},\Delta ,{\mathcal{Q}}^{\ast }\rangle$, where $\mathcal{O}$ is a topological operator from $\alpha$-type and ${\mathcal{Q}}^{\ast }$ is a temporal operator from $\beta$-type, where $\alpha ,\beta \in \{cl,in\}$.

As we are working here with three operators (standard topological, temporal-topological, and modal), we must have three groups of Kuratowski’s conditions. The operators must satisfy Equalities (3) and (4), and we have three equalities (one for each the pair operators) of the same form as Equality (5).

In the present paper, we introduce as particular cases some TTSs from the area of IFSs. For this purpose, it should be mentioned that when we have a fixed universe E and its subset A, the set

$$A^{\ast }=\{\langle x,{\mu }_A(x),{\nu }_A(x)\rangle |x\in E\},$$

where

$$0\le {\mu }_A(x)+{\nu }_A(x)\le 1$$

is called an IFS, where for $A^{\ast }$ the functions ${\mu }_A:E\to [0,1]$ and ${\nu }_A:E\to [0,1]$ represent the degree of membership (validity, etc.) and non-membership (non-validity, etc.) of element $x\in E$ with respect to the set A.

Below, for simplicity, we denote the IFS $A^{\ast }$ as A, because in what follows we use only the IFS, not the subset of E for which the membership and non-membership functions are used.

The IFSs have different geometrical interpretations. The most suitable is shown in Figure 1. It shows that two degrees are juxtaposed to each element $x\in E$, respectively, a degree of membership ${\mu }_A(x)$ and a degree of non-membership ${\nu }_A(x)$.

As mentioned in [6], for a fixed universe E and a temporal scale T, the object

$$A(T)=\{\langle \langle x,t\rangle ,{\mu }_A(x,t),{\nu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\}$$

is called a Temporal IFS (TIFS), where ${\mu }_A(x,t)$ and ${\nu }_A(x,t)$ are the degrees of membership and non-membership, respectively, of the element $x\in E$ at the time-moment $t\in T$, meaning that ${\mu }_A(x,t)+{\nu }_A(x,t)\le 1$ for every $\langle x,t\rangle \in E\times T$. The temporal scale T can be some fixed subset of positive real numbers.

Temporal IFSs represent an extension of IFSs. They were introduced by the author in [29], described in more detail in [28], and have subsequently become an object of research by numerous other authors (see, e.g., [30,31,32]).

In [6], the unary operation “negation” and the binary operations “union” and “intersection” over two TIFSs, as well as the relations between two IFTTSs, were defined as follows:

$$\neg A(T)=\{\langle \langle x,t\rangle ,{\nu }_A(x,t),{\mu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\},$$

$$A(T)\cup B(T)=\{\langle \langle x,t\rangle ,max({\mu }_A(x,t),{\mu }_B(x,t)),min({\nu }_A(x,t),{\nu }_A(x,t))\rangle ,|\langle x,t\rangle \in E\times T\},$$

$$A(T)\cap B(T)=\{\langle \langle x,t\rangle ,min({\mu }_A(x,t),{\mu }_B(x,t)),max({\nu }_A(x,t),{\nu }_A(x,t))\rangle ,|\langle x,t\rangle \in E\times T\},$$

$$\begin{array}{ccc}A(T)\subseteq B(T)\hfill & \mathrm{iff}\hfill & (\forall x\in E)(\forall t\in T)({\mu }_{A(T)}(x,t)\le {\mu }_{B(T)}(x,t)\hfill \\ & & \&{\nu }_{A(T)}(x,t)\ge {\nu }_{B(T)}(x,t));\hfill \\ A(T)\supseteq B(T)\hfill & \mathrm{iff}\hfill & B(T)\subseteq A(T);\hfill \\ A(T)=B(T)\hfill & \mathrm{iff}\hfill & (\forall x\in E)(\forall t\in T)({\mu }_{A(T)}(x,t)={\mu }_{B(T)}(x,t)\hfill \\ & & \&{\nu }_{A(T)}(x,t)={\nu }_{B(T)}(x,t)).\hfill \end{array}$$

Several other operations from each of these types were defined there, as well. Here, as in [6], we work only with the simplest forms of these operations, as described above.

The geometrical interpretation of the TIFS that corresponds to the one from Figure 1 is shown in Figure 2 (in two different ways for the sake of greater clarity).

Following [28], let us define

$$\begin{array}{cc}\hfill O^{\ast }(T)& =\{\langle \langle x,t\rangle ,0,1\rangle |\langle x,t\rangle \in E\times T\},\hfill \\ \hfill E^{\ast }(T)& =\{\langle \langle x,t\rangle ,1,0\rangle |\langle x,t\rangle \in E\times T\}.\hfill \end{array}$$

Below, we use the set

$$\mathcal{P}(E^{\ast }(T))=\{A(T)|A(T)\subseteq E^{\ast }(T)\}.$$

The standard intuitionistic fuzzy topological operators have the following forms:

$$\begin{array}{cc}\hfill \mathcal{C}(A(T))& =\{\langle \langle x,t\rangle ,\underset{y\in E}{sup}{\mu }_{A(T)}(y,t),\underset{y\in E}{inf}{\nu }_{A(T)}(y,t)\rangle |\langle x,t\rangle \in E\times T\},\hfill \\ \hfill \mathcal{I}(A(T))& =\{\langle \langle x,t\rangle ,\underset{y\in E}{inf}{\mu }_{A(T)}(y,t),\underset{y\in E}{sup}{\nu }_{A(T)}(y,t)\rangle |\langle x,t\rangle \in E\times T\},\hfill \end{array}$$

while the intuitionistic fuzzy temporal topological operators over the TIFSs have the forms

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\ast }(A(T))& =\{\langle \langle x,t\rangle ,\underset{u\in T}{sup}{\mu }_{A(T)}(x,u),\underset{u\in T}{inf}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\},\hfill \\ \hfill {\mathcal{I}}^{\ast }(A(T))& =\{\langle \langle x,t\rangle ,\underset{u\in T}{inf}{\mu }_{A(T)}(x,u),\underset{u\in T}{sup}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\}.\hfill \end{array}$$

The intuitionistic fuzzy modal operators over TIFSs have the following forms:

$$\begin{array}{cc}\hfill ◻A(T)& =\{\langle \langle x,t\rangle ,{\mu }_{A(T)}(x,t),1-{\mu }_{A(T)}(x,t)\rangle |\langle x,t\rangle \in E\times T\},\hfill \\ \hfill ◊A(T)& =\{\langle \langle x,t\rangle ,1-{\nu }_{A(T)}(x,t),{\nu }_{A(T)}(x,t)\rangle |\langle x,t\rangle \in E\times T\}.\hfill \end{array}$$

We illustrate all definitions above with the following example.

Example 1.

Let the universal set $E=\{a,b,c\}$ and $T=\{3,7\}.$ Then,

$$E^{\ast }(T)=\{\langle \langle a,3\rangle ,1,0\rangle ,\langle \langle a,7\rangle ,1,0\rangle ,\langle \langle b,3\rangle ,1,0\rangle ,\langle \langle b,7\rangle ,1,0\rangle ,\langle \langle c,3\rangle ,1,0\rangle ,\langle \langle c,7\rangle ,1,0\rangle \}.$$

Let

$$\begin{array}{cc}\hfill A(T)=& \{\langle \langle a,3\rangle ,0.2,0,5\rangle ,\langle \langle a,7\rangle ,0.7,0.1\rangle ,\langle \langle b,3\rangle ,0.4,0.4\rangle ,\langle \langle b,7\rangle ,0.5,0.3\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.6,0.4\rangle ,\langle \langle c,7\rangle ,0.3,0.4\rangle \},\hfill \\ \hfill B(T)=& \{\langle \langle a,3\rangle ,0.5,0,3\rangle ,\langle \langle a,7\rangle ,0.4,0.1\rangle ,\langle \langle b,3\rangle ,0.2,0.6\rangle ,\langle \langle b,7\rangle ,0.7,0.2\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.6,0.3\rangle ,\langle \langle c,7\rangle ,0.5,0.4\rangle \}.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill A(T)\cap B(T)=& \{\langle \langle a,3\rangle ,0.2,0,5\rangle ,\langle \langle a,7\rangle ,0.4,0.1\rangle ,\langle \langle b,3\rangle ,0.2,0.6\rangle ,\langle \langle b,7\rangle ,0.5,0.3\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.6,0.4\rangle ,\langle \langle c,7\rangle ,0.3,0.4\rangle \},\hfill \\ \hfill A(T)\cup B(T)=& \{\langle \langle a,3\rangle ,0.5,0,3\rangle ,\langle \langle a,7\rangle ,0.7,0.1\rangle ,\langle \langle b,3\rangle ,0.4,0.4\rangle ,\langle \langle b,7\rangle ,0.7,0.2\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.6,0.3\rangle ,\langle \langle c,7\rangle ,0.5,0.4\rangle \},\hfill \\ \hfill ◻A(T)=& \{\langle \langle a,3\rangle ,0.2,0,8\rangle ,\langle \langle a,7\rangle ,0.7,0.3\rangle ,\langle \langle b,3\rangle ,0.4,0.6\rangle ,\langle \langle b,7\rangle ,0.5,0.5\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.6,0.4\rangle ,\langle \langle c,7\rangle ,0.3,0.7\rangle \},\hfill \\ \hfill ◊B(T)=& \{\langle \langle a,3\rangle ,0.7,0,3\rangle ,\langle \langle a,7\rangle ,0.9,0.1\rangle ,\langle \langle b,3\rangle ,0.4,0.6\rangle ,\langle \langle b,7\rangle ,0.8,0.2\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.7,0.3\rangle ,\langle \langle c,7\rangle ,0.6,0.4\rangle \},\hfill \\ \hfill \mathcal{C}(A(T))=& \{\langle \langle a,3\rangle ,0.6,0,4\rangle ,\langle \langle a,7\rangle ,0.7,0.1\rangle ,\langle \langle b,3\rangle ,0.6,0.4\rangle ,\langle \langle b,7\rangle ,0.7,0.1\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.6,0.4\rangle ,\langle \langle c,7\rangle ,0.7,0.1\rangle \},\hfill \\ \hfill \mathcal{I}(B(T))=& \{\langle \langle a,3\rangle ,0.2,0,6\rangle ,\langle \langle a,7\rangle ,0.4,0.4\rangle ,\langle \langle b,3\rangle ,0.2,0.6\rangle ,\langle \langle b,7\rangle ,0.4,0.4\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.2,0.6\rangle ,\langle \langle c,7\rangle ,0.4,0.4\rangle \},\hfill \\ \hfill {\mathcal{C}}^{\ast }(A(T))=& \{\langle \langle a,3\rangle ,0.7,0,1\rangle ,\langle \langle a,7\rangle ,0.7,0.1\rangle ,\langle \langle b,3\rangle ,0.5,0.3\rangle ,\langle \langle b,7\rangle ,0.5,0.3\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.6,0.4\rangle ,\langle \langle c,7\rangle ,0.6,0.4\rangle \},\hfill \\ \hfill {\mathcal{I}}^{\ast }(B(T))=& \{\langle \langle a,3\rangle ,0.4,0,3\rangle ,\langle \langle a,7\rangle ,0.4,0.3\rangle ,\langle \langle b,3\rangle ,0.2,0.6\rangle ,\langle \langle b,7\rangle ,0.2,0.6\rangle ,\hfill \\ & \langle \langle c,3\rangle ,0.4,0.4\rangle ,\langle \langle c,7\rangle ,0.4,0.4\rangle \}.\hfill \end{array}$$

Below, as a notation of TMTS, we use records in the form $\alpha$-$\beta$-$\gamma$ (in this order), where $\alpha ,\beta ,\gamma \in \{cl,in\}$. The first symbol $(\alpha )$ represents the type (closure or interior) of the topological operator, the second symbol $(\beta )$ represents the temporal-topological operator, and the third symbol $(\gamma )$ represents the modal operator.

Therefore, the $\alpha$-$\beta$-$\gamma$-TMTS over the set X is denoted by $\langle \mathcal{P}(X),\mathcal{O},\Delta ,{\mathcal{Q}}^{\ast },\circ \rangle$, where $\mathcal{O}$ is a topological operator from $\alpha$-type generated by operation $\Delta$, ${\mathcal{Q}}^{\ast }$ is a temporal operator from $\beta$-type, and ∘ is a modal operator from $\gamma$-type.

It must be mentioned here that in the particular case of intuitionistic fuzziness we are not able to construct a structure with the participation of the topological operator $\mathcal{C}$ and the temporal operator ${\mathcal{I}}^{\ast }$ or with the participation of the topological operator $\mathcal{I}$ and the temporal operator ${\mathcal{C}}^{\ast }$. This is because the equalities

$$\begin{array}{cc}\hfill \mathcal{C}({\mathcal{I}}^{\ast }(A))& ={\mathcal{I}}^{\ast }(\mathcal{C}(A)),\hfill \\ \hfill \mathcal{I}({\mathcal{C}}^{\ast }(A))& ={\mathcal{C}}^{\ast }(\mathcal{I}(A)),\hfill \end{array}$$

(6)

which are particular cases of condition (5), do not hold. The argument for this is that, for any numerical set $x_{1,1},x_{1,2},\dots ,x_{m,n}$, the equality

$$\underset{1\le i\le m}{max}\underset{1\le j\le n}{min}{x}_{i,j}=\underset{1\le i\le m}{min}\underset{1\le j\le n}{max}{x}_{i,j}$$

does not necessarily hold. For this reason, the structures $\langle \mathcal{P}(E^{\ast }(T)),\mathcal{C},\cup ,{\mathcal{I}}^{\ast }\rangle$, $\langle \mathcal{P}(E^{\ast }(T)),\mathcal{I},\cap ,{\mathcal{C}}^{\ast }\rangle$ and their extensions with the addition of modal operators are impossible. An open problem is whether other intuitionistic fuzzy operators exist for which the two equalities in (6) hold true.

We now illustrate the new concept of TMTS with four particular cases of these structures from the area of intuitionistic fuzziness, formulating and proving the following four assertions.

Theorem 1.

For each universe E and each temporal scale T, $\langle \mathcal{P}(E^{\ast }(T)),\mathcal{C},\cup ,{\mathcal{C}}^{\ast },◊\rangle$ is an IF-$cl$-$cl$-$cl$-TMTS.

Proof. 

The validity of conditions C1–C4 for the operator $\mathcal{C}$ is proven in [1]; respectively, the validity of C1–C4 for the temporal operator ${\mathcal{C}}^{\ast }$ is established in [6] and for the modal operator ◊ in [28]. Equality (5) is checked for operators $\mathcal{C}$ and ${\mathcal{C}}^{\ast }$ in [6] and proven for operators $\mathcal{C}$ and ◊ in [1].

Therefore, it remains only to check Equality (5) for operators ${\mathcal{C}}^{\ast }$ and ◊. We have

$$\begin{array}{cc}{\mathcal{C}}^{\ast }(◊A(T))\hfill & ={\mathcal{C}}^{\ast }(◊\{\langle \langle x,t\rangle ,{\mu }_A(x,t),{\nu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & ={\mathcal{C}}^{\ast }(\{\langle \langle x,t\rangle ,1-{\nu }_A(x,t),{\nu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,\underset{u\in T}{sup}(1-{\nu }_A(x,u)),\underset{u\in T}{inf}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,1-\underset{u\in T}{inf}{\nu }_A(x,u),\underset{u\in T}{inf}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◊\{\langle \langle x,t\rangle ,\underset{u\in T}{sup}{\mu }_A(x,u),\underset{u\in T}{inf}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◊{\mathcal{C}}^{\ast }(A(T)),\hfill \end{array}$$

therefore, Equality (5) is valid for operators ${\mathcal{C}}^{\ast }$ and ◊. □

Corollary 1.

For each IFS $A\in E^{\ast }$ and for each temporal scale T,

$$\begin{array}{cc}{\mathcal{C}}^{\ast }(\mathcal{C}(◊A(T)))\hfill & ={\mathcal{C}}^{\ast }(◊\mathcal{C}(A(T)))=◊{\mathcal{C}}^{\ast }(\mathcal{C}(A(T)))=◊\mathcal{C}({\mathcal{C}}^{\ast }(A(T)))\hfill \\ & =\mathcal{C}(◊{\mathcal{C}}^{\ast }(A(T)))=\mathcal{C}({\mathcal{C}}^{\ast }(◊A(T))).\hfill \end{array}$$

Theorem 2.

For each universe E and each temporal scale T, $\langle \mathcal{P}(E^{\ast }(T)),\mathcal{C},\cup ,{\mathcal{C}}^{\ast },◻\rangle$ is an IF-$cl$-$cl$-$in$-TMTS.

Proof. 

As above, the validity of conditions C1–C4 for the operator $\mathcal{C}$ is checked in [1], for the temporal operator ${\mathcal{C}}^{\ast }$ in [6], and for the modal operator □ in [28]. Equality (5) is checked for operators $\mathcal{C}$ and ${\mathcal{C}}^{\ast }$ in [6] and for operators $\mathcal{C}$ and □ in [28]. Thus, here we must check only Equality (5) for operators ${\mathcal{C}}^{\ast }$ and □. We have

$$\begin{array}{cc}{\mathcal{C}}^{\ast }(◻A(T))\hfill & ={\mathcal{C}}^{\ast }(◻\{\langle \langle x,t\rangle ,{\mu }_A(x,t),{\nu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & ={\mathcal{C}}^{\ast }(\{\langle \langle x,t\rangle ,{\mu }_A(x,t),1-{\mu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,\underset{u\in T}{sup}{\mu }_A(x,u),\underset{u\in T}{inf}(1-{\mu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,\underset{u\in T}{sup}{\mu }_A(x,u)),1-\underset{u\in T}{sup}{\mu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◻\{\langle \langle x,t\rangle ,\underset{u\in T}{sup}{\mu }_A(x,u),\underset{u\in T}{inf}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◻{\mathcal{C}}^{\ast }(A(T)),\hfill \end{array}$$

therefore, Equality (5) holds true for operators ${\mathcal{C}}^{\ast }$ and □. This completes the proof. □

Corollary 2.

For each IFS $A\in E^{\ast }$ and for each temporal scale T,

$$\begin{array}{cc}{\mathcal{C}}^{\ast }(\mathcal{C}(◻A(T)))\hfill & ={\mathcal{C}}^{\ast }(◻\mathcal{C}(A(T)))=◻{\mathcal{C}}^{\ast }(\mathcal{C}(A(T)))=◻\mathcal{C}({\mathcal{C}}^{\ast }(A(T)))\hfill \\ & =\mathcal{C}(◻{\mathcal{C}}^{\ast }(A(T)))=\mathcal{C}({\mathcal{C}}^{\ast }(◻A(T))).\hfill \end{array}$$

The next assertions can be proved in the same manner.

Theorem 3.

For each universe E and each temporal scale T, $\langle \mathcal{P}(E^{\ast }(T)),\mathcal{I},\cap ,{\mathcal{I}}^{\ast },◊\rangle$ is an IF-$in$-$in$-$cl$-TMTS.

Proof. 

The validity of conditions I1–I4 for the operator $\mathcal{I}$ is checked in [1] and for the temporal operator ${\mathcal{I}}^{\ast }$ in [6]. The validity of of conditions C1–C4 for the modal operator ◊ is checked in in [28]. Equality (5) is checked for operators $\mathcal{I}$ and ${\mathcal{I}}^{\ast }$ in [6] and for operators $\mathcal{I}$ and ◊ in [28]. Thus, we must check only Equality (5) for operators ${\mathcal{I}}^{\ast }$ and ◊, which is valid because

$$\begin{array}{cc}{\mathcal{I}}^{\ast }(◊A(T))\hfill & ={\mathcal{I}}^{\ast }(◊\{\langle \langle x,t\rangle ,{\mu }_A(x,t),{\nu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & ={\mathcal{I}}^{\ast }(\{\langle \langle x,t\rangle ,1-{\nu }_A(x,t),{\nu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,\underset{u\in T}{inf}(1-{\nu }_A(x,u)),\underset{u\in T}{sup}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,1-\underset{u\in T}{sup}{\nu }_A(x,u)),\underset{u\in T}{sup}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◊\{\langle \langle x,t\rangle ,\underset{u\in T}{inf}{\nu }_A(x,u),\underset{u\in T}{sup}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◊{\mathcal{C}}^{\ast }(A(T)),\hfill \end{array}$$

i.e., (5) is valid for operators ${\mathcal{I}}^{\ast }$ and ◊. □

Corollary 3.

For each IFS $A\in E^{\ast }$ and for each temporal scale T,

$$\begin{array}{cc}{\mathcal{I}}^{\ast }(\mathcal{I}(◊A(T)))\hfill & ={\mathcal{I}}^{\ast }(◊\mathcal{I}(A(T)))=◊{\mathcal{I}}^{\ast }(\mathcal{I}(A(T)))=◊\mathcal{I}({\mathcal{I}}^{\ast }(A(T)))\hfill \\ & =\mathcal{I}(◊{\mathcal{I}}^{\ast }(A(T)))=\mathcal{I}({\mathcal{I}}^{\ast }(◊A(T))).\hfill \end{array}$$

Theorem 4.

For each universe E and each temporal scale T, $\langle \mathcal{P}(E^{\ast }(T)),\mathcal{I},\cap ,{\mathcal{I}}^{\ast },◻\rangle$ is an IF-$in$-$in$-$in$-TMTS.

Proof. 

The validity of conditions I1–I4 for the operator $\mathcal{I}$ is checked in [1], for the temporal operator ${\mathcal{I}}^{\ast }$ in [6], and for the modal operator □ in [28]. Equality (5) is checked for the operators $\mathcal{C}$ and ${\mathcal{C}}^{\ast }$ in [6] and for the operators $\mathcal{C}$ and □ in [28]. Thus, here we must check only Equality (5) for operators ${\mathcal{I}}^{\ast }$ and □, which is valid, as above, because

$$\begin{array}{cc}{\mathcal{I}}^{\ast }(◻A(T))\hfill & ={\mathcal{I}}^{\ast }(\{\langle \langle x,t\rangle ,{\mu }_A(x,t),1-{\mu }_A(x,t)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,\underset{u\in T}{inf}{\mu }_A(x,u),\underset{u\in T}{sup}(1-{\mu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =\{\langle \langle x,t\rangle ,\underset{u\in T}{inf}{\mu }_A(x,u)),1-\underset{u\in T}{inf}{\mu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◻\{\langle \langle x,t\rangle ,\underset{u\in T}{inf}{\mu }_A(x,u),\underset{u\in T}{sup}{\nu }_A(x,u)\rangle |\langle x,t\rangle \in E\times T\})\hfill \\ & =◻{\mathcal{I}}^{\ast }(A(T)),\hfill \end{array}$$

i.e., (5) is valid for operators ${\mathcal{I}}^{\ast }$ and ◻. This completes the proof. □

Corollary 4.

For each IFS $A\in E^{\ast }$ and for each temporal scale T,

$$\begin{array}{cc}{\mathcal{I}}^{\ast }(\mathcal{I}(◻A(T)))\hfill & ={\mathcal{I}}^{\ast }(◻\mathcal{I}(A(T)))=◻{\mathcal{I}}^{\ast }(\mathcal{I}(A(T)))=◻\mathcal{I}({\mathcal{I}}^{\ast }(A(T)))\hfill \\ & =\mathcal{I}(◻{\mathcal{I}}^{\ast }(A(T)))=\mathcal{I}({\mathcal{I}}^{\ast }(◻A(T))).\hfill \end{array}$$

3. Intuitionistic Fuzzy Multi-Temporal Modal Topological Structures

Let us consider a finite or infinite temporal scale T where $U\subseteq T$. Using the definitions of the operators ${\mathcal{C}}^{\ast }$ and ${\mathcal{I}}^{\ast }$, we can now provide the following definition.

Definition 3.

For each IFS A and temporal scale T, operators ${\mathcal{C}}^{\ast }$ and ${\mathcal{I}}^{\ast }$ are defined as

$$\begin{array}{cc}\hfill {\mathcal{C}}_U^{\ast }(A(T))& =\{\langle \langle x,t\rangle ,\underset{u\in U}{sup}{\mu }_{A(T)}(x,u),\underset{u\in U}{inf}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\},\hfill \\ \hfill {\mathcal{I}}_U^{\ast }(A(T))& =\{\langle \langle x,t\rangle ,\underset{u\in U}{inf}{\mu }_{A(T)}(x,u),\underset{u\in U}{sup}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\}.\hfill \end{array}$$

For the subsets $T_1,T_2,\dots ,T_n$ of T, let them satisfy the following inclusions:

$$T_1\subseteq T_2\subseteq \cdots \subseteq T_n\subseteq T.$$

(7)

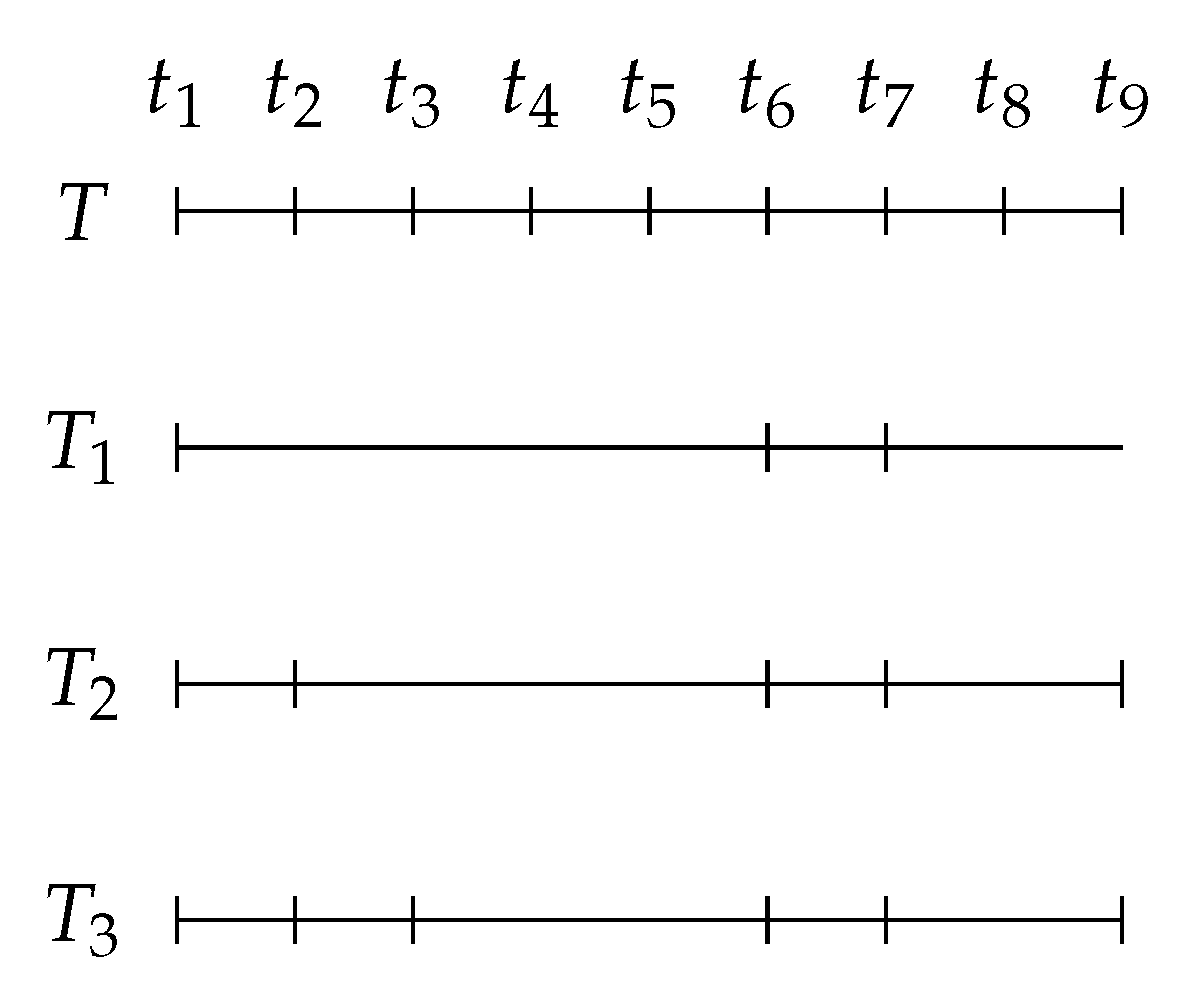
Example 2.

For example, in Figure 3, along the temporal scale $T=\{t_1,t_2,t_3,\dots ,t_9\}$ we have the subscale $T_1=\{t_1,t_6,t_7.\}$, which is a subscale of $T_2=\{t_1,t_2,t_6,t_7,t_9\}$, which is in turn a subscale of $T_3=\{t_1,t_2,t_3,t_6,t_7,t_9\}$.

At this stage, we can prove the following lemma.

Lemma 1.

For each TIFS $A(T)$:

$$\begin{array}{cc}\hfill {\mathcal{I}}_{T_n}^{\ast }(A(T))& \subseteq {\mathcal{I}}_{T_{n-1}}^{\ast }(A(T))\subseteq \cdots \subseteq {\mathcal{I}}_{T_1}^{\ast }(A(T))\hfill \\ \hfill & \subseteq A(T)\hfill \\ \hfill & \subseteq {\mathcal{C}}_{T_1}^{\ast }(A(T))\subseteq \cdots \subseteq {\mathcal{C}}_{T_{n-1}}^{\ast }(A(T))\hfill \\ \hfill & \subseteq {\mathcal{C}}_{T_n}^{\ast }(A(T)).\hfill \end{array}$$

(8)

Proof. 

Let $1\le i<j\le n$ be natural numbers and let the TIFS $A(T)$ be given, with $T_1,\dots ,T_n$ satisfying (7). Then,

$$\begin{array}{cc}{\mathcal{I}}_{T_j}^{\ast }(A(T))\hfill & =\{\langle \langle x,t\rangle ,\underset{u\in T_j}{inf}{\mu }_{A(T)}(x,u),\underset{u\in T_j}{sup}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\}\hfill \\ & \subseteq \{\langle \langle x,t\rangle ,\underset{u\in T_i}{inf}{\mu }_{A(T)}(x,u),\underset{u\in T_i}{sup}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\}\hfill \\ & ={\mathcal{I}}_{T_i}^{\ast }(A(T)),\hfill \end{array}$$

because, as is obvious from $T_i\subseteq T_j$, it follows that it is possible that an element may exist in the set $T_i$ that exhibits a lower degree of membership (respectively, a higher degree of non-membership) than the respective degrees of the all elements of $T_j$. Then,

$$\underset{u\in T_j}{inf}{\mu }_{A(T)}(x,u)\le \underset{u\in T_i}{inf}{\mu }_{A(T)}(x,u)$$

and

$$\underset{u\in T_j}{sup}{\nu }_{A(T)}(x,u)\ge \underset{u\in T_i}{sup}{\nu }_{A(T)}(x,u).$$

In the same way, it is apparent that

$${\mathcal{C}}_{T_i}^{\ast }(A(T))\subseteq {\mathcal{C}}_{T_j}^{\ast }(A(T)).$$

Finally, for the TIFS $A(T)$, it holds that

$$\begin{array}{cc}{\mathcal{I}}_{T_1}^{\ast }(A(T))\hfill & =\{\langle \langle x,t\rangle ,\underset{u\in T_1}{inf}{\mu }_{A(T)}(x,u),\underset{u\in T_1}{sup}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\}\hfill \\ & \subseteq A(T)\hfill \\ & \subseteq \{\langle \langle x,t\rangle ,\underset{u\in T_1}{sup}{\mu }_{A(T)}(x,u),\underset{u\in T_1}{inf}{\nu }_{A(T)}(x,u)\rangle |\langle x,t\rangle \in E\times T\}\hfill \\ & ={\mathcal{C}}_{T_1}^{\ast }(A(T)).\hfill \end{array}$$

Therefore, temporal topological operators satisfy Lemma 1 and the inclusions in (6). □

In the general case, we use the notation “$\alpha$-$(m,\beta )$-$\gamma$-Multi-Temporal Modal Topological Structure” (abbreviated: $\alpha$-$(m,\beta )$-$\gamma$-Multi-TMTS) to refer to the structure of the form

$$\langle \mathcal{P}(X),\mathcal{O},\Delta ,{\mathcal{O}}_1^{\ast },\dots ,{\mathcal{O}}_m^{\ast },\circ \rangle ,$$

where:

• $\alpha ,\beta ,\gamma \in \{cl,in\}$;
• $\mathcal{O}$ is a topological operator of $\alpha$-type generated by the operation $\Delta$ and satisfying conditions C1–C4 or I1–I4 with respect to $\alpha$;
• m is the number of closure or interior temporal operators with respect to $\beta$;
• ${\mathcal{O}}_1^{\ast },\dots ,{\mathcal{O}}_m^{\ast }$ are temporal operators of $\beta$-type, all satisfying conditions C1–C4 or I1–I4 with respect to $\beta$;
• ∘ is a modal operator of $\gamma$-type that satisfies conditions C1–C4 or I1–I4 with respect to $\gamma$.

Each of the pairs $\langle \mathcal{O},{\mathcal{O}}_i^{\ast }\rangle$ for $1\le i\le m$ must satisfy Equality (5) and the operators ${\mathcal{O}}_1^{\ast },\dots ,{\mathcal{O}}_m^{\ast }$ must satisfy their part of Inequality (8).

Now, we can prove the validity of the following assertions related to a particular case of $\alpha$-$(m,\beta )$-$\gamma$-Multi-Temporal Modal Topological Structure based on intuitionistic fuzziness.

Theorem 5.

For each universe E and for every m temporal scales $T_1,\dots ,T_m$ that satisfy (7),

$$\langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_1^{\ast },\dots ,{\mathcal{C}}_m^{\ast },◊\rangle$$

is an IF-$cl$-(m-$cl$)-$cl$-TMTS.

Proof. 

Really, this assertion is valid because, as mentioned in the proof of Theorem 1, the validity of conditions C1–C4 for the operator $\mathcal{C}$ is proven in [1], for the i-th temporal operators ${\mathcal{C}}_i^{\ast }$ in [6] for each $1\le i\le m$, and for the modal operator ◊ in [28]. Equality (5) is checked for operators $\mathcal{C}$ and ${\mathcal{C}}^{\ast }$ in [6] and for operators $\mathcal{C}$ and ◊ in [1], respectively, while the proof that this equality holds for operators ${\mathcal{C}}_i^{\ast }$ and ◊ is the same as in the proof of Theorem 1. □

The following Theorems 6–8 are proven identically.

Theorem 6.

For each universe E and for every m temporal scales $T_1,\dots ,T_m$ that satisfy (7),

$$\langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_1^{\ast },\dots ,{\mathcal{C}}_m^{\ast },◻\rangle$$

is an IF-$cl$-(m-$cl$)-$in$-TMTS.

Theorem 7.

For each universe E and for every m temporal scales $T_1,\dots ,T_m$ that satisfy (7),

$$\langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_1^{\ast },\dots ,{\mathcal{I}}_m^{\ast },◊\rangle$$

is an IF-$in$-(m-$inl$)-$cl$-TMTS.

Theorem 8.

For each universe E and for every m temporal scales $T_1,\dots ,T_m$ that satisfy (7),

$$\langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_1^{\ast },\dots ,{\mathcal{I}}_m^{\ast },◻\rangle$$

is an IF-$in$-(m-$in$)-$in$-TMTS.

Definition 4

(Dual structures). We say that two α-(m-β)-γ-TMTSs

$$\langle \mathcal{P}(X),\mathcal{O},\Delta ,{\mathcal{O}}_1^{\ast },\dots ,{\mathcal{O}}_m^{\ast },\circ \rangle$$

and

$$\langle \mathcal{P}(Y),\mathcal{Q},\nabla ,{\mathcal{Q}}_1^{\ast },\dots ,{\mathcal{Q}}_m^{\ast },\ast \rangle$$

are dual structures if:

1.

$X=Y$

2.

For each set $A\in \mathcal{P}(X)$, Equalities (1)–(4) and

$$\begin{array}{cc}\hfill \circ A& =\neg \ast \neg A,\hfill \\ \hfill A& =\neg \circ \neg A\hfill \end{array}$$

hold true.

Therefore, it can be seen directly that

$$\langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_1^{\ast },\dots ,{\mathcal{C}}_m^{\ast },◊\rangle and\langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_1^{\ast },\dots ,{\mathcal{I}}_m^{\ast },◻\rangle$$

are dual structures, just as

$$\langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_1^{\ast },\dots ,{\mathcal{C}}_m^{\ast },◻\rangle and\langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_1^{\ast },\dots ,{\mathcal{I}}_n^{\ast },◊\rangle$$

are dual structures.

Having in mind that the eequalities in (6) do not always hold true, it is obvious that each IF-$cl$-(m-cl)-$\gamma$-TMTS can be interpreted as a set of a total number of m IF-$cl$-$cl$-$\gamma$-TMTSs, where $\gamma \in \{cl,in\}.$

Conversely, let us consider the set of structures

$$\begin{array}{cc}\hfill & \langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_1^{\ast },\gamma \rangle ,\hfill \\ \hfill & \langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_2^{\ast },\gamma \rangle ,\hfill \\ \hfill & \cdots \hfill \\ \hfill & \langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_m^{\ast },\gamma \rangle .\hfill \end{array}$$

We can construct a new extended topological structure $\langle \mathcal{P}(E^{\ast }),\mathcal{C},\cup ,{\mathcal{C}}_1^{\ast },\dots ,{\mathcal{C}}_m^{\ast },\gamma \rangle$. By analogy, when we have the structures

$$\begin{array}{cc}\hfill & \langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_1^{\ast },\gamma \rangle ,\hfill \\ \hfill & \langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_2^{\ast },\gamma \rangle ,\hfill \\ \hfill & \cdots \hfill \\ \hfill & \langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_n^{\ast },\gamma \rangle ,\hfill \end{array}$$

we can construct an extended topological structure $\langle \mathcal{P}(E^{\ast }),\mathcal{I},\cap ,{\mathcal{I}}_1^{\ast },\dots ,$${\mathcal{I}}_n^{\ast },\gamma \rangle$.

In this regard, we can follow an idea from [1,33] generated from the definitions of maps and atlases in differential geometry (see, e.g., [34,35]). In [1,33], this idea is transferred for different topological structures with a joint universe. As mentioned in [33], while these maps and atlases are similar to those from differential geometry, there are differences (in the author’s paper, additional details about this idea in the IF-case are provided). They are related to the modal and the topological operators of the structures.

Here, we rewrite this idea, for the case of temporal-topological operators. As shown in the above lemma, the inclusions in (8) are valid.

Therefore, we can interpret each of the above total number of n$in$-structures as a map, and the sets of the maps can be ordered and enumerated by a function $\mathcal{N}$, as follows:

$$\mathcal{N}({\mathcal{I}}_i^{\ast })=i(i=1,\dots ,n).$$

Hence, the maps constructed in this way generate an $in$-atlas. By analogy, each of the above total number of m $cl$-structures can be interpreted as a map, and their set can be ordered and enumerated by the same function $\mathcal{N}$, as follows:

$$\mathcal{N}({\mathcal{C}}_j^{\ast })=j(j=1,\dots ,m).$$

Therefore, by collecting these maps, we obtain a $cl$-atlas.

Finally, we can enumerate all of the above mentioned $m+n$ structures (or maps) by

$$\begin{array}{cc}\hfill \mathcal{N}({\mathcal{I}}_i^{\ast })& =i(i=1,\dots ,n),\hfill \\ \hfill \mathcal{N}({\mathcal{C}}_j^{\ast })& =n+j(j=1,\dots ,m).\hfill \end{array}$$

Hence, the arguments of the temporal topological operators generate a pagination of the set of all $in$- and $cl$-maps; in this case, we obtain an atlas that contains $in$-maps as well as $cl$-maps (see Figure 4).

4. Conclusions

In the present paper, continuing the idea from [6], the concept of Multi-Temporal Modal Topological Structures is constructed and illustrated with some IF-multi-TMTSs. Having in mind that in IFS theory there are modal, topological, temporal, and level operators of different types, it is possible to construct more complex structures. For example, in the near future, using the modal operators from [33], we will construct Multi-Temporal Multi-Modal Topological Structures that can be illustrated with examples from the area of intuitionistic fuzziness.

This research can find applications in different areas. For example, it is possible to interpret the complex procedure for decision-making from [36] as a multi-TMTS. In this case, we have three types of objects: experts, criteria, and some objects that the experts must evaluate using the criteria provided by the organizers of procedure or determined by the experts beforehand. The experts can be assigned intuitionistic fuzzy scores corresponding to the number of procedures in which they have provided correct evaluations (degree of correctness) and the number of procedures in which they were incorrect (degree of incorrectness). The degree of uncertainty corresponds to the number of procedures for which the respective expert stops participating after starting the process of decision-making. Each expert’s estimation for a given object about some criterion can have an intuitionistic fuzzy form as well (i.e., the degrees of validity and non-validity of the criterion for the object). Therefore, this situation can be represent by an IFMTS. If we would like to represent the previous expert’s attempt to evaluate the same objects, then we can use the set of the previous expert’s evaluations as well. In this case, we obtain an IFTMTS. Having in mind that different experts, each with their own history, participate in the process of concrete decision-making, we can use different temporal scales for the different experts, and thereby obtain IF-multi-TMTSs.

Finally, it is important to note that in the present paper, as well as in the author’s previous papers on this theme, this discussion is related only to the forms of the topological structures extended with modal, temporal, or other operators. In the future, the attention of the author will be directed to the topological spaces of these structures as well.