Abstract
The purpose of this paper is to generalize the concept of classical fuzzy set to vector-valued fuzzy set which can attend values not only in the real interval , but in an ordered interval of a Banach algebra as well. This notion allows us to introduce the concept of vector-valued fuzzy metric space which generalizes, extends and unifies the notion of classical fuzzy metric space and complex-valued fuzzy metric space and permits us to consider the fuzzy sets and metrics in a larger domain. Some topological properties of such spaces are discussed and some fixed point results in this new setting are proved. Multifarious examples are presented which clarify and justify our claims and results.
Keywords:
vector-valued fuzzy set; vector-valued fuzzy metric space; strongly minihedral cone; fuzzy contractive mapping; fixed point MSC:
54H25; 47H10; 03E72
1. Introduction
A fuzzy set is considered as a class of objects whose grade of membership lies not only in the set but in the interval [1]. The approach of fuzzy sets is very useful in the study of systems of uncertain nature. Kramosil and Michalek used this approach to define a fuzzy version of classical metrics and introduced a notion of fuzzy metric space in [2]. Later on, George and Veeramani [3] suggested some modifications in the definition of fuzzy metric introduced in [2] and showed that with the modified definition the fuzzy metrics generate a topology which is first countable and Hausdorff. Then, some works contributed to the study of both aforesaid notions of fuzzy metrics. Among them, it is worth noting [4] in which the authors proved that fuzzy metrics given by George and Veeramani are metrizable. Moreover, on account of the one exposed in [4], one can derive such a conclusion also for fuzzy metrics introduced by Kramosil and Michalek. So, from the topological point of view fuzzy metrics and classical metrics are the same object. Nonetheless, fuzzy metrics show some differences compared with classical ones which still make their study of interest nowadays. On the one hand, they differ in some purely metric topics as completeness or fixed point theory, which are two active topics of research in the literature (see, for instance, the following recent references [5,6,7,8,9,10,11]). On the other hand, fuzzy metrics have been successfully used, compared with their classical counterparts, in engineering problems such as model estimation, modelling multi-agent systems or image filtering (see, for instance, [12,13,14,15,16,17] and references therein). With the aim of obtaining a fuzzy version of the celebrated Banach fixed point theorem, Ref. [18] introduced a notion of Cauchy sequence and completeness for fuzzy metric spaces in the sense of Kramosil and Michalek. However, Ref. [3] pointed out some drawbacks of the assumptions of [18] and defined the Cauchy sequences and completeness of fuzzy metric spaces in a new sense. Coming back to the fixed point theorem established in [18], the contractive condition used in it is directly associated with the parameter with respect to which the fuzzy distance is measured. In contrast with [18,19] (see also, [20]) where a more natural contractive condition is used, which is different in nature, to prove fixed point results. In this sequel, Refs. [21,22,23,24] and several others introduced various generalized contractive conditions. Recently, Ref. [25] introduced the notion of complex-valued fuzzy metric spaces and extended the idea of t-norm and fuzzy metric from the set to a subset of complex numbers. They also proved some fixed point theorems and discussed some possible applications of such spaces.
On the other hand, the fixed point theory in the vector-valued metric spaces was initiated by [26]. In such spaces, the metric function can take values not only in the set of real numbers, but in a cone associated with a Banach space. This interesting generalization of metric attracted several researchers. An important improvement to the notion due to [26] was given by [27]. They introduced the cone metric spaces over Banach algebras and showed the extensive nature of contractive conditions and fixed point theorems in such spaces.
Topological algebras consist of a very useful subclass known as Banach algebras. Banach algebras have a norm structure and hence have applications in various branches of pure and applied mathematics as well as in other branches of sciences, e.g., in solving nonlinear integral equations, functional integral equations, in the study of Fourier series, representation theory, harmonic analysis and other significant areas of sciences. Nowadays, the class of Banach algebras is an interesting and vast discipline with a variety of specializations and applications (see, e.g., [28,29,30,31,32]). Ref. [27] introduced a kind of space in which metric function attains values in the form of vectors in a Banach algebra and utilized the properties of Banach algebras to show the superiority of such vector-valued metric functions over the usual ones. The space of the complex numbers is a particular type of Banach algebra and has great significance in the study of mathematical and physical systems. Ref. [25] utilized the space of complex numbers to introduce the complex-valued fuzzy sets and complex-valued fuzzy metric spaces and proved some fixed point results in complex-valued fuzzy metric spaces. Ref. [25] discussed significance and applications of such spaces and their fixed point results. The motivation for this work comes from the question: “can fuzzy sets (fuzzy metrics) be extended to a vector-valued version in such a way that this notion generalizes and unifies to both the usual fuzzy sets (usual fuzzy metrics) and complex-valued fuzzy sets (complex-valued fuzzy metrics) and are the previously mentioned fixed point results provable in this new generalized setting”?
In this paper, we introduce the notion of vector-valued t-norm and vector-valued fuzzy metric space and prove some fixed point theorems for contractive mappings in such spaces. The notion of vector-valued fuzzy metric space generalizes, extends and unifies the usual fuzzy metric spaces and the complex-valued fuzzy metric spaces. A new class of mappings in this new setting called the class of generalized -contractions is introduced. The fixed point theorems for the mappings of such class generalize and extend some results established in the literature. Concretely, Theorems 3, 5 and 6 generalize and extend the main results provided in [23,25], due to their being established in a more general framework. Some topological properties of such spaces are also discussed. We present suitable examples which illustrate the new notions and justify our claims.
2. Preliminaries
We first state some basic notions and definitions about the fuzzy metric and complex-valued fuzzy metric spaces which will be useful throughout the paper.
Definition 1.
A triangular norm (briefly, t-norm) is a binary operation ∗ on such that, for all , the following axioms are satisfied:
(T1) (Commutativity) (T2) (Associativity) (T3) whenever (Monotonicity) (T4) (Boundary Condition)
Definition 2 ([3]).
A tripleis called a fuzzy metric space if X is a nonempty set, ∗ is a continuous t-norm and is a fuzzy set satisfying the following conditions:
- (GV1);
- (GV2)if and only if;
- (GV3);
- (GV4);
- (GV5)is a continuous mapping;
for alland. Then, the tripletis called a fuzzy metric space and M is called a fuzzy metric onFor various properties of a fuzzy metric space the reader is referred to [3].
Let and denote by and ℓ the elements , , respectively (see [25]). Then, the relation ⪯ on such that (or, equivalently, ) if and only if defines a partial ordering on . (or, equivalently, ) indicates that and . Define and
Definition 3.
Let X be a nonempty set. A complex fuzzy set M is characterized by a mapping with domain X and values in complex interval
Definition 4 ([25]).
A binary operationis called a complex-valued t-norm if (i); (ii)whenever ; (iii) ; (iv) ; for all
Definition 5 ([25]).
Let X be a nonempty set, ∗ a continuous complex-valued t-norm and M a complex fuzzy set on satisfying the following conditions:
- (CV1)
- (CV2) if and only if
- (CV3)
- (CV4)
- (CV5) is continuous;
- for all and Then, the triplet is called a complex-valued fuzzy metric space and M is called a complex-valued fuzzy metric on A complex-valued fuzzy metric can be thought of as the degree of nearness between two points of X with respect to a complex parameter For the examples of complex-valued t-norms and complex-valued fuzzy metric spaces, the reader is referred to [25].
In the next section, we introduce the vector-valued fuzzy sets and vector-valued fuzzy metric spaces and study their properties.
3. Vector-Valued Fuzzy Sets and Vector-Valued Fuzzy Metric Spaces
Let always be a real Banach algebra with zero vector and multiplicative unit e. A subset of is called a cone if:
- (C1) is nonempty closed and ;
- (C2) for all nonnegative real numbers ;
- (C3) ;
- (C4).
Given a cone , we define a partial ordering ⪯ in with respect to by (or equivalently ) if and only if . We shall write (or equivalently ) to indicate that but , while (or equivalently ) will stand for , where denotes the interior of .
A cone is said to be solid if . For , the spectral radius of a is denoted by By an ordered interval in with the end points , we mean a set which contains all vectors c such that and it is denoted by , i.e.,
We denote by a particular ordered interval , i.e.,
We call the unit vector interval.
Remark 1 ([33]).
Let be a cone in a Banach space and .
- (i)
- If and then .
- (ii)
- If and then .
- (iii)
- If for every then .
Definition 6.
Let X be a nonempty set, be a Banach algebra with unit e and be a cone in . A vector-valued or -valued fuzzy set on X is a function .
Note that for with usual norm, ordinary multiplication and , we have the real unit interval; the above definition reduces into the definition of usual fuzzy sets given by [1].
Definition 7.
A mapping is called a -valued (or vector-valued) triangular norm (-norm for short) if ∗ satisfies the following conditions:
- (i)
- ∗ is commutative and associative, i.e., and , for all
- (ii)
- , for all
- (iii)
- , whenever and with
Note that for the Banach algebra of real numbers with usual norm, ordinary multiplication and and the real unit interval, the above definition reduces into the definition of t-norm given by [34]. While, for the Banach algebra of complex numbers with coordinate-wise multiplication, maximum norm , , and , the above definition reduces into the definition of complex-valued t-norm given by [25]. Therefore, all the examples of complex-valued t-norms given in [25] are the examples of -norms.
In the next example, part (A) shows that for every given t-norm one can construct a -norm. While part (B) defines a -norm with a structure disimilar to part (A). Thus, these parts show the novelty and generalized nature of -norms.
Example 1.
Let be the Banach algebra with multiplication defined by , the norm defined by and with unit Define , then Then:
- (A)
- For each given usual t-norm , the mapping defined by:is a -norm.
- (B)
- The mapping defined by:is a -norm which cannot be expressed as , where each is a usual t-norm.
Example 2.
Suppose , where , . Then, is a Banach algebra with usual matrix addition and multiplication, with unit as unit vector and the norm defined by for all . Then, is a cone in and For every given usual t-norm , the mapping ∗ defined by for all is a -norm.
Example 3.
Let with pointwise multiplication and norm defined by . Then, is a Banach algebra with Define for all ; then
Then, the mapping defined by for all , i.e., the pointwise multiplication, is a -norm.
In what follows, for by we denote the set and by we denote the set .
Definition 8.
Let X be a nonempty set and be a Banach algebra with cone . Then, a vector-valued fuzzy metric space over is a triplet such that ∗ is a continuous -norm and M is a -valued fuzzy set on satisfying the following conditions:
- (i)
- ;
- (ii)
- if and only if
- (iii)
- ;
- (iv)
- ;
- (v)
- is continuous
for all and . In this case, M is said to be a vector-valued fuzzy metric.
Remark 2.
While, condition (iv) shows that if , then we have .
Condition (ii) of the above definition is equivalent to the following:
Remark 3.
Note that for the Banach algebra of real numbers with usual norm, ordinary multiplication, and the real unit interval, the above definition reduces into the definition of fuzzy metric spaces given by [3]. On the other hand, if is a complex-valued fuzzy metric space (in the sense of [25]), then is a vector-valued fuzzy metric space with the Banach algebra of complex numbers with coordinate-wise multiplication and with maximum norm , in which , , .
Thus, the notion of vector-valued fuzzy metric spaces generalizes and unifies the classical fuzzy metric spaces and the notion of complex-valued fuzzy metric spaces (in the sense of [25]).
The following two examples show that for every fuzzy metric space (in the sense of [3]) there exists a vector-valued fuzzy metric space.
Example 4.
Let be a fuzzy metric space (in the sense of [3]). Let and ∗ be taken from Example 2, then is a vector-valued fuzzy metric space over , where M is defined by:
The following proposition shows that the vector-valued fuzzy metric spaces can be constructed in a more general way.
Proposition 1.
Let be a cone metric space (see [27]) over a Banach algebra with cone such that every pair of points in the ordered interval is comparable and for all . Then is a vector-valued fuzzy metric space over , where and
Indeed, it is sufficient to assume that every pair of points in has a supremum (instead pair is comparable) and to take .
Example 5.
Let , and be the Banach algebra with the norm , with the multiplication “·” defined by and the unit . Let , then . Define a cone metric by for all Then, for all and is a vector-valued fuzzy metric space over , where for all and
Example 6.
Let , with pointwise multiplication “·" and supremum norm. Let , then is a Banach algebra with and . Define a cone metric by for all Then, for every the vector is invertible; indeed, the pointwise multiplicative inverse with respect to ordinary multiplication is the inverse of in . Then is a vector-valued fuzzy metric space over , where ∗ is the pointwise multiplication and
Definition 9.
A sequence in is said to be an e-sequence if, for each , there exists such that for all .
Proposition 2.
In a Banach algebra with cone :
- (A)
- If are such that , then we can find an such that ;
- (B)
- For every we can find such that and .
Proof.
(A) Suppose, are such that and
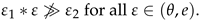 Then, we can choose a sequence in such that as and
Then, we can choose a sequence in such that as and 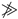 , i.e.,
Since is open, ∗ is continuous and as ; the above inclusion yields
This shows that (a contradiction) and proves the result.
, i.e.,
Since is open, ∗ is continuous and as ; the above inclusion yields
This shows that (a contradiction) and proves the result.
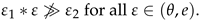
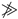 , i.e.,
, i.e.,
- (B) It can be proved by following a process similar to the one used in part (A). □
Proposition 3.
In a Banach algebra with cone . If and are two e-sequences in , then is an e-sequence in .
Proof.
Let be given; then, we have . Then, by Proposition 2, there exists such that Again, since and and are e-sequences in there exists such that
As ∗ is nondecreasing, it yields
Hence, is an e-sequence. □
Definition 10.
Let be a vector-valued fuzzy metric space over a Banach algebra with cone and be a sequence in Then is called a Cauchy sequence if for each and each , there is such that .
On the other hand, is called a weak Cauchy sequence if for each and each , there is such that Or equivalently, is called a weak Cauchy sequence if is an e-sequence for all
It is easy to see that every Cauchy sequence is a weak Cauchy sequence, but the converse is not necessarily true.
Sequence is called convergent and converges to if, for each and each , there exists such that , for all Or equivalently, is called a convergent and converges to if is an e-sequence for all
Remark 4.
In a fuzzy metric space , for the convergence of a sequence to a point the necessary and sufficient condition is that the limit must exist and be equal to 1 for all . The same is true for convergent sequences in complex-valued fuzzy metric spaces (with the mentioned limit equal to ℓ). On the other hand, in cases of vector-valued fuzzy metric spaces this condition is much weaker. Indeed, in a vector-valued fuzzy metric space the limit may not exist for some and for all , although the sequence may converge to some . For instance, let with pointwise multiplication “·” and the norm and let , then is a Banach algebra with , . Suppose that , then is a vector-valued fuzzy metric space over , where ∗ is the pointwise multiplication and
for all . Now consider the sequence in X, where . Note that does not exist for all (otherwise, in which is not true). This sequence is convergent and converges to in X. Indeed, for each and each , we can find such that for all . The above example reflects the fact that the concepts introduced here are not trivial analogues of the usual versions, it also reflects the case when existing concepts cannot be applied but new concepts can be applied.
Proposition 4.
If is a vector-valued fuzzy metric space over a Banach algebra with cone , then every convergent sequence in X is a Cauchy (therefore weak Cauchy) sequence in X.
Proof.
Suppose that the sequence converges to some ; i.e., is an e-sequence for all Since is an e-sequence for all , by Proposition 3 is an e-sequence. Hence, for each there exists such that for all . Since
for all , we must have for all . Hence, is a Cauchy sequence. □
It is easy to see that the converse of the above proposition is not necessarily true; hence, we define the following:
Definition 11.
We say that the space is complete (respectively, strong-complete) if every Cauchy (respectively, weak-Cauchy) sequence in X converges to some .
Remark 5.
The types of the Cauchy sequences (respectively, weak Cauchy sequences) and the completeness (respectively, strong completeness) defined here are a vector-valued analogue of M-Cauchy sequences defined by [3] (respectively, G-Cauchy sequences defined by [18]) and M-completeness (respectively, G-completeness), respectively, in classical fuzzy metric spaces. Hence, every G-complete (respectively, M-complete) fuzzy metric space is a particular case of strong complete (respectively, complete) vector-valued fuzzy metric spaces.
Remark 6.
In a Banach algebra, we observe that the set may be empty, e.g., let be the Banach algebra with the norm , with the multiplication “·" defined by , cone and the unit . Then, it is easy to see that Therefore, in a vector-valued fuzzy metric space with such Banach algebra and cone, every sequence is a Cauchy sequence as well as convergent and so such spaces are trivially complete (strong-complete). Hence, we can say that the presented concepts of Cauchyness and completeness are new and quite different from the Cauchyness and completeness of ordinary fuzzy metric spaces and complex-valued fuzzy metric spaces.
Note that is nonempty if and only if . Therefore, throughout the paper, we assume that .
Proposition 5.
In a vector-valued fuzzy metric space over a Banach algebra with cone , if are such that , then we can find such that .
Proof.
We prove the result by contradiction. Then, suppose that are such that and
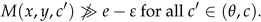 Since for all it follows from the above that , i.e.,
Since is continuous and is open, the above inclusion yields
This shows that
Since for all it follows from the above that , i.e.,
Since is continuous and is open, the above inclusion yields
This shows that 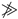 (a contradiction) and proves the result. □
(a contradiction) and proves the result. □
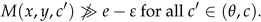
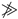 (a contradiction) and proves the result. □
(a contradiction) and proves the result. □Definition 12.
Let be a vector-valued fuzzy metric space over a Banach algebra with cone , , and . Then, the open ball with center x and radius ε is denoted by and it is defined by:
A subset is called open if for every , there exist and such that .
Theorem 1.
In a vector-valued fuzzy metric space every open ball is an open set.
Proof.
Consider an open ball and suppose . Then we have:
Therefore, by Proposition 5, there exists such that . Let . As , there exists such that . Therefore, by Proposition 2 there exists such that . Now consider the open ball . If , then we have . Therefore:
Therefore, and hence This shows that is an open set. □
It is obvious that, if is a vector-valued fuzzy metric space, then the collection
is a topology on X. Also, by properties of a cone in a Banach algebra, for given and we can always find such that ; hence, Remark 2 yields that for every the collection:
is a local base at . Therefore, the topology is first countable.
We next show that this topology is Hausdorff.
Theorem 2.
The topology is Hausdorff.
Proof.
Let be the given vector-valued fuzzy metric space and with . Then, by definition we have
Therefore, for any fixed we have . Therefore, by (iii) of Remark 1, there exists such that 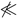 . Without loss of generality, we can assume that .
. Without loss of generality, we can assume that .
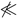 . Without loss of generality, we can assume that .
. Without loss of generality, we can assume that .Since , by Proposition 2, there exists such that . We claim that
If there exists
then and and hence
i.e., . This contradiction proves the result. □
In the next section, we prove some fixed point results in vector-valued fuzzy metric spaces.
4. Fixed Point Theorems
Let be a vector-valued fuzzy metric space over a Banach algebra with cone . We say that the mapping is a generalized Tirado contraction or a generalized fuzzy Banach contraction with contractive vector k if the following condition is satisfied: such that and
for all and
Note that for the Banach algebra of real numbers with ordinary multiplication, usual norm, and the real unit interval, the generalized Tirado contractions reduce into the contractions considered by [19] (see also [20]). Hence, Tirado’s contraction is a particular case of generalized Tirado contractions.
Let denote the family of all functions satisfying the following properties:
- (ξ1)
- is nondecreasing;
- (ξ2)
- if is an e-sequence, then is an e-sequence, where ;
- (ξ3)
- is an e-sequence for all .
Example 7.
Consider the Banach algebra with pointwise multiplication and norm defined by and with unit Let , then If we define by for all and , then it is easy to see that .
By we denote the family of all functions such that is continuous, nondecreasing and (or equivalently, ) for all [23].
Example 8.
Let with Euclidian norm, coordinate-wise multiplication and . Then . If for , then the function , where
is a member of
Note that every member of the family is a member of for .
Remark 7.
Consider the family of nondecreasing functions such that for all (see [35]). In the above example, all are assumed to be continuous, but note that even if we omit the continuity of these functions the conclusion remains same. More precisely, we have the proper inclusion:
Definition 13.
Let be a vector-valued fuzzy metric space over Banach algebra with cone and be a mapping. Then, T is called a generalized ξ-contraction if there exists a such that the following condition is satisfied:
for all and
Example 9.
If and (i.e., ), then every generalized Tirado contraction with a contractive vector k is a generalized ξ-contraction with for all .
Remark 8.
In the above example, we assume that . We point out that this assumption is necessary. In fact, if we discard this assumption, the conclusion of the above example may not be valid. Indeed, if , then , so, if , then we have ; i.e., we obtain such that . Hence,
Remark 9.
On a fuzzy metric space (in the sense of [3]), we say that a mapping is a ψ-contraction ([23]) if there exists such that the following condition is satisfied:
In view of Remark 3, it is easy to see that every ψ-contraction is a generalized ξ-contraction with for all . As the contractions considered by [21,24] (see [36]) are included in the class of ψ-contractions, these types of contractions are also members of the family .
On the other hand, in view of Remark 3, it is easy to see that every fuzzy Banach contraction (considered by [25]) with fuzzy contractive constant is a generalized Tirado contraction with contractive vector . Hence, the contractions considered by [25] are also a particular type of generalized ξ-contractions.
We next prove some fixed point theorems for generalized -contractions in strong complete and complete vector-valued fuzzy metric spaces.
Theorem 3.
Let be a strong complete vector-valued fuzzy metric space over a Banach algebra with cone . If T is a generalized ξ-contraction, then T has a unique fixed point.
Proof.
We start with an arbitrary and define an iterative sequence by:
We shall show that this sequence is a weak Cauchy sequence. Then, for every , we have:
Replacing n by in the above inequality, we obtain
Since is nondecreasing, the above inequality yields
Therefore
Repeating this process, we obtain:
By () we have is an e-sequence. So, for every there exists such that
It follows from the above inequality and (1) that
This shows that is a weak Cauchy sequence.
Since is strong complete, converges to some . We now show that u is a fixed point of T.
Fix an arbitrary . As converges to u, the sequence is an e-sequence; hence, by () we have is an e-sequence. By Proposition 3, the sequence is an e-sequence. This shows that for every there exists such that
Using (2), we obtain the following: for all
This shows that . As is arbitrary, ∗ is continuous and is closed, we must have . Because by definition of we obtain . Taking into account that is arbitrary, we conclude .
For uniqueness of fixed point, in contrast, suppose that is another fixed point of T and . Let be arbitrary; since T is a generalized -contraction, we have:
Since is nondecreasing, it follows from the above inequality that
By (), the sequence is an e-sequence; hence, for every there exists such that
We obtain from (3) and the above that ; i.e., So, we obtain and due to c being arbitrary we conclude that , a contradiction. □
Example 10.
Consider the Banach algebra with coordinate-wise multiplication, the Euclidean norm, zero vector and unit . Consider the cone in , then Note that the partial ordering “⪯" induced by on is not a linear order; nevertheless, we can always find the infimum (supremum) of any pair of elements of ; i.e., the pair is a lattice. Indeed, . Hence, we define by:
Let and consider a -valued fuzzy set M on defined by:
for all and . Then is a vector-valued fuzzy metric space. It is easy to see that if a sequence is weak Cauchy in X, then it must be convergent to e. Hence, is a strong complete vector-valued fuzzy metric space. Let , be such that and let be such that for all
Let be a mapping defined by
Now consider the mapping defined by
Then, one can verify easily that and T is a generalized ξ-contraction. Thus, all the conditions of Theorem 3 are satisfied. Hence, by Theorem 3 we can conclude the existence and uniqueness of the fixed point of the mapping T. Indeed, is the unique fixed point of T.
Remark 10.
Theorems 3.1 and 3.7 of [25] are the main results of them. We show that the results from [25] are not applicable to the above example.
It is obvious that the vector-valued fuzzy metric space in the above example is indeed a complex-valued fuzzy metric space. Set and for all . We first show that there exists no such that
for all and for all . In contrast, suppose that such a k exists. Then, taking and , we have
If , take ; then, (4) yields a contradiction. If then again take and (4) yields a contradiction. Hence, Theorem 3.1 of [25] cannot be used here.
Next, we observe that the value of is independent of c; hence, the condition “ for all , whenever " (i.e., a necessary condition in Theorem 3.7 of [25]) is not satisfied. Hence, Theorem 3.7 of [25] cannot be used here.
The following corollary is an extension and a generalization of the result of [23] in strong complete vector-valued fuzzy metric spaces. Note that the assumption of continuity (or even of semi-continuity) of function is not needed.
Corollary 1.
Let be a strong complete vector-valued fuzzy metric space over a Banach algebra with cone . If there exists a nondecreasing continuous function such that and for all and
for all and , then T has a unique fixed point.
In view of Example 9, we obtain the following corollaries which generalize and extend the fixed point result of [19] in strong complete vector-valued fuzzy metric space.
Corollary 2.
Let be a strong complete vector-valued fuzzy metric space over a Banach algebra with cone . If T is a generalized Tirado contraction with contractive vector k such that and , then T has a unique fixed point.
Different authors have pointed out the drawbacks of the notion of strong completeness used in the preceding results (see [3,37,38]). So we are interested in proving a fixed point result for generalized -contraction in a complete vector-valued fuzzy metric space. However, it will be established only for a class of vector-valued fuzzy metric spaces, which are defined below.
Definition 14.
Let be a vector-valued fuzzy metric space over Banach algebra with cone . We will say that (or simply M) is a non-Archimedean vector-valued fuzzy metric space if (in addition), for each and , the following inequality is satisfied:
Theorem 4.
Let be a complete non-Archimedean vector-valued fuzzy metric space over a Banach algebra with cone such that for all . If is a generalized ξ-contraction, then T has a unique fixed point.
Proof.
Let and define an iterative sequence by:
If for some , then is a fixed point of T and the existence is proved. In contrast, suppose for all . It is not hard to check by induction on n that, for every , we have for all . In addition, by () we have is an e-sequence for every . Therefore, is an e-sequence, for every .
Next we will show that is a Cauchy sequence.
Let and . Taking into account that is an e-sequence, given there exists such that for all . Now consider such that . Then,
This shows that is a Cauchy sequence.
Since is complete, converges to some . We now show that u is a fixed point of T. Fix an arbitrary , then:
As converges to some , the sequence is an e-sequence. Also, for every we have
As is an e-sequence, the above inequality and () imply that is an e-sequence. Hence, by Proposition 3 the sequence is an e-sequence. Therefore, for each there exists such that
Using the above inequality in (7) we obtain , i.e., for all This inequality with Remark 1 yields that i.e., . Due to being arbitrary, we conclude .
For uniqueness of fixed point, in contrast, suppose that there exists a fixed point of T and .
Fix an arbitrary . Then, since T is a generalized -contraction, we have:
Since is nondecreasing, it follows from the above inequality that
By (), the sequence is an e-sequence; hence, for each there exists such that
We obtain from (8) and the above inequality that , i.e., By Remark 1, we have and, since is arbitrary, we conclude . This contradiction proves the uniqueness. □
Example 11.
Consider the Banach algebra with pointwise multiplication, norm defined by , zero vector and with unit Let , then Define by pointwise minimum: for each
for all Then, for all . Hence, for all Let and consider a -valued fuzzy set M on defined by the following: for each
for all and . Then, it is easy to verify that is a vector-valued fuzzy metric space. Also, since every Cauchy sequence in X must converge to 1, is complete. Let be a mapping defined by for all . Consider defined by for all . Then T is a generalized ξ-contraction. Thus, all the conditions of Theorem 4 are satisfied. Hence, by Theorem 4 we can conclude the existence and uniqueness of fixed point of the mapping T. Indeed, is the unique fixed point of T.
The following result is an extension of the result of [23] in a complete non-Archimedean vector-valued fuzzy metric space which establishes the existence and uniqueness of fixed point. Note that conditions demanded on are more restrictive than those fulfilled by the functions included in . So, the hypothesis imposed on the -norm can be deleted.
Theorem 5.
Let be a complete non-Archimedean vector-valued fuzzy metric space over a Banach algebra with cone . If there exists a nondecreasing function such that and for all and
for all and , then T has a unique fixed point.
Proof.
Let and define an iterative sequence by:
Following the same arguments as those used in the proof of Theorem 4, we obtain that is an e-sequence for every . Next, we will show that is a Cauchy sequence by contradiction.
So assume that is not Cauchy. Then, there exists and such that for all we can find such that 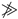 . Under such an assumption, we construct a subsequence of as follows.
. Under such an assumption, we construct a subsequence of as follows.
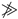 . Under such an assumption, we construct a subsequence of as follows.
. Under such an assumption, we construct a subsequence of as follows.First of all, is an e-sequence, so there exists such that for all . Let . Now, we take, for all , as the (unique) integer greater than such that , for all and 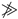 . Observe that our assumption allows us to obtain such a construction. In addition, for each we have that since for each satisfied . Then, we have, for all , the following
By (A) in Proposition 2, there exists such that . In addition, since is an e-sequence we can find such that for every . So, on account of inequality (9) we have, for every , the following:
a contradiction. Hence, is a Cauchy sequence. Then, the remainder of the proof follows the same argumentation used in the proof of Theorem 4. □
. Observe that our assumption allows us to obtain such a construction. In addition, for each we have that since for each satisfied . Then, we have, for all , the following
By (A) in Proposition 2, there exists such that . In addition, since is an e-sequence we can find such that for every . So, on account of inequality (9) we have, for every , the following:
a contradiction. Hence, is a Cauchy sequence. Then, the remainder of the proof follows the same argumentation used in the proof of Theorem 4. □
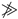 . Observe that our assumption allows us to obtain such a construction. In addition, for each we have that since for each satisfied . Then, we have, for all , the following
. Observe that our assumption allows us to obtain such a construction. In addition, for each we have that since for each satisfied . Then, we have, for all , the following
The following corollary extends the fixed point result of [19] in complete vector-valued fuzzy metric spaces.
Corollary 3.
Let be a complete non-Archimedean vector-valued fuzzy metric space over a Banach algebra with cone . If T is a generalized Tirado contraction with contractive vector k such that and , then T has a unique fixed point.
The above corollary is established for non-Archimedean vector-valued fuzzy metric spaces; therefore, the above corollary cannot be treated as a proper generalization of the main fixed point result of [25] (because in their main fixed point result no such assumption was imposed). In the next theorem, we establish a fixed point result by omitting such a requirement and applying a strong condition on cone in such a way that the fixed point result of [25] is generalized in vector-valued fuzzy metric spaces. Before stating the theorem, we recall some definitions.
The following definitions are well known (see, e.g., [39]):
Definition 15.
Let be a Banach algebra and a cone in . Then:
- (a)
- is called normal if there is a number such that for all , implies that .
- (b)
- is called regular if every monotonic nondecreasing sequence which is bounded from above is convergent.
- (c)
- is called minihedral if exists for all and strongly minihedral if every subset of which is bounded from above has a supremum or equivalently, if every subset of which is bounded from below has an infimum.
Lemma 1
([40]). In a Banach space:
- (a)
- Every strongly minihedral (closed) cone is normal;
- (b)
- Every strongly minihedral normal (not necessarily closed) cone is regular.
Theorem 6.
Let be a complete vector-valued fuzzy metric space over a Banach algebra with strongly minihedral cone . If T is a generalized Tirado contraction with contractive vector k such that and , then T has a unique fixed point.
Proof.
For any , we define a sequence in X by We can assume that for all ; otherwise, T will have a fixed point. Suppose that for all We shall show that is a Cauchy sequence.
Fix an arbitrary . Since is strongly minihedral, for all ; therefore, for every the infimum exists. Let
Obviously, for all . Since T is a generalized Tirado contraction with contractive vector k, for every and we have
Since and , the above inequality implies that
As is strongly minihedral, taking infimum over and using the definition of in the above inequality we obtain
Thus, is a monotonic nondecreasing sequence in which is strongly minihedral (therefore regular); hence, there exists such that
Inequality (10) implies that
for all . Again, since is strongly minihedral, taking infimum over and using the definition of in the above inequality we obtain , for every . Hence, by the closedness of we obtain . So, and
Therefore, for every given there exists such that
By the definition of , we have for all ; hence, it follows from the above inequality that
Thus, is a Cauchy sequence in Hence, by the completeness of X there exists such that the sequence is an e-sequence for all
We shall show that u is the fixed point of T. Since T is a generalized Tirado contraction we have , i.e.,
Since is an e-sequence for every , for given there exists such that
By the use of (12) and (13), we obtain the following: for every and for all
Since ∗ and multiplication in both are continuous, the above inequality shows that , i.e., for all . Thus, i.e., u is a fixed point of T.
If is another fixed point of T, then we must have:
Since , the above inequality yields i.e., Thus, u is the unique fixed point of T. □
Corollary 4
([25]). Let be a complete complex-valued fuzzy metric space. If T is a fuzzy Banach contraction with contractive constant k, then T has a unique fixed point in X.
Proof.
In view of Remark 3, is a complex-valued fuzzy metric space over the Banach algebra of complex numbers with coordinate-wise multiplication, maximum norm , , cone and . We notice that this cone is strongly minihedral. Also, as T is a fuzzy Banach contraction with contractive constant k, it is a generalized Tirado contraction with contractive vector . Hence, the existence and uniqueness of the fixed point of T follows from Theorem 6. □
5. Conclusions
The abstract spaces have several applications in various branches of science, e.g., in the theory of relativity, quantum mechanics and in engineering problems where the use of vector variables and functions makes procedures of calculations and finding solutions much simpler (see [41,42,43]). The establishment of most of the scientific processes and problems are influenced directly by some mathematical structures in the form of distance spaces with some particular properties, e.g., complexification of Minkowski spacetime and quantum decoherence involves the role of complex spaces (see, e.g., [44,45,46]). From a mathematical point of view, the solutions of various problems involve the uses of Banach spaces, Hilbert spaces and several other generalized spaces. The use of generalized spaces permits us to deal with the systems more effectively and simply. This shows the preponderance of generalized spaces over the spaces without generalized structure.
On the other hand, the concept of distance plays an important role in the analysis of systems and processes that frequently occur in practical problems. The deportment of systems having an uncertain nature is successfully analyzed through the concept of fuzzyness. In contrast with the classical notion of distances (metrics), the fuzzy distances have a larger domain of applicability and can be used for the analysis of such systems. In [47], authors showed how the use of fuzzy metrics makes the filtering computationally simpler and more efficient than the usual distances. In [48], the proximity of two pixels in a color image in image filtering and processing is analyzed with the fuzzy metrics.
Here, we have presented a new type of fuzzy metric space in which the fuzzy metric and t-norm can attain the values in generalized spaces (Banach algebras, e.g., in ) instead of the real numbers. This approach can be used for the systems in which the proximity of objects is desirable with respect to various components of a vector parameter, e.g., the proximity of two objects is measured with respect to some parameter (variable) associated with the t-norm; the new approach can make us able to consider the proximity of objects with respect to not only one, but more than one (n) variable simultaneously through the n-dimensional vectors. For instance, when comparing two pixels we can use a vector valued fuzzy metric that attains values in which could provide a degree of similarity of red, green and blue with respect to a parameter (not necessarily the same), respectively, in each component. Moreover, theoretically this is not limited to the finite dimensional cases; therefore, this concept can be used for infinite dimensional cases as well. The fixed point results in fuzzy metric spaces can be applied on the problems associated with recursive algorithms (see [49,50,51]). In the papers [52,53], authors applied the fixed point results of contractive mappings in fuzzy metric spaces to the analysis of quicksort algorithms. Here, we have extended the fixed point results of ordinary fuzzy metric spaces into the vector-valued fuzzy metric spaces, so the new results can be applied on a larger domain of problems.
From a theoretical point of view, we have extended the ordinary t-norm and ordinary fuzzy metrics to their vector-valued versions and proved the fixed point results for contractive type mappings in both strong complete and complete vector-valued fuzzy metric spaces. We use the class of the functions in contractive condition which is a generalized and extended form of the class introduced by [23,54] and so several fixed point results in ordinary fuzzy metric spaces have been extended and generalized to this new type of fuzzy metric space.
Thus, we have extended the notion of t-norms to their vector-valued version, and unified and generalized the notions of ordinary and complex-valued fuzzy metric spaces and corresponding fixed point theorems in vector-valued fuzzy metric spaces. An attempt to generalize some existing fixed point results in new generalized settings was made. In our fixed point result on vector-valued fuzzy metric space we have used a strong condition on the underlying cone, i.e., the cone is strongly minihedral. As we know, there are several examples of important cones which are not minihedral. Due to this fact, the applicability of our fixed point result for generalized Tirado contractions is limited and therefore we conclude this paper with the following open problem:
- Can we prove Theorem 6 for vector-valued fuzzy metric spaces with cones not necessarily miniheral?
Furthermore, following the ideas of the presented work, it may be investigated whether some important generalized notions, such as fuzzy partial metric space [55] and fuzzy metric-like spaces [56], can be extended to their vector-valued versions. Apart from this, the fixed point result for generalized contractions, e.g., for -contractions [57] in the new setting and their applications (e.g., to integral differential systems and dynamic systems) can be investigated.
Author Contributions
Conceptualization, S.S. and N.D.; Methodology, S.S. and N.D.; Validation, S.S. and J.-J.M.; Formal analysis, S.S., N.D. and J.-J.M.; Investigation, S.S. and N.D.; Writing—original draft, S.S. and N.D.; Writing—review & editing, S.S., N.D. and J.-J.M.; Visualization, S.S., N.D. and J.-J.M.; Supervision, S.S. and J.-J.M.; Funding acquisition, J.-J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science and Engineering Research Board (SERB) grant number TAR/2022/000131 and MCIN/AEI/10.13039/501100011033 y FEDER “Una manera de hacer Europa” under grants PID2022-140189OB-C21 and PID2022-139248NB-I00 and Generalitat Valenciana under grant CIAICO/2022/051 and European Union’s Horizon 2020 research and innovation programme under grant agreements No. 871260.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The first author is thankful to M.K. Dube for his regular encouragement and motivation for research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kramosil, I.; Michalek, J. Fuzzy metric and statistical metric spaces. Kybernetica 1975, 15, 326–334. [Google Scholar]
- George, A.; Veeramani, P. On some results in fuzzy metric spaces. Fuzzy Sets Syst. 1994, 64, 395–399. [Google Scholar] [CrossRef]
- Gregori, V.; Romaguera, S. Some properties of fuzzy metric spaces. Fuzzy Sets Syst. 2000, 115, 485–489. [Google Scholar] [CrossRef]
- Adhya, S.; Ray, A. On weak G-completeness for fuzzy metric spaces. Soft Comput. 2023, 26, 2099–2105. [Google Scholar] [CrossRef]
- Gopal, D.; Situnavarat, W.; Ranadive, A.S.; Shukla, S. The investigation of k-fuzzy metric spaces with the first contraction principle in such spaces. Soft Comput. 2023, 27, 11081–11089. [Google Scholar] [CrossRef]
- Gregori, V.; Miñana, J.; Roig, B.; Sapena, A. On Completeness and Fixed Point Theorems in Fuzzy Metric Spaces. Mathematics 2024, 12, 287. [Google Scholar] [CrossRef]
- Jain, M.; Atangana, A. 3-Dimensional computational analysis of φ-contraction in GV-fuzzy metric spaces with applications. Chaos Solitons Fractals 2024, 179, 1–11. [Google Scholar] [CrossRef]
- Miñana, J.; Šostak, A.; Valero, O. On metrization of fuzzy metrics and application to fixed point theory. Fuzzy Sets Syst. 2023, 468, 1–20. [Google Scholar] [CrossRef]
- Moussaoui, A.; Hussain, N.; Melliani, S.; Nasr, H.; Imdad, M. Fixed point results via extended FZ-simulation functions in fuzzy metric spaces. J. Inequalities Appl. 2022, 2022, 1–24. [Google Scholar] [CrossRef]
- Moussaoui, A.; Radenovic, S.; Melliani, S. Fixed point theorems involving FZ-ϑ-contractions in GV-fuzzy metrics. Filomat 2024, 38, 1973–1985. [Google Scholar]
- Ortiz, A.; Ortiz, E.; Miñana, J.J.; Valero, O. On the use of fuzzy metrics for robust model estimation: A RANSAC-based Approach. In Advances in Computational Intelligence; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2021; Volume 12861, pp. 165–177. [Google Scholar]
- Miñana, J.J.; Ortiz, A.; Ortiz, E.; Valero, O. On the standard fuzzy metric: Generalizations and application to model estimation. In Proceedings of the Conference of the Spanish Association for Artificial Intelligence (CAEPIA), Málaga, Spain, 22–24 September 2021; pp. 311–316. [Google Scholar]
- Guerrero, J.; Miñana, J.J.; Valero, O.; Oliver, G. Indistinguishability operators applied to task allocation problems in multi-agent systems. Appl. Sci. 2017, 7, 963. [Google Scholar] [CrossRef]
- Bibiloni-Femenias, M.d.M.; Guerrero, J.; Miñana, J.J.; Valero, O. Indistinguishability operators via Yager t-norms and their applications to swarm multi-agent task allocation. Mathematics 2021, 9, 190. [Google Scholar] [CrossRef]
- Camarena, J.; Gregori, V.; Morillas, S.; Sapena, A. Fast detection and removal of impulsive noise using peer groups and fuzzy metrics. J. Vis. Commun. Image Represent. 2008, 19, 20–29. [Google Scholar] [CrossRef]
- Gregori, V.; Miñana, J.J.; Morillas, S. Some questions in fuzzy metric spaces. Fuzzy Sets Syst. 2012, 204, 71–85. [Google Scholar] [CrossRef]
- Grabiec, M. Fixed points in fuzzy metric spaces. Fuzzy Sets Syst. 1988, 27, 385–389. [Google Scholar] [CrossRef]
- Tirado, P. Contraction mappings in fuzzy quasi-metric spaces and [0,1]-fuzzy posets. Fixed Point Theory 2012, 13, 273–283. [Google Scholar]
- Sherwood, H. Complete Probabilistic Metric Spaces and Random Variables Generated Spaces. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1965. [Google Scholar]
- Gregori, V.; Sapena, A. On fixed-point theorems in fuzzy metric spaces. Fuzzy Sets Syst. 2002, 125, 245–252. [Google Scholar] [CrossRef]
- Radu, V. Some remarks on the probabilistic contractions on fuzzy Menger spaces. In Proceedings of the the Eight International Conference on Applied Mathematics, Computer Science and Mechanics, Cluj-Napoca, Romania, 30 May–2 June 2002; Volume 11, pp. 125–131. [Google Scholar]
- Miheţ, D. Fuzzy ψ-contractive mappings in non-Archimedean fuzzy metric spaces. Fuzzy Sets Syst. 2008, 159, 739–744. [Google Scholar] [CrossRef]
- Wardowski, D. Fuzzy contractive mappings and fixed points in fuzzy metric spaces. Fuzzy Sets Syst. 2013, 222, 108–114. [Google Scholar] [CrossRef]
- Shukla, S.; López, R.R.; Abbas, M. Fixed point results for contractive mappings in complex valued fuzzy metric spaces. Fixed Point Theory 2018, 19, 751–774. [Google Scholar] [CrossRef]
- Huang, L.G.; Zhang, X. Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 2007, 332, 1468–1476. [Google Scholar] [CrossRef]
- Liu, H.; Xu, S.Y. Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings. Fixed Point Theory Appl. 2013, 2013, 320. [Google Scholar] [CrossRef]
- Taqdir, H. Topology, General. In Encyclopedia of Physical Science and Technology, 3rd ed.; Meyers, R.A., Ed.; Academic Press: New York, NY, USA, 2003; pp. 879–903. [Google Scholar] [CrossRef]
- Dhage, B. On a fixed point theorem in Banach algebras with applications. Appl. Math. Lett. 2005, 18, 273–280. [Google Scholar] [CrossRef]
- Lau, A.; Runde, V. Banach Algebras and Their Applications, Proceedings of the Sixteenth International Conference on Banach Algebras, University of Alberta in Edmonton, Canada, 27 July–9 August 2003; Contemporary Mathematics; American Mathematical Society: Providence, RI, USA, 2004. [Google Scholar]
- Monfared, M. On certain products of Banach algebras with applications to harmonic analysis. Stud. Math. 2007, 178, 277–294. [Google Scholar] [CrossRef]
- Zeidler, E. Applied Functional Analysis: Main Principles and Their Applications; Applied Mathematical Sciences; Springer: New York, NY, USA, 1995. [Google Scholar]
- Jungck, G.; Radenović, S.; Radojević, S.; Rakočević, V. Common fixed point theorems for weakly compatible pairs on cone metric spaces. Fixed Point Theory Appl. 2009, 2009, 643840. [Google Scholar] [CrossRef]
- Schweizer, B.; Sklar, A. Statistical Metric Spaces. Pac. J. Math. 1960, 10, 313–334. [Google Scholar] [CrossRef]
- Shukla, S.; Gopal, D.; Roldán-López-De-Hierro, A. Some fixed point theorems in 1-M-complete fuzzy metric-like spaces. Int. J. Gen. Syst. 2016, 45, 815–829. [Google Scholar] [CrossRef]
- Gregori, V.; Miñana, J.J. Some remarks on fuzzy contractive mappings. Fuzzy Sets Syst. 2014, 251, 101–103. [Google Scholar] [CrossRef]
- Gregori, V.; Miñana, J.J.; Sapena, A. On Banach contraction principles in fuzzy metric spaces. Fixed Point Theory 2018, 19, 235–248. [Google Scholar] [CrossRef]
- Tirado, P. On compactness and G-completeness in fuzzy metric spaces. Iran. J. Fuzzy Syst. 2012, 9, 151–158. [Google Scholar]
- Aliprantis, C.D.; Tourky, R. Cones and Duality; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2007; Volume 84. [Google Scholar]
- Karapınar, E. Some nonunique fixed point theorems of Ćirić type on cone metric spaces. Abstr. Appl. Anal. 2010, 2010, 123094. [Google Scholar] [CrossRef]
- Emch, G.G. Chapter 8. The Hilbert Space Formulation of Quantum Mechanics. In Mathematical and Conceptual Foundations of 20Th-Century Physics; North-Holland Mathematics Studies; North-Holland: Amsterdam, The Netherlands, 1984; Volume 100, pp. 249–359. [Google Scholar]
- Davies, E.B. Linear Operators and their Spectra, Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, NY, USA, 2007. [Google Scholar]
- Nowinski, J.L. Applications of Functional Analysis in Engineering; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Mejias, A.; Sigalotti, L.; Sira, E.; Felice, F.D. On El Naschie’s complex time, Hawking’s imaginary time and special relativity. Chaos Solitons Fractals 2004, 19, 773–777. [Google Scholar] [CrossRef]
- Naschie, M.E. On the unification of the fundamental forces and complex time in the space. Chaos Solitons Fractals 2000, 11, 1149–4462. [Google Scholar] [CrossRef]
- Okeng’o, G.; Awuor, J. On the complexification of Minkowski spacetime. Afr. J. Phys. Sci. 2015, 2, 73–76. [Google Scholar]
- Morillas, S.; Gregori, V.; Peris-Fajarnés, G.; Latorre, P. A fast impulsive noise color image filter using fuzzy metrics. Real-Time Imaging 2005, 11, 417–428. [Google Scholar] [CrossRef]
- Morillas, S.; Sapena, A. Fuzzy metrics and color image filtering. In Proceedings of the XVI Encuentro de Topología, Almería, Spain, 23–24 October 2009. [Google Scholar]
- Castro-Company, F. Fuzzy Quasi-Metric Spaces: Bicompletion, Contractions on Product Spaces and Applications to Access Predictions. Ph.D. Thesis, Universidad Politécnica de Valencia, Valencia, Spain, 2010. [Google Scholar]
- Castro-Company, F.; Romaguera, S. Experimental results for information systems based on accesses locality via intuitionistic fuzzy metrics. Open Cybern. Syst. J. 2008, 2, 158–172. [Google Scholar] [CrossRef][Green Version]
- Castro-Company, F.; Romaguera, S.; Tirado, P. Application of the Banach fixed point theorem on fuzzy quasi-metric spaces to study the cost of algorithms with two recurrence equations. In Proceedings of the International Conference on Fuzzy Computation (ICFC), Valencia, Spain, 24–26 October 2010; pp. 105–109. [Google Scholar]
- Mihet, D. Fuzzy quasi-metric version of a theorem of Gregori and Sapena. Iran. J. Fuzzy Syst. 2010, 7, 59–64. [Google Scholar] [CrossRef]
- Romaguera, S.; Sapena, A.; Tirado, P. The banach fixed point theorem in fuzzy quasi-metric spaces with application to the domain of words. Topol. Appl. 2007, 154, 105–109. [Google Scholar] [CrossRef]
- Miheţ, D. A class of contractions in fuzzy metric spaces. Fuzzy Sets Syst. 2010, 161, 1131–1137. [Google Scholar] [CrossRef]
- Gregori, V.; Miñana, J.; Miravet, D. Fuzzy partial metric spaces. Int. J. Gen. Syst. 2019, 48, 260–279. [Google Scholar] [CrossRef]
- Shukla, S.; Abbas, M. Fixed point results in fuzzy metric-like spaces. Iran. J. Fuzzy Syst. 2014, 11, 81–92. [Google Scholar]
- Shukla, S.; Gopal, D.; Sintunavarat, W. A new class of fuzzy contractive mappings and fixed point theorems. Fuzzy Sets Syst. 2018, 350, 85–94. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
