Satisfiability Threshold of Random Propositional S5 Theories
Abstract
1. Introduction
- It proves that any S5 formula can be translated into a reduced 3-c-S5 formula, which is proposed in this paper as a new form of S5 formula maintaining the satisfiability.
- It shows that the frequency of modal operators occurring in each reduced k-S5 clause is a key factor affecting the phase transition in a random reduced k-S5 formula.
- It presents the phase transition threshold, i.e.,where are the probability of □ and ◊ occurring in a random reduced 3-1-S5 clause, and represents the ratio of clause quantity to atom quantity in a random 3-1-S5 formula, and its correctness has been proved with a large number of random experimental results which are consistent with this result.
2. Preliminaries
2.1. Modal Logic S5
- W is a nonempty set of states,
- is a state transition relationship on W,
- is a labeling function that maps each state into a subset of .
2.2. From S5-SAT to SAT
3. The Satisfiability Threshold of Random Reduced 3-S5 Formulas
3.1. Reduced k-S5 Formulas
| Algorithm 1 Generate a random reduced 3-S5 formula |
| Input: : the probability of ◊ appearing in a modal clause, : the probability of □ appearing in a modal clause, n: the number of atoms, m: the number of clauses, c: the number of literals occurring in modality. Output: A 3-c-S5 formula Let ; Let ;
|
3.2. The Satisfiability Threshold Analysis
4. Experiment
4.1. Random Instance Generation Model for S5-SAT
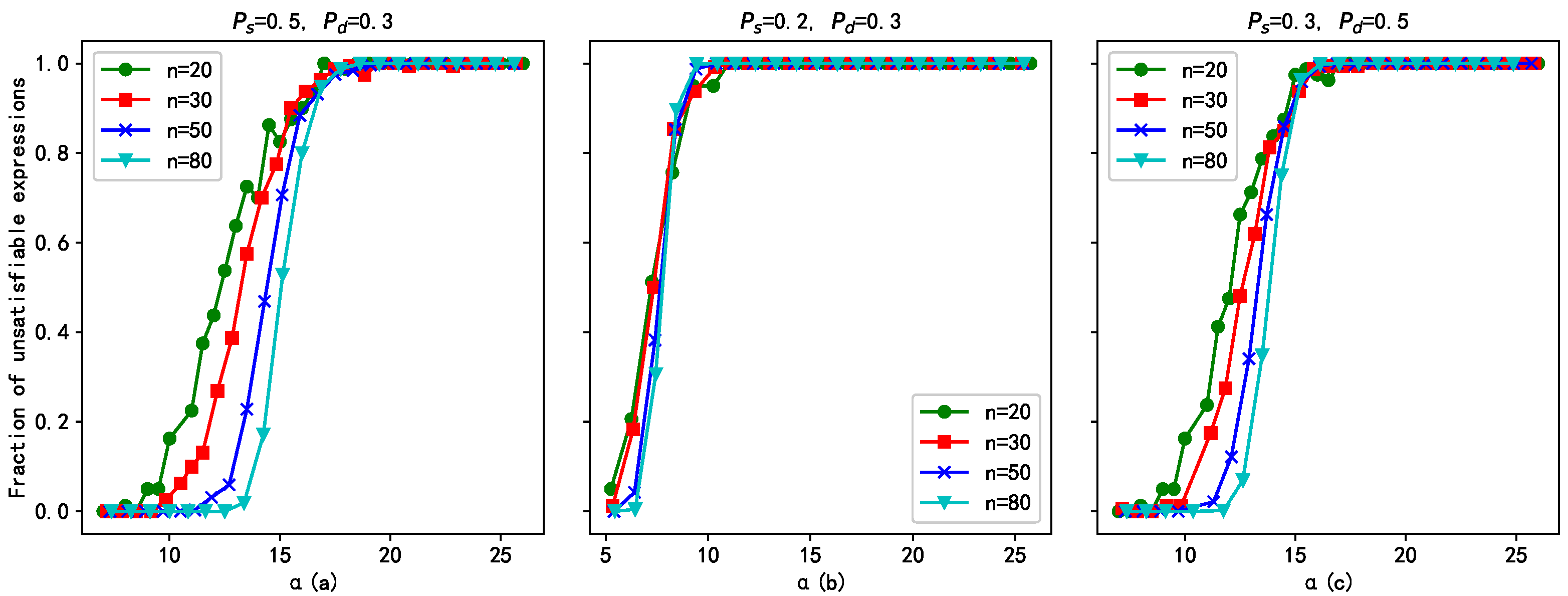
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stanley, H.E. Phase Transitions and Critical Phenomena; Clarendon Press: Oxford, UK, 1971; Volume 7. [Google Scholar]
- Mitchell, D.G.; Selman, B.; Levesque, H.J. Hard and Easy Distributions of SAT Problems. In Proceedings of the 10th National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; Swartout, W.R., Ed.; AAAI Press: Washington, DC, USA; The MIT Press: Cambridge, MA, USA, 1992; pp. 459–465. [Google Scholar]
- Kirkpatrick, S.; Selman, B. Critical Behavior in the Satisfiability of Random Boolean Expressions. Science 1994, 264, 1297–1301. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, D. Properties of the satisfiability threshold of the strictly d-regular random (3, 2s)-SAT problem. Front. Comput. Sci. 2020, 14, 146404. [Google Scholar] [CrossRef]
- Mo, X.; Xu, D.; Yan, K.; Zhang, Z. Satisfiability threshold of the random regular (s, c, k)-SAT problem. Front. Comput. Sci. 2022, 16, 163408. [Google Scholar] [CrossRef]
- Nie, G.; Xu, D.; Wang, X.; Zhang, Z. Exact satisfiability and phase transition analysis of the regular (k, d)-cnf formula. Front. Comput. Sci. 2024, 18, 181405. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, D.; Zhou, J. On the upper bounds of (1,0)-super solutions for the regular balanced random (k,2s)-sat problem. Front. Comput. Sci. 2024, 18, 184403. [Google Scholar] [CrossRef]
- Xu, K.; Li, W. Exact Phase Transitions in Random Constraint Satisfaction Problems. J. Artif. Intell. Res. 2000, 12, 93–103. [Google Scholar] [CrossRef]
- Wen, L.; Wang, K.; Shen, Y.D.; Lin, F. A Model for Phase Transition of Random Answer-Set Programs. ACM Trans. Comput. Log. 2016, 17, 22. [Google Scholar] [CrossRef]
- Fitting, M. Modality and Databases. In Automated Reasoning with Analytic Tableaux and Related Methods, International Conference, TABLEAUX 2000, St Andrews, Scotland, UK, 3–7 July 2000, Proceedings; Vol. 1847 of Lecture Notes in Computer Science; Dyckhoff, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 19–39. [Google Scholar]
- Fairtlough, M.; Mendler, M. An Intuitionistic Modal Logic with Applications to the Formal Verification of Hardware. In Computer Science Logic, 8th International Workshop, CSL ’94, Kazimierz, Poland, 25–30 September 1994; Selected Papers. Vol. 933 of Lecture Notes in Computer Science; Pacholski, L., Tiuryn, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 354–368. [Google Scholar]
- VII, T.M.; Crary, K.; Harper, R. Distributed Control Flow with Classical Modal Logic. In Computer Science Logic, 19th International Workshop, CSL 2005, 14th Annual Conference of the EACSL, Oxford, UK, 22–25 August 2005; Proceedings. Vol. 3634 of Lecture Notes in Computer Science; Ong, C.H.L., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 51–69. [Google Scholar]
- Lorini, E.; Schwarzentruber, F. A Modal Logic of Epistemic Games. Games 2010, 1, 478–526. [Google Scholar] [CrossRef]
- Giunchiglia, F.; Sebastiani, R. Building Decision Procedures for Modal Logics from Propositional Decision Procedures: The Case Study of Modal K(m). Inf. Comput. 2000, 162, 158–178. [Google Scholar] [CrossRef]
- Bienvenu, M.; Fargier, H.; Marquis, P. Knowledge Compilation in the Modal Logic S5. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2010, Atlanta, GA, USA, 11–15 July 2010; Fox, M., Poole, D., Eds.; AAAI Press: Washington, DC, USA, 2010; pp. 261–266. [Google Scholar]
- Niveau, A.; Zanuttini, B. Efficient Representations for the Modal Logic S5. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, IJCAI 2016, New York, NY, USA, 9–15 July 2016; Kambhampati, S., Ed.; IJCAI/AAAI Press: Washington, DC, USA, 2016; pp. 1223–1229. [Google Scholar]
- Wan, H.; Yang, R.; Fang, L.; Liu, Y.; Xu, H. A complete epistemic planner without the epistemic closed world assumption. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, IJCAI 2015, Buenos Aires, Argentina, 25–31 July 2015; Yang, Q., Wooldridge, M.J., Eds.; AAAI Press: Washington, DC, USA, 2015; pp. 3257–3263. [Google Scholar]
- Ladner, R.E. The Computational Complexity of Provability in Systems of Modal Propositional Logic. SIAM J. Comput. 1977, 6, 467–480. [Google Scholar] [CrossRef]
- Brünnler, K. Deep sequent systems for modal logic. Arch. Math. Log. 2009, 48, 551–577. [Google Scholar] [CrossRef]
- D’Agostino, M.; Gabbay, D.M.; Hähnle, R.; Posegga, J. Handbook of Tableau Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Fitting, M. Proof Methods for Modal and Intuitionistic Logics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 169. [Google Scholar]
- Salhi, Y.; Sioutis, M. A Resolution Method for Modal Logic S5. In Global Conference on Artificial Intelligence, GCAI 2015, Tbilisi, Georgia, 16–19 October 2015; Volume 36 of EPiC Series in Computing; Gottlob, G., Sutcliffe, G., Voronkov, A., Eds.; EasyChair: Stockport, UK, 2015; pp. 252–262. [Google Scholar]
- Huang, P.; Liu, M.; Wang, P.; Zhang, W.; Ma, F.; Zhang, J. Solving the satisfiability problem of modal logic S5 guided by graph coloring. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, 10–16 August 2019; Kraus, S., Ed.; IJCAI.ORG: Occitania, France, 2019; pp. 1093–1100. [Google Scholar]
- Alviano, M.; Batsakis, S.; Baryannis, G. Modal Logic S5 Satisfiability in Answer Set Programming. Theory Pract. Log. Program. 2021, 21, 527–542. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y. Knowledge forgetting: Properties and applications. Artif. Intell. 2009, 173, 1525–1537. [Google Scholar] [CrossRef]
- Hughes, G.E.; Cresswell, M.J. A New Introduction to Modal Logic; Psychology Press: London, UK, 1996; pp. 96–97. [Google Scholar]
- Caridroit, T.; Lagniez, J.; Berre, D.L.; de Lima, T.; Montmirail, V. A SAT-Based Approach for Solving the Modal Logic S5-Satisfiability Problem. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Singh, S., Markovitch, S., Eds.; AAAI Press: Washington, DC, USA, 2017; pp. 3864–3870. [Google Scholar]
- Feng, R.; Wang, Y.; Chen, P.; Zhou, J. Strongest necessary and weakest sufficient conditions in S5. In Proceedings of the 13th International Conference on Intelligent Systems and Knowledge Engineering (ISKE2018), Belfast, UK, 21–24 August 2018; Proceedings. World Scientific: Singapore, 2018; pp. 832–839. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Wang, Y.; Feng, R.; Zhou, C. Satisfiability Threshold of Random Propositional S5 Theories. Axioms 2024, 13, 241. https://doi.org/10.3390/axioms13040241
Su Z, Wang Y, Feng R, Zhou C. Satisfiability Threshold of Random Propositional S5 Theories. Axioms. 2024; 13(4):241. https://doi.org/10.3390/axioms13040241
Chicago/Turabian StyleSu, Zaihang, Yisong Wang, Renyan Feng, and Chan Zhou. 2024. "Satisfiability Threshold of Random Propositional S5 Theories" Axioms 13, no. 4: 241. https://doi.org/10.3390/axioms13040241
APA StyleSu, Z., Wang, Y., Feng, R., & Zhou, C. (2024). Satisfiability Threshold of Random Propositional S5 Theories. Axioms, 13(4), 241. https://doi.org/10.3390/axioms13040241





