Efficient Numerical Solutions for Fuzzy Time Fractional Convection Diffusion Equations Using Two Explicit Finite Difference Methods
Abstract
1. Introduction
2. Fuzzy Environmental Considerations in the Context of the TFCDE
3. The FTCS Method for Solving the FTFCDE
4. The Saulyev Method for Solving the FTFCDE
5. The Stability Analysis
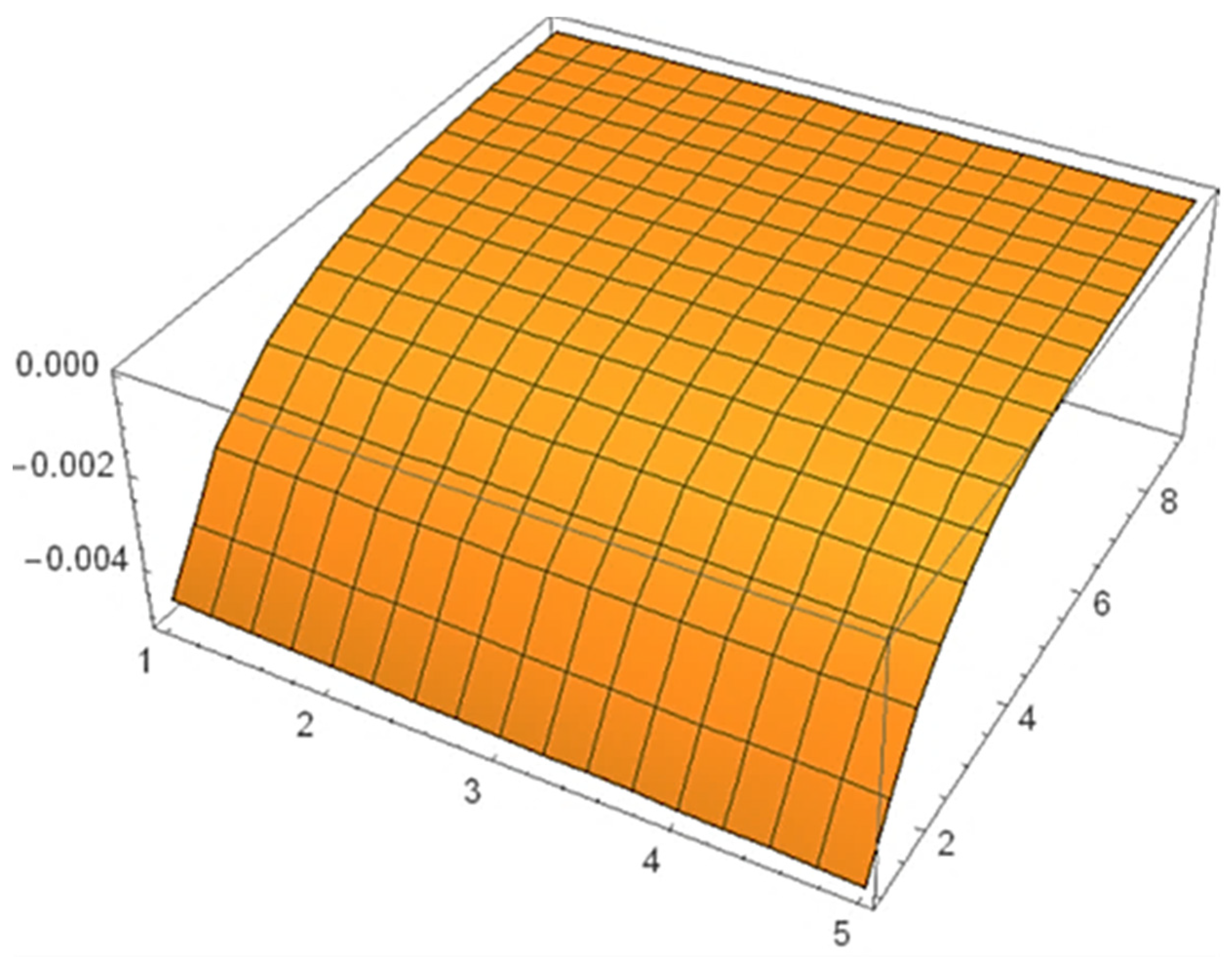
6. Numerical Example
| FTCS | Saulyev | ||||
|---|---|---|---|---|---|
| ψ | r | ||||
| Lower Solution When ψ = 0 | 0 | −0.0004929227 | 4.09024 × 10−5 | −0.0004478379 | 8.59872 × 10−5 |
| 0.2 | −0.0003943382 | 3.27219 × 10−5 | −0.0003582703 | 6.87898 × 10−5 | |
| 0.4 | −0.0002957536 | 2.45414 × 10−5 | −0.0002687027 | 5.15923 × 10−5 | |
| 0.6 | −0.0001971691 | 1.63610 × 10−5 | −0.0001791352 | 3.43949 × 10−5 | |
| 0.8 | −0.0000985845 | 8.18048 × 10−6 | −0.0000895676 | 1.71974 × 10−5 | |
| 1 | 0 | 0 | 0 | 0 | |
| Upper Solution When ψ = 1 | 0 | 0.0004929227 | 4.09024 × 10−5 | 0.0004478379 | 8.59872 × 10−5 |
| 0.2 | 0.0003943382 | 3.27219 × 10−5 | 0.0003582703 | 6.87898 × 10−5 | |
| 0.4 | 0.0002957536 | 2.45414 × 10−5 | 0.0002687027 | 5.15923 × 10−5 | |
| 0.6 | 0.0001971691 | 1.63610 × 10−5 | 0.0001791352 | 3.43949 × 10−5 | |
| 0.8 | 0.0000985845 | 8.18048 × 10−6 | 0.0000895676 | 1.71974 × 10−5 | |
| 1 | 0 | 0 | 0 | 0 | |
| FTCS | Saulyev | ||||
|---|---|---|---|---|---|
| ψ | r | ||||
| ψ = 0.4 | 0 | −0.0000985845 | 8.18048 × 10−6 | −0.0000895676 | 1.71974 × 10−5 |
| 0.2 | −0.0000788676 | 6.54438 × 10−6 | −0.0000716541 | 1.3758 × 10−5 | |
| 0.4 | −0.0000591507 | 4.90829 × 10−6 | −0.0000537405 | 1.03185 × 10−5 | |
| 0.6 | −0.0000394338 | 3.27219 × 10−6 | −0.0000358270 | 6.87898 × 10−6 | |
| 0.8 | −0.0000197169 | 1.6361 × 10−6 | −0.0000179135 | 3.43949 × 10−6 | |
| 1 | 0 | 0 | 0 | 0 | |
| ψ = 0.6 | 0 | 0.0000985845 | 8.18048 × 10−6 | 0.0000895676 | 1.71974 × 10−5 |
| 0.2 | 0.0000788676 | 6.54438 × 10−6 | 0.0000716541 | 1.3758 × 10−5 | |
| 0.4 | 0.0000591507 | 4.90829 × 10−6 | 0.0000537405 | 1.03185 × 10−5 | |
| 0.6 | 0.0000394338 | 3.27219 × 10−6 | 0.0000358270 | 6.87898 × 10−6 | |
| 0.8 | 0.0000197169 | 1.6361 × 10−6 | 0.0000179135 | 3.43949 × 10−6 | |
| 1 | 0 | 0 | 0 | 0 | |

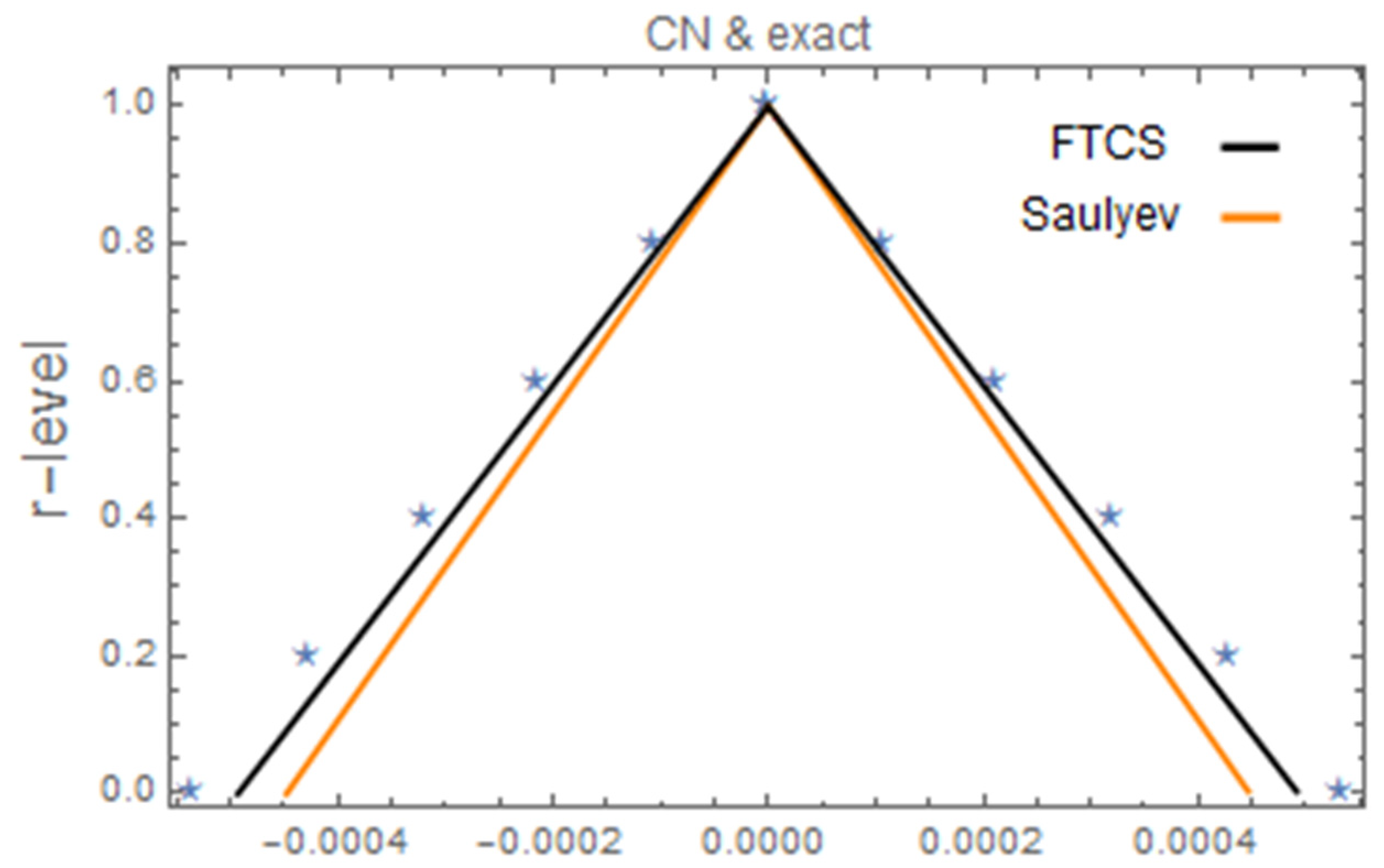
7. Summary
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Smadi, M.; Arqub, O.A. Computational algorithm for solving fredholsm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar]
- Bira, B.; Raja Sekhar, T.; Zeidan, D. Exact solutions for some time-fractional evolution equations using Lie group theory. Math. Methods Appl. Sci. 2018, 41, 6717–6725. [Google Scholar] [CrossRef]
- Zureigat, H.; Al-khateeb, A.; Abuteen, E.; Abu-Ghurra, S. Numerical Solution of Fuzzy Heat Equation with Complex Dirichlet Conditions. Int. J. Fuzzy Log. Intell. Syst. 2023, 23, 11–19. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical solutions of the space-time fractional advection-dispersion equation. Numer. Meth. Partial. Differ. Equ. Int. J. 2008, 24, 1416–1429. [Google Scholar] [CrossRef]
- Al-Smadi, M. Simplified iterative reproducing kernel method for handling time-fractional BVPs with error estimation. Ain Shams Eng. J. 2017, 9, 2517–2525. [Google Scholar] [CrossRef]
- Zureigat, H.; Al-Omari, S.; Al-Smadi, M.; Momani, S. A Solution of Complex Fuzzy Time-Fractional Heat Equation by an Explicit Scheme. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA), Ajman, United Arab Emirates, 14–16 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Batiha, B.; Ghanim, F.; Alayed, O.; Hatamleh, R.E.; Heilat, A.S.; Zureigat, H.; Bazighifan, O. Solving Multispecies Lotka–Volterra Equations by the Daftardar-Gejji and Jafari Method. Int. J. Math. Math. Sci. 2022, 2022, 1839796. [Google Scholar] [CrossRef]
- Tasbozan, O.; Senol, M.; Kurt, A.; Ozkan, O. New solutions of fractional Drinfeld-Sokolov-Wilson system in shallow water waves. Ocean. Eng. 2018, 161, 62–68. [Google Scholar] [CrossRef]
- Zureigat, H.; Al-Smadi, M.; Al-Khateeb, A.; Al-Omari, S.; Alhazmi, S. Numerical Solution for Fuzzy Time-Fractional Cancer Tumor Model with a Time-Dependent Net Killing Rate of Cancer Cells. Int. J. Environ. Res. Public. Health 2023, 20, 3766. [Google Scholar] [CrossRef]
- Zeidan, D.; Sekhar, T.R. On the wave interactions in the drift-flux equations of two-phase flows. Appl. Math. Comput. 2018, 327, 117–131. [Google Scholar]
- Almutairi, M.; Zureigat, H.; Izani Ismail, A.; Fareed Jameel, A. Fuzzy numerical solution via finite difference scheme of wave equation in double parametrical fuzzy number form. Mathematics 2021, 9, 667. [Google Scholar] [CrossRef]
- Abu Arqub, O.; El-Ajou, A.; Momani, S.; Shawagfeh, N. Analytical solutions of fuzzy initial value problems by HAM. Appl. Math. Info Sci. 2013, 7, 1903–1919. [Google Scholar] [CrossRef]
- Zureigat, H.H.; Ismail AI, M. Numerical solution of fuzzy heat equation with two different fuzzifications. In Proceedings of the 2016 SAI Computing Conference (SAI), London, UK, 13–15 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 85–90. [Google Scholar]
- Agarwal, R.P.; Lakshmikantham, V.; Nieto, J.J. On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal. Theory Methods Appl. 2010, 726, 2859–2862. [Google Scholar] [CrossRef]
- Arshad, S.; Lupulescu, V. Fractional differential equation with the fuzzy initial condition. Electron. J. Differ. Equ. 2011, 2011, 1–8. [Google Scholar]
- Salahshour, S.; Ahmadian, A.; Chan, C.S.; Baleanu, D. Toward the existence of solutions of fractional sequential differential equations with uncertainty. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Istanbul, Turkey, 2–5 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Long, H.V.; Son, N.T.K.; Hoa, N.V. Fuzzy fractional partial differential equations in partially ordered metric spaces. Iran. J. Fuzzy Syst. 2017, 14, 107–126. [Google Scholar]
- Souahi, A.; Guezane-Lakoud, A.; Hitta, A. On the existence and uniqueness for high order fuzzy fractional differential equations with uncertainty. Adv. Fuzzy Syst. 2016, 2016, 1–9. [Google Scholar] [CrossRef][Green Version]
- Salahshour, S.; Allahviranloo, T.; Abbasbandy, S. Solving fuzzy fractional differential equations by fuzzy Laplace transforms. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1372–1381. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Salahshour, S.; Abbasbandy, S. Explicit solutions of fractional differential equations with uncertainty. Soft Comput. 2012, 16, 297–302. [Google Scholar] [CrossRef]
- Mazandarani, M.; Kamyad, A.V. Modified fractional Euler method for solving fuzzy fractional initial value problem. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 12–21. [Google Scholar] [CrossRef]
- Ahmadian, A.; Suleiman, M.; Salahshour, S.; Baleanu, D. A Jacobi operational matrix for solving a fuzzy linear fractional differential equation. Adv. Differ. Equ. 2013, 2013, 104. [Google Scholar] [CrossRef]
- Jafarian, A.; Golmankhaneh, A.K.; Baleanu, D. On fuzzy fractional Laplace transformation. Adv. Math. Phys. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Raj, S.R.; Saradha, M. Solving hybrid fuzzy fractional differential equations by Adam-Bash forth method. Appl. Math. Sci. 2015, 9, 1429–1432. [Google Scholar] [CrossRef]
- Ahmadian, A.; Salahshour, S.; Chan, C.S. Fractional differential systems: A fuzzy solution based on operational matrix of shifted Chebyshev polynomials and its applications. IEEE Trans. Fuzzy Syst. 2017, 25, 218–236. [Google Scholar] [CrossRef]
- Salah, A.; Khan, M.; Gondal, M.A. A novel solution procedure for fuzzy fractional heat equations by homotopy analysis transform method. Neural Comput. Appl. 2013, 23, 269–271. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Dutt, H.M.; Arefin, M.A. Novel Evaluation of Fuzzy Fractional Cauchy Reaction-Diffusion Equation. J. Funct. Spaces 2022, 2022, 6499384. [Google Scholar] [CrossRef]
- Saadeh, R. Numerical solutions of fractional convection-diffusion equation using finite-difference and finite-volume schemes. J. Math. Comput. Sci. 2021, 11, 7872–7891. [Google Scholar]
- Zureigat, H.; Al-Smadi, M.; Al-Khateeb, A.; Al-Omari, S.; Alhazmi, S.E. Fourth-order numerical solutions for a fuzzy time-fractional convection–diffusion equation under Caputo generalized Hukuhara derivative. Fractal Fract. 2022, 7, 47. [Google Scholar] [CrossRef]
- Chakraverty, S.; Tapaswini, S. Non-probabilistic solutions of imprecisely defined fractional-order diffusion equations. Chin. Phys. B. 2014, 23, 120–202. [Google Scholar] [CrossRef][Green Version]
- Al-Shibani, F.S.; Ismail, A.M.; Abdullah, F.A. Explicit finite difference methods for the solution of the one dimensional time fractional advection-diffusion equation. In Proceedings of the AIP Conference Proceedings 2014, Boulder, CO, USA, 20–25 July 2014; American Institute of Physics: College Park, PA, USA, 2014; Volume 1605, pp. 380–385. [Google Scholar]
- Batiha, B.; Al-khateeb, A.; Zureigat, H. Improving Numerical Solutions for the Generalized Huxley Equation: The New Iterative Method (NIM). Appl. Math 2023, 1, 427–493. [Google Scholar]
- Zureigat, H.; Ismail, A.I.; Sathasivam, S. A compact Crank–Nicholson scheme for the numerical solution of fuzzy time fractional diffusion equations. Neural Comput. Appl. 2020, 32, 6405–6412. [Google Scholar] [CrossRef]
- Zureigat, H.; Ismail, A.I.; Sathasivam, S. Numerical solutions of fuzzy time fractional advection-diffusion equations in double parametric form of fuzzy number. Math. Methods Appl. Sci. 2021, 44, 7956–7968. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Khateeb, A. Efficient Numerical Solutions for Fuzzy Time Fractional Convection Diffusion Equations Using Two Explicit Finite Difference Methods. Axioms 2024, 13, 221. https://doi.org/10.3390/axioms13040221
Al-Khateeb A. Efficient Numerical Solutions for Fuzzy Time Fractional Convection Diffusion Equations Using Two Explicit Finite Difference Methods. Axioms. 2024; 13(4):221. https://doi.org/10.3390/axioms13040221
Chicago/Turabian StyleAl-Khateeb, Areen. 2024. "Efficient Numerical Solutions for Fuzzy Time Fractional Convection Diffusion Equations Using Two Explicit Finite Difference Methods" Axioms 13, no. 4: 221. https://doi.org/10.3390/axioms13040221
APA StyleAl-Khateeb, A. (2024). Efficient Numerical Solutions for Fuzzy Time Fractional Convection Diffusion Equations Using Two Explicit Finite Difference Methods. Axioms, 13(4), 221. https://doi.org/10.3390/axioms13040221






