Freeness of Signed Graphic Arrangements

Abstract

Freeness occupies an important position in the study of hyperplane arrangements. In this paper, we conclude the freeness of three special classes of signed graphic arrangements based on the addition–deletion theorem and Abe’s free path theory.

1. Introduction

It is known that the Coxeter arrangements are free; see V. I. Arnold [1,2], and K. Saito [3]. This was generalized to the case of unitary reflection groups by H. Terao [4]. T. Józefiak and B. E. Sagan [5] explicitly constructed the basic derivations of some classes of subarrangements of Coxeter arrangements. P. H. Edelman and V. Reiner [6] characterized the freeness and supersolvability of subarrangements between $A_{n-1}$ and $B_n$ combinatorially. Stanley [7] characterized the freeness and supersolvabilitiy of graphic arrangements associated with chordal graphs. Abe [8] also gave the characteristic polynomial of a multiarrangement. T. Zaslavsky [9] described that graphic and sign-symmetric arrangements can be reduced to ordinary graph theory; arrangements that are neither graphic nor sign-symmetric can also be handled, but they require a theory of signed graphs. At present, the graphic arrangements associated with signed graphs are still very active areas of research, especially the freeness of hyperplane arrangements (e.g., M. Yoshinaga [10], Ziegler [11] and Bailey [12]). In this paper, we focus on the freeness of signed graphic arrangements.

A hyperplane arrangement $\mathcal{A}$ is a collection of finite hyperplanes, H, which comprise the kernel of a linear form of variables $x_1,\dots ,x_l$ in the vector space ${\mathbb{K}}^l$. A graph $G=(V,E)$ is an ordered pair in which $V=V_G=\{1,2,\dots ,l\}=\left[l\right]$, called the vertex set, and $E=E_G$ is called the edge set of G, which is the collection of two-element subsets of V.

A signed graph is a tuple $G=(V_G,E_G^{+},E_G^{-},L_G)$ [13] where

(1)

$V_G$ is a finite set called the set of vertices;

(2)

$E_G^{+}$ is a subset of $\left(\begin{array}{c}{V}_G\\ 2\end{array}\right)$ called the set of positive edges;

(3)

$E_G^{-}$ is a subset of $\left(\begin{array}{c}{V}_G\\ 2\end{array}\right)$ called the set of negative edges;

(4)

$L_G$ is a subset of $V_G$ called the set of loops.

Let G be a signed graph with l vertices, let $\mathbb{K}$ be a field, let $V={\mathbb{K}}^l$, and let $x_1,\dots ,x_l$ be a basis for the dual space $V^{\ast }$. Associated with the signed graph G, the signed graphic arrangement $\mathcal{A}\left(G\right)$ in the l-dimensional vector space over $\mathbb{K}$ is defined as follows:

$$\mathcal{A}\left(G\right)=\{x_i-x_j=0\mid \{i,j\}\in E_G^{+}\}\cup \{x_i+x_j=0\mid \{i,j\}\in E_G^{-}\}\cup \{x_i=0\mid \left\{i\right\}\in L\}$$

where L is the loop set of the graph G; in this paper, we focus on the case of $E_G^{-}\cup E_G^{+}=E$ and $E_G^{-}\cap E_G^{+}=\varnothing$, and we assume that $L=\varnothing$.

Some results for the freeness of signed graphic arrangements have been obtained. Suyama, Michele, and Tsujie [14] characterized the freeness of signed graphic arrangements corresponding to graphs in the case $G^{+}\supseteq G^{-}$, and they show that when the signed graph G with $G^{+}\supseteq G^{-}$, the arrangement $\mathcal{A}\left(G\right)$ is free if and only if $\mathcal{A}\left(G\right)$ is divisionally free or G is a balanced chordal. Michele and Tsujie [15] generalized this result, and they give a complete characterization for the freeness of arrangements between Boolean arrangements and Weyl arrangements of type $B_l$ in terms of signed graphs. However, there are many unknown results for the freeness of signed graphic arrangements. In this article, we characterized the freeness of three other kinds of signed graphic arrangements. The following theorems are our main results.

Theorem 1.

For a signed graph G, denoted by V and E, the vertex set and the edge set, respectively, T is a chordal subgraph of G, $E\left(T\right)\subset E_G^{+}$, and $E(G-T)=\varnothing$. The signed graphic arrangement $\mathcal{A}=\mathcal{A}\left(G\right)$ is free if the vertex $v\in V(G-T)$ satisfies one of the following conditions:

(1)

For all $v_i\in V\left(T\right)$, $v{v}_i\notin E\left(G\right)$, i.e., v is an isolated point.

(2)

There exists only $v_i\in V\left(T\right)$ such that $v{v}_i\in E\left(G\right)$.

(3)

If there exist two different $v_i,v_j\in V\left(T\right)$ and $v{v}_i,v{v}_j\in E_G^{-}$, then it implies $v_i{v}_j\in E_G^{+}$.

Theorem 2.

If the signed graphic hyperplane arrangement $\mathcal{A}=\mathcal{A}\left(G\right)$ satisfies the following conditions, then it is free.

(1)

The graph $G=T\cup Q$, T is a chordal graph, and $E\left(T\right)\subset E_G^{+}$, Q satisfies $V\left(Q\right)\cap V\left(T\right)=\{v_1,v_2\}$ and $E\left(Q\right)\cap E\left(T\right)=\left\{v_1{v}_2\right\}$.

(2)

The graph Q is switching equivalent to $K_4^{\prime }$ or $K_4^{\prime }\setminus e$, where e is an edge of $K_4^{\prime }$.

Theorem 3.

For a graph $G=T\cup U=(V_G,E_G^{+},E_G^{-})$, T is a chordal subgraph of G, $E\left(T\right)\subset E_G^{+}$, $E\left(T\right)\cap E\left(U\right)=\left\{v_1{v}_2\right\}$, and the subgraph U is a cycle containing an odd number of negative edges. Then, the signed graphic hyperplane arrangement $\mathcal{A}=\mathcal{A}\left(G\right)$ is free.

The organization of this article is as follows. In Section 2, we review some basic definitions and results of the hyperplane arrangement, including the combinatorial and algebraic properties, which are helpful for studying freeness. Some related examples and theorems are also shown in this section. In Section 3, we mainly characterize the freeness of four signed graphic arrangements, $\mathcal{A}\left(K_3^2\right)$, $\mathcal{A}\left(K_3^1\right)$, $\mathcal{A}\left(K_4^{\prime }\right)$, and $\mathcal{A}(K_4^{\prime }\setminus e)$; their corresponding graphs are the subgraphs in our main theorems. In Section 4, we focus on proving the main theorems. In Section 5, we raise some questions about the freeness of signed graphic arrangements for further research.

2. Preliminaries

In this section, we briefly review some basic definitions and results from [16].

Let $\mathcal{A}$ be a finite hyperplane arrangement denoted by

$$L\left(\mathcal{A}\right)=\{B\mid B=\bigcap _{H\in \mathcal{A}}H\ne \varnothing \}$$

the intersection partial ordered set of $\mathcal{A}$.

An arrangement $\mathcal{A}$ is central if the intersection of all hyperplanes is not empty, and $L=L\left(\mathcal{A}\right)$ is a geometric lattice for central arrangements. We only discuss the central case in this paper since every signed graphic arrangement contains the origin as its center.

For an arrangement $\mathcal{A}$, the meet of $X,Y\in L\left(\mathcal{A}\right)$ is defined by $X\wedge Y=\bigcap \{Z\in L\mid Z\supseteq X\cup Y\}$, and their join is defined by $X\vee Y=X\cup Y$. A pair $(X,Y)\in L\times L$ is called a modular pair if for all $Z\le Y$, one has $Z\vee (X\wedge Y)=(Z\wedge X)\vee Y$. A pair $(X,Y)\in L\times L$ is a modular pair if and only if $r\left(X\right)+r\left(Y\right)=r(X\vee Y)+r(X\wedge Y)$, where r is the rank function of L. An element X is called a modular element if it forms a modular pair with each $Y\in L$.

For an $X\in L\left(\mathcal{A}\right)$, the localization of $\mathcal{A}$ at $X\in \mathcal{A}$ is the subarrangement

$${\mathcal{A}}_X:=\{H\in \mathcal{A}\mid H\supseteq X\},$$

and the restriction ${\mathcal{A}}^X$ is the arrangement

$${\mathcal{A}}^X=\{X\cap H:H\in \mathcal{A}\setminus {\mathcal{A}}_X,H\cap X\ne \varnothing \}.$$

For a given hyperplane $H\in \mathcal{A}$, we have a triple $(\mathcal{A},{\mathcal{A}}^{\prime },{\mathcal{A}}^{″})$ of arrangements where ${\mathcal{A}}^{\prime }=\mathcal{A}-\left\{H\right\}$ and ${\mathcal{A}}^{″}={\mathcal{A}}^H$.

The characteristic polynomial $\chi (\mathcal{A},t)$ of an arrangement $\mathcal{A}$ is defined by

$$\chi (\mathcal{A},t)=\sum _{X\in L\left(\mathcal{A}\right)}\mu \left(X\right)t^{dim\left(X\right)}$$

where $\mu \left(X\right)$ denotes the Möbius function of $L\left(\mathcal{A}\right)$, defined recursively by

$$\mu \left({\mathbb{K}}^l\right):=1,\mu \left(X\right):=-\sum _{Y<X}\mu \left(Y\right).$$

For a vector space V, $S=S\left(V^{\ast }\right)$ is the symmetric algebra of the dual space $V^{\ast }$. Given a basis of $V^{\ast }$, then S is isomorphic to a polynomial ring $\mathbb{K}[x_1,\dots ,x_l]$. Denoted by Der$\left(S\right)$, the module of derivations of S is

$$\mathrm{Der}\left(S\right):=\{\theta :S\to S\mid \theta \mathrm{is}\mathbb{K}-\mathrm{linear},\theta (fg)=\theta (f)g+f\theta (g)\mathrm{for}f,g\in S\}.$$

Let $\mathcal{A}$ be an arrangement in V with the defining polynomial

$$Q\left(\mathcal{A}\right)=\prod _{H\in \mathcal{A}}{\alpha }_H$$

where $H=$ ker$\left({\alpha }_H\right)$. We define $D\left(\mathcal{A}\right)$ as a module over the polynomial ring S as follows

$$D\left(\mathcal{A}\right)=D\left(Q\left(\mathcal{A}\right)\right)=\{\delta \in \mathrm{Der}\left(S\right)\mid \delta \left({\alpha }_H\right)\subset {\alpha }_{H}S,\forall H\in \mathcal{A}\}.$$

If $D\left(\mathcal{A}\right)$ is a free S-module of rank l, we call the arrangement $\mathcal{A}$ a free arrangement. It is known that if $\mathcal{A}$ is free, there exists a homogeneous basis ${\eta }_1,\dots ,{\eta }_l$ for $D\left(\mathcal{A}\right)$ satisfying the following property: for each ${\eta }_i=f_{ij}\frac{\partial }{\partial x_j}$ where $f_{ij}$ is zero or a homogeneous polynomial of the degree $b_j$, the degree sequence $b_1,\dots ,b_l$ is called the exponent of $\mathcal{A}$ and is denoted by $exp\mathcal{A}=(b_1,\dots ,b_l)$.

According to Terao’s factorization theorem [17], if $\mathcal{A}$ is a central and free arrangement with $exp\mathcal{A}=(b_1,\dots ,b_l)$, then its characteristic polynomial $\chi (\mathcal{A},t)$ can be factorable as follows:

$$\chi (\mathcal{A},t)=(t-b_1)(t-b_2)\cdots (t-b_l).$$

This theorem can help us to distinguish whether some arrangements are free or not; in particular, the arrangement is not free if its characteristic polynomial is not factorable.

Example 1.

Let $K_n$ be a complete graph with n vertices; for any two vertices joined by an edge, the corresponding arrangement $\mathcal{A}\left(K_n\right)=\{x_i-x_j=0\mid 1\le i<j\le n\}$ is called the braid arrangement, and it is free. The intersection of the partially ordered set $L\left(\mathcal{A}\left(K_n\right)\right)$ is isomorphic to the partition lattice, and its characteristic polynomial can be calculated through its Möbius function; it is factorable as follows:

$$\chi (\mathcal{A}\left(K_n\right),t)=t(t-1)(t-2)\cdots (t-n+1).$$

People have found many other ways to study the freeness of a hyperplane arrangement. We will introduce the corresponding definitions and theorems in the following section.

An induction table between two free arrangements $\mathcal{A}$ and $\mathcal{B}$ is a sequence of free arrangements.

$$\mathcal{A}={\mathcal{A}}_0\prec {\mathcal{A}}_1\prec ···\prec {\mathcal{A}}_k=\mathcal{B}.$$

If an l-arrangement $\mathcal{A}$ has a maximal chain of modular elements, we then call $\mathcal{A}$ supersolvable; see [6].

An equivalent definition of the modular coatom is given in [18]. A subarrangement ${\mathcal{A}}^{\prime }$ is a modular coatom of an arrangement $\mathcal{A}$ if

(1)

For all hyperplane pairs $H_1,H_2\in \mathcal{A}-{\mathcal{A}}^{\prime }$, there always exists a hyperplane $H_3\in {\mathcal{A}}^{\prime }$ such that $H_1\cap H_2\subset H_3$.

(2)

Rank ${\mathcal{A}}^{\prime }$ = rank $\mathcal{A}-1$.

An arrangement is supersolvable if $\mathcal{A}$ has an M-chain

$$\varnothing ={\mathcal{A}}_0\subset {\mathcal{A}}_1\subset ···\subset {\mathcal{A}}_r=\mathcal{A}$$

of subarrangements in which each ${\mathcal{A}}_{i-1}$ is a modular coatom of ${\mathcal{A}}_i$ for $1\le i\le r$.

The following statements are known.

(1)

If $\mathcal{A}$ is supersolvable, then $\mathcal{A}$ is free [16].

(2)

If $\mathcal{A}$ is an arrangement associated with a chordal graph, then $\mathcal{A}$ is supersolvable [6].

We now give some properties of a signed graph [13].

For a given signed graph $G=(V_G,E_G^{+},E_G^{-},L_G)$, the sign function of G is the function $sgn:E_G^{+}\cup E_G^{-}\cup L_G\to \{+,-\}$, defined by

$$sgn\left(e\right)=\left\{\begin{array}{cc}+,\hfill & e\in E_G^{+};\hfill \\ -,\hfill & e\in E_G^{-}\cup L_G.\hfill \end{array}\right.$$

For a given signed graph G and a map $\sigma :V_G\to \{+,-\}$, we find a signed graph $G^{\prime }$ which has the same underlying graph and is equivalent to a permutation on the coordinates of G. If $e=\{i,j\}\in E_G$, then $sg{n}_{G^{\prime }}\left(e\right)=\sigma \left(i\right)sg{n}_G\left(e\right)\sigma \left(j\right)$. We call $G^{\prime }$ the switching of G by $\sigma$ and denote it as $G^{\sigma }$.

If there exists a switching function $\sigma$ such that $G_2=G_1^{\sigma }$, we say they are switching equivalent and write $G_1\sim G_2$.

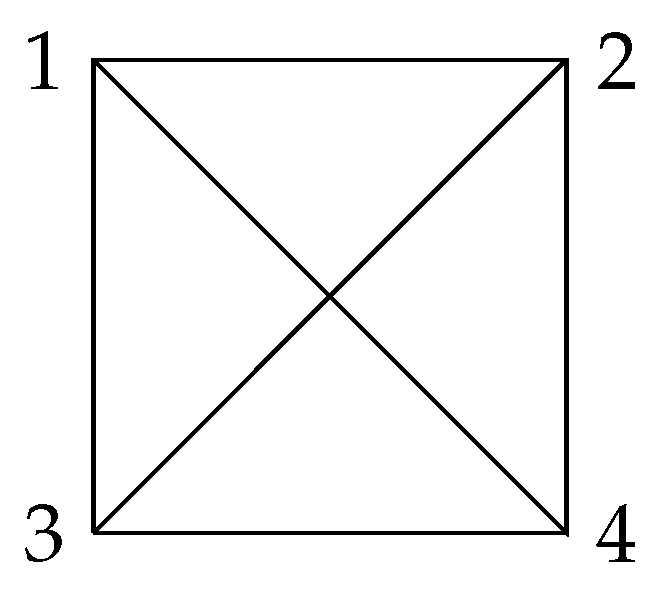
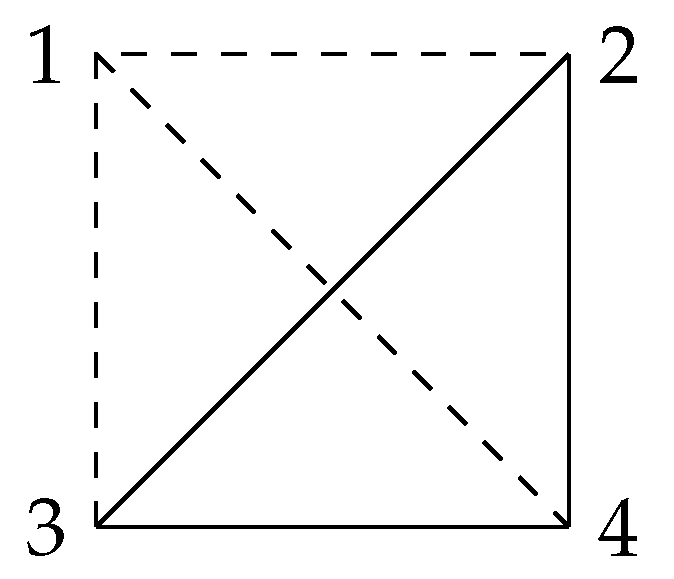
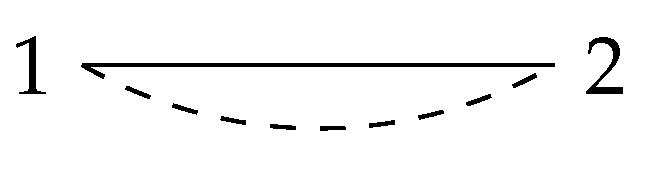
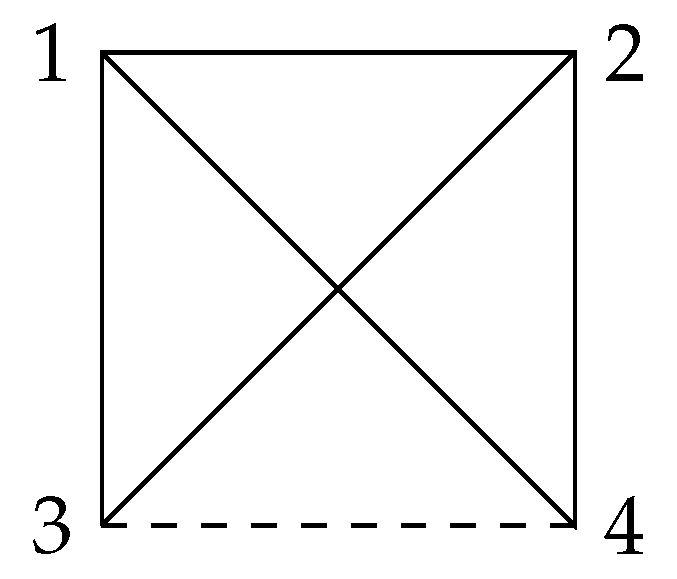
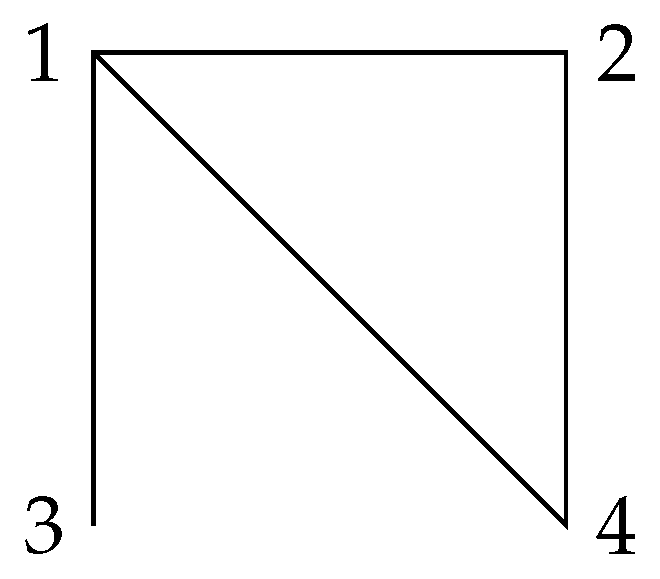
Since switching is an equivalent relationship, switching operations classify signed graphs into different classes. In this paper, our discussion is always based on switching equivalence because the degrees of freeness of two switching-equivalent arrangements are same. For example, the following two graphs, $K_4$ in Figure 1 and $K_4^{\sigma }$ in Figure 2, are switching equivalent, while the corresponding arrangements $\mathcal{A}\left(K_4\right)$ and $\mathcal{A}\left(K_4^{\sigma }\right)$ are both free with the same factorable characteristic polynomials.

$$\chi (\mathcal{A}\left(K_4\right),t)=\chi (\mathcal{A}\left(K_4^{\sigma }\right),t)=t(t-1)(t-2)(t-3).$$

The following theorems are used frequently in this paper. Abe and Yamaguchi gave a theorem on the free path [19].

Theorem 4.

Let $\mathcal{A}\supset \{H_1,H_2\}$, ${\mathcal{A}}_i:=\mathcal{A}\setminus \left\{H_i\right\}$$(i=1,2)$ and let $\mathcal{B}:=\mathcal{A}\setminus \{H_1,H_2\}$. If $\mathcal{A}$ and $\mathcal{B}$ are both free, then at least one of ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ is free.

Orlik and Terao gave the theorems as follows in [16].

Theorem 5 (addition).

Let $(\mathcal{A},{\mathcal{A}}^{\prime },{\mathcal{A}}^{″})$ be a triple of arrangements. If ${\mathcal{A}}^{\prime }$ and ${\mathcal{A}}^{″}$ are both free with $exp{\mathcal{A}}^{\prime }=(b_1,\dots ,b_{l-1},b_l-1)$ and $exp{\mathcal{A}}^{″}=(b_1,\dots ,b_{l-1})$, i.e., $exp{\mathcal{A}}^{″}\subset exp{\mathcal{A}}^{\prime }$, then $\mathcal{A}$ is free with $exp\mathcal{A}=(b_1,\dots ,b_{l-1},b_l)$.

Theorem 6 (deletion).

Let $(\mathcal{A},{\mathcal{A}}^{\prime },{\mathcal{A}}^{″})$ be a triple of arrangements. If $\mathcal{A}$ and ${\mathcal{A}}^{″}$ are both free with $exp\mathcal{A}=(b_1,\dots ,b_{l-1},b_l)$ and $exp{\mathcal{A}}^{″}=(b_1,\dots ,b_{l-1})$, i.e., $exp{\mathcal{A}}^{″}\subset exp\mathcal{A}$, then ${\mathcal{A}}^{\prime }$ is free with $exp{\mathcal{A}}^{\prime }=(b_1,\dots ,b_{l-1},b_l-1)$.

Theorem 7 (addition–deletion).

Let $(\mathcal{A},{\mathcal{A}}^{\prime },{\mathcal{A}}^{″})$ be a triple. Any two of the following statements imply the third.

(1)

$\mathcal{A}$ is free with $exp\mathcal{A}=\{b_1,\dots ,b_{l-1},b_l\}$.

(2)

${\mathcal{A}}^{\prime }$ is free with $exp{\mathcal{A}}^{\prime }=\{b_1,\dots ,b_{l-1},b_l-1\}$.

(3)

${\mathcal{A}}^{″}$ is free with $exp{\mathcal{A}}^{″}=\{b_1,\dots ,b_{l-1}\}$.

3. Some Lemmas

In this section, we will give some lemmas regarding the signed graphic arrangements (see [9,20]) which help us prove our main results.

Lemma 1.

For the signed graph $K_3^2$ shown in Figure 3, its corresponding signed graphic hyperplane arrangement $\mathcal{A}\left(K_3^2\right)$ is free.

Proof. 

The signed graphic hyperplane arrangement $\mathcal{A}\left(K_3^2\right)$ has a modular coatom ${\mathcal{A}}^{\prime }\left(K_3\right)$ which is associated with Figure 4, and ${\mathcal{A}}^{\prime }\left(K_3\right)$ is a braid arrangement and is supersolvable. Thus, the signed graphic hyperplane arrangement $\mathcal{A}\left(K_3^2\right)$ definitely is a supersolvable arrangement, and it is free. □

Remark 1.

To show Terao’s factorization theorem, we will calculate the characteristic polynomial of $\mathcal{A}\left(K_3^2\right)$ through its Hasse diagram of the lattice $L\left(\mathcal{A}\left(K_3^2\right)\right)$ in Figure 5 below.

The hyperplanes in $\mathcal{A}\left(K_3^2\right)$ are

$$\left\{\begin{array}{c}{H}_1:x_1-x_2=0\hfill \\ H_2:x_2-x_3=0\hfill \\ H_3:x_3-x_1=0\hfill \\ H_4:x_1+x_3=0\hfill \\ H_5:x_2+x_3=0.\hfill \end{array}\right.$$

From the Hasse diagram, we can obtain the Möbius function of every element in $L\left(\mathcal{A}\left(K_3^2\right)\right)$. For example, the element ${\mathbb{K}}^3$ with a rank of 0 is $1,$ while $\mu \left(H_i\right)=-1$ for $1\le i\le 5,$ $\mu (H_1,H_2,H_3)=2,$ $\mu (H_2,H_4)=1.$ Finally, we can obtain its characteristic polynomial,

$$\chi (\mathcal{A}\left(K_3^2\right),t)=(t-1){(t-2)}^2,$$

which is factorable.

Lemma 2.

For the signed graph $K_3^1$ shown in Figure 6, the corresponding signed graphic hyperplane arrangement $\mathcal{A}\left(K_3^1\right)$ is free and supersolvable.

Proof. 

According to Theorem 4 and Lemma 1, the arrangement $\mathcal{A}\left(K_3^1\right)$ is in the free path $\mathcal{A}\left(K_3\right)\subset \mathcal{A}\left(K_3^1\right)\subset \mathcal{A}\left(K_3^2\right)$; the freeness of $\mathcal{A}\left(K_3^1\right)$ is obvious. And we can find a modular coatom $\mathcal{A}\left(K_2^1\right)$ (Figure 7).

Therefore we have an M-chain of $K_3^1$:

$$\varnothing =\mathcal{A}\left(K_2^1\right)\subset \mathcal{A}\left(K_3^1\right).$$

So, $\mathcal{A}\left(K_3^1\right)$ is supersolvable. □

Lemma 3.

For the signed graph $K_4^{\prime }$ shown in Figure 8, the hyperplane arrangement $\mathcal{A}\left(K_4^{\prime }\right)$ is free.

Proof. 

The hyperplane arrangement $\mathcal{A}\left(K_4^{\prime }\right)$ is

$$\left\{\begin{array}{c}{H}_1:x_1-x_2=0\hfill \\ H_2:x_2-x_4=0\hfill \\ H_3:x_3+x_4=0\hfill \\ H_4:x_3-x_1=0\hfill \\ H_5:x_1-x_4=0\hfill \\ H_6:x_2-x_3=0\hfill \end{array}\right.$$

For hyperplane $H_3:x_3+x_4=0$ and ${\mathcal{A}}^{\prime }\left(G_1\right)=\mathcal{A}\left(K_4^{\prime }\right)-H_3$ (Figure 9), the restriction ${\mathcal{A}}^{″}\left(K_3^2\right)=\mathcal{A}{\left(K_4^{\prime }\right)}^{H_3}$ (which is isomorphic to $\mathcal{A}\left(K_3^2\right)$ in Figure 10) is

$$\left\{\begin{array}{c}{H}_1:x_1-x_2=0\hfill \\ H_2:x_2-x_3^{\prime }=0\hfill \\ H_3:x_1-x_3^{\prime }=0\hfill \\ H_4:x_2+x_3^{\prime }=0\hfill \\ H_5:x_1+x_3^{\prime }=0\hfill \end{array}\right.$$

Since ${\mathcal{A}}^{\prime }\left(G_1\right)$ is an arrangement associated with a chordal graph, the triple $(\mathcal{A},{\mathcal{A}}^{\prime },{\mathcal{A}}^{″})$ satisfies the conditions of the addition–deletion theorem, so $\mathcal{A}\left(K_4^{\prime }\right)$ is free according to the addition–deletion theorem. □

Lemma 4.

For the signed graph $K_4^{\prime }\setminus e$ shown in Figure 11, the corresponding signed graphic hyperplane arrangement $\mathcal{A}(K_4^{\prime }\setminus e)$ is free.

Proof. 

The hyperplane arrangement $\mathcal{A}(K_4^{\prime }\setminus e)$ is

$$\left\{\begin{array}{c}{H}_1:x_1-x_2=0\hfill \\ H_2:x_2-x_4=0\hfill \\ H_3:x_3+x_4=0\hfill \\ H_4:x_3-x_1=0\hfill \\ H_5:x_1-x_4=0\hfill \end{array}\right.$$

For hyperplane $H_3:x_3+x_4=0$ and ${\mathcal{A}}^{\prime }\left(G_2\right)=\mathcal{A}(K_4^{\prime }\setminus e)-H_3$ (Figure 12), the restriction ${\mathcal{A}}^{″}\left(K_3^1\right)=\mathcal{A}{(K_4^{\prime }\setminus e)}^{H_3}$ (which is isomorphic to $\mathcal{A}\left(K_3^1\right)$ in Figure 5) is

$$\left\{\begin{array}{c}{H}_1:x_1-x_2=0\hfill \\ H_2:x_2-x_3^{\prime }=0\hfill \\ H_3:x_1-x_3^{\prime }=0\hfill \\ H_4:x_1+x_3^{\prime }=0\hfill \end{array}\right.$$

Since ${\mathcal{A}}^{\prime }\left(G_2\right)$ is an arrangement associated with a chordal graph, the triple $(\mathcal{A},{\mathcal{A}}^{\prime },{\mathcal{A}}^{″})$ satisfies the conditions of the addition–deletion theorem, so $\mathcal{A}(K_4^{\prime }\setminus e)$ is free according to the addition–deletion theorem. □

4. Proof of Main Results

In this section, we prove our main results.

Proof of Theorem 1.

If the vertex $v\in V(G-T)$ satisfies conditions (1) and (2), the graph G is obviously switching equivalent to a chordal graph, so we only need to prove (3).

Firstly, we prove the situation in which there is only one vertex $v\in V(G-T)$ that satisfies condition (3). Assume the hyperplanes $H_1,H_2$ correspond to the edges $v{v}_i,v{v}_j$, respectively; then, $H_1\cap H_2$ are contained in the hyperplane $H_3:x_i-x_j=0$ of $\mathcal{A}$. Let ${\mathcal{A}}_{r-1}=\mathcal{A}\setminus \{H_1,H_2\}$; then, ${\mathcal{A}}_{r-1}$ is a modular coatom of $\mathcal{A}$, and we can obtain a modular coatom chain according to the same method.

$${\mathcal{A}}_0\subset {\mathcal{A}}_1\subset ···\subset {\mathcal{A}}_r=\mathcal{A}.$$

We denote by ${\mathcal{A}}_0$ the arrangement associated with $G_0$ in which $G_0$ has two cases.

CASE 1. If the number of edges incident to the vertex v is even, we can finally obtain an isolated vertex of $G_0$; then, $G_0$ is a chordal graph. Therefore, ${\mathcal{A}}_0$ is supersolvable, and $\mathcal{A}$ is also supersolvable and free.

CASE 2. If the number of edges incident to the vertex v is odd, then there only exists a vertex $u\in V\left(G_0\right)$ such that $\left\{vu\right\}\in E\left(G_0\right)$. In this case, $G_0$ is switching equivalent to a chordal graph, so ${\mathcal{A}}_0$ is supersolvable. Therefore, $\mathcal{A}$ is also supersolvable and free.

If there are more than one vertices in $G-T$ satisfying condition (3), we can prove the freeness of $\mathcal{A}$ by induction using the number of such vertices in $G-T$. □

Proof of Theorem 2.

According to Theorem 7, for the hyperplane H associated with the negative edge, the deletion ${\mathcal{A}}^{\prime }\left(Q\right)=\mathcal{A}\left(Q\right)-H$ is as same as $\mathcal{A}\left(G_1\right)$ or $\mathcal{A}\left(G_2\right)$. The restriction ${\mathcal{A}}^{″}\left(Q\right)={\mathcal{A}}^H$ is the same as $\mathcal{A}\left(K_3^2\right)$ or $\mathcal{A}\left(K_3^1\right)$.

The deletion arrangement ${\mathcal{A}}^{\prime }\left(G\right)=\mathcal{A}(G-e_H)$ is obviously associated with a chordal graph; thus, ${\mathcal{A}}^{\prime }\left(G\right)=\mathcal{A}\left(G\right)-H$ is free. Next, we prove the freeness of ${\mathcal{A}}^{″}\left(G\right)=\mathcal{A}{\left(G\right)}^H$. According to Lemmas 1 and 2, ${\mathcal{A}}^{″}\left(Q\right)$ is supersolvable, so we can obtain a modular coatom $\mathcal{A}\left(Q^{\ast }\right)$ of ${\mathcal{A}}^{″}\left(Q\right)$ by deleting two hyperplanes in ${\mathcal{A}}^{″}\left(Q\right)$ associated with two positive edges. For the the arrangement ${\mathcal{A}}^{″}\left(G\right)$, if we delete the same two hyperplanes, we can then obtain a modular coatom $\mathcal{A}\left(G^{\ast }\right)$ associated with the graph $G^{\ast }$, which is switching equivalent to a chordal graph; then, $\mathcal{A}\left(G^{\ast }\right)$ is supersolvable., and we can obtain an M-chain of ${\mathcal{A}}^{″}\left(G\right)$,

$$\varnothing \subset ···\subset \mathcal{A}\left(G^{\ast }\right)\subset {\mathcal{A}}^{″}\left(G\right).$$

So, ${\mathcal{A}}^{″}\left(G\right)$ is supersolvable and free, and $\mathcal{A}$ is free by Theorem 7. □

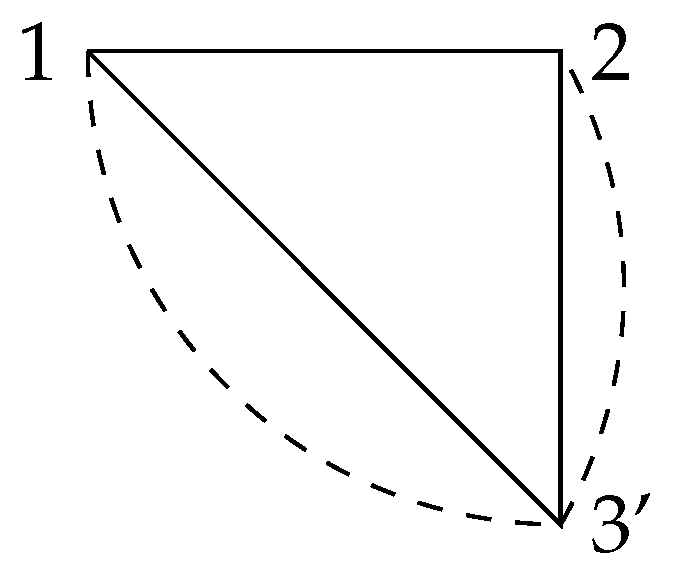
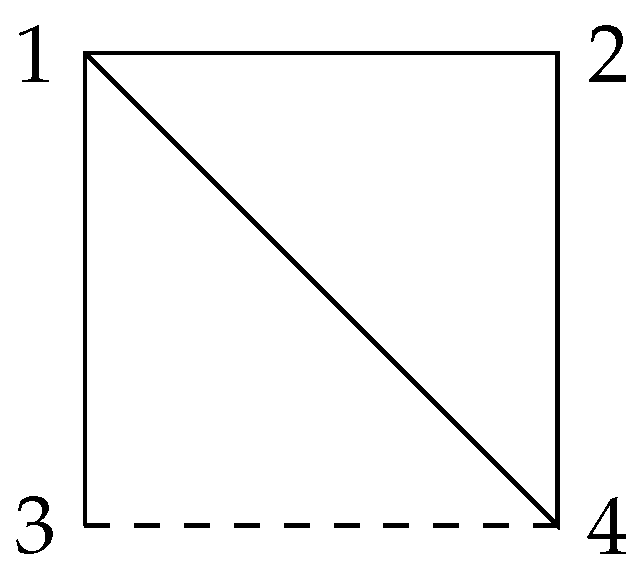
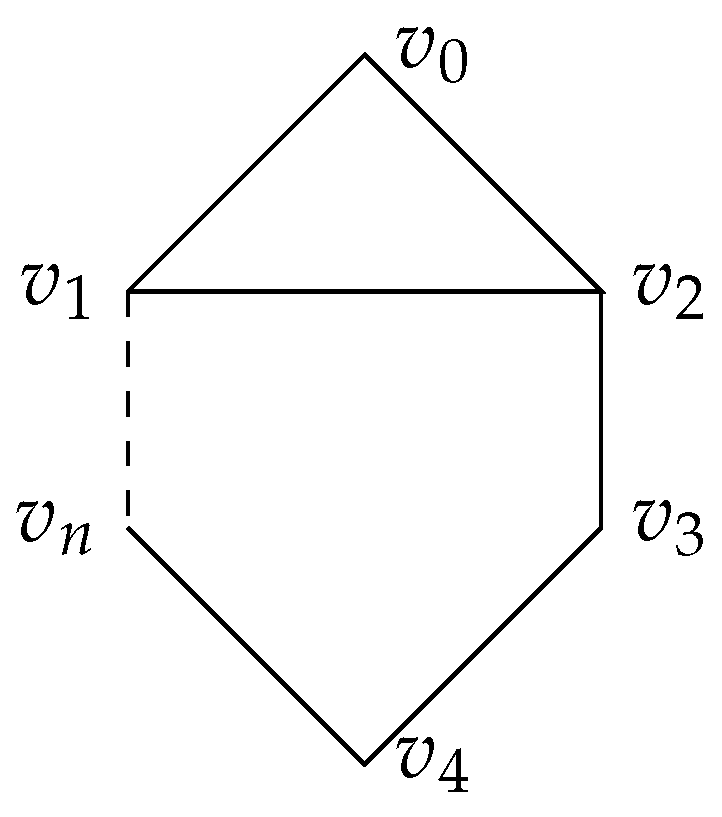
Next we will prove Theorem 3 through the signed graph ${\Sigma }_1$ (Figure 13) containing a cycle with 5 vertices.

Proof of Theorem 3.

Assume $V_G=\{v_0,v_1,\dots ,v_n\}$. Firstly, we consider $n=5$ and T to be a triangle and prove that the arrangement $\mathcal{A}\left({\Sigma }_1\right)$ associated with the graph ${\Sigma }_1$ in Figure 13 is free. For the hyperplane H that is associated with one negative edge, the deletion ${\mathcal{A}}^{\prime }=\mathcal{A}\left({\Sigma }_1\right)-H$ is always associated with a chordal graph, and $\mathcal{A}\left({\Sigma }_2\right)$ is a restriction of $\mathcal{A}\left({\Sigma }_1\right)$ in which ${\Sigma }_2$ in Figure 14 is a restriction of the graph ${\Sigma }_1$. According to Theorem 7, to prove that $\mathcal{A}\left({\Sigma }_2\right)$ is free, it suffices to prove that $\mathcal{A}\left({\Sigma }_1\right)$ is free. Similarly, for another hyperplane $H^{\prime }$ that is associated with the negative edge, the deletion $\mathcal{A}\left({\Sigma }_2\right)-H$ is always associated with a chordal graph, and $\mathcal{A}(K_4^{\prime }\setminus e)$ is a restriction of $\mathcal{A}\left({\Sigma }_2\right)$ in which $K_4^{\prime }\setminus e$ is a restriction of the graph ${\Sigma }_2$. According to Lemma 4, the signed graphic hyperplane arrangement $\mathcal{A}\left({\Sigma }_1\right)$ is free.

When $n\ge 6$ and T is a triangle, we can also conclude the freeness of $\mathcal{A}$ by the same deletions and restrictions. If T is not a triangle, then after the same process, the final arrangement we need to prove satisfies the condition of Theorem 2. □

The characteristic polynomial of a free arrangement is factorable. When $V_G=\{v_0,v_1,\dots ,v_n\}$ and T is a triangle, we calculate the characteristic polynomial of $\mathcal{A}$, which is also factorable

$$\chi \left(\mathcal{A}\right)=(2t+1){(t+1)}^n.$$

5. Discussion

Since K. Saito [3] studied logarithmic vector fields and differential forms of hyper-surfaces and defined their freeness in 1980, research on freeness has played an important role connecting the algebra, topology, combinatorics, and geometry of hyperplane arrangements. Although H. Terao, Abe, and others have obtained a large number of significant results, there are still many unknown facts. It is very fundamental and important to construct free arrangements.

In this article, we construct three kinds of signed graphic arrangements which can generalize the results on simple graphic arrangements. However, the necessary condition for the freeness of these signed graphic arrangements is still unknown. We conjecture that the necessary condition is related to the sufficient conditions in our theorems. In order to further study the algebraic and topological properties of the free signed graphic arrangements in this article, it is necessary but difficult to construct the basis of a derivation module $D\left(\mathcal{A}\right)$.