1. Introduction
Acquired immune deficiency syndrome (AIDS), caused by infection with the human immunodeficiency virus (HIV), has been one of the deadliest and most persistent epidemics in humankind since the reporting of the first AIDS cases in 1981 [
1]. It is well known that the common pathways for transmitting HIV include engaging in sexual intercourse with the infected individual, mother-to-child infection, sharing of injecting equipment, and exposure to contaminated blood in healthcare settings [
2]. The signs and symptoms of HIV differ based on the stage of the infection. During the early stages of HIV infection, individuals may exhibit no symptoms or flu-like symptoms such as fever, fatigue, sore throat, swollen lymph nodes, and skin rashes. As the infection progresses to the chronic phase, there may be no clinical symptoms for several years, but the virus continues actively assaulting and debilitating the immune system during this stage. This is why HIV is often referred to as a silent infection. In the final stage of infection, individuals with HIV develop AIDS, wherein the immune system is severely impaired, resulting in a range of symptoms and opportunistic infections. As of the end of 2022, there were an estimated 39.0 million [33.1–45.7 million] people living with HIV, including 1.5 million [1.2–2.1 million] children (0–14 years old). HIV remains a significant global public health concern, having claimed the lives of an estimated 40.4 million [32.9–51.3 million] individuals to date [
3]. This is a reminder of the need to take appropriate preventive measures for effective HIV control.
To gain a deeper understanding of AIDS/HIV mechanisms and develop more effective control strategies, numerous scholars have utilized mathematical models to investigate this disease. For example, McCluskey et al. [
4], concerned that each HIV-infected individual has the potential to progress through multiple stages of infection before reaching the advanced stage of AIDS, proposed an HIV/AIDS model with multiple stages of infection, in which the infected individual is divided into different infectious groups. In the study conducted by [
5], researchers focused on the varying transmission abilities of individuals in different stages of infection, and a nonautonomous stage-structured model was developed to simulate the spread of HIV/AIDS between hosts. In addition, mathematical modeling of HIV/AIDS based on within-host dynamics are increasingly being used to obtain a comprehensive view of the HIV-1 viral infection. As in the mid-1990s, an introductory model, including both healthy and infected cells as well as free virus particles, was developed by Perelson et al. [
6] to study the virus–cell interactions, which laid a foundation for HIV-1 infection modeling. The immune response is the body’s defensive response to alien or mutated autologous components, which play a vital role in eliminating or controlling the disease during viral infection [
7]. As a result, work on HIV-1 infection models that focus on the relationship between immune responses and invading pathogens has been developed and progressed considerably. For example, since the role of humoral immunity is crucial and cannot be replaced within the broader scope of human immunity [
8,
9], some scholars have incorporated humoral immunity into a basic HIV-1 virus model [
10,
11]. This is based on the B cells, which are produced by antigenic stimulation and are specifically programmed to kill viruses.
For many infectious diseases, such as tuberculosis, measles, AIDS, and so on, following sufficient exposure to the disease-causing agent, the susceptible individual becomes infected but is not yet capable of transmitting the infection to others, and the disease incubates within the body for a certain period of time until the exposed individual becomes infectious, and this time between infection and becoming infective is called the latent period. Capturing this feature, the introduction of the delay,
, or exposed class,
E, in modeling the dynamics of infectious diseases has received widespread consideration [
12,
13,
14]. In particular, Tipsri et al. [
15] focused on examining a
(susceptible, exposed, infected, recovered) model that incorporated a saturated incidence rate and discrete delay in three different cases. Their theoretical analysis revealed that introducing a time delay in the transmission term could potentially disrupt the stability of the system, and periodic solutions could be generated through a phenomenon known as Hopf bifurcation when utilizing the delay as a bifurcation parameter. In [
16], Jiang et al. proposed a
model with two delays (where one delay is the length of the immunity period and the other delay is the latent period of the disease) and the general nonlinear incidence rate, to discuss the the impact of delay on the disease transmission dynamics.
Additionally, delay has also been incorporated into within-host virus models to investigate HIV-1 infection more accurately [
17,
18,
19]. For instance, to characterize the time required for the infected cells to produce new virions after viral invasion and the time needed for the adaptive immune response to emerge to control viral replication, intracellular delay and immune delay were introduced by Pawelek et al. [
20]. And their results suggest that incorporating the intracellular delay into the model does not affect the stability results, but introducing the immune delay generates diverse and complex dynamics. Lin et al. [
21] extended the classical HIV model by adding cell-to-cell transmission and intracellular delay, and established the threshold dynamics that were determined by the immune-inactivated reproduction number,
, and immune-activated reproduction number,
. In fact, when HIV invades the body, it takes time for both the infection and the immune response to occur. Thus, Yang et al. [
22] incorporated two discrete delays into an HIV model, respectively, modeling intracellular delay and immune delay. Conclusions show that immune delay,
, will change the positive equilibrium from stable to unstable and cause population oscillations.
As we all know, when the virus enters the human body, it replicates and survives with the help of the host cell, destroys host cellular tissues, and than induces an innate immune response. The complex interactions between the virus and host cells directly affect the infection severity of the host. Then, the susceptible individual becomes infected after close contact with the infected individual and the disease transmission between hosts begins. That is to say, two of the important processes in transmission of viral infectious diseases are the immunological process concerning the virus–cell interactions at the individual level and the epidemiological process of disease transmission at the population level [
23]. Yet, traditional infectious diseases models are often focused on one of these two processes. In fact, numerous researchers have shown that the higher the viral load in the host is, the greater is ability of the disease to spread from host to host [
24,
25], implying that the within-host and between-host dynamics are not independent but interrelated. Initially, researchers introduced a nested modeling approach to simulate the evolutionary dynamics of host–parasite interactions [
26,
27,
28]. Since then, several attempts have been made to integrate the dynamics of pathogen progression within a host with those of transmission between hosts in the context of infectious diseases. For instance, Feng et al. [
29,
30,
31] proposed a coupled model that links the cell–parasite interaction and the between-host infection via the contaminated environment to analyze the transmission of Toxoplasma Gondii, and found that backward bifurcations can be generated by coupled models. Recently, in order to understand the connection between pathogens, hosts, and the environment better, Wang et al. [
32] developed a multiscale model to analyze the dynamics of COVID-19, and assumed that the person-to-person transmission rates depend on the viral load within the human body, and the within-host viral load depends on the environmental pathogen concentration, which enables two-way coupling of micro within-host and macro between-host dynamics. It should be noted that, for some environment-driven infectious diseases, scholars have effectively integrated both micro and macro models bidirectionally [
29,
30,
31,
32]. However, for HIV, it remains unclear how to reflect the impact of host-to-host transmission on viral loads within the hosts, or how to build a bridge that can be coupled from epidemiological models to viral dynamics models. Under this incentive, Xue et al. [
33] proposed a bidirectional coupling HIV-1 model with standard incidence, in which the entry of viruses from infected individuals into the within-host system is based on the fact that the virus can be transmitted through direct contact with HIV-positive individuals and AIDS patients.
The purpose of this paper, motivated by the above works, is to discuss the impact of immune response and delay on the multiscale HIV-1 model coupling within-host and between-host dynamics. The subsequent sections of this paper are organized as following. In
Section 2, the virus infection model with humoral immunity, intracellular delay, and immune delay in the host, and the disease transmission model with latency delay between hosts, are proposed at fast and slow time scales, respectively. In
Section 3, some properties and important results of the virus infection model are given. In
Section 4, the positivity and boundedness of solutions for the coupled slow time model without an immune response are discussed, and criteria on the existence and local stability of equilibria are established. In
Section 5, we further study the coupled slow time model with an immune response. The basic reproduction number is calculated, the existence and stability of equilibria are studied, and the uniform persistence of the model is obtained. In
Section 6, the stability of the periodic solution for the coupled slow time model with an immune response is analyzed. The basic reproduction number is defined and the global dynamics are illustrated in terms of this value. In
Section 7, numerical simulations are conducted to explain the main findings further, and a brief summary is provided in the last section.
2. Model Formulation
Following the transmission process of HIV-1 at the host level, the total number of hosts at time
t is divided into four classes: susceptible,
, exposed,
, HIV-positive,
(individuals without clinical symptoms), and AIDS patients,
(individuals that have developed clinical symptoms). Inspired by the studies [
32,
33], it is assumed that the transmission rates and disease-induced mortality of infectious individuals depend on the viral load,
V, within the host, thereby embedding micro virus dynamics into macro epidemic dynamics. Supposing that infectivity is saturated with an increasing number of infectious individuals,
represents the inhibitory effect exerted by the infected individuals, which determines the level of infectivity saturation. In addition, based on the transmission characteristics of HIV, assume that susceptible individuals first undergo a latent period after infection, which is described by a delay
, before becoming infected. From these, a between-host disease transmission slow time model reads
All the parameters in Model (
1) are nonnegative constants, and their biological interpretations are provided in
Table 1.
Remark 1. The transmission rate is assumed to satisfy , , , . One of the simplest function forms for is ; other forms for include and , where and are positive constants.
Next, taking into account the infection process of HIV-1 at the individual host level, let
,
,
, and
denote the densities of susceptible cells (healthy cells or uninfected cells), infected cells, viral load, and
B cells at time
s in the host, respectively. For HIV, in order to construct a bridge coupling the macro level to the micro scale, investigate the effect of disease transmission on the dynamics within the hosts, motivated by the works of [
33], where we suppose that the viral load in the host can increase by directly contact with infected individuals, which is characterized by saturation incidence. Humoral immunity plays an essential role in the whole human immunity [
34]. In fact, after the virus enters the human body, it does not immediately stimulate the production of
B cells; therefore, based on [
21], the immune response with time delay
is considered. According to the assumptions above, a within-host HIV-1 infection fast time model takes the form
Similarly, all the parameters of Model (
2) are nonnegative constants, and their biological interpretations are given in
Table 2.
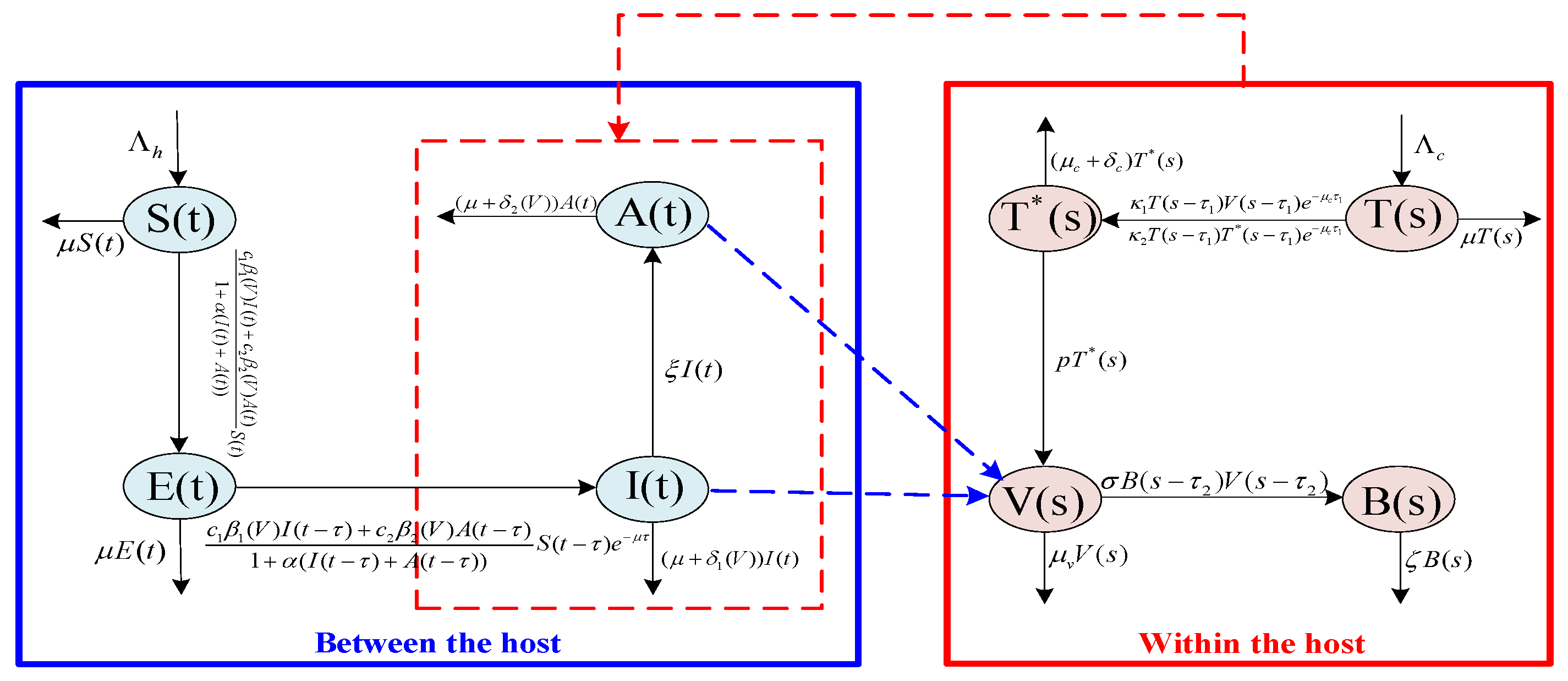
Remark 2. The flowchart of Model (1) and Model (2) are shown by the Figure 1. In addition, the multiscale model is characterized by two distinct time scales, denoted by t and s, respectively. The former represents the transmission time at the population level, while the latter represents the evolution time at the individual host level. Typically, the virus–cell dynamics within the host occur on a faster time scale than those between hosts. Therefore, s is a faster time scale than t (see [29,30,31]). Without loss of generality, we suppose that , where ϵ is a small positive constant. Since the second equation of Model (
1) is decoupled from the other equations, in the analysis below, it suffices to study the following between-host model
7. Numerical Simulation and Discussion
In this section, some numerical simulations are performed to explain our theoretical results and examine the effect of delay and immune response on the transmission of HIV-1 using the Runge-Kutta method in software MATLAB. More specifically, numerical simulations will be fulfilled for three examples: the first one considers the transmission dynamics of the coupled between-host model without an immune response, the second case considers the coupled slow time model with an immune response, in which the immune delay is in its stable interval, and the third example is dedicated to discuss the impact of the stable periodic solution formed in the host as a result of the immune delay on the disease transmission between hosts.
For the convenience of numerical simulations, we also take
,
, as mentioned in
Section 4.3 for the first example, and take
,
for the last two examples. And the parameter values for the within-host model were obtained from [
11,
21,
47]. For the between-host model, the parameter values were derived from [
33].
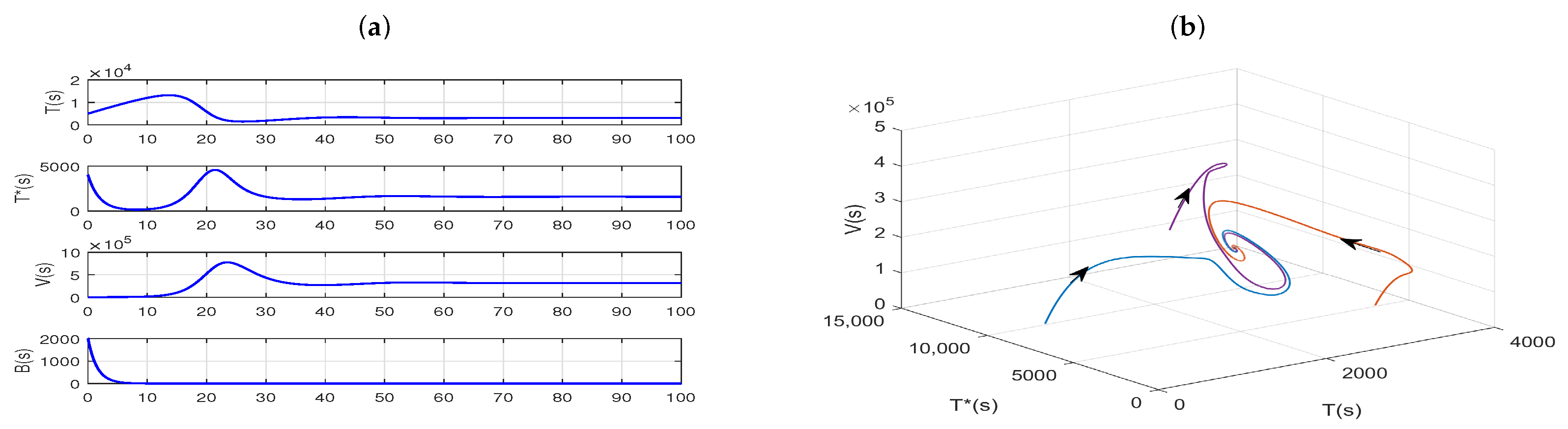
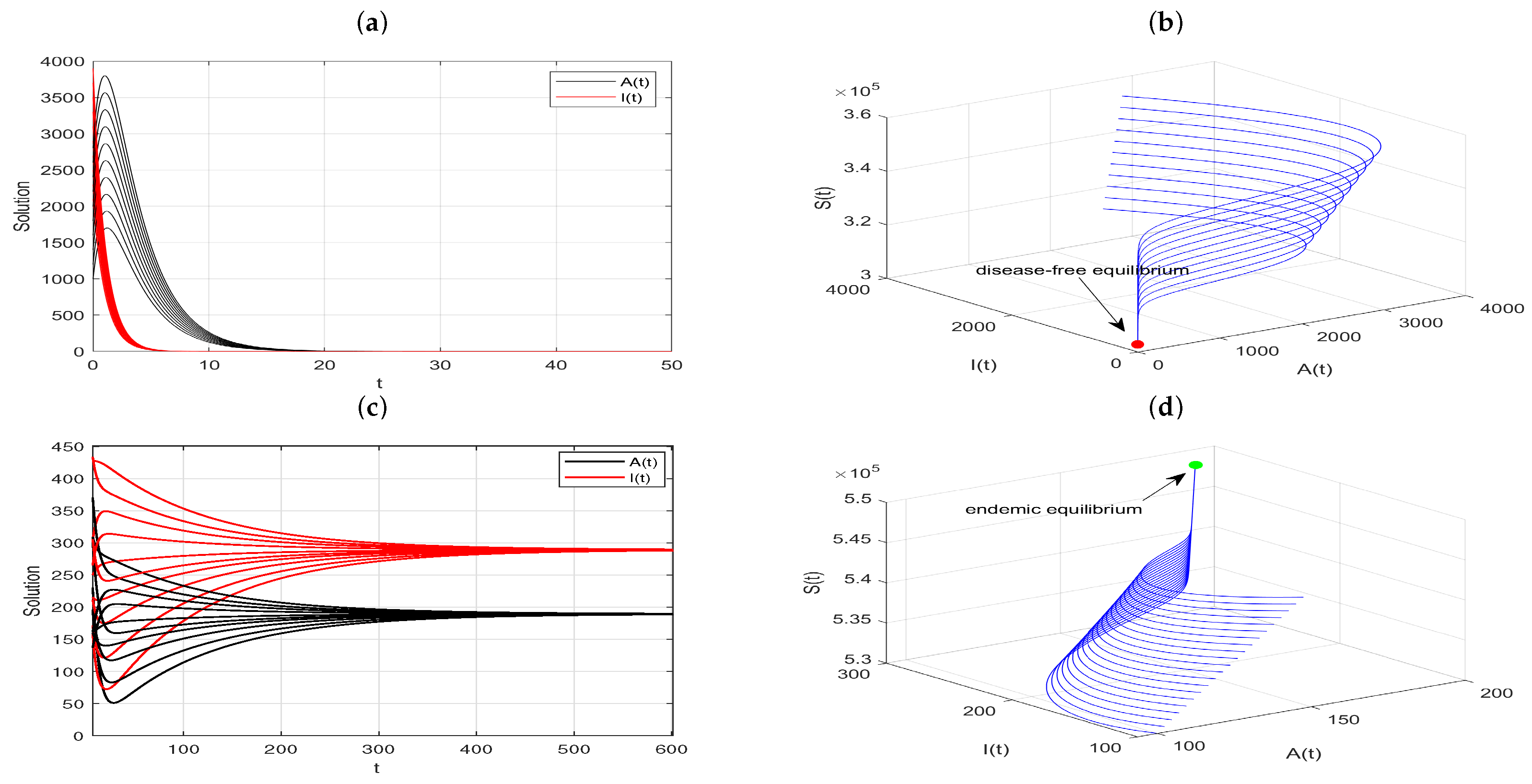
Example 1. The dynamics of the coupled slow time model, where the fast time model is without an immune response.
In Model (
4), we choose parameters as follows:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
. By the direct calculation, one has
. As shown in
Figure 2a,b,
is globally asymptotically stable, which coincides with the conclusion
of Theorem 3.
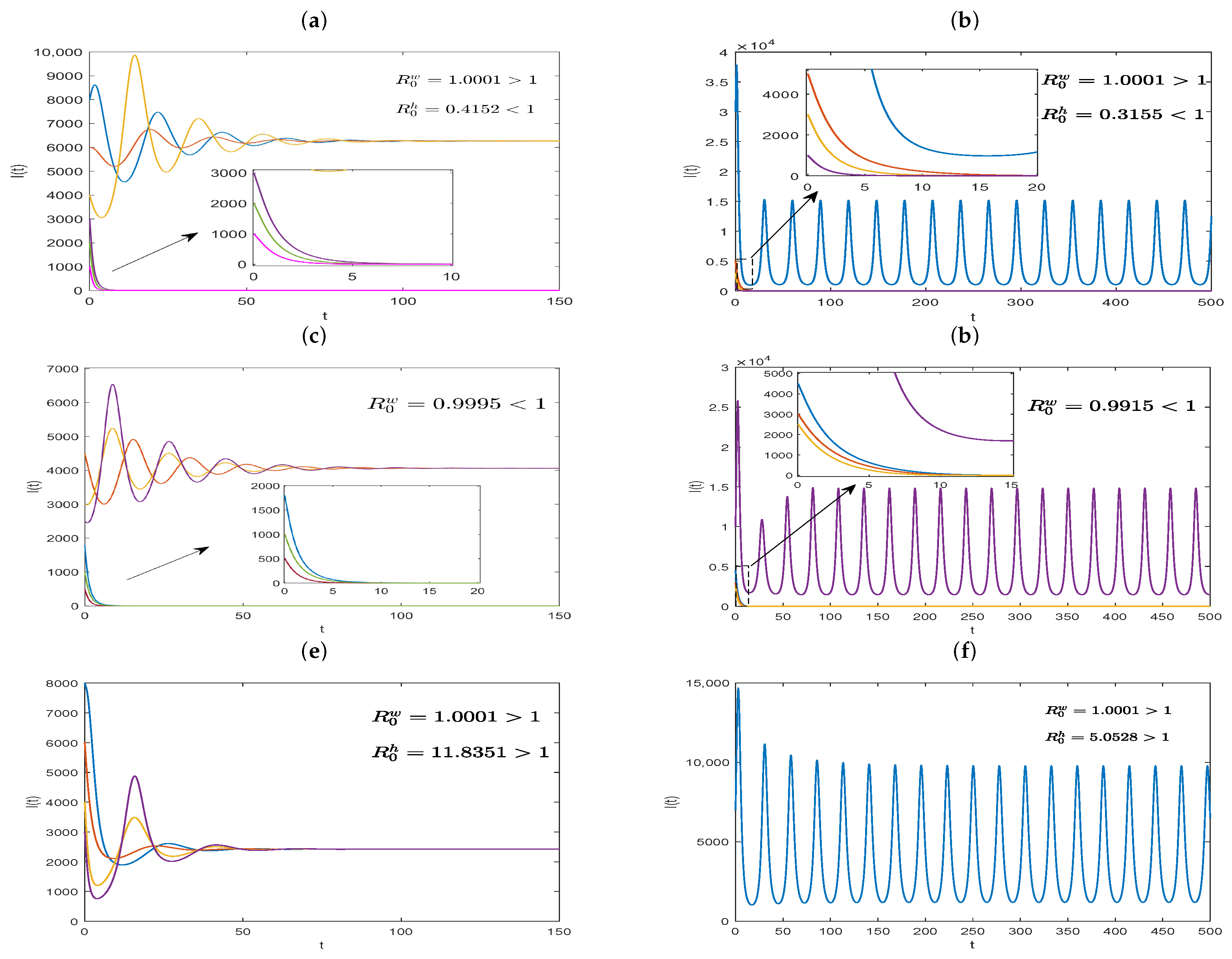
Further, taking the parameters
,
,
,
,
,
,
, and
, we can calculate
and
. Therefore, Model (
20) has two positive equilibriums,
and
, as stated in Theorem 9, where one is unstable, and the other is locally asymptotically stable. As depicted in
Figure 3a, the solutions converge to either the disease-free equilibrium or the positive equilibrium, depending on initial conditions. However, when
and other parameters are fixed, as in
Figure 3a, we obtain
and
. In this case, we find that the solutions with a lower initial value converge to the disease-free equilibrium, whereas the others with a higher initial value may oscillate periodically, which can be observed in
Figure 3b. Next, we just change the values of parameters as
,
, and other model parameters are chosen, as in
Figure 3a, and we obtain
, and the dynamical behavior is shown in
Figure 3c. What is more, if we tack
, then
, which corresponds to
Figure 3d. Clearly, the stability of equilibria given in
Figure 3c,d are similar to those in
Figure 3a and b, respectively. These show that the system may exhibit more diverse dynamics, except for the backward bifurcation, and the basic reproduction number,
, no longer serves as a threshold condition determining disease persistence or extinction. Lastly, let
,
, with other parameter values unchanged in Model (
20). By numerical calculations, we obtain
and
. Therefore, from Theorem 9, Model (
20) has a unique positive equilibrium,
. And
Figure 3e illustrate that
is globally asymptotically stable. However, if we take
and fix other model parameter values as above, then the basic reproduction numbers
and
can be obtained. In this situation, as shown in
Figure 3f, Model (
20) has a positive periodic solution.
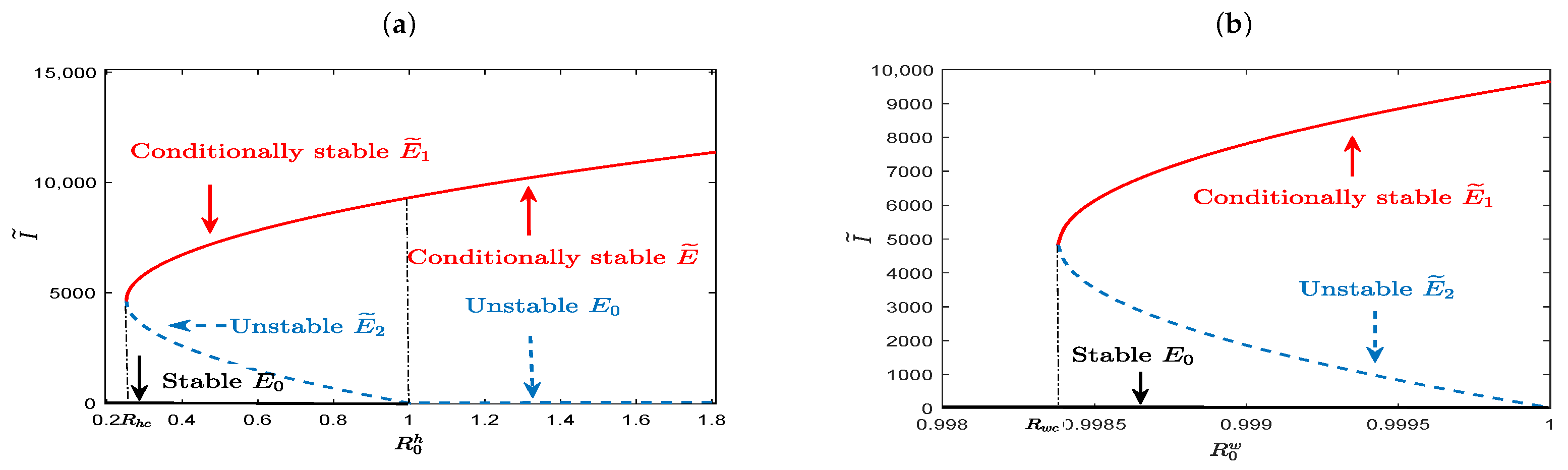
It is noticed that the existence of equilibria concluded in Theorem 9 and their stability revealed in
Figure 3a–f may indicate the existence of saddle-node bifurcation, backward bifurcation, and Hopf bifurcation for our coupled slow time model (
20). That is, Model (
20) has bistable attractors for
(or
), and a unique stable positive equilibrium for
and
. These are shown in
Figure 4a,b, in which the number of infected individuals at positive equilibrium is expressed as a function of
and
, with the black solid curve, red solid curve, and blue dashed curve representing the locally asymptotically stable, conditionally stable, and unstable equilibrium, respectively. Especially,
Figure 4a shows that the model has two positive equilibria,
and
, in which one is conditionally stable and the other is unstable for
, and has no positive equilibrium for
. This implies that the threshold value for disease eradication is not
, but
. That is to say, the infectious disease may become extinct until
. And starting from
, with the increase of
, Model (
20) undergoes saddle-node bifurcation at
, forward Hopf bifurcation that changes the stability of the positive equilibrium,
, from unstable to stable, and backward bifurcation at
in turn. When
, Model (
20) has a unique conditionally stable positive equilibrium,
, which exhibits different dynamical behavior under different values of
. That is, it is globally asymptotically stable for larger
, but loses stability for smaller
, and the solution of the model oscillates periodically around it. These complex phenomena highlight the challenges in the control of disease. Similar to the situation revealed in
Figure 4a,
Figure 4b shows that complex dynamic behaviors can exist for
, and the lower bound of the threshold condition for disease control is
. This suggests that between-host disease may still persist, resulting from contact with infected individuals, even though the virus can be cleared within the host. The parameter values used in
Figure 4a are
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
, and
. In
Figure 4b, parameters have the same values as in
Figure 4a except that
.
Example 2. The dynamics of the coupled slow time model, where the fast time model has an immune response.
Now, we choose the values of parameters in Model (
4) as follows:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
, then the immune-activated reproduction number
and
can be calculated. Therefore, the fast time model (
4) has a globally asymptotically stable immunity-activated infection equilibrium,
, from Theorem 3, and
. These are shown in
Figure 5a,b.
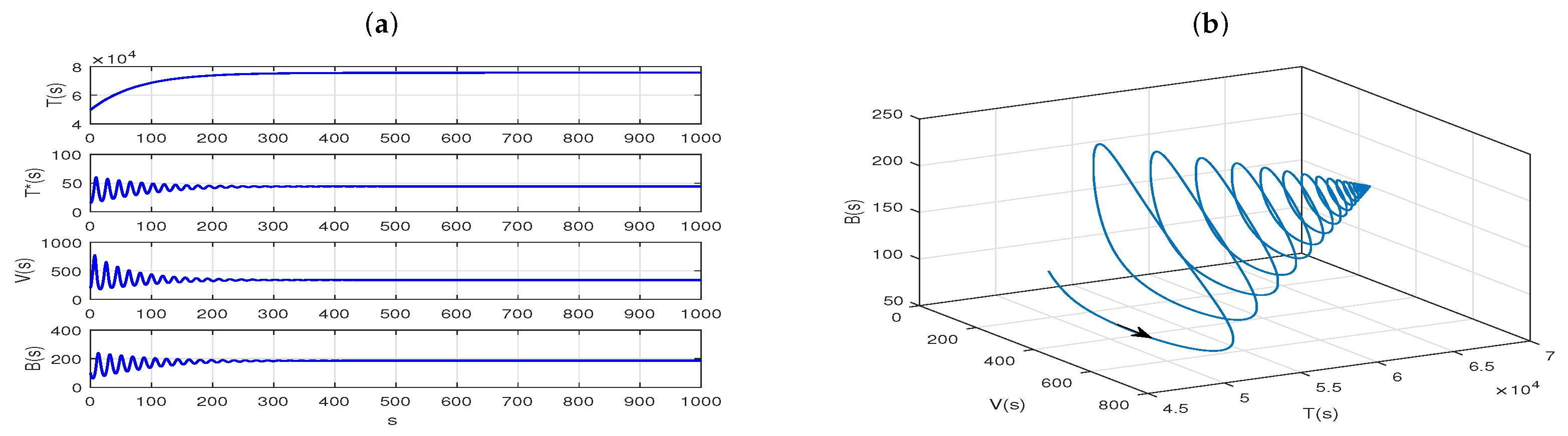
Further, we let
,
,
,
,
,
,
,
,
, and replace the
in the coupled slow time model (
28), then
. And Theorem 12 suggests that the Model (
28) has a unique equilibrium,
, which is globally asymptotically stable. Our numerical simulations confirm this result, as shown in
Figure 6a,b. Next, if we take
,
,
,
,
,
,
,
, and
, then
. As depicted in
Figure 6c,d, the solutions originating from various initial values converge to the unique endemic equilibrium,
. Thus, the global asymptotic stability of
stated in Remark 8 would be reasonable. Clearly, if immune cells are stimulated to produce, that is, humoral immunity is involved in host defense mechanisms, and the immune delay,
, is in its stable interval, then whether the infectious disease between hosts is extinct simply depends on whether
is less than 1.
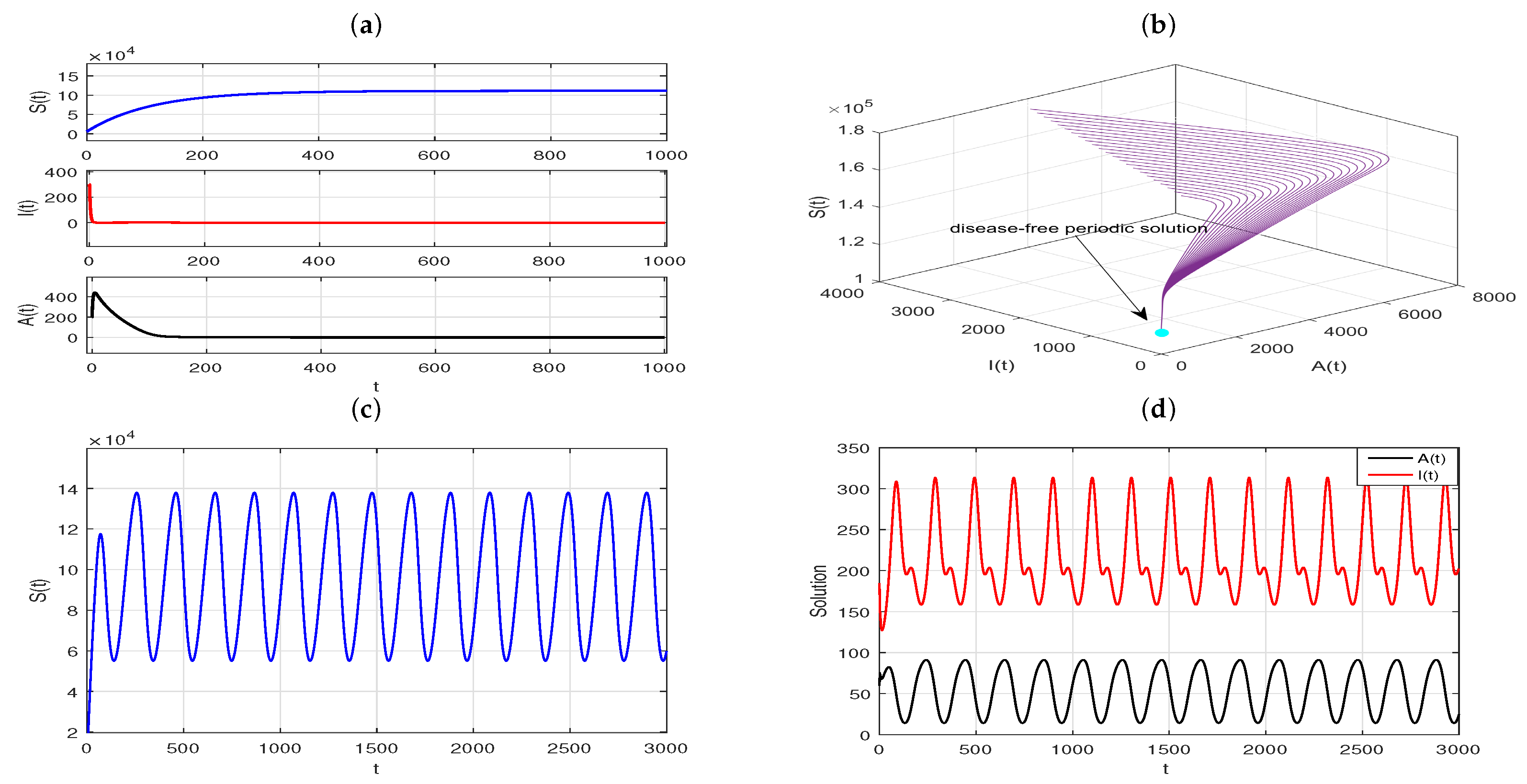
Example 3. The transmission dynamics of the coupled slow time model, where the fast time model has an immune response and stable periodic solution.
Taking the same parameter values as
Figure 5 in the fast time model (
4), except for
(that is, the delay
is not in its stability interval, for more details see Theorem 5), as shown in
Figure 7a, the infection equilibrium,
, of Model (
4) is unstable. And the plots in
Figure 7b–d show that the solutions starting from a different initial value gradually move away from
and eventually converge to a stable limit cycle.
In
Section 6, we discuss in detail the dynamics of the coupled slow time model in the presence of a stable periodic solution for the fast time model (
4). Since the exact expression for the periodic solution
of the model is not available, we obtain an approximate expression for
by function fitting. This is shown in
Figure 8a, where
exhibits a periodic oscillatory behavior when
s is sufficiently large, which is exactly the starting point for our search for this periodic solution. Fortunately, one can observe in
Figure 8b that the red curve described by function
where
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
, is established through the software MATLAB, which fits almost exactly with
.
In the following simulations, we take
,
,
,
,
,
,
,
,
and
in Model (
34). And the estimations for the periodic parameters are given by
,
,
, and
. Using the above parameter values and the direct method presented in [
48], we can calculate
. In this case, the HIV-positive individuals,
, and the AIDS individuals,
, tend to 0, which can be noticed in
Figure 9a,b. The plots mean that the disease eventually goes extinct, which is exactly what Theorem 16 describes. However, if we take
,
,
,
,
, with other parameters values unchanged, then
. As ensured by Theorem 17, a positive
-periodic solution,
, exists for Model (
34) under this scenario. And the plots in
Figure 9c,d illustrate that the disease will persist and exhibit periodic fluctuation eventually.
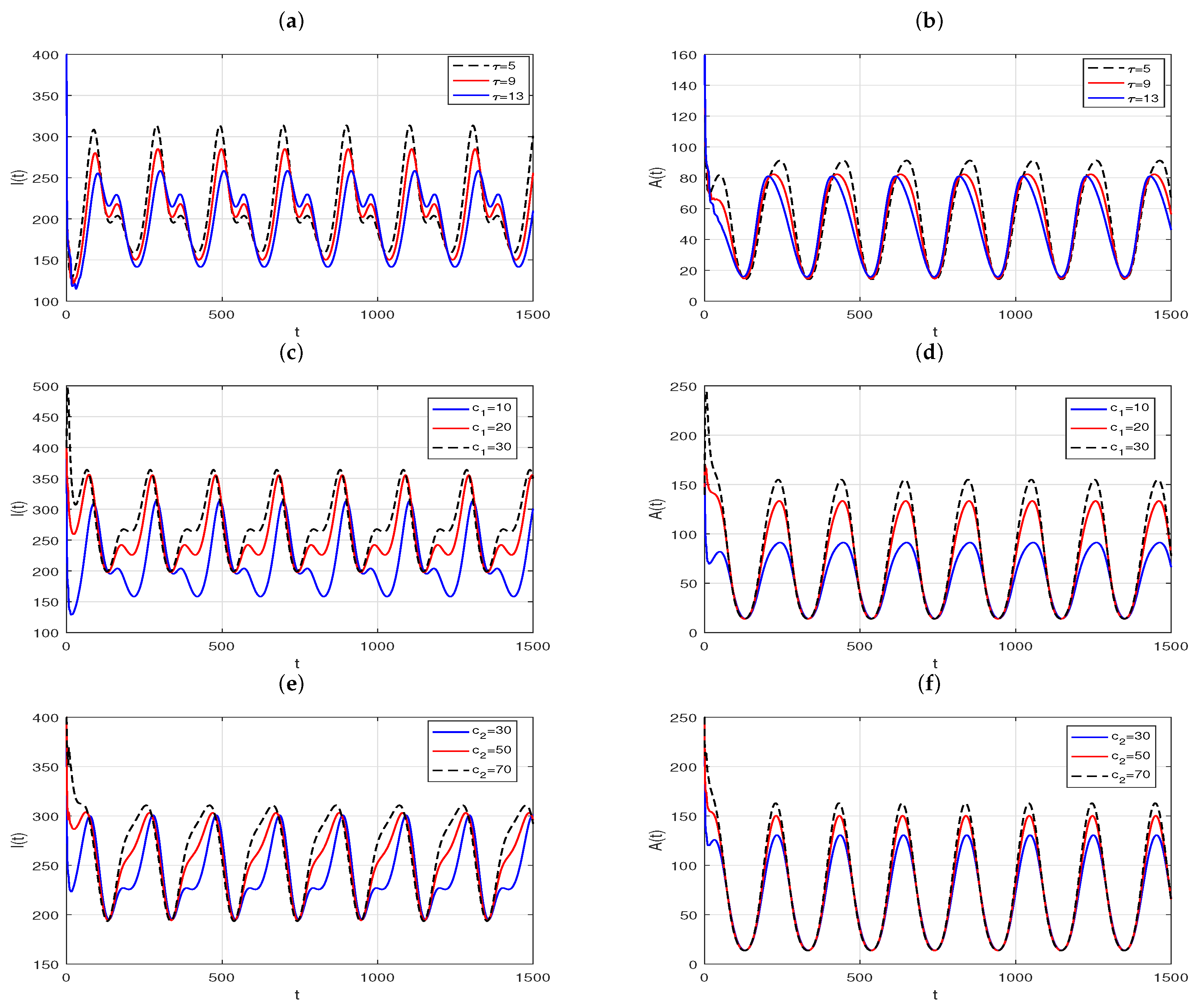
What is more, with the effect of delay
, the contact rates,
and
, on the positive periodic solutions in the case of
are demonstrated in
Figure 10. The plots in
Figure 10a,b suggest that the amplitude and period of the periodic solution of the slow time model (
33) vary with delay. More specifically, in an infection cycle, for the number of HIV-positive,
, as the latency delay increases, the time of the first peak is delayed and the intensity of the outbreak decreases, while the time of the second peak is earlier and the peak increases. However, for the number of AIDS patients,
, with the increase of delay, the time when
reach the peak is advanced, and the peak is reduced. The contact rates,
and
, rates have a more significant effect on the distribution of infectious individuals than latency delay. As the contact rates decrease, although the moment of peak arrival and the peak value of
do not change significantly, the duration of the high run of infected cases decreases dramatically, and the peak value of
decreases dramatically.
8. Conclusions
In this paper, a multiscale dynamical model based on the nested modeling approach to describe the transmission of HIV-1 is proposed. The model is described by a within-host virus infection fast time model with intracellular delay and immune delay, and a between-host disease transmission slow time model with latency delay. The two models are coupled bidirectionally by enhancing the generation rate of the virus in the host, which is based on the fact that the viral load will increase by direct contact with infected individuals, and introducing between-host parameters that explicitly depend on the within-host viral load. In addition, given the intricacy of the HIV-1 transmission process, in this model, we divided infected individuals into HIV-positive individuals and confirmed AIDS patients, and introduced saturation incidence, which makes theoretical analysis more challenging but realistic. This is one of the highlights of this article. In addition, the results suggest that the immune response in the host has a great influence on HIV-1 transmission between hosts. After the virus invades the human body, if humoral immunity does not work or has a weak effect in the host, the theoretical analysis and corresponding numerical simulation results in
Section 4 show that backward bifurcation and Hopf bifurcation could occur. That is to say, even if the basic reproduction number is less than 1, the disease may persist or erupt periodically between hosts, which undoubtedly poses many challenges in controlling the spread of this epidemic and makes it difficult to treat the disease effectively. When hosts have an extensive immune response and the time required between viral appearance and the production of new immune particles is short, the results obtained in
Section 5 indicate that the spread of disease between hosts will be easy to control. In the presence of an immune response, the basic reproduction number,
, can be less than 1. If it is possible to reduce the contact rate with infected individuals, increase the production rate of B cells, and prolong the latent period of infected individuals, the epidemic can be effectively controlled. However, if the time required for new immune particles to emerge in response to antigenic stimulation exceeds a certain range, which is entirely possible for the mechanism of HIV infection, then the disease persists between hosts in periodic outbreaks when
is greater than 1, as can be concluded from
Section 6. This is another highlight of this paper and something that has not yet been discussed in existing multiscale infectious disease models. In the event of a disease outbreak, it can be more difficult to control the spread of the disease once it has sustained periodic outbreaks, compared with a situation where the disease becomes endemic over time. Therefore, taking effective therapeutic measures to maximize the inhibition of viral replication, shorten the time that antigenic stimulation needs for generating B cells, and improve immune function is the treatment goal of AIDS. Globally, more than seventy percent of people living with HIV have undetectable or suppressed viral loads as a result of antiretroviral treatment, meaning they have a zero or negligible risk of transmitting HIV to their sexual partners [
49].
In order to analyze the effects of immune response and delay on HIV-1 transmission, factors such as population heterogeneity, social networks, and population mobility influencing the HIV-1 transmission are ignored in our paper. For example, population heterogeneity is an important influencing factor in epidemics, since people of different ages have different behavioral capabilities; therefore, a multiscale model bidirectional coupling within- and between-host dynamics with age structure is worth investigating. Moreover, in reality, all individuals are not homogeneously mixed and the probability of an infected individual coming into contact with others is quite different. Thus, multiscale models for characterizing the communicable disease transmission on complex networks are also to be considered in future work.