Exponential Stability of Dynamical Systems on Time Scales with Application to Multi-Agent Systems

Abstract

The exponential stability criteria of systems with time delays on time scales are established, which unifies and generalizes the continuous and discrete cases. The time derivatives of Lyapunov functions (functionals) along solutions are allowed to be indefinite, namely, to take both negative and positive value, which reduces conservatism of the criteria. Moreover, the stability criteria are applicable to both linear and nonlinear systems on time scales, which expands the scope of application of the criteria. Furthermore, the improved stability theorem is applied to solve a leader-following consensus problem of multi-agents on time scales. Sufficient conditions are derived for the leader-following consensus of multi-agent systems under directed interaction topology. A numerical example is given to illustrate the feasibility and effectiveness of the theoretical results.

1. Introduction

Stability is an important indicator for the control of dynamical systems, and stability analysis provides a macro theoretical basis for the regulation of systems. Due to the fact that dynamical systems involving information transmission, energy exchange, or control protocol execution are often affected by time delay, the stability analysis of time-delay systems is very important. For the two commonly used techniques for systems with time delay, both the Lyapunov–Krasovskii functional method [1,2] and Razumikhin functional method [3] require constructing a positive definite functional with a negative time derivative. The stability criteria are relatively conservative and difficult to meet in some cases. The conservatism of the criteria needs to be further reduced and the methods need to be further improved.

As an important information transmission system, multi-agent systems (MASs) have become a hot research topic, which is widely used in sensor network [4], robot coordinated control [5], intelligent transportation system [6], UAV formation flight [7], spacecraft docking [8], and many other fields. Continuous [9,10,11] or discrete [12,13,14] MASs have been widely studied. Liu et al. [9] investigated the consensus problem for continuous-time and discrete-time MASs under directed topologies. Cao et al. [10] studied the event-triggered consensus of continuous-time stochastic MASs under undirected topologies. Yu et al. [11] established event-triggered control protocol to achieve finite-time consensus for second-order continuous-time MAS under directed topology. Liu et al. [12] discussed the switching controllability of discrete-time MASs under undirected topologies. Yu et al. [13] studied the consensus problem for fourth-order discrete-time MAS under directed topologies. Zhao et al. [14] investigated the controllability of discrete-time MASs with directed and weighted signed networks.

However, it is troublesome to study the consensus of continuous and discrete MASs, respectively. Furthermore, in some practical situations, on the one hand, due to sensor failure, data packet dropouts or communication obstacles, the information transmission between agents may occur intermittently. On the other hand, continuous information transmission requires the continuous monitoring of the current state, which leads to high energy consumption. Information exchange in discrete situations may encounter problems such as transmission delay and data packet loss. In some cases, for example, in a hybrid multi-agent system, information transmission is unable or unsuitable to be described by simple continuous or discrete systems, which requires new models to be established to unify and generalize the continuous and discrete systems. The theory on time scales proposed by Hilger [15] provides a way to solve the problems. At present, the study of consensus of MASs on time scales are mainly focused on systems without time delay. For example, the consensus of linear MASs without time delay on time scales are studied in [16,17]. Babenko et al. [18] studied the exponential consensus of nonlinear MAS without time delay on time scales by Lyapunov functions. Lu et al. [19] investigated the consensus of nonlinear MAS without time delay on time scales with an improved stability theorem. However, the consensus of MASs with time delay on a time scale needs to be further investigated. The basic properties and the form and applicable conditions of calculus theory in continuous or discrete cases have significant changes on time scale, which poses difficulties in handling time-delay terms in MASs on time scale.

In this paper, the improved exponential theory of stability analysis of systems with time delay on a time scale is established, which can unify and generalize continuous and discrete cases. It is applicable to both linear and nonlinear systems on time scale, which expands the application scope of the criteria. The time derivatives of Lyapunov functions (functionals) along solutions are allowed to be indefinite, which reduce the difficulty of constructing Lyapunov functions (functionals). The stability criteria are further applied to the consensus problem of MASs on the time scale. The rest of this paper is organized as follows: the basic concepts and properties of the time scale are given in Section 2. The exponential stability criteria of dynamical systems with time delay on time scale are studied in Section 3. The application in MASs and numerical example are given in Section 4. Finally, some conclusions are made in Section 5.

2. Preliminaries

Definition 1

([20] (Time scale)). A time scale is an arbitrary non-empty closed subset of real numbers.

Definition 2

([20,21] (Jump operator)). Let $\mathbb{T}$ be a time scale. Set $\sigma \left(t\right)=t$ if $\mathbb{T}$ has a maximum t.

1. 

The forward jump operator is defined by

$$\sigma \left(t\right):=inf\{s\in \mathbb{T}:s>t\}.$$

2. 

The graininess of the time scale $\mathbb{T}$ is determined by

$$\mu \left(t\right):=\sigma \left(t\right)-t.$$

Definition 3

([20] (Regressive and exponential functions on time scales)).

1. 

A function $f:\mathbb{T}\to \mathbb{R}$ is called rd-continuous if it is continuous at right-dense points in $\mathbb{T}$ and its left-side limits exist (finite) at left-dense points in $\mathbb{T}$.

2. 

A function $\alpha :\mathbb{T}\to \mathbb{R}$ is called regressive if $1+\mu \left(t\right)\alpha \left(t\right)\ne 0$ holds for all $t\in {\mathbb{T}}^{\kappa }$, where ${\mathbb{T}}^{\kappa }=\mathbb{T}-\left\{m\right\}$ if the maximum m of $\mathbb{T}$ is left-scattered. Otherwise, ${\mathbb{T}}^{\kappa }=\mathbb{T}$. The set of all regressive and rd-continuous functions $f:\mathbb{T}\to \mathbb{R}$ is denoted by $\mathcal{R}$.

3. 

If $\alpha \in \mathcal{R}$, the exponential function on time scales is defined by

$$e_{\alpha }(t,s)=exp\left({\int }_s^t{\xi }_{\mu \left(\tau \right)}\left(\alpha \left(\tau \right)\right)\Delta \tau \right)fors,t\in \mathbb{T},$$

where ${\xi }_h\left(z\right)=\frac{1}{h}Log(1+zh)$.

Definition 4

([20] (Delta derivative)). A function $f:\mathbb{T}\to \mathbb{R}$ is called delta differential at $t\in {\mathbb{T}}^{\kappa }$ if there is $f^{\Delta }\left(t\right)$ such that, for all $\epsilon >0$, there exists a neighborhood U of t (i.e., $U=(t-\delta ,t+\delta )\bigcap \mathbb{T}$ for some $\delta >0$) such that

$$\left|f\left(\sigma \left(t\right)\right)-f\left(s\right)-f^{\Delta }\left(t\right)(\sigma \left(t\right)-s)\right|\le \epsilon \left|\sigma \left(t\right)-s\right|,\mathit{for}\mathit{all}s\in U.$$

$f^{\Delta }\left(t\right)$ is called the delta derivative of f at t.

In this paper, we denote by ${\Delta }_{t}f:=f^{\Delta }\left(t\right)$ for the ease of expression.

Lemma 1

([20]). If $f:\mathbb{T}\to \mathbb{R}$ is differentiable at $t\in {\mathbb{T}}^{\kappa }$, then

$$f\left(\sigma \left(t\right)\right)=f\left(t\right)+\mu \left(t\right)f^{\Delta }\left(t\right).$$

Lemma 2

([20]). If $\alpha ,\beta \in \mathcal{R}$ and $a,b,c\in \mathbb{T}$, then

1. 

${\left(e_{\alpha }(c,t)\right)}^{\Delta }=-\alpha \left(t\right)\left(e_{\alpha }(c,\sigma \left(t\right))\right).$

2. 

${\int }_a^b\alpha \left(t\right)e_{\alpha }(c,\sigma \left(t\right))\Delta t=e_{\alpha }(c,a)-e_{\alpha }(c,b).$

3. 

The function $\ominus \alpha$ is also elements of $\mathcal{R}$, where $(\ominus \alpha )\left(t\right)=-\frac{\alpha \left(t\right)}{1+\mu \left(t\right)\alpha \left(t\right)},\forall t\in {\mathbb{T}}^{\kappa }.$

4. 

$\alpha \ominus \beta =\frac{\alpha -\beta }{1+\mu \left(t\right)\beta }$.

5. 

$e_{\alpha }(\sigma \left(t\right),s)=(1+\mu \left(t\right)\alpha \left(t\right))e_{\alpha }(t,s)$.

Using Theorem 2.62 in [20], the following Lemma is easy to prove.

Lemma 3

([20]). If $\alpha \in \mathcal{R}$, then ${\left(e_{\alpha }(t,s)\right)}^{\Delta }=\alpha \left(t\right)e_{\alpha }(t,s).$

Lemma 4

([22]). If $\beta \in {\mathcal{R}}^{+}$ and $\beta \left(t\right)<0$ for $t\in \mathbb{T}$, then for $\forall s\le t$ and $s\in \mathbb{T}$,

$$0<e_{\beta }(t,s)\le exp\left({\int }_s^t\beta \left(r\right)\Delta r\right)<1.$$

For more detailed properties on the time scale, we refer to Theorem 1.16, Theorem 1.20, and Theorem 1.60 in Chapter 1 by Bohner et al. in [20].

3. Stability Analysis of Dynamical Systems with Time Delay on Time Scales

Consider dynamical systems with time delay on time–space scales

$${\Delta }_{t}u=F\left(t,x,u\left(\delta \right(t),x)\right),t\in {[t_0,\infty )}_{{\mathbb{T}}_1},$$

(1)

with initial data

$$u(t,x)=\phi (t,x),t\in {[\delta \left(t_0\right),t_0]}_{{\mathbb{T}}_1},$$

(2)

where $x\in \mathsf{\Omega }\subset {\mathbb{T}}_2$, $u\in {\mathbb{R}}^n$, the delay function $\delta :{[t_0,\infty )}_{{\mathbb{T}}_1}\to {[\delta \left(t_0\right),\infty )}_{{\mathbb{T}}_1}$ is a strictly monotonically increasing and invertible $\Delta$-differentiable function satisfying $\delta \left(t\right)<t$, $\left|{\delta }^{\Delta }\left(t\right)\right|<\infty$, $\delta \left(t_0\right)\in {\mathbb{T}}_1$. $C_H$ represents the set of right dense continuous function $\phi (t,x):{[\delta \left(t_0\right),t_0]}_{{\mathbb{T}}_1}\times \mathsf{\Omega }\to {\mathbb{R}}^n$ about t with norm ${∥\phi ∥}_c=sup\{∥\phi (s,·)∥:s\in {[\delta \left(t_0\right),t_0]}_{{\mathbb{T}}_1}\}$.

Combined with Definition 2.2.1 and Definition 2.4.5 of the exponential stability of trivial solutions of systems on time scales in [23], the (uniform) exponential stability and instability of the equilibrium point $u^{*}$ of the system (1) and (2) can be defined as follows.

Definition 5.

We say that the equilibrium point of systems (1) and (2) is exponential stable if there are constants $\alpha >0$, $\gamma >0$, and $M\in {\mathbb{R}}^{+}$, satisfying for the equilibrium point $u^{*}$ of system (1) and (2) and the solution $u(t,x)$ determined by initial data $u_0$, there exists

$$∥u-u^{*}∥\le M({∥\phi -u^{*}∥}_c,t_0){\left(e_{\ominus \alpha }(t,t_0)\right)}^{\gamma },\forall t\in {[t_0,\infty )}_{{\mathbb{T}}_1}.$$

The equilibrium point is said to be uniformly exponentially stable on ${[t_0,\infty )}_{\mathbb{T}}$ if M is independent of $t_0$.

Based on definition of a positive-definite function of dynamical systems on general time scale [23,24], the positive-definite function of dynamical systems on time–space scales can be defined as follows.

Definition 6

([23,24]). (1) Define function $\kappa \left(r\right)\in \mathcal{K}$ if and only if $\kappa \in C[[0,\rho ),{\mathbb{R}}_{+}]$, where ρ is a positive real number. $\kappa \left(0\right)=0$ and $\kappa \left(r\right)$ increase monotonically about r.

(2) The real valued function $V(t,x,z(t,x\left)\right)$ is called positive definite if and only if $V(t,x,0)=0$ holds for an arbitrary $t\in {\mathbb{T}}_1$, and there exists $\kappa \left(r\right)\in \mathcal{K}$ satisfying $\kappa \left(r\right)\le V(t,x,z(t,x\left)\right)$, where $∥z∥=r$, $(t,x,z)\in {\mathbb{T}}_1\times {\mathbb{T}}_2\times S_{\rho }$ and $S_{\rho }=\{z\in {\mathbb{R}}^n:∥z∥\le \rho \}$.

Let $\varphi (\theta ,x)=u(t+\theta ,x)-u^{*}$, ${∥\varphi (\theta ,·)∥}_c=sup\{∥\varphi (\theta ,·)∥:\theta \in [-\tau ,0],t+\theta \in {\left[\delta \left(t_0\right),t\right]}_{\mathbb{T}}\}$, $\overline{z}(t,x)=u(t,x)-u^{*}$. Combining the properties of an exponential function on the time scale and exponential stability of dynamical systems without time delay on time scales [23], we give some exponential estimators of systems with the time delay on time–space scales, i.e., the following Propositions 1 and 2.

Proposition 1.

If there exists a functional $V(t,x,\varphi )$ satisfying for any $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$\begin{array}{cc}& {\kappa }_1\left(∥\varphi (0,·)∥\right)\le V(t,x,\varphi )\le {\kappa }_2\left({∥\varphi ∥}_c\right),\end{array}$$

(3)

$$\begin{array}{cc}& {\Delta }_{t}V(t,x,\varphi )\le {\displaystyle \frac{-{\kappa }_3\left({∥\varphi ∥}_c\right)-\alpha L}{1+\mu \left(t\right)\alpha }},\end{array}$$

(4)

$$\begin{array}{cc}& -{\kappa }_3\left({\kappa }_2^{-1}\left(V(t,x,\varphi )\right)\right)+\alpha V(t,x,\varphi )\le 0,\end{array}$$

(5)

then the solution of systems (1) and (2) satisfies the exponential estimation equation

$$∥u-u^{*}∥\le {\kappa }_1^{-1}\left(\left({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)+L\right)e_{\ominus \alpha }(t,t_0)\right),\forall t\in {[t_0,\infty )}_{{\mathbb{T}}_1},$$

where ${\kappa }_1,{\kappa }_2,{\kappa }_3\in \mathcal{K}$, $L\ge 0$, $\alpha >0$ are constants.

Proof. 

Using (3)–(5), Lemmas 2 and 3,

$$\begin{array}{cc}\hfill {\Delta }_t\left(V(t,x,\varphi )e_{\alpha }(t,0)\right)& ={\Delta }_{t}V(t,x,\varphi )·e_{\alpha }(\sigma \left(t\right),0)+V(t,x,\varphi )·{\Delta }_t\left(e_{\alpha }(t,0)\right)\hfill \\ \hfill & \le \left(-{\kappa }_3\left({∥\varphi ∥}_c\right)-\alpha L\right)e_{\alpha }(t,0)+\alpha V(t,x,\varphi )e_{\alpha }(t,0)\hfill \\ \hfill & \le \left(-{\kappa }_3\left({\kappa }_2^{-1}\left(V(t,x,\varphi )\right)\right)+\alpha V(t,x,\varphi )-\alpha L\right)e_{\alpha }(t,0)\hfill \\ \hfill & \le -\alpha L{e}_{\alpha }(t,0).\hfill \end{array}$$

(6)

Integrating both sides of (6) from $t_0$ to t, one obtains for $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$\begin{array}{cc}\hfill V(t,x,\varphi )e_{\alpha }(t,0)& =V(t,x,\overline{z}(t+\theta ,x))e_{\alpha }(t,0)\hfill \\ & \le V(t_0,x,\overline{z}(t_0+\theta ,x))e_{\alpha }(t_0,0)-L{e}_{\alpha }(t,0)+L{e}_{\alpha }(t_0,0)\hfill \\ & \le V(t_0,x,\overline{z}(t_0+\theta ,x))e_{\alpha }(t_0,0)+L{e}_{\alpha }(t_0,0)\hfill \\ & \le \left(V(t_0,x,\overline{z}(t_0+\theta ,x))+L\right)e_{\alpha }(t_0,0)\hfill \\ & \le \left({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)+L\right)e_{\alpha }(t_0,0).\hfill \end{array}$$

Then

$$V(t,x,\varphi )\le \left({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)+L\right)e_{\ominus \alpha }(t,t_0).$$

It follows from (3) that

$$∥u(t,x)-u^{*}∥=∥\varphi (0,x)∥\le {\kappa }_1^{-1}V(t,x,\varphi )\le {\kappa }_1^{-1}\left(\left({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)+L\right)e_{\ominus \alpha }(t,t_0)\right),$$

i.e., $∥u-u^{*}∥\le {\kappa }_1^{-1}\left(\left({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)+L\right)e_{\ominus \alpha }(t,t_0)\right),\forall t\in {[t_0,\infty )}_{{\mathbb{T}}_1}.$ □

Remark 1.

(1) In the analysis of specific systems, the constants $L,\alpha$, and functions ${\kappa }_1,{\kappa }_2,{\kappa }_3$ can be obtained using the minimum eigenvalue and maximum eigenvalue of the matrix derived from the calculation of ${\Delta }_{t}V$ and the reducing and preserving transformations of inequality (4).

(2) It can be found that it requires finding a positive definite functional with a negative derivative about time in Proposition 1, which is similar to the Lyapunov–Krasovskii functional method [1,2] and Razumikhin functional method [3] for dealing with time-delay systems. The conditions are relatively conservative and difficult to satisfy in some cases. We propose an improved stability criterion. If condition (4) in Proposition 1 is changed to be

$${\Delta }_{t}V(t,x,\varphi )\le \frac{-{\kappa }_3{∥\varphi ∥}_c+\lambda \left(t\right)e_{\ominus \beta }(t,0)}{1+\mu \left(t\right)\alpha },$$

(7)

the exponential estimation that the solution satisfies can still be obtained without changing other conditions. However, in condition (4), $\alpha L>0$, i.e., ${\Delta }_{t}V(t,x,\varphi )$ is non-positive. While in condition (7), $\lambda \left(t\right)\ge 0$, which reduced its non-positive requirements of ${\Delta }_{t}V$ and the conservatism of the criterion.

Using (7), the following Proposition 2 can be concluded.

Proposition 2.

If there exists a functional $V(t,x,\varphi )$ satisfying for any $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$\begin{array}{c}\hfill {\kappa }_1\left(∥\varphi (0,·)∥\right)\le V(t,x,\varphi )\le {\kappa }_2\left({∥\varphi ∥}_c\right),\end{array}$$

(8)

$$\begin{array}{c}\hfill {\Delta }_{t}V(t,x,\varphi )\le {\displaystyle \frac{-{\kappa }_3{∥\varphi ∥}_c+\lambda \left(t\right)e_{\ominus \beta }(t,0)}{1+\mu \left(t\right)\alpha }},\end{array}$$

(9)

$$\begin{array}{c}\hfill -{\kappa }_3\left({\kappa }_2^{-1}\left(V(t,x,\varphi )\right)\right)+\alpha V(t,x,\varphi )\le 0.\end{array}$$

(10)

Then, the solution of system (1) and (2) satisfies the exponential estimation

$$∥u-u^{*}∥\le {\kappa }_1^{-1}\left(({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)-r)e_{\ominus \alpha }(t,t_0)\right),\forall t\in {[t_0,\infty )}_{{\mathbb{T}}_1},$$

(11)

where ${\kappa }_1,{\kappa }_2,{\kappa }_3\in \kappa$, $\lambda \left(t\right)\ge 0$, $r={\displaystyle \underset{t\in {[t_0,\infty )}_{\mathbb{T}}}{inf}}\left(\lambda \left(t\right)/(\alpha \ominus \beta )\left(t\right)\right)$, $\beta >\alpha >0$ is constant.

Proof. 

It follows from (8)–(10), Lemmas 2 and 3, that

$$\begin{array}{cc}\hfill & {\Delta }_t\left(V(t,x,\varphi )e_{\alpha }(t,0)\right)\hfill \\ \hfill =& {\Delta }_{t}V(t,x,\varphi )·e_{\alpha }(\sigma \left(t\right),0)+V(t,x,\varphi )·{\Delta }_t\left(e_{\alpha }(t,0)\right)\hfill \\ \hfill \le & \left(-{\kappa }_3\left({∥\varphi ∥}_c\right)+\lambda \left(t\right)e_{\ominus \beta }(t,0)\right)e_{\alpha }(t,0)+\alpha V(t,x,\varphi )e_{\alpha }(t,0)\hfill \\ \hfill \le & \left(-{\kappa }_3\left({\kappa }_2^{-1}\left(V(t,x,\varphi )\right)\right)+\alpha V(t,x,\varphi )+\lambda \left(t\right)e_{\ominus \beta }(t,0)\right)e_{\alpha }(t,0)\hfill \\ \hfill \le & \lambda \left(t\right)e_{\alpha \ominus \beta }(t,0).\hfill \end{array}$$

(12)

It follows from Lemma 2 and $\lambda \left(t\right)\ge 0$, $\beta >\alpha >0$ that

$$\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}=\frac{(\alpha -\beta )\lambda \left(t\right)}{1+\mu \left(t\right)\beta }\le 0.$$

Integrating both sides of (12) from $t_0$ to t, one obtains for $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$\begin{array}{cc}& V(t,x,\varphi )e_{\alpha }(t,0)\hfill \\ \hfill \le & V(t_0,x,\overline{z}(t_0+\theta ,x))e_{\alpha }(t_0,0)+\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}{e}_{\alpha \ominus \beta }(t,0)-\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}{e}_{\alpha \ominus \beta }(t_0,0)\hfill \\ \hfill \le & \left(V(t_0,x,\overline{z}(t_0+\theta ,x))-\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}\right)e_{\alpha }(t_0,0)\hfill \\ \hfill \le & \left({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)-\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}\right)e_{\alpha }(t_0,0).\hfill \end{array}$$

Using the method in proof of Proposition 1, one obtains

$$\begin{array}{cc}& ∥u-u^{*}∥\hfill \\ \hfill \le & {\kappa }_1^{-1}\left(\left({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)-\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}\right)e_{\ominus \alpha }(t,t_0)\right)\hfill \\ \hfill \le & {\kappa }_1^{-1}\left(({\kappa }_2\left({∥\phi -u^{*}∥}_c\right)-r)e_{\ominus \alpha }(t,t_0)\right),\hfill \end{array}$$

where $r={\displaystyle \underset{t\in {[t_0,\infty )}_{{\mathbb{T}}_1}}{inf}}\left(\lambda \left(t\right)/(\alpha \ominus \beta )\left(t\right)\right)$. □

Next, based on the properties of the exponential function on time scales, two improved exponential stability criteria of the delayed system on the time–space scales are given, i.e., the following Theorems 1 and 2.

Theorem 1.

If there exists a functional $V(t,x,\varphi )$ satisfying for any $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$\begin{array}{cc}& K_1\left(t\right){∥\varphi (0,·)∥}^p\le V(t,x,\varphi )\le K_2\left(t\right){∥\varphi ∥}_c^q,\end{array}$$

(13)

$$\begin{array}{cc}& {\Delta }_{t}V(t,x,\varphi )\le {\displaystyle \frac{-K_3\left(t\right){∥\varphi ∥}_c^{\gamma }+\lambda \left(t\right)e_{\ominus \beta }(t,0)}{1+\mu \left(t\right)\alpha }},\mathit{for}\mathit{some}\mathit{fixed}\mathit{number}\gamma >0,\end{array}$$

(14)

$$\begin{array}{cc}& V(t,x,\varphi )\le V^{\frac{\gamma }{q}}(t,x,\varphi ),\end{array}$$

(15)

where $K_1\left(t\right),K_2\left(t\right),K_3\left(t\right)>0$, $\lambda \left(t\right)\ge 0$, $K_1\left(t\right)$ is a non-decreasing function, $\gamma ,q$ are positive constants. $\alpha ={\displaystyle \underset{t\in {[t_0,\infty )}_{\mathbb{T}}}{inf}}\frac{K_3\left(t\right)}{K_2^{\gamma /q}\left(t\right)}$. β is a constant satisfying $\beta >\alpha >0$. Then, the equilibrium of (1) and (2) is exponential stable.

Proof. 

Using (14) and (15), Lemmas 2 and 3,

$$\begin{array}{cc}\hfill & {\Delta }_t\left(V(t,x,\varphi )e_{\alpha }(t,0)\right)\hfill \\ \hfill =& {\Delta }_{t}V(t,x,\varphi )·e_{\alpha }(\sigma \left(t\right),0)+V(t,x,\varphi )·{\Delta }_t\left(e_{\alpha }(t,0)\right)\hfill \\ \hfill \le & \left(-K_3\left(t\right){∥\varphi ∥}_c^{\gamma }+\lambda \left(t\right)e_{\ominus \beta }(t,0)\right)e_{\alpha }(t,0)+\alpha V(t,x,\varphi )e_{\alpha }(t,0)\hfill \\ \hfill \le & \left(-K_3\left(t\right)K_2^{-\gamma /q}\left(t\right)V^{\gamma /q}(t,x,\varphi )+\alpha V(t,x,\varphi )+\lambda \left(t\right)e_{\ominus \beta }(t,0)\right)e_{\alpha }(t,0)\hfill \\ \hfill \le & \lambda \left(t\right)e_{\alpha \ominus \beta }(t,0).\hfill \end{array}$$

(16)

Integrating (16) from $t_0$ to t, one obtains for $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$V(t,x,\varphi )e_{\alpha }(t,0)\le \left(K_2\left(t_0\right)\left({∥\phi -u^{*}∥}_c^q\right)-\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}\right)e_{\alpha }(t_0,0).$$

(17)

Using (13) and considering $K_1\left(t\right)$ to be a non-decreasing function, one obtains

$$∥u-u^{*}∥=∥\varphi (0,·)∥\le K_1^{-1/p}\left(t\right)V^{1/p}(t,x,\varphi ).$$

(18)

Substituting (17) into (18), one obtains

$$∥u-u^{*}∥\le K_1^{-1/p}\left(t_0\right){\left((K_2\left(t_0\right)\left({∥\phi -u^{*}∥}_c^q\right)-r)e_{\ominus \alpha }(t,t_0)\right)}^{1/p},$$

where $r={\displaystyle \underset{t\in {[t_0,\infty )}_{{\mathbb{T}}_1}}{inf}}\left(\lambda \left(t\right)/(\alpha \ominus \beta )\left(t\right)\right)$, then the equilibrium of (1) and (2) is exponentially stable. □

Remark 2.

(1) In the analysis of specific systems, the parameters $K_1\left(t\right)$ and $K_2\left(t\right)$ can be obtained using the minimum eigenvalue and maximum eigenvalue of the matrix related to V, respectively. The constants $\alpha ,\beta$ and parameters $K_3\left(t\right)$, $\lambda \left(t\right)$ can be derived using the minimum eigenvalue and maximum eigenvalue of the matrix derived from the calculation of ${\Delta }_{t}V$ and the reducing and preserving transformations of the inequality (14).

(2) In Theorem 1, if, for $i=1,2,3$, $K_i\left(t\right)=K_i>0$ is constant, then the equilibrium of (1) and (2) is uniformly exponential stable.

Theorem 2.

If there exists functional $V(t,x,\varphi )$ satisfying for any $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$\begin{array}{cc}& K_1\left(t\right){∥\varphi (0,·)∥}^p\le V(t,x,\varphi ),\end{array}$$

(19)

$$\begin{array}{cc}& {\Delta }_{t}V(t,x,\varphi )\le {\displaystyle \frac{-K_{3}V(t,x,\varphi )+\lambda \left(t\right)e_{\ominus \beta }(t,0)}{1+\mu \left(t\right)\alpha }},\end{array}$$

(20)

where $K_1\left(t\right),K_3>0$, $K_1\left(t\right)$ is a non-decreasing function, $\lambda \left(t\right)\ge 0$, $0<\alpha <min\{K_3,\beta \}$. Then, the equilibrium of (1) and (2) is exponentially stable.

Proof. 

Using (20), Lemmas 2 and 3, one obtains

$$\begin{array}{cc}\hfill & {\Delta }_t\left(V(t,x,\varphi )e_{\alpha }(t,0)\right)\hfill \\ \hfill =& {\Delta }_{t}V(t,x,\varphi )·e_{\alpha }(\sigma \left(t\right),0)+V(t,x,\varphi )·{\Delta }_t\left(e_{\alpha }(t,0)\right)\hfill \\ \hfill \le & \left(-K_{3}V(t,x,\varphi )+\lambda \left(t\right)e_{\ominus \beta }(t,0)\right)e_{\alpha }(t,0)+\alpha V(t,x,\varphi )e_{\alpha }(t,0)\hfill \\ \hfill \le & \lambda \left(t\right)e_{\alpha \ominus \beta }(t,0).\hfill \end{array}$$

(21)

Integrating both sides of (21) from $t_0$ to t, one obtains for $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$,

$$V(t,x,\varphi )e_{\alpha }(t,0)\le \left(V(t_0,x,\phi -u^{*})-\frac{\lambda \left(t\right)}{(\alpha \ominus \beta )\left(t\right)}\right)e_{\alpha }(t_0,0).$$

(22)

Using (19) and considering $K_1\left(t\right)$ as a non-decreasing function, one obtains

$$∥u-u^{*}∥=∥\varphi (0,·)∥\le K_1^{-1/p}\left(t\right)V^{1/p}(t,x,\varphi ).$$

(23)

Substituting (22) into (23), we have

$$∥u-u^{*}∥\le K_1^{-1/p}\left(t_0\right){\left((V(t_0,x,\phi -u^{*})-r)e_{\ominus \alpha }(t,t_0)\right)}^{1/p},$$

where $r={\displaystyle \underset{t\in {[t_0,\infty )}_{\mathbb{T}}}{inf}}\left(\lambda \left(t\right)/(\alpha \ominus \beta )\left(t\right)\right)$. Then, the equilibrium of (1) and (2) is exponential stable. □

Remark 3.

In Theorem 2, if $K_1\left(t\right)=K_1>0$ is constant, then the equilibrium of (1) and (2) is uniformly exponentially stable.

The property of the uniformly asymptotically stable function (UASF) in the following lemma provides a new approach to the study of the exponential stability of systems on time scales.

Lemma 5

([25]). $\alpha \in {\mathcal{R}}^{+}$ is a UASF if and only if there exist $k>0$, $\beta <0$ and $\beta \in {\mathcal{R}}^{+}$ satisfying for any $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$, $e_{\alpha }(t,t_0)\le k{e}_{\beta }(t,t_0)$ holds.

Next, we propose an improved stability criterion for a delayed system on time–space scales combining with Lemma 5. It does not require the time derivative of the functional to be negative definite, which expands the applicability of the criteria.

Theorem 3.

If there exists a functional $V(t,x,\varphi )$ and function ${\kappa }_1,{\kappa }_2\in \mathcal{K}$ satisfying for any $t\in {[t_0,\infty )}_{{\mathbb{T}}_1}$, then there exists a uniformly asymptotically stable function $\alpha \left(t\right)$ satisfying

$$\begin{array}{cc}& K_1\left(t\right){∥\varphi (0,·)∥}^2\le V(t,x,\varphi )\le K_2\left(t\right){∥\varphi ∥}_c^2,\end{array}$$

(24)

$$\begin{array}{cc}& {\Delta }_{t}V(t,x,\varphi )\le \alpha \left(t\right)V(t,x,\varphi )+\epsilon ,\end{array}$$

(25)

where $K_1\left(t\right),K_2\left(t\right)>0$, $K_1\left(t\right)$ is a non-decreasing function, $\epsilon >0$ are constants, and systems (1) and (2) exponentially converge to the bounded set $B=\{\left.\xi \right|{∥\xi \left(t\right)∥}^2<-\frac{k\epsilon }{\beta K_1\left(t_0\right)}\}.$ If $\epsilon =0$, then the equilibrium point of the system (1) and (2) is exponentially stable. This is especially true if $\epsilon =0$ and, for $i=1,2$, $K_i\left(t\right)=K_i$ is not related to t, then the equilibrium of system (1) and (2) is uniformly exponentially stable.

Proof. 

Using (25), one obtains

$$V(t,x,\varphi )\le e_{\alpha }(t,t_0)V(t_0,x,\varphi )+\epsilon {\int }_{t_0}^t{e}_{\alpha }(t,\sigma \left(\tau \right))\Delta \tau .$$

(26)

Since $\alpha \left(t\right)$ is a uniformly asymptotically stable function, it follows from (26) that $k>0$, $\beta <0$, and $\beta \in {\mathcal{R}}^{+}$, which satisfy

$$V(t,x,\varphi )\le k{e}_{\beta }(t,t_0)V(t_0,x,\varphi )+k\epsilon {\int }_{t_0}^t{e}_{\beta }(t,\sigma \left(\tau \right))\Delta \tau .$$

(27)

Using Lemmas 2 and 4, one obtains

$$\begin{array}{cc}\hfill V(t,x,\varphi )& \le k{e}_{\beta }(t,t_0)V(t_0,x,\varphi )-\frac{k\epsilon }{\beta }{\int }_{t_0}^t{\Delta }_{\tau }\left(e_{\beta }(t,\tau )\right)\Delta \tau \hfill \\ & \le k{e}_{\beta }(t,t_0)V(t_0,x,\varphi )-\frac{k\epsilon }{\beta }\hfill \\ & \le k{e}_{\beta }(t,t_0)K_2\left(t_0\right){∥\phi -u^{*}∥}_c^2-\frac{k\epsilon }{\beta }\hfill \end{array}$$

from (27). Then,

$$\begin{array}{cc}\hfill {∥u(t,x)-u^{*}∥}^2=& {∥\varphi (0,x)∥}^2\le \frac{1}{K_1\left(t\right)}V(t,x,\varphi )\hfill \\ \hfill \le & \frac{k{K}_2\left(t_0\right)}{K_1\left(t_0\right)}{e}_{\beta }(t,t_0){∥\phi -u^{*}∥}_c^2-\frac{k\epsilon }{\beta K_1\left(t_0\right)},\hfill \end{array}$$

(28)

which means systems (1) and (2) exponentially converge to the bounded set

$$B=\left\{\left.\xi \right|{∥\xi \left(t\right)∥}^2<-\frac{k\epsilon }{\beta K_1\left(t_0\right)}\right\}.$$

If $\epsilon =0$, the equilibrium point of systems (1) and (2) is exponential stable. If $\epsilon =0$ and for $i=1,2$, $K_i\left(t\right)=K_i$ is not related to t, it follows from (28) that the equilibrium of (1) and (2) is uniformly exponentially stable. □

Remark 4.

Theorem 3 gives (uniform) exponential stability criteria in combination with the uniform asymptotic stability function. It does not require the derivative of the functional V to be negative definite with respect to time, which reduces the difficulty of constructing the functional V and expand the applicability of the criterion.

4. Some Applications in Consensus of Multi-Agent Systems

4.1. Consensus of Multi-Agent System

Consider first-order MAS with time delay on the time scale

$$\begin{array}{cc}\hfill & x_i^{\Delta }\left(t\right)=A{x}_i\left(t\right)+f(t,x_i\left(t\right),x_i(t-\tau \left(t\right)))+B{u}_i\left(t\right)+w_i\left(t\right),i=1,2,\cdots ,N,\hfill \\ \hfill & x_0^{\Delta }\left(t\right)=A{x}_0\left(t\right)+f(t,x_0\left(t\right),x_0(t-\tau \left(t\right)))+w_0\left(t\right),\hfill \end{array}$$

(29)

where $t\in \mathbb{T}$ with ${\mu }_{max}=sup\{\mu \left(t\right),t\in \mathbb{T}\}$. $x_i\in {\mathbb{R}}^m$ is the state vector of agent i. $x_0\in {\mathbb{R}}^m$ is the state vector of the leader. $A\in {\mathbb{R}}^{m\times m}$, $B\in {\mathbb{R}}^{m\times 1}$ are the constant real matrices. The function $f(t,x_i\left(t\right),x_i(t-\tau \left(t\right)))$ describes the nonlinear dynamics of the agents, which satisfies

$$\begin{array}{cc}& ∥f(t,x_i\left(t\right),x_i(t-\tau \left(t\right)))-f(t,x_j\left(t\right),x_j(t-\tau \left(t\right)))∥\hfill \\ \hfill \le & L(∥x_i\left(t\right)-x_j\left(t\right)∥+∥x_i(t-\tau \left(t\right))-x_j(t-\tau \left(t\right))∥)\hfill \end{array}$$

with the Lipschitz constant $L\ge 0$ for $i,j=0,1,\cdots ,N$. $w_i\left(t\right)$ and $w_0\left(t\right)$ are external disturbances satisfying ${\displaystyle \underset{i}{max}}{\displaystyle \underset{t\in \mathbb{T}}{sup}}{∥w_i\left(t\right)∥}^2\le \overline{B}$, ${\displaystyle \underset{t\in \mathbb{T}}{sup}}{∥w_0\left(t\right)∥}^2\le B_0$. Suppose that N followers are represented by a node set $\mathcal{V}=\{1,2,\cdots ,N\}$. The communication connection between the followers is represented by the edge set $\epsilon \subseteq \mathcal{V}\times \mathcal{V}$ of graph $\mathcal{G}=\{\mathcal{V},\epsilon \}$. Design the following controller

$$u_i\left(t\right)=-K\left(\sum _{j=1}^N{a}_{ij}\left(t\right)(x_i\left(t\right)-x_j\left(t\right))+b_i\left(t\right)(x_i\left(t\right)-x_0\left(t\right))\right),$$

where the weighted adjacency matrix $E=\left\{a_{ij}\right\}\in {\mathbb{R}}^{N\times N}$ is defined by $a_{ij}\left(t\right)>0$ if $(j,i)\in \epsilon$ at t, otherwise $a_{ij}\left(t\right)=0$. $C_i$ represents the maximum number of nodes j satisfying $(j,i)\in \epsilon$ for all $t\in \mathbb{T}$. The interconnection relationship between the leader and followers is defined by $b_i\left(t\right)$ with $b_i\left(t\right)>0$ if the information of the leader is accessible by the ith follower at t, otherwise $b_i\left(t\right)=0$. K is a state feedback matrix.

Definition 7

([26]). For a given $\epsilon >0$, MAS (29) can reach the leader-following bound consensus if

$$\underset{t\to +\infty }{lim}∥x_i\left(t\right)-x_0\left(t\right)∥\le \epsilon ,i=1,2,\cdots ,N.$$

If ${\displaystyle \underset{t\to +\infty }{lim}}∥x_i\left(t\right)-x_0\left(t\right)∥=0$, then the MAS can reach leader-following consensus.

Lemma 6

([27]). For any $x\in {\mathbb{R}}_{+}^N$ and $p>0$,

$${\left(\sum _{i=1}^N{x}_i\right)}^p\le N^{(p-1)\vee 0}\sum _{i=1}^N{x}_i^p.$$

In the following, we denote $\epsilon =2(1+5{\mu }_{max})(\overline{B}+B_0)$, and

$$\begin{array}{cc}\hfill g_i\left(t\right)& =\left((2A+4L+1)-2BK(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left(t\right)+b_i\left(t\right))+\left|BK\right|(\sum _{j\in {\mathcal{N}}_i}{C}_j{a}_{ji}^2\left(t\right)+1)\right)\hfill \\ & +{\mu }_{max}\left(5(A^2+4L^2)+10{\left|BK\right|}^2\sum _{j\in {\mathcal{N}}_i}(C_i{a}_{ij}^2\left(t\right)+C_j{a}_{ji}^2\left(t\right))+5{\left|BK\right|}^2{b}_i^2\left(t\right)\right).\hfill \end{array}$$

$$\begin{array}{cc}\hfill h_i\left(t\right)& =\left((2A+4L)-2BK(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left(t\right)+b_i\left(t\right))+\left|BK\right|(\sum _{j\in {\mathcal{N}}_i}{C}_j{a}_{ji}^2\left(t\right)+1)\right)\hfill \\ & +{\mu }_{max}\left(4(A^2+4L^2)+8{\left|BK\right|}^2\sum _{j\in {\mathcal{N}}_i}(C_i{a}_{ij}^2\left(t\right)+C_j{a}_{ji}^2\left(t\right))+4{\left|BK\right|}^2{b}_i^2\left(t\right)\right).\hfill \end{array}$$

Using Theorem 1, the criterion for the exponential consensus of MAS (29) on the time scale with $m=1$ can be obtained as follows. The analysis can be similarly extended to arbitrary dimensions.

Theorem 4.

If there exists $K_3\left(t\right)>0$, $\lambda \left(t\right)\ge 0$ and $\beta >p>0$ satisfying

$$(1+\mu \left(t\right)p)\underset{i}{max}{g}_i\left(t\right)\le -K_3\left(t\right),(1+\mu \left(t\right)p)\epsilon \le \lambda \left(t\right)e_{\ominus \beta }(t,0),$$

(30)

then the exponential consensus of MAS (29) can be achieved.

Proof. 

Denote the tracking error $z_i\left(t\right)=x_i\left(t\right)-x_0\left(t\right)$. It follows from (29) that

$$\begin{array}{cc}\hfill z_i^{\Delta }\left(t\right)& =A{z}_i\left(t\right)+f(t,z_i\left(t\right),z_i(t-\tau \left(t\right)))\hfill \\ & -BK(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left(t\right)(z_i\left(t\right)-z_j\left(t\right))+b_i\left(t\right)z_i\left(t\right))+w_i\left(t\right)-w_0\left(t\right).\hfill \end{array}$$

Consider

$$V=\sum _{i=1}^N{z}_i^2\left(t\right)+(L+10{\mu }_{max}{L}^2){\int }_{t-\tau \left(t\right)}^t{z}_i^2\left(s\right)\Delta s.$$

(31)

It follows from Lemma 1 that

$$\begin{array}{cc}\hfill {\Delta }_{t}V& =\sum _{i=1}^N{z}_i^{\Delta }\left(t\right)(2z_i\left(t\right)+\mu \left(t\right)z_i^{\Delta }\left(t\right))+(L+10{\mu }_{max}{L}^2)(z_i^2\left(t\right)-z_i^2(t-\tau \left(t\right))),\hfill \end{array}$$

(32)

where

$$\begin{array}{cc}\hfill & 2z_i^{\Delta }\left(t\right)z_i\left(t\right)\hfill \\ \hfill =& 2(A{z}_i\left(t\right)+f(t,z_i\left(t\right),z_i(t-\tau \left(t\right)))\hfill \\ \hfill -& BK(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left(t\right)(z_i\left(t\right)-z_j\left(t\right))+b_i\left(t\right)z_i\left(t\right))+(w_i\left(t\right)-w_0\left(t\right)))z_i\left(t\right)\hfill \\ \hfill \le & ((2A+3L+1)-2BK(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left(t\right)+b_i\left(t\right))\hfill \\ \hfill +& \left|BK\right|(\sum _{j\in {\mathcal{N}}_i}{C}_j{a}_{ji}^2\left(t\right)+1))z_i^2\left(t\right)+L{z}_i^2(t-\tau \left(t\right))+{(w_i\left(t\right)-w_0\left(t\right))}^2\hfill \end{array}$$

(33)

and

$$\begin{array}{cc}\hfill & \mu \left(t\right){\left(z_i^{\Delta }\left(t\right)\right)}^2\hfill \\ \hfill =& \mu \left(t\right)(A{z}_i\left(t\right)+f(t,z_i\left(t\right),z_i(t-\tau \left(t\right)))\hfill \\ \hfill -& BK(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left(t\right)(z_i\left(t\right)-z_j\left(t\right))+b_i\left(t\right)z_i\left(t\right))+(w_i\left(t\right)-w_0\left(t\right)){)}^2\hfill \\ \hfill \le & \mu \left(t\right)(5(A^2+2L^2)z_i^2\left(t\right)+10{\left|BK\right|}^2\sum _{j\in {\mathcal{N}}_i}(C_i{a}_{ij}^2\left(t\right)+C_j{a}_{ji}^2\left(t\right))z_i^2\left(t\right)\hfill \\ \hfill +& 5{\left|BK\right|}^2{b}_i^2\left(t\right)z_i^2\left(t\right)+10L^2{z}_i^2(t-\tau \left(t\right))+5{(w_i\left(t\right)-w_0\left(t\right))}^2).\hfill \end{array}$$

(34)

Substituting (33) and (34) into (32), it follows from (31) that

$${\Delta }_{t}V\le \underset{i}{max}{g}_i\left(t\right)\sum _{i=1}^N{z}_i^2\left(t\right)+\epsilon .$$

Choose $K_1\left(t\right)=1,K_2\left(t\right)=1+\tau \left(t\right)(L+10{\mu }_{max}{L}^2)$, $\gamma =q=2$, $p={\displaystyle \underset{t\in {[t_0,\infty )}_{\mathbb{T}}}{inf}}\frac{K_3\left(t\right)}{K_2\left(t\right)}$. If (30) holds, then (13)–(15) are satisfied. Therefore, the exponential consensus of MAS (29) can be achieved. □

Using Theorem 3, the improved criterion for the exponential consensus of MAS (29) on the time scale with $m=1$ can be obtained as follows, which reduces the non-positive requirement of ${\Delta }_{t}V$ and the conservatism of the criterion. The analysis can be similarly extended to arbitrary dimensions.

Theorem 5.

(1) If there exists UASF $\alpha \left(t\right)$ satisfying

$$\underset{i}{max}{g}_i\left(t\right)\le \alpha \left(t\right),$$

(35)

then MAS (29) can reach a leader-following bound consensus.

(2) If $w_i\left(t\right)=w_0\left(t\right)$ and there exists UASF $\alpha \left(t\right)$ satisfying

$$\underset{i}{max}{h}_i\left(t\right)\le \alpha \left(t\right),$$

(36)

then MAS (29) can reach a leader-following consensus.

Proof. 

(1) It follows from (31)–(34) that

$${\Delta }_{t}V\le \underset{i}{max}{g}_i\left(t\right)V+\epsilon .$$

If there exists UASF $\alpha \left(t\right)$ satisfying (35), then

$${\Delta }_{t}V\le \underset{i}{max}{g}_i\left(t\right)V+\epsilon \le \alpha \left(t\right)V+\epsilon .$$

(37)

Using Theorem 3, it follows from (37) that the MAS (29) can reach leader-following bound consensus.

(2) If $w_i\left(t\right)=w_0\left(t\right)$, then it can be obtained that

$$\begin{array}{cc}\hfill 2z_i^{\Delta }\left(t\right)z_i\left(t\right)& \le ((2A+3L)-2BK(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left(t\right)+b_i\left(t\right))\hfill \\ & +\left|BK\right|(\sum _{j\in {\mathcal{N}}_i}{C}_j{a}_{ji}^2\left(t\right)+1))z_i^2\left(t\right)+L{z}_i^2(t-\tau \left(t\right))\hfill \end{array}$$

(38)

and

$$\begin{array}{cc}\hfill \mu \left(t\right){\left(z_i^{\Delta }\left(t\right)\right)}^2\le & \mu \left(t\right)(4(A^2+2L^2)z_i^2\left(t\right)+8{\left|BK\right|}^2\sum _{j\in {\mathcal{N}}_i}(C_i{a}_{ij}^2\left(t\right)+C_j{a}_{ji}^2\left(t\right))z_i^2\left(t\right)\hfill \\ \hfill +& 4{\left|BK\right|}^2{b}_i^2\left(t\right)z_i^2\left(t\right)+8L^2{z}_i^2(t-\tau \left(t\right))).\hfill \end{array}$$

(39)

It follows from (31), (38) and (39) that, if there exists UASF $\alpha \left(t\right)$ satisfying (36), then MAS (29) can reach the leader-following consensus. □

4.2. Numerical Example

The interconnection relationship between the followers is described by $a_{ij}\left(t\right)$ with $a_{ij}\left(t\right)=1$ if $(j,i)\in \epsilon$ at t, otherwise $a_{ij}\left(t\right)=0$. The interconnection relationship between the leader and followers is described by $b_i\left(t\right)$ with $b_i\left(t\right)=0.5$ if the information of the leader is accessible by the ith follower at t, otherwise $b_i\left(t\right)=0$. $B=0.1$. The function f with time delays possesses the form of $f(t,x_i\left(t\right),x_i(t-\tau \left(t\right)))=0.01sin\left(x_i\left(t\right)\right)+0.01sin\left(x_i(t-0.3)\right).$ $w_i\left(t\right)=w_0\left(t\right)=0.5sin\left(0.2t\right)$. Next, we consider the leader-following consensus of different MASs.

Example 1.

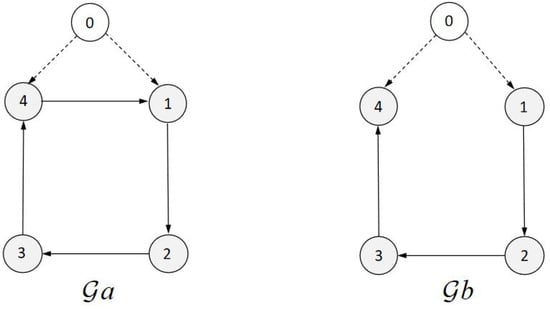
Leader agent with four following agents. Let $\mathbb{T}=0.3\mathbb{Z}$. The interaction topology switches from $\mathcal{G}a$ to $\mathcal{G}b$ at $t=0.9k$, and then from $\mathcal{G}b$ to $\mathcal{G}a$ at $t=0.9k+0.3$ for $k\in {\mathbb{Z}}^{+}$. The switching mode and communication connection between agents are shown in Figure 1.

Figure 1. Switching mode and communication connection between agents.

MAS (29) with the parameters $A=-0.08$ is considered. To achieve the consensus target, we design the parameter $K=1$ in the controller. Choosing $\alpha \left(t\right)=0.05$ if $t=0.9k$, $k\in {\mathbb{Z}}^{+}$ and $\alpha \left(t\right)=-0.05$ otherwise. Then $e_{\alpha }(t,t_0)\le e_{-1/60}(t,t_0)$, which means $\alpha \left(t\right)$ is a UASF. It can be verified that (36) holds for (29) with the above parameters. Thus, the consensus can be realized by Theorem 5. Figure 2 shows the state between the leader and followers of MAS (29). Figure 3 shows the tracking errors between the leader and followers of MAS (29). This implies that leader-following consensus can be achieved for MAS (29) with a time delay on a time scale under the above conditions, which reflect the effectiveness of the proposed criterion.

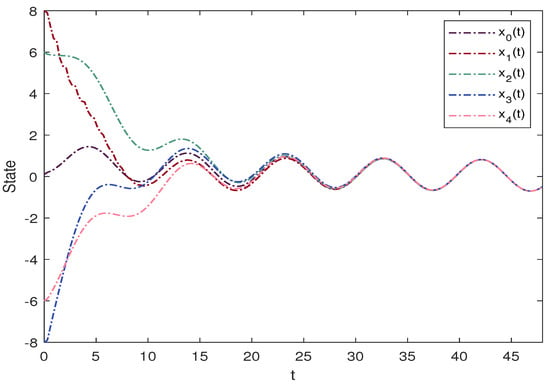
Figure 2. State trajectories of MAS (29) with parameters in example 1.

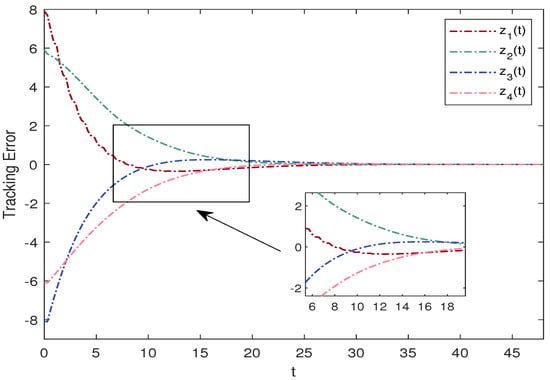
Figure 3. Tracking errors of MAS (29) with the parameters in example 1.

Example 2.

Leader agent with the six following agents.

Case 1. Let $\mathbb{T}=0.3\mathbb{Z}$. The interaction topology switches from $\mathcal{G}c$ to $\mathcal{G}d$ at $t=0.9k$, and then from $\mathcal{G}d$ to $\mathcal{G}c$ at $t=0.9k+0.3$ for $k\in {\mathbb{Z}}^{+}$. The switching mode and communication connection between agents are shown in Figure 4.

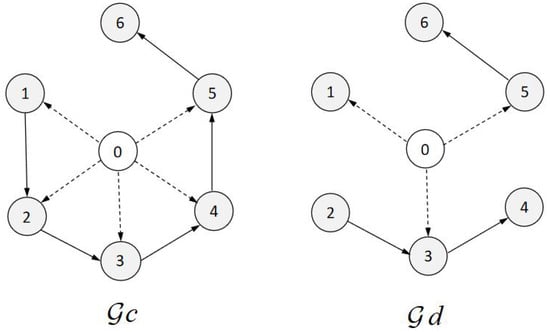
Figure 4. Switching mode and communication connection between agents.

MAS (29) with the parameters $A=-0.12$ is considered. To achieve the consensus target, we design the parameter $K=1$ in the controller. Choosing $\alpha \left(t\right)=0.05$ if $t=0.9k$, $k\in {\mathbb{Z}}^{+}$ and $\alpha \left(t\right)=-0.05$ otherwise. Then, $e_{\alpha }(t,t_0)\le e_{-1/60}(t,t_0)$, which means $\alpha \left(t\right)$ is a UASF. It can be verified that (36) holds for (29) with the above parameters. Thus, the consensus can be realized by Theorem 5. Figure 5 shows the state between the leader and followers of MAS (29). Figure 6 shows the tracking errors between the leader and the followers of MAS (29), which implies that the leader-following consensus can be achieved for MAS (29) with a time delay on a time scale under the above conditions.

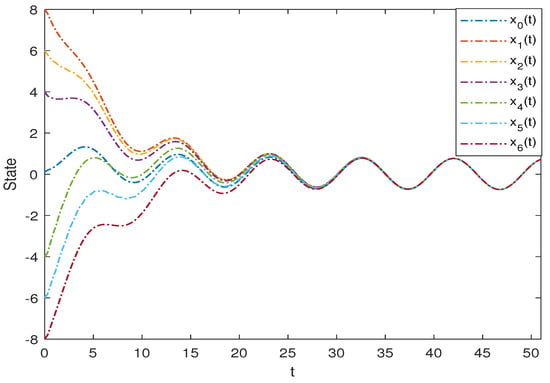
Figure 5. State trajectories of MAS (29) with parameters in example 2.

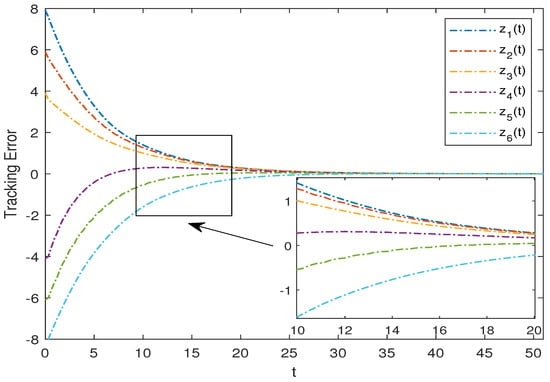
Figure 6. Tracking errors of MAS (29) with parameters in example 2.

Case 2. The interaction topology switches from $\mathcal{G}c$ to $\mathcal{G}d$ at $t=1.8k$, and then from $\mathcal{G}d$ to $\mathcal{G}c$ at $t=1.8k+0.6$ for $k\in {\mathbb{Z}}^{+}$. We take agent 3 as an example to provide its state on time scales $\mathbb{T}=0.3\mathbb{Z}$ and $\mathbb{T}=0.6\mathbb{Z}$, respectively, (c.f. Figure 7), which implies that the change in time scale has influence on the state of MASs.

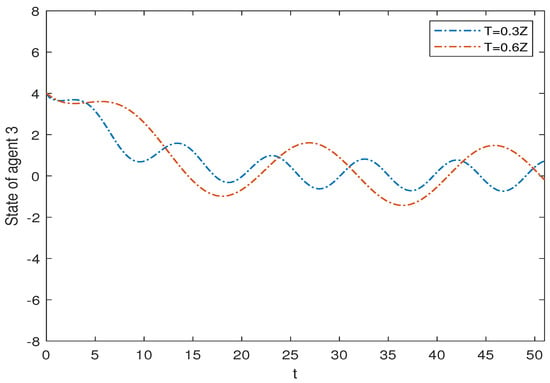
Figure 7. State trajectories for $x_3\left(t\right)$ of MAS (29) on time scales $\mathbb{T}=0.3\mathbb{Z}$ and $\mathbb{T}=0.6\mathbb{Z}$.

5. Conclusions

Criteria for the exponential stability of dynamical systems with a delay on the time scale were investigated, and were found to be more convenient and less conservative to apply in the unification and generalization of continuous and discrete cases. Based on the criteria for the exponential stability of dynamical systems on time scales, the exponential consensus problem for MASs with time delays on time scales are further studied. The algorithm for the estimation of the constants in the exponential stability criteria is important for applications and the development of numerical algorithms, which deserve to be further studied. Different forms of multi-agents with a more adaptive consensus protocol on time scales and other consensus problems, such as asymptotic consensus, are expected to be further considered.