Richard Kerner’s Path Integral Approach Aims to Understand the Self-Organized Matter Agglomeration and Its Translation into the Energy Landscape Kinetics Paradigm
Abstract
1. Introduction
2. Richard Kerner Agglomeration Model
- The number of ways in which a bond can be made.
- The bond energy.
- The concentration of atomic species.
- The temperature.
- u + Se;
- u + As;
- v + Se;
- v + As;
- w + Se;
- w + As; .
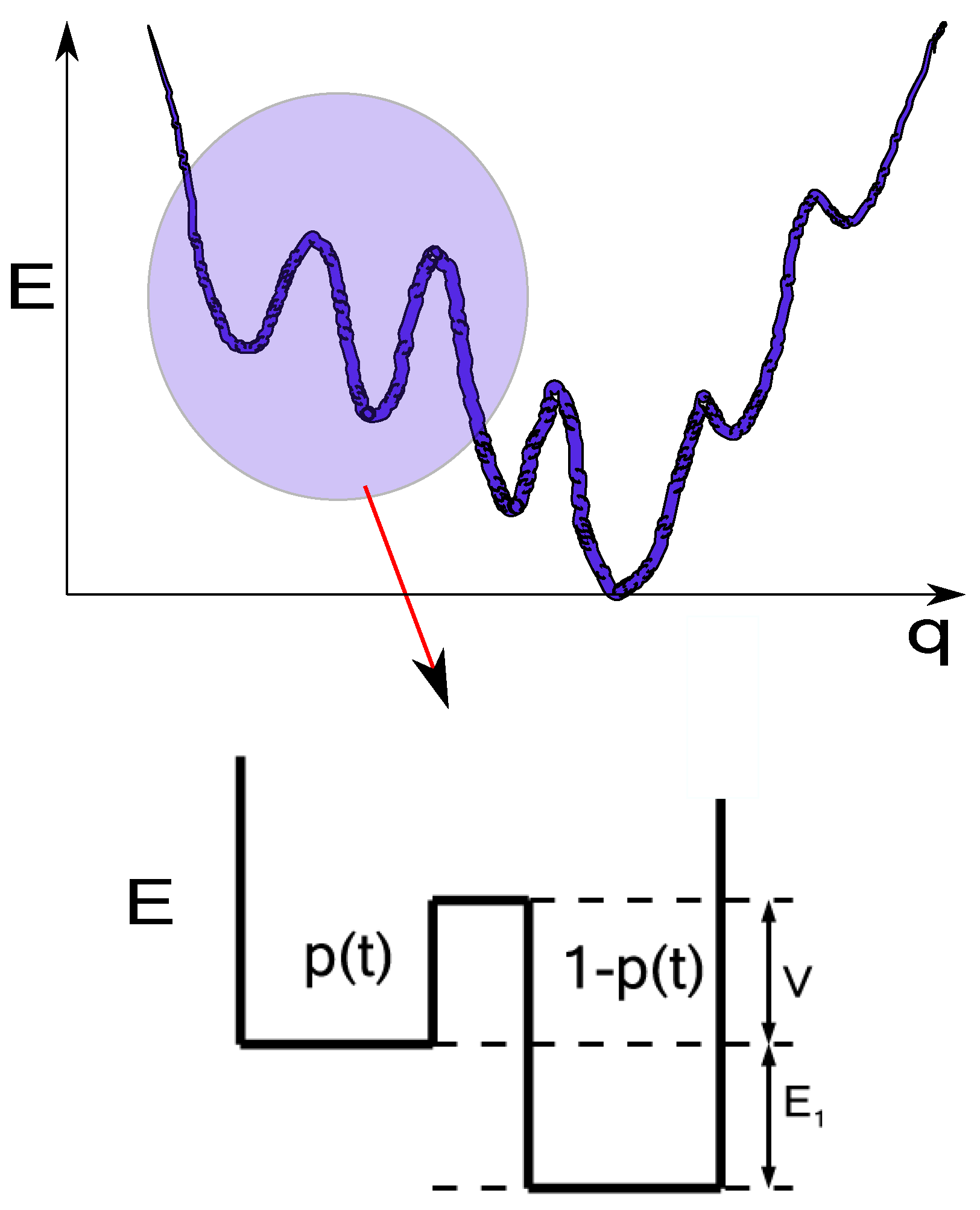
3. Translation to the Energy Landscape Paradigm and Path Integrals
4. Transition Probabilities of the Agglomeration Process
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RK | Richard Kerner |
References
- Chaikin, P.; Lubensky, T. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kerner, R. Models of Agglomeration and Glass Transition; Imperial College Press: London, UK, 2006. [Google Scholar]
- Jooss, C. Self-Organization of Matter: A Dialectical Approach to Evolution of Matter in the Microcosm and Macrocosmos; De Gruyter: Berlin, Germany, 2020. [Google Scholar]
- Sethna, J. Statistical Mechanics: Entropy, Order Parameters and Complexity; Oxford Master Series in Physics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Rylance, G.J.; Johnston, R.L.; Matsunaga, Y.; Li, C.B.; Baba, A.; Komatsuzaki, T. Topographical complexity of multidimensional energy landscapes. Proc. Natl. Acad. Sci. USA 2006, 103, 18551–18555. [Google Scholar] [CrossRef] [PubMed]
- Parisi, G.; Urbani, P.; Zamponi, F. Theory of Simple Glasses: Exact Solutions in Infinite Dimensions; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Welch, R.S.; Zanotto, E.D.; Wilkinson, C.J.; Cassar, D.R.; Montazerian, M.; Mauro, J.C. Cracking the Kauzmann paradox. Acta Mater. 2023, 254, 118994. [Google Scholar] [CrossRef]
- Bore, S.L.; Paesani, F. Realistic phase diagram of water from first principles data-driven quantum simulations. Nat. Commun. 2023, 14, 3349. [Google Scholar] [CrossRef] [PubMed]
- Roder, K.; Joseph, J.A.; Husic, B.E.; Wales, D.J. Energy Landscapes for Proteins: From Single Funnels to Multifunctional Systems. Adv. Theory Simulations 2019, 2, 1800175. [Google Scholar] [CrossRef]
- Tapia-Rojo, R.; Mora, M.; Board, S.; Walker, J.; Boujemaa-Paterski, R.; Medalia, O.; Garcia-Manyes, S. Enhanced statistical sampling reveals microscopic complexity in the talin mechanosensor folding energy landscape. Nat. Phys. 2023, 19, 52–60. [Google Scholar] [CrossRef]
- Dobson, C.M. Protein-misfolding diseases: Getting out of shape. Nature 2002, 418, 729–730. [Google Scholar] [CrossRef]
- Levinthal, C. Are there pathways for protein folding? J. Chim. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Dill, K.A.; Chan, H.S. From Levinthal to pathways to funnels. Nat. Struct. Biol. 1997, 4, 10–19. [Google Scholar] [CrossRef]
- Wales, D.J. Discrete path sampling. Mol. Phys. 2002, 100, 3285–3305. [Google Scholar] [CrossRef]
- Roder, K.; Wales, D.J. The Energy Landscape Perspective: Encoding Structure and Function for Biomolecules. Front. Mol. Biosci. 2022, 9, 820792. [Google Scholar] [CrossRef]
- Hiranuma, N.; Park, H.; Baek, M.; Anishchenko, I.; Dauparas, J.; Baker, D. Improved protein structure refinement guided by deep learning based accuracy estimation. Nat. Commun. 2021, 12, 1340. [Google Scholar] [CrossRef] [PubMed]
- Susskind, L. The Cosmic Landscape: String Theory and the Illusion of Intelligent Design; Little Brown and Company: Boston, MA, USA, 2008. [Google Scholar]
- Kerner, R. Phenomenological Lagrangian for the amorphous solid state. Phys. Rev. B 1983, 28, 5756–5761. [Google Scholar] [CrossRef]
- Kerner, R.; dos Santos, D.M.L.F. Nucleation and amorphous and crystalline growth: A dynamical model in two dimensions. Phys. Rev. B 1988, 37, 3881–3893. [Google Scholar] [CrossRef] [PubMed]
- Kerner, R.; Penson, K.A.; Bennemann, K.H. Model for the Growth of Fullerenes (C60, C70) from Carbon Vapour. Europhys. Lett. 1992, 19, 363. [Google Scholar] [CrossRef]
- Kerner, R.; Micoulaut, M. On the glass transition temperature in covalent glasses. J. Non-Cryst. Solids 1997, 210, 298–305. [Google Scholar] [CrossRef]
- Kerner, R. Nucleation and growth of fullerenes. Comput. Mater. Sci. 1994, 2, 500–508. [Google Scholar] [CrossRef]
- Kerner, R. Geometrical approach to the glass transition problem. J. Non-Cryst. Solids 1985, 71, 19–27. [Google Scholar] [CrossRef]
- Naumis, G.G.; Kerner, R. Stochastic matrix description of glass transition in ternary chalcogenide systems. J. Non-Cryst. Solids 1998, 231, 111–119. [Google Scholar] [CrossRef]
- Kerner, R.; Naumis, G.G. Stochastic matrix description of the glass transition. J. Phys. Condens. Matter 2000, 12, 1641. [Google Scholar] [CrossRef]
- dos Santos-Loff, D.M.; Micoulaut, M.; Kerner, R. Statistics of Boroxol Rings in Vitreous Boron Oxide. Europhys. Lett. 1994, 28, 573. [Google Scholar] [CrossRef]
- Barrio, R.A.; Kerner, R.; Micoulaut, M.; Naumis, G.G. Evaluation of the concentration of boroxol rings in vitreous by the stochastic matrix method. J. Phys. Condens. Matter 1997, 9, 9219. [Google Scholar] [CrossRef]
- Phillips, J.C.; Kerner, R. Structure and function of window glass and Pyrex. J. Chem. Phys. 2008, 128, 174506. [Google Scholar] [CrossRef] [PubMed]
- Kerner, R. Self-Assembly of Icosahedral Viral Capsids: The Combinatorial Analysis Approach. Math. Model. Nat. Phenom. 2011, 6, 136–158. [Google Scholar] [CrossRef]
- Aldrovandi, R. Special Matrices of Mathematical Physics: Stochastic, Circulant, and Bell Matrices; World Scientific: Singapore, 2001. [Google Scholar]
- Micoulaut, M.; Naumis, G.G. Glass transition temperature variation, cross-linking and structure in network glasses: A stochastic approach. Europhys. Lett. 1999, 47, 568. [Google Scholar] [CrossRef][Green Version]
- Phillips, J. Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys. J. Non-Cryst. Solids 1979, 34, 153–181. [Google Scholar] [CrossRef]
- Thorpe, M. Continuous deformations in random networks. J. Non-Cryst. Solids 1983, 57, 355–370. [Google Scholar] [CrossRef]
- He, H.; Thorpe, M.F. Elastic Properties of Glasses. Phys. Rev. Lett. 1985, 54, 2107–2110. [Google Scholar] [CrossRef]
- Boolchand, P.; Bauchy, M.; Micoulaut, M.; Yildirim, C. Topological Phases of Chalcogenide Glasses Encoded in the Melt Dynamics. Phys. Status Solidi B 2018, 255, 1870122. [Google Scholar] [CrossRef]
- Naumis, G.G.; Cocho, G. The tails of rank-size distributions due to multiplicative processes: From power laws to stretched exponentials and beta-like functions. New J. Phys. 2007, 9, 286. [Google Scholar] [CrossRef]
- Naumis, G.; Phillips, J. Bifurcation of stretched exponential relaxation in microscopically homogeneous glasses. J. Non-Cryst. Solids 2012, 358, 893–897. [Google Scholar] [CrossRef][Green Version]
- Huerta, A.; Naumis, G.G. Evidence of a glass transition induced by rigidity self-organization in a network-forming fluid. Phys. Rev. B 2002, 66, 184204. [Google Scholar] [CrossRef]
- Naumis, G.G. Energy landscape and rigidity. Phys. Rev. E 2005, 71, 026114. [Google Scholar] [CrossRef] [PubMed]
- Flores-Ruiz, H.M.; Naumis, G.G. The transverse nature of the Boson peak: A rigidity theory approach. Phys. B Condens. Matter 2013, 418, 26–31. [Google Scholar] [CrossRef]
- Flores-Ruiz, H.M.; Naumis, G.G.; Phillips, J.C. Heating through the glass transition: A rigidity approach to the boson peak. Phys. Rev. B 2010, 82, 214201. [Google Scholar] [CrossRef]
- Flores-Ruiz, H.M.; Naumis, G.G. Excess of low frequency vibrational modes and glass transition: A molecular dynamics study for soft spheres at constant pressure. J. Chem. Phys. 2009, 131, 154501. [Google Scholar] [CrossRef]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Gupta, P.K.; Allan, D.C. Viscosity of glass-forming liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 19780–19784. [Google Scholar] [CrossRef]
- Van Kampen, N. Stochastic Processes in Physics and Chemistry; North-Holland Personal Library, Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Gutzow, I.; Schmelzer, J. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Ahmad, S.; Khan, S.D.; Manzoor, S. The degenerate Fermi gas of π electrons in fullerenes and the σ surface instabilities. Nanotechnology 2006, 17, 1686. [Google Scholar] [CrossRef]
- Grassia, L.; D’Amore, A. On the interplay between viscoelasticity and structural relaxation in glassy amorphous polymers. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 724–739. [Google Scholar] [CrossRef]
- Gupta, P.K.; Cassar, D.R.; Zanotto, E.D. Role of dynamic heterogeneities in crystal nucleation kinetics in an oxide supercooled liquid. J. Chem. Phys. 2016, 145, 211920. [Google Scholar] [CrossRef]
- Abyzov, A.S.; Fokin, V.M.; Rodrigues, A.M.; Zanotto, E.D.; Schmelzer, J.W. The effect of elastic stresses on the thermodynamic barrier for crystal nucleation. J. Non-Cryst. Solids 2016, 432, 325–333. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Truskett, T.M.; Lewis, C.P.; Stillinger, F.H. Theory of supercooled liquids and glasses: Energy landscape and statistical geometry perspectives. Adv. Chem. Eng. 2001, 28, 21–79. [Google Scholar]
- Ohmura, S.; Shimojo, F. Mechanism of atomic diffusion in liquid B2O3: An ab initio molecular dynamics study. Phys. Rev. B 2008, 78, 224206. [Google Scholar] [CrossRef]
- Ohmura, S.; Shimojo, F. Ab initio molecular-dynamics study of structural, bonding, and dynamic properties of liquid B2O3 under pressure. Phys. Rev. B 2010, 81, 014208. [Google Scholar] [CrossRef]
- Binder, K.; Kob, W. Glassy Materials and Disordered Solids: An Introduction to Their Statistical Mechanics; World Scientific: Singapore, 2011. [Google Scholar]
- Maurya, R. Inorganic Chemistry: Some New Facets; De Gruyter: Berlin, Germany, 2021. [Google Scholar]
- Atkins, P. Shriver and Atkins’ Inorganic Chemistry; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Bartenev, G.M. The Structure and Mechanical Properties of Inorganic Glasses; Jaray, P.; Jaray, F.F., Translators; Wolters-Noordhoff Groningen: Groningen, The Netherlands, 1970. [Google Scholar]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587–645. [Google Scholar] [CrossRef]
- Zanotto, E.D.; Mauro, J. The glassy state of matter: Its definition and ultimate fate. J. Non-Cryst. Solids 2017, 471, 490–495. [Google Scholar] [CrossRef]
- Cugliandolo, L.F. Out-of-equilibrium dynamics of classical and quantum complex systems. Comptes Rendus Phys. 2013, 14, 685–699. [Google Scholar] [CrossRef]
- Pauling, L. General Chemistry; Dover Books on Chemistry; Dover Publications: Mineola, NY, USA, 2014. [Google Scholar]
- Akola, J.; Jones, R.O.; Kohara, S.; Usuki, T.; Bychkov, E. Density variations in liquid tellurium: Roles of rings, chains, and cavities. Phys. Rev. B 2010, 81, 094202. [Google Scholar] [CrossRef]
- Takeuchi, H.; Roe, R. Molecular dynamics simulation of local chain motion in bulk amorphous polymers. I. Dynamics above the glass transition. J. Chem. Phys. 1991, 94, 7446–7457. [Google Scholar] [CrossRef]
- Nascimento, M.L.F.; Fokin, V.M.; Zanotto, E.D.; Abyzov, A.S. Dynamic processes in a silicate liquid from above melting to below the glass transition. J. Chem. Phys. 2011, 135, 194703. [Google Scholar] [CrossRef]
- Wolynes, P.G.; Lubchenko, V. Structural Glasses and Supercooled Liquids: Theory, Experiment, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zanotto, E.D.; Cassar, D.R. The race within supercooled liquids—Relaxation versus crystallization. J. Chem. Phys. 2018, 149, 024503. [Google Scholar] [CrossRef]
- Eisenberg, A.; Tobolsky, A.V. Equilibrium polymerization of selenium. J. Polym. Sci. 1960, 46, 19–28. [Google Scholar] [CrossRef]
- Keezer, R.; Bailey, M. The structure of liquid selenium from viscosity measurements. Mater. Res. Bull. 1967, 2, 185–192. [Google Scholar] [CrossRef]
- Misawa, M.; Suzuki, K. Structure of Chain Molecule in Liquid Selenium by Time-of-Flight Pulsed Neutron Diffraction. Trans. Jpn. Inst. Met. 1977, 18, 427–434. [Google Scholar] [CrossRef]
- Enderby, J.; Gay, M. Liquid Te and its alloys. J. Non-Cryst. Solids 1980, 35–36, 1269–1275. [Google Scholar] [CrossRef]
- Faivre, G.; Gardissat, J.L. Viscoelastic properties and molecular structure of amorphous selenium. Macromolecules 1986, 19, 1988–1996. [Google Scholar] [CrossRef]
- Menelle, A.; Bellissent, R.; Flank, A.M. A Neutron Scattering Study of Supercooled Liquid Tellurium. Europhys. Lett. (EPL) 1987, 4, 705–708. [Google Scholar] [CrossRef]
- Phillips, W.A.; Buchenau, U.; Nücker, N.; Dianoux, A.J.; Petry, W. Dynamics of glassy and liquid selenium. Phys. Rev. Lett. 1989, 63, 2381–2384. [Google Scholar] [CrossRef]
- Hohl, D.; Jones, R.O. First-principles molecular-dynamics simulation of liquid and amorphous selenium. Phys. Rev. B 1991, 43, 3856–3870. [Google Scholar] [CrossRef]
- Foret, M.; Hehlen, B.; Taillades, G.; Courtens, E.; Vacher, R.; Casalta, H.; Dorner, B. Neutron Brillouin and Umklapp Scattering from Glassy Selenium. Phys. Rev. Lett. 1998, 81, 2100–2103. [Google Scholar] [CrossRef]
- Gopala Rao, R.V.; Venkatesh, R.J. Collective excitations and dynamic structure factor of liquid tellurium. Indian J. Chem. 2000, 39A, 247–252. [Google Scholar]
- Inui, M.; Kajihara, Y.; Hosokawa, S.; Matsuda, K.; Tsuchiya, Y.; Tsutsui, S.; Baron, A.Q. Dynamical sound speed and structural inhomogeneity in liquid Te studied by inelastic x-ray scattering. J. Non-Cryst. Solids X 2019, 1, 100006. [Google Scholar] [CrossRef]
- Boolchand, P.; Feng, X.; Bresser, W. Rigidity transitions in binary Ge–Se glasses and the intermediate phase. J. Non-Cryst. Solids 2001, 293–295, 348–356. [Google Scholar] [CrossRef]
- Rowlands, R.F.; Zeidler, A.; Fischer, H.E.; Salmon, P.S. Structure of the Intermediate Phase Glasses GeSe3 and GeSe4: The Deployment of Neutron Diffraction With Isotope Substitution. Front. Mater. 2019, 6, 133. [Google Scholar] [CrossRef]
- Flores-Ruiz, H.M.; Toledo-Marín, J.Q.; Moukarzel, C.F.; Naumis, G.G. Space-time rigidity and viscoelasticity of glass forming liquids: The case of chalcogenides. J. Non-Cryst. Solids X 2022, 15, 100117. [Google Scholar] [CrossRef]
- Bureau, B.; Boussard-Pledel, C.; Lucas, P.; Zhang, X.; Lucas, J. Forming glasses from Se and Te. Molecules 2009, 14, 4337–4350. [Google Scholar] [CrossRef] [PubMed]
- Cotton, F.; Wilkinson, G.; Murillo, C.; Bochmann, M. Advanced Inorganic Chemistry; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Prewitt, C.T.; Shannon, R.D. Crystal structure of a high-pressure form of B2O3. Acta Crystallogr. Sect. B 1968, 24, 869–874. [Google Scholar] [CrossRef]
- Naumis, G.G. Simple solvable energy-landscape model that shows a thermodynamic phase transition and a glass transition. Phys. Rev. E 2012, 85, 061505. [Google Scholar] [CrossRef]
- Flores-Ruiz, H.M.; Naumis, G.G.; Micoulaut, M. Glass transition and rigidity in the aging linear harmonic oscillator model. J. Non-Cryst. Solids 2020, 540, 120127. [Google Scholar] [CrossRef]
- Huse, D.A.; Fisher, D.S. Residual Energies after Slow Cooling of Disordered Systems. Phys. Rev. Lett. 1986, 57, 2203–2206. [Google Scholar] [CrossRef] [PubMed]
- Weber, M.F.; Frey, E. Master equations and the theory of stochastic path integrals. Rep. Prog. Phys. 2017, 80, 046601. [Google Scholar] [CrossRef]
- Karpen, M.E.; Tobias, D.J.; Brooks, C.L.I. Statistical clustering techniques for the analysis of long molecular dynamics trajectories: Analysis of 2.2-ns trajectories of YPGDV. Biochemistry 1993, 32, 412–420. [Google Scholar] [CrossRef] [PubMed]
- Husic, B.E.; Pande, V.S. Markov State Models: From an Art to a Science. J. Am. Chem. Soc. 2018, 140, 2386–2396. [Google Scholar] [CrossRef] [PubMed]
- Langer, S.A.; Sethna, J.P. Entropy of Glasses. Phys. Rev. Lett. 1988, 61, 570–573. [Google Scholar] [CrossRef] [PubMed]
- Langer, S.A.; Sethna, J.P.; Grannan, E.R. Nonequilibrium entropy and entropy distributions. Phys. Rev. B 1990, 41, 2261–2278. [Google Scholar] [CrossRef] [PubMed]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Waveland Press: Long Grove, IL, USA, 2009. [Google Scholar]
- Huerta, A.; Naumis, G. Relationship between glass transition and rigidity in a binary associative fluid. Phys. Lett. A 2002, 299, 660–665. [Google Scholar] [CrossRef]
- Huerta, A.; Naumis, G.G. Role of Rigidity in the Fluid-Solid Transition. Phys. Rev. Lett. 2003, 90, 145701. [Google Scholar] [CrossRef]
- Huerta, A.; Naumis, G.G.; Wasan, D.T.; Henderson, D.; Trokhymchuk, A. Attraction-driven disorder in a hard-core colloidal monolayer. J. Chem. Phys. 2004, 120, 1506–1510. [Google Scholar] [CrossRef]
- Flores-Ruiz, H.M.; Naumis, G.G. Boson peak as a consequence of rigidity: A perturbation theory approach. Phys. Rev. B 2011, 83, 184204. [Google Scholar] [CrossRef]
- Naumis, G.G. Glass transition phenomenology and flexibility: An approach using the energy landscape formalism. J. Non-Cryst. Solids 2006, 352, 4865–4870. [Google Scholar] [CrossRef]
- Martell, A.; Hancock, R.; Motekaitis, R. Factors affecting stabilities of chelate, macrocyclic and macrobicyclic complexes in solution. Coord. Chem. Rev. 1994, 133, 39–65. [Google Scholar] [CrossRef]
- Broderix, K.; Bhattacharya, K.K.; Cavagna, A.; Zippelius, A.; Giardina, I. Energy landscape of a Lennard-Jones liquid: Statistics of stationary points. Phys. Rev. Lett. 2000, 85, 5360. [Google Scholar] [CrossRef] [PubMed]
- Doliwa, B.; Heuer, A. Energy barriers and activated dynamics in a supercooled lennard-jones liquid. Phys. Rev. E 2003, 67, 031506. [Google Scholar] [CrossRef] [PubMed]
- Naumis, G.G. Electronic properties of 2D materials and its heterostructures: A minimal review. Rev. Mex. Física 2021, 67, 1–22. [Google Scholar]
- Naumis, G.G.; Herrera, S.A.; Poudel, S.P.; Nakamura, H.; Barraza-Lopez, S. Mechanical, electronic, optical, piezoelectric and ferroic properties of strained graphene and other strained monolayers and multilayers: An update. Rep. Prog. Phys. 2023, 87, 016502. [Google Scholar] [CrossRef]
- Boratav, M.; Kerner, R. Relativite; G-Reference, Information and Interdisciplinary Subjects Series; Ellipses: Paris, France, 1991. [Google Scholar]
- Kerner, R. Methodes Classiques de Physique Theorique: Cours et Problemes Resolus; Ellipses: Paris, France, 2014. [Google Scholar]
- Kerner, R. Our Celestial Clockwork: From Ancient Origins to Modern Astronomy of the Solar System; G-Reference, Information and Interdisciplinary Subjects Series; World Scientific Publishing Company Pte Limited: Singapore, 2021. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naumis, G.G. Richard Kerner’s Path Integral Approach Aims to Understand the Self-Organized Matter Agglomeration and Its Translation into the Energy Landscape Kinetics Paradigm. Axioms 2024, 13, 8. https://doi.org/10.3390/axioms13010008
Naumis GG. Richard Kerner’s Path Integral Approach Aims to Understand the Self-Organized Matter Agglomeration and Its Translation into the Energy Landscape Kinetics Paradigm. Axioms. 2024; 13(1):8. https://doi.org/10.3390/axioms13010008
Chicago/Turabian StyleNaumis, Gerardo G. 2024. "Richard Kerner’s Path Integral Approach Aims to Understand the Self-Organized Matter Agglomeration and Its Translation into the Energy Landscape Kinetics Paradigm" Axioms 13, no. 1: 8. https://doi.org/10.3390/axioms13010008
APA StyleNaumis, G. G. (2024). Richard Kerner’s Path Integral Approach Aims to Understand the Self-Organized Matter Agglomeration and Its Translation into the Energy Landscape Kinetics Paradigm. Axioms, 13(1), 8. https://doi.org/10.3390/axioms13010008





