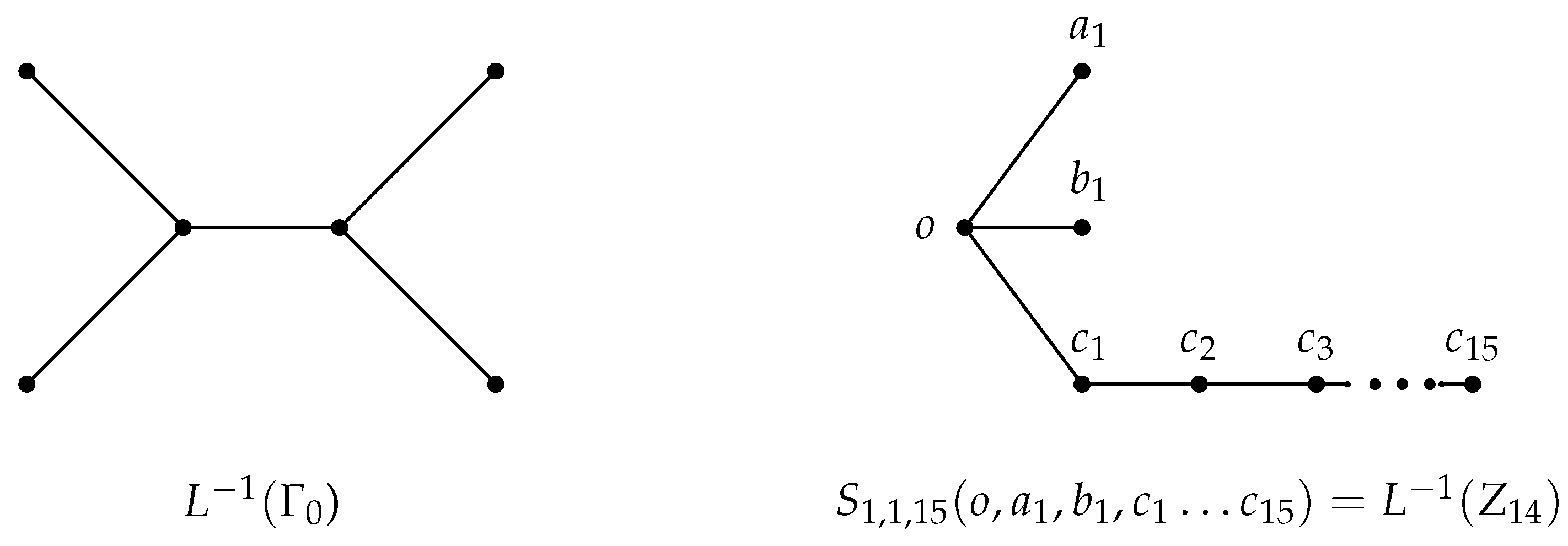Paw-Type Characterization of Hourglass-Free Hamilton-Connected Graphs

Abstract

This paper introduces the forbidden subgraph conditions for Hamilton-connected graphs. If the degree sequence of the graph is $(4,2,2,2,2)$ and it is connected, then it is called hourglass ${\mathrm{\Gamma }}_0$. For integers $i\ge 1$, the graph $Z_i$ is paw, which is obtained by attaching one of the vertices of the triangle to one of the end vertices of a path with a number of edges i. We show that every graph G is Hamilton-connected if G is a ${\mathrm{\Gamma }}_0$-free, $K_{1,3}$-free, $Z_{14}$-free, and a 3-connected graph. Moreover, we give an example to show the sharpness of a paw-type forbidden subgraph in a 3-connected, Hamilton-connected graph. Our focus on the Hamilton-connected problem can be applied to data center networks (DCNs). In the future, we will remove the forbidden subgraph families from our conclusions when building the network to obtain the optimal communication cost. Our result extends the result of Ryjáček and Vrána (Discrete Mathematics 344: 112350, 2021).

1. Introduction

In this paper, for some undefined concepts, please refer to [1].The next part introduces common graph theory symbols and terminology. A graph always refers to a finite undirected simple graph, and is denoted by $G=\left(V\right(G),E(G\left)\right)$; if multiedges (where at least two edges in an induced subgraph have the same pair of end vertices) are allowed, then the graph G is called a multigraph. If a graph G does not have an induced subgraph that is the same as the sets of vertices and edges of F, then it is called an F-free graph. $C_i$ is a cycle with a number of edges and edges i, and $P_i$ is a path with a number of vertices i. We use $N_G\left(v\right)$ to denote the neighborhood of the vertex v in G, and the degree $d\left(G\right)$ of a vertex v denotes the number of elements of $N_G\left(v\right)$. We denote the neighborhood and the degree of a vertex v in G with $N_G\left(v\right)$ and $d_G\left(v\right)$, respectively. For simplicity, we can remove the subscript with G in this paper, e.g., we will write $N\left(x\right)$ as $N_G\left(x\right)$. We use $\mathrm{\Delta }\left(G\right)$ and $\delta \left(G\right)$ to represent the maximum and the minimum degrees of a graph G, respectively.

Given a subgraph H of G, if the vertex set of H is the vertex set of G, then H is a spanning subgraph of G. Given the definition of a spanning subgraph, if G has a spanning cycle, then G is also Hamiltonian; for any pair vertices of G, there exists a spanning path with them as end vertices, and the graph G is Hamilton-connected. It is a difficult, well-studied, and meaningful problem to determine whether a graph is Hamilton-connected. They are central to graph theory. 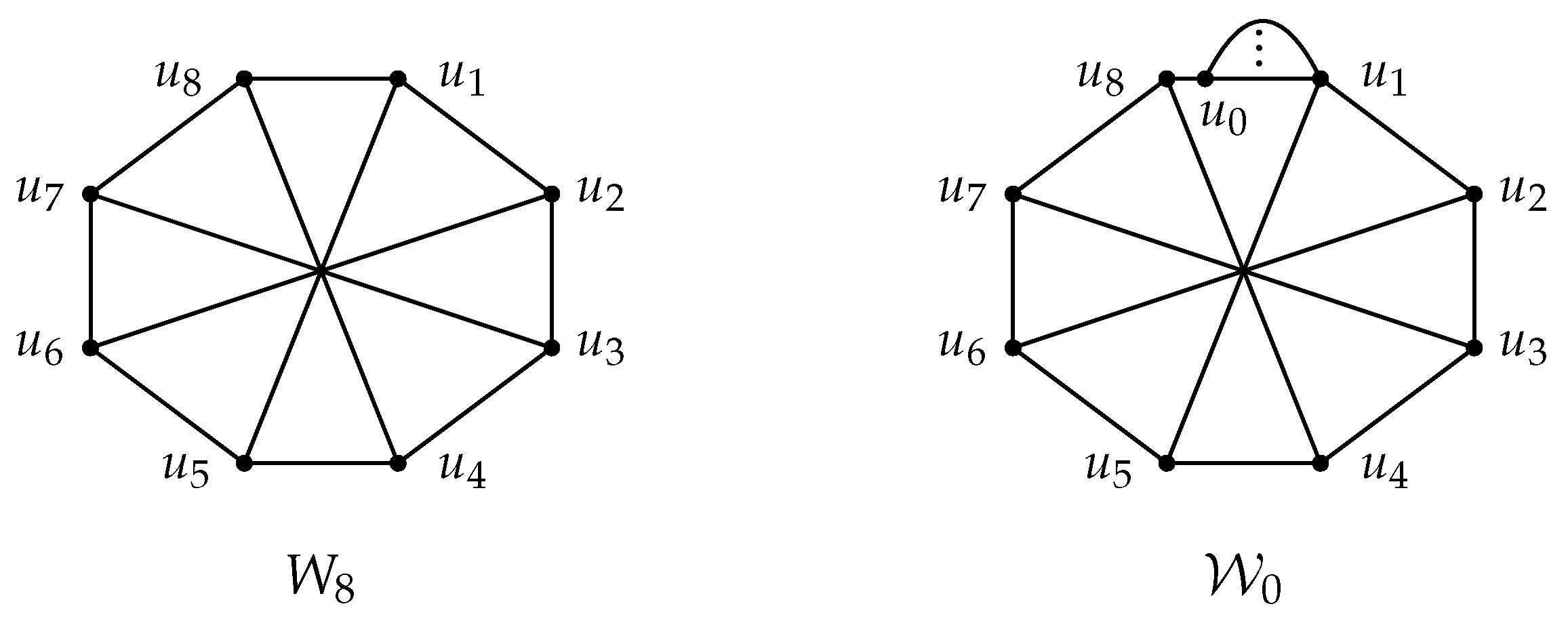Some forbidden subgraphs used in this paper are shown in Figure 1. Theorem 1 lists known results on the Hamilton-connectedness of the forbidden subgraph pairs of the 3-connected graph.

Figure 1. Some forbidden graphs.

Theorem 1.

Let G be $K_{1,3}$-free and a 3-connected graph. Then:

(1) 

(Ryjáček and Vrána [2]) G is Hamilton-connected if G is a $Z_7$-free graph of order $n\ge 21$.

(2) 

(Bian et al. [3]) G is Hamilton-connected if G is a $P_9$-free graph.

(3) 

(Liu et al. [4]) G is Hamilton-connected if G is an $N_{1,2,4}$-free graph.

We are very interested in the problem of forbidden subgraphs and, recently, many scholars have begun to pay attention to the problem of forbidden subgraph triples. Liu and Xiong [5] continued in this direction to prove Theorem 1 (2).

Theorem 2.

(Liu and Xiong [5]) Every ${\mathrm{\Gamma }}_0$-free, $K_{1,3}$-free, $P_{16}$-free, and 3-connected graph G is Hamilton-connected.

Liu and Xiong add a “${\mathrm{\Gamma }}_0$-free” assumption condition in Theorem 2, which allows the results to be substantially strengthened. In this paper, according to the research direction of several researchers, we obtain a strengthened version of Theorem 1 (1), which adds the condition of “${\mathrm{\Gamma }}_0$-free”.

Theorem 3.

Let a graph G be a ${\mathrm{\Gamma }}_0$-free, $K_{1,3}$-free, $Z_{14}$-free, and 3-connected graph; then, it is Hamilton-connected.

In reality, the Hamilton-connected problem can be applied to communication networks where we remove the family of forbidden subgraphs in our conclusions when building the data center network; this is performed to better optimize the network cloud era and data center interconnection. For the application of other graphs, refer to [6].

In the study of any problem, an effective tool is always indispensable, and closure is a very effective mathematical model for dealing with the problem of the $K_{1,3}$-free graph. In Section 2, we introduced tools and some important results for solving the forbidden subgraph problem, and the claw-free graph problem is no exception. Closure is a very effective mathematical model for dealing with forbidden subgraphs, especially claw-free graphs. The proof of Theorem 3 starts with some special edges; we consider their structure in the original graph, use their particularity, classify them, and prove the feasibility of the result one by one. It is deferred to Section 3.

2. Preliminaries

To make it easier to prove our result, we further introduce the following concepts.

Let $S\subseteq V\left(G\right)$, with S as the vertex set of the subgraph and all edges whose end vertices are in S, as the edge set is called the subgraph induced from the vertex set S (or simply induced subgraph), denoted by $G\left[S\right]$.

In Section 2.1, Section 2.2, Section 2.3, we have listed some relevant facts to prove Theorem 3.

2.1. A Line Graph of Multigraph and Its Preimage

A line graph of G is a simple graph; its vertices are all edges of G and the edges e and f of G have a common vertex in G, which is the edge $ef$ of the line graph, denoted as $L\left(G\right)$. If $H=L\left(G\right)$, then the preimage of H is G and $G=L^{-1}\left(H\right)$.

If $G\left[N\right(x\left)\right]$ is a connected graph and is not complete, then the vertex x is eligible; all eligible vertices of G are placed in the set $V_{EL}\left(G\right)$. And if $G\left[N\right(x\left)\right]$ is a complete graph, then x is simplicial. For given a vertex v in G, the graph resulting from adding all edges between two nonadjacent vertices in $N\left(x\right)$ is called local completion $G_x^{\ast }$. Clearly, when G is $K_{1,3}$-free, so is $G_x^{\ast }$.

When H is the preimage of G, The graph $G_x^{\ast }$ obtained by contracting the edge $L^{-1}\left(x\right)$ into a vertex and replacing the created loop with a new pendant edge is a line graph. Some properties of an eligible vertex are introduced in the following.

Lemma 1

(Ryjáček et al. [7]). If G is $K_{1,3}$-free, where the center vertex of every induced $H_0$ of G is an eligible vertex, and $x\in V_{EL}\left(G\right)$, then the center vertex of every induced $H_0$ of $G_x^{\ast }$ is an eligible vertex.

Theorem 4

(Brousek and Ryjáček [8,9]). For $F\in \{Z_i,{\mathrm{\Gamma }}_0\}$ and some vertex $x\in V_{EL}\left(G\right)$, if G is F-free and is also a $K_{1,3}$-free graph, then so is $G_x^{\ast }$.

2.2. SM-Closure

For a given $K_{1,3}$-free graph G, the graph that can be obtained by recursive local completion of all eligible vertices of G is called its closure$cl\left(G\right)$, for as long as possible. If $G=cl\left(G\right)$, then G is closed. The graph $G^M$ constructed on $K_{1,3}$-free graphs is introduced in [10].

1.

If G is not Hamilton-connected, then all eligible vertices are locally completed in turn until the operation cannot proceed or the final graph that can be obtained is Hamilton-connected. This operation produces a series of graphs $G_1,\dots ,G_k$ satisfying:

(1)

G is the starting graph $G_1$;

(2)

$G_{i+1}={\left(G_i\right)}_{x_i}^{\ast }$, where $i=1,\dots ,k-1$, for some eligible vertex $x_i$ of $G_i$;

(3)

For some vertices $a,b$ of $G_k$, $G_k$ does not contain Hamiltonian $(a,b)$-path; and

(4)

${\left(G_k\right)}_x^{\ast }$ is Hamilton-connected with any eligible vertex x of $G_k$, and set $G^M=G_k$.

2.

If G is Hamilton-connected, then we define $G^M$ as its closure.

The final resulting graph $G^M$, obtained after the above multi-step iterative process, is called the $SM$-closure of G. Then, there is a definition of $SM$-closure that if a graph G is an $SM$-closure, then its equivalent is to say that this graph is $SM$-closed.

An $(x,y)$-path is a path with $x,y$ as its end vertices. And $(e,f)$-trail is a trail with $e,f$ as its terminal edges. The interior vertices in a trail T are denoted by the set Int$\left(T\right)$. If an edge e has at least one vertex in vertex set $M\in V\left(G\right)$, then Mdominatese. If all the edges of G are dominated by the trail T, then the closed trail T is called a dominated closed trail (DTC). If all the edges of G are dominated by Int$\left(T\right)$, then $(e,f)$-trail is called an internally dominating $(e,f)$-trail ($(e,f)$-IDT).

The graph G cannot uniquely determine its $SM$-closure. We will use some necessary features in the $SM$-closure as follows.

Theorem 5

(Kužel et al. [10]). Let $G^M$ be one of the $SM$-closures of the $K_{1,3}$-free graph G. Then,

(1) 

$E\left(G\right)\subset E\left(G^M\right)$ and $V\left(G\right)=V\left(G^M\right)$;

(2) 

The fact that G is Hamilton-connected is equivalent to the fact that $G^M$ is Hamilton-connected;

(3) 

The graph obtained by a series of local completions of G at eligible vertices is called $G^M$;

(4) 

Given a graph H, $G^M$ is its line graph, that is, $H=L^{-1}\left(G^M\right)$, satisfying:

(A) 

H is simple graph and is also triangle-free, or;

(B) 

For some edges $e,f$, or H such that H is triangle-free and two edges $e,f$ are the only multiedges in H, there does not exist an $(e,f)$-IDT, or at least one edge of $\{e,f\}$ is in a triangle of H, and H is a simple graph and has at most two triangles, and the triangles have no common edge if H has two triangles.

(5) 

For some vertices $a,b$ of $G^M$, let $G^M$ have no Hamiltonian path and $(a,b)$-path. Then,

(A) 

$E\left(X\right)=\{L_{G^M}^{-1}\left(a\right),L_{G^M}^{-1}\left(b\right)\}$ if $X\in E\left(H\right)$ is a multiedge.

(B) 

$E\left(X\right)\cap \{L_{G^M}^{-1}\left(a\right),L_{G^M}^{-1}\left(b\right)\}\ne Ø$ if $X\in E\left(H\right)$ is a triangle.

Lemma 2

(Ryjáček and Vrána [11]). If G is a line graph of H and an $SM$-closed graph, then the triangle in H has no vertices with vertex degree 2.

Lemma 3

(Ryjáček et al. [7]). If $G^M$ be the $SM$-closure of a $K_{1,3}$-free graph G, and let $G^M$ be a line graph of H, then v is an eligible vertex in $G^M$ and is equivalent to $e=L^{-1}\left(v\right)$ and is a multiedge or a triangle in H.

In the above lemmas, we introduce some results on the $SM$-closed graphs.

2.3. Strongly Spanning Trailable Multigraphs

The edges $e_1,e_2$ in H are replaced by paths $u_1{v}_{e_1}{v}_1$, $u_2{v}_{e_2}{v}_2$, respectively, where $v_{e_1},v_{e_2}$ denote vertices; this type of graph is called multigraph $H(e_1,e_2)$. If any pair of edges $e_1,e_2\in E\left(H\right)$ (possible $e_1=e_2$) has a spanning $(v_{e_1},v_{e_2})$-trail in multigraph H, then H is strongly spanning trailable (abbreviated SST).

Here, Wagner graph $W_8$ and ${\mathcal{W}}_0$ are shown in Figure 2, where edges $w_0{w}_1$ are multiedges. For example, in [12], Wagner graphs are known in the theory of networks-on-chip under the name of Spidergon topology and even implemented as an STNoC software solution. The line graphs of [13,14] strongly-spanning trailable graphs are known to be Hamilton-connected. In the graph G, the edge connectivity and circumference of G are denoted by the symbols ${\kappa }^{\prime }\left(G\right)$ and $c\left(G\right)$, respectively. In the following proof of Theorem 3, we also need to know the following results about SST.

Figure 2. The graphs $W_8$ and ${\mathcal{W}}_0$.

Theorem 6

(Liu et al. [4]).

(1) 

Let H be a 3-edge-connected multigraph of an order not greater than 9. Then, H is SST, except for the members of $W_8\cup {\mathcal{W}}_0$.

(2) 

Let H be a 2-connected, 3-edge-connected multigraph where its circumference is at most 8. Then, H is SST, except for the members of $W_8$.

If removing a(n) vertex(edge)-cut X from G results in at least two nontrivial components of G, then X is called essential; if there does not exist an essential vertex(edge)-cut X (the number of elements in X is less than k) in multigraph G, then G is called essentially k(-edge)-connected.

Given a multigraph H that is essentially 3-edge-connected, the resulting graph from the multigraph H replacing the path $xyz$ for each vertex y of degree 2 with an edge $xz$ and deleting all the pendant vertices is called the core $H_0$ of H. In multigraph H, $P{I}_H\left(F\right)$ denotes the preimage of any subgraph F of $H_0$, referring to the maximal subgraph of H obtained under the core operation. Next, we list some well-known results.

Theorem 7

(Shao, [15]). If H is a multigraph that is essentially 3-edge-connected, then the core $H_0$ of H has the following results:

(1) 

$H_0$ is uniquely defined and ${\kappa }^{\prime }\left(H_0\right)\ge 3$;

(2) 

All edges of H are dominated by $V\left(H_0\right)$;

(3) 

$L\left(H\right)$ is Hamilton-connected if $H_0$ is SST;

(4) 

H has a DCT if $H_0$ has a spanning-closed trail.

3. Proof of Theorem 3

Let $X_1$ and $X_2$ be subsets of G such that $X_1\subseteq X_2$; if G is $X_1$-free, then the further G is also $X_2$-free. The shortest path in G connecting two vertices $u_1$ and $u_2$ is defined by $P_G[u_1,u_2]$, where $P_G(u_1,u_2)=P_G[u_1,u_2]\backslash \{u_1,u_2\}$, and we assume $P_G[u_1,u_2]$ and $P_G(u_1,u_2)$ to be oriented from $u_1$ to $u_2$. If a subpath with the smaller number of vertices among the two subpaths with end vertices $u_1$ and $u_2$ in cycle C has l internal vertices and $u_1{u}_2\in V\left(C\right)$, then $u_1{u}_2$ is a l-chord. An equivalent condition for a graph F is a subgraph of H is that the line graph of F is an induced subgraph of a line graph of G.

We use $S_{1,1,i}(o,a_1,b_1,c_1{c}_2\dots c_i)$ (for simply $S_{1,1,i}$ or $S(o,a_1,b_1,c_1{c}_2\dots c_i)$) in the resulting graph obtained by $K_{1,3}$, subdividing its one edge $i-1$ times, where the labels of these vertices are given in Figure 3, and the vertex o will be called the center vertex.

Figure 3. The graphs $L^{-1}\left({\mathrm{\Gamma }}_0\right)$ and $L^{-1}\left(Z_{14}\right)$.

Proof of Theorem 3.

Given a graph H, and letting G be its line graph, we suppose G is 3-connected and is not Hamilton-connected and let $H_0$ be the core of H. By Theorems 4 and 5 (3) and Lemma 1, we suppose that G is $SM$-closed, the center vertex of every induced $H_0$ in G is an eligible vertex. Suppose that the condition “G is a ${\mathrm{\Gamma }}_0$-free, $K_{1,3}$-free and $Z_{14}$-free graph” of Theorem 3 is true. It suffices to show that H must contain a subgraph $S_{1,1,15}$. By Theorem 7 (4), $H_0$ is not SST. By Theorem 7 (1),

$$\begin{array}{c}\hfill {\kappa }^{\prime }\left(H_0\right)\ge 3.\end{array}$$

Set

$$\begin{array}{c}\hfill \mathcal{E}=\{e\in E(H):e\mathrm{is}\mathrm{an}\mathrm{edge}\mathrm{of}\mathrm{multiedges}\mathrm{or}\mathrm{triangle}\}.\end{array}$$

By Theorem 5 (4), either H is triangle-free and contains a multiedge, or H has no more than two triangles, and is a simple graph. Then, if H contains no more than two triangles, then $\left|\mathcal{E}\right|\in \{0,3,6\}$ and if H has a pair of multiedges, then $\left|\mathcal{E}\right|\in \{0,2\}$. By Lemma 3, for an edge e in $E\left(H_0\right)\backslash \mathcal{E}$, the vertex $L\left(e\right)$ does not correspond to the eligible vertex in G, there will exist e, which is not the center edge of a subgraph $L^{-1}\left({\mathrm{\Gamma }}_0\right)$. Thus, we can get that

$$\begin{array}{c}\hfill \mathrm{subdividing}\mathrm{each}\mathrm{edge}\mathrm{of}E\left(H_0\right)\backslash \mathcal{E}\mathrm{by}\mathrm{a}\mathrm{vertex}\mathrm{of}2\mathrm{degrees}\mathrm{of}H.\end{array}$$

(1)

Claim 1.

$\left|V\right(H_0\left)\right|\ge 10$ and $c\left(H_0\right)\ge 9$.

Proof. 

Assume, to the contrary, that $c\left(H_0\right)\le 8$ or $\left|V\right(H_0\left)\right|\le 9$. We know for a fact that the equivalent condition for every graph to be essentially 3-edge connected is that its line graph is 3-connected. By Theorem 6, $H_0\in \left\{W_8\right\}\cup {\mathcal{W}}_0$. Then $H_0$ has a 8-cycle $u_1{u}_2\dots u_8{u}_1$ or 9-cycle $u_1{u}_2\dots u_8{u}_0{u}_1$ with $\{u_1{u}_5,u_2{u}_6,u_3{u}_7$, $u_4{u}_8\}\subseteq E\left(H_0\right)$ and $u_0{u}_1$ is a multiedge if there exists (see Figure 2).

By (1), for some integers $1\le m<n\le 8$, subdividing each edge $u_m{u}_n$ of $H_0$ through a given vertex $u_{m,n}$ of degree 2, we can easily get that H contains subgraphs,

$$\begin{array}{cc}\hfill & S_{1,1,15}\subseteq S(u_1,u_{1,8},u_{1,5},u_{1,2}{u}_2{u}_{2,3}{u}_3{u}_{3,4}{u}_4{u}_{4,5}{u}_5{u}_{5,6}{u}_6{u}_{6,7}{u}_7{u}_{7,8}{u}_8{u}_{4,8}),\hfill \\ \hfill & S_{1,1,15}\subseteq S(u_1,u_0,u_{1,5},u_{1,2}{u}_2{u}_{2,3}{u}_3{u}_{3,4}{u}_4{u}_{4,5}{u}_5{u}_{5,6}{u}_6{u}_{6,7}{u}_7{u}_{7,8}{u}_8{u}_{4,8}),\hfill \end{array}$$

a contradiction. □

By Claim 1, we have that $\left|V\right(H_0\left)\right|\ge 10$ and $c\left(H_0\right)\ge 9$. Next, using the following notation:

• $C_{c\left(H_0\right)}=v_1{v}_2\dots v_{c\left(H_0\right)}{v}_1$ always denotes a longest cycle of $H_0$;
• $C:=P{I}_H\left(C_{c\left(H_0\right)}\right)$;
• $m^{{}^{\prime }}:=|\mathcal{E}\cap E\left(C_{c\left(H_0\right)}\right)|$;
• ${\mathcal{D}}_{H_0}:=V\left(H_0\right)\setminus V\left(C_{c\left(H_0\right)}\right)$;
• Let $E_{H_0}^1$ be the set of all edges between $C_{c\left(H_0\right)}$ and ${\mathcal{D}}_{H_0}$. Then, $|E_{H_0}^1|\ge 3$.

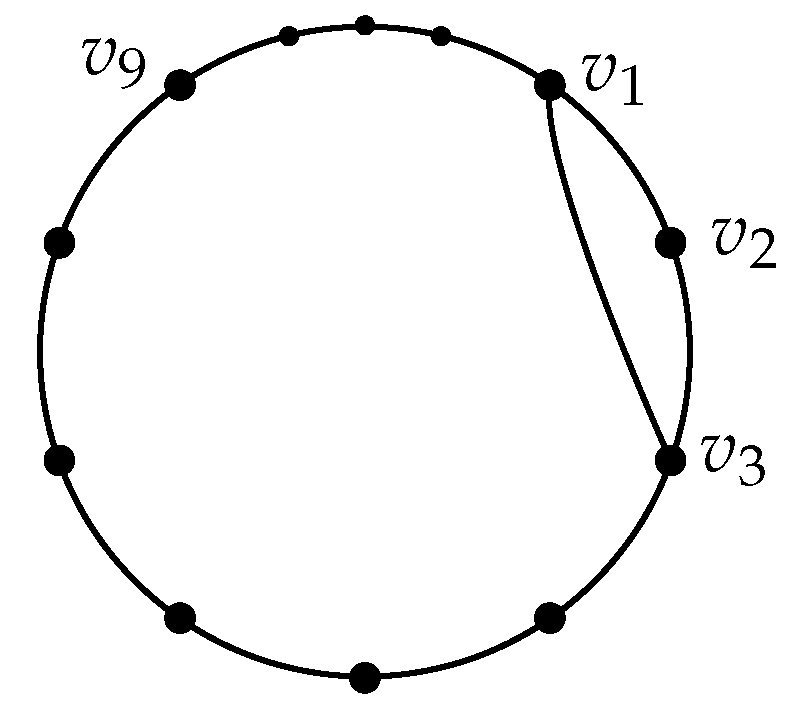
Claim 2.

For $x,y\in V\left(C_{c\left(H_0\right)}\right)$, let $P_{H_0\setminus C_{c\left(H_0\right)}}(x,y)$ be an $(x,y)$-path, where $E(P_{H_0\setminus C_{c(H_0)}}(x,y))\cap E\left(C_{c(H_0)}\right)=Ø$, and let $P_{C_{c\left(H_0\right)}}(x,y)$ be a shorter $(x,y)$-path with their vertices in $C_{c\left(H_0\right)}$. Then, $|P_{C_{c\left(H_0\right)}}(x,y)|\ge |P_{H_0\setminus C_{c\left(H_0\right)}}(x,y)|$ (see Figure 4).

Figure 4. The graph of Claim 2.

Proof. 

Suppose Claim 2 is false, $|P_{C_{c\left(H_0\right)}}(x^{\prime },y^{\prime })|<|P_{H_0\setminus C_{c\left(H_0\right)}}(x^{\prime },y^{\prime })|$ for some $x^{\prime },y^{\prime }$ satisfying the hypothesis Claim 2. Then, $C^{\prime }=H_0\left[\right(E(C_{c\left(H_0\right)})\cup E(P_{H_0\setminus C_{c\left(H_0\right)}}(x^{\prime },y^{\prime }))\setminus E(P_{C_{c\left(H_0\right)}}(x^{\prime },y^{\prime })]$ is a cycle with no less than $c\left(H_0\right)+1$ vertices, which contradicts the choice of $C_{c\left(H_0\right)}$. □

By (1) and the choice of $C_{c\left(H_0\right)}$, the longest cycle C of H is obtained by subdividing $c\left(H_0\right)-m^{\prime }$ edges of the cycle $C_{c\left(H_0\right)}$ by $c\left(H_0\right)-m^{\prime }$ vertices of degree 2, respectively. Then, $\left|V\left(C\right)\right|=2c\left(H_0\right)-m^{\prime }$. For integers $1\le r<s\le c\left(H_0\right)$, we always use vertex $v_{r,s}$ to subdivide edge $v_r{v}_s$.

Claim 3.

$V\left(\mathcal{E}\right)\cap V\left(C_{c\left(H_0\right)}\right)\ne Ø$.

Proof. 

Suppose $V\left(\mathcal{E}\right)\cap V\left(C_{c\left(H_0\right)}\right)=Ø$ by contradiction. By (1), $\left|V\left(C\right)\right|=2c\left(H_0\right)\ge 18$. Since ${\kappa }^{\prime }\left(H_0\right)⩾3$, $d\left(v_2\right)⩾3$. Moreover, in addition to vertices $v_1$ and $v_3$, there is at least one vertex v that satisfies $v{v}_2\in E\left(H_0\right)$. Then, H contains a subgraph,

$$\begin{array}{c}\hfill S_{1,1,15}\subseteq S(v_2,P_H(v_2,v],v_{2,3},v_{1,2}{v}_1\dots v_{3,4}),\end{array}$$

a contradiction. □

Claim 4.

H has no multiedges.

Proof. 

Assume, to the contrary, that H contains multiegdes. By Theorem 5 (4) (B), H contains at most two multiedges and no other multiedge. Let $\{e_1^{\prime },e_2^{\prime }\}\subseteq E\left(H\right)$ be a pair of multiedges, with $u_1,u_2$ as their end-vertices.

Suppose first that $|V\left(H_0\right)|=c\left(H_0\right)$. In this case, $u_1,u_2\in V\left(C_{c\left(H_0\right)}\right)$, so we may assume $u_1=v_i$ and $u_2=v_{i+1}$. Then $T=v_i{e}_1^{\prime }{v}_{i+1}\dots v_i{e}_2^{\prime }{v}_{i+1}$ is an $(e_1^{\prime },e_2^{\prime })$-IDT in H, contradicting Theorem 5 (5) (A). Now suppose that $|V\left(H_0\right)|>c\left(H_0\right)$.

Firstly, suppose that $m^{{}^{\prime }}=2$, but then $c\left(H_0\right)=2$, contradicting $c\left(H_0\right)\ge 9$.

Then, suppose that $m^{{}^{\prime }}=0$. By Claim 3, $\{u_1,u_2\}\cap V\left(C_{c\left(H_0\right)}\right)\ne Ø$. We suppose that $|\{u_1,u_2\}\cap V\left(C_{c\left(H_0\right)}\right)|=2$ and $u_1{u}_2\notin E\left(C_{c\left(H_0\right)}\right)$. Since H is triangle-free, $e_1^{\prime }$ is a l-chord of $C_{c\left(H_0\right)}$ with $l\ge 2$, we get that ${\mathrm{\Gamma }}_0\subseteq L^{-1}\left(H[N_H\left(u_1\right)\cup N_H\left(u_2\right)]\right)$, a contradiction. Then, suppose that $\{u_1,u_2\}\cap V\left(C_{c\left(H_0\right)}\right)=\left\{u_1\right\}=\left\{v_1\right\}$ and $u_2$ is not in $C_{c\left(H_0\right)}$, by (1), $\left|V\left(C\right)\right|=2c\left(H_0\right)\ge 18$. Then, H contains a subgraph,

$$\begin{array}{c}\hfill S_{1,1,15}\subseteq S(v_1,u_2,v_{1,c\left(H_0\right)},v_{1,2}{v}_2\dots v_{8,9}),\end{array}$$

a contradiction.

Finally, suppose that $m^{\prime }=1$, say $e_1^{\prime }=v_i{v}_{i+1}\in E\left(C_{c\left(H_0\right)}\right)$. By (1), $\left|V\left(C\right)\right|=2c\left(H_0\right)-1\ge 17$. Moreover, there is at least one edge in $E_{H_0}^1$ with $v_j\in V\left(C_{c\left(H_0\right)}\right)$ as its end-vertex should be a subdivided $x_0$ of degree 2 in H. Then, H contains a subgraph,

$$\begin{array}{c}\hfill S_{1,1,15}\subseteq H[V\left(C\right)\cup \left\{x_0\right\}],\end{array}$$

with its center vertex $v_j$, a contradiction.

Thus H has no multiedges. □

By Claims 3 and 4, we obtain that H is a simple graph.

Claim 5.

H contains at least one triangle and is a simple graph.

Proof. 

Assume that H is triangle-free and is a simple graph by contradiction. Since ${\kappa }^{\prime }\left(H_0\right)\ge 3$, the degree of $v_i\in V\left(C_{c\left(H_0\right)}\right)$ is at least 3. By (1), $\left|V\left(C\right)\right|=2c\left(H_0\right)\ge 18$. Then, H contains a subgraph,

$$\begin{array}{c}\hfill S_{1,1,15}\subseteq S(v_1,v_{1,c\left(H_0\right)},x^{\prime },v_{1,2}{v}_2\dots v_{8,9})\mathrm{with}{x}^{\prime }\in N_H\left(v_1\right)\setminus \{v_{1,2},v_{1,c\left(H_0\right)}\},\end{array}$$

a contradiction. □

By Claim 5, H contains either one triangle or two triangles. By Lemma 2, each vertex of the triangle in H has a degree of at least 3. The definition of $H_0$ shows that the edges of the triangle in H are also the edges of the triangle in $H_0$.

Claim 6.

Let $u_1{u}_2{u}_3{u}_1$ be a triangle of $H_0$. Then,

(1)

$d_{H_0}\left(u_i\right)=3$ with $i\in \{1,2,3\}$.

(2)

$m^{\prime }\in \{2,4\}$ if $H_0$ contains at least one triangle.

Proof. 

(1) Suppose that, for any $i\in \{1,2,3\}$, $d_{H_0}\left(u_i\right)\ne 3$ by contradiction. And since ${\kappa }^{\prime }\left(H_0\right)\ge 3$, $d_{H_0}\left(u_1\right)\ge 4$ and $d_{H_0}\left(u_3\right)\ge 4$, then ${\mathrm{\Gamma }}_0\subseteq L^{-1}\left(H[N_H\left(u_1\right)\cup N_H\left(u_3\right)]\right)$, a contradiction.

(2) We only need to prove that $m^{\prime }\notin \{0,1,3,5,6\}$. Firstly, suppose that $m^{\prime }=3$, but then $c\left(H_0\right)=3$, contradicting $c\left(H_0\right)\ge 9$. Therefore, $m^{\prime }\ne 3$, and we can easily get that $m^{\prime }\notin \{3,5,6\}$.

Then, suppose that $m^{\prime }=0$. By Claim 3, $\{u_1,u_2,u_3\}\cap V\left(C_{c\left(H_0\right)}\right)\ne Ø$. Then $d_{H_0}\left(u_i\right)\ge 4$ with $i\in \{1,2,3\}$, which contradicts $d_{H_0}\left(u_i\right)=3$, a contradiction. Therefore, $m^{\prime }\ne 0$.

Finally, suppose that $m^{\prime }=1$, let $u_1{u}_2\in E\left(C_{c\left(H_0\right)}\right)$. By Claim 2, $u_3\in V\left(C_{c\left(H_0\right)}\right)$. Then $d_{H_0}\left(u_3\right)\ge 4$, a contradiction. Therefore, $m^{\prime }\ne 1$. □

Next, we consider the case of $m^{\prime }=2$. For convenience, suppose that the vertices of a triangle in $C_{c\left(H_0\right)}$ are denoted by $v_1,v_2$ and $v_3$ (see Figure 5). By Claim 6 (1), we have that $d_{H_0}\left(v_1\right)=d_{H_0}\left(v_2\right)=d_{H_0}\left(v_3\right)=3$. Then, $E_{H_0}^1\cap \mathcal{E}=Ø$. By (1), $\left|V\left(C\right)\right|=2c\left(H_0\right)-2\ge 16$. Since ${\kappa }^{\prime }\left(H_0\right)\ge 3$, suppose that $\{v_{3,4},v_{4,5},x^{\prime }\}\subseteq N_H\left(v_4\right)$ and $\{v_{4,5},v_{5,6},y^{\prime }\}\subseteq N_H\left(v_5\right)$ such that $x^{\prime }\ne y^{\prime }$. Then, H contains a subgraph,

$$\begin{array}{c}\hfill S_{1,1,15}\subseteq S(v_4,v_{4,5},x^{\prime },v_{3,4}{v}_3\dots v_{5,6}{v}_5{y}^{\prime }),\end{array}$$

a contradiction. Therefore, $m^{\prime }\ne 2$.

Figure 5. A cycle C of circumference at least 9 in $H_0$ and $m^{\prime }=2$.

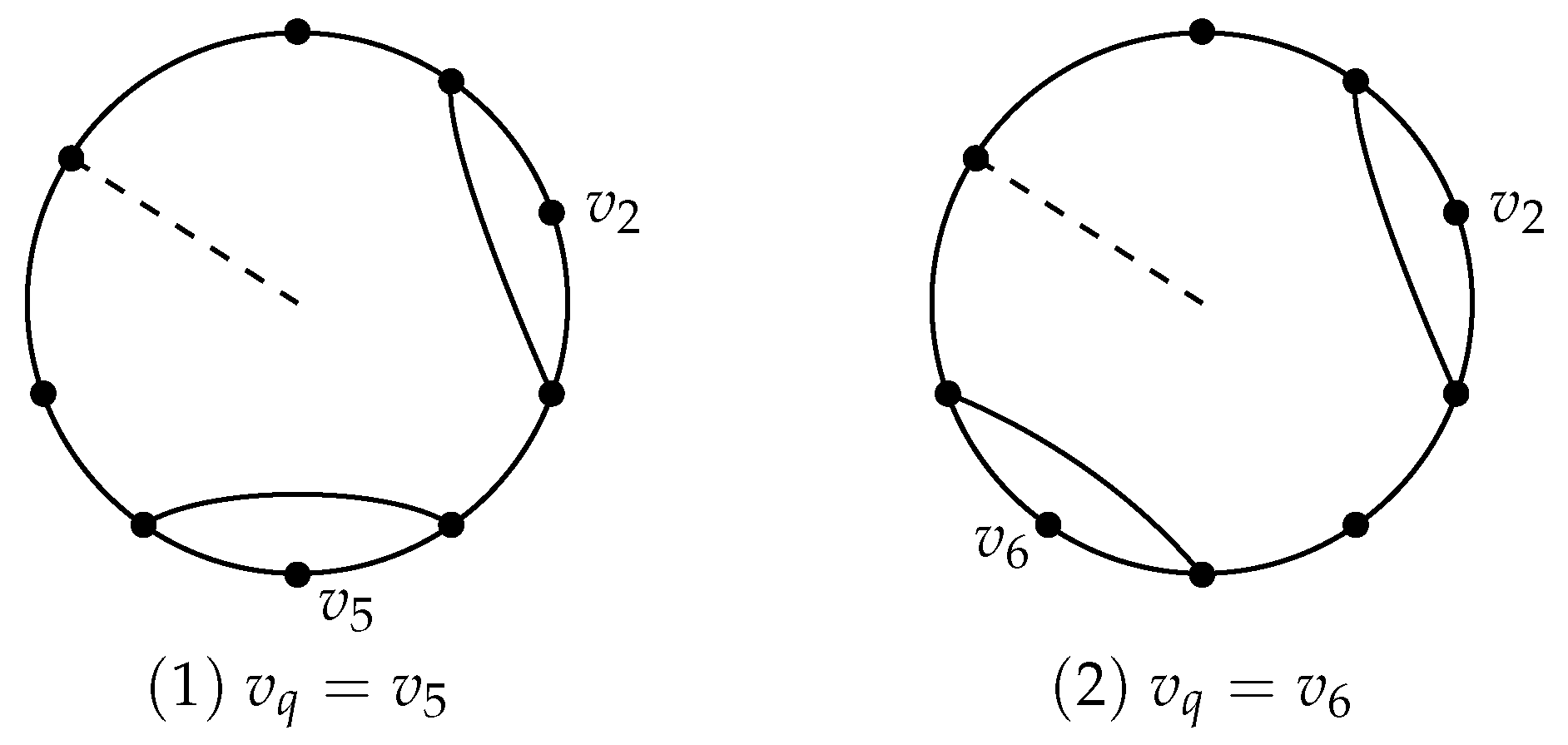
Choose a shortest path $P_{H\setminus C}(v_r,v_s)$ in H with their vertices not in C and $v_r,v_s\in V\left(C\right)$. Then, we consider the case of $m^{\prime }=4$. In the following proof of Theorem 3, we denote two triangles by $v_1{v}_2{v}_3{v}_1$ and $v_{q-1}{v}_q{v}_{q+1}{v}_{q-1}$, by symmetry, $q\in \{5,6,\dots ,\lceil \frac{c\left(H_0\right)+3}{2}\rceil \}$. By Claim 6 (1), we have that $d_{H_0}\left(v_1\right)=d_{H_0}\left(v_2\right)=d_{H_0}\left(v_3\right)=3$ and $d_{H_0}\left(v_{q-1}\right)=d_{H_0}\left(v_q\right)=d_{H_0}\left(v_{q-1}\right)=3$.

Claim 7.

Suppose that $m^{\prime }=4$ and $\left|V\right(H_0\left)\right|\ge 10$. Then, $c\left(H_0\right)\ne 9$.

Proof. 

Assume, to the contrary, that $c\left(H_0\right)=9$ (say $C_{c\left(H_0\right)}=v_1{v}_2\dots v_9{v}_1$). Then $v_q\in \{v_5,v_6\}$, and $\left|V\right({\mathcal{D}}_{H_0}\left)\right|\ge 1$ and $E_{H_0}^1\cap \mathcal{E}=Ø$. By (1), $\left|V\left(C\right)\right|=2c\left(H_0\right)-2\ge 14$.

Case 1.

$v_q=v_5$ (see Figure 6(1)).

Figure 6. The cycle C with a circumference of 9 in $H_0$ and $m^{\prime }=4$.

Suppose that $N_{H_0}\left(v_8\right)\cap V\left({\mathcal{D}}_{H_0}\right)\ne Ø$. Then, there exists a path $P_{H\setminus C}(v_r,v_8)$ in H for any possibility $v_r\in \{v_2,v_5,v_8\}$ and H contains a subgraph

$$\begin{array}{cc}\hfill & S_{1,1,15}\subseteq S(v_9,v_{8,9},x,v_{1,9}{v}_1\dots v_8{P}_{H\setminus C}(v_8,v_2))\mathrm{with}x\in N_H\left(v_9\right)\setminus \{v_{8,9},v_{1,9}\},\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_9,v_{8,9},x,v_{1,9}{v}_1\dots v_8{P}_{H\setminus C}(v_8,v_5))\mathrm{with}x\in N_H\left(v_9\right)\setminus \{v_{8,9},v_{1,9}\}\mathrm{or}\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_1,v_{1,9},v_2,v_3{v}_{3,4}\dots v_8{P}_{H\setminus C}(v_8,v_8)),\hfill \end{array}$$

a contradiction. Hence, $v_8$ is an end vertex of the chord in $C_{c\left(H_0\right)}$, that is,

$$\begin{array}{c}\hfill v_2{v}_8\in E\left(H_0\right)\mathrm{or}{v}_5{v}_8\in E\left(H_0\right).\end{array}$$

(2)

Suppose that $N_{H_0}\left(v_9\right)\cap V\left({\mathcal{D}}_{H_0}\right)\ne Ø$. Then, there exists a path $P_{H\setminus C}(v_r,v_9)$ in H for any possibility $v_r\in \{v_2,v_5,v_7,v_9\}$ and H contain a subgraph,

$$\begin{array}{cc}\hfill & S_{1,1,15}\subseteq S(v_9,v_{1,9},v_{8,9},P_{H\setminus C}(v_9,v_2)v_2{v}_1{v}_3{v}_{3,4}\dots v_8{v}_{5,8}),\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_9,v_{1,9},v_{8,9},P_{H\setminus C}(v_9,v_5)v_5{v}_4{v}_{3,4}{v}_3{v}_1{v}_2{v}_{2,8}{v}_8{v}_{7,8}\dots v_6),\hfill \\ & S_{1,1,15}\subseteq S(v_8,v_{2,8}\left(v_{5,8}\right),v_{7,8},v_{8,9}{P}_{H\setminus C}(v_9,v_7)v_7{v}_{6,7}\dots v_{1,9})\mathrm{or}\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_1,v_{1,9},v_2,v_3{v}_{3,4}\dots v_9{P}_{H\setminus C}(v_9,v_9)),\hfill \end{array}$$

a contradiction. Hence, $v_9$ is an end vertex of the chord in $C_{c\left(H_0\right)}$ ($v_5{v}_9\in E\left(H_0\right)$). Similarly, $v_2{v}_7\in E\left(H_0\right)$. Hence, by Claim 6 (1), $v_8{v}_2\notin E\left(H_0\right)$ and $v_8{v}_5\notin E\left(H_0\right)$, contradicting (2). This proves Case 1.

Case 2.

$v_q=v_6$ (see Figure 6 (2)).

Suppose that $N_{H_0}\left(v_8\right)\cap V\left({\mathcal{D}}_{H_0}\right)\ne Ø$. Then there exists a path $P_{H\setminus C}(v_r,v_8)$ in H for any possibility $v_r\in \{v_2,v_4,v_6,v_8\}$, and H contains a subgraph,

$$\begin{array}{cc}\hfill & S_{1,1,15}\subseteq S(v_8,v_{8,9},v_{7,8},P_{H\setminus C}(v_8,v_6)v_6{v}_7{v}_5\dots v_9{x}_1),\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_9,v_{8,9},x_1,v_{1,9}{v}_1\dots v_4{P}_{H\setminus C}(v_4,v_8)v_8{v}_{7,8}\dots v_{4,5}),\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_9,v_{1,9},x_1,v_{8,9}{v}_8{P}_{H\setminus C}(v_8,v_2)v_2{v}_1{v}_3\dots v_{7,8})\mathrm{with}{x}_1\in N_H\left(v_9\right)\setminus \{v_{1,9},v_{8,9}\}\mathrm{or}\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_1,v_{1,9},v_2,v_3{v}_{3,4}\dots v_8{P}_{H\setminus C}(v_8,v_8)),\hfill \end{array}$$

a contradiction. Hence, $v_8$ is an end vertex of the chord in $C_{c\left(H_0\right)}$. Similarly, $v_9$ is an end vertex of the chord in $C_{c\left(H_0\right)}$. Next, suppose that $N_{H_0}\left(v_2\right)\cap V\left({\mathcal{D}}_{H_0}\right)\ne Ø$. Then there exists a path $P_{H\setminus C}(v_2,v_s)$ in H for any possibility $v_s\in \{v_2,v_4,v_6\}$, and H contains a subgraph,

$$\begin{array}{cc}\hfill & S_{1,1,15}\subseteq S(v_5,v_{4,5},v_6,v_7{v}_{7,8}\dots v_2{P}_{H\setminus C}(v_2,v_2)),\hfill \\ \hfill & S_{1,1,15}\subseteq S(v_4,v_{3,4},v_{4,5},P_{H\setminus C}(v_4,v_2)v_2{v}_3{v}_1\dots v_7{v}_5{v}_6{x}_2)\mathrm{with}{x}_2\in N_H\left(v_6\right)\setminus \{v_5,v_7\}\mathrm{or}\hfill \\ & S_{1,1,15}\subseteq S(v_4,v_{3,4},x_3,v_{4,5}{v}_5{v}_6{P}_{H\setminus C}(v_6,v_2)v_2{v}_3{v}_1\dots v_7)\mathrm{with}{x}_3\in N_H\left(v_4\right)\setminus \{v_{3,4},v_{4,5}\},\hfill \end{array}$$

a contradiction. Hence, $v_2$ is an end vertex of the chord in $C_{c\left(H_0\right)}$. Similarly, $v_6$ is an end vertex of the chord in $C_{c\left(H_0\right)}$. Then we have that $v_4$ is an end vertex of the chord in $C_{c\left(H_0\right)}$, Then, we have that $v_4$ lies on a chord of $C_{c\left(H_0\right)}$, otherwise H contains a subgraph $S_{1,1,15}\subseteq S(v_3,v_{3,4},v_2,v_1{v}_{1,9}\dots v_4{P}_{H\setminus C}(v_4$, $v_4\left)\right)$, a contradiction. Therefore, $\left|V\right(H_0\left)\right|=9$, a contradiction. □

By Claims 1 and 4–7, we can get that $c\left(H_0\right)\ge 10$ and $\left|V\right(H_0\left)\right|\ge 10$ and $m^{\prime }=4$, where $E_{H_0}^1\cap \mathcal{E}=Ø$. By (1), $\left|V\left(C\right)\right|=2c\left(H_0\right)-2\ge 16$. Since ${\kappa }^{\prime }\left(H_0\right)\ge 3$, $v_r\in N_{H_0}\left(v_2\right)\setminus \{v_1,v_3\}$. We can get that H contains a subgraph such that there are two edges $v_{c\left(H_0\right)}{x}_1,v_2{x}_2\in$$E\left(H_0\right)$ with $x_1,x_2\in V\left(C_{c\left(H_0\right)}\right)$ and $x_1\ne x_2$. By (1), $v_{c\left(H_0\right)}{x}_1,v_2{x}_2$ should be subdivided by two vertex of degree 2, say $x_1^{\prime },x_2^{\prime }\in V\left(H\right)$, respectively. We have that H contains a subgraph,

$$\begin{array}{c}\hfill S_{1,1,15}\subseteq S(v_{c\left(H_0\right)},v_{1,c\left(H_0\right)},x_1^{\prime },v_{c\left(H_0\right)-1,c\left(H_0\right)}{v}_{c\left(H_0\right)-1}\dots v_3{v}_1{v}_2{x}_2^{\prime }),\end{array}$$

a contradiction. This proves Theorem 3. □

4. Conclusions

Remark 1.

As shown in Figure 7, we give a family of graphs $\mathcal{G}$. Then, any graph $G\in \mathcal{G}$ is a 3-connected, ${\mathrm{\Gamma }}_0$-free, and $K_{1,3}$-free graph, and G is not Hamilton-connected. It is easy to see that the graphs in Figure 7 contain a subgraph $Z_{14}$, but they are $Z_{15}$-free. Thus, these examples of these graphs presented in Figure 7 show that our result of Theorem 3 “$Z_{14}$-free” is sharp.

Figure 7. The family of graphs $\mathcal{G}$.

Remark 2.

In this paper, we are mainly concerned with the effect of an induced hourglass on existing results. We list the results to show how to effect a graph to be Hamilton-connected, when we add the $H_0$-free condition to 3-connected, $Z_i$-free, and $K_{1,3}$-free graphs. Our results show that the subscript 14 ($Z_{2i}$) is almost double the original one 7 ($Z_i$).

Remark 3.

In Figure 7, we can easily find that these graphs are also $N_{2i+1,2j,2k}$-free, $N_{2i,2j+1,2k}$-free, and $N_{2i,2j,2k+1}$-free with integers $i+j+k=7$. Also, we guess Theorem 1 (3) that adds the condition “${\mathrm{\Gamma }}_0$-free”, and the following problem may occur with the forbidden subgraphs condition of the Net-type.

Question 1.

Let G be a 3-connected graph. If G is a ${\mathrm{\Gamma }}_0$-free, $K_{1,3}$-free, and $N_{2,4,8}$-free graph, then G is Hamilton-connected.

5. Discussion

The Hamilton-connected problem has many applications in computer science, communication networks, and coding theory, and they can help create a hierarchical organization; this organization does not contain forbidden subgraphs in our results, which determines optimal communication cost, fastest computer response time, or the shortest distance of a computer network. This paper discussed the sufficient conditions for the existence of Hamilton-connection. By combining the paw-type stability with Hamilton-connected graphs, we aim to build a suitable mathematical model and apply it to reality, in order to lay a foundation and theoretical support.