An Improved Sparrow Search Algorithm for Global Optimization with Customization-Based Mechanism
Abstract
1. Introduction
- By utilizing cube mapping to initialize the population, the inherent randomness of chaos and the irregular orderliness are exploited to make the initial population state dispersion more reasonable.
- By introducing the adaptive spiral predation mechanism to change the predation mechanism of followers, better exploitation is accomplished.
- For position updating of sparrows with different search abilities in the whole population, a novel customized learning strategy is proposed. The combination of this strategy makes full use of essential positional information and achieves a balance between exploration and exploitation.
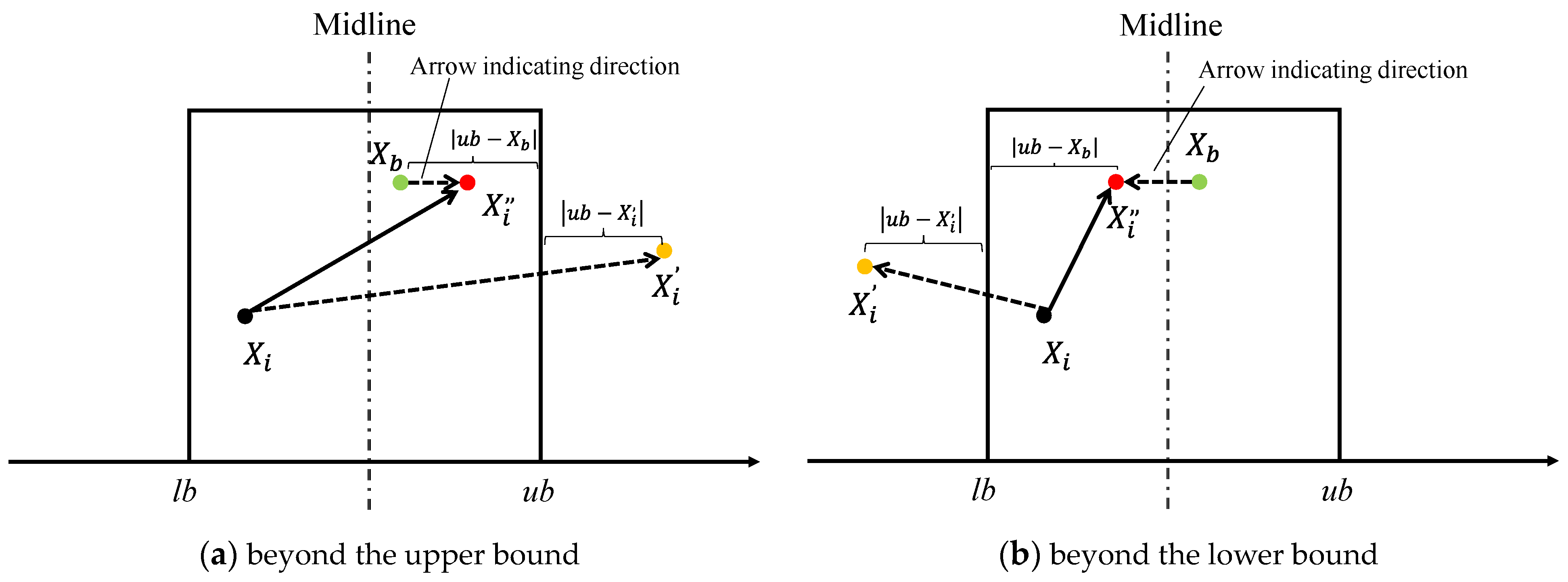
- In view of the different abilities and division of labor of the three roles, a novel boundary processing mechanism is proposed to improve the rationality of boundary processing, which effectively avoids the accumulation of the population on the boundary, thus increasing the population diversity.
- The feasibility of the CLSSA in engineering optimization is verified with three classical discrete engineering optimization problems.
2. Sparrow Search Algorithm
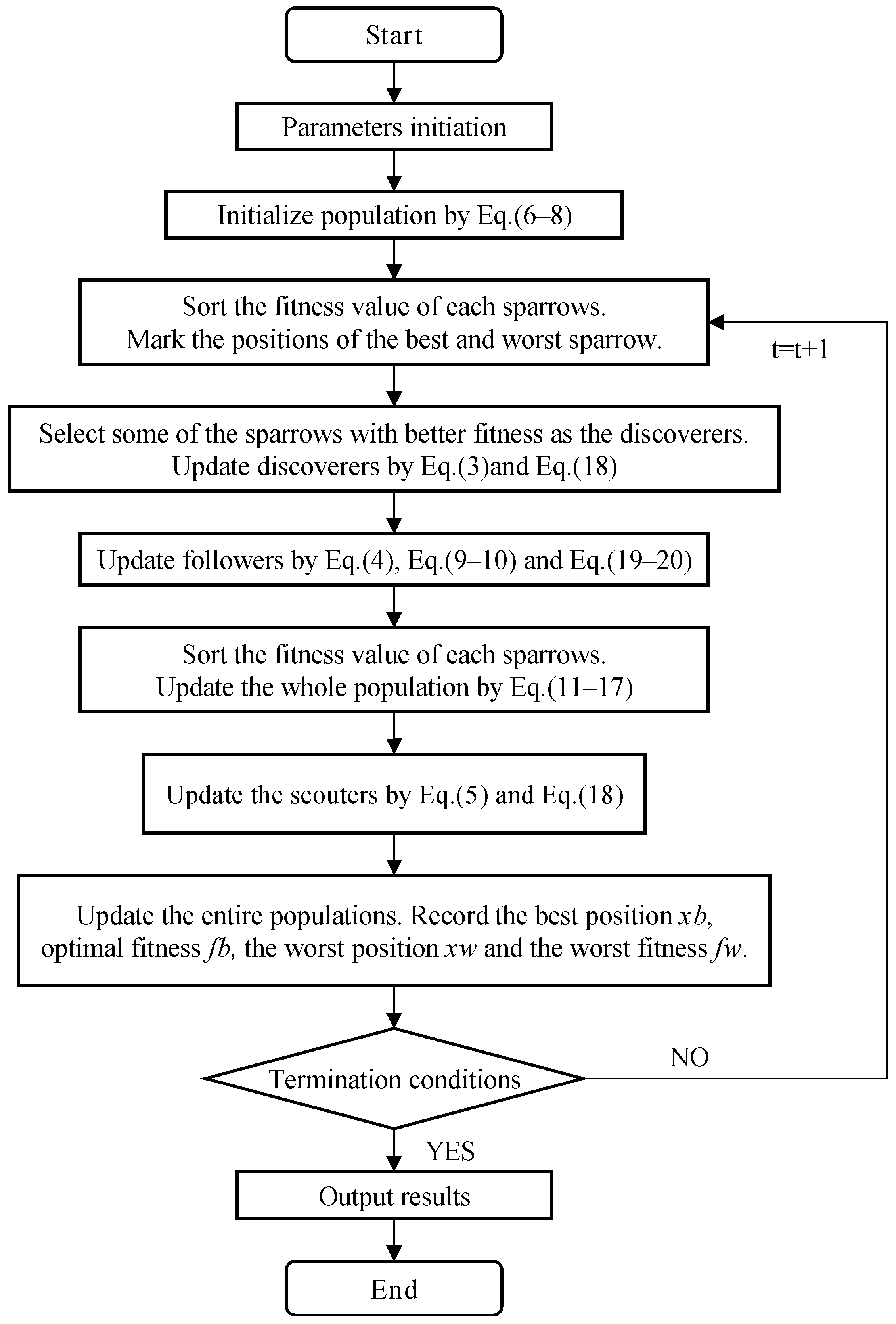
3. CLSSA
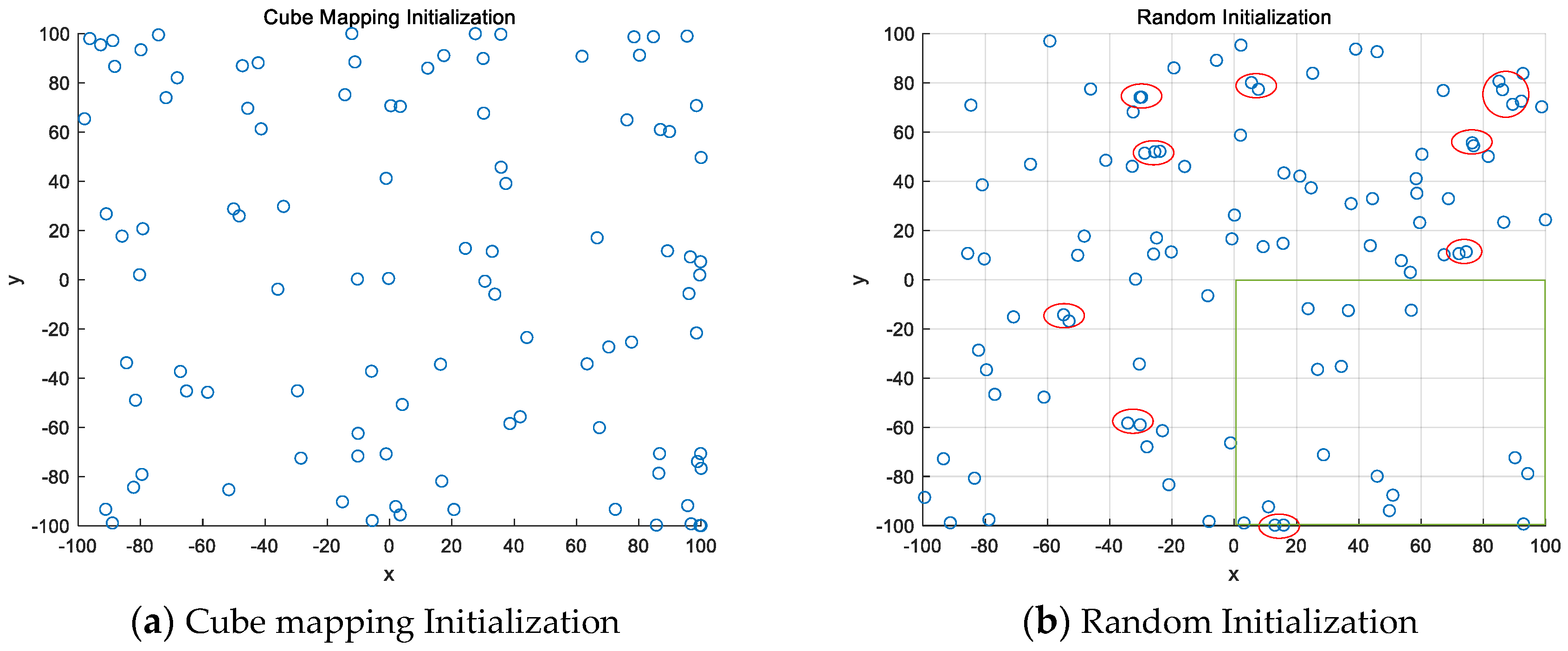
3.1. Cube Chaos Mapping Initialization Population
- A d-dimensional vector is randomly generated, the process is denoted as , each dimension satisfies , and y is used to denote the first individual position.
- A new d-dimensional vector is generated using Equation (6).
- The values of Equation (6) are brought into Equation (7) to obtain the values of each dimension of the individual.where and denote the lower and upper bounds of the search interval, respectively.
- Individual positions were obtained as:
3.2. Adaptive Spiral Predation
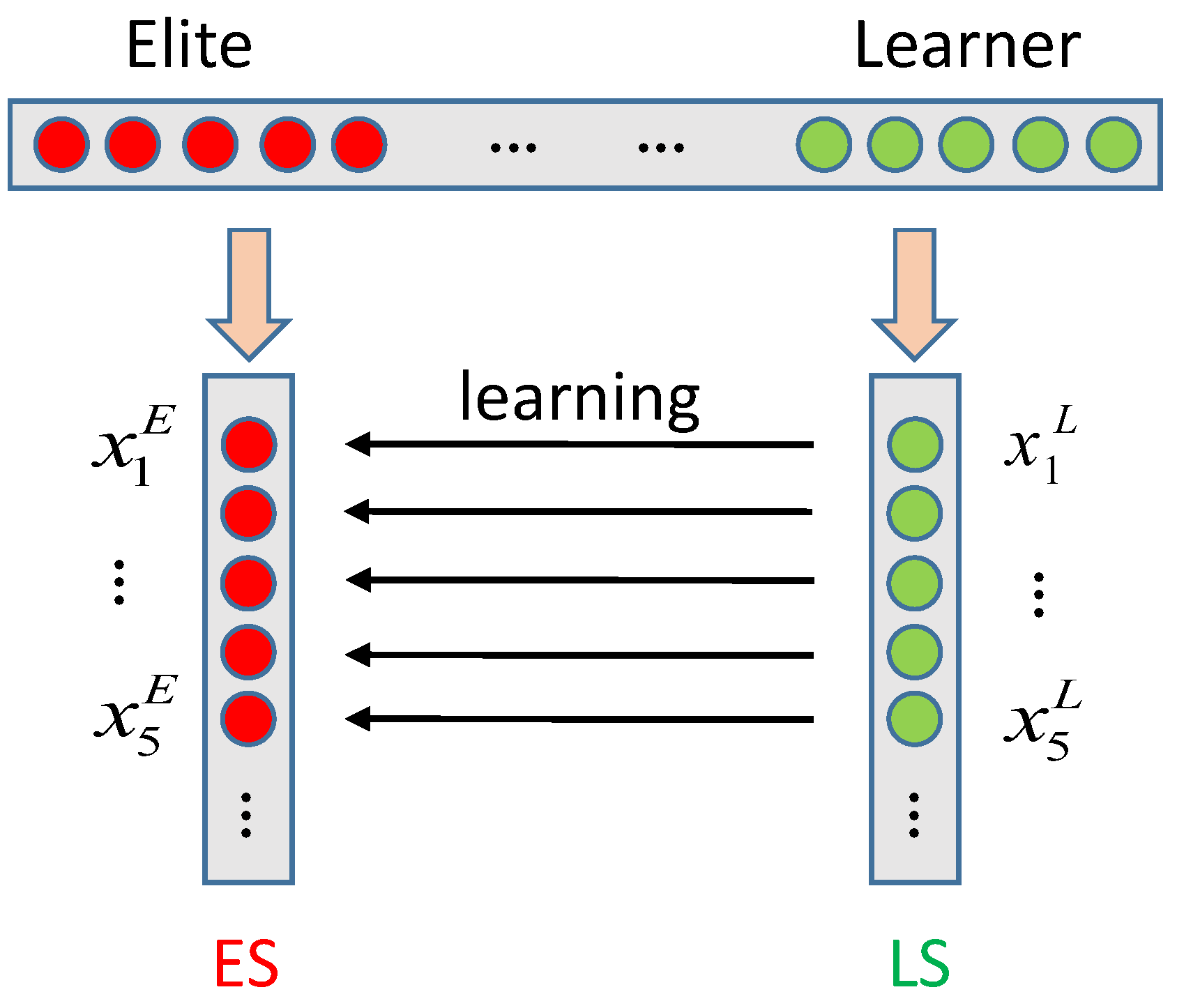
3.3. Customized Learning
3.3.1. Elite–Learner Paired Learning
3.3.2. Selected Learning
3.3.3. Multi-Example Learning
3.4. Customized Learning
3.5. CLSSA Flow
3.6. Time Complexity Analysis
4. Performance Analysis
4.1. Initialization Strategy Selection Test
4.2. Comparison of Contributions by Strategy
4.3. Benchmark Function Test
4.3.1. Comparison with the SSA
4.3.2. Comparison with Classical Algorithms and Variants
4.4. CEC2017
5. Application to Engineering Optimization Problems
5.1. Gear Train Design Problem
5.2. Pressure Vessel Design Problem
5.3. Corrugated Bulkhead Design
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rao, S.S. Optimization Theory and Application, 2nd ed.; Halsted Press: New Delhi, India, 1984; ISBN 978-0470274835. [Google Scholar]
- Dem’yanov, V.F.; Vasil’ev, V. Nondifferentiable Optimization; Springer: New York, NY, USA, 2012; ISBN 978-1461382706. [Google Scholar]
- Akyol, S.; Alatas, B. Plant intelligence based metaheuristic optimization algorithms. Artif. Intell. Rev. 2017, 47, 417–462. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Shi, Y. Brain storm optimization algorithm. In Proceedings of the Advances in Swarm Intelligence: Second International Conference, ICSI 2011, Chongqing, China, 12–15 June 2011; pp. 303–309. [Google Scholar]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mora-Gutiérrez, R.A.; Ramírez-Rodríguez, J.; Rincón-García, E.A. An optimization algorithm inspired by musical composition. Artif. Intell. Rev. 2014, 41, 301–315. [Google Scholar] [CrossRef]
- Alatas, B. ACROA: Artificial chemical reaction optimization algorithm for global optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Elaziz, M.A.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Cai, Z.; Gao, S.; Yang, X.; Yang, G.; Cheng, S.; Shi, Y. Alternate search pattern-based brain storm optimization. Knowl.-Based Syst. 2022, 238, 107896. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, H. Wireless Sensor Network Deployment of 3D Surface Based on Enhanced Grey Wolf Optimizer. IEEE Access 2020, 8, 57229–57251. [Google Scholar] [CrossRef]
- Liu, S.J.; Yang, Y.; Zhou, Y.Q. A Swarm Intelligence Algorithm—Lion Swarm Optimization. Pattern Recognit. Artif. Intell. 2018, 31, 431–441. [Google Scholar]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Lv, X.; Mu, X.D.; Zhang, J.; Zhen, W. Chaos Sparrow Search Optimization Algorithm. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 1712–1720. [Google Scholar]
- Wang, Z.; Huang, X.; Zhu, D. A Multistrategy-Integrated Learning Sparrow Search Algorithm and Optimization of Engineering Problems. Comput. Intell. Neurosci. 2022, 2022, 2475460. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Yang, P.; Zhu, D.; Zheng, W.; Wu, F. Improved Sparrow Search Algorithm Based on Iterative Local Search. Comput. Intell. Neurosci. 2021, 2021, 6860503. [Google Scholar] [CrossRef]
- Gad, A.G.; Sallam, K.M.; Chakrabortty, R.K.; Ryan, M.J. An improved binary sparrow search algorithm for feature selection in data classification. Neural Comput. Appl. 2022, 34, 15705–15752. [Google Scholar] [CrossRef]
- Yang, P.; Yan, S.; Zhu, D.; Wang, J.; Wu, F.; Yan, Z.; Yan, S. Improved sparrow algorithm based on game predatory mechanism and suicide mechanism. Comput. Intell. Neurosci. 2022, 2022, 4925416. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, H.; Zhang, C.; Hua, Y.; Zhang, W.; Chen, Q.; Gu, G.; Sui, X. Wavefront-shaping focusing based on a modified sparrow search algorithm. Optik 2021, 244, 167516. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.; Yang, H. Research on economic optimization of microgrid cluster based on chaos sparrow search algorithm. Comput. Intell. Neurosci. 2021, 2021, 5556780. [Google Scholar] [CrossRef]
- Zhu, Y.; Yousefi, N. Optimal parameter identification of PEMFC stacks using Adaptive Sparrow Search Algorithm. Int. J. Hydrog. Energy 2021, 46, 9541–9552. [Google Scholar] [CrossRef]
- Tian, H.; Wang, K.; Yu, B.; Jermsittiparsert, K.; Song, C. Hybrid improved Sparrow Search Algorithm and sequential quadratic programming for solving the cost minimization of a hybrid photovoltaic, diesel generator, and battery energy storage system. Energy Sources Part A Recovery Util. Environ. Eff. 2021, in press. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, A.; Han, Y.; Nan, J.; Li, K. Fast stochastic configuration network based on an improved sparrow search algorithm for fire flame recognition. Knowl.-Based Syst. 2022, 245, 108626. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, Y.; Guo, B.; Luo, X.; Peng, Q.; Jin, Z. A hybrid sparrow search algorithm of the hyperparameter optimization in deep learning. Mathematics 2022, 10, 3019. [Google Scholar]
- Zhang, X.; Xiao, F.; Tong, X.; Yun, J.; Liu, Y.; Sun, Y.; Tao, B.; Kong, J.; Xu, M.; Chen, B. Time optimal trajectory planning based on improved sparrow search algorithm. Front. Bioeng. Biotechnol. 2022, 10, 852408. [Google Scholar]
- Chen, G.; Lin, D.; Chen, F.; Chen, X. Image segmentation based on logistic regression sparrow algorithm. J. Beijing Univ. Aeronaut. Astronaut. 2021, 1, 14. [Google Scholar]
- Lei, Y.; De, G.; Fei, L. Improved sparrow search algorithm based DV-Hop localization in WSN. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 2240–2244. [Google Scholar]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, in press. [Google Scholar] [CrossRef]
- Ouyang, C.; Qiu, Y.; Zhu, D. Adaptive spiral flying sparrow search algorithm. Sci. Program. 2021, 2021, 6505253. [Google Scholar]
- Alatas, B. Chaotic bee colony algorithms for global numerical optimization. Expert Syst. Appl. 2010, 37, 5682–5687. [Google Scholar]
- Gao, S.; Yu, Y.; Wang, Y.; Wang, J.; Cheng, J.; Zhou, M. Chaotic local search-based differential evolution algorithms for optimization. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3954–3967. [Google Scholar]
- Gui, C.Z. Application of Chaotic Sequences in Optimization Theory. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2006. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Wang, H.; Wu, Z.; Rahnamayan, S.; Liu, Y.; Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 2011, 181, 4699–4714. [Google Scholar]
- Cheng, R.; Jin, Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. Cybern. 2014, 45, 191–204. [Google Scholar] [CrossRef]
- Ouyang, C.; Zhu, D.; Qiu, Y. Lens learning sparrow search algorithm. Math. Probl. Eng. 2021, 2021, 9935090. [Google Scholar] [CrossRef]
- Ouyang, C.; Zhu, D.; Wang, F. A learning sparrow search algorithm. Comput. Intell. Neurosci. 2021, 2021, 3946958. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Lin, Q. Three-learning strategy particle swarm algorithm for global optimization problems. Inf. Sci. 2022, 593, 289–313. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; Yu, F.; Wu, H.; Wei, B.; Zhang, Y.-L.; Zhan, Z.-H. Triple archives particle swarm optimization. IEEE Trans. Cybern. 2019, 50, 4862–4875. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Peng, L.; Zhang, H.; Yang, B.; Chen, Z. Ranking-based biased learning swarm optimizer for large-scale optimization. Inf. Sci. 2019, 493, 120–137. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar]
- Ziyu, T.; Dingxue, Z. A modified particle swarm optimization with an adaptive acceleration coefficient. In Proceedings of the 2009 Asia-Pacific Conference on Information Processing, Wuhan, China, 28–29 November 2009; pp. 330–332. [Google Scholar]
- Mirjalili, S.; Lewis, A.; Sadiq, A.S. Autonomous particles groups for particle swarm optimization. Arab. J. Sci. Eng. 2014, 39, 4683–4697. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Wang, Z.D.; Wang, J.B.; Li, D.H. Study on WSN optimization coverage of an enhanced sparrow search algorithm. Chin. J. Sens. Actuators 2021, 34, 818–828. [Google Scholar]
- Bingol, H.; Alatas, B. Chaos based optics inspired optimization algorithms as global solution search approach. Chaos Solitons Fractals 2020, 141, 110434. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical Report; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Tang, A.; Zhou, H.; Han, T.; Xie, L. A chaos sparrow search algorithm with logarithmic spiral and adaptive step for engineering problems. Comput. Model. Eng. Sci. 2022, 130, 331–364. [Google Scholar] [CrossRef]
- Peng, H.; Zhu, W.; Deng, C.; Wu, Z. Enhancing firefly algorithm with courtship learning. Inf. Sci. 2021, 543, 18–42. [Google Scholar] [CrossRef]
- Bayzidi, H.; Talatahari, S.; Saraee, M.; Lamarche, C.P. Social network search for solving engineering optimization problems. Comput. Intell. Neurosci. 2021, 2021, 8548639. [Google Scholar] [CrossRef] [PubMed]
- Sandgren, E. Nonlinear integer and discrete programming in mechanical design optimization. J. Mech. Des. 1990, 111, 223–229. [Google Scholar] [CrossRef]
- Yadav, A.; Kumar, N. Artificial electric field algorithm for engineering optimization problems. Expert Syst. Appl. 2020, 149, 113308. [Google Scholar]
- Ravindran, A.; Reklaitis, G.V.; Ragsdell, K.M. Engineering Optimization: Methods and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 978-0471558149. [Google Scholar]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.A.; Abualigah, L.; Oliva, D.; Algamal, Z.Y.; Anter, A.M.; Ali Ibrahim, R.; Ghoniem, R.M.; Abd Elaziz, M. Boosting arithmetic optimization algorithm with genetic algorithm operators for feature selection: Case study on cox proportional hazards model. Mathematics 2021, 9, 2321. [Google Scholar] [CrossRef]
- Anter, A.M.; Hassenian, A.E.; Oliva, D. An improved fast fuzzy c-means using crow search optimization algorithm for crop identification in agricultural. Expert Syst. Appl. 2019, 118, 340–354. [Google Scholar] [CrossRef]



| SSA | Tent | Logistic | ICMIC | Cube | |
| Avg | 2.76 × 10−15 | 3.06 × 10−15 | 3.08 × 10−15 | 2.51 × 10−15 | 2.45 × 10−15 |
| Std | 8.25 × 10−15 | 9.25 × 10−15 | 8.36 × 10−15 | 7.66 × 10−15 | 5.23 × 10−15 |
| Best | 6.20 × 10−21 | 1.93 × 10−20 | 1.27 × 10−20 | 9.89 × 10−21 | 1.44 × 10−21 |
| Generalized Penalized Function No. 01 | |||||
| SSA | Tent | Logistic | ICMIC | Cube | |
| Avg | 1.743 | 2.314 | 1.926 | 1.887 | 1.34 |
| Std | 2.339 | 3.235 | 2.555 | 2.455 | 1.275 |
| Best | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| De Jong Function N.5 | |||||
| Function | Index | Avg | Std | Best | Function | Index | Avg | Std | Best |
|---|---|---|---|---|---|---|---|---|---|
| F1 | SSA | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | F2 | SSA | 4.36 × 10−192 | 0.00 × 10+00 | 0.00 × 10+00 |
| ISSA-1 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-1 | 1.76 × 10−201 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-2 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-2 | 3.26 × 10−193 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-3 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-3 | 1.59 × 10−199 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-4 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-4 | 2.73 × 10−194 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-5 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-5 | 1.73 × 10−214 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-6 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-6 | 2.85 × 10−204 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-7 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-7 | 4.68 × 10−202 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-8 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-8 | 1.06 × 10−216 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| CLSSA | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | CLSSA | 8.83 × 10−229 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| F3 | SSA | 6.96 × 10−279 | 0.00 × 10+00 | 0.00 × 10+00 | F4 | SSA | 2.55 × 10−199 | 0.00 × 10+00 | 0.00 × 10+00 |
| ISSA-1 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-1 | 3.86 × 10−188 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-2 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-2 | 4.14 × 10−222 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-3 | 3.46 × 10−271 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-3 | 1.09 × 10−255 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-4 | 2.39 × 10−271 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-4 | 1.34 × 10−261 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-5 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-5 | 1.19 × 10−194 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-6 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-6 | 1.07 × 10−244 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-7 | 6.69 × 10−302 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-7 | 5.73 × 10−213 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-8 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ISSA-8 | 3.96 × 10−195 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| CLSSA | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | CLSSA | 2.18 × 10−270 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| F5 | SSA | 1.08 × 10−05 | 2.54 × 10−05 | 9.67 × 10−11 | F6 | SSA | 3.42 × 10−10 | 1.65 × 10−09 | 1.81 × 10−13 |
| ISSA-1 | 2.11 × 10−05 | 6.85 × 10−05 | 2.01 × 10−09 | ISSA-1 | 1.80 × 10−10 | 3.22 × 10−10 | 1.89 × 10−13 | ||
| ISSA-2 | 1.02 × 10−08 | 1.98 × 10−08 | 8.86 × 10−11 | ISSA-2 | 2.70 × 10−10 | 5.71 × 10−10 | 1.25 × 10−13 | ||
| ISSA-3 | 4.81 × 10−06 | 8.17 × 10−06 | 5.42 × 10−09 | ISSA-3 | 3.46 × 10−10 | 8.45 × 10−10 | 2.78 × 10−14 | ||
| ISSA-4 | 9.23 × 10−06 | 1.72 × 10−05 | 1.67 × 10−10 | ISSA-4 | 1.25 × 10−10 | 2.66 × 10−10 | 5.06 × 10−13 | ||
| ISSA-5 | 7.98 × 10−09 | 2.03 × 10−08 | 4.32 × 10−11 | ISSA-5 | 1.57 × 10−10 | 3.42 × 10−10 | 1.27 × 10−13 | ||
| ISSA-6 | 1.32 × 10−05 | 2.83 × 10−05 | 1.92 × 10−08 | ISSA-6 | 7.67 × 10−11 | 1.49 × 10−10 | 5.35 × 10−14 | ||
| ISSA-7 | 1.16 × 10−08 | 2.42 × 10−08 | 3.19 × 10−11 | ISSA-7 | 1.03 × 10−10 | 2.15 × 10−10 | 2.98 × 10−13 | ||
| ISSA-8 | 1.61 × 10−08 | 3.30 × 10−08 | 3.09 × 10−11 | ISSA-8 | 1.89 × 10−10 | 5.93 × 10−10 | 3.73 × 10−13 | ||
| CLSSA | 2.19 × 10−08 | 4.01 × 10−08 | 3.06 × 10−14 | CLSSA | 3.26 × 10−10 | 4.01 × 10−10 | 4.51 × 10−14 | ||
| F7 | SSA | 1.11 × 10−04 | 9.95 × 10−05 | 4.54 × 10−06 | F9 | SSA | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 |
| ISSA-1 | 1.84 × 10−04 | 1.45 × 10−04 | 1.39 × 10−05 | ISSA-1 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-2 | 1.91 × 10−04 | 1.42 × 10−04 | 7.01 × 10−06 | ISSA-2 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-3 | 1.49 × 10−04 | 1.05 × 10−04 | 2.49 × 10−06 | ISSA-3 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-4 | 1.48 × 10−04 | 1.50 × 10−04 | 2.79 × 10−06 | ISSA-4 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-5 | 1.94 × 10−04 | 1.76 × 10−04 | 4.38 × 10−06 | ISSA-5 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-6 | 1.89 × 10−04 | 1.30 × 10−04 | 9.56 × 10−07 | ISSA-6 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-7 | 1.25 × 10−04 | 1.01 × 10−04 | 1.17 × 10−05 | ISSA-7 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-8 | 1.55 × 10−04 | 1.51 × 10−04 | 8.79 × 10−07 | ISSA-8 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| CLSSA | 1.13 × 10−04 | 7.15 × 10−05 | 2.06 × 10−06 | CLSSA | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| F10 | SSA | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | F11 | SSA | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 |
| ISSA-1 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-1 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-2 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-2 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-3 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-3 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-4 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-4 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-5 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-5 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-6 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-6 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-7 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-7 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| ISSA-8 | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | ISSA-8 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| CLSSA | 8.88 × 10−16 | 9.86 × 10−32 | 8.88 × 10−16 | CLSSA | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | ||
| F12 | SSA | 9.46 × 10−12 | 1.54 × 10−11 | 6.06 × 10−17 | F13 | SSA | 7.39 × 10−11 | 1.40 × 10−10 | 4.12 × 10−15 |
| ISSA-1 | 4.63 × 10−12 | 8.62 × 10−12 | 5.91 × 10−17 | ISSA-1 | 1.40 × 10−10 | 2.75 × 10−10 | 4.32 × 10−14 | ||
| ISSA-2 | 3.26 × 10−16 | 8.90 × 10−16 | 8.66 × 10−20 | ISSA-2 | 1.18 × 10−13 | 2.84 × 10−13 | 1.93 × 10−17 | ||
| ISSA-3 | 7.74 × 10−12 | 2.07 × 10−11 | 1.01 × 10−15 | ISSA-3 | 1.67 × 10−10 | 4.15 × 10−10 | 3.01 × 10−14 | ||
| ISSA-4 | 3.38 × 10−12 | 8.46 × 10−12 | 3.18 × 10−16 | ISSA-4 | 1.18 × 10−10 | 3.43 × 10−10 | 1.12 × 10−13 | ||
| ISSA-5 | 4.72 × 10−16 | 1.55 × 10−15 | 4.63 × 10−21 | ISSA-5 | 1.04 × 10−13 | 2.74 × 10−13 | 2.97 × 10−19 | ||
| ISSA-6 | 2.58 × 10−12 | 6.57 × 10−12 | 4.28 × 10−17 | ISSA-6 | 1.67 × 10−10 | 6.42 × 10−10 | 1.33 × 10−13 | ||
| ISSA-7 | 3.85 × 10−16 | 1.25 × 10−15 | 4.79 × 10−20 | ISSA-7 | 7.81 × 10−14 | 1.72 × 10−13 | 4.74 × 10−18 | ||
| ISSA-8 | 4.85 × 10−16 | 9.86 × 10−16 | 1.43 × 10−19 | ISSA-8 | 1.34 × 10−13 | 2.64 × 10−13 | 5.54 × 10−18 | ||
| CLSSA | 8.78 × 10−16 | 1.23 × 10−15 | 2.59 × 10−21 | CLSSA | 7.29 × 10−13 | 1.56 × 10−12 | 7.04 × 10−20 | ||
| F14 | SSA | 4 | 4.47 × 10+00 | 1 | F15 | SSA | 3.08 × 10−04 | 1.02 × 10−09 | 3.08 × 10−04 |
| ISSA-1 | 3 | 4.04 × 10+00 | 1 | ISSA-1 | 3.07 × 10−04 | 2.94 × 10−09 | 3.07 × 10−04 | ||
| ISSA-2 | 4 | 4.57 × 10+00 | 1 | ISSA-2 | 3.07 × 10−04 | 1.44 × 10−09 | 3.07 × 10−04 | ||
| ISSA-3 | 3 | 3.92 × 10+00 | 1 | ISSA-3 | 3.43 × 10−04 | 1.89 × 10−04 | 3.07 × 10−04 | ||
| ISSA-4 | 2 | 1.83 × 10+00 | 1 | ISSA-4 | 3.07 × 10−04 | 4.80 × 10−08 | 3.07 × 10−04 | ||
| ISSA-5 | 3 | 4.53 × 10+00 | 1 | ISSA-5 | 3.08 × 10−04 | 7.95 × 10−07 | 3.07 × 10−04 | ||
| ISSA-6 | 2 | 2.92 × 10+00 | 1 | ISSA-6 | 3.07 × 10−04 | 7.17 × 10−10 | 3.07 × 10−04 | ||
| ISSA-7 | 2 | 2.92 × 10+00 | 1 | ISSA-7 | 3.07 × 10−04 | 1.54 × 10−08 | 3.07 × 10−04 | ||
| ISSA-8 | 2 | 3.32 × 10+00 | 1 | ISSA-8 | 3.38 × 10−04 | 1.64 × 10−04 | 3.07 × 10−04 | ||
| CLSSA | 1 | 1.78 × 10+00 | 1 | CLSSA | 3.08 × 10−04 | 2.45 × 10−07 | 3.08 × 10−04 | ||
| F16 | SSA | −1.032 | 0.00 × 10+00 | −1.032 | F18 | SSA | 3.9 | 4.85 × 10+00 | 3 |
| ISSA-1 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-1 | 3 | 3.09 × 10−15 | 3 | ||
| ISSA-2 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-2 | 3 | 3.43 × 10−15 | 3 | ||
| ISSA-3 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-3 | 3 | 1.92 × 10−15 | 3 | ||
| ISSA-4 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-4 | 3 | 3.09 × 10−15 | 3 | ||
| ISSA-5 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-5 | 3.9 | 4.85 × 10+00 | 3 | ||
| ISSA-6 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-6 | 3 | 2.67 × 10−15 | 3 | ||
| ISSA-7 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-7 | 3 | 2.98 × 10−15 | 3 | ||
| ISSA-8 | −1.032 | 0.00 × 10+00 | −1.032 | ISSA-8 | 3 | 2.67 × 10−15 | 3 | ||
| CLSSA | −1.032 | 0.00 × 10+00 | −1.032 | CLSSA | 3 | 3.57 × 10−15 | 3 | ||
| F19 | SSA | −3.86 | 3.11 × 10−15 | −3.86 | F20 | SSA | −3.27 | 5.89 × 10−02 | −3.32 |
| ISSA-1 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-1 | −3.24 | 5.45 × 10−02 | −3.32 | ||
| ISSA-2 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-2 | −3.26 | 5.94 × 10−02 | −3.32 | ||
| ISSA-3 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-3 | −3.27 | 5.82 × 10−02 | −3.32 | ||
| ISSA-4 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-4 | −3.28 | 5.73 × 10−02 | −3.32 | ||
| ISSA-5 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-5 | −3.25 | 5.73 × 10−02 | −3.32 | ||
| ISSA-6 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-6 | −3.25 | 5.73 × 10−02 | −3.32 | ||
| ISSA-7 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-7 | −3.26 | 5.94 × 10−02 | −3.32 | ||
| ISSA-8 | −3.86 | 3.11 × 10−15 | −3.86 | ISSA-8 | −3.25 | 5.82 × 10−02 | −3.32 | ||
| CLSSA | −3.86 | 3.11 × 10−15 | −3.86 | CLSSA | −3.24 | 5.60 × 10−02 | −3.32 | ||
| F21 | SSA | −10 | 3.24 × 10−16 | −10 | F22 | SSA | −10 | 8.39 × 10−07 | −10 |
| ISSA-1 | −10 | 9.15 × 10−01 | −10 | ISSA-1 | −10 | 9.54 × 10−01 | −10 | ||
| ISSA-2 | −10 | 4.82 × 10−08 | −10 | ISSA-2 | −10 | 0.00 × 10+00 | −10 | ||
| ISSA-3 | −10 | 9.15 × 10−01 | −10 | ISSA-3 | −10 | 2.46 × 10−06 | −10 | ||
| ISSA-4 | −10 | 3.60 × 10−14 | −10 | ISSA-4 | −10 | 9.54 × 10−01 | −10 | ||
| ISSA-5 | −10 | 1.27 × 10+00 | −10 | ISSA-5 | −10 | 9.54 × 10−01 | −10 | ||
| ISSA-6 | −10 | 9.15 × 10−01 | −10 | ISSA-6 | −10 | 4.84 × 10−05 | −10 | ||
| ISSA-7 | −10 | 5.39 × 10−14 | −10 | ISSA-7 | −10 | 0.00 × 10+00 | −10 | ||
| ISSA-8 | −10 | 3.24 × 10−16 | −10 | ISSA-8 | −10 | 0.00 × 10+00 | −10 | ||
| CLSSA | −10 | 5.96 × 10−07 | −10 | CLSSA | −10 | 4.42 × 10−11 | −10 | ||
| F23 | SSA | −11 | 8.88 × 10−15 | −11 | |||||
| ISSA-1 | −11 | 8.88 × 10−15 | −11 | ||||||
| ISSA-2 | −11 | 5.42 × 10−12 | −11 | ||||||
| ISSA-3 | −11 | 8.88 × 10−15 | −11 | ||||||
| ISSA-4 | −11 | 1.98 × 10−14 | −11 | ||||||
| ISSA-5 | −10 | 1.62 × 10+00 | −11 | ||||||
| ISSA-6 | −11 | 5.87 × 10−10 | −11 | ||||||
| ISSA-7 | −11 | 8.88 × 10−15 | −11 | ||||||
| ISSA-8 | −11 | 6.37 × 10−05 | −11 | ||||||
| CLSSA | −10 | 9.71 × 10−01 | −11 |
| Dim = 30 | Dim = 100 | ||||
|---|---|---|---|---|---|
| Function | Results | SSA | CLSSA | SSA | CLSSA |
| F1 | Avg | 0 | 0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | |
| Best | 0 | 0 | 0 | 0 | |
| F2 | Avg | 4.4 × 10−192 | 8.8 × 10−229 | 5.2 × 10−219 | 7.9 × 10−247 |
| Std | 0 | 0 | 0 | 0 | |
| Best | 0 | 0 | 0 | 0 | |
| F3 | Avg | 7 × 10−279 | 0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | |
| Best | 0 | 0 | 0 | 0 | |
| F4 | Avg | 2.5 × 10−199 | 2.2 × 10−270 | 3.2 × 10−231 | 1.7 × 10−241 |
| Std | 0 | 0 | 0 | 0 | |
| Best | 0 | 0 | 0 | 0 | |
| F5 | Avg | 1.04 × 10−05 | 2.19 × 10−08 | 3.27 × 10−05 | 1.62 × 10−07 |
| Std | 2.23 × 10−05 | 4.01 × 10−08 | 5.26 × 10−05 | 2.84 × 10−07 | |
| Best | 1.52 × 10−14 | 3.06 × 10−14 | 6.33 × 10−09 | 2.3 × 10−09 | |
| F6 | Avg | 3.42 × 10−10 | 3.26 × 10−10 | 1.62 × 10−07 | 1.56 × 10−07 |
| Std | 1.65 × 10−09 | 4.01 × 10−10 | 1.94 × 10−07 | 2.4 × 10−07 | |
| Best | 1.81 × 10−13 | 4.51 × 10−14 | 4.22 × 10−10 | 2.07 × 10−10 | |
| F7 | Avg | 1.11 × 10−04 | 1.11 × 10−04 | 1.11 × 10−04 | 1.11 × 10−04 |
| Std | 9.95 × 10−05 | 7.15 × 10−05 | 1.11 × 10−04 | 1.11 × 10−04 | |
| Best | 4.54 × 10−06 | 2.06 × 10−06 | 1.17 × 10−05 | 1.29 × 10−05 | |
| F9 | Avg | 0 | 0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | |
| Best | 0 | 0 | 0 | 0 | |
| F10 | Avg | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 |
| Std | 9.86 × 10−32 | 9.86 × 10−32 | 9.86 × 10−32 | 9.86 × 10−32 | |
| Best | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | |
| F11 | Avg | 0 | 0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | |
| Best | 0 | 0 | 0 | 0 | |
| F12 | Avg | 2.23 × 10−11 | 8.78 × 10−16 | 2.55 × 10−09 | 3.01 × 10−14 |
| Std | 6.8 × 10−11 | 1.23 × 10−15 | 8.51 × 10−09 | 3.94 × 10−14 | |
| Best | 1.52 × 10−15 | 2.59 × 10−21 | 5.17 × 10−13 | 8.89 × 10−18 | |
| F13 | Avg | 7.39 × 10−11 | 7.29 × 10−13 | 7.69 × 10−08 | 7.85 × 10−11 |
| Std | 1.4 × 10−10 | 1.56 × 10−12 | 1.21 × 10−07 | 2.06 × 10−10 | |
| Best | 4.12 × 10−15 | 7.04 × 10−20 | 2.74 × 10−10 | 2.55 × 10−16 | |
| Function | Results | SSA | CLSSA |
|---|---|---|---|
| F14 | Avg | 3.53 × 10+00 | 1.39 × 10+00 |
| Std | 4.47 × 10+00 | 1.78 × 10+00 | |
| Best | 0.998 | 0.998 | |
| F15 | Avg | 3.08 × 10−04 | 3.08 × 10−04 |
| Std | 1.02 × 10−09 | 2.45 × 10−07 | |
| Best | 3.08 × 10−04 | 3.08 × 10−04 | |
| F16 | Avg | −1.032 | −1.032 |
| Std | 0 | 0 | |
| Best | −1.032 | −1.032 | |
| F18 | Avg | 3.9 | 3 |
| Std | 4.847 | 3.57 × 10−15 | |
| Best | 3 | 3 | |
| F19 | Avg | −3.86 | −3.86 |
| Std | 3.11 × 10−15 | 3.11 × 10−15 | |
| Best | −3.86 | −3.86 | |
| F20 | Avg | −3.27 | −3.24 |
| Std | 5.89 × 10−02 | 5.60 × 10−02 | |
| Best | −3.32 | −3.32 | |
| F21 | Avg | −10 | −10 |
| Std | 3.24 × 10−16 | 5.96 × 10−07 | |
| Best | −10 | −10 | |
| F22 | Avg | −10 | −10 |
| Std | 8.39 × 10−07 | 4.42 × 10−11 | |
| Best | −10 | −10 | |
| F23 | Avg | −10.5364 | −10.3561 |
| Std | 8.88 × 10−15 | 0.970753 | |
| Best | −10.5364 | −10.5364 |
| Function | Algorithms | Avg | Std | Best |
|---|---|---|---|---|
| F1 | PSO | 5.87 × 10+00 | 3.40 × 10+00 | 2.17 × 10+00 |
| TACPSO | 2.27 × 10+02 | 8.98 × 10+02 | 1.02 × 10+01 | |
| AGPSO3 | 4.10 × 10+01 | 5.24 × 10+01 | 4.12 × 10+00 | |
| GWO | 1.03 × 10−11 | 2.11 × 10−11 | 1.92 × 10−14 | |
| IGWO | 2.00 × 10−08 | 2.82 × 10−08 | 1.28 × 10−11 | |
| SSA | 6.96 × 10−279 | 0 | 0 | |
| IHSSA | 8.96 × 10−264 | 0 | 0 | |
| ESSA | 1.57 × 10−121 | 8.45 × 10−121 | 0 | |
| CSSA | 0 | 0 | 0 | |
| CLSSA | 0 | 0 | 0 | |
| F2 | PSO | 3.65 × 10+01 | 3.46 × 10+01 | 1.09 × 10+00 |
| TACPSO | 4.86 × 10+01 | 3.49 × 10+01 | 4.82 × 10+00 | |
| AGPSO3 | 9.66 × 10+01 | 1.41 × 10+02 | 1.28 × 10+01 | |
| GWO | 2.63 × 10+01 | 7.04 × 10−01 | 2.52 × 10+01 | |
| IGWO | 2.32 × 10+01 | 2.18 × 10−01 | 2.28 × 10+01 | |
| SSA | 1.08 × 10−05 | 2.54 × 10−05 | 9.67 × 10−11 | |
| IHSSA | 7.72 × 10−07 | 3.54 × 10−06 | 8.74 × 10−12 | |
| ESSA | 2.21 × 10−06 | 7.70 × 10−06 | 2.45 × 10−12 | |
| CSSA | 2.03 × 10−06 | 2.48 × 10−06 | 3.59 × 10−10 | |
| CLSSA | 2.19 × 10−08 | 4.01 × 10−08 | 3.06 × 10−14 | |
| F3 | PSO | 4.49 × 10−02 | 8.75 × 10−02 | 5.87 × 10−14 |
| TACPSO | 2.95 × 10−01 | 5.29 × 10−01 | 2.91 × 10−07 | |
| AGPSO3 | 4.37 × 10−01 | 6.53 × 10−01 | 1.92 × 10−07 | |
| GWO | 1.67 × 10−02 | 9.03 × 10−03 | 2.46 × 10−06 | |
| IGWO | 2.16 × 10−06 | 6.02 × 10−07 | 1.15 × 10−06 | |
| SSA | 9.46 × 10−12 | 1.54 × 10−11 | 6.06 × 10−17 | |
| IHSSA | 4.23 × 10−12 | 7.02 × 10−12 | 2.85 × 10−14 | |
| ESSA | 1.17 × 10−13 | 2.75 × 10−13 | 2.92 × 10−17 | |
| CSSA | 7.09 × 10−12 | 1.29 × 10−11 | 1.08 × 10−15 | |
| CLSSA | 8.78 × 10−16 | 1.23 × 10−15 | 2.59 × 10−21 | |
| F4 | PSO | 1.46 × 10−03 | 3.73 × 10−03 | 2.74 × 10−13 |
| TACPSO | 1.98 × 10−02 | 5.33 × 10−02 | 6.56 × 10−08 | |
| AGPSO3 | 1.73 × 10−02 | 3.54 × 10−02 | 9.74 × 10−07 | |
| GWO | 1.65 × 10−01 | 1.04 × 10−01 | 2.26 × 10−05 | |
| IGWO | 8.93 × 10−03 | 2.72 × 10−02 | 1.83 × 10−05 | |
| SSA | 7.39 × 10−11 | 1.40 × 10−10 | 4.12 × 10−15 | |
| IHSSA | 3.53 × 10−11 | 8.74 × 10−11 | 4.07 × 10−16 | |
| ESSA | 3.75 × 10−12 | 9.42 × 10−12 | 5.01 × 10−17 | |
| CSSA | 2.01 × 10−11 | 3.21 × 10−11 | 4.39 × 10−14 | |
| CLSSA | 7.29 × 10−13 | 1.56 × 10−12 | 7.04 × 10−20 | |
| F5 | PSO | −9.26251 | 2.24 × 10−01 | −9.58030 |
| TACPSO | −8.79606 | 4.93 × 10−01 | −9.59818 | |
| AGPSO3 | −9.14907 | 4.49 × 10−01 | −9.61348 | |
| GWO | −8.13552 | 7.87 × 10−01 | −9.23937 | |
| IGWO | −8.68436 | 8.47 × 10−01 | −9.56575 | |
| SSA | −8.59376 | 6.47 × 10−01 | −9.55150 | |
| IHSSA | −8.59020 | 7.45 × 10−01 | −9.54755 | |
| ESSA | −8.85708 | 4.38 × 10−01 | −9.49070 | |
| CSSA | −8.98927 | 5.12 × 10−01 | −9.62254 | |
| CLSSA | −8.52505 | 5.77 × 10−01 | −9.66015 | |
| F6 | PSO | 1.20 × 10−03 | 1.18 × 10−03 | 1.55 × 10−06 |
| TACPSO | 6.56 × 10−08 | 1.11 × 10−07 | 4.33 × 10−12 | |
| AGPSO3 | 3.98 × 10−06 | 6.96 × 10−06 | 7.44 × 10−09 | |
| GWO | 6.99 × 10−01 | 7.57 × 10−01 | 1.62 × 10−05 | |
| IGWO | 4.20 × 10−05 | 3.00 × 10−05 | 9.68 × 10−06 | |
| SSA | 2.49 × 10−08 | 4.80 × 10−08 | 7.05 × 10−13 | |
| IHSSA | 2.16 × 10−08 | 5.86 × 10−08 | 9.40 × 10−13 | |
| ESSA | 7.10 × 10−08 | 1.47 × 10−07 | 2.54 × 10−15 | |
| CSSA | 1.89 × 10−08 | 4.05 × 10−08 | 7.15 × 10−17 | |
| CLSSA | 3.58 × 10−11 | 8.06 × 10−11 | 5.41 × 10−18 | |
| F7 | PSO | 1.50 × 10−03 | 7.21 × 10−04 | 5.80 × 10−04 |
| TACPSO | 1.46 × 10+00 | 7.84 × 10+00 | 2.47 × 10−04 | |
| AGPSO3 | 2.51 × 10+00 | 1.35 × 10+01 | 8.35 × 10−04 | |
| GWO | 7.57 × 10−06 | 7.20 × 10−06 | 5.40 × 10−07 | |
| IGWO | 2.11 × 10−05 | 1.28 × 10−05 | 5.27 × 10−06 | |
| SSA | 0 | 0 | 0 | |
| IHSSA | 1.76 × 10−09 | 5.05 × 10−09 | 1.35 × 10−14 | |
| ESSA | 6.74 × 10−165 | 0 | 0 | |
| CSSA | 0 | 0 | 0 | |
| CLSSA | 0 | 0 | 0 | |
| F8 | PSO | 2.39 × 10+43 | 1.13 × 10+43 | 5.64 × 10+42 |
| TACPSO | 1.83 × 10+17 | 1.06 × 10+17 | 5.30 × 10+15 | |
| AGPSO3 | 3.17 × 10+38 | 1.62 × 10+39 | 4.08 × 10+15 | |
| GWO | 3.92 × 10+14 | 7.61 × 10+15 | 1.85 × 10+14 | |
| IGWO | 4.48 × 10+14 | 3.05 × 10+14 | 7.44 × 10+13 | |
| SSA | 0 | 0 | 0 | |
| IHSSA | 7.43 × 10+13 | 4.00 × 10+14 | 0.00 × 10+00 | |
| ESSA | 7.23 × 10−173 | 0.00 × 10+00 | 0.00 × 10+00 | |
| CSSA | 0 | 0 | 0 | |
| CLSSA | 0 | 0 | 0 |
| Function | PSO | TACPSO | AGPSO3 | GWO | IGWO | SSA | IHSSA | ESSA | CSSA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.61 × 10−01 | 2.16 × 10−02 | 3.45 × 10−07 | NaN |
| F2 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.00 × 10−09 | 1.12 × 10−01 | 1.81 × 10−01 | 9.06 × 10−08 |
| F3 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.98 × 10−11 | 3.02 × 10−11 | 1.89 × 10−04 | 6.70 × 10−11 |
| F4 | 1.55 × 10−09 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 6.01 × 10−08 | 9.06 × 10−08 | 5.94 × 10−02 | 6.05 × 10−07 |
| F5 | 5.09 × 10−08 | 9.63 × 10−02 | 8.15 × 10−05 | 4.68 × 10−02 | 4.21 × 10−02 | 5.79 × 10−01 | 4.64 × 10−01 | 8.68 × 10−03 | 1.11 × 10−03 |
| F6 | 3.02 × 10−11 | 4.62 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.60 × 10−07 | 9.83 × 10−08 | 1.73 × 10−07 | 4.74 × 10−06 |
| F7 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | 1.21 × 10−12 | 6.61 × 10−05 | NaN |
| F8 | 1.21 × 10−12 | 7.58 × 10−13 | 1.05 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | 3.34 × 10−01 | 1.61 × 10−01 | NaN |
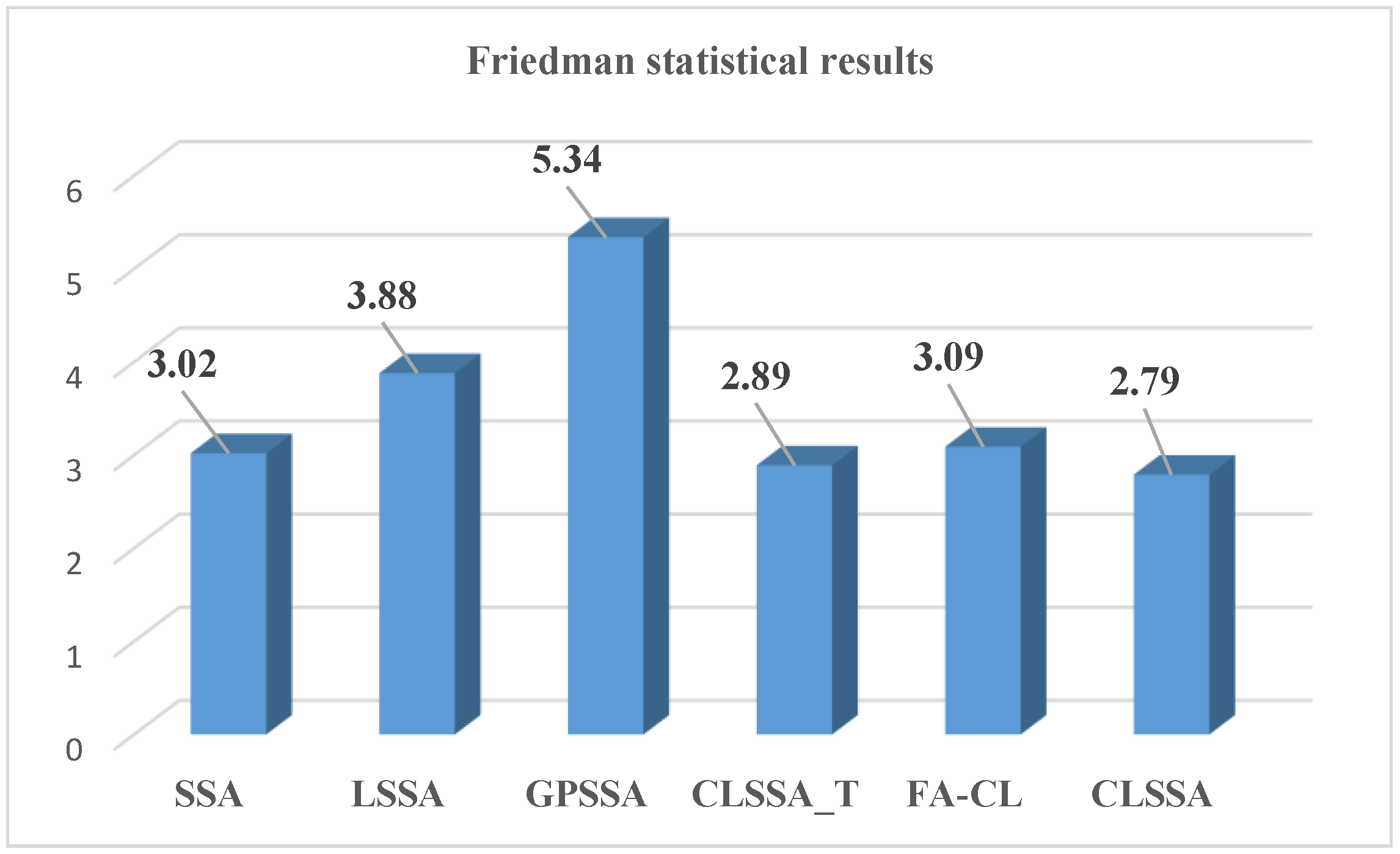
| Function | Index | SSA | LSSA | GPSSA | CLSSA_T | FA-CL | CLSSA |
|---|---|---|---|---|---|---|---|
| F1 | Best | 1.06 × 10+02 | 1.54 × 10+02 | 7.81 × 10+10 | 1.22 × 10+02 | 6.29 × 10+05 | 1.00 × 10+02 |
| Worst | 1.92 × 10+04 | 7.05 × 10+10 | 7.81 × 10+10 | 1.88 × 10+04 | 1.42 × 10+06 | 8.94 × 10+03 | |
| Median | 1.46 × 10+03 | 3.33 × 10+03 | 7.81 × 10+10 | 2.07 × 10+03 | 9.22 × 10+05 | 5.63 × 10+02 | |
| Mean | 3.82 × 10+03 | 2.62 × 10+09 | 7.81 × 10+10 | 4.53 × 10+03 | 9.61 × 10+05 | 1.48 × 10+03 | |
| Std | 5.36 × 10+03 | 1.28 × 10+10 | 2.95 × 10−01 | 5.50 × 10+03 | 1.85 × 10+05 | 1.92 × 10+03 | |
| F3 | Best | 9.62 × 10+02 | 1.09 × 10+03 | 8.38 × 10+04 | 2.52 × 10+03 | 6.83 × 10+03 | 7.82 × 10+02 |
| Worst | 4.56 × 10+03 | 1.96 × 10+04 | 9.00 × 10+04 | 1.59 × 10+04 | 1.78 × 10+04 | 6.74 × 10+03 | |
| Median | 2.54 × 10+03 | 9.38 × 10+03 | 8.48 × 10+04 | 7.99 × 10+03 | 1.11 × 10+04 | 2.72 × 10+03 | |
| Mean | 2.75 × 10+03 | 8.41 × 10+03 | 8.50 × 10+04 | 7.96 × 10+03 | 1.14 × 10+04 | 3.12 × 10+03 | |
| Std | 1.03 × 10+03 | 4.30 × 10+03 | 1.38 × 10+03 | 3.14 × 10+03 | 2.63 × 10+03 | 1.64 × 10+03 | |
| F4 | Best | 4.04 × 10+02 | 4.04 × 10+02 | 2.04 × 10+04 | 4.04 × 10+02 | 4.28 × 10+02 | 4.04 × 10+02 |
| Worst | 5.17 × 10+02 | 8.30 × 10+02 | 1.82 × 10+04 | 5.36 × 10+02 | 5.29 × 10+02 | 4.89 × 10+02 | |
| Median | 4.86 × 10+02 | 5.11 × 10+02 | 2.04 × 10+04 | 5.10 × 10+02 | 5.15 × 10+02 | 4.77 × 10+02 | |
| Mean | 4.79 × 10+02 | 5.31 × 10+02 | 2.03 × 10+04 | 4.97 × 10+02 | 5.06 × 10+02 | 4.68 × 10+02 | |
| Std | 3.36 × 10+01 | 8.72 × 10+01 | 4.06 × 10+02 | 2.69 × 10+01 | 2.24 × 10+01 | 2.30 × 10+01 | |
| F5 | Best | 6.55 × 10+02 | 6.55 × 10+02 | 8.14 × 10+02 | 6.25 × 10+02 | 6.27 × 10+02 | 6.47 × 10+02 |
| Worst | 8.20 × 10+02 | 8.25 × 10+02 | 9.70 × 10+02 | 7.97 × 10+02 | 7.33 × 10+02 | 8.24 × 10+02 | |
| Median | 7.48 × 10+02 | 7.48 × 10+02 | 9.70 × 10+02 | 7.06 × 10+02 | 6.61 × 10+02 | 7.46 × 10+02 | |
| Mean | 7.48 × 10+02 | 7.50 × 10+02 | 9.53 × 10+02 | 7.05 × 10+02 | 6.64 × 10+02 | 7.56 × 10+02 | |
| Std | 4.47 × 10+01 | 3.92 × 10+01 | 4.56 × 10+01 | 3.47 × 10+01 | 2.65 × 10+01 | 4.46 × 10+01 | |
| F6 | Best | 6.23 × 10+02 | 6.47 × 10+02 | 6.67 × 10+02 | 6.14 × 10+02 | 6.27 × 10+02 | 6.21 × 10+02 |
| Worst | 6.64 × 10+02 | 6.89 × 10+02 | 7.15 × 10+02 | 6.55 × 10+02 | 6.59 × 10+02 | 6.59 × 10+02 | |
| Median | 6.39 × 10+02 | 6.63 × 10+02 | 7.06 × 10+02 | 6.34 × 10+02 | 6.47 × 10+02 | 6.37 × 10+02 | |
| Mean | 6.40 × 10+02 | 6.63 × 10+02 | 7.04 × 10+02 | 6.34 × 10+02 | 6.44 × 10+02 | 6.38 × 10+02 | |
| Std | 1.14 × 10+01 | 7.65 × 10+00 | 9.95 × 10+00 | 7.97 × 10+00 | 8.41 × 10+00 | 1.08 × 10+01 | |
| F7 | Best | 1.08 × 10+03 | 1.02 × 10+03 | 1.50 × 10+03 | 9.58 × 10+02 | 9.49 × 10+02 | 1.02 × 10+03 |
| Worst | 1.35 × 10+03 | 1.35 × 10+03 | 1.58 × 10+03 | 1.23 × 10+03 | 1.27 × 10+03 | 1.35 × 10+03 | |
| Median | 1.23 × 10+03 | 1.27 × 10+03 | 1.53 × 10+03 | 1.12 × 10+03 | 1.09 × 10+03 | 1.24 × 10+03 | |
| Mean | 1.24 × 10+03 | 1.24 × 10+03 | 1.52 × 10+03 | 1.13 × 10+03 | 1.10 × 10+03 | 1.23 × 10+03 | |
| Std | 8.33 × 10+01 | 1.06 × 10+02 | 1.95 × 10+01 | 7.08 × 10+01 | 8.39 × 10+01 | 9.50 × 10+01 | |
| F8 | Best | 9.31 × 10+02 | 9.07 × 10+02 | 1.16 × 10+03 | 9.29 × 10+02 | 8.87 × 10+02 | 9.24 × 10+02 |
| Worst | 1.02 × 10+03 | 1.04 × 10+03 | 1.24 × 10+03 | 1.05 × 10+03 | 9.50 × 10+02 | 1.02 × 10+03 | |
| Median | 9.81 × 10+02 | 9.81 × 10+02 | 1.22 × 10+03 | 9.79 × 10+02 | 9.15 × 10+02 | 9.80 × 10+02 | |
| Mean | 9.80 × 10+02 | 9.76 × 10+02 | 1.21 × 10+03 | 9.77 × 10+02 | 9.15 × 10+02 | 9.74 × 10+02 | |
| Std | 2.15 × 10+01 | 3.33 × 10+01 | 1.93 × 10+01 | 3.47 × 10+01 | 1.67 × 10+01 | 2.63 × 10+01 | |
| F9 | Best | 5.02 × 10+03 | 4.01 × 10+03 | 6.58 × 10+03 | 4.65 × 10+03 | 2.73 × 10+03 | 3.73 × 10+03 |
| Worst | 5.48 × 10+03 | 6.73 × 10+03 | 1.42 × 10+04 | 5.71 × 10+03 | 5.34 × 10+03 | 5.65 × 10+03 | |
| Median | 5.39 × 10+03 | 5.36 × 10+03 | 1.34 × 10+04 | 5.23 × 10+03 | 4.01 × 10+03 | 5.23 × 10+03 | |
| Mean | 5.32 × 10+03 | 5.34 × 10+03 | 1.32 × 10+04 | 5.25 × 10+03 | 4.06 × 10+03 | 5.06 × 10+03 | |
| Std | 1.25 × 10+02 | 5.25 × 10+02 | 1.26 × 10+03 | 2.25 × 10+02 | 6.25 × 10+02 | 5.25 × 10+02 | |
| F10 | Best | 4.14 × 10+03 | 4.26 × 10+03 | 8.18 × 10+03 | 4.27 × 10+03 | 4.07 × 10+03 | 3.32 × 10+03 |
| Worst | 6.62 × 10+03 | 6.98 × 10+03 | 8.89 × 10+03 | 6.65 × 10+03 | 6.60 × 10+03 | 6.51 × 10+03 | |
| Median | 5.28 × 10+03 | 5.66 × 10+03 | 8.88 × 10+03 | 5.21 × 10+03 | 5.15 × 10+03 | 5.29 × 10+03 | |
| Mean | 5.35 × 10+03 | 5.57 × 10+03 | 8.69 × 10+03 | 5.33 × 10+03 | 5.13 × 10+03 | 5.24 × 10+03 | |
| Std | 6.54 × 10+02 | 5.96 × 10+02 | 2.68 × 10+02 | 6.68 × 10+02 | 6.04 × 10+02 | 7.11 × 10+02 | |
| F11 | Best | 1.15 × 10+03 | 1.15 × 10+03 | 2.58 × 10+03 | 1.16 × 10+03 | 1.17 × 10+03 | 1.16 × 10+03 |
| Worst | 1.43 × 10+03 | 1.41 × 10+04 | 9.90 × 10+03 | 1.42 × 10+03 | 1.30 × 10+03 | 1.32 × 10+03 | |
| Median | 1.30 × 10+03 | 1.22 × 10+03 | 6.15 × 10+03 | 1.25 × 10+03 | 1.23 × 10+03 | 1.22 × 10+03 | |
| Mean | 1.28 × 10+03 | 1.66 × 10+03 | 6.92 × 10+03 | 1.25 × 10+03 | 1.23 × 10+03 | 1.22 × 10+03 | |
| Std | 7.99 × 10+01 | 2.34 × 10+03 | 2.26 × 10+03 | 5.39 × 10+01 | 3.60 × 10+01 | 4.33 × 10+01 | |
| F12 | Best | 2.59 × 10+04 | 4.81 × 10+04 | 7.39 × 10+09 | 1.09 × 10+05 | 1.13 × 10+06 | 6.43 × 10+04 |
| Worst | 1.02 × 10+06 | 1.84 × 10+08 | 2.47 × 10+10 | 3.15 × 10+06 | 6.08 × 10+06 | 6.12 × 10+06 | |
| Median | 1.98 × 10+05 | 4.44 × 10+05 | 2.47 × 10+10 | 9.96 × 10+05 | 3.38 × 10+06 | 4.13 × 10+05 | |
| Mean | 2.68 × 10+05 | 7.61 × 10+06 | 2.35 × 10+10 | 1.10 × 10+06 | 3.38 × 10+06 | 8.15 × 10+05 | |
| Std | 2.31 × 10+05 | 3.36 × 10+07 | 4.38 × 10+09 | 8.57 × 10+05 | 1.23 × 10+06 | 1.20 × 10+06 | |
| F13 | Best | 1.46 × 10+03 | 2.97 × 10+03 | 7.15 × 10+07 | 1.68 × 10+03 | 5.35 × 10+04 | 1.36 × 10+03 |
| Worst | 6.10 × 10+04 | 1.31 × 10+07 | 9.35 × 10+09 | 6.08 × 10+04 | 1.49 × 10+05 | 1.47 × 10+05 | |
| Median | 8.48 × 10+03 | 1.27 × 10+04 | 9.35 × 10+09 | 8.66 × 10+03 | 9.44 × 10+04 | 3.07 × 10+04 | |
| Mean | 1.72 × 10+04 | 4.53 × 10+05 | 8.56 × 10+09 | 1.60 × 10+04 | 9.61 × 10+04 | 3.99 × 10+04 | |
| Std | 1.91 × 10+04 | 2.39 × 10+06 | 2.48 × 10+09 | 1.80 × 10+04 | 2.22 × 10+04 | 3.87 × 10+04 | |
| F14 | Best | 2.55 × 10+03 | 2.44 × 10+03 | 2.13 × 10+05 | 2.40 × 10+03 | 2.22 × 10+03 | 4.48 × 10+03 |
| Worst | 4.92 × 10+04 | 7.81 × 10+04 | 2.19 × 10+05 | 1.07 × 10+05 | 3.96 × 10+04 | 8.39 × 10+04 | |
| Median | 1.24 × 10+04 | 1.63 × 10+04 | 2.15 × 10+05 | 2.56 × 10+04 | 9.95 × 10+03 | 2.68 × 10+04 | |
| Mean | 1.83 × 10+04 | 1.99 × 10+04 | 2.16 × 10+05 | 3.65 × 10+04 | 1.13 × 10+04 | 3.47 × 10+04 | |
| Std | 1.46 × 10+04 | 1.58 × 10+04 | 1.21 × 10+03 | 3.36 × 10+04 | 8.47 × 10+03 | 2.35 × 10+04 | |
| F15 | Best | 1.75 × 10+03 | 1.77 × 10+03 | 3.50 × 10+03 | 1.66 × 10+03 | 1.32 × 10+04 | 1.56 × 10+03 |
| Worst | 4.33 × 10+04 | 2.77 × 10+04 | 9.26 × 10+07 | 4.24 × 10+04 | 6.22 × 10+04 | 6.08 × 10+04 | |
| Median | 1.06 × 10+04 | 4.50 × 10+03 | 4.63 × 10+07 | 3.35 × 10+03 | 3.09 × 10+04 | 5.14 × 10+03 | |
| Mean | 1.47 × 10+04 | 6.81 × 10+03 | 4.63 × 10+07 | 7.09 × 10+03 | 3.20 × 10+04 | 1.24 × 10+04 | |
| Std | 1.36 × 10+04 | 6.62 × 10+03 | 4.71 × 10+07 | 9.26 × 10+03 | 1.13 × 10+04 | 1.90 × 10+04 | |
| F16 | Best | 2.49 × 10+03 | 2.05 × 10+03 | 5.28 × 10+03 | 1.89 × 10+03 | 2.65 × 10+03 | 2.06 × 10+03 |
| Worst | 3.62 × 10+03 | 3.56 × 10+03 | 6.42 × 10+03 | 3.57 × 10+03 | 3.56 × 10+03 | 3.26 × 10+03 | |
| Median | 2.94 × 10+03 | 2.93 × 10+03 | 5.60 × 10+03 | 3.07 × 10+03 | 3.03 × 10+03 | 2.80 × 10+03 | |
| Mean | 2.93 × 10+03 | 2.89 × 10+03 | 5.63 × 10+03 | 3.06 × 10+03 | 3.07 × 10+03 | 2.79 × 10+03 | |
| Std | 3.02 × 10+02 | 3.88 × 10+02 | 2.46 × 10+02 | 4.47 × 10+02 | 2.67 × 10+02 | 3.30 × 10+02 | |
| F17 | Best | 1.83 × 10+03 | 1.95 × 10+03 | 2.80 × 10+04 | 1.77 × 10+03 | 1.76 × 10+03 | 2.00 × 10+03 |
| Worst | 3.07 × 10+03 | 3.00 × 10+03 | 2.87 × 10+04 | 3.01 × 10+03 | 2.52 × 10+03 | 2.92 × 10+03 | |
| Median | 2.57 × 10+03 | 2.47 × 10+03 | 2.84 × 10+04 | 2.49 × 10+03 | 2.13 × 10+03 | 2.54 × 10+03 | |
| Mean | 2.57 × 10+03 | 2.46 × 10+03 | 2.83 × 10+04 | 2.45 × 10+03 | 2.12 × 10+03 | 2.49 × 10+03 | |
| Std | 3.38 × 10+02 | 2.79 × 10+02 | 1.63 × 10+02 | 3.24 × 10+02 | 2.23 × 10+02 | 2.51 × 10+02 | |
| F18 | Best | 7.86 × 10+04 | 3.20 × 10+04 | 5.94 × 10+07 | 3.38 × 10+04 | 8.36 × 10+04 | 4.73 × 10+04 |
| Worst | 5.09 × 10+05 | 5.36 × 10+05 | 6.04 × 10+07 | 7.42 × 10+05 | 6.42 × 10+05 | 6.15 × 10+05 | |
| Median | 2.05 × 10+05 | 1.41 × 10+05 | 5.97 × 10+07 | 2.50 × 10+05 | 1.63 × 10+05 | 2.31 × 10+05 | |
| Mean | 2.28 × 10+05 | 1.66 × 10+05 | 5.97 × 10+07 | 2.92 × 10+05 | 1.98 × 10+05 | 2.55 × 10+05 | |
| Std | 1.23 × 10+05 | 1.19 × 10+05 | 2.12 × 10+05 | 1.95 × 10+05 | 1.26 × 10+05 | 1.57 × 10+05 | |
| F19 | Best | 2.05 × 10+03 | 2.04 × 10+03 | 1.54 × 10+09 | 1.95 × 10+03 | 8.51 × 10+04 | 1.95 × 10+03 |
| Worst | 5.38 × 10+04 | 2.41 × 10+04 | 1.54 × 10+09 | 4.66 × 10+04 | 1.30 × 10+06 | 2.95 × 10+04 | |
| Median | 6.67 × 10+03 | 4.23 × 10+03 | 1.54 × 10+09 | 1.11 × 10+04 | 8.35 × 10+05 | 6.98 × 10+03 | |
| Mean | 1.10 × 10+04 | 5.78 × 10+03 | 1.54 × 10+09 | 1.37 × 10+04 | 7.85 × 10+05 | 7.26 × 10+03 | |
| Std | 1.03 × 10+04 | 4.64 × 10+03 | 2.79 × 10−02 | 9.90 × 10+03 | 2.57 × 10+05 | 5.35 × 10+03 | |
| F20 | Best | 2.26 × 10+03 | 2.18 × 10+03 | 2.81 × 10+03 | 2.11 × 10+03 | 2.26 × 10+03 | 2.13 × 10+03 |
| Worst | 3.10 × 10+03 | 3.18 × 10+03 | 3.19 × 10+03 | 3.10 × 10+03 | 2.72 × 10+03 | 3.02 × 10+03 | |
| Median | 2.74 × 10+03 | 2.75 × 10+03 | 3.08 × 10+03 | 2.56 × 10+03 | 2.52 × 10+03 | 2.69 × 10+03 | |
| Mean | 2.68 × 10+03 | 2.74 × 10+03 | 3.03 × 10+03 | 2.62 × 10+03 | 2.46 × 10+03 | 2.65 × 10+03 | |
| Std | 1.94 × 10+02 | 2.20 × 10+02 | 1.23 × 10+02 | 2.49 × 10+02 | 1.40 × 10+02 | 2.43 × 10+02 | |
| F21 | Best | 2.42 × 10+03 | 2.42 × 10+03 | 2.74 × 10+03 | 2.41 × 10+03 | 2.41 × 10+03 | 2.45 × 10+03 |
| Worst | 2.62 × 10+03 | 2.69 × 10+03 | 2.92 × 10+03 | 2.64 × 10+03 | 2.53 × 10+03 | 2.60 × 10+03 | |
| Median | 2.50 × 10+03 | 2.54 × 10+03 | 2.90 × 10+03 | 2.52 × 10+03 | 2.45 × 10+03 | 2.52 × 10+03 | |
| Mean | 2.51 × 10+03 | 2.55 × 10+03 | 2.87 × 10+03 | 2.51 × 10+03 | 2.46 × 10+03 | 2.51 × 10+03 | |
| Std | 4.59 × 10+01 | 7.11 × 10+01 | 6.56 × 10+01 | 6.32 × 10+01 | 3.07 × 10+01 | 3.88 × 10+01 | |
| F22 | Best | 2.30 × 10+03 | 2.30 × 10+03 | 7.78 × 10+03 | 2.30 × 10+03 | 2.31 × 10+03 | 2.30 × 10+03 |
| Worst | 8.20 × 10+03 | 8.05 × 10+03 | 1.11 × 10+04 | 8.44 × 10+03 | 7.50 × 10+03 | 7.26 × 10+03 | |
| Median | 6.49 × 10+03 | 6.55 × 10+03 | 9.81 × 10+03 | 6.86 × 10+03 | 2.31 × 10+03 | 6.41 × 10+03 | |
| Mean | 6.14 × 10+03 | 5.31 × 10+03 | 9.70 × 10+03 | 5.88 × 10+03 | 2.48 × 10+03 | 6.30 × 10+03 | |
| Std | 1.87 × 10+03 | 2.48 × 10+03 | 7.50 × 10+02 | 2.09 × 10+03 | 9.47 × 10+02 | 9.53 × 10+02 | |
| F23 | Best | 2.74 × 10+03 | 2.82 × 10+03 | 3.87 × 10+03 | 2.77 × 10+03 | 2.83 × 10+03 | 2.86 × 10+03 |
| Worst | 3.11 × 10+03 | 3.21 × 10+03 | 4.55 × 10+03 | 2.98 × 10+03 | 3.06 × 10+03 | 3.14 × 10+03 | |
| Median | 2.88 × 10+03 | 2.96 × 10+03 | 4.51 × 10+03 | 2.83 × 10+03 | 2.94 × 10+03 | 3.02 × 10+03 | |
| Mean | 2.89 × 10+03 | 2.97 × 10+03 | 4.41 × 10+03 | 2.86 × 10+03 | 2.94 × 10+03 | 3.01 × 10+03 | |
| Std | 7.74 × 10+01 | 9.42 × 10+01 | 2.29 × 10+02 | 6.50 × 10+01 | 4.70 × 10+01 | 7.03 × 10+01 | |
| F24 | Best | 2.95 × 10+03 | 3.02 × 10+03 | 4.39 × 10+03 | 2.93 × 10+03 | 2.98 × 10+03 | 3.11 × 10+03 |
| Worst | 3.27 × 10+03 | 3.25 × 10+03 | 4.43 × 10+03 | 3.31 × 10+03 | 3.18 × 10+03 | 3.49 × 10+03 | |
| Median | 3.11 × 10+03 | 3.16 × 10+03 | 4.41 × 10+03 | 3.15 × 10+03 | 3.08 × 10+03 | 3.27 × 10+03 | |
| Mean | 3.10 × 10+03 | 3.15 × 10+03 | 4.41 × 10+03 | 3.13 × 10+03 | 3.08 × 10+03 | 3.28 × 10+03 | |
| Std | 6.27 × 10+01 | 6.17 × 10+01 | 1.07 × 10+01 | 9.69 × 10+01 | 4.66 × 10+01 | 9.97 × 10+01 | |
| F25 | Best | 2.88 × 10+03 | 2.88 × 10+03 | 3.64 × 10+03 | 2.88 × 10+03 | 2.90 × 10+03 | 2.88 × 10+03 |
| Worst | 2.94 × 10+03 | 3.59 × 10+03 | 5.49 × 10+03 | 2.94 × 10+03 | 2.95 × 10+03 | 2.90 × 10+03 | |
| Median | 2.89 × 10+03 | 2.89 × 10+03 | 5.49 × 10+03 | 2.90 × 10+03 | 2.94 × 10+03 | 2.88 × 10+03 | |
| Mean | 2.90 × 10+03 | 2.93 × 10+03 | 5.43 × 10+03 | 2.90 × 10+03 | 2.94 × 10+03 | 2.88 × 10+03 | |
| Std | 1.85 × 10+01 | 1.29 × 10+02 | 3.37 × 10+02 | 1.33 × 10+01 | 1.55 × 10+01 | 5.12 × 10+00 | |
| F26 | Best | 2.80 × 10+03 | 4.19 × 10+03 | 1.40 × 10+04 | 2.80 × 10+03 | 3.02 × 10+03 | 2.80 × 10+03 |
| Worst | 8.44 × 10+03 | 9.60 × 10+03 | 1.54 × 10+04 | 7.67 × 10+03 | 8.03 × 10+03 | 8.77 × 10+03 | |
| Median | 6.70 × 10+03 | 7.53 × 10+03 | 1.50 × 10+04 | 6.34 × 10+03 | 6.66 × 10+03 | 6.35 × 10+03 | |
| Mean | 6.45 × 10+03 | 7.16 × 10+03 | 1.49 × 10+04 | 6.12 × 10+03 | 6.37 × 10+03 | 6.00 × 10+03 | |
| Std | 1.28 × 10+03 | 1.46 × 10+03 | 3.04 × 10+02 | 1.25 × 10+03 | 1.23 × 10+03 | 1.46 × 10+03 | |
| F27 | Best | 3.22 × 10+03 | 3.23 × 10+03 | 3.20 × 10+03 | 3.21 × 10+03 | 3.34 × 10+03 | 3.20 × 10+03 |
| Worst | 3.46 × 10+03 | 3.42 × 10+03 | 3.20 × 10+03 | 3.34 × 10+03 | 3.62 × 10+03 | 3.20 × 10+03 | |
| Median | 3.26 × 10+03 | 3.30 × 10+03 | 3.20 × 10+03 | 3.26 × 10+03 | 3.50 × 10+03 | 3.20 × 10+03 | |
| Mean | 3.28 × 10+03 | 3.31 × 10+03 | 3.20 × 10+03 | 3.26 × 10+03 | 3.50 × 10+03 | 3.20 × 10+03 | |
| Std | 6.05 × 10+01 | 4.70 × 10+01 | 5.65 × 10−05 | 2.66 × 10+01 | 6.81 × 10+01 | 2.56 × 10−04 | |
| F28 | Best | 3.10 × 10+03 | 3.19 × 10+03 | 3.30 × 10+03 | 3.10 × 10+03 | 3.20 × 10+03 | 3.10 × 10+03 |
| Worst | 3.26 × 10+03 | 3.63 × 10+03 | 8.27 × 10+03 | 3.26 × 10+03 | 3.36 × 10+03 | 3.30 × 10+03 | |
| Median | 3.19 × 10+03 | 3.23 × 10+03 | 8.27 × 10+03 | 3.20 × 10+03 | 3.27 × 10+03 | 3.20 × 10+03 | |
| Mean | 3.17 × 10+03 | 3.26 × 10+03 | 7.94 × 10+03 | 3.20 × 10+03 | 3.26 × 10+03 | 3.22 × 10+03 | |
| Std | 6.00 × 10+01 | 9.42 × 10+01 | 1.26 × 10+03 | 3.11 × 10+01 | 3.05 × 10+01 | 6.11 × 10+01 | |
| F29 | Best | 3.85 × 10+03 | 3.73 × 10+03 | 7.67 × 10+03 | 3.53 × 10+03 | 3.82 × 10+03 | 3.39 × 10+03 |
| Worst | 4.57 × 10+03 | 5.22 × 10+03 | 8.69 × 10+03 | 4.35 × 10+03 | 4.85 × 10+03 | 4.35 × 10+03 | |
| Median | 4.28 × 10+03 | 4.25 × 10+03 | 7.99 × 10+03 | 4.08 × 10+03 | 4.38 × 10+03 | 3.83 × 10+03 | |
| Mean | 4.27 × 10+03 | 4.26 × 10+03 | 8.07 × 10+03 | 4.06 × 10+03 | 4.36 × 10+03 | 3.86 × 10+03 | |
| Std | 1.82 × 10+02 | 3.40 × 10+02 | 1.88 × 10+02 | 2.09 × 10+02 | 2.78 × 10+02 | 2.41 × 10+02 | |
| F30 | Best | 5.22 × 10+03 | 6.57 × 10+03 | 4.74 × 10+08 | 7.09 × 10+03 | 4.38 × 10+05 | 3.28 × 10+03 |
| Worst | 1.91 × 10+04 | 1.25 × 10+09 | 5.12 × 10+08 | 2.43 × 10+04 | 3.05 × 10+06 | 5.86 × 10+04 | |
| Median | 9.46 × 10+03 | 1.16 × 10+04 | 4.99 × 10+08 | 1.22 × 10+04 | 1.53 × 10+06 | 8.29 × 10+03 | |
| Mean | 9.94 × 10+03 | 4.20 × 10+07 | 4.98 × 10+08 | 1.28 × 10+04 | 1.56 × 10+06 | 1.30 × 10+04 | |
| Std | 3.72 × 10+03 | 2.28 × 10+08 | 5.45 × 10+06 | 4.47 × 10+03 | 5.86 × 10+05 | 1.33 × 10+04 |
| Algorithm | x1 | x2 | x3 | x4 | f(X) |
|---|---|---|---|---|---|
| GA | 49 | 19 | 16 | 43 | 2.70 × 10−12 |
| PSO | 34 | 13 | 20 | 53 | 2.31 × 10−11 |
| CS | 43 | 16 | 19 | 49 | 2.70 × 10−12 |
| ABC | 49 | 16 | 19 | 43 | 2.70 × 10−12 |
| GWO | 49 | 19 | 16 | 43 | 2.70 × 10−12 |
| MFO | 43 | 19 | 16 | 49 | 2.70 × 10−12 |
| ISA | 43 | 19 | 16 | 49 | 2.70 × 10−12 |
| WSA | 43 | 16 | 19 | 49 | 2.70 × 10−12 |
| APSO | 43 | 16 | 19 | 49 | 2.70 × 10−12 |
| SSA | 51 | 30 | 13 | 53 | 2.31 × 10−11 |
| CLSSA | 49 | 19 | 16 | 43 | 2.70 × 10−12 |
| ABC | GWO | WOA | HPSO | CPSO | CDE | MCEO | SSA | CLSSA | |
|---|---|---|---|---|---|---|---|---|---|
| x1 | 8.13 × 10−01 | 8.13 × 10−01 | 8.13 × 10−01 | 8.13 × 10−01 | 8.13 × 10−01 | 8.13 × 10−01 | 8.13 × 10−01 | 1.28 × 10+01 | 1.29 × 10+01 |
| x2 | 4.38 × 10−01 | 4.35 × 10−01 | 4.38 × 10−01 | 4.38 × 10−01 | 4.38 × 10−01 | 4.38 × 10−01 | 4.38 × 10−01 | 6.77 × 10+00 | 7.00 × 10+00 |
| x3 | 4.21 × 10+01 | 4.21 × 10+01 | 4.21 × 10+01 | 4.21 × 10+01 | 4.21 × 10+01 | 4.21 × 10+01 | 4.21 × 10+01 | 4.21 × 10+01 | 4.23 × 10+01 |
| x4 | 1.77 × 10+02 | 1.77 × 10+02 | 1.77 × 10+02 | 1.77 × 10+02 | 1.77 × 10+02 | 1.77 × 10+02 | 1.77 × 10+02 | 1.77 × 10+02 | 1.75 × 10+02 |
| g1(X) | 0.00 × 10+00 | −1.79 × 10−04 | −3.39 × 10−06 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | −1.13 × 10−10 | −5.09 × 10−04 | 3.11 × 10−03 |
| g2(X) | −3.59 × 10−02 | −3.30 × 10−02 | −3.59 × 10−02 | −3.58 × 10−02 | −3.60 × 10−04 | −3.58 × 10−02 | −3.76 × 10−02 | −3.61 × 10−02 | −3.43 × 10−02 |
| g3(X) | −2.30 × 10−04 | −4.06 × 10+01 | −1.25 × 10+00 | 3.12 × 10+00 | −1.19 × 10+02 | −3.71 × 10+00 | −4.73 × 10−04 | −2.46 × 10+00 | −2.63 × 10+03 |
| g4(X) | −6.34 × 10+01 | −6.32 × 10+01 | −6.34 × 10+01 | −6.34 × 10+01 | −6.33 × 10+01 | −6.34 × 10+01 | −6.34 × 10+01 | −6.30 × 10+01 | −6.49 × 10+01 |
| f(X) | 6.06 × 10+03 | 6.05 × 10+03 | 6.06 × 10+03 | 6.06 × 10+03 | 6.06 × 10+03 | 6.06 × 10+03 | 6.06 × 10+03 | 6.06 × 10+03 | 6.05 × 10+03 |
| CS | VIGMM3 | AEFA-C | SNS | SSA | CLSSA | |
|---|---|---|---|---|---|---|
| x1 | 37.11795 | 57.69231 | 57.69277 | 57.69231 | 57.64028 | 57.68799 |
| x2 | 33.03502 | 34.14762 | 34.13296 | 34.14762 | 34.14786 | 34.14703 |
| x3 | 37.19395 | 57.69231 | 57.55294 | 57.69231 | 57.69584 | 57.68531 |
| x4 | 0.73063 | 1.05000 | 1.05007 | 1.05000 | 1.05004 | 1.05004 |
| g1(X) | −23.35377 | −0.25839 | −240.89634 | −240.69462 | −240.45294 | −240.72862 |
| g2(X) | −1.60 × 10+01 | −2.22 × 10−16 | −1.16 × 10+01 | −1.47 × 10−05 | −9.59 × 10−01 | −1.53 × 10+00 |
| g3(X) | −1.59 × 10−03 | −9.77 × 10−15 | −6.86 × 10−05 | −5.80 × 10−09 | −8.54 × 10−04 | −1.08 × 10−04 |
| g4(X) | −4.00 × 10−04 | −5.55 × 10−16 | −2.25 × 10−03 | −6.21 × 10−09 | 1.24 × 10−05 | −1.50 × 10−04 |
| g5(X) | 3.19 × 10−01 | 0.00 × 10+00 | −7.58 × 10−05 | −6.51 × 10−13 | −4.28 × 10−05 | −4.09 × 10−05 |
| g6(X) | −4.158927 | 0.68949 | −23.41997 | −23.544687 | −23.54798517 | −23.53828095 |
| f(X) | 5.89433 | 6.84296 | −6.84584 | 6.84296 | 6.84350 | 6.84338 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Huang, X.; Zhu, D.; Zhou, C.; He, K. An Improved Sparrow Search Algorithm for Global Optimization with Customization-Based Mechanism. Axioms 2023, 12, 767. https://doi.org/10.3390/axioms12080767
Wang Z, Huang X, Zhu D, Zhou C, He K. An Improved Sparrow Search Algorithm for Global Optimization with Customization-Based Mechanism. Axioms. 2023; 12(8):767. https://doi.org/10.3390/axioms12080767
Chicago/Turabian StyleWang, Zikai, Xueyu Huang, Donglin Zhu, Changjun Zhou, and Kerou He. 2023. "An Improved Sparrow Search Algorithm for Global Optimization with Customization-Based Mechanism" Axioms 12, no. 8: 767. https://doi.org/10.3390/axioms12080767
APA StyleWang, Z., Huang, X., Zhu, D., Zhou, C., & He, K. (2023). An Improved Sparrow Search Algorithm for Global Optimization with Customization-Based Mechanism. Axioms, 12(8), 767. https://doi.org/10.3390/axioms12080767








