Enhancing Contractor Selection Process by a New Interval-Valued Fuzzy Decision-Making Model Based on SWARA and CoCoSo Methods
Abstract
:1. Introduction
2. Literature Review
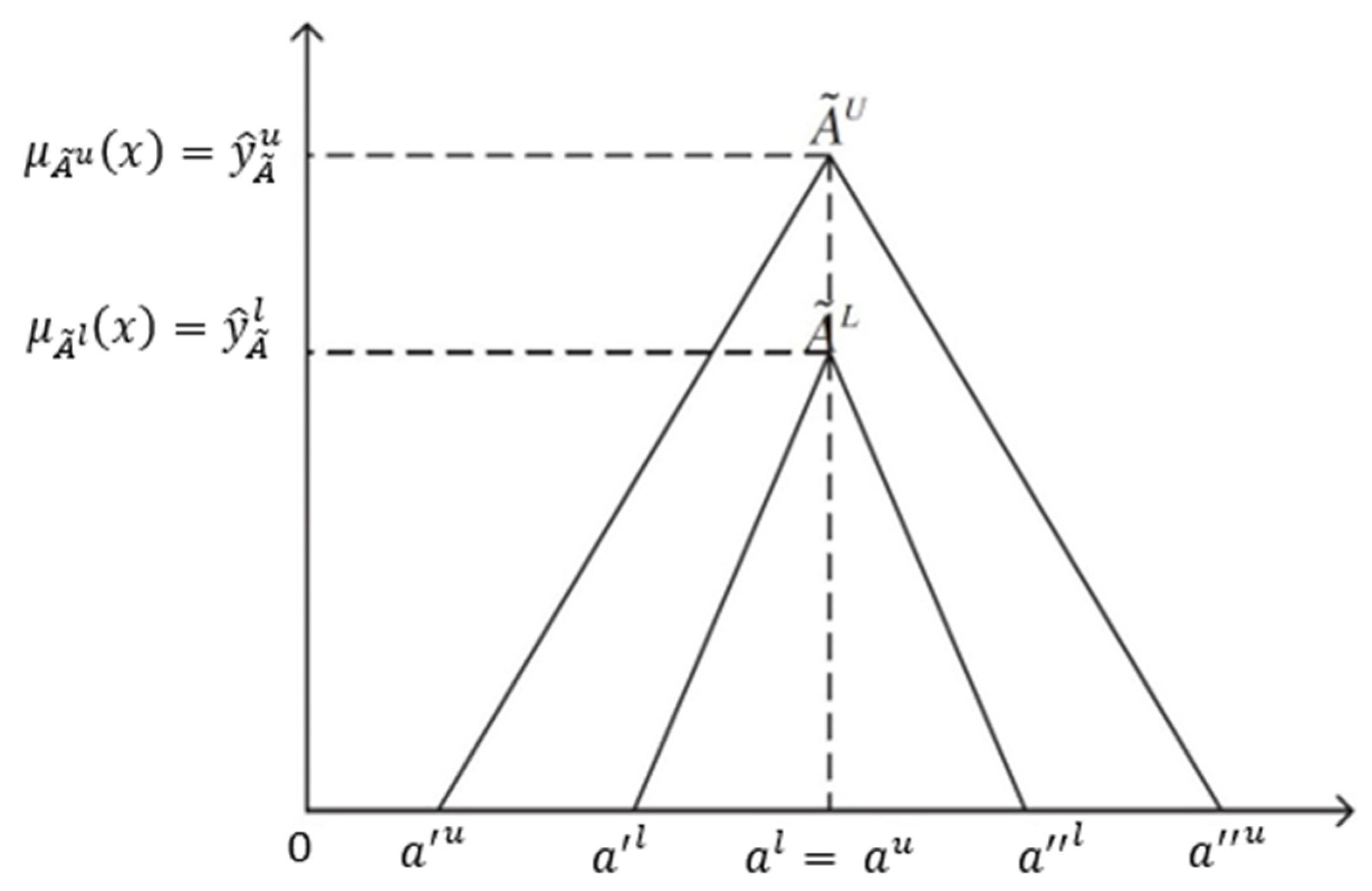
3. Interval-Valued Fuzzy Numbers
- i
- If , then the triangular IVFN can be considered as a generalized triangular fuzzy number.
- ii
- If and , then the triangular IVFN is a crisp value.
- iii
- If and , then the triangular IVFN can be represented as .
- Addition of IVFNs :
- Subtraction of IVFNs :
- Multiplication of IVFNs :
- Generalized division of IVFNs :
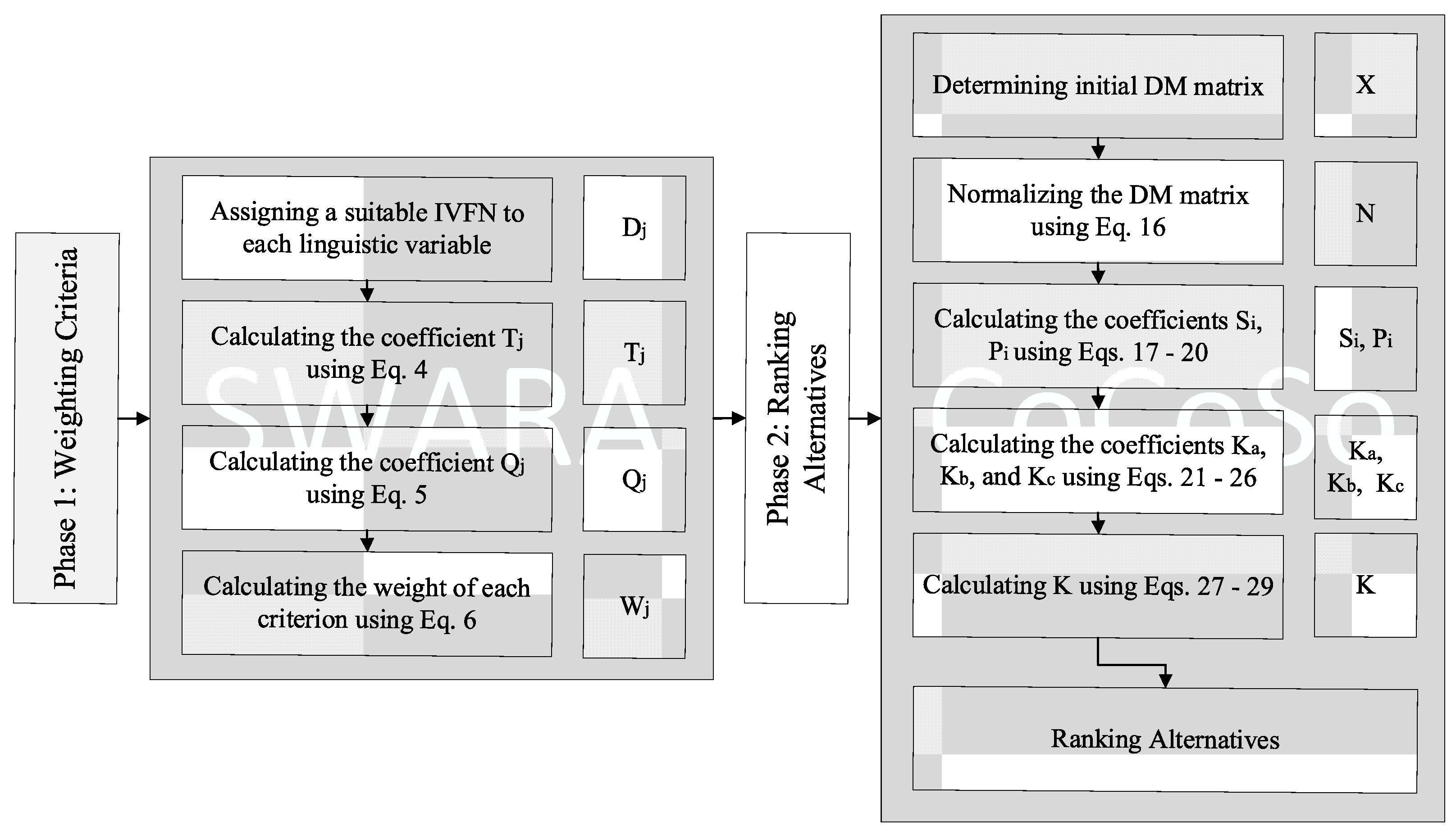
4. Proposed Methodology
4.1. Primitive SWARA and CoCoSo Methods
4.1.1. SWARA Method
4.1.2. CoCoSo Method
4.2. Proposed IVF-SWARA and IVF-CoCoSo Methods
4.2.1. Proposed IVF-SWARA Method
4.2.2. Proposed IVF-CoCoSo Method
5. Numerical Example
6. Result Discussion and Sensitivity Analysis
6.1. Result Discussion
6.2. Sensitivity Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hwang, B.-G.; Ng, W.J. Project management knowledge and skills for green construction: Overcoming challenges. Int. J. Proj. Manag. 2013, 31, 272–284. [Google Scholar]
- Cristóbal, S.; Fernández, J. Contractor Selection for Project Execution Using Multi-Attribute Decision Making. Procedia Comput. Sci. 2023, 219, 1760–1768. [Google Scholar]
- Nemati-Lafmejani, R.; Davari-Ardakani, H. Multi-mode resource constrained project scheduling and contractor selection: Mathematical formulation and metaheuristic algorithms. Appl. Soft Comput. 2019, 81, 105533. [Google Scholar]
- Akintoye, A.; Beck, M. Public Private Partnerships: A Global Review; Routledge: London, UK, 2020. [Google Scholar]
- El-Sawalhi, N.; Eaton, D. Contractor pre-qualification model: State-of-the-art. Int. J. Proj. Manag. 2007, 25, 465–474. [Google Scholar]
- El-Sayegh, S. Multi-criteria decision support model for selecting the appropriate construction management at risk firm. Constr. Manag. Econ. 2009, 27, 385–398. [Google Scholar]
- Vasiljević, M.; Fazlollahtabar, H. A rough multicriteria approach for evaluation of the supplier criteria in automotive industry. Decis. Mak. Appl. Manag. Eng. 2018, 1, 82–96. [Google Scholar]
- Madić, M.; Petrović, G. Application of the ORESTE method for solving decision making problems in transportation and logistics. Mech. Eng. 2016, 78, 83–94. [Google Scholar]
- Zhang, J.; Qi, X. Tackling Complexity in Green Contractor Selection for Mega Infrastructure Projects: A Hesitant Fuzzy Linguistic MADM Approach with considering Group Attitudinal Character and Attributes’ Interdependency. Complexity 2018, 2018, 4903572. [Google Scholar]
- Saaty, T.; Vargas, L. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Oyatoye, E.; Odulana, A. A Prototype AHP System for Contractor Selection Decision; IntechOpen: Rijeka, Yugoslavia, 2016. [Google Scholar]
- Afolayan, A.; Ojokoh, B. Performance analysis of fuzzy analytic hierarchy process multi-criteria decision support models for contractor selection. Sci. Afr. 2020, 9, e00471. [Google Scholar]
- Hussain, S.; Baruah, D. Evaluating the impact of service quality on the dynamics of customer satisfaction in the telecommunication industry of Jorhat, Assam. Telecommun. Syst. 2019, 71, 31–53. [Google Scholar]
- Wang, H.; Wang, X. Multi-objective optimization of water and fertilizer management for potato production in sandy areas of northern China based on TOPSIS. Field Crops Res. 2019, 240, 55–68. [Google Scholar]
- Kaya, T.; Kahraman, C. A fuzzy approach to e-banking website quality assessment based on an integrated AHP-ELECTRE method. Technol. Econ. Dev. Econ. 2011, 17, 313–334. [Google Scholar]
- Wu, M.C.; Chen, T.Y. The ELECTRE multicriteria analysis approach based on Atanassov’s intuitionistic fuzzy sets. Expert Syst. Appl. 2011, 38, 12318–12327. [Google Scholar]
- Morkunaite, Z.; Podvezko, V. Contractor selection for renovation of cultural heritage buildings by PROMETHEE method. Arch. Civ. Mech. Eng. 2019, 19, 1056–1071. [Google Scholar]
- Gul, M.; Celik, E. A fuzzy logic based PROMETHEE method for material selection problems. Beni-Suef Univ. J. Basic Appl. Sci. 2018, 7, 68–79. [Google Scholar]
- Mardani, A.; Zavadskas, E. VIKOR Technique: A Systematic Review of the State of the Art Literature on Methodologies and Applications. Sustainability 2016, 8, 37. [Google Scholar]
- Hashemi, H.; Mousavi, S. A New Group Decision Model Based on Grey-Intuitionistic Fuzzy-ELECTRE and VIKOR for Contractor Assessment Problem. Sustainability 2018, 10, 1635. [Google Scholar]
- Naghizadeh Vardin, A.; Ansari, R. An Integrated Decision Support Model Based on BWM and Fuzzy-VIKOR Techniques for Contractor Selection in Construction Projects. Sustainability 2021, 13, 6933. [Google Scholar]
- Geetha, S.; Narayanamoorthy, S. Extended hesitant fuzzy SWARA techniques to examine the criteria weights and VIKOR method for ranking alternatives. AIP Conf. Proc. 2020, 2261, 030144. [Google Scholar]
- Julong, D. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Sun, S.; Zhou, S. Analysis of Construction Contractor Selection and Evaluation Based on AHP and GRA. In ICCREM 2013: Construction and Operation in the Context of Sustainability; Amercian Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- Gholipour, R.; Jandaghi, G. Contractor selection in MCDM context using fuzzy AHP. Iran. J. Manag. Stud. 2014, 7, 151–173. [Google Scholar]
- Cao, Q.; Esangbedo, M. Grey SWARA-FUCOM Weighting Method for Contractor Selection MCDM Problem: A Case Study of Floating Solar Panel Energy System Installation. Energies 2019, 12, 2481. [Google Scholar]
- Yazdani, M.; Zarate, P. A Combined Compromise Solution (CoCoSo) Method for Multi-Criteria Decision-Making Problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar]
- Yazdani, M.; Wen, Z. A grey combined compromise solution (CoCoSo-G) method for supplier selection in construction management. J. Civ. Eng. Manag. 2019, 25, 858–874. [Google Scholar]
- Kumar, V.; Kalita, K. A SWARA-CoCoSo-Based Approach for Spray Painting Robot Selection. Informatica 2022, 33, 35–54. [Google Scholar]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 327–348. [Google Scholar]
- Zimmermann, H.-J. Fuzzy set theory and mathematical programming. In Fuzzy Sets Theory and Applications; Springer: Dordrecht, The Netherlands, 1986; pp. 99–114. [Google Scholar]
- Grattan-Guinness, I. Fuzzy Membership Mapped onto Intervals and Many-Valued Quantities. Math. Log. Q. 1976, 22, 149–160. [Google Scholar]
- Karnik, N.N.; Mendel, J.M. Operations on type-2 fuzzy sets. Fuzzy Sets Syst. 2001, 122, 327–348. [Google Scholar]
- Ashtiani, B.; Haghighirad, F. Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets. Appl. Soft Comput. 2009, 9, 457–461. [Google Scholar]
- Vahdani, B.; Hadipour, H. Extension of VIKOR method based on interval-valued fuzzy sets. Int. J. Adv. Manuf. Technol. 2010, 47, 1231–1239. [Google Scholar]
- Gorzałczany, M.B. A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst. 1987, 21, 1–17. [Google Scholar]
- Yao, J.S.; Lin, F.T. Constructing a fuzzy flow-shop sequencing model based on statistical data. Int. J. Approx. Reason. 2002, 29, 215–234. [Google Scholar]
- Chen, S. Fuzzy system reliability analysis based on vague set theory. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 2, pp. 1650–1655. [Google Scholar]
- Hong, D.H.; Lee, S. Some algebraic properties and a distance measure for interval-valued fuzzy numbers. Inf. Sci. 2002, 148, 1–10. [Google Scholar]
- Chen, S.J.; Chen, S.M. Fuzzy risk analysis based on measures of similarity between interval-valued fuzzy numbers. Comput. Math. Appl. 2008, 55, 1670–1685. [Google Scholar]
- Keršuliene, V.; Zavadskas, E.K. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (Swara). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar]
- Zelany, M. A concept of compromise solutions and the method of the displaced ideal. Comput. Oper. Res. 1974, 1, 479–496. [Google Scholar]
- Hatush, Z.; Skitmore, M. Evaluating contractor prequalification data: Selection criteria and project success factors. Constr. Manag. Econ. 1997, 15, 129–147. [Google Scholar]
- Dorfeshan, Y.; Jolai, F. A new risk quantification method in project-driven supply chain by MABACODAS method under interval type-2 fuzzy environment with a case study. Eng. Appl. Artif. Intell. 2023, 119, 105729. [Google Scholar]
- Davoudabadi, R.; Mousavi, S.M. A new fuzzy simulation approach for project evaluation based on concepts of risk, strategy, and group decision making with interval-valued intuitionistic fuzzy sets. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 8923–8941. [Google Scholar]
- Salimian, S.; Mousavi, S.M. A multi-criteria decision-making model with interval-valued intuitionistic fuzzy sets for evaluating digital technology strategies in COVID-19 pandemic under uncertainty. Arab. J. Sci. Eng. 2023, 48, 7005–7017. [Google Scholar]
- Mohagheghi, V.; Mousavi, S.M. Group decision-making based on last aggregation approach under interval-valued Pythagorean fuzzy environment for sustainable project decision. Sci. Iran. 2023, 30, 260–272. [Google Scholar]
- Mohagheghi, V.; Mousavi, S.M. Sustainable project portfolio selection and optimization with considerations of outsourcing decisions, financing options and staff assignment under interval type-2 fuzzy uncertainty. Neural Comput. Appl. 2022, 34, 14577–14598. [Google Scholar]
- Salimian, S.; Mousavi, S.M. Evaluation of infrastructure projects by a decision model based on RPR, MABAC, and WASPAS methods with interval-valued intuitionistic fuzzy sets. Int. J. Strateg. Prop. Manag. 2022, 26, 106–118. [Google Scholar]
- Dorfeshan, Y.; Mousavi, S.M. A new enhanced ARAS method for critical path selection of engineering projects with interval type-2 fuzzy sets. Int. J. Inf. Technol. Decis. Mak. 2021, 20, 37–65. [Google Scholar]


| Linguistic Variable | Abbreviation | IVFN |
|---|---|---|
| Absolutely Low | AL | [(0, 0.025), 0.075, (0.15, 0.2)] |
| Very Low | VL | [(0.1, 0.125), 0.175, (0.25, 0.3)] |
| Low | L | [(0.2, 0.225), 0.275, (0.35, 0.4)] |
| Medium Low | ML | [(0.3, 0.325), 0.375, (0.45, 0.5)] |
| Medium | M | [(0.4, 0.425), 0.475, (0.55, 0.6)] |
| Medium High | MH | [(0.5, 0.525), 0.575, (0.65, 0.7)] |
| High | H | [(0.6, 0.625), 0.675, (0.75, 0.8)] |
| Very High | VH | [(0.7, 0.725), 0.775, (0.85, 0.9)] |
| Absolutely High | AH | [(0.8, 0.825), 0.875, (0.95, 1)] |
| Linguistic Variable | Abbreviation | IVFN |
|---|---|---|
| Extremely Unimportant/Extremely Bad | EU/EB | [(0, 0.25), 0.75, (1.5, 2)] |
| Very Unimportant/Very Bad | VU/VB | [(1, 1.25), 1.75, (2.5, 3)] |
| Unimportant/Bad | U/B | [(2, 2.25), 2.75, (3.5, 4)] |
| Moderately Unimportant/Moderately Bad | MU/MB | [(3, 3.25), 3.75, (4.5, 5)] |
| Fair | F | [(4, 4.25), 4.75, (5.5, 6)] |
| Moderately Important/Moderately Good | MI/MG | [(5, 5.25), 5.75, (6.5, 7)] |
| Important/Good | I/G | [(6, 6.25), 6.75, (7.5, 8)] |
| Very Important/Very Good | VI/VG | [(7, 7.25), 7.75, (8.5, 9)] |
| Extremely Important/Excellent | EI/E | [(8, 8.25), 8.75, (9.5, 10)] |
| Decision Maker | R | FS | TA | HS | MC |
|---|---|---|---|---|---|
| DM1 | MU | U | VI | F | EI |
| DM2 | MI | MU | VI | F | I |
| DM3 | MU | VU | I | I | EI |
| DM4 | F | U | VI | MI | EI |
| DM5 | I | MU | I | MI | VI |
| DM6 | MU | F | I | F | EI |
| Decision Maker | R | FS | TA | HS | MC |
|---|---|---|---|---|---|
| DM1 | [(3, 3.25), 3.75, (4.5, 5)] | [(2, 2.25), 2.75, (3.5, 4)] | [(7, 7.25), 7.75, (8.5, 9)] | [(4, 4.25), 4.75, (5.5, 6)] | [(8, 8.25), 8.75, (9.5, 10)] |
| DM2 | [(5, 5.25), 5.75, (6.5, 7)] | [(3, 3.25), 3.75, (4.5, 5)] | [(7, 7.25), 7.75, (8.5, 9)] | [(4, 4.25), 4.75, (5.5, 6)] | [(6, 6.25), 6.75, (7.5, 8)] |
| DM3 | [(3, 3.25), 3.75, (4.5, 5)] | [(1, 1.25), 1.75, (2.5, 3)] | [(6, 6.25), 6.75, (7.5, 8)] | [(6, 6.25), 6.75, (7.5, 8)] | [(8, 8.25), 8.75, (9.5, 10)] |
| DM4 | [(4, 4.25), 4.75, (5.5, 6)] | [(2, 2.25), 2.75, (3.5, 4)] | [(7, 7.25), 7.75, (8.5, 9)] | [(5, 5.25), 5.75, (6.5, 7)] | [(8, 8.25), 8.75, (9.5, 10)] |
| DM5 | [(6, 6.25), 6.75, (7.5, 8)] | [(3, 3.25), 3.75, (4.5, 5)] | [(6, 6.25), 6.75, (7.5, 8)] | [(5, 5.25), 5.75, (6.5, 7)] | [(7, 7.25), 7.75, (8.5, 9)] |
| DM6 | [(3, 3.25), 3.75, (4.5, 5)] | [(4, 4.25), 4.75, (5.5, 6)] | [(6, 6.25), 6.75, (7.5, 8)] | [(4, 4.25), 4.75, (5.5, 6)] | [(8, 8.25), 8.75, (9.5, 10] |
| Average | [(4, 4.25), 4.75, (5.5, 6)] | [(2.5, 2.75), 3.25, (4, 4.5)] | [(6.5, 6.75), 7.25, (8, 8.5)] | [(4.67, 4.92), 5.42, (6.2, 6.67)] | [(7.5, 7.75), 8.25, (9, 9.5)] |
| Criteria | DM1 | DM2 | DM3 | DM4 | DM5 | DM6 |
|---|---|---|---|---|---|---|
| MC | - | - | - | - | - | - |
| TA | VL | AL | L | VL | VL | L |
| HS | ML | ML | AL | L | VL | L |
| R | VL | VL | ML | VL | VL | VL |
| FS | VL | L | L | L | ML | VL |
| Criteria | DM1 | DM2 | DM3 |
|---|---|---|---|
| MC | [(0, 0), 0, (0, 0)] | [(0, 0), 0, (0, 0)] | [(0, 0), 0, (0, 0)] |
| TA | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0, 0.025), 0.075, (0.15, 0.2)] | [(0.2, 0.225), 0.275, (0.35, 0.4)] |
| HS | [(0.3, 0.325), 0.375, (0.45, 0.5)] | [(0.3, 0.325), 0.375, (0.45, 0.5)] | [(0, 0.025), 0.075, (0.15, 0.2)] |
| R | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.3, 0.325), 0.375, (0.45, 0.5)] |
| FS | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.2, 0.225), 0.275, (0.35, 0.4)] | [(0.2, 0.225), 0.275, (0.35, 0.4)] |
| DM4 | DM5 | DM6 | |
| MC | [(0, 0), 0, (0, 0)] | [(0, 0), 0, (0, 0)] | [(0, 0), 0, (0, 0)] |
| TA | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.2, 0.225), 0.275, (0.35, 0.4)] |
| HS | [(0.2, 0.225), 0.275, (0.35, 0.4)] | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.2, 0.225), 0.275, (0.35, 0.4)] |
| R | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.1, 0.125), 0.175, (0.25, 0.3)] | [(0.1, 0.125), 0.175, (0.25, 0.3)] |
| FS | [(0.2, 0.225), 0.275, (0.35, 0.4)] | [(0.3, 0.325), 0.375, (0.45, 0.5)] | [(0.1, 0.125), 0.175, (0.25, 0.3)] |
| Average | |||
| MC | [(0, 0), 0, (0, 0)] | ||
| TA | [(0.117, 0.142), 0.191, (0.267, 0.317)] | ||
| HS | [(0.183, 0.208), 0.258, (0.333, 0.383)] | ||
| R | [(0.133, 0.158), 0.208, (0.283, 0.333)] | ||
| FS | [(0.183, 0.208), 0.258, (0.333, 0.383)] |
| Criteria | ||||
|---|---|---|---|---|
| MC | [(0, 0), 0, (0, 0)] | [(1, 1), 1, (1, 1)] | [(1, 1), 1, (1, 1)] | [(0.257, 0.267), 0.286, (0.314, 0.331)] |
| TA | [(0.117, 0.142), 0.192, (0.267, 0.317)] | [(1.117, 1.142), 1.192, (1.267, 1.317)] | [(0.759, 0.789), 0.839, (0.876, 0.896)] | [(0.196, 0.211), 0.240, (0.275, 0.297)] |
| HS | [(0.183, 0.208), 0.258, (0.333, 0.383)] | [(1.183, 1.208), 1.258, (1.333, 1.383)] | [(0.549, 0.592), 0.667, (0.725, 0.757)] | [(0.141, 0.158), 0.191, (0.227, 0.251)] |
| R | [(0.133, 0.158), 0.208, (0.283, 0.333)] | [(1.133, 1.158), 1.208, (1.283, 1.333)] | [(0.412, 0.461), 0.552, (0.626, 0.668)] | [(0.106, 0.123), 0.158, (0.196, 0.221)] |
| FS | [(0.183, 0.208), 0.258, (0.333, 0.383)] | [(1.183, 1.208), 1.258, (1.333, 1.383)] | [(0.298, 0.346), 0.439, (0.518, 0.564)] | [(0.077, 0.092), 0.125, (0.162, 0.187)] |
| Decision Maker | Reputation | |||||
|---|---|---|---|---|---|---|
| Contractor 1 | Contractor 2 | Contractor 3 | Contractor 4 | Contractor 5 | Contractor 6 | |
| DM1 | MG | MB | MG | B | VG | EB |
| DM2 | MG | B | VG | MB | G | VB |
| DM3 | MG | B | VG | MB | VG | EB |
| DM4 | F | MB | G | MB | G | B |
| DM5 | MB | F | G | VB | VG | VB |
| DM6 | MB | F | MG | MB | VG | EB |
| Financial soundness | ||||||
| Contractor 1 | Contractor 2 | Contractor 3 | Contractor 4 | Contractor 5 | Contractor 6 | |
| DM1 | F | MG | MB | G | MG | MG |
| DM2 | MG | MG | MB | VG | MB | G |
| DM3 | MG | VG | F | MG | MG | VG |
| DM4 | MG | G | MB | VG | B | E |
| DM5 | F | VG | MG | G | F | G |
| DM6 | G | G | F | G | MB | E |
| Technical ability | ||||||
| Contractor 1 | Contractor 2 | Contractor 3 | Contractor 4 | Contractor 5 | Contractor 6 | |
| DM1 | MG | MG | MB | EB | F | MB |
| DM2 | MG | MG | MB | MB | G | MB |
| DM3 | F | G | MB | EB | F | B |
| DM4 | MG | G | MB | B | MG | F |
| DM5 | G | MG | MB | EB | MG | MB |
| DM6 | G | G | MG | MB | F | MB |
| Health and safety | ||||||
| Contractor 1 | Contractor 2 | Contractor 3 | Contractor 4 | Contractor 5 | Contractor 6 | |
| DM1 | B | B | G | G | MB | G |
| DM2 | B | B | MG | G | F | F |
| DM3 | MB | VB | VG | G | MB | G |
| DM4 | MB | EB | VG | VG | MG | G |
| DM5 | F | EB | MG | E | F | F |
| DM6 | B | B | G | G | MG | MG |
| Management capability | ||||||
| Contractor 1 | Contractor 2 | Contractor 3 | Contractor 4 | Contractor 5 | Contractor 6 | |
| DM1 | F | MG | G | MB | VG | VG |
| DM2 | F | MG | MG | F | VG | VG |
| DM3 | F | MG | MG | F | VG | VG |
| DM4 | MG | F | MG | MB | G | VG |
| DM5 | MG | F | MG | B | G | MG |
| DM6 | MB | MB | G | MB | G | VG |
| Contractor | R | FS | TA | HS | MC |
|---|---|---|---|---|---|
| Cont 1 | [(4.17, 4.42), 4.92, (5.67, 6.17)] | [(4.83, 5.08), 5.58, (6.33, 6.83)] | [(5.17, 5.42), 5.92, (6.67, 7.17)] | [(2.67, 2.92), 3.42, (4.17, 4.67)] | [(4.17, 4.42), 4.92, (5.67, 6.17)] |
| Cont 2 | [(2.75, 3.25), 3.75, (4.25, 4.75)] | [(6.00, 6.25), 6.75, (7.50, 8.00)] | [(5.50, 5.75), 6.25, (7.00, 7.50)] | [(1.17, 1.42), 1.92, (2.67, 3.17)] | [(4.33, 4.58), 5.08, (5.83, 6.33)] |
| Cont 3 | [(5.75, 6.25), 6.75, (7.25, 7.75)] | [(3.67, 3.92), 4.42, (5.17, 5.67)] | [(3.33, 3.58), 4.08, (4.83, 5.33)] | [(6.00, 6.25), 6.75, (7.50, 8.00)] | [(5.33, 5.58), 6.08, (6.83, 7.33)] |
| Cont 4 | [(2.25, 2.75), 3.25, (3.75, 4.25)] | [(6.17, 6.42), 6.92, (7.67, 8.17)] | [(1.33, 1.58), 2.08, (2.83, 3.33)] | [(6.50, 6.75), 7.25, (8.00, 8.50)] | [(3.17, 3.42), 3.92, (4.67, 5.17)] |
| Cont 5 | [(6.42, 6.92), 7.42, (7.92, 8.42)] | [(3.67, 3.92), 4.42, (5.17, 5.67)] | [(4.67, 4.92), 5.42, (6.17, 6.67)] | [(4.00, 4.25), 4.75, (5.50, 6.00)] | [(6.50, 6.75), 7.25, (8.00, 8.50)] |
| Cont 6 | [(0.42, 0.92), 1.42, (1.92, 2.42)] | [(6.67, 6.92), 7.42, (8.17, 8.67)] | [(3.00, 3.25), 3.75, (4.50, 5.00)] | [(5.17, 5.42), 5.92, (6.67, 7.17)] | [(6.67, 6.92), 7.42, (8.17, 8.67)] |
| Contractor | R | FS | TA | HS | MC |
|---|---|---|---|---|---|
| Cont 1 | [(0.47, 0.50), 0.56, (0.66, 0.72)] | [(0.23, 0.28), 0.38, (0.53, 0.63)] | [(0.62, 0.66), 0.74, (0.86, 0.95)] | [(0.20, 0.24), 0.31, (0.41, 0.48)] | [(0.18, 0.23), 0.32, (0.45, 0.55)] |
| Cont 2 | [(0.29, 0.35), 0.42, (0.48, 0.54)] | [(0.47, 0.52), 0.62, (0.77, 0.87)] | [(0.68, 0.72), 0.80, (0.92, 1.00)] | [(0.00, 0.03), 0.10, (0.20, 0.27)] | [(0.21, 0.26), 0.35, (0.48, 0.58)] |
| Cont 3 | [(0.67, 0.73), 0.79, (0.85, 0.92)] | [(0.00, 0.05), 0.15, (0.30, 0.40)] | [(0.32, 0.36), 0.45, (0.57, 0.65)] | [(0.66, 0.69), 0.76, (0.86, 0.93)] | [(0.39, 0.44), 0.53, (0.67, 0.76)] |
| Cont 4 | [(0.23, 0.29), 0.35, (0.42, 0.48)] | [(0.50, 0.55), 0.65, (0.80, 0.90)] | [(0.00, 0.04), 0.12, (0.24, 0.32)] | [(0.73, 0.76), 0.83, (0.93, 1.00)] | [(0.00, 0.05), 0.14, (0.27, 0.36)] |
| Cont 5 | [(0.75, 0.81), 0.88, (0.94, 1.00)] | [(0.00, 0.05), 0.15, (0.30, 0.40)] | [(0.54, 0.58), 0.66, (0.78, 0.86)] | [(0.39, 0.42), 0.49, (0.59, 0.66)] | [(0.61, 0.65), 0.74, (0.88, 0.97)] |
| Cont 6 | [(0.00, 0.06), 0.13, (0.19, 0.25)] | [(0.60, 0.65), 0.75, (0.90, 1.00)] | [(0.27, 0.31), 0.39, (0.51, 0.59)] | [(0.55, 0.58), 0.65, (0.75, 0.82)] | [(0.64, 0.68), 0.77, (0.91, 1.00)] |
| Contractor | ||||
|---|---|---|---|---|
| Contractor 1 | 0.493 | 0.529 | 4.276 | 4.301 |
| Contractor 2 | 0.480 | 0.515 | 4.159 | 3.989 |
| Contractor 3 | 0.575 | 0.610 | 4.377 | 4.149 |
| Contractor 4 | 0.389 | 0.424 | 3.925 | 3.650 |
| Contractor 5 | 0.649 | 0.685 | 4.482 | 4.255 |
| Contractor 6 | 0.580 | 0.616 | 4.350 | 4.140 |
| Contractor | ||||||
|---|---|---|---|---|---|---|
| Contractor 1 | 0.166 | 0.173 | 2.356 | 2.428 | 0.929 | 0.969 |
| Contractor 2 | 0.161 | 0.162 | 2.293 | 2.308 | 0.904 | 0.903 |
| Contractor 3 | 0.172 | 0.171 | 2.591 | 2.577 | 0.965 | 0.954 |
| Contractor 4 | 0.150 | 0.146 | 2.000 | 2.000 | 0.841 | 0.817 |
| Contractor 5 | 0.179 | 0.177 | 2.810 | 2.784 | 1.000 | 0.991 |
| Contractor 6 | 0.172 | 0.171 | 2.598 | 2.588 | 0.961 | 0.954 |
| Contractors | Rank | |||
|---|---|---|---|---|
| Contractor 1 | 1.864 | 1.931 | 1.898 | 4 |
| Contractor 2 | 1.814 | 1.820 | 1.817 | 5 |
| Contractor 3 | 1.998 | 1.983 | 1.991 | 3 |
| Contractor 4 | 1.629 | 1.608 | 1.619 | 6 |
| Contractor 5 | 2.124 | 2.105 | 2.115 | 1 |
| Contractor 6 | 1.997 | 1.987 | 1.992 | 2 |
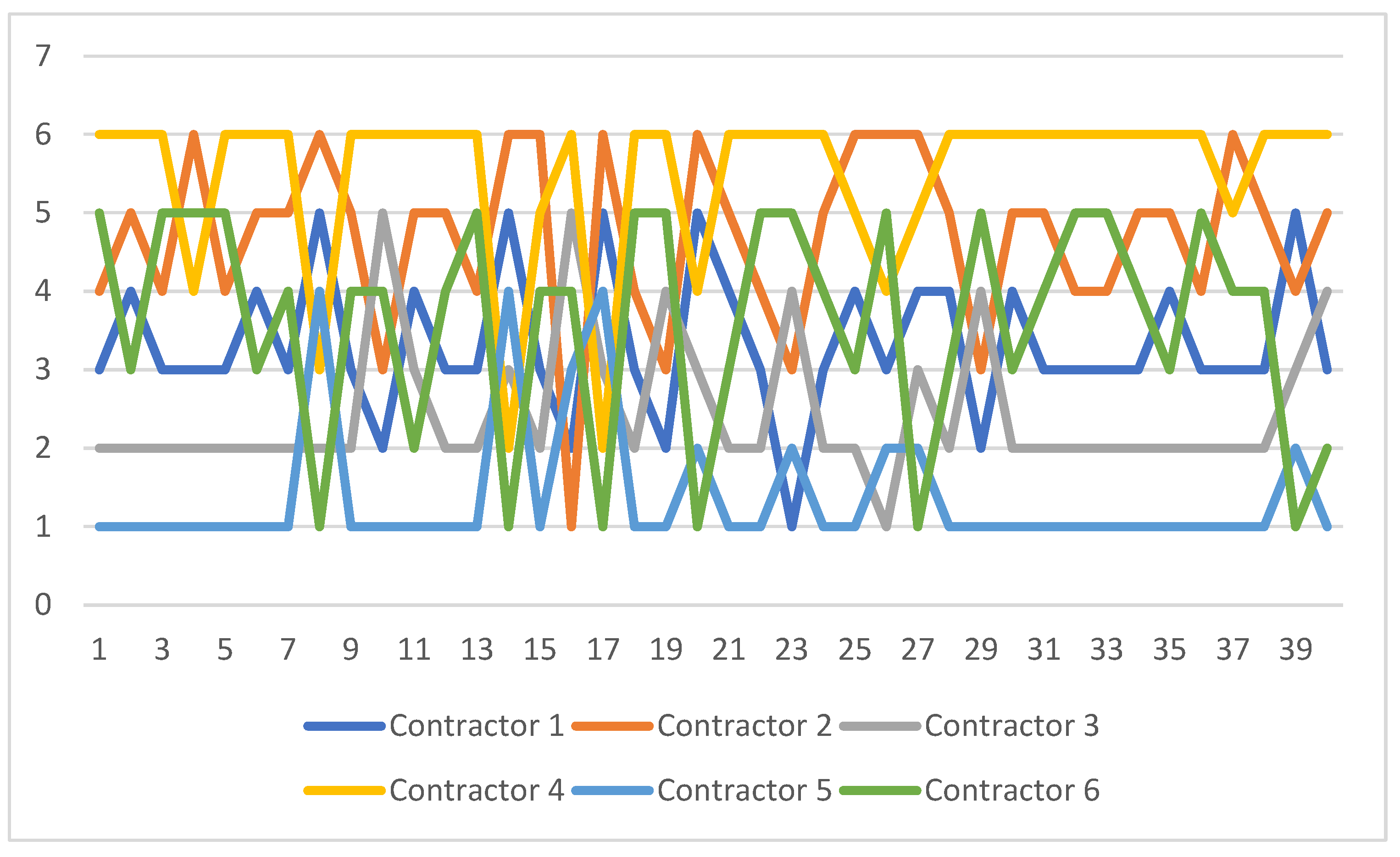
| Test | Rank | |||||
|---|---|---|---|---|---|---|
| Contractor 1 | Contractor 2 | Contractor 3 | Contractor 4 | Contractor 5 | Contractor 6 | |
| Test 1 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 2 | 4 | 5 | 2 | 6 | 1 | 3 |
| Test 3 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 4 | 3 | 6 | 2 | 4 | 1 | 5 |
| Test 5 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 6 | 4 | 5 | 2 | 6 | 1 | 3 |
| Test 7 | 3 | 5 | 2 | 6 | 1 | 4 |
| Test 8 | 5 | 6 | 2 | 3 | 4 | 1 |
| Test 9 | 3 | 5 | 2 | 6 | 1 | 4 |
| Test 10 | 2 | 3 | 5 | 6 | 1 | 4 |
| Test 11 | 4 | 5 | 3 | 6 | 1 | 2 |
| Test 12 | 3 | 5 | 2 | 6 | 1 | 4 |
| Test 13 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 14 | 5 | 6 | 3 | 2 | 4 | 1 |
| Test 15 | 3 | 6 | 2 | 5 | 1 | 4 |
| Test 16 | 2 | 1 | 5 | 6 | 3 | 4 |
| Test 17 | 5 | 6 | 3 | 2 | 4 | 1 |
| Test 18 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 19 | 2 | 3 | 4 | 6 | 1 | 5 |
| Test 20 | 5 | 6 | 3 | 4 | 2 | 1 |
| Test 21 | 4 | 5 | 2 | 6 | 1 | 3 |
| Test 22 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 23 | 1 | 3 | 4 | 6 | 2 | 5 |
| Test 24 | 3 | 5 | 2 | 6 | 1 | 4 |
| Test 25 | 4 | 6 | 2 | 5 | 1 | 3 |
| Test 26 | 3 | 6 | 1 | 4 | 2 | 5 |
| Test 27 | 4 | 6 | 3 | 5 | 2 | 1 |
| Test 28 | 4 | 5 | 2 | 6 | 1 | 3 |
| Test 29 | 2 | 3 | 4 | 6 | 1 | 5 |
| Test 30 | 4 | 5 | 2 | 6 | 1 | 3 |
| Test 31 | 3 | 5 | 2 | 6 | 1 | 4 |
| Test 32 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 33 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 34 | 3 | 5 | 2 | 6 | 1 | 4 |
| Test 35 | 4 | 5 | 2 | 6 | 1 | 3 |
| Test 36 | 3 | 4 | 2 | 6 | 1 | 5 |
| Test 37 | 3 | 6 | 2 | 5 | 1 | 4 |
| Test 38 | 3 | 5 | 2 | 6 | 1 | 4 |
| Test 39 | 5 | 4 | 3 | 6 | 2 | 1 |
| Test 40 | 3 | 5 | 4 | 6 | 1 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami, S.; Mousavi, S.M.; Antucheviciene, J. Enhancing Contractor Selection Process by a New Interval-Valued Fuzzy Decision-Making Model Based on SWARA and CoCoSo Methods. Axioms 2023, 12, 729. https://doi.org/10.3390/axioms12080729
Karami S, Mousavi SM, Antucheviciene J. Enhancing Contractor Selection Process by a New Interval-Valued Fuzzy Decision-Making Model Based on SWARA and CoCoSo Methods. Axioms. 2023; 12(8):729. https://doi.org/10.3390/axioms12080729
Chicago/Turabian StyleKarami, Sajjad, Seyed Meysam Mousavi, and Jurgita Antucheviciene. 2023. "Enhancing Contractor Selection Process by a New Interval-Valued Fuzzy Decision-Making Model Based on SWARA and CoCoSo Methods" Axioms 12, no. 8: 729. https://doi.org/10.3390/axioms12080729
APA StyleKarami, S., Mousavi, S. M., & Antucheviciene, J. (2023). Enhancing Contractor Selection Process by a New Interval-Valued Fuzzy Decision-Making Model Based on SWARA and CoCoSo Methods. Axioms, 12(8), 729. https://doi.org/10.3390/axioms12080729










