Limiting Behaviors of Stochastic Spread Models Using Branching Processes

Abstract

In this paper, we introduce a spread model using multi-type branching processes to investigate the evolution of the population during a pandemic in which individuals are classified into different types. We study some limiting behaviors of the population including the growth rate of the population and the spread rate of each type. In particular, the work in this paper focuses on the cases where the offspring mean matrices are non-primitive but can be decomposed into two primitive components, A and B, with maximal eigenvalues ${\rho }_A$ and ${\rho }_B$, respectively. It is shown that the growth rate and the spread rate heavily depend on the conditions of these two maximal eigenvalues and are related to the corresponding eigenvectors. In particular, we find the spread rates for the case with ${\rho }_B>{\rho }_A>1$ and the case with ${\rho }_A>{\rho }_B>1$. In addition, some numerical examples and simulations are also provided to support the theoretical results.

1. Introduction

When a pandemic spreads rapidly and widely around the world, developing a mathematical model becomes a useful tool to investigate the impact and spread of the viruses. Numerous models have been proposed in the literature to predict the spread of the diseases in order to come out with better disease control policies and measures. To describe the spread of the disease, techniques and ideas from different fields of study have been applied. For example, Altan and Kaasu [1] proposed a model consisting of a two-dimensional curvelet transformation, a met-heuristic optimization algorithm, and a deep learning technique to diagnose the infected patient from X-ray images. Balli [2] used a machine learning time series prediction model to obtain the disease curve and forecast the epidemic trend, while Bassey and Atsu [3] considered the model using dual-bilinear control treatment functions arising from dual non-pharmaceutical controls and dual pharmaceutical therapies to compute the system reproduction numbers and to analyze the system stability. Butt et al. [4] and Hanif et al. [5] proposed the Caputo–Fabrizio-fractional model to study the dynamical behavior of the pandemic and to prove the existence and uniqueness of the solutions using fractional calculus and a functional analysis, and so on.

Among the various models, the compartmental models are a very useful and common modelling technique. The most frequently investigated mathematical model of epidemics is the susceptible (S)–infected (I)–recovered (R) (SIR) model. It is a deterministic epidemic model in which the individuals are classified into three individuals that can only move from S to I and from I to R. Afterwards, many studies were conducted by generalizing this simplest compartment model. For example, Wu et al. [6] used the susceptible–exposed–infected–recovered metapopulation model (the SEIR model) to simulate epidemics and estimated the basic reproduction number via Markov Chain Monte Carlo methods, while Khajanchi and Sarkar [7] proposed a mathematical model called the SAIUQR model with six compartments, namely, susceptible (S), asymptomatic (A), reported symptomatic (I), unreported symptomatic (U), quarantine (Q), and recovered (R), in order to study the feasible equilibria and the stability with respect to the basic reproduction number, etc. However, it has been noticed that many compartment models are valid only in the case of sufficiently large populations, and hence, some stochastic models are presented. Britton [8] defined the standard stochastic SIR epidemic model for a closed population in order to study small population properties and a large population approximation. Bittihn and Golestanian [9] used a stochastic SIR metapopulation model for disease transmission and divided this large population into some sub-populations in which the number of infected individuals was low to estimate the effects of extinction and desynchronization. Faranda and Alberti [10] used the stochastic SEIR model in which the incubation, infection, and recovery rates are stochastically perturbed to investigate the long-term behavior of the epidemic evolution. He et al. [11] developed a discrete-time stochastic epidemic model with binomial distribution to forecast the spread of the disease in the next period and to evaluate the risk in order to provide suggestions on the returning timing to the routine. Khan et al. [12] used the stochastic Volterra integro-differential equation to model the disease transmission and used the spectral collocation method to approximate the solution of the equation.

In particular, multitype branching processes provide another stochastic approach to model the spread of the disease. Jacob [13] introduced various settings of branching processes for modeling the epidemic. According to the aims of the study, branching processes with different offspring distributions, initial conditions, or parameters are chosen to fit the population evolution. Britton [8] constructed the stochastic SIR model using the branching process with the exponential distributed infected period for an approximation of the early stage of an outbreak. Hellewell et al. [14] considered a branching process with a negative binomial offspring distribution to measure the success of controlling outbreaks using isolation and contact tracing. Levesque et al. [15] used a continuous time branching processes with a negative binomial offspring distribution to develop the efficacy of contact tracing strategies. Laha [16] considered a time-varying multitype branching process model for the spread of infectious disease in which it is assumed that all detected individuals are completely contact traced and the expected numbers of detected infected individuals, undetected infected individuals, and the total number of cases up to generation n are computed. Laha and Majumdar [17] extended the multitype branching model to the case in which the contact tracing is only partial and used Poisson offspring distributions whose parameters may vary over time to investigate the expected number of individuals in each category. Yanev et al. [18] considered both two-type (infected undetected vs infected detected) branching processes with or without immigration and studied the growth rate and so on.

In this article, we introduced a stochastic model using the multitype branching processes with a general offspring distribution for which the offspring mean matrix is no longer primitive but can be broken down into two primitive components. We investigated the asymptotic growth rate of the population vector and the spread rate of each type in an infectious disease according to the magnitude of the maximal eigenvalues of these two component matrices of the offspring mean matrix.

This paper is organized as follows. In Section 2, we introduce the setting of the stochastic spread model using branching processes. In Section 3, we present the results on the asymptotic growth rate, the properties of the population vector, and the spread rate of each type. Finally, the proofs of the main results are provided in Section 4.

2. Random Spread Models Using Branching Processes

To introduce a spread model using the multitype branching processes, we considered a population in which individuals are classified into K types, say $a_1,a_2,\cdots ,a_K$, where individuals in different categories can be considered as patients in different categories such as highly contagious, moderately contagious, mildly contagious, and so on. We assume that this population starts with one individual, i.e., the spread of the disease initiated by one individual at time 0 (or in the 0th generation). During the pandemic, the viruses are passed from person to person. We call an individual who is infected a “child” or an offspring of the individual who passes the viruses on, while the one passing the viruses on is called the “parent”. When the infected population evolves over time, we are interested only in the number of “children” each parent has. So, we assume that each individual lives (the time when this individual is able to infect others) a unit of time and, upon its death (recovery), produces its offspring according to the probability distribution ${\left\{p^{\left(i\right)}(·)\right\}}_{i=1}^K$, where $p^{\left(j\right)}(j_1,j_2,\cdots ,j_K)$ is the probability that an individual of type $a_i$ produces $j_1$ children of type $a_1$, $j_2$ children of type $a_2$, ⋯, and $j_K$ children of type $a_K$. This reproduction is also assumed to be independent of others in the same generation and in the past of the population. Let

$$\begin{array}{c}{\mathbf{Z}}_n=(Z_{n,1},Z_{n,2},\cdots ,Z_{n,K})\end{array}$$

be the population vector in the nth generation (or at time n), where $Z_{n,i}$ is the number of individuals of type $a_i$ in the nth generation, $i=1,2,\cdots ,K$. Then, the process ${\left\{{\mathbf{Z}}_n\right\}}_{n\ge 0}$ is called a K-type branching process with offspring distribution ${\left\{p^{\left(i\right)}(·)\right\}}_{i=1}^K$.

Let $m_{ij}=E\left(Z_{1,j}\right|{\mathbf{Z}}_0={\mathbf{e}}_i)$ be the expected value of the number of children of type $a_j$ produced by an individual of type $a_i$, where ${\mathbf{e}}_i$ is the unit vector with 1 as its ith component. Then, the matrix

$$\mathbf{M}\equiv \left[m_{ij}\right]=\left[\begin{array}{cccc}{m}_{11}& m_{12}& \cdots & m_{1K}\\ m_{21}& m_{22}& \cdots & m_{2K}\\ ⋮& ⋮& & ⋮\\ m_{K1}& m_{K2}& \cdots & m_{KK}\end{array}\right]$$

is called the offspring mean matrix for this branching process ${\left\{{\mathbf{Z}}_n\right\}}_{n\ge 0}$. Moreover, if ${\mathbf{M}}^2=\mathbf{M}·\mathbf{M}$ and ${\mathbf{M}}^n={\mathbf{M}}^{n-1}·\mathbf{M}$ for all $n\ge 3$; then, the $(i,j)$-entry $m_{i,j}^{\left(n\right)}$ of the matrix ${\mathbf{M}}^n$ is the expected value

$$\begin{array}{c}{m}_{ij}^{\left(n\right)}=E\left(Z_{n,j}\right|{\mathbf{Z}}_0={\mathbf{e}}_i)\end{array}$$

of the number of offspring of type $a_j$ in the nth generation of the population initiated by an ancestor of type $a_i$.

We know from the classical theory of branching processes that the behavior of the offspring matrix provides information about the branching process in the long run. In particular, the classical limit theorem tells that, when the branching process is non-singular and the offspring mean matrix $\mathbf{M}$ is primitive with a maximal eigenvalue $\rho \left(\mathbf{M}\right)>1$, under some proper conditions, the population vector grows geometrically almost surely:

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{Z}}_n}{\rho {\left(\mathbf{M}\right)}^n}={\mathbf{v}}_{\mathbf{M}}Wa.s.}\end{array}$$

(1)

where ${\mathbf{v}}_{\mathbf{M}}$ is the normalized left eigenvector associated with $\rho \left(\mathbf{M}\right)$ and W is a random variable. We refer readers to Athreya and Ney [19] for more details.

To analyze the population composition in the long run, we define the spread rate of each type $a_i$ as the limit, if it exists in some sense, of the proportion of individuals of type $a_i$ in the nth generation of the population initiated with one individual of type $a_l$ as $n\to \infty$. Namely, conditioned on the event of ${\mathbf{Z}}_0={\mathbf{e}}_l$,

$$\begin{array}{c}{\displaystyle s_{a_l}\left(a_i\right)=\underset{n\to \infty }{lim}\frac{Z_{n,i}}{{\displaystyle \sum _{j=1}^K}{Z}_{n,j}}}\end{array}$$

where $l,i=1,2,\cdots ,K$. The geometric convergence of the population vector stated in (1) above is usually the key to studying the spread rate of each type. However, in some situations, the offspring mean matrix is no longer primitive. For example, the spread model with frozen symbols proposed by Ban et al. [20] forms the non-primitive case. So, in this paper, we focus on the stochastic spread model with a non-primitive offspring mean matrix.

In addition, we define the covariance matrix ${\mathbf{V}}^{\left(l\right)}$ as the following:

$$\begin{array}{c}{\mathbf{V}}^{\left(l\right)}=Var\left({\mathbf{Z}}_1\right|{\mathbf{Z}}_0={\mathbf{e}}_l)\end{array}$$

where its $(i,j)$-entry is

$$\begin{array}{c}E\left(Z_{1,i}{Z}_{1,j}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)-E\left(Z_{1,i}\right|{\mathbf{Z}}_1={\mathbf{e}}_l)E\left(Z_{1,j}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)\end{array}$$

for all $i,j=1,2,\cdots ,K$. For each $l=1,2,\cdots ,K$, we also define the matrix ${\mathbf{C}}_n^{\left(l\right)}$ in which the $(i,j)$-entry is

$$\begin{array}{c}E\left(Z_{n,i}{Z}_{n,j}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)\end{array}$$

for all $i,j=1,2,\cdots ,K$. Note that this matrix ${\mathbf{C}}_n^{\left(l\right)}$ is symmetric, and the only nonzero entry in ${\mathbf{C}}_0^{\left(l\right)}$ is the $(l,l)$-entry. According to Harris [21] (p. 37), ${\mathbf{C}}_n^{\left(l\right)}$ can be written in the following form:

$$\begin{array}{c}\hfill {\displaystyle {\mathbf{C}}_n^{\left(l\right)}={\left({\mathbf{M}}^t\right)}^n{\mathbf{C}}_0^{\left(l\right)}{\mathbf{M}}^n+\sum _{s=1}^n{\left({\mathbf{M}}^t\right)}^{n-s}(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}E\left(Z_{s-1,r}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)){\mathbf{M}}^{n-s}.}\end{array}$$

(2)

With the proper condition of the covariance matrices ${\mathbf{V}}^{\left(l\right)}$, we can show the geometric growth rate of ${\mathbf{C}}_n^{\left(l\right)}$, which leads to the geometric growth of the population vector.

3. Main Results on the Growth and Spread Rates

Throughout this paper, the branching process is assumed to be non-singular and the offspring mean matrix is assumed to be of the following form:

$$\mathbf{M}=\left[\begin{array}{cc}A& O\\ C& B\end{array}\right].$$

where the $d\times d$ matrix A and the $(K-d)\times (K-d)$ matrix B are primitive and C is a non-zero matrix. Then, by induction and computation, we can find the form of ${\mathbf{M}}^n$:

$${\mathbf{M}}^n=\left[\begin{array}{cc}{A}^n& O\\ C_n& B^n\end{array}\right].$$

As shown in Ban et al. [20], there exists an N such that $C_N>0$.

We adapt the following notations: for any square matrix M, ${\rho }_M$ denotes the maximal eigenvalue of M, and ${\mathbf{w}}_M$ and ${\mathbf{v}}_M$ denote the right and left eigenvectors of M associated with ${\rho }_M$, respectively. In particular, if $M=\mathbf{M}$ is the offspring mean matrix, we write $\rho$ for ${\rho }_{\mathbf{M}}$, $\mathbf{w}$ for ${\mathbf{w}}_{\mathbf{M}}$ and $\mathbf{v}$ for ${\mathbf{v}}_{\mathbf{M}}$, respectively. We also normalize $\mathbf{v}=(v_1,\cdots ,v_K)$ and $\mathbf{w}={(w_1,\cdots ,w_K)}^t$ such that

$$\begin{array}{c}{\displaystyle \sum _{i=1}^K{v}_i=1\mathrm{and}\sum _{i=1}^K{w}_i{v}_i=1.}\end{array}$$

The first theorem in this section reveals the geometric growth of the population vector:

Theorem 1.

If $\rho >1$ and the covariance matrices ${\mathbf{V}}^{\left(l\right)}$’s are finite for all $l=1,2,\cdots ,K$, then there exists a random vector $\mathbf{W}={(W_1,W_2,\cdots ,W_K)}^t$ with $E\left({\mathbf{W}}^t\mathbf{W}\right)<\infty$ such that

$$\begin{array}{c}{\displaystyle \frac{{\mathbf{Z}}_n}{{\rho }^n}\to \mathbf{W}\mathrm{as} n\to \infty }\end{array}$$

both in mean square and with probability 1.

The next theorem tells us the property of the limit vector $\mathbf{W}$. Namely, it has the same direction as the left eigenvector $\mathbf{v}$ of the offspring mean matrix $\mathbf{M}$.

Theorem 2.

If $\rho >1$, the covariance matrices ${\mathbf{V}}^{\left(l\right)}$ are finite for all $l=1,2,\cdots ,K$ and the random vector $\mathbf{W}$ is defined as in Theorem 1. Then, there exists a random variable W such that

$$\begin{array}{c}\mathbf{W}=\mathbf{v}W\end{array}$$

with probability 1. Moreover, $E\left(W\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=w_l$ for all $l=1,2,\cdots ,K$.

Remark 1.

The left eigenvector $\mathbf{v}=({\mathbf{v}}_1,{\mathbf{v}}_2)$ of the offspring matrix $\mathbf{M}$ associated with the maximal eigenvalue ρ, where ${\mathbf{v}}_1\in {\mathrm{R}}^d$ and ${\mathbf{v}}_2\in {\mathrm{R}}^{K-d}$, has the following properties:

(i)

If ${\rho }_B>{\rho }_A>1$, then ${\mathbf{v}}_1>0$, ${\mathbf{v}}_2>0$ and ${\mathbf{v}}_2$ is a left eigenvector associated with ${\rho }_B$;

(ii)

If ${\rho }_A>{\rho }_B>1$, then ${\mathbf{v}}_1>0$, ${\mathbf{v}}_2=0$ and ${\mathbf{v}}_1$ is a left eigenvector associated with ${\rho }_A$.

Similar results also hold for the right eigenvector $\mathbf{w}={({\mathbf{w}}_1,{\mathbf{w}}_2)}^t$ of the offspring matrix $\mathbf{M}$ associated with ρ, where ${\mathbf{w}}_1\in {\mathrm{R}}^d$ and ${\mathbf{w}}_2\in {\mathrm{R}}^{K-d}$:

(i)

If ${\rho }_B>{\rho }_A>1$, then ${\mathbf{w}}_1=0$, ${\mathbf{w}}_2>0$ and ${\mathbf{w}}_2$ is a right eigenvector associated with ${\rho }_B$;

(ii)

If ${\rho }_A>{\rho }_B>1$, then ${\mathbf{w}}_1>0$, ${\mathbf{w}}_2>0$ and ${\mathbf{w}}_1$ is a right eigenvector associated with ${\rho }_A$.

We refer the readers to Ban et al. [20] for more details.

As a consequence of Theorems 1 and 2, we obtain the spread rate for the random spread model in the next two theorems according to the magnitude of ${\rho }_A$ and ${\rho }_B$.

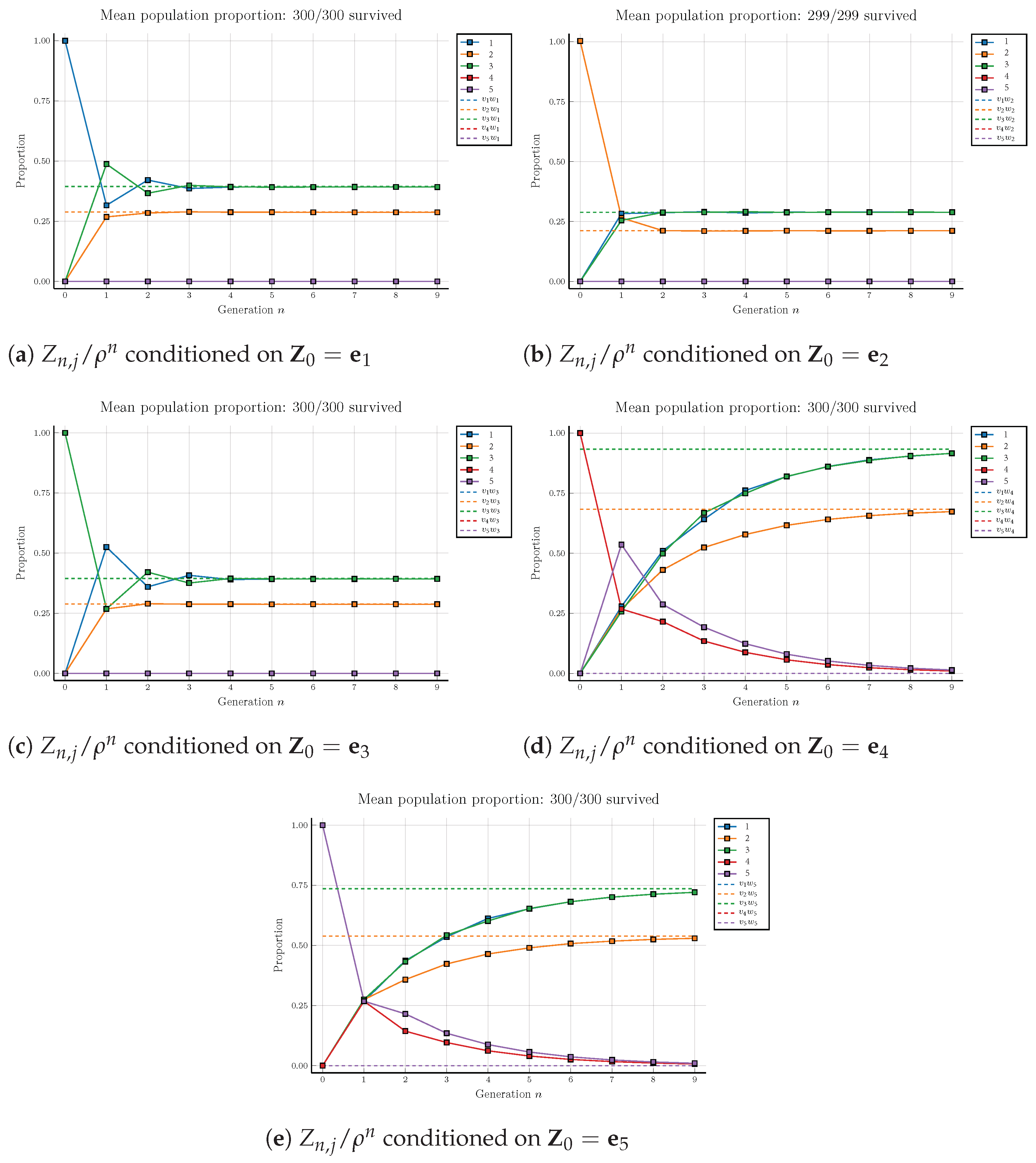
Theorem 3.

Let $\rho ={\rho }_B>{\rho }_A>1$ and the covariance matrices ${\mathbf{V}}^{\left(l\right)}$ be finite, and let ${\mathbf{Z}}_0={\mathbf{e}}_l$. Then, in the event $\left\{\parallel {\mathbf{Z}}_n\parallel \to \infty \right\}$, the spread rate

$$s_{a_l}\left(a_i\right)=\left\{\begin{array}{cc}{v}_i,\hfill & \mathit{for} l=d+1,\cdots ,K \mathit{and} i=1,2,\cdots ,K;\hfill \\ v_i^{\prime },\hfill & \mathit{for} l=1,\cdots ,d \mathit{and} i=1,2,\cdots ,d;\hfill \\ 0,\hfill & \mathit{for} l=1,\cdots ,d \mathit{and} i=d+1,\cdots ,K\hfill \end{array}\right.$$

with probability 1, where ${\mathbf{v}}_A=(v_1^{\prime },\cdots ,v_d^{\prime })$, is the normalized left eigenvector of A associated with the maximal eigenvalue ${\rho }_A$.

Theorem 4.

Let $\rho ={\rho }_A>{\rho }_B>1$ and the covariance matrices ${\mathbf{V}}^{\left(l\right)}$ be finite and let ${\mathbf{Z}}_0={\mathbf{e}}_l$. Then, in the event $\left\{\parallel {\mathbf{Z}}_n\parallel \to \infty \right\}$, the spread rate

$$s_{a_l}\left(a_i\right)=\left\{\begin{array}{cc}{v}_i,\hfill & \mathit{for} l=1,\cdots ,K \mathit{and} i=1,2,\cdots ,d;\hfill \\ 0,\hfill & \mathit{for} l=1,\cdots ,K \mathit{and} i=d+1,\cdots ,K\hfill \end{array}\right.$$

with probability 1.

4. Proofs of the Main Results

4.1. Lemmas

In order to make the proofs for Theorems 1–4 in Section 3 clearer, we state and prove the lemmas needed for establishing the theorems first.

More precisely, since the offspring mean is closely related to the evolution of the population, we first show the geometric growth rate of the power of the offspring mean matrix ${\mathbf{M}}^n$ in Lemma 1. This key property is used to study the growth rate of the matrices ${\mathbf{C}}_n^{\left(l\right)}$, $n=1,2,\cdots$, later in Lemmas 2–4 and allows us to further study the growth rate of the population vector in Theorem 1.

Lemma 1.

If ${\rho }_B>{\rho }_A>1$ or ${\rho }_B>{\rho }_A>1$, then, for any $i,j=1,2,\cdots ,K$, we have that

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^n}=w_i{v}_j.}\end{array}$$

Proof. 

Let $A=P_A{D}_A{P}_A^{-1}$ and $B=P_B{D}_B{P}_B^{-1}$ be the Jordan decompositions of A and B, respectively. Then, $\mathbf{M}=PD{P}^{-1}$, where

$$P=\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right],D=\left[\begin{array}{cc}{D}_A& O\\ O& D_B\end{array}\right],P^{-1}=\left[\begin{array}{cc}{P}_A^{-1}& O\\ R& P_B^{-1}\end{array}\right],$$

Q and R are $(K-d)\times d$ matrices, and O denotes the matrices in which all the elements are zero.

We assume that ${\rho }_A$ and ${\rho }_B$ are the $(1,1)$-elements in $D_A$ and $D_B$, respectively. Also, the matrices $P_A$ and $P_B$ are chosen such that the $(d+1)$st row in $P^{-1}$ is the normalized left eigenvector $\mathbf{v}$ of $\mathbf{M}$ associated with the maximal eigenvalue $\rho$ when ${\rho }_B>{\rho }_A>1$ or the first row in $P^{-1}$ is $\mathbf{v}$ when ${\rho }_A>{\rho }_B>1$. Note that this choice of $P_A$ and $P_B$ leads to the property that the $(d+1)$st column of P is the normalized right eigenvector $\mathbf{w}$ when ${\rho }_B>{\rho }_A>1$ and the first column of P is the normalized right eigenvector $\mathbf{w}$ when ${\rho }_A>{\rho }_B>1$. Therefore,

$${\mathbf{M}}^n=P{D}^n{P}^{-1}=\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]\left[\begin{array}{cc}{D}_A^n& O\\ O& D_B^n\end{array}\right]\left[\begin{array}{cc}{P}_A^{-1}& O\\ R& P_B^{-1}\end{array}\right]$$

and hence,

$$\begin{array}{ccc}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^n}}& =& {\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]\left[\begin{array}{cc}{D}_A^n& O\\ O& D_B^n\end{array}\right]\left[\begin{array}{cc}{P}_A^{-1}& O\\ R& P_B^{-1}\end{array}\right]{\mathbf{e}}_j}{{\rho }^n}}\\ & =& {\displaystyle \underset{n\to \infty }{lim}{\mathbf{e}}_i^t\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]\left[\begin{array}{cc}\frac{D_A^n}{{\rho }^n}& O\\ O& \frac{D_B^n}{{\rho }^n}\end{array}\right]\left[\begin{array}{cc}{P}_A^{-1}& O\\ R& P_B^{-1}\end{array}\right]{\mathbf{e}}_j}\\ & =& {\displaystyle {\mathbf{e}}_i^t\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]\left[\begin{array}{cc}{\displaystyle \underset{n\to \infty }{lim}\frac{D_A^n}{{\rho }^n}}& O\\ O& {\displaystyle \underset{n\to \infty }{lim}\frac{D_B^n}{{\rho }^n}}\end{array}\right]\left[\begin{array}{cc}{P}_A^{-1}& O\\ R& P_B^{-1}\end{array}\right]{\mathbf{e}}_j.}\end{array}$$

If ${\rho }_B>{\rho }_A>1$, then $\rho ={\rho }_B$ and since B is primitive, we have that

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{D_A^n}{{\rho }^n}=O\mathrm{and}\underset{n\to \infty }{lim}\frac{D_B^n}{{\rho }^n}=\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 0& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & 0\end{array}\right].}\end{array}$$

So,

$$\begin{array}{ccc}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^n}}& =& {\displaystyle \mathrm{the}i\mathrm{th}\mathrm{row}\mathrm{of}\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]·\left[\begin{array}{ccc}0& \cdots & 0\\ ⋮& & ⋮\\ 0& \cdots & 0\\ e_{d+1}^t& \left(\mathrm{in}\mathrm{the}\right(d+1\left)\mathrm{st}\mathrm{row}\right)& \\ 0& \cdots & 0\\ ⋮& & ⋮\\ 0& \cdots & 0\end{array}\right]}\hfill \\ & & ·\mathrm{the}j\mathrm{th}\mathrm{column}\mathrm{of}\left[\begin{array}{cc}{P}_A^{-1}& O\\ R& P_B^{-1}\end{array}\right]\hfill \\ & =& \mathrm{the}i\mathrm{th}\mathrm{row}\mathrm{of}\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]·v_j{\mathbf{e}}_{d+1}\hfill \\ & =& w_i{v}_j.\hfill \end{array}$$

Similarly, if ${\rho }_A>{\rho }_B>1$, then $\rho ={\rho }_A$ and, by the primivitity of A, we have that

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{D_A^n}{{\rho }^n}=\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 0& \cdots & 0\\ ⋮& ⋮& & ⋮\\ 0& 0& \cdots & 0\end{array}\right]\mathrm{and}\underset{n\to \infty }{lim}\frac{D_B^n}{{\rho }^n}=O}\end{array}$$

and then,

$$\begin{array}{ccc}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^n}}& =& {\displaystyle \mathrm{the}i\mathrm{th}\mathrm{row}\mathrm{of}\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]·\left[\begin{array}{ccc}& e_1^t& \\ 0& \cdots & 0\\ ⋮& & ⋮\\ 0& \cdots & 0\end{array}\right]}\hfill \\ & & ·\mathrm{the}j\mathrm{th}\mathrm{column}\mathrm{of}\left[\begin{array}{cc}{P}_A^{-1}& O\\ R& P_B^{-1}\end{array}\right]\hfill \\ & =& \mathrm{the}i\mathrm{th}\mathrm{row}\mathrm{of}\left[\begin{array}{cc}{P}_A& O\\ Q& P_B\end{array}\right]·v_j{\mathbf{e}}_1\hfill \\ & =& w_i{v}_j.\hfill \end{array}$$

So, the proof Lemma 1 is complete. □

Next, for each $l=1,2,\cdots ,K$ and each $n=1,2,\cdots$, we divide the form of ${\mathbf{C}}_n^{\left(l\right)}$ introduced in (2) in Section 2 into two parts and exam the growth rate for each part separately by letting

$$\begin{array}{c}{\mathbf{I}}_{n,1}^{\left(l\right)}={\left({\mathbf{M}}^t\right)}^n{\mathbf{C}}_0^{\left(l\right)}{\mathbf{M}}^n\end{array}$$

and

$$\begin{array}{c}{\displaystyle {\mathbf{I}}_{n,2}^{\left(l\right)}=\sum _{s=1}^n{\left({\mathbf{M}}^t\right)}^{n-s}(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}E\left(Z_{s-1,r}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)){\mathbf{M}}^{n-s}}\end{array}$$

and then, we have that ${\mathbf{C}}_n^{\left(l\right)}={\mathbf{I}}_{n,1}^{\left(l\right)}+{\mathbf{I}}_{n,2}^{\left(l\right)}$.

Lemma 2.

For each $i,j,l=1,2,\cdots ,K$,

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{I}}_{n,1}^{\left(l\right)}{\mathbf{e}}_j}{{\rho }^{2n}}=w_l^2{v}_i{v}_j.}\end{array}$$

Proof. 

By Lemma 1, we have that

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_l^t{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^n}=w_l{v}_j}\end{array}$$

and hence,

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^n{\mathbf{e}}_l}{{\rho }^n}=\underset{n\to \infty }{lim}{\left(\frac{{\mathbf{e}}_l^t{\mathbf{M}}^n{\mathbf{e}}_i}{{\rho }^n}\right)}^t=w_l{v}_i.}\end{array}$$

So,

$$\begin{array}{cc}& {\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{I}}_{n,1}^{\left(l\right)}{\mathbf{e}}_j}{{\rho }^{2n}}=\underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^n{\mathbf{C}}_0^{\left(l\right)}{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^{2n}}=\underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^n{\mathbf{e}}_l}{{\rho }^n}·{\mathbf{e}}_l^t{\mathbf{C}}_0^{\left(l\right)}{\mathbf{e}}_l·\frac{{\mathbf{e}}_l^t{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^n}}\hfill \\ =\hfill & {\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^n{\mathbf{e}}_l}{{\rho }^n}·\underset{n\to \infty }{lim}\frac{{\mathbf{e}}_l^t{\mathbf{M}}^n{\mathbf{e}}_j}{{\rho }^n}=w_l{v}_i·w_l{v}_j=w_l^2{v}_i{v}_j.}\hfill \end{array}$$

□

Lemma 3.

For each $i,j,l=1,2,\cdots ,K$,

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{I}}_{n,2}^{\left(l\right)}{\mathbf{e}}_j}{{\rho }^{2n}}=w_l^2{v}_i{v}_{j}A}\end{array}$$

for some non-negative constant A.

Proof. 

By Lemma 1, for any $ϵ>0$, there exists an $N=N(i,j,l,ϵ)\in \mathrm{N}$ such that for every $n\ge N$, we have that

$$\begin{array}{c}{\displaystyle |\frac{{\mathbf{e}}_i^t{\mathbf{M}}^n{\mathbf{e}}_l}{{\rho }^n}·\frac{{\mathbf{e}}_l^t{\left({\mathbf{M}}^t\right)}^n{\mathbf{e}}_j}{{\rho }^n}-w_l^2{v}_i{v}_j|<ϵ.}\end{array}$$

For $n>2N$,

$$\begin{array}{cc}& {\displaystyle \frac{{\mathbf{e}}_i^t{\mathbf{I}}_{n,2}^{\left(l\right)}{\mathbf{e}}_j}{{\rho }^{2n}}}\hfill \\ =\hfill & {\displaystyle {\displaystyle \frac{1}{{\rho }^{2n}}{\mathbf{e}}_i^t\left[\sum _{s=1}^n{\left({\mathbf{M}}^t\right)}^{n-s}(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}E\left(Z_{s-1,r}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)){\mathbf{M}}^{n-s}\right]{\mathbf{e}}_j}}\hfill \\ =\hfill & {\displaystyle \sum _{s=1}^N\frac{1}{{\rho }^{2s}}\frac{{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^{n-s}{\mathbf{e}}_l}{{\rho }^{n-s}}·{\mathbf{e}}_l^t(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}E\left(Z_{s-1,r}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)){\mathbf{e}}_l·\frac{{\mathbf{e}}_l^t{\mathbf{M}}^{n-s}{\mathbf{e}}_j}{{\rho }^{n-s}}}\hfill \\ & {\displaystyle +\sum _{s=N+1}^{n-N}\frac{1}{{\rho }^{s+1}}\frac{{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^{n-s}{\mathbf{e}}_l}{{\rho }^{n-s}}·{\mathbf{e}}_l^t(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}\frac{E\left(Z_{s-1,r}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)}{{\rho }^{s-1}}){\mathbf{e}}_l·\frac{{\mathbf{e}}_l^t{\mathbf{M}}^{n-s}{\mathbf{e}}_j}{{\rho }^{n-s}}}\hfill \\ & {\displaystyle +\frac{1}{{\rho }^n}\sum _{s=n-N+1}^n\frac{1}{{\rho }^{n-s+1}}{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^{n-s}{\mathbf{e}}_l·{\mathbf{e}}_l^t(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}\frac{E\left(Z_{s-1,r}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)}{{\rho }^{s-1}}){\mathbf{e}}_l·{\mathbf{e}}_l^t{\mathbf{M}}^{n-s}{\mathbf{e}}_j}\hfill \\ \equiv \hfill & J_{n,1}^{\left(l\right)}+J_{n,2}^{\left(l\right)}+J_{n,3}^{\left(l\right)}.\hfill \end{array}$$

First of all, if $s\le N$, then $n-s>N$ and $s-1<N$. Let

$$\begin{array}{c}{\displaystyle A_1\equiv \sum _{s=1}^N\frac{1}{{\rho }^{2s}}{\mathbf{e}}_l^t(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}E\left(Z_{s-1,r}\right|{\mathbf{Z}}_0={\mathbf{e}}_l)){\mathbf{e}}_l}\end{array}$$

and we have that $0\le A_1<\infty$ and

$$\begin{array}{c}{J}_{n,1}^{\left(l\right)}\to w_l^2{v}_i{v}_j{A}_1,\mathrm{as} n\to \infty .\end{array}$$

Secondly, if $N+1\le s\le n-N$ and $n>2N$, then $n-s\ge N$ and $s-1\ge N$. Hence, let

$$\begin{array}{c}{\displaystyle A_2\equiv \sum _{s=N+1}^{\infty }\frac{1}{{\rho }^{s+1}}{w}_l{\mathbf{e}}_l^t(\sum _{r=1}^K{\mathbf{V}}^{\left(r\right)}{v}_r){\mathbf{e}}_l}\end{array}$$

and note that, since $\rho >1$, $A_2$ is a non-negative and convergent series. Therefore, we have that

$$\begin{array}{c}{J}_{n,2}^{\left(l\right)}\to w_l^2{v}_i{v}_j{A}_2,\mathrm{as} n\to \infty .\end{array}$$

Thirdly, if $n-N+1\le s\le n$ and $n>2N$, then $0\le n-s\le N-1$ and $s-1>N$; then, using similar arguments, we can see that $J_{n,3}^{\left(l\right)}=O\left({\rho }^{-n}\right)$ as $n\to \infty$.

Therefore, we have that

$$\begin{array}{c}{\displaystyle \frac{{\mathbf{e}}_j^t{\mathbf{I}}_{n,2}^{\left(l\right)}{\mathbf{e}}_i}{{\rho }^{2n}}=J_{n,1}^{\left(l\right)}+J_{n,2}^{\left(l\right)}+J_{n,3}^{\left(l\right)}\to w_l^2{v}_i{v}_{j}A,\mathrm{as} n\to \infty ,}\end{array}$$

where $A=A_1+A_2\ge 0$. □

Lemmas 2 and 3 together give the following lemma:

Lemma 4.

For all $i,j,l=1,2,\cdots ,K$, there exists a constant $A^{\prime }>0$ such that

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}\frac{{\mathbf{e}}_j^t{\mathbf{C}}_n^{\left(l\right)}{\mathbf{e}}_i}{{\rho }^{2n}}=w_l^2{v}_i{v}_j{A}^{\prime }}\end{array}$$

Now, we are ready to prove Theorem 1.

4.2. Proof of Theorem 1

Proof  of Theorem 1.

For $n=0,1,2,\cdots$, let ${\displaystyle {\mathbf{W}}_n=\frac{{\mathbf{Z}}_n}{{\rho }^n}}$, and we first show that $\left\{{\mathbf{W}}_n\right\}$ is Cauchy in the means square sense, i.e.,

$$\begin{array}{c}E\left({({\mathbf{W}}_{n+m}-{\mathbf{W}}_n)}^t({\mathbf{W}}_{n+m}-{\mathbf{W}}_n)|{\mathbf{Z}}_0={\mathbf{e}}_l\right)\to 0,\mathrm{as}m,n\to \infty .\end{array}$$

and hence is convergent.

Note that

$$\begin{array}{cc}& E\left({({\mathbf{W}}_{n+m}-{\mathbf{W}}_n)}^t({\mathbf{W}}_{n+m}-{\mathbf{W}}_n)|{\mathbf{Z}}_0={\mathbf{e}}_l\right)\hfill \\ =\hfill & E\left({\mathbf{W}}_{n+m}^t{\mathbf{W}}_{n+m}|{\mathbf{Z}}_0={\mathbf{e}}_l\right)-E\left({\mathbf{W}}_{n+m}^t{\mathbf{W}}_n|{\mathbf{Z}}_0={\mathbf{e}}_l\right)\hfill \\ & -E\left({\mathbf{W}}_n^t{\mathbf{W}}_{n+m}|{\mathbf{Z}}_0={\mathbf{e}}_l\right)+E\left({\mathbf{W}}_n^t{\mathbf{W}}_n|{\mathbf{Z}}_0={\mathbf{e}}_l\right)\hfill \end{array}$$

and by the Markov property of branching process, i.e., for $n,m=0,1,2,\cdots$,

$$\begin{array}{c}E\left({\mathbf{Z}}_{n+m}\right|{\mathbf{Z}}_n)={\mathbf{Z}}_n{\mathbf{M}}^m,\end{array}$$

we have that

$$\begin{array}{c}{\displaystyle E\left({\mathbf{W}}_{n+m}^t{\mathbf{W}}_n|{\mathbf{Z}}_0={\mathbf{e}}_l\right)=\frac{{\left({\mathbf{M}}^t\right)}^m{\mathbf{C}}_n^{\left(l\right)}}{{\rho }^{2n+m}}}\end{array}$$

and

$$\begin{array}{c}{\displaystyle E\left({\mathbf{W}}_n^t{\mathbf{W}}_{n+m}|{\mathbf{Z}}_0={\mathbf{e}}_l\right)=\frac{{\mathbf{C}}_n^{\left(l\right)}{\mathbf{M}}^m}{{\rho }^{2n+m}}.}\end{array}$$

By the same arguments in the proofs of Lemmas 2 and 3, we can show that, as $m,n\to \infty$, for any $i,j,l=1,2,\cdots ,K$,

$$\begin{array}{c}{\displaystyle {\mathbf{e}}_i^{t}E\left({\mathbf{W}}_{n+m}^t{\mathbf{W}}_n|{\mathbf{Z}}_0={\mathbf{e}}_l\right){\mathbf{e}}_j=\frac{{\mathbf{e}}_i^t{\left({\mathbf{M}}^t\right)}^m{\mathbf{C}}_n^{\left(l\right)}{\mathbf{e}}_j}{{\rho }^{2n+m}}\to w_l^2{v}_i{v}_j{A}^{\prime }}\end{array}$$

and

$$\begin{array}{c}{\displaystyle {\mathbf{e}}_i^{t}E\left({\mathbf{W}}_n^t{\mathbf{W}}_{n+m}|{\mathbf{Z}}_0={\mathbf{e}}_l\right){\mathbf{e}}_j=\frac{{\mathbf{e}}_i^t{\mathbf{C}}_n^{\left(l\right)}{\mathbf{M}}^m{\mathbf{e}}_j}{{\rho }^{2n+m}}\to w_l^2{v}_i{v}_j{A}^{\prime }.}\end{array}$$

Moreover, as $n\to \infty$,

$$\begin{array}{c}{\displaystyle {\mathbf{e}}_i^{t}E\left({\mathbf{W}}_n^t{\mathbf{W}}_n\right|{\mathbf{Z}}_0={\mathbf{e}}_l){\mathbf{e}}_j=\frac{{\mathbf{e}}_i^{t}E\left({\left({\mathbf{Z}}_n\right)}^t{\mathbf{Z}}_n\right|{\mathbf{Z}}_0={\mathbf{e}}_l){\mathbf{e}}_j}{{\rho }^{2n}}=\frac{{\mathbf{e}}_i^t{\mathbf{C}}_n^{\left(l\right)}{\mathbf{e}}_j}{{\rho }^{2n}}\to w_l^2{v}_i{v}_j{A}^{\prime }.}\end{array}$$

Therefore, as $m,n\to \infty$,

$$\begin{array}{cc}& {\mathbf{e}}_j^{t}E\left({({\mathbf{W}}_{n+m}-{\mathbf{W}}_n)}^t({\mathbf{W}}_{n+m}-{\mathbf{W}}_n)|{\mathbf{Z}}_0={\mathbf{e}}_l\right){\mathbf{e}}_i\hfill \\ =\hfill & {\displaystyle \frac{{\mathbf{e}}_j^t{\mathbf{C}}_{n+m}^{\left(l\right)}{\mathbf{e}}_i}{{\rho }^{2(n+m)}}-\frac{{\mathbf{e}}_j^t{\mathbf{M}}^m{\mathbf{C}}_n^{\left(l\right)}{\mathbf{e}}_i}{{\rho }^{2n+m}}-\frac{{\mathbf{e}}_j^t{\mathbf{C}}_n^{\left(l\right)}{\left({\mathbf{M}}^t\right)}^m{\mathbf{e}}_i}{{\rho }^{2n+m}}+\frac{{\mathbf{e}}_j^t{\mathbf{C}}_n^{\left(l\right)}{\mathbf{e}}_i}{{\rho }^{2n}}\to 0.}\hfill \end{array}$$

So, the sequence ${\left\{{\mathbf{W}}_n\right\}}_{n\ge 0}$ is a Cauchy and hence convergent in mean square. Therefore, there exists a random vector $\mathbf{W}$ with $E\left({\mathbf{W}}^t\mathbf{W}\right)$ finite such that

$$\begin{array}{c}{\displaystyle {\mathbf{W}}_n=\frac{{\mathbf{Z}}_n}{{\rho }^n}\to \mathbf{W}\mathrm{in}\mathrm{mean}\mathrm{square},\mathrm{as}n\to \infty .}\end{array}$$

In addition, as $n\to \infty$,

$$\begin{array}{cc}& {\mathbf{e}}_i^{t}E\left({(\mathbf{W}-{\mathbf{W}}_n)}^t(\mathbf{W}-{\mathbf{W}}_n)|{\mathbf{Z}}_0={\mathbf{e}}_l\right){\mathbf{e}}_j\hfill \\ =\hfill & {\displaystyle \underset{m\to \infty }{lim}{\mathbf{e}}_i^{t}E\left({({\mathbf{W}}_m-{\mathbf{W}}_n)}^t({\mathbf{W}}_m-{\mathbf{W}}_n)|{\mathbf{Z}}_0={\mathbf{e}}_l\right){\mathbf{e}}_j=O\left({\rho }^{-2n}\right)}\hfill \end{array}$$

and hence,

$$\begin{array}{cc}& {\displaystyle E\left({\mathbf{e}}_i^t(\sum _{n=0}^{\infty }{(\mathbf{W}-{\mathbf{W}}_n)}^t(\mathbf{W}-{\mathbf{W}}_n)){\mathbf{e}}_j|{\mathbf{Z}}_0={\mathbf{e}}_l\right)}\hfill \\ =\hfill & {\displaystyle \sum _{n=0}^{\infty }E\left({\mathbf{e}}_i^t\left({(\mathbf{W}-{\mathbf{W}}_n)}^t(\mathbf{W}-{\mathbf{W}}_n)\right){\mathbf{e}}_j\right|{\mathbf{Z}}_0={\mathbf{e}}_l)<\infty .}\hfill \end{array}$$

So, given ${\mathbf{Z}}_0={\mathbf{e}}_l$, for all l, ${\displaystyle {\mathbf{e}}_i^t(\sum _{n=0}^{\infty }{(\mathbf{W}-{\mathbf{W}}_n)}^t(\mathbf{W}-{\mathbf{W}}_n)){\mathbf{e}}_j<\infty }$ with probability 1 and, therefore, for all $i,j=1,2,\cdots ,K$,

$$\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}{\mathbf{e}}_i^t{(\mathbf{W}-{\mathbf{W}}_n)}^t(\mathbf{W}-{\mathbf{W}}_n){\mathbf{e}}_j=0\mathrm{with}\mathrm{probability}1.}\end{array}$$

It follows that ${\mathbf{e}}_i^t(\mathbf{W}-{\mathbf{W}}_n){\mathbf{e}}_j\to 0$ with probability 1 for all $i,j=1,2,\cdots ,K$ and hence gives that, as $n\to \infty$,

$$\begin{array}{c}{\mathbf{W}}_n\to \mathbf{W}\mathrm{with}\mathrm{probability}1.\end{array}$$

So, ${\mathbf{W}}_n$ converges to $\mathbf{W}$ both in mean square and with probability 1, and the proof of Theorem 1 is complete. □

4.3. Proof of Theorem 2

Next, we are going to prove Theorem 2, which says that the vectors $\mathbf{W}$ and $\mathbf{v}$ share the same direction.

Proof of Theorem 2.

Let $\mathbf{W}=(W_1,W_2,\cdots ,W_K)$, where $W_1,\cdots ,W_K$ are random variables. From the proof of Theorem 1, we have that

$$\begin{array}{cc}& {\mathbf{e}}_i^{t}E\left({\mathbf{W}}^t\mathbf{W}\right|{\mathbf{Z}}_0={\mathbf{e}}_l){\mathbf{e}}_j\hfill \\ =\hfill & {\displaystyle \underset{n\to \infty }{lim}{\mathbf{e}}_i^{t}E\left(\frac{{\left({\mathbf{Z}}_n\right)}^t}{{\rho }^n}·\frac{{\mathbf{Z}}_n}{{\rho }^n}|{\mathbf{Z}}_0={\mathbf{e}}_l\right){\mathbf{e}}_i=\underset{n\to \infty }{lim}\frac{{\mathbf{e}}_i^t{\mathbf{C}}_n^{\left(l\right)}{\mathbf{e}}_j}{{\rho }^{2n}}=w_l{v}_i{v}_j{A}^{\prime },}\hfill \end{array}$$

So, for $v_i>0$ and $v_j>0$,

$$\begin{array}{cc}& E\left({(v_i{W}_j-v_j{W}_i)}^2|{\mathbf{Z}}_0={\mathbf{e}}_l\right)\hfill \\ =\hfill & v_i^{2}E\left(W_j^2\right|{\mathbf{Z}}_0={\mathbf{e}}_l)-2v_i{v}_{j}E\left(W_i{W}_j\right|{\mathbf{Z}}_0={\mathbf{e}}_l)+v_j^{2}E\left(W_i^2\right|{\mathbf{Z}}_0={\mathbf{e}}_l)\hfill \\ =\hfill & v_i^2{\mathbf{e}}_j^{t}E\left({\mathbf{W}}^t\mathbf{W}\right|{\mathbf{Z}}_0={\mathbf{e}}_l){\mathbf{e}}_j-2v_i{v}_j{\mathbf{e}}_i^{t}E\left({\mathbf{W}}^t\mathbf{W}\right|{\mathbf{Z}}_0={\mathbf{e}}_l){\mathbf{e}}_j\hfill \\ & +v_j^2{\mathbf{e}}_i^{t}E\left({\mathbf{W}}^t\mathbf{W}\right|{\mathbf{Z}}_0={\mathbf{e}}_l){\mathbf{e}}_i\hfill \\ =\hfill & v_i^2{w}_l^2{v}_j{v}_j{A}^{\prime }-2v_i{v}_j{w}_l^2{v}_i{v}_j{A}^{\prime }+v_j^2{w}_l^2{v}_i{v}_i{A}^{\prime }\hfill \\ =\hfill & 0.\hfill \end{array}$$

and hence, $v_i{W}_j=v_j{W}_i$ with probability 1. Therefore,

$$\begin{array}{c}{\displaystyle \frac{W_i}{v_i}=\frac{W_j}{v_j}\mathrm{with}\mathrm{probability}1}\end{array}$$

for all $i,j$ such that $v_i>0$ and $v_j>0$. Note that, if ${\rho }_B>{\rho }_A>1$, then $v_i>0$ for all $i=1,2,\cdots ,K$, and if ${\rho }_A>{\rho }_B>1$, then $v_i=0$ for $i=d+1,\cdots .K$. When $v_i=0$, we have that

$$\begin{array}{c}E\left(W_i^2\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=e_i^{t}E\left({\mathbf{W}}^t\mathbf{W}\right|{\mathbf{Z}}_0={\mathbf{e}}_l){\mathbf{e}}_i=w_l^2{v}_i^2=0\end{array}$$

which implies that $W_i=0$ with probability 1.

Therefore, there exists a random variable W such that

$$\begin{array}{c}\mathbf{W}=(W_1,W_2,\cdots ,W_k)=(v_{1}W,v_{2}W,\cdots ,v_{K}W)=\mathbf{v}W\end{array}$$

and

$$\begin{array}{c}{\displaystyle \frac{{\mathbf{Z}}_n}{{\rho }^n}\to \mathbf{v}W}\end{array}$$

with probability 1. Moreover, since

$$\begin{array}{c}E\left({\mathbf{Z}}_n\right|{\mathbf{Z}}_0={\mathbf{e}}_l)={\mathbf{e}}_l^t{\mathbf{M}}^n,\end{array}$$

we have that

$$\begin{array}{c}{\displaystyle E\left({\mathbf{W}}_n\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=\frac{1}{{\rho }^n}E\left({\mathbf{Z}}_n\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=\frac{{\mathbf{e}}_l^t{\mathbf{M}}^n}{{\rho }^n}}\end{array}$$

and then,

$$\begin{array}{c}{\displaystyle E\left(W_i\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=\underset{n\to \infty }{lim}E\left({\mathbf{W}}_n{\mathbf{e}}_i\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=\underset{n\to \infty }{lim}\frac{{\mathbf{e}}_l^t{\mathbf{M}}^n{\mathbf{e}}_i}{{\rho }^n}=w_l{v}_i,}\end{array}$$

that is, $E\left(v_{i}W\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=w_l{v}_i$. Therefore, $E\left(W\right|{\mathbf{Z}}_0={\mathbf{e}}_l)=w_l$ for all $l=1,2,\cdots ,K$, and it completes the proof of Theorem 2.

□

4.4. Proofs of Theorems 3 and 4

The proofs of Theorem 3 and 4 are straightforward from the results in Theorem 2:

Proof of Theorem 3.

First, we consider the case where $l=d+1,d+2,\cdots ,K$. Given ${\mathbf{Z}}_0={\mathbf{e}}_l$, we have that, for all $i=1,2,\cdots ,K$, the spread rate of $a_i$ is

$$\begin{array}{cc}& {\displaystyle s_{a_l}\left(a_j\right)=\underset{n\to \infty }{lim}\frac{Z_{n,i}}{{\displaystyle \sum _{j=1}^K}{Z}_{n,j}}=\underset{n\to \infty }{lim}\frac{Z_{n,i}/{\rho }^n}{{\displaystyle \sum _{j=1}^K}{Z}_{n,j}/{\rho }^n}=\frac{W_i}{{\displaystyle \sum _{j=1}^K}{W}_j}}\hfill \\ =\hfill & {\displaystyle \frac{v_{i}W}{{\displaystyle \sum _{j=1}^K}{v}_{j}W}=\frac{v_i}{{\displaystyle \sum _{j=1}^K}{v}_j}=v_i\mathrm{with}\mathrm{probability}1.}\hfill \end{array}$$

Next, if $l=1,2,\cdots ,d$, from the form of the offspring mean matrix

$$\mathbf{M}=\left[\begin{array}{cc}A& O\\ C& B\end{array}\right].$$

where the $d\times d$ matrix A and the $(K-d)\times (K-d)$ matrix B are primitive and C is a non-zero matrix, we can see that every individual of type $a_l$ only produces individuals of type $a_i$ for $i=1,2,\cdots ,d$. So, $s_{a_l}\left(a_j\right)=0$ for $i=d+1,\cdots ,K$. Moreover, by the primitivity of A and the classical limit results in the theory of branching processes, we have that, for $i=1,\cdots ,d$,

$$\begin{array}{c}{\displaystyle s_{a_l}\left(a_j\right)=\underset{n\to \infty }{lim}\frac{Z_{n,i}}{{\displaystyle \sum _{j=1}^d}{Z}_{n,j}}=\underset{n\to \infty }{lim}\frac{Z_{n,i}/{\rho }_A^n}{{\displaystyle \sum _{j=1}^d}{Z}_{n,j}/{\rho }_A^n}=v_i^{\prime }}\end{array}$$

with probability 1 and the proof is complete. □

Similar arguments in the proof of Theorem 3 can be adapted to prove the results in Theorem 4.

5. Numerical Examples

In this section, we provide two examples to demonstrate the numerical evidence for our main theorems. In both examples, the mean ratios and the mean populations are numerically approximated by empirical averages with about 300 realizations.

5.1. The Example with ${\rho }_B>{\rho }_A>1$

We consider the branching process with five types and the following offspring distribution:

$$\begin{array}{c}{p}^{\left(1\right)}(1,2,0,0,0)=1;\hfill \\ p^{\left(2\right)}(4,1,0,0,0)=\frac{1}{4},p^{\left(2\right)}(0,1,0,0,0)=\frac{3}{4};\hfill \\ p^{\left(3\right)}(2,1,1,0,4)=\frac{1}{2},p^{\left(3\right)}(0,1,1,2,0)=\frac{1}{2};\hfill \\ p^{\left(4\right)}(1,0,1,1,0)=\frac{2}{3},p^{\left(4\right)}(1,3,1,1,3)=\frac{1}{3};\hfill \\ p^{\left(5\right)}(0,1,2,1,1)=\frac{1}{2},p^{\left(5\right)}(2,1,2,1,1)=\frac{1}{2}.\hfill \end{array}$$

So, its offspring mean matrix is

$$\mathbf{M}=\left[\begin{array}{ccccc}1& 2& 0& 0& 0\\ 1& 1& 0& 0& 0\\ 1& 1& 1& 1& 2\\ 1& 1& 1& 1& 1\\ 1& 1& 2& 1& 1\end{array}\right]$$

where

$$A=\left[\begin{array}{cc}1& 2\\ 1& 1\end{array}\right]\mathrm{and}B=\left[\begin{array}{ccc}1& 1& 2\\ 1& 1& 1\\ 2& 1& 1\end{array}\right]$$

are the two primitive components. In this example, the maximal eigenvalues for the primitive component matrices A and B are

$$\begin{array}{c}{\rho }_A=1+\sqrt{2}\mathrm{and}{\rho }_B=2+\sqrt{3},\end{array}$$

respectively, and hence, the maximal eigenvalue of $\mathbf{M}$ is $\rho ={\rho }_B=2+\sqrt{3}$. We can see from Figure 1 that, when the population is initiated by an individual of type $a_i$, $i=1,2,3,4,5$, the population size ${\sum }_{j=1}^5{Z}_{n,j}$ grows like $w_i{\rho }^n$ asymptotically. This geometric growth has been shown in Theorem 1.

Moreover, the spread rates of all five types, given that the population is initiated by an individual of different types, are also simulated and presented in Figure 2. In Figure 2c–e, we can see that, when the population is initiated by an individual of type $a_i$, $i=3,4,5$, the population of type $a_j$ converges to $w_i{v}_j$, $j=1,2,3,4,5$. Therefore, the spread rate $s_{a_i}\left(a_j\right)$ (the proportion of individuals of each type $a_j$) is the same as the jth component in the normalized left eigenvector of $\mathbf{M}$ associated with $\rho$:

$$\begin{array}{c}\mathbf{v}=(v_1,v_2,v_3,v_4,v_5)\approx (0.44,0.26,0.11,0.08,0.11).\end{array}$$

This is unlike what happens to the population initiated with the individual of type $a_3$, $a_4$, or $a_5$, when the initial individual is of type $a_i$, $i=1,2$; the tendency of the population of each type is presented in Figure 2a,b. The spread rates of type $a_1$ and $a_2$ are $\frac{1}{1+\sqrt{2}}$ and $\frac{\sqrt{2}}{1+\sqrt{2}}$, respectively, which are the components of the normalized left eigenvector ${\mathbf{v}}_A$ of the primitive component matrix A associated with the maximal eigenvalue ${\rho }_A$. These simulation results are also consistent with the theoretical results in Theorem 3.

5.2. The Case Where ${\rho }_A>{\rho }_B>1$

Now, we consider the branching process with 5 types and the following offspring distribution:

$$\begin{array}{c}{p}^{\left(1\right)}(2,1,1,0,0)=\frac{1}{2},p^{\left(1\right)}(0,1,3,0,0)=\frac{1}{2};\hfill \\ p^{\left(2\right)}(1,2,1,0,0)=\frac{1}{3},p^{\left(2\right)}(2,1,0,0,0)=\frac{1}{3},p^{\left(2\right)}(0,0,2,0,0)=\frac{1}{3};\hfill \\ p^{\left(3\right)}(3,1,1,0,0)=\frac{2}{3},p^{\left(3\right)}(0,1,1,0,0)=\frac{1}{3};\hfill \\ p^{\left(4\right)}(2,1,0,1,2)=\frac{1}{2},p^{\left(4\right)}(0,1,2,1,2)=\frac{1}{2};\hfill \\ p^{\left(5\right)}(1,2,2,1,1)=\frac{1}{2},p^{\left(5\right)}(1,0,0,1,1)=\frac{1}{2};\hfill \end{array}$$

and the corresponding offspring mean matrix is

$$\mathbf{M}=\left[\begin{array}{ccccc}1& 1& 2& 0& 0\\ 1& 1& 1& 0& 0\\ 2& 1& 1& 0& 0\\ 1& 1& 1& 1& 2\\ 1& 1& 1& 1& 1\end{array}\right]$$

where

$$A=\left[\begin{array}{ccc}1& 1& 2\\ 1& 1& 1\\ 2& 1& 1\end{array}\right]\mathrm{and}B=\left[\begin{array}{cc}1& 2\\ 1& 1\end{array}\right].$$

So, the maximal eigenvalues for the primitive component matrices A and B are

$$\begin{array}{c}{\rho }_A=2+\sqrt{3}\mathrm{and}{\rho }_B=1+\sqrt{2},\end{array}$$

respectively, and hence, the maximal eigenvalue of $\mathbf{M}$ is $\rho ={\rho }_A=2+\sqrt{3}$. When the population is initiated with an individual of type $a_i$, $i=1,2,3,4,5$, the geometric growth again is observed in Figure 3. On the other hand, Figure 4 also shows that the number of individuals of type $a_j$ converges to $w_i{v}_j$ and the spread rates of all five types approach the corresponding components of the normalized left eigenvector of $\mathbf{M}$ associated with $\rho$:

$$\begin{array}{c}\mathbf{v}=(v_1,v_2,v_3,v_4,v_5)\approx (0.36,0.28,0.36,0,0)\end{array}$$

as proved in Theorem 4.

6. Discussion and Conclusions

To model the random phenomenon of the spread of the disease during a pandemic, we propose a spread model using the multitype branching process. Due to the discreteness of the processes, we are able to study the spread pattern at any time n by studying the behavior of the nth power of the offspring mean matrix. However, in order to be able to consider more applications which are not supported by the classical results in the theory of the branching processes due to the non-primitive offspring mean matrix, we consider the non-primitive offspring mean matrix which is of the form

$$\mathbf{M}=\left[\begin{array}{cc}A& O\\ C& B\end{array}\right].$$

with primitive components A and B and positive component C and study the asymptotic growth rate of the population vector and the spread rate of each type in the long run. In this work, we prove that the population vector grows geometrically (Theorem 1) and the limit of the normalized population vector share the same direction as the left eigenvector of the offspring mean associated with the maximal eigenvalue (Theorem 2). Moreover, we show that the limit of the type composition is proportional to the left eigenvector associated with the maximal eigenvalue of the offspring mean matrix and find the spread rates (Theorems 3 and 4). Although we only state the results and provide the proofs for the cases when the offspring mean matrix has two primitive components, similar discussions should be adapted to establish the spread rate for even more general forms such as

$$\mathbf{M}=\left[\begin{array}{ccccc}{A}_{11}& O& \cdots & & O\\ C_{21}& A_{22}& O& \cdots & O\\ C_{31}& C_{32}& A_{33}& \cdots & O\\ ⋮& \cdots & & & ⋮\\ C_{r1}& C_{r2}& \cdots & & A_{rr}\end{array}\right].$$

with primitive components $A_{ii}$, $i=1,2,\cdots ,r$ and the results could be achieved under weaker conditions on the moment conditions of the offspring matrix.