Higher-Order Blended Compact Difference Scheme on Nonuniform Grids for the 3D Steady Convection-Diffusion Equation
Abstract
1. Introduction
2. BCD Scheme on Nonuniform Grids
2.1. The Fifth-Order Compact Schemes for the First Derivatives
2.2. The Fifth-Order Compact Schemes for the Second Derivatives
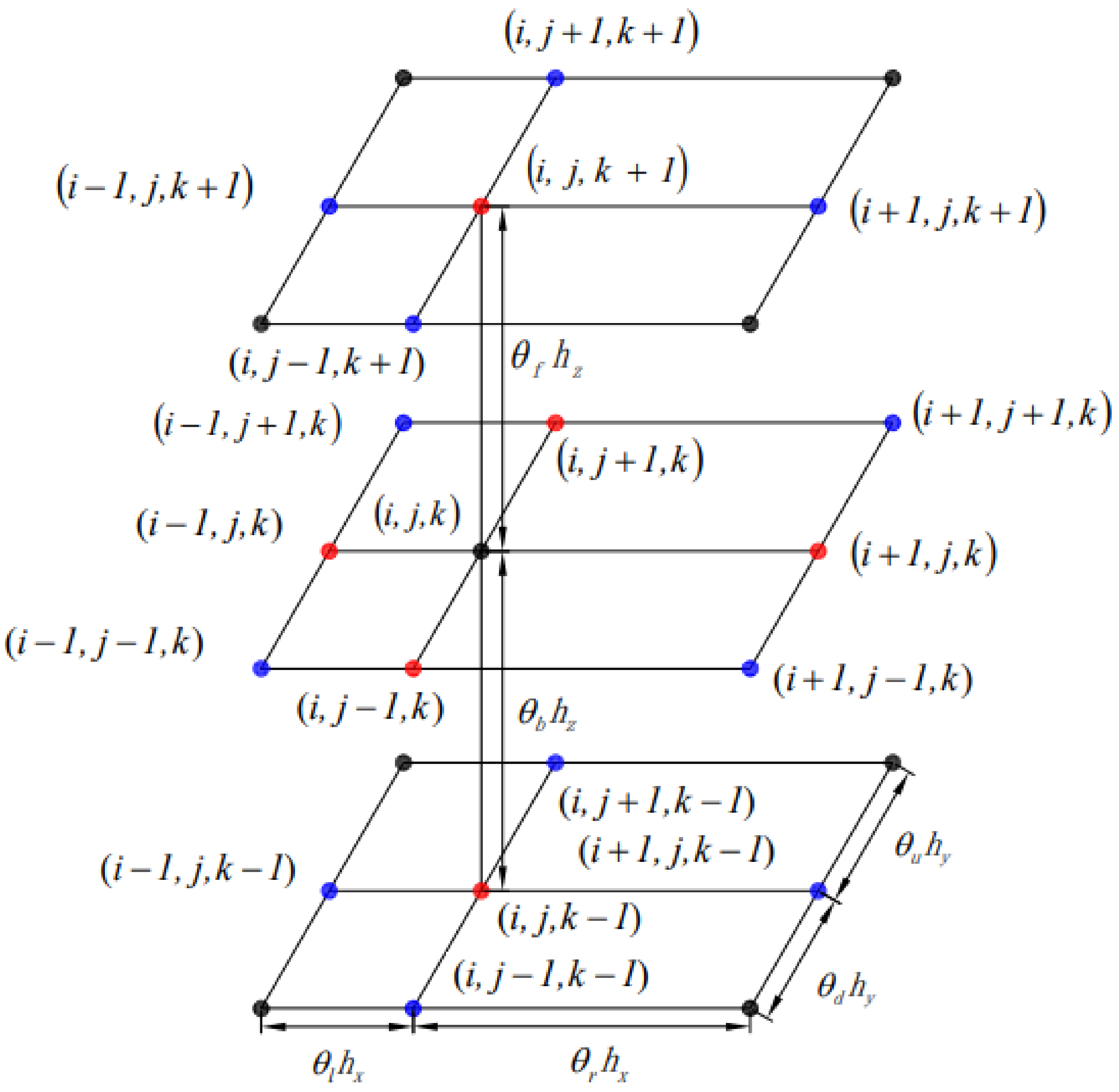
2.3. BCD Schemes of the 3D CDE on Nonuniform Grids
2.4. The High-Order Boundary Schemes on Nonuniform Grids
3. Numerical Experiments
3.1. Problem 1
3.2. Problem 2
3.3. Problem 3
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ashraf, M.; Khan, A.; Abbas, A.; Hussanan, A.; Ghachem, K.; Maatki, C.; Kolsi, L. Finite difference method to evaluate the characteristics of optically dense gray nanofluid heat transfer around the surface of a sphere and in the plume region. Mathematics 2023, 11, 908. [Google Scholar] [CrossRef]
- Ishtiaq, A.; Saleem, M.T.; Din, A.U. Special functions and its application in solving two dimensional hyperbolic partial differential equation of telegraph type. Symmetry 2023, 15, 847. [Google Scholar]
- Amo-Navarro, J.; Vinuesa, R.; Alberto Conejero, J.; Sergio, H. Two-dimensional compact-finite-difference schemes for solving the bi-laplacian operator with homogeneous wall-normal derivatives. Mathematics 2021, 19, 2508. [Google Scholar] [CrossRef]
- Choo, J.Y.; Schultz, D.H. A stable high-order method for the heated cavity problem. Int. J. Numer. Meth. Fluids 2010, 15, 1313–1332. [Google Scholar] [CrossRef]
- Dennis, S.; Hudson, J. Compact h4 finite-difference approximations to operators of Navier-Stokes type. J. Comput. Phys. 1989, 85, 390–416. [Google Scholar] [CrossRef]
- Pillai, A. Fourth-order exponential finite difference methods for boundary value problems of convective diffusion type. Int. J. Numer. Meth. Fluids 2001, 37, 87–106. [Google Scholar] [CrossRef]
- Tian, Z.; Ge, Y.B. A fourth-order compact finite difference scheme for the steady stream function-vorticity formulation of the Navier-Stokes/Boussinesq equations. Int. J. Numer. Meth. Fluids 2003, 41, 495–518. [Google Scholar] [CrossRef]
- Gupta, M.M.; Zhang, J. High accuracy multigrid solution of the 3D convection- diffusion equation. Appl. Math. Comput. 2000, 113, 249–274. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Ge, Y.B. A high order finite difference method with Richardson extrapolation for 3D convection diffusion equation. Appl. Math. Comput. 2010, 215, 3408–3417. [Google Scholar]
- Ananthakrishnaiah, U.; Manohar, R.; Stephenson, J. High-order methods for elliptic equations with variable coefficients. Numer. Methods Partial. Differ. Equ. 1987, 3, 219–227. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, J. Symbolic computation of high order compact difference schemes for three dimensional linear elliptic partial differential equations with variable coefficients. J. Comput. Appl. Math. 2002, 143, 9–27. [Google Scholar] [CrossRef]
- Mohamed, N.S.; Seddek, L.F. Exponential higher-order compact scheme for 3D steady convection-diffusion problem. Appl. Math. Comput. 2014, 232, 1046–1061. [Google Scholar] [CrossRef]
- Tian, Z.F.; Dai, S. High-order compact exponential finite difference methods for convection-diffusion type problems. J. Comput. Phys. 2007, 220, 952–974. [Google Scholar] [CrossRef]
- Chen, G.Q.; Gao, Z.; Yang, Z.F. A perturbational h4 exponential finite difference scheme for the convective diffusion equation. J. Comput. Phys. 1992, 104, 129–139. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Chu, P.C.; Fan, C. A three-point combined compact difference scheme. J. Comput. Phys. 1998, 140, 370–399. [Google Scholar] [CrossRef]
- Mahesh, K. A family of high order finite difference schemes with good spectral resolution. J. Comput. Phys. 1998, 145, 332–358. [Google Scholar] [CrossRef]
- Lakshmanan, T.K.V.; Vijay, V. A new combined stable and dispersion relation preserving comp Sengupta, act scheme for non-periodic problems. J. Comput. Phys. 2009, 228, 3048–3071. [Google Scholar]
- Deng, X.; Maekawa, H. Compact high-order accurate nonlinear schemes. J. Comput. Phys. 1997, 130, 77–91. [Google Scholar] [CrossRef]
- Ma, T.F.; Ge, Y.B. A Blended Compact Difference (BCD) Method for Solving 3D Convection-Diffusion Problems with Variable Coefficients. Int. J. Comput. Methods 2019, 16, 1950022. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, H.; Zhao, J.J. High order compact scheme with multigrid local mesh refinement procedure for convection diffusion problems. Comput. Methods Appl. Mech. Eng. 2002, 199, 4661–4674. [Google Scholar] [CrossRef]
- Kalita, J.C.; Dass, A.K.; Dalal, D. A transformation-free HOC scheme for steady convection-diffusion on non-uniform grids. Int. J. Numer. Meth. Fluids 2004, 44, 33–53. [Google Scholar] [CrossRef]
- Ge, Y.B.; Cao, F.J. Multigrid method based on the transformation-free HOC scheme on nonuniform grids for 2D convection diffusion problems. J. Comput. Phys. 2011, 230, 4051–4070. [Google Scholar] [CrossRef]
- Pandit, S.K.; Kalita, J.C.; Dalal, D. A fourth-order accurate compact scheme for the solution of steady Navier-Stokes equations on non-uniform grids. Comput. fluids 2008, 37, 121–134. [Google Scholar] [CrossRef]
- Yu, P.X.; Tian, Z.F. A compact streamfunction-velocity scheme on nonuniform grids for the 2D steady incompressible Navier-Stokes equations. Comput. Math. Appl. 2013, 66, 1192–1212. [Google Scholar] [CrossRef]
- Spotz, W.F.; Flow, F. Formulation and experiments with high-order compact schemes for nonuniform grids. Int. J. Numer. Methods Heat Fluid Flow 1998, 8, 288–303. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Ge, L.; Gupta, M.M. Fourth order compact difference scheme for 3D convection diffusion equation with boundary layers on nonuniform grids. Neural Parallel Sci. Comput. 2000, 8, 373–392. [Google Scholar]
- Ray, R.K.; Kalita, J.C. A transformation-free HOC scheme for incompressible viscous flows on nonuniform polar grids. Int. J. Numer. Meth. Fluids 2010, 62, 683–708. [Google Scholar] [CrossRef]
- Chu, P.C.; Fan, C. A three-point sixth-order nonuniform combined compact difference scheme. J. Comput. Phys. 1999, 148, 663–674. [Google Scholar] [CrossRef]
- Shukla, R.K.; Zhong, X. Derivation of high-order compact finite difference schemes for non-uniform grid using polynomial interpolation. J. Comput. Phys. 2005, 204, 404–429. [Google Scholar] [CrossRef]
- Shukla, R.K.; Tatineni, M.; Zhong, X. Very high-order compact finite difference schemes on non-uniform grids for incompressible Navier-Stokes equations. J. Comput. Phys. 2007, 224, 1064–1094. [Google Scholar] [CrossRef]
- Ge, Y.B.; Cao, F.J.; Zhang, J. A transformation-free HOC scheme and multigrid method for solving the 3D Poisson equation on nonuniform grids. J. Comput. Phys. 2013, 234, 199–216. [Google Scholar] [CrossRef]
- Shanab, R.A.; Seddek, L.F.; Mohamed, S.A. Non-uniform HOC scheme for the 3D convection-diffusion equation. Appl. Comput. Math. 2013, 2, 64–77. [Google Scholar] [CrossRef]
- Chertovskih, R.; Zheligovsky, V. Large-scale weakly nonlinear perturbations of convective magnetic dynamos in a rotating layer. Phys. D Nonlinear Phenom. 2015, 313, 99–116. [Google Scholar] [CrossRef]
- Sleijpen, G.L.G.; van der Vorst, H.A. Reliable updated residuals in hybrid BiCG methods. Computing 1996, 56, 141–163. [Google Scholar] [CrossRef]
- Boscain, U.V.; Chertovskih, R.; Gauthier, J.P.; Prandi, D.; Remizov, A. Highly corrupted image inpainting through hypoelliptic diffusion. J. Math. Imaging Vis. 2018, 60, 1231–1245. [Google Scholar] [CrossRef]
- Staritsyn, M.; Pogodaev, N.; Pereira, F.L. Linear-quadratic problems of optimal control in the space of probabilities. IEEE Control. Syst. Lett. 2022, 6, 3271–3276. [Google Scholar] [CrossRef]
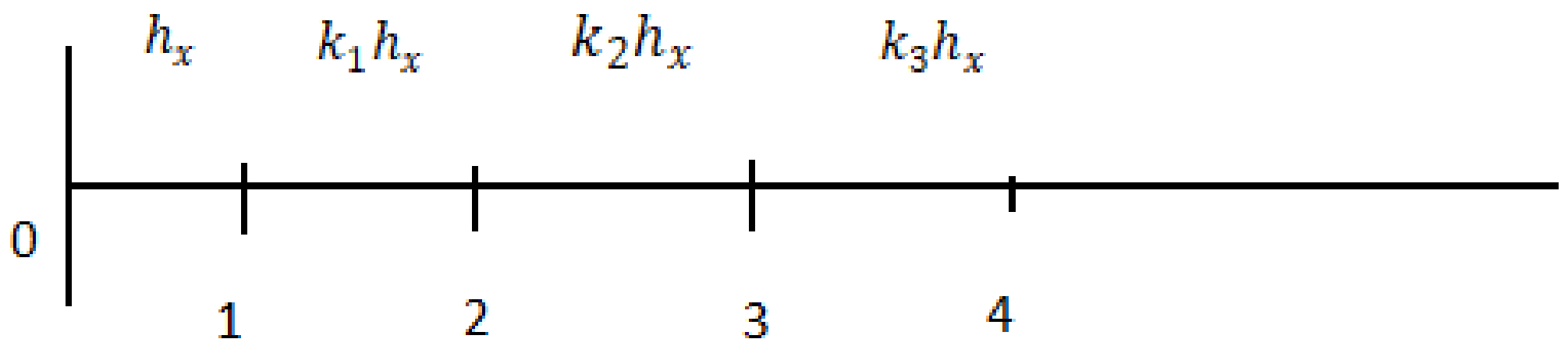

| Grid Number | BCD on Uniform Grids | BCD on Nonuniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 4.50 × 10−4 | 1.38 × 10−5 | ||
| 243 | 4.33 × 10−5 | 5.77 | 6.08 × 10−7 | 7.70 |
| 323 | 7.54 × 10−6 | 6.07 | 8.88 × 10−8 | 6.69 |
| 403 | 1.82 × 10−6 | 6.37 | 1.98 × 10−8 | 6.72 |
| 643 | 8.57 × 10−8 | 6.50 | 8.12 × 10−10 | 6.79 |
| 163 | 1.64 × 10−2 | 3.94 × 10−5 | ||
| 243 | 2.32 × 10−3 | 4.82 | 4.47 × 10−6 | 5.37 |
| 323 | 4.92 × 10−4 | 5.39 | 8.83 × 10−7 | 5.64 |
| 403 | 1.37 × 10−4 | 5.73 | 2.44 × 10−7 | 5.76 |
| 643 | 7.82 × 10−6 | 6.09 | 1.49 × 10−8 | 5.95 |
| 163 | 8.94 × 10−1 | 3.59 × 10−3 | ||
| 243 | 6.18 × 10−1 | 0.91 | 4.21 × 10−4 | 5.28 |
| 323 | 3.74 × 10−1 | 1.74 | 8.54 × 10−5 | 5.54 |
| 403 | 2.17 × 10−1 | 2.44 | 2.38 × 10−5 | 5.73 |
| 643 | 4.45 × 10−2 | 3.37 | 1.87 × 10−6 | 5.41 |
| Grid Number | HOC [34] on Uniform Grids | BCD on Uniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 3.28 × 10−4 | 4.50 × 10−4 | ||
| 323 | 2.13 × 10−5 | 3.94 | 7.54 × 10−6 | 5.92 |
| 643 | 1.36 × 10−6 | 3.97 | 8.57 × 10−8 | 6.44 |
| 163 | 5.01 × 10−3 | 1.64 × 10−2 | ||
| 323 | 3.26 × 10−4 | 3.94 | 4.92 × 10−4 | 5.06 |
| 643 | 2.12 × 10−5 | 3.94 | 7.82 × 10−6 | 5.97 |
| 163 | 6.65 × 10−1 | 8.94 × 10−1 | ||
| 323 | 1.45 × 10−1 | 2.20 | 3.74 × 10−1 | 1.26 |
| 643 | 1.38 × 10−2 | 3.39 | 4.45 × 10−2 | 3.07 |
| Grid Number | HOC [34] on Nonuniform Grids | BCD on Nonuniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 5.05 × 10−5 | 1.38 × 10−5 | ||
| 323 | 3.19 × 10−6 | 3.98 | 8.88 × 10−8 | 7.28 |
| 643 | 2.00 × 10−7 | 4.00 | 8.12 × 10−10 | 6.77 |
| 163 | 3.60 × 10−4 | 3.94 × 10−5 | ||
| 323 | 2.24 × 10−5 | 4.01 | 8.83 × 10−7 | 5.48 |
| 643 | 1.39 × 10−6 | 4.01 | 1.49 × 10−8 | 5.89 |
| 163 | 8.46 × 10−3 | 3.59 × 10−3 | ||
| 323 | 5.06 × 10−4 | 4.06 | 8.54 × 10−5 | 5.39 |
| 643 | 3.12 × 10−5 | 4.02 | 1.87 × 10−6 | 5.50 |
| Grid Number | HOC [34] on Nonuniform Grids | BCD on Nonuniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 1.23 × 10−6 | 1.20 × 10−6 | ||
| 323 | 7.57 × 10−8 | 4.02 | 1.27 × 10−8 | 6.56 |
| 643 | 4.72 × 10−9 | 4.00 | 1.21 × 10−10 | 6.71 |
| 163 | 1.58 × 10−5 | 1.71 × 10−5 | ||
| 323 | 9.37 × 10−7 | 4.08 | 7.73 × 10−8 | 7.79 |
| 643 | 5.79 × 10−8 | 4.02 | 6.97 × 10−10 | 6.79 |
| 163 | 1.24 × 10−3 | 1.56 × 10−4 | ||
| 323 | 6.08 × 10−5 | 4.35 | 7.08 × 10−6 | 4.46 |
| 643 | 3.86 × 10−6 | 3.98 | 1.39 × 10−7 | 5.67 |
| Grid Number | HOC [34] on Uniform Grids | BCD on Uniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 5.89 × 10−6 | 2.30 × 10−6 | ||
| 323 | 3.67 × 10−7 | 4.00 | 2.56 × 10−8 | 6.49 |
| 643 | 2.29 × 10−8 | 4.00 | 2.46 × 10−10 | 6.70 |
| 163 | 1.25 × 10−4 | 3.57 × 10−4 | ||
| 323 | 7.95 × 10−6 | 3.97 | 6.01 × 10−6 | 5.89 |
| 643 | 4.95 × 10−7 | 4.01 | 7.04 × 10−10 | 6.42 |
| Grid Number | BCD on Uniform Grids | BCD on Nonuniform Grids | ||||
|---|---|---|---|---|---|---|
| Error | Rate | CPU | Error | Rate | CPU | |
| 163 | 2.30 × 10−6 | 377.02 | 1.20 × 10−6 | 368.76 | ||
| 243 | 1.71 × 10−7 | 6.41 | 945.70 | 8.65 × 10−8 | 6.48 | 935.80 |
| 323 | 2.56 × 10−8 | 6.60 | 1979.74 | 1.27 × 10−8 | 6.67 | 1938.75 |
| 403 | 5.84 × 10−9 | 6.62 | 3294.52 | 2.88 × 10−9 | 6.65 | 3267.10 |
| 643 | 2.46 × 10−10 | 6.73 | 11,497.21 | 1.21 × 10−10 | 6.74 | 11,607.82 |
| 163 | 3.57 × 10−4 | 370.28 | 1.71 × 10−5 | 349.66 | ||
| 243 | 3.46 × 10−6 | 5.75 | 1434.50 | 5.28 × 10−7 | 8.58 | 892.31 |
| 323 | 6.01 × 10−6 | 6.08 | 1881.50 | 7.73 × 10−8 | 6.68 | 1948.70 |
| 403 | 1.48 × 10−6 | 6.28 | 3121.33 | 1.69 × 10−8 | 6.81 | 3184.98 |
| 643 | 7.04 × 10−8 | 6.48 | 11,867.19 | 6.97 × 10−10 | 6.78 | 12,392.76 |
| 163 | 2.59 × 10−1 | 1.37 | 449.88 | 1.56 × 10−4 | 7.59 | 534.23 |
| 243 | 9.99 × 10−2 | 2.35 | 1085.34 | 2.99 × 10−5 | 4.07 | 1041.01 |
| 323 | 3.99 × 10−2 | 2.70 | 2191.68 | 7.08 × 10−6 | 4.46 | 2360.45 |
| 403 | 1.71 × 10−2 | 3.80 | 3647.55 | 2.08 × 10−6 | 5.49 | 3771.67 |
| 643 | 2.00 × 10−3 | 4.32 | 21,577.83 | 1.39 × 10−7 | 5.76 | 22,842.95 |
| Grid Number | HOC [34] on Nonuniform Grids | BCD on Nonuniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 3.13 × 10−5 | 1.30 × 10−5 | ||
| 323 | 1.97 × 10−6 | 3.99 | 1.25 × 10−7 | 6.70 |
| 643 | 1.23 × 10−7 | 4.00 | 1.12 × 10−9 | 6.80 |
| 163 | 2.28 × 10−4 | 4.38 × 10−5 | ||
| 323 | 1.40 × 10−5 | 4.03 | 9.09 × 10−7 | 5.59 |
| 643 | 8.68 × 10−7 | 4.01 | 1.82 × 10−8 | 5.64 |
| 163 | 5.54 × 10−3 | 3.63 × 10−3 | ||
| 323 | 3.37 × 10−4 | 4.04 | 8.68 × 10−5 | 5.39 |
| 643 | 2.11 × 10−5 | 4.00 | 1.52 × 10−6 | 5.84 |
| Grid Number | HOC [34] on Uniform Grids | BCD on Uniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 6.17 × 10−4 | 5.09 × 10−4 | ||
| 323 | 3.91 × 10−5 | 3.98 | 8.01 × 10−6 | 5.99 |
| 643 | 2.46 × 10−6 | 3.99 | 8.96 × 10−8 | 6.48 |
| 163 | 9.90 × 10−3 | 1.74 × 10−2 | ||
| 323 | 6.48 × 10−4 | 3.93 | 5.10 × 10−4 | 5.09 |
| 643 | 4.10 × 10−5 | 3.98 | 8.01 × 10−4 | 5.99 |
| Grid Number | BCD on Uniform Grids | BCD on Nonuniform Grids | ||
|---|---|---|---|---|
| Error | Rate | Error | Rate | |
| 163 | 5.09 × 10−4 | 1.30 × 10−5 | ||
| 243 | 4.66 × 10−5 | 5.89 | 8.58 × 10−7 | 6.70 |
| 323 | 8.01 × 10−6 | 6.12 | 1.25 × 10−7 | 6.69 |
| 403 | 1.92 × 10−6 | 6.40 | 2.74 × 10−8 | 6.80 |
| 643 | 8.96 × 10−8 | 6.52 | 1.12 × 10−9 | 6.80 |
| 163 | 1.74 × 10−2 | 4.38 × 10−5 | ||
| 243 | 2.35 × 10−3 | 4.94 | 5.84 × 10−6 | 4.97 |
| 323 | 5.10 × 10−4 | 5.30 | 9.09 × 10−7 | 6.47 |
| 403 | 1.39 × 10−4 | 5.82 | 1.77 × 10−7 | 7.33 |
| 643 | 8.01 × 10−6 | 6.07 | 1.82 × 10−8 | 4.84 |
| 163 | 8.97 × 10−1 | 3.63 × 10−3 | ||
| 243 | 6.60 × 10−1 | 0.76 | 4.45 × 10−4 | 5.18 |
| 323 | 3.79 × 10−1 | 1.93 | 8.68 × 10−5 | 5.68 |
| 403 | 3.80 × 10−1 | 0.01 | 2.52 × 10−5 | 5.54 |
| 643 | 4.49 × 10−2 | 4.54 | 1.52 × 10−6 | 5.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Lan, B.; Ge, Y.; Wu, L. Higher-Order Blended Compact Difference Scheme on Nonuniform Grids for the 3D Steady Convection-Diffusion Equation. Axioms 2023, 12, 651. https://doi.org/10.3390/axioms12070651
Ma T, Lan B, Ge Y, Wu L. Higher-Order Blended Compact Difference Scheme on Nonuniform Grids for the 3D Steady Convection-Diffusion Equation. Axioms. 2023; 12(7):651. https://doi.org/10.3390/axioms12070651
Chicago/Turabian StyleMa, Tingfu, Bin Lan, Yongbin Ge, and Lili Wu. 2023. "Higher-Order Blended Compact Difference Scheme on Nonuniform Grids for the 3D Steady Convection-Diffusion Equation" Axioms 12, no. 7: 651. https://doi.org/10.3390/axioms12070651
APA StyleMa, T., Lan, B., Ge, Y., & Wu, L. (2023). Higher-Order Blended Compact Difference Scheme on Nonuniform Grids for the 3D Steady Convection-Diffusion Equation. Axioms, 12(7), 651. https://doi.org/10.3390/axioms12070651






