1. Introduction
Entrepreneurship has been recognized as a significant driver of economic growth, both directly and indirectly, and as well as a catalyst for more investments in knowledge creation and generation [
1]. Notably, technology-based startups can transform the traditional economy into a digital economy through innovation [
2]. The key determinants of entrepreneurial success encompass a range of factors, including entrepreneurs’ networks, leadership skills, financial competency, aptitude, knowledge, and support services [
3]. Stam [
3] defined the entrepreneurial ecosystem as a complex network of interconnected actors and factors that collaborate to facilitate productive entrepreneurship. Among the factors, accelerators are the primary players in the entrepreneurial ecosystem and are actively engaged in fostering innovation and nurturing startups. They develop startup projects, including financing, services, networking, mentoring, and training [
4]. Not only do accelerators support through networking services, mentorships, and educational endeavors, but they also play a crucial role in augmenting the financial capabilities of entrepreneurial firms. However, despite their critical role, exploring the selection process employed by accelerators in identifying and evaluating entrepreneurial firms and the underlying selection criteria remains relatively scarce [
5].
The initial phase in the process of the entry-boost-exit process is to select a suitable startup. Accelerators whose financial gains are contingent upon the successful exit of the startups in which they invest must exercise discernment when evaluating prospective projects [
5]. The selection process encompasses three distinct steps: soliciting startup submissions, conducting comprehensive examinations and evaluations of the projects, and, based on the input of key decision-makers (DMs), eliminating unpromising projects while investing in those that exhibit promise [
6]. Lin et al. [
7] used the hesitant fuzzy linguistic (HFL) multi-criteria decision-making (MCDM) method to evaluate startups from a technology business incubator perspective, taking into account DMs’ psychology. The researchers developed a ratio of score value to deviation degree to compare HFL term sets and defined the HFL information envelopment efficiency, analysis, and preference model. Their numerical example showed the method’s applicability, and they concluded that it is more flexible and general. Nonetheless, it should be noted that this method exclusively applies to HFL information environments with unrevealed criteria weight values. Furthermore, the authors acknowledged the limited extent of research on ranking startups within the existing literature.
The process of selecting startups for acceleration programs involves intricate consideration of both qualitative and quantitative criteria. Qualitative criteria encompass factors such as competitive advantage and demand validation, while quantitative criteria include investment costs and team size. Consequently, the ranking of startups poses an MCDM problem. MCDM, as a research field, contributes to the development and implementation of decision-support methodologies and tools [
8]. Additionally, MCDM methods are valuable in resolving multiplex problems involving objectives, multiple criteria, and alternatives rated by DMs. It is important to note that the DMs’ judgment through qualitative criteria is crucial to the decision-making process, despite its inherent subjectivity and vagueness. Fuzzy numbers (FNs) offer a more effective means of modeling human thought compared to their crisp counterparts.
However, the conventional MCDM method solely adheres to classical mathematical theory, and different methods must be improved or combined to adapt to actual MCDM [
9]. Moreover, the amalgamation of DEMATEL-ANP-based fuzzy PROMETHEE II has not been previously applied. This study aims to bridge this gap by investigating the technology startup selection process from the perspective of accelerators, utilizing the DEMATEL-ANP-based fuzzy PROMETHEE II approach. To the best of our knowledge, no prior research has scrutinized this hybrid method in evaluating startups. Accordingly, our study explores its feasibility and effectiveness. A ranking method based on spread areas is proposed with formulas to support the decision-making process, and a comparison is conducted to demonstrate the method’s advantages. Subsequently, a numerical example is presented to elucidate the complete process of the hybrid method.
The subsequent sections of this paper are structured as follows.
Section 2 provides a literature review of the accelerator, selection criteria, and MCDM techniques.
Section 3 introduces the classical concept of fuzzy set theory and outlines the hybrid DEMATEL-ANP-based fuzzy PROMETHEE II method. In
Section 4, a comparative analysis is presented to underscore the advantages of the ranking technique.
Section 5 presents a numerical example that illustrates the applicability and implementation of the hybrid approach in real-world problems. Finally,
Section 6 concludes the work by summarizing key findings and suggesting potential avenues for future research.
3. Model Establishment
3.1. Fuzzy Set Theory
where
x is an element in the space of points
U,
A is a fuzzy set in
U,
is the membership function of
A at
x [
44]. The larger
, the stronger the grade of membership for
x in
A.
A real FN
A is described as any fuzzy subset of the real line
R with a membership function
that possesses the following properties [
50].
is a continuous mapping from
R to [0, 1],
.
is strictly increasing on the left membership function
and is strictly decreasing on the right membership function
.
and
, where
a,
b,
c, and
d are real numbers.
We may let , or a = b, or b = c, or c = d, or d = . Unless elsewhere defined, A is assumed to be convex, normalized, and bounded, i.e., , . A can be indicated as , . Let represent and represent the left and the right membership function of A, respectively, and .
In this research, TFNs will be used. The FN
A is a TFN if its membership function
is given as follows [
51].
where
a,
b, and
c are real numbers.
The α-cuts of FN
A can be determined as
, where
is a non-empty bounded closed interval is contained in
R and can be denoted by
, where
are lower bounds and
are upper bounds [
64].
Given FNs
A and
B,
,
and
. By the interval arithmetic, some primary operations of
A and
B can be described as follows [
64].
A linguistic variable is a variable whose values are represented in linguistic terms. It is advantageous for dealing with complicated matters or is ambiguous to be rationally described in traditional quantitative information [
51,
65]. DMs are assumed to have agreed to weight alternatives over criteria using linguistic values such as
Extremely Poor (EP),
Very Poor (VP),
Poor (P),
Moderate (M),
High (H),
Very High (VH), and
Extremely High (EH) which can also be represented by TFNs such as
EP = (0,0.1,0.25),
VP = (0.1,0.2,0.35),
P = (0.25,0.35,0.5),
M = (0.35,0.5,0.65),
H = (0.5,0.65,0.75),
VH = (0.65,0.8,0.9), and
EH = (0.75,0.9,1).
3.2. Relative Maximizing and Minimizing Sets
Chu and Nguyen [
63] suggested a technique to improve Chen’s [
51] maximizing and minimizing set to rank FNs. In their study, numerical comparisons and examples were conducted to demonstrate that the RMMS can consistently and logically rank fuzzy values of alternatives. The RMMS [
63] technique is introduced as follows.
Assume there are n FNs , . , FNs and are added to the right and left sides of the above n FNs respectively. Assume , , and . Let and , where , , , . The new supremum element is defined as and the new infimum element is defined as , where .
The relative maximizing set
and the relative minimizing set
are determined as:
Herein,
k is set to 1. The value of
k can be varied to suit the application. The total relative utility of each
Ai is denoted as in Equation (8).
where the first right relative utility
, the first left relative utility
, the second left relative utility
and the second right relative utility
.
3.3. Spread Area-Based RMMS
In 2011, Nejad and Mashinchi [
59] pointed out the shortcomings of Wang et al.’s [
54] deviation degree method that when the values of the left area, the right area, the transfer coefficient
or
is zero, the ranking result is inaccurate. Hence, to prevent these problems from occurring, expanding
and
is needed when ranking. Chu and Nguyen [
63] also found out that when adding a new FN,
and
must be modified by adding equal values to consider both sides of membership functions. Consequently, four utilities need to be accounted for to reduce the inconsistency of Chen’s [
51] maximizing and minimizing set. However, if a set of FNs with
, then a new FN
is added, there is no extended value applicable in this situation. Therefore, this work suggests integrating confidence levels in ranking FNs to solve the mentioned problems.
Yeh and Kuo [
66] in their research on evaluating passenger service quality of Asia-Pacific international airports, suggested incorporating a DM’s confidence level α and a preference index λ to obtain an overall service performance index. In the evaluation procedure, DMs give the value α, based on the concept of an α-cut, with respect to the criteria’s weights and alternative performance ratings.
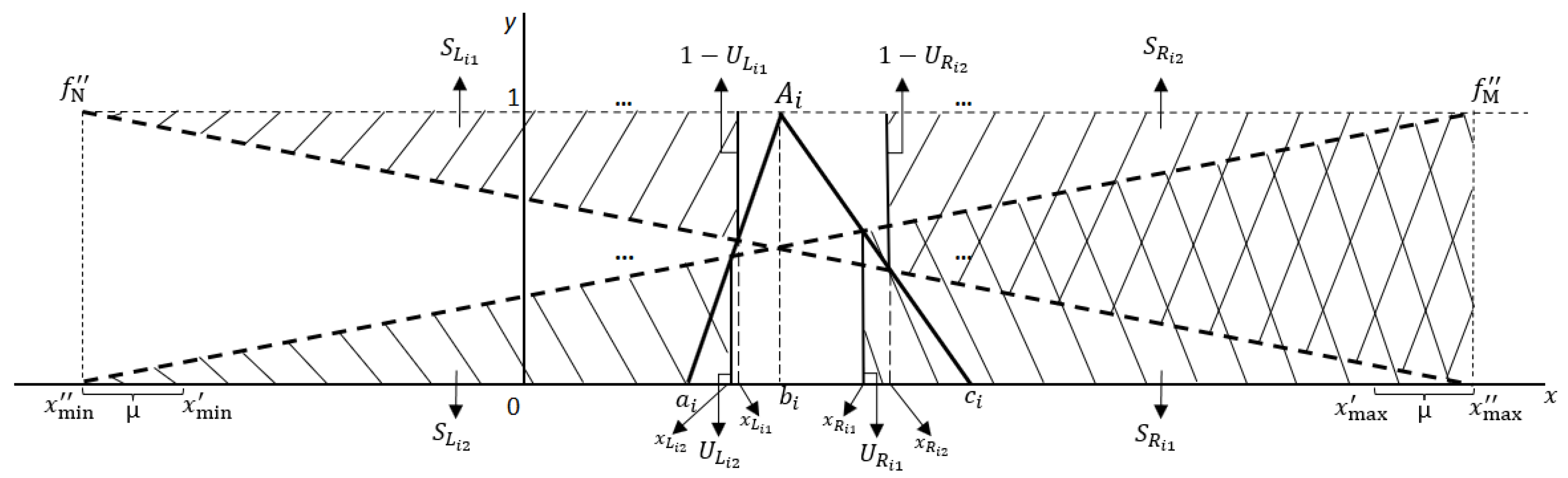
This work proposes to use confidence level in a new perspective, which is confidence level, symbolized as
μ, will be integrated into measuring areas spreading based on the RMMS model to assist the ranking FNs procedure, as shown in
Figure 1. First,
h experts in the group of DMs,
are asked to specify their confidence
, representing their confidence for alternatives to obtain
. The greater the
μ, the more assured is the decision-maker on the alternative.
Since DMs’ confidence in an alternative will influence their confidence level in other alternatives, the confidence level μ, calculated by the average of all DMs’ evaluation, should be engaged simultaneously with the immensity of the RMMS concept. Accordingly, value μ is integrated by shifting the RMMS’s infimum element to the left, provided that the new infimum element is obtained as . Similarly, the average value of μ will be integrated by shifting the RMMS’s infimum element to the right, provided that the new supremum element is obtained as .
The coordinates of the intersection of the
with the relative maximizing set
and the relative minimizing set
can be seen in
Figure 1 and are determined as the following equations.
The first left spread area
is defined as follows.
If the first left spread area
is larger, the fuzzy number
is larger. The second left spread area
is defined as Equation (14); and if
is larger, the fuzzy number
is also larger. The first right spread area
is defined as Equation (15); but if
is larger, the fuzzy number
is smaller. Finally, the second right spread area
is defined as Equation (16); and if
is larger, the fuzzy number
is also smaller. Therefore, the above four areas must be considered when ranking FNs. The detailed derivation for Equations (14)–(16) is placed in
Appendix A.
Finally, the ranking value of each
is determined as Equation (17) to classify FNs. An FN is more prominent if its value is larger.
3.4. The Hybrid DEMATEL-ANP Based Fuzzy PROMETHEE II Model
3.4.1. DEMATEL
The DEMATEL method is first used to demonstrate the interrelationships between criteria and produce the influential network relationship map. The constructing equations of the classical DEMATEL model can be summarized as follows [
67].
Assume that h experts in a decision group are asked to indicate the direct effect of factor (criterion) Ci has on factor (criterion) Cj in a system with m factors (criteria) using an integer scale of No Effect (0), Low Effect (1), Medium Low Effect (2), Medium Effect (3), Medium High Effect (4), High Effect (5) and Extremely Strong Effect (6). Next, the individual direct-influence matrix provided by the eth expert can be constructed, where all main diagonal components are equal to zero and represent the respondent’s evaluation of DM on the degree to which criterion Ci affects Cj.
Step 1. Generating the group direct-influence matrix. By aggregating
h DMs’ judgments, the group direct-influence matrix
can be constructed by
Step 2. Acquiring the normalized direct-influence matrix. At this step, the normalized direct-influence matrix by the eth expert is .
The following equations calculate the average matrix X
Step 3. Computing the total-influence matrix
T. The total-influence matrix
is computed as the summation of the direct impacts and all the indirect impacts by Equation (21)
when
in the identity matrix, known as
I.
Step 4. Setting up a threshold value and producing the causal diagram.
The sum of columns and the sum of rows are symbolized as
R and
D, respectively, within the total-relation matrix
by the following formulas:
The horizontal axis vector (
D +
R) called “Prominence” demonstrates the power of influence degree that is given and received by the criteria. The vertical axis vector (
D −
R) named “Relation” shows the system’s criteria effect. If (
D −
R) is positive, the criterion
Cj influences other criteria and can be grouped into a causal group; if (
D +
R) is negative, the criterion
Cj is being influenced by the other criteria and can be grouped into an effect group. A causal diagram can be produced by mapping the (D + R, D − R) dataset, yielding valuable assessment perception. A threshold value can be defined to screen out the negligible factors [
68,
69]. In this work, factors that have a value higher than the average value of the “Prominence” (
D +
R) and/or (
D −
R) is positive are selected to use in the next step.
3.4.2. ANP
Next, the present work applied the ANP method to produce the weights of the criteria. The generalized ANP process from previous studies is summarized as follows [
30,
70,
71]. In this work, a set of importance scales [
28] is adopted to weight each criterion using linguistic values, including 1—
Identically Important (II), 3—
Moderately Important (MI), 5—
Highly Important (HI), 7—
Very Highly Importance (VHI),
9—Extremely Important (EI), and 2, 4, 6, 8 are the median values. Reciprocal values are used for inverse comparison.
Step 1. Obtaining Pairwise Comparison Matrix (PCM). Assume that h experts in a decision group
are responsible for evaluating criteria
that are screened through the previous step. The PCM is generated by comparing the
ith row with the
jth column. The weights of components are formed as shown in matrix
A. The diagonal components with identical importance are illustrated by 1.
As there are several DMs, the pairwise comparison values from different DMs may vary. Experts can decide together, or each assessment can be integrated into a PCM by the geometric mean
GM as in Equation (24).
Step 2. Computing eigenvectors and the unweighted supermatrix. In this step, eigenvector
Ei is obtained through Equation (25), which is computed by each row’s average.
Then, the eigenvectors of each matrix are consolidated to form the unweighted matrix.
Step 3. Examining the consistency. To guarantee consistency among the judgments of the DMs, it is necessary to test the consistency by three metrics, including Consistency Measure (CM), Consistency Index (CI), and Consistency Ratio (CR).
The general form for
CM values is obtained through Equation (26).
where
j = 1,2,3, …,
m,
aj is the corresponding row of the comparison matrix,
E is Eigenvector and
Ej represents the corresponding component in
E.
Then,
λmax is obtained by the average of the
CM vector. The
CI is calculated as shown in Equation (27).
Next, a random index, as listed in
Table 1 [
28], is computed following the order of the PCM. Consequently, the Consistency Ratio
CR is obtained by Equation (28).
The value of CR ≤ 0.1 is in the satisfactory range; otherwise, the pairwise comparison is required to be revised.
Step 4. Obtain the weighted supermatrix. A weighted supermatrix is obtained to evaluate the relation between criteria. Then, the unweighted matrix is converted into a weighted supermatrix to make the sum of each column 1, called column stochastic.
Step 5. Determining stable weights by obtaining limit supermatrix. The values produced from the previous step are elevated to the power of 2k until the values are firmly established, where k is an arbitrarily large number. The final priorities can be determined using the normalization function on each block of the limit matrix. The most significant value represents the most critical criterion among other criteria. The stable weights w constructed from this step are utilized in the following steps.
3.4.3. Fuzzy PROMETHEE-Based Ranking Method
The same group of
h experts
will assess
n alternatives
under
m criteria
that are screened through the previous steps. Let
be the rating assigned to an alternative
under the criterion
by a decision-maker
. Criteria chosen from the earlier steps are first categorized into the cost-benefit framework as qualitative benefit criteria,
quantitative benefit criteria,
cost qualitative criteria,
and cost quantitative criteria
The fuzzy PROMETHEE II process is summarized as follows [
72,
73].
Step 1. Constructing the fuzzy decision matrix. Aggregated rating
is:
where
,
,
.
Step 2. Computing the normalized matrix. The normalization is completed using the Chu and Nguyen [
63] approach. The ranges of normalized TFNs belong to [0, 1]. Suppose
is the value of an alternative
versus a benefit (B) criterion or a cost (C) criterion. The normalized value
lij can be as
where
.
Step 3. Calculating the evaluative differences. Pairwise comparison is made by calculating the evaluative differences of
ith alternative with respect to other alternatives. The intensity of the fuzzy preference
of an alternative
Ai over
Ai’ is obtained by Equations (32) and (33), based on Equation (3)
where
Pj is the fuzzy preference function for the
jth criterion and
Cj(
Ai) is the evaluation of alternative
Ai corresponding to criterion
Cj.
Step 4. Determining the preference function. To avoid the complexity and be in a more practicable form, the simplified fuzzy preference function is applied in this study as in Equations (34) and (35).
Step 5. Reckoning the aggregated fuzzy preference function. Calculate the aggregated fuzzy preference function considering the criteria weights computed from the ANP method.
The higher is, the stronger preference for the ith alternative will be.
Step 6. Determining the fuzzy leaving flow and the fuzzy entering flow
The fuzzy leaving flow of
Ai is determined as
The fuzzy entering flow of
Ai is determined as
Step 7. Calculating the fuzzy net outranking flow for each alternative
Step 8. Defuzzifying the fuzzy net outranking flow value and obtaining the ranking of alternatives. In this step, the spread area-based RMMS model is proposed to apply to assist defuzzification and obtain the final ranking using Equations (12)–(20). An FN is more prominent if its value is more significant.
4. Numerical Comparison and Consistency Test
In this section, various examples of comparisons are established to investigate the effectiveness of the proposed method. The first example illustrates the ranking orders of the method compared with the methods of Wang et al. [
54] and Nejad and Mashinchi [
59]. We used FNs in Examples 2–4 from Nejad and Mashinchi [
59], and then different situations were generated through the addition of new FNs for testing the consistency of the ranking results, as shown in
Table 2. In Situation (1), methods from both Nejad and Mashinchi and Wang et al. produce
, but the proposed method can discriminate between three FNs with the order
. Furthermore, the ranking order is
, and either
is added (see Situation (1.1)) or
is added (see Situation (1.2)). In Situation (2), the proposed method yields the same ranking,
, as that of the method of Nejad and Mashinchi when either
or
is added. However, the method of Wang et al. highlights the inconsistency and produces
in Situation (2.2). In Situation (3), the proposed method yields the same ranking
as that of Nejad and Mashinchi when
or
is added, but the method of Wang et al. compensates for the inconsistency and produces
in Situation (3.2). The first comparison demonstrates the usefulness of the proposed method in discriminating FNs.
Second, three sets of FNs are created to further examine the proposed method’s stability and credibility, as shown in
Table 3. In all previous situations, the method of Wang et al. is ineffective in distinguishing FNs. For example, in Situation (1.1), the method of Nejad and Mashinchi yields an FN ranking,
, but yields
in cases (1) and (1.2), indicating inconsistency, but the proposed method yields
in all Situations (1), (1.1), and (1.2). Similarly, in Situations (2) and (2.2), the ranking order obtained using the method of Nejad and Mashinchi is
; however, when
is added, the order changes to
, as in Situation (2.1); whereas the suggested method persistently ranks in the following order:
. In Situations (3) and (3.2), both the proposed method and the method of Nejad and Mashinchi yield a ranking order of
; however, in (3.1), when
is added, the method of Nejad and Mashinchi yields
; however, the proposed method yields a persistent rank order of
. Hence, the second comparison has demonstrated the effectiveness of the proposed method in discriminating FNs compared to Wang et al.’s technique and the consistency compared with the method of Nejad and Mashinchi.
Additionally, a consistency test is designed to examine the reliability of the proposed method, as shown in
Table 4 and
Table 5. In Example 1, the result is
,
for all assumed various
µ values. In Example 2, when
is added, the classifying order remains the same as
for all
. Finally, in Example 3, when
is added, the proposed method consistently yields an order of
for all tested values of
µ. The results of the numerical comparison demonstrate the credibility and effectiveness of the suggested ranking method based on spread area-based RMMS.
5. Numerical Example
Suppose 4 DMs
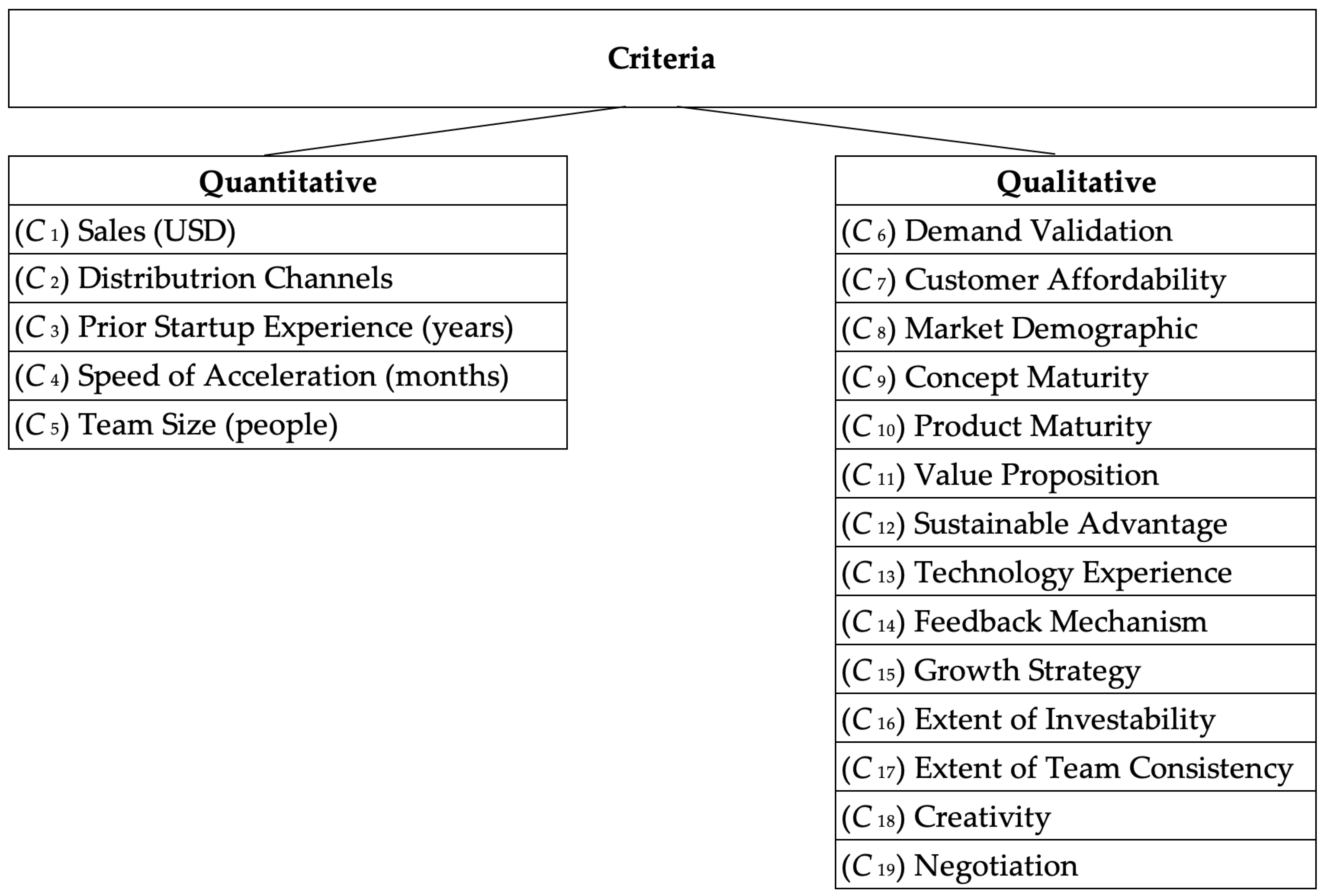
of an accelerator must establish criteria and analyze the criteria’s effect on a technology-based acceleration program. To achieve this goal, the methods DEMATEL and ANP are performed. Assume
are the qualitative criteria and quantitative criteria under consideration, as shown in
Figure A1 (see
Appendix B for details). Assuming that DMs have reached a consensus, the effects of criteria on each other are indicated using a scale of
No Effect (1),
Low Effect (2),
Medium Low Effect (3),
Medium Effect (4),
Medium High Effect (5),
High Effect (6), and
Extremely Strong Effect (7). After each DM rates the alternatives, the aggregating direct-relation matrix is determined using Equation (18) and is shown in
Table A1 (see
Appendix C for details).
Subsequently, values of the normalized direct-relation matrix are obtained using Equations (19) and (20) and are shown in
Table A2 (see
Appendix D for details). Finally, the total-relation matrix is attained using Equation (21), as shown in
Table A3 (see
Appendix E for details). Next, the prominence (
D +
R) and relation (
D −
R) values are calculated using Equations (22) and (23). Thereafter, the threshold value is set, which determines the filtered factors. The causal relationship and notable factors are displayed in
Table 6 and
Figure 2. According to
Table 6, “(
C6) demand validation” has the greatest (
D +
R) value and is the most critical factor, followed by “(
C7) customer affordability” and “(
C8) market demographic”. All these factors need to be evaluated in the initial steps when building a product or service. Additionally, the (
D −
R) values of “(
C3) prior startup experience”, “(
C1) sales”, and “(
C2) product development cost” demonstrate that these criteria have net influences on other factors. Other medium value factors that are selected when proceeding to the next steps are “(
C9) concept maturity”, “(
C10) product maturity”, “(
C11) value proposition”, “(
C13) technology experience”, “(
C15) growth strategy”, “(
C18) creativity”, and “(
C19) negotiation”.
Next, the pairwise comparison must be carefully evaluated by DMs according to the criteria. In this study, the statistical software Super Decisions was used for the analysis. Super Decisions is a decision-support program that implements AHP and ANP to calculate the weights of the dimensions and tests the expert’s competency. After obtaining the integrated PCM, the values are entered into the software to compute
CR values. First, the integrated matrix is computed with respect to each criterion, including the Consistency Ratio
CR ≤ 0.1, as shown in Equations (24)–(28) (see
Table A4,
Table A5,
Table A6,
Table A7,
Table A8,
Table A9,
Table A10,
Table A11,
Table A12,
Table A13,
Table A14,
Table A15 and
Table A16 in
Appendix F for details). Then, the unweighted supermatrix and weighted matrix are created, as shown in
Table 7 and
Table 8. Finally, the limited matrix with the stable weights and the final weight order can be determined, as shown in
Table 9 and
Table 10. According to
Table 10, “(
C8) market demographics” has the highest value with 0.1253, followed by “(
C6) demand validation” with 0.1196 and “(
C3) prior startup experience” with 0.0940. The lowest weight value is “(
C11) value proposition” with 0.0215.
Finally, the fuzzy PROMETHEE II-based spread area ranking method is applied. Suppose the same DM group assesses four technology-based startup projects
under 13 criteria that are screened during the previous steps. The ratings of the alternatives over qualitative criteria and quantitative criteria are shown in
Table A17 and
Table A18 (see
Appendix G and
Appendix H, respectively, for details). Subsequently, the mean ratings are calculated using Equation (29), as shown in
Table 11, and the alternatives’ normalized gradings versus quantitative criteria are produced using Equations (30) and (31), as shown in
Table 12. The confidence level ratings on alternatives are also collected to produce
µ value, as shown in
Table 13.
The aggregated fuzzy preference is attained using Equations (32)–(36), as shown in
Table 14. Subsequently, the fuzzy leaving flow
, the fuzzy entering flow
, and the fuzzy net outranking flow for each alternative are computed using Equations (37)–(39), as presented in
Table 15. Using the proposed spread area-based RMMS model, the fuzzy net outranking flow of each alternative is defuzzified using Equations (9)–(17) and yields values of
A1 (−0.0519),
A2 (0.0905),
A3 (0.0594) and
A4 (−0.0980) as presented in
Table 16. The final ranking of four startup projects
indicates that startup project
A2 has the highest comprehensive potential, followed by startup project
A3.
The utilization of the DEMATEL-ANP-based fuzzy PROMETHEE II provides a comprehensive procedure for ranking alternatives. The DEMATEL investigated the cause–effect relationships between criteria and filtered out the nonsignificant criteria. Subsequently, ANP helped to determine the criteria weights because it permits criterion dependency. Finally, the final ranking was generated by the fuzzy-based PROMETHEE II method, which includes a proposed ranking model to enhance consistency and discrimination ability. The numerical results demonstrated the feasibility of the hybrid model for various decision-making management applications.
6. Conclusions
Language has naturally evolved to reflect human judgment and fuzzy ranking is required to turn assessments into decision-making. An extension on ranking FNs using spread area-based RMMS was proposed to improve the applicability and differentiation of the methods of Wang et al. [
54], Nejad and Mashinchi [
59], and Chu and Nguyen [
63]. The algorithm and equations were derived by implementing a ranking method. Comparative examples demonstrated the strengths of the proposed method in discriminating fuzzy numbers and consistency ranking. Finally, the suggested ranking method was integrated into a hybrid DEMATEL-ANP-based fuzzy PROMETHEE II model to inspect the interrelationships among factors, obtain critical criteria weights, and organize startups for a comprehensive decision-making procedure. The numerical example has illustrated the feasibility of the hybrid fuzzy MCDM method.
In future studies, the proposed fuzzy ranking method can be amalgamated into different MCDM methods to further investigate its validity and apply the method to various practices in entrepreneurial problems, such as project selections, business investment evaluation, accelerator evaluation, risk management, performance evaluation, and other areas where decision-making involves subjective judgment and uncertainty. Hybrid fuzzy ranking methods enable comprehensive evaluation and prioritization of project proposals or initiatives by considering multiple criteria and incorporating fuzzy logic, aiding decision-makers in selecting projects aligned with their strategic objectives. In addition, fuzzy ranking methods can aid in evaluating and comparing different accelerators based on their offerings, mentorship quality, network strength, success rate, and other relevant criteria. This helps entrepreneurs make informed decisions about which accelerator program would best suit their needs and increase their chances of success. The fuzzy ranking approach adds a layer of flexibility to handle uncertain or imprecise data in investment decision-making.