Some Optimal Classes of Estimators Based on Multi-Auxiliary Information

Abstract

Ranked set sampling (RSS) has been proven an efficient alternative to simple random sampling (SRS). The use of auxiliary information also helps to improve the efficiency of the estimation procedures. Therefore, to accomplish higher efficiency and discuss the optimality issues, we proffer some optimal classes of estimators under RSS by employing multi-auxiliary information. It is seen that the ordinary mean estimator, traditional regression, and ratio estimators are the subsets of the proffered estimators. The expressions of the bias and mean square error are reported. An analytical comparison under some optimality conditions points out the ascendancy of the proffered classes of estimators over all reviewed works. The theoretical results have been furnished with computational study by employing some artificial and natural populations. The computational results show that the proffered estimators outperform the conventional estimators reviewed in this study. Furthermore, apposite advices are suggested to the survey persons.

1. Introduction

In the survey literature, usually more efficient estimates can be obtained by making appropriate utilization of additional data pertaining to the supplementary variables linked to the study variable. The data associated with the auxiliary variables are used either at the evaluation phase or at the design phase or at both. The ratio, regression, and product methods of evaluation are utilized widely at the estimation stage, whereas stratification of population and choice of units with probability relative to the size of the units are used at the design phase. Sometimes in vast surveys, the efficacy of the estimation procedures may increase by accumulating information on several auxiliary variables. Ref. [1] was the first who envisaged the ratio estimator in SRS by considering multi-auxiliary information (MAI) correlated positively with the study variable. Subsequently, many renowned statisticians like [2,3,4,5,6,7,8,9] suggested some estimators in SRS by using MAI.

The primary goal of any surveyor during survey is to achieve the observational economy by utilizing frugal and effective sampling schemes. In this context, ref. [10] envisaged the thought of RSS as a cost proficient substitute of SRS without any numerical support to his thought. Ref. [11] put up the requisite numerical support to the RSS theory. The circumstances of perfectly ranked units in RSS were studied simultaneously by [10,11]. Ref. [12] proved that the ranked set sample mean is an unbiased estimator of the population mean when the units are ranked imperfectly and perfectly. Ref. [13] deduced the estimates of the parameters in simple linear regression using RSS. Ref. [14] proved that the efficiency of the ratio estimator can be enhanced by ranking the denominator variable. Ref. [15] suggested a ratio estimation of the population mean utilizing auxiliary information under SRS and median RSS. Ref. [16] investigated a double quartile RSS for computing the population ratio utilizing auxiliary information. Ref. [17] developed the ratio estimators of the population mean in case of missing values under RSS. Ref. [18] examined a ratio estimation approach based on multistage median RSS. Ref. [19] investigated a novel class of regression cum ratio estimators of population mean based on RSS. Some comprehensive studies based on RSS were presented by [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].

Furthermore, in extensive surveys, in the case of bivariate auxiliary information (BAI), ref. [35] deliberated the ratio type population mean estimators utilizing supplementary information in RSS. An enhanced ratio estimator consisting of BAI under RSS was analyzed by [36]. Refs. [37,38] discussed the improved ratio kind of estimators by using BAI in RSS. Ref. [39] investigated efficient population mean estimators based on BAI under RSS. Ref. [40] suggested some efficient population mean estimation methods under stratified RSS consisting of BAI.

Under the ranked set sampling framework, when multi-auxiliary information is available, then no prominent works are available till date. Therefore, we extended the multivariate version of the existing estimators as well as proffered our estimators using bivariate and multi-auxiliary information. The main contributions of this study to the existing body of knowledge is:

(i).

to provide some optimal classes of estimators based on multi-auxiliary information having the maximum relative efficiency and the least $MSE$,

(ii).

to provide a comparative study theoretically,

(iii).

to provide an extensive simulation study and a real data application for comparison with the existing estimators.

The further manuscript is designed in a few sections. Section 2 describes the sampling methodology and notations used throughout this study. Section 3 describes a concise review of the conventional estimators under RSS. The proffered estimators are suggested in Section 4 with the properties. The conditions of optimality are deduced by comparing the proffered estimators with the conventional aspirants in Section 5, whereas Section 6 comprises the computational study and discussion of the results administered to enhance the theoretical findings. The conclusion is drafted in Section 7.

2. Methodology and Notations

The methodology of RSS is consisting of drawing m simple random samples independently, m elements without replacement from the population of length N. Here, m is a design parameter known as set size which should kept small to avoid large ranking errors. Let the ranking be performed over the characteristic of either the research variable or the auxiliary variable. Suppose the research variable is notified by y and the auxiliary variables are notified by $w_1$ and $w_2$, then $m^2$ trivariate random samples are drawn from the population and randomly allocated in m sets, all of length m. Every set is now ranked regarding one of the auxiliary variable $w_1$ or $w_2$. Here, ranking is performed on the basis of the auxiliary variable $w_1$. Now, from the first set, the element assigned the lowest rank of $w_1$, along with the variables y and $w_2$ linked to the lowest rank of $w_1$ is quantified. From the second set of length m, the variables y and $w_2$ linked to the second lowest rank of $w_1$ are quantified. The above procedure is kept on until the y and $w_2$ values assigned the largest rank of $w_1$ are quantified from the set m. The above sampling process consummates one cycle. The iteration of this cycle with r count furnishes $n=mr$ ranked set samples. Hence, in RSS, overall $m^{2}r$ elements are extracted from the population out of which only $mr$ elements are quantified for further study.

Let $\Omega =({\Omega }_1,{\Omega }_2,\dots ,{\Omega }_N)$ be a finite population having N identifiable units from which a ranked set sample of size n is quantified. Let $\overline{Y}$, ${\sigma }_y^2$, and $C_y$ be, respectively, the population mean, population variance, and population coefficient of variation of the research variable y. The information on supplementary variables $w_1$ and $w_2$ are used to estimate the population mean $\overline{Y}$. Let ${\overline{W}}_i$, ${\sigma }_i^2$ and $C_{w_i},i=1,2$ be the population mean, population variance, and population coefficient of variation of auxiliary variables $w_1$ and $w_2$, respectively, which are supposed to be available. Let the ranking be carried out here over the auxiliary variable $w_1$. Let $y_{\left[i\right]j}$ and $w_{2\left[i\right]j}$ be, respectively, the $i^{th}$ judgement order statistics and $w_{1\left(i\right)j}$ denote the $i^{th}$ order statistics of a sample of size m in the cycle j of the variables y, $w_2$ and $w_1$ consist of $n=mr$ ranked set sample quantified from the population $\Omega$. Here, the units are perfectly ranked according to $w_1$, denoted by $\left(\right)$ and therefore, ranking of y and $w_2$ are imperfect, denoted by $\left[\right]$, meaning thereby that they may not be sorted in the same order as that of $w_1$.

To determine the mean square error ($MSE$) and bias of the proffered estimators, we assume the undermentioned terminologies in this paper.

Let ${ϵ}_0=({\overline{y}}_{\left[n\right]}-\overline{Y})/\overline{Y},{ϵ}_1=({\overline{w}}_{1\left(n\right)}-{\overline{W}}_1)/{\overline{W}}_1,\mathrm{and}{ϵ}_2=({\overline{w}}_{2\left[n\right]}-{\overline{W}}_2)/{\overline{W}}_2$ be the error terms provided $E\left({ϵ}_a\right)=0,a=0,1,2$, $E\left(w_{1_{\left(i\right)}}\right)={\mu }_{w_{1\left(i\right)}}$, $E\left(w_{2_{\left[i\right]}}\right)={\mu }_{w_{2\left[i\right]}}$, and $E\left(y_{\left[i\right]}\right)={\mu }_{y_{\left[i\right]}}$. Also,

$$\begin{array}{cc}\hfill E\left({{ϵ}_0}^2\right)& =(\gamma C_y^2-D_{y_{\left[i\right]}}^2)=U_0,\hfill \\ \hfill E\left({{ϵ}_1}^2\right)& =(\gamma C_{w_1}^2-D_{w_{1\left(i\right)}}^2)=U_1,\hfill \\ \hfill E\left({{ϵ}_2}^2\right)& =(\gamma C_{w_2}^2-D_{w_{2\left[i\right]}}^2)=U_2,\hfill \\ \hfill E\left({ϵ}_0,{ϵ}_1\right)& =(\gamma {\rho }_{w_{1}y}{C}_{w_1}{C}_y-D_{{w_{1}y}_{\left[i\right]}})=U_{01},\hfill \\ \hfill E\left({ϵ}_0,{ϵ}_2\right)& =(\gamma {\rho }_{w_{2}y}{C}_{w_2}{C}_y-D_{{w_{2}y}_{\left[i\right]}})=U_{02},\hfill \\ \hfill E\left({ϵ}_1,{ϵ}_2\right)& =(\gamma {\rho }_{w_1{w}_2}{C}_{w_1}{C}_{w_2}-D_{{w_1{w}_2}_{\left[i\right]}})=U_{12},\hfill \end{array}$$

where $\gamma =1/mr$, $C_{w_1}=S_{w_1}/{\overline{W}}_1$, $C_{w_2}=S_{w_2}/{\overline{W}}_2$, $C_y=S_y/\overline{Y}$, $S_y=$$\sqrt{{\sum }_{i=1}^N{(y_i-\overline{Y})}^2/(N-1)}$, $S_{w_1}=\sqrt{{\sum }_{i=1}^N{(w_{1_i}-{\overline{W}}_1)}^2/(N-1)}$, $S_{w_2}=$$\sqrt{{\sum }_{i=1}^N{(w_{2_i}-{\overline{W}}_2)}^2/(N-1)}$, $D_{w_{1\left(i\right)}}^2={\sum }_{i=1}^m{\tau }_{w_{1\left(i\right)}}^2/m^{2}r{\overline{W}}_1^2$, $D_{w_{2\left[i\right]}}^2={\sum }_{i=1}^m{\tau }_{w_{2\left[i\right]}}^2/m^{2}r{\overline{W}}_2^2$, $D_{y_{\left[i\right]}}^2={\sum }_{i=1}^m{\tau }_{y_{\left[i\right]}}^2/m^{2}r{\overline{Y}}^2$, $D_{w_1{y}_{\left[i\right]}}={\sum }_{i=1}^m{\tau }_{w_1{y}_{\left[i\right]}}/m^{2}r{\overline{W}}_1\overline{Y}$, $D_{w_2{y}_{\left[i\right]}}={\sum }_{i=1}^m{\tau }_{w_2{y}_{\left[i\right]}}/m^{2}r{\overline{W}}_2\overline{Y}$, $D_{{w_1{w}_2}_{\left[i\right]}}={\sum }_{i=1}^m{\tau }_{{w_1{w}_2}_{\left[i\right]}}/m^{2}r{\overline{W}}_1{\overline{W}}_2$, ${\tau }_{w_{{}_{1\left(i\right)}}}=({\mu }_{w_{{}_{1\left(i\right)}}}-{\overline{W}}_1)$, ${\tau }_{w_{{}_{2\left[i\right]}}}=({\mu }_{w_{{}_{2\left[i\right]}}}-{\overline{W}}_2)$ ${\tau }_{y_{{}_{\left[i\right]}}}=({\mu }_{y_{{}_{\left[i\right]}}}-\overline{Y})$, ${\tau }_{{w_{1}y}_{{}_{\left[i\right]}}}=({\mu }_{w_{{}_{1\left(i\right)}}}-{\overline{W}}_1)({\mu }_{y_{{}_{\left[i\right]}}}-\overline{Y})$, ${\tau }_{{w_{2}y}_{{}_{\left[i\right]}}}=({\mu }_{w_{{}_{2\left[i\right]}}}-{\overline{W}}_2)({\mu }_{y_{{}_{\left[i\right]}}}-\overline{Y})$, ${\tau }_{{w_1{w}_2}_{{}_{\left[i\right]}}}=({\mu }_{w_{{}_{1\left(i\right)}}}-{\overline{W}}_1)({\mu }_{w_{{}_{2\left[i\right]}}}-{\overline{W}}_2)$, ${\mu }_{y_{{}_{\left[i\right]}}}=E\left(y_{\left[i\right]}\right)$, ${\mu }_{w_{{}_{1\left(i\right)}}}=E\left(w_{1\left(i\right)}\right)$, and ${\mu }_{w_{{}_{2\left[i\right]}}}=E\left(w_{2\left[i\right]}\right)$.

Here, ${\overline{y}}_{\left[n\right]}={\sum }_{i=1}^m{y}_{\left[i\right]}/rm$, ${\overline{w}}_{1\left(n\right)}={\sum }_{i=1}^m{w}_{1\left(i\right)}/rm$, and ${\overline{w}}_{2\left[n\right]}={\sum }_{i=1}^m{w}_{2\left[i\right]}/rm$ are the ranked set sample mean of variables y, $w_1$, and $w_2$, respectively.

We elucidate that the quantities ${\mu }_{y_{{}_{\left[i\right]}}}$, ${\mu }_{w_{{}_{1\left(i\right)}}}$, and ${\mu }_{w_{{}_{2\left[i\right]}}}$ rely upon order statistics from any particular distribution are taken from [41], but, when the error judgement orderings are absent, then the values ${\mu }_{y_{{}_{\left[i\right]}}}$, ${\mu }_{w_{{}_{1\left(i\right)}}}$, and ${\mu }_{w_{{}_{2\left[i\right]}}}$ are taken as equal given that both auxiliary variables $w_1$ and $w_2$, and the study variable y possess the identical distribution (see [12]).

3. Review

The present section discusses the prominent conventional estimators suggested under RSS by using BAI and MAI, respectively.

The traditional unbiased estimator of the population mean is considered under RSS as

$$\begin{array}{c}\hfill {\overline{y}}_m={\overline{y}}_{\left[n\right]}\end{array}$$

When study and auxiliary variables are strongly positively correlated and when the regression line of y on $w_1$ and $w_2$ follows a straight line through the origin, then the ratio estimator is more effective. Considering this benefit, we define the RSS based conventional ratio estimator envisaged by [14] using BAI as

$${\overline{y}}_r={\overline{y}}_{\left[n\right]}\left(\frac{{\overline{W}}_1}{{\overline{w}}_{1\left(n\right)}}\right)\left(\frac{{\overline{W}}_2}{{\overline{w}}_{2\left[n\right]}}\right)$$

The conventional ratio estimator consisting of MAI is given by

$$\begin{array}{c}\hfill {\overline{y}}_{r_{multi}}={\overline{y}}_{\left[n\right]}\prod _{l=1}^q\left(\frac{{\overline{W}}_l}{{\overline{w}}_{l\left(n\right)}}\right)\end{array}$$

Sometimes the study and auxiliary variables are linearly regressed but the regression line passes a location far from the origin. In such situations, the efficiency of the ratio estimator is very poor. Regression estimator is the best option in these situations. Therefore, on the lines of [42], we consider BAI and define the RSS based conventional regression estimator as

$${\overline{y}}_l={\overline{y}}_{\left[n\right]}+b_1({\overline{W}}_1-{\overline{w}}_{1\left(n\right)})+b_2({\overline{W}}_2-{\overline{w}}_{2\left[n\right]})$$

where $b_1$ and $b_2$ denote, respectively, the regression coefficients of y on $w_1$ and $w_2$.

The conventional regression estimator consisting of MAI is defined as

$$\begin{array}{c}\hfill {\overline{y}}_{l_{multi}}={\overline{y}}_{\left[n\right]}+\sum _{l=1}^q{b}_l({\overline{W}}_l-{\overline{w}}_{l\left(n\right)})\end{array}$$

where $b_l$ denotes the regression coefficient of y on $w_l,l=1,2,\dots ,q$, respectively.

Ref. [35] developed some ratio type estimators based on BAI as

$$\begin{array}{cc}\hfill {\overline{y}}_a& ={\overline{y}}_{\left[n\right]}{\left(\frac{{\overline{W}}_1}{{\overline{w}}_{1\left(n\right)}}\right)}^{a_1}{\left(\frac{{\overline{W}}_2}{{\overline{w}}_{2\left[n\right]}}\right)}^{a_2}\hfill \\ \hfill {\overline{y}}_w& ={\overline{y}}_{\left[n\right]}\left\{w_1{\left(\frac{{\overline{W}}_1}{{\overline{w}}_{1\left(n\right)}}\right)}^{a_1}+w_2{\left(\frac{{\overline{W}}_2}{{\overline{w}}_{2\left[n\right]}}\right)}^{a_2}\right\}\hfill \end{array}$$

where $a_1,a_2,w_1,\mathrm{and}{w}_2$ are properly selected scalars and $w_1+w_2=1$.

The estimators of [35] consisting of MAI are defined as

$$\begin{array}{cc}\hfill {\overline{y}}_{a_{multi}}& ={\overline{y}}_{\left[n\right]}\prod _{l=1}^q{\left(\frac{{\overline{W}}_l}{{\overline{w}}_{l\left(n\right)}}\right)}^{a_l}\hfill \\ \hfill {\overline{y}}_{w_{multi}}& ={\overline{y}}_{\left[n\right]}\sum _{l=1}^q{w}_l{\left(\frac{{\overline{W}}_l}{{\overline{w}}_{l\left(n\right)}}\right)}^{a_l}\hfill \end{array}$$

where $a_l$ and $w_l$ are properly selected scalars and the sum of $w_l$ is 1.

Motivated by [1,36] suggested the ratio type estimator as

$${\overline{y}}_{mm}={\overline{y}}_{\left[n\right]}\left\{d_1\left(\frac{{\overline{W}}_1}{{\overline{w}}_{1\left(n\right)}}\right)+d_2\left(\frac{{\overline{W}}_2}{{\overline{w}}_{2\left[n\right]}}\right)\right\}$$

where $d_1$ and $d_2$ are properly selected scalars.

The estimator of [36] using MAI is stated as

$$\begin{array}{cc}\hfill {\overline{y}}_{m{m}_{multi}}& ={\overline{y}}_{\left[n\right]}\sum _{l=1}^q{d}_l\left(\frac{{\overline{W}}_l}{{\overline{w}}_{l\left(n\right)}}\right)\hfill \end{array}$$

Following [43], we define some RSS based ratio-cum-product type estimators using BAI as

$$\begin{array}{cc}\hfill {\overline{y}}_{m{m}_1}& ={\overline{y}}_{\left[n\right]}\left(\frac{{\overline{W}}_1+C_{w_1}}{{\overline{w}}_{1\left(n\right)}+C_{w_1}}\right)\left(\frac{{\overline{W}}_2+C_{w_2}}{{\overline{w}}_{2\left[n\right]}+C_{w_2}}\right)\hfill \\ \hfill {\overline{y}}_{m{m}_2}& ={\overline{y}}_{\left[n\right]}\left(\frac{{\overline{W}}_1+{\beta }_2\left(w_1\right)}{{\overline{w}}_{1\left(n\right)}+{\beta }_2\left(w_1\right)}\right)\left(\frac{{\overline{W}}_2+{\beta }_2\left(w_2\right)}{{\overline{w}}_{2\left[n\right]}+{\beta }_2\left(w_2\right)}\right)\hfill \\ \hfill {\overline{y}}_{m{m}_3}& ={\overline{y}}_{\left[n\right]}\left(\frac{{\overline{W}}_1{C}_{w_1}+{\beta }_2\left(w_1\right)}{{\overline{w}}_{1\left(n\right)}{C}_{w_1}+{\beta }_2\left(w_1\right)}\right)\left(\frac{{\overline{W}}_2{C}_{w_2}+{\beta }_2\left(w_2\right)}{{\overline{w}}_{2\left[n\right]}{C}_{w_2}+{\beta }_2\left(w_2\right)}\right)\hfill \\ \hfill {\overline{y}}_{m{m}_4}& ={\overline{y}}_{\left[n\right]}\left(\frac{{\overline{w}}_{1\left(n\right)}{C}_{w_1}+{\beta }_2\left(w_1\right)}{{\overline{W}}_1{C}_{w_1}+{\beta }_2\left(w_1\right)}\right)\left(\frac{{\overline{w}}_{2\left[n\right]}{C}_{w_2}+{\beta }_2\left(w_2\right)}{{\overline{W}}_2{C}_{w_2}+{\beta }_2\left(w_2\right)}\right)\hfill \end{array}$$

where ${\beta }_2\left(w_1\right)$ and ${\beta }_2\left(w_2\right)$ are the coefficient of kurtosis of auxiliary variables $w_1$ and $w_2$, respectively.

The above estimators utilizing MAI are prescribed as

$$\begin{array}{cc}\hfill {\overline{y}}_{{m{m}_1}_{multi}}& ={\overline{y}}_{\left[n\right]}\prod _{l=1}^q\left(\frac{{\overline{W}}_l+C_{w_l}}{{\overline{w}}_{l\left(n\right)}+C_{w_l}}\right)\hfill \\ \hfill {\overline{y}}_{{m{m}_2}_{multi}}& ={\overline{y}}_{\left[n\right]}\prod _{l=1}^q\left(\frac{{\overline{W}}_l+{\beta }_2\left(w_l\right)}{{\overline{w}}_{l\left(n\right)}+{\beta }_2\left(w_l\right)}\right)\hfill \\ \hfill {\overline{y}}_{{m{m}_3}_{multi}}& ={\overline{y}}_{\left[n\right]}\prod _{l=1}^q\left(\frac{{\overline{W}}_l{C}_{w_l}+{\beta }_2\left(w_l\right)}{{\overline{w}}_{l\left(n\right)}{C}_{w_l}+{\beta }_2\left(w_l\right)}\right)\hfill \\ \hfill {\overline{y}}_{{m{m}_4}_{multi}}& ={\overline{y}}_{\left[n\right]}\prod _{l=1}^q\left(\frac{{\overline{w}}_{l\left(n\right)}{C}_{w_l}+{\beta }_2\left(w_l\right)}{{\overline{W}}_l{C}_{w_l}+{\beta }_2\left(w_l\right)}\right)\hfill \end{array}$$

where $b_2\left(w_l\right)$ is the coefficient of kurtosis of supplementary variable $w_l$.

Ref. [37] considered BAI and introduced the following estimators as

$$\begin{array}{c}\hfill {\overline{y}}_{k_1}={\overline{y}}_{\left[n\right]}{\left(\frac{{\overline{W}}_1}{{\overline{w}}_{1\left(n\right)}}\right)}^{{\eta }_1}{\left(\frac{{\overline{W}}_2}{{\overline{w}}_{2\left[n\right]}}\right)}^{{\eta }_2}\left\{k_1\exp \left(\frac{{\overline{W}}_1-{\overline{w}}_{1\left(n\right)}}{{\overline{W}}_1+{\overline{w}}_{1\left(n\right)}}\right)+k_2\exp \left(\frac{{\overline{W}}_2-{\overline{w}}_{2\left[n\right]}}{{\overline{W}}_2+{\overline{w}}_{2\left[n\right]}}\right)\right\}\end{array}$$

where ${\eta }_1$ and ${\eta }_2$ are properly selected scalars and $k_1$, and $k_2$ are the weights such that $k_1+k_2=1$.

The estimator of [37] based on MAI is expressed as

$$\begin{array}{c}\hfill {\overline{y}}_{{k_1}_{multi}}={\overline{y}}_{\left[n\right]}\prod _{l=1}^q{\left(\frac{{\overline{W}}_l}{{\overline{w}}_{l\left(n\right)}}\right)}^{{\eta }_l}\sum _{l=1}^q{k}_l\exp \left(\frac{{\overline{W}}_l-{\overline{w}}_{l\left(n\right)}}{{\overline{W}}_l+{\overline{w}}_{l\left(n\right)}}\right)\end{array}$$

where ${\eta }_l,l=1,2,\dots ,q$ is a properly selected scalars and $k_l,l=1,2,\dots ,q$ are weights whose sum is 1.

Ref. [38] suggested the following estimator utilizing two auxiliary variables in RSS as

$$\begin{array}{c}\hfill {\overline{y}}_{k_2}={\overline{y}}_{\left[n\right]}\exp \left(\frac{{\overline{W}}_1-{\overline{w}}_{1\left(n\right)}}{{\overline{W}}_1+(b_1-1){\overline{w}}_{1\left(n\right)}}\right)\exp \left(\frac{{\overline{W}}_2-{\overline{w}}_{2\left[n\right]}}{{\overline{W}}_2+(b_2-1){\overline{w}}_{2\left[n\right]}}\right)\end{array}$$

where $b_1$ and $b_2$ are properly selected scalars.

The estimator of [38] utilizing MAI is expressed as

$$\begin{array}{c}\hfill {\overline{y}}_{{k_2}_{multi}}={\overline{y}}_{\left[n\right]}\prod _{l=1}^q\exp \left(\frac{{\overline{W}}_l-{\overline{w}}_{l\left(n\right)}}{{\overline{W}}_l+(b_l-1){\overline{w}}_{l\left(n\right)}}\right)\end{array}$$

where $b_l,l=1,2,\dots ,q$ is a properly selected scalar.

Ref. [39] introduced the following estimators considering BAI under RSS as

$$\begin{array}{c}\hfill {\overline{y}}_{k_3}=\{{\overline{y}}_{\left[n\right]}+{\Phi }_1({\overline{W}}_1-{\overline{w}}_{1\left(n\right)})+{\Phi }_2({\overline{W}}_2-{\overline{w}}_{2\left[n\right]})\}\left\{\begin{array}{c}{k}_1\exp \left(\frac{{\overline{W}}_1-{\overline{w}}_{1\left(n\right)}}{{\overline{W}}_1+{\overline{w}}_{1\left(n\right)}}\right)\hfill \\ +k_2\exp \left(\frac{{\overline{W}}_2-{\overline{w}}_{2\left[n\right]}}{{\overline{W}}_2+{\overline{w}}_{2\left[n\right]}}\right)\hfill \end{array}\right\}\end{array}$$

where ${\Phi }_1$ and ${\Phi }_2$ are properly selected scalars and $k_1$ and $k_2$ are the same as defined earlier.

The estimator of [39] consisting of MAI is defined as

$$\begin{array}{c}\hfill {\overline{y}}_{{k_3}_{multi}}=\left\{{\overline{y}}_{\left[n\right]}+\sum _{l=1}^q{\Phi }_l({\overline{W}}_l-{\overline{w}}_{l\left(n\right)})\right\}\sum _{l=1}^q{k}_l\exp \left(\frac{{\overline{W}}_l-{\overline{w}}_{l\left(n\right)}}{{\overline{W}}_l+{\overline{w}}_{l\left(n\right)}}\right)\end{array}$$

where ${\Phi }_l,l=1,2,\dots ,q$ is a properly selected scalars.

The $MSEs$ of these estimators are reported in Appendix A.

4. Proposed Estimators

The inspiration of this study is to proffer some optimal classes of estimators as an optimal choice over the reviewed estimators. Motivated by [20], we extended the work of [21] using BAI and MAI and proffer some difference and ratio type estimators under RSS.

4.1. Proposed Estimators Using BAI

The proffered classes of estimators consisting of BAI are given as

$$\begin{array}{cc}\hfill T_{{bk}_1}& ={\varphi }_1{\overline{y}}_{\left[n\right]}+{\zeta }_1({\overline{w}}_{1\left(n\right)}-{\overline{W}}_1)+{\zeta }_2({\overline{w}}_{2\left[n\right]}-{\overline{W}}_2)\hfill \\ \hfill T_{{bk}_2}& ={\varphi }_2{\overline{y}}_{\left[n\right]}{\left(\frac{{\overline{W}}_1}{{\overline{w}}_{1\left(n\right)}}\right)}^{{\delta }_1}{\left(\frac{{\overline{W}}_2}{{\overline{w}}_{2\left[n\right]}}\right)}^{{\delta }_2}\hfill \\ \hfill T_{{bk}_3}& ={\varphi }_3{\overline{y}}_{\left[n\right]}\left\{\frac{{\overline{W}}_1}{{\overline{W}}_1+{\theta }_1({\overline{w}}_{1\left(n\right)}-{\overline{W}}_1)}\right\}\left\{\frac{{\overline{W}}_2}{{\overline{W}}_2+{\theta }_2({\overline{w}}_{2\left[n\right]}-{\overline{W}}_2)}\right\}\hfill \end{array}$$

where ${\varphi }_1$, ${\zeta }_i$, ${\varphi }_2$, ${\delta }_i$, ${\varphi }_3$, and ${\theta }_i$; $i=1,2$ are properly selected scalars.

4.2. Proposed Estimators Using MAI

The proffered classes of estimators based on MAI are given as

$$\begin{array}{cc}\hfill T_{b{k}_4}& ={\varphi }_4{\overline{y}}_{\left[n\right]}+\sum _{l=1}^q{\zeta }_l({\overline{w}}_{l\left(n\right)}-{\overline{W}}_l)\hfill \\ \hfill T_{b{k}_5}& ={\varphi }_5{\overline{y}}_{\left[n\right]}\prod _{l=1}^q{\left(\frac{{\overline{W}}_l}{{\overline{w}}_{l\left(n\right)}}\right)}^{{\delta }_l}\hfill \\ \hfill T_{b{k}_6}& ={\varphi }_6{\overline{y}}_{\left[n\right]}\prod _{l=1}^q\left\{\frac{{\overline{W}}_l}{{\overline{W}}_l+{\theta }_l({\overline{w}}_{l\left(n\right)}-{\overline{W}}_l)}\right\}\hfill \end{array}$$

where ${\varphi }_4,{\varphi }_5,{\varphi }_6,{\zeta }_l,{\delta }_l,\mathrm{and}{\theta }_l$; $l=1,2,...,q$ are properly selected scalars.

It can be easily seen that the class $T_{b{k}_1}$ and $T_{b{k}_4}$ are generalized classes of regression type estimators and we get the regression type estimators as their special cases by putting ${\varphi }_1=1$ and ${\varphi }_4=1$. Similarly, the estimators $T_{b{k}_2}$ and $T_{b{k}_5}$ are generalized classes of ratio and product type estimators, and we get the ratio and product estimators as their special cases by putting ${\varphi }_2=1$, ${\delta }_i=(1,-1),i=1,2$ and ${\varphi }_5=1$, ${\delta }_l=(1,-1)$, respectively. Furthermore, the ratio cum product estimators can also be obtained by suitably choosing ${\delta }_l$ to be either −1 or +1. Similarly, it can be easily seen that the class $T_{b{k}_3}$ and $T_{b{k}_6}$ are generalized classes of ratio type estimators and we get the ratio estimators as their special cases by putting ${\theta }_1=1$, ${\theta }_2=1$ and ${\theta }_l=1$. Similarly, some other subclasses can also be provided.

4.3. Bias and Minimum MSE of the Proffered Estimators

Theorem 1. 

The expressions of bias and minimum MSE of the proffered difference type estimators $T_{b{k}_i},i=1,4$ are given below as

$$\begin{array}{cc}\hfill Bias\left(T_{b{k}_i}\right)& =\overline{Y}({\varphi }_i-1)\hfill \\ \hfill minMSE\left(T_{b{k}_i}\right)& ={\overline{Y}}^2(1-{\varphi }_{i\left(opt\right)})\hfill \end{array}$$

(1)

where

$$\begin{array}{cc}\hfill {\varphi }_{1\left(opt\right)}& =\frac{1}{\left\{1+U_0-\frac{\left(\begin{array}{c}{U}_1{U}_{02}^2+U_2{U}_{01}^2-2U_{01}{U}_{02}{U}_{12}\hfill \end{array}\right)}{\begin{array}{c}(U_1{U}_2-U_{12}^2)\hfill \end{array}}\right\}}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\varphi }_{4\left(opt\right)}& =\frac{1}{\left\{1+U_0-\frac{\left(\begin{array}{c}{\displaystyle \sum _{l=1}^q}{U}_l{\displaystyle U_{0q-l+1}^2}-2\sum {\displaystyle \sum _{i>l}^q}{U}_{0i}{U}_{0l}{U}_{il}\hfill \end{array}\right)}{\begin{array}{c}\left({\displaystyle \prod _{l=1}^q}{U}_l-\sum {\displaystyle \sum _{i>l}^q}{\displaystyle U_{il}^2}\right)\hfill \end{array}}\right\}}\hfill \end{array}$$

(3)

Proof. 

Appendix B contains the proof’s outline. □

Theorem 2. 

The expressions of bias and minimum MSE of the proffered ratio type estimators $T_{b{k}_i},i=2,3,5,6$ are given below as

$$\begin{array}{cc}\hfill Bias\left(T_{b{k}_i}\right)& =\overline{Y}({\varphi }_i{B}_i-1)\hfill \\ \hfill minMSE\left(T_{b{k}_i}\right)& ={\overline{Y}}^2\left(1-\frac{B_i^2}{A_i}\right)\hfill \end{array}$$

(4)

Proof. 

Appendix B contains the proof’s outline. The definitions of ${\varphi }_i$, $A_i$, and $B_i$ are given in Appendix B. □

The $MSE$ of the proposed estimator $T_{b{k}_1}$ obtained in (1) depends on the values of $\overline{Y}$ and ${\varphi }_1$, while the $MSE$ of the proposed estimators $T_{b{k}_i},i=2,3$ obtained in (4) depends on the values of $\overline{Y}$ and $B_i^2/A_i$, when the population size is large. In the numerical study section, following [44,45], we will examine the effect of the variations of the $\overline{Y}$, ${\varphi }_1$, and $B_i^2/A_i$ values on the $MSE$ of the proposed estimators.

Corollary 1. 

The proffered ratio type estimators $T_{b{k}_i},i=2,3$ are superior than the proffered difference type estimator $T_{b{k}_1}$, iff

$$\begin{array}{c}\hfill \frac{B_i^2}{A_i}>{\varphi }_{1\left(opt\right)}\end{array}$$

(5)

and vice-versa. Otherwise, these are evenly effective provided that the equality sustains in (5).

Proof. 

By comparing (1) and (4), we obtain (5). □

The inequality given in (5) can merely be obtained. Therefore, to check whether it holds practically, we perform a computational study in Section 5.

5. Optimality Conditions

The minimum $MSE$s of the suggested estimators $T_{b{k}_i},i=1,2,3$ and the reviewed estimators are theoretically compared in this part, and the optimality conditions are reported.

The proffered estimator $T_{b{k}_1}$ dominates the usual mean estimator ${\overline{y}}_m$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_m\right)\hfill \\ \hfill {\overline{Y}}^2(1-{\varphi }_{1\left(opt\right)})& <{\overline{Y}}^2{U}_0\hfill \\ \hfill (1-{\varphi }_{1\left(opt\right)})& <U_0\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0\hfill \end{array}$$

(6)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate the usual mean estimator ${\overline{y}}_m$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_m\right)\hfill \\ \hfill {\overline{Y}}^2\left(1-\frac{B_i^2}{A_i}\right)& <{\overline{Y}}^2{U}_0\hfill \\ \hfill \left(1-\frac{B_i^2}{A_i}\right)& <U_0\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0\hfill \end{array}$$

(7)

The proffered estimator $T_{b{k}_1}$ dominates the usual ratio estimator ${\overline{y}}_r$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_r\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0-U_1-U_2+2U_{01}+2U_{02}-2U_{12}\hfill \end{array}$$

(8)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate the usual ratio estimator ${\overline{y}}_r$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_r\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0-U_1-U_2+2U_{01}+2U_{02}-2U_{12}\hfill \end{array}$$

(9)

The proffered estimator $T_{b{k}_1}$ dominates the usual regression estimator ${\overline{y}}_l$, ref. [35] estimator ${\overline{y}}_a$ and [38] estimator ${\overline{y}}_{k_2}$ if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_t\right);{\overline{y}}_t={\overline{y}}_l,{\overline{y}}_a\mathrm{and}{\overline{y}}_{k_2}\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\hfill \end{array}$$

(10)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate the usual regression estimator ${\overline{y}}_l$, ref. [35] estimator ${\overline{y}}_a$ and [38] estimator ${\overline{y}}_{k_2}$ if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_t\right);{\overline{y}}_t={\overline{y}}_l,{\overline{y}}_a\mathrm{and}{\overline{y}}_{k_2}\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\hfill \end{array}$$

(11)

The proffered estimator $T_{b{k}_1}$ dominates [35] estimator ${\overline{y}}_w$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_w\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0-a_2^2{U}_2+2a_2{U}_{02}+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\hfill \end{array}$$

(12)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [35] estimator ${\overline{y}}_w$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_w\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0-a_2^2{U}_2+2a_2{U}_{02}+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\hfill \end{array}$$

(13)

The proffered estimator $T_{b{k}_1}$ dominates [36] estimator ${\overline{y}}_{mm}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_{mm}\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-(U_0+U_2+2U_{02})+\frac{{(U_{02}-U_2-U_{01}+U_{12})}^2}{(U_1+U_2-2U_{12})}\hfill \end{array}$$

(14)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [36] estimator ${\overline{y}}_{mm}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_{mm}\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-(U_0+U_2+2U_{02})+\frac{{(U_{02}-U_2-U_{01}+U_{12})}^2}{(U_1+U_2-2U_{12})}\hfill \end{array}$$

(15)

The proffered estimator $T_{b{k}_1}$ dominates [43] estimator ${\overline{y}}_{m{m}_1}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_{m{m}_1}\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0-{\lambda }_1^2{U}_1-{\lambda }_2^2{U}_2+2{\lambda }_1{U}_{01}+2{\lambda }_2{U}_{02}-2{\lambda }_1{\lambda }_2{U}_{12}\hfill \end{array}$$

(16)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [43] estimator ${\overline{y}}_{m{m}_1}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_{m{m}_1}\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0-{\lambda }_1^2{U}_1-{\lambda }_2^2{U}_2+2{\lambda }_1{U}_{01}+2{\lambda }_2{U}_{02}-2{\lambda }_1{\lambda }_2{U}_{12}\hfill \end{array}$$

(17)

The proffered estimator $T_{b{k}_1}$ dominates [43] estimator ${\overline{y}}_{m{m}_2}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_{m{m}_2}\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0-{\Lambda }_1^2{U}_1-{\Lambda }_2^2{U}_2+2{\Lambda }_1{U}_{01}+2{\Lambda }_2{U}_{02}-2{\Lambda }_1{\Lambda }_2{U}_{12}\hfill \end{array}$$

(18)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [43] estimator ${\overline{y}}_{m{m}_1}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_{m{m}_2}\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0-{\Lambda }_1^2{U}_1-{\Lambda }_2^2{U}_2+2{\Lambda }_1{U}_{01}+2{\Lambda }_2{U}_{02}-2{\Lambda }_1{\Lambda }_2{U}_{12}\hfill \end{array}$$

(19)

The proffered estimator $T_{b{k}_1}$ dominates [43] estimator ${\overline{y}}_{m{m}_3}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_{m{m}_3}\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0-{\gamma }_1^2{U}_1-{\gamma }_2^2{U}_2+2{\gamma }_1{U}_{01}+2{\gamma }_2{U}_{02}-2{\gamma }_1{\gamma }_2{U}_{12}\hfill \end{array}$$

(20)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [43] estimator ${\overline{y}}_{m{m}_1}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_{m{m}_3}\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0-{\gamma }_1^2{U}_1-{\gamma }_2^2{U}_2+2{\gamma }_1{U}_{01}+2{\gamma }_2{U}_{02}-2{\gamma }_1{\gamma }_2{U}_{12}\hfill \end{array}$$

(21)

The proffered estimator $T_{b{k}_1}$ dominates [43] estimator ${\overline{y}}_{m{m}_4}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_{m{m}_4}\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-U_0-{\xi }_1^2{U}_1-{\xi }_2^2{U}_2-2{\xi }_1{U}_{01}-2{\xi }_2{U}_{02}-2{\xi }_1{\xi }_2{U}_{12}\hfill \end{array}$$

(22)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [43] estimator ${\overline{y}}_{m{m}_4}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_{m{m}_4}\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-U_0-{\lambda }_4^2{U}_1-{\Lambda }_4^2{U}_2-2{\lambda }_4{U}_{01}-2{\Lambda }_4{U}_{02}-2{\lambda }_4{\Lambda }_4{U}_{12}\hfill \end{array}$$

(23)

The proffered estimator $T_{b{k}_1}$ dominates [37] estimator ${\overline{y}}_{k_1}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_{k_1}\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >1-\left[\begin{array}{c}{U}_0+\frac{1}{4}{(k_1+2{\eta }_1)}^2{U}_1+\frac{1}{4}{(k_2+2{\eta }_2)}^2{U}_2-(k_1+2{\eta }_1)U_{01}\hfill \\ -(k_2+2{\eta }_2)U_{02}+\frac{1}{2}(k_1+2{\eta }_1)(k_2+2{\eta }_2)U_{12}\hfill \end{array}\right]\hfill \end{array}$$

(24)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [37] estimator ${\overline{y}}_{k_1}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_{k_1}\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-\left[\begin{array}{c}{U}_0+\frac{1}{4}{(k_1+2{\eta }_1)}^2{U}_1+\frac{1}{4}{(k_2+2{\eta }_2)}^2{U}_2-(k_1+2{\eta }_1)U_{01}\hfill \\ -(k_2+2{\eta }_2)U_{02}+\frac{1}{2}(k_1+2{\eta }_1)(k_2+2{\eta }_2)U_{12}\hfill \end{array}\right]\hfill \end{array}$$

(25)

The proffered estimator $T_{b{k}_1}$ dominates [39] estimator ${\overline{y}}_{k_3}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_1}\right)& <MSE\left({\overline{y}}_{k_3}\right)\hfill \\ \hfill {\varphi }_{1\left(opt\right)}& >\frac{1}{{\overline{Y}}^2}\left[\begin{array}{c}{\overline{Y}}^2-{\overline{Y}}^2{U}_0-\frac{1}{4}{(k_1\overline{Y}+2{\Phi }_1{\overline{W}}_1)}^2{U}_1-\frac{1}{4}{(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)}^2{U}_2\hfill \\ +\overline{Y}(\overline{Y}{k}_1+2{\Phi }_1{\overline{W}}_1)U_{01}+\overline{Y}(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{02}\hfill \\ -\frac{1}{2}(k_2\overline{Y}-2{\Phi }_1{\overline{W}}_1)(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{12}\hfill \end{array}\right]\hfill \end{array}$$

(26)

The proffered estimators $T_{b{k}_i},i=2,3$ dominate [39] estimator ${\overline{y}}_{k_3}$, if

$$\begin{array}{cc}\hfill MSE\left(T_{b{k}_i}\right)& <MSE\left({\overline{y}}_{k_3}\right)\hfill \\ \hfill \frac{B_i^2}{A_i}& >1-\frac{1}{{\overline{Y}}^2}\left[\begin{array}{c}{\overline{Y}}^2-{\overline{Y}}^2{U}_0-\frac{1}{4}{(k_1\overline{Y}+2{\Phi }_1{\overline{W}}_1)}^2{U}_1-\frac{1}{4}{(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)}^2{U}_2\hfill \\ +\overline{Y}(\overline{Y}{k}_1+2{\Phi }_1{\overline{W}}_1)U_{01}+\overline{Y}(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{02}\hfill \\ -\frac{1}{2}(k_2\overline{Y}-2{\Phi }_1{\overline{W}}_1)(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{12}\hfill \end{array}\right]\hfill \end{array}$$

(27)

Under the conditions (6)–(27), the proffered classes of estimators are superior in comparison with the conventional estimators. These conditions are illustrated numerically in the next section using a real population.

6. Computational Study

Four subsections—a numerical study utilizing real populations, a simulation study utilizing real populations, a simulation study utilizing artificially created populations, and a discussion of computational results are used to conduct a computational study in the current section.

6.1. Numerical Study Utilizing Real Populations

To exemplify the practicability of the proffered classes of estimators in real life scenarios, we carry out a numerical study by utilizing some real populations. These populations are discussed hereunder.

Population 1: 

Origine: [46], page no. 662–665, $w_1$ = 1983 import (in millions of U.S. dollar), $w_2$ = 1983 export (in millions of U.S. dollars), y = 1983 population (in millions), ${\overline{W}}_1$ = 14,604.49, ${\overline{W}}_2$ = 14,276.03, $\overline{Y}$ = 36.6516, $S_y=116.80$, $S_{w_1}=\mathrm{34,064.88}$, $S_{w_2}=\mathrm{31,431.81}$, ${\rho }_{w_{1}y}=0.2271$, ${\rho }_{w_1{w}_2}=0.9758$, ${\rho }_{w_{2}y}=0.2225$, and N = 124.

Population 2: 

Origine: [47] page no. 1115, y = 1996 seasonal average price (in U.S. dollar) per pound, $w_1$ = 1995 seasonal average price (in U.S. dollar) per pound, $w_2$ = 1994 seasonal average price (in U.S. dollar) per pound, $\overline{Y}$ = 0.2032, ${\overline{W}}_1$ = 0.1856, ${\overline{W}}_2$ = 0.1708, $S_y=0.0803$, $S_{w_1}=0.0752$, $S_{w_2}=0.0634$, ${\rho }_{w_{1}y}=0.8775$, ${\rho }_{w_{2}y}=0.8577$, ${\rho }_{w_1{w}_2}=0.8780$, and N = 36.

Population 3: 

Origine: [47], page no. 1116, y = quantity of fish caught in 1995, $w_1$ = quantity of fish caught in 1994, $w_2$ = quantity of fish caught in 1993, $\overline{Y}$ = 4514.89, ${\overline{W}}_1$ = 4954.43, ${\overline{W}}_2$ = 4591.07, $S_y=6099.14$, $S_{w_1}=7058.98$, $S_{w_2}=6315.21$, ${\rho }_{w_{1}y}=0.9601$, ${\rho }_{w_{2}y}=0.9564$, ${\rho }_{w_1{w}_2}=0.9729$, and N = 69.

Population 4: 

Origine: [46], page no. 652–659, y = real estate values as per 1984 assessment (in millions of kroner), $w_1$ = 1975 population (in thousand), $w_2$ = number of municipal employees in 1984, $\overline{Y}$ = 3077.52, ${\overline{W}}_1$ = 29.28, ${\overline{W}}_2$ = 1779.06, $S_y=4745.52$, $S_{w_1}=53.36$, $S_{w_2}=4253.13$, ${\rho }_{w_{1}y}=0.9687$, ${\rho }_{w_{2}y}=0.9400$, ${\rho }_{w_1{w}_2}=0.9601$, and N = 284.

We quantify a ranked set sample with m = 3 and r = 4 provided $n=rm$ = 12 units from Populations 1–4. The $MSE$ and percent relative efficiency (PRE) are tabulated for each population utilizing the formula given as

$$\begin{array}{c}\hfill PRE=\frac{MSE\left({\overline{y}}_m\right)}{MSE\left(T\right)}\times 100\end{array}$$

(28)

The numerical results are shown by $MSE$ and PRE in Table 1.

Table 1. Results of numerical study for real populations.

Estimators	Population 1		Population 2		Population 3		Population 4
	MSE	PRE	MSE	PRE	MSE	PRE	MSE	PRE
${\overline{y}}_m$	1133.892	100.000	0.000532	100.000	3,027,926	100.000	1,876,164	100.000
${\overline{y}}_r$	1997.891	56.754	0.000652	81.633	3,863,125	78.380	5,765,568	32.540
${\overline{y}}_l$	1082.504	104.747	0.000103	512.413	212,002	1428.252	228,686	820.410
${\overline{y}}_a$	1082.504	104.747	0.000103	512.413	212,002	1428.252	228,686	820.410
${\overline{y}}_w$	1078.606	105.125	0.000210	252.303	355,522	851.682	223,294	840.219
${\overline{y}}_{mm}$	2034.186	55.741	0.001860	28.609	11,959,036	25.319	4,111,339	45.633
${\overline{y}}_{m{m}_1}$	1997.496	56.765	0.000150	353.911	3,859,104	78.461	5,334,283	35.171
${\overline{y}}_{m{m}_2}$	1994.011	56.864	0.000439	121.090	3,834,538	78.964	1,412,015	132.871
${\overline{y}}_{m{m}_3}$	1996.164	56.803	0.000493	107.817	3,842,672	78.797	2,032,861	92.291
${\overline{y}}_{m{m}_4}$	3618.840	31.333	0.000572	92.942	27,886,266	10.858	15,976,676	11.743
${\overline{y}}_{k_1}$	1238.466	91.556	0.000488	108.913	6,838,612	44.276	13,330,568	14.074
${\overline{y}}_{k_2}$	1082.504	104.747	0.000103	512.413	212,002	1428.252	228,686	820.410
${\overline{y}}_{k_3}$	1262.336	89.824	0.000585	90.885	17,524,939	17.277	57,190,391	3.280
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{1}}}$	599.449	189.155	0.000103	513.702	209,820	1443.107	214,423	874.981
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{2}}}$	555.289	204.198	0.000103	514.386	201,387	1503.533	104,759	1790.933
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{3}}}$	586.707	193.263	0.000103	513.414	206,611	1465.516	149,486	1255.072

The bold values are representing minimum $MSE$ and maximum PRE.

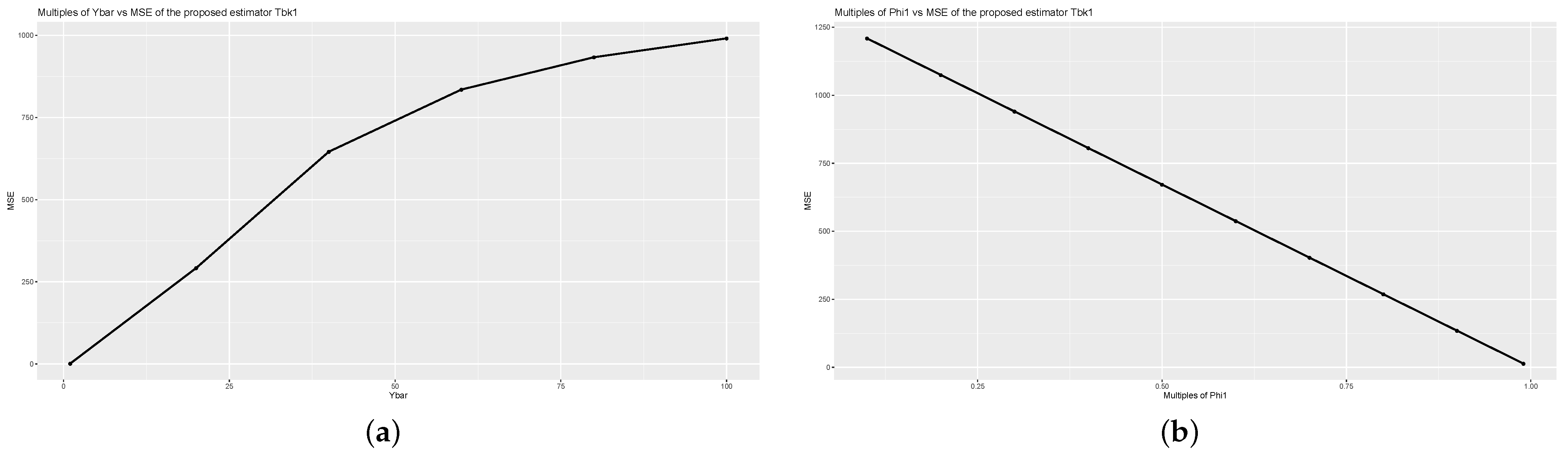
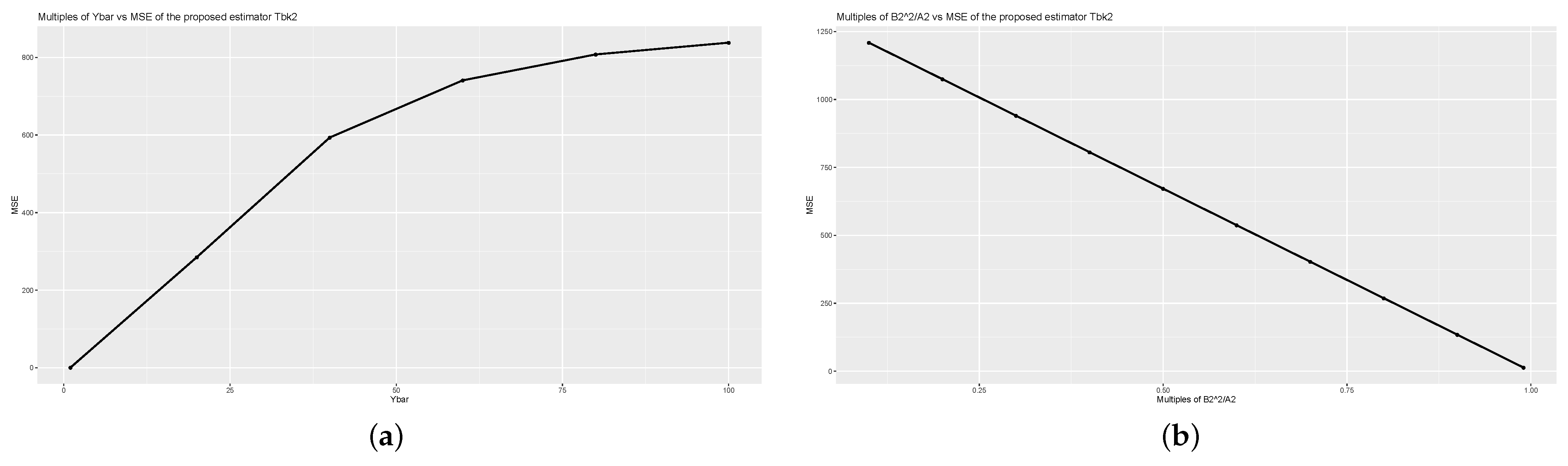
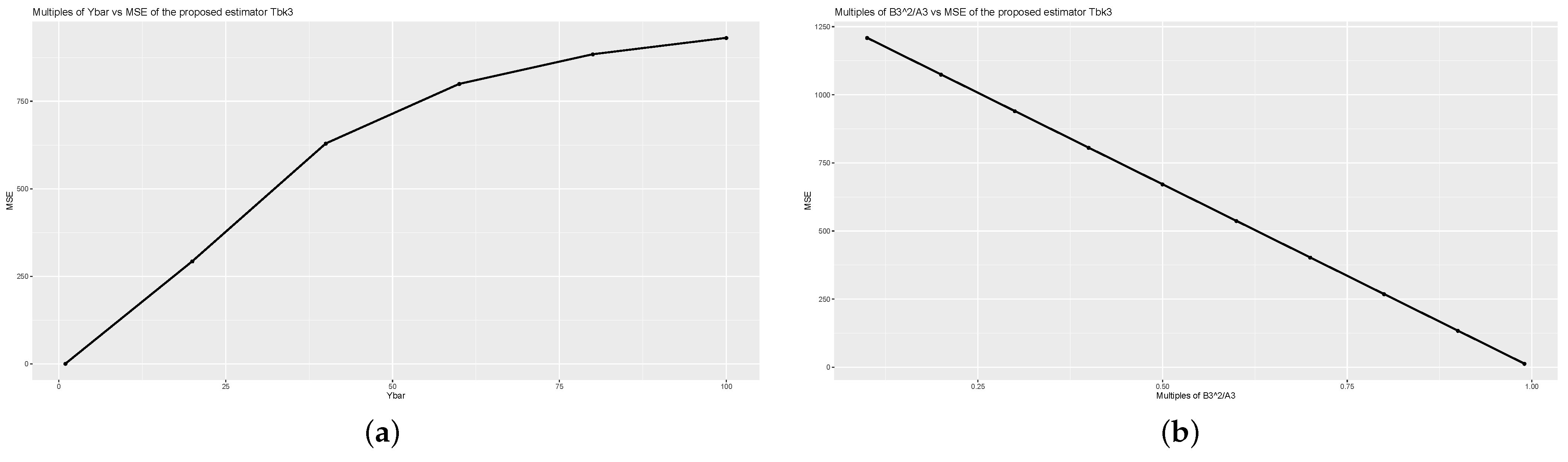
For a detailed analysis of the $MSE$ values of the proposed estimators computed using (1) and (4), we examine the $MSE$ values for different values of $\overline{Y}$, ${\Phi }_1$, and $B_i^2/A_i,i=2,3$ using Population 1 as shown in Figure 1, Figure 2 and Figure 3. We observe the effect of the $MSE$ values when $\overline{Y}$, ${\Phi }_1$, and $B_i^2/A_i,i=2,3$ values increase. Note that when $\overline{Y}$ increases, $MSE$ increases, while ${\Phi }_1$ and $B_i^2/A_i,i=2,3$ increases, $MSE$ decrease.

Figure 1. Graph of (a) Multiples of $\overline{Y}$ and $MSE$ of estimator $T_{b{k}_1}$ (b) Multiples of ${\Phi }_1$ and $MSE$ of estimator $T_{b{k}_1}$ for the Population 1.

Figure 2. Graph of (a) Multiples of $\overline{Y}$ and $MSE$ of estimator $T_{b{k}_2}$ (b) Multiples of $\frac{B_2^2}{A_2}$ and $MSE$ of estimator $T_{b{k}_2}$ for the Population 1.

Figure 3. Graph of (a) Multiples of $\overline{Y}$ and $MSE$ of estimator $T_{b{k}_3}$ (b) Multiples of $\frac{B_3^2}{A_3}$ and $MSE$ of estimator $T_{b{k}_3}$ for the Population 1.

In Figure 1, Figure 2 and Figure 3, for graphs (a), we multiply $\overline{Y}$ by 1 to 100, and for graphs (b), we vary ${\Phi }_1$ and $B_i^2/A_i,i=2,3$ from 0.1 to 0.99, given on x-axis. The $MSE$ values are shown on the y-axis. From Figure 1, Figure 2 and Figure 3, we observe that the increasing values of $\overline{Y}$ increase the $MSE$ values, while the increasing values of ${\Phi }_1$ and $B_i^2/A_i,i=2,3$, decrease the $MSE$ values of the proposed estimators. From these results, an optimal point might be found to obtain the minimum $MSE$ for the data sets. The similar effect can be shown using other data sets.

Furthermore, the efficiency conditions obtained in Section 5 are numerically illustrated in Table 2 using the real Population 1.

Table 2. Numerical illustration of the efficiency conditions obtained in Section 5 using Population 1.

Conditions	Numerical Illustration Using Population 1
Condition 6	${\varphi }_{1\left(opt\right)}>1-U_0\Rightarrow$0.5537 > 0.1559
Condition 7	$\frac{B_2^2}{A_2}>1-U_0\Rightarrow$0.5866 > 0.1559
Condition 7	$\frac{B_3^2}{A_3}>1-U_0\Rightarrow$0.5632 > 0.1559
Condition 8	${\varphi }_{1\left(opt\right)}>1-U_0-U_1-U_2+2U_{01}+2U_{02}-2U_{12}\Rightarrow$0.5537 > −0.4872
Condition 9	$\frac{B_2^2}{A_2}>1-U_0-U_1-U_2+2U_{01}+2U_{02}-2U_{12}\Rightarrow$0.5866 > −0.4872
Condition 9	$\frac{B_2^2}{A_2}>1-U_0-U_1-U_2+2U_{01}+2U_{02}-2U_{12}\Rightarrow$0.5632 > −0.4872
Condition 10	${\varphi }_{1\left(opt\right)}>1-U_0+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\Rightarrow$0.5537 > 0.1941
Condition 11	$\frac{B_2^2}{A_2}>1-U_0+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\Rightarrow$0.5866 > 0.1941
Condition 11	$\frac{B_3^2}{A_3}>1-U_0+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\Rightarrow$0.5632 > 0.1941
Condition 12	${\varphi }_{1\left(opt\right)}>1-U_0-a_2^2{U}_2+2a_2{U}_{02}+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\Rightarrow$0.5537 > 0.2666
Condition 13	$\frac{B_2^2}{A_2}>1-U_0-a_2^2{U}_2+2a_2{U}_{02}+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\Rightarrow$0.5866 > 0.2666
Condition 13	$\frac{B_3^2}{A_3}>1-U_0-a_2^2{U}_2+2a_2{U}_{02}+\frac{(U_2{U}_{01}^2+U_1{U}_{02}^2-2U_{01}{U}_{02}{U}_{12})}{(U_1{U}_2-U_{12}^2)}\Rightarrow$0.5632 > 0.2666
Condition 14	${\varphi }_{1\left(opt\right)}>1-(U_0+U_2+2U_{02})+\frac{{(U_{02}-U_2-U_{01}+U_{12})}^2}{(U_1+U_2-2U_{12})}\Rightarrow$0.5537 > −0.5142
Condition 15	$\frac{B_2^2}{A_2}>1-(U_0+U_2+2U_{02})+\frac{{(U_{02}-U_2-U_{01}+U_{12})}^2}{(U_1+U_2-2U_{12})}\Rightarrow$0.5866 > −0.5142
Condition 15	$\frac{B_3^2}{A_3}>1-(U_0+U_2+2U_{02})+\frac{{(U_{02}-U_2-U_{01}+U_{12})}^2}{(U_1+U_2-2U_{12})}\Rightarrow$0.5632 > −0.5142
Condition 16	${\varphi }_{1\left(opt\right)}>1-U_0-{\lambda }_1^2{U}_1-{\lambda }_2^2{U}_2+2{\lambda }_1{U}_{01}+2{\lambda }_2{U}_{02}-2{\lambda }_1{\lambda }_2{U}_{12}\Rightarrow$0.5537 > −0.4869
Condition 17	$\frac{B_2^2}{A_2}>1-U_0-{\lambda }_1^2{U}_1-{\lambda }_2^2{U}_2+2{\lambda }_1{U}_{01}+2{\lambda }_2{U}_{02}-2{\lambda }_1{\lambda }_2{U}_{12}\Rightarrow$0.5866 > −0.4869
Condition 17	$\frac{B_3^2}{A_3}>1-U_0-{\lambda }_1^2{U}_1-{\lambda }_2^2{U}_2+2{\lambda }_1{U}_{01}+2{\lambda }_2{U}_{02}-2{\lambda }_1{\lambda }_2{U}_{12}\Rightarrow$0.5632 > −0.4869
Condition 18	${\varphi }_{1\left(opt\right)}>1-U_0-{\Lambda }_1^2{U}_1-{\Lambda }_2^2{U}_2+2{\Lambda }_1{U}_{01}+2{\Lambda }_2{U}_{02}-2{\Lambda }_1{\Lambda }_2{U}_{12}\Rightarrow$0.5537 > −0.4843
Condition 19	$\frac{B_2^2}{A_2}>1-U_0-{\Lambda }_1^2{U}_1-{\Lambda }_2^2{U}_2+2{\Lambda }_1{U}_{01}+2{\Lambda }_2{U}_{02}-2{\Lambda }_1{\Lambda }_2{U}_{12}\Rightarrow$0.5866 > −0.4843
Condition 19	$\frac{B_3^2}{A_3}>1-U_0-{\Lambda }_1^2{U}_1-{\Lambda }_2^2{U}_2+2{\Lambda }_1{U}_{01}+2{\Lambda }_2{U}_{02}-2{\Lambda }_1{\Lambda }_2{U}_{12}\Rightarrow$0.5632 > −0.4843
Condition 20	${\varphi }_{1\left(opt\right)}>1-U_0-{\gamma }_1^2{U}_1-{\gamma }_2^2{U}_2+2{\gamma }_1{U}_{01}+2{\gamma }_2{U}_{02}-2{\gamma }_1{\gamma }_2{U}_{12}\Rightarrow$0.5537 > −0.4859
Condition 21	$\frac{B_2^2}{A_2}>1-U_0-{\gamma }_1^2{U}_1-{\gamma }_2^2{U}_2+2{\gamma }_1{U}_{01}+2{\gamma }_2{U}_{02}-2{\gamma }_1{\gamma }_2{U}_{12}\Rightarrow$0.5866 > −0.4859
Condition 21	$\frac{B_3^2}{A_3}>1-U_0-{\gamma }_1^2{U}_1-{\gamma }_2^2{U}_2+2{\gamma }_1{U}_{01}+2{\gamma }_2{U}_{02}-2{\gamma }_1{\gamma }_2{U}_{12}\Rightarrow$0.5632 > −0.4859
Condition 22	${\varphi }_{1\left(opt\right)}>1-U_0-{\xi }_1^2{U}_1-{\xi }_2^2{U}_2-2{\xi }_1{U}_{01}-2{\xi }_2{U}_{02}-2{\xi }_1{\xi }_2{U}_{12}\Rightarrow$0.5537 > −1.6939
Condition 23	$\frac{B_2^2}{A_2}>1-U_0-{\xi }_1^2{U}_1-{\xi }_2^2{U}_2-2{\xi }_1{U}_{01}-2{\xi }_2{U}_{02}-2{\xi }_1{\xi }_2{U}_{12}\Rightarrow$0.5866 > −1.6939
Condition 23	$\frac{B_3^2}{A_3}>1-U_0-{\xi }_1^2{U}_1-{\xi }_2^2{U}_2-2{\xi }_1{U}_{01}-2{\xi }_2{U}_{02}-2{\xi }_1{\xi }_2{U}_{12}\Rightarrow$0.5632 > −1.6939
Condition 24	${\varphi }_{1\left(opt\right)}>1-\left[\begin{array}{c}{U}_0+\frac{1}{4}{(k_1+2{\eta }_1)}^2{U}_1+\frac{1}{4}{(k_2+2{\eta }_2)}^2{U}_2-(k_1+2{\eta }_1)U_{01}\hfill \\ -(k_2+2{\eta }_2)U_{02}+\frac{1}{2}(k_1+2{\eta }_1)(k_2+2{\eta }_2)U_{12}\hfill \end{array}\right]\Rightarrow$0.5537 > 0.0780
Condition 25	$\frac{B_2^2}{A_2}>1-\left[\begin{array}{c}{U}_0+\frac{1}{4}{(k_1+2{\eta }_1)}^2{U}_1+\frac{1}{4}{(k_2+2{\eta }_2)}^2{U}_2-(k_1+2{\eta }_1)U_{01}\hfill \\ -(k_2+2{\eta }_2)U_{02}+\frac{1}{2}(k_1+2{\eta }_1)(k_2+2{\eta }_2)U_{12}\hfill \end{array}\right]\Rightarrow$0.5866 > 0.0780
Condition 25	$\frac{B_3^2}{A_3}>1-\left[\begin{array}{c}{U}_0+\frac{1}{4}{(k_1+2{\eta }_1)}^2{U}_1+\frac{1}{4}{(k_2+2{\eta }_2)}^2{U}_2-(k_1+2{\eta }_1)U_{01}\hfill \\ -(k_2+2{\eta }_2)U_{02}+\frac{1}{2}(k_1+2{\eta }_1)(k_2+2{\eta }_2)U_{12}\hfill \end{array}\right]\Rightarrow$0.5632 > 0.0780
Condition 26	${\varphi }_{1\left(opt\right)}>\frac{1}{{\overline{Y}}^2}\left[\begin{array}{c}{\overline{Y}}^2-{\overline{Y}}^2{U}_0-\frac{1}{4}{(k_1\overline{Y}+2{\Phi }_1{\overline{W}}_1)}^2{U}_1-\frac{1}{4}{(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)}^2{U}_2\hfill \\ +\overline{Y}(\overline{Y}{k}_1+2{\Phi }_1{\overline{W}}_1)U_{01}+\overline{Y}(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{02}\hfill \\ -\frac{1}{2}(k_2\overline{Y}-2{\Phi }_1{\overline{W}}_1)(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{12}\hfill \end{array}\right]\Rightarrow$0.5537 > −0.0136
Condition 27	$\frac{B_2^2}{A_2}>\frac{1}{{\overline{Y}}^2}\left[\begin{array}{c}{\overline{Y}}^2-{\overline{Y}}^2{U}_0-\frac{1}{4}{(k_1\overline{Y}+2{\Phi }_1{\overline{W}}_1)}^2{U}_1-\frac{1}{4}{(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)}^2{U}_2\hfill \\ +\overline{Y}(\overline{Y}{k}_1+2{\Phi }_1{\overline{W}}_1)U_{01}+\overline{Y}(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{02}\hfill \\ -\frac{1}{2}(k_2\overline{Y}-2{\Phi }_1{\overline{W}}_1)(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{12}\hfill \end{array}\right]\Rightarrow$0.5866 > −0.0136
Condition 27	$\frac{B_3^2}{A_3}>\frac{1}{{\overline{Y}}^2}\left[\begin{array}{c}{\overline{Y}}^2-{\overline{Y}}^2{U}_0-\frac{1}{4}{(k_1\overline{Y}+2{\Phi }_1{\overline{W}}_1)}^2{U}_1-\frac{1}{4}{(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)}^2{U}_2\hfill \\ +\overline{Y}(\overline{Y}{k}_1+2{\Phi }_1{\overline{W}}_1)U_{01}+\overline{Y}(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{02}\hfill \\ -\frac{1}{2}(k_2\overline{Y}-2{\Phi }_1{\overline{W}}_1)(\overline{Y}{k}_2+2{\Phi }_2{\overline{W}}_2)U_{12}\hfill \end{array}\right]\Rightarrow$0.5632 > −0.0136

6.2. Simulation Study Utilizing Real Populations

To extrapolate the numerical results, we administer a simulation study by utilizing real populations. The simulation study is based on the following points.

(i).

Take the natural populations reported in Section 6.1.

(ii).

Select a ranked set sample with r = 4 and m = 3 so that size $n=rm=12$ units using RSS from every population.

(iii).

Obtain the necessary summary statistics.

(iv).

Repeat the aforementioned steps 15,000 times and tabulate the $MSE$ and PRE for each population.

The simulated PRE is tabulated as

$$\begin{array}{cc}\hfill PRE& =\frac{{\sum }_{i=1}^{\mathrm{15,000}}{({\overline{y}}_m-\overline{Y})}^2}{{\sum }_{i=1}^{\mathrm{15,000}}{(T-\overline{Y})}^2}\times 100\hfill \end{array}$$

(29)

Table 3 lists the results of the simulation study by $MSE$ and PRE for each real population.

Table 3. Results of simulation study for real populations.

Estimators	Population 1		Population 2		Population 3		Population 4
	MSE	PRE	MSE	PRE	MSE	PRE	MSE	PRE
${\overline{y}}_m$	1090.342	100.000	0.000492	100.000	2,860,741	100.000	17,71,020	100.000
${\overline{y}}_r$	2239.336	48.690	0.001346	36.544	8,330,842	34.339	4,055,247	43.672
${\overline{y}}_l$	891.551	122.297	0.000406	121.148	2,362,351	121.097	1,463,237	121.034
${\overline{y}}_a$	891.551	122.297	0.000406	121.148	2,362,351	121.097	1,463,237	121.034
${\overline{y}}_w$	907.034	120.209	0.000416	118.052	2,419,359	118.243	1,492,140	118.690
${\overline{y}}_{mm}$	1234.764	88.303	0.000640	76.830	3,718,263	76.937	1,959,909	90.362
${\overline{y}}_{m{m}_1}$	2238.959	48.698	0.000575	85.420	8,327,452	34.353	3,985,200	44.439
${\overline{y}}_{m{m}_2}$	2238.008	48.719	0.000496	99.112	8,316,689	34.397	3,783,187	46.812
${\overline{y}}_{m{m}_3}$	2238.632	48.705	0.000492	99.841	8,320,640	34.381	3,833,795	46.194
${\overline{y}}_{m{m}_4}$	2250.034	48.458	0.000492	99.825	8,222,207	34.792	3,822,069	46.336
${\overline{y}}_{k_1}$	5070.206	21.504	0.000495	99.243	4,947,819	57.818	4,080,352	43.403
${\overline{y}}_{k_2}$	891.551	122.297	0.000406	121.148	2,362,351	121.097	1,463,237	121.034
${\overline{y}}_{k_3}$	4344.361	25.097	0.000482	101.874	4,504,028	63.515	3,793,459	46.686
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{1}}}$	617.772	176.495	0.000401	122.552	2,103,387	136.006	1,181,170	149.937
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{2}}}$	652.059	167.215	0.000401	122.393	2,143,901	133.436	1,217,474	145.466
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{3}}}$	605.853	179.968	0.000401	122.580	2,095,924	136.490	1,169,544	151.428

The bold values are representing minimum $MSE$ and maximum PRE.

6.3. Simulation Study Using Artificially Drawn Populations

In the sequence of having better perception about the proffered estimators regarding the reviewed estimators, a simulation experiment has been executed utilizing artificially drawn populations which are discussed below.

Population 1: 

The trivariate population having N = 500 is generated from the multivariate normal distribution using R language with parameters ${\overline{W}}_1$ = 15, ${\overline{W}}_2$ = 20, $\overline{Y}=10$, ${\sigma }_{w_1}$ = 5, ${\sigma }_{w_2}$ = 6, ${\sigma }_y=4$, and varying amount of correlation coefficients ${\rho }_{w_{1}y}$, ${\rho }_{w_{2}y}$ and ${\rho }_{w_1{w}_2}$ in between their respective subscripts.

Population 2: 

The trivariate population of size N = 500 is generated using Weibull distribution such that $w_1\sim$ Weibull(2, 3), $e\sim$ N(0, 1), $w_2$ = 1.5$w_1^{0.5}+e$ and y = 1.2$w_1$ + 0.2$w_2$ + e where ${\rho }_{w_{1}y}>{\rho }_{w_{2}y}$.

Population 3: 

The trivariate population of size N = 500 is generated using gamma distribution such that $w_1\sim$ Gamma(2.5, 1), $e\sim$ N(0, 1), $w_2$ = 1.5$w_1^{0.5}+e$ and $y=1.2w_1+0.2w_2+e$ where ${\rho }_{w_{1}y}>{\rho }_{w_{2}y}$.

Population 4: 

The trivariate population of size N = 500 is generated utilizing an exponential distribution provided that $w_1\sim$ Exponential(1.2), $e\sim$ N(0, 1), $w_2$ = 1.5$w_1^{0.5}+e$ and $y=1.2w_1+0.2w_2+e$ where ${\rho }_{w_{1}y}>{\rho }_{w_{2}y}$.

Population 5: 

The trivariate population having N = 500 is generated employing ${\chi }^2$-distribution provided $w_1\sim$${\chi }^2\left(8\right)$, $e\sim$ N(0, 1), $w_2$ = 1.5$w_1^{0.5}+e$ and $y=1.2w_1+0.2w_2+e$ where ${\rho }_{w_{1}y}>{\rho }_{w_{2}y}$.

Taking RSS methodology into consideration, we select a ranked set sample of length n = 12 with r = 4 and m = 3 from each population. Using 15,000 repeated samples, the $MSE$ and PRE of the proffered estimators are calculated for each population and the outcomes are disclosed from Table 4 to Table 5. The simulation study is described in the points as:

Table 4. Results of simulation study for first artificially generated population.

${\mathit{\rho }}_{{\mathit{w}}_1\mathit{y}}$	0.5		0.7		0.9		0.5		0.7		0.9
${\mathit{\rho }}_{{\mathit{w}}_2\mathit{y}}$	0.3		0.5		0.7		0.5		0.7		0.9
${\mathit{\rho }}_{{\mathit{w}}_1{\mathit{w}}_2}$	0.1		0.3		0.5		0.5		0.7		0.9
Estimators	MSE	PRE	MSE	PRE	MSE	PRE	MSE	PRE	MSE	PRE	MSE	PRE
${\overline{y}}_m$	1.191	100.000	1.181	100.000	1.201	100.000	1.173	100.000	1.171	100.000	1.291	100.000
${\overline{y}}_r$	1.874	63.547	1.429	82.628	1.000	120.038	1.700	68.992	1.262	92.810	0.819	157.650
${\overline{y}}_l$	0.882	135.073	0.703	167.892	0.462	259.853	0.750	156.375	0.512	228.751	0.201	642.228
${\overline{y}}_a$	0.882	135.073	0.703	167.892	0.462	259.853	0.750	156.375	0.512	228.751	0.201	642.228
${\overline{y}}_w$	0.919	129.512	0.758	155.736	0.534	224.604	0.793	147.882	0.558	209.665	0.225	572.178
${\overline{y}}_{mm}$	1.983	60.069	2.506	47.129	3.026	39.685	2.536	46.265	3.006	38.973	3.642	35.447
${\overline{y}}_{m{m}_1}$	1.829	65.114	1.390	84.957	0.967	124.081	1.652	70.996	1.220	95.971	0.790	163.314
${\overline{y}}_{m{m}_2}$	1.621	73.465	1.214	97.245	0.827	145.212	1.432	81.915	1.034	113.321	0.666	193.752
${\overline{y}}_{m{m}_3}$	1.368	87.033	1.025	115.166	0.703	170.631	1.184	99.029	0.850	137.720	0.565	228.465
${\overline{y}}_{m{m}_4}$	2.491	47.815	2.896	40.780	3.333	36.030	2.823	41.563	3.224	36.339	3.827	33.737
${\overline{y}}_{k_1}$	1.027	115.934	0.874	135.082	0.698	171.973	0.913	128.480	0.696	168.154	0.430	299.966
${\overline{y}}_{k_2}$	0.882	135.073	0.703	167.892	0.462	259.853	0.750	156.375	0.512	228.751	0.201	642.228
${\overline{y}}_{k_3}$	1.036	114.920	0.885	133.353	0.745	161.043	0.925	126.775	0.740	158.320	0.717	179.937
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{1}}}$	0.871	136.753	0.696	169.588	0.459	261.612	0.742	157.996	0.508	230.384	0.200	643.787
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{2}}}$	0.870	136.881	0.695	169.820	0.458	261.778	0.742	158.128	0.508	230.440	0.200	643.923
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{3}}}$	0.870	136.787	0.696	169.591	0.459	261.521	0.742	158.020	0.508	230.380	0.200	643.849

The bold values are representing minimum $MSE$ and maximum PRE.

Table 5. Results of simulation study for artificially generated Populations 2–5.

Estimators	Population 2		Population 3		Population 4		Population 5
	MSE	PRE	MSE	PRE	MSE	PRE	MSE	PRE
${\overline{y}}_m$	0.151	100.000	0.164	100.000	0.050	100.000	1.154	100.000
${\overline{y}}_r$	0.292	51.603	0.315	52.239	0.473	10.694	1.252	92.140
${\overline{y}}_l$	0.085	176.481	0.079	206.521	0.026	189.187	0.452	255.040
${\overline{y}}_a$	0.085	176.481	0.079	206.521	0.026	189.187	0.452	255.040
${\overline{y}}_w$	0.091	164.875	0.086	189.816	0.028	175.540	0.510	226.182
${\overline{y}}_{mm}$	0.406	37.171	0.497	33.106	0.162	31.113	2.897	39.842
${\overline{y}}_{m{m}_1}$	0.212	71.074	0.213	77.121	0.045	110.216	1.137	101.466
${\overline{y}}_{m{m}_2}$	0.135	111.316	0.135	121.326	0.039	127.234	0.886	130.236
${\overline{y}}_{m{m}_3}$	0.123	122.502	0.126	130.135	0.076	66.501	0.827	139.559
${\overline{y}}_{m{m}_4}$	0.312	48.274	0.379	43.395	0.146	34.669	2.743	42.081
${\overline{y}}_{k_1}$	0.126	118.973	0.132	124.488	0.101	50.056	0.806	143.069
${\overline{y}}_{k_2}$	0.085	176.481	0.079	206.521	0.026	189.187	0.452	255.040
${\overline{y}}_{k_3}$	0.143	105.453	0.152	107.739	0.119	42.234	0.878	131.473
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{1}}}$	0.084	179.351	0.078	209.808	0.025	198.876	0.448	257.327
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{2}}}$	0.083	180.143	0.077	211.013	0.024	204.165	0.448	257.471
${\mathbf{T}}_{{\mathbf{bk}}_{\mathbf{3}}}$	0.084	179.430	0.078	209.883	0.025	199.719	0.448	257.197

The bold values are representing minimum $MSE$ and maximum PRE.

(i).

Quantify $m^2$ simple random samples from the parent population with replacement.

(ii).

Extract $n=mr$ ranked set sample by utilizing the RSS methodology.

(iii).

Calculate the required statistics.

(iv).

Calculate the $MSE$ and PRE of several estimators by repeating the prior points 15,000 times.

The simulated $MSE$ and PRE are calculated as

$$\begin{array}{cc}\hfill MSE\left(T\right)& =\frac{1}{\mathrm{15,000}}\sum _{i=1}^{\mathrm{15,000}}{(T-\overline{Y})}^2\hfill \\ \hfill PRE& =\frac{MSE\left({\overline{y}}_m\right)}{MSE\left(T\right)}\times 100\hfill \end{array}$$

(30)

6.4. Discussion of Computational Findings

After carefully observing the results of the computational study revealed from Table 1, Table 2, Table 3, Table 4 and Table 5, we draw the following discussion.

(i).

The numerical findings tabulated using real populations are displayed in Table 1 that show that the proffered estimators $T_{b{k}_i},i=1,2,3$ repress the existing estimators ${\overline{y}}_m$, ${\overline{y}}_r$, ${\overline{y}}_l$, ${\overline{y}}_a$, ${\overline{y}}_w$, ${\overline{y}}_{mm}$, ${\overline{y}}_{m{m}_i},i=1,2,3,4$ and ${\overline{y}}_{k_i},i=1,2,3$ by lowest $MSE$ and highest PRE.

(ii).

The simulation findings displayed in Table 3 for real populations show that the proffered estimators $T_{b{k}_i},i=1,2,3$ are found to be superior than the existing estimators.

(iii).

The simulation findings displayed in Table 4 for the artificially generated normal population exhibit that the proffered estimators $T_{b{k}_i},i=1,2,3$ attain the lowest $MSE$ and highest PRE regarding the existing estimators for various values of correlation coefficients. Moreover, it is also observed that the $MSE$ decreases as the correlation coefficient increases and vice versa in the sense of PRE.

(iv).

From Table 5 consisting of the findings of the simulation study for artificially generated asymmetric populations, the proffered estimators $T_{b{k}_i},i=1,2,3$ repress the conventional estimators with the lowest $MSE$ and highest PRE.

(v).

Moreover, from the findings of Table 1, Table 4 and Table 5 consisting of a numerical study using real populations and a simulation study using artificially generated populations, the proffered estimator $T_{b{k}_2}$ is established to be superior among the proffered classes of estimators whereas the proffered estimator $T_{b{k}_3}$ is found to be superior among the proffered classes of estimators from the results of Table 3 based on simulation study using real populations.

7. Conclusions

The present article has considered some optimal classes of estimators under RSS based on MAI with their properties. It is noteworthy that the conventional mean estimator, conventional regression and ratio estimators, and [35] estimators are found out to be the subclass of the proffered classes of estimators for properly selected values of the characterizing scalars as discussed in Section 4. The conditions of optimality have been determined under which the proffered estimators prevail on the conventional aspirants. From the results of the computational study, it is observed that the proffered classes of estimators $T_{b{k}_i},i=1,2,3$ exhibit their dominance by the lowest $MSE$ and highest PRE over the existing estimators, namely, usual mean estimator ${\overline{y}}_m$, conventional ratio estimator ${\overline{y}}_r$, conventional regression estimator ${\overline{y}}_l$, ref. [35] estimators ${\overline{y}}_a$, ${\overline{y}}_w$, ref. [36] estimator ${\overline{y}}_{mm}$, ref. [43] estimators ${\overline{y}}_{m{m}_i},i=1,2,3,4$, ref. [37] estimator ${\overline{y}}_{k_1}$, ref. [38] estimator ${\overline{y}}_{k_2}$, ref. [39] estimator ${\overline{y}}_{k_3}$ owing to the satisfaction of the optimality conditions derived in Section 5. Thus, the ensured deportment of the proffered classes of estimators will encourage the survey persons to consider the suggested classes of estimators for real life use, whenever MAI is available.

The proffered optimal classes of estimators can also be developed for the imputation of missing data under different sampling designs and it is the authors next supervision of this work.