Dynamics in an n-Species Lotka–Volterra Cooperative System with Delays

Abstract

We studied a class of generalized n-species non-autonomous cooperative Lotka–Volterra (L-V) systems with time delays. We obtained new criteria on the dynamic properties of the systems. First, we obtained the boundedness and permanence of the system using the inequality analysis technique and comparison method. Then, the existence of positive periodic solutions was investigated using the coincidence degree theory. The global attractivity of the system was obtained by constructing suitable Lyapunov functionals and utilizing Barbalat’s lemma. The existence and global attractivity of the periodic solutions were also obtained. Finally, we conducted two numerical simulations to validate the feasibility and practicability of our results.

1. Introduction

In recent decades, humans have caused the diversity of species on Earth to change at an unprecedented rate. Large-scale human disturbances endanger the survival and diversity of animal species. Predicting survival and diversity is one of the cutting-edge interdisciplinary research directions and hot issues in Earth science and ecology. Given the large timescales associated with population evolution and the inherent complexity of ecosystems, many important scientific questions such as these cannot be solved using traditional field observations and statistical analysis alone. The study and prediction of the dynamic behavior of relevant ecosystems are becoming increasingly popular [1].

A cooperative population system is an ecosystem formed by many individuals working together whose dynamic behavior is closely related to the cooperative relationship between the individuals. Cooperative populations can help us understand collaborative behavior in ecosystems. Cooperation is a common behavior in ecosystems; for example, bees gathering nectar together, or birds and fish migrating in large numbers [2].

Studying the dynamics of cooperative population systems can help us better understand these cooperative behaviors and how they function. Factors such as climate change and human activity can impact populations and collaborative behavior in ecosystems. It can also help us understand the effects of these changes on ecosystems and how to respond to the impacts of climate change. Understanding collaborative behavior in ecosystems can help us design more effective environmental management and conservation measures to protect the balance and stability of ecosystems and promote environmental management and protection [3]. The dynamic behavior of cooperative systems can provide a reference for the further research of new technologies, disease prevention, and regulation and control development trends of species [4,5,6].

The L-V system is a population dynamics model for representing the behavior of species in ecosystems. It is worth noting that understanding the survival of populations in biological systems is one of the most fundamental and important issues in biomathematics. Coexistence is a well-known way to achieve species survival. Many scholars have studied cooperative systems and obtained good results. For example, authors that considered the problem of determining the permanence or persistence of non-autonomous multi-species L-V systems with and without delays managed to obtain some criteria for the permanence or persistence of the systems they studied [7,8,9,10,11,12,13].

The problem of the uniform persistence (permanence) of autonomous and non-autonomous two-species L-V cooperative systems with or without delays has been studied, and the researchers derived some criteria for the uniform persistence of the systems [14,15,16,17,18,19,20].

In [7], the authors studied the following n-species cooperative system without delays and they obtained some criteria for the persistence of this system.

$$\frac{d{r}_j\left(\mu \right)}{d\mu }=r_j\left(\mu \right)[d_j\left(\mu \right)-c_{jj}{y}_j\left(\mu \right)+\sum _{i\ne j}^n{c}_{ji}{r}_i\left(\mu \right)],j=1,2,\dots ,n.$$

(1)

However, in the real world, a population’s environment often changes over time, leading to changes in population growth. Therefore, the impact of time delays on biological systems cannot be ignored.

Over the past few years, there have been many interesting results published on L-V cooperative systems with delays. For example, in [8], the authors discuss an autonomous two-species cooperative model with multiple discrete delays and they derived conditions for the permanence of system (2).

$$\begin{array}{cc}{\dot{r}}_1\left(\mu \right)=\hfill & {\displaystyle r_1\left(\mu \right)[b_1\left(\mu \right)-\sum _{l=1}^{l_{11}}{a}_{11l}\left(\mu \right)r_1(\mu -{\tau }_{11l})+\sum _{l=1}^{l_{12}}{a}_{12l}\left(t\right)r_2(\mu -{\tau }_{12l})],}\hfill \\ {\dot{r}}_2\left(\mu \right)=\hfill & {\displaystyle r_2\left(\mu \right)[b_2\left(\mu \right)+\sum _{l=1}^{l_{21}}{a}_{21l}\left(\mu \right)r_1(\mu -{\tau }_{21l})-\sum _{l=1}^{l_{22}}{a}_{22l}\left(\mu \right)r_2(\mu -{\tau }_{22l})].}\hfill \end{array}$$

(2)

The authors also considered an autonomous two-species L-V cooperative model, based on system (2), with several discrete delays and established a new sufficient condition for its permanence. Furthermore, the authors presented an open problem on a class of n-species L-V cooperative systems with delays.

In [9], the authors discussed a class of n-species L-V systems with time delays, and they established some criteria for the permanence of system.

$$\begin{array}{cc}{\dot{r}}_1\left(t\right)=\hfill & {\displaystyle r_1\left(\mu \right)[c_1\left(\mu \right)-\sum _{j=1,j\ne 2}^n\sum _{l=0}^m{a}_{1j}^l\left(\mu \right)r_j(\mu -l\tau )+a_{12}^1\left(\mu \right)r_2(\mu -\tau )],}\hfill \\ {\dot{r}}_i\left(\mu \right)=\hfill & {\displaystyle r_i\left(\mu \right)[c_i\left(\mu \right)-\sum _{j=1,j\ne i+1}^n\sum _{l=0}^m{a}_{ij}^l\left(\mu \right)r_j(\mu -l\tau )+\sum _{l=0}^m{a}_{ii+1}^l\left(\mu \right)r_{i+1}(\mu -l\tau )],}\hfill \\ {\dot{r}}_n\left(t\right)=\hfill & {\displaystyle r_n\left(\mu \right)[c_n\left(\mu \right)-\sum _{j=2}^n\sum _{l=0}^m{a}_{nj}^l\left(\mu \right)r_j(\mu -l\tau )+\sum _{l=0}^m{a}_{n1}^l\left(\mu \right)r_{i+1}(\mu -l\tau )],}\hfill \\ & i=2,\cdots ,n-1.\hfill \end{array}$$

(3)

The following general L-V cooperative system with both varying and distributed time delays was studied in [11]. They obtained sufficient conditions for the extinction and permanence of model (4).

$$\begin{array}{cc}\hfill \frac{d{r}_i\left(\mu \right)}{d\mu }=& r_i\left(\mu \right)[d_i\left(\mu \right)-e_{ii}\left(\mu \right)r_i\left(\mu \right)+\sum _{j\ne i}^n{e}_{ij}\left(\mu \right)r_j(\mu -{\tau }_{ij}\left(\mu \right))+\sum _{j\ne i}^n{\int }_{-{\sigma }_{ij}}^0{f}_{ij}(\mu ,s)r_j(\mu +s)ds],\hfill \\ & i=1,2,\dots ,n.\hfill \end{array}$$

(4)

As we all know, periodic phenomena are commonplace in nature. In an ecosystem, environmental factors such as the season, availability of food, and physiological characteristics always show periodic changes, which implies that these system parameters are periodic functions of time and that the population has multiple dynamic equilibrium states. Therefore, studying the periodic solutions and its stability in dynamic population systems has great practical significance. In [12], the author studied the following periodic cooperative systems (5) and derived several conditions of periodic solutions for them.

$$\begin{array}{cc}\hfill {\dot{r}}_i\left(\mu \right)=& r_i\left(t\right)[c_i\left(\mu \right)-p_{ii}\left(\mu \right)r_i\left(\mu \right)+\sum _{k\ne i}^n{p}_{ik}\left(\mu \right)r_k\left(\mu \right)-\sum _{j=1}^n{q}_{ij}\left(\mu \right)r_i\left(\mu -{\tau }_{ij}\left(\mu \right)\right)\hfill \\ & +\sum _{k\ne i}^n\sum _{j=1}^n{d}_{ikj}\left(\mu \right)r_k(\mu -{\gamma }_{ikj}\left(\mu \right))],(i=1,2,\dots ,n).\hfill \end{array}$$

(5)

In [8,9,10,11,13,15,16,17,18,19], the authors derived conditions for the persistence, permanence, and extinction of the considered systems. However, while studying the dynamics of those systems, they ignore the periodic solutions and the global attractivity of the cooperative models. Furthermore, there have been few relevant studies on the permanence, periodic solutions, and the global attractivity of multispecies cooperative systems with delays.

Considering these factors, and inspired by the studies cited above, we investigated the following delayed n-species L-V cooperative systems:

$$\begin{array}{cc}\hfill {\dot{z}}_i\left(t\right)& =z_i\left(t\right)\left[s_i\left(t\right)-b_{i0}\left(t\right)z_i\left(t\right)-\sum _{k=1}^m{b}_{ik}\left(t\right)z_i(t-kϵ)+\sum _{j=1,j\ne i}^n{c}_{ij}\left(t\right)z_j\left(t\right)\right],\hfill \\ & i=1,2,\dots ,n.\hfill \end{array}$$

(6)

where $z_i\left(t\right)$ corresponds to the density of n cooperative species, respectively; $c_{ij}\left(t\right)$ denotes the cooperative coefficients between n species, respectively; $b_{ij}\left(t\right)$ represents the intra-patch restriction density, respectively; $s_i\left(t\right)$ represents the intrinsic growth rate, respectively; and $ϵ$ is a time delay.

The purpose of this study is to obtain further conditions on global attractivity, permanence, and periodic solutions. We will achieve this by constructing appropriate Lyapunov functionals, using inequality techniques and a comparison method, coincidence degree theory, and knowledge of differential equations.

2. Preliminaries

In this paper, we always use $\mathcal{I}\triangleq \{1,2,\dots ,n\}$, and we define

$$\begin{array}{c}{\mathcal{A}}^l=\underset{s\in [0,+\infty )}{min}\mathcal{A}\left(s\right),{\mathcal{A}}^u=\underset{s\in [0,+\infty )}{max}\mathcal{A}\left(s\right),\overline{\mathcal{F}}=\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}\mathcal{F}\left(s\right)ds.\end{array}$$

where $\mathcal{A}\left(s\right)$ is any bounded continuous function defined on $[0,+\infty )$ and $\mathcal{F}\left(s\right)$ is any $\mathrm{\Omega }$-periodic continuous function on $[0,+\infty )$.

Now, we shall give some assumptions for convenience.

Hypothesis 1 (H1).

$ϵ>0,s_i\left(t\right)>0,b_{ij}\left(t\right)>0,c_{ij}\left(t\right)>0(i,j\in \mathcal{I})$ are all continuous bounded functions on $[0,+\infty )$.

Hypothesis 2 (H2).

$ϵ>0,s_i\left(t\right)>0,b_{ij}\left(t\right)>0,c_{ij}\left(t\right)>0(i,j\in \mathcal{I})$ are all continuous bounded and Ω-periodic functions on $[0,+\infty )$.

The initial conditions associated with system (6) are given by

$$z_i\left(t\right)={\mathrm{\Gamma }}_i\left(t\right),\forall t\in [-\sigma ,0],i\in \mathcal{I},$$

(7)

where ${\mathrm{\Gamma }}_i\left(t\right)$$(i\in \mathcal{I})$ are satisfying ${\mathrm{\Gamma }}_i\left(0\right)>0$ and continuous non-negative functions defined on $[-\sigma ,0]$.

For further study, we need the following lemmas in this paper.

Lemma 1

([21]). If $p>0,q>0$ and $\dot{s}\left(\mu \right)\le q-ps\left(\mu \right)$, we have

$$s\left(\mu \right)\le \frac{q}{p}[1+(\frac{ps(0)}{q}-1)e^{-p\mu })],$$

when $\mu \ge 0$ and $s\left(0\right)>0$.

Lemma 2

([22]). If $s\left(\mu \right)\ge 0$ and ${lim}_{\mu \to \infty }s\left(\mu \right)\le M_s$ such that

$$\dot{s}\left(\mu \right)\ge s\left(\mu \right)[\theta -\sum _{l=0}^m{\lambda }^{l}s(\mu -kϵ)],\lambda =\sum _{l=0}^m{\lambda }^l,$$

then there is a $0<m_s<\infty$, such that

$$\underset{\mu \to \infty }{lim}s\left(\mu \right)\ge m_s=\frac{\theta }{\lambda }{e}^{(\theta -\lambda M_s)m\tau }>0.$$

3. Main Results

Theorem 1.

If H1 holds and $A_i>0(i\in \mathcal{I})$, then system (6) is permanent. Where

$$A_i=\underset{t\in R}{min}\{b_{i0}\left(t\right)-\frac{1}{2}\sum _{j=1,j\ne i}^n(c_{ij}\left(t\right)+c_{ji}\left(t\right))\}.$$

Proof. 

Suppose that $(z_1\left(t\right),z_2\left(t\right),\cdots ,z_n\left(t\right))$ is a solution of system (6) with initial conditions (7). We firstly define that

$$W\left(t\right)=\sum _{i=1}^n{z}_i\left(t\right),s=\underset{i\in \mathcal{I}}{min}{s}_i\left(t\right),S=\underset{i\in \mathcal{I}}{max}{s}_i\left(t\right),t\in R.$$

Then, we have

$$\begin{array}{cc}\hfill \dot{W}\left(t\right)+sW\left(t\right)\le & 2\sum _{i=1}^{n}S{z}_i\left(t\right)-\sum _{i=1}^n{b}_{i0}\left(t\right)z_i^2\left(t\right)+z_i\left(t\right)\sum _{j=1,j\ne i}^n{c}_{ij}\left(t\right)z_j\left(t\right)\hfill \\ \hfill =& 2\sum _{i=1}^{n}S{z}_i\left(t\right)-\sum _{i=1}^n{b}_{i0}\left(t\right)z_i^2\left(t\right)+\frac{1}{2}\sum _{i=1}^n\sum _{j=1,j\ne i}^n(c_{ij}\left(t\right)+c_{ji}\left(t\right))z_i^2\left(t\right)\hfill \\ \hfill =& -\sum _{i=1}^n[(b_{i0}\left(t\right)-\frac{1}{2}\sum _{j=1,j\ne i}^n(c_{ij}\left(t\right)+c_{ji}\left(t\right)))z_i^2\left(t\right)-2S{z}_i(t)]\hfill \\ \hfill \le & -\sum _{i=1}^n\left[A_i{z}_i^2\left(t\right)-2S{z}_i\left(t\right)\right].\hfill \end{array}$$

(8)

Since $A_i>0$, then one can easily obtain

$$A_i{z}_i^2\left(t\right)-2S{z}_i\left(t\right)=A_i[z_i\left(t\right)-\frac{2S}{A_i}{z}_i\left(t\right)+{(\frac{S}{A_i})}^2-{(\frac{S}{A_i})}^2]=A_i{(z_i\left(t\right)-\frac{S}{A_i})}^2-\frac{S^2}{A_i}.$$

Hence, from (8), we derive that

$$\dot{W}\left(t\right)+sW\left(t\right)\le \sum _{i=1}^n\frac{S^2}{A_i}:=\theta .$$

Then, by using the Lemma 1, we can find that

$$W(t)\le \frac{\theta }{s}+(W(0)-\frac{\theta }{s})e^{-\theta t}.$$

(9)

It follows from (9) when $t\to \infty$,

$$\underset{t\to \infty }{lim}W(t)\le \underset{t\to \infty }{lim}(\frac{\theta }{s}+(W(0)-\frac{\theta }{s})e^{-\theta t})=\frac{\theta }{s}:=M.$$

(10)

Hence, there exists a $T_0>0$ such that $z_i(t)\le M(i\in \mathcal{I})$ for $t>T_0$.

Next, for each $z_i(t)$, we can find that

$${\dot{z}}_i(t)\ge z_i(t)[s_i^l-\sum _{k=0}^m{b}_{ik}^u{z}_i(t-kϵ)].$$

Let $B_i={\sum }_{k=0}^m{b}_{ik}^u$, then by Lemma 2, for $t>T_0$, we directly obtain

$$\underset{t\to \infty }{lim}{z}_i(t)\ge \frac{s_i^l}{B_i}{e}^{(s_i^l-B_{i}M)mϵ}:=m_i>0,i\in \mathcal{I}.$$

(11)

Then, there is a $T_1>T_0$ such that $z_i(t)\ge m_i$ for $t>T_1$. This implies that system (6) is permanent. □

Theorem 2.

If H2 holds and

$$\underset{t\in R}{min}\{b_{i0}(t)+\sum _{k=1}^m{b}_{ik}(t+kϵ)-\sum _{j=1,j\ne i}^n{c}_{ji}(t)\}:=D_i>0,i\in \mathcal{I},$$

and the system of algebraic equations

$${\overline{s}}_i-{\overline{b}}_{i0}{v}_i-\sum _{k=1}^m{\overline{b}}_{ik}{v}_i+\sum _{j\ne i}^n{\overline{c}}_{ij}{v}_j=0,i\in \mathcal{I},$$

has a unique positive solution, then system (6) has a positive Ω-periodic solution. Where $v_i>0$ is a constant.

Proof. 

Let

$$z_i(t)=e^{u_i(t)},i\in \mathcal{I}.$$

Then, we obtain

$${\dot{u}}_i(t)=s_i(t)-b_{i0}(t)e^{u_i(t)}-\sum _{k=1}^m{b}_{ik}(t)e^{u_i(t-kϵ)}+\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)}.$$

(12)

Let $\mathcal{Z}$ and $\mathcal{X}$ be the normed vector spaces, and $\mathcal{C}\left(\mathcal{R},{\mathcal{R}}^n\right)$ the space of all continuous functions $u(t)=$$\left(u_1(t),u_2(t),\dots ,u_n(t)\right):\mathcal{R}\to {\mathcal{R}}^n$. We take

$$\mathcal{X}=\mathcal{Z}=\left\{u(t)\in \mathcal{C}\left(\mathcal{R},{\mathcal{R}}^n\right):u(t)\mathrm{is}\mathrm{an}\mathrm{\Omega }-\mathrm{periodic}\mathrm{function}\right\},$$

with norm

$$\parallel u\parallel =\sum _{i=1}^n\underset{t\in [0,\mathrm{\Omega }]}{max}\left|u_i(t)\right|.$$

Then, $\mathcal{X}$ and $\mathcal{Z}$ are the Banach spaces. We let $\mathcal{L}:Dom\mathcal{L}\subset \mathcal{X}\to \mathcal{Z}$ be a linear operator and $\mathcal{N}:\mathcal{X}\to \mathcal{Z}$ be a continuous operator satisfying:

$$\begin{array}{c}\mathcal{L}u(t)=\dot{u}(t),\\ \mathcal{N}u(t)=(\mathcal{N}{u}_1(t),\mathcal{N}{u}_2(t),\dots ,\mathcal{N}{u}_n(t)),\end{array}$$

where

$$\mathcal{N}{u}_i(t)=s_i(t)-b_{i0}(t)e^{u_i(t)}-\sum _{k=1}^m{b}_{ik}(t)e^{u_i(t-kϵ)}+\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)}.$$

(13)

Next, we let $\mathcal{P}:\mathcal{X}\to \mathcal{X}$ and $\mathcal{Q}:\mathcal{Z}\to \mathcal{Z}$ are continuous projectors satisfying:

$$\mathcal{P}u(t)=\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}u(t)dt,\mathcal{Q}v(t)=\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}v(t)dt.$$

Then, $Im\mathcal{L}=\{v\in Z:{\int }_0^{\mathrm{\Omega }}v(t)dt=0\}$ and $Ker\mathcal{L}={\mathcal{R}}^n$. Further, $Im\mathcal{L}$ is closed in $\mathcal{Z}$ and $dimKer\mathcal{L}=n$. Since for any $v\in \mathcal{Z}$ there are unique $v_1\in R^n$ and $v_2\in Im\mathcal{L}$ with

$$v_1=\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}v(t)dt,v_2(t)=v(t)-v_1,$$

such that $v(t)=v_1+v_2(t)$, we obtain codimIm $\mathcal{L}=n$. Thus, $\mathcal{L}$ is a Fredholm mapping of index zero. Moreover, the following form is the generalized inverse (to $\mathcal{L}$ ) ${\mathcal{K}}_{\mathcal{P}}:Im\mathcal{L}\to Ker\mathcal{P}\cap Dom\mathcal{L}$:

$${\mathcal{K}}_{\mathcal{P}}v(t)={\int }_0^{t}v(s)ds-\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}{\int }_0^{t}v(s)dsdt.$$

Let $\mathcal{F}(t)=\left({\mathcal{F}}_1(t),{\mathcal{F}}_2(t),\dots ,{\mathcal{F}}_n(t)\right)$ as follows:

$${\mathcal{F}}_i(t)=s_i(t)-b_{i0}(t)e^{u_i(t)}-\sum _{k=1}^m{b}_{ik}(t)e^{u_i(t-kϵ)}+\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)}.$$

(14)

Thus, we have

$$\mathcal{Q}\mathcal{N}u(t)=\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}\mathcal{F}(t)dt,$$

(15)

and

$$\begin{array}{cc}\hfill {\mathcal{K}}_{\mathcal{P}}(I-\mathcal{Q})\mathcal{N}u(t)=& {\mathcal{K}}_{\mathcal{P}}I\mathcal{N}u(t)-{\mathcal{K}}_{\mathcal{P}}\mathcal{Q}\mathcal{N}u(t)\hfill \\ \hfill =& {\int }_0^t\mathcal{F}(s)ds-\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}{\int }_0^t\mathcal{F}(s)dsdt\hfill \\ & +\left(\frac{1}{2}-\frac{t}{\mathrm{\Omega }}\right){\int }_0^{\mathrm{\Omega }}\mathcal{F}(s)ds.\hfill \end{array}$$

(16)

So, one can see that $\mathcal{Q}\mathcal{N}$ and ${\mathcal{K}}_{\mathcal{P}}(I-\mathcal{Q})\mathcal{N}$ are continuous operators. Further, using the Arzela–Ascoli theorem, $\mathcal{Q}\mathcal{N}({\overline{\mathrm{\Omega }}}_0)$ is bounded and $\overline{{\mathcal{K}}_{\mathcal{P}}(I-\mathcal{Q})\mathcal{N}({\overline{\mathrm{\Omega }}}_0)}$ is compact for any open bounded set ${\mathrm{\Omega }}_0\subset \mathcal{X}$. Hence, $\mathcal{N}$ is $\mathcal{L}$-compact on ${\overline{\mathrm{\Omega }}}_0$ for any open bounded subset ${\mathrm{\Omega }}_0\subset \mathcal{X}$.

Corresponding to $\mathcal{L}u(t)=\lambda \mathcal{N}u(t)$ with $\lambda \in (0,1)$ and from (14), we obtain

$${\dot{u}}_i(t)=\lambda {\mathcal{F}}_i(t),i\in \mathcal{I}.$$

(17)

Suppose that $u(t)=\left(u_1(t),u_2(t),\dots ,u_n(t)\right)\in \mathcal{X}$ is a solution of system (7) for some parameter $\lambda \in (0,1)$. Then, integrating system (12) over the interval $[0,\mathrm{\Omega }]$, we have

$$\begin{array}{c}\hfill {\overline{s}}_i\mathrm{\Omega }-{\int }_0^{\mathrm{\Omega }}(b_{i0}(t)e^{u_i(t)}+\sum _{k=1}^m{b}_{ik}(t+kϵ)e^{u_i(t)}-\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)})dt=0,i\in \mathcal{I}.\end{array}$$

consequently, we have

$${\int }_0^{\mathrm{\Omega }}(b_{i0}(t)e^{u_i(t)}+\sum _{k=1}^m{b}_{ik}(t+kϵ)e^{u_i(t)}-\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)})dt={\overline{s}}_i\mathrm{\Omega },i\in \mathcal{I}.$$

(18)

For each $b_{ik}(t)$, we have

$$\begin{array}{cc}\hfill {\int }_0^{\mathrm{\Omega }}\sum _{i=1}^m{b}_{ik}(t)e^{u_i(t-k\epsilon )}dt& ={\int }_{k\epsilon }^{\mathrm{\Omega }+\epsilon }\sum _{i=1}^m{b}_{ik}(s+k\epsilon )e^{u_i(s)}ds\hfill \\ & ={\int }_0^{\mathrm{\Omega }}\sum _{i=1}^m{b}_{ik}(s+k\epsilon )e^{u_i(s)}ds\hfill \\ & ={\int }_0^{\mathrm{\Omega }}\sum _{i=1}^m{b}_{ik}(t+k\epsilon )e^{u_i(t)}dt.\hfill \end{array}$$

(19)

From (17) and (18), one can easily obtain

$$\begin{array}{cc}\hfill {\int }_0^{\mathrm{\Omega }}|{\dot{u}}_i(t)|dt& ={\int }_0^{\mathrm{\Omega }}|s_i(t)-b_{i0}(t)e^{u_i(t)}-\sum _{k=1}^m{b}_{ik}(t+kϵ)e^{u_i(t)}\hfill \\ & +\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)}|dt\hfill \\ & \le {\int }_0^{\mathrm{\Omega }}|s_i(t)|dt+{\int }_0^{\mathrm{\Omega }}[b_{i0}(t)e^{u_i(t)}+\sum _{k=1}^m{b}_{ik}(t+kϵ)e^{u_i(t)}\hfill \\ & +\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)}]dt\hfill \\ & \le ({\overline{s}}_i+{\overline{S}}_i)w:=C_i,i\in \mathcal{I},\hfill \end{array}$$

(20)

where ${\overline{S}}_i=\frac{1}{\mathrm{\Omega }}{\int }_0^{\mathrm{\Omega }}|s_i|dt.$

From the properties of solutions $u(t)=(u_1(t),u_2(t),\dots ,u_n(t))$, we have some constants ${\xi }_i,{\eta }_i\in [0,\mathrm{\Omega }](i\in \mathcal{I})$ and satisfying

$$\begin{array}{cc}\hfill u_i({\xi }_i)& =\underset{t\in [0,\mathrm{\Omega }]}{max}{u}_i(t),u_i({\eta }_i)=\underset{t\in [0,\mathrm{\Omega }]}{min}{u}_i(t),i\in \mathcal{I}.\hfill \end{array}$$

(21)

Considering the integration of periodic functions, we have

$${\int }_0^{\mathrm{\Omega }}{b}_{ik}(t+k\epsilon )dt={\int }_{k\epsilon }^{\mathrm{\Omega }+k\epsilon }{b}_{ik}(s)ds={\int }_0^{\mathrm{\Omega }}{b}_{ik}(t)dt,i\in \mathcal{I}.$$

(22)

Then from (18) and (22), we have

$$\begin{array}{cc}\hfill {\overline{s}}_i\mathrm{\Omega }& \le {\int }_0^{\mathrm{\Omega }}{b}_{i0}(t)e^{u_i({\xi }_i)}dt+\sum _{k=1}^m{\int }_0^{\mathrm{\Omega }}{b}_{ik}(t+kϵ)e^{u_i({\xi }_i)}dt\hfill \\ & ={\int }_0^{\mathrm{\Omega }}{b}_{i0}(t)e^{u_i({\xi }_i)}dt+\sum _{k=1}^m{\int }_0^{\mathrm{\Omega }}{b}_{ik}(t)e^{u_i({\xi }_i)}dt\hfill \\ & =e^{u_i({\xi }_i)}{\int }_0^{\mathrm{\Omega }}[b_{i0}(t)+\sum _{k=1}^m{b}_{ik}(t)]dt,i\in \mathcal{I}.\hfill \end{array}$$

(23)

Therefore, we find that

$$u_i({\xi }_i)\ge ln(\frac{{\overline{s}}_i}{{\overline{b}}_{i0}+{\sum }_{k=1}^m{\overline{b}}_{ik}}),i\in \mathcal{I}.$$

(24)

On the other hand from (18) and (19), we have

$${\int }_0^{\mathrm{\Omega }}[b_{i0}(t)e^{u_i(t)}+\sum _{k=1}^m{b}_{ik}(t+kϵ)e^{u_i(t)}-\sum _{j=1,j\ne i}^n{c}_{ij}(t)e^{u_j(t)}]dt={\overline{s}}_i\mathrm{\Omega },i\in \mathcal{I}.$$

(25)

From (25), we obtain

$$\begin{array}{cc}& {\int }_0^{\mathrm{\Omega }}[b_{10}(t)e^{u_1(t)}+\sum _{k=1}^m{b}_{1k}(t+kϵ)e^{u_1(t)}-\sum _{j=1,j\ne i}^n{c}_{1j}(t)e^{u_j(t)}]dt\hfill \\ & +{\int }_0^{\mathrm{\Omega }}[b_{20}(t)e^{u_2(t)}+\sum _{k=1}^m{b}_{2k}(t+kϵ)e^{u_2(t)}-\sum _{j=1,j\ne i}^n{c}_{2j}(t)e^{u_j(t)}]dt\hfill \\ & +\cdots +{\int }_0^{\mathrm{\Omega }}[b_{n0}(t)e^{u_2(t)}+\sum _{k=1}^m{b}_{nk}(t+kϵ)e^{u_n(t)}-\sum _{j=1,j\ne i}^n{c}_{nj}(t)e^{u_j(t)}]dt\hfill \\ \hfill =& {\int }_0^{\mathrm{\Omega }}[b_{10}(t)+\sum _{k=1}^m{b}_{1k}(t+kϵ)-\sum _{j=1,j\ne i}^n{c}_{j1}(t)]e^{u_1(t)}dt\hfill \\ & +{\int }_0^{\mathrm{\Omega }}[b_{20}(t)+\sum _{k=1}^m{b}_{2k}(t+kϵ)-\sum _{j=1,j\ne i}^n{c}_{j2}(t)]e^{u_2(t)}dt\hfill \\ & +\cdots +{\int }_0^{\mathrm{\Omega }}[b_{n0}(t)+\sum _{k=1}^m{b}_{nk}(t+kϵ)-\sum _{j=1,j\ne i}^n{c}_{jn}(t)]e^{u_n(t)}dt\hfill \\ \hfill =& \sum _{i=1}^n{\overline{s}}_i\mathrm{\Omega }.\hfill \end{array}$$

(26)

Thus, we have

$${\int }_0^{\mathrm{\Omega }}[b_{i0}(t)+\sum _{k=1}^m{b}_{ik}(t+kϵ)-\sum _{j=1,j\ne i}^n{c}_{ji}(t)]e^{u_i(t)}dt\le \sum _{i=1}^n{\overline{s}}_i\mathrm{\Omega },i\in \mathcal{I},$$

and

$${\int }_0^{\mathrm{\Omega }}{e}^{u_i(t)}dt\le \frac{{\sum }_{i=1}^n{\overline{s}}_i\mathrm{\Omega }}{D_i},i\in \mathcal{I}.$$

(27)

From (21) and (27), we further obtain

$$u({\eta }_i)\le ln\frac{{\sum }_{i=1}^n{\overline{s}}_i}{D_i}:=B_i,i\in \mathcal{I}.$$

(28)

From (20) and (28), we have

$$\begin{array}{cc}& u_i(t)\le u_i({\eta }_i)+{\int }_0^{\mathrm{\Omega }}|{\dot{u}}_i(t)|dt\le B_i+C_i:=M_i,\hfill \\ & u_i(t)\ge u_i({\epsilon }_i)-{\int }_0^{\mathrm{\Omega }}|{\dot{u}}_i(t)|dt:=N_i,\hfill \end{array}$$

(29)

and

$$max|u_i(t)|\le max(M_i,N_i):=H_i.$$

(30)

It is obvious that the constants $H_i$ are independent of parameter $\lambda \in (0,1)$. For any $u=$$\left(u_1,u_2,\dots ,u_n\right)\in {\mathcal{R}}^n$, from (13) we obtain

$$\begin{array}{c}\mathcal{Q}\mathcal{N}u=(\mathcal{Q}\mathcal{N}{u}_1,\mathcal{Q}\mathcal{N}{u}_2,\dots ,\mathcal{Q}\mathcal{N}{u}_n),\\ \mathcal{Q}\mathcal{N}{u}_i={\overline{s}}_i-{\overline{b}}_{i0}{e}^{u_i}-{\displaystyle \sum _{k=1}^m}{\overline{b}}_{ik}{e}^{u_i}+{\displaystyle \sum _{j\ne i}^n}{\overline{c}}_{ij}{e}^{u_j},i\in \mathcal{I}.\end{array}$$

Let $0<\mathcal{B}<+\infty$ be big enough, satisfying $\left|u_1^{*}\right|+$ $\left|u_2^{*}\right|+\cdots +\left|u_n^{*}\right|<\mathcal{B}$ and $\mathcal{B}>B_1+B_2+\cdots +B_n$. Let ${\mathrm{\Omega }}_0\subset \mathcal{X}$ be a bounded open set, satisfying

$${\mathrm{\Omega }}_0=\{u\in X:\parallel u\parallel <\mathcal{B}\}.$$

One can see that ${\mathrm{\Omega }}_0$ fulfills the first two conditions of coincidence degree theory [23]. Moreover, we can obtain

$$\begin{array}{c}deg\{\mathcal{J}\mathcal{Q}\mathcal{N},{\mathrm{\Omega }}_0\cap Ker\mathcal{L},(0,0,\dots ,0)\}=sgn\left|\begin{array}{cccc}{f}_{u_1}^1& f_{u_2}^1& \cdots & f_{u_n}^1\\ f_{u_1}^2& f_{u_2}^2& \cdots & f_{u_n}^2\\ \cdots & \cdots & \cdots & \cdots \\ f_{u_1}^n& f_{u_2}^n& \cdots & f_{u_n}^n\end{array}\right|\ne 0.\end{array}$$

It can be seen that the ${\mathrm{\Omega }}_0$ satisfies the last condition of coincidence degree theory [23]. Therefore, system (12) has an $\mathrm{\Omega }$-periodic solution $u^{*}(t)=$$\left(u_1^{*}(t),u_2^{*}(t),\dots ,u_n^{*}(t)\right)\in {\overline{\mathrm{\Omega }}}_0$. Finally, we find that system (6) has a positive $\mathrm{\Omega }$-periodic solution. □

Theorem 3.

If H1 and $\mathrm{\Theta }>0$ hold, the system (6) is globally attractive. Where

$$\mathrm{\Theta }=min\{{\mathrm{\Theta }}_1,{\mathrm{\Theta }}_2,\cdots ,{\mathrm{\Theta }}_n\},$$

and

$${\mathrm{\Theta }}_i=\underset{t\in R}{min}\left\{b_{i0}(t)-\sum _{k=1}^m{b}_{ik}(t+k\epsilon )-\sum _{j=1,j\ne i}^n{c}_{ji}(t)\right\},i\in \mathcal{I}.$$

Proof. 

Suppose that $(x_1(t),x_2(t),\dots ,x_n(t))$ and $(z_1(t),z_2(t),\dots ,z_n(t))$ are any two positive solutions of system (6), then from the conditions of Theorem 3, there exist real numbers $T^{*}$ and $M>m_0>0$ such that

$$m_0\le x_i(t),z_i(t)\le M,$$

(31)

as $t\ge T^{*}$. Construct the following Lyapunov functional:

$$\mathcal{V}(t)=\sum _{i=1}^n\left[|ln{x}_i(t)-ln{z}_i(t)|+\sum _{k=1}^m{\int }_{t-k\epsilon }^t{b}_{ik}(s+k\epsilon )|x_i(s)-z_i(s)|ds\right],$$

then we obtain

$$\begin{array}{cc}\hfill D^{+}\mathcal{V}(t)=& \sum _{i=1}^{n}sign(x_i(t)-z_i(t))[-b_{i0}(t)(x_i(t)-z_i(t))+\sum _{j=1,j\ne i}^n{c}_{ij}(t)(x_j(t)-z_j(t))\hfill \\ & -\sum _{k=1}^m{b}_{ik}(t)(x_i(t-k\epsilon )-z_i(t-k\epsilon ))]+\sum _{i=1}^n\sum _{k=1}^m[b_{ik}(t+k\epsilon )|x_i(t)-z_i(t)|\hfill \\ & -b_{ik}(t)|x_i(t-k\epsilon )-z_i(t-k\epsilon )|]\hfill \\ \hfill \le & \sum _{i=1}^n[-b_{i0}(t)|x_i(t)-z_i(t)|+\sum _{k=1}^m{b}_{ik}(t)|x_i(t-k\epsilon )-z_i(t-k\epsilon )|\hfill \\ & +\sum _{j=1,j\ne i}^n{c}_{ij}(t)|x_j(t)-z_j(t)|]-\sum _{i=1}^n\sum _{k=1}^m{b}_{ik}(t)|x_i(t-k\epsilon )-z_i(t-k\epsilon )|\hfill \\ & +\sum _{i=1}^n\sum _{k=1}^m{b}_{ik}(t+k\epsilon )|x_i(t)-z_i(t)|\hfill \\ \hfill \le & \sum _{i=1}^n[-b_{i0}(t)|x_i(t)-z_i(t)|+\sum _{k=1}^m{b}_{ik}(t+k\epsilon )|x_i(t)-z_i(t)|\hfill \\ & +\sum _{j=1,j\ne i}^n{c}_{ij}(t)|x_j(t)-z_j(t)|]\hfill \\ \hfill \le & -\sum _{i=1}^n\left[b_{i0}(t)-\sum _{k=1}^m{b}_{ik}(t+k\epsilon )-\sum _{j=1,j\ne i}^n{c}_{ji}(t)\right]|x_i(t)-z_i(t)|\hfill \\ \hfill \le & -\mathrm{\Theta }|x_i(t)-z_i(t)|.\hfill \end{array}$$

(32)

Integrating from $T_{*}$ to t on both sides of (32), we obtain

$$\mathcal{V}(t)+{\int }_{T^{*}}^t\mathrm{\Theta }|x_i(t)-z_i(t)|\le \mathcal{V}(T^{*}).$$

(33)

Then, from (31) and the similar method in [22], we can find that $(x_i(t)-z_i(t))$ and $({\dot{x}}_i(t)-{\dot{z}}_i(t))$ are bounded on $[T_{*},\infty )$ and $|x_i(t)-z_i(t)|\in L^1[T^{*},+\infty )$. Then, by Barbalat’s lemma, we find that for $i\in \mathcal{I}$,

$$\underset{t\to +\infty }{lim}\left|x_i(t)-z_i(t)\right|=0.$$

From the conditions and proofs of the above theorems, we can derive the following result for system (6). □

Corollary 1.

If H2 holds and

$$\underset{t\in R}{min}\{b_{i0}(t)-\sum _{k=1}^m{b}_{ik}(t+kϵ)-\sum _{j=1,j\ne i}^n{c}_{ji}(t)\}:={\Pi }_i>0,i\in \mathcal{I},$$

and the system of algebraic equations

$${\overline{s}}_i-{\overline{b}}_{i0}{v}_i-\sum _{k=1}^m{\overline{b}}_{ik}{v}_i+\sum _{j\ne i}^n{\overline{c}}_{ij}{v}_j=0,i\in \mathcal{I},$$

a unique positive solution, then system (6) is permanent and has a global attractive positive ω-periodic solution.

Remark 1.

Because model (6) can be specialized as systems in [7,8,9,11,14,15,16,17,18], and compared with the results in [7,8,9,11,14,15,16,17,18], in the present paper we derived the aforementioned results. Therefore, system (6) and the results in this paper can be seen as the supplements and extensions of the previously known results and models in [7,8,9,11,14,15,16,17,18].

4. Examples

In this section, we provide two examples to validate the practicability and feasibility of our results.

Example 1.

$$\begin{array}{cc}\hfill {\dot{z}}_1(t)=z_1(t)[& 3+sin(t)-(4+0.5sin(t))z_1(t)-(0.2+0.1sin(t))z_1(t-0.4)\hfill \\ & -(0.2+0.1cos(t))z_1(t-0.8)+(0.4+0.2sin(t))z_2(t)\hfill \\ & +(0.4+0.2cos(t))z_3(t)],\hfill \\ \hfill {\dot{z}}_2(t)=z_2(t)[& 2+sin(t)-(5+1.5sin(t))z_2(t)-(0.3+0.1sin(t))z_2(t-0.4)\hfill \\ & -(0.3+0.1cos(t))z_2(t-0.8)+(0.5+0.2sin(t))z_1(t)\hfill \\ & +(0.5+0.2cos(t))z_3(t)],\hfill \\ \hfill {\dot{z}}_3(t)=z_3(t)[& 2+sin(t)-(6+2sin(t))z_3(t)-(0.2+0.1cos(t))z_3(t-0.4)\hfill \\ & -(0.3+0.1sin(t))z_3(t-0.8)+(0.3+0.1sin(t))z_1(t)\hfill \\ & +(0.3+0.1cos(t))z_2(t)].\hfill \end{array}$$

(34)

From direct calculation, we obtain

$$\begin{array}{c}\hfill \underset{t\in R}{min}\{b_{10}(t)-\sum _{k=1}^2{b}_{1k}(t+kϵ)-\sum _{j=2,j\ne 1}^3{c}_{j1}(t)\}\approx 1.7>0,\\ \hfill \underset{t\in R}{min}\{b_{20}(t)-\sum _{k=1}^2{b}_{2k}(t+kϵ)-\sum _{j=1,j\ne 2}^3{c}_{j2}(t)\}\approx 1.3>0,\\ \hfill \underset{t\in R}{min}\{b_{30}(t)-\sum _{k=1}^2{b}_{3k}(t+kϵ)-\sum _{j=1,j\ne 3}^3{c}_{j3}(t)\}\approx 2.5>0,\end{array}$$

and

$$\begin{array}{c}\hfill 4.4v_1-0.4v_2-0.4v_3=3,\\ \hfill 5.6v_2-0.5v_1-0.5v_3=2,\\ \hfill 6.5v_3-0.3v_1-0.3v_2=2,\end{array}$$

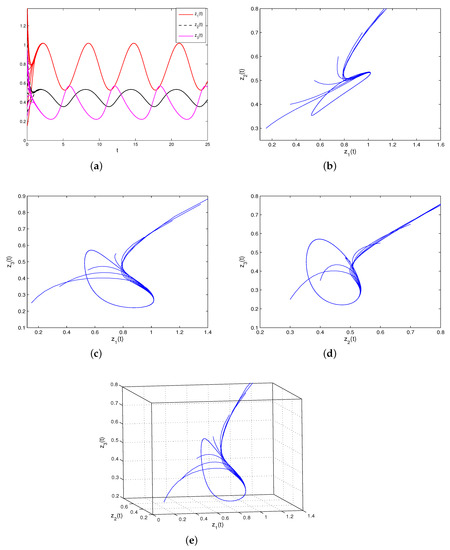
has a unique positive solution $v_1=0.7564,v_2=0.4572,v_3=0.3537$. Obviously, the assumptions of Corollary 1 are all satisfied. Therefore, system (34) is permanent and has a globally attractive $2\pi$-periodic solution. The corresponding simulations demonstrated in Figure 1.

As shown in Figure 1, numerical simulations suggest that system (34) is permanent and has a global attractive $2\pi$-periodic solution.

Example 2.

$$\begin{array}{cc}\hfill {\dot{z}}_1(t)=z_1(t)[& 3.5+0.5cos(t)-(3+0.5cos(t))z_1(t)-(5.2+0.1cos(t))z_1(t-0.65)\hfill \\ & -(5.3+0.1cos(t))z_1(t-1.3)+(0.89+0.02cos(t))z_2(t)\hfill \\ & +(0.85+0.02cos(t))z_3(t)],\hfill \\ \hfill {\dot{z}}_2(t)=z_2(t)[& 4+0.45cos(t)-(3+0.55cos(t))z_2(t)-(5.8+0.1cos(t))z_2(t-0.4)\hfill \\ & -(5.7+0.1cos(t))z_2(t-0.8)+(0.9+0.02cos(t))z_1(t)\hfill \\ & +(0.88+0.02cos(t))z_3(t)],\hfill \\ \hfill {\dot{z}}_3(t)=z_3(t)[& 5+0.55cos(t)-(3+0.45cos(t))z_3(t)-(5.5+0.1cos(t))z_3(t-0.4)\hfill \\ & -(5.6+0.1cos(t))z_3(t-0.8)+(0.93+0.01cos(t))z_1(t)\hfill \\ & +(0.91+0.01cos(t))z_2(t)].\hfill \end{array}$$

(35)

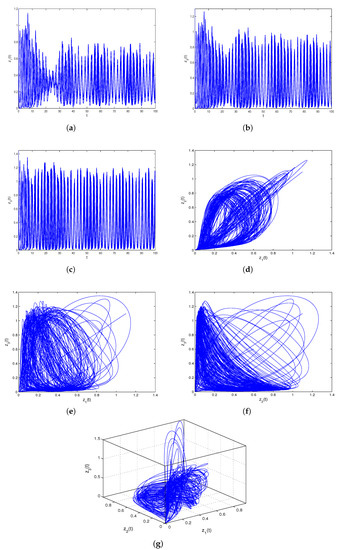
From direct calculation, we obtain

$$\begin{array}{cc}\hfill \underset{t\in R}{min}\{b_{10}(t)-\frac{1}{2}\sum _{j=2,j\ne 1}^3(c_{1j}(t)+c_{j1}(t))\}& \approx 0.68>0,\hfill \\ \hfill \underset{t\in R}{min}\{b_{20}(t)-\frac{1}{2}\sum _{j=1,j\ne 2}^3(c_{2j}(t)+c_{j2}(t))\}& \approx 0.645>0,\hfill \\ \hfill \underset{t\in R}{min}\{b_{30}(t)-\frac{1}{2}\sum _{j=1,j\ne 3}^3(c_{3j}(t)+c_{j3}(t))\}& \approx 0.735>0,\hfill \end{array}$$

$$\begin{array}{c}\hfill \underset{t\in R}{min}\{b_{10}(t)+\sum _{k=1}^2{b}_{1k}(t+kϵ)-\sum _{j=2,j\ne 1}^3{c}_{j1}(t)\}\approx 10.94>0,\\ \hfill \underset{t\in R}{min}\{b_{20}(t)+\sum _{k=1}^2{b}_{2k}(t+kϵ)-\sum _{j=1,j\ne 2}^3{c}_{j2}(t)\}\approx 11.92>0,\\ \hfill \underset{t\in R}{min}\{b_{30}(t)+\sum _{k=1}^2{b}_{3k}(t+kϵ)-\sum _{j=1,j\ne 3}^3{c}_{j3}(t)\}\approx 11.68>0,\end{array}$$

and

$$\begin{array}{cc}\hfill 13.5v_1-0.89v_2-0.87v_3& =3.5,\hfill \\ \hfill 14.5v_2-0.9v_1-0.88v_3& =4,\hfill \\ \hfill 14.1v_3-0.93v_1-0.91v_2& =5,\hfill \end{array}$$

has a unique positive solution $v_1=0.3058,v_2=0.3188,v_3=0.3954$.

However, we find that

$$\begin{array}{cc}\hfill \underset{t\in R}{min}\{b_{10}(t)-\sum _{k=1}^2{b}_{1k}(t+kϵ)-\sum _{j=2,j\ne 1}^3{c}_{j1}(t)\}& \approx -10.06<0,\hfill \\ \hfill \underset{t\in R}{min}\{b_{20}(t)-\sum _{k=1}^2{b}_{2k}(t+kϵ)-\sum _{j=1,j\ne 2}^3{c}_{j2}(t)\}& \approx -11.08<0,\hfill \\ \hfill \underset{t\in R}{min}\{b_{30}(t)-\sum _{k=1}^2{b}_{3k}(t+kϵ)-\sum _{j=1,j\ne 3}^3{c}_{j3}(t)\}& \approx -10.52<0.\hfill \end{array}$$

Obviously, the assumptions of Theorems 1 and 2 are all satisfied. However, the assumptions of Theorem 3 do not hold. The corresponding simulation is demonstrated in Figure 2.

As shown in Figure 2, numerical simulations suggest that system (35) is permanent, but has no globally attractive positive periodic solution.

5. Conclusions

By considering the non-negligible nature of time delay and cooperative relationships between populations, and by extending and generalizing previous works, in this paper, we established and investigated an n-species Lotka–Volterra cooperative system with time delays (6). First, we obtained new conditions for the boundedness, permanence, and periodic solution by using inequality techniques, the comparison principle, and the coincidence degree theory. Second, by means of the Lyapunov method, we obtained conditions for the global attractiveness of the system. Moreover, we derived the conditions for the existence and global attractivity of the periodic solution. Finally, numerical simulations were employed to illustrate the effectiveness and feasibility of our results. Recently, the dynamic properties of fractional-order delay differential equations have been extensively investigated both in theory and applications [24,25]. Therefore, we have interesting future work such as the dynamical behavior on the fractional-order n-species Lotka–Volterra cooperative population systems with delays.