Quaternionic Shape Operator and Rotation Matrix on Ruled Surfaces

Abstract

In this article, we examine the relationship between Darboux frames along parameter curves and the Darboux frame of the base curve of the ruled surface. We derive the equations of the quaternionic shape operators, which can rotate tangent vectors around the normal vector, and find the corresponding rotation matrices. Using these operators, we examine the Gauss curvature and mean curvature of the ruled surface. We explore how these properties are found by the use of Frenet vectors instead of generator vectors. We provide illustrative examples to better demonstrate the concepts and results discussed.

1. Introduction

The universal cover of the special orthogonal group in three dimensions SO(3) is a Lie group known as Spin(3). The group Spin(3) is isomorphic to the special unitary group SU(2). Additionally, Spin(3) is diffeomorphic to the three-dimensional unit sphere $S^3$, and it can be understood as the group of versors, which are quaternions with an absolute value of 1. In computer graphics, the connection between quaternions and rotations is commonly used. This connection is explained in detail on the topic of quaternions and spatial rotations. The map from $S^3$ onto SO(3) identifies antipodal points of $S^3$, and it is a surjective homomorphism of Lie groups. Topologically, this map is a two-to-one covering map. The group SU(2) is isomorphic to the quaternions of unit norm via a map determined by

$$q=a1+bi+cj+dk=\alpha +\beta j⟷\left[\begin{array}{cc}\alpha & -\overline{\beta }\\ \beta & \overline{\alpha }\end{array}\right]=\mathbf{U}$$

restricted to $a^2+b^2+c^2+d^2=\mid \alpha {\mid }^2+\mid \beta {\mid }^2=1$ where $a,b,c,d\in \mathbb{R},$ $\mathbf{U}\in$ SU(2), and $\alpha =a+bi,\beta =c+di\in \mathbb{C},$ where $\mathbb{R}$ denote the set of real numbers. The Pauli matrices ${\sigma }_1=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],{\sigma }_2=\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right],{\sigma }_3=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ are three $2\times 2$ complex matrices that satisfy three important properties: Hermiticity, involution, and unitarity. These matrices produce an algebra that is isomorphic to the Clifford algebra [1]. In the field of transformations, certain equations relying on the use of Pauli matrices have been discovered. The application of Pauli matrices has been explored in various studies across different fields of research, including condensed matter physics, quantum computing, and soliton surfaces. The authors introduce and analyze a specific class of exact solutions to the equations related to the localized-induction approximation. These solutions are characterized by three parameters and are considered one-soliton excitations, also known as Bäcklund transforms, of circular vortex motion [2]. The formulation of the Darboux–Bäcklund transformation is achieved using Clifford numbers, resulting in a simpler process for constructing explicit solutions. This transformation is particularly useful in the field of differential equations and provides a way to transform a known solution into a new one [3]. Sym develops the concept of a soliton surface, which provides a geometric interpretation of the equivalence relation [4]. Schief show that the natural geodesic coordinate systems on Razzaboni surfaces and their mates are related by a reciprocal transformation. The geodesic coordinate system on the Razzaboni transform generated by a Bäcklund transformation is given explicitly in terms of Razzaboni’s pseudopotential obeying a compatible Frobenius system [5].

The (unital associative) algebra generated by $i{\sigma }_1,i{\sigma }_2,i{\sigma }_3$ is effectively isomorphic to that of quaternions. The study conducted by Rogers et al. focuses on the Bäcklund and Darboux transformations, their geometry, and modern applications in soliton theory [6]. Quaternions represent three-dimensional rotations about an arbitrary axis and offer a solution to employ quaternion algebra in kinematics equations. As a result, several new application areas emerged such as programming, robotics, animation and navigation systems. To describe the rotations of objects, a four-coordinate system called quaternions is commonly used. The most appropriate quaternions for animation are those located on the unit sphere. However, little attention has been given to the problem of constructing curves on spheres. Shoemake proposes a solution by introducing a novel type of spline curve designed to be created on a sphere, and capable of smoothly interpolating arbitrary sequences of rotations [7]. Xu et al. propose the quaternion calibration algorithm to calibrate large misalignment angles between Strapdown Inertial Navigation System (SINS) and Doppler Velocity Log (DVL) in SINS/DVL integrated navigation system [8]. In addition to these areas, quaternions are also important for the theory of surfaces. Bobenko utilizes analytic methods to construct and study surfaces. To facilitate this, the author finds it more convenient to use $2\times 2$ matrices instead of $3\times 3$ matrices. As a result, it is calculated certain equations for the moving frame in terms of quaternions, allowing for better control over the spin structure of the immersion [9]. Babaarslan and Yaylı examine constant slope surfaces with quaternions [10]. The quaternion rational surfaces are introduced by Wang and Goldman. Analyzing these surfaces, they investigate how to use syzygies [11]. Şenyurt and Çalışkan express ruled surface as quaternionic and compute integral invariants of ruled surface [12]. In the differential geometry of surfaces, interesting studies have been made on the orthonormal frames. In one of these studies, Cui and Dai investigate the kinematics of the spin-rolling motion of rigid objects [13]. Li et al. introduce partner-ruled surfaces according to the Flc frame. Then, the conditions of each couple of two partners ruled surfaces to be simultaneously developable and minimal are investigated. Moreover, some special curves of the partner ruled surfaces are characterized [14]. Şenyurt and Çalışkan examine ruled surfaces as dual quaternions and explain the characterization of this surface [15]. Aslan and Yaylı define the quaternionic shape operator expressed in the surface. They aim to find a way to calculate the invariants of the surface using Darboux frames and quaternions [16]. Ruled surfaces are one of the simplest objects in geometric modeling. A practical application of ruled surfaces is that they are used in civil engineering. In addition to civil engineering, ruled surfaces are also important for robot kinematics. Ryuh suggests the idea that ruled surfaces play an important role in robot end effectors [17]. In another study, parallel q-equidistant ruled surfaces are defined. When the surfaces are considered to be closed, then the integral invariants are given [18]. López investigate surfaces whose mean curvature H satisfies the equation $H=\alpha ⟨N,x⟩+\lambda$. These surfaces generalize self-shrinkers and self-expanders of the mean curvature flow. He categorizes the ruled and the translation surfaces [19]. Some authors give crucial results about the curves and surfaces in different spaces [12,15,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. We can find more motivations of our work from some articles (see [38,39,40,41,42,43,44,45,46,47,48,49,50]).

In Section 2, we provide some necessary background information about the problem of the paper that was mentioned in the introduction. In Section 3, we examine the relationship between Darboux frames along parameter curves and the Darboux frame of the base curve of the ruled surface. We derive the equations of the quaternionic shape operators and we investigate the rotation matrix, the Gauss curvature, and the mean curvature of the surface with these operators. In Section 4, we explore the ruled surfaces that can be drawn using Frenet vectors and we derive the equations of the quaternionic shape operators and exemplify the findings. In Section 5, we give a conclusion for our findings and discuss potential directions for future research.

2. Preliminaries

Let $\alpha :I\to {\mathbb{R}}^3$ be a unit-speed curve, hence $\parallel {\alpha }^{\prime }\left(s\right)\parallel =1$ for each s in I. We call $T\left(s\right)={\alpha }^{\prime }\left(s\right)$ the unit tangent vector field of $\alpha$, since it points in the direction of the curve. The derivative of $T\left(s\right)$ with respect to arc length, denoted $T^{\prime }\left(s\right)={\alpha }^{″}\left(s\right)$, measures the way the curve is turning in ${\mathbb{R}}^3$. Differentiation of $⟨T\left(s\right),T\left(s\right)⟩=1$ yields $2⟨T^{\prime }\left(s\right),T\left(s\right)⟩=0$, which means that $T^{\prime }\left(s\right)$ is orthogonal to $T\left(s\right)$ at each point. We call $T^{\prime }\left(s\right)$ the curvature vector field of $\alpha$ and denote $\kappa \left(s\right)=\parallel T^{\prime }\left(s\right)\parallel$, which is called the curvature of the curve. Thus $\kappa \ge 0,$ and the larger $\kappa$ is, the sharper the turning of $\alpha$. If we assume that $\kappa >0$ for all $s\in I$, we can define the principal normal vector field $N=T^{\prime }/\kappa$, which tells us the direction in which the curve is turning at each point. The binormal vector field $B\left(s\right)$ is then defined as the vector field $B\left(s\right)=T\left(s\right)\times N\left(s\right)$.

(Frenet formulas:) If $\alpha :I\to {\mathbb{R}}^3$ is a unit-speed curve with first curvature $\kappa >0$ and second curvature (torsion) $\tau$, then [51]

$$T^{\prime }\left(s\right)=\kappa \left(s\right)N\left(s\right),N^{\prime }\left(s\right)=-\kappa \left(s\right)T\left(s\right)+\tau \left(s\right)B\left(s\right),B^{\prime }\left(s\right)=-\tau \left(s\right)N\left(s\right).$$

A quaternion can be expressed as $q=d+a{e}_1+b{e}_2+c{e}_3$, where d is the real part and $a{e}_1+b{e}_2+c{e}_3$ is the pure part. We call quaternions with zero real parts ($d=0$) pure quaternions. A pure quaternion can also be represented as $q=a{e}_1+b{e}_2+c{e}_3;$ equivalently, it satisfies $q+\overline{q}=0$ [52,53].

The Hamiltonian quaternions H are the unitary $\mathbb{R}$-algebra generated by the symbols $e_1,e_2,e_3$ with the relations

$$\left\{\begin{array}{cc}{e}_1\ast e_1=e_2\ast e_2=e_3\ast e_3=-1,\hfill & \\ e_1\ast e_2=e_3,e_2\ast e_3=e_1,e_3\ast e_1=e_2.\hfill \end{array}\right.$$

where it is implied that the product of any two terms in the above expressions is the quaternion product. The general form of the quaternion product is as follows:

Definition 1 

([52,53]). Let $q_1=d_1+a_1{e}_1+b_1{e}_2+c_1{e}_3$ and $q_2=d_2+a_2{e}_1+b_2{e}_2+c_2{e}_3$ be two quaternions. where $a_1,b_1,c_1,d_1,a_2,b_2,c_2,d_2\in \mathbb{R}$, and $e_1,e_2,e_3$ are the imaginary units of the quaternion algebra. The quaternion multiplication of $q_1$ and $q_2$, denoted as $q_1\ast q_2$, is defined as follows:

$$\begin{array}{ccc}\hfill q_1\ast q_2& =& d_1{d}_2-(a_1{a}_2+b_1{b}_2+c_1{c}_2)+(d_1{a}_2+a_1{d}_2+b_1{c}_2-c_1{b}_2)e_1\hfill \\ & +& (d_1{b}_2+b_1{d}_2+c_1{a}_2-a_1{c}_2)e_2+(d_1{c}_2+c_1{d}_2+a_1{b}_2-b_1{a}_2)e_3.\hfill \end{array}$$

The quaternion multiplication of two pure quaternions is

$$q\ast p=-⟨q,p⟩+q\times p.$$

(1)

where $⟨,⟩$ is the inner product and × is the cross product.

The conjugate of a quaternion is denoted as $\overline{q}=d-a{e}_1-b{e}_2-c{e}_3$. The norm of the quaternion is given by $N\left(q\right)=\sqrt{d^2+a^2+b^2+c^2}$. It follows that $q\ast q=-N\left(q\right)$.

Substituting $q(\phi ,w)=cos\phi +sin\phi w$, where $w=(w_1,w_2,w_3)\in {\mathbb{R}}^3$ and $\parallel w\parallel =1$ is a unit three-vector lying on the two-sphere $S^2,$ where ${\mathbb{R}}^3$ denote the 3-dimensional Euclidean space. The matrix $R(\phi ,w)$ becomes the standard matrix for a rotation by $\phi$ in the plane perpendicular to $w.$ The quadratic form certifies that the two distinct unit quaternions q and $-q$ in $S^3$ correspond to the same $SO\left(3\right)$ rotation. Let p be a pure quaternion. Then $Rot\left(p\right)=q\ast p\ast q^{-1}$ is p rotated $2\phi$ about the axis $w.$ Moreover, the rotation matrix $R(\phi ,w)$ has the following explicit form [52]:

$$R(\phi ,w)=\left[\begin{array}{ccc}1+{sin}^2\phi (w_1^2-w_2^2-w_3^2-1)& -sin2\phi w_3+2{sin}^2\phi w_1{w}_2& sin2\phi w_2+2{sin}^2\phi w_1{w}_3\\ \\ sin2\phi w_3+2{sin}^2\phi w_1{w}_2& 1+{sin}^2\phi (w_2^2-w_1^2-w_3^2-1)& 2{sin}^2\phi w_2{w}_3-sin2\phi w_1\\ \\ 2{sin}^2\phi w_1{w}_3-sin2\phi w_2& sin2\phi w_1+2{sin}^2\phi w_2{w}_3& 1+{sin}^2\phi (w_3^2-w_2^2-w_1^2-1)\end{array}\right].$$

(2)

Definition 2 

([51]). Let $U\subset {\mathbb{R}}^2$ be an open set. M is a regular surface in ${\mathbb{R}}^3$, if the $\varphi :U\subset {\mathbb{R}}^2⟶M\subset {\mathbb{R}}^3$ mapping is one-to-one, regular and homeomorphism.

Let the surface M be given by the parameterization $\varphi (u,t)=\left(f\right(u,t),f_2(u,t),f_3(u,t))$ for $u,t\in U$. If we keep the first parameter u constant, then $t\to r(u,t)$ is a curve on the surface. Similarly, if t is constant, then $u\to r(u,t)$ traces a curve on the surface. These curves are called parameter curves [54].

If p is a point of M, so for each tangent vector X to M at p,

$$S_p\left(X\right)=-{\nabla }_{X}Z.$$

Herein Z is the unit normal vector field. $S_p$ is defined as the shape operator of M at p. The shape operator is the symmetric linear map [51,54].

Definition 3 

([51]). Let M be a regular surface in ${\mathbb{R}}^3$. The Gaussian curvature $K\left(p\right)$ of M at a point $p\in M$ is defined as the determinant of the shape operator S of M at p, i.e., $K\left(p\right)=det\left(S\right(p\left)\right)$. Similarly, the mean curvature $H\left(p\right)$ of M at a point $p\in M$ is defined as the trace of the shape operator S of M at p, i.e., $H\left(p\right)=tr\left(S\right(p\left)\right)$.

Lemma 1 

([51]). Let $E_1\left(u\right)$ and $E_2\left(t\right)$ be the tangent vectors of $\beta \left(u\right)$ and $\zeta \left(t\right)$, respectively. If $E_1\left(u\right)$ and $E_2\left(t\right)$ are linearly independent tangent vectors at a point p of $M\subset {\mathbb{R}}^3$, then the Gauss and mean curvatures are found with the equations

$$K=\frac{\parallel S\left(E_1\left(u\right)\right)\times S\left(E_2\left(t\right)\right)\parallel }{\parallel E_1\left(u\right)\times E_2\left(t\right)\parallel },H=\frac{\parallel S\left(E_1\left(u\right)\right)\times E_2\left(t\right)+E_1\left(u\right)\times S\left(E_2\left(t\right)\right)\parallel }{2\parallel E_1\left(u\right)\times E_2\left(t\right)\parallel }·$$

Let M be an oriented regular surface with a unit normal Z, and let $\alpha :I\to M$ be a curve with parameter s on M. Denote by the vector $Y\left(s\right)$, and write $Z\left(s\right)\times T\left(s\right)=Y\left(s\right)$. The orthonormal frame $\left\{T\right(s),Y(s),Z(s\left)\right\}$ is called Darboux frame. The equations of motion of the Darboux frame can be written as

$$\left[\begin{array}{c}{T}^{\prime }\left(s\right)\\ Y^{\prime }\left(s\right)\\ Z^{\prime }\left(s\right)\end{array}\right]=\parallel {\alpha }^{\prime }\left(s\right)\parallel \left[\begin{array}{ccc}0& k_g\left(s\right)& k_n\left(s\right)\\ -k_g\left(s\right)& 0& t_g\left(s\right)\\ -k_n\left(s\right)& -t_g\left(s\right)& 0\end{array}\right]\left[\begin{array}{c}T\left(s\right)\\ Y\left(s\right)\\ Z\left(s\right)\end{array}\right]$$

where $k_g,$$k_n$, and $t_g$ are the geodesic curvature, the normal curvature, and the geodesic torsion, respectively [51,54].

Definition 4 

([51]). A regular curve α in M is called a principal curve if its velocity vector α always points in a principal direction, which means that the geodesic torsion along the curve is zero.

Theorem 1 

([16]). Let M be a surface with parameters u and t, and $\beta \left(u\right)$ be a parameter curve in M. By using the quaternion operator $Q\left(u\right)=k_n\left(u\right)+t_g\left(u\right)Z\left(u\right)$, the shape operator can be given as

$$S\left(E_1\left(u\right)\right)=Q\left(u\right)\ast E_1\left(u\right).$$

(3)

The quaternion Q will be called a quaternionic shape operator.

Theorem 2 

([16]). Let M be a surface in ${\mathbb{R}}^3$ with a unit normal vector field Z and $p\left(u\right)=cos2\phi \left(u\right)+sin2\phi \left(u\right)Z\left(u\right)$ be a unit quaternion. Let $Q\left(u\right)$ be the quaternionic shape operator given by

$$Q\left(u\right)=\sqrt{{k_n}^2\left(u\right)+{t_g}^2\left(u\right)}\left(\cos 2\phi \left(u\right)+\sin 2\phi \left(u\right)Z\left(u\right)\right).$$

The quaternionic shape operator $Q\left(s\right)$ rotates the tangent vector $E_1\left(u\right)$ in the tangent plane of the surface around the normal vector $Z\left(u\right)$ of the surface.

Theorem 3 

([16]). Let M be a surface with parameters u and v and $\beta \left(u\right)$ and $\zeta \left(t\right)$ be the parameter curves on M. The unit tangent vectors of these curves are $E_1\left(u\right)$ and $E_2\left(t\right)$, respectively. By using the quaternionic shape operators, the Gauss curvature K and the mean curvature H can be written by

$$\begin{array}{ccc}\hfill K& =& \frac{\parallel (Q\left(u\right)\ast E_1\left(u\right))\times (Q\left(t\right)\ast E_2\left(t\right))\parallel }{\parallel E_1\left(u\right)\times E_2\left(t\right)\parallel },\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill H& =& \frac{\parallel (Q\left(u\right)\ast E_1\left(u\right))\times E_2\left(t\right)+E_1\left(u\right)\times (Q\left(t\right)\ast E_2\left(t\right))\parallel }{2\parallel E_1\left(u\right)\times E_2\left(t\right)\parallel }·\hfill \end{array}$$

(5)

Corollary 1 

([16]). If the curves in the surface are the principal curve, the quaternionic shape operator is given by

$$Q\left(u\right)\ast E_1\left(u\right)=|k_n\left(u\right)|I{E}_1\left(u\right)=\left|k_n\left(u\right)\right|E_1\left(u\right),$$

(6)

where I is the unit matrix.

A surface is said to be ruled if it is generated by moving a straight line continuously in ${\mathbb{R}}^3$. Thus a ruled surface has a parametrization in the form

$$\begin{array}{ccc}\hfill \phi :I\times \mathbb{R}& \to & {\mathbb{R}}^3\hfill \\ \hfill (s,v)& \to & \phi (s,v)=\alpha \left(s\right)+vx\left(s\right)\hfill \end{array}$$

(7)

where we call $\alpha$ the base curve of the ruled surface, $x\left(s\right)$ the generator unit vector of ruled surface [54]. Let the unit vector $n\left(s\right)$ be the normal vector of the surface and the Darboux frame $\left\{T\right(s),x(s),n(s\left)\right\}$ be at the point of $\alpha \left(s\right)$ of the ruled surface. The derivative of $T\left(s\right),x\left(s\right)$ and $n\left(s\right)$ can be written by [55]

$$\left\{\begin{array}{cc}{T}^{\prime }\left(s\right)=a\left(s\right)x\left(s\right)+b\left(s\right)n\left(s\right)\hfill & \\ x^{\prime }\left(s\right)=-a\left(s\right)T\left(s\right)+c\left(s\right)n\left(s\right)\hfill & \\ n^{\prime }\left(s\right)=-b\left(s\right)T\left(s\right)-c\left(s\right)x\left(s\right)\hfill \end{array}\right.$$

(8)

where $a\left(s\right),b\left(s\right)$ and $c\left(s\right)$ are real-valued functions.

3. Quaternion Shape Operator and Rotation Matrix on Ruled Surface

A ruled surface $\phi (s,v)=\alpha \left(s\right)+vx\left(s\right)$ has special curves, namely the parametric curves $\beta \left(s\right)$ and $\zeta \left(v\right)$, and the base curve $\alpha$. There are Darboux frames $\{E_1\left(s\right),Y\left(s\right),Z\left(s\right)\}$ and $\{E_1\left(v\right),Y\left(v\right),Z\left(v\right)\}$ belonging to parametric curves $\beta \left(s\right)$ and $\zeta \left(v\right)$ of the ruled surface $\phi$ at p. There is a Darboux frame $\left\{T\right(s),x(s),n(s\left)\right\}$ belonging to the base curve of the ruled surface $\phi$ at $\alpha \left(s\right).$ In this section, we investigate the relationship between Darboux frames along parameter curves and the Darboux frame of the base curve of the ruled surface. We derive the equations of the quaternionic shape operators, which rotate tangent vectors around the normal vector. We also find the corresponding rotation matrices. By using the quaternionic shape operators, we examine the Gauss curvature and the mean curvature of the surface.

Theorem 4. 

Let $\phi (s,v)=\alpha \left(s\right)+vx\left(s\right)$ be a ruled surface and let $\beta \left(s\right)$ and $\zeta \left(v\right)$ s parameter and v parameter curves on the ruled surface, respectively. Then the following relations hold between the Darboux frames of φ:

$$\left[\begin{array}{c}{E}_1\left(s\right)\\ Y\left(s\right)\\ Z\left(s\right)\end{array}\right]=\left[\begin{array}{ccc}\frac{1-av}{\sqrt{{(1-av)}^2+c^2{v}^2}}& 0& \frac{cv}{\sqrt{{(1-av)}^2}}\\ 0& 1& 0\\ \frac{-cv}{\sqrt{{(1-av)}^2}}& 0& \frac{1-av}{\sqrt{{(1-av)}^2+c^2{v}^2}}\end{array}\right]\left[\begin{array}{c}T\left(s\right)\\ x\left(s\right)\\ n\left(s\right)\end{array}\right]$$

and

$$\left[\begin{array}{c}{E}_2\left(v\right)\\ Y\left(v\right)\\ Z\left(v\right)\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ \frac{-1+av}{\sqrt{{(1-av)}^2+c^2{v}^2}}& 0& \frac{-cv}{\sqrt{{(1-av)}^2}}\\ \frac{-cv}{\sqrt{{(1-av)}^2}}& 0& \frac{1-av}{\sqrt{{(1-av)}^2+c^2{v}^2}}\end{array}\right]\left[\begin{array}{c}T\left(s\right)\\ x\left(s\right)\\ n\left(s\right)\end{array}\right].$$

Proof. 

By using (7) and (8), it then follows that the tangents of s and v parameter curves are found by

$$\begin{array}{ccc}\hfill E_1\left(s\right)& =& \frac{{\phi }_s}{\parallel {\phi }_s\parallel }=\frac{(1-av)T\left(s\right)+cvn\left(s\right)}{\sqrt{{(1-av)}^2+c^2{v}^2}},\hfill \\ \hfill E_2\left(v\right)& =& \frac{{\phi }_v}{\parallel {\phi }_v\parallel }=x\left(s\right).\hfill \end{array}$$

The unit normal vector of the ruled surface $\phi$ is given as

$$\begin{array}{ccc}\hfill Z& =& E_1\left(s\right)\times E_2\left(v\right)=\frac{-cvT\left(s\right)+(1-av)n\left(s\right)}{\sqrt{{(1-av)}^2+c^2{v}^2}}·\hfill \end{array}$$

(9)

$Y\left(s\right)$ and $Y\left(v\right)$ can be obtained

$$\begin{array}{ccc}\hfill Y\left(s\right)& =& Z\left(s\right)\times E_1\left(s\right)=x\left(s\right),\hfill \\ \hfill Y\left(v\right)& =& Z\left(v\right)\times E_2\left(v\right)=-E_1\left(s\right)=\frac{(-1+av)T\left(s\right)-cvn\left(s\right)}{\sqrt{{(1-av)}^2+c^2{v}^2}}·\hfill \end{array}$$

The proof is completed. □

Theorem 5. 

Let φ be a ruled surface and let $\beta \left(s\right)$ and $\zeta \left(v\right)$ parameter curves on the ruled surface, respectively. The quaternionic shape operators $Q\left(s\right)$ and $Q\left(v\right)$ are calculated by

$$\begin{array}{ccc}\hfill Q(s)\ast E_1(s)& =& \frac{(c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb))((1-av)T(s)+cvn(s))}{{({(1-av)}^2+c^2{v}^2)}^2}\hfill \\ & & +\frac{cx(s)}{({(1-av)}^2+c^2{v}^2)},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill Q(v)\ast E_2(v)& =& \frac{c(1-av)T\left(s\right)+c^{2}vn\left(s\right)}{{({(1-av)}^2+c^2{v}^2)}^{\frac{3}{2}}}·\hfill \end{array}$$

(11)

Proof. 

From the Equations (1) and (3), the quaternionic shape operator for the vector $E_1\left(s\right)$ is quaternionically obtained by

$$\begin{array}{ccc}\hfill Q\left(s\right)\ast E_1\left(s\right)& =& (k_n\left(s\right)+t_g\left(s\right)Z\left(s\right))\ast E_1\left(s\right)\hfill \\ & =& \left(k_n\left(s\right)E_1\left(s\right)+t_g\left(s\right)Y\left(s\right)\right).\hfill \end{array}$$

The normal curvature $k_n\left(s\right)$ and the geodesic torsion $t_g\left(s\right)$ can be calculated as:

$$\begin{array}{ccc}\hfill k_n\left(s\right)& =& -\frac{1}{\parallel {\phi }_s\parallel }\left(⟨Z^{\prime }\left(s\right),E_1\left(s\right)⟩\right)=\frac{c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)}{{({(1-av)}^2+c^2{v}^2)}^{\frac{3}{2}}},\hfill \\ \hfill t_g(s)& =& -\frac{1}{\parallel {\phi }_s\parallel }(⟨Z^{\prime }(s),Y(s)⟩)=\frac{c}{{(1-av)}^2+c^2{v}^2}.\hfill \end{array}$$

Substituting these values into the expression for the quaternionic shape operator, we obtain:

$$\begin{array}{ccc}\hfill Q(s)\ast E_1(s)& =& \frac{\left(c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)\right)\left((1-av)T(s)+cvn(s)\right)}{{({(1-av)}^2+c^2{v}^2)}^2}\hfill \\ & & +\frac{-c^{2}v(1-av)(T(s)\ast T(s))-c^3{v}^2(T(s)\ast n(s))}{{({(1-av)}^2+c^2{v}^2)}^2}\hfill \\ & & +\frac{c{(1-av)}^2(n(s)\ast T(s))+c^{2}v(1-av)(n(s)\ast n(s))}{{({(1-av)}^2+c^2{v}^2)}^2}\hfill \\ & =& \frac{\left(c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)\right)((1-av)T(s)+cvn(s))}{{({(1-av)}^2+c^2{v}^2)}^2}\hfill \\ & & +\frac{cx(s)}{({(1-av)}^2+c^2{v}^2)}.\hfill \end{array}$$

Similarly, we can find the quaternionic shape operator $Q(v)\ast E_2\left(v\right)$ using the same method. □

Using this operator, we can give the following theorem regarding the rotation of the tangent vector $E_1\left(s\right)$.

Theorem 6. 

The quaternionic shape operator $Q\left(s\right)$ rotates the tangent vector $E_1\left(s\right)$ in the tangent plane of the surface around the normal vector $Z(s,v)$ of the ruled surface. The yielding rotation matrix is given by

$$R_1=\frac{1}{\xi }\left[\begin{array}{ccc}{\displaystyle \frac{\sigma {(1-av)}^2+c^2{v}^2\xi }{{(1-av)}^2+c^2{v}^2}}& -c(1-av)& \frac{(-\xi +\sigma )cv(1-av)}{{(1-av)}^2+c^2{v}^2}\\ c(1-av)& \sigma ({(1-av)}^2+c^2{v}^2)& c^{2}v\\ {\displaystyle \frac{(-\xi +\sigma )cv(1-av)}{{(1-av)}^2+c^2{v}^2}}& -c^{2}v& {\displaystyle \frac{\xi {(1-av)}^2+\sigma c^2{v}^2}{{(1-av)}^2+c^2{v}^2}}\end{array}\right]$$

where $\sigma =c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb),\xi =\sqrt{{\sigma }^2+c^2({(1-av)}^2+c^2{v}^2)}$.

Proof. 

We begin by noting that the equation $Q\left(s\right)=k_n\left(s\right)+t_g\left(s\right)Z\left(s\right)$ holds, where $k_n\left(s\right)$ is the normal curvature and $t_g\left(s\right)$ is the geodesic torsion. Then, we obtain

$$\begin{array}{ccc}\hfill Q\left(s\right)& =& k_n\left(s\right)+t_g\left(s\right)Z\left(s\right)\hfill \\ & =& \sqrt{{k_n}^2\left(s\right)+{t_g}^2\left(s\right)}(\frac{k_n\left(s\right)}{\sqrt{{k_n}^2\left(s\right)+{t_g}^2\left(s\right)}}+\frac{t_g\left(s\right)}{\sqrt{{k_n}^2\left(s\right)+{t_g}^2\left(s\right)}}Z\left(s\right))\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& =& \sqrt{{k_n}^2\left(s\right)+{t_g}^2\left(s\right)}\left(cos2\phi \left(s\right)+sin2\phi \left(s\right)Z\left(s\right)\right).\hfill \end{array}$$

(13)

Next, we calculate the expressions for $k_n\left(s\right)$ and $t_g\left(s\right)$ and substitute them in the above equation, we obtain

$$\begin{array}{ccc}\hfill cos2\phi (s)& =& \frac{c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)}{\sqrt{{\left(c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)\right)}^2+c^2{({(1-av)}^2+c^2{v}^2)}^2}},\hfill \\ \hfill sin2\phi (s)& =& \frac{c\sqrt{{(1-av)}^2+c^2{v}^2}}{\sqrt{{\left(c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)\right)}^2+c^2{({(1-av)}^2+c^2{v}^2)}^2}}·\hfill \end{array}$$

Using Equation (2), we can conclude that the quaternionic shape operator $Q(s)$ rotates the tangent vector $E_1(s)$ in the tangent plane of the surface around the normal vector $Z(s)$ of the surface. This completes the proof. □

We can give the following result for the tangent vector $E_2(v)$.

Corollary 2. 

The quaternionic shape operator $Q(v)$ rotates the tangent vector $E_2(v)$ in the tangent plane of the surface around the normal vector $Z(s,v)$ of the ruled surface. The yielding rotation matrix is given by

$$R_2=\left[\begin{array}{ccc}\frac{c^2{v}^2}{{(1-av)}^2+c^2{v}^2}& \frac{-1+av}{\sqrt{{(1-av)}^2+c^2{v}^2}}& \frac{-cv(1-av)}{{(1-av)}^2+c^2{v}^2}\\ \frac{1-av}{\sqrt{{(1-av)}^2+c^2{v}^2}}& 0& \frac{cv}{{(1-av)}^2+c^2{v}^2}\\ \frac{-cv(1-av)}{{(1-av)}^2+c^2{v}^2}& \frac{-cv}{{(1-av)}^2+c^2{v}^2}& \frac{{(1-av)}^2}{{(1-av)}^2+c^2{v}^2}\end{array}\right]$$

where $R_2$ is an orthogonal matrix.

Theorem 7. 

Let φ be a ruled surface. The Gauss curvature K and the mean curvature H of the ruled surface are obtained by

$$\begin{array}{ccc}\hfill K& =& \frac{c^2}{{\left({(1-av)}^2+c^2{v}^2\right)}^2},H=\frac{c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)}{2{\left({(1-av)}^2+c^2{v}^2\right)}^2}·\hfill \end{array}$$

Proof. 

The Gauss curvature of the ruled surface $\phi$ is defined as quaternionic as follows:

$$\begin{array}{ccc}\hfill K& =& \frac{\parallel \left(Q(s)\ast E_1(s)\right)\times \left(Q(v)\ast E_2(v)\right)\parallel }{\parallel E_1(s)\times E_2(v)\parallel }·\hfill \end{array}$$

Using (10) and (11), it can be found

$$\begin{array}{ccc}& & \left(Q(s)\ast E_1(s)\right)\times \left(Q(v)\ast E_2(v)\right)=(\frac{(c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb))(1-av)T(s)}{{({(1-av)}^2+c^2{v}^2)}^2}\hfill \\ & & +\frac{\left(c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)\right)cvn(s)}{{({(1-av)}^2+c^2{v}^2)}^2}+\frac{cx(s)}{({(1-av)}^2+c^2{v}^2)})\times \left(\frac{c(1-av)T(s)+c^{2}vn(s)}{{({(1-av)}^2+c^2{v}^2)}^{\frac{3}{2}}}\right),\hfill \\ & & \left(Q(s)\ast E_1(s)\right)\times \left(Q(v)\ast E_2(v)\right)=\frac{c^{3}vT(s)-c^2(1-av)n(s)}{{({(1-av)}^2+c^2{v}^2)}^{\frac{5}{2}}}·\hfill \end{array}$$

If we calculate the norm of the above equation, we have

$$\begin{array}{c}\hfill \parallel \left(Q(s)\ast E_1(s)\right)\times \left(Q(v)\ast E_2(v)\right)\parallel =\frac{c^2}{{\left({(1-av)}^2+c^2{v}^2\right)}^2}·\end{array}$$

From (9), we know that $\parallel E_1(s)\times E_2(v)\parallel =1$. Then we obtain

$$\begin{array}{ccc}\hfill K& =& \frac{c^2}{{\left({(1-av)}^2+c^2{v}^2\right)}^2}·\hfill \end{array}$$

When the required calculations are completed, the resulting mean curvature is

$$\begin{array}{c}\hfill H=\frac{c^{\prime }v(1-av)+b{(1-av)}^2+c{v}^2(a^{\prime }+cb)}{2{\left({(1-av)}^2+c^2{v}^2\right)}^2}·\end{array}$$

□

The picture of the ruled surface and quaternion shape operators see Figure 1.

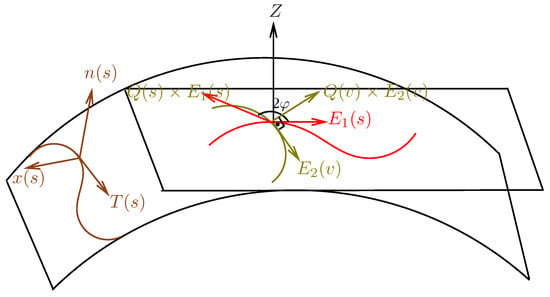
Figure 1. Ruled surface and quaternion shape operators.

4. Quaternion Shape Operator and Rotation Matrices on Special Ruled Surfaces

In this section, we explore the ruled surfaces that can be drawn using Frenet vectors and we derive the equations of the quaternionic shape operators. Through quaternionic shape operators, we uncover a variety of interesting results, including rotation matrices, Gauss curvatures, and mean curvatures.

4.1. The Ruled Surface Drawn by Tangent Vector

Theorem 8. 

Let ${\phi }_T(s,v)=\alpha (s)+vT(s)$ be a ruled surface and α be a base curve of the surface. The expressions of the Darboux frames constructed on the $\beta (s)$ and $\zeta (v)$ parameter curves on the ruled surface, according to the Frenet vectors, are

$$\left[\begin{array}{c}{E}_1(s)\\ Y(s)\\ Z(s)\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& -1\end{array}\right]\left[\begin{array}{c}T(s)\\ N(s)\\ B(s)\end{array}\right]$$

and

$$\left[\begin{array}{c}{E}_2(v)\\ Y(v)\\ Z(v)\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right]\left[\begin{array}{c}T(s)\\ N(s)\\ B(s)\end{array}\right].$$

Proof. 

For the ruled surface ${\phi }_T$, the partial derivative is taken according to s and v, it is found

$$\begin{array}{ccc}\hfill {({\phi }_T)}_s& =& T(s)+v\kappa (s)N(s)=X_1,\hfill \\ \hfill {({\phi }_T)}_v& =& T(s)=X_2.\hfill \end{array}$$

Taking into account the inner product, we have $⟨{({\phi }_T)}_s,{({\phi }_T)}_v⟩\ne 0.$

Using the Gram–Schmidt process, the vectors of orthonormal base for ${({\phi }_T)}_s=X_1$ and ${({\phi }_T)}_v=X_2$ are

$$\begin{array}{ccc}\hfill Y_1& =& X_2=T(s),\hfill \\ \hfill Y_2& =& -\frac{⟨Y_1,X_1⟩}{⟨Y_1,Y_1⟩}{Y}_1+X_1=v\kappa (s)N(s),\hfill \\ \hfill E_1(s)& =& \frac{Y_2}{\parallel Y_2\parallel }=N(s),E_2(v)=\frac{Y_1}{\parallel Y_1\parallel }=T(s).\hfill \end{array}$$

The unit normal vector of the ${\phi }_T$ is given as

$$\begin{array}{ccc}\hfill Z& =& E_1(s)\times E_2(v)=-B(s)·\hfill \end{array}$$

(14)

$Y(s)$ and $Y(v)$ depending Frenet frame at point $\alpha (s)$ can be obtained

$$\begin{array}{ccc}\hfill Y(s)& =& Z(s)\times E_1(s)=T(s),\hfill \\ \hfill Y(v)& =& Z(v)\times E_2(v)=-N(s).\hfill \end{array}$$

□

Theorem 9. 

Let ${\phi }_T$ be a ruled surface. The quaternionic shape operators $Q(s)$ and $Q(v)$ are obtained by

$$Q(s)\ast E_1(s)=\frac{-\tau }{\sqrt{1+v^2{\kappa }^2}}N,Q(v)\ast E_2(v)=0.$$

Proof. 

By considering the Equation (3), The quaternionic shape operators $Q(s)$ and $Q(v)$ are expressed by

$$\begin{array}{ccc}\hfill Q(s)\ast E_1(s)& =& k_n(s)E_1(s)+t_g(s)Y(s)=\frac{-\tau }{\sqrt{1+v^2{\kappa }^2}}N,\hfill \\ \hfill Q(v)\ast E_2(v)& =& k_n(v)E_2(v)+t_g(v)Y(v)=0.\hfill \end{array}$$

 □

Corollary 3. 

The cosine and sine of the angle of between $E_1(s)$ and $Q(s)\ast E_1(s)$ are explicitly shown as

$$cos2\phi (s)=\frac{k_n(s)}{\sqrt{{k_n}^2(s)+{t_g}^2(s)}}=1,sin2\phi (s)=\frac{t_g(s)}{\sqrt{{k_n}^2(s)+{t_g}^2(s)}}=0.$$

(15)

This means that the $E_1(s)$ and $Q(s)\ast E_1(s)$ vectors are linearly dependent, so the rotation matrix has to be the unit matrix. If we use the Equations (2), (14) and (15), rotation matrix can be obtained as

$$R_T=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right].$$

Theorem 10. 

The ruled surface ${\phi }_T$ is flat. The mean curvature H of this surface is obtained by

$$\begin{array}{ccc}\hfill H& =& \frac{\tau }{2\sqrt{1+v^2{\kappa }^2}}·\hfill \end{array}$$

Proof. 

It is very similar to the proof of Theorem 7, therefore we omit it. □

4.2. The Ruled Surface Drawn by Principal Normal Vector

The relation between frames according to surface ${\phi }_N(s,v)=\alpha (s)+vN(s)$ can be obtained as it is similar to Theorem 8.

$$\left[\begin{array}{c}{E}_1(s)\\ Y(s)\\ Z(s)\end{array}\right]=\left[\begin{array}{ccc}\frac{1-v\kappa }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}& 0& \frac{v\tau }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}\\ 0& 1& 0\\ \frac{-v\tau }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}& 0& \frac{1-v\kappa }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}\end{array}\right]\left[\begin{array}{c}T(s)\\ N(s)\\ B(s)\end{array}\right]$$

and

$$\left[\begin{array}{c}{E}_2(v)\\ Y(v)\\ Z(v)\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ \frac{-1+v\kappa }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}& 0& \frac{-v\tau }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}\\ \frac{-v\tau }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}& 0& \frac{1-v\kappa }{\sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}\end{array}\right]\left[\begin{array}{c}T(s)\\ N(s)\\ B(s)\end{array}\right].$$

Theorem 11. 

Let ${\phi }_N$ be a ruled surface. The quaternionic shape operators $Q(s)$ and $Q(v)$ are obtained by

$$\begin{array}{ccc}\hfill Q(s)\ast E_1(s)& =& \frac{(v{\tau }^{\prime }(1-v\kappa )+v^2\tau {\kappa }^{\prime })((1-v\kappa )T(s)+v\tau B(s)}{{({(1-v\kappa )}^2+v^2{\tau }^2)}^2}\hfill \\ & & +\frac{\tau N(s)}{{(1-v\kappa )}^2+v^2{\tau }^2},\hfill \\ \\ \hfill Q(v)\ast E_2(v)& =& \frac{(1-v\kappa )\tau T(s)+v{\tau }^{2}B(s)}{{({(1-v\kappa )}^2+v^2{\tau }^2)}^{\frac{3}{2}}}·\hfill \end{array}$$

Proof. 

The theorem is similar to Theorem 9, therefore we omit its proof. □

Corollary 4. 

The cosine and sine of the angle of between $E_1(s)$ and $Q(s)\ast E_1(s)$ are explicitly shown as

$$\begin{array}{ccc}\hfill cos2\phi (s)& =& \frac{v{\tau }^{\prime }(1-v\kappa )+v^2\tau {\kappa }^{\prime }}{\sqrt{{(v{\tau }^{\prime }(1-v\kappa )+v^2\tau {\kappa }^{\prime })}^2+{\tau }^2({(1-v\kappa )}^2+v^2{\tau }^2)}},\hfill \\ \hfill sin2\phi (s)& =& \frac{\tau \sqrt{{(1-v\kappa )}^2+v^2{\tau }^2}}{\sqrt{{(v{\tau }^{\prime }(1-v\kappa )+v^2\tau {\kappa }^{\prime })}^2+{\tau }^2({(1-v\kappa )}^2+v^2{\tau }^2)}}·\hfill \\ \hfill \end{array}$$

The rotation matrix can be obtained as

$$R_N=\frac{1}{\xi }\left[\begin{array}{ccc}\frac{\sigma {(1-v\kappa )}^2+v^2{\tau }^2\xi }{{(1-v\kappa )}^2+v^2{\tau }^2}& -\tau (1-v\kappa )& \frac{(-\xi +\sigma )v\tau (1-v\kappa )}{{(1-v\kappa )}^2+v^2{\tau }^2}\\ \tau (1-v\kappa )& \sigma ({(1-v\kappa )}^2+v^2{\tau }^2)& v{\tau }^2\\ \frac{(-\xi +\sigma )v\tau (1-v\kappa )}{{(1-v\kappa )}^2+v^2{\tau }^2}& -v{\tau }^2& \frac{\xi {(1-v\kappa )}^2+\sigma v^2{\tau }^2}{{(1-v\kappa )}^2+v^2{\tau }^2}\end{array}\right]$$

where $\sigma ={\tau }^{\prime }v(1-v\kappa )+v^2\tau {\kappa }^{\prime },\xi =\sqrt{{\sigma }^2+{\tau }^2({(1-v\kappa )}^2+v^2{\tau }^2)}$.

Theorem 12. 

Let ${\phi }_N$ be ruled surface. The Gauss curvature K and the mean curvature H of this surface are obtained by

$$\begin{array}{ccc}\hfill K& =& \frac{{\tau }^2}{{({(1-v\kappa )}^2+v^2{\tau }^2)}^2},H=\frac{{\tau }^{\prime }v(1-v\kappa )+v^2\tau {\kappa }^{\prime }}{2{({(1-v\kappa )}^2+v^2{\tau }^2)}^{\frac{3}{2}}}·\hfill \end{array}$$

Proof. 

It is very similar to the proof of Theorem 7. Thus, we omit it. □

4.3. The Ruled Surface Drawn by Binormal Vector

The relation between frames according to surface ${\phi }_B(s,v)=\alpha (s)+vB(s)$ can be obtained as it is similar to Theorem 8.

$$\left[\begin{array}{c}{E}_1(s)\\ Y(s)\\ Z(s)\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{\sqrt{1+v^2{\tau }^2}}& \frac{-v\tau }{\sqrt{1+v^2{\tau }^2}}& 0\\ 0& 0& 1\\ \frac{-v\tau }{\sqrt{1+v^2{\tau }^2}}& \frac{-1}{\sqrt{1+v^2{\tau }^2}}& 0\end{array}\right]\left[\begin{array}{c}T(s)\\ N(s)\\ B(s)\end{array}\right]$$

(16)

and

$$\left[\begin{array}{c}{E}_2(v)\\ Y(v)\\ Z(v)\end{array}\right]=\left[\begin{array}{ccc}0& 0& 1\\ \frac{-1}{\sqrt{1+v^2{\tau }^2}}& \frac{v\tau }{\sqrt{1+v^2{\tau }^2}}& 0\\ \frac{-v\tau }{\sqrt{1+v^2{\tau }^2}}& \frac{-1}{\sqrt{1+v^2{\tau }^2}}& 0\end{array}\right]\left[\begin{array}{c}T(s)\\ N(s)\\ B(s)\end{array}\right].$$

Theorem 13. 

Let ${\phi }_B$ be a ruled surface. The quaternionic shape operators of $Q(s)$ and $Q(v)$ are obtained by

$$\begin{array}{ccc}\hfill Q(s)\ast E_1(s)& =& \frac{(v{\tau }^{\prime }-\kappa -v^2{\tau }^2\kappa )(T(s)-v\tau N(s))}{{(1+v^2{\tau }^2)}^2}+\frac{\tau }{1+v^2{\tau }^2}B(s),\hfill \\ \hfill Q(v)\ast E_2(v)& =& \frac{\tau T(s)-v{\tau }^{2}N(s)}{({(1+v^2{\tau }^2)}^{\frac{3}{2}}}·\hfill \end{array}$$

Proof. 

The theorem is similar to Theorem 9, therefore we omit its proof. □

Corollary 5. 

The cosine and sine of the angle of between $E_1(s)$ and $Q(s)\ast E_1(s)$ are explicitly shown as

$$\begin{array}{ccc}\hfill cos2\phi (s)& =& \frac{v{\tau }^{\prime }-\kappa -v^2{\tau }^2\kappa }{\sqrt{{(v{\tau }^{\prime }-\kappa -v^2{\tau }^2\kappa )}^2+{\tau }^2(1+v^2{\tau }^2)}},\hfill \\ \hfill sin2\phi (s)& =& \frac{\tau \sqrt{1+v^2{\tau }^2}}{\sqrt{{(v{\tau }^{\prime }-\kappa -v^2{\tau }^2\kappa )}^2+{\tau }^2(1+v^2{\tau }^2)}}·\hfill \end{array}$$

The rotation matrix is given by

$$R_B=\frac{1}{\xi }\left[\begin{array}{ccc}\frac{\sigma +v^2{\tau }^2\xi }{1+v^2{\tau }^2}& \frac{(\xi -\sigma )v\tau }{1+v^2{\tau }^2}& -\tau \\ \\ \frac{(\xi -\sigma )v\tau }{1+v^2{\tau }^2}& \frac{\xi +v^2{\tau }^2\sigma }{1+v^2{\tau }^2}& v{\tau }^2\\ \\ \tau & -v{\tau }^2& \sigma \end{array}\right]$$

where $\sigma ={\tau }^{\prime }v-\kappa -v^2{\tau }^2\kappa ,\xi =\sqrt{{\sigma }^2+{\tau }^2(1+v^2{\tau }^2)}$.

Theorem 14. 

Let ${\phi }_B$ be a ruled surface. The Gauss curvature K and the mean curvature H of this surface are obtained by

$$K=\frac{{\tau }^2}{{(1+v^2{\tau }^2)}^2},H=\frac{{\tau }^{\prime }v-\kappa -v^2{\tau }^2\kappa }{2{(1+v^2{\tau }^2)}^{\frac{3}{2}}}·$$

Proof. 

It is very similar to the proof of Theorem 7. Therefore, we omit it. □

Example 1. 

The straight circular cylinder of radius 1 about the z-axis has the following parametric representation:

$$\phi (s,v)=(coss,sins,v).$$

A ruled surface is a surface swept out by a straight line as it moves through space. For example, a cylinder is formed by moving a straight line around a curve in a plane, keeping it perpendicular to the plane at all times. Hence, the parametric equation of the cylinder is

$$\phi (s,v)=(\cos s,\sin s,0)+v(0,0,1)$$

where base curve is $\alpha (s)=(\cos s,\sin s,0)$ and generator vector is $B(s)=(0,0,1).$ It is shown that curvature and torsion of the base curve are 1 and 0, respectively. By taking into account (6), we can obtain

$$Q(s)\ast E_1(s)=\left|k_n\right|I{E}_1(s)=E_1(s).$$

In similar way, we find that $Q(v)\ast E_1(v)=0.$ Considering (4) and (5), we have $K=0$ and $H=1/2$.

Example 2. 

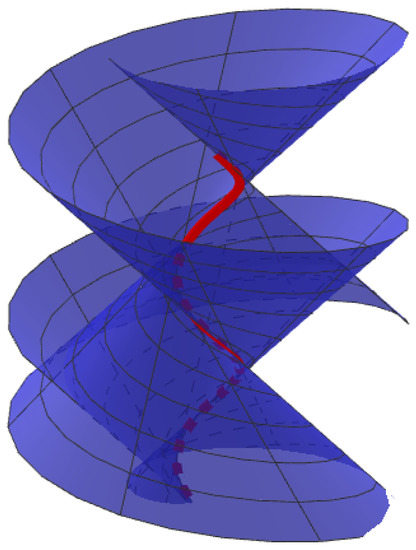
Let $\alpha (s)=\frac{1}{\sqrt{2}}(-\cos (s),-\sin (s),s)$ be a circular helix. A ruled surface can be constructed as follows:

$$\phi (s,v)=\alpha (s)+vB(s)=\frac{1}{\sqrt{2}}(-\cos (s),-\sin (s),s)+v\frac{1}{\sqrt{2}}(-\sin (s),\cos (s),1)$$

(17)

where $B(s)=\frac{1}{\sqrt{2}}(-\sin (s),\cos (s),1)$ is binormal vector of circular helix. It is easy to determined $E_1(s)=\frac{1}{\sqrt{1+v^2}}T(s)-\frac{v}{\sqrt{2+2v^2}}N.$

Concentrating on the investigation of the quaternionic shape operator $Q(s)$ in the Equation (17), it is solved via the rotation method

$$Q(s)\ast E_1=q\ast E_1(s)\ast q^{\prime },q=\cos \phi +\sin \phi Z(s).$$

Then doing the required simplifications, we find the quaternionic shape operator as

$$\begin{array}{ccc}\hfill Q(s)\ast E_1(s)& =& (\cos \phi +\sin \phi Z(s))\ast E_1(s)\ast (\cos \phi -\sin \phi Z(s)),\hfill \\ & =& \cos 2\phi (\frac{1}{\sqrt{1+v^2}}T(s)-\frac{v}{\sqrt{2+2v^2}}N)+\sin 2\phi N(s).\hfill \end{array}$$

Considering the appropriate scaling of s and $2\phi$ should be ${90}^{\circ }$ and ${135}^{\circ }$; respectively, the quaternionic shape operator is obtained as $Q(s)=\frac{\sqrt{2}}{2}-(\frac{v}{2\sqrt{2+v^2}},\frac{1}{\sqrt{2+v^2}},\frac{v}{2\sqrt{2+v^2}}).$ The ruled surface can see Figure 2.

Figure 2. The ruled surface (blue) with the base curve (red).

The quaternionic shape operator $Q(s)$ rotates the tangent vector $E_1(s)$ in the tangent plane of the surface around the normal vector $Z(s)$ of the surface. The yielding rotation matrix $(R_B)$ is given by

$$R_B=\frac{\sqrt{6}(2+v^2)}{4}\left[\begin{array}{ccc}\frac{\sqrt{2}(v^2\sqrt{3}-2)}{4}& \frac{v(\sqrt{3}+1)}{4}& -\frac{1}{\sqrt{2}}\\ \\ \frac{v(\sqrt{3}+1)}{4}& \frac{\sqrt{2}(2\sqrt{3}-v^2)}{4}& v\frac{1}{2}\\ \\ \frac{1}{\sqrt{2}}& -v\frac{1}{2}& -\frac{\sqrt{2}(2+v^2)}{4}\end{array}\right].$$

5. Conclusions and Discussion

Combining the mathematical tools of quaternions with the theory of ruled surfaces has the potential to yield new insights and applications. In this article, we attempted to unify certain aspects of two important subjects. Furthermore, we explored the relationship between Darboux frames along parameter curves and the Darboux frame of the base curve of a ruled surface. Our investigation has led us to derive the equations for quaternionic shape operators, which can rotate tangent vectors around the normal vector, and find the corresponding rotation matrices. Using these operators, we examined the Gauss curvature and mean curvature of the ruled surface and have explored how these properties differ when Frenet vectors are used instead of generator vectors. Our study uncovers several interesting findings about the geometry of ruled surfaces and the interplay between their various properties. In particular, we show the importance of Darboux frames in understanding these surfaces and how they can be used to derive useful equations. Furthermore, we provide a range of illustrative examples to help clarify the concepts and results presented throughout the article. Our investigation also opens up new avenues for future research in this field, including the study of ruled surfaces in different spaces such as Lorentz and dual space. In the future work, we are going to study some applications of ruled surfaces combine with singularity theory, submanifold theory, etc., in [56,57,58,59,60,61,62,63,64,65,66], to obtain more new results.