Aperiodic Sampled-Data Control for Anti-Synchronization of Chaotic Nonlinear Systems Subject to Input Saturation
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
3. Main Results
- Step 1:
- Guaranteeing the stability of discrete instants with the help of the DTLM;
- Step 2:
- Estimating the trivial solutions inside the sampling interval by using the squeeze theory.
4. Optimization Algorithms
4.1. Optimization of the AIA
4.2. Optimization of the UBSP
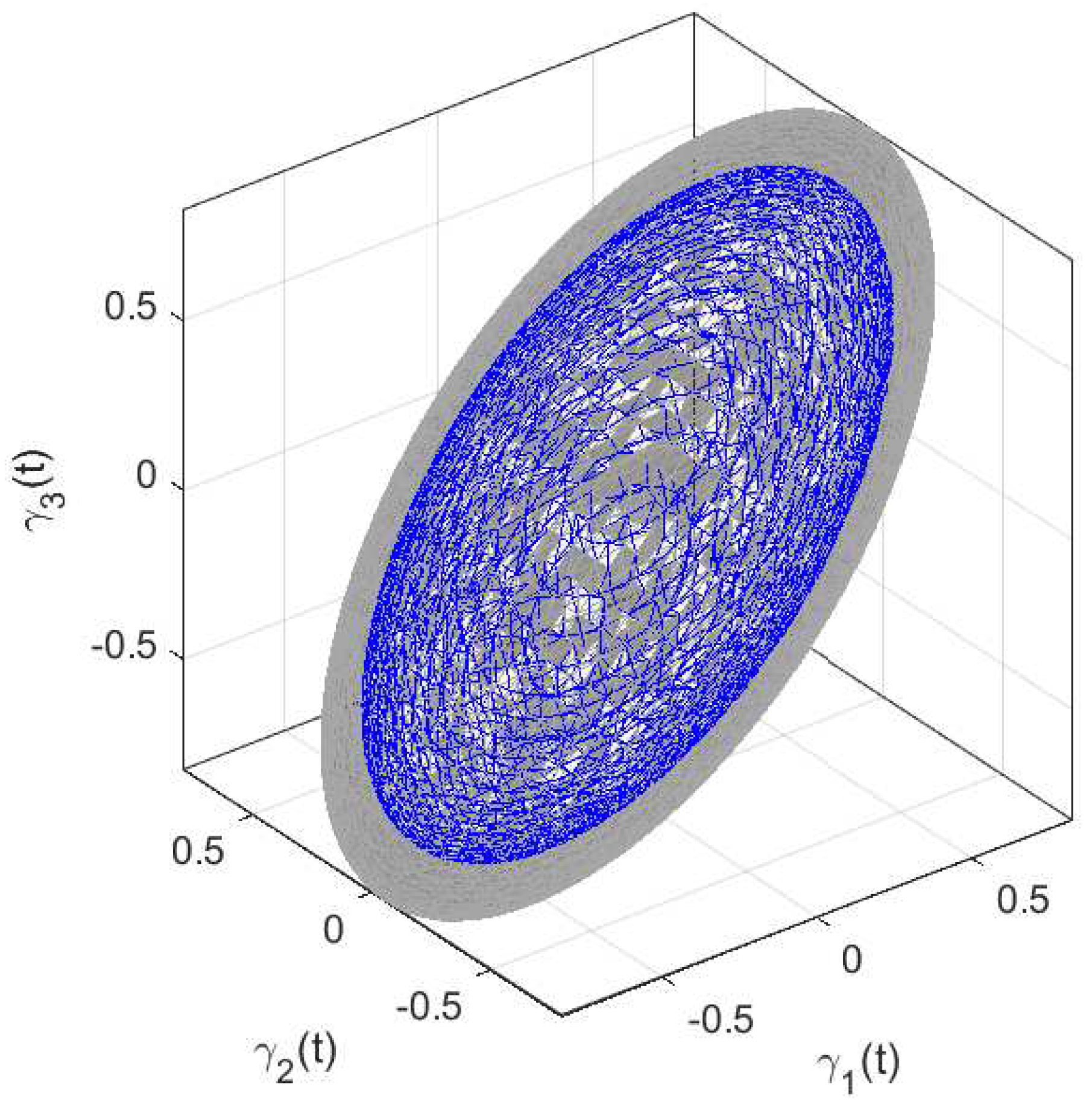
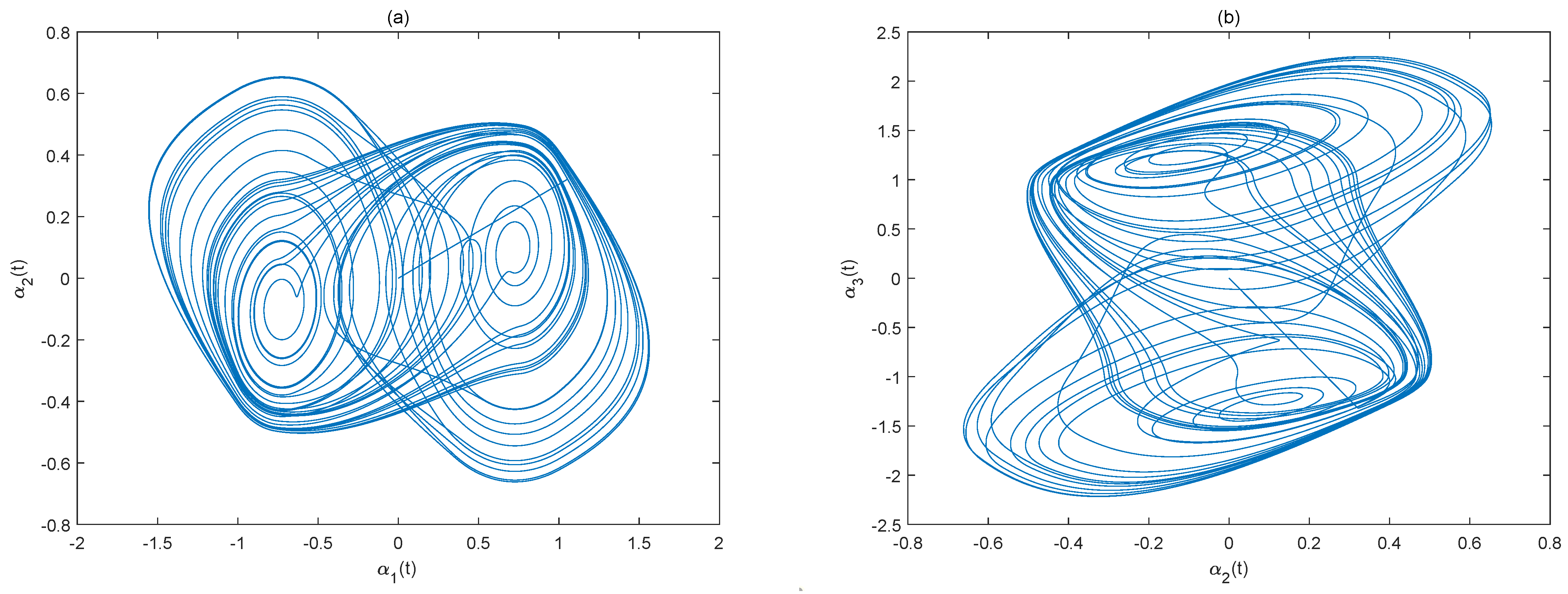
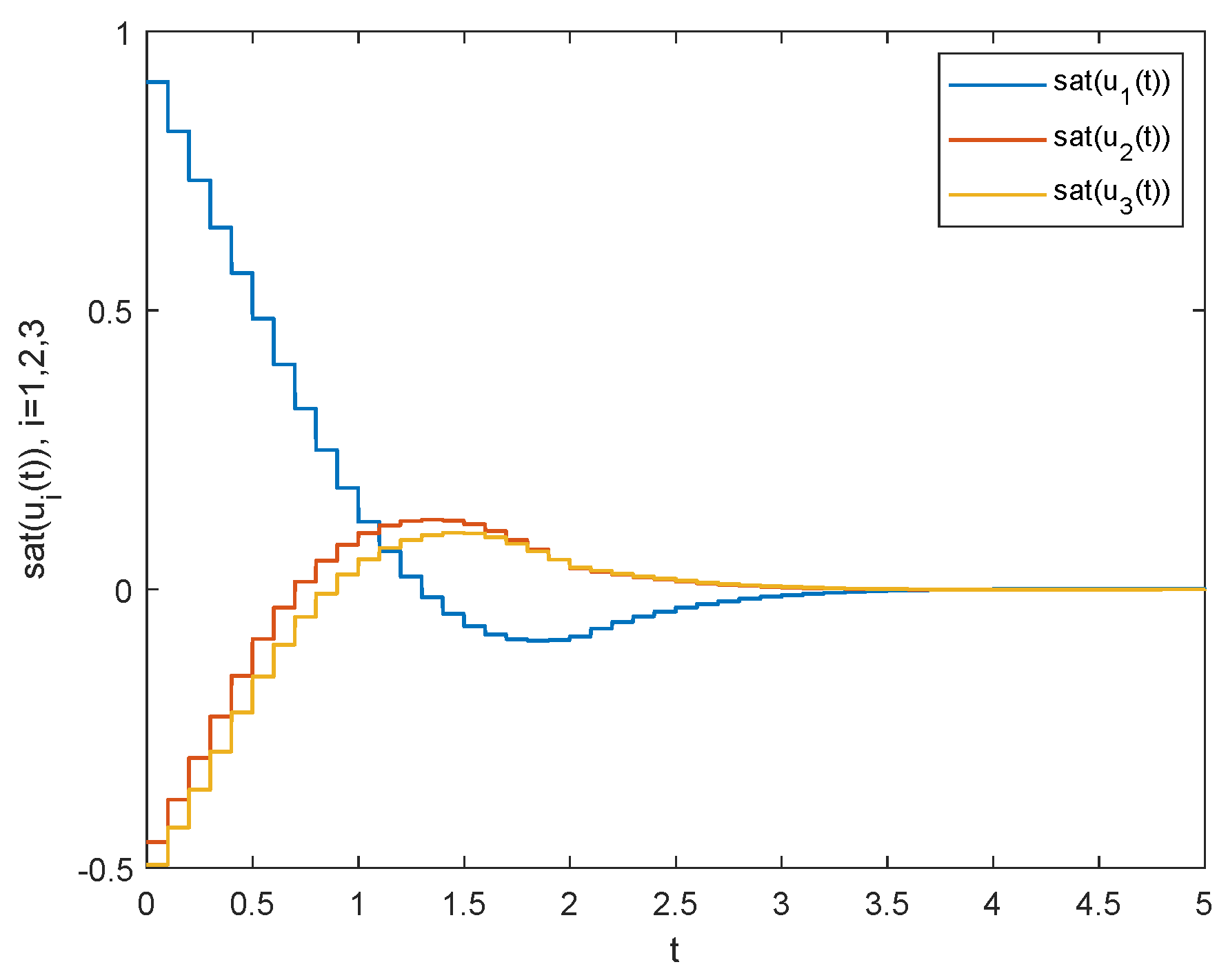
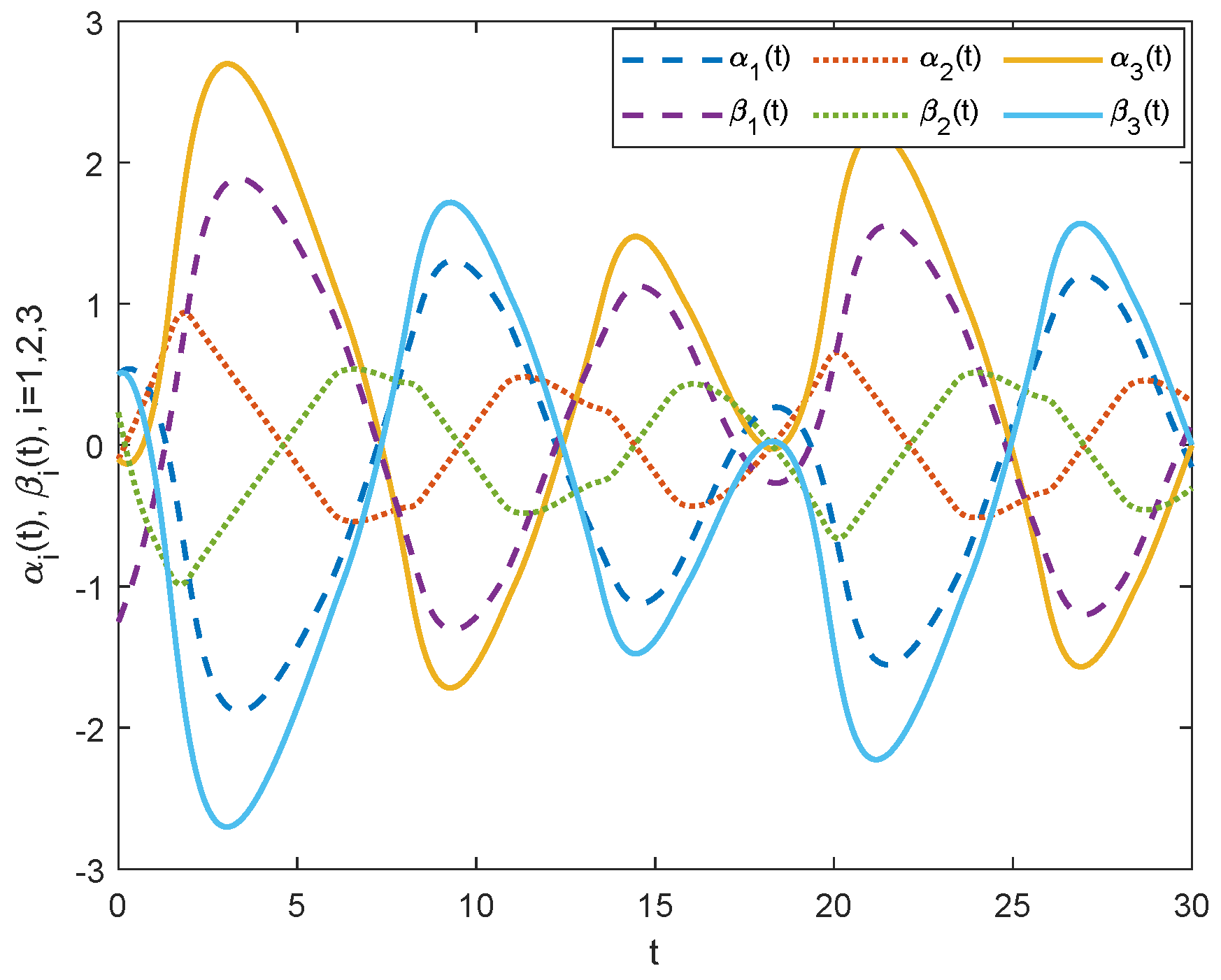
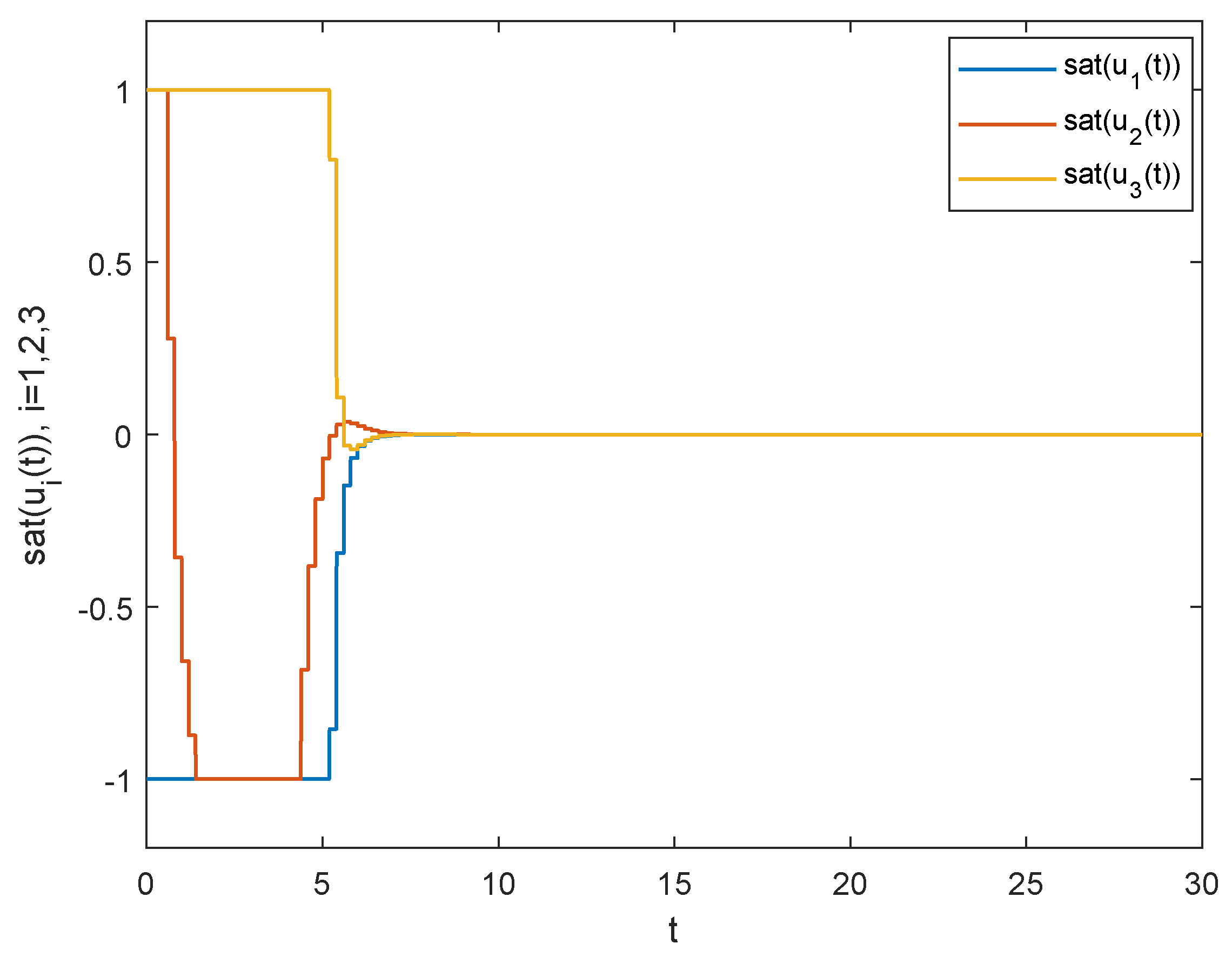
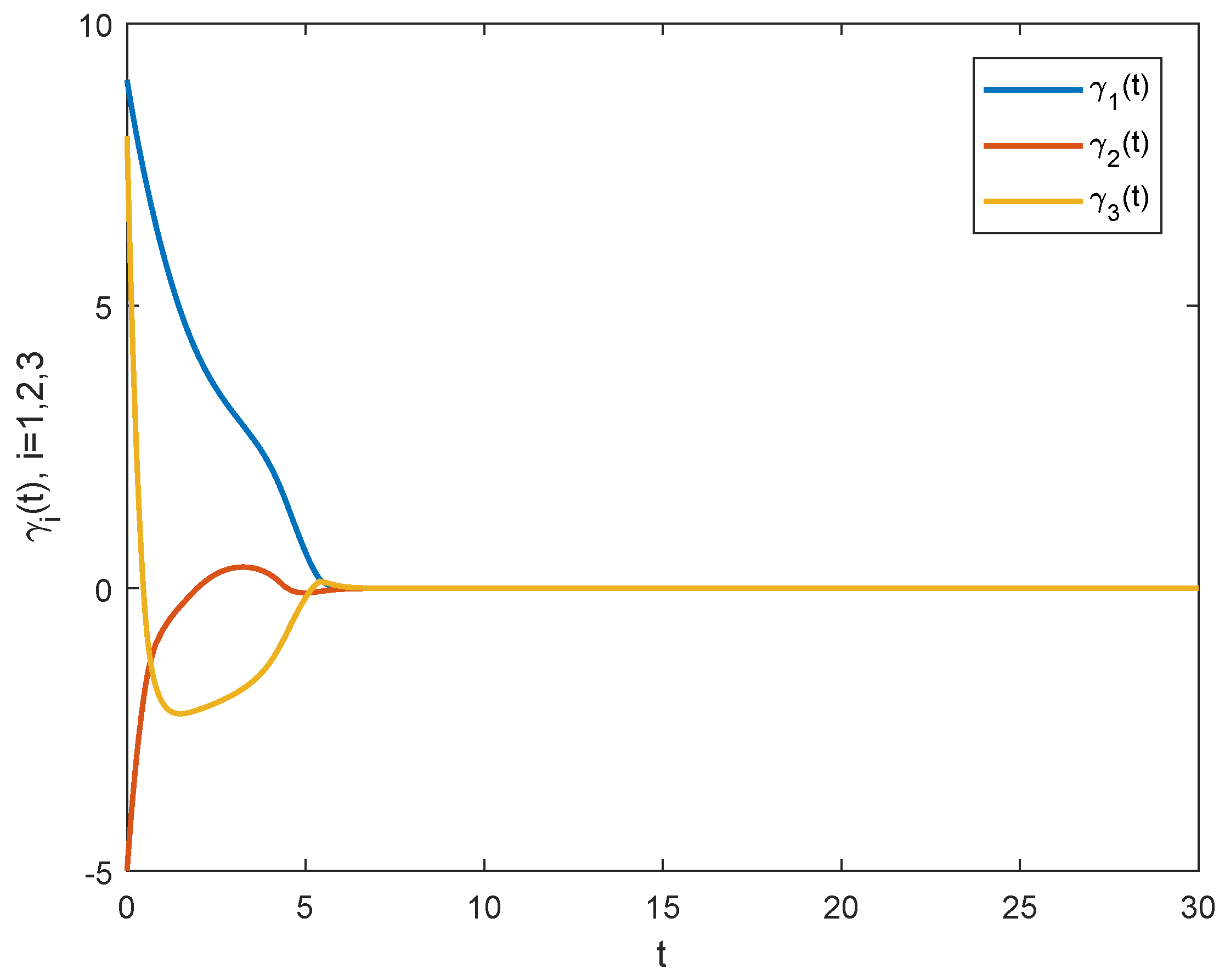
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, J.; Zang, M.; Liu, P.; Wang, Y. A secure communication scheme of three-variable chaotic coupling synchronization based on DNA chemical reaction networks. IEEE Trans. Signal Process. 2022, 70, 2362–2373. [Google Scholar] [CrossRef]
- Kano, T.; Umeno, K. Chaotic synchronization of mutually coupled systems-arbitrary proportional linear relations. Chaos 2022, 32, 113137. [Google Scholar] [CrossRef]
- Jiang, H.; Zhuang, L.; Chen, C.; Wang, Z. Hidden dynamics and hybrid synchronization of fractional-order memristive systems. Axioms 2022, 11, 645. [Google Scholar] [CrossRef]
- Xin, L.; Shi, X.; Xu, M. Dynamical analysis and generalized synchronization of a novel fractional-order hyperchaotic system with hidden attractor. Axioms 2023, 12, 6. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Synchronization of delayed fuzzy neural networks with probabilistic communication delay and its application to image encryption. IEEE Trans. Fuzzy Syst. 2023, 31, 930–940. [Google Scholar] [CrossRef]
- Dong, S.; Liu, X.; Zhong, S.; Shi, K.; Zhu, H. Practical synchronization of neural networks with delayed impulses and external disturbance via hybrid control. Neural Netw. 2023, 157, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Si, X.; Wang, Z.; Fan, Y. Quantized control for finite-time synchronization of delayed fractional-order memristive neural networks: The Gronwall inequality approach. Expert Syst. Appl. 2023, 215, 119310. [Google Scholar] [CrossRef]
- Li, H.L.; Jiang, Y.L.; Wang, Z.L. Anti-synchronization and intermittent anti-synchronization of two identical hyperchaotic Chua systems via impulsive control. Nonlinear Dyn. 2015, 79, 919–925. [Google Scholar] [CrossRef]
- Hou, J.; Huang, Y.; Yang, E. Finite-time anti-synchronization of multi-weighted coupled neural networks with and without coupling delays. Neural Process. Lett. 2019, 50, 2871–2898. [Google Scholar] [CrossRef]
- Shi, J.; Zeng, Z. Anti-synchronization of delayed state-based switched inertial neural networks. IEEE Trans. Cybern. 2021, 51, 2540–2549. [Google Scholar] [CrossRef]
- Sakthivel, R.; Anbuvithya, R.; Mathiyalagan, K.; Ma, Y.K.; Prakash, P. Reliable anti-synchronization conditions for BAM memristive neural networks with different memductance functions. Appl. Math. Comput. 2016, 275, 213–228. [Google Scholar] [CrossRef]
- Yuan, M.; Wang, W.; Luo, X.; Liu, L.; Zhao, W. Finite-time anti-synchronization of memristive stochastic BAM neural networks with probabilistic time-varying delays. Chaos Solitons Fractals 2018, 113, 244–260. [Google Scholar] [CrossRef]
- Min, F.; Luo, A.C. Complex dynamics of projective synchronization of Chua circuits with different scrolls. Int. J. Bifurc. Chaos 2015, 25, 1530016. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Y.; Zhang, X. Modified projective and modified function projective synchronization of a class of real nonlinear systems and a class of complex nonlinear systems. Nonlinear Dyn. 2014, 78, 1755–1764. [Google Scholar] [CrossRef]
- Zhang, W.; Sha, C.; Cao, J.; Wang, G.; Wang, Y. Adaptive quaternion projective synchronization of fractional order delayed neural networks in quaternion field. Appl. Math. Comput. 2021, 400, 126045. [Google Scholar] [CrossRef]
- Gasri, A.; Ouannas, A.; Ojo, K.S.; Pham, V.T. Coexistence of generalized synchronization and inverse generalized synchronization between chaotic and hyperchaotic systems. Nonlinear Anal. Model. Control. 2018, 23, 583–598. [Google Scholar] [CrossRef]
- Wang, D.; Huang, L.; Tang, L.; Zhuang, J. Generalized pinning synchronization of delayed Cohen-Grossberg neural networks with discontinuous activations. Neural Netw. 2018, 104, 80–92. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, W.; Ren, S.; Zheng, Z. Analysis and pinning control for generalized synchronization of delayed coupled neural networks with different dimensional nodes. J. Frankl. Inst. 2018, 355, 5968–5997. [Google Scholar] [CrossRef]
- Shi, K.; Wang, B.; Yang, L.; Jian, S.; Bi, J. Takagi-Sugeno fuzzy generalized predictive control for a class of nonlinear systems. Nonlinear Dyn. 2017, 89, 169–177. [Google Scholar] [CrossRef]
- Califano, C.; Moog, C.H. Accessibility of nonlinear time-delay systems. IEEE Trans. Autom. Control. 2017, 62, 1254–1268. [Google Scholar] [CrossRef]
- Araújo, R.F.; Torres, L.A.; Palhares, R.M. Reinaldo Martine, Distributed control of networked nonlinear systems via interconnected Takagi-Sugeno fuzzy systems with nonlinear consequent. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 4858–4867. [Google Scholar] [CrossRef]
- Wu, Z.G.; Shi, P.; Su, H.; Chu, J. Exponential synchronization of neural networks with discrete and distributed delays under time-varying sampling. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1368–1376. [Google Scholar]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Sampled memory-event-triggered fuzzy load frequency control for wind power systems subject to outliers and transmission delays. IEEE Trans. Cybern. 2022. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.G.; Shi, P.; Su, H.; Chu, J. Sampled-data synchronization of chaotic Lur’e systems with time delays. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 410–421. [Google Scholar] [PubMed]
- Chen, G.; Xia, J.; Park, J.H.; Shen, H.; Zhuang, G. Sampled-data synchronization of stochastic Markovian jump neural networks with time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3829–3841. [Google Scholar] [CrossRef]
- Wang, Z.; He, H.; Jiang, G.P.; Cao, J. Quasi-synchronization in heterogeneous harmonic oscillators with continuous and sampled coupling. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1267–1277. [Google Scholar] [CrossRef]
- Yang, W.; Huang, J.; Wang, X. Fixed-time synchronization of neural networks with parameter uncertainties via quantized intermittent control. Neural Process. Lett. 2022, 54, 2303–2318. [Google Scholar] [CrossRef]
- Sang, H.; Zhao, J. Intermittent pinning synchronization for directed networks with switching technique. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1432–1436. [Google Scholar] [CrossRef]
- Wang, Z.P.; Wu, H.N.; Wang, J.L.; Li, H.X. Quantized sampled-data synchronization of delayed reaction-diffusion neural networks under spatially point measurements. IEEE Trans. Cybern. 2021, 51, 5740–5751. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Yang, S.; Yang, X. Synchronization criteria for neural networks with proportional delays via quantized control. Nonlinear Dyn. 2018, 94, 541–551. [Google Scholar] [CrossRef]
- Li, J.; Jiang, H.; Wang, J.; Hu, C.; Zhang, G. H∞ Exponential synchronization of complex networks: Aperiodic sampled-data-based event-triggered control. IEEE Trans. Cybern. 2022, 52, 7968–7980. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Zhuang, G.; Xia, J.; Wang, Y.; Chen, G. Stochastic admissibility and H∞ output feedback control for singular Markov jump systems under dynamic measurement output event-triggered strategy. Chaos Solitons Fractals 2022, 164, 112635. [Google Scholar] [CrossRef]
- Lv, X.; Cao, J.; Li, X.; Abdel-Aty, M.; Al-Juboori, U.A. Synchronization analysis for complex dynamical networks with coupling delay via event-triggered delayed impulsive control. IEEE Trans. Cybern. 2021, 51, 5269–5278. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. A delay-kernel-dependent approach to saturated control of linear systems with mixed delays. Automatica 2023, 152, 110984. [Google Scholar] [CrossRef]
- Fridman, E. A refined input delay approach to sampled-data control. Automatica 2010, 46, 421–427. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.L.; He, Y. A new looped-functional for stability analysis of sampled-data systems. Automatica 2017, 82, 328–331. [Google Scholar] [CrossRef]
- Seuret, A. A novel stability analysis of linear systems under asynchronous samplings. Automatica 2012, 48, 177–182. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Z.; Huang, X.; Li, Y.; Shen, H.; Chen, G. Aperiodic sampled-data control for exponential stabilization of delayed neural networks: A refined two-sided looped-functional approach. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3217–3221. [Google Scholar] [CrossRef]
- Seuret, A.; Da Silva, J.M.G., Jr. Taking into account period variations and actuator saturation in sampled-data systems. Syst. Control Lett. 2012, 61, 3217–3221. [Google Scholar] [CrossRef]
- Luo, D.; Zhu, Q.; Luo, Z. A novel result on averaging principle of stochastic Hilfer-type fractional system involving non-Lipschitz coefficients. Appl. Math. Lett. 2021, 122, 107549. [Google Scholar] [CrossRef]
- Menz, P.; Mulberry, N.; Guichard, D.; Team, L.L. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences; SFU: Vancouver BC, Canada, 2018. [Google Scholar]
- Liu, A.; Huang, X.; Fan, Y.; Wang, Z. A control-interval-dependent functional for exponential stabilization of neural networks via intermittent sampled-data control. Appl. Math. Comput. 2021, 411, 126494. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Fan, Y. Aperiodic Sampled-Data Control for Anti-Synchronization of Chaotic Nonlinear Systems Subject to Input Saturation. Axioms 2023, 12, 403. https://doi.org/10.3390/axioms12040403
Li M, Fan Y. Aperiodic Sampled-Data Control for Anti-Synchronization of Chaotic Nonlinear Systems Subject to Input Saturation. Axioms. 2023; 12(4):403. https://doi.org/10.3390/axioms12040403
Chicago/Turabian StyleLi, Meixuan, and Yingjie Fan. 2023. "Aperiodic Sampled-Data Control for Anti-Synchronization of Chaotic Nonlinear Systems Subject to Input Saturation" Axioms 12, no. 4: 403. https://doi.org/10.3390/axioms12040403
APA StyleLi, M., & Fan, Y. (2023). Aperiodic Sampled-Data Control for Anti-Synchronization of Chaotic Nonlinear Systems Subject to Input Saturation. Axioms, 12(4), 403. https://doi.org/10.3390/axioms12040403