Abstract
This article investigates the seventh-order Lax’s Korteweg–de Vries equation using the Yang transform decomposition method (YTDM) and the homotopy perturbation transform method (HPTM). The physical phenomena that emerge in physics, engineering and chemistry are mathematically expressed by this equation. For instance, the KdV equation was constructed to represent a wide range of physical processes involving the evolution and interaction of nonlinear waves. In the Caputo sense, the fractional derivative is considered. We employed the Yang transform, the Adomian decomposition method and the homotopy perturbation method to obtain the solution to the time-fractional Lax’s Korteweg–de Vries problem. We examined and compared a particular example with the actual result to verify the approaches. By utilizing these methods, we can construct recurrence relations that represent the solution to the problem that is being proposed, and we are then able to present graphical representations that enable us to visually examine all of the results in the proposed case for different fractional order values. Furthermore, the results of the current approach exhibit a good correlation with the precise solution to the problem being studied. Furthermore, the present study offers an example of error analysis. The numerical outcomes obtained by applying the provided approaches demonstrate that the techniques are easy to use and have superior computational performance.
Keywords:
Yang transform; Caputo operator; time-fractional Lax’s Korteweg–de Vries equation; Adomian decomposition method; homotopy perturbation method MSC:
34A25; 26A33; 35Q53; 35A20
1. Introduction
Researchers have become more interested in fractional calculus (FC) due to the fractional modeling it offers for various natural processes. FC is helpful in illustrating the memory and hereditary properties of numerous events. Fractional differentiation is the expansion of the integer to the non-integer order of differentiation. FC is related to practical efforts and is commonly employed in various fields. This is because fractional calculus is a valuable tool for explaining the dynamic behavior of numerous physical systems. Fractional differential equations (FDEs) are notable for providing memory and transmission qualities for numerous mathematical models [1,2]. The integer order differential operator is commonly considered a local operator, whereas the fractional order differential operator is non-local. This explains how the past and present states of a system influence its future state. This enables fractional calculus to be more useful, which is one of the reasons it is becoming more popular [3,4,5,6]. Fractional differential equations have grown in importance and popularity as a result of their various engineering and scientific applications. For instance, these equations are more frequently employed to explain issues in a variety of physical systems, including quantum physics [7], diffusion processes [8], viscoelasticity and fluid mechanics [9], propagation of complex acoustic oscillations [10], human diseases [11], optics [12], biomathematics [13], chaos theory [14] and many more. In these and other applications, the major benefit of fractional differential equations is their non-locality.
Nonlinear equations are essential for explaining a wide range of events, not just in physics but also in other fields of science and engineering. In order to adequately represent physical processes, a mathematical model involving nonlinear partial differential equations (PDEs) was constructed, because relatively few issues in physics, or in fact in any field of natural science, can be resolved by direct solutions. An overview of the related phenomena is given by the PDE solution’s features. Due to their importance in a wide range of fields, numerous technologies have been implemented to examine the precise and computational solutions of fractional differential equations. Along with modeling, the solutions’ divergence and convergence are equally important. In some cases, it can be very difficult to find analytical solutions to fractional differential equations. This has increased the significance of developing numerical solutions to these issues. There are numerous effective methods in the literature for constructing semi-analytical and computational solutions of fractional differential equations, including the first integral method [15], the extended direct algebraic method [16], the modified Kudryashov method [17], the finite difference method [18], the optimal homotopy asymptotic method (OHAM) [19], the Adomian decomposition method [20], the standard reductive perturbation method [21], the homotopy perturbation transform technique [22,23], the Elzaki transform decomposition method [24], the Haar wavelet method [25], the fractional sub-equation method [26], the differential transform method [27], the Khater method [28] and the variational iteration procedure with transformation [29].
An example of a partial differential equation is the Korteweg–de Vries (KdV) equation, which has been used to explain a variety of physical phenomena as a model for the evolution and interaction of nonlinear waves. It was derived as an evolution equation that governed the propagation of one-dimensional, long, low-amplitude surface gravity waves in a shallow water channel [30]. The KdV equation has now been used in many different branches of physics, including collision-free hydromagnetic waves, stratified internal waves, ion-acoustic waves, plasma physics, and lattice dynamics [31]. Using a KdV model, some hypothetical physical events in the context of quantum mechanics have been expressed. It is used as a model for shock wave propagation, turbulence, solitons, mass transport in fluid dynamics, boundary layer behavior, continuum mechanics and aerodynamics [32]. Hence, in the literature, various finite-difference- [33] and finite-element-based (continuous [34,35,36] and discontinuous [37,38] Galerkin/Petrov–Galerkin) numerical approaches are found to address transport, dispersion, and convection–diffusion problems. The general form of the seventh-order time-fractional Lax’s Korteweg–de Vries equation is given as
where the fractional derivative’s order is indicated by the parameter and the constant parameters are finite and cannot be zero. is a function of the dynamic wave profile of the spatiotemporal patterns that will be eventually derived. The complicated physical processes that arise in physics, biology, engineering and chemistry are mathematically modeled by these equations. Examples include quantum mechanics, plasma physics, the propagation of long waves in shallow water under gravity, fluid mechanics and nonlinear optics. The pseudospectral method [39], variational iteration method [40] and modified Cole–Hopf transformation method [41] are a few of the analytical techniques utilized by numerous scholars to solve the seventh-order Lax’s Korteweg–de Vries equation. The residual power series approach and perturbation iteration algorithm were used in [42] to analyze numerical solutions of the time-fractional Rosenau–Hyman equation, a model that is similar to the KdV model.
The adomian decomposition approach, the homotopy perturbation method (HPM) and the Yang transform (YT) are presented in this paper. The homotopy perturbation method (HPM), developed by Ji-Huan He of Shanghai University, was first used to address nonlinear problems in science and technology in 1998 [43,44]. Many mathematicians used the homotopy perturbation method to solve nonlinear equations that came up in engineering and scientific studies [45,46,47,48]. It is simpler to estimate the series terms using the proposed method than it is using the usual Adomian approach since it does not compute the fractional derivative or fractional integrals in the recursive mechanism. Since YTDM does not require prescribed assumptions, discretization, perturbation and round-off errors are avoided. In the literature, YTDM has been used to solve a wide range of differential equations, including the time-fractional Belousov–Zhabotinskii reaction [49], fractional-order diffusion equations [50] and the time-fractional Fisher equation [51].
The current article is structured as follows: We start with the fundamental idea of fractional calculus in Section 2. We discuss the fundamental concepts of the suggested methods in Section 3 and Section 4. The time-fractional Lax’s Korteweg–de Vries problem is solved using these techniques in Section 5 with the provided initial conditions. Lastly, Section 6 provides the conclusion.
2. Preliminaries
The FC and the Yang transform (YT) are discussed here which will be employed in this framework.
Definition 1.
The fractional derivative Caputo operator is given by [4]
Definition 2.
The YT of the function is given by [52]
where u is the transform variable.
The inverse YT is
Definition 3.
The inverse Yang transform is defined by
Definition 4.
The YT of the fractional derivative function is given by [52]
3. General Implementation of HPTM
Let us assume the general fractional PDE of the form:
with initial guess
where illustrates the Caputo operator, is a linear function and is a nonlinear function.
On taking YT, we obtain
By simplification of the above equation, we have
On taking inverse YT, we have
Now, in terms of HPM
with parameter .
The nonlinear term is taken as
In addition, illustrates He’s polynomial and is written as
where
By inserting (14) and (15) into (12), we obtain
Comparing the coefficients of like powers of yields
Lastly, the HPTM solution in series form is taken as
4. General Implementation of the YTDM
Let us assume the general fractional PDE of the form:
with initial guess
where illustrates the Caputo operator, is a linear function and is a non-linear function.
On taking YT, we obtain
By simplification of the above equation, we have
On taking inverse YT, we have
Now, in terms of the YTDM,
The nonlinear term is taken as
with
By inserting (24) and (26) into (23), we obtain
Comparing both sides of the above equation yields
Lastly, the YTDM general solution for is
5. Application
Example 1.
Let us assume the seventh order TFLK–dV equation with as:
with initial guess
where ρ is an arbitrary constant.
On taking YT, we obtain
By simplification of the above equation, we have
On taking inverse YT, we have
Now, by means of the HPM, the non-linear term is represented by as
Comparing the coefficients of like powers of ϵ yields
Lastly, the HPTM solution in series form is taken as
The YTDM for solving the TFLK–dV equation
On taking YT, we obtain
By simplification of the above equation, we have
On taking inverse YT, we have
Now, in terms of the ADM,
The nonlinear term is taken as
Thus, we obtain
Comparing both sides of the above equation yields
On :
On :
Lastly, the YTDM solution for is easy to obtain as
By inserting we have
6. Numerical Simulation Studies
This section offers the approximate analytical solution to the mathematical equation . The numerical results show the method’s applicability, and its accuracy is evaluated in the context of exact results. The implementation of our approach gives outcomes with good performance and simplicity. The actual solution plot is depicted in Figure 1a, whereas the suggested approaches solution plot of is depicted in Figure 1b. The graphical representations of for and are shown in Figure 2a,b. Similarly, Figure 3a,b shows the plots of for and 1, while Figure 4 shows the behavior of absolute error for the same equation generated using both techniques. The approximate solution to the equation is provided in Table 1 for different values of and , while the absolute error comparison is shown in Table 2 for different values of and . It should be noted that we used third-order approximate solutions throughout the calculations and that we obtained a good approximation of the exact solutions for the addressed problem. Better approximation solutions would have been found if we increased the order of the approximation, which would increase the number of terms in the solution.
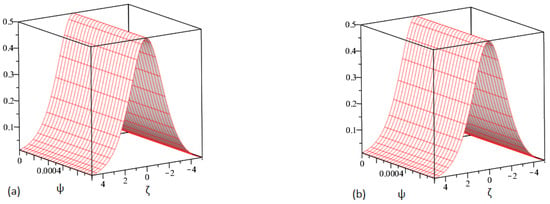
Figure 1.
Graphical depiction of our techniques and the accurate solution.
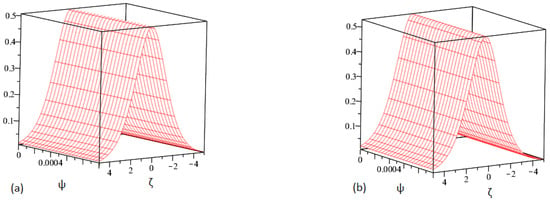
Figure 2.
Graphical depiction of our techniques solution at and .
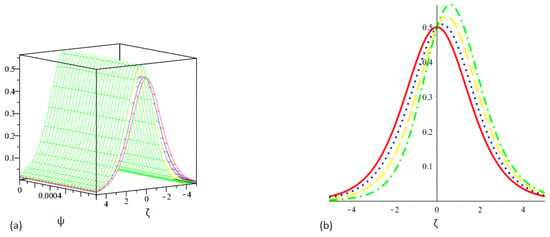
Figure 3.
Graphical depiction of our techniques solution for various values of .
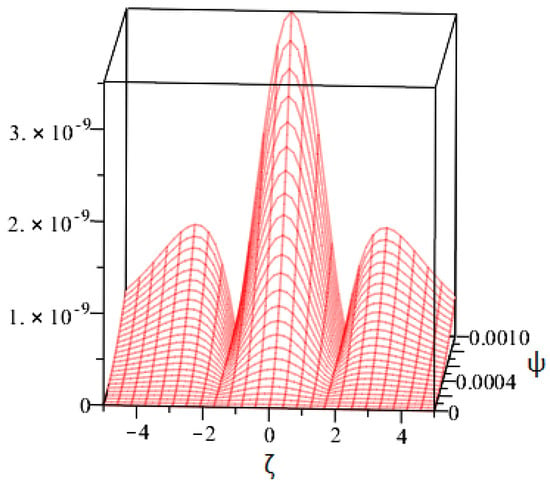
Figure 4.
Graphical depiction our techniques solution in terms of error.

Table 1.
Exact and approximate solutions of the TFLK–dV equation at different values of .

Table 2.
Absolute error comparison of our techniques at different values of .
7. Conclusions
This article uses Lax’s Korteweg–de Vries equation using the Yang transform and the Caputo derivative. The YTDM and the HPTM are methods that combine the Yang transform, decomposition and perturbation. A numerical example shows the efficacy and precision of the presented approaches. To explain the theoretical perspective and visualize dynamic behavior, two-dimensional and three-dimensional graphical representations of particular solutions are given. We gave the error estimate in terms of absolute error, shown in Table 2, to demonstrate the applicability and consistency of the two approaches utilized in this current work. The approaches utilized are very effectively explained by the tables and plots, which are comparable with the exact solution in the standard situation when . Finally, multidimensional problems, variable-order nonlinear fractional differential equations and many other problems can be successfully resolved by combining the methodologies that have been considered with the fractional operator.
Author Contributions
Conceptualization, N.K.M., M.M.A., A.K. and A.H.G.; methodology, N.K.M., M.M.A., A.K. and A.H.G.; software, A.K.; validation, N.K.M., M.M.A., A.K. and A.H.G.; formal analysis, A.K.; investigation, A.K.; resources, N.K.M., M.M.A., A.K. and A.H.G.; data curation, A.K. and A.H.G.; writing—original draft preparation, A.K.; writing—review and editing, A.K.; visualization, A.K. and A.H.G.; supervision, A.K. and A.H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The numerical data used to support the findings of this study are included within the article.
Acknowledgments
The authors are pleased to the reviewers for their meticulous reading and suggestions which improved the presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goyal, M.; Baskonus, H.M.; Prakash, A. An efficient technique for a time fractional model of lassa hemorrhagic fever spreading in pregnant women. Eur. Phys. J. Plus 2019, 134, 482. [Google Scholar] [CrossRef]
- Alaoui, K.M.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical investigation of fractional-order Cahn-Hilliard and gardner equations using two novel techniques. Mathematics 2022, 10, 1643. [Google Scholar] [CrossRef]
- Ganie, A.H. New Bounds For Variables of Fractional Order. Pak. J. Stat. 2022, 38, 211–218. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific Publishing Company: Singapore; Hackensack, NJ, USA; Hong Kong, China, 2000; pp. 87–130. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Chen, W. An Intuitive Study of Fractional Derivative Modeling and Fractional Quantum in Soft Matter. J. Vib. Control 2008, 14, 1651–1657. [Google Scholar] [CrossRef]
- Acioli, P.S.; Xavier, F.A.; Moreira, D.M. Mathematical Model Using Fractional Derivatives Applied to the Dispersion of Pollutants in the Planetary Boundary Layer. Bound.-Layer Meteorol. 2019, 170, 285–304. [Google Scholar] [CrossRef]
- Jamil, B.; Anwar, M.S.; Rasheed, A.; Irfan, M. MHD Maxwell flow modeled by fractional derivatives with chemical reaction and thermal radiation. Chin. J. Phys. 2020, 67, 512–533. [Google Scholar] [CrossRef]
- Fellah, M.; Fellah, Z.E.A.; Mitri, F.; Ogam, E.; Depollier, C. Transient ultrasound propagation in porous media using Biot theory and fractional calculus: Application to human cancellous bone. J. Acoust. Soc. Am. 2013, 133, 1867–1881. [Google Scholar] [CrossRef]
- Yadav, R.P.; Verma, R. A numerical simulation of fractional order mathematical modeling of COVID-19 disease in case of Wuhan China. Chaos Solitons Fractals 2020, 140, 110124. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.B.; Tenreiro Machado, J.A. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2010. [Google Scholar]
- Baleanu, D.; Wu, G.-C.; Zeng, S.-D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Eslami, M.; Vajargah, B.F.; Mirzazadeh, M.; Biswas, A. Application of first integral method to fractional partial differential equations. Indian J. Phys. 2014, 88, 177–184. [Google Scholar] [CrossRef]
- Younis, M.; Iftikhar, M. Computational examples of a class of fractional order nonlinear evolution equations using modified extended direct algebraic method. J. Comput. Methods 2015, 15, 359–365. [Google Scholar] [CrossRef]
- Gaber, A.A.; Aljohani, A.F.; Ebaid, A.; Machado, J.T. The generalized Kudryashov method for nonlinear space-time fractional partial differential equations of Burgers type. Nonlinear Dyn. 2019, 95, 361–368. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Sarwar, S.; Alkhalaf, S.; Iqbal, S.; Zahid, M.A. A note on optimal homotopy asymptotic method for the solutions of fractional order heat-and wave-like partial differential equations. Comput. Math. Appl. 2015, 70, 942–953. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Elhanbaly, A.; Abdou, M.A. Adomian decomposition method for solving fractional nonlinear differential equations. Appl. Math. Comput. 2006, 182, 313–324. [Google Scholar] [CrossRef]
- Uddin, M.F.; Hafez, M.G.; Hwang, I.; Park, C. Effect of Space Fractional Parameter on Nonlinear Ion Acoustic Shock Wave Excitation in an Unmagnetized Relativistic Plasma. Front. Phys. 2022, 9, 766035. [Google Scholar] [CrossRef]
- Mishra, N.K.; AlBaidani, M.M.; Khan, A.; Ganie, A.H. Numerical Investigation of Time-Fractional Phi-Four Equation via Novel Transform. Symmetry 2023, 15, 687. [Google Scholar] [CrossRef]
- Fathima, D.; Alahmadi, R.A.; Khan, A.; Akhter, A.; Ganie, A.H. An Efficient Analytical Approach to Investigate Fractional Caudrey-Dodd-Gibbon Equations with Non-Singular Kernel Derivatives. Symmetry 2023, 15, 850. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Wang, L.; Ma, Y.; Meng, Z. Haar wavelet method for solving fractional partial differential equations numerically. Appl. Math. Comput. 2014, 227, 66–76. [Google Scholar] [CrossRef]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194–199. [Google Scholar] [CrossRef]
- Ali, U.; Naeem, M.; Alahmadi, R.; Abdullah, F.A.; Khan, M.A.; Ganie, A.H. An investigation of a closed-form solution for non-linear variable-order fractional evolution equations via the fractional Caputo derivative. Front. Phys. 2023, 11, 73. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana-Baleanu-Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Fung, M.K. KdV equation as an Euler–Poincare equation. Chin. J. Phys. 1997, 35, 789–796. [Google Scholar]
- Elwakil, S.A.; Abulwafa, E.M.; Zahran, M.A.; Mahmoud, A.A. Time-fractional KdV equation: Formulation and solution using variational methods. Nonlinear Dyn. 2011, 65, 55–63. [Google Scholar] [CrossRef]
- Sukhinov, A. The Construction and Research of the Modified Upwind Leapfrog Difference Scheme with Improved Dispersion Properties for the Korteweg-de Vries Equation. Mathematics 2022, 10, 2922. [Google Scholar] [CrossRef]
- Salnikov, N.N. On construction of finite-dimensional mathematical model of convection-diffusion process with usage of the PetrovGalerkin method. J. Autom. Inf. Sci. 2010, 42, 67–83. [Google Scholar] [CrossRef]
- Salnikov, N.N. Analysis of lumped approximations in the finite-element method for convection-diffusion problems. Cybern. Syst. Anal. 2013, 49, 774–784. [Google Scholar]
- Siryk, S.V.; Salnikov, N.N. Numerical solution of Burgers equation by Petrov-Galerkin method with adaptive weighting functions. J. Autom. Inf. Sci. 2012, 44, 50–67. [Google Scholar] [CrossRef]
- Kashkool, H.A. Space-Time Petrov-Discontinuous Galerkin Finite Element Method for Solving Linear Convection-Diffusion Problems. J. Phys. Conf. Ser. 2022, 2322, 012007. [Google Scholar]
- Kashkool, H.A. hp-discontinuous Galerkin Finite Element Method for Incompressible Miscible Displacement in Porous Media. J. Phys. Conf. Ser. 2020, 1530, 012001. [Google Scholar] [CrossRef]
- Akinyemi, L. q-Homotopy analysis method for solving the seventh-order time-fractional Lax’s Korteweg-de Vries and Sawada-Kotera equations. Comput. Appl. Math. 2019, 38, 191. [Google Scholar] [CrossRef]
- Soliman, A.A. A numerical simulation and explicit solutions of KdV-Burgers and Lax’s seventh-order KdV equations. Chaos Solitons Fractals 2006, 29, 294–302. [Google Scholar] [CrossRef]
- Salas, A.H.; Gómez, S.; Cesar, A. Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation. Math. Probl. Eng. 2010, 2010, 194329. [Google Scholar] [CrossRef]
- Senol, M.; Tasbozan, O.; Kurt, A. Comparison of two reliable methods to solve fractional Rosenau-Hyman equation. Math. Methods Appl. Sci. 2021, 44, 7904–7914. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Compt. Meth. Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A new perturbation technique which is also valid for large parameters. J. Sound Vib. 2000, 229, 1257–1263. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ganji, D.D.; Dinarvand, S. Explicit analytical solutions of the generalized Burger and Burger-Fisher equations by homotopy perturbation method. Numer. Meth. 2009, 25, 409–417. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ganji, D.D. Homotopy Perturbation Combined with Padé Approximation for Solving Two Dimensional Viscous Flow in the Extrusion Process. Int. J. Nonlinear Sci. 2009, 7, 387–394. [Google Scholar]
- Yildirim, A. An algorithm for solving the fractional nonlinear Schrödinger equation by means of the homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 445–451. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, O.P. Numerical Inversion of the Abel Integral Equation using Homotopy Perturbation Method. Z. Naturforschung 2010, 65, 677–682. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).