Abstract
In this study, we analyzed the inertia effect on the axisymmetric squeeze flow of slightly viscoelastic fluid film between two disks. A system of nonlinear partial differential equations (PDEs) in cylindrical coordinates, along with nonhomogenous boundary conditions, illustrates the phenomenon of fluid flow caused by squeezing with the inertia effect. The Langlois recursive approach was applied to obtain the analytical solution of the system having a stream function, axial and radial velocities, pressure distribution, normal and tangential stresses and normal squeeze force. These flow variables are also portrayed graphically to describe the effects of the Reynolds number and slightly viscoelastic parameter. The results show that by increasing the Reynolds number, the velocity profile decreases, and both the pressure distribution and shear stresses increase. Moreover, there is a small increase in normal squeeze force. When the slightly viscoelastic parameter approaches zero, the obtained solution of flow variables matches with the classical results. This study can be applied to understand the mechanism of load-bearing features in thrust bearings and in arthrodial human joint (knee and hip) diseases.
Keywords:
inertia effect; Langlois recursive approach; axisymmetric squeeze flow; slightly viscoelastic fluid; Reynolds number MSC:
76A10
1. Introduction
The applications of squeeze flow are discussed in various fields of science and engineering, including lubrication in thrust bearings, knee and hip joints, food texture, the compress molding process of polymers, journal bearings, motors, the processing of dampers [1,2,3] and so on. In addition, squeezing flow is used to examine the rheological behavior of non-Newtonian (soft materials and complex) fluids [4,5,6]. Bubble boundaries grow biaxially and thin out during the evolution of foams, acting much like squeezing films. The elastohydrodynamic lubrication theory states that the squeezing effect is crucial in preserving the unstable film thickness during the walking cycle [7].
Various researchers have examined the hydrodynamics of viscous and power-law fluid films between two disks in relative motion since the 19th century [8,9,10]. Later, Jackson [11], Kuzma [12] and Hamza and MacDonald [13] investigated the numerical and perturbation solution of the squeezing flow of viscous fluid with an inertia effect. In the last few years, most researchers [14,15,16,17,18] have explored the analytical and semi-analytical solutions for the steady and unsteady squeezing flow of viscous fluid with a slip boundary in a porous medium. The solution of the velocity components was determined—but not estimated—by the analytical expressions of pressure distribution and squeeze force.
However, researchers are quite interested in studying viscoelastic fluids. As a large number of biological and industrial fluids are non-Newtonian fluids, the Navier–Stokes theory is insufficient to elaborate on the intricate viscoelastic features of these fluids. The constitutive equations of viscoelastic fluids are significantly classified into integral, differential and rate-type fluids. At the end of the 19th century, researchers found asymptotic and numerical solutions for the squeeze flow of rate-type fluids. Phan Thein et al. [19,20,21] presented the asymptotic and numerical solution for the squeeze flow of rate-type Maxwell and Oldroyd-B fluids with and without the inertia effect, respectively. These studies illustrated that less squeeze force is required to compress the shear-thinning viscoelastic fluid than the Newtonian fluid between two disks. Recently, Muhammad et al. [22] worked on the axisymmetric squeeze flow of slightly viscoelastic fluid film using a recursive approach, which is the special class of the differential type of third-grade fluid. Hayat et al. [23] examined the analytical solution for the squeeze flow of third-grade fluid with convective conditions. Anum et al. [24] investigated the analytical solution for the axisymmetric squeezing flow of third-grade fluid in presence of the Cattaneo–Christov theory. Azlina explored the influences of the chemical reaction and viscous dissipation on the MHD squeezing flow of Casson nanofluid in a horizontal channel with slip condition. Azlina discussed the effects of a chemical reaction on the magneto-hydrodynamic (MHD) squeeze flow of Casson fluid in a porous medium under slip conditions with viscous dissipation [25,26,27]. Shankar and Naduvinamani numerically simulated features of the Cattaneo–Christov heat and mass fluxes in an unsteady two-dimensional squeeze flow of a magnetohydrodynamic (MHD) Casson fluid between two parallel plates with radiation and Joule dissipation effects under the impact of time-dependent homogenous first-order chemical reactions [28]. Chemical reactions and viscous dissipation on the hydromagnetic squeeze flow of Jeffrey fluid across two plates over a porous medium in slip conditions with the effects of heat generation, absorption, thermal radiation and chemical reaction were examined by Azlina [29,30,31,32] using the Keller–Box technique. Hameedullah et al. [33,34] examined the analytical result of the creeping flow of slightly viscoelastic fluid through a porous slit with constant reabsorption using the recursive approach. There is a crucial need to examine the slightly viscoelastic fluid film that is squeezed between two disks in the presence of the inertia effect.
The governing equations of the flow are a highly nonlinear system of partial differential equations with nonhomogeneous boundary conditions. The analytical and numerical solutions of these equations are puzzling task for the researchers. Therefore, the main thought of this research is to analyze the impact of inertia on the squeezed flow of slightly viscoelastic fluid film between the surfaces of two disks. In this regard, the recursive technique of Langlois [35,36] is applied to determine the analytical solution. Langlois is also applied for computing the solution of the creeping flow of viscoelastic fluid in the absence of inertia. This approach is extended to find the solution of the highly nonlinear two-dimensional governing equation along the inertia effect in cylindrical coordinates. This is a step forward in research. The impact of the Reynolds number and the slightly viscoelastic parameter on the achieved analytical expressions of velocity components, pressure distribution, shear stress and squeeze force are illustrated graphically.
2. Mathematical Formulation
In this study, the quasi-steady axisymmetric flow of slightly viscoelastic fluid film with constant density and viscosity squeezed between two circular disks of radius is assumed, and its geometry is illustrated in Figure 1. The fluid film thickness between two disks is taken as , and both disks move towards each other with constant velocity . The cylindrical coordinates are used to study the dynamics of the fluid because the fluid contains velocities in both radial and axial directions. The origin of the coordinate system is considered at the center of the channel. There is symmetry in the z-axis.
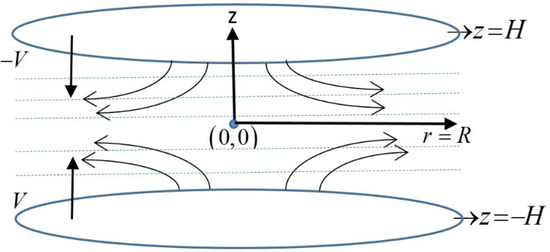
Figure 1.
Geometry of the squeeze flow when both disks approach each other.
The velocity vector for axisymmetric flow is considered in Equation (1).
where and represent the radial and axial components of the velocity, respectively.
The following governing equations of the motion for incompressible slightly viscoelastic fluid [22,37] in the absence of body force are considered.
Here and denote the velocity vector, constant fluid density, pressure distribution, Cauchy stress tensor, material time derivative, viscosity, identity tensor, material constant, first Rivlin–Erickson tensor and trace of the tensor, respectively.
The governing equations of flow have been expressed in component form [22] by Equation (1) as follows:
where . The four nonzero stress components are defined in Equation (9).
The above equations are solved together with appropriate boundary conditions. The boundary conditions due to the symmetry of the axisymmetric flow at the center plane and the no-slip condition on both disks are given as
where is a dimensionless number and shows the small perturbation in flow properties of the viscoelastic fluid model; is the velocity of both disks and is symbolically defined as .
3. Analytical Solution of Flow Variables
The Langlois recursive approach [36] is applied for the solution of the couple system of nonlinear PDEs (6)–(9) subject to nonhomogeneous boundary conditions (10)–(11). The following solutions of the flow variables are assumed.
where is a small dimensionless number. Substituting the Equations (12)–(15) in Equations (6)–(11) and comparing the coefficients of the same order ‘’, we have the following three problems:
First-order problem:
Subject to the boundary conditions
Second-order problem:
Subject to conditions
Third-order problem:
Subject to the boundary conditions
3.1. Solution of Stream Function and Velocity Profile
The solution of the first-order problem of Equations (16)–(19) corresponding to boundary conditions (20) is obtained by reducing the equations in terms of stream function. By using the relation of stream function and velocity , Equation (16) is satisfied identically and excluding the pressure from Equations (17)–(18) by the cross-differentiation acquired as follows.
Subject to conditions
where , . The solution of Equation (31) is subjected to the boundary conditions of Equation (32), and is assumed as . Using this assumption in Equations (31) and (32), the following solution is obtained:
Invoking Equation (33) in the assumption of stream function, the expressions of stream function and radial and axial velocity for the first-order problem are found as follows:
It is noticed that first-order velocity components (35)–(36) are identical to the result of the squeeze flow of Newtonian fluid between two disks [38].
The governing equations of the second-order problem (21)–(25) are reduced by substituting the first-order solution and then transforming it into a stream function using the relation and eliminating the pressure, which is obtained in the following form:
Subject to conditions
where represents the Reynolds number. According to the aspect of Equations (37) and (38), the stream function is considered, and substituting in Equations (37) and (38) obtains the following boundary value problem:
Corresponding to conditions
Thus, the following is the interpreted solution of Equation (39) with the boundary condition (40).
Inserting Equation (41) into the assumed solution of stream function, the solution of the stream function and velocity components for the second-order approximation is found as
The second-order solution contributes in terms of the Reynolds number.
Here, we are computing the solution of the third-order problem (26)–(28) corresponding to homogeneous boundary conditions (30) for the velocity field. Putting the first- and second-order solution into Equations (26)–(28), the resulting equations are transformed into the stream function by the relation , and eliminating the resulting pressure, one can reach the following form:
Subject to conditions
The inverse solution [39] of Equation (45) with boundary conditions (46) is obtained by considering the stream function . Using this assumption in Equations (45) and (46) and equating the leading terms of , we found the following boundary value problems.
Subject to conditions
Solving the boundary value problems (47)–(50), we achieved the following solution:
Using Equations (51) and (52) in the assumed solution of the stream function, we obtain the following third-order approximation of the stream function and velocity components:
It is noted that the Reynolds number and viscoelastic parameter are present in the third-order approximation solution of the velocity profile and stream function. Ultimately, the outcomes of the velocity components and stream function up to third-order approximation are achieved by consolidating the first-, second- and third-order solutions.
3.2. Pressure Distribution
This section contains the computed pressure distribution on each order. Initially, the first-order pressure equations are formulated by corresponding Equations (35)–(36) into Equations (17) and (18).
The following solution of first-order pressure distribution is obtained by integrating Equation (56) over and then differentiating with respect to .
The equations of pressure distribution for second-order approximation are given by adding the solution of velocity components (43) and (44) in Equations (22) and (23).
Similarly, the pressure distribution for second-order approximation is achieved by determining the solution of Equations (61) and (62)
The required equations of pressure distribution for third-order approximation are found by implementing the solution of velocity components (54) and (55) in Equations (27) and (28).
Consequently, the pressure distribution for third-order approximation is obtained by formulating the solution of Equations (64) and (65).
Moreover, by combining the solution of all three estimated orders, (58), (61) and (64), the pressure distribution is obtained:
where . The integral constant is found by the zero normal stress at ; however, the expression is dependent on . Therefore, by following Lee [38], the average boundary condition is used.
Substituting the result of Equation (9) in Equation (68), after simplification, we found
Putting the value of in Equation (67) the pressure distribution correct to the third-order approximation is
3.3. Tangential and Normal Stresses
The analytical expressions for tangential and normal stresses correct to third-order approximations are obtained by substituting the solution of the velocity components and pressure distribution of all orders in Equation (9).
Here, it is clear that the second-order shear and normal stresses have no impact on the slightly viscoelastic term , but there is the influence of the Reynolds number due to inertial forces. The third-order shear and normal stresses are highly contributed by the slightly viscoelastic parameter .
3.4. Normal Force on the Upper Disk
The squeeze force applied to the circular disks for compressing the viscoelastic material between them is the crucial factor in squeeze flow with constant velocity. The total force at the upper disk is evaluated by integrating the negative for the normal axial stress over the disk surface. Therefore, it is expressed mathematically as
By inserting Equation (72) in Equation (74), the following result is obtained.
For the viscoelastic parameter , the proposed results given in Equations (56), (57), (70) and (75) of axial and radial velocities, pressure and squeeze force are verified with the result of Ghori [40]. The outcomes of the flow variables for and are coherent with Lee et al.’s findings [38].
3.5. Fluid Film Thickness
For a deeper understanding of the squeezing process, it is necessary to determine the evolution of the film thickness based on the mechanical system dynamics. An equation of motion for the upper disk is written in dimensionless form as follows:
subject to initial conditions with
where is the mass of the upper disk, and is the gravity acceleration.
The numerical solution of film thickness is evaluated by the computational tool of the Maple ODE analyzer. The following values of the parameters are considered for the numerical solution of Equation (76).
The following Figure 2 illustrates the solution of fluid film thickness .
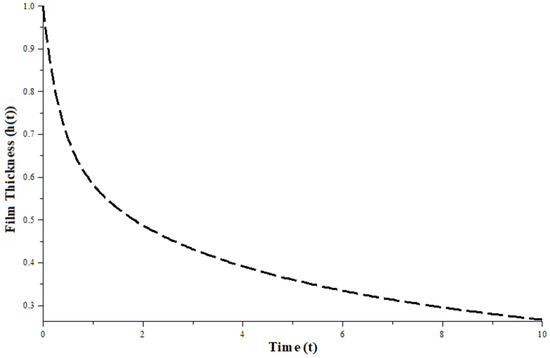
Figure 2.
Film thickness.
4. Results and Discussion
The Langlois recursive approach is successfully used to find the analytical solution for the squeezing flow of slightly viscoelastic fluid films between two disks, including the inertia effect. The dimensionless variables (76) are used to determine the effect of the slightly viscoelastic parameter and the Reynolds number on the given variables, such as velocity components, pressure distribution, normal shear stress and normal squeezing force as follows:
Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 were produced using the mathematically based program Mathematica, and portray the nondimensional flow variables for various values of pertinent parameters without the use of asterisks. The outcomes of the radial velocity by the Langlois recursive approach of viscous fluid at distinct Reynolds number values are compared with the homotopy perturbation method in Figure 3. It is clear that the outcomes of both methods agree with each other.
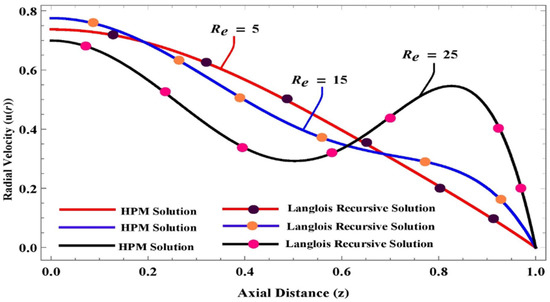
Figure 3.
Comparison between homotopy perturbation method (HPM) [40] and Langlois recursive solutions for viscous fluid at different Reynolds number values.
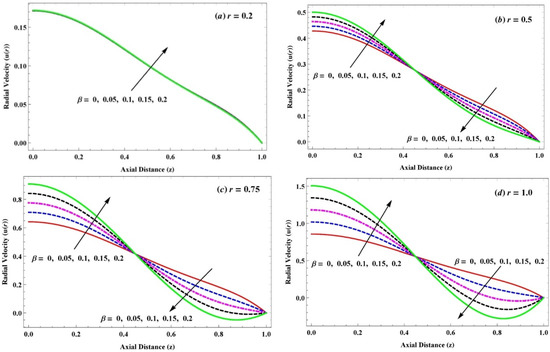
Figure 4.
(a–d) Variation in radial velocity due to slightly viscoelastic parameter when for .
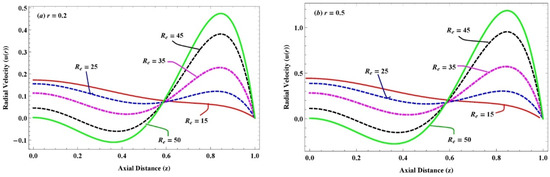
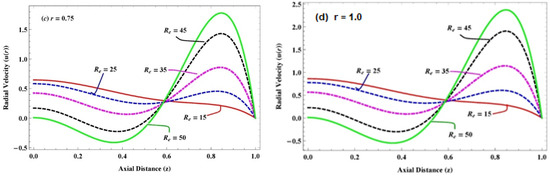
Figure 5.
(a–d) Variation in radial velocity due to Reynolds number when and for .
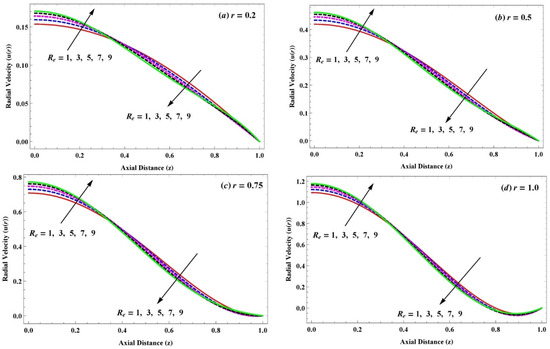
Figure 6.
(a–d) Variation in radial velocity due to small Reynolds number when and for .
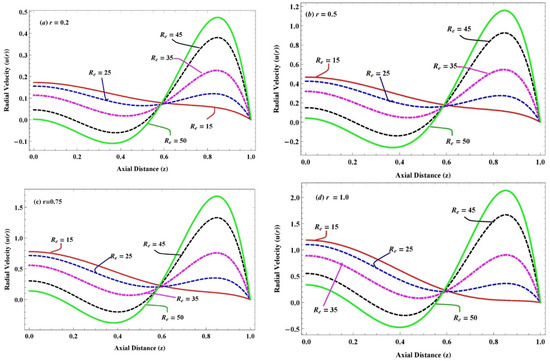
Figure 7.
(a–d) Variation in radial velocity due to large Reynolds number when and for .
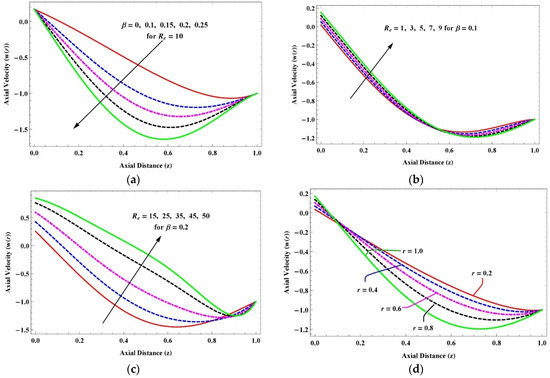
Figure 8.
(a–d) Variation in axial velocity due to (a) rise in with ; (b) rise with small ; (c) rise with large ; (d) variation in radial points with .
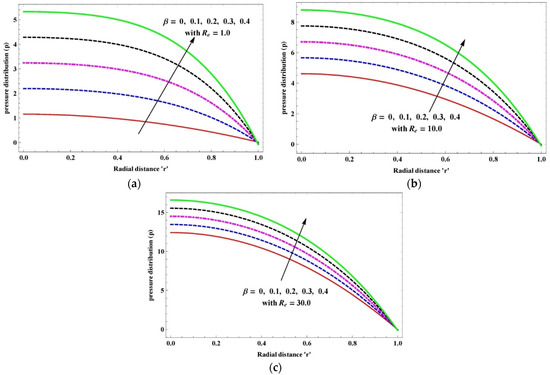
Figure 9.
(a–c) Variation in pressure distribution due to slightly viscoelastic parameter when (a) (b) (c) .
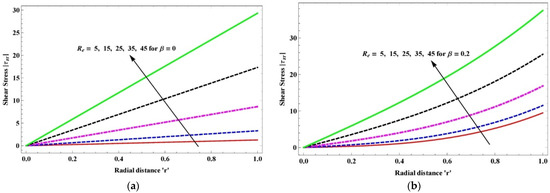
Figure 10.
(a,b) Variation in wall absolute shear stress due to Reynolds number for (a) viscous fluid; (b) slightly viscoelastic fluid.
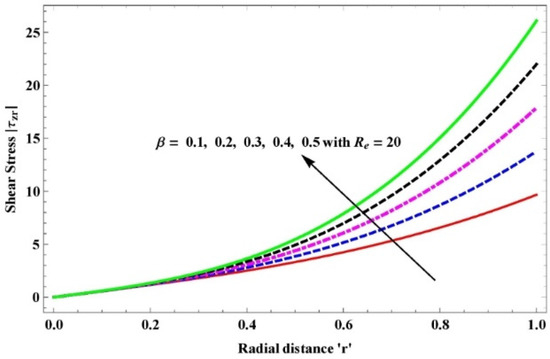
Figure 11.
Variation in wall absolute shear stress due to the slightly viscoelastic parameter in the presence of .
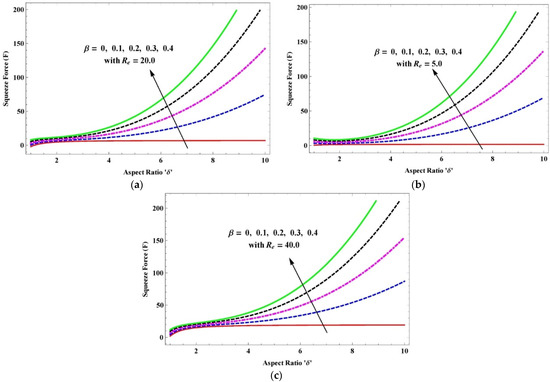
Figure 12.
(a–c) Variation in squeeze force at upper disk due to slightly viscoelastic parameter when (a) ; (b) ; (c) .
Figure 4a–c demonstrates the influence of a slightly viscoelastic parameter through the inertia effect on the radial velocity at different values. The radial velocity is identical near the center of the channel for different values of . The radial velocity on the rise of is increased at the center line of the channel in the radial direction and it diminished in the vicinity of the upper disk. The radial velocity sharpens when the disks approach each other; further, the decline in the velocity is due to the thickness of the material, and this signifies the behavior of the shear-thickening fluid. In addition, the backward flow arises in the presence of the inertia effect from at the edges of the channel, and cross-flow is seen in the middle of the channel .
The impact of large Reynolds numbers (from 10 to 50) on radial velocity of the slightly viscoelastic and Newtonian fluid at distinct radial points is illustrated in Figure 4 and Figure 6. Therefore, it is noticed from the figures that the radial velocities of both fluids accelerate near the edges of the channel on the surging in Reynolds number, but it declines around the central region of the channel. Moreover, it is observed that boundary layer thickness decreases in Newtonian fluid as compared to slightly viscoelastic fluid, and the backward flow is initiated from the Reynolds numbers . In contrast, the reverse behavior (boundary layer thickness is increasing) appears for the effect of small Reynolds numbers (from 1 to 10) on the radial velocity, as shown in Figure 6a–d, while a similar pattern of the velocity profile on the rise of the Reynolds number is validated by the work of Anum Shafiq [24].
Figure 8a–d reveals the effects of the slightly viscoelastic parameter , Reynolds numbers and radial points , respectively, on the axial velocity. The value of the velocity is negative in the graph, which interprets the flow as moving in a downward direction. The magnitude of the axial velocity with the effect of inertia amplifies with surges in , but the boundary layer thickness drops. Moreover, the axial velocity of the slightly viscoelastic fluid with a fixed value of increases in the radial direction, and the magnitude of the axial velocity diminishes due to the increment in Reynolds number for large and small values. The backward flow in axial velocity is initiated from .
Figure 9a–c demonstrates the influence of the various Reynolds numbers with variation in the slightly viscoelastic parameter on the pressure distribution. The pressure distribution escalates with variation in the slightly viscoelastic parameter, and it greatly surges when increases. It is observed that the escalation in pressure indicates the thickness of the fluid; this fluid is mostly called shear-thickening fluid.
The effects of inertia on the wall tangential shear stress for viscous and slightly viscoelastic fluids are shown in Figure 10a,b. It is observed that tangential shear stress increases the viscoelastic fluid slightly more than the viscous fluid under the increment in Reynolds number and the maximum value occurs on the edges. Further, the tangential shear stress for viscous fluid and slightly viscoelastic fluid extends linearly and nonlinearly with the increase in Reynolds number along the radial direction, respectively. This is in nice consensus with Newton’s law of viscosity. Figure 10 illustrates the change in shear stress due to the variation in along at . Tangential shear stress extends accordingly with the rise in ; this is the behavior of shear-thickening fluid.
The change in squeeze force is exemplified in Figure 12a–c due to the slightly viscoelastic parameter along (a) (b) (c) . The squeeze force surges because of the increment in B with the inertia effect, but it has a slight increase with the variation in Reynolds number. The increment in increases the thickness of the fluid, so it requires more force to squeeze the slightly viscoelastic fluid. Thus, the fluid behavior indicates the shear-thickening fluid.
5. Conclusions
The impact of inertia on the axisymmetric squeezing flow of a slightly viscoelastic fluid film between two disks was analyzed by an analytical study. The mathematical model consists of a highly nonlinear system of PDEs in cylindrical coordinates, and its analytical solution was achieved by using the Langlois recursive approach. All possible expressions of flow variables were obtained, and the impact of the Reynolds number and the slightly viscoelastic parameter are graphically illustrated by transforming them into dimensionless variables in axial and radial directions. The following are the concluded remarks:
- The result of the radial velocity in the absence of the slightly viscoelastic parameter by the Langlois recursive approach was compared with the squeeze flow of viscous fluid by the homotopy perturbation method [40]. An excellent consensus was observed between the results.
- The flow variables at have identical results with the creeping squeeze flow of viscous fluid [38].
- The radial velocity on the values of surges at the center line of the channel with the radial direction and decreases in the vicinity of the upper disk. The backward flow initiated from on the edges due to the inertia effect.
- The radial velocity accelerates with the maximum value near the edges, and it reduces around the center of the channel due to the rise in Reynolds number.
- The shear-thickening and -thinning behavior of the slightly viscoelastic fluid are observed in the center region of the channel and the vicinity of the upper disk, respectively.
- The magnitude of axial velocity increases with the rise of and it also increases towards the radial direction.
- A reduction in the magnitude of axial velocity for the slightly viscoelastic fluid is seen due to the rising value of the Reynolds number .
- An increasing trend is seen in the pressure distribution when the slightly viscoelastic parameter and Reynolds number increase.
- The tangential shear stress at the upper disk surges significantly by increment in and .
- The squeeze force is boosted with the increase in , and this signifies that the fluid has shear-thickening properties.
Author Contributions
Conceptualization, M.M., A.M.S. and S.K.S.; Methodology, M.M. and W.A.S.; Software, M.M. and W.A.S.; Validation W.A.S., A.A.S. and M.D.L.S.; Formal analysis, A.M.S. and A.A.S.; Investigation, M.M. and W.A.S.; Writing—original draft preparation, M.M., W.A.S. and S.K.S.; writing—review and editing, A.A.S. and S.K.S.; Supervision; S.K.S.; Funding Acquisition, M.D.L.S. All authors have read and agreed to the published version of the manuscript.
Funding
Basque Government Grants IT1555-22 and KK-2022/00090; and MCIN/AEI 269.10.13039/501100011033 for Grant PID2021-1235430B-C21/C22.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the Basque Government for its support through Grants IT1555-22 and KK-2022/00090; and to MCIN/AEI 269.10.13039/501100011033 for Grant PID2021-1235430B-C21/C22.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Yousfi, M.; Bou-Saïd, B.; Tichy, J. An analytical study of the squeezing flow of synovial fluid. Mech. Ind. 2013, 14, 59–69. [Google Scholar] [CrossRef]
- Venerus, D.C. Squeeze flows in liquid films bound by porous disks. J. Fluid Mech. 2018, 855, 860–881. [Google Scholar] [CrossRef]
- Meeten, G. Constant-force squeeze flow of soft solids. Rheol. Acta 2002, 41, 557–566. [Google Scholar] [CrossRef]
- Engmann, J.; Servais, C.; Burbidge, A.S. Squeeze flow theory and applications to rheometry: A review. J. Non-Newton. Fluid Mech. 2005, 132, 1–27. [Google Scholar] [CrossRef]
- Coussot, P. Yield stress fluid flows: A review of experimental data. J. Non-Newton. Fluid Mech. 2014, 211, 31–49. [Google Scholar] [CrossRef]
- Liu, F.; Jin, Z.; Hirt, F.; Rieker, C.; Roberts, P.; Grigoris, P. Transient elastohydrodynamic lubrication analysis of metal-on-metal hip implant under simulated walking conditions. J. Biomech. 2006, 39, 905–914. [Google Scholar] [CrossRef]
- Stefan, J. Versuche über die Scheinbare Adhäsion. Ann. Phys. 1875, 230, 316–318. [Google Scholar] [CrossRef]
- Reynolds, O. IV. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Scott, J. Theory and application of the parallel-plate plastimeter. Part 2. Rubber Chem. Technol. 1935, 8, 587–596. [Google Scholar] [CrossRef]
- Jackson, J. A study of squeezing flow. Appl. Sci. Res. Sect. A 1963, 11, 148–152. [Google Scholar] [CrossRef]
- Jones, A.; Wilson, S. On the failure of lubrication theory in squeezing flows. J. Lubr. Technol. 1975, 97, 101–104. [Google Scholar] [CrossRef]
- Hamza, E.; MacDonald, D. A fluid film squeezed between two parallel plane surfaces. J. Fluid Mech. 1981, 109, 147–160. [Google Scholar] [CrossRef]
- Li, Y.-M.; Ullah, I.; Ameer Ahammad, N.; Ullah, I.; Muhammad, T.; Asiri, S.A. Approximation of unsteady squeezing flow through porous space with slip effect: DJM approach. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Qayyum, M.; Khan, H.; Rahim, M.T.; Ullah, I. Modeling and analysis of unsteady axisymmetric squeezing fluid flow through porous medium channel with slip boundary. PLoS ONE 2015, 10, e0117368. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.; Rahim, M.; Khan, H. Application of Daftardar Jafari method to first grade MHD squeezing fluid flow in a porous medium with slip boundary condition. Abstr. Appl. Anal. 2014, 2014, 479136. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Haroon, T.; Bhatti, S.; Ansari, A.R. A comparison of the adomian and homotopy perturbation methods in solving the problem of squeezing flow between two circular plates. Math. Model. Anal. 2010, 15, 491–504. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Irum, S.; Ansari, A.R. Unsteady squeezing flow of a viscous MHD fluid between parallel plates, a solution using the homotopy perturbation method. Math. Model. Anal. 2008, 13, 565–576. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Dudek, J.; Boger, D.; Tirtaatmadja, V. Squeeze film flow of ideal elastic liquids. J. Non-Newton. Fluid Mech. 1985, 18, 227–254. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Tanner, R. Viscoelastic squeeze-film flows–Maxwell fluids. J. Fluid Mech. 1983, 129, 265–281. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Sugeng, F.; Tanner, R. The squeeze-film flow of a viscoelastic fluid. J. Non-Newton. Fluid Mech. 1987, 24, 97–119. [Google Scholar] [CrossRef]
- Memon, M.; Shaikh, A.A.; Siddiqui, A.M.; Kumar, L. Analytical Solution of Slow Squeeze Flow of Slightly Viscoelastic Fluid Film between Two Circular Disks Using Recursive Approach. Math. Probl. Eng. 2022, 2022, 4043909. [Google Scholar] [CrossRef]
- Hayat, T.; Nazar, H.; Imtiaz, M.; Alsaedi, A.; Ayub, M. Axisymmetric squeezing flow of third grade fluid in presence of convective conditions. Chin. J. Phys. 2017, 55, 738–754. [Google Scholar] [CrossRef]
- Shafiq, A.; Jabeen, S.; Hayat, T.; Alsaedi, A. Cattaneo–Christov heat flux model for squeezed flow of third grade fluid. Surf. Rev. Lett. 2017, 24, 1750098. [Google Scholar] [CrossRef]
- Noor, N.A.M.; Admon, M.A.; Shafie, S. Unsteady MHD Squeezing Flow of Casson Fluid Over Horizontal Channel in Presence of Chemical Reaction. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 92, 49–60. [Google Scholar] [CrossRef]
- Noor, N.A.M.; Shafie, S.; Admon, M.A. Effects of viscous dissipation and chemical reaction on MHD squeezing flow of Casson nanofluid between parallel plates in a porous medium with slip boundary condition. Eur. Phys. J. Plus 2020, 135, 855. [Google Scholar] [CrossRef]
- Noor, N.A.M.; Shafie, S.; Admon, M.A. MHD squeezing flow of Casson nanofluid with chemical reaction, thermal radiation and heat generation/absorption. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 68, 94–111. [Google Scholar] [CrossRef]
- Shankar, U.; Naduvinamani, N.B. Magnetized impacts of Cattaneo-Christov double-diffusion models on the time-dependent squeezing flow of Casson fluid: A generalized perspective of Fourier and Fick's laws. Eur. Phys. J. Plus 2019, 134, 344. [Google Scholar] [CrossRef]
- Mat Noor, N.A.; Shafie, S.; Admon, M.A. Slip effects on MHD squeezing flow of Jeffrey nanofluid in horizontal channel with chemical reaction. Mathematics 2021, 9, 1215. [Google Scholar] [CrossRef]
- Mat Noor, N.A.; Shafie, S.; Admon, M.A. Heat and mass transfer on MHD squeezing flow of Jeffrey nanofluid in horizontal channel through permeable medium. PLoS ONE 2021, 16, e0250402. [Google Scholar] [CrossRef]
- Mat Noor, N.A.; Shafie, S.; Admon, M.A. Heat Transfer on Magnetohydrodynamics Squeezing Flow of Jeffrey Fluid Through Permeable Medium with Slip Boundary. J. Nanofluids 2022, 11, 31–38. [Google Scholar] [CrossRef]
- Noor, N.A.M.; Shafie, S.; Admon, M.A. Impacts of chemical reaction on squeeze flow of MHD Jeffrey fluid in horizontal porous channel with slip condition. Phys. Scr. 2021, 96, 035216. [Google Scholar] [CrossRef]
- Ullah, H.; Siddiqui, A.M.; Sun, H.; Haroon, T. Slip effects on creeping flow of slightly non-Newtonian fluid in a uniformly porous slit. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 412. [Google Scholar] [CrossRef]
- Ullah, H.; Sun, H.; Siddiqui, A.M.; Haroon, T. Creeping flow analysis of slightly non-Newtonian fluid in a uniformly porous slit. J. Appl. Anal. Comput. 2019, 9, 140–158. [Google Scholar] [CrossRef]
- Mehboob, H.; Maqbool, K.; Ullah, H.; Siddiqui, A.M. Computational analysis of an axisymmetric flow of Jeffrey fluid in a permeable micro channel. Appl. Math. Comput. 2022, 418, 126826. [Google Scholar] [CrossRef]
- Langlois, W. A Recursive Approach to the Theory of Slow, Steady-State Viscoelastic Flow. Trans. Soc. Rheol. 1963, 7, 75–99. [Google Scholar] [CrossRef]
- Kacou, A.; Rajagopal, K.; Szeri, A. A thermohydrodynamic analysis of journal bearings lubricated by a non-Newtonian fluid. J. Tribol. 1988, 110, 414–420. [Google Scholar] [CrossRef]
- Lee, S.; Denn, M.; Crochet, M.; Metzner, A. Compressive flow between parallel disks: I. Newtonian fluid with a transverse viscosity gradient. J. Non-Newton. Fluid Mech. 1982, 10, 3–30. [Google Scholar] [CrossRef]
- Siddiqui, A.; Kaloni, P. Certain inverse solutions of a non-Newtonian fluid. Int. J. Non-Linear Mech. 1986, 21, 459–473. [Google Scholar] [CrossRef]
- Ghori, Q.K.; Ahmed, M.; Siddiqui, A.M. Application of Homotopy Perturbation Method to Squeezing Flow of a Newtonian Fluid. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 179–184. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).