Abstract
Computational analysis is performed for turbulent free convection and surface thermal radiation in an air-filled cavity with solid obstacle on the bottom wall. A partition of finite thickness is considered, the position, length, and heat conductivity of which vary for certain values of the Rayleigh number. The coupled heat transmission by thermal radiation, free convection and heat conduction through the solid obstacle and walls is studied. The governing equations are solved by the finite difference method. This work also contains a detailed description of the computational grid thickening procedure. Temperature patterns and airflow field are scrutinized for some specific conditions using streamlines and isotherms. The overall heat transfer within the cavity is analyzed in terms of the mean convective and radiative Nusselt numbers, and many of the data are presented in detail for various partition positions, heat conductivities of the partition and walls of the cavity, and Rayleigh numbers. The results report that the participation of partitions within the cavities in the heat exchange processes decreases the overall heat transfer rate compared to the simpler case of cavities without partitions.
Keywords:
numerical simulation; coordinate transformation; finite difference technique; coupled heat transfer MSC:
35Q30; 76F60; 76R10
1. Introduction
Free convection is the most economical type of convection compared to other types of convection. The characteristic advantages of this mode of energy transfer include its noiselessness and reliability. In some cases, when the characteristic dimensions of the cavity are significant or a significant temperature drop is observed, the flow regime becomes turbulent. There are many studies of turbulent convection in enclosures [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18], as indicated and summarized in [19], as this is the main form that can be found in various engineering systems.
The effect of turbulent free convection on heat transfer in shallow cavity was investigated by Qaddah et al. [20]. They aimed to analyze in detail the various phenomena of heat transport in a cavity with seasonal fluctuations in ground temperature. Turbulent free convection in a cave, radiative heat transfer between walls and heat conduction inside walls were analyzed. The results showed that the horizontal temperature drop determines the average direction of flow rotation. It was also established that the intensity of flow and the level of turbulence have a weak effect on the magnitude of the heat transport parameter. Numerical analysis of turbulent free convection in heated from below cavity was performed by Chai et al. [21]. Such processes occurring in a small reactor affect the removal of residual thermal energy from the top header of the pressure vessel in severe accidents. The authors used least squares regression analysis to construct correlations for the average Nu as a function of Ra. So, the average Nusselt number is proportional to Ra0.2. Benyahia et al. [22] studied the complex heat transfer by turbulent natural convection, conduction and heat radiation in an enclosure having high aspect ratio. The enclosure had the shape of a parallelepiped and sides length was 0.076 × 2.18 × 0.52 m. The impact of surface radiation on heat transfer and airflow was investigated through various values of surface emissivity of internal walls. As a result of the research, it was found that the emissivity of the inner surfaces significantly affects the velocity patterns near the horizontal surfaces, without affecting the flow in the core of the enclosure. Fabregat and Pallares [23] investigated heat transfer via both laminar and turbulent natural convection in differently heated cube. Using the method of direct numerical simulation, the authors obtained correlations for the mean Nu depending on Ra ranged from 105 to 5.5 × 108.
The intensity of heat transfer inside the cavity can be changed either by taking into account the temperature difference between the walls, or by creating obstacles (various blocks, fins and partitions). Such obstacles can essentially affect the fluid motion and therefore the heat transport within the entire cavity. Thermophysical properties of obstacles, location, geometry, length are the main parameters to consider when studying such problems. Experimental analysis of turbulent free convection in non-partitioned or partitioned cavity was carried out by Ampofo [24]. The scale dimensions of the study area were 0.75 × 0.75 × 1.5 m3. Cold and hot enclosure walls were isothermal at temperatures 50 and 10 °C, respectively. Five baffles were installed on the hot isothermal wall made of a material with a higher thermal conductivity than that of the enclosure. The experiments carried out with a sufficiently high accuracy helped to establish experimental reference results and will undoubtedly be useful in testing numerical algorithms.
Priam et at. [25] performed a computational analysis of conjugate thermal convection within a cavity separated by a wavy obstacle filled with air and water. As an obstacle, the authors used a corrugated thermally-conducting block with three various thicknesses and three various materials. They have investigated the impact of the corrugation frequency and amplitude, heat conductivity, location and thickness of the corrugated obstacle on fluid and air flow and heat transfer. The outcomes presented that a growth of the heat conductivity of the obstacle increases the heat transport strength up to 25%. The use of a low frequency corrugation allowed a slight improvement in heat transfer, but this effect is negligible. Saha and Gu [26] studied heat transfer in a triangular cavity having a conducting obstacle. The authors received outcomes for a wide range of control characteristics such as Ra (105–108) and aspect ratio (0.2–1.0). It was established that for a fixed Ra, the energy transport is higher for small values of the aspect ratio. However, if aspect ratio is fixed, then the intensity of energy transport can be raised with a growth of Ra. The influence of aspect ratio on energy transport in a cavity having mutually orthogonal warmed partitions was investigated by Kandaswamy et al. [27]. The enclosure had two isothermal thin partitions (horizontal and vertical). All surfaces of the cavity were kept at a constant temperature, namely, they were isothermal. It was found that energy transport in the enclosure can be significantly improved by raising the length of the vertical partition, regardless of its location. At the same time, a growth of the length of the horizontal partition increases the intensity of heat transfer only in the case when the partition is located below the center of the cavity.
It is very useful to highlight that the effect of surface radiation on heat transfer in a chamber has been experimentally studied in [28,29]. In these papers, the average Nusselt number correlations for combined convection and radiation are presented in terms of Grashof number. As a result of the research, it has been found that surface thermal radiation is important in a chamber. Percentages of the contribution of each heat transfer mechanism for the case of heat transfer through hollow building element is presented in [30]. It has been shown that the contribution of the radiation heat transfer is about 25.5% while the convection contribution does not exceed 15.4%.
Some of the leading studies on heat transfer in a partitioned enclosures are presented in Table 1. The presented studies show that the main attention was paid mainly to laminar problems and partitions with infinite thermal conductivity. In this paper, all the main mechanisms of heat transfer (thermal conduction in the baffle and walls, convection inside the cavity, and thermal radiation between the surfaces) will be considered.

Table 1.
Several studies on heat transfer in partitioned enclosures.
2. Governing Equations and Numerical Method
Two-dimensional square air-filled cavity having a partition is depicted in Figure 1 together with boundary limitations. Cartesian coordinates (x, y) combined corresponding velocity projections (u1, u2) are considered. The heat-conducting partition is placed vertically for various heights inside the cavity (h/L = 0.2, 0.5 and 0.7). A cavity with characteristic size of L is heated by setting a fixed temperature Th for the wall x = 0 and cooled by setting a fixed temperature Tc for the wall x = 1 + 2l/L. Bottom and top walls at y = 0 and y = 1 + 2l/L respectively are considered adiabatic. Boussinesq approximation was employed, assuming an incompressible viscous Newtonian fluid. As assumptions used in modeling radiative heat transfer, the following can be noted, namely, the inner walls are gray, and the radiation is diffuse. Physical properties of air at reference temperature T0 = (Th + Tc)/2 presented in Table 2.
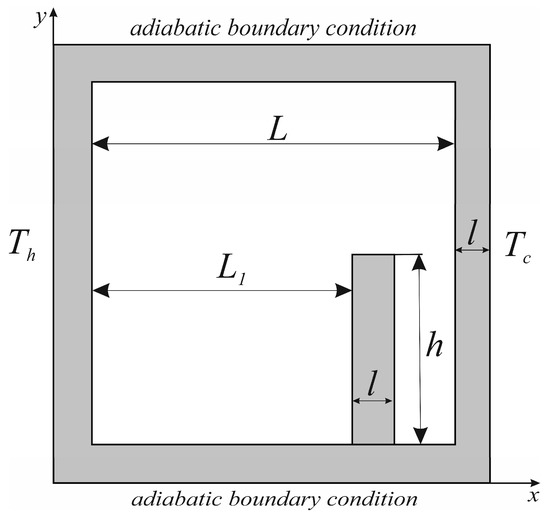
Figure 1.
A sketch of the analyzed region.

Table 2.
Physical properties of air at T0 = 15 °C.
The control equations can be written in following form
The system of Equations (1)–(4) is formulated in terms of “velocity-pressure” variables. One of the approaches to solving the equations of natural convection is the transition to the variables “stream function-vorticity”. The implementation of this approach makes it possible to diminish the number of equations to be solved, and also eliminates the pressure field definition.
The stream function and vorticity are given as follows:
In a number of theoretical studies, as well as in modeling physical processes, the transition to dimensionless dependences between parameters provides great convenience. For dimensionless values, the coordinates and parameters of the object are divided into characteristic dimensions and parameters chosen as measurement scales and having the same dimensions. The scales of distance L, time , temperature , velocity , stream function , kinetic energy of turbulence , dissipation rate of turbulence kinetic energy and vorticity are used in this work.
The initial restrictions for the control equations in variables “stream function-vorticity” are:
The border limitations are shown in Table 3.

Table 3.
Border limitations.
The boundary-value problem was worked out by the finite difference technique on a nonuniform mesh. The mesh thickening within the heat boundary layer was specified using a relation of the form [39]
Here is a compaction parameter, a, b are the shape coefficients. Computational region and used grid are presented in Figure 2.
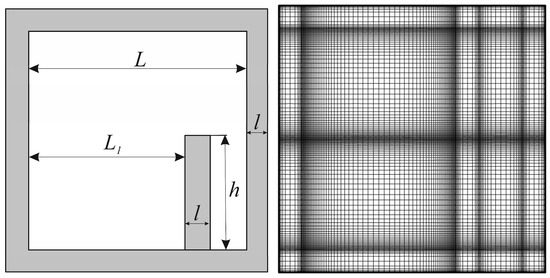
Figure 2.
Computational region and used grid.
The average Nusselt numbers (convective and radiative) are taken as dimensionless heat transfer coefficients. These numbers are defined in the following form:
Here Nuconv is an average convective Nusselt number that illustrates a ratio of the heat transfer by convection to the heat transfer by conduction, while Nurad is an average radiative Nusselt number that illustrates a ratio of the heat transfer by radiation to the heat transfer by conduction. Qrad is dimensionless net radiative heat flux. The dimensional form of Qrad is defined as the difference between the effective and incident radiation. Nrad is a radiation parameter. The radiation of real bodies differs from the radiation of a completely black body. At equal temperatures, real bodies radiate less thermal energy than a completely black body. To describe the radiation of real bodies, the concept of the surface emissivity is introduced, which characterizes the ratio of the flux density of the own radiation of a real body to the flux density of its own radiation of an absolutely black body. The wall emissivity varies between 0 and 1. The radiation of real bodies in this work is modeled by the radiation of a gray body.
To find the dimensionless net radiative heat flux Qrad, the following equations should be solved
The view factor of radiation is called the value that determines the proportion of radiant energy coming to a given body from another body. The view factor of radiation depends only on the relative position of the bodies in space and therefore it is a purely geometric quantity. In this paper, to find the view factors, the Hottel crossed string method is used [40].
In this work, an in-house computational procedure was developed using C++ programming language to analyze the influence of different parameters on energy transport and airflow in a cavity having partition on the bottom solid wall. The problem of free convection in a differentially-heated cavity is studied to validate the developed computational algorithm. As a part of the validation, the computed outcomes were checked using the experimental work [41]. Figure 3 demonstrates the temperature and vertical velocity patterns at the middle section.
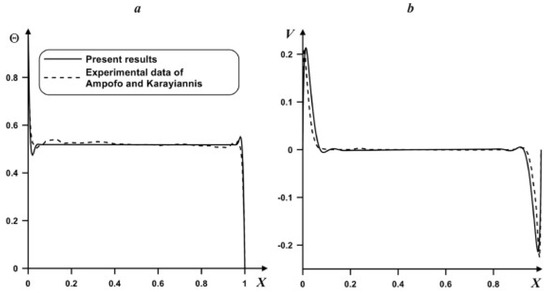
Figure 3.
Thermal profiles (a) and vertical velocity (b) in comparison with outcomes from [41].
In order to make the obtained numerical solutions independent on the mesh, an additional analysis was conducted using three various grids (96 × 96, 120 × 120, 180 × 180) for the case of Ra = 109, Pr = 0.7, λw,air = 10,000, h/L = 0.2, . The resulting time series of the average Nurad at the heated surface are shown in Figure 4. Moreover, the difference of outcomes between the grids of 120 × 120 elements and 180 × 180 elements is less than 2.5% for the average convective Nu and the 120 × 120 elements grid is chosen as the grid for numerical analysis in present research.
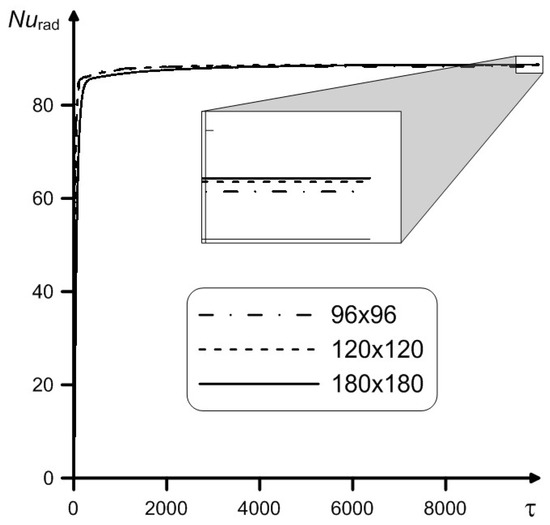
Figure 4.
Dependences of the average radiative Nusselt number at left wall vs. various grids and dimensionless time.
3. Results
A total of 33 runs were performed in this study for three partitions heights (i.e., h/L = 0.2, 0.5, and 0.7), four magnitudes of wall emissivity (i.e., , 0.3, 0.6, and 0.9), three Rayleigh numbers (i.e., Ra = 109, 1.5∙109, and 1010), four values of thermal conductivity ratio (i.e., λw,air = 10, 100, 1000, and 10,000). For all these runs, Pr = 0.7 and L1 = 0.7L are used. The thermal conductivity of materials λw,air chosen for this study corresponds to a wide range of materials with various industrial applications. Insulating materials such as foam concrete, aerated concrete or wood modeling by selecting λw,air ≈ 10. Sandstone and granite are among the materials that have λw,air ≈ 100. Aluminum nitride, aluminum, silicon have λw,air ≈ 1000.
An influence of inner wall emissivity on energy transport and airflow at Ra = 109, Pr = 0.7, λw,air = 10,000, h/L = 0.2 is shown in Figure 5. The obtained patterns are considered in the steady state, which corresponds to the dimensionless time . In the central part of the cavity, the isotherms take a horizontal position. Near solid vertical walls, one can see an appearance of a heat boundary layer (thickening of temperature isolines close to walls).
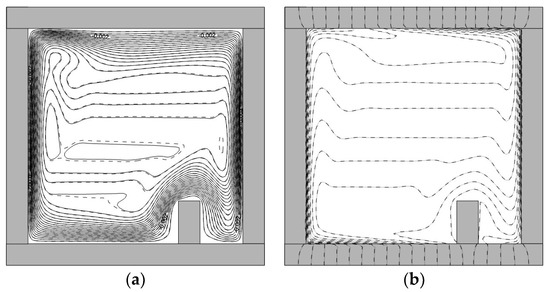
Figure 5.
Isolines of stream function Ψ (a) and temperature Θ (b) at Ra = 109, Pr = 0.7, λw,air = 10,000, h/L = 0.2: —dashed lines, —solid lines.
A growth of the emissivity of the inner walls does not lead to significant changes in the thermal field in the cavity. The streamlines demonstrate that the flow nature is not complicated.
The contribution of the radiative mechanism of energy transfer in problems of natural convection in closed cavities is quite significant [42]. An influence of walls emissivity values on Nurad can be seen in Figure 6. Numerical results show that, as expected, a growth of the values of results to a significant intensification of the radiative mechanism of energy transfer. At the mean radiative Nu raises up to 3.46 times at changing of surface emissivity values from 0.3 to 0.9. It should be noted that when solving the boundary-value problem, the internal medium (air) was considered diathermic, that is, transparent to radiation.
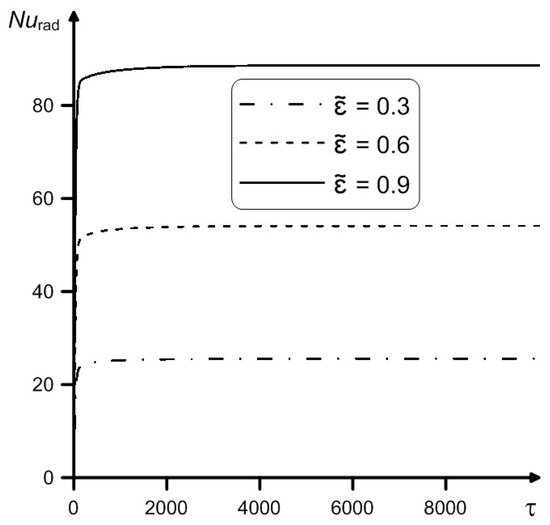
Figure 6.
Profiles of the average radiative Nu vs. time and surface emissivity at Ra = 109, Pr = 0.7, λw,air = 10,000, h/L = 0.2.
Table 4 shows the values of two various parameters considered, namely, maximum absolute value of Ψ and mean convective Nu for Ra = 109, Pr = 0.7, λw,air = 10,000, h/L = 0.2. According to the presented tabular data, it can be found that with a growth of the surface emissivity values, a slight reduction of the strength of convective energy transport is shown. The mean convective Nu diminishes up to 0.16% as the surface emissivity changes from 0 to 0.9. Maximum absolute value of Ψ also decreases with increasing surface emissivity values. This is due to a reduction of the temperature gradient, and a growth of the radiative thermal flux. A similar effect of the parameter on convective energy transport in closed cavities for the case of laminar flow was studied by Martyushev and Sheremet [43] and Miroshnichenko et al. [44].

Table 4.
Variations of various considered parameters.
The impact of Ra on the patterns of local parameters (streamlines and isotherms) for , Pr = 0.7, λw,air = 10,000, h/L = 0.2 can been seen in Figure 7. A single convective cell is appeared within the cavity, regardless of the Rayleigh number. The occurrence of this recirculation air flow is due to the geometric features of the problem, as well as the formulated boundary conditions. A growth of Ra manifests itself in a characteristic increase in the thickness of the heat boundary layer near the inner vertical borders. Visually, the isotherms are similar, but the difference in the distribution of temperature isolines can be traced by the isotherm of .
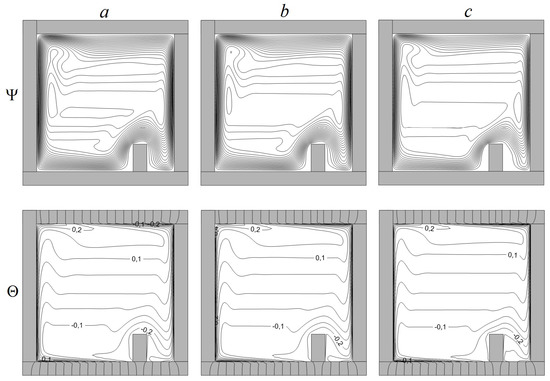
Figure 7.
Isolines of Ψ and Θ at , Pr = 0.7, λw,air = 10,000, h/L = 0.2: Ra = 109 (a), Ra = 1.5 × 109 (b), Ra = 1010 (c).
Figure 8 demonstrates and at the left internal wall for different Rayleigh numbers and heat-conducting partition heights. The outcomes show that an increase in Ra results to an increase in the time required for the flow in the cavity become stationary.
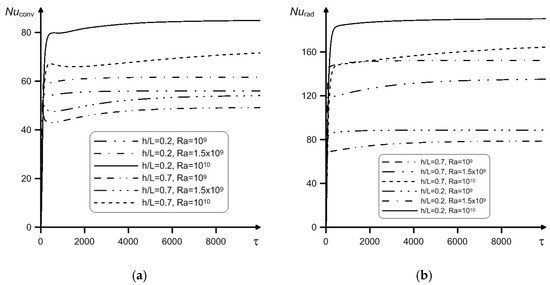
Figure 8.
Dependences of the mean convective (a) and radiative (b) Nusselt numbers at the left border vs. Rayleigh number, heat-conducting partition heights and dimensionless time at , Pr = 0.7, λw,air = 10,000.
The presence of a heat-conducting obstacle results to a reduction of the intensity of energy transport in the cavity. It can be seen that changing the height of the partition from h/L = 0.2 to h/L = 0.7 results to a diminution of the integral energy transport coefficients. For thermal radiation, the partition plays the role of an obstacle, forming shading zones. The in-house numerical code includes the calculation of the view factors. This represents some mathematical complexity due to the need to calculate the view factors for each elementary surface area. The correctness of the calculation was checked by the main property of the view factors (property arising from the law of conservation of energy). The results show that when the height of the partition changes from h/L = 0.2 to h/L = 0.7 the average convective Nu reduces up to 14.8% at 1010, and decreases up to 12.2% at 109. The mean radiative Nu also reduces up to 13.6% and 11.2% respectively. An increment of Ra from 109 to 1010 results in an increment of the mean convective Nu up to 31.4% at h/L = 0.7 and up to 34.12% at h/L = 0.2.
Figure 9 presents the snapshots of temperature contours and streamlines for the case of , Ra = 109, Pr = 0.7, h/L = 0.7. A growth of the heat conductivity ratio by a factor of 10 due to a raise of the heat conductivity of the solid wall material results to both more intensive cooling and heating of the analyzed area. At and λw,air = 100 the flow in the cavity does not yet correspond to a stationary position. This can be seen from the temperature patterns within the heat-conducting walls.
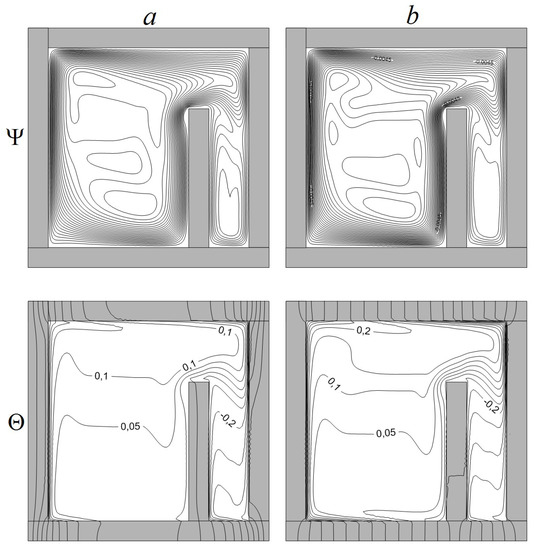
Figure 9.
Isolines of Ψ and Θ at , Ra = 109, Pr = 0.7, h/L = 0.7: λw,air = 100 (a), λw,air = 1000 (b).
An increase in of an air circulation rate is observed with a growth of the heat conductivity ratio:
Figure 10 presents the time series of mean convective Nu on the left border for different thermal conductivity ratio values at , Ra = 109, Pr = 0.7, h/L = 0.2. According to the values of the mean convective Nu depending on Ra, two facts can be noted, namely, with a growth of heat conductivity ratio, the time required to achieve a steady flow in the cavity decreases significantly, and a growth of λw,air results to a raising the values of the average convective Nusselt number. A similar dependence is also found for the average radiative Nu at the characteristic boundary.
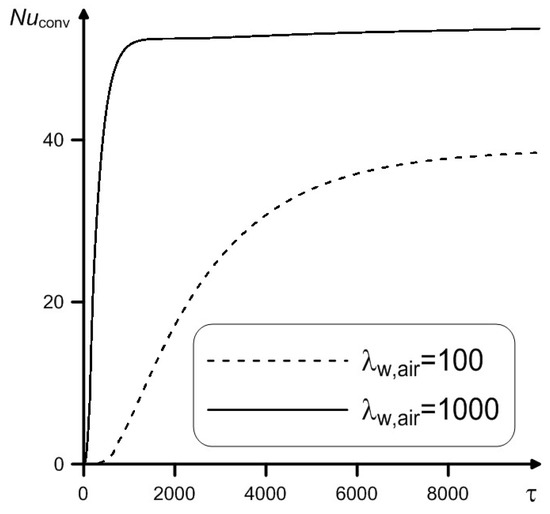
Figure 10.
Time profiles of the average convective Nu vs. thermal conductivity ratio at , Ra = 109, Pr = 0.7, h/L = 0.2.
4. Conclusions
In this study, turbulent free convection combined with surface thermal radiation in a cavity with a solid obstacle was computationally studied for a wide range of partition heights, surface emissivity values, Rayleigh numbers and thermal conductivity values. The heat flux in the cavity arises due to the temperature difference at the outer surfaces of vertical walls. The problem was worked out by the finite difference algorithm on a non-uniform mesh. The presence of a partition has an essential influence on the temperature and velocity properties of the considered cavity. Mean convective Nu is an increasing function of heat conductivity and Ra but it is a decreasing function of surface emissivity. It was shown that by changing the height of the partition it is possible to manage the processes of energy transport in the solution area. This work demonstrates a significant impact of surface thermal radiation on the fluid flow and heat transport within the bounded cavity. In this regard, it is necessary to include in thermal analysis the radiation as one of the main phenomenon of heat transport.
Author Contributions
I.V.M. and M.A.S. conceived the main concept. I.V.M. and M.A.S. contributed to the investigation and data analysis. I.V.M. wrote the manuscript. All authors contributed to the writing of the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of Russia (agreement No. 075-02-2022-884).
Data Availability Statement
All data can be found in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Fk–i | view factor between k-th and i-th elements of a cavity |
| L | size (m) |
| g | gravity acceleration (m/s2) |
| k | turbulence kinetic energy (m2/s2) |
| h | partition heights (m) |
| K | non-dimensional turbulent kinetic energy |
| generation/destruction of buoyancy turbulent kinetic energy | |
| E | non-dimensional dissipation rate of turbulent kinetic energy |
| Rayleigh number | |
| average convective Nusselt number | |
| radiation parameter | |
| Prandtl number | |
| average radiative Nusselt number | |
| shearing production | |
| turbulent Prandtl number | |
| Rk | non-dimensional radiosity of the k-th element of an enclosure |
| Qrad | non-dimensional net radiative heat flux |
| Th | temperature at the left border (K) |
| t | time (s) |
| Tc | temperature at the right border (K) |
| T | temperature (K) |
| Θf | non-dimensional temperature of fluid |
| Θ | non-dimensional temperature |
| u1, u2 | velocity components for x and y axis (m/s) |
| U1, U2 | non-dimensional velocity components for X and Y axis |
| Θw | non-dimensional temperature of walls |
| X, Y | non-dimensional Cartesian coordinates |
| ε | dissipation rate of turbulent kinetic energy (m2/s3) |
| temperature parameter | |
| β | factor of volumetric heat expansion (1/K) |
| thermal diffusivity of the wall material (m2/s) | |
| air thermal diffusivity (m2/s) | |
| thermal diffusivity ratio | |
| surface emissivity of inner surfaces | |
| air heat conductivity (W/mK) | |
| heat conductivity of the wall material (W/mK) | |
| heat conductivity ratio | |
| ν | kinematic viscosity (m2/s) |
| ψ | stream function (m2/s) |
| ω | vorticity (s−1) |
| turbulent viscosity (m2/s) | |
| Ψ | non-dimensional stream function |
| new dimensionless independent variables | |
| Ω | non-dimensional vorticity |
| τ | non-dimensional time |
| σ | Stefan–Boltzmann constant (W/m2K4) |
References
- Sharma, A.K.; Velusamy, K.; Balaji, C. Turbulent Natural Convection in an Enclosure with Localized Heating from Below. Int. J. Therm. Sci. 2007, 46, 1232–1241. [Google Scholar] [CrossRef]
- Dixit, H.N.; Babu, V. Simulation of High Rayleigh Number Natural Convection in a Square Cavity Using the Lattice Boltzmann Method. Int. J. Heat Mass Transf. 2006, 49, 727–739. [Google Scholar] [CrossRef]
- Zhuo, C.; Zhong, C. LES-Based Filter-Matrix Lattice Boltzmann Model for Simulating Turbulent Natural Convection in a Square Cavity. Int. J. Heat Fluid Flow 2013, 42, 10–22. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A.; Mohamad, A.A. The influence of surface radiation on the passive cooling of a heat-generating element. Energies 2019, 12, 980. [Google Scholar] [CrossRef]
- Baudoin, A.; Saury, D.; Boström, C. Optimized Distribution of a Large Number of Power Electronics Components Cooled by Conjugate Turbulent Natural Convection. Appl. Therm. Eng. 2017, 124, 975–985. [Google Scholar] [CrossRef]
- Ibrahim, A.; Saury, D.; Lemonnier, D. Coupling of Turbulent Natural Convection with Radiation in an Air-Filled Differentially-Heated Cavity at Ra = 1.5 × 109. Comput. Fluids 2013, 88, 115–125. [Google Scholar] [CrossRef]
- Shati, A.K.A.; Blakey, S.G.; Beck, S.B.M. A dimensionless solution to radiation and turbulent natural convection in square and rectangular enclosures. J. Eng. Sci. Technol. 2012, 7, 257–279. [Google Scholar]
- Tian, Y.S.; Karayiannis, T.G. Low turbulence natural convection in an air filled square cavity Part I: The thermal and fluid flow fields. Int. J. Heat Mass Transf. 2000, 43, 849–866. [Google Scholar] [CrossRef]
- Tian, Y.S.; Karayiannis, T.G. Low turbulence natural cosnvection in an air filled square cavity Part II: The turbulence quantities. Int. J. Heat Mass Transf. 2000, 43, 867–884. [Google Scholar] [CrossRef]
- Zhang, X.; Su, G.; Yu, J.; Yao, Z.; He, F. PIV measurement and simulation of turbulent thermal free convection over a small heat source in a large enclosed cavity. Build. Environ. 2015, 90, 105–113. [Google Scholar] [CrossRef]
- Altac, Z.; Ugurlubilek, N. Assessment of turbulence models in natural convection from two- and three-dimensional rectangular enclosures. Int. J. Therm. Sci. 2016, 107, 237–246. [Google Scholar] [CrossRef]
- Shati, A.K.A.; Blakey, S.G.; Beck, S.B.M. An empirical solution to turbulent natural convection and radiation heat transfer in square and rectangular enclosures. Appl. Therm. Eng. 2013, 51, 364–370. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Toilibayev, A.A.; Sheremet, M.A. Simulation of Thermal Radiation and Turbulent Free Convection in an Enclosure with a Glass Wall and a Local Heater. Fluids 2021, 6, 91. [Google Scholar] [CrossRef]
- Cui, H.; An, H.; Wang, W.; Han, Z.; Hu, B.; Xu, F.; Liu, Q.; Saha, S.C. Numerical Study of Mixed Convection and Heat Transfer in Arc-Shaped Cavity with Inner Heat Sources. Appl. Sci. 2023, 13, 1029. [Google Scholar] [CrossRef]
- Serrano-Arellano, J.M.; Belman-Flores, J.; Xamán, J.; M. Aguilar-Castro, K.; V. Macías-Melo, E. Numerical Study of the Double Diffusion Natural Convection inside a Closed Cavity with Heat and Pollutant Sources Placed near the Bottom Wall. Energies 2020, 13, 3085. [Google Scholar] [CrossRef]
- Balam, N.B.; Alam, T.; Gupta, A.; Blecich, P. Higher Order Accurate Transient Numerical Model to Evaluate the Natural Convection Heat Transfer in Flat Plate Solar Collector. Processes 2021, 9, 1508. [Google Scholar] [CrossRef]
- Yao, J.; Yao, Y. Unsteady Flow Oscillations in a 3-D Ventilated Model Room with Convective Heat Transfer. Fluids 2022, 7, 192. [Google Scholar] [CrossRef]
- Ovando-Chacon, G.E.; Rodríguez-León, A.; Ovando-Chacon, S.L.; Hernández-Ordoñez, M.; Díaz-González, M.; Pozos-Texon, F.d.J. Computational Study of Thermal Comfort and Reduction of CO2 Levels inside a Classroom. Int. J. Environ. Res. Public Health 2022, 19, 2956. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A. Turbulent Natural Convection Heat Transfer in Rectangular Enclosures Using Experimental and Numerical Approaches: A Review. Renew. Sustain. Energy Rev. 2018, 82, 40–59. [Google Scholar] [CrossRef]
- Qaddah, B.; Soucasse, L.; Doumenc, F.; Mergui, S.; Riviиre, P.; Soufiani, A. Influence of turbulent natural convection on heat transfer in shallow caves. Int. J. Therm. Sci. 2022, 177, 107524. [Google Scholar] [CrossRef]
- Chai, X.; Li, W.; Chen, B.; Liu, X.; Xiong, J.; Cheng, X. Numerical simulation of turbulent natural convection in an enclosure with a curved surface heated from below. Prog. Nucl. Energy 2020, 126, 103392. [Google Scholar] [CrossRef]
- Benyahia, N.; Aksouh, M.; Mataoui, A.; Oztop, H.F. Coupling turbulent natural convection-radiation-conduction in differentially heated cavity with high aspect ratio. Int. J. Therm. Sci. 2020, 158, 106518. [Google Scholar] [CrossRef]
- Fabregat, A.; Pallarès, J. Heat transfer and boundary layer analyses of laminar and turbulent natural convection in a cubical cavity with differently heated opposed walls. Int. J. Heat Mass Transf. 2020, 151, 119409. [Google Scholar] [CrossRef]
- Ampofo, F. Turbulent natural convection of air in a non-partitioned or partitioned cavity with differentially heated vertical and conducting horizontal walls. Exp. Therm. Fluid Sci. 2005, 29, 137–157. [Google Scholar] [CrossRef]
- Priam, S.S.; Ikram, M.M.; Saha, S.; Saha, S.C. Conjugate natural convection in a vertically divided square enclosure by a corrugated solid partition into air and water regions. Therm. Sci. Eng. Prog. 2021, 25, 101036. [Google Scholar] [CrossRef]
- Saha, S.C.; Gu, Y.T. Transient air flow and heat transfer in a triangular enclosure with a conducting partition. Appl. Math. Model. 2014, 38, 3879–3887. [Google Scholar] [CrossRef]
- Kandaswamy, P.; Lee, J.; Hakeem, A.K.A.; Saravanan, S. Effect of baffle–cavity ratios on buoyancy convection in a cavity with mutually orthogonal heated baffles. Int. J. Heat Mass Transf. 2008, 51, 1830–1837. [Google Scholar] [CrossRef]
- Ramesh, N.; Venkateshan, S.P. Effect of surface radiation on natural convection in a square enclosure. J. Thermophys. Heat Transf. 1999, 13, 299–301. [Google Scholar] [CrossRef]
- Balaji, C.; Venkateshan, S.P. Correlations for free convection and surface radiation in a square cavity. Int. J. Heat Fluid Flow 1994, 15, 249–251. [Google Scholar] [CrossRef]
- Boukendil, M.; Abdelbaki, A.; Zrikem, Z. Detailed numerical simulation of coupled heat transfer by conduction, natural convection and radiation through double honeycomb walls. Build. Simul. 2012, 5, 337–344. [Google Scholar] [CrossRef]
- Khatamifar, M.; Lin, W.; Dong, L. Transient conjugate natural convection heat transfer in a differentially-heated square cavity with a partition of finite thickness and thermal conductivity. Case Stud. Therm. Eng. 2021, 25, 100952. [Google Scholar] [CrossRef]
- Wu, W.; Ching, C.Y. Laminar natural convection in an air-filled square cavity with partitions on the top wall. Int. J. Heat Mass Transf. 2010, 53, 1759–1772. [Google Scholar] [CrossRef]
- Costa, V.A.F. Natural convection in partially divided square enclosures: Effects of thermal boundary conditions and thermal conductivity of the partitions. Int. J. Heat Mass Transf. 2012, 55, 7812–7822. [Google Scholar] [CrossRef]
- Said, S.A.M.; Habib, M.A.; Khan, M.A.R. Turbulent natural convection flow in partitioned enclosure. Comput. Fluids 1997, 26, 541–563. [Google Scholar] [CrossRef]
- Xu, F. Unsteady coupled thermal boundary layers induced by a fin on the partition of a differentially heated cavity. Int. Commun. Heat Mass Transf. 2015, 67, 59–65. [Google Scholar] [CrossRef]
- Famouri, M.; Hooman, K. Entropy generation for natural convection by heated partitions in a cavity. Int. Commun. Heat Mass Transf. 2008, 35, 492–502. [Google Scholar] [CrossRef]
- Khatamifara, M.; Lina, W.; Armfieldc, S.W.; Holmesa, D.; Kirkpatrickc, M.P. Conjugate natural convection heat transfer in a partitioned differentially-heated square cavity. Int. Commun. Heat Mass Transf. 2017, 81, 92–103. [Google Scholar] [CrossRef]
- Al-Farhany, K.; Al-Muhja, B.; Ali, F.; Khan, U.; Zaib, A.; Raizah, Z.; Galal, A.M. The Baffle Length Effects on the Natural Convection in Nanofluid-Filled Square Enclosure with Sinusoidal Temperature. Molecules 2022, 27, 4445. [Google Scholar] [CrossRef] [PubMed]
- Kublbeck, K.; Merker, G.P.; Straub, J. Advanced numerical computation of two-dimensional time-dependent free convection in cavities. Int. J. Heat Mass Transf. 1980, 23, 203–217. [Google Scholar] [CrossRef]
- Howell, J.R.; Menguc, M.P.; Siegel, R. Thermal Radiation Heat Transfer, 6th ed.; CRC Press: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Ampofo, F.; Karayiannis, T.G. Experimental benchmark data for turbulent natural convection in an air filled square cavity. Int. J. Heat Mass Transf. 2003, 46, 3551–3572. [Google Scholar] [CrossRef]
- Kogawa, T.; Okajima, J.; Sakurai, A.; Komiya, A.; Maruyama, S. Influence of radiation effect on turbulent natural convection in cubic cavity at normal temperature atmospheric gas. Int. J. Heat Mass Transf. 2017, 104, 456–466. [Google Scholar] [CrossRef]
- Martyushev, S.G.; Sheremet, M.A. Conjugate natural convection combined with surface thermal radiation in an air filled cavity with internal heat source. Int. J. Therm. Sci. 2014, 76, 51–67. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Gibanov, N.S.; Sheremet, M.A. Numerical Analysis of Heat Transfer through Hollow Brick Using Finite-Difference Method. Axioms 2022, 11, 37. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).