A Novel Fractional Multi-Order High-Gain Observer Design to Estimate Temperature in a Heat Exchange Process
Abstract
:1. Introduction
2. Fractional Calculus Definitions
Numerical Algorithms to Solve Fractional-Order Differential Equations
3. Mathematical Model of a Double Pipe Heat Exchanger (DPHE)
- The thermophysical properties of the fluids are constant.
- The overall heat transfer coefficient remains constant and uniform along the axial direction.
- The process is adiabatic, meaning there is no heat exchange with the surrounding environment.
- The fluids are incompressible and monophasic.
- The walls do not store energy.
- The volume in the tubes is constant.
4. High-Gain Observer (HGO) Design
4.1. Numerical Example
4.2. Fractional-Order Representation
4.3. Numerical Solution of the FMO-HGO
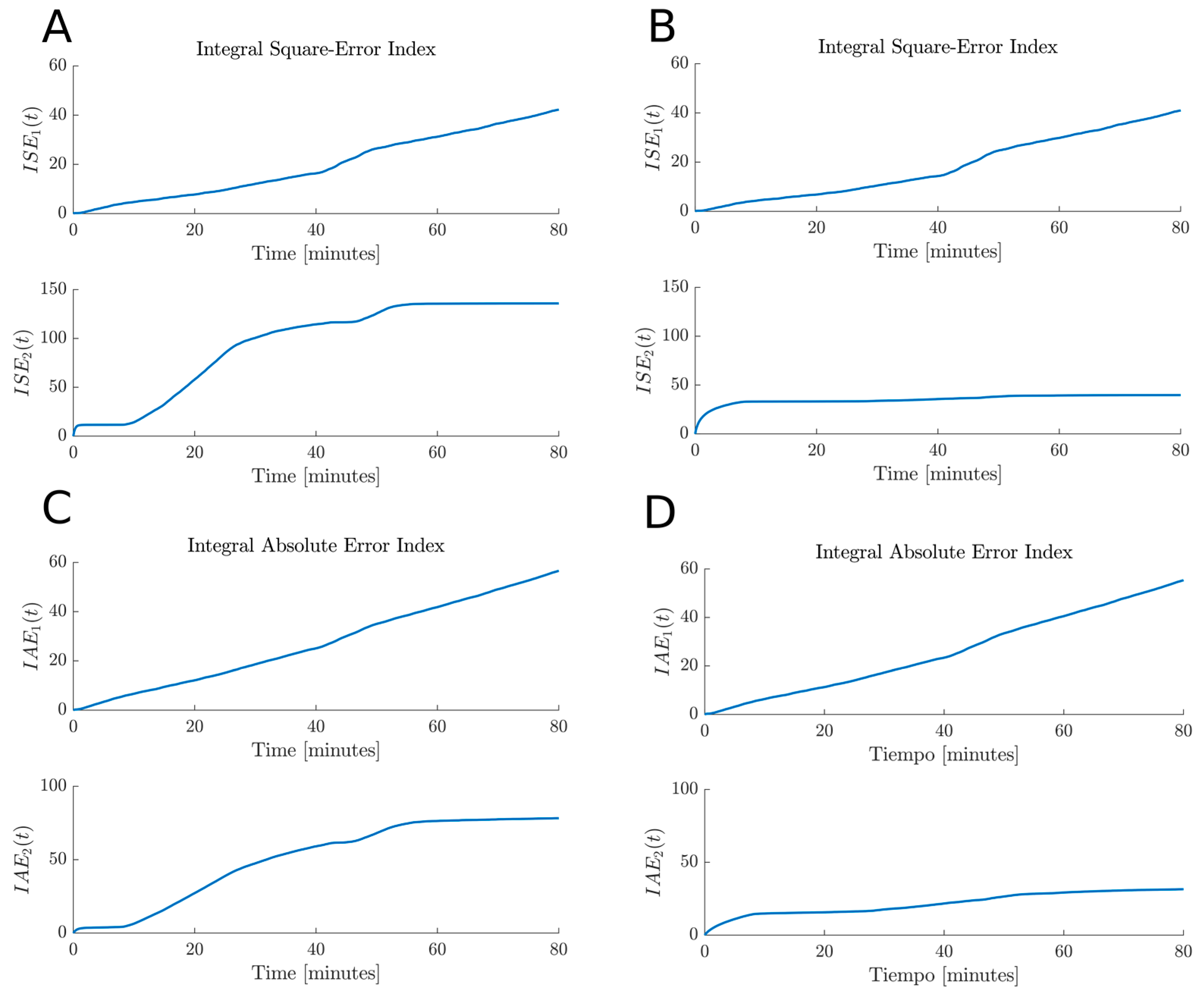
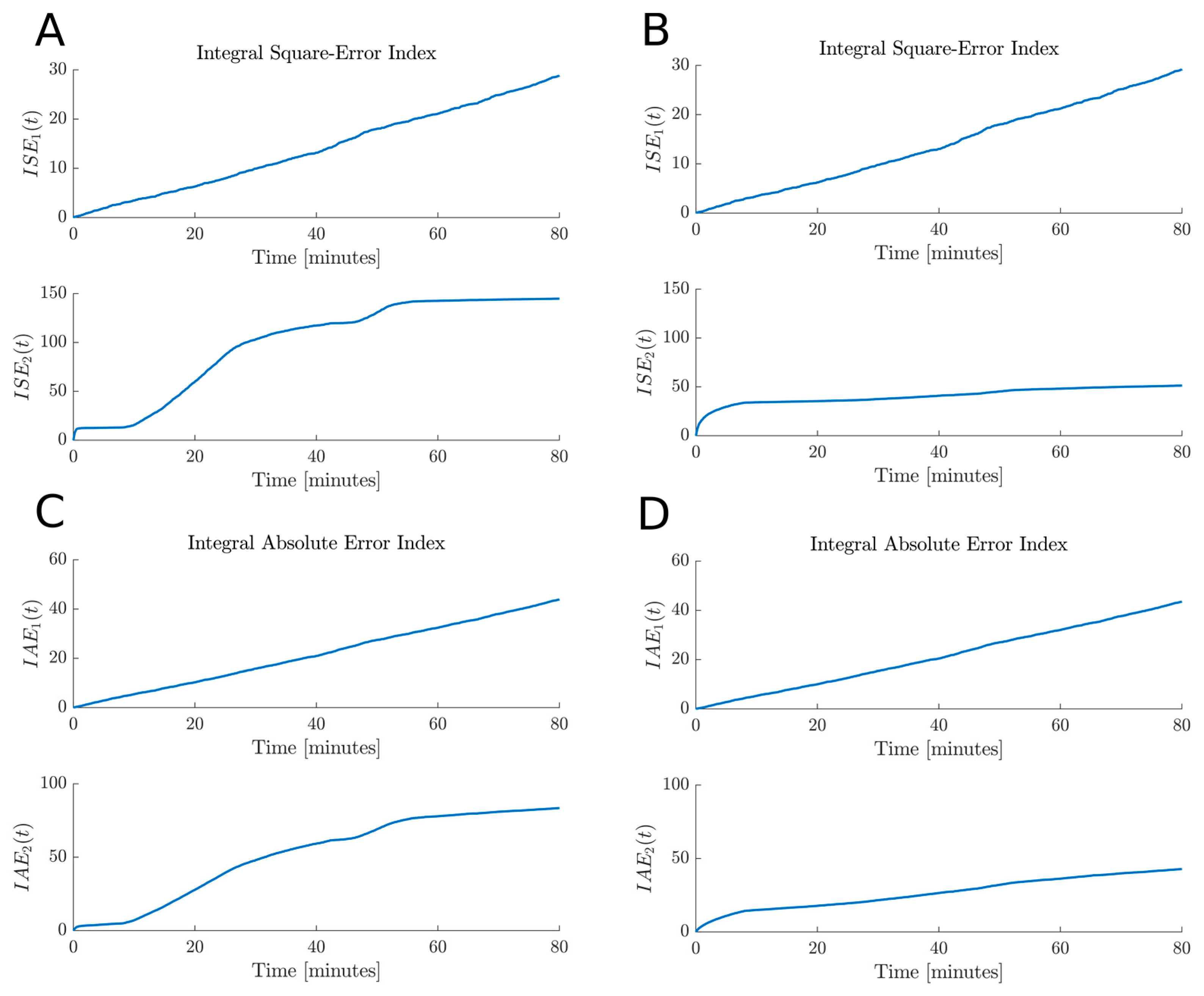
5. Results
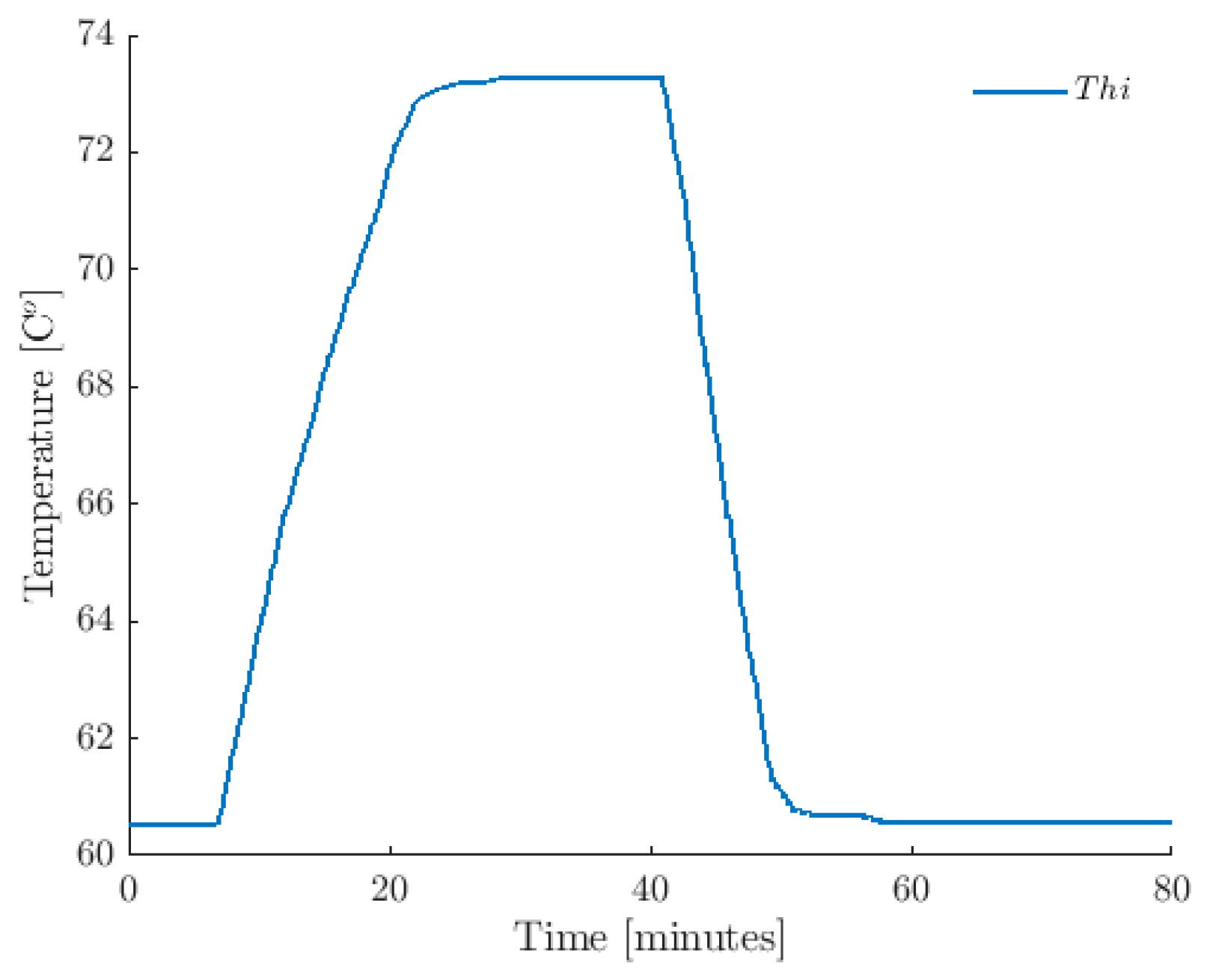
5.1. Experiment Configuration
5.2. Performance Analyses of the Proposed FMO-HGO
5.2.1. Case 1. Estimation Test under Ideal Conditions
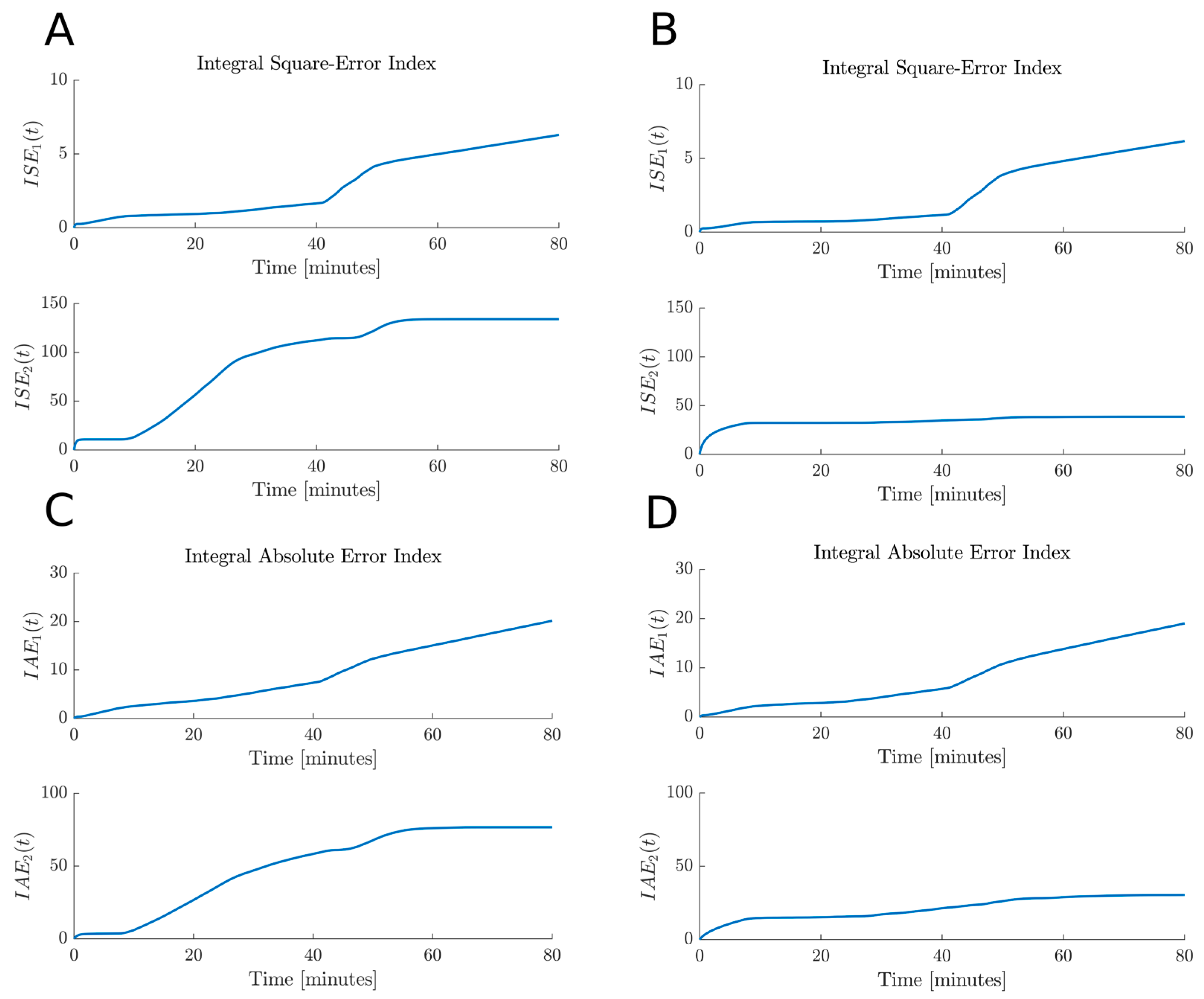
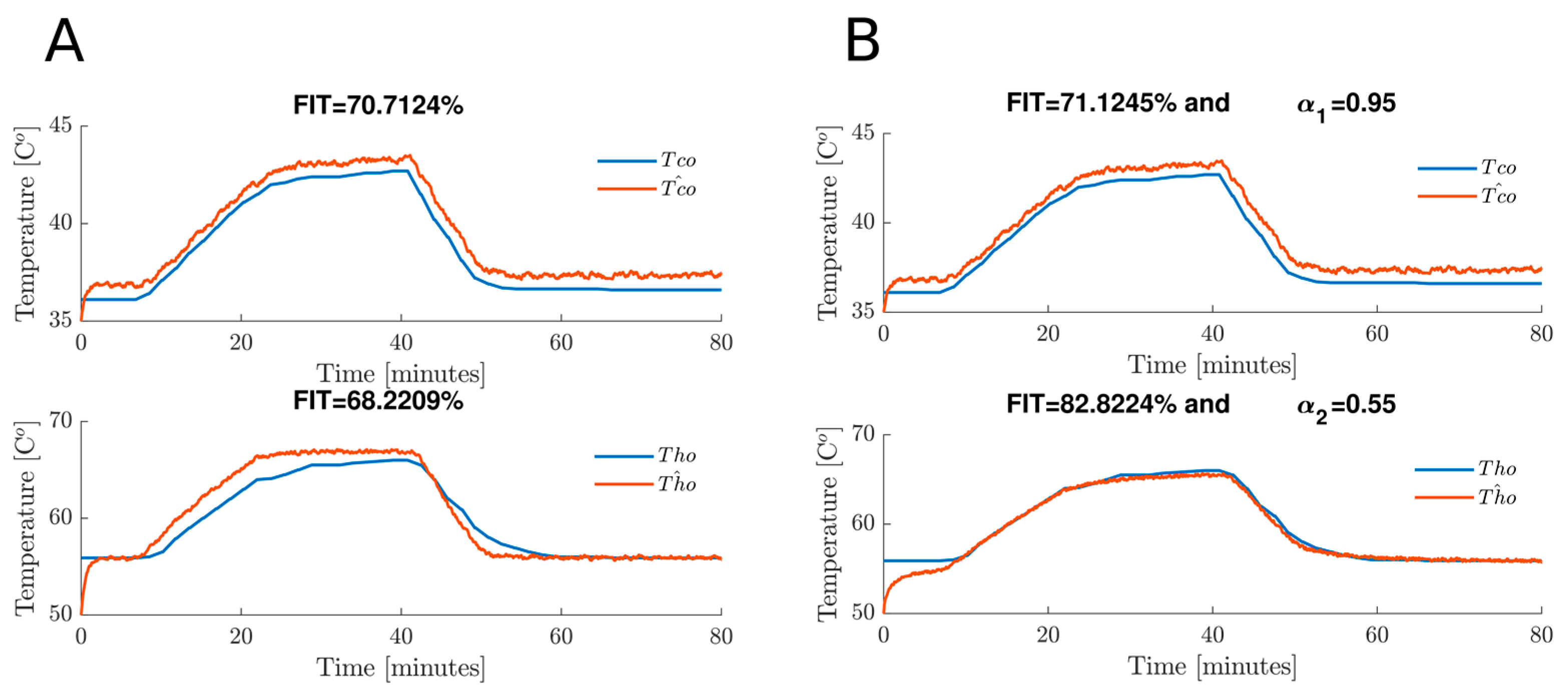
5.2.2. Case 2. Estimation Test under Noise Conditions in the Measurable Variable
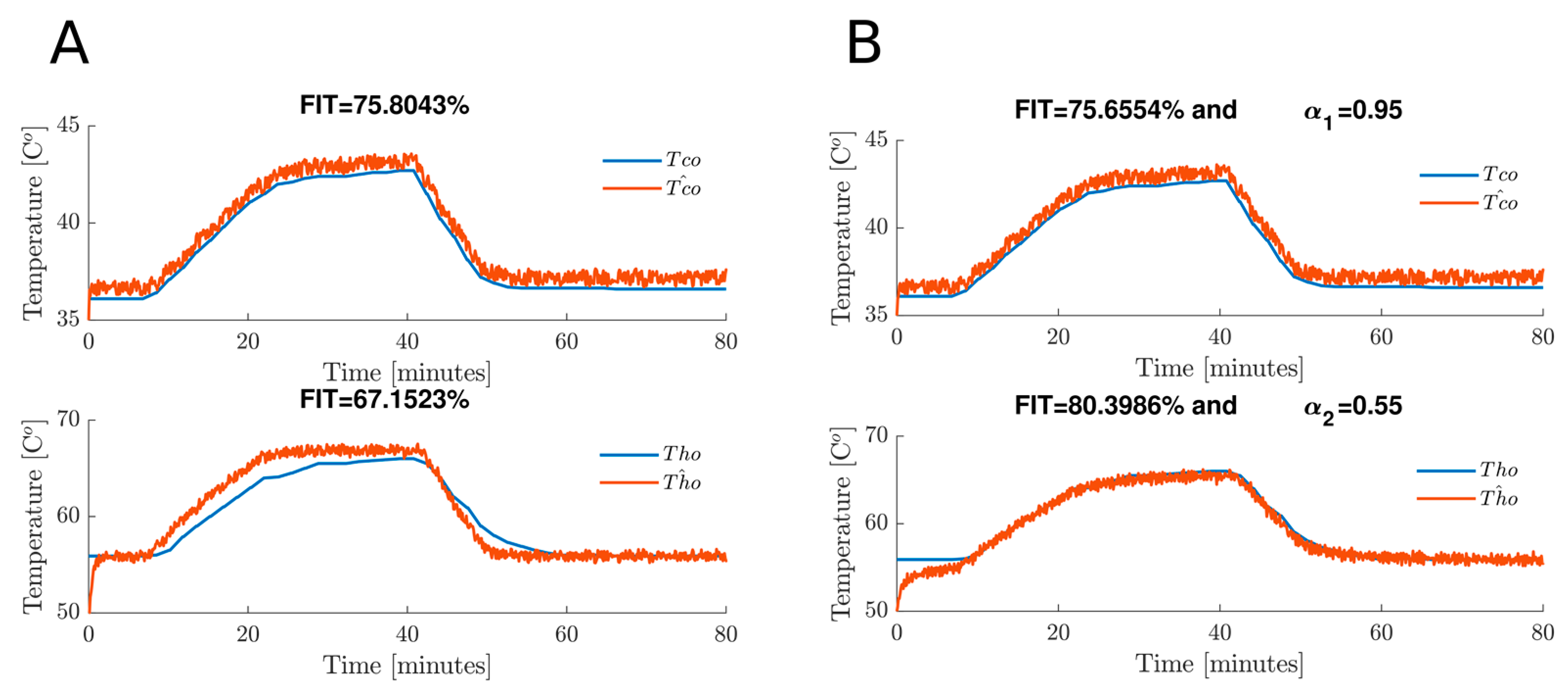
5.2.3. Case 3. Estimation Test Involving Noise Conditions in the Measurable Variable and a Change in the Observer Gains
6. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alam, T.; Kim, M.-H. A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew. Sustain. Energy Rev. 2018, 81, 813–839. [Google Scholar] [CrossRef]
- Omidi, M.; Farhadi, M.; Jafari, M. A comprehensive review on double pipe heat exchangers. Appl. Therm. Eng. 2017, 110, 1075–1090. [Google Scholar] [CrossRef]
- Srimuang, W.; Amatachaya, P. A review of the applications of heat pipe heat exchangers for heat recovery. Renew. Sustain. Energy Rev. 2012, 16, 4303–4315. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Han, Y.; Li, W.; Yang, L.; Guo, J.; Liu, Y.; Zhang, J.; Zhang, M.; Jiang, F. A comprehensive review of heat transfer enhancement and flow characteristics in the concentric pipe heat exchanger. Powder Technol. 2022, 397, 117037. [Google Scholar] [CrossRef]
- Wallhäußer, E.; Hussein, M.; Becker, T. Detection methods of fouling in heat exchangers in the food industry. Food Control 2012, 27, 1–10. [Google Scholar] [CrossRef]
- Padhee, S. Controller Design for Temperature Control of Heat Exchanger System: Simulation Studies. WSEAS Trans. Syst. Control 2014, 9, 485–491. [Google Scholar]
- Borja-Jaimes, V.; Adam-Medina, M.; López-Zapata, B.Y.; Valdés, L.G.V.; Pachecano, L.C.; Coronado, E.M.S. Sliding Mode Observer-Based Fault Detection and Isolation Approach for a Wind Turbine Benchmark. Processes 2021, 10, 54. [Google Scholar] [CrossRef]
- Borja-Jaimes, V.; Adam-Medina, M.; García-Morales, J.; Guerrero-Ramírez, G.V.; López-Zapata, B.Y.; Coronado, E.M.S. Actuator FDI Scheme for a Wind Turbine Benchmark Using Sliding Mode Observers. Processes 2023, 11, 1690. [Google Scholar] [CrossRef]
- Diaz-Bejarano, E.; Coletti, F.; Macchietto, S. A Model-Based Method for Visualization, Monitoring, and Diagnosis of Fouling in Heat Exchangers. Ind. Eng. Chem. Res. 2020, 59, 4602–4619. [Google Scholar] [CrossRef]
- Nagarsheth, S.H.; Bhatt, D.S.; Hirpara, R.H.; Sharma, S.N. Non-linear filter design for a counter-flow heat exchanger: Some investigations. Int. J. Dyn. Control 2021, 9, 922–934. [Google Scholar] [CrossRef]
- Thibault, É.; Désilets, F.L.; Poulin, B.; Chioua, M.; Stuart, P. Comparison of signal processing methods considering their optimal parameters using synthetic signals in a heat exchanger network simulation. Comput. Chem. Eng. 2023, 178, 108380. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.-H. Fault detection and diagnostics analysis of air conditioners using virtual sensors. Appl. Therm. Eng. 2021, 191, 116848. [Google Scholar] [CrossRef]
- Wang, J.; Sun, J.; Ge, W.; Zhang, F.; Gao, R.X. Virtual Sensing for Online Fault Diagnosis of Heat Exchangers. IEEE Trans. Instrum. Meas. 2022, 71, 9508708. [Google Scholar] [CrossRef]
- Ahilan, C.; Dhas, J.E.R.; Somasundaram, K.; Sivakumaran, N. Performance assessment of heat exchanger using intelligent decision making tools. Appl. Soft Comput. 2015, 26, 474–482. [Google Scholar] [CrossRef]
- Sridharan, M. Application of fuzzy logic expert system in predicting cold and hot fluid outlet temperature of counter-flow double-pipe heat exchanger. In Advanced Analytic and Control Techniques for Thermal Systems with Heat Exchangers; Academic Press: Cambridge, MA, USA, 2020; pp. 307–323. [Google Scholar] [CrossRef]
- Apio, A.; Martinelli, G.B.; Trierweiler, L.F.; Farenzena, M.; Trierweiler, J.O. Fouling monitoring of a heat exchanger network of an actual crude oil distillation unit by constrained extended Kalman filter with smoothing. Chem. Eng. Commun. 2023, 210, 2229–2248. [Google Scholar] [CrossRef]
- Kazaku, J.K.; Dochain, D.; Winkin, J.; Kahilu, M.M.; Kasongo, J.K.K. Port-Hamiltonian Sliding Mode Observer Design for a Counter-current Heat Exchanger. IFAC-PapersOnLine 2020, 53, 4910–4915. [Google Scholar] [CrossRef]
- Han, X.; Li, Z.; Cabassud, M.; Dahhou, B. A comparison study of nonlinear state ob-server design: Application to an intensified heat-exchanger/reactor. In Proceedings of the 2020 28th Mediterranean Conference on Control and Automation, MED 2020, Saint-Raphaël, France, 15–18 September 2020; pp. 162–167. [Google Scholar] [CrossRef]
- Khalil, H.K. High-gain observers in nonlinear feedback control. In Proceedings of the 2008 International Conference on Control, Automation and Systems, Seoul, Republic of Korea, 14–17 October 2008. [Google Scholar] [CrossRef]
- Ahrens, J.H.; Khalil, H.K. High-gain observers in the presence of measurement noise: A switched-gain approach. Automatica 2009, 45, 936–943. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin, Germany, 2010; Available online: https://books.google.es/books?hl=es&lr=&id=c4fV9WeCiEwC&oi=fnd&pg=PR9&dq=fractional+order+calculus+fundamentals+&ots=E1uXM6iMMF&sig=i7vpaCR8Pin5f2LGSeG-P9-lv9w#v=onepage&q=fractional%20order%20calculus%20fundamentals&f=false (accessed on 1 October 2023).
- Gutiérrez, R.E.; Rosário, J.M.; Machado, J.T. Fractional Order Calculus: Basic Concepts and Engineering Applications. Math. Probl. Eng. 2010, 2010, 375858. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Tuladhar, R.; Stamova, I.; Santamaria, F. Fractional-order dynamics to study neuronal function. In Fractional-Order Modeling of Dynamic Systems with Applications in Optimization, Signal Processing, and Control; Academic Press: Cambridge, MA, USA, 2022; pp. 429–456. [Google Scholar] [CrossRef]
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer: Berlin/Heidelberg, Germany, 2017; Available online: https://books.google.es/books?hl=es&lr=&id=NswWDgAAQBAJ&oi=fnd&pg=PP7&dq=fractional+order+calculus&ots=jwao5TX84_&sig=5tF-2ojzCsWNqX1z6_HMjX2a0oM#v=onepage&q=fractional%20order%20calculus&f=false (accessed on 1 October 2023).
- Martínez-Fuentes, O.; Martínez-Guerra, R. A high-gain observer with Mittag–Leffler rate of convergence for a class of nonlinear fractional-order systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104909. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.; Torres-Jiménez, J.; Mousa, A.; Elagan, S. Fractional synchronization involving fractional derivatives with nonsingular kernels: Application to chaotic systems. Math. Methods Appl. Sci. 2023, 46, 7987–8003. [Google Scholar] [CrossRef]
- Boroujeni, E.A.; Momeni, H.R. Non-fragile nonlinear fractional order observer design for a class of nonlinear fractional order systems. Signal Process. 2012, 92, 2365–2370. [Google Scholar] [CrossRef]
- Dinh, T.N.; Kamal, S.; Pandey, R.K. Fractional-Order System: Control Theory and Applications; MDPI AG: Basel, Switzerland, 2023; p. 204. [Google Scholar] [CrossRef]
- de Almeida, A.M.; Lenzi, M.K.; Lenzi, E.K. A Survey of Fractional Order Calculus Applications of Multiple-Input, Multiple-Output (MIMO) Process Control. Fractal Fract. 2020, 4, 22. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gomez-Aguilar, J.F.; Stamova, I.; Santamaria, F. Fractional order controllers increase the robustness of closed-loop deep brain stimulation systems. Chaos Solitons Fractals 2020, 140, 110149. [Google Scholar] [CrossRef]
- Bettayeb, M.; Djennoune, S.; Al-Saggaf, U.M. High gain observer design for fractional-order non-linear systems with delayed measurements: Application to synchronisation of fractional-order chaotic systems. IET Control Theory Appl. 2017, 11, 3171–3178. [Google Scholar] [CrossRef]
- Rodriguez-Mata, A.E.; Bustos-Terrones, Y.; Gonzalez-Huitrón, V.; Lopéz-Peréz, P.A.; Hernández-González, O.; Amabilis-Sosa, L.E. A Fractional High-Gain Nonlinear Observer Design—Application for Rivers Environmental Monitoring Model. Math. Comput. Appl. 2020, 25, 44. [Google Scholar] [CrossRef]
- Deng, W.; Li, C.; Guo, Q. Analysis of fractional differential equations with multi-orders. Fractals 2011, 15, 173–182. [Google Scholar] [CrossRef]
- Ahmadova, A.; Huseynov, I.T.; Fernandez, A.; Mahmudov, N.I. Trivariate Mittag-Leffler functions used to solve multi-order systems of fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2021, 97, 105735. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Multi-order fractional differential equations and their numerical solution. Appl. Math. Comput. 2004, 154, 621–640. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Petras, I.; Xue, D. Fractional order control—A tutorial. In Proceedings of the 2009 American Control Conference (ACC), St. Louis, MO, USA, 10–12 July 2009; pp. 1397–1411. [Google Scholar]
- Yang, Y.; Zhang, H.H. Fractional Calculus with Its Applications in Engineering and Technology; Springer Science and Business Media LLC: Dordrecht, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 2011; Available online: http://link.springer.com/10.1007/978-3-642-18101-6 (accessed on 4 October 2023).
- McGraw-Hill Education. Giorgio Carta, Heat and Mass Transfer for Chemical Engineers: Principles and Applications; McGraw-Hill Education: New York, NY, USA, 2021; Available online: https://www.accessengineeringlibrary.com/content/book/9781264266678 (accessed on 9 July 2023).
- Cao, E. Heat Transfer in Process Engineering; McGraw-Hill Education: New York, NY, USA, 2010; Available online: https://www.accessengineeringlibrary.com/content/book/9780071624084 (accessed on 20 September 2023).
- Serth, R.W.; Lestina, T.G. Process Heat Transfer: Principles, Applications and Rules of Thumb, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1–609. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.; Incropera, F.P. Fundamentals of Heat and Mass Transfer. 2018. Available online: https://www.wiley.com/en-us/Fundamentals+of+Heat+and+Mass+Transfer%2C+8th+Edition-p-9781119353881 (accessed on 9 July 2023).
- Khalil, H.K.; Praly, L. High-gain observers in nonlinear feedback control. Int. J. Robust Nonlinear Control 2014, 24, 993–1015. [Google Scholar] [CrossRef]
- Prasov, A.A.; Khalil, H.K. A Nonlinear High-Gain Observer for Systems With Measurement Noise in a Feedback Control Framework. IEEE Trans. Autom. Control 2013, 58, 569–580. [Google Scholar] [CrossRef]
- Ball, A.A.; Khalil, H.K. Analysis of a nonlinear high-gain observer in the presence of measurement noise. In Proceedings of the 2011 American Control Conference IEEE, San Francisco, CA, USA, 29 June–1 July 2011; pp. 2584–2589. [Google Scholar] [CrossRef]
- Gauthier, J.; Hammouri, H.; Othman, S. A simple observer for nonlinear systems applications to bioreactors. IEEE Trans. Autom. Control 1992, 37, 875–880. [Google Scholar] [CrossRef]
- Gauthier, J.; Hammouri, H.; Kupka, I. Observers for nonlinear systems. In Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, UK, 11–13 December 1991; pp. 1483–1489. [Google Scholar] [CrossRef]
- Atassi, A.; Khalil, H. Separation results for the stabilization of nonlinear systems using different high-gain observer designs. Syst. Control Lett. 2000, 39, 183–191. [Google Scholar] [CrossRef]
- Khalil, H.K. High-Gain Observers in Nonlinear Feedback Control; Society for Industrial & Applied Mathematics (SIAM): Philadelphia, PA, USA, 2017. [Google Scholar] [CrossRef]
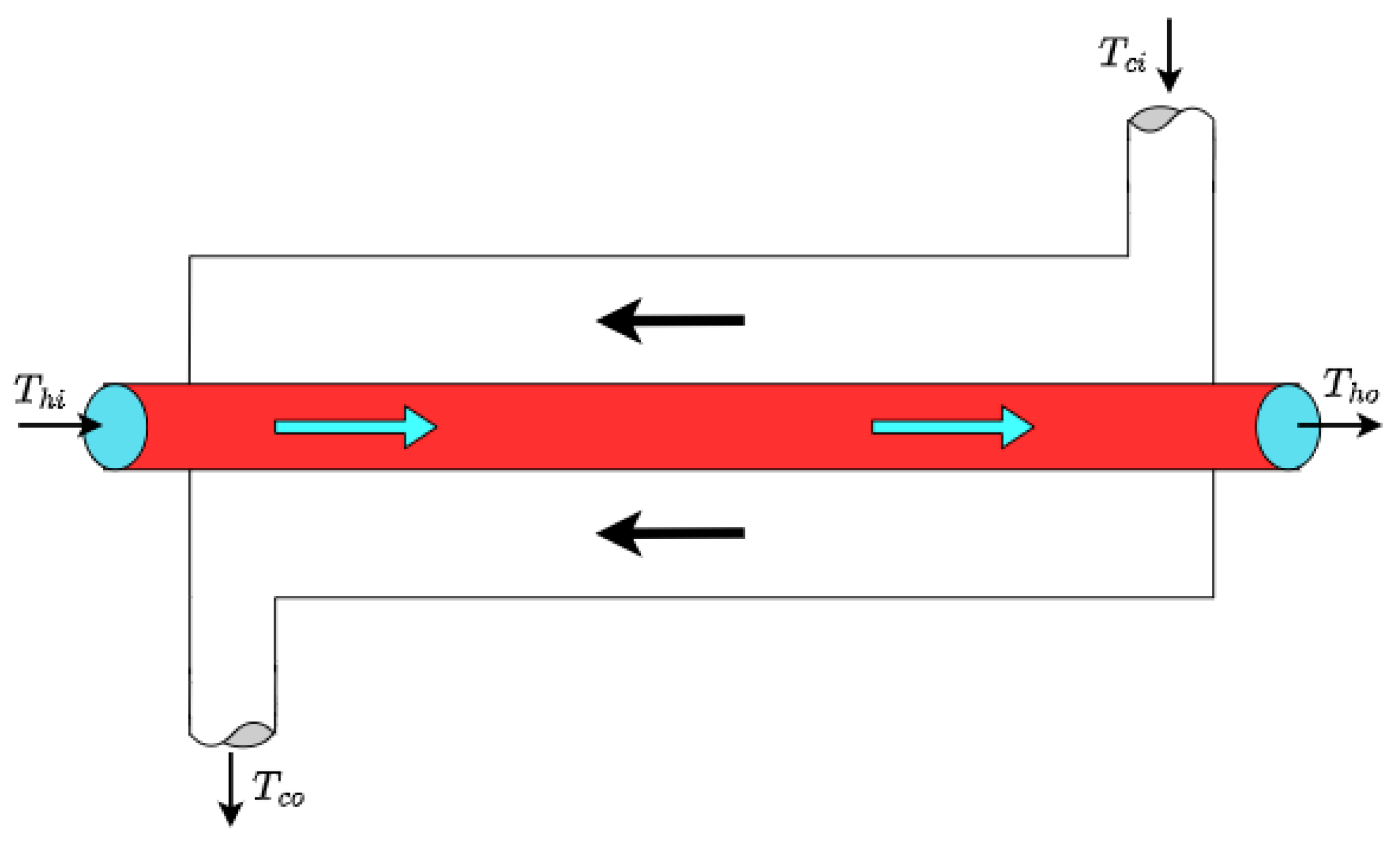


| Notation | Description | Notation | Description |
|---|---|---|---|
| Inlet temperature on the cold side. | Specific heat on the hot side. | ||
| Inlet temperature on the hot side. | Density of the cold fluid. | ||
| Outlet temperature on the cold side. | Density of the hot fluid. | ||
| Outlet temperature on the hot side. | Volume on the cold side. | ||
| Heat transfer coefficient. | Volume on the hot side. | ||
| Shell side area. | Flow rate on the cold side. | ||
| Tube side area. | Flow rate on the hot side. | ||
| Specific heat on the cold side. | - | - |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 26.5 °C | 4179 J/(Kg K) | ||
| 60.55 °C | 991.8 Kg/m3 | ||
| 36.10 °C | 983.3 Kg/m3 | ||
| 55.9 °C | 1.3499 × 10−4 m3 | ||
| 1050 J/(m2 °C s) | 1.5512 × 10−5 m3 | ||
| 0.0154 m2 | 6.6667 × 10−6 m3/s | ||
| 0.0124 m2 | 1.6667 × 10−6 m3/s | ||
| 4174 J/(Kg °C) | - | - |
| Experiment | Normalized Root-Mean-Square Error FIT | Integral Square Error ISE | Integral Absolute Error IAE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | ||||||||||||
| HGO | FMO-HGO | HGO | FMO-HGO | HGO | FMO-HGO | HGO | FMO-HGO | HGO | FMO-HGO | HGO | FMO-HGO | |
| 88.79% | 88.89% | 68.44% | 83.08% | 6.28 | 6.10 | 134 | 38.51 | 20.16 | 19.01 | 76.65 | 30.45 | |
| 70.71% | 71.12% | 68.22% | 82.82% | 42.28 | 41.04 | 135.8 | 39.67 | 56.6 | 55.0 | 78.28 | 31.48 | |
| 3 | 75.80% | 75.65% | 67.15% | 80.39% | 28.84 | 28.12 | 144.8 | 51.22 | 43.93 | 42.85 | 83.47 | 42.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borja-Jaimes, V.; Adam-Medina, M.; García-Morales, J.; Cruz-Rojas, A.; Gil-Velasco, A.; Coronel-Escamilla, A. A Novel Fractional Multi-Order High-Gain Observer Design to Estimate Temperature in a Heat Exchange Process. Axioms 2023, 12, 1107. https://doi.org/10.3390/axioms12121107
Borja-Jaimes V, Adam-Medina M, García-Morales J, Cruz-Rojas A, Gil-Velasco A, Coronel-Escamilla A. A Novel Fractional Multi-Order High-Gain Observer Design to Estimate Temperature in a Heat Exchange Process. Axioms. 2023; 12(12):1107. https://doi.org/10.3390/axioms12121107
Chicago/Turabian StyleBorja-Jaimes, Vicente, Manuel Adam-Medina, Jarniel García-Morales, Alan Cruz-Rojas, Alfredo Gil-Velasco, and Antonio Coronel-Escamilla. 2023. "A Novel Fractional Multi-Order High-Gain Observer Design to Estimate Temperature in a Heat Exchange Process" Axioms 12, no. 12: 1107. https://doi.org/10.3390/axioms12121107
APA StyleBorja-Jaimes, V., Adam-Medina, M., García-Morales, J., Cruz-Rojas, A., Gil-Velasco, A., & Coronel-Escamilla, A. (2023). A Novel Fractional Multi-Order High-Gain Observer Design to Estimate Temperature in a Heat Exchange Process. Axioms, 12(12), 1107. https://doi.org/10.3390/axioms12121107







